Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 21)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 21)
-
339 lượt thi
-
79 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
Phần tư duy đọc hiểu
Theo đoạn [1], công ti khởi nghiệp muốn biến carbon dioxide thành protein vì không thể loại bỏ lượng khí thải đó trong bầu khí quyển. Đúng hay sai?
 Xem đáp án
Xem đáp án
Đọc lại nội dung đoạn [1] xác định nội dung quan trọng: “bơm carbon dioxide vào bầu khí quyển”, “cơ hội có lợi nhuận khá thấp”, “biến carbon dioxide thành protein”. Nội dung đoạn [1] có nêu lên vấn đề: nhiều công ti/doanh nghiệp đưa ra giải pháp loại bỏ carbon dioxide nhưng sự khác biệt khi biến carbon dioxide thành protein chính là “lợi nhuận”.
Chọn B
Câu 2:
Dựa vào đoạn [2], hãy điền một cụm từ không quá hai tiếng để hoàn thành nhận định sau:
Đẩy mạnh những tiến bộ về (1) _______ , công ti NovoNutrients đầu tư trang thiết bị kĩ thuật cao, tìm ra cơ sở trong quá trình trao đổi chất của vi khuẩn, sử dụng khí thải làm năng lượng.
 Xem đáp án
Xem đáp án
Đáp án
Dựa vào đoạn [2], hãy điền một cụm từ không quá hai tiếng để hoàn thành nhận định sau:
Đẩy mạnh những tiến bộ về (1) công nghệ, công ti NovoNutrients đầu tư trang thiết bị kĩ thuật cao, tìm ra cơ sở trong quá trình trao đổi chất của vi khuẩn, sử dụng khí thải làm năng lượng.
Giải thích
Đọc lại đoạn [2] và xác định thông tin, chú ý nội dung: “dựa vào vi khuẩn để làm công việc bẩn thỉu. Công ti đã khảo sát các tài liệu khoa học để tìm ra những loài có thể sử dụng carbon dioxide trong quá trình trao đổi chất của chúng, cho phép chúng sử dụng khí thải làm năng lượng” và “công nghiệp hóa quá trình trao đổi chất” nên từ cần điền là “công nghệ”.
Câu 3:
Theo đoạn [2], cụm từ “công việc bẩn thỉu” được hiểu như thế nào? Chọn Từ khóa đúng nhất.
 Xem đáp án
Xem đáp án
Đọc kĩ đoạn [2] để hiểu được: “công việc bẩn thỉu” do vi khuẩn thực hiện: “NovoNutrients dựa vào vi khuẩn để làm công việc bẩn thỉu”, “sử dụng carbon dioxide trong quá trình trao đổi chất của chúng, cho phép chúng sử dụng khí thải làm năng lượng”.
Chọn D
Câu 4:
hoạt động, đậm đặc, tái tạo, chế tạo
Việc phát triển các lò phản ứng sinh học trở thành yêu cầu cấp thiết và nguyên liệu chính là cacbon dioxide _______ - sản phẩm từ bất kì _______ gây ô nhiễm nào trong đời sống và từ đó _______ thành nhiều sản phẩm khác nhau.
 Xem đáp án
Xem đáp án
Đáp án
Việc phát triển các lò phản ứng sinh học trở thành yêu cầu cấp thiết và nguyên liệu chính là cacbon dioxide đậm đặc - sản phẩm từ bất kì hoạt động gây ô nhiễm nào trong đời sống và từ đó tái tạo thành nhiều sản phẩm khác nhau.
Giải thích
Căn cứ vào từ khoá “lò phản ứng sinh học”, đọc lại nội dung đoạn [3] và tìm thông tin thích hợp: “Nguồn gốc của carbon dioxide có thể là bất kì hoạt động nào đang gây ô nhiễm ngày nay, cho dù đó là hoạt động dầu khí, nhà máy hóa chất, nhà máy phân bón hay nhà máy xi măng. Tất cả những gì cần thiết là cung cấp đủ carbon dioxide đậm đặc. Mặt khác, các nhà máy của NovoNutrients sẽ sản xuất một loại bột khô có thể được tinh chế thành một số sản phẩm khác nhau, bao gồm chất bổ sung protein cho người, động vật và cá nuôi”.
Việc phát triển các lò phản ứng sinh học trở thành yêu cầu cấp thiết và nguyên liệu chính là cacbon dioxide [đậm đặc] - sản phẩm từ bất kì [hoạt động] gây ô nhiễm nào trong đời sống và từ đó [tái tạo] thành nhiều sản phẩm khác nhau.
Câu 5:
 Xem đáp án
Xem đáp án
Căn cứ vào từ khóa “cải thiện hiệu suất” xác định được nội dung cần tìm nằm ở đoạn [4]: “Một cách khác mà công ti khởi nghiệp có thể tăng sản lượng là sử dụng nhiều chủng khác nhau trong một bể”. Chú ý “công ti khởi nghiệp” chính là NovoNutrients và “chủng” ở đây là các chủng vi khuẩn.
Chọn C
Câu 6:
Hãy điền một cụm từ không quá ba tiếng để hoàn thành nhận định sau:
Bên cạnh các mục tiêu thương mại, NovoNutrients hướng tới việc cung cấp (1) ______ cho các doanh nghiệp và đào tạo quy trình hoạt động cho những cơ sở có nhu cầu sử dụng công nghệ này.
 Xem đáp án
Xem đáp án
Đáp án
Hãy điền một cụm từ không quá ba tiếng để hoàn thành nhận định sau:
Bên cạnh các mục tiêu thương mại, NovoNutrients hướng tới việc cung cấp (1) giải pháp cho các doanh nghiệp và đào tạo quy trình hoạt động cho những cơ sở có nhu cầu sử dụng công nghệ này.
Giải thích
Đọc lại nội dung đoạn [5] xác định: “bán các vi khuẩn để duy trì hoạt động của mọi thứ”, “lấy tiền bản quyền giấy phép công nghệ”, “cung cấp toàn bộ gói công nghệ”, “đào tạo nhân viên điều hành và sẽ sẵn sàng hỗ trợ.”. Mục tiêu của doanh nghiệp ngoài kinh doanh chính là cung cấp các giải pháp cho doanh nghiệp cần tới công nghệ.
Câu 7:
 Xem đáp án
Xem đáp án
Căn cứ vào từ khóa “cung cấp”, “đối tác” để xác định nội dung cần tìm nằm ở đoạn [5]: “Và tất nhiên, chúng tôi sẽ cung cấp toàn bộ gói công nghệ - cả sinh học và phần cứng” (đáp án A); “làm việc với các công ti xây dựng mua sắm kĩ thuật, do đối tác được cấp phép của chúng tôi lựa chọn để xây dựng công trình đó” (đáp án D); “Chúng tôi sẽ đào tạo nhân viên điều hành” (đáp án B).
Sử dụng phương pháp loại trừ, chọn đáp án C. Thông tin trong đoạn là “công ti đối tác sẽ quyết định sản phẩm nào họ muốn sản xuất” chứ không phải do NovoNutrients quyết định.
Chọn C
Câu 8:
công nghệ, thu mua, cung cấp, tiêu dùng
Công ti NovoNutrients lấy _______ làm trung tâm và cấp phép cho công nghệ cốt lõi của mình. Với vai trò là một công ti _______ dịch vụ, NovoNutrients tư vấn cho các công ti đối tác về quy trình xây dựng, vận hành và hỗ trợ tiếp cận người _______.
 Xem đáp án
Xem đáp án
Công ti NovoNutrients lấy công nghệ làm trung tâm và cấp phép cho công nghệ cốt lõi của mình. Với vai trò là một công ti cung cấp dịch vụ, NovoNutrients tư vấn cho các công ti đối tác về quy trình xây dựng, vận hành và hỗ trợ tiếp cận người tiêu dùng.
Câu 9:
Theo thông tin trong đoạn [6], các công ti khởi nghiệp gặp thất bại chủ yếu vì:
 Xem đáp án
Xem đáp án
Đọc kĩ đoạn [6] để xác định nội dung chính: “Cách tiếp cận cấp phép và dịch vụ có thể hạn chế tăng doanh thu cuối cùng, nhưng nó chắc chắn hạn chế rủi ro vốn” cho thấy, các doanh nghiệp gặp thất bại do sự kì vọng tạo nên chuỗi cung ứng toàn bộ, thiếu sự hợp tác chiến lược, chọn A.
Câu 10:
 Xem đáp án
Xem đáp án
Đọc nội dung nhan đề và đoạn [1] xác định mục đích chính của bài viết: “dành một thế kỉ rưỡi qua để bơm carbon dioxide vào bầu khí quyển”, “dành những thập kỉ tới để loại bỏ một phần đáng kể lượng đó”, “Nhưng sau đó chúng ta sẽ làm gì với tất cả?” và “Một công ti khởi nghiệp nghĩ rằng câu trả lời là biến carbon dioxide thành protein.” nên Từ khóa đúng là C.
Chọn C
Câu 11:
Theo bài viết, giải pháp đơn giản nhất để giảm gánh nặng nhiệt cho cư dân đô thị hiện nay là gì?
 Xem đáp án
Xem đáp án
Đọc thông tin trong phần sapo, đoạn [1] và tiến hành loại trừ các phương án không chính xác: "Ở đô thị, mái che nhỏ gọn, dễ lắp đặt tại các trạm dừng xe buýt, trở thành giải pháp đơn giản để chiếu sáng và che mát cho những hành khách đang chờ đợi."
Chọn A
Câu 12:
 Xem đáp án
Xem đáp án
Đọc thông tin trong đoạn [2] kết hợp với việc giải nghĩa cụm từ, xác định: "sa mạc bóng râm" là nơi thiếu bóng râm trong đô thị, áp lực cần được giải quyết để đảm bảo chất lượng cuộc sống cho nhân dân.
Chọn B
Câu 13:
Trong việc quy hoạch đô thị, các nhà quản lí, nghiên cứu do đặt ưu tiên hàng đầu về vấn đề sử dụng và mục tiêu xây dựng công trình kiến trúc của thành phố nên đã bỏ qua việc thiết kế hệ thống mái che là đúng hay sai?
 Xem đáp án
Xem đáp án
Đọc thông tin trong đoạn [3] xác định: "hiện nay các nhà nghiên cứu và chính quyền đô thị còn rất thiếu hiểu biết hoặc ít quan tâm đo lường gánh nặng nhiệt" là nguyên nhân chính cho việc "lập kế hoạch bóng râm" chứ không phải ưu tiên mục đích sử dụng công trình kiến trúc.
Chọn B
Câu 14:
suy giảm, áp lực, nguy cơ, gia tăng, bức xạ
Nếu không thể giảm _______ nhiệt từ môi trường, con người không chỉ cảm thấy khó chịu ở thời điểm đó mà còn làm _______ các vấn đề liên quan tới sức khỏe, một trong những vấn đề đó chính là _______ mặt trời.
 Xem đáp án
Xem đáp án
Đáp án
Nếu không thể giảm áp lực nhiệt từ môi trường, con người không chỉ cảm thấy khó chịu ở thời điểm đó mà còn làm gia tăng các vấn đề liên quan tới sức khỏe, một trong những vấn đề đó chính là bức xạ mặt trời.
Giải thích
Căn cứ vào từ khóa "sức khỏe", xác định thông tin cần tìm nằm trong đoạn [2]: ‘Sa mạc bóng râm’ đô thị — những nơi thiếu bóng râm cần thiết để giảm ‘gánh nặng nhiệt’ và bảo vệ sức khỏe con người ở ngoài trời — là một vấn đề nghiêm trọng đối với các cộng đồng thu nhập thấp và làm gia tăng gánh nặng về sức khỏe. Bóng râm có thể giảm tổng ‘gánh nặng nhiệt’ từ môi trường của một người bằng cách giảm nhiệt độ không khí, độ ẩm khí quyển, tốc độ gió và tổng mức phơi nhiễm bức xạ. Tổng hợp thông tin có thể thấy, vấn đề lớn nhất mà con người phải đối mặt chính là nhiễm bức xạ mặt trời, gây ảnh hưởng nghiêm trọng tới sức khỏe.
Câu 15:
Điền cụm từ thích hợp (không quá bốn tiếng) để hoàn thành nhận định sau:
“Với đặc thù của đô thị - không gian chật hẹp, diện tích đất ở trên đầu người thấp, đa số vật liệu trong các cơ sở hạ tầng thường giữ nhiệt nên các thành phố thường phải đối diện với hiện tượng (1)_________ .”
 Xem đáp án
Xem đáp án
Đáp án
“Với đặc thù của đô thị - không gian chật hẹp, diện tích đất ở trên đầu người thấp, đa số vật liệu trong các cơ sở hạ tầng thường giữ nhiệt nên các thành phố thường phải đối diện với hiện tượng (1) đảo nhiệt đô thị.”
Giải thích
Căn cứ vào từ khóa "cơ sở hạ tầng", nội dung liên quan đến việc tăng nhiệt tại các đô thị xác định thông tin cần tìm kiếm nằm trong đoạn [4]: "Các thành phố thường gánh chịu hiện tượng ‘đảo nhiệt đô thị’ – nóng hơn khu vực nông thôn rất nhiều, do mật độ xây dựng dày đặc, và vật liệu trong các cơ sở hạ tầng thường giữ nhiệt."
Câu 16:
Theo bài viết, để có thể giải quyết các vấn đề liên quan tới nhiệt độ đô thị, chính quyền các cấp nên quan tâm tới điều gì?
 Xem đáp án
Xem đáp án
Câu hỏi đề cập tới vấn đề chính quyền đô thị quan tâm tới các chỉ số nào để giảm tải áp lực nhiệt đô thị nên cần đọc thông tin trong đoạn [5]: "thay vì tập trung vào nhiệt độ không khí hoặc các bề mặt, chính quyền đô thị nên theo dõi nhiệt độ bức xạ trung bình: sự trao đổi nhiệt ròng giữa cơ thể con người và môi trường xung quanh."
Chọn C
Câu 17:
Trong quá trình thiết kế nhà ở, phương án nào thường được các kiến trúc sư lựa chọn để giảm áp lực nhiệt?
 Xem đáp án
Xem đáp án
Đọc và xác định thông tin trong đoạn [5] của văn bản: Người La Mã đã thiết kế những ngôi nhà có sân trong để cung cấp bóng râm và đài phun nước để làm mát không khí xung quanh. Các tòa nhà ở những vùng nóng thường kết hợp sân trong và ô văng, và ở một số thành phố, đường phố được định hướng để chắn Mặt trời. Tổng hợp thông tin cho thấy, trong việc thiết kế nhà cửa, các kiến trúc sư sẽ lựa chọn việc làm mát không khí xung quanh nhà bằng cách tạo không gian đệm với khu vực sống: sân trong, đài phun nước trong sân, ô văng chắn nắng...
Chọn C
Câu 18:
kế hoạch, cộng đồng, quy hoạchnguy hại, tổn thương
Với đặc trưng của một thành phố có hơn 200 ngày nhiệt độ trên 32 độ, Phoenix là thành phố đầu tiên có _______ về cây và bóng râm, mục tiêu tăng 25% diện tích tán cây và hướng tới _______ những người thu nhập thấp, dễ bị _______ do nhiệt.
 Xem đáp án
Xem đáp án
Đáp án
Với đặc trưng của một thành phố có hơn 200 ngày nhiệt độ trên 32 độ, Phoenix là thành phố đầu tiên có kế hoạch về cây và bóng râm, mục tiêu tăng 25% diện tích tán cây và hướng tới cộng đồng những người thu nhập thấp, dễ bị tổn thương do nhiệt.
Giải thích
Đọc và tìm kiếm thông tin trong đoạn [6] của văn bản: Phoenix, nơi thường trải qua gần 200 ngày trên 32 °C, đã nhận ra tầm quan trọng của bóng râm và là thành phố đầu tiên công bố kế hoạch tổng thể về cây và bóng râm từ năm 2010, ban đầu kêu gọi tăng 25% diện tích tán cây, nhắm mục tiêu đến các cộng đồng dễ bị tổn thương do nhiệt.
Câu 19:
Vì sao Singapore yêu cầu "chỗ ngồi được che nắng vào lúc 9 giờ sáng, 12 giờ trưa và 4 giờ chiều vào giữa mùa hè"?
 Xem đáp án
Xem đáp án
Đọc thông tin trong văn bản, kết hợp với những hiểu biết cá nhân, xác định: 9h, 12h, 16h là những thời điểm nắng nhất trong ngày, tia cực tím nhiều nhất và dễ gây ung thư da; ngoài ra trong câu chủ đề của đoạn có nội dung: Kể từ những năm 1990, các nhà nghiên cứu, quản lý về y tế công cộng đã kêu gọi việc đưa bóng râm vào kế hoạch phòng ngừa ung thư da do tia cực tím.
Chọn C
Câu 20:
Sau những khuyến cáo về y tế, các Quốc gia đã xây dựng những bộ tiêu chuẩn khác nhau về quy hoạch bóng râm và thống nhất ở mục tiêu "bóng râm liên tục" là đúng hay sai?
 Xem đáp án
Xem đáp án
Đọc thông tin trong đoạn [7] xác định: Các Quốc gia dựa trên điều kiện thực tế có những mục tiêu khác nhau cho từng thời điểm nhưng về cơ bản đề hướng tới "bóng râm liên tục" ở các khu vực công cộng để giảm tải áp lực nhiệt thành phố.
Chọn ACâu 21:
Phần tư duy khoa học / giải quyết vấn đề
Phát biểu sau đây đúng hay sai?
Các liên kết bền bị phá vỡ ở nhiệt độ cao hơn các liên kết yếu.
 Xem đáp án
Xem đáp án
Văn bản đã cung cấp thông tin “Các liên kết bền hơn cần được cung cấp nhiệt độ cao hơn để phá vỡ liên kết đó”.
Chọn A
Câu 22:
Điền từ/cụm từ thích hợp vào chỗ trống.
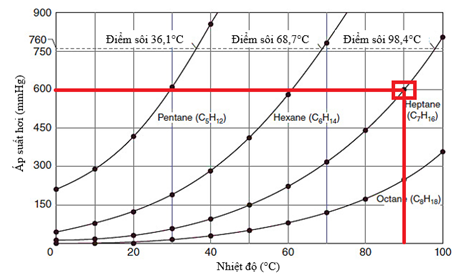
Theo Hình 1, tại nhiệt độ 90°C, áp suất hơi của heptane là (1) ________.
 Xem đáp án
Xem đáp án
Đáp án
Điền từ/cụm từ thích hợp vào chỗ trống.
Theo Hình 1, tại nhiệt độ 90°C, áp suất hơi của heptane là (1) 600 mmHg.
Giải thích
Đối chiếu với Hình 1 có thể dễ dàng nhìn thấy tại nhiệt độ 90°C, áp suất hơi của heptane là 600 mmHg.
Câu 23:
Phát biểu sau đây đúng hay sai?
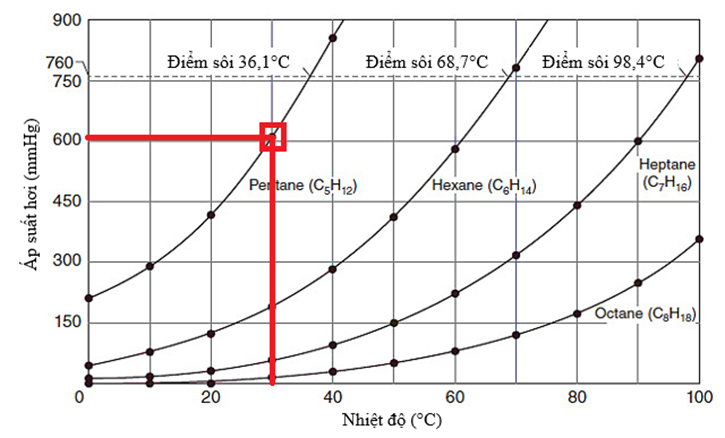
Theo Hình 1, tại nhiệt độ 30°C, áp suất hơi của pentane là 225 mmHg.
 Xem đáp án
Xem đáp án
Dựa vào Hình 1, tìm nhiệt độ tại 30°C, dễ dàng nhận thấy áp suất hơi của pentane vào khoảng 600 mmHg.
Chọn B
Câu 24:
Hợp chất nào trong bốn hợp chất trong Bảng 2 có khả năng chứa liên kết hydrogen kép nhất?
 Xem đáp án
Xem đáp án
Đáp án
Propionic acid
Giải thích
Theo Bảng 1, carboxylic acid chứa liên kết hydrogen kép. Dựa vào Hình 2 có thể xác định được propionic acid là carboxylic acid (hợp chất 3 carbon, nhiệt độ sôi 140°C).
Chọn C
Câu 25:
Phát biểu sau đây đúng hay sai?
Các hợp chất hữu cơ chứa liên kết Van der Waals trong phân tử là alkane, alkene và alkyne.
 Xem đáp án
Xem đáp án
Dựa vào Bảng 1, ta thấy các hợp chất hữu cơ chứa liên kết Van der Waals trong phân tử là alkane, alkene và alkyne.
Chọn A
Câu 26:
 Xem đáp án
Xem đáp án
Trong Bảng 2, khối lượng phân tử của mỗi phân tử tương đối giống nhau, nhưng điểm sôi thì không. Điều này cho thấy khối lượng phân tử không phải yếu tố ảnh hưởng trực tiếp đến điểm sôi.
Chọn A
Câu 27:
Các phát biểu sau đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Trong các liên kết được liệt kê ở Bảng 1, liên kết hydrogen là liên kết bền nhất. |
||
|
Độ bền liên kết được sắp xếp theo thứ tự giảm dần là: liên kết hydrogen kép, liên kết hydrogen, liên kết lưỡng cực và liên kết Van der Waals. |
||
|
Đối với hợp chất hữu cơ alkane, khi áp suất hơi tăng thì nhiệt độ sôi tăng. |
||
|
Trong các hợp chất hữu cơ, khối lượng phân tử tỉ lệ thuận với nhiệt độ sôi. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Trong các liên kết được liệt kê ở Bảng 1, liên kết hydrogen là liên kết bền nhất. |
X | |
|
Độ bền liên kết được sắp xếp theo thứ tự giảm dần là: liên kết hydrogen kép, liên kết hydrogen, liên kết lưỡng cực và liên kết Van der Waals. |
X | |
|
Đối với hợp chất hữu cơ alkane, khi áp suất hơi tăng thì nhiệt độ sôi tăng. |
X | |
|
Trong các hợp chất hữu cơ, khối lượng phân tử tỉ lệ thuận với nhiệt độ sôi. |
X |
Giải thích
1. Trong các liên kết được liệt kê ở Bảng 1, liên kết hydrogen là liên kết bền nhất.
Sai, vì: Dựa vào Hình 2, carboxylic acid có nhiệt độ sôi cao nhất => Liên kết hydrogen kép trong nhóm chức này khó bị phá vỡ nhất. Nói cách khác, liên kết hydrogen kép là liên kết bền nhất.
2. Độ bền liên kết được sắp xếp theo thứ tự giảm dần là: liên kết hydrogen kép, liên kết hydrogen, liên kết lưỡng cực và liên kết Van der Waals.
Đúng, vì: Dựa vào Hình 2, nhiệt độ sôi của các hợp chất hữu cơ được sắp xếp theo thứ tự giảm dần là: Carboxylic acid; Alcohol; (Amine, Ester, Ketone); (Alkane, Alkene, Alkyne). Nhiệt độ sôi càng cao thì liên kết càng bền => liên kết hydrogen kép là liên kết bền nhất, tiếp theo là liên kết hydrogen, liên kết lưỡng cực và liên kết Van der Waals.
3. Đối với hợp chất hữu cơ alkane, khi áp suất hơi tăng thì nhiệt độ sôi tăng.
Đúng, vì: Dựa vào Hình 1, ta thấy khi áp suất hơi tăng thì nhiệt độ sôi cũng tăng theo.
4. Trong các hợp chất hữu cơ, khối lượng phân tử tỉ lệ thuận với nhiệt độ sôi.
Sai. vì: Theo số liệu trong Bảng 2, hợp chất hữu cơ có khối lượng phân tử giống nhau nhưng nhiệt độ sôi khác nhau. Nghĩa là, khối lượng phân tử không phải yếu tố ảnh hưởng trực tiếp đến nhiệt độ sôi.
Câu 28:
 Xem đáp án
Xem đáp án
Thể tích là phép đo lượng không gian mà một vật nào đó chiếm giữ. Theo số liệu ở Bảng 1, mẫu 6 có thể tích 44,8 lít, đây là thể tích lớn nhất trong số các mẫu.
Chọn C
Câu 29:
Phát biểu sau đây đúng hay sai?
Xét cùng một loại khí tại cùng điều kiện áp suất và nhiệt độ, thể tích khí tăng thì khối lượng khí tăng.
 Xem đáp án
Xem đáp án
Dựa vào số liệu Bảng 1, có thể rút ra được thể tích của mỗi khí tỉ lệ thuận với khối lượng của khí đó.
Chọn A
Câu 30:
Định luật Avogadro dựa trên căn bản Hóa học nói lên sự liên hệ giữa khối lượng phân tử và tỉ trọng của
 Xem đáp án
Xem đáp án
Dựa vào thông tin văn bản đã cung cấp, có thể rút ra được: Định luật Avogadro là định luật chỉ áp dụng cho chất khí hoặc hơi.
Chọn B
Câu 31:
 Xem đáp án
Xem đáp án
Mẫu 1 và mẫu 3 có cùng thể tích, tuy nhiên, mẫu 3 có khối lượng 10 g, trong khi mẫu 1 chỉ có khối lượng khoảng 1 g.
Chọn B
Câu 32:
Dựa vào định luật Avogadro và Bảng 1, hãy sắp xếp các mẫu khí theo thứ tự số lượng phân tử từ ít nhất đến nhiều nhất?
 Xem đáp án
Xem đáp án
Định luật Avogadro được phát biểu rằng các thể tích khí bằng nhau ở cùng áp suất và nhiệt độ sẽ có số phân tử bằng nhau. Cả ba mẫu đều có thể tích 11,2 lít.
Chọn D
Câu 33:
Về mặt lý thuyết, số Avogadro (được kí hiệu là NA) cho biết số nguyên tử hay phân tử có trong 1 mol chất đó (NA ≈ 6,022.1023 mol−1). Hãy tính số phân tử H2O có trong 1,08 gam nước.
(Biết biểu thức biểu diễn mối quan hệ giữa số mol của chất và số phân tử: số phân tử = nchất.NA)
 Xem đáp án
Xem đáp án
\({n_{{{\rm{H}}_2}{\rm{O}}}} = \frac{{{m_{{{\rm{H}}_2}{\rm{O}}}}}}{{{M_{{{\rm{H}}_2}{\rm{O}}}}}} = \frac{{1,08}}{{18}} = 0,06\,\,({\rm{mol}}).\)
Số phân tử \({{\rm{H}}_2}{\rm{O}} = {n_{{{\rm{H}}_2}{\rm{O}}}}{\rm{.}}{{\rm{N}}_{\rm{A}}} \approx 0,06.6,{022.10^{23}} \approx 3,{613.10^{22}}\) (phân tử).
Chọn A
Câu 34:
Kéo thả từ hoặc cụm từ vào vị trí thích hợp:
gấp 2 lần, khối lượng riêng, độ âm, khối lượng, thể tích, gấp 4 lần
Xét tại cùng điều kiện áp suất, nhiệt độ và _______, một mẫu khí helium nặng _______ một mẫu khí hydrogen.
 Xem đáp án
Xem đáp án
Xét tại cùng điều kiện áp suất, nhiệt độ và thể tích, một mẫu khí helium nặng gấp 2 lần một mẫu khí hydrogen.
Câu 35:
 Xem đáp án
Xem đáp án
Dựa vào phần dẫn, chiết suất của vật liệu là thước đo lượng ánh sáng bị bẻ cong khi chiếu vào vật liệu.
Chọn A
Câu 36:
 Xem đáp án
Xem đáp án
Dựa vào cột thứ 2 của Bảng: Chiết suất của vật liệu luôn lớn hơn 1.
Chọn B
Câu 37:
Trong các vật liệu sau, vật liệu nào có khả năng kháng hóa chất là lớn nhất?
 Xem đáp án
Xem đáp án
Dựa vào cột thứ 5 của Bảng Tính chất vật lí của vật liệu quang phổ thì thạch anh và thủy tinh đá lửa có khả năng kháng hóa chất rất tốt.
Chọn B
Câu 38:
Khi nói về việc pha tạp oxide chì vào thạch anh tinh khiết thì các nhận xét sau đây là đúng hay là sai?
|
Phát biểu |
Đúng |
Sai |
|
Thạch anh tinh khiết được bổ sung oxide chì có tác dụng tăng chiết suất của vật liệu. |
||
|
Thạch anh tinh khiết được bổ sung oxide chì có tác dụng giảm chiết suất của vật liệu. |
||
|
Thạch anh tinh khiết được bổ sung oxide chì có tác dụng tăng cự ly truyền của của vật liệu. |
||
|
Thạch anh tinh khiết được bổ sung oxide chì có tác dụng giảm cự ly truyền của của vật liệu. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Thạch anh tinh khiết được bổ sung oxide chì có tác dụng tăng chiết suất của vật liệu. |
X | |
|
Thạch anh tinh khiết được bổ sung oxide chì có tác dụng giảm chiết suất của vật liệu. |
X | |
|
Thạch anh tinh khiết được bổ sung oxide chì có tác dụng tăng cự ly truyền của của vật liệu. |
X | |
|
Thạch anh tinh khiết được bổ sung oxide chì có tác dụng giảm cự ly truyền của của vật liệu. |
X |
Giải thích
Theo chú thích trong bảng, thạch anh pha với oxide chì thành thủy tinh đá lửa. So sánh các tính chất của thạch anh tinh khiết và thủy tinh đá lửa cho thấy: cự ly truyền của thủy tinh đá lửa nhỏ hơn so với cự ly truyền của thạch anh nhưng chiết suất của nó lại lớn hơn.
Câu 39:
 Xem đáp án
Xem đáp án
Ánh sáng có thể truyền qua một vật liệu khi bước sóng của nó nhỏ hơn hoặc bằng cự li truyền qua của ánh sáng đó đối với vật liệu.
→ Chỉ potassium bromide (0,3–29 μm) và caesium iodide (0,3–70 μm) thỏa mãn.
Chọn B
Câu 40:
Hiện tượng phản xạ toàn phần có thể xảy ra nếu ánh sáng truyền từ
 Xem đáp án
Xem đáp án
Hiện tượng phản xạ toàn phần chỉ có thể xảy ra khi ánh sáng truyền từ môi trường có chiết suất lớn sang môi trường có chiết suất bé hơn.
Từ Bảng ta thấy thủy tinh đá lửa có chiết suất là 1,66 trong khi chiết suất của calcium fluoride chỉ là 1,43 nên hiện tượng phản xạ toàn phần có thể xảy ra nếu ánh sáng truyền từ thủy tinh đá lửa sang calcium fluoride.
Chọn D
Câu 41:
Một nhà khoa học đưa ra giả thuyết rằng bất kỳ vật liệu nào có khả năng kháng hóa chất kém sẽ có cự ly truyền lớn hơn 10 μm. Tính chất của vật liệu nào sau đây mâu thuẫn với giả thuyết này?
 Xem đáp án
Xem đáp án
Vật liệu có tính chất mâu thuẫn với giả thuyết này sẽ có khả năng kháng hóa chất kém nhưng cự ly truyền nhỏ hơn 10 μm. Lithium fluoride có khả năng kháng hóa chất kém và cự ly truyền của nó dưới 6 μm.
Thủy tinh đá lửa và thạch anh đều có khả năng kháng hóa chất rất tốt.
Caesium iodide có cự ly truyền gần 70 μm.
Chọn A
Câu 42:
bệnh nhân 3, bệnh nhân 5, bênh nhân 1, bệnh nhân 4, bệnh nhân 2
Giả sử virus SARS-CoV-2 chưa phát sinh thêm đột biến mới, ban đầu chỉ có 1 chủng gây bệnh, thì những người nên ưu tiên tiêm vaccine phòng ngừa bệnh viêm đường hô hấp cấp là _______ và _______.
 Xem đáp án
Xem đáp án
Đáp án
Giả sử virus SARS-CoV-2 chưa phát sinh thêm đột biến mới, ban đầu chỉ có 1 chủng gây bệnh, thì những người nên ưu tiên tiêm vaccine phòng ngừa bệnh viêm đường hô hấp cấp là bệnh nhân số 5 và bệnh nhân số 1.
Giải thích
Nhìn vào bảng 1, ta thấy bệnh nhân số 1 và số 5 đều không mắc bệnh Covid-19, tức là trong cơ thể của 2 người này đều chưa tồn tại kháng thể đặc hiệu với chủng virus SARS-CoV-2 này. Nên những người bệnh này cần được ưu tiên tiêm vaccine.
Những người bệnh còn lại đều đưa ra kết quả xét nghiệm là đã từng, hoặc đang mắc bệnh Covid-19, những bệnh nhân này cơ thể đã/đang/sẽ sinh ra kháng thể tương ứng, và kháng thể IgG có trí nhớ miễn dịch, có khả năng nhận diện lại nếu kháng nguyên này xâm nhập vào một lần nữa.
Câu 43:
Bệnh nhân đang bị nhiễm virus SARS-CoV-2 chưa biểu hiện thành triệu chứng là bệnh nhân số (1) ________.
 Xem đáp án
Xem đáp án
Đáp án
Bệnh nhân đang bị nhiễm virus SARS-CoV-2 chưa biểu hiện thành triệu chứng là bệnh nhân số (1) __ 2 __ .
Giải thích
Nhìn vào bảng 1, ta thấy bệnh nhân số 2 xét nghiệm PCR ra kết quả dương tính, trong khi đó không có biểu hiện bệnh, xét nghiệm kháng thể IgG và IgM đều âm tính, chứng tỏ bệnh ở giai đoạn mới đầu, chưa sinh ra kháng thể, chỉ khi xét nghiệm RT-PCR nhằm xác định sự có mặt của vật chất di truyền virus thì mới phát hiện bệnh.
Câu 44:
Trong trường hợp tất cả các bệnh nhân đều chưa tiêm vaccine thì bệnh nhân có khả năng cao nhất bị nhiễm virus SARS-CoV-2 nhưng đã được điều trị khỏi bệnh là bệnh nhân số (1) ________.
 Xem đáp án
Xem đáp án
Đáp án
Trong trường hợp tất cả các bệnh nhân đều chưa tiêm vaccine thì bệnh nhân có khả năng cao nhất bị nhiễm virus SARS-CoV-2 nhưng đã được điều trị khỏi bệnh là bệnh nhân số (1) __ 3 __ .
Giải thích
IgG cùng với IgM là hai kháng thể đặc biệt giúp chống lại virus SARS-CoV-2. IgG có trong máu người đã nhiễm Covid 19 sau một khoảng thời gian nhất định (thường là giai đoạn phục hồi), hoặc ở những người đã tiêm vaccine phòng Covid-19.
Trong trường hợp này, đề bài loại trừ trường hợp kháng thể IgG xuất hiện do tiêm vaccine, nên sự xuất hiện của kháng thể IgG ở người nào chứng tỏ người đó đã từng nhiễm Covid-19. Nhìn vào bảng 1, ta chỉ thấy duy nhất bệnh nhân số 3 có kết quả dương tính với IgG, ngoài ra không biểu hiện triệu chứng nào, đồng thời kết quả xét nghiệm RT-PCR và IgM đều âm tính chứng tỏ người này đã từng nhiễm virus SARS-CoV-2 nhưng đã được điều trị khỏi bệnh
Câu 45:
 Xem đáp án
Xem đáp án
Theo giả thuyết đồng tiến hóa: “...những chuỗi khác được đóng gói bên trong các protein.”
Theo giả thuyết nguồn gốc tế bào: “...các chuỗi này liên kết với protein để tạo vỏ capsid bên ngoài.”
Theo giả thuyết hồi quy: “...Kết quả là mỗi hạt virus chỉ chứa nucleic acid, vỏ capsid, và đôi khi có thêm lớp vỏ ngoài.”
Như vậy điểm chung của cả ba giả thuyết là đều công nhận virus có cấu tạo gồm vỏ protein.
Chọn A
Câu 46:
 Xem đáp án
Xem đáp án
Theo Giả thuyết đồng tiến hóa thì “virus có thể đã tiến hóa từ các phân tử phức tạp của protein và nucleic acid cùng lúc với tế bào xuất hiện lần đầu tiên trên Trái Đất. Và nó đã không phụ thuộc vào sự sống của tế bào trong hàng tỷ năm” như vậy có thể thấy rằng quan điểm này cho rằng ban đầu virus không hề có sự kí sinh nội bào bắt buộc.
Chọn C
Câu 47:
 Xem đáp án
Xem đáp án
Theo thông tin văn bản “Bệnh não xốp hay còn gọi là bệnh bò điên (viết tắt là BSE) thường xảy ra chủ yếu ở bò” nên suy ra được đáp án cần chọn là C – bò.
Chọn C
Câu 48:
 Xem đáp án
Xem đáp án
Theo thông tin văn bản “Nguyên nhân gây ra bệnh được cho là do các protein prion cuộn gập sai” nên suy ra được đáp án cần chọn là A – prion cuộn gập sai.
Chọn A
Câu 49:
Có thể xác định chính xác bệnh não xốp bò (BSE) ở bò bằng việc quan sát biểu hiện bên ngoài của chúng, đúng hay sai?
 Xem đáp án
Xem đáp án
Sai. Vì theo thông tin đưa ra: “Hiện tại, không có phương pháp nào có thể đưa ra kết luận chắc chắn một con bò mắc bệnh bò điên khi chúng còn sống” tức là không thể dựa vào biểu hiện để xác định chính xác chúng có bị bệnh BSE hay không. Cách duy nhất là kiểm tra mô não sau khi chúng chết đi.
Chọn B
Câu 50:
Dựa vào bảng kết quả thí nghiệm, cho biết nhóm bò có số lượng mắc bệnh BSE cao nhất thuộc nhóm nào sau đây?
 Xem đáp án
Xem đáp án
Dựa vào bảng kết quả thí nghiệm, ta thấy số lượng bò mắc bệnh BSE nhiều nhất (12) thuộc nhóm B – mà theo thông tin văn bản thì nhóm B là nhóm bò có nguồn thức ăn được lấy từ những con cừu nhiễm bệnh.
Chọn B
Câu 51:
 Xem đáp án
Xem đáp án
Trong 2 thí nghiệm, các nhà nghiên cứu đã kiểm tra não của các con bò thí nghiệm sau thời gian 18 tháng (1 năm rưỡi) kể từ khi tiến hành thí nghiệm. Điều này tương ứng với việc các nhà nghiên cứu đã ngầm công nhận khoảng thời gian này đủ để bệnh não xốp bò phát triển. Nếu các giả định này sai lệch thì có thể kết quả thí nghiệm sẽ sai lệch, và các nhà nghiên cứu sẽ phải thực hiện thêm các thí nghiệm với khoảng thời gian dài hơn.
Chọn B
Câu 52:
 Xem đáp án
Xem đáp án
Dựa vào Hình 1, ta thấy vật A có tỉ lệ phần trăm thể tích phần vật bị chìm trong chất lỏng là thấp nhất nên vật A có tỉ lệ phần trăm thể tích phần vật nổi trên bề mặt chất lỏng lớn nhất.
Chọn A
Câu 53:
Khi một vật nổi trên bề mặt chất lỏng thì toàn bộ thể tích của vật nằm ở phía trên bề mặt chất lỏng, đúng hay sai?
 Xem đáp án
Xem đáp án
Theo đoạn thứ nhất của phần dẫn: Khi một vật nổi trên bề mặt chất lỏng thì một phần thể tích của vật vẫn ở trên bề mặt chất lỏng, trong khi phần thể tích còn lại của vật chìm trong chất lỏng.
Chọn B
Câu 54:
 Xem đáp án
Xem đáp án
Dựa vào hình 1, ta thấy : Khi tỉ trọng của vật giảm thì phần trăm thể tích của nó chìm trong chất lỏng giảm. Đối với 4 chất lỏng trên thì quy luật này đều đúng.
Chọn B
Câu 55:
Khi xét sự nổi của vật B trong dung dịch bromine thì lời giải thích nào sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Khối lượng vật B chìm trong dung dịch bromine chiếm khoảng 10% tổng khối lượng của nó. |
||
|
Khối lượng vật B chìm trong dung dịch bromine chiếm khoảng 20% tổng khối lượng của nó. |
||
|
Thể tích vật B chìm trong dung dịch bromine chiếm khoảng 10% tổng khối lượng của nó |
||
|
Thể tích vật B chìm trong dung dịch bromine chiếm khoảng 20% tổng khối lượng của nó |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Khối lượng vật B chìm trong dung dịch bromine chiếm khoảng 10% tổng khối lượng của nó. |
X | |
|
Khối lượng vật B chìm trong dung dịch bromine chiếm khoảng 20% tổng khối lượng của nó. |
X | |
|
Thể tích vật B chìm trong dung dịch bromine chiếm khoảng 10% tổng khối lượng của nó |
X | |
|
Thể tích vật B chìm trong dung dịch bromine chiếm khoảng 20% tổng khối lượng của nó |
X |
Giải thích
Theo Bảng 1, Vật B có tỉ trọng là 0,300.
Theo Hình 1, một vật có tỉ trọng là 0,300 sẽ chìm trong dung dịch brom khoảng 10%.
Tại một nhiệt độ nhất định, khối lượng riêng của vật: \({\rho _v} = \frac{m}{V}\) với V = const
Mà tỉ trọng là tỉ lệ giữa khối lượng riêng của một vật so với khối lượng riêng của nước ở một nhiệt độ nhất định
→ Khối lượng của vật chìm trong dung dịch bromine chiếm khoảng 10% tổng khối lượng của nó.
Câu 56:
Tỉ trọng có đơn vị đo là gì?
 Xem đáp án
Xem đáp án
Tỉ trọng là tỉ lệ giữa khối lượng riêng của một vật so với khối lượng riêng của nước ở một nhiệt độ nhất định nên tỉ trọng không có đơn vị đo.
Chọn D
Câu 57:
Giả sử một vật có tỉ trọng là 1,00 nổi trong một bình chứa nước trong điều kiện nhiệt độ là 20°C. Cho rằng nếu nhiệt độ của cả vật và nước đều tăng lên nhiệt độ 85°C, và vật không nở ra cũng không co lại khi nhiệt độ tăng. Các phát biểu sau đây là đúng hay là sai?
|
Phát biểu |
Đúng |
Sai |
|
Vật có nhiều khả năng sẽ nổi lên. |
||
|
Vật có nhiều khả năng sẽ chìm xuống. |
||
|
Khối lượng của nước không đổi. |
||
|
Thể tích của nước không đổi |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Vật có nhiều khả năng sẽ nổi lên. |
X | |
|
Vật có nhiều khả năng sẽ chìm xuống. |
X | |
|
Khối lượng của nước không đổi. |
X | |
|
Thể tích của nước không đổi |
X |
Giải thích
Khối lượng riêng : \(\rho = \frac{m}{V}\)
Khi nước nóng lên thì m không đổi nhưng V của nước tăng nên khối lượng riêng giảm. Nói cách khác thì khi nước nóng lên, nó sẽ trở nên ít nhẹ hơn, dẫn đến vật có nhiều khả năng chìm xuống thay vì tiếp tục nổi.
Câu 58:
Một khối lập phương đồng chất có tỉ trọng ở 20℃ là 0,700. Độ dài mỗi cạnh của khối lập phương là 10 cm. Khối lập phương nổi trong bình chứa benzene. Theo Hình 1, thể tích của khối lập phương bị chìm trong benzene gần nhất với giá trị nào sau đây?
 Xem đáp án
Xem đáp án
Thể tích của khối lập phương là: \[V = {a^3} = {10^3} = 1000\;\,\,{\rm{c}}{{\rm{m}}^3}\]
Do khối lập phương này có tỉ trọng ở 20℃ là 0,700 và nổi trong bình chứa benzene nên theo hình 1 thì có khoảng hơn 80% thể tích khối lập phương bị chìm.
→ Thể tích của khối lập phương bị chìm trong benzene: \({V_c} = V.80\)
Chọn CCâu 59:
 Xem đáp án
Xem đáp án
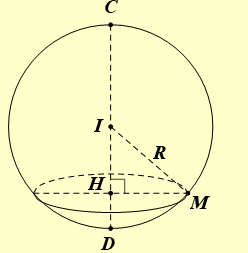
Gọi \(M\) là một giao điểm của \(\left( S \right)\) và \(\left( \alpha \right)\).
Vì mặt phẳng \(\left( \alpha \right)\) giao mặt cầu \(\left( S \right)\) theo một đường tròn có chu vi \(16\pi {\rm{cm}}\)
\( \Rightarrow 2\pi HM = 16\pi \Leftrightarrow HM = 8\left( {{\rm{cm}}} \right)\).
Gọi bán kính của \(\left( S \right)\) là \(R\).
Ta có: \(CH = R + IH \Leftrightarrow R + IH = 16 \Leftrightarrow IH = 16 - R\).
Áp dụng định lí Pythagore đối với tam giác vuông \(IHM\) :
\(I{M^2} = I{H^2} + H{M^2} \Leftrightarrow {R^2} = {(16 - R)^2} + {8^2} \Leftrightarrow - 32R + 320 = 0 \Leftrightarrow R = 10\left( {{\rm{cm}}} \right)\).
Vậy diện tích mặt cầu \(\left( S \right)\) là \(S = 4\pi {R^2} = 400\pi \left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Chọn A
Câu 60:
Mỗi phát biểu sau là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Tổng của hai số nguyên dương là một số nguyên dương. |
||
|
Tích của hai số nguyên âm là một số nguyên âm. |
||
|
Tích của hai số nguyên bằng 0 khi và chỉ khi ít nhất một trong hai số nguyên đó bằng 0. |
||
|
Hiệu \(a - b\) là một số nguyên âm nếu a dương và b dương. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Tổng của hai số nguyên dương là một số nguyên dương. |
X | |
|
Tích của hai số nguyên âm là một số nguyên âm. |
X | |
|
Tích của hai số nguyên bằng 0 khi và chỉ khi ít nhất một trong hai số nguyên đó bằng 0. |
X | |
|
Hiệu \(a - b\) là một số nguyên âm nếu a dương và b dương. |
X |
Giải thích
Khẳng định sai là:
+) "Tích của hai số nguyên âm là một số nguyên âm". Ví dụ: -1 ). -3 ) \( = 3 > 0\).
+) "Hiệu \(a - b\) là một số nguyên âm nếu a dương và b dương". Ví dụ: \(3 - 2 = 1 > 0\).
Câu 61:
 Xem đáp án
Xem đáp án
Giải thích
Trong 1 phút, Minh hoàn thành được \(\frac{1}{{40}}\) công việc, An hoàn thành được \(\frac{1}{{30}}\) công việc và Chi hoàn thành được \(\frac{1}{{24}}\) công việc.
Trong 1 phút, cả ba bạn hoàn thành được \(\frac{1}{{40}} + \frac{1}{{30}} + \frac{1}{{24}} = \frac{1}{{10}}\) công việc.
Vậy ba người sẽ mất \(1:\frac{1}{{10}} = 10\) phút để cùng nhau gõ xong file tài liệu.
Chọn B
Câu 62:
Một công ty sản xuất linh kiện điện tử nghiên cứu sản xuất bóng bán dẫn theo các phương pháp khác nhau. Có một lượng bóng bán dẫn được sản xuất với 3 phương pháp khác nhau trong cùng khoảng thời gian. Số lượng bóng bán dẫn được sản xuất theo mỗi phương pháp được cho dưới bảng sau:
|
Phương pháp |
Số lượng |
|
|
Thành phẩm |
Sản phẩm lỗi |
|
|
1 |
88 |
12 |
|
2 |
165 |
35 |
|
3 |
260 |
65 |
Mỗi phát biểu sau là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Phương pháp 2 có tỉ lệ thành phẩm thấp nhất. |
||
|
Năng suất sản xuất bóng bán dẫn của phương pháp 1 là tốt nhất. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Phương pháp 2 có tỉ lệ thành phẩm thấp nhất. |
X | |
|
Năng suất sản xuất bóng bán dẫn của phương pháp 1 là tốt nhất. |
X |
Giải thích
Ta có:
|
Phương pháp |
Số lượng |
Tổng số lượng sản phẩm |
Tỉ lệ thành phẩm |
|
|
Thành phẩm |
Sản phẩm lỗi |
|||
|
1 |
88 |
12 |
100 |
\(\frac{{88}}{{100}} = 88\) |
|
2 |
165 |
35 |
200 |
\(\frac{{165}}{{200}} = 82,5\) |
|
3 |
260 |
65 |
325 |
\(\frac{{260}}{{325}} = 80\) |
Vậy phương pháp 3 có tỉ lệ thành phẩm thấp nhất.
Vì trong cùng khoảng thời gian, một lượng bóng bán dẫn được sản xuất với 3 phương pháp khác nhau nên phương pháp nào có số lượng sản phẩm thành công nhiều nhất thì có năng suất tốt nhất. Vậy năng suất sản xuất bóng bán dẫn của phương pháp 3 là tốt nhất.
Câu 63:
Trong thời gian liên tục 25 năm, một người lao động luôn gửi đúng 4 000 000 đồng vào một ngày cố định của tháng ở ngân hàng \(M\) với lãi suất không thay đổi trong suốt thời gian gửi tiền là 0,6%/tháng. Số tiền người đó có được sau 25 năm là (1) ______ triệu đồng. (Kết quả làm tròn đến chữ số thập phân thứ ba).
 Xem đáp án
Xem đáp án
Đáp án
định của tháng ở ngân hàng \(M\) với lãi suất không thay đổi trong suốt thời gian gửi tiền là 0,6%/tháng. Số tiền người đó có được sau 25 năm là (1) ___3364,867___ triệu đồng. (Kết quả làm tròn đến chữ số thập phân thứ ba).
Giải thích
Sau tháng thứ 1 người lao động có: \(4\left( {1 + 0,6{\rm{\% }}} \right)\) triệu đồng.
Sau tháng thứ 2 người lao động có:
\(\left( {4\left( {1 + 0,6{\rm{\% }}} \right) + 4} \right)\left( {1 + 0,6{\rm{\% }}} \right) = 4\left[ {{{(1 + 0,6{\rm{\% }})}^2} + \left( {1 + 0,6{\rm{\% }}} \right)} \right]\) triệu đồng.
…
Sau tháng thứ 300 người lao động có:
\(4\left[ {{{(1 + 0,6{\rm{\% }})}^{300}} + {{(1 + 0,6{\rm{\% }})}^{299}} \ldots + \left( {1 + 0,6{\rm{\% }}} \right)} \right] = 4\left( {1 + 0,6{\rm{\% }}} \right)\frac{{{{(1 + 0,6{\rm{\% }})}^{300}} - 1}}{{\left( {1 + 0,6{\rm{\% }}} \right) - 1}} \approx 3364,867\) (triệu đồng).
Câu 64:
 Xem đáp án
Xem đáp án
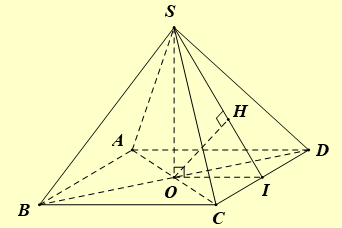
Vì \(I\) là trung điểm của \(CD \Rightarrow OI \bot CD,CD = 2OI\).
Kẻ \(OH \bot SI\) tại \(H \Rightarrow OH \bot \left( {SCD} \right) \Rightarrow d\left( {O,\left( {SCD} \right)} \right) = d\left( {O,SI} \right) = OH = 1\).
Ta có \(\left\{ {\begin{array}{*{20}{l}}{(SCD) \cap (ABCD) = CD}\\{SI \subset (SCD),SI \bot CD}\\{OI \subset (ABCD),OI \bot CD}\end{array}} \right. \Rightarrow ((SCD),(ABCD)) = (SI,OI) = (SI,AD) = \widehat {SIO} = {45^^\circ }\)
Xét tam giác vuông \(HIO \Rightarrow OI = \frac{{OH}}{{{\rm{sin}}\widehat {SIO}}} = \frac{1}{{{\rm{sin}}{{45}^ \circ }}} = \sqrt 2 \Rightarrow CD = 2OI = 2\sqrt 2 \).
Ta có \({\rm{\Delta }}SIO\) là tam giác vuông cân tại \(O \Rightarrow SO = OI = \sqrt 2 \).
Vậy \({V_{S.ABCD}} = \frac{1}{3}C{D^2}.SO = \frac{1}{3}{(2\sqrt 2 )^2}.\sqrt 2 = \frac{{8\sqrt 2 }}{3}\).
Chọn D
Câu 65:
Hằng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu \(h\) (mét) của mực nước trong kênh tính theo thời gian \(t\) (giờ) trong một ngày \((0 \le t < 24)\) được cho bởi công thức\(h\left( t \right) = 2{\rm{sin}}\left( {\frac{{3\pi t}}{{14}}} \right)\left( {1 - 4{\rm{si}}{{\rm{n}}^2}\left( {\frac{{\pi t}}{{14}}} \right)} \right) + 12\).
Trong một ngày có bao nhiêu lần mực nước trong kênh đạt độ sâu 12m?
 Xem đáp án
Xem đáp án
Giải thích
Đặt \(x = \frac{{\pi t}}{{14}}\). Với \(t \in \left[ {0;24} \right)\) thì \(x \in \left[ {0;\frac{{12\pi }}{7}} \right)\). Khi đó, \(h\left( x \right) = 2{\rm{sin}}\left( {3x} \right)\left( {1 - 4{\rm{si}}{{\rm{n}}^2}x} \right) + 12\)
Để mực nước trong kênh đạt độ sau \(12{\rm{\;m}}\) thì \(h\left( t \right) = 12\).
\( \Leftrightarrow h\left( x \right) = 12 \Leftrightarrow 2{\rm{sin}}\left( {3x} \right)\left( {1 - 4{\rm{si}}{{\rm{n}}^2}x} \right) + 12 = 12\)
\( \Leftrightarrow {\rm{sin}}\left( {3x} \right)\left( {1 - 4{\rm{si}}{{\rm{n}}^2}x} \right) = 0\)
\( \Leftrightarrow 2{\rm{sin}}\left( {3x} \right)\left( {1 - 2{\rm{sin}}x} \right)\left( {1 + 2{\rm{sin}}x} \right) = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{\rm{sin}}\left( {3x} \right) = 0}\\{1 - 2{\rm{sin}}x = 0}\\{1 + 2{\rm{sin}}x = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{{k\pi }}{3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\{x = \pm \frac{\pi }{6} + k2\pi }\\{x = \frac{{5\pi }}{6} + k2\pi }\\{x = \frac{{7\pi }}{6} + k2\pi }\end{array}} \right.} \right.\)
Vì \(x \in \left[ {0;\frac{{12\pi }}{7}} \right);k \in \mathbb{Z}\) nên:
|
\(x\) |
\(k\) |
|
\(x = \frac{{k\pi }}{3}\) \(0 \le \frac{\pi }{6} + k2\pi < \frac{{12\pi }}{7}\) |
\(k \in \left\{ {0;1; \ldots ;4;5} \right\}\) |
|
\(x = \frac{\pi }{6} + k2\pi \) |
\(k = 0\) |
|
\(x = - \frac{\pi }{6} + k2\pi \) |
\(k \in \emptyset \) |
|
\(x = \frac{{5\pi }}{6} + k2\pi \) |
\(k = 0\) |
|
\(x = \frac{{7\pi }}{6} + k2\pi \) |
\(k = 0\) |
Vậy có 9 giá trị thỏa mãn hay trong một ngày có 9 lần mực nước trong kênh đạt độ sâu \(12{\rm{\;m}}\).
Chọn D
Câu 66:
 Xem đáp án
Xem đáp án
Giải thích
Điều kiện: \(\left\{ {\begin{array}{*{20}{c}}{x \ne 0}\\{{\rm{lo}}{{\rm{g}}_2}\frac{4}{{{x^2}}} > 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ne 0}\\{ - 2 < x < 2}\end{array} \Rightarrow D = \left( { - 2;2} \right) \setminus \left\{ 0 \right\}} \right.} \right.\).
Cách 1. Sử dụng Casio \({\rm{FX}} - 580\)
Ấn MENU +8 và nhập hàm số \(f\left( x \right) = {\rm{lo}}{{\rm{g}}_2}\frac{4}{{{x^2}}} - {2^{x + 2}}\) với phạm vi bảng như sau:

Khi đó, ta có bảng giá trị:

Từ bảng giá trị ta có phương trình đã cho có nghiệm duy nhất \(x = - 1\).
Cách 2. Sử dụng phương pháp hàm số.
Chọn B
Câu 67:
 Xem đáp án
Xem đáp án
Giải thích
Ta có \[\left| {{x^2} + x - 2} \right| = 2m + {x^2} - x - 6 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x^2} + x - 2 = 2m + {x^2} - x - 6\quad ({\rm{khi }}x \ge 1 \vee x \le - 2)}\\{ - {x^2} - x + 2 = 2m + {x^2} - x - 6\,\,({\rm{khi }} - 2 \le x \le 1)}\end{array}} \right.\].
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m = x + 2{\rm{\;}}\,\,\left( {x \ge 1 \vee x \le - 2} \right)}\\{m = - {x^2} + 4\,\,\left( { - 2 \le x \le 1} \right)}\end{array}} \right.\). Ta vẽ các đồ thị như hình vẽ.
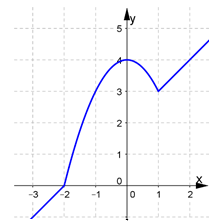
Từ đó ta suy ra để phương trình có 3 nghiệm phân biệt thì \(3 < m < 4\).
Vậy không có giá trị nguyên của \(m\) thỏa mãn.
Chọn C
Câu 68:
 Xem đáp án
Xem đáp án
Giải thích
Sử dụng Casio nhập ta được kết quả \( \approx - {10^5} \to - \infty \).
Vậy \(\mathop {{\rm{lim}}}\limits_{x \to {{( - 2)}^ - }} \frac{{ - 3}}{{{x^2} + x - 2}} = - \infty \).
Chọn A
Câu 69:
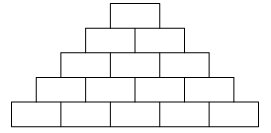
Bà chủ quán trà sữa \(X\) muốn trang trí quán cho đẹp nên quyết định thuê nhân công xây một bức tường bằng gạch với xi măng (như hình vẽ bên dưới), biết hàng dưới cùng có 500 viên, mỗi hàng tiếp theo đều có ít hơn hàng trước 1 viên và hàng trên cùng có 1 viên. Hỏi số gạch cần dùng để hoàn thành bức tường trên là bao nhiêu viên?
 Xem đáp án
Xem đáp án
Giải thích
Ta có số gạch ở mỗi hàng là các số hạng của 1 cấp số cộng: \(500,499,498,.,2,1\).
\( \Rightarrow \) Tổng số gạch cần dùng là tổng của cấp số cộng trên và bằng
\({S_{500}} = \frac{{500\left( {500 + 1} \right)}}{2} = 250.501 = 125250\) (viên).
Chọn D
Câu 70:
 Xem đáp án
Xem đáp án
Giải thích
\({2^{{x^2} - x + 8}} = {4^{1 - 3x}} \Leftrightarrow {2^{{x^2} - x + 8}} = {2^{2 - 6x}} \Leftrightarrow {x^2} - x + 8 = 2 - 6x \Leftrightarrow {x^2} + 5x + 6 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 2}\\{x = - 3}\end{array}} \right.\).
Vậy phương trình có 2 nghiệm thực.
Chọn A
Câu 71:
 Xem đáp án
Xem đáp án
Giải thích
Từ công thức truy hồi \({u_1} = 2;{u_n} = 2{u_{n - 1}} + 3n - 1\) ta suy ra: \(\left\{ {\begin{array}{*{20}{l}}{{u_2} = 9}\\{{u_3} = 26}\\{{u_4} = 63}\end{array}} \right.\).
Mà \({u_n} = a{.2^n} + bn + c,n \ge 2\) nên ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{4a + 2b + c = 9}\\{8a + 3b + c = 26}\\{16a + 4b + c = 63}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 5}\\{b = - 3}\\{c = - 5}\end{array}} \right.} \right.\).
Do đó \(a + b + c = - 3\).
Chọn D
Câu 72:
Ta định nghĩa, một hình nón gọi là nội tiếp một mặt cầu nếu mặt cầu chứa đỉnh và đường tròn đáy của hình nón.
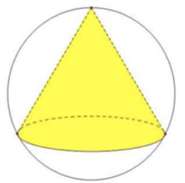
Cho mặt cầu \(\left( S \right)\) có đường kính bằng \(24{\rm{\;cm}}\). Xét tất cả các hình nón nội tiếp mặt cầu \(\left( S \right)\), gọi \(\left( N \right)\) là hình nón có thể tích của khối nón được tạo bởi \(\left( N \right)\) là lớn nhất. Khi đó, chiều cao của hình nón \(\left( N \right)\) bằng
 Xem đáp án
Xem đáp án
Chọn A
Câu 73:
 Xem đáp án
Xem đáp án
Giải thích
Trước hết, ta chia cho mỗi đứa trẻ 7 chiếc kẹo. Số kẹo còn lại là \(100 - 12.7 = 16\) chiếc.
Ta cần chia 16 chiếc kẹo còn lại cho 12 em nhỏ sao cho mỗi em được thêm ít nhất 1 chiếc kẹo.
Xếp 16 chiếc kẹo thành 1 hàng ngang, giữa chúng có 15 chỗ trống.
Số cách chia kẹo thỏa mãn là số cách đặt 11 vách ngăn vào 11 chỗ trống trong số 15 chỗ trống trên, 11 vách ngăn đó chia thành 12 khoảng, là số kẹo chia cho 12 em.
Vậy số cách chia thỏa mãn là \(C_{15}^{11} = 1365\) cách.
Chọn D
Câu 74:
Một chiếc cốc có phần chứa nước có dạng hình nón (không có nắp) đựng đầy nước. Người ta thả vào đó một khối cẩu có đường kính bằng chiều cao của phần chứa nước của chiếc cốc và đo được thể tích nước tràn ra ngoài là \(18\pi {\rm{c}}{{\rm{m}}^3}\). Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa của khối cầu chìm trong nước (minh họa như hình vẽ). Thể tích lượng nước còn lại trong cốc bằng
 Xem đáp án
Xem đáp án
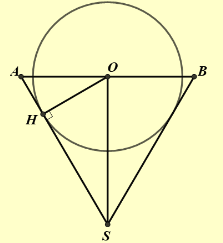
Đường kính của khối cầu bằng chiều cao của phần chứa nước của cốc nước nên \(OS = 2OH\).
Thể tích nước tràn ra là thể tích của một nửa khối cầu (phần chìm trong nước):
\(18\pi = \frac{{{V_C}}}{2} = \frac{{2\pi .O{H^3}}}{3}\) suy ra \(OH = 3\).
Xét tam giác \(AOS\) vuông tại \(O\), đường cao \(OH\) :
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{S^2}}}\) hay
\(\frac{1}{{O{A^2}}} = \frac{1}{{O{H^2}}} - \frac{1}{{O{S^2}}} = \frac{1}{{O{H^2}}} - \frac{1}{{4O{H^2}}} = \frac{3}{{4O{H^2}}} = \frac{3}{{{{4.3}^2}}} = \frac{1}{{12}}\).
Suy ra \(OA = 2\sqrt 3 \).
Thể tích lượng nước còn lại trong cốc là:
\(V = {V_n} - \frac{{{V_c}}}{2} = \frac{1}{3}\pi .O{A^2}.OS - 18\pi = \frac{1}{3}\pi .{(2\sqrt 3 )^2}.6 - 18\pi = 6\pi \left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Chọn B
Câu 75:
Một hình hộp đứng có đáy là hình vuông chứa đồng hồ cát. Thiết diện qua trục của hình hộp như hình vẽ.
Tỉ số thể tích của đồng hồ cát và phần còn lại giữa đồng hồ cát và hình hộp đứng là
 Xem đáp án
Xem đáp án
Giải thích
Gọi \({V_{\left( H \right)}},{V_{\left( {DH} \right)}},{V_{\left( {CL} \right)}}\) lần lượt là thể tích của hộp đứng, đồng hồ cát và phần còn lại.
Cho cạnh đáy hộp bằng 6 , chiều cao hộp bằng 8 . Đồng hồ cát tạo bởi 2 nón bằng nhau và chiều cao nón bằng 4 ; bán kính đáy nón bằng 3 .
Ta có: \({V_{\left( H \right)}} = {8.6^2} = 288;{V_{\left( {DH} \right)}} = 2.\frac{1}{3}.4.\pi {.3^2} = 24\pi ;\)
\({V_{\left( {CL} \right)}} = {V_{\left( H \right)}} - {V_{\left( {DH} \right)}} = 288 - 24\pi \).
\( \Rightarrow \frac{{{V_{\left( {DH} \right)}}}}{{{V_{\left( {CL} \right)}}}} = \frac{{24\pi }}{{288 - 24\pi }} = \frac{\pi }{{12 - \pi }}\).
Chọn A
Câu 76:
 Xem đáp án
Xem đáp án
Giải thích
Áp dụng bất đẳng thức trị tuyệt đối \(\left| a \right| + \left| b \right| \ge \left| {a + b} \right|\), ta có:
\[\left| {{{\log }_2}2(x + y)} \right| + \left| {{{\log }_2}\frac{{2(x + y)}}{{{x^2} + 4{y^2} + 1}}} \right| = \left| {{{\log }_2}(x + y) + 1} \right| + \left| {1 - {{\log }_2}\frac{{{x^2} + 4{y^2} + 1}}{{x + y}}} \right|\]
\( = \left| {{\rm{lo}}{{\rm{g}}_2}\left( {x + y} \right) + 1} \right| + \left| {{\rm{lo}}{{\rm{g}}_2}\frac{{{x^2} + 4{y^2} + 1}}{{x + y}} - 1} \right| \ge \left| {{\rm{lo}}{{\rm{g}}_2}\left( {{x^2} + 4{y^2} + 1} \right)} \right| = {\rm{lo}}{{\rm{g}}_2}\left( {{x^2} + 4{y^2} + 1} \right)\)
Mặt khác theo bất đẳng thức \({\rm{AM}} - {\rm{GM}}\) ta lại có: \({\rm{lo}}{{\rm{g}}_2}\left( {{x^2} + 4{y^2} + 1} \right) \ge {\rm{lo}}{{\rm{g}}_2}\left( {4xy + 1} \right) = VP\)
Dấu "=" xảy ra khi và chỉ khi \(\left\{ {\begin{array}{*{20}{l}}{\left( {1 - {\rm{lo}}{{\rm{g}}_2}\frac{{{x^2} + 4{y^2} + 1}}{{x + y}}} \right).\left[ {{\rm{lo}}{{\rm{g}}_2}\left( {x + y} \right) + 1} \right] \ge 0}\\{x = 2y}\end{array}} \right.\).
Thế vào \(P\) ta được \(P = \sqrt {2x} - {x^2} = g\left( x \right)\). Vì \(x,y \ge 1\) và \(x = 2y\) nên ta xét \(g\left( x \right)\) trên \(\left[ {2; + \infty } \right)\).
Ta có: \(g'\left( x \right) = 0 \Leftrightarrow \frac{1}{{\sqrt {2x} }} - 2x = 0 \Leftrightarrow \frac{1}{{\sqrt {2x} }} = 2x \Leftrightarrow x = \frac{1}{2}\) (Loại).
\( \Rightarrow g'\left( x \right) < 0\) trên \(\left[ {2; + \infty } \right) \Rightarrow g\left( x \right)\) luôn nghịch biến trên \(\left[ {2; + \infty } \right)\).
\( \Rightarrow \mathop {{\rm{max}}}\limits_{\left[ {2; + \infty } \right)} g\left( x \right) = g\left( 2 \right) = - 2\).
Chọn A
Câu 77:
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Yến có 20 cuốn sách khác nhau và bạn định chia đều số sách vào 2 chiếc thùng giấy để chở tới trường.
Số cách Yến có thể xếp sách vào hai chiếc thùng có màu sắc khác nhau là _______.
Số cách Yến có thể xếp sách vào hai chiếc thùng giống hệt nhau là _______.
 Xem đáp án
Xem đáp án
Đáp án
Số cách Yến có thể xếp sách vào hai chiếc thùng có màu sắc khác nhau là 184756.
Câu 78:
 Xem đáp án
Xem đáp án
Giải thích
Gọi \(M\left( {x;y} \right)\) là điểm biểu diễn của số phức \(z\) trong mặt phẳng \(Oxy\) và điểm \(I\left( {0;2} \right)\).
Ta có \(\left| {z - 2i} \right| + \left| z \right| = 2 \Leftrightarrow MI + OM = 2\).
Mặt khác, \(IO = 2\) nên \(M\) thuộc đoạn thẳng \(OI\) có độ dài bằng 2 .
Chọn B
Câu 79:
Một du khách vào hội chợ và chơi trò chơi ném vòng trúng thưởng. Lần đầu du khách mua 1 lượt ném vòng với giá 1000 đồng, kể từ lần sau tiền mua số lượt ném vòng gấp đôi số tiền lần trước. Người đó thua 10 lần liên tiếp và thắng ở 2 lần cuối. Biết mỗi lần thắng, giá trị phần thưởng của người chơi nhận được gấp đôi số tiền mua ban đầu (không kể số tiền đã đặt). Giá trị phần thưởng cuối cùng người đó nhận được là (1) _________ đồng.
 Xem đáp án
Xem đáp án
Đáp số
Một du khách vào hội chợ và chơi trò chơi ném vòng trúng thưởng. Lần đầu du khách mua 1 lượt ném vòng với giá 1000 đồng, kể từ lần sau tiền mua số lượt ném vòng gấp đôi số tiền lần trước. Người đó thua 10 lần liên tiếp và thắng ở 2 lần cuối. Biết mỗi lần thắng, giá trị phần thưởng của người chơi nhận được gấp đôi số tiền mua ban đầu (không kể số tiền đã đặt). Giá trị phần thưởng cuối cùng người đó nhận được là (1) __5121000___ đồng.
Giải thích
Số tiền mỗi lần du khách mua số lượt ném vòng là một số hạng của một cấp số nhân có \({u_1} = 1000\) và công bội \(q = 2\).
Du khách thua trong 10 lần đầu tiên nên tổng số tiền du khách đã bỏ ra mua lượt ném vòng là
\({S_{10}} = {u_1} + {u_2} + \ldots + {u_{10}} = \frac{{{u_1}\left( {1 - {q^{10}}} \right)}}{{1 - q}} = 1023000\) (đồng).
Giá trị phần thưởng mà du khách thắng trong 2 lần cuối (lần thứ 11 và 12) là
\(2{u_{11}} + 2{u_{12}} = 2{u_1}\left( {{q^{10}} + {q^{11}}} \right) = 6144000\) (đồng).
Ta có \(2{u_{11}} + 2{u_{12}} - {S_{10}} = 5121000\) nên du khách nhận được 5121000 đồng.
