Mặt nón, khối nón
-
332 lượt thi
-
31 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Công thức tính diện tích xung quanh hình nón có bán kính đáy r và độ dài đường sinh l là
 Xem đáp án
Xem đáp án
Công thức tính diện tích xung quanh hình nón có bán kính đáy r và độ dài đường sinh l là:
Đáp án cần chọn là: D
Câu 2:
Công thức tính diện tích toàn phần hình nón có bán kính đáy r, độ dài đường cao h và độ dài đường sinh l là:
 Xem đáp án
Xem đáp án
Công thức tính diện tích toàn phần hình nón có bán kính đáy r và độ dài đường sinh l là:
Đáp án cần chọn là: A
Câu 3:
Công thức tính thể tích khối nón có bán kính đáy r, độ dài đường sinh l và chiều cao h là:
 Xem đáp án
Xem đáp án
Công thức tính thể tích khối nón:
Đáp án cần chọn là: C
Câu 4:
 Xem đáp án
Xem đáp án
Ta có:
Đáp án cần chọn là: C
Câu 5:
Diện tích xung quanh hình nón có bán kính đáy r = 3cm và độ dài đường sinh 4cm là:
 Xem đáp án
Xem đáp án
Áp dụng công thức ta được:
Đáp án cần chọn là: C
Câu 6:
Cho hình nón có các kích thước r = 1cm; l = 2cm với r, l lần lượt là bán kính đáy và độ dài đường sinh hình nón. Diện tích toàn phần hình nón là:
 Xem đáp án
Xem đáp án
Áp dụng công thức ta được:
Đáp án cần chọn là: C
Câu 7:
Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a. Diện tích xung quanh của hình nón bằng:
 Xem đáp án
Xem đáp án
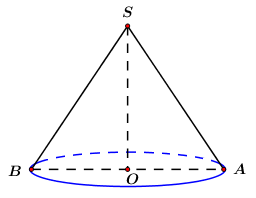
Thiết diện qua trục của hình nón là vuông cân tại S và có
Ta có: vuông cân tại
⇒ Diện tích xung quanh của hình nón đã cho là:
Đáp án cần chọn là: C
Câu 8:
Cho hình nón có góc ở đỉnh bằng 1200 và đường cao bằng 2. Tính diện tích xung quanh của hình nón đã cho.
 Xem đáp án
Xem đáp án
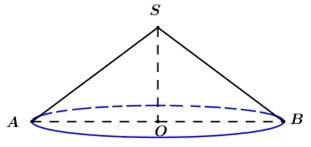
Gọi S là đỉnh hình nón, AB là 1 đường kính của hình nón và O là tâm đường tròn đáy của hình nón.
Khi đó ta có và
Ta có: cân tại S suy ra SO là phân giác của
Xét tam giác vuông SOA có:
Vậy diện tích xung quanh của hình nón là:
Đáp án cần chọn là: B
Câu 9:
Cho hình nón đỉnh S có bán kính đáy R = 2. Biết diện tích xung quanh của hình nón là . Tính thể tích khối nón.
 Xem đáp án
Xem đáp án
Ta có :
Lại có
Vậy thể tích khối nón là :
Đáp án cần chọn là: CCâu 10:
Cho hình nón có các kích thước r = 1; h = 2 với r,hr,h lần lượt là bán kính đáy và độ dài đường cao hình nón. Diện tích toàn phần hình nón là:
 Xem đáp án
Xem đáp án
Ta có:
Do đó
Đáp án cần chọn là: D
Câu 11:
 Xem đáp án
Xem đáp án
Áp dụng công thức tính thể tích khối nón
Đáp án cần chọn là: A
Câu 12:
Cho tam giác ABO vuông tại O, có góc Quay tam giác ABO quanh trục AO ta được một hình nón có diện tích xung quanh bằng:
 Xem đáp án
Xem đáp án
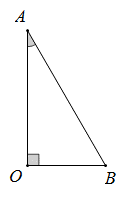
Hình nón thu được có đường sinh l = AB = a; bán kính đáy
và diện tích xung quanh là
Đáp án cần chọn là: C
Câu 13:
Một hình nón tròn xoay có đường sinh bằng đường kính đáy. Diện tích đáy của hình nón bằng . Khi đó chiều cao h của hình nón bằng:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Câu 14:
Hình nón có thiết diện qua trục là tam giác đều cạnh a = 3 . Tính độ dài đường cao của hình nón.
 Xem đáp án
Xem đáp án
Độ dài đường cao của hình nón cũng chính là chiều cao của tam giác đều
Đáp án cần chọn là: D
Câu 15:
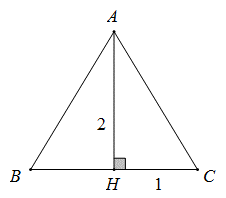
Một hình nón có bán kính đáy bằng 1, chiều cao nón bằng 2. Khi đó góc ở đỉnh của nón là thỏa mãn
 Xem đáp án
Xem đáp án
Giả sử thiết diện qua trục của hình nón đã cho là cân tại A với A là đỉnh nón, BC là đường kính đáy của nón.
Gọi H là tâm đáy nón ⇒H là trung điểm
Ta có . Ta có
Đáp án cần chọn là: C
Câu 16:
Người ta đặt được vào một hình nón hai khối cầu có bán kính lần lượt là a và 2a sao cho các khối cầu đều tiếp xúc với mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và khối cầu lớn tiếp xúc với đáy của hình nón. Bán kính đáy của hình nón đã cho là:
 Xem đáp án
Xem đáp án
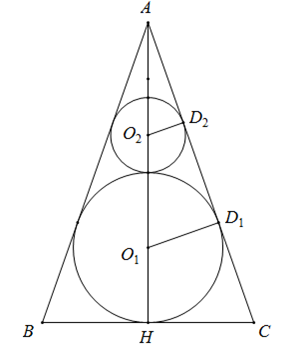
Giả sử thiết diện qua trục của hình nón là với A là đỉnh nón, BC là đường kính đáy nón.
Gọi H là tâm đường tròn đáy của hình nón, O1,O2 lần lượt là tâm của mặt cầu lớn và nhỏ, D1,D2 lần lượt là tiếp điểm của AC với (O1) và (O2).
Vì O1D1//O2D2 (cùng vuông góc với AC) nên theo hệ thức Ta – let ta có:
là trung điểm của
Xét tam giác vuông có:
Dễ thấy:
Đáp án cần chọn là: C
Câu 17:
Cho hình nón có diện tích xung quanh bằng và bán kính đáy bằng a. Tính độ dài đường sinh l của hình nón đã cho.
 Xem đáp án
Xem đáp án
Ta có:
Đáp án cần chọn là: D
Câu 18:
Cho mặt cầu tâm O bán kính R. Xét mặt phẳng (P) thay đổi cắt mặt cầu theo giao tuyến là đường tròn (C). Hình nón N có đỉnh S nằm trên mặt cầu, có đáy là đường tròn (C) và có chiều cao h (h > R). Tìm hh để thể tích khối nón được tạo nên bởi (N) có giá trị lớn nhất.
 Xem đáp án
Xem đáp án
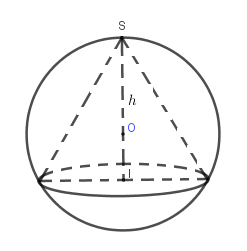
Ta có: Gọi bán kính (C) với tâm là I là r thì dễ có S phải thuộc OI và :
Tới đây ta sẽ khảo sát hàm số:
Đáp án cần chọn là: C
Câu 19:
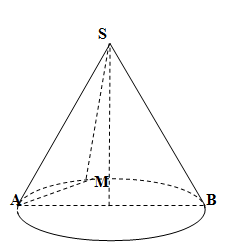
Cho hình nón đỉnh S, tâm đáy là O, góc ở đỉnh là 1350. Trên đường tròn đáy lấy điểm A cố định và điểm M di động. Tìm số vị trí M để diện tích SAM đạt giá trị lớn nhất
 Xem đáp án
Xem đáp án
Ta có:
Dấu “=” xảy ra khi
Có 2 điểm M như vậy (hai điểm đối xứng với nhau qua AB).
Đáp án cần chọn là: C
Câu 20:
Một que kem ốc quế gồm hai phần: phần kem có dạng hình cầu, phần ốc quế có dạng hình nón. Giả sử hình cầu và hình nón có bán kính bằng nhau; biết rằng nếu kem tan chảy hết thì sẽ làm đầy phần ốc quế. Biết thể tích phần kem sau khi tan chảy chỉ bằng 75% thể tích kem đóng băng ban đầu. Gọi h và r lần lượt là chiều cao và bán kính của phần ốc quế. Tính tỉ số .
 Xem đáp án
Xem đáp án
Theo đầu bài ta có bán kính của khối cầu và khối nón đều bằng r.
Từ dữ kiện đầu bài ta suy ra :
Đáp án cần chọn là: A
Câu 21:
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD); tứ giác ABCD là hình thang vuông với cạnh đáy AD,BC; AD = 3BC = 3a, AB = a,. Điểm I thỏa mãn ; M là trung điểm SD, H là giao điểm của AM và SI. Gọi E, F lần lượt là hình chiếu của A lên SB, SC. Tính thể tích V của khối nón có đáy là đường tròn ngoại tiếp tam giác EFH và đỉnh thuộc mặt phẳng (ABCD).
 Xem đáp án
Xem đáp án
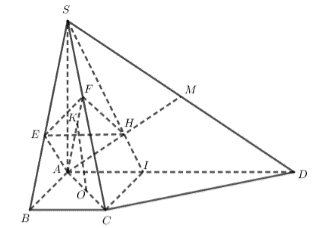
Xét tam giác SAD vuông tại A có
Lại có tam giác SAI vuông tại A có nên tam giác AHI có hay
Mà do nên
Ngoài ra,
Mà nên và AEFH là tứ giác có nên nội tiếp đường tròn tâm K là trung điểm AF đường kính AF.
Gọi O là trung điểm AC thì OK//SC, mà nên hay O chính là đỉnh hình nón và đường tròn đáy là đường tròn đường kính AF.
Ta tính AF,OK.
Xét tam giác SAC vuông tại A đường cao AF nên
Vậy thể tích
Đáp án cần chọn là: C
Câu 22:
Cho hình vuông ABCD cạnh bằng 2. Gọi M là trung điểm AB. Cho tứ giác AMCD và các điểm trong của nó quay quanh trục AD ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.
 Xem đáp án
Xem đáp án
Kéo dài CM cắt DA tại E. Quay hình thang vuông AMCD quanh trục AD ta được hình nón cụt như hình vẽ.
Quay tam giác EDC quanh trục ED ta được hình nón.
Dễ thấy V1V1 là thể tích khối nón đỉnh E, bán kính đáy DC = 2DC = 2 và V2 là thể tích khối nón đỉnh E, bán kính đáy AM = 1
Có
Vậy
Đáp án cần chọn là: C
Câu 23:
Cho tam giác ABC đều, có diện tích bằng s1 và AH là đường cao. Quay tam giác ABC quanh đường thẳng AH ta thu được hình nón có diện tích xung quanh bằng s2. Tính .
 Xem đáp án
Xem đáp án
Giả sử tam giác ABC đều cạnh a
Quay tam giác ABC quanh đường thẳng AH ta thu được hình nón có đường sinh bán kính đáy do đó diện tích xung quanh của hình nón bằng:
Vậy
Đáp án cần chọn là: B
Câu 24:
Một cái phễu có dạng hình nón có chiều cao 15(cm). Người ta đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng chiều cao ban đầu của cái phễu (hình 1). Hỏi nếu bịt kín miệng phễu rồi lộn ngược phễu lên (hình 2) thì chiều cao của nước xấp xỉ bằng bao nhiêu (làm tròn đến hàng phần nghìn).
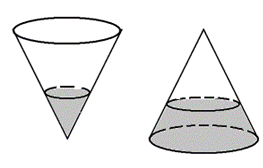
 Xem đáp án
Xem đáp án
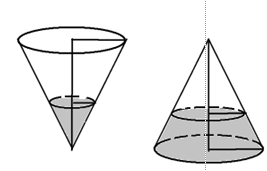
Gọi là bán kính đáy phễu, là bán kính đáy phần nước, và là chiều cao phễu và chiều cao cột nước ta có
Khi úp phễu xuống thì thể tích của phần nón không chứa nước là:
với r,h là bán kính và chiều cao của hình nón không chứa nước
Ta có
Vậy chiều cao của nước sau khi úp phếu xuống là
Đáp án cần chọn là: D
Câu 25:
Một cái phễu có dạng hình nón. Chiều cao của phễu là 20 cm. Người ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu bằng 10cm. Nếu bịt kín miệng phễu rồi lật ngược phễu lên thì chiều cao của cột nước trong phễu gần bằng với giá trị nào sau đây?
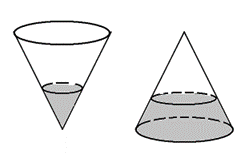
 Xem đáp án
Xem đáp án
Gọi thể tích của phễu là V, bán kính đáy phễu là R, bán kính của cột nước có dạng khối nón trong H1 là R1
Ta có:
Gọi là thể tích của nước ta có:
Sau khi úp ngược phễu lên, thể tích của phần không có nước có dạng khối nón có thể tích là
Gọi là chiều cao và bán kính đáy của khối nón không chứa nước ở H2 ta có
và :
⇒ Chiều cao của cột nước trong H2 là
Đáp án cần chọn là: C
Câu 26:
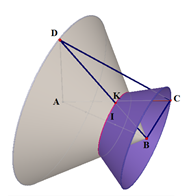
 Xem đáp án
Xem đáp án
* Xét mặt phẳng (ABD):
Gọi C’ là điểm ở trong (ABD) sao cho: C’B vuông góc AB và C’B = BC = a.
Gọi
Theo Ta – lét ta có:
Thể tích của phần chung là:
Đáp án cần chọn là: B
Câu 27:
Cho hình nón N1 có chiều cao bằng 40cm. Người ta cắt hình nón N1 bằng một mặt phẳng song song với đáy của có để được một hình nón nhỏ N2 có thể tích bằng 18 thể tích N1. Tính chiều cao h của hình nón N2?
 Xem đáp án
Xem đáp án
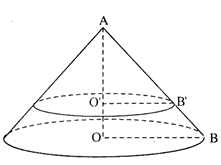
(Quan sát kí hiệu trên hình vẽ)
Áp dụng định lí Ta lét ta có:
Tỉ số thể tích giữa 2 khối nón:
Vậy chiều cao h của hình nón N2 là: 20cm.
Đáp án cần chọn là: A
Câu 28:
Một hình nón đỉnh S có bán kính đáy bằng , góc ở đỉnh là 1200. Thiết diện qua đỉnh của hình nón là một tam giác. Diện tích lớn nhất Smax của thiết diện đó là bao nhiêu?
 Xem đáp án
Xem đáp án
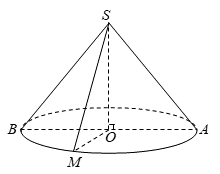
Giả sử O là tâm đáy và AB là một đường kính của đường tròn đáy hình nón.
Thiết diện qua đỉnh của hình nón là tam giác cân SAM. Theo giả thiết hình nón có bán kính đáy
nên
Xét tam giác SOA vông tại O, ta có
Diện tích thiết diện là
Do nên lớn nhất khi và chỉ khi hay khi tam giác ASM vuông cân đỉnh S (vì nên tồn tại tam giác ASM thoả mãn).
Vậy diện tích thiết diện lớn nhất là (đvdt).
Đáp án cần chọn là: A
Câu 29:
Cho hình hộp có đáy là hình thoi cạnh a và góc . Mặt chéo ACC′A′ nằm trong mặt phẳng vuông góc với đáy, đồng thời là hình thoi có góc .
Tính tan góc giữa hai mặt phẳng (BCC′B′) và (ABCD).
 Xem đáp án
Xem đáp án
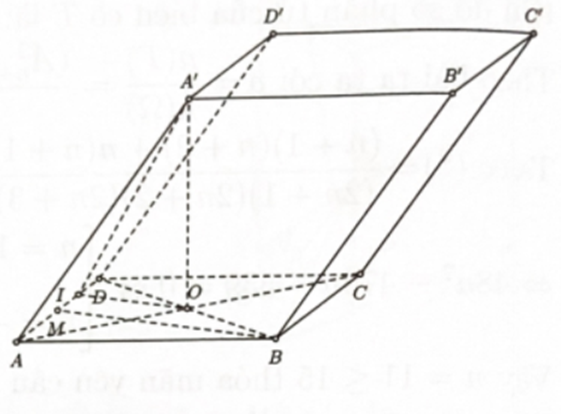
Bước 1: Xác định góc giữa hai mặt phẳng (BCC′B′) và (ABCD)
Gọi M là trung điểm AD
giác ABD I là trung điểm M D
góc giữa hai mặt phẳng (BCC′B′) và (ABCD) bằng
Bước 2: Tính
Ta có
Xét tam giác AA′O vuông tại O có:
Xét có:
Xét tam giác A′IO vuông tại O có:
Đáp án cần chọn là: A
Câu 30:
Cho hình hộp có đáy là hình thoi cạnh a và góc . Mặt chéo ACC′A′ nằm trong mặt phẳng vuông góc với đáy, đồng thời là hình thoi có góc .
Tính thể tích khối tứ diện ACB′D′.
 Xem đáp án
Xem đáp án

Bước 1: Tính
Ta có
Bước 2: Tính
Đáp án cần chọn là: C
Câu 31:
Cho hình hộp có đáy là hình thoi cạnh a và góc . Mặt chéo ACC′A′ nằm trong mặt phẳng vuông góc với đáy, đồng thời là hình thoi có góc .
Tính diện toàn phần của hình nón có đáy là đường tròn nội tiếp và chiều cao bằng chiều cao của lăng trụ.
 Xem đáp án
Xem đáp án
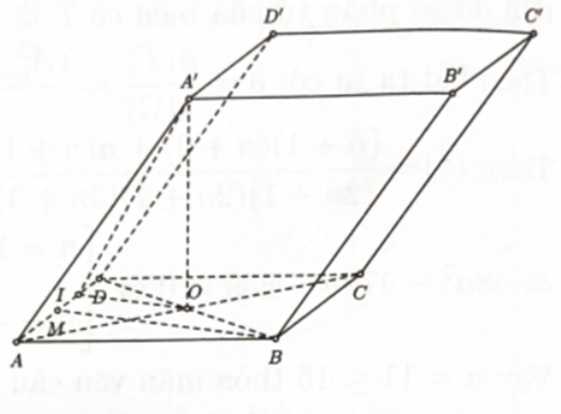
Bước 1: Tính bán kính đường tròn đáy của hình nón.
Vì đều nên tâm đường tròn nội tiếp tam giác trùng với trọng tâm của tam giác
⇒ Bán kính đường tròn đáy của hình nón là:
Bước 2: Tính diện tích xung quanh của hình nón
Vì chiều cao của hình nón bằng chiều cao của lăng trụ nên ta có độ dài đường sinh là
Vậy diện tích xung quanh của hình nón là:
Đáp án cần chọn là: C
