Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 4)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 3)
-
236 lượt thi
-
93 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
Phần tư duy đọc hiểu
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Văn bản được mở đầu bằng cách kể lại một câu chuyện ngụ ngôn.
Đúng hay sai?
 Xem đáp án
Xem đáp án
Lời giải
→ Ý kiến trên: Đúng.
- Căn cứ vào nội dung ở đoạn 3:
Sam, ông chợt nhớ lại câu chuyện ngụ ngôn này khi nghĩ tới những tấm bản đồ dẫn đường cho chúng ta.
- Văn bản được mở đầu bằng cách kể lại một câu chuyện ngụ ngôn về người đàn ông tìm kiếm chiếc chìa khoá dưới ngọn đèn đường.
Câu 2:
Tấm bản đồ dẫn đường là gì?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [4].
Lời giải
Theo thông tin đoạn [4]:
Tấm bản đồ dẫn đường là cách nhìn về cuộc đời này, bao gồm cả cách nhìn về con người. Thường thì cách nhìn này được truyền từ bố mẹ cho chúng ta, rồi qua năm tháng, được điều chỉnh theo từng hoàn cảnh sống, theo tôn giáo hay từ những kinh nghiệm của chính bản thân chúng ta…
- Phân tích, loại trừ:
Ý A: Một loại bản đồ chỉ dẫn các con đường để đi lại. Đây là một ý sai vì nó không liên quan đến nội dung. Nội dung không nói về các con đường để đi lại mà nói về các cách nhìn về cuộc sống và con người.
Ý B: Một loại bản đồ chỉ dẫn các mối quan hệ giữa con người. Đây là một ý sai vì nó quá hẹp so với khái niệm của tấm bản đồ dẫn đường. Nội dung không chỉ nói về các mối quan hệ giữa con người mà còn nói về các giá trị và niềm tin của cuộc sống.
Ý C: Một loại bản đồ chỉ dẫn các giá trị và niềm tin của cuộc sống. Đây là một ý sai vì nó cũng quá hẹp so với khái niệm của tấm bản đồ dẫn đường. Nội dung không chỉ nói về các giá trị và niềm tin của cuộc sống mà còn nói về các cách nhìn về con người.
Ý D: Một loại bản đồ chỉ dẫn các cách nhìn về cuộc sống và con người. Đây là một ý đúng vì nó phù hợp với nội dung. Nội dung nói rằng tấm bản đồ dẫn đường là cách nhìn về cuộc đời này, bao gồm cả cách nhìn về con người.
Câu 3:
Những khó khăn của “ông” khi tìm kiếm “tấm bản đồ” cho mình là gì?
Chọn các đáp án đúng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ nội dung đoạn trích.
Liên kết với những câu văn cả đoạn trích để tìm đáp án đúng.
Lời giải
Phân tích, suy luận và loại trừ:
- Bị ảnh hưởng bởi những quan điểm tiêu cực về cuộc sống, về mọi người và về chính bản thân của bố mẹ ông.
Đây là một đáp án đúng, vì nó phản ánh được nội dung của đoạn [4] và [8] trong bài đọc. Ông cho biết mẹ ông luôn nhìn cuộc đời này như một nơi đầy hiểm nguy, và bố ông cũng phần nào đồng ý với quan điểm đó. Những quan điểm tiêu cực này đã ảnh hưởng đến cách nhìn của ông về cuộc sống, về mọi người và về chính bản thân.
- Không biết cách tận dụng những trải nghiệm khó khăn để học hỏi và phát triển.
Đây là một đáp án sai, vì nó không phản ánh được nội dung của bài đọc. Ngược lại, ông đã biết cách tận dụng những trải nghiệm khó khăn để học hỏi và phát triển. Đoạn [11] trong bài đọc cho biết sau khi trải qua một tai nạn nghiêm trọng, ông đã đi vào bóng tối để tìm xem mình là ai và ý nghĩa của cuộc sống là gì. Điều này đã giúp ông tìm kiếm “tấm bản đồ” cho cuộc sống của mình.
- Không có sự tự tin và khẳng định với quan điểm của mình, bị gia đình ông cho rằng là sai lầm.
Đây cũng là một đáp án đúng, vì nó phản ánh được nội dung của đoạn [9] trong bài đọc. Ông cho biết quan điểm của mình khác biệt với gia đình, và chưa bao giờ ông cảm thấy tự tin với quan điểm của mình. Gia đình ông luôn cho rằng quan điểm của ông là hoàn toàn sai lầm, và mỗi thể nào mẹ ông cũng ngán ngầm: “Cứ chờ mà xem!”. Điều này đã khiến ông gặp khó khăn trong việc tự tin và khẳng định với quan điểm của mình.
- Không có một ngọn đèn đường nào để đứng cạnh mà tìm kiếm “tấm bản đồ” phù hợp với bản thân.
Câu 4:
Hãy tìm một cụm từ không quá hai tiếng để hoàn thành nhận định sau từ nội dung của đoạn 4:
Tấm bản đồ dẫn đường là cách nhìn về cuộc đời này và cả cách nhìn về con người. Đó chính là hai ___________ của hình ảnh ẩn dụ “tấm bản đồ” được tác giả dùng những lí lẽ và bằng chứng để thuyết phục người đọc.
 Xem đáp án
Xem đáp án
Đáp án: “khía cạnh”
Phương pháp giải
Căn cứ vào nội dung đoạn [4 ] và cách dùng từ
Lời giải
Tấm bản đồ dẫn đường là cách nhìn về cuộc đời này và cả cách nhìn về con người: Đây là một hình ảnh ẩn dụ, trong đó tấm bản đồ được dùng để biểu thị cho cách nhìn về cuộc đời và con người. Cách nhìn này có thể khác nhau tùy theo người và hoàn cảnh, giống như có nhiều tấm bản đồ khác nhau cho một vùng đất.
Đó chính là hai khía cạnh của hình ảnh ẩn dụ “tấm bản đồ”: Đây là một cách nói rằng hình ảnh ẩn dụ “tấm bản đồ” có thể được phân tích theo hai góc độ: cách nhìn về cuộc đời và cách nhìn về con người. Hai khía cạnh này liên quan chặt chẽ với nhau và ảnh hưởng lẫn nhau.
Được tác giả dùng những lí lẽ và bằng chứng để thuyết phục người đọc: Đây là một cách nói rằng tác giả không chỉ nêu ra hình ảnh ẩn dụ “tấm bản đồ” mà còn giải thích cho người đọc hiểu được ý nghĩa và tầm quan trọng của nó. Tác giả dùng những lí lẽ so sánh, nêu câu hỏi, kết luận và ví dụ để minh họa cho hai khía cạnh của hình ảnh ẩn dụ “tấm bản đồ”.
Câu 5:
Hãy xác định tương quan cách nhìn nhận về cuộc đời của “ông” và của “mẹ ông”:
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ đoạn [8] và đoạn [9] để trả lời câu hỏi.
Lời giải
Tương quan cách nhìn nhận về cuộc đời của “ông” và của “mẹ ông” là: Hoàn toàn trái ngược nhau. Bởi vì:
- Mẹ ông luôn nhìn cuộc đời này như một nơi đầy hiểm nguy, phải luôn đề phòng và cảnh giác.
- Ông lại cảm thấy yêu mến và tin tưởng tất cả mọi người xung quanh, thấy cuộc sống là chốn bình yên và an toàn.
- Mẹ ông cho rằng quan điểm của ông là hoàn toàn sai lầm và không tự tin với nó.
Câu 6:
Câu chuyện của “ông” và “mẹ ông” được nêu trong đoạn trích nhằm thể hiện:
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ đoạn [8] và đoạn [9] để trả lời câu hỏi.
Lời giải
Câu chuyện của “ông” và “mẹ ông” được nêu trong đoạn trích nhằm thể hiện: Sự bế tắc của “ông” trong việc tìm kiếm “tấm bản đồ” của riêng mình. Bởi vì:
Đoạn trích tập trung vào những khó khăn và mâu thuẫn mà “ông” gặp phải khi cố gắng tìm ra cách nhìn về cuộc đời phù hợp với bản thân.
“Ông” không thể chấp nhận quan điểm của “mẹ ông”, nhưng cũng không tự tin với quan điểm của mình, nên cảm thấy bị lạc lõng và không có hướng đi rõ ràng.
Câu 7:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Những tấm bản đồ của cuộc đời chỉ dẫn người ta đi theo những con đường khác nhau. Nếu tấm bản đồ chỉ dẫn nhấn mạnh rằng: “Cuộc sống chỉ toàn những chuỗi lo âu, đau khổ, còn niềm vui lại hiếm hoi và dễ dàng vụt mất như cánh chim trời” thì tấm bản đồ định hướng cho rằng: “Cuộc sống là một món quà quý mà chúng ta phải trân trọng”.
Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [5]
Lời giải
→ Ý kiến trên: Sai.
- Căn cứ vào nội dung ở đoạn 5:
Tấm bản đồ định hướng: “Cuộc sống chỉ toàn những chuỗi lo âu, đau khổ, còn niềm vui thì hiếm hoi và dễ dàng vụt mất như cánh chim trời
Tấm bản đồ chỉ dẫn: “Cuộc sống là một món quà quý mà chúng ta phải trân trọng”.
- Phân tích, loại trừ:
+ Tấm bản đồ định hướng: Tấm bản đồ này cho rằng cuộc sống chỉ toàn những chuỗi lo âu, đau khổ, còn niềm vui lại hiếm hoi và dễ dàng vụt mất như cánh chim trời. Đây là một cách nhìn bi quan và tiêu cực về cuộc sống. Người có tấm bản đồ này thường cảm thấy buồn chán, thất vọng, hoặc tức giận với cuộc sống. Họ không tin vào khả năng của bản thân và không có niềm tin vào tương lai. Họ thường tránh giao tiếp với người khác và không có nhiều mục tiêu hay ước mơ.
+ Tấm bản đồ chỉ dẫn: Tấm bản đồ này cho rằng cuộc sống là một món quà quý mà chúng ta phải trân trọng. Đây là một cách nhìn lạc quan và tích cực về cuộc sống. Người có tấm bản đồ này thường cảm thấy vui vẻ, biết ơn, hoặc yêu thương cuộc sống. Họ tin vào khả năng của bản thân và có niềm tin vào tương lai. Họ thường giao tiếp với người khác và có nhiều mục tiêu hay ước mơ.
Câu 8:
Nội dung chính của đoạn [5] là gì?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [5]
Lời giải
Nội dung chính của đoạn [5] là: Những tấm bản đồ khác nhau sẽ dẫn người ta đi theo những con đường khác nhau.
Đoạn 5 tập trung vào việc so sánh hai tấm bản đồ dẫn đường khác nhau về cách nhìn về cuộc đời: một tấm bản đồ nhìn cuộc đời là chuỗi lo âu và đau khổ, một tấm bản đồ nhìn cuộc đời là món quà quý giá.
Đoạn trên cho thấy hai quan điểm khác nhau này sẽ ảnh hưởng đến cảm nhận của mỗi người về cuộc sống, dù điều kiện sống có giống nhau hay không.
Câu 9:
Nội dung chính của bài đọc trên là gì?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung chính của văn bản, chú ý các nội dung và từ khoá được lặp lại trong mỗi đoạn văn.
Lời giải
Nội dung chính của bài đọc trên là: Giải thích tầm quan trọng của DHA và D3 cho sự phát triển trí não và xương của trẻ.
- Phân tích, loại trừ:
A -> sai: Bởi vì bài đọc không tập trung vào việc giới thiệu sản phẩm, mà chỉ đề cập đến một sản phẩm cụ thể ở cuối bài. Mục đích chính của bài đọc là giải thích tầm quan trọng của DHA và D3 cho sự phát triển của trẻ.
B -> đúng: Bởi vì bài đọc có hai phần chính: phần đầu giải thích lợi ích của DHA và D3 cho sự phát triển trí não, mắt, hệ miễn dịch và xương của trẻ; phần sau đưa ra các lưu ý khi bổ sung hai dưỡng chất này cho trẻ.
C -> sai: Bởi vì bài đọc không so sánh các nguồn cung cấp DHA và D3 cho trẻ từ thực phẩm và thực phẩm bảo vệ sức khỏe, mà chỉ nói về nguồn gốc của DHA từ vi tảo biển. Bài đọc không nói gì về các nguồn cung cấp D3 cho trẻ.
Câu 10:
Để trẻ có sự phát triển ________ về trí tuệ và thể chất, chế độ dinh dưỡng là ________ _______. Trẻ cần được cấp đủ các chất dinh dưỡng như năng lượng, đạm, béo, đường, vitamin, khoáng chất và xơ. Bên cạnh đó, trẻ cũng nên được __________ hai dưỡng chất quan trọng khác là DHA và vitamin D3.Bổ sung DHA và D3 sẽ giúp bé phát triển __________, phòng tránh còi xương và tăng cường hệ miễn dịch.
 Xem đáp án
Xem đáp án
Đáp án
Để trẻ có sự phát triển toàn diện về trí tuệ và thể chất, chế độ dinh dưỡng là yếu tố then chốt. Trẻ cần được cấp đủ các chất dinh dưỡng như năng lượng, đạm, béo, đường, vitamin, khoáng chất và xơ. Bên cạnh đó, trẻ cũng nên được bổ sung hai dưỡng chất quan trọng khác là DHA và vitamin D3.Bổ sung DHA và D3 sẽ giúp bé phát triển trí não, phòng tránh còi xương và tăng cường hệ miễn dịch.
Phương pháp giải
Đọc kĩ nội dung đoạn [1] và đoạn [2] và chọn từ ngữ phù hợp để điền vào chỗ trống.
Lời giải
Căn cứ vào nội dung đoạn 1 và đoạn 2:
Toàn diện: Đây là từ thích hợp để diễn tả sự phát triển về mọi mặt của trẻ, không chỉ về thể chất mà còn về trí tuệ.
Yếu tố: Đây là từ thích hợp để diễn tả vai trò của chế độ dinh dưỡng đối với sự phát triển của trẻ.
Then chốt: Đây là từ thích hợp để nhấn mạnh sự “vô cùng quan trọng” của chế độ dinh dưỡng đối với sự phát triển của trẻ.
Bổ sung: Đây là từ thích hợp để diễn tả việc cung cấp thêm cho trẻ hai dưỡng chất quan trọng là DHA và vitamin D3.
Trí não: Đây là từ thích hợp để diễn tả một trong những lợi ích của việc bổ sung DHA và D3 cho trẻ.
Dựa vào nội dung đoạn trên cùng cách sử dụng từ ngữ trong bài đọc, ta có các từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: toàn diện
- Vị trí thả 2: yếu tố
- Vị trí thả 3: then chốt
- Vị trí thả 4: bổ sung
Câu 11:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai từ nội dung của đoạn 2.
DHA có thể giúp trẻ học tốt hơn bằng cách tăng số lượng tế bào thần kinh trong não.
Đúng hay Sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ đoạn [2] và trả lời câu hỏi.
Lời giải
→ Ý kiến trên: SAI
Căn cứ vào nội dung đoạn 2:
Câu 12:
Từ nội dung của đoạn 4, việc bổ sung đầy đủ DHA có tác dụng gì đối với trẻ sơ sinh?
(Chọn các đáp án đúng)
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ đoạn [4] và chú ý các ý chính
Lời giải
Phân tích, loại trừ:
Đáp án A -> Đúng: vì DHA là thành phần chiếm đến 60% cấu trúc của võng mạc, nơi tổng chỉ huy sự nhìn của mắt.
Đáp án B -> Đúng: vì DHA có tác dụng kích thích hệ miễn dịch và giảm viêm nhiễm ở trẻ sơ sinh.
Đáp án C -> Sai: vì DHA không có tác dụng trực tiếp đối với hệ xương của trẻ sơ sinh, mà là do các chất khác như canxi, vitamin D, protein, v.v.
Câu 13:
Tại sao cha mẹ nên cho trẻ uống DHA và vitamin D3 ngay từ những ngày đầu sau sinh, đặc biệt với bé sinh non?
Chọn ba đáp án đúng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung văn bản và kiến thức bản thân.
Lời giải
Phân tích, loại trừ:
A ->Đúng: vì đây là giai đoạn quan trọng nhất cho sự phát triển của não bộ, võng mạc mắt, hệ xương và hệ miễn dịch của trẻ. Nếu thiếu DHA và vitamin D3 trong giai đoạn này, trẻ có thể gặp phải các vấn đề về sức khỏe và trí tuệ sau này.
B -> Sai: vì DHA và vitamin D3 không có tác dụng trực tiếp đối với béo phì và tiểu đường ở trẻ, mà là do các yếu tố khác như chế độ ăn uống, hoạt động thể chất, di truyền, v.v.
C -> Đúng: vì DHA là thành phần chiếm đến 60% cấu trúc của võng mạc và 20% cấu trúc của não bộ, giúp trẻ hoàn thiện chức năng nhìn và tư duy. Vitamin D3 là chất dẫn để hấp thu canxi, giúp trẻ tăng cường xương và răng. Cả hai dưỡng chất này còn giúp tăng cường hệ miễn dịch và giảm viêm nhiễm ở trẻ.
Câu 14:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Chỉ nên bổ sung DHA từ vi tảo biển cho trẻ sơ sinh vì trong vi tảo có chứa DHA tinh khiết, do đó chúng sẽ phù hợp với cơ địa của trẻ sơ sinh.
Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [7]
Lời giải
→ Ý kiến trên: SAI
Bổ sung DHA từ vi tảo biển cho trẻ sơ sinh có thể cải thiện thị lực và phát triển não bộ của trẻ Tuy nhiên, không phải chỉ có vi tảo biển mới là nguồn cung cấp DHA cho trẻ sơ sinh. Các sản phẩm bổ sung DHA từ cá hoặc các loại thực phẩm giàu DHA như cá hồi, cá ngừ, cá trích cũng có thể giúp bổ sung DHA cho trẻ sơ sinh
Câu 15:
VitaDHA Baby Drops có những lợi ích gì cho trẻ sơ sinh và trẻ nhỏ?
Chọn 2 đáp án đúng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn trích
Lời giải
Những lợi ích VitaDHA Baby Drops mang lại cho trẻ sơ sinh và trẻ nhỏ là: Bổ sung DHA cho não bộ và thị lực và Bổ sung vitamin E cho da và tóc
- Giải thích, suy luận:
+ A -> đúng: vì DHA là một axit béo thuộc nhóm acid béo Omega-3 rất cần thiết cho sự phát triển trí não, thị giác của trẻ. DHA chiếm 20% khối lượng não, loại acid béo này hỗ trợ sự phát triển hệ thần kinh và não ở trẻ, giúp tăng cường trí thông minh (IQ) cho trẻ, ngăn ngừa mắc các bệnh về hành vi và khuyết tật hay thiểu năng, tự kỷ. DHA cũng đóng vai trò quan trọng trong sự phát triển của võng mạc mắt, giúp bé có thị lực tốt hơn.
+ B -> sai: vì VitaDHA Baby Drops không có thành phần sắt. Sắt là một khoáng chất cần thiết cho sự hình thành hồng cầu trong máu và vận chuyển oxy đến các cơ quan trong cơ thể. Sắt cũng có vai trò trong việc tăng cường hệ miễn dịch và chống nhiễm trùng. Tuy nhiên, sắt không có trong sản phẩm này.
+ C -> đúng: vì VitaDHA Baby Drops có chứa vitamin E. Vitamin E là một hợp chất hòa tan trong chất béo, đóng vai trò quan trọng đối với cơ thể trong việc chuyển hóa các dưỡng chất, hỗ trợ cơ thể hấp thu các chất khác một cách tốt nhất. Vitamin E cũng có tác dụng chống oxy hóa tế bào, giúp củng cố da, tóc, móng và giúp bé có đôi mắt sáng khỏe hơn.
Câu 16:
Dựa trên dữ liệu trong hình 1 và hình 2, nhận định nào sau đây phù hợp nhất về nồng độ trung bình trong huyết tương và điểm số triệu chứng trung bình theo thời gian sau khi dùng thuốc?
 Xem đáp án
Xem đáp án
Phương pháp giải
Kết hợp xem hình 1 và hình 2
Lời giải
Theo hình 2, phải mất 1 khoảng thời gian để thuốc bắt đầu phát huy tác dụng, sau đó thuốc phát huy tác dụng, các triệu chứng giảm đi trong 1 khoảng thời gian, sau đó các triệu chứng trở lại (có thể là thuốc bắt đầu trơ đi và mất tác dụng)
Hơn nữa, theo hình 1 cho thấy sự thuyên giảm triệu chứng tỉ lệ nghịch với nồng độ thuốc trong cơ thể
=> Nồng độ trung bình trong huyết tương tăng sau đó giảm và điểm số triệu chứng trung bình giảm sau đó tăng.
Câu 17:
Theo hình 1, nồng độ trung bình trong huyết tương của thành phần A được sử dụng ở dạng phóng thích tức thời tăng nhiều nhất trong khoảng thời gian nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào hình 1
Lời giải
Câu 18:
Nhận định nào sau đây đúng hay sai
Nồng độ trong huyết tương trung bình của thành phần B được sử dụng dưới dạng viên nang phóng thích tức thời luôn thấp hơn nồng độ trong huyết tương trung bình của thành phần A trong khoảng 24 giờ sau khi dùng thuốc, đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào hình 1
Lời giải
Theo hình 1, nồng độ trong huyết tương trung bình của thành phần B được sử dụng dưới dạng viên nang phóng thích hoạt chất tức luôn thấp hơn nồng độ trong huyết tương trung bình của thành phần A trong khoảng 24 giờ sau khi dùng thuốc
Câu 19:
Điểm triệu chứng của một đối tượng thử nghiệm lâm sàng được dùng viên nang dạng giải phóng kéo dài của thuốc theo toa không thay đổi trong 8 giờ. Dựa vào bảng 2, khoảng thời gian đó rất có thể bắt đầu sau bao lâu sử dụng thuốc?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào bảng 2
Lời giải
Dựa vào hình 2, ta dễ dàng nhận thấy khoảng thời gian sau 14 giờ sử dụng đến 22 giờ sau sử dụng có đường cong với độ dốc thay đổi ít nhất
=> Điểm triệu chứng của một đối tượng thử nghiệm lâm sàng được dùng viên nang dạng giải phóng kéo dài của thuốc theo toa không thay đổi trong khoảng thời gian này.
Câu 20:
Giả sử thành phần A có tác dụng phụ là làm người sử dụng có cảm giác buồn nôn và chỉ có tác dụng khi đạt nồng độ trong huyết tương trung bình trên 25 ng/ml. Một người sử dụng thuốc có chứa viên nén nêu trên, nhận định nào sau đây chính xác?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào bảng 1
Lời giải
Vì sau khoảng 8 giờ nồng độ trong huyết tương trung bình của thành phần A đạt khoảng 25 ng/ml, và sau khoảng 10 giờ sẽ giảm xuống dưới mức 25 ng/ml
=> Người sử dụng viên nén nêu trên sau khoảng 8 giờ sử dụng sẽ cảm thấy buồn nôn và hết sau khoảng 10 giờ.
Câu 21:
Điền đáp án chính xác vào chỗ trống
Phần trăm cá thể ở lứa tuổi trước sinh sản của quần thể trước khi bị săn bắt là: _________%
 Xem đáp án
Xem đáp án
Đáp án: “51”
Phương pháp giải
Dựa vào kết quả điều tra
Lời giải
Trước và sau khi bị săn bắt đều không thấy xuất hiện nhóm tuổi sau sinh sản. Trước khi bị săn bắt, quần thể có 51% cá thể ở lứa tuổi trước sinh sản, 49% cá thể ở lứa tuổi sinh sản => Đặc điểm đặc trưng của loài
Câu 22:
Nhận xét nào đúng về kích thước quần thể sau 2 năm bị khai thác?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào kết quả điều tra
Lời giải
Sau hai năm bị săn bắt, số cá thể ở lứa tuổi sinh sản giảm mạnh => chủ yếu khai thác nhóm tuổi trưởng thành => Tỷ lệ nhóm tuổi thay đổi, quần thể có 75% cá thể ở lứa tuổi trước sinh sản, 25% cá thể ở lứa tuổi sinh sản.
Kích thước quần thể ít biến động (trước khai thác: 3062, sau hai năm khai thác: 3021)
=> việc khai thác nằm trong khả năng tự phục hồi của quần thể
Câu 23:
Nếu việc săn bắt dừng lại, thành phần nhóm tuổi của quần thể sẽ như thế nào? Biết khi dừng khai thác thì mật độ quần thể tăng lên?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào kết quả điều tra
Lời giải
Khi dừng khai thác, mật độ quần thể tăng => quần thể tự điều chỉnh, giảm khả năng sinh sản của các cá thể => số lượng cá thể giảm => quần thể quay lại tỷ lệ nhóm tuổi ban đầu
Câu 24:
Điền đáp án phù hợp vào chỗ trống
Theo WHO, béo phì là do tích tụ __________ quá mức trong cơ thể.
 Xem đáp án
Xem đáp án
Đáp án: “chất béo”
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Thừa cân và béo phì được WHO (tổ chức y tế thế giới) định nghĩa là sự tích tụ chất béo bất thường hoặc quá mức có thể làm giảm sức khỏe.
Câu 25:
Nhận định dưới đây đúng hay sai?
Theo bảng 1, ở tất cả các nhóm tuổi, tỉ lệ béo phì đều tăng dần qua các năm từ 2007 đến 2016.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Nhận định trên không đúng
Vì ở nhóm 6-11 tuổi, ta nhận thấy tỉ lệ béo phì giảm dần qua các năm từ 2007 đến 2016.
Câu 26:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Theo bảng 1, trong giai đoạn nghiên cứu, nhóm tuổi luôn có tỉ lệ béo phì cao nhất là 20-74 tuổi.
Câu 27:
Theo bảng 1, trong giai đoạn nghiên cứu, nhóm tuổi có biến động về tỉ lệ béo phì thấp nhất qua các năm là?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Nhóm tuổi 2-5: chỉ số biến động 13,9% - 8,4% = 5,5
Nhóm tuổi 6-11: chỉ số biến động 19,6% - 17,4% = 2,2
Nhóm tuổi 12-19: chỉ số biến động 20,6% - 18,1% = 2,5
Nhóm tuổi 20 – 74: chỉ số biến động 39,6% - 33,7% = 5,9
Nhóm tuổi có biến động về tỉ lệ béo phì thấp nhất qua các năm là nhóm tuổi 6-11
Câu 28:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin bảng 1
Lời giải
Dung dịch có pH càng lớn thì có tính bazo càng mạnh
Câu 29:
Dãy dung dịch được sắp xếp theo chiều tăng dần tính axit là
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin bảng 1
Lời giải
Dung dịch có tính axit cành mạnh thì pH càng nhỏ
=> Chiều sắp xếp giảm dần giá trị pH là bột giặt, giấm, nước chanh, nước tẩy rửa bồn cầu
Câu 30:
Bạn sinh viên sẽ cố gắng tô màu trong hình 1 bằng màu thích hợp mà chất chỉ thị sẽ chuyển sang các độ pH khác nhau. Từ trái sang phải của hình 1, thứ tự màu sắc được thể hiện đúng là
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin bảng 1
Lời giải
Ở bảng 1 liệt kê các hoá chất có độ pH từ thấp nhất đến cao nhất
=> Liệt kê các màu tương ứng với các giá trị pH tăng dần này theo thứ tự danh sách trong bảng 1
Câu 31:
Chọn đúng/ sai cho kết quả ở thí nghiệm 2 (Đúng nếu có phản ứng tạo bọt khí xảy ra, sai nếu không có phản ứng tạo bọt khí xảy ra)
|
|
ĐÚNG |
SAI |
|
Nước tẩy rửa bồn cầu |
||
|
Nước ngọt có gas |
||
|
Nước chanh |
||
|
Giấm |
||
|
Nước |
||
|
Bột nở |
||
|
Bột giặt |
||
|
Nước thông cống |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Nước tẩy rửa bồn cầu |
X | |
|
Nước ngọt có gas |
X | |
|
Nước chanh |
X | |
|
Giấm |
X | |
|
Nước |
X | |
|
Bột nở |
X | |
|
Bột giặt |
X | |
|
Nước thông cống |
X |
Phương pháp giải
Xem thành phần trong muối nở gồm chất gì và có tính chất gì
Lời giải
Muối nở chứa thành phần NaHCO3 có phản ứng tạo bọt khí khi tác dụng với dung dịch có tính axit
Câu 32:
2-4, 8-10, nước ngọt có gas đến giấm, muối nở đến nươc thông cống
Chất chỉ thị vạn năng là chất chỉ thị pH chứa hỗn hợp của một số chất chỉ thị khác nhau có màu sắc thay đổi rõ rệt trong các phạm vi khác nhau của thang đo pH để cho biết chính xác độ pH của bất kỳ dung dịch nào. Mặc dù chất chỉ thị bắp cải tím là một chất chỉ thị tốt cho hầu hết các độ pH, nhưng nó có một phạm vi không có sự thay đổi màu đủ mạnh để cho biết chính xác độ pH trong vùng của _______________.Vì vậy cần bổ sung thêm một chất chỉ thị bổ sung khác. Khoảng pH _________
mà chất chỉ thị bổ sung có màu sắc thay đổi mạnh để cải thiện chất chỉ thị bắp cải tím
 Xem đáp án
Xem đáp án
Đáp án
Chất chỉ thị vạn năng là chất chỉ thị pH chứa hỗn hợp của một số chất chỉ thị khác nhau có màu sắc thay đổi rõ rệt trong các phạm vi khác nhau của thang đo pH để cho biết chính xác độ pH của bất kỳ dung dịch nào. Mặc dù chất chỉ thị bắp cải tím là một chất chỉ thị tốt cho hầu hết các độ pH, nhưng nó có một phạm vi không có sự thay đổi màu đủ mạnh để cho biết chính xác độ pH trong vùng của nước ngọt có gas đến giấm.Vì vậy cần bổ sung thêm một chất chỉ thị bổ sung khác. Khoảng pH 2 - 4 mà chất chỉ thị bổ sung có màu sắc thay đổi mạnh để cải thiện chất chỉ thị bắp cải tím
Phương pháp giải
Dựa vào bảng 1 tìm khoảng pH khi dùng chất chỉ thị bắp cải tím không làm thay đổi màu sắc nhiều
Lời giải
Từ bảng 1 có chất chỉ thị bắp cải tím không thay đổi nhiều màu sắc từ độ pH của nước ngọt có gas (2,5) đến giấm (4,5)
Câu 33:
Một chất chỉ thị mới, được gọi là Methyl Red, cũng được sử dụng để kiểm tra các hóa chất gia dụng từ Thí nghiệm 1 và 2. Người ta nhận thấy rằng chất chỉ thị chuyển sang màu đỏ khi có chất tẩy rửa bồn cầu, nước ngọt có ga hoặc nước chanh; nó chuyển sang màu cam khi có giấm; nó chuyển sang màu vàng khi có mặt các hóa chất còn lại. Khoảng pH nào có nhiều khả năng nhất chứa giá trị pH mà tại đó Methyl Red có sự chuyển màu, hoặc pH tại đó chất chỉ thị sẽ hết màu đỏ và chuyển sang màu vàng?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào bảng 1 và thông tin đề bài cho
Lời giải
Theo thông tin đề bài cho có khoảng pH cần tìm có nhiều khả năng nhất chứa giá trị pH mà tại đó Methyl Red có sự chuyển màu hay chất chỉ thị sẽ hết màu đỏ và chuyển sang màu vàng
Mà Methyl Red chuyển sang màu đỏ khi có chất tẩy rửa bồn cầu, nước ngọt có ga hoặc nước chanh; nó chuyển sang màu cam khi có giấm; nó chuyển sang màu vàng khi có mặt các hóa chất còn lại
=> Khoảng pH cần tìm xung quanh độ pH của giấm
Theo bảng 1 độ pH của giấm là 4,5
Câu 34:
Điền số thích hợp vào chỗ trống sau:
Theo đoạn văn, ngôi nhà ____________ có nhiều khả năng có bếp ga được điều chỉnh kém
 Xem đáp án
Xem đáp án
Đáp án: “1”
Phương pháp giải
Dựa vào đoạn văn và bảng 1
Lời giải
Đoạn văn nói rằng, “Mức độ gần bếp ga được điều chỉnh đúng cách thường là 5,0 đến 15,0 ppm và những mức độ gần bếp được điều chỉnh kém có thể là 30,0 ppm hoặc cao hơn.”
Câu 35:
Phát biểu sau đây đúng hay sai?
Một thiết bị cảm biến đã được cài đặt trong Nhà 2 để kiểm tra mức CO. Kết quả cho thấy lượng khí thải CO dưới mức trung bình
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào bảng 1 về số liệu liên quan đến nhà 2
Lời giải
Theo Bảng 1, Nhà 2 có mức CO từ 15,0 đến 25,0 ppm. Đoạn văn nói rằng mức CO trung bình trong những ngôi nhà không có bếp ga là từ 0,5 đến 5,0 ppm, có nghĩa là mức CO trong Nhà 2 ở trên mức trung bình.
Câu 36:
Theo đoạn văn, mức độ carbon monoxide nào sau đây sẽ được coi là có hại nhất?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn văn
Lời giải
Đoạn văn nói rằng, “Mức gần bếp gas được điều chỉnh đúng cách thường là 5,0 đến 15,0 ppm và mức gần bếp được điều chỉnh kém có thể là 30,0 ppm hoặc cao hơn. Mức CO từ 0,5 đến 15,0 ppm được coi là an toàn.”
Câu 37:
Phát biểu sau đây đúng hay sai?
Theo đoạn văn, nếu Nhà 4 có bếp ga thì nên bỏ đi
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn văn
Lời giải
Câu 38:
Giả sử một ngôi nhà thứ 6 được kiểm tra carbon monoxide và kết quả cho thấy mức carbon monoxide là 10,0 ppm. Theo đoạn văn, kết luận nào sau đây có thể đạt được?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn văn
Lời giải
Câu 39:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào kiến thức thực tế
Lời giải
Câu 40:
Điền từ/cụm từ vào chỗ trống:
Trong thí nghiệm 1, khi khối lượng quả nặng tăng lên thì vị trí cân bằng của nó dịch chuyển sang _______
 Xem đáp án
Xem đáp án
Đáp án: “trái | bên trái”
Phương pháp giải
Quan sát hình ảnh và bảng số liệu 1
Vận dụng kiến thức đã học về cân bằng vật rắn
Lời giải
Cách 1:
Ta có trọng lượng được xác định bằng công thức: P = mg
⇒khi khối lượng tăng lên thì trọng lượng của vật cũng tăng lên
Theo bảng số liệu 1 ta thấy rằng khi trọng lượng vật tăng lên thì vị trí cân bằng của vật sẽ dịch sang phía bên trái.
Cách 2:
Câu 41:
Câu nào sau đây so sánh Thí nghiệm 1 với Thí nghiệm 2 là SAI?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin từ đề bài
Lời giải
Từ các thí nghiệm và số liệu ta bài ta thấy rằng:
- Thí nghiệm 1 đã sử dụng các khối đã biết trọng lượng; Thí nghiệm 2 đã sử dụng khối chưa biết trọng lượng.
- Thí nghiệm 1 liên quan đến một vị trí điểm tựa cố định; Thí nghiệm 2 liên quan đến một điểm tựa có thể di chuyển.
- Thí nghiệm 1 và 2 liên quan đến các trọng lượng tạo ra mô-men xoắn bằng nhau ở cả hai bên của điểm tựa.
Câu 42:
Giả sử nếu học sinh thực hiện Thí nghiệm 2 trên Sao Hỏa, ở đó gia tốc do trọng trường bằng 3,7m/s2. Kết quả của thí nghiệm sẽ:
|
|
ĐÚNG |
SAI |
|
Có thay đổi, vì trọng lượng của các khối sẽ thay đổi. |
||
|
Có thay đổi, bởi vì mối quan hệ giữa trọng số của các khối sẽ thay đổi. |
||
|
Không thay đổi, vì trọng lượng của các khối sẽ không thay đổi. |
||
|
Không thay đổi, bởi vì mối quan hệ giữa trọng lượng của các khối sẽ không thay đổi. |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Có thay đổi, vì trọng lượng của các khối sẽ thay đổi. |
X | |
|
Có thay đổi, bởi vì mối quan hệ giữa trọng số của các khối sẽ thay đổi. |
X | |
|
Không thay đổi, vì trọng lượng của các khối sẽ không thay đổi. |
X | |
|
Không thay đổi, bởi vì mối quan hệ giữa trọng lượng của các khối sẽ không thay đổi. |
X |
Phương pháp giải
Dựa vào thông tin bài cung cấp và kiến thức đã học về lực
Lời giải
Câu 43:
Giả sử rằng học sinh đã sử dụng một khối khác trong Thí nghiệm 1 và vị trí của khối đó là 0,5675 m. Trọng lượng của khối rất có thể là:
 Xem đáp án
Xem đáp án
Phương pháp giải
Quan sát hình ảnh và bảng số liệu 1
Vận dụng kiến thức đã học về cân bằng vật rắn
Lời giải
Ta có r = 0,5675m < 0,575m - là khoảng cách của khối có trọng lượng là 60N
Mà ta trọng lượng của vật càng tăng khi vị trí cân bằng của vật sẽ càng dịch sang phía bên trái
Câu 44:
Dựa vào kết quả của thí nghiệm 2, hãy cho biết thứ tự đúng của 4 khối từ khối lượng lớn nhất đến khối lượng nhỏ nhất là bao nhiêu?
 Xem đáp án
Xem đáp án
Phương pháp giải
Quan sát hình ảnh và bảng số liệu 2
Vận dụng kiến thức đã học về cân bằng vật rắn
Lời giải
Câu 45:
Đơn vị nào sau đây viết đúng đơn vị của momen lực trong những thí nghiệm này?
 Xem đáp án
Xem đáp án
Phương pháp giải
Quan sát hình ảnh và bảng số liệu 2
Vận dụng kiến thức đã học về cân bằng vật rắn
Lời giải
Câu 46:
Giả sử rằng học sinh từ Thí nghiệm 1 tác dụng một lực nhỏ hướng lên trên thước đo ở phía bên trái của đòn bẩy. Điều này có ảnh hưởng gì, nếu có, đối với vị trí cân bằng của các quả nặng trong thí nghiệm này?
 Xem đáp án
Xem đáp án
Phương pháp giải
Quan sát hình ảnh và bảng số liệu 1
Vận dụng kiến thức đã học về cân bằng vật rắn
Lời giải
Câu 47:
Trong nghiên cứu 2, sử dụng quả nặng có trọng lượng 10N và lực đó phân bố đều giữa các cân A và B, các nhận xét sau đây đúng hay sai?
|
|
ĐÚNG |
SAI |
|
Trọng lực vật nặng phân bố đều trong lần thứ 4 |
||
|
Trọng lực vật nặng phân bố đều trong lần thứ 5 |
||
|
Trọng lực vật nặng phân bố đều trong lần thứ 6 |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Trọng lực vật nặng phân bố đều trong lần thứ 4 |
X | |
|
Trọng lực vật nặng phân bố đều trong lần thứ 5 |
X | |
|
Trọng lực vật nặng phân bố đều trong lần thứ 6 |
X |
Phương pháp giải
Phân tích các thông tin từ bài cung cấp
Lời giải
Quan sát hình 4 ta thấy được: trong lần thử nghiệm thứ 5, kim chỉ thị trên mặt cân của 2 cân chỉ cùng một giá trị.
Câu 48:
Dựa trên kết quả của Thử nghiệm 1 và 2, cân A và cân B có trọng lượng ________
 Xem đáp án
Xem đáp án
Đáp án: “5N | 5 N”
Phương pháp giải
Phân tích các thông tin từ bài cung cấp
Lời giải
Xét thử nghiệm (1):
- Cân A chưa có vật nặng ⇒ trọng lượng lúc này của cân A là 0N
- Cân B đặt phía dưới và kim chỉ thị quay \(\frac{1}{4}\)⇒ là trọng lượng của cân A
Xét thử nghiệm 2:
- Vật nặng có trọng lượng 5N đặt lên cân A⇒lúc này kim chỉ thị của cân quay \(\frac{1}{4}\) vòng
- Đồng thời kim của cân B quay được \(\frac{1}{2}\) vòng
Từ các số liệu đã quan sát được ta thấy rằng khi đặt một vật 5,0 N lên một trong 2 chiếc cân giống nhau thì kim của chiếc cân đó quay được 1/4 quãng đường quanh mặt số của chiếc cân.
Đồng thời ta rút ra được Cân A nặng 5,0 N vì khi đó nó được đặt trên Cân B, kim của Cân B quay được 1/4 vòng quay của Cân B.
Câu 49:
Giả sử rằng mỗi khi đặt một quả nặng lên mặt cân thì một lò xo bên trong cân bị nén lại. Cũng giả sử rằng trọng lượng thêm vào càng lớn thì lượng nén càng lớn. Lượng thế năng dự trữ trong lò xo của cân A lớn hơn trong Thử nghiệm 1 hay trong Thử nghiệm 3?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích các thông tin từ bài cung cấp
Vận dụng lí thuyết về thế năng của con lắc lò xo
Lời giải
Ta có công thức xác định thế năng \({{\rm{W}}_t} = \frac{1}{2}k{{\rm{x}}^2}\)
ta thấy rằng khi lò xo bị nén càng nhiều thì thế năng dự trữ trong lò xo càng lớn
Từ đề bài ta cũng có khi trọng lượng trên mặt cân càng lớn thì lượng nén ở lò xo càng lớn
Câu 50:
Trong một nghiên cứu mới, giả sử cân A được đặt lộn ngược trên cân B, sao cho mặt cân của cân A nằm trực tiếp trên mặt cân của cân B. Hình vẽ nào sau đây thể hiện đúng nhất kết quả có khả năng thu được nhất cho sự sắp xếp này?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích các thông tin từ bài cung cấp
Lời giải
Từ kết quả của nghiên cứu 1 ta thấy được mỗi cân có trọng lượng 5N và kim sẽ quay theo chiều kim đồng hồ.
Câu 51:
Trong Nghiên cứu 2, khi khoảng cách giữa quả nặng 10,0 N và chiếc bút chì trên mặt cân B tăng lên, thì lực tác dụng lên bề mặt của cân B:
|
|
ĐÚNG |
SAI |
|
giữ nguyên |
||
|
tăng lên |
||
|
giảm đi |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
giữ nguyên |
X | |
|
tăng lên |
X | |
|
giảm đi |
X |
Phương pháp giải
Phân tích các thông tin từ bài cung cấp
Lời giải
Quan sát nghiên cứu 2 ta có kết luận sau:
(1) Khi lực tác dụng lên mặt cân của Cân B là lớn nhất (Thử nghiệm 4) thì khoảng cách giữa quả cân và bút chì là nhỏ nhất (0,10 m).
(2) Khi lực tác dụng lên mặt cân của Cân B là nhỏ nhất (Thử nghiệm 6) thì khoảng cách giữa quả cân và bút chì là lớn nhất (0,30 m).
Câu 52:
Phát biểu nào sau đây rất có thể mô tả lý do quan trọng cho việc phải điều chỉnh số chỉ của kim về số 0 sau Nghiên cứu 1, trước mỗi Thử nghiệm 4-6?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích các thông tin từ bài cung cấp
Lời giải
Câu 53:
Học sinh đặt một chồng sách lên cân và kim chỉ thị quay đến giá trị 15N. Khối lượng của chồng sách đó là bao nhiêu, lấy g = 10m/s2
 Xem đáp án
Xem đáp án
Phương pháp giải
Áp dụng công thức tính P = mg
Lời giải
Ta có kim chỉ 15N hay trọng lượng của chồng sách đó là 15N
Vậy khối lượng của chồng sách được xác định như sau: \(m = \frac{P}{g} = \frac{{15}}{{10}} = 1,5\;{\rm{kg}}\)
Chọn C
Câu 54:
Xét tính chẵn lẻ của 3 hàm số sau đây:
\[f(x) = \frac{{|x - 1| - |x + 1|}}{{ - x}}\]
\[g(x) = {x^2}(|x + 1| - |x - 1|)\]
\[h(x) = {x^3} - x + 1\]
Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Phương pháp giải
Áp dụng định nghĩa về tính chẵn lẻ của 1 hàm số
Tính f(-x), g(-x), h(-x) và kết luận
Đại cương về hàm số
Lời giải
Xét hàm số f(x)
Ta có \(f( - x) = \frac{{| - x - 1| - | - x + 1|}}{x} = \frac{{|x + 1| - |x - 1|}}{x}\)
\( = \frac{{|x - 1| - |x + 1|}}{{ - x}} = f(x)\)
⇒ f là hàm số chẵn
Xét hàm số g(x)
\(\begin{array}{l}g( - x) = {( - x)^2}(| - x + 1| - | - x - 1|)\\ = {x^2}(|x - 1| - |x + 1|)\\ = - {x^2}(|x + 1| - |x - 1|)\\ = - g(x)\end{array}\)
⇒ g là hàm số lẻ
Xét hàm số h(x)
\(\left. {\begin{array}{*{20}{l}}{h( - x) = {{( - x)}^3} + x + 1 = - {x^3} + x + 1}\\{ - h(x) = - {x^3} + x - 1}\end{array}} \right\} \Rightarrow \) h là hàm số không chẵn không lẻ
Chọn C
Câu 55:
Tập hợp các giá trị của tham số m để hàm số \(y = 2{x^2} + 2mx - 2m + 1\) đồng biến trên khoảng (3;+∞) là
 Xem đáp án
Xem đáp án
Phương pháp giải
Bước 1: Tìm khoảng đồng biến của hàm số đã cho bằng cách sử dụng kiến thức: Hàm số \(y = a{x^2} + bx + c(a > 0)\) đồng biến trên khoảng \(\left( { - \frac{b}{{2a}}; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\).
Bước 2: Tìm \(m\) bằng cách sử dụng kiến thức: Để hàm số đã cho đồng biến trên khoảng \((3; + \infty )\) thì \((3; + \infty ) \subset \left( { - \frac{b}{{2a}}; + \infty } \right)\). Tức là, \( - \frac{b}{{2a}} \le 3\).
Bước 3: Kết luận.
Lời giải
Ta có \( - \frac{b}{{2a}} = - \frac{{2m}}{{2.2}} = - \frac{m}{2}\).
Suy ra hàm số \(y = 2{x^2} + 2mx - 2m + 1\) đồng biến trên khoảng \(\left( { - \frac{m}{2}; + \infty } \right)\).
Hàm số đã cho đồng biến trên khoảng \((3; + \infty )\) khi và chỉ khi \((3; + \infty ) \subset \left( { - \frac{m}{2}; + \infty } \right)\).
Tức là, \( - \frac{m}{2} \le 3\).
\( \Leftrightarrow m \ge - 6.{\rm{ }}\)
Vậy \(m \in [ - 6; + \infty )\) thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án B.
Câu 56:
Có bao nhiêu giá trị nguyên âm của tham số m để hàm số \({f_{(x)}} = \sqrt {(m + 4){x^2} - (m - 4)x - 2m + 1} \) xác định \(\forall x \in R\)?
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm ĐKXĐ của biểu thức chứa dấu căn bậc 2
Giải bất phương trình trên tập \(\forall x \in R\) và biện luận giá trị của m
Lời giải
\({f_{(x)}}\) xác định \(\forall x \in R \Leftrightarrow (m + 4){x^2} - (m - 4)x - 2m + 1 \ge 0\forall x \in R\)
Đặt \({g_{(x)}} = (m + 4){x^2} - (m - 4)x - 2m + 1\)
Xét \(m = - 4:{g_{(x)}} = 8x + 9 \le 0 \Leftrightarrow x \le \frac{{ - 9}}{8}\) (loại)
Xét \(m \ne - 4:{g_{(x)}} \ge 0\forall x \in R \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m > 4}\\{{{(m - 4)}^2} - 4(m + 4)( - 2m + 1) \le 0}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m > - 4}\\{9{m^2} + 20m \le 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m > - 4}\\{\frac{{ - 20}}{9} \le m \le 0}\end{array} \Leftrightarrow \frac{{ - 20}}{9} \le m \le 0} \right.} \right.\)
Mà \(m\) nguyên âm \( \Rightarrow m \in \{ - 2; - 1\} \Rightarrow \) Có 2 giá trị của \(m\) thỏa mãn
Chọn B
Câu 57:
Cho \(f(x) = m{x^2} - 2mx + 4\). Tập hợp tất cả các giá trị của tham số \(m\) để \(f(x) > 0,\forall x \in \mathbb{R}\) là
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
TH 1: \(m = 0:f(x) = 4 > 0,\forall x \in \mathbb{R}\) (đúng) \( \Rightarrow m = 0\) thỏa mãn.
TH 2: Yêu cầu bài toán \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a > 0}\\{{\Delta ^\prime } < 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m > 0}\\{{m^2} - 4m < 0}\end{array} \Leftrightarrow m \in (0;4)} \right.} \right.\).
Vậy \(m \in [0;4)\).
⇒ Chọn đáp án D
Câu 58:
Số nghiệm nguyên của bất phương trình \(\frac{{{x^2} - 4x + 3}}{{{x^2} - 16}} \le 0\) là
 Xem đáp án
Xem đáp án
Phương pháp giải
Dấu của tam thức bậc hai
Lời giải
Đặt \(M = \frac{{{x^2} - 4x + 3}}{{{x^2} - 16}}\).
Ta có:
+) \({x^2} - 4x + 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = 3}\end{array}} \right.\)
+) \({x^2} - 16 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 4}\\{x = - 4}\end{array}} \right.\)
Bảng xét dấu biểu thức M:

Vậy tập nghiệm của bất phương trình đã cho là S = (−4;1] ∪ [3;4)
Vậy có 6 nghiệm nguyên.
Câu 59:
Tìm m để phương trình \(\sqrt {{x^2} - 2{\rm{x}} + m} = 2x + 1\) có nghiệm?
 Xem đáp án
Xem đáp án
Phương pháp giải
- Biết đổi phương trình để cô lập m có dạng m = g(x)
- Khảo sát và vẽ bảng biến thiên g(x)
- Quan sát bảng biến thiên g(x)để chọn mthỏa mãn
Phương trình chứa căn cơ bản
Lời giải
Ta có \(\sqrt {{x^2} - 2x + m} = 2x + 1\)
Điều kiện \({x^2} - 2x + m \ge 0 \Rightarrow m \ge 1\)
\(\begin{array}{l} \Leftrightarrow {x^2} - 2x + m = 4{x^2} + 4x + 1\\ \Leftrightarrow m = 3{x^2} + 6x + 1\end{array}\)
Đặt \(g(x) = 3{x^2} + 6x + 1 \Rightarrow g'(x) = 6x + 6\)
\(g'(x) = 0 \Rightarrow x = - 1\)
Ta có bảng biến thiên g(x)
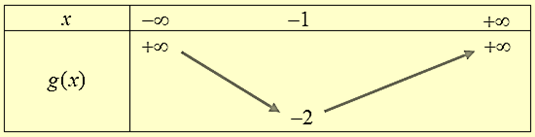
⇒ m ≥ −2 thì phương trình có nghiệm
Kết hợp điều kiện m ≥ 1
Câu 60:
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
Hàm số \(y = 3\sin \frac{x}{2}\) tuần hoàn với chu kì π. |
¡ |
¡ |
|
Tập giá trị của hàm số \(y = \sqrt 3 \sin x - \cos x - 2\) là [−4;0]. |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
Hàm số \(y = 3\sin \frac{x}{2}\) tuần hoàn với chu kì π. |
¡ |
¤ |
|
Tập giá trị của hàm số \(y = \sqrt 3 \sin x - \cos x - 2\) là [−4;0]. |
¤ |
¡ |
Phương pháp giải
Hàm số y = k.sin(ax + b) có chu kì là \(T = \frac{{2\pi }}{{|a|}}\)
Lời giải
Hàm số \(y = 3\sin \frac{x}{2}\) tuần hoàn với chu kì \(T = \frac{{2\pi }}{{|a|}}\)
Mệnh đề 1 sai
Xét hàm số \(y = \sqrt 3 \sin x - \cos x - 2\)
Ta có: \(\sqrt 3 \sin x - \cos x = 2.\left( {\frac{{\sqrt 3 }}{2}\sin x - \frac{1}{2}\cos x} \right)\)
\( = 2.\sin \left( {x - \frac{\pi }{6}} \right)\)
Ta có:
\(\begin{array}{l} - 1 \le \sin \left( {x - \frac{\pi }{6}} \right) \le 1\\ \Rightarrow - 2 \le 2\sin \left( {x - \frac{\pi }{6}} \right) \le 2\\ \Rightarrow - 4 \le \sqrt 3 \sin x - \cos x - 2 \le 0\end{array}\)
⇒ Hàm số \(y = \sqrt 3 \sin x - \cos x - 2\) là [−4;0]
Câu 61:
Cho dãy số un xác định bởi: \({u_1} = 1,\,\,{u_{n + 1}} = 2{u_n} + 3\,\,(n \ge 2)\) .
Các khẳng định sau là đúng hay sai?
|
|
ĐÚNG |
SAI |
|
un lập thành cấp số nhân. |
¡ |
¡ |
|
Số hạng tổng quát của dãy là 2n+1 − 3 |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
un lập thành cấp số nhân. |
¡ |
¤ |
|
Số hạng tổng quát của dãy là 2n+1 − 3 |
¤ |
¡ |
Phương pháp giải
- Tính u1; u2;... rồi đoán quy luật của dãy số.
Lời giải
u1 = 1
u2 = 2.1 + 3 = 5 = 23 − 3
u3 = 2.5 + 3 = 13 = 24 − 3
u4 = 2.13 + 3 = 29 = 25 − 3
...
un = 2n+1 − 3
Câu 62:
Một chiếc guồng nước có dạng hình tròn bán kính 2,5m; trục của nó đặt cách mặt nước 2m. Khi guồng quay đều, khoảng cách h (mét) từ một chiếc gầu gắn tại điểm A của guồng đến mặt nước được tính theo công thức h = |y|, trong đó \(y = 2 + 2,5\sin \left[ {2\pi \left( {t - \frac{1}{4}} \right)} \right]\)
với t (phút) là thời gian quay của guồng. Ta quy ước y > 0 khi gầu ở trên mặt nước và y < 0 khi gầu ở dưới nước.
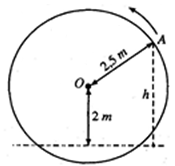
Điền số thích hợp vào ô trống:
Sau khi guồng nước bắt đầu quay, thời điểm đầu tiên chiếc gầu ở vị trí thấp nhất là _______ phút.
 Xem đáp án
Xem đáp án
Đáp án “1”
Phương pháp giải
Lời giải
Chiếu gầu ở vị trí thấp nhất khi
\(\sin x = - 1 \Leftrightarrow x = - \frac{\pi }{2} + k2\pi \)
Vậy chiếc gầu ở vị trí thấp nhất tại các thời điểm 0 phút, 1 phút, 2 phút, …
Câu 63:
Số điểm biểu diễn nghiệm của phương trình \({\sin ^2}x - 2\cos x.\sin x + 1 = 0\) trên đường tròn lượng giác là
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
\(\begin{array}{l}{\sin ^2}x - 2\cos x\sin x + 1 = 0\\ \Leftrightarrow \frac{{1 - \cos 2x}}{2} - \sin 2x + 1 = 0\\ \Leftrightarrow 1 - \cos 2x - 2\sin 2x + 2 = 0\\ \Leftrightarrow \cos 2x + 2\sin 2x = 3\end{array}\)
Ta thấy: \({1^2} + {2^2} < {3^2}\). Vậy phương trình trên vô nghiệm.
Câu 64:
Khi một vận động viên nhảy dù nhảy ra khỏi máy bay, giả sử quãng đường người ấy rơi tự do (tính theo feet) trong mỗi giây liên tiếp theo thứ tự trước khi bung dù lần lượt là: 16; 48;80;112;144;…(các quãng đường này tạo thành cấp số cộng).
Khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
Công sai của cấp số cộng trên là d = 30 |
¡ |
¡ |
|
Tổng chiều dài quãng đường rơi tự do của người đó trong 10 giây đầu tiên là 1060 feet |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
Công sai của cấp số cộng trên là d = 30 |
¡ |
¤ |
|
Tổng chiều dài quãng đường rơi tự do của người đó trong 10 giây đầu tiên là 1060 feet |
¡ |
¤ |
Phương pháp giải
- Tính công sai d = u2 − u1
- Sử dụng công thức tính tổng n số hạng đầu tiên.
Lời giải
a) Công sai của cấp số cộng trên là: d = 32
b) \({S_{10}} = \frac{{10.[2.16 + (10 - 1).32]}}{2} = 1600\)
Câu 65:
Cho dãy số \(\left( {{a_n}} \right)\) có \({a_n} = \frac{n}{{{n^2} + 100}},\forall n \in \mathbb{N}*\). Tìm số hạng lớn nhất của dãy số \(\left( {{a_n}} \right)\).
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng bất đẳng thức Cô – si đánh giá GTLN của số hạng tổng quát
Lời giải
Ta có \({a_n} = \frac{n}{{{n^2} + 100}} \le \frac{n}{{2\sqrt {{n^2} \cdot 100} }} = \frac{1}{{20}}\).
Dấu bằng xảy ra khi \({n^2} = 100 \Leftrightarrow n = 10\).
Vậy số hạng lớn nhất của dãy là số hạng bằng \(\frac{1}{{20}}\).
Câu 66:
Cho cấp số cộng un = 5n − 1. Tính A = u26 + u27 + ... + u100
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào công thức tính tổng n số hạng đầu tiên của cấp số cộng.
Vì biết công thức tổng quát của CSC nên có thể dụng máy tính để tính ra đáp án.
Tính tổng n số hạng đầu tiên của dãy
Lời giải
Cách 1:
Ta có:\({S_{100}} = \frac{{100}}{2}\left( {{u_1} + {u_{100}}} \right) = 50(4 + 499) = 25150\)
Và \({\rm{ }}{S_{25}} = \frac{{25}}{2}\left( {{u_1} + {u_{25}}} \right) = \frac{{25}}{2}(4 + 124) = 1600\)
\( \Rightarrow A = {S_{100}} - {S_{25}} = 23550\)
Cách 2:
Ta sử dụng máy tính cầm tay: \(\sum\limits_{26}^{100} 5 {\rm{x}} - 1\), sau đó nhấn "=" ta được kết quả \(A = 23550\).
Câu 67:
Bốn góc lượng giác có số đo dương lập thành 1 cấp số nhân có tổng là 360∘. Tìm số đo góc lớn nhất, biết rằng số đo của góc đó gấp 8 lần số đo của góc nhỏ nhất.
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng tính chất của cấp số nhân
Gọi số đo góc nhỏ nhất là a, biểu diễn các số đo còn lại theo a
Lời giải
Gọi a là số đo góc lượng giác nhỏ nhất trong 4 góc ( \(a > 0)\).
Giả sử cấp số nhân có công bội là q
Ta có cấp số nhân theo thứ tự: \(a,\,\,a.q,\,\,a{q^2},\,\,a{q^3}\)
Do \(a{q^3} = 8a \Rightarrow {q^3} = 8 \Rightarrow q = 2\)
\( \Rightarrow \) Cấp số nhân theo thứ tự: a, 2a, 4a, 8a
Mà \(a + 2a + 4a + 8a = {360^^\circ }\)
\( \Rightarrow a = {24^^\circ }\)
\( \Rightarrow \) Số đo góc lớn nhất là: \({24^^\circ }{.2^3} = {192^^\circ }\)
Câu 68:
Cho hình vuông ABCD có các cạnh bằng a và có diện tích bằng S1. Nối bốn trung điểm A1, B1, C1, D1 theo thứ tự của bốn cạnh AB, BC, CD, DA ta được hình vuông thứ hai có diện tích S2.
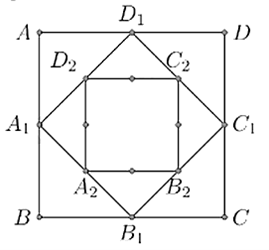
Tiếp tục quá trình trên ta được hình vuông thứ ba là A2B2C2D2 có diện tích S3 … và cứ tiếp tục như thế ta được các hình vuông lần lượt có diện tích S4, S5, ... , S50 (tham khảo hình vẽ).
Tổng S = S1 + S2 + ... + S50 bằng
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Diện tích hình vuông thứ nhất là \({S_1} = {a^2}\).
Cạnh hình vuông thứ hai là: \({a_2} = \frac{{a\sqrt 2 }}{2}\) nên diện tích hình vuông thứ hai là \({S_2} = a_2^2 = \frac{1}{2}{S_1}\)
Tiếp tục quá trình trên, ta được: Diện tích các hình vuông lập thành cấp số nhân với \({S_1} = {a^2},q = \frac{1}{2}\).
Vậy \(S = \frac{{{S_1}\left( {1 - {q^{50}}} \right)}}{{1 - q}} = \frac{{{a^2}\left( {{2^{50}} - 1} \right)}}{{{2^{49}}}}\).
Câu 69:
Giá trị của giới hạn \[L = \lim \left[ {\left( {1 - \frac{1}{{{2^2}}}} \right)\left( {1 - \frac{1}{{{3^2}}}} \right)...\left( {1 - \frac{1}{{{n^2}}}} \right)} \right]\] bằng \[\frac{a}{b}\] (phân số tối giản)
Khi đó, tổng a + b bằng _____________.
 Xem đáp án
Xem đáp án
Đáp án: “3”
Phương pháp giải
- Xét dãy số \(\left( {{u_n}} \right)\), với \({u_n} = \left( {1 - \frac{1}{{{2^2}}}} \right)\left( {1 - \frac{1}{{{3^2}}}} \right) \ldots \left( {1 - \frac{1}{{{n^2}}}} \right),n \ge 2,n \in \mathbb{N}.\)
- Chứng minh bằng phương pháp qui nạp để khẳng định \({u_n} = \frac{{n + 1}}{{2n}},\forall n \ge 2\)
Lời giải
Xét dãy số \(\left( {{u_n}} \right)\), với \({u_n} = \left( {1 - \frac{1}{{{2^2}}}} \right)\left( {1 - \frac{1}{{{3^2}}}} \right) \ldots \left( {1 - \frac{1}{{{n^2}}}} \right),n \ge 2,n \in \mathbb{N}.\)
Ta có:
\({u_2} = 1 - \frac{1}{{{2^2}}} = \frac{3}{4} = \frac{{2 + 1}}{{2.2}}\)
\({u_3} = \left( {1 - \frac{1}{{{2^2}}}} \right).\left( {1 - \frac{1}{{{3^2}}}} \right) = \frac{3}{4}.\frac{8}{9} = \frac{4}{6} = \frac{{3 + 1}}{{2.3}};\)
\({u_4} = \left( {1 - \frac{1}{{{2^2}}}} \right).\left( {1 - \frac{1}{{{3^2}}}} \right)\left( {1 - \frac{1}{{{4^2}}}} \right) = \frac{3}{4}.\frac{8}{9}.\frac{{15}}{{16}} = \frac{5}{8} = \frac{{4 + 1}}{{2.4}}\)
\({u_n} = \frac{{n + 1}}{{2n}}.\)
Dễ dàng chứng minh bằng phương pháp qui nạp để khẳng định \({u_n} = \frac{{n + 1}}{{2n}},\forall n \ge 2\)
Khi đó \(\lim \left[ {\left( {1 - \frac{1}{{{2^2}}}} \right)\left( {1 - \frac{1}{{{3^2}}}} \right) \ldots \left( {1 - \frac{1}{{{n^2}}}} \right)} \right] = \lim \frac{{n + 1}}{{2n}} = \frac{1}{2}\)
Câu 70:
Tính giới hạn \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} + 2} }}{x}\)
 Xem đáp án
Xem đáp án
Phương pháp giải
Dạng vô định ∞ / ∞
Lời giải
Cách 1: \(\mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2} + 2} }}{x} = \mathop {\lim }\limits_{x \to - \infty } \frac{{|x|.\sqrt {1 + \frac{2}{{{x^2}}}} }}{x} = - 1\)
Cách 2: Tính giá trị của hàm số tại -999999999
Câu 71:
Cho hàm số y = |x − 1|. Chọn phát biểu đúng?
 Xem đáp án
Xem đáp án
Phương pháp giải
Áp dụng điều kiện để hàm số liên tục và có đạo hàm tại 1 điểm
Lời giải
Ta có: \(y = f(x) = |x - 1| = \left\{ {\begin{array}{*{20}{l}}{x - 1,{\rm{ khi}}:x \ge 1}\\{1 - x,{\rm{ khi}}:x < 1}\end{array}} \right.\)
\(\left. {\begin{array}{*{20}{l}}{\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} (x - 1) = 0}\\{\mathop {\lim }\limits_{x \to {1^ - }} f(x) = \mathop {\lim }\limits_{x \to {1^ - }} (1 - x) = 0}\\{{f_{(1)}} = 1 - 1 = 0}\end{array}} \right\}\) ⇒Hàm số liên tục tại x = 1
\(\left. {\begin{array}{*{20}{l}}{f_{\left( {{1^ + }} \right)}^\prime = 1}\\{f_{\left( {{1^ - }} \right)}^\prime = - 1}\end{array}} \right\} \Rightarrow f_{\left( {{1^ + }} \right)}^\prime \ne f_{\left( {{1^ - }} \right)}^\prime \)
Hàm số không có đạo hàm tại x = 1
Chọn B
Câu 72:
Biết hàm số \(f(x) = a{x^3} + b{x^2} + cx + d(a > 0)\) có đạo hàm là \(f'(x) > 0\) với \(\forall x \in \mathbb{R}\). Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Phương pháp giải
+ Tính đạo hàm
+ Biện luận nghiệm của bất phương trình.
Đạo hàm của một số hàm số thường gặp
Lời giải
\(f'(x) = 3a{x^2} + 2bx + c > 0;\,\,\forall x \in \mathbb{R}\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a > 0}\\{\Delta ' < 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a > 0\,\,\,\,\,\,\,\,\,\,\,\,\,}\\{{b^2} - 3ac < 0}\end{array}} \right.} \right.\).
Câu 73:
Một vật rơi tự do theo phương thẳng đứng có quãng đường dịch chuyển , với t là thời gian tính bằng giây (s) kể từ lúc vật bắt đầu rơi, S là quãng đường tính bằng mét (m), g = 9,8 m/s2. Vận tốc tức thời của vật tại thời điểm t = 6 s là
 Xem đáp án
Xem đáp án
Phương pháp giải
Bước 1: Tìm hàm v(t) = S′(t)
Bước 2: Tìm v(6).
Lời giải
Ta có \(S(t) = \frac{1}{3}g{t^2}\)
Suy ra \(v(6) = \frac{2}{3}.9,8.6 = 39,2\,\,(\;{\rm{m/s}})\).
Vậy vận tốc tức thời của vật tại thời điểm t = 6 s là 39,2 m/s.
Do đó ta chọn phương án A.
Câu 74:
A,B,C,D,E,F cùng đi xem phim. 6 bạn mua được 3 vé chẵn, 3 vé lẻ. A và F muốn được ngồi ghế chẵn, C và D muốn được ngồi ghế lẻ. B và E không có yêu cầu gì.
Các nhận định sau Đúng hay Sai?
|
|
ĐÚNG |
SAI |
|
Số cách để sắp xếp vị trí cho 6 bạn là 72 cách |
¡ |
¡ |
|
B và E có thể cùng chẵn hoặc cùng lẻ |
¡ |
¡ |
|
Số cách để sắp xếp vị trí cho 6 bạn là 720 cách |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
Số cách để sắp xếp vị trí cho 6 bạn là 72 cách |
¤ |
¡ |
|
B và E có thể cùng chẵn hoặc cùng lẻ |
¡ |
¤ |
|
Số cách để sắp xếp vị trí cho 6 bạn là 720 cách |
¡ |
¤ |
Phương pháp giải
- Xếp A và F
- Xếp C và D
- Sau đó mới xếp vị trí cho B và E.
Lời giải
Số cách xếp A và F là \(A_3^2\)
Số cách xếp C và D là \(A_3^2\)
Số cách xếp B và E là 2!
Số cách xếp vị trí cho 6 bạn là \(A_3^2\).\(A_3^2\).2! = 72
=> Mệnh đề 1 đúng, mệnh đề 3 sai.
Sau khi xếp vị trí cho A, C, D, F thì chỉ còn đúng 1 vị trí chẵn và 1 vị trí lẻ.
=> B và E khác tính chẵn lẻ
=> Mệnh đề 2 sai.
Câu 75:
Cho tập hợp A = {1;2;3;4;5;6}.
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
Tập hợp A có 64 tập con khác rỗng. |
¡ |
¡ |
|
Tập hợp A có 20 tập con có 3 phần tử. |
¡ |
¡ |
|
Số tập con có 2 phần tử của A bằng số tập con có 4 phần tử của A. |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
Tập hợp A có 64 tập con khác rỗng. |
¡ |
¤ |
|
Tập hợp A có 20 tập con có 3 phần tử. |
¤ |
¡ |
|
Số tập con có 2 phần tử của A bằng số tập con có 4 phần tử của A. |
¤ |
¡ |
Phương pháp giải
Tập A có n phần tử thì số tập con khác rỗng của A là \({2^n} - 1\)
Số tập con có k phần tử của tập A có n phần tử là \(C_n^k\)
Lời giải
Số tập con khác rỗng của A là 26 − 1 = 63
=> Mệnh đề 1 sai
Số tập con có 3 phần tử là số cách chọn 3 phần tử trong 6 phần tử: \(C_6^3 = 20\)
=> Mệnh đề 2 đúng
Số tập con có 2 phần tử là: \(C_6^2 = 15\)
Số tập con có 4 phần tử là: \(C_6^4 = 15\)
=> Mệnh đề 3 đúng
Câu 76:
Cho khai triển \({(1 - 2x)^{20}} = {a_0} + {a_1}x + {a_2}{x^2} + \ldots + {a_{20}}{x^{20}}{\rm{. }}\)
Trong các khẳng định sau, khẳng định nào đúng?
|
|
ĐÚNG |
SAI |
|
Giá trị của \[{a_0} - {a_1} + {a_2}\] bằng 801. |
¡ |
¡ |
|
Tổng \({a_0} + {a_1} + {a_2} + \ldots + {a_{20}}\) bằng −1. |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
Giá trị của \[{a_0} - {a_1} + {a_2}\] bằng 801. |
¤ |
¡ |
|
Tổng \({a_0} + {a_1} + {a_2} + \ldots + {a_{20}}\) bằng −1. |
¡ |
¤ |
Phương pháp giải
Xét từng mệnh đề.
Sử dụng công thức:
\({(a + b)^n} = \sum\limits_{k = 0}^n {C_n^k} {a^{n - k}}{b^k}\)
Số chỉnh hợp chập k của n phần tử là:
\(A_n^k = \frac{{n!}}{{(n - k)!}} = n(n - 1)(n - 2) \ldots (n - k + 1)\)
Lời giải
+) Ta có \({(1 - 2x)^{20}} = \sum\limits_{k = 0}^{20} {C_{20}^k} {( - 2)^k}{x^k},(k \in Z) \Rightarrow {a_0} = C_{20}^0,{a_1} = - 2.C_{20}^1,{a_2} = {( - 2)^2}C_{20}^2 = 4C_{20}^2\) .
Vậy \({a_0} - {a_1} + {a_2} = C_{20}^0 + 2C_{20}^1 + 4C_{20}^2 = 801.\)
+) Ta có: \({(1 - 2x)^{20}} = {a_0} + {a_1}x + {a_2}{x^2} + \cdots + {a_{20}}{x_{20}}\) (1).
Thay x = 1 vào (1) ta có: \({a_0} + {a_1} + {a_2} + \cdots + {a_{20}} = {( - 1)^{20}} = 1.\)
Câu 77:
Có bao nhiêu số có 5 chữ số đôi một khác nhau và trong đó có đúng một chữ số lẻ?
 Xem đáp án
Xem đáp án
Đáp án: “2520”
Phương pháp giải
- Trường hợp 1: Chọn một chữ số lẻ, ba chữ số chã̃n khác 0 và xếp vào các vị trí còn lại.
- Trường hợp 2: số tạo thành không có chữ số 0
Lời giải
Chọn một chữ số lẻ, ba chữ số chã̃n khác 0 và xếp vào các vị trí còn lại, có: cách.
Trong trường hợp này có 4 × 480 = 1920 số.
- Trường hợp 2: số tạo thành không có chữ số 0 , khi đó: chọn một chữ số lè cùng với bốn chữ số chẵn rồi xếp vào các vị trí có: 5 × 5! = 600 số.
Vậy tất cả có 1920 + 600 = 2520 số thỏa mãn đề bài.
Câu 78:
Cho tập hợp A = {1;2;3;4;5}. Gọi S là tập hợp tất cả các số tự nhiên có ít nhất 3 chữ số, các chữ số đôi một khác nhau được lập thành từ các chữ số thuộc tập A. Chọn ngẫu nhiên một số từ tập S, xác xuất để số được chọn có tổng các chữ số bằng 10 được viết dưới dạng phân số tối giản \(\frac{a}{b}\,\,(a,b \in \mathbb{Z}).\)
Tổng a + b bằng
 Xem đáp án
Xem đáp án
Đáp án: “28”
Phương pháp giải
Vì S là tập hợp tất cả các số tự nhiên có ít nhất 3 chữ số, các chữ số đôi một khác nhau được lập thành từ các chữ số thuộc tập A
Lời giải
Vì S là tập hợp tất cả các số tự nhiên có ít nhất 3 chữ số, các chữ số đôi một khác nhau được lập thành từ các chữ số thuộc tập A nên ta tính số phần tử thuộc tập Snhư sau:
+ Số các số thuộc S có 3 chữ số là \(A_5^3\).
+ Số các số thuộc S có 4 chữ số là \(A_5^4\).
+ Số các số thuộc S có 5 chữ số là \(A_5^5\).
Suy ra số phần tử của tập S là \(A_5^3 + A_5^4 + A_5^5 = 300.\)
Số phần tử của không gian mẫu là \({n_\Omega } = C_{300}^1 = 300\)
Gọi X là biến cố “Số được chọn có tổng các chữ số bằng 10”. Các tập con của A có tổng số phần tử bằng 10 là A1 = {1;2;3;4}, A2 = {2;3;5}, A3 = {1;4;5}.
+ Từ A1 lập được các số thuộc S là 4!.
+ Từ A2 lập được các số thuộc S là 3!.
+ Từ A3 lập được các số thuộc S là 3!.
Suy ra số phần tử của biến cố X là nX = 4! + 3! + 3! = 36.
Vậy xác suất cần tính \(P(X) = \frac{{{n_X}}}{{{n_\Omega }}} = \frac{{36}}{{300}} = \frac{3}{{25}}.\)
Câu 79:
Tại buổi tất niên công ty, Dương và Nguyên cùng tham gia trò chơi và giành chiến thắng. Phần quà của hai bạn được đặt trong 1 hộp kín, gồm 6 tờ 20.000 và 4 tờ 50.000. Dương lấy trước, Nguyên lấy sau. Xác suất để Nguyên lấy được tờ 50.000 là a/b (a/b là phân số tối giản).
Tổng a + b = ?
 Xem đáp án
Xem đáp án
Đáp án: “7”
Phương pháp giải
TH1: Dương lấy trước và lấy đúng tờ 20.000
TH2: Dương lấy trước và lấy đúng tờ 50.000
Lời giải
TH1: Dương lấy trước và lấy đúng tờ 20.000, xác suất lấy trúng tờ 20.000 là \(\frac{6}{{10}}\)
Khi đó xác suất để Nguyên lấy được tờ 50.000 là \(\frac{4}{9}\)
TH2: Dương lấy trước và lấy đúng tờ 50.000, xác suất lấy trúng tờ 50.000 là \(\frac{4}{{10}}\)
Khi đó xác suất để Nguyên lấy được tờ 50.000 là\(\frac{3}{9}\)
Xác suất để Nguyên lấy được tờ 50.000 là \(\frac{6}{{10}}.\frac{4}{9} + \frac{4}{{10}}.\frac{3}{9} = \frac{2}{5}.\)
Câu 80:
Cho hình chóp S.ABC có đáy là tam giác vuông tại A, cạnh huyền BC = 6(cm), các cạnh bên cùng tạo với đáy một góc 600.
Kéo biểu thức trong các ô thả vào vị trí thích hợp trong các câu sau:

Các cạnh bên của hình chóp bằng ...
Diện tích mặt cầu ngoại tiếp hình chóp S.ABC bằng ....
 Xem đáp án
Xem đáp án
Các cạnh bên của hình chóp bằng 6cm
Diện tích mặt cầu ngoại tiếp hình chóp S.ABC bằng 48
Phương pháp giải
- Gọi H là hình chiếu vuông góc của S lên mặt phẳng (ABC). Gọi O là trung điểm của BC.
- Tam giác ABC vuông tại A,O là trung diểm của cạnh huyền BC, suy ra OA = OB = OC
- Chứng minh ΔSHA = ΔSHB = ΔSHC
- Trong ΔSAH dựng trung trực của SA cắt SH tại I.
- Chứng minh IA = IB = IC = IS.
Lời giải
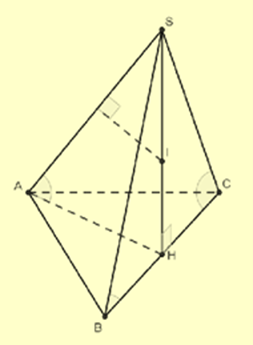
Gọi H là hình chiếu vuông góc của S lên mặt phẳng (ABC). Gọi O là trung điểm của BC.
Tam giác ABC vuông tại A,O là trung diểm của cạnh huyền BC, suy ra OA = OB = OC (1).
Xét các tam giác ΔSHA, ΔSHB, ΔSHC có:
\(\left\{ {\begin{array}{*{20}{l}}{{\rm{ SH}}\,\,{\rm{chung }}}\\{\widehat {SHA} = \widehat {SHB} = \widehat {SHC} = {{90}^^\circ } \Rightarrow \Delta SHA = \Delta SHB = \Delta SHC\,\,({\rm{g}}{\rm{.c}}{\rm{.g) }}}\\{\widehat {SAH} = \widehat {SBH} = \widehat {SCH} = {{60}^^\circ }}\end{array}} \right.\)
\( \Rightarrow HA = HB = HC\)
\(\widehat {SAH} = \widehat {SBH} = \widehat {SCH} = {60^^\circ }\)
⇒ ΔSBC đều cạnh bằng 6 (cm)
Từ (1) và (2) suy ra H trùng O. Khi đó SH là trục đường tròn ngoại tiếp ΔABC
Trong ΔSAH dựng trung trực của SA cắt SH tại I.
Khi đó IA = IB = IC = IS. Vậy I là tâm mặt cầu ngoại tiếp hình chóp S.ABC.
ΔSBC đều cạnh bằng 6(cm) \( \Rightarrow SO = 3\sqrt 3 \Rightarrow SI = \frac{2}{3}.SO = \frac{2}{3}.3\sqrt 3 = 2\sqrt 3 \) .
Diện tích mặt cầu ngoại tiếp hình chóp S.ABC là: \(S = 4\pi {(2\sqrt 3 )^2} = 48\pi \left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Câu 81:
Cho hình chóp S.ABCD có đáy là một hình vuông cạnh \(a\), mặt bên (SAD) là một tam giác đều và \((SAD) \bot (ABCD)\). Tính chiều cao của hình chóp.
 Xem đáp án
Xem đáp án
Phương pháp giải
Tính khoảng cách từ một điểm đến một mặt phẳng
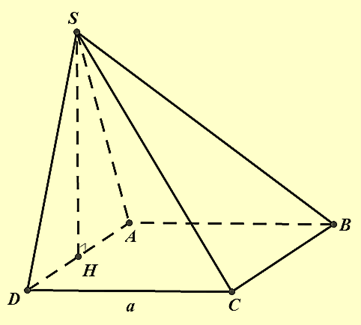
Kẻ SH vuông góc với AD.
Vì (SAD) ⊥ (ABCD) nên (SAD) chứa đường cao của hình chóp.
SAD là tam giác đều nên \(H = \frac{{\sqrt 3 AD}}{2} = \frac{{\sqrt 3 a}}{2}\)
Vậy chiều cao của hình chóp là \(\frac{{\sqrt 3 a}}{2}\)
Câu 82:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh \(a,SA \bot (ABC)\), góc giữa SC và mặt phẳng \((ABC)\) bằng . Tính khoảng cách giữa hai đường thẳng SB và AC.
 Xem đáp án
Xem đáp án
Phương pháp giải
Bước 1: Do \(SA \bot (ABC)\) nên góc giữa SC và mặt phẳng \((ABC)\) là góc \(\widehat {SCA}\). Tìm SA
Bước 2: Lấy điểm \(D\) sao cho ACBD là hình bình hành. Khi đó \(d(SB,AC) = d(AC,(SBD)) = d(A,(SBD))\).
Ta có \(\Delta ABD\) đều cạnh \(a\). Gọi \(M\) là trung điểm \(BD \to AM\)
Bước 3: Trong \(\Delta SAM\) kẻ \(AH \bot SM\) với \(H \in SM\). Suy ra \(AH \bot (SAM) \Rightarrow d(A,(SBD)) = AH\)
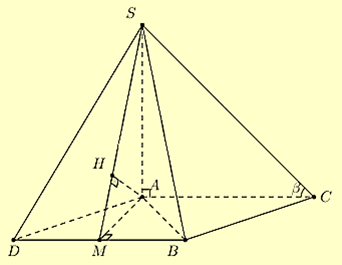
Do \(SA \bot (ABC)\) nên góc giữa SC và mặt phẳng \((ABC)\) là góc \(\widehat {SCA}\). Suy ra \(\widehat {SCA} = {30^^\circ }\) Trong tam giác SCA vuông tại \(A\):
Có \(\tan \widehat {SCA} = \frac{{SA}}{{AC}} \leftrightarrow SA = AC.\tan \widehat {SCA} = a.\tan {30^^\circ } = \frac{{a\sqrt 3 }}{3}\)
Lấy điểm \(D\) sao cho ACBD là hình bình hành.
Khi đó \(d(SB,AC) = d(AC,(SBD)) = d(A,(SBD))\).
Ta có \(AB = BD = AD \Rightarrow \Delta ABD\) đều cạnh \(a\).
Gọi \(M\) là trung điểm BD. Suy ra \(AM \bot BD\) và \(AM = \frac{{a\sqrt 3 }}{2}\).
Trong \(\Delta SAM\) kẻ \(AH \bot SM\) với \(H \in SM\).
Do \(\left. {\begin{array}{*{20}{l}}{BD \bot AM}\\{BD \bot SA}\end{array}} \right\} \Rightarrow BD \bot (SAM) \Rightarrow BD \bot AH\).
Suy ra \(AH \bot (SAM) \Rightarrow d(A,(SBD)) = AH\).
Trong \(\Delta SAM\) vuông tại \(A\) ta có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{M^2}}} + \frac{1}{{S{A^2}}} \Leftrightarrow \frac{1}{{A{H^2}}} = \frac{4}{{3{a^2}}} + \frac{9}{{3{a^2}}}\)
\( \Leftrightarrow \frac{1}{{A{H^2}}} = \frac{{13}}{{3{a^2}}} \Leftrightarrow AH = \frac{{a\sqrt 3 }}{{\sqrt {13} }}\)
Vậy\(d(SB,AC) = \frac{{a\sqrt 3 }}{{\sqrt {13} }} = \frac{{a\sqrt {39} }}{{13}}\).
Câu 83:
Cho hình chóp S.ABCD có đáy ABCD là một hình thang với đáy AD và BC. Biết AD = a,BC = b. Gọi I và J lần lượt là trọng tâm các tam giác SAD và SBC. Mặt phẳng (ADJ) cắt SB, SC lần lượt tại M, N. Mặt phẳng (BCI) cắt SA, SD tại P, Q. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
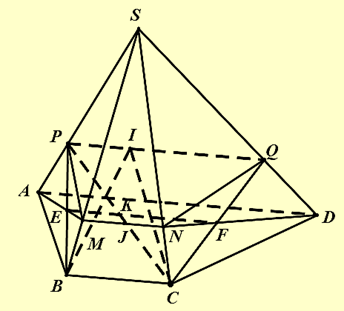
Ta có .
Vậy (1)
Tương tự
Vậy (2)
Từ (1) và (2) suy ra MN ∥ PQ.
Câu 84:
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), SA = a, đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Góc giữa hai mặt phẳng (SBC) và (SCD) bằng
 Xem đáp án
Xem đáp án
Phương pháp giải
Bước 1: CM vuông tại \(C,AK \bot SC \Rightarrow AK \bot (SAC)\)
Bước 2: Từ đó góc giữa hai mặt phẳng \((SBC)\) và \((SCD)\) bằng góc giữa AH và AK bằng \(\widehat {HAK};AH \bot (SBC) \Rightarrow AH \bot HK\)
Bước 3: Tính AH, AK và tam giác vuông AHK có \(\cos \widehat {HAK} = \frac{{AH}}{{AK}} \to \widehat {HAK}\)
Có \(SA \bot (ABCD)\), đáy ABCD là hình thang vuông tại \(A\) và \(B\) nên
\(\left. {\begin{array}{*{20}{l}}{SA \bot BC}\\{AB \bot BC}\end{array}} \right\} \Rightarrow BC \bot (SAB){\rm{. }}\)
Trong dựng đường cao \(AH \bot SB \Rightarrow AH \bot (SBC)\).
Ta có \(AC = a\sqrt 2 ;SD = a\sqrt 5 ;CD = a\sqrt 2 ;SC = a\sqrt 3 \). Do đó vuông tại \(C\).
Có \(\left. {\begin{array}{*{20}{l}}{SC \bot CD}\\{SA \bot CD}\end{array}} \right\} \Rightarrow CD \bot (SAC)\).
Trong dựng đường cao \(AK \bot SC \Rightarrow AK \bot (SDC)\)
Từ đó góc giữa hai mặt phẳng \((SBC)\) và \((SCD)\) bằng góc giữa AH và AK bằng \(\widehat {HAK}\)
\(AH \bot (SBC) \Rightarrow AH \bot HK\).
Có \(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} \Rightarrow AH = \frac{a}{{\sqrt 2 }};\frac{1}{{A{K^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{C^2}}} \Rightarrow AK = \frac{{a\sqrt 2 }}{{\sqrt 3 }}\)
Tam giác vuông AHK có \(\cos \widehat {HAK} = \frac{{AH}}{{AK}} = \frac{{\sqrt 3 }}{2} \to \widehat {HAK} = {30^^\circ }\).
Câu 85:
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
Chữ số tận cùng của \[{9^{{9^{10}}}}\]là 9 |
¡ |
¡ |
|
Số dư của 31000 khi chia cho 5 là 2 |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
Chữ số tận cùng của \[{9^{{9^{10}}}}\]là 9 |
¤ |
¡ |
|
Số dư của 31000 khi chia cho 5 là 2 |
¡ |
¤ |
Phương pháp giải
a) Tìm chữ số tận cùng của một số là tìm dư trong phép chia số đó cho 10 .
\(a \equiv x(\,\bmod \,m)\)
\(b \equiv y(\,\bmod \,m)\)
\(a.b \equiv x.y(\,\bmod \,m)\)
\({a^n} \equiv {x^n}(\,\bmod \,m)\)
b) Tìm hai chữ số tận cùng của một số là tìm dư trong phép chia số đó cho 100 .
Lời giải
a) Tìm chữ số tận cùng của một số là tìm dư trong phép chia số đó cho 10 . Vì \({9^{2n + 1}} = {9.81^n} \equiv 9(\,\bmod \,10)\).
Do \({9^{10}}\) là số lẻ nên số \({9^{{9^{10}}}}\) có chữ số tận cùng là 9 .
b) Tìm hai chữ số tận cùng của một số là tìm dư trong phép chia số đó cho 100 .
Ta có \({3^4} = 81 \equiv - 19(\,\bmod \,100) \Rightarrow {3^8} \equiv {( - 19)^2}(\,\bmod \,100)\)
Mà \({( - 19)^2} = 361 \equiv 61(\,\bmod \,100)\)
Vậy \({3^8} \equiv 61(\,\bmod \,100)\)
\({3^{10}} \equiv 61.9 \equiv 549 \equiv 49(\,\bmod \,100)\)
\({3^{20}} \equiv {49^2} \equiv 01(\,\bmod \,100)\quad \left( {{\mathop{\rm do}\nolimits} \,\,{{49}^2} = 2401 = 24.100 + 1} \right)\)
Do đó \({3^{1000}} \equiv 01(\,\bmod \,100)\) nghĩa là hai chữ số sau cùng của \({3^{1000}}\) là 01.
Tất cả các số là bội của 100 đều chia hết cho 5 , do đó số dư khi chia \({3^{1000}}\) cho 5 là 1
Câu 86:
- Hình thang cân.
- Hình thoi.
- Hình tam giác đều.
- Hình bình hành
 Xem đáp án
Xem đáp án
Đáp án
Hình thang cân.
Hình thoi. - Đ
Hình tam giác đều. - Đ
Hình bình hành.
Phương pháp giải
Xét từng đáp án.
Lời giải
Hình thang cân chỉ có 1 trục đối xứng.
Hình thoi có 2 trục đối xứng (là hai đường chéo).
Tam giác đều có 3 trục đối xứng (nối đỉnh với trung điểm cạnh đối diện).
Hình hình hành không có trục đối xứng.
Câu 87:
Tìm số tự nhiên k để dãy : k + 1, k + 2, …, k + 10 chứa nhiều số nguyên tố nhất
Khi đó k =...
 Xem đáp án
Xem đáp án
Đáp án: “1”
Phương pháp giải
- Với k = 0; 1; 2
- Với k ≥ 3 và chứng minh số nguyên tố trong dãy có ít hơn 5 số nguyên tố.
Lời giải
- Với k = 0 ta có dãy 1, 2, 3,…, 10 chứa 4 số nguyên tố là 2, 3, 5, 7.
- Với k = 1 ta có dãy 2, 3, 4,…, 11 chứa 5 số nguyên tố là 2, 3, 5, 7, 11.
- Với k = 2 ta có dãy 3, 4, 5,…, 12 chứa 4 số nguyên tố là 3, 5, 7, 11.
- Với k ≥ 3 dãy k + 1, k + 2, …, k + 10 chứa 5 số lẻ liên tiếp, các số lẻ này đều lớn hơn 3 nên có một số chia hết cho 3 , mà 5 số chẵn trong dãy hiển nhiên không là số nguyên tố. Vậy trong dãy có ít hơn 5 số nguyên tố.
Tóm lại với k = 1 thì dãy k + 1, k + 2,…, k + 10 chứa nhiều số nguyên tố nhất.
Câu 88:
Gọi \(S\) là tập có \(n\) phần tử. Mỗi phân hoạch của \(S\) được định nghĩa là tập gồm \(k\) tập con \({S_1},{S_2}, \ldots ,{S_k}\) khác rỗng của \(S\), đôi một rời nhau và hợp của chúng là \(S\). Tức là:
\(S = {S_1} \cup {S_2} \cup \ldots \cup {S_k},\,\,{S_i} \ne \emptyset ,\,\,{S_i} \cap {S_j} = \emptyset \,\,(i \ne j),\,\,\forall i,j = 1;2; \ldots ;k\)$
Ví dụ: Tập hợp \(A = \{ a,b\} \) chỉ có 1 phân hoạch là \({A_1} = \{ \{ a\} ,\{ b\} \} \).
Tập hợp \(B = \{ a,b,c\} \) có 4 phân hoạch làCho tập \(C = \{ a,b,c,d\} \).
Hỏi tập \(C\) có bao nhiêu phân hoạch?
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Các phân hoạch của C là:
C1 = {{a},{b},{c},{d}}
C2 ={{a},{b,c,d}}, C3 = {{b},{a,c,d}}, C4 = {{c},{a,b,d}}, C5 = {{d},{a,b,c}}
C6 = {{a,b},{c,d}}, C7 = {{a,c},{b,d}}, C8 = {{a,d},{b,c}}
Câu 89:
Bạn Hải lấy một cặp số tự nhiên phân biệt rồi tính số dư khi chia tổng lập phương của hai số cho tổng các chữ số của số lớn trong hai số đó. Nếu làm theo đúng quy tắc của bạn Hải với cặp số (31, 175) ta thu được kết quả bằng.
 Xem đáp án
Xem đáp án
Phương pháp giải
- Tổng lập phương của hai số 31 và 175.
- Tổng các chữ số của số lớn hơn.
- Lấy hai số vừa tìm được chia cho nhau.
Lời giải
Tổng lập phương của hai số 31 và 175 là A = 313 + 1753 = 5389166.
Tổng các chữ số của số lớn hơn là: B = 1 + 7 + 5 = 13.
Theo quy tắc của Hải, lấy A : B được 414551 dư 3.
Câu 90:
Khoảng 200 năm trước, hai nhà khoa học Pháp là Clô-zi-ut và Cla-pay-rông đã thấy rằng áp suất p của hơi nước (đo bằng milimet thủy ngân, kí hiệu là mmHg) gây ra khi nó chiếm khoảng trống phía trên của mặt nước chứa trong một bình kín được tính theo công thức , với t là nhiệt độ ∘C của nước, a và k là hằng số. Cho biết k ≈ −2258,624 và khi nhiệt độ của nước là 100∘C thì áp suất của hơi nước là 760mmHg. Tìm [a], với [a] có giá trị nguyên không vượt quá a.
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Ta có : .\(p = a{.10^{\frac{k}{{t + 273}}}}\)
Câu 91:
Cho phương trình (m là tham số thực). Có tất cả bao nhiêu giá trị nguyên của m để phương trình có đúng hai nghiệm phân biệt thuộc (−π; π).
 Xem đáp án
Xem đáp án
Phương pháp giải
Bước 1: Đặt t = sin2x tìm điều kiện của t khi x ∈ (−π; π).
Bước 2:Đưa phương trình ban đầu về phương trình ẩn t và giải phương trình với điều kiện ở bước 1.
Bước 3: Nếu có nghiệm t không phụ thuộc vào m thì thay vào t = sin2x tìm nghiệm x ∈ (−π; π).
Bước 4: Biện luận m.
Một số phương trình lượng giác thường gặp
Lời giải
Bước 1:\((2m + 1){\cos ^2}2x - (3m - 1)\sin 2x - 3m + 1 = 0\)
Ta có \((2m + 1){\cos ^2}2x - (3m - 1)\sin 2x - 3m + 1 = 0\) (∗).
Đặt \(t = \sin 2x \Rightarrow - 1 \le t \le 1\,\,(x \in ( - \pi ;\pi ))\)
Bước 2:
Khi đó phương trình (*) có dạng:
\(\begin{array}{l}(2m + 1)\left( {1 - {t^2}} \right) - (3m - 1)t - 3m + 1 = 0\\ \Leftrightarrow (2m + 1){t^2} + (3m - 1)t + m - 2 = 0\\ \Leftrightarrow (t + 1)((2m + 1)t + m - 2) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t = - 1}\\{(2m + 1)t + m - 2 = 0}\end{array}} \right.\end{array}\)
Bước 3:
Nếu: \(t = - 1\,\,(tm) \Rightarrow \sin 2x = - 1\)
\(\begin{array}{l} \Leftrightarrow 2x = \frac{{ - \pi }}{2} + k2\pi (k \in {\rm{Z}})\\ \Leftrightarrow x = \frac{{ - \pi }}{4} + k\pi \in ( - \pi ;\pi )\\ \Rightarrow \frac{{ - 3}}{4} < k < \frac{5}{4} \Rightarrow k \in \{ 0;1\} \end{array}\)
Khi đó phương trình (*) có 2 nghiệm phân biệt là \(\frac{{ - \pi }}{4};\frac{{3\pi }}{4}\)
Bước 4:
\[\left( {2m + 1} \right)t = 2 - m\] (1).
+) Nếu \(m = \frac{{ - 1}}{2}{\rm{ }}\)
Từ (1)\( \Rightarrow m = 2\,\,({\rm{ktm}})\)
+) \(m \ne \frac{{ - 1}}{2} \Rightarrow t = \frac{{2 - m}}{{2m + 1}}\)
Để phương trình (*) có 2 nghiệm phân biệt thì
\(\left[ {\begin{array}{*{20}{l}}{t = \frac{{2 - m}}{{2m + 1}} = - 1}\\{t < - 1}\\{t > 1}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = - 3}\\{\frac{{m + 3}}{{2m + 1}} < 0 \Leftrightarrow - 3 < m < \frac{{ - 1}}{2} \Leftrightarrow m \in \{ - 2; - 1\} }\\{\frac{{3m - 1}}{{2m + 1}} < 0 \Leftrightarrow \frac{{ - 1}}{2} < m < \frac{1}{3} \Leftrightarrow m = 0}\end{array}} \right.} \right.\)
Vậy có 4 giá trị của m thỏa mãn.
Câu 92:
Cho biết \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {a{x^2} + 1} - bx - 2}}{{{x^3} - 3x + 2}}(a,b \in \mathbb{R})\) có kết quả là một số thực. Giá trị của biểu thức \({a^2} + {b^2}\) bằng?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dạng vô định ∞ - ∞
Lời giải
Ta có \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {a{x^2} + 1} - bx - 2}}{{{x^3} - 3x + 2}} = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {a{x^2} + 1} - bx - 2}}{{{{(x - 1)}^2}(x + 2)}} = L,\) với \(L \in \mathbb{R}\)(*)
Khi đó \(\sqrt {a + 1} - b - 2 = 0 \Leftrightarrow \sqrt {a + 1} = b + 2 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b \ge - 2}\\{a + 1 = {b^2} + 4b + 4}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b \ge - 2}\\{a = {b^2} + 4b + 3}\end{array}} \right.\)
Thay \(a = {b^2} + 4b + 3\) vào (*):
\(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {a{x^2} + 1} - bx - 2}}{{{x^3} - 3x + 2}} = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} - bx - 2}}{{{{(x - 1)}^2}(x + 2)}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {{b^2} + 4b + 3} \right){x^2} + 1 - {{(bx + 2)}^2}}}{{{{(x - 1)}^2}(x + 2)\left[ {\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} + bx + 2} \right]}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{{(4b + 3){x^2} - 4bx - 3}}{{{{(x - 1)}^2}(x + 2)\left[ {\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} + bx + 2} \right]}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{{(4b + 3)x + 3}}{{(x - 1)(x + 2)\left[ {\sqrt {\left( {{b^2} + 4b + 3} \right){x^2} + 1} + bx + 2} \right]}} = L,\,\,L \in \mathbb{R}\)
Khi đó: \((4b + 3) + 3 = 0 \Leftrightarrow b = - \frac{3}{2} \Rightarrow a = - \frac{3}{4}.\)
Vậy \({a^2} + {b^2} = \frac{{45}}{{16}}\)
Câu 93:
Cho lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy ABCD là hình thoi,. Góc giữa đường thẳng \({\rm{AC'}}\) và mặt phẳng \(\left( {{\rm{ADD'A'}}} \right)\) là . M là trung điểm \({\rm{A'D'}},\) N là trung điểm \({\rm{BB'}}\). Tính khoảng cách từ \({\rm{N}}\) đến mặt phẳng (\({\rm{C'MA}}\))
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng phương pháp đổi điểm để tính khoảng cách
Lời giải
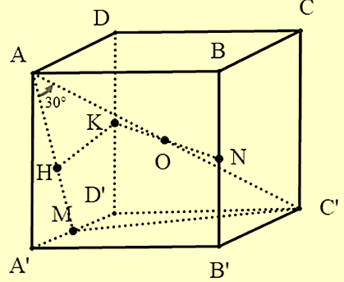
ΔA′D′C′ đều ⇒ C′M ⊥ A′D′
⇒ C′M ⊥ (AA′D′D)
\[ \Rightarrow \left( {\widehat {AC\prime ;\left( {ADD\prime A\prime } \right)}} \right) = \widehat {C\prime AM} = {30^ \circ }\]
Gọi O là trung điểm của AC′
K là trung điểm của DD′
⇒ K và N đối xứng nhau qua O
⇒ d[N,(C′MA)] = d[K,(C′MA)]
Do (C′MA) ⊥ (AA′D′D) theo giao tuyến AM nên kẻ KH ⊥ AM, ta có: KH ⊥ (C′MA)
⇒ d[K,(C′MA)] = KH
Ta có: \(C'M = a\sqrt 3 .\frac{{\sqrt 3 }}{2} = \frac{{3a}}{2}\)
Xét ΔAMC′:
Xét ΔA′AM: \(A'A = \sqrt {A{M^2} - A'{M^2}} = \sqrt {{{\left( {\frac{{3a\sqrt 3 }}{2}} \right)}^2} - {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}} = a\sqrt 6 \)
Ta có: SAA′D′D = AA′.A′D′ = \(a\sqrt 6 .a\sqrt 3 = 3{a^2}\sqrt 2 \)
\({S_{AA'M}} = \frac{1}{2}a\sqrt 6 .\frac{{a\sqrt 3 }}{2} = \frac{{3{a^2}\sqrt 2 }}{4}\)
\({S_{MD'K}} = \frac{1}{2}.\frac{{a\sqrt 3 }}{2}.\frac{{a\sqrt 6 }}{2} = \frac{{3{a^2}\sqrt 2 }}{8}\)
\({S_{ADK}} = \frac{1}{2}.\frac{{a\sqrt 6 }}{2}.a\sqrt 3 = \frac{{3{a^2}\sqrt 2 }}{4}\)
\({S_{\Delta AMK}} = {S_{AA'D'D}} - \left( {{S_{\Delta A'AM}} + {S_{\Delta MD'K}} + {S_{\Delta ADK}}} \right)\)
\( = 3{a^2}\sqrt 2 - \left( {\frac{{3{a^2}\sqrt 2 }}{4} + \frac{{3{a^2}\sqrt 2 }}{8} + \frac{{3{a^2}\sqrt 2 }}{4}} \right) = \frac{{9{a^2}\sqrt 2 }}{8}\)
Mặt khác: \[{S_{\Delta AMK}} = \frac{1}{2}AM.KH\]
\( \Rightarrow \frac{{9{a^2}\sqrt 2 }}{8} = \frac{1}{2}.\frac{{3a\sqrt 3 }}{2}.KH\)
\( \Rightarrow KH = \frac{{a\sqrt 6 }}{2}\). Chọn C
