Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 22)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 22)
-
81 lượt thi
-
86 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
Phần tư duy đọc hiểu
Từ đoạn số [1], cụ Kép nghĩ rằng mình không phù hợp để chơi hoa vì lí do nào sau đây?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn số [1].
Lời giải
- Đáp án A sai vì đây là lời giới thiệu về cụ Kép chứ không phải lí do cho việc cụ không phù hợp để chơi hoa.
- Đáp án B đúng vì theo đoạn [1] có viết “Nhưng nghĩ rằng mình chỉ là một anh nhà nho sống vào giữa buổi Tây Tàu nhố nhăng làm lạc mất cả quan niệm cũ, làm tiêu hao mất bao nhiêu giá trị tinh thần; nhưng nghĩ mình chỉ là một kẻ chọn nhầm thế kỷ với hai bàn tay không có lợi khí mới, thì riêng lo cho thân thế, lo cho sự mất còn của mình cũng chưa xong, nói chi đến chuyện chơi hoa”. Có thể thấy, cụm từ “mình chỉ là…nói chi đến chuyện chơi hoa” đã khẳng định trước đây cụ Kép cho rằng mình không phù hợp chơi hoa vì lí do như đáp án B đề cập.
- Đáp án C sai vì đây là điều kiện đặt ra với một người chơi hoa là phải có thời gian để săn sóc hoa.
- Đáp án D sai vì ý này nói tới thái độ, cách ứng xử của con người đối với việc chăm hoa.
Chọn B
Câu 2:
Cụ Kép đối xử với hoa bằng tình cảm, thái độ như thế nào? (Chọn 2 đáp án đúng)
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung văn bản, đặc biệt đoạn số [1]
Lời giải
- Từ đoạn [1] có thể thấy “Cụ muốn nói rằng người chơi hoa nhiều khi phải lấy cái chí thành chí tình ra mà đối đãi với giống hoa cỏ không bao giờ biết lên tiếng” như vậy đáp án D là chính xác.
- Trong cả văn bản, cách cụ Kép chăm hoa, nói về hoa là đủ thấy sự trân trọng, nâng niu của cụ nhưng không phải cái đắm đuối đến quên ăn quên ngủ mà vô cùng chừng mực. Vậy nên đáp án đúng là A.
Chọn A, D
Câu 3:
Dựa vào đoạn số [3], điền một từ ngữ không quá một tiếng có trong bài đọc vào chỗ trống.
Kẹo mạch nha được nấu vô cùng cẩn thận và kĩ lưỡng, người trông nồi kẹo cần phải điều chỉnh được độ to nhỏ của ngọn lửa, nếu không sẽ dễ gây ra tình trạng nồi kẹo bị _______.
 Xem đáp án
Xem đáp án
Đáp án: "khê"
Phương pháp giải
Căn cứ vào nội dung đoạn số [3].
Lời giải
Trong đoạn số [3] có thông tin sau đây “Cụ Kép dặn bõ già phải cẩn thận xem lửa kẻo lơ đễnh một chút là khê mất nồi kẹo”. Như vậy có thể thấy, nếu người trông nồi kẹp không cẩn thận điều chỉnh lửa thì nồi kẹp mạch nha sẽ dễ bị khê.
=> Đáp án: khê.
Câu 4:
Hoàn thành câu hỏi bằng cách chọn đáp án đúng hoặc sai.
Hai ông ấm – con trai cụ Kép là những người con hiếu thảo, luôn cố gắng làm cha vui lòng khi toại được sở thích của mình.
Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn số [3], [4].
Lời giải
Qua đoạn số [4] có thể nhận thấy thông tin “Họ rất vui sướng vì họ tin đã làm toại được sở thích của cha già”. Thêm vào đó là một số chi tiết ở đoạn số [3] như “Hai ông ấm, con trai cụ Kép, người lớn tuổi đứng đắn như thế, mà lại ngồi gần đấy, phất giấy vào những nan lồng”. Điều này cho thấy dù đã lớn tuổi nhưng hai người con của cụ Kép rất hiếu thảo, sẵn sàng làm mọi chuyện để cha vui lòng. Song, những việc như phất lồng bàn giấy là sở thích của người cha già chứ không phải sở thích của chính họ. Vì vậy, nhận định của đề bài là chưa chính xác.
Chọn B
Câu 5:
uống rượu thưởng trăng, làm thơ, nấu kẹo mạch nha, cúng bái, bình thơ, uống rượu thưởng hoa
Không khí Tết cổ truyền được miêu tả qua những chi tiết: Cụ Kép cùng con cháu quây quần chăm chút cho vườn lan nở đúng dịp Tết, _______ ướp hương lan, _______ đêm giao thừa, _______ cùng những người bạn già, _______ và thưởng thức cái không khí êm đềm của mùa xuân.
 Xem đáp án
Xem đáp án
Đáp án
Không khí Tết cổ truyền được miêu tả qua những chi tiết: Cụ Kép cùng con cháu quây quần chăm chút cho vườn lan nở đúng dịp Tết, nấu kẹo mạch nha ướp hương lan, cúng bái đêm giao thừa, uống rượu thưởng hoa cùng những người bạn già, bình thơ và thưởng thức cái không khí êm đềm của mùa xuân.
Phương pháp giải
Căn cứ vào nội dung văn bản.
Lời giải
Theo thông tin từ văn bản, đúng trình tự kể chuyện của tác giả thì ở đoạn [3] đã xuất hiện chi tiết “Đêm giao thừa, bên cạnh nồi bánh chưng sôi sình sịch, bõ già đang chăm chú canh nồi kẹo mạch nha”. Như vậy, từ khóa còn thiếu phù hợp với ô số 1 là nấu kẹo mạch nha ướp hương lan.
=> [vị trí thả 1]: nấu kẹo mạch nha
Sau đó đến đoạn số [6], khi nồi kẹo mạch nha đã nấu xong và hoàn tất mọi công đoạn thì xuất hiện chi tiết “Úp xong lồng bàn giấy lên mười chậu Mặc lan thì vừa cúng giao thừa. Ba ông con, khăn lượt áo thâm lạy trước bàn thờ đặt ngoài trời”. Đây là hành động cúng bái vào đêm giao thừa – một trong những nghi lễ truyền thống của người Việt.
=> [vị trí thả 2]: cúng bái
Ngay trong đoạn số [6] tiếp tục đề cập đến thông tin “Trước khi ra đình cụ đã dặn bõ già ở nhà phải sửa soạn cho đủ để đến quá trưa, cụ và vài cụ nữa đi việc đình làng về sẽ cùng uống rượu thưởng hoa”. Như vậy không phải uống rượu thưởng trăng mà phải là thưởng hoa.
=> [vị trí thả 3]: uống rượu thưởng hoa
Vị trí ô trống cuối cùng sẽ dễ bị nhầm lẫn hai hành động làm thơ hoặc bình thơ. Tuy nhiên có thể thấy ở đoạn [8], các cụ không phải đang làm thơ, sáng tác ngay tức khắc mà đã chuẩn bị trước và mang đến nhờ mọi người cùng góp ý. Như vậy đáp án đúng là bình thơ.
=> [vị trí thả 4]: bình thơ
Đáp án:
[vị trí thả 1]: nấu kẹo mạch nha
[vị trí thả 2]: cúng bái
[vị trí thả 3]: uống rượu thưởng hoa
[vị trí thả 4]: bình thơ
Câu 6:
nho sĩ, lòng yêu nước, truyền thống văn hóa, ngườ nghệ sĩ, tinh hoa văn hóa, bậc hiền triết
Tác phẩm “Hương cuội” đã thể hiện tinh thần dân tộc sâu sắc với một số biểu hiện sau: - Ca ngợi vẻ đẹp _______ của dân tộc: Uống rượu, ngâm thơ, thưởng hoa, đặc biệt là thú làm kẹo hương cuội vào dịp Tết cổ truyền.- Ca ngợi những _______ thanh cao, có tâm hồn và thú vui tao nhã luôn có ý thức trong việc gìn giữ truyền lại cho con cháu vẻ đẹp truyền thống của dân tộc.- Bất hòa với hiện thực, Nguyễn Tuân đã tìm về quá khứ của dân tộc, ca ngợi vẻ đẹp văn hóa, vẻ đẹp của con người Việt một thời nay còn vang bóng. Đó cũng chính là một cách để Nguyễn Tuân cũng như các nhân vật của ông bày tỏ _______ và sự chán ghét những biểu hiện nhố nhăng của xã hội đương thời.
 Xem đáp án
Xem đáp án
Đáp án
Tác phẩm “Hương cuội” đã thể hiện tinh thần dân tộc sâu sắc với một số biểu hiện sau: - Ca ngợi vẻ đẹp truyền thống văn hóa của dân tộc: Uống rượu, ngâm thơ, thưởng hoa, đặc biệt là thú làm kẹo hương cuội vào dịp Tết cổ truyền.- Ca ngợi những nho sĩ thanh cao, có tâm hồn và thú vui tao nhã luôn có ý thức trong việc gìn giữ truyền lại cho con cháu vẻ đẹp truyền thống của dân tộc.- Bất hòa với hiện thực, Nguyễn Tuân đã tìm về quá khứ của dân tộc, ca ngợi vẻ đẹp văn hóa, vẻ đẹp của con người Việt một thời nay còn vang bóng. Đó cũng chính là một cách để Nguyễn Tuân cũng như các nhân vật của ông bày tỏ lòng yêu nước và sự chán ghét những biểu hiện nhố nhăng của xã hội đương thời.
Phương pháp giải
Căn cứ vào nội dung văn bản.
Lời giải
Có thể thấy các thú chơi như uống rượu, ngâm thơ, thưởng hoa, đặc biệt là thú làm kẹo hương cuội đều là những phong tục truyền thống của Tết cổ truyền mà chúng ta thường gọi là truyền thống văn hóa của dân tộc.
=> [vị trí thả 1]: truyền thống văn hóa
Lớp người như cụ Kép và những người bạn của cụ trong thời kì phong kiến, hoặc những năm đầu thế kỉ XX được gọi là những nhà nho, hay còn gọi là nho sĩ.
=> [vị trí thả 2]: nho sĩ
Những biểu hiện như tìm về quá khứ của dân tộc, ca ngợi vẻ đẹp văn hóa, vẻ đẹp của con người Việt đều thể hiện một tấm lòng yêu đất nước sâu nặng, cháy bỏng của tác giả Nguyễn Tuân.
=> [vị trí thả 3]: lòng yêu nước
Đáp án:
[vị trí thả 1]: truyền thống văn hóa
[vị trí thả 2]: nho sĩ
[vị trí thả 3]: lòng yêu nước
Câu 7:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung văn bản.
Lời giải
Trước hết cần xác định thú vui của cụ Kép trong văn bản là gì? Có thể nhận thấy nổi bật lên là cụ thích chơi hoa, làm kẹo mạch nha, uống rượu thưởng hoa,… Những thú vui kể trên đều là những điều vô cùng cao đẹp, là những giá trị văn hóa gắn liền với truyền thống của dân tộc. Vậy nên, thú vui của cụ Kép là thú vui thanh cao và tao nhã.
Chọn A
Câu 8:
Với tính cách của cụ Kép, theo em vì sao cụ KHÔNG trồng lan Bạch ngọc?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn số [2].
Lời giải
- Đáp án A sai vì trong đoạn số [2] có thông tin “Không phải vì lan Bạch ngọc đắt giá mỗi giò mười đồng bạc, mà cụ Kép không trồng giống hoa này”. Có thể thấy chính đoạn văn đã khẳng định giá đắt không phải lí do khiến cụ Kép không trồng giống hoa này.
- Đáp án B đúng vì “Tôi tự biết không chăm được lan Bạch ngọc. Công phu lắm, ông ạ”. Điều này chứng tỏ hoa Bạch ngọc rất khó chăm, tốn nhiều công sức của người trồng.
- Đáp án C sai vì “Lan Bạch ngọc hay ưa hơi đàn bà. Trồng nó ở vườn các tiểu thư thì phải hơn” tức là lan Bạch ngọc phù hợp, ưa thích bàn tay người phụ nữ chăm sóc hơn, chứ không phải bắt buộc phải là người phụ nữ. Như vậy đáp án D là chính xác.
Chọn B, D
Câu 9:
Dựa vào văn bản, điền hai từ ngữ phù hợp, mỗi từ không quá hai tiếng vào chỗ trống.
Nhan đề “Hương cuội” trong văn cảnh truyện ngắn này có nghĩa là mùi hương của _______. Nó được chọn làm _______ và được ướp hương lan nên có mùi hương của hoa lan.
 Xem đáp án
Xem đáp án
Đáp án:
Nhan đề “Hương cuội” trong văn cảnh truyện ngắn này có nghĩa là mùi hương của đá cuội. Nó được chọn làm nhân kẹo và được ướp hương lan nên có mùi hương của hoa lan.
Phương pháp giải
Căn cứ vào nội dung văn bản, nhan đề.
Lời giải
- Dựa vào nội dung văn bản, đặc biệt là đoạn số [5] có thể thấy cách làm kẹo mạch nha được miêu tả như sau “Bây giờ thêm được bõ già đỡ một tay nữa, cả ba ông con đều lấy những hòn cuội để riêng ban nãy ra mẹt, đem dúng đá cuội vào nồi kẹo, quấn kẹo bọc kín lấy đá, được viên nào liền đem đặt luôn vào lồng chậu hoa. Những viên đá bọc kẹo được đặt nhẹ nhàng lên trên lượt đá lót lên nền đất chậu hoa”. Từ chi tiết này có thể thấy, “hương cuội” chính là mùi hương của viên đá cuội đã được chọn lọc kĩ lưỡng, ướp hương hoa lan và sau đó được sử dụng để làm nhân kẹo mạch nha. Qua cách làm đó kẹo mạch nha tự nhiên mang mùi hương hoa lan thơm ngát.
- Đáp án: đá cuội/nhân kẹo
Câu 10:
Hoàn thành câu hỏi bằng cách chọn đáp án đúng hoặc sai:
Tình cảm, thái độ của tác giả Nguyễn Tuân đối với nhân vật cụ Kép trong văn bản trên là gì?
|
|
ĐÚNG |
SAI |
|
- Nguyễn Tuân trân trọng, cảm phục, khát vọng nhập vào thú chơi tao nhã của nhân vật. |
||
|
- Nguyễn Tuân lí tưởng hóa nhân vật lên hàng nghệ sĩ trong lĩnh vực chơi hoa. |
||
|
Vì lan Bạch ngọc yếu ớt buộc phải có phụ nữ chăm sóc. |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
- Nguyễn Tuân trân trọng, cảm phục, khát vọng nhập vào thú chơi tao nhã của nhân vật. |
X | |
|
- Nguyễn Tuân lí tưởng hóa nhân vật lên hàng nghệ sĩ trong lĩnh vực chơi hoa. |
X | |
|
Vì lan Bạch ngọc yếu ớt buộc phải có phụ nữ chăm sóc. |
X |
Phương pháp giải
Căn cứ vào nội dung văn bản.
Lời giải
- Thông tin thứ nhất sai vì Nguyễn Tuân có thể hiện sự trân trọng và cảm phục nhân vật nhưng không bày tỏ khát vọng nhập vào thú chơi của nhân vật. Tác giả chỉ đóng vai trò của người đứng ngoài nhìn vào.
- Thông tin thứ hai đúng vì Nguyễn Tuân đã lí tưởng hóa nhân vật cụ Kép trở thành một người nghệ sĩ trong lĩnh vực chơi hoa, thưởng hoa uống rượu với giá trị văn hóa truyền thống tốt đẹp. Từng cử chỉ, động tác, yêu cầu của cụ Kép trong thú chơi tao nhã này đều khắt khe và đầy nghệ thuật.
- Thông tin thứ ba đúng vì tác phẩm được đặt trong tập truyện “Vang bóng một thời”, điều nà chứng tỏ tất cả các thú chơi trong tác phẩm dù tao nhã, thanh cao đến nhường nào đều cũng chỉ còn là quá khứ vọng lại, vì vậy nên tác giả luôn thường trực cảm xúc nuối tiếc trước những người đã qua.
Câu 11:
Mục đích chính của văn bản là gì?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung văn bản, nhan đề.
Lời giải
Từ nội dung văn bản và tên nhan đề có thể thấy bài viết đang nói về mối quan hệ giữa DNA bạch tuộc và phiến băng Nam cực, cụ thể hơn là các nhà khoa học đang nỗ lực tìm kiếm và chứng minh DNA bạch tuộc có khả năng cung cấp manh mối, dự báo về tương lai của phiến băng Nam cực.
Đáp án: C. Làm rõ khả năng của DNA bạch tuộc trong việc cung cấp thông tin về phiến băng Nam cực.
Chọn C
Câu 12:
thực vật, lục địa, sự sản sinh, sự di truyền, động vật, chu vi
Nếu băng tan chảy, bạch tuộc ở các vùng khác nhau có thể di chuyển và gặp gỡ nhau, bằng chứng của điều này là _______ có thể có trong DNA. Nhưng nếu phiến băng không tan chảy, sự lai giống sẽ chỉ xảy ra trong phạm vi các quần thể bạch tuộc thuộc cùng một _______. Và bằng kết quả nghiên cứu DNA đã cho thấy, thực sự đã có những kết nối trực tiếp giữa ba quần thể bạch tuộc khác nhau trong quá trình băng tan. Điều này đã chứng minh DNA _______ như một đại diện/bằng chứng cho những thay đổi của phiến băng.
 Xem đáp án
Xem đáp án
Đáp án
Nếu băng tan chảy, bạch tuộc ở các vùng khác nhau có thể di chuyển và gặp gỡ nhau, bằng chứng của điều này là sự sinh sản có thể có trong DNA. Nhưng nếu phiến băng không tan chảy, sự lai giống sẽ chỉ xảy ra trong phạm vi các quần thể bạch tuộc thuộc cùng một lục địa. Và bằng kết quả nghiên cứu DNA đã cho thấy, thực sự đã có những kết nối trực tiếp giữa ba quần thể bạch tuộc khác nhau trong quá trình băng tan. Điều này đã chứng minh DNA động vật như một đại diện/bằng chứng cho những thay đổi của phiến băng.
Phương pháp giải
Căn cứ vào nội dung văn bản.
Lời giải
Đoạn [6] của văn bản đề cập đến thông tin “Nếu băng tan chảy, các hải lưu có thể mở rộng và kết nối những vũng vịnh với nhau. Bạch tuộc có thể di chuyển trực tiếp sang các vùng đó và bằng chứng của sự sản sinh có thể có trong DNA”. Như vậy, có thể thấy ô trống cần điền là sự sinh sản.
=> [vị trí thả 1]: sự sinh sản
Tiếp đó, trong đoạn [6] cũng đề cập tới thông tin thứ 2 như sau “Nhưng nếu phiến băng không tan chảy, chúng ta chỉ có thể thấy bằng chứng của sự lai giống giữa các quần thể bạch tuộc theo chu vi của lục địa này”. Tức là khi băng không tan chảy, sẽ không có các dòng hải lưu cuốn bạch tuộc đến các vùng khác thì chúng se chỉ lai giống trong cùng một lục địa.
=> [vị trí thả 2]: lục địa
Ở đoạn [7] thông tin có ô trống thứ [3] được nhắc trực tiếp “Để sử dụng DNA động vật như một đại diện/bằng chứng cho những thay đổi của phiến băng, chúng tôi đã phải kết hợp nhiều ngành và nhiều quốc gia”.
[vị trí thả 3]: động vật
Đáp án:
[vị trí thả 1]: sự sinh sản
[vị trí thả 2]: lục địa
[vị trí thả 3]: động vật
Câu 13:
Dựa vào đoạn số [2], điền một cụm từ không quá hai tiếng có trong bài đọc vào chỗ trống.
Điểm giống nhau giữa thời đại của chúng ta và khoảng thời gian 125.000 năm trước chính là nhiệt độ Trái đất đang dần _______
 Xem đáp án
Xem đáp án
Đáp án: "ấm hơn"
Phương pháp giải
Căn cứ vào nội dung đoạn số [2].
Lời giải
- Trong đoạn số [2] đã cung cấp những thông tin khá đầy đủ rằng “Khoảng 125.000 năm trước, trái đất trong thời kỳ ấm cuối cùng giữa những thời kỳ băng hà. Nhiệt độ toàn cầu trong suốt thời kỳ gian băng ấm hơn khoảng 0,5 đến 1,5° C hơn các mức nhiệt độ ở thời kỳ tiền công nghiệp.
- Điều này hết sức tương đồng với thời đại chúng ta. Bởi khoảng một phần ba của năm 2023, nhiệt độ trái đất ấm hơn 1,5° C so với thời kỳ tiền công nghiệp, do biến đổi khí hậu.”
- Điều này cho thấy nhiệt độ trái đất ấm lên khoảng 1,5° C chính là điểm giống nhau của hai thời điểm này.
Câu 14:
Theo đoạn số [4], lí do nào đã khiến các nhà khoa học chọn nghiên cứu DNA của bạch tuộc Turquet? (Chọn 2 đáp án đúng)
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn số [4].
Lời giải
- Đáp án A sai vì đây là đặc điểm không liên quan tới việc nghiên cứu DNA của bạch tuộc Turquet.
- Đáp án B đúng vì việc bạch tuộc Turquet sống ở khắp chốn quanh Nam Cực sẽ là điều kiện thuận lợi để tiến hành thí nghiệm trên một loài vật đặc trưng của vùng biển này.
- Đáp án C sai vì thông tin này không xuất hiện trong văn bản, thậm chí trong đoạn [4] còn có thông tin “không có con nào di chuyển xa khỏi khu nhà mình”.
- Đáp án D đúng vì việc bạch tuộc Turquet không di chuyển khởi nhà mình, không lai giống là một điều kiện thuận lợi để nghiên cứu AND của chúng.
Chọn B, D
Câu 15:
Hoàn thành câu hỏi bằng cách chọn đáp án đúng hoặc sai.
Theo đoạn [6], nếu nhiệt độ trái đất ấm lên vượt mức cảnh báo từ 1,5° C hoặc thậm chí là 2°C của Thỏa thuận Paris thì phiến băng Tây Nam cực sẽ sụp đổ hết.
Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn số [6]
Lời giải
Theo thông tin ở đoạn [6] thì “Công trình nghiên cứu của chúng tôi đem lại bằng chứng thực nghiệm đầu tiên về phiến băng Tây Nam cực có thể bắt đầu suy sụp nếu chúng ta vượt quá mục tiêu giới hạn cảnh báo từ 1,5° C hoặc thậm chí là 2°C của Thỏa thuận Paris”. Ở đây, ngữ liệu sử dụng cách diễn đạt là “có thể bắt đầu suy sụp” nghĩa là khi nhiệt độ tăng đến mức độ đó sẽ có dấu hiệu của việc băng tan chứ không phải băng sẽ sụp đổ/tan hết.
Đáp án: B
Câu 16:
Theo đoạn [8], để hiểu những gì xảy ra khi băng tan do trái đất nóng lên, chúng ta nên sử dụng phương pháp nghiên cứu nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn số [8].
Lời giải
Trong đoạn [8] có thông tin như sau “Chúng tôi hy vọng sẽ tiếp tục sử dụng DNA như một đại diện để khám phá những phần khác nhau của Nam Cực với lịch sử khí hậu vẫn còn được ít hiểu biết”. Như vậy có thể thấy từ tín hiệu tích cực khi nghiên cứu DNA của bạch tuộc Turquet, các nhà khoa học hi vọng có thể tiếp tục dùng cách thức này để nghiên cứu nhiều hiện tượng tự nhiên khác, đặc biệt là hiện tượng băng tan.
Đáp án: A. Cách tiếp cận sử dụng DNA của loài vật.
Câu 17:
Các nhà khoa học đã tìm thấy những kết nối trực tiếp giữa ba quần thể bạch tuộc ở Weddell, Amundsen và Ross trong những thời điểm nào? (Chọn 2 đáp án đúng)
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn số [6].
Lời giải
- Đáp án A và B là hai đáp án không được nhắc tới trong văn bản.
- Đáp án C và D đều được đề cập tới ở đoạn số [6] với thông tin như sau: “đầu tiên chúng tôi tìm thấy những kết nối trực tiếp giữa ba quần thể trong suốt thời kỳ Pliocene giữa, vào khoảng 3 triệu đến 3,6 triệu năm trước, khi nhiệt độ nóng hơn 2 đến 3° C và mực nước hiển cao hơn hiện nay 25 mét” và thông tin thứ hai là “Những dấu hiệu về kết nối trực tiếp trong DNA được tìm thấy gần đây giữa bạch tuộc ở ba vùng biển đã xảy ra trong thời kỳ gian băng cuối cùng khoảng 125.000 năm trước”.
=> Đáp án: C và D
Câu 18:
Dựa vào thông tin bài đọc, hoàn thành câu hỏi bằng cách chọn đáp án đúng hoặc sai.
|
|
ĐÚNG |
SAI |
|
- Băng tan chảy đã tạo nên sự lai giống giữa các quần thể bạch tuộc không cùng thuộc một khu vực. |
||
|
- Chưa tìm ra sự kết nối giữa các quần thể bạch tuộc ở Weddell, Amundsen và Ross. |
||
|
- Các quần thể bạch tuộc ở Weddell, Amundsen và Ross có nhiều cách để liên hệ với nhau và tạo ra sự lai giống. |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
- Băng tan chảy đã tạo nên sự lai giống giữa các quần thể bạch tuộc không cùng thuộc một khu vực. |
X | |
|
- Chưa tìm ra sự kết nối giữa các quần thể bạch tuộc ở Weddell, Amundsen và Ross. |
X | |
|
- Các quần thể bạch tuộc ở Weddell, Amundsen và Ross có nhiều cách để liên hệ với nhau và tạo ra sự lai giống. |
X |
Phương pháp giải
Căn cứ vào nội dung đoạn số [5].
Lời giải
Thông tin thứ nhất đúng vì theo đoạn số [5] “Nếu băng tan chảy, các hải lưu có thể mở rộng và kết nối những vũng vịnh với nhau. Bạch tuộc có thể di chuyển trực tiếp sang các vùng đó và bằng chứng của sự sản sinh có thể có trong DNA” chứng tỏ sự tan chảy của các tảng băng chính là nguyên nhân tạo nên sự lai giống của các quần thể bạch tuộc ở các khu vực khác nhau. Nhưng ngữ liệu dùng từ nêu giả thiết “Nếu…” chứng tỏ đây là thông tin chưa xác định. Tuy nhiên, ngay bên dưới kết quả nghiên cứu đã cho thấy “đúng, có những kết nối trực tiếp giữa ba quần thể bạch tuộc đó”. Điều này kết luận nhận định số 1 là chính xác.
Thông tin thứ hai sai vì như đã nói ở trên, ngữ liệu đã khẳng định “đúng, có những kết nối trực tiếp giữa ba quần thể bạch tuộc đó”.
Thông tin số 3 là sai vì đoạn số [5] nói rõ thông tin “Những quần thể đó có thể chỉ đến từ liên hệ qua những dòng hải lưu mà giờ bị khối băng Tây Nam cực ngăn cản”. Tức là chỉ khi băng tan và nhờ những dòng hải lưu thì 3 quần thể bạch tuộc này mới có thể có mối liên hệ với nhau.
Câu 19:
Hãy hoàn thành câu sau bằng cách kéo thả các cụm từ vào đúng vị trí.
mọi loài vật, cuốn sách lịch sử, tính di truyền, các sinh vật, tính sinh sản, bách khoa toàn thư
Để có được câu trả lời chính xác hơn về thời gian phiến băng bị tách khỏi nơi nó tồn tại, các nhà khoa học nghiên cứu _______ của động vật chân đầu (cephalopod). Các nhà khoa học cho rằng họ có thể sử dụng DNA của _______ để nhìn lại và điểm ra sự khác biệt của các quần thể động vật được lai giống. Bởi vì mỗi DNA của chúng là một _______ và giờ chúng ta có công nghệ để đọc được nó.
 Xem đáp án
Xem đáp án
Đáp án
Để có được câu trả lời chính xác hơn về thời gian phiến băng bị tách khỏi nơi nó tồn tại, các nhà khoa học nghiên cứu tính di truyền của động vật chân đầu (cephalopod). Các nhà khoa học cho rằng họ có thể sử dụng DNA của các sinh vật để nhìn lại và điểm ra sự khác biệt của các quần thể động vật được lai giống. Bởi vì mỗi DNA của chúng là một cuốn sách lịch sử và giờ chúng ta có công nghệ để đọc được nó.
Phương pháp giải
Căn cứ vào nội dung văn bản.
Lời giải
Trong đoạn [4] có đề cập tới “Để có được câu trả lời chính xác hơn, chúng tôi nhìn vào tính di truyền của động vật chân đầu (cephalopod)”. Kết nối với nội dung trước đó thì nhận thấy, để hiểu hơn về thời gian băng tan, các nhà khoa học đã chọn nghiên cứu tính di truyền của động vật chân đầu, tiêu biểu là bạch tuộc.
=> [vị trí thả 1]: tính di truyền
Đoạn số [4] có đề cập đến thông tin “Mỗi DNA của các sinh vật là một cuốn sách lịch sử và giờ chúng ta có công nghệ để đọc được nó. Chúng tôi có thể sử dụng DNA để nhìn lại và điểm ra sự khác biệt của các quần thể động vật được lai giống”. Từ phần in đậm của thể thấy, các nhà nghiên cứu sẽ chọn đối tượng là DNA của các sinh vật chứ không phải mọi loài vật, ít nhất trong bài viết này là động vật chứ không phải thực vật. Và mỗi DNA này lại giống một cuốn sách lịch sử gợi mở cho khoa học về đời sống của hiện tượng tự nhiên trước đó.
=> [vị trí thả 2]: các sinh vật
[vị trí thả 3]: cuốn sách lịch sử
Đáp án:
[vị trí thả 1]: tính di truyền
[vị trí thả 2]: các sinh vật
[vị trí thả 3]: cuốn sách lịch sử
Câu 20:
Điền một cụm từ không quá bốn tiếng có trong bài đọc vào chỗ trống.
Sử dụng DNA động vật như một đại diện/bằng chứng cho những thay đổi của phiến băng là một nghiên cứu _______. Bởi vì điều này đòi hỏi kết hợp nhiều nhà khoa học vật lý và sinh học lại với nhau đem lại những cách thức mới để trả lời những câu hỏi tồn tại đã lâu và có tầm quan trọng sống còn với tất cả chúng ta.
 Xem đáp án
Xem đáp án
Đáp án: "khoa học liên ngành"
Phương pháp giải
Căn cứ vào nội dung đoạn số [7].
Lời giải
Trong đoạn số [7] có thông tin sau "Để sử dụng DNA động vật như một đại diện/bằng chứng cho những thay đổi của phiến băng, chúng tôi đã phải kết hợp nhiều ngành và nhiều quốc giA. Kết hợp nhiều nhà khoa học vật lý và sinh học lại với nhau đem lại những cách thức mới để trả lời những câu hỏi tồn tại đã lâu và có tầm quan trọng sống còn với tất cả chúng ta". Lĩnh vực khoa học có sự kết hợp của nhiềus ngành nghề được gọi là khoa học liên ngành. Thuật ngữ này cũng được nhắc tới ngay chính trong đoạn số [7] "Nhưng thật khó để đảm bảo cho khoa học liên ngành bởi nó đòi hỏi thời gian, nỗ lực và tư duy mở để đánh giá cao về thuật ngữ mới, các quy mô và các cách tiếp cận mới"
Câu 21:
Phần tư duy khoa học / giải quyết vấn đề
Điền các cụm từ thích hợp vào chỗ trống.
- Khi dịch hai khe lại gần màn chắn thì khoảng vân sẽ _______
- Khi giảm khoảng cách hai khe thì khoảng vân sẽ _______
 Xem đáp án
Xem đáp án
Đáp án:
- Khi dịch hai khe lại gần màn chắn thì khoảng vân sẽ giảm
- Khi giảm khoảng cách hai khe thì khoảng vân sẽ tăng
Phương pháp giải
Sử dụng công thức tính khoảng vân bài cung cấp.
Lời giải
Ta có khoảng vân được xác định bằng: \[i = \frac{{\lambda D}}{a}\]
ta thấy rằng:
- Khi dịch hai khe lại gần màn chắn thì khoảng vân sẽ giảm
- Khi giảm khoảng cách hai khe hẹp đi thì khoảng vân sẽ tăng
Câu 22:
Một trong hai khe hẹp được làm mờ sao cho nó chỉ truyền ánh sáng được bằng ½ cường độ sáng của khe còn lại. Kết quả xảy ra là:
 Xem đáp án
Xem đáp án
Phương pháp giải
Hiện tượng giao thoa là hiện tượng khi hai sóng kết hợp gặp nhau thì có những điểm ở đó hai sóng luôn đồng pha thì dao động mạnh; có những điểm ở đó hai sóng luôn ngược pha thì đứng yên
Lời giải
Khi ta làm mờ 1 khe thì tại nơi giao thoa cực đại ánh sáng là giao thoa bởi 2 ánh sáng khác cường độ nên tối hơn , còn ở nơi giao thoa cực tiểu ánh sáng không bị triệt tiêu bởi ánh sáng có cùng cường độ nên yếu hơn
Đáp án: D
Câu 23:
Trong thí nghiệm Young về giao thoa ánh sáng, khoảng vân sẽ thay đổi thế nào khi ta thay nguồn sáng đơn sắc có bước sóng λ bằng ánh sáng đơn sắc có bước sóng là 1,2λ? Nếu khoảng cách từ hai khe đến màn quan sát giữ cố định, ta phải thay đổi khoảng cách giữa hai khe như thế nào để khoảng vẫn lại có độ lớn như ban đầu?
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng công thức tính khoảng vân bài cung cấp.
Lời giải
Ta có khoảng vân được xác định bằng: \[i = \frac{{\lambda D}}{a}\]
Từ công thức ta thấy nếu λ tăng thành 1,2λ để giữ nguyên i thì phải tăng a thành 1,2a
Chọn A
Câu 24:
Giả sử tại điểm M trên màn quan sát là vân sáng bậc 3. Khi đó, vị trí của M được xác định bằng biểu thức nào sau đây?
 Xem đáp án
Xem đáp án
Phương pháp giải
Vận dụng thông tin bài cung cấp.
Lời giải
Ta có khoảng vân i là khoảng cách giữa hai vân sáng hoặc vân tối liên tiếp.
Với M là vân sáng bậc 3 thì khi đó: xM = 3i
Chọn A
Câu 25:
Trong thí nghiệm giao thoa, khoảng cách hai khe hẹp là 1mm, khoảng cách D là 2m. Tại điểm M trên màn quan sát cách vân trung tâm 3mm có 1 vân sáng bậc 4. Bước sóng của ánh sáng trên là:
 Xem đáp án
Xem đáp án
Phương pháp giải
Vận dụng lí thuyết giao thoa ánh sáng.
Áp dụng công thức tính khoảng vân.
Lời giải
Vị trí vân sáng được sáng được xác định bằng: xM = ki
Ta có: \[i = \frac{{\lambda D}}{a}\]
\[ \Rightarrow 4.\frac{{\lambda .2}}{{{{1.10}^{ - 3}}}} = {3.10^{ - 3}}\]
\( \Rightarrow \lambda = 3,{75.10^{ - 7}}\;{\rm{m}} = 375\;{\rm{nm}}\)
Chọn C
Câu 26:
Cho hai từ: sóng, hạt. Hay chọn từ thích hợp điền vào chỗ trống:
Giao thoa ánh sáng là thí nghiệm chứng minh ánh sáng có tính chất _______
 Xem đáp án
Xem đáp án
Đáp án: "sóng"
Phương pháp giải
Phân tích thông tin bài cung cấp.
Lời giải
Giao thoa ánh sáng sẽ chứng minh ánh sáng có tính chất sóng.
Tương tự với giao thoa sóng cơ, sự giao thoa xảy ra khi sự tổng hợp của hai hoặc nhiều ánh sáng kết hợp trong không gian, tạo ra các vân sáng tối xen kẽ. Hai nguồn kết hợp ở đây là hai nguồn có cùng bước sóng và độ lệch pha giữa hai nguồn không thay đổi theo thời gian.
Câu 27:
Chọn các đáp án chính xác
Tế bào ung thư có đặc điểm nào sau đây?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào các thông tin có trong đoạn đọc liên quan đến tế bào ung thư.
Lời giải
Tế bào ung thư có đặc điểm:
- Có thể hình thành ở bất kỳ tế bào nào trong cơ thể và sẽ hoạt động rất khác so với một tế bào bình thường -> A sai.
- Tế bào ung thư liên tục phát triển và phân chia vượt khỏi tầm kiểm soát -> B đúng.
- Tế bào ung thư không thể trưởng thành như các tế bào khỏe mạnh khác mà vẫn ở mãi trạng thái chưa hoàn chỉnh -> C không đúng, D đúng.
Đáp án: B, D
Câu 28:
Điền đáp án chính xác vào chỗ trống.
Khối u được hình thành khi các tế bào unh thư không ngừng _______.
 Xem đáp án
Xem đáp án
Đáp án: "tăng sinh"
Phương pháp giải
Dựa vào các thông tin có trong đoạn đọc liên quan đến tế bào ung thư.
Lời giải
Khi các tế bào ung thư không ngừng tăng sinh, khối u cũng dần hình thành.
Đáp án: tăng sinh.
Câu 29:
carbon dioxide, oxygen, máu, ống tiêu hóa
Khối u sau khi hình thành sẽ phát triển nhờ lấy _______ và chất dinh dưỡng từ _______
 Xem đáp án
Xem đáp án
Đáp án
Khối u sau khi hình thành sẽ phát triển nhờ lấy oxygen và chất dinh dưỡng từ máu
Phương pháp giải
Dựa vào các thông tin có trong đoạn đọc liên quan đến tế bào ung thư.
Lời giải
Tế bào ung thư cũng có nhu cầu về oxy và chất dinh dưỡng từ máu như những tế bào bình thường khác để phát triển và tồn tại.
Một khối u nhỏ có thể dễ dàng phát triển nhờ được các mạch máu gần đó nuôi dưỡng.
Đáp án: oxygen/máu.
Câu 30:
Quan sát kết quả thí nghiệm, hãy xác định loại tế bào phát triển tốt nhất khi nồng độ glucose là 0.4 μM?
I. Tế bào A.
II. Tế bào B.
III. Tế bào C.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào kết quả thí nghiệm xác định ảnh hưởng của nồng độ glucose và calcium đối với sự phát triển của ba loại tế bào ung thư khác nhau.
Lời giải
Quan sát kết quả thí nghiệm, ta nhận thấy rõ có cả hai loại tế bào A và B đều có số lượng tế bào bằng nhau và lớn hơn tế bào C khi nồng độ glucose là 0.4 μM
Nên khi nồng độ glucose là 0.4 μM, tế bào A và B phát triển tốt nhất.
Đáp án: Chọn B
Câu 31:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào kết quả thí nghiệm xác định ảnh hưởng của nồng độ glucose và calcium đối với sự phát triển của ba loại tế bào ung thư khác nhau.
Lời giải
Số lượng tế bào A khoảng 3,5 triệu tế bào khi nồng độ calcium là 20 μM.
Đáp án: B
Câu 32:
Nhận định dưới đây đúng hay sai?
Các tế bào ung thư xâm lấn là các tế bào ung thư xuất hiện tại các mô lân cận vị trí cũ và trong quá trình phát triển không thể ảnh hưởng đến các tế bào khỏe mạnh tại đó.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào các thông tin có trong đoạn đọc liên quan đến tế bào ung thư.
Lời giải
Tế bào ung thư cũng tạo ra các enzyme khiến những tế bào và mô khỏe mạnh khác bị phá vỡ. Ung thư xuất hiện tại các mô lân cận vị trí cũ ban đầu được gọi là tế bào ung thư xâm lấn hoặc ung thư ác tính.
Đáp án: B. Sai.
Câu 33:
tuần hoàn, thần kinh, hô hấp
Khi cơ thể bị nhiễm virus cúm có thể dẫn đến suy _______ và tử vong.
 Xem đáp án
Xem đáp án
Đáp án
Khi cơ thể bị nhiễm virus cúm có thể dẫn đến suy hô hấp và tử vong.
Phương pháp giải
Đọc thông tin khái quát về virus cúm.
Lời giải
Virus cúm là tác nhân chủ yếu gây bệnh đường hô hấp trên ở chim, thú và người.
Khi cơ thể bị nhiễm bệnh nặng có thể dẫn đến suy hô hấp và tử vong.
Đáp án: hô hấp.
Câu 34:
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc thông tin về sự lây nhiễm của virus cúm.
Lời giải
Khi vào trong cơ thể người, virus xâm nhiễm vào các tế bào biểu mô đường hô hấp; virus cũng có thể xâm nhiễm vào các tế bào phế nang, tế bào tuyến nhày và đại thực bào.
Đáp án: B
Câu 35:
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc thông tin của virus cúm và quan sát hình ảnh virus cúm A.
Lời giải
- Dựa vào thông tin đoạn đọc ta nhận thấy vật chất di truyền của virus cúm là ARN.
- Khi quan sát ảnh, ta thấy nucleocapsid của virus cúm A là sợi đơn.
-> Nên Vật chất di truyền của virus cúm A là: ARN sợi đơn.
Đáp án: B
Câu 36:
Các nhận định dưới đây đúng hay sai?
|
|
ĐÚNG |
SAI |
|
A. Trên bề mặt virus cúm có hai loại kháng nguyên là gai H và gai N. |
||
|
B. Gai H khi xâm nhập vào cơ thể vật chủ sẽ làm ngưng kết hồng cầu vật chủ. |
||
|
C. Gai N làm giảm khả năng tự bảo vệ của đường hô hấp vật chủ. |
||
|
D. Trong cơ thể người, không có kháng thể kháng các kháng nguyên virus cúm. |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
A. Trên bề mặt virus cúm có hai loại kháng nguyên là gai H và gai N. |
X | |
|
B. Gai H khi xâm nhập vào cơ thể vật chủ sẽ làm ngưng kết hồng cầu vật chủ. |
X | |
|
C. Gai N làm giảm khả năng tự bảo vệ của đường hô hấp vật chủ. |
X | |
|
D. Trong cơ thể người, không có kháng thể kháng các kháng nguyên virus cúm. |
X |
Phương pháp giải
Đọc thông tin đặc điểm của virus cúm.
Lời giải
Ý A đúng, các loại virus cúm A được xác định dựa vào hai kháng nguyên bề mặt, đó là gai H (Hemagglutinin) và gai N (Neuraminidase).
Ý B đúng, gai H còn được gọi là nhân tố ngưng kết hồng cầu giúp virus bám vào tế bào niêm mạc đường hô hấp, từ đó xâm nhập vào trong tế bào.
Ý C đúng, gai N làm loãng chất nhầy ở đường hô hấp, từ đó làm giảm khả năng lọc không khí của đường hô hấp.
Ý D sai, kháng thể tương ứng với gai H là kháng thể ngăn ngưng kết hồng cầu có tác dụng bảo vệ, kháng thể tương ứng gai N có tác dụng bảo vệ cơ thể.
Đáp án: A, B, C đúng; D sai.
Câu 37:
Điền đáp án chính xác vào chỗ trống.
Các biến chủng virus cúm mới được hình thành khi các _______ trên bề mặt virus thay đổi.
 Xem đáp án
Xem đáp án
Đáp án: "kháng nguyên"
Phương pháp giải
Đọc thông tin đặc điểm của virus cúm.
Lời giải
Khi các kháng nguyên trên bề mặt virus thay đổi sẽ tạo ra những biến chủng virus mới
Đáp án: kháng nguyên
Câu 38:
Kéo thả đáp án chính xác vào chỗ trống
antigenic shift, antigenic drift
Để nghiên cứu độc lực của một chủng virus cúm, người ta cho chủng đó lây nhiễm vào cơ thể vật chủ thí nghiệm. Sau một thời gian, người ta phát hiện trong cơ thể vật chủ thí nghiệm, người ta phát hiện một biến chủng virus cúm mới khác với chủng virus cúm ban đầu.Biến chủng virus cúm mới có thể được hình thành từ cơ chế _________.
 Xem đáp án
Xem đáp án
Đáp án
Để nghiên cứu độc lực của một chủng virus cúm, người ta cho chủng đó lây nhiễm vào cơ thể vật chủ thí nghiệm. Sau một thời gian, người ta phát hiện trong cơ thể vật chủ thí nghiệm, người ta phát hiện một biến chủng virus cúm mới khác với chủng virus cúm ban đầu.Biến chủng virus cúm mới có thể được hình thành từ cơ chế antigenic drift.
Phương pháp giải
Đọc thông tin đặc điểm của virus cúm.
Lời giải
- Theo thông tin đề bài, ban đầu chỉ lây nhiễm vào cơ thể 1 chủng virus cúm nên không thể xảy ra quá trình hoán vị kháng nguyên (antigenic shift) (xảy ra khi có 2 hoặc nhiều chủng virus với nhiều đoạn ARN khác biệt nhau về mặt di truyền và cùng lúc xâm nhiễm vào một tế bào).
- Biến chủng virus cúm mới có thể được hình thành từ cơ chế biến thể kháng nguyên (antigenic drift).
Đáp án: antigenic drift
Câu 39:
Nhận định dưới đây đúng hay sai?
Sau khoảng 5 giờ, kể từ sau khi virus xâm nhiễm vào cơ thể, virus đã nhân lên, phát tán và lây nhiễm sang hầu hết các tế bào lân cận.
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc thông tin về sự lây nhiễm của virus cúm.
Lời giải
Ở trong các tế bào bị nhiễm, virus nhân lên trong vòng 4 - 6 giờ, sau đó phát tán và lây nhiễm sang các tế bào và vùng lân cận rồi biểu hiện bệnh trong vòng 18 - 72 giờ.
Do đó, sau khoảng 5 giờ, virus mới bắt đầu nhân lên trong tế bào xâm nhiễm.
Đáp án: Sai.
Câu 40:
Công thức phân tử của hợp chất phenolphtalein là
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào phương trình tổng hợp phenolphtalein, sản phẩm cuối cùng là công thức cấu tạo của phenolphtalein. Từ công thức cấu tạo suy ra được công thức phân tử.
Lời giải
Công thức phân tử của phenolphtalein là C20H14O4.
Chọn A
Câu 41:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào hình ảnh về công thức cấu tạo phenolphtalein.
Lời giải
Những đáp án mô tả thành phần và cấu trúc đúng của phân tử phenolphtalein là:
- Vòng thơm 6 cạnh.
- Phenol.
- Xeton.
- Dị vòng có chứa O.
Chọn A, C, F, I
Câu 42:
Chọn các đáp án đúng:
Những yếu tố chỉ ra rằng phenolphtalein là axit yếu là
|
|
ĐÚNG |
SAI |
|
Trong cấu trúc của phenolphtalein có 2 vòng phenol có tính axit yếu nên gây cho phenolphtalein có tính axit yếu. |
||
|
Trong cấu trúc của phenolphtalein có nhóm chức của axit cacboxylic nên gây ra tính axit yếu của phenolphtalein. |
||
|
Ka của axit HIn rất nhỏ, do đó khả năng phân li ra ion H+ của axit này rất yếu, nên tính axit của HIn yếu. |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Trong cấu trúc của phenolphtalein có 2 vòng phenol có tính axit yếu nên gây cho phenolphtalein có tính axit yếu. |
X | |
|
Trong cấu trúc của phenolphtalein có nhóm chức của axit cacboxylic nên gây ra tính axit yếu của phenolphtalein. |
X | |
|
Ka của axit HIn rất nhỏ, do đó khả năng phân li ra ion H+ của axit này rất yếu, nên tính axit của HIn yếu. |
X |
Phương pháp giải
Dựa vào các thông tin về phenolphtalein.
Lời giải
- Nhận định “Trong cấu trúc của phenolphtalein có 2 vòng phenol có tính axit yếu nên gây cho phenolphtalein có tính axit yếu” là đúng.
- Nhận định “Trong cấu trúc của phenolphtalein có nhóm chức của axit cacboxylic nên gây ra tính axit yếu của phenolphtalein” là sai, vì trong cấu trúc của phenolphtalein không có nhóm chức axit cacboxylic.
- Nhận định “Ka của axit HIn rất nhỏ, do đó khả năng phân li ra ion H+ của axit này rất yếu, nên tính axit của HIn yếu”.
Câu 43:
Điền số thích hợp vào chỗ trống (Làm tròn đến chữ số thập phân thứ nhất)
pH trung gian mà tại đó người ta mong chờ có sự đổi màu của chỉ thị phenolphtalein là _______.
 Xem đáp án
Xem đáp án
Đáp án: "9,5"
Phương pháp giải
Dựa vào công thức của phương trình Henderson – Hasselbalch: \(pH = p{K_a} + \log \frac{{\left[ {I{n^ - }} \right]}}{{[HIn]}}\).
Lời giải
Ka của HIn là 3×10−10, thay vào phương trình Henderson – Hasselbalch ta có:
\(pH = - \log \left( {3 \times {{10}^{ - 10}}} \right) + \log 1 = 9,5\)
Vậy số cần điền là 9,5.
Câu 44:
Kéo thả cụm từ thích hợp vào chỗ trống
không màu, màu hồng, HIn, In-, từ không màu sang màu hồng nhạt, từ màu hồng nhạt sang không màu
- Khi cho phenolphtalein vào cốc đựng dung dịch nước chanh có pH = 2,4 thì chỉ thị có màu _______.Khi cho phenolphtalein vào cốc đựng dung dịch Ba(OH)2 nồng độ 0,1M thì nồng độ của _______ trong dung dịch lớn hơn nồng độ của _______.- Trong phép chuẩn độ dung dịch HCl bằng dung dịch NaOH, sự đổi màu của dung dịch HCl trộn thêm chất chỉ thị phenolphtalein là _______.
 Xem đáp án
Xem đáp án
Đáp án
- Khi cho phenolphtalein vào cốc đựng dung dịch nước chanh có pH = 2,4 thì chỉ thị có màu không màu .Khi cho phenolphtalein vào cốc đựng dung dịch Ba(OH)2 nồng độ 0,1M thì nồng độ của In− trong dung dịch lớn hơn nồng độ của HIn .
- Trong phép chuẩn độ dung dịch HCl bằng dung dịch NaOH, sự đổi màu của dung dịch HCl trộn thêm chất chỉ thị phenolphtalein là từ không màu sang màu hồng nhạt.
Phương pháp giải
Dựa vào quá trình chuẩn độ bằng chất chỉ thị phenolphtalein.
Lời giải
- Khi cho phenolphtalein vào cốc đựng dung dịch nước chanh có pH = 2,4 thì chỉ thị có màu không màu vì môi trường 0 < pH < 8 thì phenolphtalein khộng đổi màu.
- Khi cho phenolphtalein vào cốc đựng dung dịch Ba(OH)2 nồng độ 0,1M thì nồng độ của In− trong dung dịch lớn hơn nồng độ của HIn.
- Trong phép chuẩn độ dung dịch HCl bằng dung dịch NaOH, sự đổi màu của dung dịch HCl trộn thêm chất chỉ thị phenolphtalein là từ không màu sang màu hồng nhạt.
Câu 45:
Để tổng hợp 18 mol phenolphtalein theo quá trình đã được Adolf van Bayer đã phát hiện ra vào năm 1871 cần bao nhiêu gam chất phản ứng? Biết phản ứng có hiệu suất 90%.
 Xem đáp án
Xem đáp án
Phương pháp giải
Tính số mol phenolphtalein theo lý thuyết thu được, từ đó tính được số mol các chất phản ứng tham gia
⇒ tính tổng khối lượng các chất phản ứng bao gồm khối lượng của phenol với anhyđrit phthaliC.
Lời giải
Phương trình tổng hợp phenolphtalein theo Adolf van Bayer là:
\({{\rm{C}}_6}{{\rm{H}}_5}{\rm{OH}} + {{\rm{C}}_6}{{\rm{H}}_4}{({\rm{CO}})_2}{\rm{O}} \to {{\rm{C}}_{20}}{{\rm{H}}_{14}}{{\rm{O}}_4}\)
Vì hiệu suất của phản ứng là 90% ⇒ Số mol HIn lý thuyết thu được là nHIn = 18 : 90% = 20mol
\( \Rightarrow {n_{{C_6}{{\rm{H}}_5}{\rm{OH}}}} = {n_{{{\rm{C}}_6}{{\rm{H}}_4}{{({\rm{CO}})}_2}{\rm{O}}}} = 20\;{\rm{mol}}\)
⇒ Khối lượng chất phản ứng là:
\(m = {m_{{C_6}{{\rm{H}}_5}{\rm{OH}}}} + {m_{{{\rm{C}}_6}{{\rm{H}}_4}{{({\rm{CO}})}_2}{\rm{O}}}} = 20.94 + 20.148 = 4840\,\,{\rm{gam}}\)
Chọn A
Câu 46:
Nhận định dưới đây là đúng hay sai
Nồng độ ion H+ ảnh hưởng tới trạng thái tồn tại của HIn.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào cân bằng của phenolphtalein
Lời giải
Nồng độ ion H+ ảnh hưởng trực tiếp tới quá trình chuyển đổi của HIn trong dung dịch. Khi nồng độ của ion H+ tăng lên, H+ sẽ tác dụng với H2O ra \({{\rm{H}}^ + } + {{\rm{H}}_2}{\rm{O}} \to {{\rm{H}}_3}{{\rm{O}}^ + }\), từ đó làm cho nồng độ H3O+ tăng lên, cân bằng chuyển dịch sang bên trái, dạng axit là HIn sẽ tồn tại chủ yếu và ngược lại.
Chọn B
Câu 47:
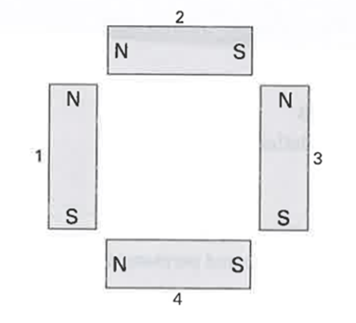
Một hệ gồm 4 nam châm được sắp xếp như hình sau. Các nhận xét sau đây về tương tác giữa các nam châm là đúng?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích hình vẽ.
Vận dụng kiến thức về từ trường và tương tác từ.
Lời giải
Ta có với nam châm hai cực trái đấu thì hút nhau, cùng dấu thì đẩy nhau. Các đáp án đúng là:
Nam châm 2 đẩy nam châm 1 và hút nam châm 3.
Chọn B
Câu 48:
Một cuộn dây điện từ tạo ra từ trường tương tự như một thanh nam châm. Hình vẽ sau minh họa cho một cuộn đây điện từ.
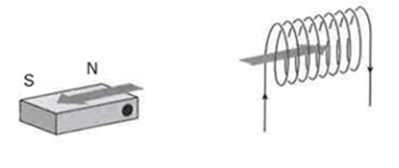
Đầu bên trái cái cuộn dây là cực _______, đầu bên phải là cực _______
 Xem đáp án
Xem đáp án
Đáp án:
Đầu bên trái cái cuộn dây là cực Bắc, đầu bên phải là cực Nam
Phương pháp giải
Dựa vào thông tin bài cung cấp.
Áp dụng lí thuyết đã học về từ trường.
Lời giải
Ta có đầu dây bên trái cuộn dây là cực Bắc, đầu bên phải là cực Nam.
Câu 49:
Hai thanh nam châm A và B được đặt như hình. Trong các cách sắp xếp sau, những trường hợp nào 2 thanh hút nhau.

 Xem đáp án
Xem đáp án
Phương pháp giải
Vận dụng lí thuyết về tương tác từ và nam châm.
Lời giải
Ta có hai cực trái trái nhau sẽ hút nhau.
=> cách sắp xếp đúng sẽ là S-N-S-N
Chọn A, D
Câu 50:
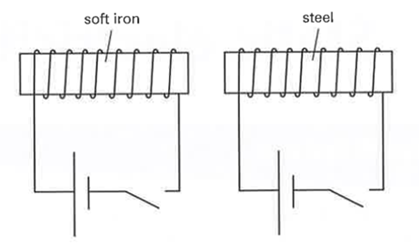
Cho biết rằng lực kháng từlà đại lượng quan trọng đặc trưng cho tính từ cứng của vật liệu từ cứng. Vì vật liệu từ cứng là khó từ hóa và khó khử từ, nên ngược lại với vật liệu từ mềm, nó có lực kháng từ cao.
Một thanh sắt mềm và một thanh thép đều có cuộn dây quấn quanh. Cả hai thanh ban đầu đều không bị nhiễm từ. Các cuộn dây được gắn vào mạch điện như sau:
Kéo thả các cụm từ sau vào chỗ trống thích hợp:
Khi công tắc đóng thì cả lõi sắt mềm và cả thép đều bị _______. Khi mở công tắc thì thanh sắt mềm sẽ _______ và thanh thép sẽ _______.
 Xem đáp án
Xem đáp án
Đáp án
Khi công tắc đóng thì cả lõi sắt mềm và cả thép đều bị nhiễm từ. Khi mở công tắc thì thanh sắt mềm sẽ mất đi từ tính và thanh thép sẽ giữ nguyên từ tính.
Phương pháp giải
Vận dụng lí thuyết về vật liệu từ.
Lời giải
Khi công tắc được bật, dòng điện chảy qua các cuộn dây và tạo ra một từ trường xung quanh chúng. Từ trường này làm cho các thanh bên trong các cuộn dây bị từ hóa hay chúng bị nhiễm từ.
Khi công tắc mở thì thanh sắt mềm sẽ mất đi từ tính nhanh do sắt mềm có độ giữ từ tính thấp. Trong khi đó, thanh thép vẫn sẽ giữ được từ tính.
Câu 51:
Một học sinh thực hiện tạo ra một cuộn dây điện từ. Ban đầu, số vòng dây quấn là a (vòng ). Sau đó, học sinh quấn thêm một số lượng vòng dây. Kết luận nào sau đây về cường độ từ trường của cuộn dây.
 Xem đáp án
Xem đáp án
Phương pháp giải
Vận dụng lí thuyết bài cung cấp.
Lời giải
Ta có khi quấn thêm vòng dây vào lõi kim loại thì cường độ từ trường của cuộn dây sẽ tăng lên.
Chọn A
Câu 52:
 Xem đáp án
Xem đáp án
Phương pháp giải
Vận dụng lí thuyết bài cung cấp.
Sử dụng công thức định luật Ohm.
Lời giải
Ta có công thức định luật Ohm: \[I = \frac{U}{R}\]
=>điện trở càng nhỏ thì cường độ càng lớn
Ta có cường độ dòng điện càng lớn thì cường độ từ trường của cuộn đây càng lớn, hay nam châm điện càng mạnh.
Vậy trường hợp cho dòng điện mạnh nhất là dòng điện có điện trở 1Ω
Chọn A
Câu 53:
Chất nào là chất mà theo hai nhà khoa học phải có mặt để tạo ra CH3 từ metan trong bầu khí quyển?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào phương trình (2).
Lời giải
Theo như quan điểm của cả hai nhà khoa học đều đồng ý với việc các phản ứng mà các nhà khoa học xây dựng đều xảy ra trong bầu khí quyển, mà O3 là chất thiết yếu đầu tiên bắt đầu sinh ra gốc hiđroxyl bắt đầu cho các phản ứng tiếp theo.
Chọn D
Câu 54:
Đồ thị nào dưới đây phản ánh giải thuyết của nhà khoa học 1 về nồng độ của HCHO trong bầu khí quyển do sự phát thải khí metan vào bầu khí quyển tăng cao?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào các phương trình biến đổi hoá học từ (2) đến (4).
Lời giải
Nồng độ khí CH4 trong khí quyển càng tăng thì chuỗi phản ứng từ (2) đến (4) càng diễn ra nhiều. Vì vậy theo sự tăng nồng độ khí CH4 thì nồng độ HCHO càng tăng cao. Với sự tăng đồng thời của cả hai chất như vậy thì đồ thị ở đáp án A là phù hợp nhất.
Chọn A
Câu 55:
Nhận định dưới đây là đúng hay sai?
Trong phản ứng 5 khối lượng phân tử của một trong hai sản phẩm ở sẽ lớn hơn khối lượng phân tử của chất phản ứng
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào phương trình (5) rồi so sánh khối lượng của chất phản ứng với chất sản phẩm.
Lời giải
Phản ứng số (5) là HCHO → CO + H2. So sánh khối lượng phân tử ta thấy khối lượng của chất HCHO đều lớn hơn cả hai sản phẩm là CO hoặc H2.
Chọn B
Câu 56:
Kéo thả đáp án thích hợp vào chỗ trống
tăng, tăng, giảm, giảm
Hiện nay đang có một hiện trạng đáng báo động là nồng độ của O3 trong bầu khí quyển tại một số khu vực bị giảm đi.Theo nhà khoa học 1, nồng độ của CH3 sẽ _______ và nồng độ của HCHO trong bầu khí quyển sẽ _______.
 Xem đáp án
Xem đáp án
Đáp án
Hiện nay đang có một hiện trạng đáng báo động là nồng độ của O3 trong bầu khí quyển tại một số khu vực bị giảm đi.Theo nhà khoa học 1, nồng độ của CH3 sẽ giảm và nồng độ của HCHO trong bầu khí quyển sẽ giảm.
Phương pháp giải
Dựa vào các phương trình theo nhà khoa học 1 từ (1) đến (4).
Lời giải
Theo nhà khoa học 1, nồng độ của CH3 và HCHO trong bầu khí quyển đều sẽ giảm.
Câu 57:
Điền số nguyên thích hợp vào chỗ trống
Một đàn bò có 100 con bò. Thể tích khí metan nhỏ nhất (tính theo m3) trong một tháng mà đàn bò này thải ra (giả sử một tháng có 30 ngày) là _______ m3.
 Xem đáp án
Xem đáp án
Đáp án: "750"
Phương pháp giải
Một con bò một ngày thải ra môi trường ít nhất 250 L khí metan.
Lời giải
Thể tích khí metan ít nhất mà một đàn bò 100 con có thể thải ra môi trường là:
250.100.30 = 750000L = 750m3
Câu 58:
Nhận định nào dưới đây là khác biệt nhất với ý kiến của nhà khoa học 2?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa theo lập luận của nhà khoa học 2.
Lời giải
Theo nhà khoa học số 2, khi có ánh sáng thì HCHO nhanh chóng phân huỷ thành CO và H2:
HCHO → CO + H2
Vậy nên khi lượng khí CH4 tăng lên, mức độ HCHO sẽ tăng lên đáng kể là khẳng định khác biệt nhất so với lập luận của nhà khoa học 2.
Chọn D
Câu 59:
Nghiên cứu sâu hơn đã chỉ ra rằng phản ứng (6) xảy ra trên quy mô lớn. Câu nào sau đây giải thích bằng chứng mới làm suy yếu lập luận của nhà khoa học 1 như thế nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào phương trình (3), (4), (5), (6).
Lời giải
Phản ứng (3) tạo ra HCHO, chất mà có thể phản ứng trong phản ứng (5) và (6)
Chọn B
Câu 60:
Phần tư duy toán học
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng định nghĩa và tính chất về trung điểm.
Lời giải
\(I\) là trung điểm của \(AB\) nên:
\(\overrightarrow {IA} + \overrightarrow {IB} = \vec 0\)
\(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \)
\(\left\{ {\begin{array}{*{20}{l}}{{x_A} + {x_B} = 2{x_I}}\\{{y_A} + {y_B} = 2{y_I}}\\{{z_A} + {z_B} = 2{z_I}}\end{array}} \right.\)
Chưa thể khẳng định được \(MA + MB < 2MI\) vì nếu MI vuông góc với \(AB\) thì điều này là sai.
Chọn D
Câu 61:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Ta có: \(y = 2{\rm{sin}}\left( {x + 1} \right) - 1\)
\( - 1 \le {\rm{sin}}\left( {x + 1} \right) \le 1\)
\( \Rightarrow - 2 \le 2{\rm{sin}}\left( {x + 1} \right) \le 2\)
\( \Rightarrow - 3 \le 2{\rm{sin}}\left( {x + 1} \right) - 1 \le 1\)
Vậy tập giá trị của hàm số \(y = 2{\rm{sin}}\left( {x + 1} \right) - 1\) là \(\left[ { - 3;1} \right]\)
Chọn B
Câu 62:
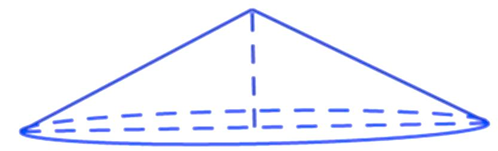
Cho hình nón có đường sinh bằng \(12{\rm{\;cm}}\) và có góc tạo bởi đường sinh và mặt đáy bằng \({30^ \circ }\). Diện tích thiết diện đi qua trục là
 Xem đáp án
Xem đáp án
Phương pháp giải
Tính chiều cao và bán kính đáy.
Lời giải
Góc tạo bởi đường sinh và mặt đáy bằng \({30^ \circ }\) nên \(h = \frac{1}{2}.12 = 6{\rm{\;cm}}\).
\(r = h.\sqrt 3 = 6\sqrt 3 \)
\(S = \frac{1}{2}.6.6\sqrt 3 = 18\sqrt 3 \left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Chọn A
Câu 63:
Có bao nhiêu số có 5 chữ số đôi một khác nhau và trong đó có đúng một chữ số lẻ?
Đáp án: ______
 Xem đáp án
Xem đáp án
Đáp án: "2520"
Phương pháp giải
- Trường hợp 1: Chọn một chữ số lẻ, ba chữ số chẵn khác 0 và xếp vào các vị trí còn lại.
- Trường hợp 2: số tạo thành không có chữ số 0
Lời giải
Ta thấy: Có 5 vị trí xếp chỗ.
- Trường hợp 1: Số tạo thành có chữ số 0.
Số vị trí điền số 0 là 4 vị trí. Còn 4 chỗ trống thì điền số lẻ \(1;3;5;7;9\) và 3 trong 4 số chẵn: \(2;4;6;8\).
Chọn một chữ số lẻ, ba chữ số chẵn khác 0 và xếp vào 4 vị trí còn lại, ta có: \(5 \times C_4^3 \times 4! = 480\) cách.
Trong trường hợp này có \(4 \times 480 = 1920\) số.
- Trường hợp 2: Số tạo thành không có chữ số 0 , khi đó: chọn một chữ số lẻ cùng với bốn chữ số chẵn rồi xếp vào các vị trí có: \(5 \times 5! = 600\) số.
Vậy tất cả có \(1920 + 600 = 2520\) số thỏa mãn đề bài.
Câu 64:
 Xem đáp án
Xem đáp án
Phương pháp giải
- Đặt \(t = {\rm{lo}}{{\rm{g}}_{100}}a = {\rm{lo}}{{\rm{g}}_{40}}b = {\rm{lo}}{{\rm{g}}_{16}}\frac{{a - 4b}}{{12}}\).
- Biến đổi \(a,b\) và \(a + b\) theo \(t\).
- Tìm \(t\).
Lời giải
Điều kiện: \(a,b > 0\) và \(a - 4b > 0\)
Đặt \({\rm{lo}}{{\rm{g}}_{100}}a = {\rm{lo}}{{\rm{g}}_{40}}b = {\rm{lo}}{{\rm{g}}_{16}}\frac{{a - 4b}}{{12}} = t \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = {{100}^t}}\\{b = {{40}^t}}\\{a - 4b = {{12.16}^t}}\end{array}} \right.\)
Suy ra \({100^t} - {4.40^t} - {12.16^t} = 0 \Leftrightarrow {\left( {\frac{5}{2}} \right)^{2t}} - 4.{\left( {\frac{5}{2}} \right)^t} - 12 = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{{\left( {\frac{5}{2}} \right)}^t} = 6}\\{{{\left( {\frac{5}{2}} \right)}^t} = - 2\left( l \right)}\end{array}} \right.\)
Vậy \(\frac{a}{b} = {\left( {\frac{5}{2}} \right)^t} = 6\).
Chọn A
Câu 65:
Cho hàm đa thức bậc ba \[y = f(x)\] có đồ thị như hình vẽ sau:
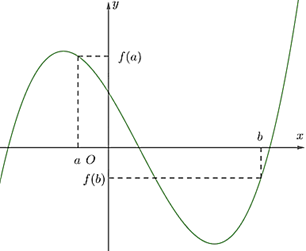
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
Với \({x_1};{x_2} \in \left( {a;b} \right)\) thỏa mãn \({x_1} < {x_2} < 0\) thì \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\) |
||
|
Với \({x_0} \in \left( {a;0} \right)\) thì \(f'\left( {{x_0}} \right) < 0\) |
||
|
Với \({x_0} \in \left( {0;b} \right)\) thì \(f\left( {{x_0}} \right) < f\left( a \right)\) |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Với \({x_1};{x_2} \in \left( {a;b} \right)\) thỏa mãn \({x_1} < {x_2} < 0\) thì \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\) |
X | |
|
Với \({x_0} \in \left( {a;0} \right)\) thì \(f'\left( {{x_0}} \right) < 0\) |
X | |
|
Với \({x_0} \in \left( {0;b} \right)\) thì \(f\left( {{x_0}} \right) < f\left( a \right)\) |
X |
Phương pháp giải
Cho hàm số \(y = f\left( x \right)\) xác định trên \(K\) (\(K\) có thể là một khoảng, đoạn hoặc nửa khoảng)
- Hàm số \(y = f\left( x \right)\) được gọi là đồng biến trên \(K\) nếu \(\forall {x_1},{x_2} \in K:{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\)
- Hàm số \(y = f\left( x \right)\) được gọi là nghịch biến trên \(K\) nếu \(\forall {x_1},{x_2} \in K:{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).
Lời giải
+) Với \({x_1};{x_2} \in \left( {a;b} \right)\) thỏa mãn \({x_1} < {x_2} < 0\) thì \({x_1};{x_2} \in \left( {a;0} \right)\)
Mà hàm số nghịch biến trên \(\left( {a;0} \right)\) nên \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
=> Mệnh đề 1 sai
+) Hàm số nghịch biến trên \(\left( {a;0} \right)\) nên với \({x_0} \in \left( {a;0} \right)\) thì \(f'\left( {{x_0}} \right) < 0\)
=> Mệnh đề 2 đúng
+) Quan sát đồ thị ta thấy khi \(x \in \left[ {a;b} \right]\) thì \(\mathop {{\rm{max}}}\limits_{\left[ {a;b} \right]} f\left( x \right) = f\left( a \right)\)
Khi đó với \({x_0} \in \left( {0;b} \right)\) thì \(f\left( {{x_0}} \right) < f\left( a \right)\)
=> Mệnh đề 3 đúng
Câu 66:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
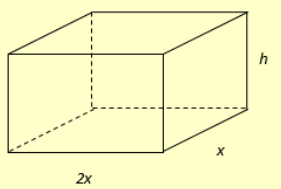
Gọi \(x,h\) lần lượt là chiều rộng đáy và chiều cao của khối hộp với \(x,h \in \left( {0; + \infty } \right)\).
Ta có chiều dài đáy là \(2x\). Thể tích \(V = 2x.x.h = 2{x^2}h \Leftrightarrow h = \frac{V}{{2{x^2}}} = \frac{2}{{3{x^2}}}\).
Diện tích vật liệu làm khối hộp là \(S\left( x \right) = {S_d} + {S_{xq}} = 2x.x + 2\left( {x + 2x} \right).h = 2{x^2} + \frac{4}{x}\).
\(S'\left( x \right) = 4x - \frac{4}{{{x^2}}}\).
Câu 67:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Gọi số lượng lá bèo ban đầu là \({M_0}\) thì số lượng lá bèo sau \(t\) giờ là :\(M\left( t \right) = {M_0}{.2^t}\).
Số lượng lá bèo sau 1 ngày là : \(M\left( {24} \right) = {M_0}{.2^{24}}\).
Khi số lượng lá bèo phủ kín \(\frac{1}{3}\) hồ ta có :
\(M\left( t \right) = \frac{1}{3}M\left( {24} \right) \Leftrightarrow {M_0}{.2^t} = \frac{1}{3}{M_0}{.2^{24}} \Leftrightarrow t = {\rm{lo}}{{\rm{g}}_2}\frac{{{2^{24}}}}{3} = 24 - {\rm{lo}}{{\rm{g}}_2}3\).
Chọn B
Câu 68:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Ta có
\(h'\left( t \right) = \frac{1}{3}\sqrt[3]{{t + 8}} \Rightarrow h\left( t \right) = \mathop \smallint \nolimits^ \frac{1}{3}\sqrt[3]{{t + 8}}dt = \frac{1}{3}\mathop \smallint \nolimits^ {(t + 8)^{\frac{1}{3}}}d\left( {t + 8} \right)\)
\(h\left( t \right) = \frac{1}{3}.\frac{{{{(t + 8)}^{\frac{1}{3} + 1}}}}{{\frac{4}{3}}} + C = \frac{{{{(t + 8)}^{\frac{4}{3}}}}}{4} + C\).
Lúc đầu bồn không có nước nên ta có: \(h\left( 0 \right) = 0\)
Suy ra: \(\frac{{{8^{\frac{4}{3}}}}}{4} + C = 0 \Leftrightarrow C = - 4 \Rightarrow h\left( t \right) = \frac{{{{(t + 8)}^{\frac{4}{3}}}}}{4} - 4\).
Khi đó \(L = h\left( {19} \right) = \frac{{65}}{4} = 16,25\left( {{\rm{cm}}} \right)\).
Chọn C
Câu 69:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Ta có : \(760 = a{.10^{\frac{{ - 2258,224}}{{100 + 273}}}} \Rightarrow \left[ a \right] = 863188841\).
Chọn D
Câu 70:
 Xem đáp án
Xem đáp án
Phương pháp giải
\(df\left( x \right) = f'\left( x \right)dx\)
Lời giải
\(df\left( 2 \right) = 3dx \Rightarrow f'\left( 2 \right) = 3\)
\(f'\left( 2 \right) = \frac{{m.2 + 4}}{{2 + 2}} = 3 \Rightarrow 2m = 8 \Rightarrow m = 4\).
Chọn B
Câu 71:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\). Đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ
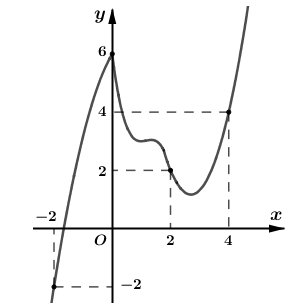
Hàm số \(g\left( x \right) = 2f\left( x \right) - {x^2}\) đồng biến trên khoảng nào trong các khoảng sau đây?
 Xem đáp án
Xem đáp án
Phương pháp giải
- Khảo sát hàm số, lập BBT.
- Tương giao đồ thị giữa một hàm số và \(f'\left( x \right)\)
Dạng 2: Tìm số giao điểm của hai đồ thị hàm số
Lời giải
Tập xác định \(D = \mathbb{R}\).
Ta có \(g'\left( x \right) = 2f'\left( x \right) - 2x \Rightarrow g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = x\).
Số nghiệm của phương trình \(g'\left( x \right) = 0\) bằng số giao điểm của đồ thị hàm số \(y = f'\left( x \right)\) và đường thẳng \(y = x\) (như hình vẽ bên dưới).
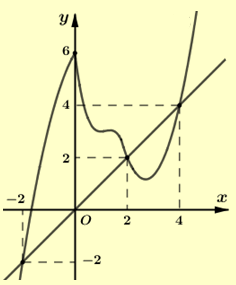
Dựa vào đồ thị, suy ra \(g'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 2}\\{x = 2}\\{x = 4}\end{array}} \right.\) .
Ta có bảng xét dấu của hàm \(g'(x)\)

Vậy hàm số \(g\left( x \right)\) đồng biến trên các khoảng \(\left( { - 2;2} \right)\) và \(\left( {4; + \infty } \right)\).
Chọn C
Câu 72:
 Xem đáp án
Xem đáp án
Phương pháp giải
Bước 1: Nhân cả 2 vế với \({e^{ - x}}\) để đưa về đạo hàm tích
Bước 2: Ta tìm được muối liên hệ ở Bước 1 và tìm được \(f\left( x \right)\)
Bước 3: Thay dữ kiện đề bài để tìm giá trị của hằng số C
Bước 4: Tìm \(f\left( 1 \right)\)
Lời giải
Ta có:
\(f'\left( x \right) - f\left( x \right) = \left( {x + 1} \right){e^{3x}}\)
\( \Leftrightarrow {e^{ - x}}f'\left( x \right) - {e^{ - x}}f\left( x \right) = \left( {x + 1} \right){e^{2x}}\)
\( \Leftrightarrow {\left( {{e^{ - x}}f\left( x \right)} \right)^{\rm{'}}} = \left( {x + 1} \right){e^{2x}}\)
Khi đó:
\(\begin{array}{l}{e^{ - x}}f(x) = \int {(x + 1)} {e^{2x}}dx\\ = \int {\frac{1}{2}} (x + 1)d\left( {{e^{2x}}} \right)\\ = \frac{1}{2}(x + 1).{e^{2x}} - \frac{1}{2}\int {{e^{2x}}} d(x + 1)\\ = \frac{1}{2}(x + 1).{e^{2x}} - \frac{1}{2}\int {{e^{2x}}} dx\\ = \frac{1}{2}(x + 1){e^{2x}} - \frac{1}{4}{e^{2x}} + C\end{array}\)
Do \(f\left( 0 \right) = \frac{5}{4}\) nên: \(\frac{1}{4} + C = \frac{5}{4} \Leftrightarrow C = 1\)\( \Rightarrow f\left( x \right) = \frac{1}{2}\left( {x + 1} \right){e^{3x}} - \frac{1}{4}{e^{3x}} + {e^x}\)
Vậy \(f\left( 1 \right) = \frac{3}{4}{e^3} + e\).
Chọn C
Câu 73:
Cho hai hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) có đồ thị như hình vẽ:
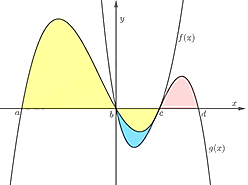
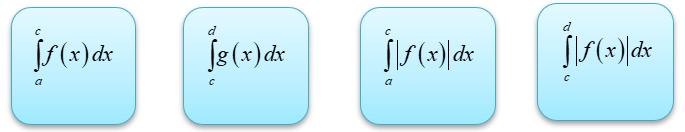
Diện tích của phần tô màu vàng là: _______
Diện tích của phần tô màu đỏ là: _______
 Xem đáp án
Xem đáp án
Đáp án
Diện tích của phần tô màu vàng là: \[\mathop \smallint \limits_a^c \left| {f\left( x \right)} \right|dx\].
Diện tích của phần tô màu đỏ là: \({\rm{\;}}\mathop \smallint \limits_c^d g\left( x \right)dx{\rm{\;}}\).
Phương pháp giải
Sử dụng định nghĩa.
Lời giải
Diện tích của phần tô màu vàng là: \[\mathop \smallint \limits_a^c \left| {f\left( x \right)} \right|dx\].
Diện tích của phần tô màu đỏ là: \({\rm{\;}}\mathop \smallint \limits_c^d g\left( x \right)dx{\rm{\;}}\).
Câu 74:
 Xem đáp án
Xem đáp án
Phương pháp giải
Bước 1: Đặt \(z = x + yi,x,y \in \mathbb{R}\). Từ đó suy ra \(\bar z = x - yi\).
Bước 2: Thế \(z\) và \(\bar z\) vào phương trình đã cho và rút gọn.
Bước 3: Cho phần thực của vế trái bằng phần thực của vế phải và phần ảo của vế trái bằng phần ảo của vế phải để tìm \(x,y\).
Bước 4: Kết luận.
Tìm phần thực, phần ảo, mô đun, … của số phức
Lời giải
Gọi \(z = x + yi,x,y \in \mathbb{R}\).
\( \Rightarrow \bar z = x - yi\).
Ta có \(\left( {x + yi} \right) - \left( {4 - 2i} \right)\left( {x - yi} \right) = 2 + 7i\)
\( \Leftrightarrow \left( { - 3x + 2y} \right) + \left( {5y + 2x} \right)i = 2 + 7i\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 3x + 2y = 2}\\{2x + 5y = 7}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = \frac{4}{{19}}}\\{y = \frac{{25}}{{19}}}\end{array}} \right.} \right.\)
Vì vậy \(z = \frac{4}{{19}} + \frac{{25}}{{19}}i\).
Vậy phần ảo của số phức \(z\) là \(\frac{{25}}{{19}}\).
Do đó ta chọn phương án \({\rm{D}}\).
Ñ Phần ảo của số phức \(z = x + yi\) là \(y\) (không phải \(yi\)).
Chọn D
Câu 75:
 Xem đáp án
Xem đáp án
Phương pháp giải
Liệt kê các số nguyên tố.
Lời giải
Ta thấy từ 1 đến 13 thì các số nguyên tố là: 2;3;5;7;11;13
Có tất cả 6 số nguyên tố.
Chọn B
Câu 76:
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng công thức tổng quát \({(a + b)^n} = \sum\limits_{k = 0}^n {C_n^k.{a^{n - k}}.{b^k}} \to \) Tìm hệ số của số hạng cần tìm.
Nhị thức Niu - tơn
Lời giải
Theo khai triển nhị thức Newton, ta có
\({\left( {x{y^2} - \frac{1}{{xy}}} \right)^8} = \sum\limits_{k = 0}^8 {C_8^k} .{\left( {x{y^2}} \right)^{8 - k}}.{\left( { - \frac{1}{{xy}}} \right)^k} = \sum\limits_{k = 0}^8 {C_8^k} .{x^{8 - k}}.{y^{16 - 2k}}.{( - 1)^k}.{(xy)^{ - k}}\)
\( = \sum\limits_{k = 0}^8 {C_8^k} .{( - 1)^k}.{x^{8 - 2k}}.{y^{16 - 3k}}\)
Số hạng không chứa \(x\) ứng với \(8 - 2k = 0 \Leftrightarrow k = 4 \to \) Số hạng cần tìm là \(C_8^4.{( - 1)^4}.{y^4} = 70{y^4}\).
Chọn A
Câu 77:
Một mật mã cửa có 6 chữ số được lập từ các chữ số từ 0 đến 9. Xác suất để mật mã không có chữ số 3 hoặc không có chữ số 5 là (kết quả làm tròn đến hàng phần mười)
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng quy tắc nhân.
Lời giải
Ta có tất cả \({10^6}\) mật mã có 6 chữ số được lập từ các chữ số từ 0 đến 9 .
\( \Rightarrow n\left( {\rm{\Omega }} \right) = {10^6}\).
Số mật mã không có chữ số 3 là: \({9^6}\) (mật mã).
Số mật mã không có chữ số 5 là: \({9^6}\) (mật mã).
Số mật mã không có chữ số 3 và không có chữ số 5 là: \({8^6}\) (mật mã).
Khi đó số mật mã không có chữ số 3 hoặc không có chữ số 5 là: \({2.9^6} - {8^6}\) (mật mã).
Vậy xác suất để lấy được mật mã không có chữ số 3 hoặc không có chữ số 5 là: \(\frac{{{{2.9}^6} - {8^6}}}{{{{10}^6}}} \approx 0,8\).
Vậy ta chọn phương án D.
Câu 78:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lập luận để xác định chiều cao và đáy.
Thể tích khối hộp, khối lăng trụ
Lời giải
Ta coi mặt có diện tích 2a2 là mặt đáy, khi đó mặt còn lại là hình vuông cạnh a là mặt khác và nằm trong mặt phẳng vuông góc với đáy
=> Chiều cao h = a
Thể tích của khối hộp là \[V = a.2{a^2} = 2{a^3}\]
Chọn B
Câu 79:
 Xem đáp án
Xem đáp án
Phương pháp giải
- Xác định trục của đường tròn đáy.
- Xác định tâm mặt cầu.
- Tính bán kính mặt cầu theo \({\rm{OA}}\) và \({\rm{OB}}\).
- Sử dụng BĐT Bu-nhi-a-cốp-xki: \(\left( {{a^2} + {b^2}} \right)\left( {{c^2} + {d^2}} \right) \ge {(ac + bd)^2}\)
Công thức tính diện tích mặt cầu, thể tích khối cầu
Lời giải
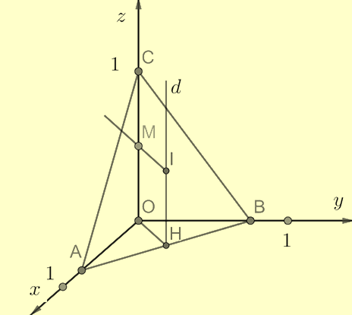
* Dựng trục \(d\) của
\( \Rightarrow d\left\{ {\begin{array}{*{20}{l}}{{\rm{\;qua\;}}H}\\{d \bot \left( {OAB} \right) \Rightarrow d//OC}\end{array}} \right.\) (với \(H\) là trung điểm của \(AB\))
* Kẻ trung trực \({\rm{\Delta }}\) của \(OC\) trong mặt phẳng \(\left( {OCH} \right)\) (\({\rm{\Delta }}\) qua trung điểm \({\rm{M}}\) của \({\rm{OC}}\))
\( \Rightarrow {\rm{\Delta }} \cap d = I\) là tâm mặt cầu ngoại tiếp tứ diện \(OABC\)
* \(R = IO = \sqrt {I{H^2} + H{O^2}} \)
+ \(IH = MO = \frac{1}{2}OC = \frac{{OC}}{2}\)
+ \(HO = \frac{1}{2}AB = \frac{1}{2}\sqrt {O{A^2} + O{B^2}} \)
\( \Rightarrow R = \sqrt {\frac{{O{C^2}}}{4} + \frac{{O{A^2} + O{B^2}}}{4}} = \frac{1}{2}\sqrt {O{A^2} + O{B^2} + O{C^2}} \)\( = \underbrace {\frac{1}{2}\sqrt {O{A^2} + O{B^2} + 1} }_{\min }\)
(Với \(OA + OB = OC = 1\))
Theo BĐT Bu-nhi-a-cốp-xki: \(\left( {{a^2} + {b^2}} \right)\left( {{c^2} + {d^2}} \right) \ge {(ac + bd)^2}\)
Dấu "\( = \)" xảy ra khi \(\frac{a}{c} = \frac{b}{d}\)
\( \Rightarrow \left( {O{A^2} + O{B^2}} \right)\left( {{1^2} + {1^2}} \right) \ge \underbrace {\left( {OA\mathop + \limits^2 OB} \right)}_{ = 1}\)
\( \Rightarrow O{A^2} + O{B^2} \ge \frac{1}{2}\)
Dấu "=" xảy ra khi \(\frac{{OA}}{1} = \frac{{OB}}{1} \Rightarrow OA = OB = \frac{1}{2}\)
\( \Rightarrow {R_{{\rm{min}}}} = \frac{1}{2}\sqrt {{{\left( {\frac{1}{2}} \right)}^2} + {{\left( {\frac{1}{2}} \right)}^2} + 1} = \frac{{\sqrt 6 }}{4}\).
Chọn A
Câu 80:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Cắt hình nón theo hai đường sinh SA, SB rồi trải ra ta được hình (H2) như sau:
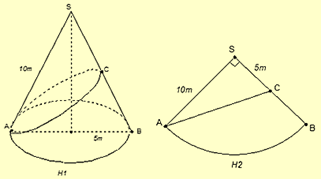
Khi đó, chiều dài dây đèn ngắn nhất là độ dài đoạn thẳng \(AC\) trên hình H2.
Chu vi cung tròn: \(C = \frac{1}{2}.2\pi .5 = 5\pi \).
\( \Rightarrow {\rm{\Delta }}SAC\) vuông tại \(S\).
\( \Rightarrow AC = \sqrt {S{A^2} + S{C^2}} = \sqrt {{{10}^2} + {5^5}} = 5\sqrt 5 {\rm{\;m}}\).
Chọn D
Câu 81:
 Xem đáp án
Xem đáp án
Phương pháp giải
Xét tính đúng, sai cho từng đáp án, dựa vào các công thức cộng véc tơ, độ dài véc tơ, các tính chất hai véc tơ cùng phương, hai véc tơ vuông góc.
Tọa độ véc tơ
Lời giải
\(\vec a + \vec b = \left( {2 + 1; - 2 - 1; - 4 + 1} \right) = \left( {3; - 3; - 3} \right)\) nên A đúng.
\(\vec a.\vec b = 2.1 + \left( { - 2} \right).\left( { - 1} \right) + \left( { - 4} \right).1 = 0\) nên \(\vec a \bot \vec b\) hay B đúng.
\(\left| {\vec b} \right| = \sqrt {{1^2} + {{( - 1)}^2} + {1^2}} = \sqrt 3 \) nên C đúng.
Câu 82:
 Xem đáp án
Xem đáp án
Đáp án
A. Khoảng cách giữa \(H,K\) luôn không đổi.
B. \(HK\) vuông góc với hai mặt phẳng \(\left( P \right),\left( Q \right)\)
Phương pháp giải
Nhận xét tính chất hình học.
Lời giải
Khi \(HK\) song song với \(Oz\) mà \(Oz\) lại vuông góc với \(\left( P \right)\) và \(\left( Q \right)\) nên \(HK\) vuông góc với hai mặt phẳng \(\left( P \right),\left( Q \right)\).
Mà \(HK = d\left( {\left( P \right),\left( Q \right)} \right) = 6\) là một số không đổi.
Chọn A, B
Câu 83:
 Xem đáp án
Xem đáp án
Phương pháp giải
+ Gọi \(M\left( {x;y;z} \right)\) và \(A',B'\) lần lượt là hình chiếu vuông góc của \(A,B\) lên \({\rm{mp}}\left( P \right)\).
+ Chứng minh \(M\) luôn thuộc một đường tròn cố định.
+ Gọi \(E\) là hình chiếu của \(I\) lên \(\left( P \right)\), tìm \(E\).
+ Gọi \(H\) là hình chiếu vuông góc của \(O\) lên \({\rm{mp}}\left( P \right)\), tìm \(H\).
+ vì \(O{M^2} = O{H^2} + H{M^2}\) nên \(OM_{{\rm{max}}}^2 \Leftrightarrow HM_{{\rm{max}}}^2\), tính \(O{M^2}\) max.
Phương pháp giải các bài toán về mặt cầu và mặt phẳng
Lời giải
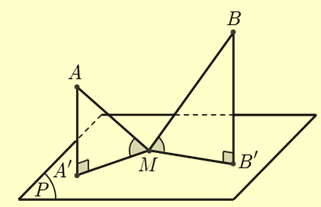
Nhận thấy đường thẳng \(AB\) không vuông góc với \({\rm{mp}}\left( P \right)\) và
\(\left( { - 1 + 0 - 0 + 2} \right).\left( {1 + 0 - 1 + 2} \right) > 0\) nên \(A,B\) nằm cùng phía so với \(\left( P \right)\).
Gọi \(M\left( {x;y;z} \right)\) và \(A',B'\) lần lượt là hình chiếu vuông góc của \(A,B\) lên \({\rm{mp}}\left( P \right)\).
Vì các đường thẳng \(MA,MB\) cùng tạo với \({\rm{mp}}\left( P \right)\) các góc bằng nhau nên \(\widehat {AMA'} = \widehat {BMB'}\)
\( \Rightarrow {\rm{\Delta }}AMA'\,\,{\rm{\Delta }}BMB' \Rightarrow \frac{{MA}}{{MB}} = \frac{{AA'}}{{BB'}} = \frac{{d\left( {A,\left( P \right)} \right)}}{{d\left( {B,\left( P \right)} \right)}} = \frac{{\left| { - 1 + 2} \right|}}{{\left| {1 - 1 + 2} \right|}} = \frac{1}{2}\)
\( \Leftrightarrow MB = 2MA \Leftrightarrow M{B^2} = 4M{A^2} \Leftrightarrow {(x - 1)^2} + {y^2} + {(z - 1)^2}\)
\( = 4\left[ {{{(x + 1)}^2} + {y^2} + {z^2}} \right]\)
\( \Leftrightarrow 3{x^2} + 3{y^2} + 3{z^2} + 10x + 2z + 2 = 0 \Leftrightarrow {x^2} + {y^2} + {z^2} + \frac{{10}}{3}x + \frac{2}{3}z + \frac{2}{3} = 0\).
Suy ra \(M\) nằm trên mặt cầu \(\left( S \right)\) tâm \(I\left( { - \frac{5}{3};0; - \frac{1}{3}} \right)\), bán kính \(R = \sqrt {{{\left( { - \frac{5}{3}} \right)}^2} + {{\left( { - \frac{1}{3}} \right)}^2} - \frac{2}{3}} = \frac{{2\sqrt 5 }}{3}\).
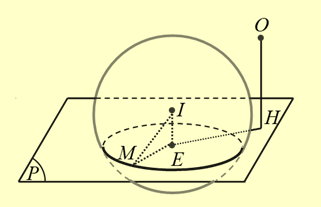
Vì \(\left\{ {\begin{array}{*{20}{l}}{M \in \left( P \right)}\\{M \in \left( S \right)}\end{array} \Rightarrow M \in \left( C \right)} \right.\), với \(\left( C \right) = \left( P \right) \cap \left( S \right)\).
Ta có \(d\left( {I,\left( P \right)} \right) = \frac{{\left| { - \frac{5}{3} + \frac{1}{3} + 2} \right|}}{{\sqrt 3 }} = \frac{2}{{3\sqrt 3 }}\).
Gọi \(E\) là hình chiếu của \(I\) lên \(\left( P \right)\).
Đường tròn \(\left( C \right)\) có tâm là \(E\) và bán kính bằng \(r = \sqrt {{R^2} - {d^2}\left( {I,\left( P \right)} \right)} = \)\(\sqrt {\frac{{20}}{9} - \frac{4}{{27}}} = \frac{{2\sqrt {42} }}{9}\).
Đường thẳng \(IE\) đi qua điểm \(I\) nhận vectơ pháp tuyến của \({\rm{mp}}\left( P \right)\) là \(\overrightarrow {{n_{\left( P \right)}}} = \left( {1;1; - 1} \right)\) làm vectơ chỉ phương nên có phương trình \(IE:\left\{ {\begin{array}{*{20}{l}}{x = - \frac{5}{3} + t}\\{y = t}\\{z = - \frac{1}{3} - t}\end{array} \Rightarrow E\left( { - \frac{5}{3} + t;t; - \frac{1}{3} - t} \right)} \right.\).
\(E \in \left( P \right) \Leftrightarrow - \frac{5}{3} + t + t + \frac{1}{3} + t + 2 = 0 \Leftrightarrow t = - \frac{2}{9} \Leftrightarrow E\left( { - \frac{{17}}{9}; - \frac{2}{9}; - \frac{1}{9}} \right)\).
Gọi \(H\) là hình chiếu vuông góc của \(O\) lên \({\rm{mp}}\left( P \right)\).
Phương trình đường thẳng \(OH:\left\{ {\begin{array}{*{20}{l}}{x = t'}\\{y = t'}\\{z = - t'}\end{array} \Rightarrow H\left( {t';t'; - t'} \right)} \right.\).
\(H\left( {t';t'; - t'} \right) \in \left( P \right) \Leftrightarrow t' + t' + t' + 2 = 0 \Leftrightarrow t' = - \frac{2}{3} \Leftrightarrow H\left( { - \frac{2}{3}; - \frac{2}{3};\frac{2}{3}} \right)\).
\(\overrightarrow {HE} = \left( { - \frac{{11}}{9};\frac{4}{9}; - \frac{7}{9}} \right) \Rightarrow HE = \sqrt {\frac{{121}}{{81}} + \frac{{16}}{{81}} + \frac{{49}}{{81}}} = \frac{{\sqrt {186} }}{9}\).
vì \(O{M^2} = O{H^2} + H{M^2}\) nên \(OM_{{\rm{max}}}^2 \Leftrightarrow HM_{{\rm{max}}}^2\)
Mà \(H{M_{{\rm{max}}}} = HE + r = \frac{{\sqrt {186} + 2\sqrt {42} }}{9}\).
Suy ra \(OM_{{\rm{max}}}^2 = \frac{4}{3} + {\left( {\frac{{\sqrt {186} + 2\sqrt {42} }}{9}} \right)^2} = \frac{4}{3} + \frac{{354 + 24\sqrt {217} }}{{81}} = \frac{{462 + 24\sqrt {217} }}{{81}}\).
Do đó \(a = 462,b = 217,c = 81\).
Vậy \(a + b + c = 760\).
Chọn C
Câu 84:
 Xem đáp án
Xem đáp án
Phương pháp giải
Bước 1: Gọi các cạnh của tam giác lần lượt là \(a,b,c\left( {a,b,c \in {\mathbb{N}^{\rm{*}}}} \right)\).
Bước 2: Sử dụng bất đẳng thức tam giác để tìm điều kiện của các cạnh.
Bước 3: Tìm bộ ba số \(\left( {a,b,c} \right)\).
Bước 4: Sử dụng công thức Hê-rông để tính diện tích của tam giác.
\(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \) với \(p = \frac{{a + b + c}}{2}\)
Lời giải
Bước 1:
Gọi các cạnh của tam giác lần lượt là \(a,b,c\left( {a,b,c \in {\mathbb{N}^{\rm{*}}}} \right)\).
Bước 2:
Theo bất đẳng thức tam giác ta có
\(2a < a + b + c = 8 \Rightarrow a < 4 \Leftrightarrow a \le 3\)
Lập luận tương tự ta có: \(b \le 3,c \le 3\).
Vì \(a \le 3,b \le 3 \Rightarrow a + b \le 6\).
Ta lại có:
\(a + b + c = 8 \Rightarrow c = 8 - \left( {a + b} \right)\)
\( \Rightarrow c \ge 8 - 6 = 2\)
Lập luận tương tự ta có: \(a \ge 2,b \ge 2\).
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a,b,c \in \mathbb{N}}\\{2 \le a,b,c \le 3}\\{a + b + c = 8}\end{array}} \right.\)
Bước 3:
Khi đó cả 3 số không đồng thời bằng 2 được và cũng không thể đồng thời bằng 3 được.
=> Có ít nhất 1 số bằng 3, giả sử là \({\rm{a}}\).
Để tổng chẵn thì một số khác cũng phải bằng 3 , giả sử là b.
Vậy số cuối cùng \(c = 2\).
Bước 4:
Theo công thức Hê - rông ta có diện tích của tam giác là:
\(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \)
\(\; = \sqrt {4.1.1.2} = 2\sqrt 2 \)
với \(p = \frac{{a + b + c}}{2} = 4\).
Chọn A
Câu 85:
 Xem đáp án
Xem đáp án
Phương pháp giải
Xác định hệ thức truy hồi của dãy số
Nhóm tổng 15 số hạng đầu tiên thành các tổng bằng nhau
Lời giải
Với \(n \ge 1\), ta có:
\({S_{n + 3}} = {\rm{sin}}\left[ {4\left( {n + 3} \right) - 1} \right]\frac{\pi }{6} = {\rm{sin}}\left[ {4n - 1 + 12} \right]\frac{\pi }{6}\)
\( = {\rm{sin}}\left[ {\left( {4n - 1} \right)\frac{\pi }{6} + 2\pi } \right] = {\rm{sin}}\left( {4n - 1} \right)\frac{\pi }{6} = {S_n}\)
Ta có: \(S = {s_1} + {s_2} + .. + {s_{15}} = \left( {{s_1} + {s_2} + {s_3}} \right) + \left( {{s_4} + {s_5} + {s_6}} \right) + \ldots \)\( + \left( {{s_{13}} + {s_{14}} + {s_{15}}} \right)\)
Mà \({s_1} = {s_4} = {s_7} = {s_{10}} = {s_{13}}\)
\({s_2} = {s_5} = {s_8} = {s_{11}} = {s_{14}}\)
\({s_3} = {s_6} = {s_9} = {s_{12}} = {s_{15}}\)
\( \Rightarrow {s_1} + {s_2} + {s_3} = {s_4} + {s_5} + {s_6} = \ldots = {s_{13}} + {s_{14}} + {s_{15}}\)
\( \Rightarrow S = 5\left( {{s_1} + {s_2} + {s_3}} \right)\)
\( = 5\left( {1 - \frac{1}{2} - \frac{1}{2}} \right)\)
\( = 0\)
Chọn C
Câu 86:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Ta có \({S_{2018}} = \frac{{2018}}{2}\left( {2{u_1} + 2017d} \right),{S_{1009}} = \frac{{1009}}{2}\left( {2{u_1} + 1008d} \right)\).
Theo giả thiết, ta có \({u_1} + {u_2} + \ldots + {u_{2018}} = 4\left( {{u_1} + {u_2} + \ldots + {u_{1009}}} \right)\)
\( \Leftrightarrow \frac{{2018}}{2}\left( {2{u_1} + 2017d} \right) = 4.\frac{{1009}}{2}\left( {2{u_1} + 1008d} \right)\)
\( \Leftrightarrow 2{u_1} + 2017d = 2\left( {2{u_1} + 1008d} \right) \Leftrightarrow {u_1} = \frac{d}{2}\)
Dãy số \(\left( {{u_n}} \right):\frac{d}{2},\frac{{3d}}{2},\frac{{5d}}{2}, \ldots \)
Ta có \(P = {\rm{log}}_3^2{u_2} + {\rm{log}}_3^2{u_5} + {\rm{log}}_3^2{u_{14}} = {\rm{log}}_3^2\frac{{3d}}{2} + {\rm{log}}_3^2\frac{{9d}}{2} + {\rm{log}}_3^2\frac{{27d}}{2}\)
\( = {\left( {1 + {\rm{lo}}{{\rm{g}}_3}\frac{d}{2}} \right)^2} + {\left( {2 + {\rm{lo}}{{\rm{g}}_3}\frac{d}{2}} \right)^2} + {\left( {3 + {\rm{lo}}{{\rm{g}}_3}\frac{d}{2}} \right)^2}\)
Đặt \({\rm{lo}}{{\rm{g}}_3}\frac{d}{2} = x\) thì \(P = {(1 + x)^2} + {(2 + x)^2} + {(3 + x)^2} = 3{x^2} + 12x + 14 \ge 2\)
Dấu bằng xảy ra khi \(x = - 2 \Leftrightarrow d = \frac{2}{9}\). Vậy giá trị nhỏ nhất của \(P\) bằng 2 .
Chọn D
