Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 16)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 16)
-
216 lượt thi
-
82 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
Các số liệu khảo sát trong đoạn [2] của bài viết cho thấy điều gì?
 Xem đáp án
Xem đáp án
Giải thích
Đọc lại văn bản kết hợp với việc sử dụng phương pháp loại trừ. Căn cứ vào các số liệu trong đoạn [2] xác định được các thông tin quan trọng: “30% số người đọc sách thường xuyên, 26% không đọc sách và 44% thỉnh thoảng đọc sách”, “có 47,26% sinh viên nhận thức được tầm quan trọng của sách, 26.37% nghĩ rằng đọc sách là cần thiết” và người trẻ đang có xu hướng sử dụng công nghệ: “41,7% số bạn trẻ trả lời là lên mạng, 20% xem phim, 16,7% nghe nhạc và chỉ có 15% trả lời là đọc sách”. Chọn A, C
Câu 2:
Theo bài viết, cách đọc sách mới giúp người đọc có thể tiết kiệm được nhiều thời gian và mang lại nhiều lợi ích hơn so với sách giấy. Đúng hay sai?
 Xem đáp án
Xem đáp án
Đáp án
B. Sai.
Giải thích
Căn cứ vào từ khóa “cách đọc sách mới” xác định nội dung cần tìm ở đoạn [5]: “với cách đọc mới này, những cuốn tiểu thuyết mấy trăm trang được tóm gọn trong vài chục trang. Những cuốn sách nâng cao kiến thức, câu chuyện lịch sử cũng chỉ gói gọn trong 3 – 4 phút trên mạng”, “cần đặc biệt lưu ý để văn chương không bị biên tập, cắt gọn tới mức biến dạng nội dung”. Cách đọc sách mới đang bị cắt gọn, biến dạng nội dung. Vậy nhận xét trên không chính xác.
Câu 3:
Theo bài viết, những đối tượng cần lan tỏa và hình thành thói quen đọc sách là:
 Xem đáp án
Xem đáp án
Căn cứ vào từ khóa “lan tỏa” và “hình thành thói quen” xác định được nội dung cần tìm ở đoạn [6] và [7]: “những người viết sách cũng cần phải đổi mới về phong cách viết, hình thức truyền tải để phù hợp với xu thế hiện nay” và “cha mẹ và thầy cô giáo hãy khuyến khích, hướng dẫn trẻ cách tìm kiếm sách, cách đọc sách sao cho hiệu quả”, “giúp hình thành thói quen đọc sách và có thể khuyến khích giới trẻ đến với sách nhiều hơn”. Chú ý “người viết sách” tương đương với “người sáng tạo nội dung”; “thầy cô” tương đương với “cơ sở giáo dục và đào tạo”. Chọn A, D
Câu 4:
Theo nội dung bài viết, những nhận định sau đây đúng hay sai?
|
Nhận định |
Đúng |
Sai |
|
Cần nhìn nhận văn hóa đọc trong nhiều mối tương quan với sự phát triển của đời sống xã hội. |
||
|
Để hình thành thói quen đọc sách nên bắt đầu từ những hành động nhỏ và sở thích cá nhân. |
||
|
Muốn lan tỏa giá trị của sách tới cộng đồng cần chú trọng tới những chính sách khuyến học. |
||
|
Phương pháp tự học không chỉ mang lại hiệu quả về kiến thức mà còn góp phần xây dựng tính cách. |
 Xem đáp án
Xem đáp án
Đáp án
|
Nhận định |
Đúng |
Sai |
|
Cần nhìn nhận văn hóa đọc trong nhiều mối tương quan với sự phát triển của đời sống xã hội. |
X | |
|
Để hình thành thói quen đọc sách nên bắt đầu từ những hành động nhỏ và sở thích cá nhân. |
X | |
|
Muốn lan tỏa giá trị của sách tới cộng đồng cần chú trọng tới những chính sách khuyến học. |
X | |
|
Phương pháp tự học không chỉ mang lại hiệu quả về kiến thức mà còn góp phần xây dựng tính cách. |
X |
Giải thích
Căn cứ vào từ khóa “văn hóa đọc”, “sự phát triển của đời sống xã hội”, “hình thành thói quen đọc sách”, “phương pháp tự học” xác định nội dung cần tìm ở đoạn [7]: “nhiều bài viết, nghiên cứu khẳng định vai trò quan trọng của việc đọc đối với mỗi cá nhân và sự phát triển của xã hội” (nhận định 1 đúng); “ngay từ khi ở bậc tiểu học… hãy khuyến khích, hướng dẫn trẻ cách tìm kiếm sách, cách đọc sách sao cho hiệu quả”, “điều đó sẽ giúp hình thành thói quen đọc sách” (nhận định 2 đúng); “đọc sách chính là phương pháp tự học hiệu quả nhất”, “văn hóa đọc… không chỉ nâng cao nhận thức mà còn hình thành nhân cách con người” (nhận định 4 đúng). Không có thông tin về “chính sách khuyến học”, chỉ có “khuyến khích giới trẻ đến với sách nhiều hơn” (nhận định 3 sai).
Câu 5:
Bài viết đề cập tới vấn đề gì?
 Xem đáp án
Xem đáp án
Câu 6:
Ý nào sau đây thể hiện rõ nhất nội dung chính của bài đọc trên?
 Xem đáp án
Xem đáp án
Ý chính các đoạn trong bài.
Đoạn 1. Tính cấp thiết của việc tái chế rác thải xây dựng.
Đoạn 2. Một số phương pháp được đề xuất để tái chế chất thải xây dựng.
Đoạn 3-5. Giới thiệu và những ưu điểm chính của phương pháp tái chế chất thải xây dựng thành hạt cốt liệu nung rỗng.
Đoạn 6-9. Quá trình thực hiện nghiên cứu chế tạo bê tông cách nhiệt chịu lực từ chất thải xây dựng.
Đoạn 10-11. Những khó khăn trong quá trình thực hiện nghiên cứu và đề xuất phương án giải quyết.
Tổng hợp các ý trên, ta có ý chính của toàn câu là: “Chế tạo bê tông nhẹ có khả năng cách nhiệt và chịu lực từ chất thải xây dựng.”
Chọn A
Câu 7:
Từ thông tin trong đoạn [1] và [2], hãy điền một cụm từ không quá ba tiếng để hoàn thành đoạn sau.
Các thành phố lớn tại Việt Nam đang phải đối mặt với nguy cơ ô nhiễm môi trường do chất thải xây dựng. Một số chuyên gia đã đề xuất sử dụng (1) ______ mới, thay thế việc chôn lấp tại các khu xử lý. Trong đó, công nghệ nghiền tái chế được cho rằng sẽ tận dụng 70-100% phế thải xây dựng ngay tại công trình.
 Xem đáp án
Xem đáp án
Đáp án
Từ thông tin trong đoạn [1] và [2], hãy điền một cụm từ không quá ba tiếng để hoàn thành đoạn sau.
Các thành phố lớn tại Việt Nam đang phải đối mặt với nguy cơ ô nhiễm môi trường do chất thải xây dựng. Một số chuyên gia đã đề xuất sử dụng (1) biện pháp mới, thay thế việc chôn lấp tại các khu xử lý. Trong đó, công nghệ nghiền tái chế được cho rằng sẽ tận dụng 70-100% phế thải xây dựng ngay tại công trình.
Giải pháp
Đọc đoạn [1], [2] trong văn bản, chú ý câu văn sử dụng từ “chôn lấp”. “Tuy nhiên, phần lớn các khu xử lý chất thải rắn hiện nay đều bị quá tải và chủ yếu sử dụng biện pháp chôn lấp.”. Nhận thấy đề bài đã thay thế “biện pháp chôn lấp” thành “việc chôn lấp”, kết hợp thông tin trong đoạn. “Đó là lý do khiến ngành xây dựng đang nghĩ đến cách tiếp cận mới. Tái chế chất thải xây dựng.” để suy luận. biện pháp chôn lấp không còn phù hợp, cần thay thế bằng một biện pháp mới. Từ cần điền trong đoạn là “biện pháp”.
HS cần lưu ý, trong bài đọc có sử dụng cụm từ “cách tiếp cận mới”, tuy nhiên, cụm từ này không phù hợp để kết hợp với từ “sử dụng” trong câu điền khuyết.
Câu 8:
Theo đoạn [2], phương án nào sau đây là thành phẩm trực tiếp của máy nghiền tái chế vật liệu xây dựng?
 Xem đáp án
Xem đáp án
Thông tin tại đoạn [2]. “máy nghiền lắp đặt ngay tại chân công trình, cho phép nghiền tại chỗ các khối bê tông, vật liệu rắn thành các hạt nhỏ 3x4cm và cát mịn mà không cần tập kết ra bãi phế liệu.”, như vậy, đáp án đúng làD. Các phương án còn lại là chế phẩm tạo ra từ vật liệu tái chế, không phải sản phẩm trực tiếp hình thành từ máy nghiền tái chế. Chọn D
Câu 9:
 Xem đáp án
Xem đáp án
Từ “này” cho thấy cụm từ/đối tượng được nhắc tới trong đoạn này đã được làm rõ trước đó để người đọc biết đến. Tìm kiếm từ khóa và thông tin liên quan trong các đoạn [1], [2] → Trong đoạn [2] có đề cập thông tin như sau. “...chẳng hạn như máy nghiền lắp đặt ngay tại chân công trình, cho phép nghiền tại chỗ các khối bê tông, vật liệu rắn thành các hạn nhỏ 3x4cm và cát mịn…”, từ đó đáp án đúng là A.
Câu 10:
 Xem đáp án
Xem đáp án
Dựa vào thông tin trong đoạn [4]. “so với gạch xây thông thường, ta có thể giảm chi phí đáng kể trong các công trình xây dựng do giảm được tải trọng tác dụng, qua đó giảm kích thước các kết cấu chịu lực và móng công trình”, chọn đáp án đúng là C.
Câu 11:
Theo đoạn [6], việc sử dụng công nghệ nung và đầu vào là phế thải xây dựng lần đầu tiên được nghiên cứu bởi một tập hợp các chuyên gia của Việt Nam. Đúng hay Sai?
 Xem đáp án
Xem đáp án
Thông tin tại đoạn [6] như sau. “...ở Việt Nam đây là một trong những nghiên cứu đầu tiên sử dụng công nghệ nung và sử dụng đầu vào là phế thải xây dựng. Để làm được điều đó, nhóm nghiên cứu đã tập hợp các chuyên gia từ nhiều lĩnh vực, ...”. Theo đó, nghiên cứu này chỉ là “một trong những nghiên cứu tiên” nên mệnh đề trên “Sai”. Chọn B
Câu 12:
Từ thông tin trong đoạn [8], hãy điền một cụm từ không quá bốn tiếng để hoàn thành đoạn sau.
Theo đoạn trích, các loại hạt cốt liệu được phân loại dựa trên (1) ________, sau đó có thể được ứng dụng trong nhiều ngành khác nhau.
 Xem đáp án
Xem đáp án
Đáp án
Từ thông tin trong đoạn [8], hãy điền một cụm từ không quá bốn tiếng để hoàn thành đoạn sau.
Theo đoạn trích, các loại hạt cốt liệu được phân loại dựa trên (1) khả năng chịu lực, sau đó có thể được ứng dụng trong nhiều ngành khác nhau.
Giải thích
Căn cứ vào thông tin trong đoạn. “Do các hạt cốt liệu nhẹ chế tạo từ phế thải xây dựng nên chúng tôi không kì vọng chúng có khả năng chịu lực quá cao.”, “Bù lại, các hạt cốt liệu nhẹ có thể có nhiều ứng dụng khác nhau ...”. Như vậy, sự phân loại các hạt thành có chất lượng thấp, chất lượng tốt hơn, có cường độ tốt nhất để ứng dụng được là căn cứ vào khả năng chịu lực. Từ cần điền để hoàn thành câu là “khả năng chịu lực”.
Câu 13:
 Xem đáp án
Xem đáp án
Đọc đoạn [10], xác định các vấn đề được đưa ra trong đoạn. “việc nung trên cơ sở lò quay vẫn là khâu thách thức nhất”, “công nghệ chế tạo lò vẫn chưa thể nội địa hóa…chi phí vẫn còn cao”, “nhiệt lượng sử dụng khá lớn và có thể khiến tổng chi phí tăng lên”, “Một số ý kiến phản hồi …chưa đủ “xanh” cho môi trường”. Như vậy, chọn đáp án đúng là B.
Câu 14:
Theo đoạn [11], phương án nào sau đây KHÔNG phải hướng hoàn thiện quy trình sản xuất hạt cốt liệu nhẹ?
 Xem đáp án
Xem đáp án
Đọc đoạn [11]. “...chẳng hạn tận dụng khí gas từ chất thải hữu cơ làm năng lượng đốt lò – để giảm thiểu tác động, hoặc tạo ra một quá trình sản xuất liên tục để giảm hao phí năng lượng và chi phí vận hành. Trong tương lai, họ cũng xem xét nghiên cứu thêm cách hạ thấp nhiệt độ nung để nâng cao hiệu quả kinh tế - kỹ thuật của sản phẩm hạt nhẹ này.”, nhận thấy phương án “Tạo ra sản phẩm hạt nhẹ có giá trị kinh tế cao” không được nhắc tới trong bài nên đáp án đúng là D.
Câu 15:
Để các hạt vật liệu nhẹ đảm bảo hiệu quả về kinh tế - kỹ thuật, các chuyên gia dự định nghiên cứu việc giảm nhiệt lượng cần thiết trong quy trình nung và nội địa hóa công nghệ chế tạo lò. Đúng hay Sai?
 Xem đáp án
Xem đáp án
Đọc đoạn [10], [11]. Trong đoạn [10], các thông tin liên quan đến chi phí (hiệu quả kinh tế) bao gồm. “Hiện công nghệ chế tạo lò vẫn chưa thể nội địa hóa mà phải nhập khẩu, do vậy chi phí vẫn còn cao. Hơn thế nữa, quy trình đòi hỏi nhiệt độ nung phải trên 12000C – tức nhiệt lượng sử dụng khá lớn và có thể khiến tổng chi phí tăng lên.”. Tuy nhiên, trong đoạn [11], thông tin được đưa ra là. “họ cũng xem xét nghiên cứu thêm cách hạ thấp nhiệt độ nung để nâng cao hiệu quả kinh tế - kỹ thuật của sản phẩm hạt nhẹ”. Như vậy, việc nội địa hóa công nghệ chế tạo lò chưa nằm trong dự định. Mệnh đề trên là “Sai”.
Chọn BCâu 16:
Phần tư duy khoa học / giải quyết vấn đề
lớn hơn, nhỏ hơn
Gia tốc trọng trường trên bề mặt Trái Đất _______ gia tốc trọng trường trên bề mặt Mặt Trăng.
Gia tốc trọng trường trên bề mặt Trái Đất _______ gia tốc trọng trường trên bề mặt Sao Mộc.
 Xem đáp án
Xem đáp án
Đáp án
Gia tốc trọng trường trên bề mặt Trái Đất lớn hơn gia tốc trọng trường trên bề mặt Mặt Trăng.
Gia tốc trọng trường trên bề mặt Trái Đất nhỏ hơn gia tốc trọng trường trên bề mặt Sao Mộc.
Giải thích
Dựa vào Bảng 1, ta có:
gTĐ = 9,8 (m/s2) > gMT = 1,6 (m/s2)
gTĐ = 9,8 (m/s2) < gSM = 24,9 (m/s2)
Câu 17:
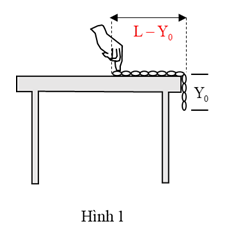
Trước khi buông tay, chiều dài của sợi dây xích nằm trên mặt bàn bằng
 Xem đáp án
Xem đáp án
Tổng chiều dài của cả sợi xích là L
Chiều dài của một phần sợi xích thòng xuống cạnh bàn là \({Y_0}\).
=> Trước khi buông sợi xích, chiều dài của sợi xích nằm trên mặt bàn bằng \(L - {Y_0}\). Chọn B
Câu 18:
Dựa vào hình 3, hãy cho biết: Nếu \({Y_0}\) là 5 cm thì thời gian rơi của sợi dây xích khi ở trên Mặt Trăng gần nhất với giá trị nào sau đây?
 Xem đáp án
Xem đáp án
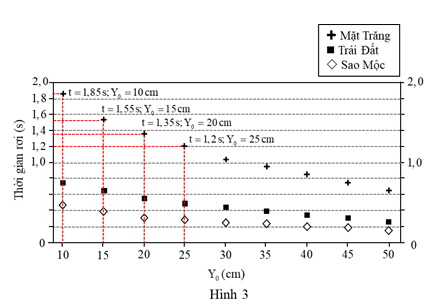
Từ hình 3, có thể thấy quy luật sự phụ thuộc của thời gian rơi t vào \({Y_0}\) của dây xích khi ở trên bề mặt Mặt Trăng như sau:
+ Khi \(\begin{array}{l}{Y_0} = 25\;{\rm{cm}} \to {Y_0} = 20\;{\rm{cm}}\\t = 1,2\;{\rm{s}} \to t = 1,35\;{\rm{s}}\end{array}\) \( \Rightarrow \Delta t = 0,15\;{\rm{s}}\)
+ Khi \(\begin{array}{l}{Y_0} = 20\;{\rm{cm}} \to {Y_0} = 15\;{\rm{cm}}\\t = 1,35s \to t = 1,55\;{\rm{s}}\end{array}\) \( \Rightarrow \Delta t = 0,2\;{\rm{s}}\)
+ Khi \(\begin{array}{l}{Y_0} = 15\;{\rm{cm}} \to {Y_0} = 10\;{\rm{cm}}\\t = 1,55\;{\rm{s}} \to t = 1,85\;{\rm{s}}\end{array}\) \( \Rightarrow \Delta t = 0,3\;{\rm{s}}\)
+ Khi \(\begin{array}{l}{Y_0} = 10\;{\rm{cm}} \to {Y_0} = 5\;{\rm{cm}}\\t = 1,85\;{\rm{s}} \to t\end{array}\) \( \Rightarrow \Delta t > 0,3\;{\rm{s}}\)
Như vậy, khi \({Y_0}\) giảm từ 10 cm còn 5 cm thì thời gian rơi tăng lên tối thiểu là 0,3 s, tức là thời gian rơi phải lớn hơn 2,15 s. Phương án phù hợp là 2,3 s
Chọn D
Câu 19:
Theo Hình 4, sợi dây xích có \({Y_0} = 20\,\,cm\) sẽ có thời gian rơi khi ở trên bề mặt Mặt Trăng là 2,0 s nếu L xấp xỉ bằng
 Xem đáp án
Xem đáp án
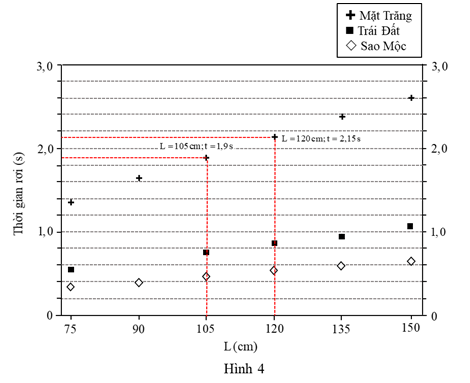
Nếu L = 105 cm thì thời gian rơi trên bề mặt Mặt Trăng là 1,9 s.
Nếu L = 120 cm thì thời gian rơi trên bề mặt Mặt Trăng là 2,15 s.
Do đó, thời gian rơi là 2,0 s sẽ xảy ra nếu L lớn hơn 105 cm và nhỏ hơn 120 cm.
Chọn C
Câu 20:
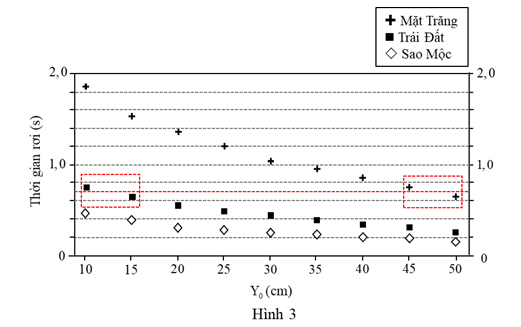
Giả sử sợi dây xích trong Hình 3 có thời gian rơi là 0,7 s khi ở trên bề mặt Trái Đất. Để sợi dây xích đó có thời gian rơi cũng là 0,7 s khi ở trên bề mặt Mặt trăng, thì \({Y_0}\) khi ở trên bề mặt Mặt Trăng phải có giá trị
 Xem đáp án
Xem đáp án
+ Quy luật sự phụ thuộc của thời gian rơi t vào \({Y_0}\) trên bề mặt Trái Đất như sau:
\(\begin{array}{l}{Y_0} = 10\;{\rm{cm}}\\t = 0,75\;{\rm{s}}\end{array}\) \( \to \) \(\begin{array}{l}{Y_0} = 15\;{\rm{cm}}\\t = 0,65\;{\rm{s}}\end{array}\) \({Y_0} \approx 13\;{\rm{cm}}\)
+ Quy luật sự phụ thuộc của thời gian rơi t vào \({Y_0}\) trên bề mặt Mặt Trăng như sau:
\(\begin{array}{l}{Y_0} = 45\;{\rm{cm}}\\t = 0,75\;{\rm{s}}\end{array}\) \( \to \) \(\begin{array}{l}{Y_0} = 50\;{\rm{cm}}\\t = 0,65\;{\rm{s}}\end{array}\) \({Y_0} \approx 48\;{\rm{cm}}\)
Để sợi dây xích đó có thời gian rơi cũng là 0,7 s trên bề mặt Mặt trăng, thì \({Y_0}\) khi ở trên bề mặt Mặt trăng phải có giá trị lớn hơn so với khi ở trên bề mặt Trái Đất là: 48 cm – 13 cm = 35 cm. Chọn A
Câu 21:
Gia tốc trọng trường trên bề mặt của Sao Hải Vương xấp xỉ 11,7 m/s2. Dựa vào Hình 3, với mỗi giá trị \({Y_0}\), hãy cho biết nhận định nào sau đây là đúng hoặc sai?
|
Phát biểu |
Đúng |
Sai |
|
Thời gian rơi của sợi dây xích khi ở trên bề mặt của Sao Hải Vương nhỏ hơn thời gian rơi của nó khi ở trên bề mặt Sao Mộc. |
||
|
Thời gian rơi của sợi dây xích khi ở trên bề mặt của Sao Hải Vương nhỏ hơn thời gian rơi của nó khi ở trên bề mặt Trái Đất. |
||
|
Thời gian rơi của sợi dây xích bề mặt của Sao Hải Vương nhỏ hơn thời gian rơi của nó khi ở trên bề mặt Mặt Trăng. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Thời gian rơi của sợi dây xích khi ở trên bề mặt của Sao Hải Vương nhỏ hơn thời gian rơi của nó khi ở trên bề mặt Sao Mộc. |
X | |
|
Thời gian rơi của sợi dây xích khi ở trên bề mặt của Sao Hải Vương nhỏ hơn thời gian rơi của nó khi ở trên bề mặt Trái Đất. |
X | |
|
Thời gian rơi của sợi dây xích bề mặt của Sao Hải Vương nhỏ hơn thời gian rơi của nó khi ở trên bề mặt Mặt Trăng. |
X |
Giải thích
Hình 3 và Bảng 1 cho thấy khi gia tốc trọng trường tăng thì thời gian rơi giảm.
Ví dụ, trong Hình 3, khi Y0 = 10 cm, thời gian rơi tại bề mặt Mặt trăng là lớn nhất và trong Bảng 1, Gia tốc trọng trường trên bề mặt Mặt trăng là nhỏ nhất. Tương tự như vậy, thời gian rơi tại bề mặt Sao Mộc là nhỏ nhất và Gia tốc trọng trường là lớn nhất tại bề mặt Sao Mộc. Vì Gia tốc trọng trường trên bề mặt của Sao Hải Vương là khoảng 11,7 m/s2, nên thời gian rơi trên bề mặt Sao Hải Vương sẽ lớn hơn thời gian rơi trên bề mặt Sao Mộc và nhỏ hơn thời gian rơi trên bề mặt Trái Đất.
1. Sai do thời gian rơi trên bề mặt Sao Hải Vương sẽ lớn hơn thời gian rơi trên bề mặt Sao Mộc
2. Đúng do thời gian rơi trên bề mặt Sao Hải Vương nhỏ hơn thời gian rơi trên bề mặt Trái Đất.
3. Sai. Do Gia tốc trọng trường ở bề mặt Sao Hải Vương lớn hơn Gia tốc trọng trường ở bề mặt Mặt Trăng. Thời gian rơi giảm khi gia tốc tự do tăng lên, vì vậy thời gian rơi trên bề mặt Mặt trăng sẽ lớn hơn trên bề mặt Sao Hải Vương.
Câu 22:
Cho tổng chiều dài của dây xích là L = 120 cm, giá trị Y tối thiểu để dây xích bắt đầu trượt trên mặt bàn là
Cho tổng chiều dài của dây xích là L = 120 cm, giá trị Y tối thiểu để dây xích bắt đầu trượt trên mặt bàn là
 Xem đáp án
Xem đáp án
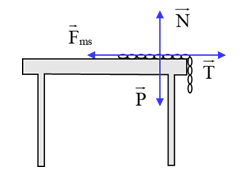
Dây bắt đầu trượt xuống khi lực căng có độ lớn lớn hơn độ lớn của lực ma sát: \[T > {F_{ms}}\]
Với \[{F_{ms}} = k.N = k.P = k.mg\]
\[T = {P_0} = {m_0}g\]
(P là trọng lượng đoạn xích nằm trên mặt bàn, P0 là trọng lượng của đoạn xích thòng xuống; m0 là khối lượng đoạn xích thòng xuống, m là khối lượng đoạn xích còn lại nằm trên mặt bàn)
\( \Rightarrow k.m = {m_0} \Leftrightarrow \frac{{{m_0}}}{m} = k \Rightarrow \frac{Y}{{L - Y}} = k \Rightarrow Y = \frac{k}{{k + 1}}.L\)
Với L = 120 cm; k = 1/3 \( \Rightarrow Y = \frac{{\frac{1}{3}}}{{\frac{1}{3} + 1}}.120 = 30\;{\rm{cm}}\)
Chọn A
Câu 23:
Phát biểu sau đây đúng hay sai?
Theo thí nghiệm 1, phân lập B có số lượng vi khuẩn phát triển lớn nhất khi được cung cấp nguồn carbon là galactose.
 Xem đáp án
Xem đáp án
Nhìn vào bảng 1, ta thấy trong môi trường nuôi cấy chứa nguồn carbon là galactose thì chủng vi khuẩn được nuôi cấy trên đĩa B có sự tăng trưởng cao nhất. Chọn A
Câu 24:
Dựa vào kết quả thí nghiệm 2, cho biết nếu đặt trong điều kiện nhiệt độ dưới nhiệt độ đóng băng của nước trong vòng 24 giờ thì sự phát triển của khuẩn lạc trong đĩa petri nào sẽ phát triển mạnh mẽ nhất?
 Xem đáp án
Xem đáp án
Nước đóng băng ở nhiệt độ 0oC, mà ta thấy ở kết quả của thí nghiệm 2, ở nhiệt độ 4oC không thấy sự sinh trưởng của vi khuẩn, nên rất có thể ở điều kiện nhiệt độ 0oC thì cũng không có khuẩn lạc nào có thể trải qua sự sinh trưởng. Chọn D
Câu 25:
Kéo thả từ/cụm từ vào vị trí thích hợp:
luôn giảm, giảm rồi tăng, tăng rồi giảm, luôn tăng
Xu hướng chung về sự phát triển của khuẩn lạc khi nhiệt độ giảm trong thí nghiệm 2 là _______.
 Xem đáp án
Xem đáp án
Đáp án
Xu hướng chung về sự phát triển của khuẩn lạc khi nhiệt độ giảm trong thí nghiệm 2 là tăng rồi giảm.
Giải thích
Quan sát bảng kết quả thí nghiệm 2, khi nhiệt độ giảm đi (42oC – 4oC) thì lượng khuẩn lạc trong thí nghiệm tăng dần rồi sau đó giảm đi.
Câu 26:
Giả sử thí nghiệm 3 được tiếp tục cho đến 34 giờ thay vì dừng lại ở 24 giờ (không xảy ra pha suy vong), thì mật độ quang học cuối cùng của đĩa C sẽ có giá trị gần nhất với
 Xem đáp án
Xem đáp án
Nhìn vào hình 1 ta thấy đường cong sinh trưởng của vi khuẩn thuộc đĩa C có xu hướng cân bằng từ 18 giờ tới 25 giờ, mà lại không xảy ra pha suy vong, thì lượng vi khuẩn sau 34h cũng sẽ xấp xỉ với giá trị tại 25 giờ, tức là gần nhất với giá trị 100. Chọn C
Câu 27:
 Xem đáp án
Xem đáp án
Xem xét bảng kết quả thí nghiệm 1 và 2, ta thấy ở môi trường có nguồn carbon là pyruvate thì có lượng vi khuẩn sinh trưởng lớn nhất, tương tự ở 30oC lượng vi khuẩn phát triển trên mỗi môi trường cũng là lớn nhất. Chọn B
Câu 28:
 Xem đáp án
Xem đáp án
Theo đoạn thông tin, máy đo quang phổ sẽ sử dụng tia laser để đo mật độ quang học của chất lỏng, khi mẫu đo càng đục thì giá trị đo được càng lớn. Nếu thay vì sử dụng nước cất, mà sử dụng nước đục để hiệu chuẩn thì giá trị OD đo được ở tất cả các môi trường đo đều sẽ có giá trị lớn hơn giá trị chuẩn. Chọn C
Câu 29:
Phát biểu sau đây đúng hay sai?
Trong thí nghiệm 3, giai đoạn đầu vi khuẩn gần như không có sự gia tăng về số lượng chủ yếu do lượng vi khuẩn còn ít, sự gia tăng không đáng kể nên đồ thị gần như nằm ngang.
 Xem đáp án
Xem đáp án
Sai. Vì trong giai đoạn đầu này vi khuẩn đang làm quen với môi trường, hình thành các enzyme cảm ứng nên chưa có sự phân chia rõ rệt, nên đồ thị gần như ở trạng thái cân bằng.
Chọn B
Câu 30:
Phát biểu sau đúng hay sai?
Theo quan điểm của học sinh 3, mẫu A và B được tạo thành từ cùng một chất.
 Xem đáp án
Xem đáp án
Văn bản đã cung cấp thông tin về quan điểm của học sinh 3: “Nếu hai mẫu có cùng khối lượng, thể tích, khối lượng riêng thì chúng được tạo thành từ cùng một chất”. So sánh dữ liệu ở Bảng 1, mẫu A và B có cùng khối lượng, thể tích, khối lượng riêng, do đó theo quan điểm của học sinh 3, mẫu A và B được tạo thành từ cùng một chất. Chọn A
Câu 31:
 Xem đáp án
Xem đáp án
Dựa vào Bảng 1, nhận thấy mẫu B và C chỉ giống nhau ở khối lượng riêng. Chọn A
Câu 32:
Dựa trên lời giải thích của Học sinh 1, hai mẫu nào sau đây được tạo thành từ cùng một chất?
 Xem đáp án
Xem đáp án
Văn bản đã cung cấp thông tin về quan điểm của học sinh 1: “Nếu 2 mẫu có cùng giá trị về cả 5 tính chất thì chúng được tạo thành bởi cùng một chất”. So sánh dữ liệu ở Bảng 1, mẫu C và D giống nhau ở cả 5 tính chất, do đó đáp án đúng là C.
Câu 33:
Cho quan điểm sau: “Hai mẫu có cùng khối lượng, thể tích, khối lượng riêng và điểm sôi được tạo thành từ cùng một chất, ngay cả khi chúng có điểm nóng chảy khác nhau”. Học sinh nào trong số học sinh 2 và 4 sẽ có khả năng đồng ý với ý kiến này?
 Xem đáp án
Xem đáp án
Theo quan điểm của học sinh 2, các mẫu phải giống nhau ở 3 tính chất bất kỳ thì mới được cấu tạo từ cùng một chất. Do đó, học sinh 2 sẽ đồng ý với quan điểm trên.
Theo quan điểm của học sinh 4, các mẫu có khối lượng riêng, nhiệt độ nóng chảy và nhiệt độ sôi giống nhau thì chúng được dự đoán tạo thành từ cùng một chất. Nếu bất kỳ tính chất nào trong số các tính chất này khác nhau, thì các mẫu không được tạo thành từ cùng một chất.
Chọn A
Câu 34:
Đơn vị tính của năng lượng liên kết hạt nhân là gì?
 Xem đáp án
Xem đáp án
Đơn vị của năng lượng liên kết là J hoặc MeV, trong đó: 1MeV = 1,6.10-13 J.
Chọn A, B
Câu 35:
Năng lượng liên kết riêng của hạt nhân có thể được tính theo công thức nào sau đây?
 Xem đáp án
Xem đáp án
Năng lượng liên kết riêng của hạt nhân, kí hiệu là \(\varepsilon \), có giá trị bằng tỷ số giữa năng lượng liên kết và tổng số nuclôn của hạt nhân: \(\varepsilon = \frac{{\Delta W}}{A} = \frac{{\Delta m{c^2}}}{A}\)
Chọn A
Câu 36:
Phát biểu nào sau đây là đúng hoặc sai?
|
Phát biểu |
Đúng |
Sai |
|
Năng lượng liên kết riêng là năng lượng liên kết tính cho một nuclôn |
||
|
Hạt nhân có độ hụt khối càng lớn thì năng lượng liên kết càng lớn. |
||
|
Hạt nhân càng bền vững khi có năng lượng liên kết càng lớn. |
||
|
Năng lượng liên kết đặc trưng cho mức độ bền vững của hạt nhân |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Năng lượng liên kết riêng là năng lượng liên kết tính cho một nuclôn |
X | |
|
Hạt nhân có độ hụt khối càng lớn thì năng lượng liên kết càng lớn. |
X | |
|
Hạt nhân càng bền vững khi có năng lượng liên kết càng lớn. |
X | |
|
Năng lượng liên kết đặc trưng cho mức độ bền vững của hạt nhân |
X |
Giải thích
1. Đúng. Năng lượng liên kết riêng là năng lượng liên kết trung bình cho một nuclôn.
2. Đúng. \(\Delta W = \Delta m.{c^2}\) nên \(\Delta m\) càng lớn thì \(\Delta W\)càng lớn.
3. Sai. Để so sánh độ bền vững giữa các hạt nhân, cần so sánh năng lượng liên kết riêng của hạt nhân.
4. Sai. Năng lượng liên kết riêng đặc trưng cho mức độ bền vững của hạt nhân.
Câu 37:
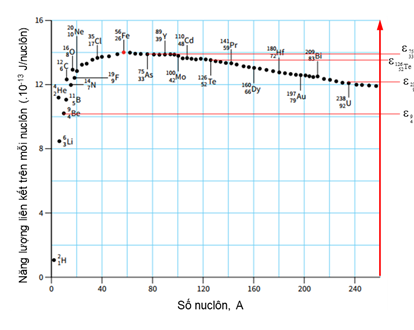
Năng lượng liên kết riêng của hạt nhân \(_{26}^{56}{\rm{Fe}}\) là (1) _______ MeV/nuclôn.
 Xem đáp án
Xem đáp án
Đáp án
Năng lượng liên kết riêng của hạt nhân \(_{26}^{56}{\rm{Fe}}\) là (1) 8,75 MeV/nuclôn.
Giải thích
Từ đồ thị ta thấy:
\({\varepsilon _{_{26}^{56}Fe}} = {14.10^{ - 13}}\) J/nuclôn \( = \frac{{{{14.10}^{ - 13}}}}{{1,{{6.10}^{ - 13}}}} = 8,75\) MeV/nuclôn.
Câu 38:
Cho các hạt nhân sau: \(_4^9{\rm{Be}};\,\,_{33}^{75}{\rm{As}};\,\,_{52}^{126}{\rm{Te}};\,\,_{92}^{238}U\). Sắp xếp các hạt nhân theo thứ tự tăng dần độ bền vững của hạt nhân là
 Xem đáp án
Xem đáp án
Giải thích
Nhìn vào biểu đồ có thể thấy: \({\varepsilon _{_4^9{\rm{Be}}}}\,\,{\rm{ < }}\,\,{\varepsilon _{_{92}^{238}{\rm{U}}}}\,\,{\rm{ < }}\,\,{\varepsilon _{_{52}^{126}{\rm{Te}}}}\,\,{\rm{ < }}\,\,{\varepsilon _{_{33}^{75}{\rm{As}}}}\). Chọn B
Câu 39:
Biết khối lượng nghỉ của protôn, nơtron, và electrôn lần lượt là 1,00728u; 1,00866u và 5,486.10-4u. Khối lượng của nguyên tử \(_7^{14}N\)có giá trị là
 Xem đáp án
Xem đáp án
Giải thích
Từ đồ thị có thể thấy \({\varepsilon _{_7^{14}N}} = {12.10^{ - 13}}\)J/nuclôn.
Mà: \(\Delta {{\rm{W}}_{_7^{14}N}} = A.{\varepsilon _{_7^{14}N}} = {14.12.10^{ - 13}} = 1,{68.10^{ - 11}}\;{\rm{J}} = 105\,\,{\rm{MeV}}\)
Mặt khác: \(\Delta {W_{_7^{14}N}} = 931,5.\Delta {m_{_7^{14}N}} \Rightarrow \Delta {m_{_7^{14}N}} = \frac{{105}}{{931,5}}u = \frac{{70}}{{621}}u{\rm{. }}\)
\(\Delta {m_{N_7^{14}}} = 7\left( {{m_n} + {m_p}} \right) - {M_{N_7^{14}}}\)
\( \Rightarrow {M_{N_7^{14}}} = 7\left( {{m_n} + {m_p}} \right) - \Delta {m_{N_7^{14}}} = 7(1,00728u + 1,00866u) - \frac{{70}}{{621}}u = 13,99886u\)
Khối lượng nguyên tử \(_7^{14}N\) là:
\(m = {M_{_7^{14}N}} + 7{m_e} = 13,99886u + 7.5,{486.10^{ - 4}}u = 14,0027u.\)
Chọn A
Câu 40:
Kéo ô vuông thả vào vị trí thích hợp:
20, 200, 50 < A < 80, bền vững, kém bền vững
Ngoại trừ các hạt sơ cấp riêng rẽ (như protôn, nơtrôn, êlectron), hạt nhân có năng lượng liên kết riêng càng lớn thì càng _______. Thực nghiệm cho thấy những hạt nhân có số khối lớn hơn _______ hoặc số khối nhỏ hơn _______ thì kém bền vững, còn những hạt nhân có số khối _______ thì rất bền.
 Xem đáp án
Xem đáp án
Đáp án
Ngoại trừ các hạt sơ cấp riêng rẽ (như protôn, nơtrôn, êlectron), hạt nhân có năng lượng liên kết riêng càng lớn thì càng bền vững. Thực nghiệm cho thấy những hạt nhân có số khối lớn hơn 200 hoặc số khối nhỏ hơn 20 thì kém bền vững, còn những hạt nhân có số khối 50 < A< 80 thì rất bền.
Giải thích
Từ bài đọc có thể rút ra nhận xét: Hạt nhân có năng lượng liên kết riêng càng lớn thì càng bền vững.
Từ đồ thị ta thấy:
- Khi A tăng dần từ 0 đến 20, năng lượng liên kết riêng tăng dần từ khoảng 10-13 J/nuclôn đến 13.10-13 J/nuclôn.
- Khi A tăng dần từ 200 trở đi, năng lượng liên kết riêng giảm dần từ khoảng 12,5.10-13 J/nuclôn.
=> Hai vùng A < 20 và A > 200 có năng lượng liên kết riêng thấp nhất nên kém bền vững nhất.
- Khi A nằm trong khoảng từ 50 đến 80, năng lượng liên kết riêng của hạt nhân có giá trị lớn nhất, vào khoảng 14.10-13 J/nuclôn. Vì vậy những hạt nhân có số khối nằm trong khoảng này là bền vững nhất.
Câu 41:
Virus nhận ra các tế bào chủ của nó theo nguyên tắc “chìa và khóa” nghĩa là
 Xem đáp án
Xem đáp án
Theo đoạn thông tin: “Virus nhận ra các tế bào chủ của nó theo nguyên tắc “chìa và khóa” giữa các protein bề mặt của virus với các phân tử thụ thể đặc hiệu trên bề mặt ngoài của tế bào chủ”, tức là không phải virus nào cũng xâm nhập được vào hết các loại tế bào, mà cần có sự liên kết đặc hiệu với tùy từng loại thụ thể trên bề mặt tế bào. Chọn B
Câu 42:
Hấp thị, Xâm nhập, Sinh tổng hợp, Lắp ráp, Giải phóng
_______ → _______ → _______ → _______ → _______.
 Xem đáp án
Xem đáp án
Đáp án
Sắp xếp các giai đoạn sau đây cho đúng chu trình nhân lên của virus?
Hấp phụ → Xâm nhập → Sinh tổng hợp → Lắp ráp → Giải phóng.
Giải thích
Theo đoạn thông tin, ta có thể sơ đồ hóa lại quá trình nhân lên của virus theo trình tự: Hấp phụ → Xâm nhập → Sinh tổng hợp → Lắp ráp → Giải phóng.
Câu 43:
Điều nào sau đây không đúng khi nói về virus?
 Xem đáp án
Xem đáp án
Theo bài: “Chúng là các dạng sống ký sinh nội bào bắt buộc”, sử dụng hệ enzyme của vật chủ để nhân lên, nên dù ở trong hay ngoài vật chủ thì virus đều không có sự sinh trưởng. Chọn D
Câu 44:
 Xem đáp án
Xem đáp án
Virus cần tự mã hóa một số loại enzyme nhất định phục vụ cho nhu cầu nhân lên của chúng, do tế bào chủ không cần thiết phải có những enzyme đó trong quá trình hoạt động của mình. Chọn A
Câu 45:
Điền số thích hợp vào chỗ trống
Cho các phương thức sau:
(1) Ức chế hoà màng/xâm nhập.
(2) Ức chế enzyme sao chép ngược.
(3) Ức chế protease.
(4) Ức chế sự tích hợp vật chất di truyền của virus.
Có (1) ______ phương thức phù hợp với việc sản xuất các loại thuốc để ức chế sự nhân lên của virus HIV.
 Xem đáp án
Xem đáp án
Đáp án
Có (1) __4__ phương thức phù hợp với việc sản xuất các loại thuốc để ức chế sự nhân lên của virus HIV.
Giải thích
4 phương thức trên đều phù hợp:
Ức chế hòa màng/xâm nhập: ngăn chặn virus xâm nhập vào tế bào.
Ức chế enzyme sao chép ngược: không tạo đủ vật chất di truyền cho các thế hệ virus.
Ức chế protease: ức chế sự tổng hợp protein, lắp ráp các vật chất virus.
Ức chế sự tích hợp vật chất di truyền của virus: ngăn chặn virus gắn hệ gene vào hệ gene tế bào.
Câu 46:
Phát biểu sau đây đúng hay sai?
Thụ thể CD4 là thụ thể của virus HIV. Nếu đưa hồng cầu có thụ thể CD4 vào bệnh nhân HIV thì bệnh nhân sẽ thiếu máu nghiêm trọng vì virus sẽ xâm nhập và phá hủy tế bào.
 Xem đáp án
Xem đáp án
Thụ thể CD4 đặc hiệu với protein bề mặt của virus. Nếu đưa hồng cầu có thụ thể CD4 vào bệnh nhân HIV thì virus sẽ xâm nhập vào nhưng không nhân lên được do hồng cầu không có nhân, không có bộ máy sao chép nucleic acid. Chọn B
Câu 47:
Các phát biểu sau đây đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Virus bám được vào tế bào chủ là nhờ các thụ thể thích hợp có sẵn trên bề mặt tế bào chủ. |
||
|
Kết quả của quá trình nhân lên là từ một virus ban đầu tạo ra vô số virus mới có độc tính tăng gấp nhiều lần. |
||
|
Virus sử dụng nguyên liệu của tế bào chủ trong quá trình nhân lên của mình. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Virus bám được vào tế bào chủ là nhờ các thụ thể thích hợp có sẵn trên bề mặt tế bào chủ. |
X | |
|
Kết quả của quá trình nhân lên là từ một virus ban đầu tạo ra vô số virus mới có độc tính tăng gấp nhiều lần. |
X | |
|
Virus sử dụng nguyên liệu của tế bào chủ trong quá trình nhân lên của mình. |
X |
Giải thích
(1), (3) đúng.
(2) sai vì kết quả của quá trình nhân lên là từ một virus ban đầu tạo ra vô số virus mới giống hệt nhau và giống virus ban đầu.
Câu 48:
Phát biểu sau đúng hay sai?
Một sinh viên dự đoán rằng khi nickel hydroxide monohydrate rắn được thu hồi bằng phương pháp lọc thông thường, CNF trong thời gian phản ứng 3 ngày sẽ lớn hơn so với thời gian phản ứng 10 phút.
 Xem đáp án
Xem đáp án
Cách 1: nhìn nhanh các giá trị CNF trong Bảng 1, ta thấy ở cả 2 thí nghiệm, CNF ở thời gian phản ứng 3 ngày đều cao hơn CNF ở thời gian phản ứng 10 phút.
Cách 2:
Thí nghiệm 1 sử dụng phương pháp lọc thông thường.
Theo Bảng 1, khi thời gian phản ứng là 3 ngày thì CNF là 39 mg/kg (thử nghiệm 2) và khi thời gian phản ứng là 10 phút thì CNF là 6 mg/kg (thử nghiệm 1).
→ CNF trong 3 ngày sẽ lớn hơn so với 10 phút (bằng phương pháp lọc thông thường). Chọn A
Câu 49:
 Xem đáp án
Xem đáp án
Theo Bảng 1, trong thí nghiệm 1:
Khi thời gian phản ứng là 10 phút thì CNF là 6 mg/kg và khi thời gian phản ứng là 3 ngày thì CNF là 39 mg/kg.
→ Thời gian phản ứng là 2 ngày thì CNF nằm trong khoảng từ 6 mg/kg đến 39 mg/kg.
Chọn B
Câu 50:
Theo quy chuẩn kỹ thuật quốc gia về chất lượng nước sạch sử dụng cho mục đích sinh hoạt (QCVN 01-1:2018/BYT), hàm lượng Ni2+ trong nước ở mức cho phép là
 Xem đáp án
Xem đáp án
Theo quy chuẩn kỹ thuật quốc gia về chất lượng nước sạch sử dụng cho mục đích sinh hoạt (QCVN 01-1:2018/BYT), hàm lượng Ni2+ trong nước phải nhỏ hơn 0,07 mg/L.
Chọn A
Câu 51:
Phát biểu sau đúng hay sai?
Trong thí nghiệm 2, nếu thời gian phản ứng là 5 ngày thì CNF có giá trị nằm trong khoảng từ 58 mg/kg đến 69 mg/kg.
 Xem đáp án
Xem đáp án
Theo Bảng 1, trong thí nghiệm 2: khi thời gian phản ứng là 3 ngày thì CNF là 69 mg/kg và khi thời gian phản ứng là 7 ngày thì CNF là 73 mg/kg.
→ Thời gian phản ứng là 5 ngày thì CNF nằm trong khoảng từ 69 mg/kg đến 73 mg/kg.
Chọn B
Câu 52:
Điền số thích hợp vào chỗ trống
Trong thí nghiệm 2, khi thời gian phản ứng là 3 ngày thì CNF đo được là (1) _____ mg/kg.
 Xem đáp án
Xem đáp án
Đáp án:
Trong thí nghiệm 2, khi thời gian phản ứng là 3 ngày thì CNF đo được là (1) __69__ mg/kg.
Câu 53:
Điền số thích hợp vào chỗ trống
Dựa vào phương trình hóa học đã cân bằng ở trên, khi 6 hydroxide phản ứng thì có (1) _____ nickel hydroxide monohydrate được tạo ra.
 Xem đáp án
Xem đáp án
Đáp án
Xét phương trình phản ứng:
Ni2+ + 2OH− + H2O → Ni(OH)2.H2O
Ta có tỉ lệ: OH– : [Ni(OH)2.H2O] = 2 : 1
Do đó, nếu 6 hydroxide (OH–) phản ứng thì có 3 [Ni(OH)2.H2O] được tạo ra.
Câu 54:
Phân tư duy toán học
 Xem đáp án
Xem đáp án
Giải thích
Đặt \(f\left( x \right) = {x^2} + x - m\). Ta có: \(f'\left( x \right) = 2x + 1;f'\left( x \right) = 0 \Leftrightarrow x = - \frac{1}{2}\)
Bảng biến thiên:
![Gọi \(S\) là tập hợp các giá trị \(m\) để giá trị nhỏ nhất của hàm số \(y = {\left( {{x^2} + x - m} \right)^2}\) trên đoạn \(\left[ { - 2;2} \right]\) bằng 9 . Tổng các phần tử của tập hợp \(S\) bằng A. \(\frac{{23}}{4}\). B. \( - \frac{{23}}{4}\). C. \(\frac{{41}}{4}\). D. \(\frac{{23}}{2}\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid0-1729741965.png)
Trường hợp 1. \( - m - \frac{1}{4} > 0 \Leftrightarrow m < - \frac{1}{4}\)
Ta có: \(\mathop {{\rm{min}}}\limits_{x \in \left[ { - 2;2} \right]} f\left( x \right) = - m - \frac{1}{4} \Rightarrow \mathop {{\rm{min}}}\limits_{x \in \left[ { - 2;2} \right]} y = {\left( { - m - \frac{1}{4}} \right)^2} = 9 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = - \frac{{13}}{4}\,\,\left( {t/m} \right)}\\{m = \frac{{11}}{4}\,\,\left( l \right)\,\,\,\,\,\,\,\,\,}\end{array}} \right.\)
Trường hợp 2. \( - m + 6 < 0 \Leftrightarrow m > 6\)
Ta có \(\mathop {{\rm{min}}}\limits_{x \in \left[ { - 2;2} \right]} f\left( x \right) = - m - \frac{1}{4} \Rightarrow \mathop {{\rm{min}}}\limits_{x \in \left[ { - 2;2} \right]} y = {( - m + 6)^2} = 9 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 3\,\,\left( l \right)\,\,\,\,\,\,\,}\\{m = 9\,\,\left( {t/m} \right)}\end{array}} \right.\)
Trường hợp 3. \( - m - \frac{1}{4} \le 0 \le - m + 6 \Leftrightarrow - \frac{1}{4} \le m \le 6\)
Ta có . Suy ra \( - \frac{1}{4} \le m \le 6\) không thỏa mãn yêu cầu bài toán.
Vậy \(m \in \left\{ { - \frac{{13}}{4};9} \right\} \Rightarrow S = \frac{{23}}{4}\).
Chọn A
Câu 55:
Ta định nghĩa, một hình nón gọi là nội tiếp một mặt cầu nếu mặt cầu chứa đỉnh và đường tròn đáy của hình nón.
Cho mặt cầu \(\left( S \right)\) có đường kính bằng \(24{\rm{\;cm}}\). Xét tất cả các hình nón nội tiếp mặt cầu \(\left( S \right)\), gọi \(\left( N \right)\) là hình nón có thể tích của khối nón được tạo bởi \(\left( N \right)\) là lớn nhất. Khi đó, chiều cao của hình nón \(\left( N \right)\) bằng
 Xem đáp án
Xem đáp án
Chọn A
Câu 56:
 Xem đáp án
Xem đáp án
Giải thích
Ta có: \(g'\left( x \right) = 2xf'\left( {{x^2}} \right) = 2x\left[ {{x^2}{{\left( {{x^2} + 1} \right)}^2}\left( {{x^4} + m{x^2} + 16} \right)} \right]\)
\(g'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{{x^4} + m{x^2} + 16 = 0\,\,\left( * \right)}\end{array}} \right.\)
Để hàm số \(g\left( x \right)\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\) thì \(g'\left( x \right) \ge 0,\forall x \in \left( {0; + \infty } \right)\)
Đặt \(t = {x^2}\left( {t \ge 0} \right)\), phương trình \(\left( {\rm{*}} \right)\) trở thành: \({t^2} + mt + 16 = 0\left( {{\rm{**}}} \right)\)
Để \(g'\left( x \right) \ge 0,\forall x \in \left( {0; + \infty } \right)\) thì \(\left( {{\rm{**}}} \right)\) vô nghiệm hoặc có nghiệm kép hoặc có hai nghiệm âm phân biệt.
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{\rm{\Delta }} \le 0}\\{\left\{ {\begin{array}{*{20}{c}}{{\rm{\Delta }} > 0}\\{ - m < 0}\end{array}} \right.}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{m^2} - 4.16 \le 0}\\{\left\{ {\begin{array}{*{20}{c}}{{m^2} - 4.16 > 0}\\{ - m < 0}\end{array}} \right.}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ - 8 \le m \le 8}\\{m > 8}\end{array} \Leftrightarrow m \ge - 8} \right.} \right.} \right.\)
Vì \(m\) nguyên âm nên \(m \in \left\{ { - 8; - 7; \ldots ; - 1} \right\}\).
Chọn C
Câu 57:
 Xem đáp án
Xem đáp án
Giải thích
Điều kiện: \(\left\{ {\begin{array}{*{20}{l}}{n \ge k}\\{n,k \in \mathbb{N}}\end{array}} \right.\).
Ta có: \(\frac{{{P_{n + 5}}}}{{\left( {n - k} \right)!}} \le 60A_{n + 3}^{k + 2} \Leftrightarrow \frac{{\left( {n + 5} \right)!}}{{\left( {n - k} \right)!}} \le 60.\frac{{\left( {n + 3} \right)!}}{{\left( {n - k + 1} \right)!}} \Leftrightarrow \left( {n + 5} \right)\left( {n + 4} \right)\left( {n - k + 1} \right) \le 60\,\,\left( {\rm{*}} \right)\)
Với \(n \ge 4\) thì \(\left( {n + 5} \right)\left( {n + 4} \right) \ge \left( {4 + 5} \right)\left( {4 + 4} \right) = 72\) nên từ \(\left( {\rm{*}} \right)\) suy ra \(n - k + 1 \le \frac{5}{6}\) (vô lí, do \(n \ge k)\).
Với \(n = 3\) thì \(\left( {\rm{*}} \right) \Leftrightarrow \left( {3 + 5} \right)\left( {3 + 4} \right)\left( {3 - k + 1} \right) \le 60 \Leftrightarrow 56\left( {4 - k} \right) \le 60 \Leftrightarrow k \ge \frac{{41}}{{14}} \Rightarrow k = 3\)
Với \(n = 2\) thì \(\left( {\rm{*}} \right) \Leftrightarrow \left( {2 + 5} \right)\left( {2 + 4} \right)\left( {2 - k + 1} \right) \le 60 \Leftrightarrow 42\left( {3 - k} \right) \le 60 \Leftrightarrow k \ge \frac{{11}}{7} \Rightarrow k = 2\)
Với \(n = 1\) thì \(\left( {\rm{*}} \right) \Leftrightarrow \left( {1 + 5} \right)\left( {1 + 4} \right)\left( {1 - k + 1} \right) \le 60 \Leftrightarrow 30\left( {2 - k} \right) \le 60 \Leftrightarrow k \ge 0 \Rightarrow k \in \left\{ {0;1} \right\}\)
Với \(n = 0\) thì \(\left( {\rm{*}} \right) \Leftrightarrow \left( {0 + 5} \right)\left( {0 + 4} \right)\left( {0 - k + 1} \right) \le 60 \Leftrightarrow 20\left( {1 - k} \right) \le 60 \Leftrightarrow k \ge - 2 \Rightarrow k = 0\)
Vậy có 5 bộ số \(\left( {n;k} \right)\) thỏa mãn.
Chọn A
Câu 58:
 Xem đáp án
Xem đáp án

Câu 59:
 Xem đáp án
Xem đáp án
Giải thích
Ta có: \(\frac{{1 + 2 + \ldots + n}}{{{n^2} + n}} \le \frac{1}{{{n^2} + 1}} + \frac{2}{{{n^2} + 2}} + \ldots + \frac{n}{{{n^2} + n}} \le \frac{{1 + 2 + \ldots + n}}{{{n^2} + 1}}\).
Mà \({\rm{lim}}\frac{{1 + 2 + \ldots + n}}{{{n^2} + n}} = {\rm{lim}}\frac{{\frac{{n\left( {n + 1} \right)}}{2}}}{{{n^2} + n}} = \frac{1}{2}\);
\({\rm{lim}}\frac{{1 + 2 + \ldots + n}}{{{n^2} + 1}} = {\rm{lim}}\frac{{\frac{{n\left( {n + 1} \right)}}{2}}}{{{n^2} + 1}} = {\rm{lim}}\frac{{{n^2} + n}}{{2\left( {{n^2} + 1} \right)}} = {\rm{lim}}\frac{{1 + \frac{1}{n}}}{{2\left( {1 + \frac{1}{{{n^2}}}} \right)}} = \frac{1}{2}\)
Nên \({\rm{lim}}\left( {\frac{1}{{{n^2} + 1}} + \frac{2}{{{n^2} + 2}} + \ldots + \frac{n}{{{n^2} + n}}} \right) = \frac{1}{2}\).
Chọn C
Câu 60:
 Xem đáp án
Xem đáp án
Giải thích
Gọi số tự nhiên có 6 chữ số khác nhau là \(\overline {abcdef} \) với \(a \ne 0;\,\,a,b,c,d,e,f \in \left\{ {0;1;2;3;4;5} \right\}\).
Số cách chọn chữ số \(a\) có 5 cách.
Số cách sắp xếp 5 chữ số còn lại vào 5 vị trí \(b;c;d;e;f\): có 5! cách
Vậy có tất cả \(5.5! = 600\) số thỏa mãn yêu cầu đề bài.
Chọn A
Câu 61:
Hai chị em Trang và Bình có sinh nhật vào tháng ba và tháng năm. Vào tháng tư năm 2023, Bình cộng tuổi của mình với năm sinh của mình và tuổi của Trang với năm sinh của Trang được số (1) _______.
 Xem đáp án
Xem đáp án
Đáp án
Hai chị em Trang và Bình có sinh nhật vào tháng ba và tháng năm. Vào tháng tư năm 2023, Bình cộng tuổi của mình với năm sinh của mình và tuổi của Trang với năm sinh của Trang được số (1) __4045_.
Giải thích
Vào tháng tư năm 2023, Trang đã qua ngày sinh nhật trong năm 2023, còn Bình chưa tới ngày sinh nhật trong năm 2023.
Tổng tuổi của Trang với năm sinh của Trang là 2023.
Tổng tuổi của Bình với năm sinh của Bình là 2022.
Ta có: .2022 + 2023 = 4045
Câu 62:
 Xem đáp án
Xem đáp án
Giải thích
Điểm thuộc giao tuyến \(d\) của \(\left( P \right)\) và \(\left( Q \right)\) là nghiệm của hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x + 4y - 2z - 6 = 0}\\{x - 2y + 4z - 6 = 0}\end{array}} \right.\).
Chọn \(x = 2 \Rightarrow y = z = 2 \Rightarrow M\left( {2;2;2} \right) \in d\).
Chọn \(x = 0 \Rightarrow y = z = 3 \Rightarrow N\left( {0;3;3} \right) \in d\).
Gọi \(A\left( {a;0;0} \right),B\left( {0;b;0} \right),C\left( {0;0;c} \right)\) lần lượt là giao điểm của \(\left( \alpha \right)\) và các trục tọa độ \(Ox,Oy,Oz\) \( \Rightarrow \left( \alpha \right):\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1{\rm{\;}}\left( {abc \ne 0} \right)\)
Vì \(d \in \left( \alpha \right)\) nên \(M,N \in \left( \alpha \right)\).
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{2}{a} + \frac{2}{b} + \frac{2}{c} = 1}\\{\frac{3}{b} + \frac{3}{c} = 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{1}{a} = \frac{1}{6}}\\{\frac{2}{a} + \frac{2}{b} + \frac{2}{c} = 1}\end{array} \Rightarrow a = 6} \right.} \right.\)
Để \(O.ABC\) là hình chóp đều thì \(OA = OB = OC \Leftrightarrow \left| a \right| = \left| b \right| = \left| c \right| \Rightarrow a = b = c = 6\).
\( \Rightarrow \left( \alpha \right):x + y + z - 6 = 0\)
Chọn A
Câu 63:
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật với \(AB = 2a,BC = a\), tam giác đều \(SAB\) nằm trên mặt phẳng vuông góc với đáy.
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\) là đường thẳng đi qua điểm \(S\) và song song với \(AB\). |
||
|
Khoảng cách giữa \(BC\) và \(SD\) bằng \(a\sqrt 3 \). |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\) là đường thẳng đi qua điểm \(S\) và song song với \(AB\). |
X | |
|
Khoảng cách giữa \(BC\) và \(SD\) bằng \(a\sqrt 3 \). |
X |
Giải thích
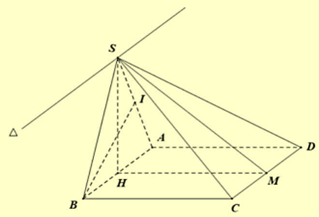
Ta có: \(\left\{ \begin{array}{l}AB//CD\\AB \subset (SAB)\\CD \subset (SCD)\\S \in (SAB) \cap (SCD)\end{array} \right.\)
\( \Rightarrow \) Đường thẳng \({\rm{\Delta }}\) đi qua \(S\) và song song với \(AB\) là giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\).
Gọi \(H\) là trung điểm \(AB\) thì \(SH \bot \left( {ABCD} \right)\).
Vì \(BC//\left( {SAD} \right)\) nên \(d\left( {BC,SD} \right) = d\left( {BC,\left( {SAD} \right)} \right) = d\left( {B,\left( {SAD} \right)} \right)\).
Gọi \(I\) là trung điểm của \(SA\) thì \(BI \bot SA\) thì \(BI \bot \left( {SAD} \right)\) (do \(AD \bot \left( {SAB} \right) \supset BI\)).
Suy ra \({\rm{d}}\left( {B,\left( {SAD} \right)} \right) = BI = \frac{{2a\sqrt 3 }}{2} = a\sqrt 3 \).
Câu 64:
Cho một đa giác đều 14 đỉnh. Chọn ngẫu nhiên 3 đỉnh của đa giác. Xác suất để 3 đỉnh được chọn tạo thành một tam giác vuông bằng (1) _______.
 Xem đáp án
Xem đáp án
Đáp án
Cho một đa giác đều 14 đỉnh. Chọn ngẫu nhiên 3 đỉnh của đa giác. Xác suất để 3 đỉnh được chọn tạo thành một tam giác vuông bằng (1) __3/13__.
Giải thích
Số phần tử của không gian mẫu là \(n\left( {\rm{\Omega }} \right) = C_{14}^3\).
Đa giác đều 14 đỉnh có 7 đường chéo đi qua tâm, với mỗi đường chéo thì số tam giác vuông nhận đường chéo là cạnh huyền là 12 nên số tam giác vuông thỏa mãn yêu cầu bài toán là \(7.12 = 84\) (tam giác).
Xác suất cần tính là \(P = \frac{{84}}{{C_{14}^3}} = \frac{3}{{13}}\).
Câu 65:
Thống kê điểm môn Toán trong một kì thi của 50 em học sinh được bảng sau:
|
Điểm |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Số học sinh |
1 |
3 |
1 |
11 |
8 |
9 |
10 |
4 |
3 |
Chọn ngẫu nhiên 2 bài làm của 2 em học sinh. Xác suất để chọn được 2 bài trên 7 điểm là (1) _____ % (Kết quả làm tròn đến chữ số thập phân thứ nhất).
 Xem đáp án
Xem đáp án
Đáp án
Chọn ngẫu nhiên 2 bài làm của 2 em học sinh. Xác suất để chọn được 2 bài trên 7 điểm là (1) __11,1__ % (Kết quả làm tròn đến chữ số thập phân thứ nhất).
Giải thích
Số phần tử của không gian mẫu là \(n\left( {\rm{\Omega }} \right) = C_{50}^2\).
Biến cố \(A\) : "Chọn được 2 bài trên 7 điểm" \( \Rightarrow n\left( A \right) = C_{10 + 4 + 3}^2 = C_{17}^2\).
Xác suất cần tìm là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( {\rm{\Omega }} \right)}} = \frac{{C_{17}^2}}{{C_{50}^2}} \approx 11,1\).
Câu 66:
Hai số nguyên dương là cặp số hứa hôn khi thoả mãn quy luật sau: Tổng các ước của số này (khác chính nó) nhiều hơn số kia đúng 1 đơn vị. Hai số nguyên dương tạo thành một cặp số thân thiết khi chúng tuân theo quy luật: Số này bằng tổng tất cả các ước của số kia (trừ chính nó) và ngược lại. Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
220 và 284 là một cặp số thân thiết. |
||
|
140 và 195 không là cặp số hứa hôn. |
||
|
48 và 75 là cặp số hứa hôn. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
220 và 284 là một cặp số thân thiết. |
X | |
|
140 và 195 không là cặp số hứa hôn. |
X | |
|
48 và 75 là cặp số hứa hôn. |
X |
Giải thích
Ta có:
\(220 = {2^2} \times 5 \times 11\). Ngoài chính nó ra, nó còn có 11 ước số khác là: \(1;2;4;5;10;11;20;44;55;110\).
Tổng của 11 ước này bằng 284 .
\(284 = {2^2} \times 71\). Ngoài chính nó, nó còn có 5 ước số khác là: 1;\(2;4;71;142\). Tổng của 5 ước này bằng 220.
Vậy 220 và 284 là một cặp số thân thiết.
\(140 = {2^2} \times 5 \times 7\). Ngoài chính nó ra, nó còn có 11 ước số khác là: \(1;2;4;5;7;10;12;20;28;35;70\).
Tổng của 11 ước này bằng 194.
\(195 = 3 \times 5 \times 13\). Ngoài chính nó ra, nó còn có 7 ước số khác là: \(1;3;5;13;15;39;65\). Tổng của 11 ước này bằng 141.
Ta thấy \(141 - 140 = 1,194 - 195 = - 1\). Vậy 140 và 195 không là cặp số hứa hôn.
\(48 = {2^4} \times 3\). Ngoài chính nó, nó còn có 9 ước số khác là: \(1;2;3;4;6;8;12;16;24\). Tổng của 9 ước này bằng \(76 \ne 75\).
\(75 = 3 \times {5^2}\). Ngoài chính nó, nó còn có 5 ước số khác là: \(1;3;5;15;25\). Tổng của 5 ước này bằng 49. Ta thấy \(76 - 75 = 1\) và \(49 - 48 = 1\). Vậy 48 và 75 là cặp số hứa hôn.
Câu 67:
 Xem đáp án
Xem đáp án
Giải thích
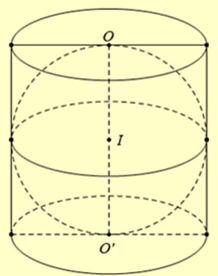
Ta có thể tích khối trụ là \({V_t} = \pi .{r^2}.OO' = 2\pi {r^3}\).
Mặt cầu tiếp xúc với hai đáy của hình trụ nên mặt cầu có bán kính \(R = \frac{1}{2}OO' = r\), suy ra thể tích khối cầu là \({V_c} = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {r^3}\).
Khi đó, \(\frac{{{V_c}}}{{{V_t}}} = \frac{{\frac{4}{3}\pi {r^3}}}{{2\pi {r^3}}} = \frac{2}{3}\).
Chọn A
Câu 68:
Một cửa chuyên bán các sản phẩm điện tử tung ra chương trình khuyến mại nhân ngày khai trương chi nhánh mới như sau: Khi khách hàng mua từ 2 loại sản phầm trở lên, giá mỗi sản phẩm giảm so với giá ban đầu. Dưới đây là bảng giá gốc của các sản phẩm khuyến mại:
|
Loại sản phẩm |
Sản phẩm |
Giá (Đơn vị: Nghìn đồng) |
|
Tai nghe |
Tai nghe có dây |
200 |
|
Tai nghe bluetooth |
540 |
|
|
Tai nghe gaming |
486 |
|
|
Loa |
Loa vi tính |
350 |
|
Loa bluetooth |
550 |
|
|
Sạc |
Sạc dự phòng |
620 |
|
Miếng dán màn hình |
Miếng dán cường lực |
70 |
Nếu Chi có 500 nghìn đồng thì Chi có thể mua được tối đa (1) _______ sản phẩm và còn thừa ít nhất (2) ________ nghìn đồng
 Xem đáp án
Xem đáp án
Đáp án
Nếu Chi có 500 nghìn đồng thì Chi có thể mua được tối đa (1) ___3___ sản phẩm và còn thừa ít nhất (2) ___4___ nghìn đồng
Giải thích
Vì khi mua từ 2 loại sản phầm trở lên, giá mỗi sản phẩm giảm so với giá ban đầu nên giả sử số sản phẩm Chi mua được ít nhất bằng 2 với tổng giá gốc là (nghìn đồng), .
Khi đó, .
Vậy tổng số tiền gốc các sản phẩm Chi mua không vượt quá 625 nghìn đồng.
Xét các sản phầm có giá từ thấp lên cao ta thấy 3 sản phẩm có giá thấp nhất (Miếng dán cường lực, tai nghe có dây, loa vi tính) có tổng giá tiền gốc là: (nghìn dồng).
Vậy Chi mua được tối đa 3 sản phầm và còn thừa (nghìn đồng).
Câu 69:
 Xem đáp án
Xem đáp án
Giải thích
Ta có:
\({\rm{lo}}{{\rm{g}}_3}\left( {{x^2} - 5x + m} \right) > {\rm{lo}}{{\rm{g}}_3}\left( {x - 2} \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x - 2 > 0}\\{{x^2} - 5x + m > x - 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x > 2}\\{m > - {x^2} + 6x - 2}\end{array}} \right.} \right.\).
Bất phương trình \({\rm{lo}}{{\rm{g}}_3}\left( {{x^2} - 5x + m} \right) > {\rm{lo}}{{\rm{g}}_3}\left( {x - 2} \right)\) có tập nghiệm chứa khoảng \(\left( {2; + \infty } \right)\)
\( \Leftrightarrow m > - {x^2} + 6x - 2\) có nghiệm với mọi \(x \in \left( {2; + \infty } \right)\).
Xét hàm số \(f\left( x \right) = - {x^2} + 6x - 2\) trên \(\left( {2; + \infty } \right)\).
Ta có \(f'\left( x \right) = - 2x + 6,f'\left( x \right) = 0 \Leftrightarrow x = 3\)
Bảng biến thiên
![Gọi \(S\) là tập hợp tất cả các giá trị của tham số \(m\) để bất phương trình \({\rm{lo}}{{\rm{g}}_3}\left( {{x^2} - 5x + m} \right) > {\rm{lo}}{{\rm{g}}_3}\left( {x - 2} \right)\) có tập nghiệm chứa khoảng \(\left( {2; + \infty } \right)\). Khẳng định nào sau đây là đúng? A. \(S = \left( {7; + \infty } \right)\) B. \(S = \left[ {6; + \infty } \right)\). C. \(S = \left( { - \infty ;4} \right)\). D. \(S = \left( { - \infty ;5} \right]\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid13-1729744217.png)
Dựa vào bảng biến thiên ta có: \(m > - {x^2} + 6x - 2\) có nghiệm với mọi \(x \in \left( {2; + \infty } \right) \Leftrightarrow m > 7\).
Chọn A
Câu 70:
 Xem đáp án
Xem đáp án
Giải thích
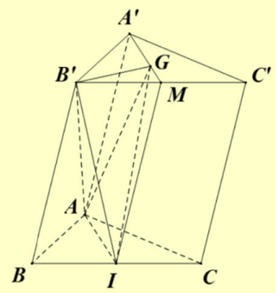
Gọi \(M\) là trung điểm của \(B'C'\) ta có: \({S_{AGI}} = \frac{1}{2}{S_{AA'MF}} \Rightarrow {V_{B'.AGI}} = \frac{1}{2}{V_{B'.AA'MI}}\).
Mà \({V_{B'.AA'MI}} = \frac{2}{3}{V_{ABI.A'B'M}} = \frac{2}{3}.\frac{1}{2}V = \frac{1}{3}V = 4\).
\( \Rightarrow {V_{B'.AGI}} = \frac{1}{2}{V_{B'.AA'MI}} = \frac{1}{2}.4 = 2\).
Chọn A
Câu 71:
Để diện tích xung quanh của hình trụ bằng tổng diện tích hai đáy thì chiều cao của hình trụ bằng (1) _______ đường kính đáy.
 Xem đáp án
Xem đáp án
Đáp án
Để diện tích xung quanh của hình trụ bằng tổng diện tích hai đáy thì chiều cao của hình trụ bằng (1) ___1/2___ đường kính đáy.
Giải thích
Vì diện tích xung quanh của hình trụ bằng diện tích hai đáy nên ta có: \(2\pi rh = 2\pi {r^2} \Leftrightarrow h = r\).
Vậy chiều cao của hình trụ bằng \(\frac{1}{2}\) đường kính đáy.
Câu 72:
Xung quanh một bờ hồ hình tròn có trồng 20 cây cau cảnh. Người ta dự định chặt bớt 5 cây sao cho không có hai cây nào kề nhau bị chặt. Có (1) ______ cách thực hiện khác nhau.
 Xem đáp án
Xem đáp án
Đáp án
Xung quanh một bờ hồ hình tròn có trồng 20 cây cau cảnh. Người ta dự định chặt bớt 5 cây sao cho không có hai cây nào kề nhau bị chặt. Có (1) ___4004___ cách thực hiện khác nhau.
Giải thích
Ta gọi một trong số 20 cây cau cảnh trong đầu bài là \(A\). Có hai trường hợp sau:
Trường hợp 1: Cây \(A\) không bị chặt.
Sau khi chặt đi 5 cây, còn lại 15 cây. Xen kẽ giữa 15 cây này có 15 khoảng trống. 5 cây bị chặt tương ứng với 5 trong số 15 khoảng trống nói trên. Do đó số cách thực hiện trong trường hợp này là \(C_{15}^5 = 3003\).
Trường hợp 2: Cây \(A\) bị chặt.
Sau khi chặt tiếp 4 cây, còn lại 15 cây. Xen kẽ giữa 15 cây này có 14 khoảng trống không kề với vị trí của cây \(A\). 4 cây bị chặt (không kể cây \(A\)) tương ứng với 4 trong số 14 khoảng trống nói trên. Do đó số cách thực hiện trong trường hợp này là \(C_{14}^4 = 1001\).
Theo quy tắc cộng, ta được số khả năng phải tìm là \(3003 + 1001 = 4004\) (cách).
Câu 73:
Gọi \({z_1}\) là nghiệm phức có phần ảo âm của phương trình \({z^2} - 2z + 5 = 0\). Điểm biểu diễn của số phức \(w = \left( {1 + i} \right){z_1}\) là điểm nào trong các điểm \(M,N,P,Q\) ở hình sau đây?

 Xem đáp án
Xem đáp án
Giải thích
Ta có \({z^2} - 2z + 5 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{z_1} = 1 - 2i}\\{{z_2} = 1 + 2i}\end{array}} \right.\)
Suy ra \(w = \left( {1 + i} \right){z_1} = \left( {1 + i} \right)\left( {1 - 2i} \right) = 3 - i\)
Vậy tọa độ điểm biểu diễn số phức \(w = \left( {1 + i} \right){z_1}\) là điểm \(P\left( {3; - 1} \right)\).
Chọn D
Câu 74:
Điền số tự nhiên thích hợp vào các chỗ trống.
Từ một miếng gỗ là khối cầu có bán kính 1dm, bác thợ mộc muốn tạo thành một khối trụ sao cho hai đường tròn đáy của khối trụ thuộc mặt cầu của khối cầu đã cho (xem hình minh họa).
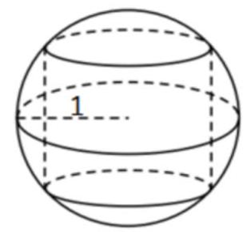
Gọi \(h,r\) lần lượt là chiều cao và bán kính đáy của khối trụ (tính theo đơn vị \(dm\)). Khi đó ta có \(4{r^2} + {h^2} = \) (1) ________.
Trong các khối trụ thỏa mãn tính chất trên, biết rằng khối trụ có diện tích toàn phần lớn nhất là \(\left( {a + \sqrt b } \right)\pi {\rm{d}}{{\rm{m}}^2}\) (với \({\rm{a}},{\rm{b}}\) là hai số nguyên). Khi đó \(a + b = \) (2) ________.
 Xem đáp án
Xem đáp án
Đáp án
Gọi \(h,r\) lần lượt là chiều cao và bán kính đáy của khối trụ (tính theo đơn vị \(dm\)). Khi đó ta có \(4{r^2} + {h^2} = \) (1) ____4____.
Trong các khối trụ thỏa mãn tính chất trên, biết rằng khối trụ có diện tích toàn phần lớn nhất là \(\left( {a + \sqrt b } \right)\pi {\rm{d}}{{\rm{m}}^2}\) (với \({\rm{a}},{\rm{b}}\) là hai số nguyên). Khi đó \(a + b = \) (2) ____6____.
Giải thích
Cách 1. Ta có: \({r^2} + \frac{{{h^2}}}{4} = 1 \Rightarrow 4{r^2} + {h^2} = 4\).
\({S_{tp}} = 2\pi r\left( {r + h} \right) = 2\pi \left( {{r^2} + rh} \right)\) (1).
Áp dụng bất đẳng thức Cô-si ta có:
\(1 = \left( {\frac{{\sqrt 5 - 1}}{2}} \right){r^2} + \left( {\frac{{3 - \sqrt 5 }}{2}{r^2} + \frac{{{h^2}}}{4}} \right) \ge \left( {\frac{{\sqrt 5 - 1}}{2}} \right){r^2} + 2\sqrt {\frac{{3 - \sqrt 5 }}{2}{r^2}.\frac{{{h^2}}}{4}} = \left( {\frac{{\sqrt 5 - 1}}{2}} \right)\left( {{r^2} + rh} \right)\,\,\left( 2 \right)\).
Kết hợp (1) và (2) ta suy ra \({S_{tp}} \le \pi \left( {1 + \sqrt 5 } \right)\).
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = 5}\end{array}} \right.\)
Cách 2. Ta có: \({r^2} + \frac{{{h^2}}}{4} = 1 \Rightarrow 4{r^2} + {h^2} = 4\).
\({S_{tp}} = 2\pi \left( {{r^2} + rh} \right) = 8\pi \left( {\frac{{{r^2} + rh}}{{4{r^2} + {h^2}}}} \right)\)
\( = 8\pi \left( {\frac{{{{\left( {\frac{r}{h}} \right)}^2} + \frac{r}{h}}}{{4{{\left( {\frac{r}{h}} \right)}^2} + 1}}} \right) = 8\pi \frac{{{t^2} + t}}{{4{t^2} + 1}}\)
Khảo sát hàm \(f\left( t \right) = \frac{{{t^2} + t}}{{4{t^2} + 1}},t > 0\) ta suy ra \({\rm{max}}{S_{tp}} = \pi \left( {1 + \sqrt 5 } \right)\).
Câu 75:
 Xem đáp án
Xem đáp án
Giải thích
Vectơ chỉ phương của \({d_1}\) và \({d_2}\) lần lượt là \({\vec u_1} = \left( {2;1;3} \right)\), \({\vec u_2} = \left( {1;2;3} \right)\).
Gọi \(AB\) là đoạn vuông góc chung của \({d_1}\) và \({d_2}\) với \(A \in {d_1},B \in {d_2}\).
Suy ra: \(A\left( { - 1 + 2a; - 1 + a; - 1 + 3a} \right);B\left( {2 + b;2b;9 + 3b} \right)\).
Khi đó: \(\overrightarrow {AB} = \left( { - 2a + b + 3; - a + 2b + 1; - 3a + 3b + 10} \right)\).
Vì \(AB\) là đoạn vuông góc chung của \({d_1}\) và \({d_2}\) nên:
\(\left\{ {\begin{array}{*{20}{l}}{\overrightarrow {AB} \bot \overrightarrow {{u_1}} }\\{\overrightarrow {AB} \bot \overrightarrow {{u_2}} }\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{14a - 13b = 37}\\{13a - 14b = 35}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = \frac{7}{3}}\\{b = - \frac{1}{3}}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{A\left( {\frac{{11}}{3};\frac{4}{3};6} \right)}\\{B\left( {\frac{5}{3}; - \frac{2}{3};8} \right)}\end{array} \Rightarrow AB = 2\sqrt 3 } \right.} \right.} \right.} \right.\).
Gọi \(I\) là tâm mặt cầu \(\left( S \right)\) có đường kính là \(AB\). Suy ra \(I\left( {\frac{8}{3};\frac{1}{3};7} \right)\) và \(R = \frac{1}{2}AB = \sqrt 3 \).
Vậy phương trình mặt cầu \(\left( S \right):{\left( {x - \frac{8}{3}} \right)^2} + {\left( {y - \frac{1}{3}} \right)^2} + {(z - 7)^2} = 3\).
Chọn C
Câu 76:
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Góc lượng giác _______ rad tương ứng với chuyển động quay 3,2 vòng ngược chiều kim đồng hồ.
Trên đường tròn đường kính bằng 4 cm, cung có số đo \(\frac{\pi }{5}\) thì có độ dài bằng _______ cm.
Góc \({100^ \circ }\) bằng _______ rad.
 Xem đáp án
Xem đáp án
Đáp án
Góc lượng giác \(\frac{{32\pi }}{5}\) rad tương ứng với chuyển động quay 3,2 vòng ngược chiều kim đồng hồ.
Trên đường tròn đường kính bằng 4 cm, cung có số đo \(\frac{\pi }{5}\) thì có độ dài bằng \(\frac{{2\pi }}{5}\) cm.
Góc \({100^ \circ }\) bằng \(\frac{{5\pi }}{9}\) rad.
Giải thích
3,2 vòng ngược chiều kim đồng hồ tương ứng với \(3,2 \times 2\pi = \frac{{32\pi }}{5}\left( {{\rm{rad}}} \right)\).
Độ dài cung có số đo \(\frac{\pi }{5}\) là \(l = \alpha R = \frac{\pi }{5}.\frac{4}{2} = \frac{{2\pi }}{5}\left( {{\rm{cm}}} \right)\).
Góc \({100^ \circ }\) bằng \(\frac{{100}}{{180}}\pi = \frac{{5\pi }}{9}\left( {{\rm{rad}}} \right)\).
Câu 77:
Cho số phức \(z = 3 - i,w = {(1 - i)^2}\). Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Mođun của số phức \(z\) là 2 . |
||
|
Điểm biểu diễn số phức \(w\) có tọa độ là \(\left( {0; - 2} \right)\). |
||
|
Mođun của số phức \(\left| {\frac{w}{z}} \right| = \frac{{\sqrt {10} }}{5}\). |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Mođun của số phức \(z\) là 2 . |
X | |
|
Điểm biểu diễn số phức \(w\) có tọa độ là \(\left( {0; - 2} \right)\). |
X | |
|
Mođun của số phức \(\left| {\frac{w}{z}} \right| = \frac{{\sqrt {10} }}{5}\). |
X |
Giải thích
Ta có:
\(w = 1 - i{)^2} = - 2i \Rightarrow \) Điểm biểu diễn số phức \(w\) có tọa độ là \(\left( {0; - 2} \right)\).
\(\left| z \right| = \sqrt {10} \)
\(\left| {\frac{w}{z}} \right| = \frac{{\left| w \right|}}{{\left| z \right|}} = \frac{{\sqrt {10} }}{5}\).
Câu 78:
Cho một dãy gồm bốn số theo thứ tự ba số hạng đầu lập thành một cấp số nhân và ba số hạng cuối lập thành một cấp số cộng. Biết tổng của hai số hạng đầu và cuối bằng 14 và tổng của hai số hạng giữa bằng 12.
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau
Số hạng đầu của dãy số là _______.
Công bội của ba số hạng đầu của dãy là _______.
Công sai của ba số hạng cuối của dãy là _______.
 Xem đáp án
Xem đáp án
Đáp án
Số hạng đầu của dãy số là \(\frac{{25}}{2}\).
Công bội của ba số hạng đầu của dãy là -3 .
Công sai của ba số hạng cuối của dãy là \(\frac{3}{5}\).
Giải thích
Gọi 4 số phải tìm là \({a_1};{a_2};{a_3};{a_4}\). Theo bài ra ta có hệ phương trình
\[\left\{ {\begin{array}{*{20}{c}}{a_2^2 = {a_1}{a_3}}\\{2{a_3} = {a_2} + {a_4}}\\{{a_1} + {a_4} = 14}\\{{a_2} + {a_3} = 12}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{a_2} + {a_4} = 2{a_3}}\\{{a_1} + {a_2} + {a_3} + {a_4}}\\{{a_2} + {a_3} = 12}\end{array} = 26 \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{a_1} + 3{a_3} = 26}\\{{a_2} + {a_3} = 12}\end{array}} \right.} \right.} \right.\]
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{a_1} + 3{q^2}{a_1} = 26}\\{q{a_1} + {q^2}{a_1} = 12}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\left( {1 + 3{q^2}} \right){a_1} = 26}\\{\left( {q + {q^2}} \right){a_1} = 12}\end{array}} \right.} \right.\)
\( \Rightarrow 12\left( {1 + 3{q^2}} \right) = 26\left( {q + {q^2}} \right)\)
\( \Leftrightarrow 5{q^2} - 13q + 6 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{q = 2 \Rightarrow {a_1} = 2 \Rightarrow {a_2} = 4;{a_3} = 8;{a_4} = 12}\\{q = \frac{3}{5} \Rightarrow {a_1} = \frac{{25}}{2} \Rightarrow {a_2} = \frac{{15}}{2};{a_3} = \frac{9}{2};{a_4} = \frac{3}{2}}\end{array}} \right.\)
Vậy có hai bộ số cần tìm: \(\left( {2,4,8,12} \right),\left( {\frac{{25}}{2},\frac{{15}}{2},\frac{9}{2},\frac{3}{2}} \right)\).
Xét các số trong bảng kéo thả ta thấy chỉ có bộ số \(\left( {\frac{{25}}{2},\frac{{15}}{2},\frac{9}{2},\frac{3}{2}} \right)\) thỏa mãn với số hạng đầu là \(\frac{{25}}{2}\); công sai là -3 và công bội là \(\frac{3}{5}\).
Câu 79:
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
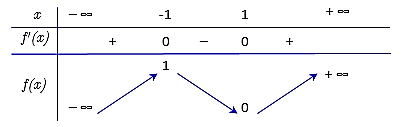
Hàm số \(f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Giải thích
Từ bảng biến thiên ta suy ra \(f'\left( x \right) > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x > 1}\\{x < - 1}\end{array}} \right.\).
Chọn C
Câu 80:
Cho hàm phân thức \(f\left( x \right) = \frac{{ax - b}}{{cx + d}}\) có đồ thị như hình vẽ.
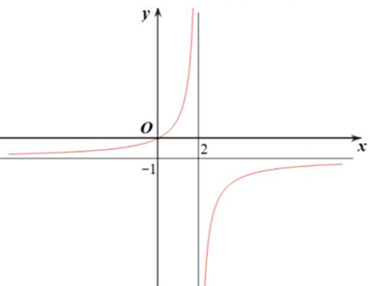

Đồ thị hàm số đã cho có đường tiệm cận đứng là \(x = \) ____ và đường tiệm cận ngang là \(y = \)____.
Giá trị của tích \(abcd\) bằng _____.
 Xem đáp án
Xem đáp án
Đáp án
Đồ thị hàm số đã cho có đường tiệm cận đứng là \(x = \) 2 và đường tiệm cận ngang là \(y = \)-1 .
Giá trị của tích \(abcd\) bằng 0 .
Giải thích
Đồ thị hàm số đã cho có đường tiệm cận ngang \(y = - 1\), đường tiệm cận đứng \(x = 2\) và đi qua điểm \(A\left( {0;0} \right)\).
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{ - \frac{d}{c} = 2}\\{\frac{a}{c} = - 1}\\{ - \frac{b}{d} = 0}\end{array} \Rightarrow b = 0 \Rightarrow abcd = 0} \right.\)
Câu 81:
 Xem đáp án
Xem đáp án
Giải thích
Giai đoạn 1: Tính số tiền bạn Hùng nợ ngân hàng sau 4 năm.
Ta xem đây là bài toán gửi tiết kiệm với người cho vay là ngân hàng.
Áp dụng công thức gửi tiết kiệm \(T = M\left( {1 + r} \right).\frac{{{{(1 + r)}^n} - 1}}{r}\) với \(\left\{ {\begin{array}{*{20}{l}}{M = {{10}^6}}\\{r = \frac{{3{\rm{\% }}}}{{12}} = 0,25{\rm{\% \;}}}\\{n = 4 \times 12 = 48}\end{array}} \right.\) ta có:
\(T = 51058536,44\) đồng.
Giai đoạn 2. Ta coi như bạn Hùng nợ ngân hàng khoản tiền ban đầu 51058 536, 44 đồng.
Số tiền này bắt đầu được tính lãi và được trả góp trong 4 năm (= 48 tháng).
Áp dụng công thức \(m = \frac{{M{{(1 + r)}^n}r}}{{{{(1 + r)}^n} - 1}}\) với \(\left\{ {\begin{array}{*{20}{l}}{M = 51058536,44}\\{r = 0,25{\rm{\% }}}\\{n = 4 \times 12 = 48}\end{array}} \right.\) ta được:
m = 1 130 146,341 ≈ 1 130 000 (đồng)
Chọn B
Câu 82:
 Xem đáp án
Xem đáp án
Giải thích
Ta có \({u_1} = \frac{1}{2},{u_4} = 32\) và \({u_n} = 2048\).
\({u_4} = {u_1}.{q^3} \Leftrightarrow 32 = \frac{1}{2}.{q^3} \Leftrightarrow q = 4\).
\({u_n} = 2048 \Leftrightarrow {u_1}.{q^{n - 1}} = 2048 \Leftrightarrow \frac{1}{2}{.4^{n - 1}} = 2048 \Leftrightarrow {4^{n - 1}} = {4^6} \Leftrightarrow n = 7\).
Khi đó tổng của cấp số nhân này là \(T = {S_7} = \frac{{\frac{1}{2}\left( {1 - {4^7}} \right)}}{{1 - 4}} = \frac{{5461}}{2}\).
Chọn C