Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 25)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 25)
-
402 lượt thi
-
79 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
Phần tư duy đọc hiểu
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Con người có xu hướng liên kết những màu sắc ấm với cảm nhận nhiệt độ cao.
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
Căn cứ đoạn [2]: “Có thể đó là nguyên nhân giải thích tại sao chúng ta bắt đầu liên kết các mức nhiệt cao hơn với những màu sắc ấm”.
=>Thông tin Đúng.
Chọn A
Câu 2:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Người tham gia trong nghiên cứu không được tiếp xúc với chất tạo mùi và không mắc các bệnh thị giác.
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
Căn cứ nội dung đoạn [3], nói rõ rằng những người tham gia không sử dụng chất khử mùi hoặc nước hoa và không có ai trong số họ mắc bệnh mù màu hoặc vấn đề liên quan đến nhận thức mùi.
=> Thông tin Đúng.
Chọn A
Câu 3:
Từ thông tin của bài đọc, hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí.
kích thích, sinh viên, cộng sự, liên kết, mở rộng
Nghiên cứu của tiến sĩ Ryan Ward và các _______ về mối liên quangiữa mùi hương và màu sắc mang đến kết quả đầy thú vị về sự tương tác phức tạp giữa các giác quan của chúng ta. Ryan cho rằng mỗi mùi hương có thể _______ sự thay đổi trong lựa chọn màu sắc của chúng ta, khẳng định giác quan của con người là một hệ thống _______, không chỉ hoạt động độc lập mà còn tương tác mạnh mẽ với nhau.
 Xem đáp án
Xem đáp án
Đáp án
Nghiên cứu của tiến sĩ Ryan Ward và các cộng sự về mối liên quan giữa mùi hương và màu sắc mang đến kết quả đầy thú vị về sự tương tác phức tạp giữa các giác quan của chúng ta. Ryan cho rằng mỗi mùi hương có thể kích thích sự thay đổi trong lựa chọn màu sắc của chúng ta, khẳng định giác quan của con người là một hệ thống liên kết, không chỉ hoạt động độc lập mà còn tương tác mạnh mẽ với nhau.
Phương pháp giải
Dựa vào logic câu từ và hiểu biết có được qua bài đọc.
Lời giải
- [Vị trí thả 1]: cộng sự -> trong ngữ cảnh câu văn, “cộng sự” là những người hỗ trợ hoặc đồng nghiệp cùng thực hiện nghiên cứu với tiến sĩ Ryan Ward.
- [Vị trí thả 2]: kích thích -> trong ngữ cảnh câu văn và nội dung bài đọc, mùi hương có thể tác động đến sự lựa chọn màu sắc, nghĩa là “kích thích” sự thay đổi trong lựa chọn màu sắc.
- [Vị trí thả 3]: liên kết -> mối liên hệ, kết nối giữa các bộ phận trong cơ thể, có thể hoạt động độc lập và tác động lẫn nhau.
Câu 4:
Liên quan đến nghiên cứu về mùi và màu sắc, đâu là một trong những kết luận của tiến sĩ Ryan Ward và đồng nghiệp?
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
- C đúng - Căn cứ nội dung đoạn [8]: “Duy chỉ có ngoại lệ khi mùi bạc hà tỏa ra: sự lựa chọn màu sắc của người tham gia khác biệt từ mối liên hệ đa mô thức điển hình liên kết với mùi khác.” -> mùi bạc hà không tạo ra liên kết đa mô thức.
- A sai - Căn cứ nội dung đoạn [5]: “chúng tôi đã chứng tỏ là mùi caramel nhìn chung tạo thành một liên kết đa phương thức với màu nâu tối và vàng”.
- B sai - Căn cứ nội dung đoạn [5]: “giống như cà phê với nâu tối và đỏ”.
- D sai - Căn cứ nội dung đoạn [9]: “những liên kết đa mô thức trong xử lý thông tin đầu vào đủ ảnh hưởng lên cách chúng ta đón nhận thông tin từ các mùi khác nhau, ở đây là giữa mùi hương và màu sắc” -> sự lựa chọn màu sắc có ảnh hưởng bởi mùi hương.
=> Đáp án cần chọn là C.
Câu 5:
Điền một từ không quá hai tiếng có trong đoạn [7] vào chỗ trống.
_______ thị trường công nghệ đang dần chuyển từ các thiết bị cầm tay sang các sản phẩm tích hợp trí tuệ nhân tạo và kết nối mạng.
 Xem đáp án
Xem đáp án
Đáp án: "Xu hướng"
Phương pháp giải
Xét logic câu từ và thông tin có được sau bài đọc.
Lời giải
Trong ngữ cảnh câu văn, thị trường công nghệ đang chuyển dịch là một “xu hướng” -> “xu hướng” xuất hiện trong đoạn [7] và [8] của bài đọc.
=> Từ cần điền là Xu hướng.
Câu 6:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Kết quả của nghiên cứu cho thấy sự liên kết giữa mùi hương và màu sắc không có ảnh hưởng đáng kể đối với cảm nhận của người tham gia.
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
Căn cứ nội dung đoạn [7], kết quả của nghiên cứu chỉ ra rằng có sự ảnh hưởng đáng kể của mùi hương đối với cảm nhận màu sắc của người tham gia. Ví dụ, khi hiển thị mùi của cà phê, họ thường nhận 'màu xám' thành màu đỏ nâu hơn là màu xám trung tính.
-> Điều này chứng tỏ mối liên quan giữa mùi hương và màu sắc có thể có ảnh hưởng đáng kể đối với cảm nhận của người tham gia.
Chọn B
Câu 7:
tinh thần, giác quan, màu sắc, phức tạp
Như cách mùi hương có thể tác động tới _______ trong bài viết, âm nhạc cũng có khả năng gắn kết với trạng thái _______ con người. Một nghiên cứu gần đây chỉ ra rằng những giai điệu nhẹ nhàng thường kết hợp tốt với trạng thái vui vẻ, trong khi những giai điệu nhanh mạnh có thể kích thích sự hoạt động.
 Xem đáp án
Xem đáp án
Đáp án
Như cách mùi hương có thể tác động tới màu sắc trong bài viết, âm nhạc cũng có khả năng gắn kết với trạng thái tinh thần con người. Một nghiên cứu gần đây chỉ ra rằng những giai điệu nhẹ nhàng thường kết hợp tốt với trạng thái vui vẻ, trong khi những giai điệu nhanh mạnh có thể kích thích sự hoạt động.
Phương pháp giải
Dựa vào logic câu từ và hiểu biết có được qua bài đọc.
Lời giải
- [Vị trí thả 1]: màu sắc -> căn cứ vào nội dung bài đọc, nói về nghiên cứu tác động của mùi hương tới nhận diện màu sắc.
- [Vị trí thả 2]: tinh thần -> căn cứ vào ngữ cảnh câu văn, đặc biệt là vế sau của câu: “vui vẻ” là một trạng thái tinh thần -> “trạng thái tinh thần” có thể bị ảnh hưởng bởi âm nhạc.
Câu 8:
Theo tiến sĩ Ryan Ward, một trong những thách thức chưa được giải quyết trong nghiên cứu về mùi và màu sắc là gì?
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
- A đúng - Căn cứ nội dung đoạn [9]: “Chúng ta cần biết mức độ mùi ảnh hưởng đến ý thức về mùi như thế nào.” -> sự cần thiết trong nghiên cứu mức độ ảnh hưởng của mùi đến màu sắc.
- B, C sai - thông tin không được nhắc đến trong bài đọc.
- D sai - “Nghiên cứu về mùi lần đầu tiên bắt gặp” là một ví dụ trong nghiên cứu về mối liên hệ giữa mùi và màu sắc, không phải thách thức mà tác giả đề cập.
=> Đáp án cần chọn là A.
Câu 9:
Trong nghiên cứu của Tiến sĩ Ryan Ward, mối liên quan giữa mùi hương và màu sắc được thử nghiệm trên nhóm người tham gia có độ tuổi nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
Căn cứ nội dung đoạn [3], nghiên cứu được thực hiện trên nhóm người trưởng thành ở độ tuổi từ 20 đến 57 -> độ tuổi 29 đến 49 có nằm trong phạm vi đối tượng nghiên cứu.
=> Đáp án cần chọn là C.
Câu 10:
Điền một từ không quá hai tiếng có trong bài văn vào chỗ trống.
Kết quả thí nghiệm cho thấy sự tương ứng giữa mùi và màu sắc trong ________ của người tham gia, đồng thời nêu cao tầm quan trọng của liên kết này trong xử lý thông tin đầu vào.
 Xem đáp án
Xem đáp án
Đáp án: "ý thức | nhận thức"
Phương pháp giải
Xét logic câu từ và hiểu biết có được từ bài đọc, đặc biệt đoạn [2] và [9].
Lời giải
Bài đọc nghiên cứu mối liên hệ giữa mùi hương và màu sắc, ảnh hưởng đến ý thức/ nhận thức về mùi của người tham gia.
=> Từ cần điền là ý thức hoặc nhận thức.
Câu 11:
Nội dung chính của đoạn trích trên là gì?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc hiểu nội dung toàn bài, suy ra nội dung chính.
Lời giải
Căn cứ nội dung toàn bài. Tác giả đề cập đến lịch sử hình thành, kiến trúc, công trình, cảnh quan nổi bật của chùa Thiên Mụ nhằm làm nổi bật vẻ đẹp và sự thiêng liêng, cổ kính của ngôi chùa.
=> Đáp án cần chọn là A.
Câu 12:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Chùa Thiên Mụ có được danh hiệu “Đệ nhất danh lam xứ Huế” nhờ vào kiến trúc độc đáo và vị trí đẹp mắt tại Huế.
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
Căn cứ nội dung toàn bài, Chùa Thiên Mụ được mệnh danh là "Đệ nhất danh lam xứ Huế" do kiến trúc uy nghiêm (đoạn [7]: “Thời cực thịnh, trong chùa có tới vài chục công trình”; đoạn [9]: “Tháp Phước Duyên là một kiến trúc đậm dấu ấn mỹ thuật Phật giáo, là một trong những biểu tượng của cố đô”) và vị trí đẹp mắt tại Huế (đoạn [2]: “nằm trên đồi Hà Khê, tả ngạn sông Hương, cách Kinh thành Huế chừng 5km về hướng Tây”) - nơi có nền văn hóa lâu dài và lịch sử Phật giáo quan trọng.
=> Thông tin Đúng.
Câu 13:
Từ thông tin của bài đọc, hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí.
dân gian, vĩnh cửu, truyền thuyết, vượt thời gian
Một trong những biểu tượng nổi bật của nền văn hóa Phật Giáo là Taj Mahal ở Ấn Độ. Taj Mahal được coi là một công trình kiến trúc độc đáo có lịch sử hình thành và văn hóa tín ngưỡng sâu sắc. Như Chùa Thiên Mụ ở Việt Nam với _______ về bà già áo đỏ, Taj Mahal cũng gắn liền với một chuyện tình cổ điển, đó là tình yêu _______ giữa Hoàng đế Shah Jahan và Hoàng hậu Mumtaz Mahal.
 Xem đáp án
Xem đáp án
Đáp án
Một trong những biểu tượng nổi bật của nền văn hóa Phật Giáo là Taj Mahal ở Ấn Độ. Taj Mahal được coi là một công trình kiến trúc độc đáo có lịch sử hình thành và văn hóa tín ngưỡng sâu sắc. Như Chùa Thiên Mụ ở Việt Nam với truyền thuyết về bà già áo đỏ, Taj Mahal cũng gắn liền với một chuyện tình cổ điển, đó là tình yêu vĩnh cửu giữa Hoàng đế Shah Jahan và Hoàng hậu Mumtaz Mahal.
Phương pháp giải
Dựa vào logic câu từ và hiểu biết có được qua bài đọc.
Lời giải
- [Vị trí thả 1]: truyền thuyết -> căn cứ nội dung đoạn [3], chuyện về bà già mặc áo đỏ là truyền thuyết dân gian gắn với Chùa Thiên Mụ.
- [Vị trí thả 2]: vĩnh cửu -> căn cứ vào hiểu biết thực tế và ngữ cảnh câu văn, chuyện tình của Hoàng đế Shah Jahan và Hoàng hậu Mumtaz Mahal là tình yêu vĩnh cửu.
Câu 14:
Đâu là nội dung KHÔNG được suy ra từ đoạn [3] của bài đọc?
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
Căn cứ nội dung đoạn [3]
A đúng: chúa Nguyễn Hoàng đã nghe về truyền thuyết và quyết định xây dựng chùa Thiên Mụ vào năm 1601.
B đúng: truyền thuyết của bà già mặc áo đỏ, nói về sự xuất hiện của một vị chân chúa để lập chùa và tụ long khí cho nước Nam.
C sai: Mặc dù chùa Thiên Mụ được mệnh danh là "đệ nhất danh lam xứ Huế," nhưng không có thông tin trong đoạn về truyền thuyết dự đoán sự hùng mạnh của nước Nam.
D đúng: sau khi nghe câu chuyện, chúa Nguyễn Hoàng đã quyết định xây dựng chùa Thiên Mụ vào năm 1601 và đặt tên là Thiên Mụ Sơn.
=> Đáp án cần chọn là C.
Câu 15:
Điền một từ không quá hai tiếng có trong bài đọc vào chỗ trống.
Trong _______ chùa Thiên Mụ, có rất nhiều di vật quý giá và công trình kiến trúc độc đáo, đại diện cho sự phong phú và lâu dài của lịch sử Phật giáo tại Huế.
 Xem đáp án
Xem đáp án
Đáp án: "quần thể"
Phương pháp giải
Đọc hiểu nội dung toàn bài, kết hợp với ngữ cảnh câu văn.
Lời giải
Căn cứ nội dung toàn bài, chùa Thiên Mụ có nhiều hạng mục kiến trúc tiêu biểu và những di vật, pháp khí lâu đời được lưu giữ trong “quần thể” kiến trúc đó -> “kiến trúc” xuất hiện trong đoạn [5], [7], [8], [10] của bài đọc.
=> Từ cần điền là quần thể.
Câu 16:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Chùa Thiên Mụ được xây dựng lần đầu vào thời kỳ của chúa Nguyễn Hoàng năm 1601 và là ngôi chùa cổ nhất xứ Huế ở Đàng Trong.
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
Căn cứ nội dung đoạn [3], “Chúa Nguyễn Hoàng cho rằng đó là điềm ứng với mình. Năm 1601, chúa cho xây dựng một ngôi chùa trên đồi, nhìn thẳng ra sông Hương và đặt tên là “Thiên Mụ.”
=> Thông tin Đúng.
Câu 17:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Công trình kiến trúc Tháp Phước Duyên tại chùa Thiên Mụ hiện vẫn giữ nguyên cấu trúc và cấu kiện gỗ ban đầu từ thời trùng tu năm 1957.
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
Căn cứ nội dung đoạn [8], “Trong lần trùng tu năm 1957, nhiều cấu kiện gỗ đã được thay bằng bê tông. Tuy nhiên, cấu trúc ngôi điện vẫn được giữ nguyên.” -> Cấu trúc chùa Thiên Mụ được giữ nguyên nhưng cấu kiện gỗ đã bị thay thế.
=> Thông tin Sai.
Câu 18:
Từ thông tin của bài đọc, hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí.
cao tăng, vua chúa, thiêng liêng, tôn giáo, kết hợp
1/ Chùa Thiên Mụ tại Huế thể hiện sự ______ hoàn hảo giữa kiến trúc tôn giáo và văn hóa lịch sử.
2/ Đọc về lịch sử và phát triển của chùa, ta thấy sự kiên trì và tận hiến của những vị _______ trong việc duy trì và phát triển nền Phật giáo xứ Đàng Trong.
3/ Chùa Thiên Mụ không chỉ là biểu tượng _______, mà còn là biểu tượng sống động của sự hòa quyện giữa lịch sử và văn hóa tại Huế.
 Xem đáp án
Xem đáp án
Đáp án
1/ Chùa Thiên Mụ tại Huế thể hiện sự kết hợp hoàn hảo giữa kiến trúc tôn giáo và văn hóa lịch sử.
2/ Đọc về lịch sử và phát triển của chùa, ta thấy sự kiên trì và tận hiến của những vị vua chúa trong việc duy trì và phát triển nền Phật giáo xứ Đàng Trong.
3/ Chùa Thiên Mụ không chỉ là biểu tượng tôn giáo, mà còn là biểu tượng sống động của sự hòa quyện giữa lịch sử và văn hóa tại Huế.
Phương pháp giải
Dựa vào logic câu từ và hiểu biết có được qua bài đọc.
Lời giải
[Vị trí thả 1]: kết hợp - căn cứ nội dung toàn bài, tác giả tập trung vào khía cạnh kiến trúc và văn hóa lịch sử của chùa Thiên Mụ.
[Vị trí thả 2]: vua chúa - căn cứ nội dung đoạn [3] [4], tác giả đề cập tới nhiều vị vua chúa đã có công xây dựng, trùng tu nhiều lần chùa Thiên Mụ.
[Vị trí thả 3]: tôn giáo - căn cứ nội dung toàn bài, kết hợp ngữ cảnh câu, chùa Thiên Mụ là biểu tượng văn hóa, cũng là biểu tượng tôn giáo độc đáo.
Câu 19:
Trong lịch sử phát triển Chùa Thiên Mụ, thông tin nào dưới đây SAI:
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
A - Căn cứ nội dung đoạn [3]: “Năm 1601, chúa cho xây dựng một ngôi chùa trên đồi” -> thông tin đúng.
B - Căn cứ nội dung đoạn [4]: “Thiệu Trị lại cho trùng tu, xây thêm tháp Phước Duyên và đình Hương Nguyện, dựng hai tấm bia đá ghi khắc thơ văn của nhà vua.” -> thông tin đúng.
C - Căn cứ nội dung đoạn [4]: “Dưới thời Tây Sơn, chùa bị binh hỏa tàn phá nặng nề. Chùa được trùng tu vào năm 1815 và 1831 dưới thời vua Gia Long và vua Minh Mạng nhà Nguyễn.” -> thông tin đúng.
D - Căn cứ nội dung đoạn [4]: “Dưới thời chúa Nguyễn Phúc Chu, chùa được xây dựng lại với quy mô lớn hơn. Chúa cho đúc Đại hồng chuông và khắc một bài minh lên chuông.” -> chuông Đại hồng được đúc dưới thời chúa Nguyễn Phúc Tần là sai.
=> Đáp án cần chọn là D.
Câu 20:
Phần tư duy khoa học / giải quyết vấn đề
Điền cụm từ (tối đa 03 từ) vào chỗ trống:
Với máy nước nóng, nguyên lí truyền nhiệt sẽ là _______
 Xem đáp án
Xem đáp án
Đáp án: "đối lưu | đối lưu nhiệt"
Phương pháp giải
Phân tích sơ đồ trong đề bài cung cấp.
Vận dụng lí thuyết đã học về các cách truyền nhiệt.
Lời giải
Trong máy nước nóng, nguyên lí truyền nhiệt diễn ra là đối lưu nhiệt. Nước nóng hơn có xu hướng di chuyển lên trên bồn chứa và nước lạnh di chuyển xuống dưới ống chân không để làm nóng. Quá trình như vậy luân phiên diễn ra cho đến khi cân bằng nhiệt ở bình và ống chân không xảy ra.
Câu 21:
Để nhiệt độ trong ống thủy tinh được hấp thụ một cách tốt nhất, tấm pin trong ống thường sẽ có màu:
 Xem đáp án
Xem đáp án
Phương pháp giải
Vận dụng lí thuyết về sự thụ nhiệt.
Lời giải
Để hấp thụ bức xạ nhiệt của Mặt trời được tốt nhất nên tấm tin trong máy thường sẽ có màu đen
Chọn A
Câu 22:
Nhận xét sau đây đúng hay sai?
Phía sau tấm pin có lớp cách nhiệt với tác dụng chính là tránh thất thoát năng lượng nhiệt (nhiệt) cần được nước hấp thụ.
 Xem đáp án
Xem đáp án
Phương pháp giải
Vận dụng lí thuyết thực tiễn đã biết và thông tin bài cung cấp.
Lời giải
Trong quá trình truyền nhiệt để hạn chế tối đa việc tiêu hao nhiệt thì người ta dùng một cách cách nhiệt sau tấm pin năng lượng.
Chọn A
Câu 23:
Điền các đáp án thích hợp vào chống trống:
Trong máy nước nóng, ________ sẽ được chuyển hóa trực tiếp thành _________ . Còn với tấm pin năng lượng mặt trời, quang năng được biến đổi tực tiếp thành __________.
 Xem đáp án
Xem đáp án
Đáp án:
Trong máy nước nóng, quang năng sẽ được chuyển hóa trực tiếp thành nhiệt năng. Còn với tấm pin năng lượng mặt trời, quang năng được biến đổi tực tiếp thành điện năng.
Phương pháp giải
Vận dụng lí thuyết đã học về chuyển hóa năng lượng.
Lời giải
Trong máy nước nóng, quang năng điện chuyển thành nhiệt năng, còn với tấm pin năng lượng mặt trời quang năng điện biến trực tiếp thành điện năng.
Câu 24:
Trung bình, mỗi mét vuông tấm pin mặt trời ở trên nhận được 1000J năng lượng từ Mặt trời mỗi giây. Công suất đầu vào mỗi giây (tính bằng kW) của tấm pin nếu diện tích bề mặt của nó là 2m2 là:
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin bài cung cấp.
Áp dụng công thức tính công suất và điện năng.
Lời giải
Công suất mỗi giây mới mỗi mét vuông của tấm pin là: \(P = \frac{A}{t} = 1000W\)
Cả tấm pin 2m2 khi đó công suất sẽ là: P′ = 2000W = 2kW
Chọn C
Câu 25:
Ngoài sử dụng trong bình nước nóng, những tấm pin năng lượng còn được sử dụng trực tiếp trong quá trình tạo ra điện năng bằng cách được đặt trực tiếp trên các mái nhà. Ở nhà bạn A, những ngày trời nắng không có mây, bề mặt có diện tích 1m2 của tấm pin Mặt Trời để ngoài nắng nhận được một năng lượng Mặt Trời là 1400J trong 1s. Hỏi cần phủ lên mái nhà một tấm pin Mặt Trời có diện tích tối thiểu là bao nhiêu để có đủ điện thắp sáng hai bóng đèn có công suất 100W và một máy thu hìnhcó công suất 75W? Biết rằng hiệu suất của pin Mặt Trời là 10%.
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin bài cung cấp.
Áp dụng công thức tính điện năng và công suất đã học.
Lời giải
Tổng công suất tiêu thụ của các thiết bị là: \({P_i} = 2.100 + 75 = 275\;{\rm{W}}\)
Hiệu suất của pin được xác định bằng: \(H = \frac{{{P_i}}}{{{P_{tp}}}}100\% \)
\( \Rightarrow {P_{tp}} = \frac{{{P_i}}}{H} = \frac{{275}}{{10\% }} = 2750\;{\rm{W}}\)
Mặt khác: \({P_{tp}} = {P_0}.S \Rightarrow S = \frac{{{P_{tp}}}}{{{P_0}}} = \frac{{2750}}{{1400}} = 1,964{m^2}\)
Vậy, diện tích của tấm pin mặt trời cần thiết là 1,964m2
Chọn C
Câu 26:
Biết bể chứa của máy có 100 kg nước. Nhiệt dung riêng của nước là 4200J/(kg0C). Cần bao nhiêu năng lượng để tăng nhiệt độ trung bình của toàn bộ nước trong bể lên 10C
 Xem đáp án
Xem đáp án
Phương pháp giải
Áp dụng công thức tính nhiệt lượng: Q = mcΔt
Lời giải
Năng lượng cần cung cấp bằng với nhiệt lượng nước thu vào:
Q = mcΔt = 100.4200.1 = 420000J = 420kJ
Chọn B
Câu 27:
Điện năng xoay chiều có khả năng truyền tải tốt hơn so với điện một chiều. Các lí do sau đây là đúng hay sai?
|
|
ĐÚNG |
SAI |
|
Điện xoay chiều có hao phí truyền tải thấp, không phụ thuộc hạ tầng truyền tải. |
||
|
Điện xoay chiều có công suất rất cao và hao phí luôn thấp. |
||
|
Điện xoay chiều có khả năng tăng điện thế tại nguồn bằng cách sử dụng máy biến áp nên có thể giảm được hao phí đường truyền. |
||
|
Điện xoay chiều có thể tăng điện thế tại nguồn nên có thể tăng được công suất tại nguồn. |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Điện xoay chiều có hao phí truyền tải thấp, không phụ thuộc hạ tầng truyền tải. |
X | |
|
Điện xoay chiều có công suất rất cao và hao phí luôn thấp. |
X | |
|
Điện xoay chiều có khả năng tăng điện thế tại nguồn bằng cách sử dụng máy biến áp nên có thể giảm được hao phí đường truyền. |
X | |
|
Điện xoay chiều có thể tăng điện thế tại nguồn nên có thể tăng được công suất tại nguồn. |
X |
Phương pháp giải
Phân tích thông tin bài cung cấp.
Vận dụng lí thuyết về dòng điện xoay chiều.
Lời giải
Ta có dòng điện xoay chiều sẽ có khả năng truyền tải ở cự li xa với hao phí thấp bằng cách tăng điện thế tại nguồn bằng cách sử dụng máy biến áp.
Câu 28:
Hệ thống tuyền tải lí tưởng với điện áp tại nguồn là 500kV. Giả sử tăng giá trị của điện áp nguồn lên 600kV khi đó công suất hao phí trên đường dây:
 Xem đáp án
Xem đáp án
Phương pháp giải
Vận dụng lí thuyết đề cung cấp: khi nâng điện áp nguồn lên k lần thì công suất hao phí giảm đi k2
Lời giải
Ta có: khi nâng điện áp nguồn lên k lần thì công suất hao phí giảm đi k2 lần.
\( \Rightarrow \frac{{{P_{hp}}}}{{{P_{hp}}^\prime }} = \frac{{U{'^2}}}{{{U^2}}} = \frac{{{{600}^2}}}{{{{500}^2}}} = 1,44\)
=> công suất hao phí giảm 1,44 lần.
Chọn A
Câu 29:
Cho các công dụng sau, đâu sẽ không phải công dụng của máy biến áp:
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin bài cung cấp.
Vận dụng lí thuyết đã học về máy biến áp.
Lời giải
Với máy biếp áp, sẽ tăng hoặc giảm điện áp của dòng điện và sẽ giảm hao phí của đường dây truyền tải.
Việc tăng cường độ của dòng điện không phải là công dụng của máy biến áp.
Chọn A
Câu 30:
Công suất hao phí dọc đường dây tải có điện áp 500 kV, khi truyền đi một công suất điện 12000 kW theo một đường dây có điện trở 10Ω10Ω là bao nhiêu? Coi hệ số công suất bằng 1.
 Xem đáp án
Xem đáp án
Phương pháp giải
Áp dụng công thức tính công suất hao phí: \(\Delta P = R{I^2}\)
Lời giải
Công suất hao phí của đường dây: \(\Delta P = R{I^2} = {\left( {\frac{P}{U}} \right)^2}R = {\left( {\frac{{12000}}{{500}}} \right)^2}.10 = 5760\;{\rm{W}}\)
Chọn C
Câu 31:
Điền số thích hợp vào chỗ trống:
Điện năng ở một trạm phát điện được truyền đi dưới điện áp 2kV và công suất truyền đi 200kW. Hiệu số chỉ của các công tơ điện ở trạm phát và ở nơi thu sau mỗi ngày đêm lệch nhau thêm 480kW.ℎ. Hiệu suất của quá trình truyển tải điện là % _______
 Xem đáp án
Xem đáp án
Đáp án: "90"
Phương pháp giải
Áp dụng công thức tính hiệu suất truyền tải: \(H = \frac{{P - \Delta P}}{P}.100\% \)
Lời giải
Hiệu số chỉ của các công tơ điện ở trạm phát và nơi thu sau mỗi ngày đêm lệch nhau thêm 480kWh là điện năng hao phí do tỏa nhiệt trên đường dây.
Công suất hao phí: \(\Delta P = \frac{P}{t} = \frac{{480kWh}}{{24h}} = 20kW = 10\% P\)
Hiệu suất của đường dây trên: \(H = \frac{{P - \Delta P}}{P}.100\% = \frac{{P - 10\% P}}{P}100\% = 90\% \)
Hiệu suất của đường dây là 90%
Câu 32:
Với trạm phát điện ở câu trên. Cần tăng điện áp ở trạm phát đến giá trị nào để điện năng hao phí trên đường dây chỉ bằng 2,5 điện năng truyền đi ? Coi công suất truyền đi ở trạm phát điện không đổi.
 Xem đáp án
Xem đáp án
Phương pháp giải
Áp dụng công thức tính công suất hao phí: \(\Delta P = R{I^2} = R\frac{{{P^2}}}{{{{(U\cos \varphi )}^2}}}\)
Lời giải
Công suất hao phí: \(\Delta P = 10\% P\)
Ta có:
\(U = {U_1} \Rightarrow \Delta P = 10\% P = R\frac{{{P^2}}}{{{{\left( {{U_1}\cos \varphi } \right)}^2}}}\)(1)
\(U = {U_2} \Rightarrow \Delta P = 2,5\% P = R\frac{{{P^2}}}{{{{\left( {{U_2}\cos \varphi } \right)}^2}}}\)(2)
Lấy (1)/(2) \( \Rightarrow \frac{{10\% P}}{{2,5\% P}} = \frac{{R{P^2}}}{{U_1^2{{\cos }^2}\varphi }}.\frac{{U_2^2{{\cos }^2}\varphi }}{{R{P^2}}}\)
\( \Rightarrow 4 = \frac{{U_2^2}}{{U_1^2}} \Rightarrow {U_2} = 2{U_1} = 4kV\)
Chọn B
Câu 33:
Nhận định dưới đây là đúng hay sai?
Trong quá trình chưng cất rượu nấu, tỉ lệ etanol/nước giảm dần.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào nhiệt độ sôi của nước và etanol, chất nào bay hơi trước thì sẽ giảm nồng độ trước.
Lời giải
Khi chưng cất rượu nấu, etanol có nhiệt độ sôi thấp hơn nước sẽ bay hơi trước nên tỉ lệ etanol/nước sẽ tăng dần. Vậy nhận định trên là nhận định sai.
Chọn B
Câu 34:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dung dịch rượu nấu là hỗn hợp của etanol và nước, nên nhiệt độ sôi của hỗn hợp này là nhiệt độ trung gian giữa nhiệt độ sôi hai chất.
Lời giải
Nhiệt độ sôi của etanol là 78,3oC, nhiệt độ sôi của nước là 100oC, thì nhiệt độ sôi của dung dịch rượu nấu sẽ cao hơn rượu và thấp hơn nước. Nhiệt độ sôi phù hợp là 85oC.
Chọn C
Câu 35:
Trong quá trình chưng cất rượu, thể tích rượu nguyên chất _______. Do vậy, sau quá trình chưng cất, nồng độ cồn của sản phẩm trong _______ sẽ _______ nồng độ dung dịch rượu nấu ban đầu.
 Xem đáp án
Xem đáp án
Đáp án
Trong quá trình chưng cất rượu, thể tích rượu nguyên chất tăng. Do vậy, sau quá trình chưng cất, nồng độ cồn của sản phẩm trong bình hứng sẽ lớn hơn nồng độ dung dịch rượu nấu ban đầu.
Phương pháp giải
Dựa vào sơ đồ chưng cất dung dịch rượu nấu và quá trình chưng cất rượu nấu.
Lời giải
Quá trình chưng cất dung dịch rượu nấu nhằm thu được rượu tinh khiết. Do vậy sau quá trình chưng cất nồng độ cồn của sản phẩm trong sản phẩm chắc chắn sẽ cao hơn nồng độ của dung dịch ban đầu. Trong thí nghiệm trên sản phẩm được thu trong bình hứng.
Câu 36:
Phương pháp chưng cất phân đoạn được ứng dụng trong quá trình sản xuất dầu mỏ đi từ nguyên liệu đầu là dầu thô. Trong chưng cất phân đoạn dầu thô, dầu thô được đun nóng tới 400oC cho bay hơi, sau đó hơi dầu thô được dẫn vào một tháp để ngưng tụ phân đoạn các sản phẩm tuỳ theo nhiệt độ sôi của chúng theo thứ tự càng lên cao nhiệt độ càng giảm dần.
Cho nhiệt độ sôi của các chất sản phẩm thu được khi chưng cất phân đoạn dầu thô như sau:
- Butan và propan: Khoảng −42oC - −0,5oC.
- Dầu diesel: Khoảng 200oC – 350oC
- Xăng: Khoảng 38oC – 205oC
- Dầu hoả: Khoảng từ 250oC – 260oC
- Dầu đốt: Có nhiệt độ sôi khoảng 600oCbutan và propan, dầu diesel, xăng, dầu hỏa, dầu đốt
Thứ tự các sản phẩm thu được từ trên đỉnh tháp xuống là: _______ → _______ → _______ → _______ → _______
 Xem đáp án
Xem đáp án
Đáp án
Thứ tự các sản phẩm thu được từ trên đỉnh tháp xuống là: butan và propan → xăng → dầu hoả → dầu diesel → dầu đốt
Phương pháp giải
Dựa vào nguyên tắc làm ngưng tụ sản phẩm trong tháp phân đoạn: Hơi dầu thô được dẫn vào một tháp để ngưng tụ phân đoạn các sản phẩm tuỳ theo nhiệt độ sôi của chúng theo thứ tự càng lên cao nhiệt độ càng giảm dần.
Lời giải
Từ trên đỉnh tháp đi xuống thì nhiệt độ sôi của các sản phẩm thu được sẽ tăng dần. Vậy thứ tự của các sản phẩm thu được từ trên đỉnh tháp xuống là: butan và propan → xăng → dầu hoả → dầu diesel → dầu đốt.
Câu 37:
Để thu được tinh dầu sả chanh từ cây sả người ta sử dụng phương pháp nào dưới đây? Biết rằng tinh dầu sả chanh không tan trong nước?
 Xem đáp án
Xem đáp án
Phương pháp giải
Thu được sản phẩm là tinh dầu sả chanh có đặc điểm là không tan trong nước.
Lời giải
Để thu được chất lỏng hữu cơ không tan trong nước người ta sử dụng phương pháp chưng cất lôi cuốn hơi nước.
Chọn B
Câu 38:
Những nhận định dưới đây là đúng hay sai?
|
|
ĐÚNG |
SAI |
|
Trong phương pháp chưng cất phân đoạn, số sản phẩm tinh khiết thu được nhiều hơn phương pháp chưng cất lôi cuốn hơi nước. |
||
|
Phương pháp chưng cất phân đoạn thực hiện đơn giản hơn phương pháp chưng cất thường. |
||
|
Để tách hai chất lỏng có nhiệt đôi sôi không tách biệt quá lớn thì nên dùng phương pháp chưng cất thường. |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Trong phương pháp chưng cất phân đoạn, số sản phẩm tinh khiết thu được nhiều hơn phương pháp chưng cất lôi cuốn hơi nước. |
X | |
|
Phương pháp chưng cất phân đoạn thực hiện đơn giản hơn phương pháp chưng cất thường. |
X | |
|
Để tách hai chất lỏng có nhiệt đôi sôi không tách biệt quá lớn thì nên dùng phương pháp chưng cất thường. |
X |
Phương pháp giải
Dựa vào quá trình thực hiện các phương pháp chưng cất.
Lời giải
- Phương pháp chưng cất phân đoạn dùng để tách hai hay nhiều chất lỏng có nhiệt độ sôi khác nhau không nhiều và tan lẫn hoàn toàn trong nhau, còn phương pháp chưng cất lôi cuốn hơi nước để tách chất lỏng có nhiệt độ sôi cao và không tan trong nước. Vậy nên nhận địnhn trên là đúng.
- Phương pháp chưng cất phân đoạn khó thực hiện hơn do cần làm ngưng tụ phân đoạn các hơi chất lỏng của sản phẩm theo mỗi nhiệt độ sôi khác nhau của mỗi chất. Vậy nên nhận định trên là sai.
- Không dùng các phương pháp chưng cất thường để tách các hợp chất hữu cơ có nhiệt độ sôi không quá khác biệt, như vậy thì sẽ chỉ thu được hỗn hợp hơi của tất cả các chất mà không có biện pháp tách riêng ra. Phương pháp chưng cất thường chỉ có thể tách các chất lỏng có nhiệt độ sôi có sự chênh lệch rõ ràng.
Câu 39:
Phương pháp chưng cất được sử dụng để
 Xem đáp án
Xem đáp án
Phương pháp giải
Mục đích của phương pháp chưng cất.
Lời giải
Phương pháp chưng cất để sản xuất tinh dầu cam chanh từ vỏ chanh.
Chọn C
Câu 40:
Điều nào sau đây mô tả đúng nhất điều gì đã xảy ra với ống tiêm 60 ml trong thí nghiệm 1?
Khi bơm propanol vào ống xúc tác, khoảng cách từ đầu pittông đến đầu ống tiêm là:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào điều kiện thực hiện thí nghiệm 2.
Lời giải
Khi phản ứng chưa xảy ra thì không có khí trong ống tiêm thu sản phẩm, trước khi có sản phẩm thì ống tiêm không đổi, sau đó tăng lên.
Chọn D
Câu 41:
Kéo thả số thứ tự phù hợp của mỗi giai đoạn trong phản ứng xúc tác dị thể: 1, 2, 3, 4
Các giai đoạn của phản ứng có xúc tác dị thể đều trải qua các giai đoạn giống nhau:- Giai đoạn ______: Có một số loại tương tác giữa bề mặt chất xúc tác và các phân tử chất phản ứng, khiến chúng phản ứng mạnh hơn.- Giai đoạn ______: Phản ứng xảy ra.- Giai đoạn ______: Một hoặc nhiều chất phản ứng được hấp phụ lên bề mặt chất xúc tác.- Giai đoạn ______: Các phân tử sản phẩm được giải hấp, nghĩa là các phân tử sản phẩm bị tách ra khỏi chất xúc tác.
 Xem đáp án
Xem đáp án
Đáp án
Các giai đoạn của phản ứng có xúc tác dị thể đều trải qua các giai đoạn giống nhau:- Giai đoạn 2 : Có một số loại tương tác giữa bề mặt chất xúc tác và các phân tử chất phản ứng, khiến chúng phản ứng mạnh hơn.- Giai đoạn 3 : Phản ứng xảy ra.- Giai đoạn 1 : Một hoặc nhiều chất phản ứng được hấp phụ lên bề mặt chất xúc tác.- Giai đoạn 4 : Các phân tử sản phẩm được giải hấp, nghĩa là các phân tử sản phẩm bị tách ra khỏi chất xúc tác.
Phương pháp giải
Đặc điểm của chất xúc tác trong đề bài được đề cập đến: Không bị biến đổi về lượng và chất sau phản ứng
Lời giải
Giai đoạn …1…: Một hoặc nhiều chất phản ứng được hấp phụ lên bề mặt chất xúc tác.
Giai đoạn …2…: Có một số loại tương tác giữa bề mặt chất xúc tác và các phân tử chất phản ứng, khiến chúng phản ứng mạnh hơn.
Giai đoạn …3…: Phản ứng xảy ra
Giai đoạn …4…: Các phân tử sản phẩm được giải hấp, nghĩa là các phân tử sản phẩm bị vỡ ra.
Câu 42:
Nhận định dưới đây là đúng hay sai?
Thí nghiệm 1 và thí nghiệm 2 đều nghiên cứu ảnh hưởng của xúc tác dị thể tới tốc độ phản ứng pha khí.
 Xem đáp án
Xem đáp án
Phương pháp giải
Cách thực hiện và chất tham gia của thí nghiệm 1 và 2.
Lời giải
Nhận định trên là sai. Chất tham gia của thí nghiệm 1 là pha lỏng còn ở thí nghiệm 2 là pha khí.
Chọn B
Câu 43:
Điền một từ thích hợp vào chỗ trống
Trong thí nghiệm 2, khi thời gian chất phản ứng đi qua chất xúc tác giảm đi thì thể tích propan tạo ra _______.
 Xem đáp án
Xem đáp án
Đáp án: "giảm"
Phương pháp giải
Dựa vào kết quả cúa thí nghiệm 2 trong bảng 2.
Lời giải
Theo thí nghiệm 2, trong bảng 2, thời gian chất phản ứng đi qua chất xúc tác càng nhiều thì propan thu được càng lớn và ngược lại. Vậy từ cần điền là "giảm".
Câu 44:
Những nhận định dưới đây là đúng hay sai?
|
|
ĐÚNG |
SAI |
|
Trong thí nghiệm 2, propan được tạo ra ở giai đoạn 2. |
||
|
Trong thí nghiệm 1, sau phản ứng có bột nhôm ở ống tiêm thu sản phẩm. |
||
|
Phản ứng hoá học ở thí nghiệm 2 là phản ứng cộng. |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Trong thí nghiệm 2, propan được tạo ra ở giai đoạn 2. |
X | |
|
Trong thí nghiệm 1, sau phản ứng có bột nhôm ở ống tiêm thu sản phẩm. |
X | |
|
Phản ứng hoá học ở thí nghiệm 2 là phản ứng cộng. |
X |
Phương pháp giải
Đọc thông tin về cách thực hiện quá trình 1 và 2.
Lời giải
- Nhận định: "Trong thí nghiệm 2, propan được tạo ra ở giai đoạn 2" là sai vì giai đoạn 3 mới là giai đoạn phản ứng xảy ra tạo ra sản phẩm.
- Nhận định: "Trong thí nghiệm 1, sau phản ứng có bột nhôm ở ống tiêm thu sản phẩm" là sai vì chất xúc tác và sản phẩm sẽ tách nhau ra chứ không đi về ống tiêm thu sản phẩm.
- Nhận định: "Phản ứng hoá học ở thí nghiệm 2 là phản ứng cộng" là đúng. Chất phản ứng là hai chất sau phản ứng chỉ thu được một sản phẩm nên phản ứng là phản ứng cộng.
Câu 45:
Điền số thích hợp vào chỗ trống
Hai thử nghiệm minh họa tác động của việc thay đổi khối lượng chất xúc tác đến thể tích propen được tạo ra là _______ và _______ trong thí nghiệm 1.
 Xem đáp án
Xem đáp án
Đáp án:
Hai thử nghiệm minh họa tác động của việc thay đổi khối lượng chất xúc tác đến thể tích propen được tạo ra là 1 | 2 và 2 | 1 trong thí nghiệm 1.
Phương pháp giải
Dựa vào bảng 1 của thí nghiệm 1.
Lời giải
Thí nghiệm 1 và 2 là thí nghiệm nghiên cứu ảnh hưởng của khối lượng chất xúc tác đến thể tích propen thu được.
Câu 46:
Lời giải thích hợp lý nhất cho việc tại sao không thu được propan trong thử nghiệm 4 của thí nghiệm 2 là
 Xem đáp án
Xem đáp án
Phương pháp giải
Quan sát các điều kiện thực hiện thí nghiệm 2 trong bảng 2.
Lời giải
Thời gian thực hiện thử nghiệm 4 quá ngắn nên không tạo ra sản phẩm.
Chọn D
Câu 47:
Chọn các đáp án chính xác
Nhóm sinh vật nào sau đây được cấu tạo từ tế bào nhân sơ?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ các thông tin được cung cấp
Lời giải
Vi khuẩn và Archaea (vi khuẩn cổ) có cấu trúc tế bào là tế bào nhân sơ. Sinh vật nguyên sinh, nấm, động vật và thực vật đều được cấu tạo từ tế bào nhân chuẩn.
Đáp án: Vi khuẩn, Archaea (vi khuẩn cổ)
Chọn A, B
Câu 48:
thành tế bào, màng sinh chất, nhân, vùng nhân
Tế bào nhân sơ được bao bọc bởi một màng chọn lọc, được gọi là _______ . DNA của tế bào nhân sơ tập trung ở một vùng không có màng bao bọc, gọi là _______
 Xem đáp án
Xem đáp án
Đáp án
Tế bào nhân sơ được bao bọc bởi một màng chọn lọc, được gọi là màng sinh chất . DNA của tế bào nhân sơ tập trung ở một vùng không có màng bao bọc, gọi là vùng nhân
Phương pháp giải
Đọc kĩ các thông tin được cung cấp
Lời giải
Tế bào nhân sơ được bao bọc bởi một màng chọn lọc, được gọi là màng sinh chất. DNA của tế bào nhân sơ tập trung ở một vùng không có màng bao bọc, gọi là vùng nhân.
Câu 49:
Nhận định dưới đây đúng hay sai?
Do ribosome có chức năng là tổng hợp nên các protein nên bào quan này có cả ở tế bào nhân sơ và tế bào nhân thực.
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ các thông tin được cung cấp
Lời giải
Có, ribosome là bào quan tổng hợp chuỗi polypeptit dựa trên khuôn mã của RNA thông tin (tổng hợp protein). Nên ribosome có mặt trong tất cả các tế bào sống, bao gồm cả tế bào nhân sơ và tế bào nhân thực.
Đáp án: Đúng
Câu 50:
Thalassemia là một bệnh di truyền nào dưới đây?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin đã cho về bệnh Thalassemia.
Lời giải
Thalassemia là một bệnh di truyền lặn trên nhiễm sắc thể thường.
Chọn C
Câu 51:
Điền đáp án chính xác vào chỗ trống
Tình trạng phổ biến của các bệnh nhân mắc bệnh Thalassemia là _______
 Xem đáp án
Xem đáp án
Đáp án: "thiếu máu"
Phương pháp giải
Đọc kĩ thông tin đã cho về bệnh Thalassemia.
Lời giải
Ở bệnh nhân Thalassemia, các hồng cầu bị phá hủy quá mức dẫn đến tình trạng thiếu máu.
Nên tình trạng phổ biến của các bệnh nhân mắc bệnh Thalassemia là thiếu máu.
Đáp án: thiếu máu
Câu 52:
Điền đáp án chính xác vào chỗ trống
Hồng cầu bị dị dạng là do sự bất thường của _______ (một cấu trúc protein trong hồng cầu có chức năng vận chuyển oxygen).
 Xem đáp án
Xem đáp án
Đáp án: "hemoglobin"
Phương pháp giải
Đọc kĩ thông tin đã cho về bệnh Thalassemia.
Lời giải
Hồng cầu bị dị dạng là do sự bất thường của hemoglobin (một cấu trúc protein trong hồng cầu có chức năng vận chuyển oxygen).
Đáp án: hemoglobin
Câu 53:
hồng cầu, tiểu cầu, bạch cầu, globin, hem, hemoglobin
Bệnh Thalassemia gây ra là do đột biến gen liên quan đến sự tổng hợp chuỗi ______ làm cho ______ bị vỡ và dẫn đến tình trạng thiếu máu.
 Xem đáp án
Xem đáp án
Đáp án
Bệnh Thalassemia gây ra là do đột biến gen liên quan đến sự tổng hợp chuỗi globin làm cho hồng cầu bị vỡ và dẫn đến tình trạng thiếu máu.
Phương pháp giải
Đọc kĩ thông tin đã cho về bệnh Thalassemia.
Lời giải
Bệnh Thalassemia gây ra là do đột biến gen liên quan đến sự tổng hợp chuỗi globin làm cho hồng cầu bị vỡ và dẫn đến tình trạng thiếu máu.
Câu 54:
Chọn nhận định chính xác?
Một bệnh nhân bị thiếu máu, khi xét nghiệm phát hiện mắc bệnh Thalassemia do đột biến gen tại gen tổng hợp chuỗi α-globin.
Bệnh nhân này đã mắc bệnh Thalassemia loại nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin đã cho về bệnh Thalassemia.
Lời giải
Thiếu hụt tổng hợp chuỗi α, do đột biến tại một hay nhiều gen tổng hợp chuỗi α-globin gây ra bệnh α-Thalassemia
-> Bệnh nhân này đã mắc bệnh α-Thalassemia.
Chọn A
Câu 55:
Nhận định dưới đây đúng hay sai?
Một cặp vợ chồng không bị bệnh Thalassemia khi đi xét nghiệm máu và phát hiện cả hai đều có gen gây bệnh này. Khi cặp vợ chồng này dự định sinh con thì xác xuất sinh con mắc bệnh Thalassemia là 50%.
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin đã cho về bệnh Thalassemia.
Lời giải
Một cặp vợ chồng không bị bệnh Thalassemia khi đi xét nghiệm máu và phát hiện cả hai đều có gen gây bệnh này.
Phép lai Aa x Aa
→ Xác xuất sinh con bị bệnh Thalassemia là \(\frac{1}{2}.\frac{1}{2} = \frac{1}{4} = 25\% \)
Đáp án: Sai
Câu 56:
Nhận định dưới đây đúng hay sai?
Với một loài phong lan quý hiếm, người ta có thể thực hiện kĩ thuật nuôi cấy In Vitro để nhân nhanh giống loài này chỉ với 1 mô lá.
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin đã cho
Lời giải
Nuôi cấy mô In Vitro là thuật ngữ dùng để chỉ quá trình nuôi cấy vô trùng trong ống nghiệm các bộ phận tách rời khác nhau của thực vật.
Chỉ với 1 mô lá người ta cũng đã có thể thực hiện nuôi cấy In Vitro.
Đáp án: Đúng
Câu 57:
Đặc điểm nào sau đây không phải của tế bào trần?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin đã cho
Lời giải
Tế bào trần có thể tách trực tiếp từ các bộ phận của thực vật (lá, rễ) bằng cơ học.
Chọn B
Câu 58:
Kéo từ thả vào ô trống thích hợp: vô tính, hữu tính
 Xem đáp án
Xem đáp án
Đáp án
Nuôi cấy tế bào thực vật có thể được coi là một ứng dụng của sinh sản vô tính ở thực vật.
Phương pháp giải
Đọc kĩ thông tin đã cho
Lời giải
Nuôi cấy tế bào thực vật dựa trên tính toàn năng của tế bào và khả năng biệt hóa, phản biệt hóa của chúng mà người ta có thể tái sinh cây từ một tế bào hay một mẫu mô nào đó.
-> Nuôi cấy tế bào thực vật có thể được coi là một ứng dụng của sinh sản vô tính ở thực vật.
Đáp án: vô tính
Câu 59:
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng tính chất: \(\mathop \smallint \nolimits^ _a^cf\left( x \right){\rm{d}}x = \mathop \smallint \nolimits^ _a^bf\left( x \right){\rm{d}}x + \mathop \smallint \nolimits^ _b^cf\left( x \right){\rm{d}}x\)
Lời giải
Chọn C
Câu 60:
 Xem đáp án
Xem đáp án
Phương pháp giải
Điều kiện cần và đủ để (2) là phương trình mặt cầu là \({a^2} + {b^2} + {c^2} - d > 0\).
Lời giải
Xét đáp án B:
\(2{x^2} + 2{y^2} + 2{z^2} - 4x + 2y + 2z + 16 = 0\,\,\left( 1 \right)\)
\( \Leftrightarrow {x^2} + {y^2} + {z^2} - 2x + y + z + 8 = 0.\)
Ta có: \(a = 1,b = - \frac{1}{2},c = - \frac{1}{2},d = 8\)
\( \Rightarrow {a^2} + {b^2} + {c^2} - d = - \frac{{13}}{2} < 0\).
Suy ra (1) không là phương trình đường tròn.
Chọn B
Câu 61:
Người ta muốn trang trí Tết bằng cách xếp xen kẽ 3 cây quất và 2 cây đào sao cho không có cây nào cùng loại xếp cạnh nhau.
Số cách xếp là _______
 Xem đáp án
Xem đáp án
Đáp án: "12"
Phương pháp giải
Sử dụng quy tắc nhân và hoán vị.
Lời giải
Số cách xếp là 3!.2!=12 cách xếp.
Câu 62:
Một cửa hàng kem Tràng Tiền có 6 vị kem khác nhau. Bạn \(A\) đi mua kem 3 vị khác nhau. Hỏi có bao nhiêu cách chọn?
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng tổ hợp chập k của n.
Lời giải
Số cách chọn 3 vị khác nhau trong 6 vị là: \(C_6^3\).
Chọn A
Câu 63:
Trong các mệnh đề cho dưới đây, mệnh đề nào là mệnh đề sai?
 Xem đáp án
Xem đáp án
Đáp án
A Nếu \(f'\left( x \right) \ge 0,\forall x \in \left( {a;b} \right)\) thì hàm số \(f\) đồng biến trên khoảng \(\left( {a;b} \right)\).
C Hàm số \(y = \frac{{2x - 1}}{{x + 1}}\) luôn đồng biến trên \(D = \left( { - \infty ; - 1} \right) \cup \left( { - 1; + \infty } \right)\).
Phương pháp giải
Xét từng mệnh đề.
Lời giải
Nếu \(f'\left( x \right) \ge 0,\forall x \in \left( {a;b} \right)\) thì hàm số \(f\) chưa chắc đã đồng biến trên khoảng \(\left( {a;b} \right)\) vì vẫn có thể xảy ra trường hợp \(f'\left( x \right) = 0\forall x \in \left( {a;b} \right) \Rightarrow \) Mệnh đề 1 sai.
Điểm \({x_0}\) là điểm cực trị của hàm số \(f\) nếu \(f'\left( x \right)\) đổi dấu khi \(x\) đi qua \({x_0} \Rightarrow \) Mệnh đề 2 đúng.
Hàm số \(y = \frac{{2x - 1}}{{x + 1}}\) luôn đồng biến trên \(D = \left( { - \infty ; - 1} \right) \cup \left( { - 1; + \infty } \right) \Rightarrow \) Mệnh đề 3 sai vì \(y = \frac{{2x - 1}}{{x + 1}}\) luôn đồng biến trên \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).
Cho hàm số \(f\) có đạo hàm cấp hai trên khoảng \(\left( {a;b} \right)\). Nếu \({x_0} \in \left( {a;b} \right)\) thỏa mãn \(f'\left( {{x_0}} \right) = 0\) và \(f''\left( {{x_0}} \right) < 0\) thì \({x_0}\) là điểm cực đại của hàm số \(f \Rightarrow \) Mệnh đề 4 đúng.
Đồ thị hàm số \(y = \frac{{ - x + 2}}{{2x - 4}}\) có tiệm cận đứng \(x = 2\) và tiệm cận ngang \(y = - \frac{1}{2} \Rightarrow \) Mệnh đề 5 đúng.
Câu 64:
Cho hàm đa thức bậc ba \[y = f(x)\;\] có đồ thị như hình vẽ sau:
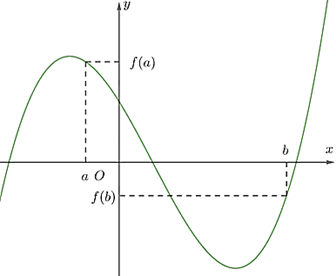
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
Với \({x_1};{x_2} \in \left( {a;b} \right)\) thỏa mãn \({x_1} < {x_2} < 0\) thì \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\) |
||
|
Với \({x_0} \in \left( {a;0} \right)\) thì \(f'\left( {{x_0}} \right) < 0\) |
||
|
Với \({x_0} \in \left( {0;b} \right)\) thì \(f\left( {{x_0}} \right) < f\left( a \right)\) |
 Xem đáp án
Xem đáp án
Đáp số
|
|
ĐÚNG |
SAI |
|
Với \({x_1};{x_2} \in \left( {a;b} \right)\) thỏa mãn \({x_1} < {x_2} < 0\) thì \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\) |
X | |
|
Với \({x_0} \in \left( {a;0} \right)\) thì \(f'\left( {{x_0}} \right) < 0\) |
X | |
|
Với \({x_0} \in \left( {0;b} \right)\) thì \(f\left( {{x_0}} \right) < f\left( a \right)\) |
X |
Phương pháp giải
Cho hàm số \(y = f\left( x \right)\) xác định trên \(K\) (\(K\) có thể là một khoảng, đoạn hoặc nửa khoảng)
- Hàm số \(y = f\left( x \right)\) được gọi là đồng biến trên \(K\) nếu \(\forall {x_1},{x_2} \in K:{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\)
- Hàm số \(y = f\left( x \right)\) được gọi là nghịch biến trên \(K\) nếu \(\forall {x_1},{x_2} \in K:{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).
Lời giải
+) Với \({x_1};{x_2} \in \left( {a;b} \right)\) thỏa mãn \({x_1} < {x_2} < 0\) thì \({x_1};{x_2} \in \left( {a;0} \right)\)
Mà hàm số nghịch biến trên \(\left( {a;0} \right)\) nên \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
=> Mệnh đề 1 sai
+) Hàm số nghịch biến trên \(\left( {a;0} \right)\) nên với \({x_0} \in \left( {a;0} \right)\) thì \(f'\left( {{x_0}} \right) < 0\)
=> Mệnh đề 2 đúng
+) Quan sát đồ thị ta thấy khi \(x \in \left[ {a;b} \right]\) thì \(\mathop {{\rm{max}}}\limits_{\left[ {a;b} \right]} f\left( x \right) = f\left( a \right)\)
Khi đó với \({x_0} \in \left( {0;b} \right)\) thì \(f\left( {{x_0}} \right) < f\left( a \right)\)
=> Mệnh đề 3 đúng
Câu 65:
Từ các chữ số 1,2,3,4,5,6 lập được bao nhiêu số tự nhiên gồm 4 chữ số?
Đáp án _______
 Xem đáp án
Xem đáp án
Đáp án: "1296"
Phương pháp giải
Sử dụng quy tắc nhân.
Lời giải
Số cách tạo một số gồm 4 chữ số từ tập hợp gồm các chữ số \(1,2,3,4,5,6\) là: \({6^4} = 1296\).
Câu 66:
Một cấp số cộng có 12 số hạng. Biết rằng tổng của 12 số hạng đó bằng 144 và số hạng thứ mười hai bằng 23. Khi đó:
Số hạng đầu tiên của cấp số cộng đó là: _______
Công sai của cấp số cộng là: _______
 Xem đáp án
Xem đáp án
Đáp án
Số hạng đầu tiên của cấp số cộng đó là: 1
Công sai của cấp số cộng là: 2
Phương pháp giải
Sử dụng công thức \({u_n} = {u_1} + \left( {n - 1} \right)d\) và \({S_n} = \frac{{n.\left( {{u_1} + {u_{12}}} \right)}}{2}\).
Lời giải
Ta có \(\left\{ {\begin{array}{*{20}{l}}{{u_{12}} = 23}\\{{S_{12}} = 144}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{u_1} + 11d = 23}\\{\frac{{12}}{2}\left( {{u_1} + {u_{12}}} \right) = 144}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{u_1} = 1}\\{d = \frac{{23 - {u_1}}}{{11}} = 2.}\end{array}} \right.} \right.} \right.\)
Câu 67:
Tại buổi tất niên công ty, Dương và Nguyên cùng tham gia trò chơi và giành chiến thắng. Phần quà của hai bạn được đặt trong 1 hộp kín, gồm 6 tờ 20.000 và 4 tờ 50.000. Dương lấy trước, Nguyên lấy sau. Xác suất để Nguyên lấy được tờ 50.000 là a/b (a/b là phân số tối giản).
Tổng a + b = _______
 Xem đáp án
Xem đáp án
Đáp án: "7"
Phương pháp giải
TH1: Dương lấy trước và lấy đúng tờ 20.000
TH2: Dương lấy trước và lấy đúng tờ 50.000
Lời giải
TH1: Dương lấy trước và lấy đúng tờ 20.000 , xác suất lấy trúng tờ 20.000 là \(\frac{6}{{10}}\)
Khi đó xác suất để Nguyên lấy được tờ 50.000 là \(\frac{4}{9}\)
TH2: Dương lấy trước và lấy đúng tờ 50.000 , xác suất lấy trúng tờ 50.000 là \(\frac{4}{{10}}\)
Khi đó xác suất để Nguyên lấy được tờ 50.000 là \(\frac{3}{9}\)
Xác suất để Nguyên lấy được tờ 50.000 là \(\frac{6}{{10}}.\frac{4}{9} + \frac{4}{{10}}.\frac{3}{9} = \frac{2}{5}\)
Câu 68:
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) diện tích \(S\) của hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b(a < b)\) được tính theo công thức
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng lý thuyết về ứng dụng diện tích.
Lời giải
Diện tích \(S\) của hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b(a < b)\) được tính theo công thức
Chọn B
Câu 69:
 Xem đáp án
Xem đáp án
Phương pháp giải
Cho hai dãy số \(\left( {{u_n}} \right),\left( {{v_n}} \right)\). Nếu \(\left| {{u_n}} \right| \le {v_n}\) với mọi \(n\) và \({\rm{lim}}{v_n} = 0\) thì \({\rm{lim}}{u_n} = 0\).
Lời giải
Ta có: \(\frac{{{{( - 1)}^n}{{.2}^{5n + 1}}}}{{{3^{5n + 2}}}} \le \frac{{{2^{5n + 1}}}}{{{3^{5n + 2}}}}\)
Mà \({\rm{lim}}\frac{{{2^{5n + 1}}}}{{{3^{5n + 2}}}} = 0\) nên \({\rm{lim}}\frac{{{{( - 1)}^n}{{.2}^{5n + 1}}}}{{{3^{5n + 2}}}} = 0\)
Chọn A
Câu 70:
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\) có đồ thị như hình bên.
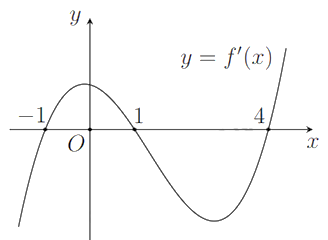
Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án
B. Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {1; + \infty } \right)\).
C. \(f\left( { - 1} \right) < f\left( 4 \right) < f\left( 1 \right)\).
Xét từng mệnh đề.
- Số cực trị của \(y = f\left( x \right)\)
- Hàm số \(y = f\left( x \right)\) đồng biến trên những khoảng mà \(f'\left( x \right) > 0\).
- Tính tích phân từ - 1 đến 1 , từ 1 đến 4 và từ -1 đến 4 rồi so sánh \(f\left( { - 1} \right),f\left( 1 \right),f\left( 4 \right)\).
Lời giải
Ta thấy \(f'\left( x \right) = 0\) cắt đường thẳng \(Ox\) tại 3 điểm phân biệt.
Khi đó hàm số \(y = f\left( x \right)\) có ba cực trị \( \Rightarrow \) Khẳng định đúng \( \Rightarrow \) Loại.
Trên khoảng \(\left( {1; + \infty } \right)\) thì hàm số \(y = f\left( x \right)\) không đồng biến \( \Rightarrow \) Khẳng định 2 sai \( \Rightarrow \) Thỏa mãn.
Tính tích phân: \(\int\limits_{ - 1}^1 {f'\left( x \right)dx = f\left( 1 \right) - f\left( { - 1} \right) > 0} \) vì \(f'\left( x \right) > 0\forall x \in \left( { - 1;1} \right)\).
\( \Rightarrow f\left( 1 \right) > f\left( { - 1} \right)\)
vì \(f'\left( x \right) < 0\forall x \in \left( {1;4} \right)\).
\( \Rightarrow f\left( 1 \right) > f\left( 4 \right)\)
do phần diện tích bên dưới lớn hơn.
\( \Rightarrow f\left( { - 1} \right) > f\left( 4 \right)\)
\( \Rightarrow f\left( 1 \right) > f\left( { - 1} \right) > f\left( 4 \right)\)
Khẳng định 3 sai \( \Rightarrow \) Thỏa mãn.
Giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 1;4} \right]\) bằng \(f\left( 4 \right)\) vì \(f\left( 1 \right) > f\left( { - 1} \right) > f\left( 4 \right)\).
\( \Rightarrow \) Khẳng định đúng \( \Rightarrow \) Loại.
Chọn B, C
Câu 71:
Cho cặp số tự nhiên \(\left( {x,y} \right)\) thỏa mãn \({x^2} - {y^2} = 91\).
Với mỗi cặp số (x, y) thỏa mãn điều kiện trên thì x.y có thể bằng:
 Xem đáp án
Xem đáp án
Đáp án
A. 30
C. 2070
Phương pháp giải
Nhận xét dấu của \(x,y\).
Lời giải
\({x^2} - {y^2} = \left( {x - y} \right).\left( {x + y} \right)\)
\(91 = 7.13 = 1.91\)
Vì \(x,y \in \mathbb{N}\) nên \(x + y > 0,x - y > 0\) và \(x - y < x + y\)
Khi đó:
\({x^2} - {y^2} = 91\)
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{x - y = 7}\\{x + y = 13}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{x - y = 1}\\{x + y = 91}\end{array}} \right.}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{x = 10}\\{y = 3}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{x = 46}\\{y = 45}\end{array}} \right.}\end{array}} \right.} \right.\]
Khi đó \(x.y = 30\) hoặc \(x.y = 2070\).
Chọn A, C
Câu 72:
 Xem đáp án
Xem đáp án
Phương pháp giải
- Hàm số \(y = f\left( x \right)\) được gọi là liên tục tại \({x_0}\) nếu \(\mathop {{\rm{lim}}}\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).
-Tìm ra a và giải bất phương trình.
Hàm số liên tục trên khoảng, đoạn
Lời giải
Ta có: \(f\left( 0 \right) = 3\)
\(\mathop {{\rm{lim}}}\limits_{x \to 0} f\left( x \right) = \mathop {{\rm{lim}}}\limits_{x \to 0} \frac{{\sqrt {4x + 1} - 1}}{{a{x^2} + \left( {2a + 1} \right)x}} = \mathop {{\rm{lim}}}\limits_{x \to 0} \frac{{4x}}{{x\left( {ax + 2a + 1} \right)\left( {\sqrt {4x + 1} + 1} \right)}}\)
\( = \mathop {{\rm{lim}}}\limits_{x \to 0} \frac{4}{{\left( {ax + 2a + 1} \right)\left( {\sqrt {4x + 1} + 1} \right)}} = \frac{2}{{2a + 1}}\)
Hàm số liên tục tại \({x_0} = 0 \Leftrightarrow \mathop {{\rm{lim}}}\limits_{x \to 0} f\left( x \right) = f\left( 0 \right) \Leftrightarrow \frac{2}{{2a + 1}} = 3 \Leftrightarrow a = - \frac{1}{6}\)
Ta có bất phương trình \({x^2} - x + 36a < 0 \Leftrightarrow {x^2} - x - 6 < 0 \Leftrightarrow - 2 < x < 3\)
Vậy số nghiệm nguyên của bất phương trình đã cho là 4.
Chọn A
Câu 73:
 Xem đáp án
Xem đáp án
Phương pháp giải
Bước 1: Giải bất phương trình tương đương
Bước 2: Biện luận để tìm giá trị của m
Tìm điều kiện của tham số để bất phương trình có nghiệm
Lời giải
Ta có bất phương trình tương đương với:
\(\left( {x - m.} \right){2^x} - 4\left( {x - m} \right) < 0 \Leftrightarrow \left( {x - m} \right)\left( {{2^x} - 4} \right) < 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{c}}{x - m > 0}\\{{2^x} - 4 < 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{x - m < 0}\\{{2^x} - 4 > 0}\end{array}} \right.}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{c}}{x > m}\\{x < 2}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{x < m}\\{x > 2}\end{array}} \right.}\end{array}} \right.} \right.\) (*). Dễ dàng thấy cụm điều kiện \(\left\{ {\begin{array}{*{20}{l}}{x > m}\\{x < 2}\end{array}} \right.\) không tồn tại giá trị nguyên dương nào với mọi m nguyên dương nên (*) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x < m}\\{x > 2}\end{array}} \right.\)
Để chứa đúng 5 số nguyên dương tức tập giá trị từ bất phương trình trên nhận từ 3 đến 7. Như vậy với \(m = 8\) thì thỏa điều kiện đề bài
Chọn D
Câu 74:
Một quyển sách có 2000 trang.
Điền đáp án vào chỗ trống:
Cần dùng _______ chữ số để đánh số trang quyển sách đó.
 Xem đáp án
Xem đáp án
Đáp án: "6893"
Phương pháp giải
Tính số trang có 1, 2, 3, 4 chữ số.
Lời giải
Số trang có 1 chữ số: 9 trang.
Số trang có 2 chữ số: 90 trang.
Số trang có 3 chữ số: 900 trang.
Số trang có 4 chữ số: 9000 trang.
Ta có: 2000 = 9+90+900+1001
Số chữ số để đánh số trang là: 9.1 + 90.2 + 900.3 + 1001.4 = 6893
Câu 75:
 Xem đáp án
Xem đáp án
Phương pháp giải
Mặt cầu có phương trình dạng \({x^2} + {y^2} + {z^2} + 2ax + 2by + 2cz + d = 0\) có tâm \(I\left( { - a; - b; - c} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \).
Nhận biết các yếu tố từ phương trình mặt cầu
Lời giải
Ta có tọa dộ tâm \(I\left( {1; - 2;0} \right)\) và bán kính \(R = 5\).
Chọn D
Câu 76:
Cho hàm số \(f\left( x \right) = {x^3} - 4{x^2} + 5x - 2\).
Phát biểu đúng là
 Xem đáp án
Xem đáp án
Đáp án
A. Hàm số đã cho xác định với mọi \(x \in \mathbb{R}\).
C. Hàm số đã cho có đạo hàm cấp 2 và \(f''\left( 1 \right) < 0\).
Phương pháp giải
Xét từng mệnh đề.
Lời giải
Hàm số \(f\left( x \right) = {x^3} - 4{x^2} + 5x - 2\) có:
\(f'\left( x \right) = 3{x^2} - 8x + 5\)
\(f''\left( x \right) = 6x - 8\)
Hàm số đã cho xác định với mọi \(x \in \mathbb{R}\).
\(f\left( { - x} \right) = {( - x)^3} - 4{( - x)^2} + 5\left( { - x} \right) - 2\)
\( = - {x^3} - 4{x^2} - 5x - 2 \ne f\left( x \right)\)
Hàm số đã cho không là hàm số chẵn.
Hàm số đã cho có đạo hàm cấp 2 và \(f''\left( 1 \right) = 6 - 8 = - 2 < 0\).
Đồ thị của hàm số đã cho không phải là một parabol.
Giới hạn \(\mathop {{\rm{lim}}}\limits_{x \to + \infty } f\left( x \right) = + \infty ,\mathop {{\rm{lim}}}\limits_{x \to - \infty } f\left( x \right) = - \infty \Rightarrow \) Mệnh đề cuối sai.
Chọn A, C
Câu 77:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Để \(\widehat {\vec u,\vec v)} < {90^ \circ } \Rightarrow {\rm{cos}}\widehat {\left( {\vec u,\vec v} \right)} > 0\).
\( \Rightarrow \vec u.\vec v > 0 \Leftrightarrow 3 + {\rm{lo}}{{\rm{g}}_3}5.{\rm{lo}}{{\rm{g}}_5}3 + 4{\rm{lo}}{{\rm{g}}_m}2 > 0\)
\( \Leftrightarrow 4 + 4{\rm{lo}}{{\rm{g}}_m}2 > 0 \Leftrightarrow {\rm{lo}}{{\rm{g}}_m}2 > - 1 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m > 1}\\{m < \frac{1}{2}}\end{array}} \right.\).
Kết hợp điều kiện \(m > 0 \Rightarrow \left[ {\begin{array}{*{20}{l}}{m > 1}\\{0 < m < \frac{1}{2}}\end{array}} \right.\)
Chọn D
Câu 78:
 Xem đáp án
Xem đáp án
Phương pháp giải
-Nhận xét giá trị của \(a\).
-Nhân liên hợp để tìm \(b\).
Dạng vô định \(\infty \) - \(\infty \)
Lời giải
Xét \(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \left( {\sqrt {{x^2} - 4x + 1} - ax + b} \right) = 5\).
+ Nếu \(a \ne 1\) thì \(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \left( {\sqrt {{x^2} - 4x + 1} - ax + b} \right)\)
\( = \mathop {{\rm{lim}}}\limits_{x \to + \infty } x\left( {\sqrt {1 - \frac{4}{x} + \frac{1}{{{x^2}}}} - a + \frac{b}{x}} \right) = \infty \)
Vì: \(\left\{ {\begin{array}{*{20}{c}}{\mathop {{\rm{lim}}}\limits_{x \to + \infty } x = + \infty }\\{\mathop {{\rm{lim}}}\limits_{x \to + \infty } \left( {\sqrt {1 - \frac{4}{x} + \frac{1}{{{x^2}}}} - a + \frac{b}{x}} \right) = 1 - a \ne 0}\end{array}} \right.\)
Do đó: \(a = 1\)
Khi đó: \(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \left( {\sqrt {{x^2} - 4x + 1} - ax + b} \right) = \mathop {{\rm{lim}}}\limits_{x \to + \infty } \left( {\sqrt {{x^2} - 4x + 1} - x + b} \right)\)
\( = \mathop {{\rm{lim}}}\limits_{x \to + \infty } \frac{{{x^2} - 4x + 1 - {{(x - b)}^2}}}{{\sqrt {{x^2} - 4x + 1} + x - b}}\)
\( = \mathop {{\rm{lim}}}\limits_{x \to + \infty } \frac{{\left( {2b - 4} \right)x + 1 - {b^2}}}{{\sqrt {{x^2} - 4x + 1} + x - b}}\)
\( = \mathop {{\rm{lim}}}\limits_{x \to + \infty } \frac{{\left( {2b - 4} \right) + \frac{{1 - {b^2}}}{x}}}{{\sqrt {1 - \frac{4}{x} + \frac{1}{{{x^2}}}} + 1 - \frac{b}{x}}} = \frac{{2b - 4}}{2} = b - 2\)
Mà \(\mathop {{\rm{lim}}}\limits_{x \to + \infty } \left( {\sqrt {{x^2} - 4x + 1} - ax + b} \right) = 5\) nên \(b - 2 = 5 \Leftrightarrow b = 7\).
Vậy \(T = {a^3} + {b^2} = 50\)
Chọn D
Câu 79:
 Xem đáp án
Xem đáp án
Phương pháp giải
Gọi số lượng lá bèo ban đầu là \({M_0}\) thì số lượng lá bèo sau \(t\) giờ là : \(M\left( t \right) = {M_0}{.2^t}\)
- Tính lượng lá bèo sau 1 ngày và khi phủ kín \(\frac{1}{4}\) hồ.
- Lập phương trình và tìm \(t\).
Lời giải
Gọi số lượng lá bèo ban đầu là \({M_0}\) thì số lượng lá bèo sau \(t\) giờ là : \(M\left( t \right) = {M_0}{.2^t}\).
Số lượng lá bèo sau 1 ngày là : \(M\left( {24} \right) = {M_0}{.2^{24}}\).
Khi số lượng lá bèo phủ kín \(\frac{1}{4}\) hồ ta có:
\(M\left( t \right) = \frac{1}{4}M\left( {24} \right) \Leftrightarrow {M_0}{.2^t} = \frac{1}{4}{M_0}{.2^{24}} \Leftrightarrow t = 22\)
Chọn B
