Hàm số bậc hai
-
844 lượt thi
-
27 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Do đó, ta có hệ phương trình
Câu 2:
 Xem đáp án
Xem đáp án
Câu 3:
 Xem đáp án
Xem đáp án
Câu 4:
 Xem đáp án
Xem đáp án
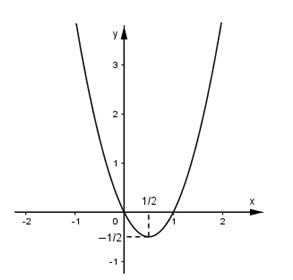
Câu 5:
 Xem đáp án
Xem đáp án
Câu 6:
Tìm các giá trị của m để hàm số luôn đồng biến trên
 Xem đáp án
Xem đáp án
Câu 7:
Tìm giá trị của m để hàm số đạt giá trị lớn nhất bằng 6
 Xem đáp án
Xem đáp án
Câu 8:
Một cái cổng hình parabol có dạng có chiều rộng d = 4m.
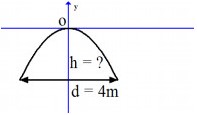
 Xem đáp án
Xem đáp án
Gọi hai điểm chân cổng là và thì ta có và
Vậy
Câu 9:
 Xem đáp án
Xem đáp án
Do đó, ta có hệ phương trình
Câu 10:
Cho phương trình của (P): biết rằng hàm số có giá trị lớn nhất bằng 1 và đồ thị hàm số đi qua các điểm A(2;0), B(−2;−8) Tính tổng
 Xem đáp án
Xem đáp án
Do đó, phương trình của (P) có dạng
Câu 11:
Biết đồ thị hàm số (P): cắt trục hoành tại hai điểm phân biệt có hoành độ x1,x2. Tìm giá trị của tham số mm để biểu thức đạt giá trị nhỏ nhất.
 Xem đáp án
Xem đáp án
Dễ thấy rằng phương trình hoành độ giao điểm có hai nghiệm phân biệt vì
Câu 12:
Tìm các giá trị của tham số mm để phương trình có hai nghiệm phân biệt trong đó có đúng một nghiệm thuộc khoảng (0;1).
 Xem đáp án
Xem đáp án
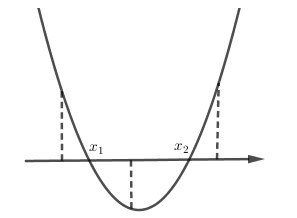
Yêu cầu bài toán tương đương
Đáp án cần chọn là: A
Câu 13:
 Xem đáp án
Xem đáp án
Parabol có hệ số a = 2 > 0 nên có bề lõm hướng lên trên đạt GTNN tại đỉnh parabol
Câu 14:
Tìm giá trị nhỏ nhất của hàm số f(x) biết rằng trên
 Xem đáp án
Xem đáp án
Đặt từ đẳng thức trên ta suy ra
Câu 15:
Tìm giá trị của m để đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ dương.
 Xem đáp án
Xem đáp án
Câu 16:
Tìm điểm A cố định mà họ đồ thị hàm số luôn đi qua.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 17:
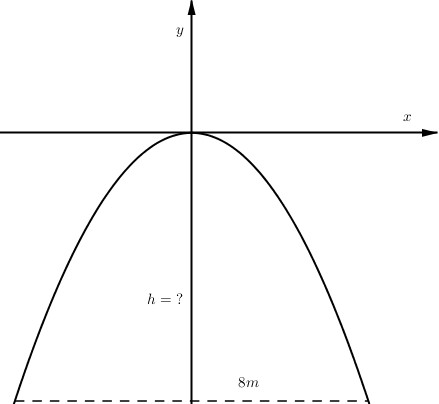
 Xem đáp án
Xem đáp án
Tung độ chân cổng là
Câu 18:
Tìm các giá trị thực của tham số m để phương trình có bốn nghiệm thực phân biệt.
 Xem đáp án
Xem đáp án
Ta có
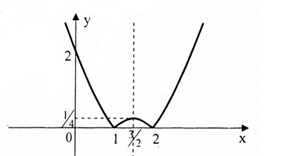
Câu 19:
Tìm các giá trị của tham số m để phương trình có 3 nghiệm thực phân biệt.
 Xem đáp án
Xem đáp án
Đồ thị hàm số được vẽ như sau :
+ Giữ nguyên nhánh bên phải trục tung của đồ thị hàm và xóa nhánh bên trái trục tung.
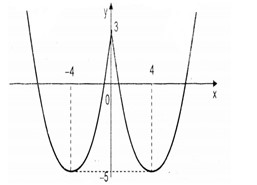
Câu 20:
Tìm các giá trị của m để phương trình có nghiệm duy nhất.
 Xem đáp án
Xem đáp án
Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số và đường thẳng y = m có tính chất song song với trục hoành.
+ Vẽ lần lượt hai đồ thị hàm số trên cùng một hệ trục tọa độ
+ Xóa đi nhánh bên trái điểm của đồ thị hàm số
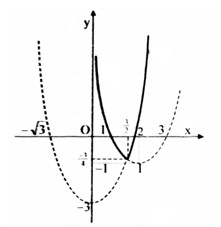
Câu 21:
 Xem đáp án
Xem đáp án
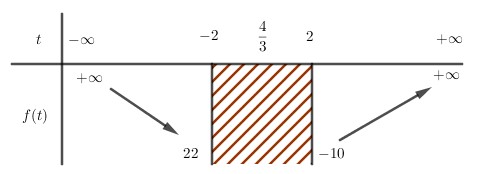
Ta có f(2 )= −10.
Vậy minP = minf(t) = −10.
Đáp án cần chọn là: D
Câu 22:

 Xem đáp án
Xem đáp án
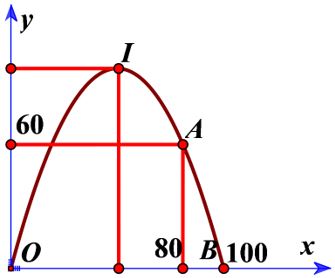
Vị trí đạn bay cao nhất cách mặt đất là
Câu 23:

 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 24:

 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Câu 25:
|
Quãng đường |
Giá cước (VNĐ/km) |
|
Từ 0 đến 10 km |
10 000 |
|
Từ trên 10 km đến 40 km |
15 000 |
|
Trên 40 km |
12 500 |
 Xem đáp án
Xem đáp án
Để xác định số tiền xe là 475000VNĐ mà người đi xe phải trả ứng với quãng đường di chuyển dài bao nhiêu, ta cần xác định công thức tương ứng
Với thì
Đáp án cần chọn là: A
Câu 26:
|
Quãng đường |
Giá cước (VNĐ/km) |
|
Từ 0 đến 10 km |
10 000 |
|
Từ trên 10 km đến 40 km |
15 000 |
|
Trên 40 km |
12 500 |
 Xem đáp án
Xem đáp án
Bước 1: Gọi là độ dài quãng đường AB.
Vì số tiền người đó phải trả ở quãng đường BC gấp 2,8 lần số tiền phải trả ở quãng đường AB nên ta có phương trình
Đáp án cần chọn là: B
Câu 27:
|
Quãng đường |
Giá cước (VNĐ/km) |
|
Từ 0 đến 10 km |
10 000 |
|
Từ trên 10 km đến 40 km |
15 000 |
|
Trên 40 km |
12 500 |
 Xem đáp án
Xem đáp án
Nếu không được giảm giá 10% thì người đi xe phải trả số tiền là:
Vì nên người đi xe đã đi được quãng đường là:
Đáp án cần chọn là: D
