Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 13)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 13)
-
399 lượt thi
-
82 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
Phần tư duy đọc hiểu
 Xem đáp án
Xem đáp án
Giải thích
Đọc lại nội dung của đoạn [1], xác định các thông tin quan trọng liên quan tới hậu quả của tình trạng tắc nghẽn giao thông: “lãng phí thời gian, tiêu hao nhiên liệu và ô nhiễm môi trường”; từ các thông tin trong bài viết cần đưa ra suy luận để tiến hành loại trừ Từ khóa: việc lãng phí thời gian và tiền bạc sẽ làm mất đi cơ hội phát triển của con người, tiêu hao nhiên liệu và ô nhiễm môi trường sẽ gây ra hậu quả về sức khỏe và việc khai thác chất đốt trong tự nhiên; Từ khóa đúng là C.
Chọn C
Câu 2:
Từ thông tin của đoạn [1] hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí
ứng dụng, xây dựng, thiết kế, áp dụng
Theo đánh giá từ Viện chiến lược và phát triển Giao thông vận tải, tình trạng tắc nghẽn giao thông đang gây ảnh hưởng nghiêm trọng tới đời sống, vậy nên, các cơ quan tổ chức đang ______ nhiều biện pháp và ______ khoa học máy tính vào việc ______ các hệ thống thu thập và xử lý dữ liệu.
 Xem đáp án
Xem đáp án
Đáp án
Từ thông tin của đoạn [1] hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí:
Theo đánh giá từ Viện chiến lược và phát triển Giao thông vận tải, tình trạng tắc nghẽn giao thông đang gây ảnh hưởng nghiêm trọng tới đời sống, vậy nên, các cơ quan tổ chức đang áp dụng nhiều biện pháp và ứng dụng khoa học máy tính vào việc thiết kế các hệ thống thu thập và xử lý dữ liệu.
Giải thích
Đọc lại thông tin trong đoạn [1] để tìm ra được một số từ khóa quan trọng: “nhiều các biện pháp được nghiên cứu và áp dụng”, “ứng dụng khoa học máy tính càng được chú ý”, “thiết kế hệ thống thị giác máy tính thu thập và xử lý dữ liệu”. Câu văn đầy đủ là: “Theo đánh giá từ Viện chiến lược và phát triển Giao thông vận tải, tình trạng tắc nghẽn giao thông đang gây ảnh hưởng nghiêm trọng tới đời sống, vậy nên, các cơ quan tổ chức đang [áp dụng] nhiều biện pháp và [ứng dụng] khoa học máy tính vào việc [thiết kế] các hệ thống thu thập và xử lý dữ liệu.”
Câu 3:
Mục đích của nhóm nghiên cứu khi tìm kiếm giải pháp phân loại phương tiện giao thông là gì?
 Xem đáp án
Xem đáp án
Giải thích
Đọc lại nội dung của đoạn [1]: Khi triển khai nghiên cứu giải pháp từ việc thu thập dữ liệu của camera giao thông để “xác định số lượng phương tiện lưu thông trên đường và tính toán mật độ lưu lượng phương tiện tham gia giao thông trong một khoảng thời gian xác định”; vậy mục tiêu cốt lõi sẽ là dự báo về tình trạng giao thông để giảm thiểu tình trạng tắc nghẽn.
Chọn D
Câu 4:
Yolov4 là phiên bản nâng cấp, có cơ chế hoạt động của mô hình mạng dùng cho việc phát hiện, nhận dạng, phân loại đối tượng; phân chia và xử lý hình ảnh sau đó đưa ra các dự đoán theo một yêu cầu xác định là đúng hay sai?
 Xem đáp án
Xem đáp án
Đáp án
A. Đúng
Giải thích
Đọc lại nội dung đoạn [2] để tìm hiểu định nghĩa về Yolo: “mô hình mạng dùng cho việc phát hiện, nhận dạng, phân lại đối tượng”, “dự đoán xem trong mỗi ô liệu có đối tượng (object) mà điểm trung tâm rơi vào ô đó không, dự đoán điểm trung tâm, kích thước của đối tượng và xác suất là đối tượng nào trong số các đối tượng cần xác định”; chú ý câu “phiên bản đang được sử dụng là thế hệ thứ 4, gọi là Yolov4”.
Câu 5:
 Xem đáp án
Xem đáp án
Giải thích
Đọc kĩ nội dung của đoạn [3], cần phân biệt Sort và Tracking-by-detection; trong đó, Tracking-by-dectection là thuật toán để giải quyết từng đối tượng (xác định, dự đoán) còn Sort là “sự phát triển của khung theo dõi nhiều đối tượng”.
Chọn B
Câu 6:
 Xem đáp án
Xem đáp án
Giải thích
Đọc nội dung của đoạn [4] xác định thông tin: “… từ đó gán địa chỉ nhận dạng ID cho từng phương tiện lưu thông và phân loại chúng… xe ô tô, xe tải, xe buýt, xe máy và xe đạp”; cần lưu ý xe đạp không phải xe cơ giới nên chọn Từ khóa B.
Chọn B
Câu 7:
 Xem đáp án
Xem đáp án
Giải thích
Căn cứ vào từ khóa “tỷ lệ chính xác” để tìm thông tin trong đoạn [5]: “với xe ô tô, xe tải và xe buýt thì tỉ lệ chính xác tương đối cao và ổn định do đặc điểm kích thước và nhận dạng của chúng”; trong đoạn có nhắc tới yếu tố góc quan sát của camera, thời tiết, ánh sáng… nhưng đó không phải yếu tố quan trọng nhất.
Chọn A
Câu 8:
Đọc đoạn [5] và tìm từ không quá ba tiếng để hoàn thành câu văn sau:
Ở Việt Nam, phương tiện di chuyển chủ yếu là (1) ______, mật độ lưu thông cao nên để xây dựng được thuật toán ổn định và chính xác là rất phức tạp, cần thời gian dài để có thể hoàn thiện mô hình.
 Xem đáp án
Xem đáp án
Đáp án
Đọc đoạn [5] và tìm từ không quá ba tiếng để hoàn thành câu văn sau:
Ở Việt Nam, phương tiện di chuyển chủ yếu là (1) xe máy, mật độ lưu thông cao nên để xây dựng được thuật toán ổn định và chính xác là rất phức tạp, cần thời gian dài để có thể hoàn thiện mô hình.
Giải thích
Đọc thông tin trong đoạn [5] xác định từ cần điền là: “xe máy” vì có thông tin “tại Việt Nam, giao thông với đặc thù lượng xe máy lớn và mật độ lưu thông cao…”.
Câu 9:
 Xem đáp án
Xem đáp án
Giải thích
Căn cứ vào từ khóa “kết quả phân loại và kiểm đếm” để đọc lại nội dung của đoạn [6] và xác định thông tin: “nhóm nghiên cứu nhận thấy khi mật độ lưu thông thấp, thuật toán cho kết quả phân loại và kiểm đếm tương đối chính xác. Với mật độ lưu thông trung bình và cao, kết quả bắt đầu có độ chênh lệch và mất định hơn ở loại phương tiện và xe đạp và xe máy”.
Chọn B
Câu 10:
Hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí:
giải quyết, đánh giá, khắc phục, điều tiết, xác định
Kết quả của quá trình thực nghiệm bằng video thực tế là cơ sở cho quá trình _____ để _____ mật độ lưu thông nhằm _____ tình trạng hệ thống giao thông bị quá tải, gây ùn tắc cho các phương tiện tham gia.
 Xem đáp án
Xem đáp án
Đáp án
Hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí:
Kết quả của quá trình thực nghiệm bằng video thực tế là cơ sở cho quá trình xác định để đánh giá mật độ lưu thông nhằm khắc phục tình trạng hệ thống giao thông bị quá tải, gây ùn tắc cho các phương tiện tham gia.
Giải thích
Căn cứ vào từ khóa “hệ thống giao thông bị quá tải”, “gây ùn tắc” tương đương với “tình trạng ùn tắc giao thông” xác định nội dung cần tìm ở đoạn [6]: “Các số liệu… được áp dụng vào việc tính toán mật độ lưu thông trên từng khoảng thời gian, từ đó đưa ra các kết luận”, “nhằm trực tiếp giảm thiểu tình trạng ùn tắc giao thông”. Chú ý “tính toán” tương đương với “xác định”, “kết luận” tương đương với “đánh giá” và “giảm thiểu” tương đương với “khắc phục”.
Câu 11:
Hãy điền một cụm từ không quá ba tiếng vào chỗ trống để hoàn thành nhận định sau:
Từ nền tảng ChatGPT đã được phát triển trước đó, một nhóm khởi nghiệp đã nghiên cứu và tìm ra phương thức giao tới với AI miễn phí thông qua (1) ________.
 Xem đáp án
Xem đáp án
Đáp án
Hãy điền một cụm từ không quá ba tiếng vào chỗ trống để hoàn thành nhận định sau:
Từ nền tảng ChatGPT đã được phát triển trước đó, một nhóm khởi nghiệp đã nghiên cứu và tìm ra phương thức giao tới với AI miễn phí thông qua (1) giọng nói.
Giải thích
Căn cứ vào thông tin trong đoạn [1] “Dựa trên dữ liệu của ChatGPT, nhóm khởi nghiệp tại TP HCM phát triển nền tảng VoiceGPT có thể giao tiếp với AI bằng giọng nói, sử dụng miễn phí.”, xác định từ cần điền là “giọng nói” hoặc “ngôn ngữ nói”.
Câu 12:
 Xem đáp án
Xem đáp án
Giải thích
Đọc đoạn [3], căn cứ vào thông tin “Mong muốn có một sản phẩm ChatGPT cho người Việt, các thành viên nhóm liên hệ với OpenAI, đơn vị phát triển sản phẩm, đề xuất phát triển ứng dụng này tại Việt Nam. xác định mục đích của nhóm là tạo ra một sản phẩm phù hợp về ngôn ngữ và dành cho người Việt. Đáp án đúng là B.
Câu 13:
Hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí
OpenAI, Chat GPT, tạo tài khoản, Voice GPT
Trong giai đoạn đầu tiên khi nghiên cứu, phát triển và đưa vào sử dụng, người dùng sẽ _______ bằng email hoặc số điện thoại Việt Nam; các câu hỏi sẽ được chuyển về máy chủ của hệ thống _______ để xử lý sau đó trả về _______ trước khi tới với người dùng.
 Xem đáp án
Xem đáp án
Đáp án
Hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí
Trong giai đoạn đầu tiên khi nghiên cứu, phát triển và đưa vào sử dụng, người dùng sẽ tạo tài khoản bằng email hoặc số điện thoại Việt Nam; các câu hỏi sẽ được chuyển về máy chủ của hệ thống ChatGPT để xử lý sau đó trả về VoiceGPT trước khi tới với người dùng.
Giải thích
Căn cứ vào từ khóa “email hoặc số điện thoại ở Việt Nam”, xác định được thông tin cần tìm kiếm nằm trong đoạn [4]: người dùng tại Việt Nam đăng kí tài khoản để dùng và hệ thống VoiceGPT đảm nhiệm chức năng trung gian từ người dùng tới ChatGPT.
Câu cần điền là: Trong giai đoạn đầu tiên khi nghiên cứu, phát triển và đưa vào sử dụng, người dùng sẽ [tạo tài khoản] bằng email hoặc số điện thoại Việt Nam; các câu hỏi sẽ được chuyển về máy chủ của hệ thống [ChatGPT] để xử lý, sau đó trả về [VoiceGPT] trước khi tới với người dùng.
Câu 14:
Theo đoạn [4], hạn chế của ứng dụng VoiceGPT là ở khả năng làm việc độc lập. Đúng hay sai?
 Xem đáp án
Xem đáp án
Đáp án
A. Đúng
Giải thích
Từ thông tin tổng hợp được qua 04 đoạn đầu tiên của văn bản, xác định được VoiceGPT chỉ là hệ thống trung gian giữa người dùng và ChatGPT nên đây không phải ứng dụng hoạt động độc lập.
Câu 15:
 Xem đáp án
Xem đáp án
Giải thích
Đọc đoạn [5], xác định được thông tin: VoiceGPT tích hợp thêm tính năng vẽ tranh thông qua gợi ý từ các văn bản.
Chọn B
Câu 16:
Hãy điền một cụm từ không quá ba tiếng vào chỗ trống để hoàn thành nhận định sau:
Để thuận tiện cho một nhóm người dùng bị hạn chế về điều kiện gõ văn bản, nhóm phát triển VoiceGPT đã phát triển thêm tính năng (1) _______ dựa trên nền tảng công cụ AI của Google.
 Xem đáp án
Xem đáp án
Đáp án
Hãy điền một cụm từ không quá ba tiếng vào chỗ trống để hoàn thành nhận định sau:
Để thuận tiện cho một nhóm người dùng bị hạn chế về điều kiện gõ văn bản, nhóm phát triển VoiceGPT đã phát triển thêm tính năng (1) trò chuyện dựa trên nền tảng công cụ AI của Google.
Giải thích
Căn cứ vào từ khóa “AI của Google” xác định thông tin cần tìm nằm trong đoạn [6] và [7]: “ngoài giao tiếp với AI bằng văn bản, nhóm phát triển thêm tính năng nói chuyện bằng giọng nói”. Vậy từ cần điền là “trò chuyện” hoặc “nói chuyện”.
Câu 17:
Theo người sáng lập Tesse, điều gì sẽ tạo điều kiện cho các startup thuộc nhiều lĩnh vực phát triển ứng dụng riêng?
 Xem đáp án
Xem đáp án
Giải thích
Xác định “người sáng lập Tesse” ở đây là Nguyễn Phạm Tuấn Anh, từ đó, đọc lướt để tìm kiếm những đoạn có đề cập đến nhân vật hoặc xuất hiện ý kiến, lời nói của nhân vật: đoạn [3], [8]. Nội dung liên quan đến câu hỏi nằm ở đoạn [8]: “Theo Tuấn Anh, việc OpenAI cho phép các đơn vị khác phát triển ứng dụng dựa trên ChatGPT sẽ giúp các startup phát triển các sản phẩm phục vụ cho lĩnh vực mình”
chọn C.
Câu 18:
Việc hạn chế số lượng câu hỏi trong một ngày đối trên ứng dụng VoiceGPT là do vấn đề bản quyền. Đúng hay sai?
 Xem đáp án
Xem đáp án
Đáp án
B. Sai
Giải thích
Việc hạn chế số lượng câu hỏi từ người dùng trong một ngày được đề cập ở đoạn [9]: “Hiện mỗi ngày một tài khoản có thể hỏi 40 câu, một giờ được hỏi tối đa 20 câu. Lý giải điều này, nhóm cho biết, hiện việc sử dụng VoiceGPT nhóm phải trả phí cho nhà cung cấp dựa trên số lượng từ ngữ, nên cần đưa ra giới hạn để người dùng hỏi những câu thật sự cần thiết.”. Như vậy, vấn đề trả phí cho nhà cung cấp dẫn đến sự giới hạn về số lượng câu hỏi, không phải vấn đề bản quyền.
Câu 19:
 Xem đáp án
Xem đáp án
Giải thích
Đoạn [10] cung cấp thông tin về trải nghiệm của người dùng thông qua đánh giá của anh Hoàng Minh, gồm cả điểm mạnh: dễ đăng ký, giao diện dễ sử dụng, thích hợp đối với những người không tiện gõ văn bản (con trai anh 5 tuổi, chưa biết mặt chữ nhưng vẫn có thể sử dụng) và điểm yếu: độ trễ khi phản hồi câu hỏi, thao tác bị treo, chọn A.
Câu 20:
Theo nhận xét của ông Lê Nhật Quang - Phó giám đốc khu công nghệ phần mềm, Đại học Quốc gia TP HCM, ứng dụng VoiceGPT là:
 Xem đáp án
Xem đáp án
Giải thích
Căn cứ vào từ khóa “Lê Nhật Quang” để xác định thông tin cần tìm kiếm trong đonạ [11]. Ở đoạn văn này, tác giả đã trích lại lời nhận xét về ứng dụng VoiceGPT: thúc đẩy việc phát triển ứng dụng, tốc độ phản hồi chậm và nội dung bị trùng lặp.
Kết hợp với phương pháp loại trừ, tìm được đáp án đúng là B (sản phẩm này có ý nghĩa về sự khởi đầu, tạo động lực cho các doanh nghiệp tiếp tục phát triển).
Chọn BCâu 21:
Cá mòi có rất nhiều ở vịnh Chiriqui và sự hiện diện của chúng ảnh hưởng đến toàn bộ hệ sinh thái của vịnh. Chim bói cá chủ yếu ăn cá mòi. Sự suy giảm số lượng của chím bói cá làm các nhà khoa học lo ngại vấn đề môi trường của vịnh Chiriqui. Lo ngại này có phù hợp quan điểm của nhà nghiên cứu 1 không?
 Xem đáp án
Xem đáp án
Giải thích
Theo đoạn thông tin: “...Quần thể chim biển và tỉ lệ sinh sản của chúng được điều chỉnh bởi sự đa dạng phong phú của con mồi, do đó sẽ phản ánh những thay đổi do môi trường gây ra ảnh hưởng tới số lượng con mồi.”
Chọn D
Câu 22:
Một nghiên cứu cho thấy rằng trong vòng hai tháng sau khi xảy ra sự cố tràn dầu ở vịnh, số lượng cá nhỏ tìm thấy trong nước đã giảm đáng kể và số lượng chim biển trong khu vực cũng giảm mạnh. Nhà nghiên cứu nào rất có thể sẽ sử dụng nghiên cứu này để hỗ trợ cho quan điểm của mình?
 Xem đáp án
Xem đáp án
Giải thích
Nhà nghiên cứu 1 cho rằng sự thay đổi của môi trường ảnh hưởng đến số lượng con mồi (cá) sẽ làm ảnh hưởng đến số lượng của loài săn mồi (chim biển). Như vậy nghiên cứu về sự cố tràn dầu này sẽ ủng hộ quan điểm của nhà nghiên cứu 1.
Chọn A
Câu 23:
Biểu đồ nào sau đây phù hợp với quan điểm của nhà nghiên cứu 1 về mối quan hệ giữa số lượng con mồi với quần thể chim biển?
 Xem đáp án
Xem đáp án
Giải thích
Nhà nghiên cứu 1 cho rằng số lượng con mồi và chim biển phụ thuộc vào nhau, số lượng con mồi tăng, thì số lượng chim biển tăng và ngược lại, số lượng con mồi giảm thì số lượng chim biển giảm.
Chọn A
Câu 24:
Phát biểu sau đây đúng hay sai?
Nhà nghiên cứu 2 cho rằng việc sử dụng chim biển làm sinh vật chỉ thị là tốn kém nhiều về mặt chi phí.
 Xem đáp án
Xem đáp án
Đáp án
B. Sai
Giải thích
Nhà nghiên cứu 2 không đề cập đến chi phí khi sử dụng chim biển làm sinh vật chỉ thị. Còn nhà nghiên cứu 1 cho rằng việc sử dụng chim biển làm sinh vật chỉ thị là phù hợp về nhu cầu chi phí.
Câu 25:
Điền số thích hợp vào chỗ trống
Cây đước là một loài thực vật ngập mặn, phát triển tốt trong môi trường rừng ngập mặn nên được chọn làm sinh vật chỉ thị cho môi trường ngập mặn. Ngược lại, cây cỏ hôi có độ rộng nồng độ muối lớn thì không có khả năng làm chỉ thị cho môi trường ngập mặn. Ví dụ này tương ứng với chỉ tiêu số (1) _______ trong việc chọn lựa sinh vật chỉ thị.
 Xem đáp án
Xem đáp án
Đáp án
Điền số thích hợp vào chỗ trống
Cây đước là một loài thực vật ngập mặn, phát triển tốt trong môi trường rừng ngập mặn nên được chọn làm sinh vật chỉ thị cho môi trường ngập mặn. Ngược lại, cây cỏ hôi có độ rộng nồng độ muối lớn thì không có khả năng làm chỉ thị cho môi trường ngập mặn. Ví dụ này tương ứng với chỉ tiêu số (1) __ 3 __ trong việc chọn lựa sinh vật chỉ thị.
Giải thích
Chỉ tiêu số 3 là: “Các loài có độ thích ứng hẹp thường là vật chỉ thị tốt hơn loài thích ứng rộng.” Độ thích ứng ở đây là khả năng phát triển trong điều kiện nồng độ muối cao.
Câu 26:
Quan điểm của nhà nghiên cứu nào cho rằng việc xử lý thông tin thu thập từ loài chim biển không thể chắc chắn hoàn toàn chính xác và hợp lệ?
 Xem đáp án
Xem đáp án
Giải thích
Theo đoạn thông tin: “...Nhưng cũng không thể phân biệt chính xác nguyên nhân gây nên những sự thay đổi đó, là từ môi trường hay từ các tác động vật lí, hóa học trong quá trình theo dõi chúng của con người.”
Chọn C
Câu 27:
Phát biểu sau đúng hay sai?
Phương trình sản xuất BD được mô tả như sau:
Dầu đậu nành + FAMES methanol
 Xem đáp án
Xem đáp án
Đáp án
B. Sai.
Giải thích
Theo đoạn văn, dầu đậu nành và methanol phản ứng với sự có mặt của chất xúc tác để tạo thành FAMES. Dầu đậu nành và methanol là chất phản ứng còn FAMES là sản phẩm.
Câu 28:
Các phát biểu sau đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Phương trình hóa học cho phản ứng giữa dầu đậu nành và methanol là: 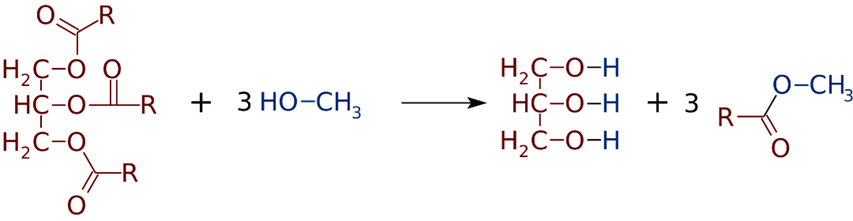 |
||
|
Dựa trên kết quả của Nghiên cứu 1, mẫu chỉ chứa FAMES sẽ hấp thụ ánh sáng ở số sóng 900 cm–1 mạnh hơn ánh sáng ở số sóng 1250 cm–1. |
||
|
Dựa trên kết quả của Nghiên cứu 2, nếu thực hiện Nghiên cứu 3 ở số sóng 1746 cm–1 thì trong các mẫu ở Nghiên cứu 3, mẫu nhiên liệu X có độ hấp thụ A lớn nhất. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Phương trình hóa học cho phản ứng giữa dầu đậu nành và methanol là: 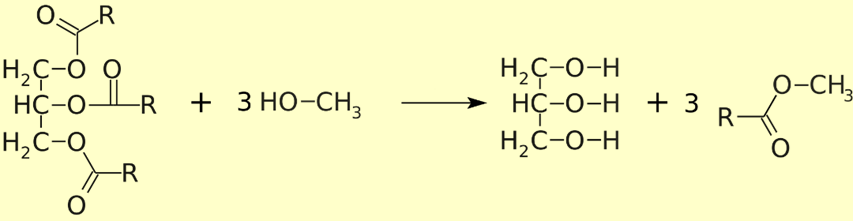 |
X | |
|
Dựa trên kết quả của Nghiên cứu 1, mẫu chỉ chứa FAMES sẽ hấp thụ ánh sáng ở số sóng 900 cm–1 mạnh hơn ánh sáng ở số sóng 1250 cm–1. |
X | |
|
Dựa trên kết quả của Nghiên cứu 2, nếu thực hiện Nghiên cứu 3 ở số sóng 1746 cm–1 thì trong các mẫu ở Nghiên cứu 3, mẫu nhiên liệu X có độ hấp thụ A lớn nhất. |
X |
Giải thích
1. Đúng, vì: Phản ứng giữa dầu đậu nành và methanol là phản ứng ester hóa giữa chất béo và CH3OH.
2. Sai, vì: Theo đoạn văn, BD chứa FAMES và PD thì không. Hình 1 cho thấy BD không hấp thụ mạnh ánh sáng ở số sóng 900 cm–1 nhưng hấp thụ mạnh ở 1250 cm–1. Mẫu chỉ chứa FAMES sẽ có khả năng hấp thụ tương tự mẫu BD. Do đó, mẫu sẽ hấp thụ ánh sáng ở số sóng 1250 cm–1 mạnh hơn ở số sóng 900 cm–1.
3. Đúng, vì: Theo Hình 2, khi tỉ lệ phần trăm BD theo thể tích giảm, độ hấp thụ A ở số sóng 1746 cm–1 cũng giảm. Mẫu nhiên liệu trong Nghiên cứu 3 với A lớn nhất sẽ là mẫu có tỉ lệ phần trăm BD theo thể tích cao nhất. Do đó, mẫu X trong Nghiên cứu 3 có độ hấp thụ A lớn nhất ở số sóng 1746 cm–1.
Câu 29:
Theo Nghiên cứu 2, trong số các mẫu được thử nghiệm, khi phần trăm theo thể tích BD tăng lên thì độ hấp thụ A ở số sóng 1746 cm–1
 Xem đáp án
Xem đáp án
Giải thích
Theo Hình 2, khi phần trăm theo thể tích BD tăng lên thì độ hấp thụ A ở mức 1746 cm–1 cũng tăng lên.
Chọn A
Câu 30:
Xét mẫu chứa hỗn hợp BD và PD với tỉ lệ phần trăm theo thể tích của BD là 60%, độ hấp thụ A ở số sóng 1746 cm–1 có giá trị
 Xem đáp án
Xem đáp án
Giải thích
Theo Hình 2, mẫu chứa hỗn hợp BD và PD với tỉ lệ phần trăm theo thể tích của BD là 60% sẽ có độ hấp thụ A ở số sóng 1746 cm–1 xấp xỉ 0,6.
Chọn C
Câu 31:
Giả sử rằng trong Nghiên cứu 1, các sinh viên đã đo độ hấp thụ ở các số sóng từ 600 cm–1 đến 1600 cm–1 (thay vì qua 1800 cm–1). Dựa vào Hình 1, có thể dự đoán sinh viên đo được độ hấp thụ trong Nghiên cứu 2 ở số sóng
 Xem đáp án
Xem đáp án
Giải thích
Để có được thông tin hữu ích cho độ hấp thụ của Nghiên cứu 2, các sinh viên phải đo độ hấp thụ ở số sóng mà tại đó BD hoặc PD hấp thụ mạnh (không phải BD và PD đều hấp thụ mạnh).
Theo Hình 1, ở số sóng 1172 cm–1, chỉ có BD hấp thụ mạnh và ở số sóng 1464 cm–1, cả BD và PD đều hấp thụ. Do đó, trong Nghiên cứu 2, các sinh viên có thể đo được độ hấp thụ ở số sóng 1172 cm–1, vì BD hấp thụ mạnh ở số sóng này.
Chọn B
Câu 32:
Điền từ/cụm từ thích hợp vào chỗ trống.
Dựa trên kết quả của Nghiên cứu 2, mẫu nhiên liệu (1) _______ trong Nghiên cứu 3 có độ hấp thụ A nhỏ nhất ở số sóng 1746 cm–1.
 Xem đáp án
Xem đáp án
Đáp án
Điền từ/cụm từ thích hợp vào chỗ trống.
Dựa trên kết quả của Nghiên cứu 2, mẫu nhiên liệu (1) __ W __ trong Nghiên cứu 3 có độ hấp thụ A nhỏ nhất ở số sóng 1746 cm–1.
Giải thích
Theo Hình 2, khi tỉ lệ phần trăm BD theo thể tích giảm, độ hấp thụ A ở số sóng 1746 cm–1 cũng giảm. Mẫu nhiên liệu trong Nghiên cứu 3 với A nhỏ nhất sẽ là mẫu có tỉ lệ phần trăm BD theo thể tích thấp nhất. Do đó, mẫu W trong Nghiên cứu 3 có độ hấp thụ A nhỏ nhất ở số sóng 1746 cm–1.
Câu 33:
Kéo thả các ô vuông vào đúng vị trí
480, 600, 400, 470, 500
Xem xét tỉ lệ phần trăm BD theo thể tích được liệt kê trong Bảng 1. Thể tích BD trong 10 lít mỗi mẫu nhiên liệu Y, X, W và Z lần lượt là ______ ml, ______ ml, ______ ml và ______ ml.
 Xem đáp án
Xem đáp án
Đáp án
Xem xét tỉ lệ phần trăm BD theo thể tích được liệt kê trong Bảng 1. Thể tích BD trong 10 lít mỗi mẫu nhiên liệu Y, X, W và Z lần lượt là 480 ml, 600 ml, 400 ml và 470 ml.
Giải thích
Theo Bảng 1, tỉ lệ BD theo thể tích trong mẫu W là 4,0%. Do đó, 10 lít mẫu X sẽ chứa
4.10:100 = 0,4 lít = 400 ml BD.
Tương tự với các mẫu X, Y và Z, thể tích BD trong 10 lít mẫu X, Y và Z lần lượt là: 600 ml, 480 ml và 470 ml.
Câu 34:
Phát biểu sau đúng hay sai?
Dựa trên thông tin trong Bảng 1 và Bảng 2, có thể kết luận rằng Mẫu nước thải 1 chứa 2 ion kim loại là Co2+ và Cd2+.
 Xem đáp án
Xem đáp án
Đáp án
B. Sai.
Giải thích
Sai, vì: Mẫu 1 có 2 đốm màu: đốm màu xanh da trời có Rf = 0,60 và đốm màu vàng có Rf = 0,78.
Theo Bảng 1, đốm màu xanh da trời (Rf = 0,60) ứng với ion Cu2+ và đốm màu vàng (Rf = 0,78) ứng với ion Cd2+.
Vậy, Mẫu 1 chứa 2 ion kim loại là Cu2+ và Cd2+.
Câu 35:
Các phát biểu sau đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Sắc ký giấy là một loại sắc ký phẳng, trong đó kỹ thuật sắc ký được thực hiện trên giấy chuyên dụng và hoạt động thông qua hiện tượng mao dẫn. |
||
|
Trong quá trình thực hiện sắc ký giấy, ta có thể sử dụng bút mực để kẻ đường thẳng trên giấy sắc ký. |
||
|
Theo thông tin có trong Bảng 1, hai ion kim loại có đốm màu giống nhau là Co2+ và Cd2+. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Sắc ký giấy là một loại sắc ký phẳng, trong đó kỹ thuật sắc ký được thực hiện trên giấy chuyên dụng và hoạt động thông qua hiện tượng mao dẫn. |
X | |
|
Trong quá trình thực hiện sắc ký giấy, ta có thể sử dụng bút mực để kẻ đường thẳng trên giấy sắc ký. |
X | |
|
Theo thông tin có trong Bảng 1, hai ion kim loại có đốm màu giống nhau là Co2+ và Cd2+. |
X |
Giải thích
1. Đúng
2. Sai, vì: Bút mực sẽ hòa tan trong dung môi và di chuyển lên giấy sắc ký, làm cho kết quả bị sai lệch.
3. Sai, vì: Theo thông tin có trong Bảng 1, hai ion kim loại có đốm màu giống nhau (màu nâu đen) là Co2+ và Hg2+.
Câu 36:
Điền số thích hợp vào chỗ trống.
Dựa trên thông tin trong Bảng 1 và Bảng 2, có thể kết luận rằng Mẫu 2 chứa (1) ____ ion kim loại.
 Xem đáp án
Xem đáp án
Đáp án
Điền số thích hợp vào chỗ trống.
Dựa trên thông tin trong Bảng 1 và Bảng 2, có thể kết luận rằng Mẫu 2 chứa (1) __ 2 _ ion kim loại.
Giải thích
Mẫu 2 có 2 đốm màu: đốm nâu đen có Rf = 0,35 và đốm nâu đen có Rf = 0,95.
Theo Bảng 1, đốm màu nâu đen (Rf = 0,35) ứng với ion Co2+ và đốm màu nâu đen (Rf = 0,95) ứng với ion Hg2+.
Vậy, Mẫu 2 chứa 2 ion kim loại là Co2+ và Hg2+.
Câu 37:
Kéo thả các ô vuông vào đúng vị trí
Dựa trên thông tin trong Bảng 1, các ion kim loại được sắp xếp theo thứ tự tốc độ di chuyển chậm dần là: _______, _______, _______, _______, _______.
 Xem đáp án
Xem đáp án
Đáp án
Dựa trên thông tin trong Bảng 1, các ion kim loại được sắp xếp theo thứ tự tốc độ di chuyển chậm dần là: Hg2+, Cd2+, Cu2+, Co2+, Ni2+.
Giải thích
Khi giá trị Rf tăng lên, tốc độ ion kim loại di chuyển lên trên tờ giấy cũng tăng lên.
Theo Bảng 1, thứ tự giảm dần giá trị Rf của các ion là: Hg2+, Cd2+, Cu2+, Co2+, Ni2+.
Câu 38:
Dựa trên thông tin trong Bảng 1 và Bảng 2, có thể kết luận rằng Mẫu 3 chứa các ion (sắp xếp theo thứ tự tốc độ di chuyển nhanh dần)
 Xem đáp án
Xem đáp án
Giải thích
Theo Bảng 2, Mẫu 3 có 3 đốm màu: đốm hồng có Rf = 0,08; đốm vàng có Rf = 0,78 và đốm nâu đen có Rf = 0,95. Ba đốm màu này tương ứng với 3 đốm màu trong Bảng 1: đốm hồng có Rf = 0,08 ứng với Ni2+, đốm vàng có Rf = 0,78 ứng với Cd2+ và đốm nâu đen có Rf = 0,95 ứng với Hg2+. Vậy Mẫu 3 chứa Ni2+, Cd2+ , và Hg2+.
Ngoài ra, nếu Mẫu 3 chứa Cu2+ thì mẫu đó phải tạo ra đốm màu xanh có Rf = 0,60. Nếu Mẫu 3 chứa Co2+ thì mẫu đó phải tạo ra đốm màu nâu đen với Rf = 0,35.
Chọn D
Câu 39:
Dựa trên thông tin trong Bảng 1, để xác định chính xác ion kim loại bằng sắc ký giấy, người ta cần biết
 Xem đáp án
Xem đáp án
Giải thích
Đốm màu có thể được sử dụng để xác định ion kim loại. Tuy nhiên, một số ion kim loại, chẳng hạn như coban và thủy ngân, có cùng đốm màu (nâu đen). Do đó, để xác định chính xác ion kim loại, người ta cần biết thêm giá trị Rf của đốm màu đó.
Chọn C
Câu 40:
Dựa trên thông tin trong Bảng 2, hình nào sau đây minh họa rõ nhất giấy lọc sau khi Mẫu 1 được phân tích?
 Xem đáp án
Xem đáp án
Giải thích
Theo Bảng 2, Mẫu 1 có đốm màu xanh và đốm màu vàng. Dựa trên công thức, đốm màu xanh đã đi được quãng đường = 0,6b và đốm màu vàng đã đi được quãng đường là 0,78b. Hình ở phương án A cho thấy vị trí chính xác của cả hai điểm.
Phương án B sai vì hình vẽ chỉ ra rằng đốm màu xanh đã di chuyển một quãng đường là 0,1b.
Phương án C sai vì hình vẽ chỉ ra rằng đốm màu xanh đã di chuyển một quãng đường là 0,48b. Tương tự, hình vẽ chỉ ra rằng đốm màu vàng đã di chuyển một quãng đường bằng 0,5b.
Phương án D sai vì hình vẽ chỉ ra rằng đốm màu xanh đã di chuyển một quãng đường là 0,1b. Tương tự, hình vẽ chỉ ra rằng đốm màu vàng đã di chuyển một quãng đường là 0,2b.
Chọn A
Câu 41:
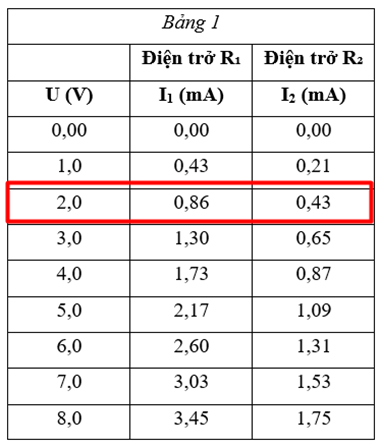
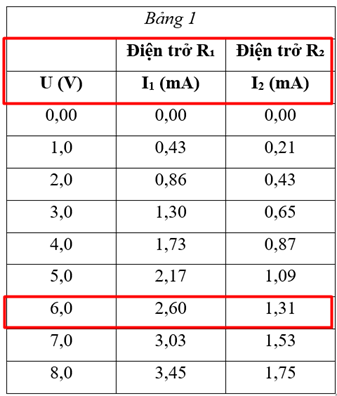
Nếu cùng đặt một hiệu điện thế vào hai đầu vật dẫn R1 và R2 thì cường độ chạy qua hai vật dẫn có giá trị như nhau, đúng hay sai?
 Xem đáp án
Xem đáp án
Đáp án
B. Sai
Giải thích
Nhìn vào bảng 1, dễ thấy ứng với mỗi giá trị U thì I1 và I2 có giá trị khác nhau.
Câu 42:
hiệu điện thế giữa 2 đầu, cường độ dòng điện đi qua, nối tiếp, điện trở, song song
Trong mạch điện ở hình 1, ampe kế A được mắc _______ với vật dẫn để đo _______ vật dẫn, vôn kế V được mắc _______ với vật dẫn để đo _______ vật dẫn.
 Xem đáp án
Xem đáp án
Đáp án
Kéo các cụm từ sau đây vào vị trí thích hợp.
Trong mạch điện ở hình 1, ampe kế A được mắc nối tiếp với vật dẫn để đo cường độ dòng điện chạy qua vật dẫn, vôn kế V được mắc song song với vật dẫn để đo hiệu điện thế giữa hai đầu vật dẫn.
Giải thích
Trong mạch điện ở hình 1, ampe kế A được mắc nối tiếp với vật dẫn để đo cường độ dòng điện chạy qua vật dẫn, vôn kế V được mắc song song với vật dẫn để đo hiệu điện thế giữa hai đầu vật dẫn.
Câu 43:
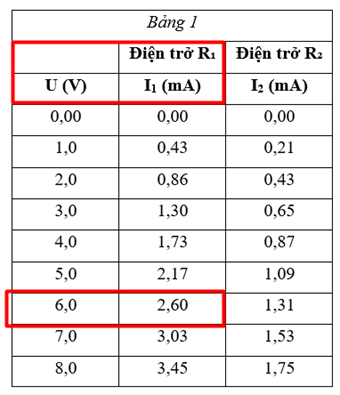
Khi hiệu điện thế của nguồn là 6 V, cường độ dòng điện chạy qua vật dẫn R1 có giá trị là (1) ______.
 Xem đáp án
Xem đáp án
Đáp án
Khi hiệu điện thế của nguồn là 6V, cường độ dòng điện chạy qua vật dẫn R1 có giá trị là (1) 2,60 .
Giải thích
Xem bảng 1
Câu 44:
Đồ thị nào sau đây thể hiện đúng đường đặc trưng vôn – ampe của hai vật dẫn R1 và R2
 Xem đáp án
Xem đáp án
Giải thích
Dựa vào dữ liệu Bảng 1:
+ Khi U tăng thì I tăng → Loại Hình C, Hình D.
+ Xét một cặp số liệu tương ứng với hiệu điện thế của nguồn - cường độ dòng điện chạy qua vật dẫn, ta có:
Đối với vật dẫn R1: (6,0 V; 2,6 mA)
Đối với vật dẫn R2: (6,0 V; 1,31 mA). Chọn B
Câu 45:
Điều chỉnh hiệu điện thế của nguồn điện đến giá trị 10 V thì cường độ dòng điện chạy qua vật dẫn R2 có giá trị xấp xỉ bằng
 Xem đáp án
Xem đáp án
Giải thích: Chọn A
|
U (V) |
I2 (mA) |
|
8,0 |
1,75 |
|
\[{R_2} = \frac{8}{{1,75}} \approx 4,57\Omega \] |
|
|
10,0 |
\({I_2} = \frac{U}{{{R_2}}} = \frac{{10}}{{4,57}} \approx 2,19\;{\rm{A}}\). |
Câu 46:
Ghép nối tiếp hai vật dẫn R1 và R2 rồi thay vào vị trí của vật dẫn R1 trong Hình 1 sau đó lặp lại các bước tiến hành như trong thí nghiệm. Khi hiệu điện thế của nguồn điện được điều chỉnh đến giá trị 8 V thì số chỉ của ampe kế A xấp xỉ là
 Xem đáp án
Xem đáp án
Giải thích: Chọn D
|
U (V) |
I1 (mA) |
I2 (mA) |
|
8,0 |
3,45 |
1,75 |
|
\({R_1} = \frac{8}{{3,45}} \approx 2,32\Omega \) |
\({R_2} = \frac{8}{{1,75}} \approx 4,57\Omega \) |
Khi R₁ nối tiếp R2, điện trở tương đương R của 2 vật dẫn là: \(R = {R_1} + {R_2} \approx 2,32 + 4,57 \approx 6,89\Omega \).
Câu 47:
 Xem đáp án
Xem đáp án
Giải thích
Theo đoạn thông tin: “Virus nhận ra các tế bào chủ của nó theo nguyên tắc “chìa và khóa” giữa các protein bề mặt của virus với các phân tử thụ thể đặc hiệu trên bề mặt ngoài của tế bào chủ”, tức là không phải virus nào cũng xâm nhập được vào hết các loại tế bào, mà cần có sự liên kết đặc hiệu với tùy từng loại thụ thể trên bề mặt tế bào.
Chọn B
Câu 48:
 Xem đáp án
Xem đáp án
Giải thích
Theo bài: “Chúng là các dạng sống ký sinh nội bào bắt buộc”, sử dụng hệ enzyme của vật chủ để nhân lên, nên dù ở trong hay ngoài vật chủ thì virus đều không có sự sinh trưởng.
Chọn D
Câu 49:
 Xem đáp án
Xem đáp án
Giải thích
Virus cần tự mã hóa một số loại enzyme nhất định phục vụ cho nhu cầu nhân lên của chúng, do tế bào chủ không cần thiết phải có những enzyme đó trong quá trình hoạt động của mình.
Chọn A
Câu 50:
Phát biểu sau đây đúng hay sai?
Thụ thể CD4 là thụ thể của virus HIV. Nếu đưa hồng cầu có thụ thể CD4 vào bệnh nhân HIV thì bệnh nhân sẽ thiếu máu nghiêm trọng vì virus sẽ xâm nhập và phá hủy tế bào.
 Xem đáp án
Xem đáp án
Đáp án
B. Sai
Giải thích
Thụ thể CD4 đặc hiệu với protein bề mặt của virus. Nếu đưa hồng cầu có thụ thể CD4 vào bệnh nhân HIV thì virus sẽ xâm nhập vào nhưng không nhân lên được do hồng cầu không có nhân, không có bộ máy sao chép nucleic acid.
Câu 51:
Các phát biểu sau đây đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Virus bám được vào tế bào chủ là nhờ các thụ thể thích hợp có sẵn trên bề mặt tế bào chủ. |
¡ |
¡ |
|
Kết quả của quá trình nhân lên là từ một virus ban đầu tạo ra vô số virus mới có độc tính tăng gấp nhiều lần. |
¡ |
¡ |
|
Virus sử dụng nguyên liệu của tế bào chủ trong quá trình nhân lên của mình. |
¡ |
¡ |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Virus bám được vào tế bào chủ là nhờ các thụ thể thích hợp có sẵn trên bề mặt tế bào chủ. |
X | |
|
Kết quả của quá trình nhân lên là từ một virus ban đầu tạo ra vô số virus mới có độc tính tăng gấp nhiều lần. |
X | |
|
Virus sử dụng nguyên liệu của tế bào chủ trong quá trình nhân lên của mình. |
X |
Giải thích
(1), (3) đúng.
(2) sai vì kết quả của quá trình nhân lên là từ một virus ban đầu tạo ra vô số virus mới giống hệt nhau và giống virus ban đầu.
Câu 52:
 Xem đáp án
Xem đáp án
Giải thích
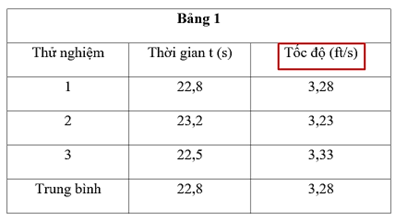
Dựa vào các bảng dữ liệu, ta có đơn vị của tốc độ được sử dụng trong các thử nghiệm là feet/s hay ft/s. Chọn C
Câu 53:
Trong Nghiên cứu 1, tốc độ trung bình của cả ba thử nghiệm lớn hơn tốc độ trung bình đo được trong Thử nghiệm 2, đúng hay sai?
 Xem đáp án
Xem đáp án
Đáp án
A. Đúng
Giải thích
Dựa trên dữ liệu trong Bảng 2, ta có: tốc độ trung bình là: 1,32 ft/s
Mà tốc độ trung bình trong các thử nghiệm của Nghiên cứu 1 là:
|
Bảng 1 |
||
|
Thử nghiệm |
Thời gian t (s) |
Tốc độ (ft/s) |
|
1 |
22,8 |
3,28 |
|
2 |
23,2 |
3,23 |
|
3 |
22,5 |
3,33 |
|
Trung bình |
22,8 |
3,28 |
→ Tốc độ trung bình của cả ba thử nghiệm trong Nghiên cứu 1 lớn hơn tốc độ trung bình đo được trong Thử nghiệm 2.
Câu 54:
 Xem đáp án
Xem đáp án
Giải thích
Dựa trên dữ liệu trong cả ba bảng, ta có:
+ Trong Bảng 1, tốc độ trung bình là: 3,28 ft/s
+ Trong Bảng 2, tốc độ trung bình là: 1,32 ft/s
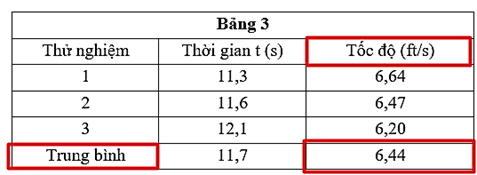
+ Trong Bảng 3, tốc độ trung bình là: 6,44 ft/s
→ Tốc độ trung bình nhanh nhất 6,44 ft/s được ghi lại trong Bảng 3 và tương ứng trong Nghiên cứu 3, loại bánh xe được sử dụng là bánh xe bằng cao su cứng, có các đinh tán.
Chọn A
Câu 55:
Kéo các cụm từ sau vào vị trí thích hợp.
giảm tốc độ, tăng tốc độ, lực ma sát, lục hướng tâm
Trong các thử nghiệm, để _______ chuyển động của xe, các học sinh nên sử dụng loại bánh xe có đinh tán hoặc có rãnh sâu nhằm tạo ra _______ lớn.
 Xem đáp án
Xem đáp án
Đáp án
Kéo các cụm từ sau vào vị trí thích hợp.
Trong các thử nghiệm, để tăng tốc độ chuyển động của xe, các học sinh nên sử dụng loại bánh xe có đinh tán hoặc có rãnh sâu nhằm tạo ra lực ma sát lớn.
Giải thích
(1) – tăng tốc độ
(2) - lực ma sát
Các vỏ lốp xe cao su cần có rãnh và gai để tăng độ bám dính lên bề mặt di chuyển, tạo ra ma sát vừa đủ để các bánh xe có thể chuyển động liên tục, thay vì chỉ quay tròn và trượt theo quán tính. Như vậy, nếu không có các rãnh, gai trên vỏ lốp xe thì sẽ không tạo ra đủ lực ma sát trên bánh xe giúp xe tiến về phía trước.
Câu 56:
Điền số thích hợp vào chỗ trống.
Tốc độ trung bình của ô tô có bánh xe bằng cao su cứng và có các đinh tán trong các thử nghiệm là (1) _______ ft/s.
 Xem đáp án
Xem đáp án
Đáp án
Điền số thích hợp vào chỗ trống.
Tốc độ trung bình của ô tô có bánh xe bằng cao su cứng và có các đinh tán trong các thử nghiệm là (1) __ 6,44 __ ft/s.
Giải thích
Trong Nghiên cứu 3, các thử nghiệm sử dụng ô tô có bánh xe bằng cao su cứng và có các đinh tán
+ Dựa vào Bảng 3, ta có tốc độ trung bình trong các thử nghiệm là 6,44 ft/s.
Câu 57:
Gọi tốc độ trung bình của ô tô có bánh xe bằng cao su cứng, có các đinh tán là v1, tốc độ trung bình của ô tô có bánh xe cao su mềm, nhẵn và không có rãnh là v2 và tốc độ trung bình của ô tô có bánh xe cao su cứng, có rãnh sâu là v3. Hệ thức nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Giải thích
Dựa trên dữ liệu trong cả ba bảng, ta có:
+ Trong Bảng 1, tốc độ trung bình của ô tô có bánh xe bằng cao su cứng, có các đinh tán là: \[{v_1} = 3,28\,\,ft/s\]
+ Trong Bảng 2, tốc độ trung bình của ô tô có bánh xe cao su mềm, nhẵn và không có rãnh là: \[{v_2} = 1,32\,\,ft/s\]
+ Trong Bảng 3, tốc độ trung bình của ô tô có bánh xe cao su cứng, có rãnh sâu là: \[{v_3} = 6,44\,\,ft/s\]
Từ các giá trị trên, ta có: \({v_1} \approx \frac{1}{2}{v_3}\).
Chọn DCâu 58:
 Xem đáp án
Xem đáp án
Giải thích
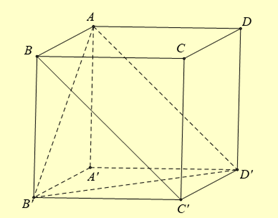
Dựng hình hộp \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Ta có \(B{C^\prime }//A{D^\prime }\) và \({A^\prime }{B^\prime }{C^\prime }{D^\prime }\) là hình thoi.
Gọi \({A^\prime }{B^\prime } = x \Rightarrow {B^\prime }{D^\prime } = x\sqrt 3 \).
Vì \(B{C^\prime }//A{D^\prime }\) và \(A{B^\prime } \bot B{C^\prime } \Rightarrow A{B^\prime } \bot A{D^\prime }\) và \(A{B^{\prime 2}} = A{A^{\prime 2}} + {A^\prime }{B^{\prime 2}} = {x^2} + 3{a^2}\).
Vì \(\Delta A{A^\prime }{D^\prime } = \Delta A{A^\prime }{B^\prime } \Rightarrow A{B^\prime } = A{D^\prime } = {x^2} + 3{a^2}\).
Ta có: \({B^\prime }{D^{\prime 2}} = A{B^{\prime 2}} + A{D^{\prime 2}} = 2{x^2} + 6{a^2} = 3{x^2} \Leftrightarrow {x^2} = 6{a^2} \Leftrightarrow x = a\sqrt 6 \).
Khi đó,
Chọn D
Câu 59:
Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) và đồ thị như hình vẽ bên. Có bao nhiêu giá trị thực của \(m\) để hàm số \(g(x) = f\left( {{2^x} - 1} \right) + \dot f(m)\) có \({\max _{[0;1]}}|g(x)| = 3\)?
![Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) và đồ thị như hình vẽ bên. Có bao nhiêu giá trị thực của \(m\) để hàm số \(g(x) = f\left( {{2^x} - 1} \right) + \dot f(m)\) có \({\max _{[0;1]}}|g(x)| = 3\)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid1-1729655896.png)
 Xem đáp án
Xem đáp án
Giải thích
Đặt \(f(m) = a\), khi đó ta có
\({\max _{[0;1]}}|g(x)| = \max \left\{ {\left| {{{\max }_{[0;1]}}g(x)} \right|;\left| {{{\min }_{[0;1]}}g(x)} \right|} \right\}\)
Xét hàm số \(g(x) = f\left( {{2^x} - 1} \right) + a\), đặt \(t = {2^x} - 1 \Rightarrow t \in [0;1]\,\,\forall x \in [0;1]\)
Dựa vào đồ thị có: \(\left\{ {\begin{array}{*{20}{l}}{{{\max }_{[0;1]}}f(t) = 3}\\{{{\min }_{[0;1]}}f(t) = - 2}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{{\max }_{[0;1]}}g(x) = 3 + a}\\{{{\min }_{[0;1]}}g(x) = - 2 + a}\end{array}} \right.} \right.\)
TH1. \(\left\{ {\begin{array}{*{20}{l}}{|3 + a| = 3}\\{|3 + a| > | - 2 + a|}\end{array} \Rightarrow a = 0 \Rightarrow f(m) = 0} \right.\) (4 nghiệm)
TH2. \(\left\{ {\begin{array}{*{20}{l}}{| - 2 + a| = 3}\\{| - 2 + a| > |3 + a|}\end{array} \Rightarrow a = - 1 \Rightarrow f(m) = - 1} \right.\) (4 nghiệm)
Vậy có tất cả 8 giá trị \(m\) thỏa mãn yêu cầu đề bài.
Chọn B
Câu 60:
 Xem đáp án
Xem đáp án
Giải thích
Ta có: \({2^x} - \left( {2 - {m^2}} \right){.2^{ - x}} > m\)
\( \Leftrightarrow {2^x} - \left( {2 - {m^2}} \right).\frac{1}{{{2^x}}} - m > 0{\rm{ }}\)
\( \Leftrightarrow {2^{2x}} - m{.2^x} - \left( {2 - {m^2}} \right) > 0\)
Đặt \(t = {2^x}(t > 0)\). Bất phương trình trở thành: \({t^2} - mt - \left( {2 - {m^2}} \right) > 0\,\,(*)\).
Bất phương trình đã cho nghiệm đúng với mọi \(x \in \mathbb{R}\)
\( \Leftrightarrow \) Bất phương trình (*) nghiệm đúng với mọi \(t > 0\).
TH1. Phương trình \({t^2} - mt - \left( {2 - {m^2}} \right) = 0\) vô nghiệm
\( \Leftrightarrow \Delta < 0 \Leftrightarrow {( - m)^2} + 4\left( {2 - {m^2}} \right) < 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m > \frac{{2\sqrt 6 }}{3}}\\{m < - \frac{{2\sqrt 6 }}{3}}\end{array}} \right.\)
TH2. Phương trình \({t^2} - mt - \left( {2 - {m^2}} \right) = 0\) có hai không dương
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\Delta \ge 0}\\{S < 0}\\{P \ge 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{{( - m)}^2} + 4\left( {2 - {m^2}} \right) \ge 0}\\{m < 0}\\{ - \left( {2 - {m^2}} \right) \ge 0}\end{array} \Leftrightarrow - \frac{{2\sqrt 6 }}{3} \le m \le - \sqrt 2 } \right.} \right.\)
Vậy \(\left[ {\begin{array}{*{20}{l}}{m > \frac{{2\sqrt 6 }}{3}}\\{m \le - \sqrt 2 }\end{array}} \right.\).
Chọn D
Câu 61:
Độ dốc của mái chính là độ nghiêng của mái nhà. Trong xây dựng, người ta cần tính toán độ dốc phù hợp với kết cấu của mỗi công trình nhằm mục đích thoát nước trên mái, tránh việc ứ đọng nước trên mái gây thấm dột. Biết độ dốc i của mái tôn là tỉ số giữa chiều cao H và chiều dài L và được tính bằng công thức: \(i = \frac{H}{L}.100\% \).
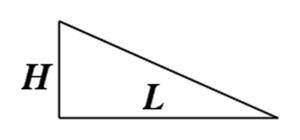
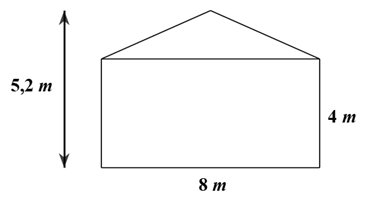
Một nhà xưởng có mái lợp tôn và có mặt cắt với các kích thước như hình vẽ. Biết độ dốc mái tôn tối thiểu là 10.
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Độ dốc mái tôn của nhà xưởng là 15%. |
||
|
Góc tạo bởi mặt phẳng mái và sàn là 17∘. (Kết quả làm tròn đến độ) |
||
|
Để tiết kiệm nguyên vật liệu, người ta chỉ có thể giảm độ dốc mái về mức tối thiểu. Khi đó, chiều cao của nhà xưởng giảm 0,8 mét. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Độ dốc mái tôn của nhà xưởng là 15%. |
X | |
|
Góc tạo bởi mặt phẳng mái và sàn là 17∘. (Kết quả làm tròn đến độ) |
X | |
|
Để tiết kiệm nguyên vật liệu, người ta chỉ có thể giảm độ dốc mái về mức tối thiểu. Khi đó, chiều cao của nhà xưởng giảm 0,8 mét. |
X |
Giải thích
Độ dốc mái tôn của nhà xưởng là \(i = \frac{{5,2 - 4}}{{8:2}}.100\% = 30\% \).
Gọi \(\alpha \) là góc tạo bởi mặt phẳng mái và sàn. Khi đó, \(\tan \alpha = \frac{H}{L} = 0,3 \Rightarrow \alpha \approx {17^^\circ }\).
Khi độ dốc mái giảm về mức tối thiểu thì \(i = \frac{{{H^\prime }}}{L}.100 \Rightarrow {H^\prime } = 0,4(m)\).
Suy ra chiều cao của nhà xưởng khi \(i = 10\% \) là 4,4 m. Vậy chiều cao của nhà xưởng giảm \(5,2 - 4,4 = 0,8(m)\).
Câu 62:
 Xem đáp án
Xem đáp án
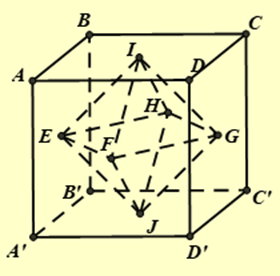
Giả sử hình lập phương \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có cạnh bằng 1 ; tâm của các mặt là I, J, E, F, G, H như hình vē.
Ta có EFGH là hình thoi.
Thể tích khối bát diện đều là: \(V = \frac{1}{3}{S_{EFGH}}.IJ = \frac{1}{3}.\frac{1}{2}EG.FH.IJ = \frac{1}{6}\).
Chọn C
Câu 63:
 Xem đáp án
Xem đáp án
Ta có: \(A{C^2} = B{A^2} + B{C^2} \Leftrightarrow 2{a^2} = 2A{B^2} \Leftrightarrow A{B^2} = {a^2}\).
Chọn B
Câu 64:
Đặt một chiếc phễu hình nón lên một chiếc cốc hình trụ như hình vẽ. Biết chiều cao của cốc bằng gấp đôi chiều cao của phễu. Giả sử độ dày thành cốc và phễu không đáng kể. Người ta đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng \(\frac{1}{2}\) chiều cao của phễu. Nước trong phễu sẽ chảy vào cốc qua lỗ nhỏ trên đỉnh phễu.
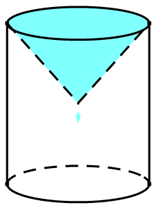
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Thể tích của cốc gấp 4 lần thể tích phễu. |
||
|
Khi nước trong phễu chảy hết vào cốc thì lượng nước trong cốc chiếm khoảng 2,08% thể tích cốc. (Coi như lượng nước không bị hao hụt và kết quả làm tròn đến chữ số thập phân thứ hai) |
||
|
Nếu mỗi lần người ta chỉ đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng \(\frac{1}{2}\) chiều cao của phễu thì cần 12 lần đổ để chiều cao của nước trong cốc vừa chạm đỉnh phễu. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Thể tích của cốc gấp 4 lần thể tích phễu. |
X | |
|
Khi nước trong phễu chảy hết vào cốc thì lượng nước trong cốc chiếm khoảng 2,08% thể tích cốc. (Coi như lượng nước không bị hao hụt và kết quả làm tròn đến chữ số thập phân thứ hai) |
X | |
|
Nếu mỗi lần người ta chỉ đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng 12 chiều cao của phễu thì cần 12 lần đổ để chiều cao của nước trong cốc vừa chạm đỉnh phễu. |
X |
Giải thích
Thể tích của cốc nước là: \[{V_0} = \pi {R^2}h\] .
Thể tích của phễu là: \({V_1} = \frac{1}{3}\pi {R^2}\frac{h}{2} = \frac{1}{6}{V_0}\).
Vậy thể tích của cốc gấp 6 lần thể tích phễu.
Vì lượng nước đổ vào phễu có chiều cao bằng \(\frac{1}{2}\) chiều cao của phễu nên bán kính của mặt nước là \(\frac{R}{2}\) (Áp dụng định lí Ta-let).
Khi đó, lượng nước đổ vào phễu là: \({V_2} = \frac{1}{3}\pi {\left( {\frac{R}{2}} \right)^2}.\frac{1}{2}.\frac{h}{2} = \frac{1}{{48}}{V_0} \approx 2,08\% {V_0}\)
⇒Chiều cao của nước trong cốc sau 1 lần đổ là \[\frac{h}{{48}}\].
Để để chiều cao của nước trong cốc vừa chạm đỉnh phễu thì cần \(\frac{h}{2}:\frac{h}{{48}} = 24\) lần đổ nước.
Câu 65:
Cho một hộp bóng bàn có dạng hình hộp chữ nhật. Biết rằng hộp chứa vừa khít ba quả bóng bàn được xếp theo chiều dọc, các quả bóng bàn có kích thước như nhau.
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Chiều cao của chiếc hộp gấp 3 lần bán kính của một quả bóng. |
||
|
Phần không gian còn trống trong hộp chiếm khoảng 47,64%. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Chiều cao của chiếc hộp gấp 3 lần bán kính của một quả bóng. |
X | |
|
Phần không gian còn trống trong hộp chiếm khoảng 47,64%. |
X |
Giải thích
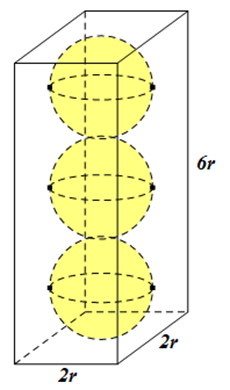
Giả sử quả bóng bàn có bán kính \(r\), thể tích 3 quả bóng bàn là \({V_1}\) và hình hộp chữ nhật có thể tích \(V\). Từ giả thiết suy ra đáy hình hộp là hình vuông cạnh 2r, chiều cao của hình hộp là 6r.
Vậy chiều cao của chiếc hộp gấp 6 lần bán kính của một quả bóng.
Ta có \(V = 24{r^3};\,\,\,{V_1} = 3.\frac{4}{3}\pi {r^3} = 4\pi {r^3}\).
Suy ra thể tích phần không gian còn trống là \({V_2} = V - {V_1} = 4{r^3}(6 - \pi )\).
Thể tích phần không gian còn trống chiếm \(\frac{{{V_2}}}{V}.100\).
Câu 66:
 Xem đáp án
Xem đáp án
Giải thích
Ta có: \(\overrightarrow {{n_P}} = (m;2 - m;1);\overrightarrow {{u_\Delta }} = (1;2;3)\).
Khi đó, \(\sin {60^o } = \frac{{\left| {\overrightarrow {{n_P}} .\overrightarrow {{u_\Delta }} } \right|}}{{\left| {\overrightarrow {{n_P}} } \right|.\left| {\overrightarrow {{u_\Delta }} } \right|}}\).
\( \Leftrightarrow \frac{{|m + 2(2 - m) + 3|}}{{\sqrt {{m^2} + {{(2 - m)}^2} + 1} .\sqrt {1 + {2^2} + {3^2}} }} = \frac{{\sqrt 3 }}{2}\)
\( \Leftrightarrow \frac{{|7 - m|}}{{\sqrt {2{m^2} - 4m + 5} }} = \frac{{\sqrt {42} }}{2}\)
\( \Leftrightarrow 4{( - m + 7)^2} = 42\left( {2{m^2} - 4m + 5} \right)\)
\( \Leftrightarrow 80{m^2} - 112m + 14 = 0\)
Vậy tổng các giá trị của tham số m thỏa mãn bài toán là \(\frac{7}{5}\).
Chọn B
Câu 67:
 Xem đáp án
Xem đáp án
Giải thích
Xét \(u(x) = \frac{{{x^4} + ax + a}}{{x + 1}}\) trên đoạn [1; 2], ta có \({u^\prime }(x) = \frac{{3{x^4} + 4{x^3}}}{{{{(x + 1)}^2}}} > 0,\forall x \in [1;2]\).
Do đó, \({\max _{[1;2]}}u = u(2) = a + \frac{{16}}{3},{\min _{[1;2]}}u = u(1) = a + \frac{1}{2}\).
TH1. Nếu \(a + \frac{1}{2} \ge 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{M = a + \frac{{16}}{3}}\\{m = a + \frac{1}{2}}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a + \frac{1}{2} \ge 0}\\{a + \frac{{16}}{3} \ge 2\left( {a + \frac{1}{2}} \right)}\end{array} \Leftrightarrow - \frac{1}{2} \le a \le \frac{{13}}{3}} \right.} \right.\).
TH2. Nếu \(a + \frac{{16}}{3} \le 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{M = - \left( {a + \frac{1}{2}} \right)}\\{m = - \left( {a + \frac{{16}}{3}} \right)}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a + \frac{{16}}{3} \le 0}\\{ - \left( {a + \frac{1}{2}} \right) \ge - 2\left( {a + \frac{{16}}{3}} \right)}\end{array} \Leftrightarrow - \frac{{61}}{6} \le a \le - \frac{{16}}{3}} \right.} \right.\).
TH3. Nếu \(\left( {a + \frac{1}{2}} \right).\left( {a + \frac{{16}}{3}} \right) \le 0 \Leftrightarrow \frac{{ - 16}}{3} \le a \le \frac{{ - 1}}{2} \Rightarrow m = 0\),
\(M = \max \left\{ {\left| {a + \frac{1}{2}} \right|,\left| {a + \frac{{16}}{3}} \right|} \right\} \Rightarrow M > 2m\) (thỏa mãn).
Vậy \( - \frac{{61}}{6} \le a \le \frac{{13}}{3}\). Mà \(a \in \mathbb{Z}\) nên \(a \in \{ - 10; \ldots ;4\} \).
Câu 68:
Cho hàm số \(y = \frac{{2x - 3}}{{2 - x}}\).
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Hàm số luôn nghịch biến trên các khoảng của tập xác định. |
||
|
Đồ thị hàm số có đường tiệm cận ngang \(y = 1\). |
||
|
Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \(x = - 1\) có hệ số góc bằng \( - \frac{1}{9}\). |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Hàm số luôn nghịch biến trên các khoảng của tập xác định. |
X | |
|
Đồ thị hàm số có đường tiệm cận ngang \(y = 1\). |
X | |
|
Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \(x = - 1\) có hệ số góc bằng \( - \frac{1}{9}\). |
X |
Giải thích
ТХĐ: \(D = \mathbb{R}\backslash \{ 2\} \).
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{2x - 3}}{{2 - x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x - 3}}{{2 - x}} = - 2 \Rightarrow y = - 2\) là đường tiệm cận ngang của đồ thị hàm số.
Ta có \(y = \frac{{2x - 3}}{{2 - x}} = \frac{{2x - 3}}{{ - x + 2}} \Rightarrow {y^\prime } = \frac{1}{{{{(2 - x)}^2}}} > 0,\forall x \in D\).
\( \Rightarrow \) Hàm số luôn đồng biến trên các khoảng của tập xác định
Hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \(x = - 1\) là \(k = {y^\prime }( - 1) = \frac{1}{9}\).
Câu 69:
Hai bạn An và Bình chơi trò gieo xúc xắc với nhau. Luật chơi như sau: hai bạn có 3 con xúc xắc, các bạn gieo 3 con xúc xắc cùng lúc, lấy con xúc xắc có số chấm nhiều nhất qua một bên (nếu có nhiều hơn 1 con xúc xắc cùng ra số chấm nhiều nhất thì bỏ ra 1 con xúc xắc bất kì trong đó), sau đó gieo 2 con xúc xắc còn lại cùng lúc, lấy con xúc xắc có số chấm nhiều nhất qua một bên và gieo con xúc xắc còn lại, sau đó cộng số chấm trên 3 con xúc xắc đó với nhau, bạn nào có tổng số chấm cao hơn thì chiến thắng. Bạn An chơi trước, tổng số chấm trên 3 con xúc xắc bạn gieo được là 16. Xác suất bạn Bình giành chiến thắng là (1) _______ (viết kết quả dưới dạng phần trăm, làm tròn đến chữ số thập phân thứ nhất).
 Xem đáp án
Xem đáp án
Đáp án
Hai bạn An và Bình chơi trò gieo xúc xắc với nhau. Luật chơi như sau: hai bạn có 3 con xúc xắc, các bạn gieo 3 con xúc xắc cùng lúc, lấy con xúc xắc có số chấm nhiều nhất qua một bên (nếu có nhiều hơn 1 con xúc xắc cùng ra số chấm nhiều nhất thì bỏ ra 1 con xúc xắc bất kì trong đó), sau đó gieo 2 con xúc xắc còn lại cùng lúc, lấy con xúc xắc có số chấm nhiều nhất qua một bên và gieo con xúc xắc còn lại, sau đó cộng số chấm trên 3 con xúc xắc đó với nhau, bạn nào có tổng số chấm cao hơn thì chiến thắng. Bạn An chơi trước, tổng số chấm trên 3 con xúc xắc bạn gieo được là 16. Xác suất bạn Bình giành chiến thắng là (1) __ 7,5% __ (viết kết quả dưới dạng phần trăm, làm tròn đến chữ số thập phân thứ nhất).
Giải thích
Tổng số chấm tối đa có thể thu được là 6.3 = 18.
Để bạn Bình giành chiến thắng thì tổng số chấm bạn thu được phải là 17hoặc 18.
TH1. Tổng số chấm là 18.
Để tổng số chấm là 18 thì con xúc xắc có số chấm nhiều nhất trong 3 lần gieo đều phải bằng 6.
Xác suất xảy ra là: \(\left[ {1 - {{\left( {\frac{5}{6}} \right)}^3}} \right].\left[ {1 - {{\left( {\frac{5}{6}} \right)}^2}} \right].\frac{1}{6} = \frac{{1001}}{{46656}}\).
TH2. Tổng số chấm là 17.
Để tổng số chấm là 17 thì con xúc xắc có số chấm nhiều nhất trong 2 lần gieo bằng 6, trong lần gieo còn lại bằng 5.
+ Số chấm cao nhất trong 3 lần gieo lần lượt là 6, 6, 5. Xác suất xảy ra là:
\(\left[ {1 - {{\left( {\frac{5}{6}} \right)}^3}} \right].\left[ {1 - {{\left( {\frac{5}{6}} \right)}^2}} \right].\frac{1}{6} = \frac{{1001}}{{46656}}\).
+ Số chấm cao nhất trong 3 lần gieo lần lượt là 6, 5, 6. Xác suất xảy ra là:
\(\left[ {1 - {{\left( {\frac{5}{6}} \right)}^3}} \right].\left( {C_2^1.\frac{1}{6}.\frac{4}{6} + \frac{1}{6}.\frac{1}{6}} \right).\frac{1}{6} = \frac{{91}}{{5184}}\).
+ Số chấm cao nhất trong 3 lần gieo lần lượt là 5, 6, 6. Xác suất xảy ra là:
\(\left[ {C_3^1.\frac{1}{6}.{{\left( {\frac{4}{6}} \right)}^2} + C_3^2.{{\left( {\frac{1}{6}} \right)}^2}.\frac{4}{6} + C_3^3.{{\left( {\frac{1}{6}} \right)}^3}} \right].\left[ {1 - {{\left( {\frac{5}{6}} \right)}^2}} \right].\frac{1}{6} = \frac{{671}}{{46656}}\) .
Xác suất để bạn Bình giành chiến thắng là:
\(\frac{{1001}}{{46656}} + \frac{{1001}}{{46656}} + \frac{{91}}{{5184}} + \frac{{671}}{{46656}} = \frac{{97}}{{1296}} \approx 7,5\% \).
Câu 70:
Cho một tam giác đều cạnh bằng 3 (hình 1). Chia mỗi cạnh của tam giác thành 3 đoạn bằng nhau và thay mỗi đoạn ở giữa bằng hai đoạn bằng nó sao cho chúng tạo với đoạn bỏ đi một tam giác đều về phía bên ngoài ta được hình 2.
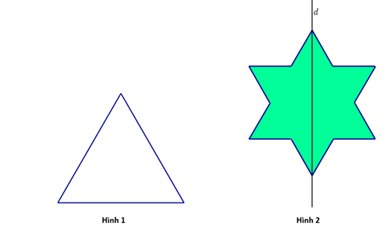
Diện tích của hình 2 bằng ______.
Thể tích khối tròn xoay khi quay hình 2 xung quanh trục d là ______π.
 Xem đáp án
Xem đáp án
Đáp án
Diện tích của hình 2 bằng \(3\sqrt 3 \).
Thể tích khối tròn xoay khi quay hình 2 xung quanh trục d là \(\frac{{5\sqrt 3 }}{3}\)π.
Giải thích
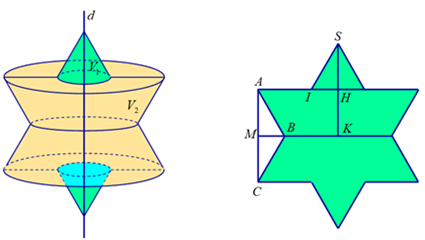
Diện tích của hình 2 bằng tổng diện tích của tam giác đều (hình 1) và 3 tam giác đều cạnh bằng 1 được vẽ thêm.
⇒ Diện tích hình 2 bằng: \(S = \frac{{{3^2}\sqrt 3 }}{4} + 3.\frac{{{1^2}\sqrt 3 }}{4} = 3\sqrt 3 .\)
Ta có thể tích khối tròn xoay tạo thành bằng 2 lần thể tích nửa trên khi cho hình SIABK quay quanh trục SK.
Tam giác SIH quay quanh trục SK tạo thành khối nón có \({r_1} = IH = \frac{1}{2};{h_1} = SH = \frac{{\sqrt 3 }}{2}\).
Thể tích khối nón này bằng \({V_1} = \frac{1}{3}\pi {r_1}^2{h_1} = \frac{1}{3}\pi .\frac{1}{4}.\frac{{\sqrt 3 }}{2} = \frac{{\sqrt 3 \pi }}{{24}}\)
Hình thang vuông HABK quay quanh trục HK tạo thành hình nón cụt có \(R = AH = \frac{3}{2}\); \(r = BK = 1;h = HK = SH = \frac{{\sqrt 3 }}{2}\).
Thể tích khối nón cụt này bằng \({V_2} = \frac{{\pi h}}{3}.\left( {{R^2} + {r^2} + R.r} \right) = \frac{\pi }{3}.\frac{{\sqrt 3 }}{2}\left( {\frac{9}{4} + 1 + \frac{3}{2}} \right) = \frac{{19\pi \sqrt 3 }}{{24}}\).
Câu 71:
 Xem đáp án
Xem đáp án
Giải thích
Ta có: \(f(1) = n\).
\(\mathop {\lim }\limits_{x \to 1} f(x) = \mathop {\lim }\limits_{x \to 1} \frac{{x + 3 - {m^2}}}{{(x - 1)(\sqrt {x + 3} + m)}}{\rm{. }}\)
Hàm số liên tục tại \(x = 1 \Leftrightarrow \mathop {\lim }\limits_{x \to 1} f(x) = f(1) \Leftrightarrow n = \mathop {\lim }\limits_{x \to 1} \frac{{x + 3 - {m^2}}}{{(x - 1)(\sqrt {x + 3} + m)}}\)(1)
\(\mathop {\lim }\limits_{x \to 1} f(x)\) tồn tại khi 1 là nghiệm của phương trình \(x + 3 - {m^2} = 0\)
\( \Leftrightarrow 1 + 3 - {m^2} = 0 \Rightarrow \left[ {\begin{array}{*{20}{l}}{m = 2}\\{m = - 2}\end{array}} \right.\).
+ Khi \(m = 2\) thì (1) \( \Rightarrow n = \mathop {\lim }\limits_{x \to 1} \frac{{x - 1}}{{(x - 1)(\sqrt {x + 3} + 2)}} \Rightarrow n = \mathop {\lim }\limits_{x \to 1} \frac{1}{{\sqrt {x + 3} + 2}} \Rightarrow n = \frac{1}{4}\).
+ Khi \(m = - 2\) thì (1) \( \Rightarrow n = \mathop {\lim }\limits_{x \to 1} \frac{1}{{\sqrt {x + 3} - 2}}\) suy ra không tồn tại \(n\).
Vậy \(m + n = 2 + \frac{1}{4} = \frac{9}{4}\).
Chọn D
Câu 72:
 Xem đáp án
Xem đáp án
Giải thích
Cách 1.
Gọi \(d\) là giao tuyến của hai mặt phẳng \((P)\) và \((Q)\).
\(\overrightarrow {{n_{(P)}}} = (1;1;1),\overrightarrow {{n_{(Q)}}} = (2;1; - 1).\)
\(\overrightarrow {{u_d}} = \left[ {\overrightarrow {{n_{(P)}}} ,\overrightarrow {{n_{(Q)}}} } \right] = ( - 2;3; - 1).\)
Chọn điểm \(M(0;4; - 1)\) thuộc hai mặt phẳng \((P)\) và \((Q)\).
Phương trình đường thẳng \(d\) là̀ \(\frac{x}{{ - 2}} = \frac{{y - 4}}{3} = \frac{{z + 1}}{{ - 1}}\).
Cách 2.
Gọi \(d\) là giao tuyến của hai mặt phẳng \((P)\) và \((Q)\) thì với mỗi điểm \(M(x;y;z) \in d\) là nghiệm của hệ phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{x + y + z = 3}\\{2x + y - z = 5}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3x + 2y = 8}\\{z = 2x + y - 5}\end{array}} \right.} \right.\)
Cho \(x = 2t(t \in \mathbb{R})\) thì từ hệ phương trình trên ta thu được \(\left\{ {\begin{array}{*{20}{l}}{y = 4 - 3t}\\{z = - 1 + t}\end{array}} \right.\).
Vậy phương trình của đường thẳng \(d\) là \(\left\{ {\begin{array}{*{20}{l}}{x = 2t}\\{y = 4 - 3t\,\,(t \in \mathbb{R}){\rm{. }}}\\{z = - 1 + t}\end{array}} \right.\)
Chọn A
Câu 73:
Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác ABC được gọi là tam giác trung bình của tam giác ABC.
Ta xây dựng dãy các tam giác \({A_1}{B_1}{C_1},{A_2}{B_2}{C_2},{A_3}{B_3}{C_3}, \ldots \) sao cho \({A_1}{B_1}{C_1}\) là một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương \(n \ge 2\), tam giác \({A_n}{B_n}{C_n}\) là tam giác trung bình của tam giác \({A_{n - 1}}{B_{n - 1}}{C_{n - 1}}\). Với mỗi số nguyên dương \(n\), kí hiệu \({S_n}\) tương ứng là diện tích hình tròn ngoại tiếp tam giác \({A_n}{B_n}{C_n}\). Tổng \(S = {S_1} + {S_2} + \ldots + {S_n} + \ldots \) có giá trị bằng (1) __________. (kết quả làm tròn đến chữ số thập phân thứ hai).
 Xem đáp án
Xem đáp án
Đáp án
Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác ABC được gọi là tam giác trung bình của tam giác ABC.
Ta xây dựng dãy các tam giác \({A_1}{B_1}{C_1},{A_2}{B_2}{C_2},{A_3}{B_3}{C_3}, \ldots \) sao cho \({A_1}{B_1}{C_1}\) là một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương \(n \ge 2\), tam giác \({A_n}{B_n}{C_n}\) là tam giác trung bình của tam giác \({A_{n - 1}}{B_{n - 1}}{C_{n - 1}}\). Với mỗi số nguyên dương \(n\), kí hiệu \({S_n}\) tương ứng là diện tích hình tròn ngoại tiếp tam giác \({A_n}{B_n}{C_n}\). Tổng \(S = {S_1} + {S_2} + \ldots + {S_n} + \ldots \) có giá trị bằng (1) __ 12,57 __ . (kết quả làm tròn đến chữ số thập phân thứ hai).
Giải thích
Vì dãy các tam giác \({A_1}{B_1}{C_1},{A_2}{B_2}{C_2},{A_3}{B_3}{C_3}, \ldots \) là các tam giác đều nên bán kính đường tròn ngoại tiếp các tam giác bằng cạnh \( \times \frac{{\sqrt 3 }}{3}\).
Với \(n = 1\) thì tam giác đều \({A_1}{B_1}{C_1}\) có cạnh bằng 3 nên đường tròn ngoại tiếp tam giác \({A_1}{B_1}{C_1}\) có bán kính \({R_1} = 3.\frac{{\sqrt 3 }}{3} \Rightarrow {S_1} = \pi {\left( {3.\frac{{\sqrt 3 }}{3}} \right)^2}\).
Với \(n = 2\) thì tam giác đều \({A_2}{B_2}{C_2}\) có cạnh bằng \(\frac{3}{2}\) nên đường tròn ngoại tiếp tam giác \({A_2}{B_2}{C_2}\) có bán kính \({R_2} = 3.\frac{1}{2}.\frac{{\sqrt 3 }}{3} \Rightarrow {S_2} = \pi {\left( {3.\frac{1}{2}.\frac{{\sqrt 3 }}{3}} \right)^2}\).
Với \(n = 3\) thì tam giác đều \({A_3}{B_3}{C_3}\) có cạnh bằng \(\frac{3}{4}\) nên đường tròn ngoại tiếp tam giác \({A_2}{B_2}{C_2}\) có bán kính \({R_3} = 3.\frac{1}{4}.\frac{{\sqrt 3 }}{3} \Rightarrow {S_3} = \pi {\left( {3.\frac{1}{4}.\frac{{\sqrt 3 }}{3}} \right)^2}\).
…………
Như vậy tam giác đều \({A_n}{B_n}{C_n}\) có cạnh bằng \(3.{\left( {\frac{1}{2}} \right)^{n - 1}}\) nên đường tròn ngoại tiếp tam giác \({A_n}{B_n}{C_n}\) có bán kính \({R_n} = 3.{\left( {\frac{1}{2}} \right)^{n - 1}}.\frac{{\sqrt 3 }}{3} \Rightarrow {S_n} = \pi {\left( {3.{{\left( {\frac{1}{2}} \right)}^{n - 1}}.\frac{{\sqrt 3 }}{3}} \right)^2}\).
Khi đó ta được dãy \({S_1},{S_2}, \ldots {S_n}\).. là một cấp số nhân lùi vô hạn với số hạng đầu \({u_1} = {S_1} = 3\pi \) và công bội \(q = \frac{1}{4}\).
Do đó tổng \(S = {S_1} + {S_2} + \ldots + {S_n} + \ldots = \frac{{{u_1}}}{{1 - q}} = 4\pi \approx 12,57\).
Câu 74:
Ta gọi số nguyên bé nhất không nhỏ hơn x là phần nguyên trên của x, ký hiệu \(\left\lceil x \right\rceil \)
Chẳng hạn \(\left\lceil { - 2,5} \right\rceil = - 2,\,\,\left\lceil {\frac{{19}}{6}} \right\rceil = 4\)
Tổng phần nguyên trên của tất cả các số có dạng \(\frac{k}{2}\) với k nguyên lấy giá trị từ -4 đến 4 bằng
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 75:
 Xem đáp án
Xem đáp án
Tổng của 50 số hạng đầu của cấp số nhân \(\left( {{u_n}} \right)\) bằng:
\({S_{50}} = {u_1}.\frac{{1 - {q^n}}}{{1 - q}} = {u_1}.\frac{{1 - {{(1 - i)}^{50}}}}{{1 - (1 - i)}} = \frac{1}{2}.\frac{{1 - {{\left[ {{{(1 - i)}^2}} \right]}^{25}}}}{i} = \frac{{1 - {{( - 2i)}^{25}}}}{{2i}} = \frac{{1 + {2^{25}}i}}{{2i}} = {2^{24}} - \frac{1}{2}i{\rm{.}}\)
Chọn B
Câu 76:
Thiết diện của hình trụ (T) cắt bởi một mặt phẳng song song với trục và cách trục một đoạn bằng 2 cm là hình chữ nhật có chiều dài gấp đôi chiều rộng. Biết diện tích xung quanh của hình trụ (T) là \(32\pi \sqrt 6 \) cm2.
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau
Bán kính đáy của hình trụ (T) là ______ cm.
Thể tích của khối trụ (T) là ______ cm3 Xem đáp án
Xem đáp án
Đáp án
Bán kính đáy của hình trụ (T) là \(2\sqrt 3 \) cm.
Thể tích của khối trụ (T) là \(48\pi \sqrt 2 \) cm3.
Giải thích
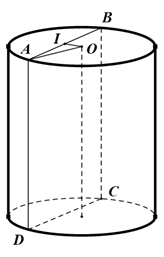
Giả sử ta có hình trụ như hình vẽ với \(I\) là trung điểm của AB.
Khi đó, \(OI = 2;OA = R \Rightarrow AB = 2AI = 2\sqrt {{R^2} - 4} \).
Vì thiết diện là hình chữ nhật có chiều dài gấp đôi chiều rộng nên \(h = AD = 2AB = 4\sqrt {{R^2} - 4} \).
Vì diện tích xung quanh của hình trụ ( \(T)\) là \(32\pi \sqrt 6 \;{\rm{c}}{{\rm{m}}^2}\) nên \({S_{xq}} = 2\pi Rh = 32\pi \sqrt 6 \).
\(\begin{array}{l} \Leftrightarrow 2\pi R.4\sqrt {{R^2} - 4} = 32\pi \sqrt 6 \\ \Leftrightarrow R\sqrt {{R^2} - 4} = 4\sqrt 6 \end{array}\)
\(\begin{array}{l} \Leftrightarrow {R^2}\left( {{R^2} - 4} \right) = 96\\ \Leftrightarrow R = 2\sqrt 3 \end{array}\)
Khi đó, thể tích của khối trụ \((T)\) là \(V = \pi {R^2}h = \pi {\left( {2\sqrt 3 } \right)^2}.2\sqrt {{{\left( {2\sqrt 3 } \right)}^2} - 4} = 48\pi \sqrt 2 \,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Câu 77:
 Xem đáp án
Xem đáp án
Chọn A
Câu 78:
 Xem đáp án
Xem đáp án
Gọi \(z = x + yi\), với \(x,y \in \mathbb{R}\). Khi đó \(M(x;y)\) là điểm biểu diễn cho số phức \(z\).
Theo giả thiết, \(5w = (2 + i)(z - 4) \Leftrightarrow 5(w + i) = (2 + i)(z - 4) + 5i\)
\( \Leftrightarrow (2 - i)(w + i) = z - 3 + 2i\)
\( \Leftrightarrow |z - 3 + 2i| = 3\). Suy ra \(M(x;y)\) thuộc đường tròn \((C)\) có tâm \(I(3; - 2)\), bán kính \(R = 3\).
Ta có \(P = |z - 1 - 2i| + |z - 5 - 2i| = MA + MB\), với \(A(1;2)\) và \(B(5;2)\).
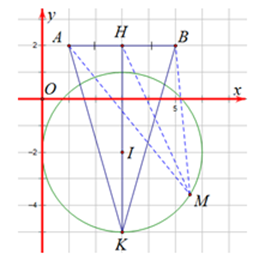
Gọi \(H\) là trung điểm của AB, ta có \(H(3;2)\) và khi đó:
\(P = MA + MB \le \sqrt {2\left( {M{A^2} + M{B^2}} \right)} {\rm{ hay }}P \le \sqrt {4M{H^2} + A{B^2}} {\rm{. }}\)
Mặt khác, \(MH \le KH\) với mọi \(M \in (C)\) và \(K(3; - 5) = HI \cap (I)\) nên
\(P \le \sqrt {4K{H^2} + A{B^2}} = \sqrt {{{4.7}^2} + {4^2}} = 2\sqrt {53} .\)
Vậy \({P_{\max }} = 2\sqrt {53} \) khi \(\left\{ {\begin{array}{*{20}{c}}{M \equiv K}\\{MA = MB}\end{array}} \right.\) hay \(z = 3 - 5i\) và \(w = \frac{3}{5} - \frac{{11}}{5}i\).
Chọn C
Câu 79:
Một xe lửa chuyển động chậm dần đều và dừng lại hẳn sau 20s kể từ lúc bắt đầu hãm phanh. Trong thời gian đó, xe chạy được 120m. Biết vận tốc của chuyển động biến đổi đều được tính bằng công thức \(v = {v_0} + at\); trong đó v (m/s) là vận tốc tại thời điểm t (s), v0 (m/s) là vận tốc của xe lửa lúc bắt đầu hãm phanh, a (m/s2) là gia tốc. Khi đó v0 = (1) _________ m/s.
 Xem đáp án
Xem đáp án
Đáp án
Một xe lửa chuyển động chậm dần đều và dừng lại hẳn sau 20s kể từ lúc bắt đầu hãm phanh. Trong thời gian đó, xe chạy được 120m. Biết vận tốc của chuyển động biến đổi đều được tính bằng công thức \(v = {v_0} + at\); trong đó v (m/s) là vận tốc tại thời điểm t (s), v0 (m/s) là vận tốc của xe lửa lúc bắt đầu hãm phanh, a (m/s2) là gia tốc. Khi đó v0 = (1) __ 12 __ m/s.
Giải thích
Tại thời điểm \(t = 20(s)\) thì \(v(20) = 0\) nên \({v_0} + 20a = 0 \Rightarrow a = - \frac{{{v_0}}}{{20}}\).
Do đó, \(v(t) = {v_0} - \frac{{{v_0}}}{{20}}t\).
Mặt khác, \(v(t) = {s^\prime }(t) \Rightarrow \int_0^{20} v (t){\rm{d}}t = \int_0^{20} {{s^\prime }} (t){\rm{d}}t = \left. {s(t)} \right|_0^{20} = s(20) - s(0) = 120\).
\( \Rightarrow \int_0^{20} {\left( {{v_0} - \frac{{{v_0}}}{{20}}t} \right)} {\rm{d}}t = 120\)
Từ đó ta có phương trình \(20{v_0} - 10{v_0} = 120 \Leftrightarrow {v_0} = 12\,\,(\;{\rm{m}}/{\rm{s}})\).
Câu 80:
Định luật Newton II cho biết: “Gia tốc của một vật có cùng hướng với lực tác dụng lên vật. Độ lớn của gia tốc tỉ lệ thuận với độ lớn của lực tác dụng lên vật và tỉ lệ nghịch với khối lượng của vật”.
Ở thời điểm ban đầu, một chất điểm có khối lượng m = 1kg có vận tốc v0 = 20 m/s. Chất điểm chịu lực cản \({F_C} = - rv\) với r = ln2 và v là vận tốc của chất điểm tính bằng m/s. Sau 3s, chất điểm đạt vận tốc là
 Xem đáp án
Xem đáp án
Gọi a là gia tốc của chất điểm.
Theo định luật II Newton ta có: \(a = \frac{F}{m} \Rightarrow {F_C} = ma = mv' = m\frac{{dv}}{{dt}}\).
Mà \({F_C} = - rv\) nên \( - rv = m\frac{{dv}}{{dt}} \Rightarrow \frac{{dv}}{v} = - \frac{r}{m}dt\)
\( \Leftrightarrow \int_{{v_0}}^v {\frac{{dv}}{v}} = \int_0^t - \frac{r}{m}dt \Leftrightarrow \ln \frac{v}{{{v_0}}} = - \frac{r}{m}t \Rightarrow v = {v_0}.{e^{ - \frac{r}{m}t}} = 2,5\,\,(m/s).\)
Chọn D
Câu 81:
 Xem đáp án
Xem đáp án
Ta có \(\left| {{x^2} + x - 2} \right| = 2m + {x^2} - x - 6 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x^2} + x - 2 = 2m + {x^2} - x - 6\,\,\,\,\,\,\,({\rm{khi }}x \ge 1 \vee x \le - 2)}\\{ - {x^2} - x + 2 = 2m + {x^2} - x - 6\,\,\,\,({\rm{khi}} - 2 \le x \le 1)}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m = x + 2\quad (x \ge 1 \vee x \le - 2)}\\{m = - {x^2} + 4\,\,( - 2 \le x \le 1)\,\,\,\,\,\,}\end{array}} \right.\). Ta vẽ các đồ thị như hình vẽ.
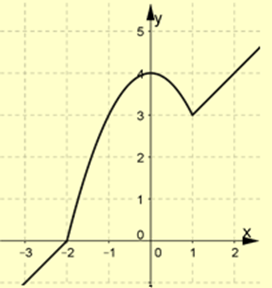
Từ đó ta suy ra để phương trình có 3 nghiệm phân biệt thì \(3 < m < 4\).
Vậy không có giá trị nguyên của m thỏa mãn.
Chọn B
Câu 82:
 Xem đáp án
Xem đáp án
Giải thích
Gọi 5 số thuộc tập hợp A thỏa mãn yêu cầu bài toán là \(x;xq;x{q^2};x{q^3};x{q^4}\,\,\left( {x,q \in {\mathbb{N}^*};q \ge 2;x \ge 1} \right)\).
Ta có: \(x{q^4} \le 2024 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{q < \sqrt[4]{{2024}}}\\{1 \le x \le \frac{{2024}}{{{q^4}}}}\end{array} \Rightarrow q \in \{ 2;3; \ldots ;6\} } \right.\) .
Với \(q = 2 \Rightarrow 1 \le x \le \frac{{253}}{2} \Rightarrow x \in \{ 1;2; \ldots ;126\} \).
Với \(q = 3 \Rightarrow 1 \le x \le \frac{{2024}}{{81}} \Rightarrow x \in \{ 1;2; \ldots ;24\} \).
Với \(q = 4 \Rightarrow 1 \le x \le \frac{{253}}{{32}} \Rightarrow x \in \{ 1;2; \ldots ;7\} \).
Với \(q = 5 \Rightarrow 1 \le x \le \frac{{2024}}{{625}} \Rightarrow x \in \{ 1;2;3\} \).
Với \(q = 6 \Rightarrow 1 \le x \le \frac{{253}}{{162}} \Rightarrow x \in \{ 1\} \).
Vậy có tất cả 126 + 24 + 7 + 3 + 1 = 161 cách chọn bộ số (x; q) thỏa mãn hay có 161 cách chọn 5 số từ tập hợp A thỏa mãn.
Chọn B
