Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 27)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 27)
-
432 lượt thi
-
80 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
Phần tư duy đọc hiểu
 Xem đáp án
Xem đáp án
Đọc lại nội dung của đoạn [1], xác định các thông tin quan trọng liên quan tới hậu quả của tình trạng tắc nghẽn giao thông: “lãng phí thời gian, tiêu hao nhiên liệu và ô nhiễm môi trường”; từ các thông tin trong bài viết cần đưa ra suy luận để tiến hành loại trừ Từ khóa: việc lãng phí thời gian và tiền bạc sẽ làm mất đi cơ hội phát triển của con người, tiêu hao nhiên liệu và ô nhiễm môi trường sẽ gây ra hậu quả về sức khỏe và việc khai thác chất đốt trong tự nhiên; Từ khóa đúng là C.
Chọn C
Câu 2:
Từ thông tin của đoạn [1] hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí:
ứng dụng, xây dựng, áp dụng, thiết kế
Theo đánh giá từ Viện chiến lược và phát triển Giao thông vận tải, tình trạng tắc nghẽn giao thông đang gây ảnh hưởng nghiêm trọng tới đời sống, vậy nên, các cơ quan tổ chức đang _______ nhiều biện pháp và _______ khoa học máy tính vào việc _______ các hệ thống thu thập và xử lý dữ liệu.
 Xem đáp án
Xem đáp án
Đáp án
Theo đánh giá từ Viện chiến lược và phát triển Giao thông vận tải, tình trạng tắc nghẽn giao thông đang gây ảnh hưởng nghiêm trọng tới đời sống, vậy nên, các cơ quan tổ chức đang áp dụng nhiều biện pháp và ứng dụng khoa học máy tính vào việc thiết kế các hệ thống thu thập và xử lý dữ liệu.
Giải thích
Đọc lại thông tin trong đoạn [1] để tìm ra được một số từ khóa quan trọng: “nhiều các biện pháp được nghiên cứu và áp dụng”, “ứng dụng khoa học máy tính càng được chú ý”, “thiết kế hệ thống thị giác máy tính thu thập và xử lý dữ liệu”. Câu văn đầy đủ là: “Theo đánh giá từ Viện chiến lược và phát triển Giao thông vận tải, tình trạng tắc nghẽn giao thông đang gây ảnh hưởng nghiêm trọng tới đời sống, vậy nên, các cơ quan tổ chức đang [áp dụng] nhiều biện pháp và [ứng dụng] khoa học máy tính vào việc [thiết kế] các hệ thống thu thập và xử lý dữ liệu.”
Câu 3:
 Xem đáp án
Xem đáp án
Đọc lại nội dung của đoạn [1]: Khi triển khai nghiên cứu giải pháp từ việc thu thập dữ liệu của camera giao thông để “xác định số lượng phương tiện lưu thông trên đường và tính toán mật độ lưu lượng phương tiện tham gia giao thông trong một khoảng thời gian xác định”; vậy mục tiêu cốt lõi sẽ là dự báo về tình trạng giao thông để giảm thiểu tình trạng tắc nghẽn.
Chọn D
Câu 4:
Yolov4 là phiên bản nâng cấp, có cơ chế hoạt động của mô hình mạng dùng cho việc phát hiện, nhận dạng, phân loại đối tượng; phân chia và xử lý hình ảnh sau đó đưa ra các dự đoán theo một yêu cầu xác định là đúng hay sai?
 Xem đáp án
Xem đáp án
Đọc lại nội dung đoạn [2] để tìm hiểu định nghĩa về Yolo: “mô hình mạng dùng cho việc phát hiện, nhận dạng, phân lại đối tượng”, “dự đoán xem trong mỗi ô liệu có đối tượng (object) mà điểm trung tâm rơi vào ô đó không, dự đoán điểm trung tâm, kích thước của đối tượng và xác suất là đối tượng nào trong số các đối tượng cần xác định”; chú ý câu “phiên bản đang được sử dụng là thế hệ thứ 4, gọi là Yolov4”.
Chọn A
Câu 5:
 Xem đáp án
Xem đáp án
Đọc kĩ nội dung của đoạn [3], cần phân biệt Sort và Tracking-by-detection; trong đó, Tracking-by-dectection là thuật toán để giải quyết từng đối tượng (xác định, dự đoán) còn Sort là “sự phát triển của khung theo dõi nhiều đối tượng”.
Chọn B
Câu 6:
 Xem đáp án
Xem đáp án
Đọc nội dung của đoạn [4] xác định thông tin: “… từ đó gán địa chỉ nhận dạng ID cho từng phương tiện lưu thông và phân loại chúng… xe ô tô, xe tải, xe buýt, xe máy và xe đạp”; cần lưu ý xe đạp không phải xe cơ giới nên chọn Từ khóa B.
Chọn B
Câu 7:
 Xem đáp án
Xem đáp án
Căn cứ vào từ khóa “tỷ lệ chính xác” để tìm thông tin trong đoạn [5]: “với xe ô tô, xe tải và xe buýt thì tỉ lệ chính xác tương đối cao và ổn định do đặc điểm kích thước và nhận dạng của chúng”; trong đoạn có nhắc tới yếu tố góc quan sát của camera, thời tiết, ánh sáng… nhưng đó không phải yếu tố quan trọng nhất.
Chọn A
Câu 8:
Đọc đoạn [5] và tìm từ không quá ba tiếng để hoàn thành câu văn sau:
Ở Việt Nam, phương tiện di chuyển chủ yếu là (1) ________, mật độ lưu thông cao nên để xây dựng được thuật toán ổn định và chính xác là rất phức tạp, cần thời gian dài để có thể hoàn thiện mô hình.
 Xem đáp án
Xem đáp án
Đáp án
Đọc đoạn [5] và tìm từ không quá ba tiếng để hoàn thành câu văn sau:
Ở Việt Nam, phương tiện di chuyển chủ yếu là (1) xe máy, mật độ lưu thông cao nên để xây dựng được thuật toán ổn định và chính xác là rất phức tạp, cần thời gian dài để có thể hoàn thiện mô hình.
Giải thích
Đọc thông tin trong đoạn [5] xác định từ cần điền là: “xe máy” vì có thông tin “tại Việt Nam, giao thông với đặc thù lượng xe máy lớn và mật độ lưu thông cao…”.
Câu 9:
Sau quá trình thử nghiệm tại các thành phố lớn, nhóm nghiên cứu đã thấy kết quả phân loại và kiểm đếm:
 Xem đáp án
Xem đáp án
Căn cứ vào từ khóa “kết quả phân loại và kiểm đếm” để đọc lại nội dung của đoạn [6] và xác định thông tin: “nhóm nghiên cứu nhận thấy khi mật độ lưu thông thấp, thuật toán cho kết quả phân loại và kiểm đếm tương đối chính xác. Với mật độ lưu thông trung bình và cao, kết quả bắt đầu có độ chênh lệch và mất định hơn ở loại phương tiện và xe đạp và xe máy”.
Chọn B
Câu 10:
Hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí:
giải quyết, đánh giá, khắc phục, điều tiết, xác định
Kết quả của quá trình thực nghiệm bằng video thực tế là cơ sở cho quá trình _______ để _______ mật độ lưu thông nhằm _______ tình trạng hệ thống giao thông bị quá tải, gây ùn tắc cho các phương tiện tham gia.
 Xem đáp án
Xem đáp án
Đáp án
Kết quả của quá trình thực nghiệm bằng video thực tế là cơ sở cho quá trình xác định để đánh giá mật độ lưu thông nhằm khắc phục tình trạng hệ thống giao thông bị quá tải, gây ùn tắc cho các phương tiện tham gia.
Giải thích
Căn cứ vào từ khóa “hệ thống giao thông bị quá tải”, “gây ùn tắc” tương đương với “tình trạng ùn tắc giao thông” xác định nội dung cần tìm ở đoạn [6]: “Các số liệu… được áp dụng vào việc tính toán mật độ lưu thông trên từng khoảng thời gian, từ đó đưa ra các kết luận”, “nhằm trực tiếp giảm thiểu tình trạng ùn tắc giao thông”. Chú ý “tính toán” tương đương với “xác định”, “kết luận” tương đương với “đánh giá” và “giảm thiểu” tương đương với “khắc phục”.
Câu 11:
Theo bài viết, mối quan hệ giữa đô thị hóa và những công trình lịch sử chứa đựng nhiều yếu tố văn hóa là sự tác động qua lại, mang đến những giá trị mới cho hình ảnh đô thị là đúng hay sai?
 Xem đáp án
Xem đáp án
Đọc nội dung phần sapo, xác định thông tin liên quan tới mối quan hệ của quá trình đô thị hóa và các công trình lịch sử là việc "làm mất nhiều dấu vết"; đô thị hóa là sản phẩm của quá trình tích lũy thặng dư" chứ không tạo nên giá trị mới cho các di tích lịch sử.
Chọn A
Câu 12:
Điền từ thích hợp trong đoạn [1] (không quá ba tiếng) hoàn thành nhận định sau:
“Trong khoảng hơn một thế kỷ nay, khi các đô thị bắt đầu hình thành, khi con người thực hiện những cải cách lớn, kiến tạo vào không gian đã có hay nói ngắn gọn là ý niệm (1) ______ dần trở nên quen thuộc thì những di sản văn hóa cũng đứng trước nỗi lo bị xóa nhòa, thậm chí biến mất.”
 Xem đáp án
Xem đáp án
Đáp án
“Trong khoảng hơn một thế kỷ nay, khi các đô thị bắt đầu hình thành, khi con người thực hiện những cải cách lớn, kiến tạo vào không gian đã có hay nói ngắn gọn là ý niệm (1) hiện đại hóa dần trở nên quen thuộc thì những di sản văn hóa cũng đứng trước nỗi lo bị xóa nhòa, thậm chí biến mất.”
Giải thích
Dọc nội dung đoạn [1], xác định việc "cải tạo cái cũ", "kiến tạo vào không gian" chính là quá trình "hiện đại hóa" và "những sự can thiệp luôn tiềm ẩn nguy cơ phá cỡ di sản".
Câu 13:
Hải Phòng, Hà Nội, EFEO, Huế
Vào khoảng cuối thế kỷ XIX, khi những cuộc triển lãm thuộc địa hay khảo cứu do _______ được tổ chức, khái niệm di sản bắt đầu được biết đến; khác với _______ - một thành phố thuộc địa, _______ và Huế đứng trước những bàn luận giữa việc hiện đại hóa và bảo tồn những giá trị di sản văn hóa.
 Xem đáp án
Xem đáp án
Đáp án
Vào khoảng cuối thế kỷ XIX, khi những cuộc triển lãm thuộc địa hay khảo cứu do EFEO được tổ chức, khái niệm di sản bắt đầu được biết đến; khác với Hải Phòng - một thành phố thuộc địa, Hà Nội và Huế đứng trước những bàn luận giữa việc hiện đại hóa và bảo tồn những giá trị di sản văn hóa.
Giải thích
Căn cứ vào các từ khóa "cuối thế kỉ XIX", "khảo cứu"... xác định thông tin nằm trong đoạn [1] của bài viết. Tổng hợp nội dung đoạn [1] xác định: vấn đề bảo tồn di sản được đặt ra trong quá trình xây dựng, cải tạo tại một số đô thị trung đại (Hà Nội, Huế), còn các đô thị mới, được xây trong quá trình khai thác thuộc địa (Hải Phòng, Nam Định, Hòn Gai...) thì không.
Câu 14:
 Xem đáp án
Xem đáp án
Căn cứ vào từ khóa "ý niệm về bảo tồn" xác định thông tin cần tìm nằm trong đoạn [2] của văn bản: "bảo tồn di sản là một ý niệm mờ nhạt với tư duy người Việt", "cuộc tranh cãi về nghi thức cung đình", "công việc đầu tiên là ứng xử với di sản tinh thần của người Việt".
Chọn B
Câu 15:
 Xem đáp án
Xem đáp án
Đọc thông tin trong đoạn [2] của văn bản, kết hợp với hiểu biết cá nhân để tìm ra câu trả lời đúng. Di sản vật thể là những công trình kiến trúc, điêu khắc, việc bảo tồn là lưu giữ những giá trị văn hóa; cần phân biệt việc "bảo tồn" - lưu giữ cái cũ với "quy hoạch" - tổ chức, sắp xếp làm ra một hệ thống, cả cái mới và cái cũ.
Chọn B
Câu 16:
Vì sao Sài Gòn lại trở thành "đô thị được đặt ra như hai phép thử cho việc kiến thiết" với Hà Nội?
 Xem đáp án
Xem đáp án
Đọc nội dung đoạn [3], xác định "Sài Gòn và Hà Nội, hai đô thị này thường được đặt ra như hai phép thử cho việc kiến thiết cũng như xử lý mối quan hệ giữa hiện đại và truyền thống" và lý do Sài Gòn không phải đối diện với "thách thức của việc bảo tồn" là do: "Những thứ được truyền thông ngày nay tranh luận về việc bảo tồn, chính là những dấu mốc của quá trình hiện đại hóa Sài Gòn" - những thứ được coi là cũ ngày nay cũng chỉ mới đc xây dựng ở thế kỉ XIX.
Chọn A
Câu 17:
 Xem đáp án
Xem đáp án
Đọc nội dung đoạn [3] và tổng hợp ý kiến của nhà văn Sơn Nam, chú ý phân biệt giữa cái ban đầu (ý định đầu tiên" và cái cuối cùng, được quy hoạch lại "sau rốt lại đảo lộn kế hoạch". Trong đó, Pháp đã quy hoạch Sài Gòn: "lấp tất cả kinh rạch với đất từ vùng cao đem xuống", "lộ xe dùng cho xe có ngựa kéo".
Chọn D
Câu 18:
Theo nghiên cứu của nhà văn Sơn Nam, những con đường lớn của Sài Gòn ngày nay, trước đây, vốn là những kinh rạch rộng rãi, đổ ra sông Sài Gòn nhằm mục đích giao thương trong vùng là đúng hay sai?
 Xem đáp án
Xem đáp án
Đọc thông tin trong đoạn [3] của văn bản, xác định hệ thống đường giao thông chính của Sài Gòn ngày này là quá trình "mở rộng những con đường mòn có sẵn từ trước" và "thêm đường"; vậy nên, không phải tất cả những con đường lớn đều do lấp kênh rạch mà thành.
Chọn A
Câu 19:
 Xem đáp án
Xem đáp án
Đọc và xác định thông tin nằm trong đoạn [4] của văn bản: "dinh Norodom mang phong cách kiến trúc cổ điển đế chế đặc trưng những năm 1860-1870".
Chọn A
Câu 20:
 Xem đáp án
Xem đáp án
Tổng hợp thông tin bài viết kết hợp với phương pháp loại trừ, xác định: bài viết nêu lên mối quan hệ giữa hiện đại hóa và bảo tồn di sản văn hóa, dẫn chứng về quá trình hiện đại hóa ở nhiều nơi khác nhau: Hà Nội, Sài Gòn, Nam Định...
Chọn DCâu 21:
Phần tư duy khoa học / giải quyết vấn đề
Sao Diêm Vương có đường kính xấp xỉ
 Xem đáp án
Xem đáp án
Dựa trên những thông tin mà Nhà khoa học 1 cung cấp thì Sao Diêm Vương có đường kính xấp xỉ 1477 Mile.
Chọn A
Câu 22:
Điền từ/cụm từ thích hợp vào chỗ trống
Theo quan điểm của Nhà khoa học 2, so với các hành tinh khác của Hệ Mặt Trời, bề mặt của Sao Diêm Vương là (1) _____.
 Xem đáp án
Xem đáp án
Đáp án
Theo quan điểm của Nhà khoa học 2, so với các hành tinh khác của Hệ Mặt Trời, bề mặt của Sao Diêm Vương là (1) băng.
Giải thích
Theo lập lập của Nhà khoa học 2, ta có:
+ Sao Diêm Vương bao gồm chủ yếu gồm đá với băng, cũng như các sao chổi trong Vành đai Kuiper, trong khi các hành tinh khác của Hệ Mặt Trời thuộc một trong hai loại: đá hoặc khí.
+ Sao Diêm Vương không phải là đá hay khí mà có sông băng khổng lồ trên bề mặt nhưng sông băng này được tạo thành từ loại băng kỳ lạ. Chúng không phải băng nước như trên Trái Đất mà là băng được tạo ra từ nitrogen và methan, những thứ ở dạng khí trong bầu khí quyển của chúng ta.
→ Theo quan điểm của Nhà khoa học 2, so với các hành tinh khác của Hệ Mặt Trời, bề mặt của Sao Diêm Vương là băng.
Câu 23:
Câu nào sau đây mô tả đúng nhất điểm khác biệt chính giữa quan điểm của hai nhà khoa học?
 Xem đáp án
Xem đáp án
Hai nhà khoa học đang thảo luận về hành tinh Sao Diêm Vương nên được phân loại là một hành tinh, hay là một thiên thể khác.
Nhà khoa học 1 cho rằng Sao Diêm Vương vẫn được coi là một hành tinh, trong khi Nhà khoa học 2 lại cho rằng Sao Diêm Vương được phân loại chính xác hơn là một sao chổi thuộc Vành đai Kuiper.
Chọn D
Câu 24:
Kéo thả các từ vào vị trí thích hợp.
Trái Đất, Sao Diêm Vương, Sao Hải Vương, Sao Mộc
Các hình tinh và tiểu hành tinh trong hệ Mặt Trời đều chuyển động xung quanh Mặt Trời với quỹ đạo xác định. Bán kính quỹ đạo chuyển động của các hình tinh được sắp xếp là:
_______ < _______ < _______ < _______.
 Xem đáp án
Xem đáp án
Đáp án
Các hình tinh và tiểu hành tinh trong hệ Mặt Trời đều chuyển động xung quanh Mặt Trời với quỹ đạo xác định. Bán kính quỹ đạo chuyển động của các hình tinh được sắp xếp là:
Trái Đất < Sao Mộc < Sao Hải Vương < Sao Diêm Vương.
Giải thích
Vị trí thả (1): Trái Đất
Vị trí thả (2): Sao Mộc
Vị trí thả (3): Sao Hải Vương
Vị trí thả (4): Sao Diêm Vương
Câu 25:
Điền từ/cụm từ thích hợp vào chỗ trống
Sao Diem Vương không phải là đá hay khí mà bề mặt sao Diêm Vương là băng được cấu tạo từ (1) ________ và (2) _______.
 Xem đáp án
Xem đáp án
Đáp án
Sao Diem Vương không phải là đá hay khí mà bề mặt sao Diêm Vương là băng được cấu tạo từ (1) nitrogen và (2) methan.
Giải thích
Theo lập lập của Nhà khoa học 2, ta có:
Sao Diêm Vương không phải là đá hay khí mà có sông băng khổng lồ trên bề mặt nhưng sông băng này được tạo thành từ loại băng kỳ lạ. Chúng không phải băng nước như trên Trái Đất mà là băng được tạo ra từ nitrogen và methan, những thứ ở dạng khí trong bầu khí quyển của chúng ta.
Câu 26:
Theo quan điểm của Nhà khoa học 2 khi so sánh Sao Diêm Vương với các sao chổi của Vành đai Kuiper thì khẳng định nào sau đây là đúng nhất?
 Xem đáp án
Xem đáp án
Theo các lập luận của Nhà khoa học 2 thì Sao Diêm Vương là một vật thể thuộc Vành đai Kuiper và cả hai đều có những đặc điểm kỳ lạ: Quỹ đạo lệch tâm của Sao Diêm Vương cũng tương tự như hơn 70 sao chổi của Vành đai Kuiper.
Chọn B
Câu 27:
Phát biểu sau đúng hay sai?
Quan điểm của nhà khoa học 1 sẽ bị suy yếu khi các nhà khoa học gần đây đã phát hiện ra một sao chổi Vành đai Kuiper với bán kính gần 1500 Mile.
 Xem đáp án
Xem đáp án
Giải thích
Đáp án: Đúng
Một trong những lập luận mà Nhà khoa học 1 đưa ra để khẳng định Sao Diêm Vương không phải là một sao chổi là Sao Diêm Vương quá lớn.
Nếu một sao chổi được phát hiện với đường kính 1500 Mile, thì nó thậm chí còn lớn hơn Sao Diêm Vương, có đường kính 1477 Mile.
→ Điều này sẽ làm suy yếu lập luận của nhà khoa học nếu cho rằng: Sao Diêm Vương không thể là sao chổi vì sao chổi nhỏ hơn nhiều so với Sao Diêm Vương.
Chọn A
Câu 28:
Phát biểu sau đây đúng hay sai?
Theo thí nghiệm 1, phân lập B có số lượng vi khuẩn phát triển lớn nhất khi được cung cấp nguồn carbon là galactose.
 Xem đáp án
Xem đáp án
Nhìn vào bảng 1, ta thấy trong môi trường nuôi cấy chứa nguồn carbon là galactose thì chủng vi khuẩn được nuôi cấy trên đĩa B có sự tăng trưởng cao nhất.
Chọn A
Câu 29:
Dựa vào kết quả thí nghiệm 2, cho biết nếu đặt trong điều kiện nhiệt độ dưới nhiệt độ đóng băng của nước trong vòng 24 giờ thì sự phát triển của khuẩn lạc trong đĩa petri nào sẽ phát triển mạnh mẽ nhất?
 Xem đáp án
Xem đáp án
Nước đóng băng ở nhiệt độ 0oC, mà ta thấy ở kết quả của thí nghiệm 2, ở nhiệt độ 4oC không thấy sự sinh trưởng của vi khuẩn, nên rất có thể ở điều kiện nhiệt độ 0oC thì cũng không có khuẩn lạc nào có thể trải qua sự sinh trưởng.
Chọn D
Câu 30:
Kéo thả các từ vào vị trí thích hợp.
luôn giảm, giảm rồi tăng, tăng rồi giảm, luôn tăng
Xu hướng chung về sự phát triển của khuẩn lạc khi nhiệt độ giảm trong thí nghiệm 2 là _______.
 Xem đáp án
Xem đáp án
Đáp án
Xu hướng chung về sự phát triển của khuẩn lạc khi nhiệt độ giảm trong thí nghiệm 2 là tăng rồi giảm.
Giải thích
Quan sát bảng kết quả thí nghiệm 2, khi nhiệt độ giảm đi (42oC – 4oC) thì lượng khuẩn lạc trong thí nghiệm tăng dần rồi sau đó giảm đi.
Câu 31:
Giả sử thí nghiệm 3 được tiếp tục cho đến 34 giờ thay vì dừng lại ở 24 giờ (không xảy ra pha suy vong), thì mật độ quang học cuối cùng của đĩa C sẽ có giá trị gần nhất với
 Xem đáp án
Xem đáp án
Nhìn vào hình 1 ta thấy đường cong sinh trưởng của vi khuẩn thuộc đĩa C có xu hướng cân bằng từ 18 giờ tới 25 giờ, mà lại không xảy ra pha suy vong, thì lượng vi khuẩn sau 34h cũng sẽ xấp xỉ với giá trị tại 25 giờ, tức là gần nhất với giá trị 100.
Chọn C
Câu 32:
 Xem đáp án
Xem đáp án
Xem xét bảng kết quả thí nghiệm 1 và 2, ta thấy ở môi trường có nguồn carbon là pyruvate thì có lượng vi khuẩn sinh trưởng lớn nhất, tương tự ở 30oC lượng vi khuẩn phát triển trên mỗi môi trường cũng là lớn nhất.
Chọn B
Câu 33:
Giả sử trong thí nghiệm 3, mỗi lần hiệu chuẩn thay vì sử dụng nước cất sẽ sử dụng nước có vẩn đục, thì điều gì có thể xảy ra với đường cong sinh trưởng của vi khuẩn?
 Xem đáp án
Xem đáp án
Theo đoạn thông tin, máy đo quang phổ sẽ sử dụng tia laser để đo mật độ quang học của chất lỏng, khi mẫu đo càng đục thì giá trị đo được càng lớn. Nếu thay vì sử dụng nước cất, mà sử dụng nước đục để hiệu chuẩn thì giá trị OD đo được ở tất cả các môi trường đo đều sẽ có giá trị lớn hơn giá trị chuẩn.
Chọn C
Câu 34:
Phát biểu sau đây đúng hay sai?
Trong thí nghiệm 3, giai đoạn đầu vi khuẩn gần như không có sự gia tăng về số lượng chủ yếu do lượng vi khuẩn còn ít, sự gia tăng không đáng kể nên đồ thị gần như nằm ngang.
 Xem đáp án
Xem đáp án
Sai. Vì trong giai đoạn đầu này vi khuẩn đang làm quen với môi trường, hình thành các enzyme cảm ứng nên chưa có sự phân chia rõ rệt, nên đồ thị gần như ở trạng thái cân bằng.
Chọn B
Câu 35:
 Xem đáp án
Xem đáp án
Theo đoạn thứ 3 của phần dẫn: Cường độ của dòng điện (lượng điện tích (q) dịch chuyển qua tiết diện thẳng của vật dẫn trong thời gian (t))
→ Ngoài đơn vị là ampe (A), cường độ dòng điện có thể có đơn vị là Culông trên giây (C/s).
Chọn D
Câu 36:
Điện lượng dịch chuyển qua tiết diện thẳng của dây dẫn kim loại làm bằng Nickel có tiết diện 7,61.10−10 m2 và chiều dài 100 m ở thí nghiệm 1 trong 10 s là
 Xem đáp án
Xem đáp án
Từ Bảng 1, ta có đối với dây dẫn kim loại có chiều dài 100 m có: I = 1.10−3A
Mà cường độ của dòng điện (lượng điện tích (q) dịch chuyển qua tiết diện thẳng của vật dẫn trong thời gian (t))
\( \to I = \frac{q}{t} \to q = I.t = {10^{ - 3}}.10 = {10^{ - 2}}{\rm{C}}\)
Chọn C
Câu 37:
Trong sơ đồ hình vẽ trên, ampe kế được mắc nối với điện trở kim loại sao cho cực dương của ampe kế được mắc về cực dương của nguồn điện và cực âm của ampe kế được mắc về phía cực âm của nguồn điện.
Nội dung trên là đúng hay sai?
 Xem đáp án
Xem đáp án
Dòng điện chạy qua ampe kế có chiều đi vào chốt dương (+) và đi ra từ chốt âm (-).
→ Ampe kế được mắc nối với điện trở kim loại sao cho cực dương của ampe kế được mắc về cực dương của nguồn điện và cực âm của ampe kế được mắc về phía cực âm của nguồn điện
Chọn A
Câu 38:
Trong thí nghiệm 1, cường độ dòng điện qua mạch tăng và điện trở giảm khi (1) ________ của điện trở kim loại giảm.
 Xem đáp án
Xem đáp án
Đáp án
Trong thí nghiệm 1, cường độ dòng điện qua mạch tăng và điện trở giảm khi (1) chiều dài của điện trở kim loại giảm.
Giải thích
Trong Thí nghiệm 1, chỉ có chiều dài của điện trở kim loại được thay đổi.
Mặt khác, dựa theo kết quả trong Bảng 1 thì khi chiều dài của điện trở kim loại giảm, dòng điện tăng và điện trở giảm.
Câu 39:
Giả sử rằng khi ρ tăng, khả năng dẫn điện của kim loại giảm. Dựa vào kết quả của thí nghiệm 3, sắp xếp 3 kim loại nào sau đây là đúng theo thứ tự khả năng dẫn điện tăng dần?
 Xem đáp án
Xem đáp án
+ Theo thông tin ở câu hỏi, khi ρ tăng, khả năng dẫn điện của kim loại giảm tức là I giảm.
Dựa vào kết quả của Thí nghiệm 3 thể hiện trong Bảng 3 chỉ ra rằng khi trở tăng và dòng điện giảm.
Vì vàng có giá trị ρ thấp nhất nên nó phải là vật dẫn điện tốt nhất. Tương tự như vậy ta có thứ tự đúng là: thiếc, nickel, vàng.
Chọn C
Câu 40:
Nhận định sau là đúng hay sai?
Khi đóng công tắc trong mạch điện được mô tả trong phần dẫn, nguồn điện có tác dụng làm cho các electron (điện tử) chuyển động theo hướng được thể hiện bằng sơ đồ dưới đây:
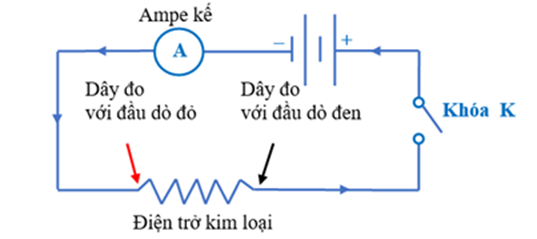
 Xem đáp án
Xem đáp án
Phần dẫn cho rằng khi mạch điện được đóng lại, các electron đi ra khỏi cực âm của nguồn, qua mạch và quay trở lại cực dương của nguồn điện.
→ Cách duy nhất để các electron có thể di chuyển từ cực âm sang cực dương khi đi qua mạch là đi ngược chiều kim đồng hồ.
Chọn A
Câu 41:
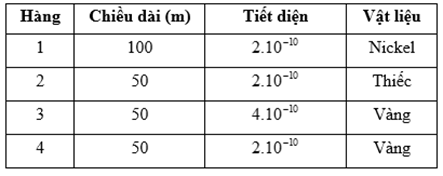
Dựa vào kết quả của cả 3 thí nghiệm hãy cho biết: Ở hiệu điện thế nhất định, dòng điện chạy qua điện trở kim loại bao gồm các thông số nào dưới dây có giá trị lớn nhất?
 Xem đáp án
Xem đáp án
Các kết quả trong Bảng 1 cho thấy dòng điện tăng khi chiều dài của điện trở kim loại giảm → Loại Hàng 1
Kết quả trong Bảng 2 cho thấy dòng điện tăng khi tiết diện của điện trở kim loại tăng
Kết quả trong Bảng 3 cho thấy kim loại vàng có độ dẫn điện cao nhất với tất cả các yếu tố khác bằng nhau
→ Hàng 3 đúng.
Chọn C
Câu 42:
Phát biểu sau đúng hay sai?
Học sinh 2 và 4 cho rằng thành phần phần trăm theo thể tích của khí argon trong không khí nhỏ hơn 1%.
 Xem đáp án
Xem đáp án
Đúng. Vì:
Theo đoạn văn, không ai trong số các sinh viên đề cập đến khí argon. Tuy nhiên, cả bốn sinh viên đều đề cập đến “gần như tất cả khí còn lại…”, điều này cho thấy rằng các loại khí khác có thể có mặt, chẳng hạn như argon. Trên thực tế, khí argon trong không khí ít hơn 1% theo thể tích.
Chọn A
Câu 43:
Điền số thích hợp vào chỗ trống
Dựa trên lời giải thích của học sinh 3, tổng hệ số của phương trình phản ứng xảy ra trong thí nghiệm là (1) _______.
 Xem đáp án
Xem đáp án
Đáp án
Dựa trên lời giải thích của học sinh 3, tổng hệ số của phương trình phản ứng xảy ra trong thí nghiệm là (1) __9__.
Giải thích
Theo học sinh 3, Fe đã phản ứng với O2 để tạo thành Fe2O3. Do đó, phương trình phản ứng sẽ là:
4Fe + 3O2 2Fe2O3.
Do đó, tổng hệ số của phương trình phản ứng xảy ra trong thí nghiệm là 9.
Câu 44:
Điền số thích hợp vào chỗ trống
Trong phản ứng hóa học, chất phản ứng hết là chất có nguồn cung cấp ít nhất và do đó hạn chế lượng sản phẩm được tạo thành. Học sinh (1) _________ đồng ý rằng chất phản ứng hết trong thí nghiệm là Fe trong len thép.
 Xem đáp án
Xem đáp án
Đáp án
Trong phản ứng hóa học, chất phản ứng hết là chất có nguồn cung cấp ít nhất và do đó hạn chế lượng sản phẩm được tạo thành. Học sinh (1) __2___ đồng ý rằng chất phản ứng hết trong thí nghiệm là Fe trong len thép.
Giải thích
Học sinh 1 cho rằng Fe đã phản ứng với toàn bộ khí N2 → N2 hết và Fe dư.
Học sinh 2 cho rằng Fe phản ứng với một phần khí O2 → Fe hết và O2 còn dư.
Học sinh 3 cho rằng Fe phản ứng với toàn bộ khí O2 → O2 hết và Fe dư.
Học sinh 4 cho rằng len thép phản ứng với toàn bộ khí CO2 → CO2 hết và Fe dư.
Câu 45:
 Xem đáp án
Xem đáp án
Nước màu được sử dụng trong thí nghiệm nhằm mục đích ngăn không khí thoát ra ngoài và xác định thể tích khí chính xác hơn.
Chọn C
Câu 46:
 Xem đáp án
Xem đáp án
Theo học sinh 1, Fe trong len thép đã phản ứng với khí N2 trong không khí tạo ra FeN.
Học sinh 2 nói rằng Fe trong len thép đã phản ứng với một phần khí O2 trong không khí tạo ra Fe2O3.
Học sinh 3 nói rằng Fe trong len thép đã phản ứng với toàn bộ khí O2 trong không khí tạo ra Fe2O3.
Học sinh 4 cho rằng Fe trong len thép đã phản ứng với khí CO2 trong không khí tạo ra FeCO3.
→ Học sinh 2 và 3 đều cho rằng Fe trong len thép đã phản ứng với khí O2 trong không khí tạo ra Fe2O3.
Chọn B
Câu 47:
Học sinh nào cho rằng sau phản ứng, khí còn lại trong thiết bị là N2 chiếm ít nhất 20,7% theo thể tích?
 Xem đáp án
Xem đáp án
Học sinh 1 và 4 đều cho rằng: sau phản ứng, gần như tất cả khí còn lại trong thiết bị là O2 và chiếm khoảng 79,3% thể tích không khí.
Học sinh 2 cho rằng: sau phản ứng, khí còn lại trong thiết bị là hỗn hợp của khoảng 75% O2 và 4,3% N2.
Học sinh 3 cho rằng: sau phản ứng, gần như tất cả khí còn lại trong thiết bị là N2 và chiếm khoảng 79,3% thể tích không khí.
→ Chỉ có học sinh 3 sẽ đồng ý rằng lượng khí còn lại trong thiết bị là N2 chiếm ít nhất 20,7% theo thể tích.
Chọn B
Câu 48:
Kéo thả các từ vào vị trí thích hợp.
quy mô quần thể, tốc độ sinh trưởng, thời gian kiếm ăn, tỉ lệ sinh sản/ tử vong
Theo nhà nghiên cứu 1, yếu tố _______ không thể theo dõi một cách dễ dàng ở loài chim biển.
 Xem đáp án
Xem đáp án
Đáp án
Theo nhà nghiên cứu 1, yếu tố tỉ lệ sinh sản/tử vong không thể theo dõi một cách dễ dàng ở loài chim biển.
Giải thích
Theo đoạn thông tin: “...Các thông số có thể dễ dàng theo dõi ở loài chim biển là quy mô quần thể, thời gian của các chuyến đi kiếm ăn, những thay đổi về khối lượng cơ thể và tốc độ tăng trưởng của con cái.”
Câu 49:
Cá mòi có rất nhiều ở vịnh Chiriqui và sự hiện diện của chúng ảnh hưởng đến toàn bộ hệ sinh thái của vịnh. Chim bói cá chủ yếu ăn cá mòi. Sự suy giảm số lượng của chím bói cá làm các nhà khoa học lo ngại vấn đề môi trường của vịnh Chiriqui. Lo ngại này có phù hợp quan điểm của nhà nghiên cứu 1 không?
 Xem đáp án
Xem đáp án
Theo đoạn thông tin: “...Quần thể chim biển và tỉ lệ sinh sản của chúng được điều chỉnh bởi sự đa dạng phong phú của con mồi, do đó sẽ phản ánh những thay đổi do môi trường gây ra ảnh hưởng tới số lượng con mồi.”
Chọn D
Câu 50:
Một nghiên cứu cho thấy rằng trong vòng hai tháng sau khi xảy ra sự cố tràn dầu ở vịnh, số lượng cá nhỏ tìm thấy trong nước đã giảm đáng kể và số lượng chim biển trong khu vực cũng giảm mạnh. Nhà nghiên cứu nào rất có thể sẽ sử dụng nghiên cứu này để hỗ trợ cho quan điểm của mình?
 Xem đáp án
Xem đáp án
Giải thích
Nhà nghiên cứu 1 cho rằng sự thay đổi của môi trường ảnh hưởng đến số lượng con mồi (cá) sẽ làm ảnh hưởng đến số lượng của loài săn mồi (chim biển). Như vậy nghiên cứu về sự cố tràn dầu này sẽ ủng hộ quan điểm của nhà nghiên cứu 1.
Chọn A
Câu 51:
Biểu đồ nào sau đây phù hợp với quan điểm của nhà nghiên cứu 1 về mối quan hệ giữa số lượng con mồi với quần thể chim biển?
 Xem đáp án
Xem đáp án
Giải thích
Nhà nghiên cứu 1 cho rằng số lượng con mồi và chim biển phụ thuộc vào nhau, số lượng con mồi tăng, thì số lượng chim biển tăng và ngược lại, số lượng con mồi giảm thì số lượng chim biển giảm.
Chọn A
Câu 52:
Phát biểu sau đây đúng hay sai?
Nhà nghiên cứu 2 cho rằng việc sử dụng chim biển làm sinh vật chỉ thị là tốn kém nhiều về mặt chi phí.
 Xem đáp án
Xem đáp án
Nhà nghiên cứu 2 không đề cập đến chi phí khi sử dụng chim biển làm sinh vật chỉ thị. Còn nhà nghiên cứu 1 cho rằng việc sử dụng chim biển làm sinh vật chỉ thị là phù hợp về nhu cầu chi phí.
Chọn B
Câu 53:
Điền số thích hợp vào chỗ trống
Cây đước là một loài thực vật ngập mặn, phát triển tốt trong môi trường rừng ngập mặn nên được chọn làm sinh vật chỉ thị cho môi trường ngập mặn. Ngược lại, cây cỏ hôi có độ rộng nồng độ muối lớn thì không có khả năng làm chỉ thị cho môi trường ngập mặn. Ví dụ này tương ứng với chỉ tiêu số (1) ________ trong việc chọn lựa sinh vật chỉ thị.
 Xem đáp án
Xem đáp án
Đáp án
Cây đước là một loài thực vật ngập mặn, phát triển tốt trong môi trường rừng ngập mặn nên được chọn làm sinh vật chỉ thị cho môi trường ngập mặn. Ngược lại, cây cỏ hôi có độ rộng nồng độ muối lớn thì không có khả năng làm chỉ thị cho môi trường ngập mặn. Ví dụ này tương ứng với chỉ tiêu số (1) ___3____ trong việc chọn lựa sinh vật chỉ thị.
Giải thích
Chỉ tiêu số 3 là: “Các loài có độ thích ứng hẹp thường là vật chỉ thị tốt hơn loài thích ứng rộng.” Độ thích ứng ở đây là khả năng phát triển trong điều kiện nồng độ muối cao.
Câu 54:
Quan điểm của nhà nghiên cứu nào cho rằng việc xử lý thông tin thu thập từ loài chim biển không thể chắc chắn hoàn toàn chính xác và hợp lệ?
 Xem đáp án
Xem đáp án
Theo đoạn thông tin: “...Nhưng cũng không thể phân biệt chính xác nguyên nhân gây nên những sự thay đổi đó, là từ môi trường hay từ các tác động vật lí, hóa học trong quá trình theo dõi chúng của con người.”
Chọn C
Câu 55:
Phát biểu sau đúng hay sai?
Dựa trên lời giải thích của học sinh 3, trong các khí được liệt kê ở Bảng 1 thì xenon lan ra nhanh nhất ở 25°C.
 Xem đáp án
Xem đáp án
Học sinh 3 cho rằng chất khí có mật độ lớn hơn thì lan chậm hơn. Trong số các chất khí được liệt kê ở Bảng 1 thì hydrogen có mật độ phân tử nhỏ nhất (0,089 kg/l) nên sẽ lan ra nhanh nhất. Trong khi xenon có mật độ phân tử lớn nhất (5,894 kg/l) nên sẽ lan ra chậm nhất.
Chọn B
Câu 56:
Điền từ/cụm từ thích hợp vào chỗ trống
Phát biểu "Ở 25°C, xenon lan chậm hơn krypton" phù hợp với lời giải thích của (1) ___________.
 Xem đáp án
Xem đáp án
Đáp án
Điền từ/cụm từ thích hợp vào chỗ trống
Phát biểu "Ở 25°C, xenon lan chậm hơn krypton" phù hợp với lời giải thích của (1) cả 3 học sinh.
Giải thích
Học sinh 1 cho rằng chất khí có khối lượng phân tử lớn hơn thì lan chậm hơn.
Học sinh 2 cho rằng chất khí có thể tích phân tử lớn hơn thì lan chậm hơn.
Học sinh 3 cho rằng chất khí có mật độ lớn hơn thì lan chậm hơn.
Theo Bảng 1, khối lượng, thể tích và mật độ phân tử của xenon đều lớn hơn krypton.
Do đó, cả 3 học sinh đều dự đoán xenon lan chậm hơn.
Câu 57:
Để giải thích cho sự khác nhau về tổng thời gian tràn khí của khí A và khí B trong thí nghiệm trên, học sinh 3 cho rằng
 Xem đáp án
Xem đáp án
Để giải thích cho sự khác nhau về tổng thời gian tràn khí của khí A và khí B trong thí nghiệm, học sinh 1 cho rằng các khí có khối lượng phân tử lớn hơn sẽ lan chậm hơn.
Chọn B
Câu 58:
Dựa trên lời giải thích của học sinh 2, trong các khí được liệt kê ở Bảng 1 thì chất khí nào lan ra nhanh nhất ở 25°C.
 Xem đáp án
Xem đáp án
Học sinh 2 cho rằng chất khí có thể tích phân tử lớn hơn thì lan chậm hơn.Trong số các chất khí được liệt kê ở Bảng 1 thì helium có thể tích phân tử nhỏ nhất (11,46 ÅÅ3) nên sẽ lan ra nhanh nhất.
Chọn C
Câu 59:
Cho các dữ liệu về carbon dioxide ở 25°C được liệt kê trong bảng sau:
|
Khối lượng phân tử (amu) |
Thể tích phân tử (Å3) |
Mật độ phân tử( kg/l) |
|
44,01 |
34,87 |
1,77 |
Học sinh nào dự đoán rằng carbon dioxide có thời gian tràn khí ngắn hơn krypton?
 Xem đáp án
Xem đáp án
Học sinh 1 cho rằng chất khí có khối lượng phân tử lớn hơn thì lan chậm hơn.
Học sinh 2 cho rằng chất khí có thể tích phân tử lớn hơn thì lan chậm hơn.
Học sinh 3 cho rằng chất khí có mật độ lớn hơn thì lan chậm hơn.
Theo thông tin được cung cấp trong bảng trên và Bảng 1, khối lượng và mật độ phân tử của krypton lớn hơn carbon dioxide, trong khi thể tích phân tử của carbon dioxide lớn hơn krypton.
Do đó, học sinh 1 và 3 sẽ dự đoán rằng carbon dioxide sẽ lan nhanh hơn krypton (thời gian tràn khí ngắn hơn).
Chọn A
Câu 60:
Điền từ/cụm từ thích hợp vào chỗ trống
Để giải thích cho sự khác nhau về tổng thời gian tràn khí của khí A và khí B trong thí nghiệm trên, học sinh 2 cho rằng các khí có (1) ________ lớn hơn sẽ lan chậm hơn.
 Xem đáp án
Xem đáp án
Đáp án
Điền từ/cụm từ thích hợp vào chỗ trống
Để giải thích cho sự khác nhau về tổng thời gian tràn khí của khí A và khí B trong thí nghiệm trên, học sinh 2 cho rằng các khí có (1) thể tích phân tử lớn hơn sẽ lan chậm hơn.
Giải thích
Để giải thích cho sự khác nhau về tổng thời gian tràn khí của khí A và khí B trong thí nghiệm, học sinh 2 cho rằng các khí có thể tích phân tử lớn hơn sẽ lan chậm hơn
Câu 61:
Một công ty vận tải cung cấp dịch vụ tour du lịch tại một số địa điểm trong địa bàn thành phố Hồ Chí Minh. Bảng số liệu sau cho ta thông tin về giá vé xe buýt tại các điểm dừng chân trong tour du lịch này như sau:
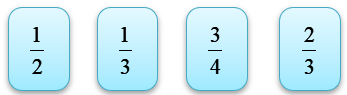
Một du khách muốn tự mình trải nghiệm nên tự bắt xe đi ngẫu nhiên giữa các địa điểm như sau:
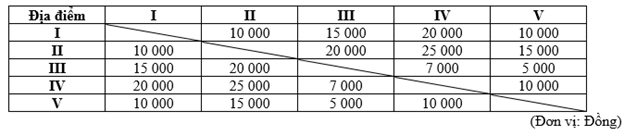
a) Bắt một chuyến xe đi từ địa điểm I đến một địa điểm bất kì. Khi đó, xác suất người đó phải trả dưới 20 000 đồng tiền vé xe buýt là _______.
b) Đi từ địa điểm I đến địa điểm III qua 1 trạm trung gian. Khi đó, xác suất người đó trả trên 25 000 đồng tiền vé xe buýt là _______.
 Xem đáp án
Xem đáp án
Đáp án
a) Bắt một chuyến xe đi từ địa điểm I đến một địa điểm bất kì. Khi đó, xác suất người đó phải trả dưới 20 000 đồng tiền vé xe buýt là \(\frac{3}{4}\).
b) Đi từ địa điểm I đến địa điểm III qua 1 trạm trung gian. Khi đó, xác suất người đó trả trên 25 000 đồng tiền vé xe buýt là \(\frac{2}{3}\).
Giải thích
a) Có 4 cách để đi từ địa điểm I đến 1 địa điểm bất kì, trong đó có 3 cách để chỉ tốn dưới 20 000 đồng tiền vé xe buýt là đi theo tuyến I – II, I – III, I – V. Vậy xác suất cần tìm là \[\frac{3}{4}\].
b) Để đi từ địa điểm I đến địa điểm III qua 1 trạm trung gian ta có bảng sau:

Từ bảng ta có 2 cách để người đó phải trả trên 25 000 đồng là đi theo tuyến I – II – III, I – IV – III .
Vậy xác suất cần tìm là \[\frac{2}{3}\].
Câu 62:
 Xem đáp án
Xem đáp án
Giải thích
Để hàm số có đạo hàm tại \(x = 2\) thì hàm số phải liên tục tại \(x = 2\).
Do đó .
Hàm số có đạo hàm tại điểm \(x = 2\) nên
\(\mathop {\lim }\limits_{x \to {2^ - }} \frac{{f(x) - f(2)}}{{x - 2}} = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{f(x) - f(2)}}{{x - 2}}\)
\( \Leftrightarrow \mathop {\lim }\limits_{x \to {2^ - }} \frac{{{x^3} - {x^2} - 8x + 10 - ( - 2)}}{{x - 2}} = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{{x^2} + ax + b - (4 + 2a + b)}}{{x - 2}}\)
\( \Leftrightarrow \mathop {\lim }\limits_{x \to {2^ - }} \left( {{x^2} + x - 6} \right) = \mathop {\lim }\limits_{x \to {2^ + }} (x + 2 + a)\)
\( \Leftrightarrow 4 + a = 0 \Leftrightarrow a = - 4\).
Suy ra \(b = 2\). Vậy \(ab = - 8\).
Chọn D
Câu 63:
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Tồn tại hình đa diện có số đỉnh bằng số mặt. |
||
|
Có 5 khối đa diện đều lần lượt là: {3;3}; {3;4}; {4;3} ;{3;5};{5;3}. |
||
|
Chỉ có duy nhất một khối đa diện đều mà mỗi mặt của nó là một tam giác đều. |
||
|
Trong một hình đa diện, mỗi cạnh là cạnh chung của ba mặt. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Tồn tại hình đa diện có số đỉnh bằng số mặt. |
X | |
|
Có 5 khối đa diện đều lần lượt là: {3;3}; {3;4}; {4;3} ;{3;5};{5;3}. |
X | |
|
Chỉ có duy nhất một khối đa diện đều mà mỗi mặt của nó là một tam giác đều. |
X | |
|
Trong một hình đa diện, mỗi cạnh là cạnh chung của ba mặt. |
X |
Giải thích
+ Khối tứ diện đều có 4 đỉnh và 4 mặt.
+ Có 5 khối đa diện đều lần lượt là: {3;3}; {3;4}; {4;3} ;{3;5};{5;3}.
+ Có ba loại khối đa diện đều mà mỗi mặt của nó là một tam giác đều là: khối tứ diện đều, khối bát diện đều và khối hai mươi mặt đều.
+ Trong một hình đa diện, mỗi cạnh là cạnh chung của hai mặt.
Câu 64:
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ.
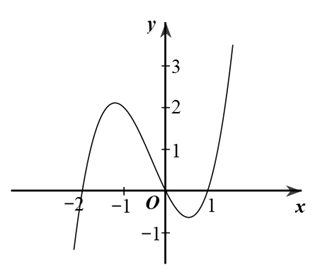
Đồ thị hàm số \(y = - \frac{1}{{f\left( x \right) + 1}}\) có bao nhiêu đường tiệm cận?
 Xem đáp án
Xem đáp án
Giải thích
Ta có:
\( \Rightarrow y = 0\) là tiệm cận ngang của đồ thị hàm số \(y = - \frac{1}{{f\left( x \right) + 1}}\).
Mặt khác, phương trình \(f\left( x \right) + 1 = 0\) có nghiệm duy nhất.
\( \Rightarrow \) Đồ thị hàm số \(y = - \frac{1}{{f\left( x \right) + 1}}\) có 1 đường tiệm cận đứng.
Vậy đồ thị hàm số đã cho có 2 đường tiệm cận.
Chọn C
Câu 65:
Ta gọi số nguyên bé nhất không nhỏ hơn x là phần nguyên trên của x, ký hiệu \(\left\lceil x \right\rceil \)
Chẳng hạn \(\left\lceil { - 2,5} \right\rceil = - 2,\left\lceil {\frac{{19}}{6}} \right\rceil = 4\)
Tổng phần nguyên trên của tất cả các số có dạng \(\frac{{\rm{k}}}{2}\) với \({\rm{k}}\) nguyên lấy giá trị từ -4 đến 4 bằng
 Xem đáp án
Xem đáp án
Chọn A
Câu 66:
Cho sơ đồ mạch điện có 6 công tắc khác nhau, trong đó mỗi công tắc có hai trạng thái đóng và mở như hình vẽ.
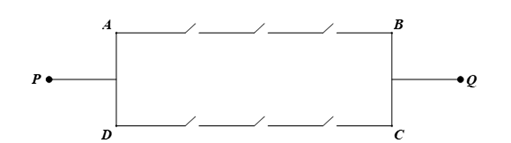
Một người bật ngẫu nhiên các công tắc. Xác suất để mạch điện thông từ P đến Q là bao nhiêu phần trăm? (Kết quả làm tròn đến chữu số thập phân thứ nhất)
 Xem đáp án
Xem đáp án
Giải thích
Mỗi cách đóng - mở 6 công tắc của mạch điện được gọi là một trạng thái của mạch điện.
Ta có: \(n\left( {\rm{\Omega }} \right) = {2^6} = 64\) trạng thái.
Gọi \(A\) là biến cố: "Mạch điện thông từ \(P\) đến \(Q\) ".
\( \Rightarrow \overline A \) là biến cố: “Mạch điện không thông từ \(P\) đến \(Q\) ”.
Vì mạch gồm hai nhánh \(A \to B\) và \(C \to D\) nên trạng thái không thông mạch xảy ra \( \Leftrightarrow \) Hai nhánh \(A \to B\) và \(C \to D\) đều không thông mạch.
Xét nhánh \(A \to B\) có \({2^3} = 8\) trạng thái trong đó có duy nhất một trạng thái thông mạch.
\( \Rightarrow \) Nhánh \(A \to B\) có \(8 - 1 = 7\) trạng thái không thông mạch.
Tương tự, nhánh \(C \to D\) có 7 trạng thái không thông mạch.
\( \Rightarrow \) Có \(7.7 = 49\) trạng thái mà hai nhánh \(A \to B\) và \(C \to D\) đều không thông mạch.
\( \Rightarrow n\left( {\overline A } \right) = 49 \Rightarrow n\left( A \right) = 64 - 49 = 15 \Rightarrow P\left( A \right) = \frac{{15}}{{64}} \approx 23,4{\rm{\% }}\).
Chọn A
Câu 67:
 Xem đáp án
Xem đáp án
Giải thích
Số phần tử của không gian mẫu là \(n\left( {\rm{\Omega }} \right) = C_{30}^6\).
Trong 30 tấm thẻ có 15 tấm thẻ mang số lẻ, 7 tấm thẻ mang số chẵn và chia hết cho 4,8 tấm thẻ mang số chẵn và không chia hết cho 4.
Gọi \(A\) là biến cố cần tính xác suất, ta có \(n\left( A \right) = C_{15}^3.C_8^2.C_7^1\).
Xác suất cần tìm là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( {\rm{\Omega }} \right)}} = \frac{{C_{15}^3.C_8^2.C_7^1}}{{C_{30}^6}} = \frac{{196}}{{1305}} \approx 15{\rm{\% }}\).
Chọn C
Câu 68:
Cho hình chóp \(S.ABCD\) có tọa độ các điểm \(A\left( { - 2;2;6} \right),B\left( { - 3;1;8} \right),C\left( { - 1;0;7} \right),D\left( {1;2;3} \right)\). Gọi \(H\) là trung điểm của \(CD\) và \(SH\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Biết \(S\left( {a;b;c} \right)\) (với \(a,b,c\) là các giá trị dương) là điểm thỏa mãn thể tích khối chóp \(S.ABCD\) bằng \(\frac{{27}}{2}\) (đvtt). Tổng giá trị của \(a + b + c\) bằng
 Xem đáp án
Xem đáp án
Giải thích
Ta có:
\(\overrightarrow {AB} = \left( { - 1; - 1;2} \right),\overrightarrow {AC} = \left( {1; - 2;1} \right) \Rightarrow \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {3;3;3} \right) \Rightarrow {S_{ABC}} = \frac{1}{2}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]} \right| = \frac{{3\sqrt 3 }}{2}\)
Lại có: \(\overrightarrow {DC} = \left( { - 2; - 2;4} \right),\overrightarrow {AB} = \left( { - 1; - 1;2} \right) \Rightarrow \overrightarrow {DC} = 2\overrightarrow {AB} \)
\( \Rightarrow ABCD\) là hình thang và \({S_{ABCD}} = 3{S_{ABC}} = \frac{{9\sqrt 3 }}{2}\).
Vì \({V_{S.ABCD}} = \frac{1}{3}SH.{S_{ABCD}} \Rightarrow SH = 3\sqrt 3 \)
Lại có \(H\) là trung điểm của \(CD \Rightarrow H\left( {0;1;5} \right)\)
Gọi \(S\left( {a;b;c} \right) \Rightarrow \overrightarrow {SH} = \left( { - a;1 - b;5 - c} \right) \Rightarrow \overrightarrow {SH} = k\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = k\left( {3;3;3} \right) = \left( {3k;3k;3k} \right)\)
Suy ra \(3\sqrt 3 = \sqrt {9{k^2} + 9{k^2} + 9{k^2}} \Rightarrow k = \pm 1\)
+) Với \(k = 1 \Rightarrow \overrightarrow {SH} = \left( {3;3;3} \right) \Rightarrow {S_1}\left( { - 3; - 2;2} \right)\)
+) Với \(k = - 1 \Rightarrow \overrightarrow {SH} = \left( { - 3; - 3; - 3} \right) \Rightarrow {S_2}\left( {3;4;8} \right)\)
\( \Rightarrow a = 3;b = 4;c = 8 \Rightarrow a + b - c = - 1\).
Chọn C
Câu 69:
 Xem đáp án
Xem đáp án
Giải thích
Số các số thuộc \(M\) là \(A_5^3 + A_5^4 + A_5^5 = 300\).
Các tập con của \(E\) có tổng các phần tử bằng 10 gồm \({E_1} = \left\{ {1;2;3;4} \right\},{E_2} = \left\{ {2;3;5} \right\}\),\({E_3} = \left\{ {1;4;5} \right\}\).
Gọi \(A\) là tập con của \(M\) sao cho mỗi số thuộc \(A\) có tổng các chữ số bằng 10 .
Từ \({E_1}\) lập được số các số thuộc \(A\) là 4!.
Từ mỗi tập \({E_2}\) và \({E_3}\) lập được các số thuộc \(A\) là 3!.
Suy ra số phần tử của \(A\) là \(4! + 2.3! = 36\).
Xác suất cần tìm là \(P = \frac{{36}}{{300}} = \frac{3}{{25}}\).
Chọn B
Câu 70:
Cho một cái hộp có nắp có dạng hình trụ có bán kính đáy là 10cm và khoảng cách giữa hai đáy là 56cm. Thả các quả bóng có dạng hình cầu vào trong hộp sao cho các quả bóng tiếp xúc với thành hộp theo một đường tròn và tiếp xúc với nhau. Gọi (P) là mặt phẳng song song với trục và cắt hình trụ theo thiết diện ABCD.
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
ĐÚNG |
SAI |
|
Thể tích của hộp là \(5600\pi {\rm{c}}{{\rm{m}}^3}\). |
||
|
Hộp đựng được tối đa 4 quả bóng. |
||
|
Để diện tích \(ABCD\) bằng \(80{\rm{\;c}}{{\rm{m}}^2}\) thì khoảng cách từ trục đến mặt phẳng \(\left( P \right)\) là \(\frac{{465}}{{49}}{\rm{\;cm}}\). |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Thể tích của hộp là \(5600\pi {\rm{c}}{{\rm{m}}^3}\). |
X | |
|
Hộp đựng được tối đa 4 quả bóng. |
X | |
|
Để diện tích \(ABCD\) bằng \(80{\rm{\;c}}{{\rm{m}}^2}\) thì khoảng cách từ trục đến mặt phẳng \(\left( P \right)\) là \(\frac{{465}}{{49}}{\rm{\;cm}}\). |
X |
Giải thích
Thể tích của hộp là \(V = \pi {R^2}h = \pi {.10^2}.56 = 5600\pi \left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Tổng chiều cao của \(n\) quả bóng thả trong hộp là: \(2nR = 2n.10 = 20n\).
Ta có: \(20n \le 56 \Leftrightarrow n \le 2,8\).
Vậy hộp chỉ đựng được tối đa 2 quả bóng.
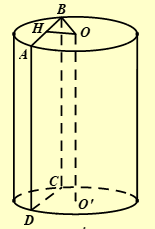
Vì \(\left( P \right)//OO'\) nên \(d\left( {OO';\left( P \right)} \right) = d\left( {O;\left( P \right)} \right) = OH\) (với \(H\) là trung điểm cạnh \(AB\))
Ta có: \({S_{ABCD}} = 80 \Leftrightarrow AB.AD = 80 \Leftrightarrow AB = \frac{{10}}{7}\left( {AD = h = 56} \right)\)
\( \Leftrightarrow 2BH = \frac{{10}}{7} \Leftrightarrow \sqrt {{R^2} - O{H^2}} = \frac{5}{7} \Leftrightarrow OH = \frac{{5\sqrt {149} }}{7}\left( {{\rm{cm}}} \right)\)
Câu 71:
 Xem đáp án
Xem đáp án
Giải thích
Ta có:
+) \(\left( P \right):x + y + z - 1 = 0\) có VTPT \(\vec a = \left( {1;1;1} \right)\)
\( + )\left( Q \right):2x + my + 2z + 3 = 0\) có VTPT \(\vec b = \left( {2;m;2} \right)\)
\( + )\left( R \right): - x + 2y + nz = 0\) có VTPT \(\vec c = \left( { - 1;2;n} \right)\)
\(\left( P \right) \bot \left( R \right) \Leftrightarrow \vec a.\vec c = 0 \Leftrightarrow n = - 1\)
\(\left( P \right)//\left( Q \right) \Leftrightarrow \frac{2}{1} = \frac{m}{1} = \frac{2}{1} \ne \frac{3}{{ - 1}} \Leftrightarrow m = 2\)
Vậy \(m + 2n = 2 + 2\left( { - 1} \right) = 0\).
Chọn C
Câu 72:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { - 1;2} \right]\) và có đồ thị như hình vẽ
![Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { - 1;2} \right]\) và có đồ thị như hình vẽ Biết diện tích các hình phẳng \(\left( K \right),\left( H \right)\) lần lượt là \(\frac{5}{{12}}\) và \(\frac{8}{3}\). Giá trị của \(I = \int\limits_{ - 3}^0 {xf'\left( {x + 2} \right)dx} \) là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/11/blobid18-1731398725.png)
Biết diện tích các hình phẳng \(\left( K \right),\left( H \right)\) lần lượt là \(\frac{5}{{12}}\) và \(\frac{8}{3}\). Giá trị của \(I = \int\limits_{ - 3}^0 {xf'\left( {x + 2} \right)dx} \) là
 Xem đáp án
Xem đáp án
Giải thích
Ta có: \(I = \int\limits_{ - 3}^0 {xf'\left( {x + 2} \right)dx} = \int\limits_{ - 1}^2 {\left( {x - 2} \right)f'\left( x \right)dx} \).
Đặt \(\left\{ {\begin{array}{*{20}{l}}{u = x - 2}\\{dv = f'\left( x \right)dx}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{du = dx}\\{v = f\left( x \right)}\end{array}} \right.} \right.\)
Chọn A
Câu 73:
 Xem đáp án
Xem đáp án
Giải thích
Cách 1.
Gọi \(d\) là giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).
\(\overrightarrow {{n_{\left( P \right)}}} = \left( {1;1;1} \right),\overrightarrow {{n_{\left( Q \right)}}} = \left( {2;1; - 1} \right)\).
\(\overrightarrow {{u_d}} = \left[ {\overrightarrow {{n_{\left( P \right)}}} ,\overrightarrow {{n_{\left( Q \right)}}} } \right] = \left( { - 2;3; - 1} \right)\).
Chọn điểm \(M\left( {0;4; - 1} \right)\) thuộc hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).
Phương trình đường thẳng \(d\) là \(\frac{x}{{ - 2}} = \frac{{y - 4}}{3} = \frac{{z + 1}}{{ - 1}}\).
Cách 2.
Gọi \(d\) là giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) thì với mỗi điểm \(M\left( {x;y;z} \right) \in d\) là nghiệm của hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x + y + z = 3}\\{2x + y - z = 5}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3x + 2y = 8}\\{z = 2x + y - 5}\end{array}} \right.} \right.\)
Cho \(x = 2t\left( {t \in \mathbb{R}} \right)\) thì từ hệ phương trình trên ta thu được \(\left\{ {\begin{array}{*{20}{l}}{y = 4 - 3t}\\{z = - 1 + t}\end{array}} \right.\)
Vậy phương trình của đường thẳng \(d\) là \(\left\{ {\begin{array}{*{20}{l}}{x = 2t}\\{y = 4 - 3t\left( {t \in \mathbb{R}} \right){\rm{.\;}}}\\{z = - 1 + t}\end{array}} \right.\)
Chọn A
Câu 74:
 Xem đáp án
Xem đáp án
Giải thích
Để đường thẳng \(x = 2\) là tiệm cận đứng của đồ thị hàm số thì \(x = 2\) là nghiệm của phương trình \({x^2} - {m^2} - 1 = 0 \Leftrightarrow {2^2} - {m^2} - 1 = 0 \Leftrightarrow m = \pm \sqrt 3 \).
Thử lại, với \(m = \pm \sqrt 3 \) ta có: \(y = x + \frac{1}{{\sqrt {{x^2} - 4} }}\)
\( \Rightarrow \) Đường thẳng \(x = 2\) là tiệm cận đứng của đồ thị hàm số.
Vậy có 2 giá trị của tham số \(m\) thỏa mãn.
Chọn C
Câu 75:
 Xem đáp án
Xem đáp án
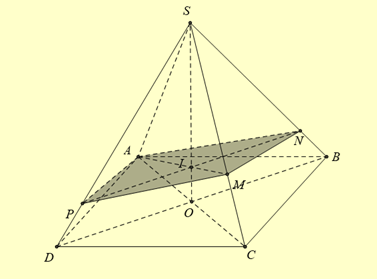
Gọi \(O = AC \cap BD,I = AM \cap SO\).
Trong \(\left( {SBD} \right)\) từ \(I\) kẻ đường thẳng \({\rm{\Delta }}\) song song với \(BD\) cắt \(SB,SD\) lần lượt tại \(N,P\).
Suy ra thiết diện là tứ giác \(ANMP\).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BD \bot AC}\\{BD \bot SO}\end{array} \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot AM} \right.\).
Mặt khác: \(BD//NP\).
\( \Rightarrow AM \bot NP \Rightarrow {S_{ANMP}} = \frac{1}{2}NP.AM\).
+ Tính \(AM\):
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{SA = SC = 3}\\{AC = 3\sqrt 2 }\end{array} \Rightarrow {\rm{\Delta }}SAC} \right.\) vuông cân tại \(S \Rightarrow AM = \sqrt {S{A^2} + S{M^2}} = \sqrt {{3^2} + {2^2}} = \sqrt {13} \).
+ Tính \(NP\):
Ta có: \(NP//BD \Rightarrow \frac{{NP}}{{BD}} = \frac{{SI}}{{SO}} \Rightarrow NP = \frac{{SI.BD}}{{SO}}\).
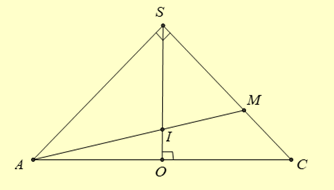
Gọi \(\frac{{SI}}{{SO}} = k\).
Ta có: \(\overrightarrow {AI} = \overrightarrow {AS} + \overrightarrow {SI} = - \overrightarrow {SA} + k\overrightarrow {SO} \).
\(\overrightarrow {AM} = \overrightarrow {AS} + \overrightarrow {SM} = - \overrightarrow {SA} + \frac{2}{3}\overrightarrow {SC} \)
\(A,I,M\) thẳng hàng \( \Leftrightarrow \overrightarrow {AI} = l\overrightarrow {AM} \Leftrightarrow - \overrightarrow {SA} + k\overrightarrow {SO} = - l\overrightarrow {SA} + \frac{2}{3}l\overrightarrow {SC} \)
\( \Leftrightarrow - \overrightarrow {SA} + \frac{k}{2}\left( {\overrightarrow {SA} + \overrightarrow {SC} } \right) = - l\overrightarrow {SA} + \frac{2}{3}l\overrightarrow {SC} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{1}{2}k + l = 1}\\{\frac{1}{2}k - \frac{2}{3}l = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{k = \frac{4}{5}}\\{l = \frac{3}{5}}\end{array}} \right.} \right.\).
\( \Rightarrow \frac{{SI}}{{SO}} = \frac{4}{5} \Rightarrow NP = \frac{4}{5}BD = \frac{{12\sqrt 2 }}{5}\).
\( \Rightarrow {S_{ANMP}} = \frac{1}{2}NP.AM = \frac{1}{2}.\frac{{12\sqrt 2 }}{5}.\sqrt {13} = \frac{{6\sqrt {26} }}{5} \approx 6,12\).
Chọn A
Câu 76:
 Xem đáp án
Xem đáp án
Giải thích
Ta có \(4{m^3} + m = 12{n^3} + n \Leftrightarrow \left( {m - n} \right)\left( {4{m^2} + 4mn + 4{n^2} + 1} \right) = 8{n^3}\)
Giả sử \(p\) là một ước nguyên tố chung của \(m - n\) và \(4{m^2} + 4mn + 4{n^2} + 1\).
Vì \(4{m^2} + 4mn + 4{n^2} + 1\) lẻ nên \(p\) là số lẻ.
Mà \(8{n^3} \vdots p\) nên suy ra \(n \vdots p\).
Mặt khác \(\left( {m - n} \right) \vdots p \Rightarrow m \vdots p\).
Mà \(4{m^2} + 4mn + 4{n^2} + 1\) cũng chia hết cho \(p\) nên 1\( \vdots \)\(p\), điều này vô lý.
Vậy \(\left( {m - n,4{m^2} + 4mn + 4{n^3} + 1} \right) = 1\).
Mà \(8{n^3} = {(2n)^3}\) nên \(m - n = {x^3}\) và \(4{m^2} + 4mn + 4{n^2} + 1 = {y^3}\left( {x,y \in \mathbb{Z}} \right)\) thỏa mãn \({x^3}.{y^3} = {(2n)^3}\).
Hay \(m - n\) là lập phương của một số nguyên.
Chọn B
Câu 77:
 Xem đáp án
Xem đáp án
Giải thích
+ Số cách chọn ngẫu nhiên 5 học \({\rm{sinh}}C_9^5\) cách.
+ Số cách chọn 5 học sinh chỉ có 2 lớp: \(C_7^5 + C_6^5 + C_5^5\)
Vậy số cách chọn 5 học sinh có cả 3 lớp là \(C_9^5 - \left( {C_7^5 + C_6^5 + C_5^5} \right) = 98\).
Chọn B
Câu 78:
Một người nông dân có một khu đất rất rộng dọc theo một con sông. Người đó muốn làm một hàng rào hình chữ E (như hình vẽ) để được một khu đất gồm hai phần đất hình chữ nhật để trồng rau và nuôi gà. Biết chi phí nguyên vật liệu của hàng rào AB là 80 nghìn đồng/mét; phần hàng rào còn lại là 40 nghìn đồng/mét và tổng chi phí vật liệu là 20 triệu đồng.
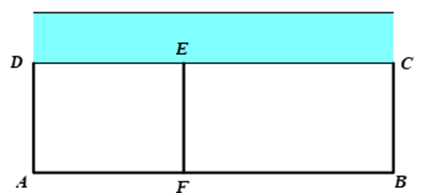
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Diện tích khu đất lớn nhất khi độ dài hàng rào AD là 125 mét. |
||
|
Diện tích khu đất lớn nhất khi chi phí nguyên vật liệu làm hàng rào AB là 7 triệu đồng. |
||
|
Diện tích khu đất lớn nhất bằng 5200 m2. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Diện tích khu đất lớn nhất khi độ dài hàng rào AD là 125 mét. |
X | |
|
Diện tích khu đất lớn nhất khi chi phí nguyên vật liệu làm hàng rào AB là 7 triệu đồng. |
X | |
|
Diện tích khu đất lớn nhất bằng 5200 m2. |
X |
Giải thích
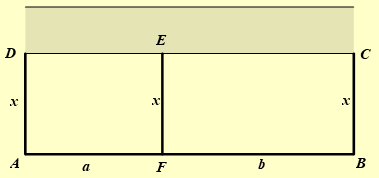
Gọi chiều rộng của hình chữ nhật là \(x\left( m \right){\rm{\;}}(x > 0)\) và chiều dài của phần đất trồng rau và nuôi gà lần lượt là \(a\left( m \right),b\left( m \right){\rm{\;}}(a > 0;b > 0)\).
Khi đó diện tích của khu đất là \(S = \left( {a + b} \right)x\left( {{m^2}} \right)\).
Mặt khác theo giả thiết tổng chi phí là 20 triệu đồng nên ta có:
\(3x.40000 + \left( {a + b} \right)80000 = 20000000 \Leftrightarrow 3x + 2\left( {a + b} \right) = 500\).
Ta có \(6S = 3x.2\left( {a + b} \right) \le \frac{{{{[3x + 2\left( {a + b} \right)]}^2}}}{4} = \frac{{{{500}^2}}}{4} \Rightarrow S \le \frac{{31250}}{3}\).
\( \Rightarrow {{\rm{S}}_{{\rm{max}}}} = \frac{{31250}}{3} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a + b = 125}\\{x = \frac{{250}}{3}}\end{array}} \right.\)
\( \Rightarrow \) Chi phí nguyên vật liệu làm hàng rào \(AB\) là: \(125.80000 = 10000000\) (đồng).
Câu 79:
 Xem đáp án
Xem đáp án
Giải thích
Điều kiện: \(\left\{ {\begin{array}{*{20}{c}}{x \ne 0}\\{{\rm{lo}}{{\rm{g}}_2}\frac{4}{{{x^2}}} > 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ne 0}\\{ - 2 < x < 2}\end{array} \Rightarrow D = \left( { - 2;2} \right) \setminus \left\{ 0 \right\}} \right.} \right.\).
Cách 1. Sử dụng Casio \({\rm{FX}}\) - 580
Ấn MENU + 8 và nhập hàm số \(f\left( x \right) = {\rm{lo}}{{\rm{g}}_2}\frac{4}{{{x^2}}} - {2^{x + 2}}\) với phạm vi bảng như sau:

Từ bảng giá trị ta có phương trình đã cho có nghiệm duy nhất x = −1.
Cách 2. Sử dụng phương pháp hàm số.
Chọn B
Câu 80:
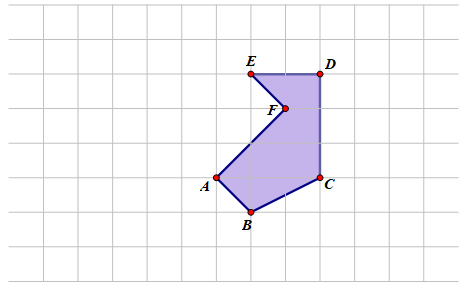
Ở hình vẽ dưới, miền đa giác thu được khi lấy hình lục giác \(ABCDEF\) hợp với ảnh của nó qua phép quay tâm \(A\) góc \({90^ \circ }\) có chu vi bằng \(a + b\sqrt 2 + c\sqrt 5 \left( {a,b,c \in \mathbb{N}} \right)\) lần so với cạnh của 1 ô vuông. Giá trị của \(a + b + c\) bằng
 Xem đáp án
Xem đáp án
Giải thích
Ta có: \({Q_{\left( {A,{{90}^ \circ }} \right)}}\left( {ABCDEF} \right) = AB'C'D'E'F'\) như hình vẽ bên dưới.
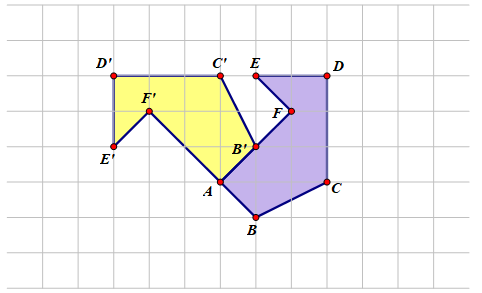
Chu vi của hình hợp bởi ảnh và tạo ảnh trên là
\(C = F'B + BC + CD + DE + EF + FB' + B'C' + C'D' + D'E' + E'F'\)
\( = 3\sqrt 2 + \sqrt 5 + 3 + 2 + \sqrt 2 + \sqrt 2 + \sqrt 5 + 3 + 2 + \sqrt 2 = 10 + 6\sqrt 2 + 2\sqrt 5 \).
Vậy \(a + b + c = 18\).
Chọn A