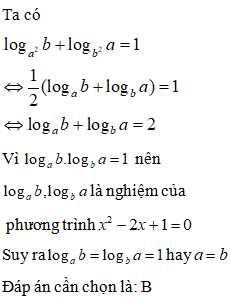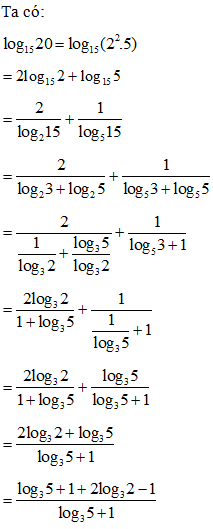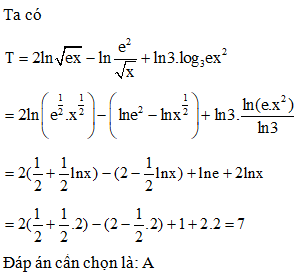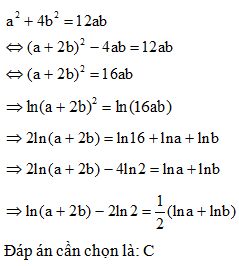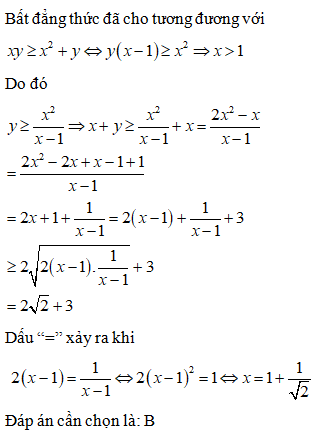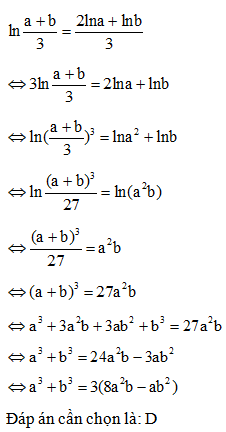Hàm số có Logarit
-
1314 lượt thi
-
38 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 3:
 Xem đáp án
Xem đáp án
Từ công thức ta thấy chỉ có đáp án A đúng.
Đáp án cần chọn là: ACâu 4:
 Xem đáp án
Xem đáp án
Từ công thức ta thấy chỉ có đáp án B đúng.
Đáp án cần chọn là: B
Câu 7:
 Xem đáp án
Xem đáp án
Ta có:
Đáp án cần chọn là: D
Câu 12:
 Xem đáp án
Xem đáp án
Điều kiện xác định:
Khi đó:
(vì nên chia cả hai vế cho
Đáp án cần chọn là: D
Câu 16:
 Xem đáp án
Xem đáp án
Ta có:
Đáp án cần chọn là: D
Câu 23:
 Xem đáp án
Xem đáp án
Gán giá trị đề bài cho bằng cách bấm:
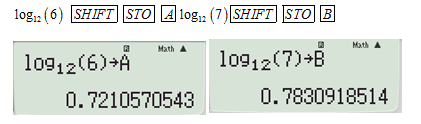
Lần lượt thử từng đáp án:
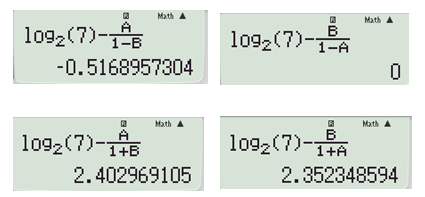
Câu 25:
 Xem đáp án
Xem đáp án
Trả lời:
Dựa vào 2 kết quả trên ta có
Đáp án cần chọn là: B
Câu 26:
Cho a>0; b>0 thỏa mãn . Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Ta có:
Logarit cơ số 10 hai vế ta được:
Đáp án cần chọn là: C
Câu 28:
 Xem đáp án
Xem đáp án
Ta có:
Ta có nên
Câu 29:
Cho các phát biểu sau:
(I). Nếu với A,B là các biểu thức luôn nhận giá trị dương.
(II).
(III).
(IV).
Số phát biểu đúng là Xem đáp án
Xem đáp án
Ta có nên I đúng
Ta có suy ra II đúng.
Logarit cơ số m hai vế ta được suy ra III sai
Ta có: đúng nên IV đúng.
Vậy có 3 phát biểu đúng.
Đáp án cần chọn là: CCâu 33:
 Xem đáp án
Xem đáp án
Theo đầu bài ta có :
Đáp án cần chọn là: C
Câu 34:
 Xem đáp án
Xem đáp án
Theo đầu bài ta có nên theo công thức ta có :
Đáp án cần chọn là: C
Câu 38:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B