Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 26)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 26)
-
358 lượt thi
-
85 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
Phần tư duy đọc hiểu
Một cuộc nghiên cứu về tinh tinh miền tây ở châu Phi đã hé lộ rằng chúng khôn khéo sử dụng chiến thuật quân sự cổ xưa của con người để tránh xa các cuộc _______ đầy nguy hiểm. Thay vì thụ động, chúng đặt mình ở vị trí cao để cảm nhận và đánh giá tình hình xung quanh, một chiến thuật mà con người từng sử dụng trong _______ cổ đại.
 Xem đáp án
Xem đáp án
Đáp án
Một cuộc nghiên cứu về tinh tinh miền tây ở châu Phi đã hé lộ rằng chúng khôn khéo sử dụng chiến thuật quân sự cổ xưa của con người để tránh xa các cuộc đụng độ đầy nguy hiểm. Thay vì thụ động, chúng đặt mình ở vị trí cao để cảm nhận và đánh giá tình hình xung quanh, một chiến thuật mà con người từng sử dụng trong quân sự cổ đại.
Phương pháp giải
Dựa vào logic câu từ và hiểu biết có được qua bài đọc.
Lời giải
- [Vị trí thả 1]: đụng độ -> sự xung đột lực lượng hai bầy tinh tinh khi tiếp cận ranh giới lãnh thổ.
- [Vị trí thả 2]: quân sự -> thuật ngữ liên quan đến quân đội, chiến thuật được chuẩn bị để thực hiện chiến tranh hay bảo vệ; trong bài đọc là chiến thuật quân sự của con người cổ đại.
Câu 2:
Nghiên cứu của Lemoine đã chứng minh điều gì trong hành vi của tinh tinh ở vườn quốc gia Taï?
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
Căn cứ nội dung đoạn [3]: “Tận dụng địa thế cao là một trong những chiến thuật quân sự cổ xưa nhất của con người trong chiến tranh, theo nhóm nghiên cứu ở Đại học Cambridge.”
=> Đáp án cần chọn là B.
Câu 3:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Sự nhận thức phức tạp giúp tinh tinh mở rộng lãnh thổ và chọn lọc tự nhiên đã thúc đẩy chiến thuật chiến đấu của chúng.
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
Căn cứ nội dung đoạn [6]: “Khả năng nhận thức phức tạp giúp tinh tinh mở rộng lãnh thổ được thúc đẩy bởi chọn lọc tự nhiên, chứng tỏ chiến thuật chiến đấu trên có nguồn gốc từ tiến hóa.”
=> Thông tin Đúng.
Câu 4:
Tác giả viết bài văn trên nhằm mục đích gì?
(chọn nhiều đáp án)
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc hiểu nội dung toàn bài, suy ra mục đích của tác giả.
Lời giải
A đúng - Căn cứ nội dung toàn bài, bài viết trình bày kết quả của cuộc nghiên cứu về tinh tinh của nhóm nghiên cứu Đại học Cambridge.
B sai - Tác giả không có thái độ phản đối và bác bỏ với những nghiên cứu tương tự trước đó.
C đúng - Căn cứ nội dung toàn bài, suy ra mục đích sau cùng của tác giả là cung cấp thông tin cho nghiên cứu sinh học.
D sai - Bài viết không đề cập đến lịch sử và không đi sâu vào đặc điểm tự nhiên của bầy tinh tinh Bờ Biển Ngà.
=> Đáp án cần chọn là A và C.
Câu 5:
Điền một từ không quá hai tiếng có trong bài đọc vào chỗ trống
Nghiên cứu của Lemoine không chỉ mở ra cái nhìn mới về chiến thuật quân sự của tinh tinh miền tây mà còn nhấn mạnh tầm quan trọng của khả năng _______ của chúng trong việc phát triển chiến thuật chiến đấu.
 Xem đáp án
Xem đáp án
Đáp án: "nhận thức"
Phương pháp giải
Xét logic câu từ và thông tin có được sau bài đọc.
Lời giải
Căn cứ nội dung đoạn toàn bài; “nhận thức” xuất hiện trong đoạn [2] và [6]. -> Khả năng nhận thức của tinh tinh trong các chiến thuật chiến đấu.
=> Từ cần điền là nhận thức.
Câu 6:
Thông tin nào KHÔNG thể suy ra từ những gì tác giả trình bày?
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
A đúng - Căn cứ nội dung đoạn [5]: “sự cân bằng quyền lực (tức số lượng ở mỗi bên) là một yếu tố quan trọng xác định bạo lực có leo thang ở một bên hay không.” -> quan trọng khiến chiến lược thay đổi -> thông tin câu không được suy ra từ đề bài.
B sai - Căn cứ nội dung đoạn [4]: “Nhóm nghiên cứu cùng với sinh viên và trợ lý người địa phương đi theo những con tinh tinh 8 - 12 giờ/ngày từ năm 2013 đến 2016, thu thập dữ liệu hành vi và GPS.” -> thông tin có suy ra được từ ngữ liệu.
C sai - Căn cứ nội dung đoạn [3]: “Tinh tinh sống theo bầy đàn cạnh tranh đất đai và tài nguyên. Hành vi thông thường của chúng bao gồm phối hợp tấn công, đôi khi gây mất mạng. Lãnh thổ giữa các đàn tinh tinh không được đánh dấu bằng đá và sự hiện diện hàng ngày của chúng ở một khu vực rất quan trọng.” -> thông tin có suy ra được từ ngữ liệu.
D sai - Căn cứ nội dung đoạn [6]: “họ cho rằng những con tinh tinh khác cũng sử dụng chiến thuật tương tự” -> thông tin có suy ra được từ ngữ liệu.
=> Đáp án cần chọn là A.
Câu 7:
Từ thông tin của bài đọc, hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí.
tự động hóa, tối ưu hóa, tận dung, sử dụng
Có vẻ như tinh tinh miền tây không chỉ sử dụng chiến thuật quân sự để đảm bảo an toàn cho bản thân mà còn để _______ cơ hội sinh tồn. Việc chúng có thể _______ địa thế cao để ngồi yên và quan sát, sau đó quyết định liệu nên tấn công hay không, là một biểu hiện rõ ràng của khả năng đánh giá tình hình xung quanh.
 Xem đáp án
Xem đáp án
Đáp án
Có vẻ như tinh tinh miền tây không chỉ sử dụng chiến thuật quân sự để đảm bảo an toàn cho bản thân mà còn để tối ưu hóa cơ hội sinh tồn. Việc chúng có thể tận dụng địa thế cao để ngồi yên và quan sát, sau đó quyết định liệu nên tấn công hay không, là một biểu hiện rõ ràng của khả năng đánh giá tình hình xung quanh.
Phương pháp giải
Dựa vào logic câu từ và hiểu biết có được qua bài đọc.
Lời giải
- [Vị trí thả 1]: tối ưu hóa -> thường liên quan đến hiệu suất: trong ngữ cảnh câu văn, “tối ưu hóa” có nghĩa là tăng cơ hội sinh tồn -> phù hợp với logic câu.
- [Vị trí thả 2]: tận dụng -> thể hiện sự thông minh của tinh tinh trọng việc sử dụng địa hình để tăng cơ hội sinh tồn.
Câu 8:
Điền một từ không quá hai tiếng có trong bài văn vào chỗ trống.
Tập tính tự nhiên là kết quả của quy luật tương tác phức tạp giữa các yếu tố môi trường, đóng góp vào sự đa dạng của hệ sinh thái và quá trình_______
 Xem đáp án
Xem đáp án
Đáp án: "tiến hóa"
Phương pháp giải
Xét logic câu từ, kết hợp với hiểu biết có được qua bài đọc.
Lời giải
Quá trình tiến hóa và tập tính tự nhiên của động vật có mối liên quan mật thiết. Tính tập tính tự nhiên của động vật là kết quả của quá trình tiến hóa, trong đó các đặc điểm và hành vi có lợi cho sự sống sót và sinh sản được chọn lọc và truyền đưa vào thế hệ kế tiếp. “Tiến hóa” xuất hiện trong đoạn [6].
=> Từ cần điền là tiến hóa.
Câu 9:
Nghiên cứu tại Bờ Biển Ngà của Lemoine đã làm thay đổi quan điểm chúng ta về gì trong lĩnh vực hành vi động vật?
(chọn nhiều đáp án)
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc hiểu nội dung toàn bài, đối chiếu ngữ liệu.
Lời giải
B đúng - Căn cứ nội dung đoạn [2]: “đây là lần đầu tiên các nhà khoa học quan sát một loài không phải con người tỉ mỉ tận dụng địa thế cao để đánh giá nguy cơ trong một cuộc xung đột lãnh thổ. "Điều này thể hiện khả năng nhận thức và hành động dựa trên những gì chưa biết để thu được nhiều thông tin hơn" -> nghiên cứu có tính mới và quan trọng để làm tiền đề cho những nghiên cứu hành vi sau này.
D đúng - Căn cứ nội dung đoạn [6]: “họ cho rằng những con tinh tinh khác cũng sử dụng chiến thuật tương tự, tùy theo địa hình.” -> góc nhìn mới được suy ra từ nghiên cứu hành vi của tinh tinh.
=> Đáp án cần chọn là B và D.
Câu 10:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Sự cân bằng quyền lực không có ảnh hưởng đến bạo lực trong cuộc xung đột của hai bầy tinh tinh.
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
Căn cứ nội dung đoạn [5]: “Lemoine để ý khi thành viên của hai đàn gặp nhau, sự cân bằng quyền lực (tức số lượng ở mỗi bên) là một yếu tố quan trọng xác định bạo lực có leo thang ở một bên hay không.” -> quan trọng = có ảnh hưởng lớn.
=> Thông tin Sai.
Câu 11:
Nội dung có thể suy ra từ truyện ngắn trên là:
(chọn nhiều đáp án)
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc hiểu nội dung toàn bài, suy ra mục đích của tác giả.
Lời giải
A đúng - Căn cứ nội dung đoạn [3]: “Trong lúc ấy tôi bỗng nhìn thấy ở dãy ghế bên phải có một khuôn mặt quen.” và [5]: “Một con người như anh ta, tôi vẫn còn nhớ” và [7]: “Riêng tôi không khỏi cảm thấy một cái gì sững sờ, thật cay đắng, thật đau xót” -> người kể chuyện gặp lại người quen cũ khiến anh ta cảm thấy sững sờ và đau lòng.
B đúng - Căn cứ nội dung đoạn [2]: “Tôi đâm lo cho cô bé. Tôi nhìn thấy trước, cô bé sẽ bị lừa đảo, mất trộm hoặc bị cướp giật ngay giữa thủ đô Hà Nội. Tôi đang nghĩ ra một cách gì giúp cô bé.” -> người kể chuyện lo lắng và quan tâm đến cô gái trẻ còn thiếu kinh nghiệm sống.
C sai - Truyện không nhắc đến sự thay đổi về tính cách con người.
D đúng - Căn cứ nội dung toàn bài -> người kể chuyện gặp người quen trong chuyến bay, gặp cả người trẻ mà anh thấy đồng cảm -> đây là sự kiện bất ngờ khiến anh suy nghĩ nhiều về ngày trước, mang lại trải nghiệm đặc biệt.
=> Đáp án cần chọn là A, B, D.
Câu 12:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Ý nghĩa của truyện ngắn có thể được hiểu thông qua những tình huống và cảm xúc mà người kể chuyện trải qua trong suốt chuyến bay.
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
Căn cứ nội dung toàn bài: tình huống truyện ngắn là người kể chuyện có cuộc gặp gỡ bất ngờ với một cô gái trẻ chuẩn bị đi xuất khẩu lao động và một người quen trong quá khứ trên chuyến bay từ Hồ Chí Minh về Hà Nội. Tác giả miêu tả rất chi tiết diễn biến tâm trạng của người kể chuyện qua tình huống trên, từ đó hình thành nên bức tranh đa chiều về mối quan hệ giữa người với người.
=> Thông tin Đúng.
Câu 13:
Từ thông tin của bài đọc, hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí.
việc làm, lao động, thực tế, tinh tế, quen thuộc gần gũi
Truyện ngắn kể về một chuyến bay của người kể chuyện, trong đó anh gặp một cô gái trẻ chuẩn bị đi xuất khẩu _______. Trong chuyến bay, anh nhận ra một người đàn ông _______ ngồi ở dãy ghế bên cạnh, khiến anh sững sờ và đau lòng khi nhớ về quá khứ. Những khía cạnh như sự ngẫu nhiên, sự đồng cảm, và khả năng đối mặt với quá khứ con người được tác giả _______ miêu tả.
 Xem đáp án
Xem đáp án
Đáp án
Truyện ngắn kể về một chuyến bay của người kể chuyện, trong đó anh gặp một cô gái trẻ chuẩn bị đi xuất khẩu lao động. Trong chuyến bay, anh nhận ra một người đàn ông quen thuộc ngồi ở dãy ghế bên cạnh, khiến anh sững sờ và đau lòng khi nhớ về quá khứ. Những khía cạnh như sự ngẫu nhiên, sự đồng cảm, và khả năng đối mặt với quá khứ con người được tác giả tinh tế miêu tả.
Phương pháp giải
Dựa vào logic câu từ và hiểu biết có được qua bài đọc.
Lời giải
- [Vị trí thả 1]: lao động -> Căn cứ nội dung đoạn [2]: “Cô đã học xong lớp 12 từ năm kia, đã trượt đại học hai năm và bây giờ ra Hà Nội để chuẩn bị đi xuất khẩu lao động ở Tiệp Khắc.” -> cụm “xuất khẩu lao động” phù hợp với logic câu.
- [Vị trí thả 2]: quen thuộc -> Căn cứ nội dung đoạn [3]: “Trong lúc ấy tôi bỗng nhìn thấy ở dãy ghế bên phải có một khuôn mặt quen.” -> phù hợp với ngữ cảnh.
- [Vị trí thả 3]: tinh tế -> Tác giả miêu tả những chi tiết nổi bật, lựa chọn ngôn từ và cấu trúc câu tinh tế giúp độc giả cảm nhận sống động tâm trạng nhân vật.
Câu 14:
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
Từ khóa chính là “bao lâu”. Căn cứ nội dung đoạn [2]: “Cô đã học xong lớp 12 từ năm kia, đã trượt đại học hai năm và bây giờ ra Hà Nội để chuẩn bị đi xuất khẩu lao động ở Tiệp KhắC.”
=> Đáp án cần chọn là B.
Câu 15:
Điền một từ không quá hai tiếng có trong đoạn [3] vào chỗ trống:
Trong cuộc hội thoại với cô gái trẻ, tôi bắt đầu ______ một kịch bản bảo vệ để giúp cô bé tránh xa khỏi những rủi ro có thể xảy ra khi cô vừa mới đến Hà Nội.
 Xem đáp án
Xem đáp án
Đáp án: "định hình"
Phương pháp giải
Xét logic câu từ và thông tin có được sau bài đọc.
Lời giải
Căn cứ nội dung đoạn [2]: “Tôi đâm lo cho cô bé. Tôi nhìn thấy trước, cô bé sẽ bị lừa đảo, mất trộm hoặc bị cướp giật ngay giữa thủ đô Hà Nội. Tôi đang nghĩ ra một cách gì giúp cô bé”. Trong ngữ cảnh câu, nhân vật chính đang nghĩ kịch bản để có thể hỗ trợ, hướng dẫn cô gái trẻ. Từ “định hình” xuất hiện trong đoạn [3], ám chỉ việc hình thành, xây dựng một quan điểm, lối tư duy.
=> Từ cần điền là định hình.
Câu 16:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Người đàn ông ngồi bất động trong máy bay đã quay đầu để nhìn thẳng vào tác giả khi bị nhận ra.
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
Từ khóa chính là “nhìn thẳng”. Căn cứ nội dung đoạn [2]: “từ lúc nãy tới giờ, anh ta có quay ngang quay ngửa hay động đậy cái cổ hoặc liếc mắt nhìn ai đâu.” -> thông tin không có trong bài.
=> Thông tin Sai.
Câu 17:
vui mừng, trò chuyện, lo lắng, xuất hiện, hội ngộ
Tình huống chính trong truyện này là cuộc _______ bất ngờ giữa người kể chuyện và một người quen từ quá khứ trong suốt chuyến bay từ thành phố Hồ Chí Minh về Hà Nội. Người quen này là một người đàn ông mà người kể chuyện đã biết từ trước, và sự _______ của ông ta khiến nhân vật chính nhớ lại nhiều kỉ niệm ngày xưa.
 Xem đáp án
Xem đáp án
Đáp án
Tình huống chính trong truyện này là cuộc hội ngộ bất ngờ giữa người kể chuyện và một người quen từ quá khứ trong suốt chuyến bay từ thành phố Hồ Chí Minh về Hà Nội. Người quen này là một người đàn ông mà người kể chuyện đã biết từ trước, và sự xuất hiện của ông ta khiến nhân vật chính nhớ lại nhiều kỉ niệm ngày xưa.
Phương pháp giải
Dựa vào logic câu từ và hiểu biết có được qua bài đọc.
Lời giải
- [Vị trí thả 1]: hội ngộ -> phù hợp với vế sau “giữa người kể chuyện và một người quen từ quá khứ” -> cụm từ “cuộc hội ngộ”
- [Vị trí thả 2]: xuất hiện -> sự xuất hiện, có mặt của người đàn ông trên chuyến bay gợi cho nhân vật chính nhiều suy tư.
Câu 18:
Người thanh niên trong truyện mặc trang phục và đồ trang sức nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
Căn cứ nội dung đoạn [6]: “Người thanh niên mặc quần áo vàng, đội mũ cát vàng đính phù hiệu công an. Trên thắt lưng to bản đeo bao súng ngắn, lại thêm một khẩu tiểu liên cầm lăm lăm trong tay.”
=> Đáp án cần chọn là C.
Câu 19:
Qua truyện ngắn trên, có thể rút ra điều gì về phong cách sáng tác của Nguyễn Minh Châu?
(chọn nhiều đáp án)
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm từ khóa chính, đối chiếu với ngữ liệu.
Lời giải
A sai - tác giả chú trọng miêu tả diễn biến tâm trạng nhân vật.
B đúng - 2 mối quan hệ chính được xây dựng trong truyện ngắn là của người kể chuyện với cô gái trẻ và với người quen cũ.
C đúng - thể hiện qua sự đồng cảm với cô gái và sự đau lòng với người quen xưa.
D sai - tình huống truyện được xây dựng đơn giản là cuộc gặp gỡ trên chuyến bay.
=> Đáp án cần chọn là B và C.
Câu 20:
Điền một từ không quá hai tiếng có trong bài văn vào chỗ trống.
Người đàn ông ngồi bất động trên máy bay tỏ ra có vẻ ________, ánh mắt chằm chằm nhìn về phía trước, toát lên một vẻ tự hào và không chịu chuyển động.
 Xem đáp án
Xem đáp án
Đáp án: "kiêu hãnh"
Phương pháp giải
Xét logic câu từ.
Lời giải
Căn cứ nội dung đoạn [3]: “Cái tư thế ngồi ấy, hai con mắt ấy và toàn bộ con người ấy toát ra một vẻ kiêu hãnh, khiến tôi hết sức khó chịu, đầy ác cảm.” -> “kiêu hãnh” phù hợp nội dung vế sau “toát lên một vẻ tự hào”.
=> Từ cần điền là kiêu hãnh.
Câu 21:
Phần tư duy khoa học / giải quyết vấn đề
Nhận định nào dưới đây đúng hay sai?
Các loài sử dụng nguồn thức ăn khác nhau nhưng cấu tạo cơ quan tiêu hóa đều giống nhau.
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin bài đọc.
Lời giải
Các loài sử dụng nguồn thức ăn khác nhau thì cấu tạo của cơ quan tiêu hóa khác nhau để phù hợp với nguồn thức ăn để tối ưu hóa hiệu quả tiêu hóa.
Đáp án: Sai
Câu 22:
Loài động vật nào dưới đây có răng phân hóa thành răng cửa, răng nanh, răng ăn thịt và răng hàm và dạ dày đơn?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin bài đọc.
Lời giải
Động vật ăn thịt: Đối với động vật ăn thịt, thức ăn rất giàu dinh dưỡng, dễ tiêu hóa cho nên cấu tạo cơ quan tiêu hóa có những đặc điểm đặc trưng: Răng phân hóa thành răng cửa, răng nanh, răng ăn thịt và răng hàm, Ống tiêu hóa nhỏ, ngắn, dạ dày đơn có khả năng co giãn lớn, manh tràng kém phát triển.
Trong các động vật trên thì sư tử là động vật ăn thịt; trâu và hươu là động vật nhai lại; thỏ là động vật ăn thực vật có dạ dày đơn.
Đáp án: B
Câu 23:
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin bài đọc.
Lời giải
Động vật ăn thịt: Đối với động vật ăn thịt, thức ăn rất giàu dinh dưỡng, dễ tiêu hóa cho nên cấu tạo cơ quan tiêu hóa có những đặc điểm đặc trưng: Răng phân hóa thành răng cửa, răng nanh, răng ăn thịt và răng hàm, răng cửa lấy thịt ra khỏi xương, răng nanh cắm vào con mồi và giữ mồi, răng ăn thịt rất phát triển, có chức năng xé thịt thành những miếng nhỏ, răng hàm kém phát triển.
Đáp án: C
Câu 24:
Chọn các đáp án chính xác
Những động vật nào sau đây có dạ dày đơn?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin bài đọc.
Lời giải
- Báo đốm là động vật ăn thịt có dạ dày đơn.
- Trâu, bò, nai là động vật nhai lại có dạ dày 4 túi.
- Ngựa là động vật ăn thực vật có dạ dày đơn.
Đáp án: Báo đốm, ngựa.
Chọn C, D
Câu 25:
dạ cỏ, dạ tổ ong, dạ lá sách, dạ múi khế
Ở thực vật nhai lại, hệ vi sinh vật phân giải xenlulozo và chuyển hóa thành protein nằm ở _______ trong dạ dày 4 túi.
 Xem đáp án
Xem đáp án
Đáp án
Ở thực vật nhai lại, hệ vi sinh vật phân giải xenlulozo và chuyển hóa thành protein nằm ở dạ cỏ trong dạ dày 4 túi.
Phương pháp giải
Đọc kĩ thông tin bài đọc.
Lời giải
Dạ dày 4 túi (Dạ cỏ, dạ tổ ong, dạ lá sách và dạ múi khế).
Dạ cỏ có chứa hệ vi sinh vật phân giải xenlulozo và chuyển hóa thành protein.
Đáp án: Dạ cỏ
Câu 26:
Điều gì giúp động vật nhai lại nghiền nát thức ăn?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin bài đọc.
Lời giải
Hàm trên có tấm sừng thay cho răng cửa và răng nanh. Hàm dưới có răng cửa và răng nanh giống nhau, có tác dụng tì cỏ vào tấm sừng hàm trên, có khoảng trống không răng tạo điều kiện .cho chuyển động của cỏ. Răng trước hàm và răng hàm có các gờ xi măng nổi trên bề mặt, làm tăng hiệu quả nghiền nát thức ăn.
Đáp án: D
Câu 27:
Điểm giống nhau của cơ quan tiêu hóa ở nai và thỏ?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin bài đọc.
Lời giải
Điểm giống nhau của cơ quan tiêu hóa ở nai (động vật nhai lại) và thỏ (động vật ăn thực vật có dạ dày đơn) là trong dạ dày đều có hệ sinh vật cộng sinh phát triển phân giải xenlulozo.
Đáp án: C
Câu 28:
Cho hình vẽ về bó cơ của chân. Lực ở gân Achilles bằng bao nhiều nếu người chơi chỉ đứng bằng một chân? Coi tất cả các xương bàn chân là một khối cứng (hình B). Bỏ qua trọng lượng của xương bàn chân và g = 9,81m/s2
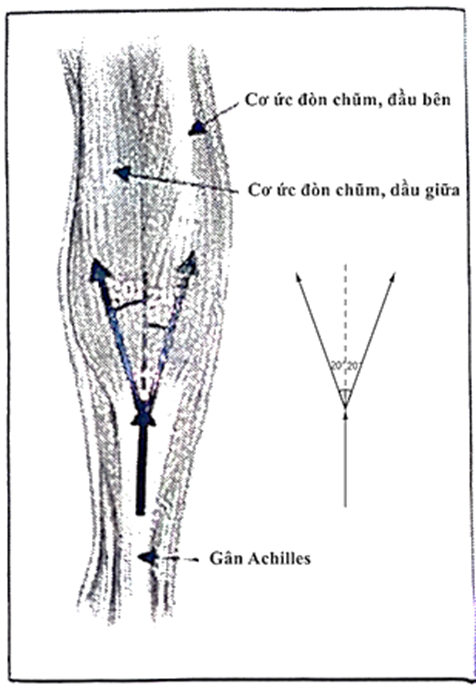
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin từ đề bài.
Vận dụng lí thuyết về momen của vật rắn
Lời giải
Khi đứng bằng một chân thì lực tác dụng lên chân hay các cơ chính là trọng lượng của cơ thể.
Áp dụng điều kiện để cân bằng lực ta có: \[T{d_1} = P{d_2}\]
\( \Rightarrow T = \frac{{P{d_2}}}{{{d_1}}} = \frac{{72.9,81.13,{{5.10}^{ - 2}}}}{{5,{{2.10}^{ - 2}}}} = 1,{83.10^3}\;{\rm{N}}\)
Chọn C
Câu 29:
Tính lực căng riêng của cơ bắp chân.
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin bài cung cấp.
Sử dụng số liệu từ câu trước.
Lời giải
Ta có lực căng đặc hiệu (lực căng tối đa trên một đơn vị diện tích) của cơ bắp chân là:
\(F = \frac{T}{S} = \frac{{1,{{83.10}^3}}}{{{{23.10}^{ - 4}}}} = 7,{96.10^5}\;{\rm{N}}/{{\rm{m}}^2}\)
Chọn A
Câu 30:
Điền số thích hợp vào chỗ trống:
Nếu hai cơ ức đòn chũm (đầu bên và đầu giữa) phân bổ như nhau vào tổng 60% lực tác động lên gân Achilles). Lực căng do hai cơ này tác động vào gân (lấy phần nguyên) là _______ N
 Xem đáp án
Xem đáp án
Đáp án: "584"
Phương pháp giải
Phân tích hình vẽ và vận dụng lí thuyết phân tích lực.
Lời giải
Hai cơ ức đòn chũm (đầu bên và đầu giữa) phân bổ như nhau vào tổng 60% lực tác động lên gân Achilles.
Lực căng do hai cơ sinh ra là: T = 1,83.103.0,6 = 1,098.103 N
Lực căng hai bên là như nhau.
Dựa vào lí thuyết tổng hợp lực ta có:
Lực phân bổ như nhau vào tổng 60% lực tác động lên gân Achilles nên lực tác động vào gân là: 2Tcos200 = 1,098.103 ⇒ T = 584 N
Câu 31:
Đối với một cầu thủ bóng đá khỏe mạnh, xương chày có thể chịu được một lực tối đa là 3,60N trên 4,90.102 (mm2) trước khi gãy. Trong một trận bóng, cầu thủ A không may sút trúng cầu thủ B. Kết quả là cầu thủ B bị trấn thương ở xương chày (giả sử xương chày của cầu thủ B đứng yên trước va chạm). Sau va chạm, chân cầu thủ B chuyển động trở lại với vận tốc 4,25m/s. Khối lượng của chân anh ta là 3,20kg và thời gian va chạm là 55,0ms và diện tích va chạm 6,20.102 mm2, biết không có ngoại lực nào khác ảnh hưởng đến chân của cầu thủ B. Khi đó lực tác dụng lên xương chày của B là bao nhiêu?
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng lí thuyết về động lượng đã được học.
Lời giải
Ta có độ biến thiên động lượng trong quá trình va chạm được xác định bằng: Δp = FΔt
Khi đó, lực tác dụng lên xương chày của B trong quá trình va chạm là: \[F = \frac{{\Delta p}}{{\Delta t}}\]
Ban đầu chưa có va chạm xảy ra thì: \[{p_1} = m{v_1} = 0\]
\( \Rightarrow F = \frac{{\Delta p}}{{\Delta t}} = \frac{{m{v_2}}}{{\Delta t}} = \frac{{3,2.4,25}}{{{{55.10}^{ - 3}}}} = 247N\)
Chọn B
Câu 32:
Chọn đúng hoặc sai cho các nhận xét sau:
|
Phát biểu |
ĐÚNG |
SAI |
|
Xương chày của cầu thủ B bị gãy. |
||
|
Xương chày của cầu thủ B không gãy. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Xương chày của cầu thủ B bị gãy. |
X | |
|
Xương chày của cầu thủ B không gãy. |
X |
Phương pháp giải
So sánh số liệu từ câu trên đã tính được.
Lời giải
Ta có lực tác dụng trong câu tính được là 247N trên 6,2.102 mm2
Mà lực chịu được tối đa là 3,60N trên 4,90.102 (mm2)
=> xương chày vẫn chưa bị gãy.
Câu 33:
Nhiều công ti thể thao phát triển miếng đệm ống chân. Miếng đệm có tác dụng hấp thụ tác động có nguy cơ gây ra thương tích khi va chạm trong các trận đấu bóng đá. Trong một thử nghiệm để so sánh hiệu quả các nhãn hiệu đệm ống khác nhau, mỗi miếng đệm của ống chân bọc ngoài một thiết bị mô phỏng xương chày của người. Mỗi thiết bị đá (tác động) được sử dụng để bắt chước chân của một cầu thủ tấn công. Một đồng hồ đo lực được đặt bên dưới miếng đệm để đo lực tác động lên xương chày. Bảng sau thể hiện kết quả:
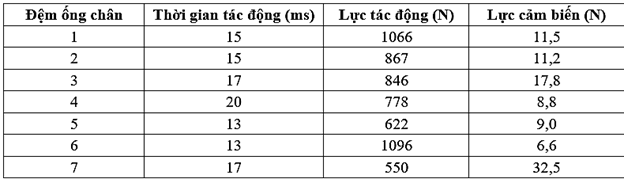
Lực hấp thụ của tấm đệm càng _______ thì tấm đệm đó càng tốt.
 Xem đáp án
Xem đáp án
Đáp án: "lớn"
Phương pháp giải
Phân tích đề bài và thông tin được mô tả.
Lời giải
Ta có lực hấp thụ càng lớn thì tấm đệm đó càng tốt.
Câu 34:
Thứ tự sắp xếp các đệm trên theo thứ tự giảm dần của khả năng hấp thụ lực cao nhất trên một đơn vị thời gian là?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích bằng số liệu bài cung cấp.
Lời giải
Ta xác định lực hấp thụ bằng cách lấy hiệu (lực tác động - lực cảm biến) chia có thời gian tác động.
Khi đó thứ tự đúng sẽ là: 6 – 1 – 2 – 3 – 5 – 4 - 7
Chọn A
Câu 35:
Cho phản ứng: 2NOCl(g) → 2NO(g) + Cl2(g) . Năng lượng hoạt hóa của phản ứng này là 100 kJ/mol. Ở 350K, hằng số tốc độ của phản ứng là 8.10−6 L/(mol.s). Hằng số tốc độ phản ứng của phản ứng này ở 400K là
 Xem đáp án
Xem đáp án
Phương pháp giải
Áp dụng phương trình Arrhenius.
Lời giải
Gọi hằng số tốc độ phản ứng của phản ứng này tại 400K là x.
Theo phương trình Arrhenius:
\(\ln \frac{{{k_{{T_2}}}}}{{{k_{{T_1}}}}} = \frac{{{E_a}}}{R}.\left( {\frac{1}{{{T_1}}} - \frac{1}{{{T_2}}}} \right) \Rightarrow \ln \frac{x}{{350}} = \frac{{{{100.10}^3}}}{{8,314}}.\left( {\frac{1}{{350}} - \frac{1}{{400}}} \right) \Rightarrow x = 5,{87.10^{ - 4}}L/({\rm{mol}}{\rm{.}}s)\)
Chọn A
Câu 36:
Trong những nhận định sau, nhận định nào là nhận định chính xác?
|
Phát biểu |
ĐÚNG |
SAI |
|
Tất cả các phân tử hóa học khi đã xảy ra sự va chạm với nhau thì đều là va chạm có hiệu quả. |
||
|
Tất cả các phân tử hóa học khi đã xảy ra sự va chạm với nhau thì đều xảy ra phản ứng hóa học. |
||
|
Năng lượng hoạt hóa của một phản ứng hóa học càng lớn thì phản ứng hóa học đó càng dễ xảy ra. |
||
|
Khi Ea càng lớn thì k càng nhỏ, tốc độ phản ứng càng nhỏ. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Tất cả các phân tử hóa học khi đã xảy ra sự va chạm với nhau thì đều là va chạm có hiệu quả. |
X | |
|
Tất cả các phân tử hóa học khi đã xảy ra sự va chạm với nhau thì đều xảy ra phản ứng hóa học. |
X | |
|
Năng lượng hoạt hóa của một phản ứng hóa học càng lớn thì phản ứng hóa học đó càng dễ xảy ra. |
X | |
|
Khi Ea càng lớn thì k càng nhỏ, tốc độ phản ứng càng nhỏ. |
X |
Phương pháp giải
Dựa vào thông tin về sự va chạm của các phân tử.
Lời giải
- Nhận định “Tất cả các phân tử hóa học khi đã xảy ra sự va chạm với nhau thì đều là va chạm có hiệu quả” là SAI vì theo như bài đọc, không phải tất cả các va chạm của các phân tử hóa học là va chamj có hiệu quả.
- Nhận định “Tất cả các phân tử hóa học khi đã xảy ra sự va chạm với nhau thì đều xảy ra phản ứng hóa học” là SAI, vì phải là những va chạm có hiệu quả thì mới có phản ứng hóa học xảy ra.
- Nhận định “Năng lượng hoạt hóa của một phản ứng hóa học càng lớn thì phản ứng hóa học đó càng dễ xảy ra” là SAI. Năng lượng hoạt hóa của một phản ứng hóa học càng lớn thì phản ứng đó càng khó xảy ra.
- Nhận định “Khi Ea càng lớn thì k càng nhỏ, tốc độ phản ứng càng nhỏ” là ĐÚNG. Dựa vào phương trình kinh nghiệm Arrhenius có thể nhận thấy điều này.
Câu 37:
Kéo thả đáp án thích hợp vào chỗ trống:
Cl, O3, ClO, O2
Sự suy giảm tầng ozone và lỗ thủng tầng ozone (O3) đã gây ra mối lo ngại về việc gia tăng nguy cơ ung thư da, cháy nắng, mù mắt và đục thủy tinh thể,… Tầng ozone hấp thụ hầu hết các tia cực tím (UV) có hại cho sự sống trên Trái Đất. Các phân tử ozone có thể bị phá hủy theo hai giai đoạn:
Cl + O3 → ClO + O2 và ClO + O3 → Cl + 2O2
Chất xúc tác trong quá trình này là _______.
 Xem đáp án
Xem đáp án
Đáp án
Chất xúc tác trong quá trình này là Cl.
Phương pháp giải
Thông tin về chất xúc tác: Chất xúc tác làm giảm năng lượng hoạt hóa của phản ứng nên làm tăng tốc độ phản ứng hóa học. Chất xúc tác không bị biến đổi về lượng và chất sau phản ứng.
Lời giải
Chất xúc tác không bị biến đổi sau phản ứng nên Cl là chất xúc tác.
Câu 38:
Thực nghiệm cho biết phản ứng 2N2O5(g) → 4NO2(g) + O2(g) ở 45oC có hằng số tốc độ phản ứng là 8,17.10−3s−1; Ea = 103,5 kJ/mol. Hằng số tốc độ phản ứng tại 65oC là
 Xem đáp án
Xem đáp án
Phương pháp giải
Đổi nhiệt độ thành độ K.
Lời giải
Gọi hằng số tốc độ phản ứng của phản ứng này tại 400K là x.
Theo phương trình Arrhenius:
\(\ln \frac{{{k_{{T_2}}}}}{{{k_{{T_1}}}}} = \frac{{{E_a}}}{R}.\left( {\frac{1}{{{T_1}}} - \frac{1}{{{T_2}}}} \right) \Rightarrow \ln \frac{x}{{8,{{17.10}^{ - 3}}}} = \frac{{103,{{5.10}^3}}}{{8,314}}.\left( {\frac{1}{{45 + 273}} - \frac{1}{{65 + 273}}} \right) \Rightarrow x = 0,083\)
Chọn B
Câu 39:
Một phản ứng đơn giản xảy ra ở nhiệt độ 100oC, trong điều kiện có xúc tác và không có xúc tác, năng lượng hoạt hóa của phản ứng lần lượt là: Ea1 = 25 kJ/mol, Ea2 = 50 kJ/mol. Nhận định dưới đây là đúng hay sai?
Khi năng lượng hoạt hóa giảm từ 50 kJ/mol về 25 kJ/mol, tốc độ phản ứng tăng 2050 lần.
 Xem đáp án
Xem đáp án
Phương pháp giải
Áp dụng phương trình Arrhenius.
Lời giải
Phương trình Arrhenius trong 2 điều kiện là:
\({k_1} = A \times {e^{\frac{{{E_{a1}}}}{{RT}}}}\)
\({k_2} = A \times {e^{\frac{{{E_{a2}}}}{{RT}}}}\)
\( \Rightarrow \frac{{{k_1}}}{{{k_2}}} = {e^{\frac{{{E_{a2}} - {E_{a1}}}}{{RT}}}} = {e^{\frac{{(50 - 25){{.10}^3}}}{{8,314.373}}}} = 3170,4\)
Vậy khi năng lượng hoạt hóa giảm từ 50 kJ/mol về 25 kJ/mol, tốc độ phản ứng tăng lên 3170,4 lần.
Chọn B
Câu 40:
Chọn nhận định sai trong những nhận định dưới đây?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đã cho trong đầu bài.
Lời giải
Đáp án sai là đáp án C. Tăng nhiệt độ không làm giảm năng lượng hoạt hóa của phản ứng.
Chọn C
Câu 41:
Cơ chế điều hòa mức độ xoắn của NST là cơ chế điều hòa hoạt động gen của sinh vật nhân thực ở cấp độ nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin đoạn đọc.
Lời giải
Điều hòa trước phiên mã được thực hiện thông qua cơ chế điều hòa mức độ xoắn của NST.
Đáp án: A
Câu 42:
Điều hòa hoạt động gen ở mức độ trước phiên mã ở sinh vật nhân thực là hình thức điều hòa _______
 Xem đáp án
Xem đáp án
Đáp án
Điều hòa hoạt động gen ở mức độ trước phiên mã ở sinh vật nhân thực là hình thức điều hòa cần ít năng lượng
Phương pháp giải
Đọc kĩ thông tin đoạn đọc.
Lời giải
Ở sinh vật nhân thực, điều hòa hoạt động gen có nhiều cấp độ khác nhau, trong đó điều hòa trước phiên mã là hình thức điều hòa ít tốn kém năng lượng.
Đáp án: cần ít năng lượng
Câu 43:
Chọn những nhận định chính xác.
Sự điều hòa biểu hiện của gen ở mức độ trước phiên mã của sinh vật nhân sơ dựa trên cơ sở khoa học nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin đoạn đọc.
Lời giải
Các gen nằm trong vùng co xoắn (vùng dị nhiễm sắc) của NST sẽ không được biểu hiện. Chỉ những gen nằm trong vùng giãn xoắn (vùng nguyên nhiễm sắc) mới có cơ hội được biểu hiện. Vì thế, tế bào có thể điều hòa sự biểu hiện của gen bằng cách co, giãn xoắn NST.
Đáp án:
- Các gen nằm trong vùng dị nhiễm sắc của NST không được biểu hiện.
- Các gen nằm trong vùng nguyên nhiễm sắc của NST sẽ được biểu hiện.
Chọn A, D
Câu 44:
Đối với cơ chế cải biến histone, hoạt động nào dẫn đến sự ức chế quá trình phiên mã của gen?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin đoạn đọc.
Lời giải
- Sự gắn nhóm methyl vào histone sẽ làm co xoắn NST, ức chế sự biểu hiện của gen.
- Các hoạt động còn lại đều dẫn đến khởi động quá trình phiên mã.
Chọn A
Câu 45:
Điền từ chính xác vào chỗ trống
Quá trình Acetyl hóa đuôi histone là sự gắn nhóm Acetyl vào các phân tử lysine tích điện _______ của đuôi histone làm giãn xoắn NST.
 Xem đáp án
Xem đáp án
Đáp án: "dương"
Phương pháp giải
Đọc kĩ thông tin đoạn đọc.
Lời giải
Sự gắn nhóm acetyl vào các phân tử lysine tích điện dương của đuôi histone sẽ làm giãn xoắn NST, khởi động quá trình phiên mã của gen.
Đáp án: dương
Câu 46:
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin đoạn đọc.
Lời giải
Sự methyl hóa ADN thường gây ra sự bất hoạt gen trong thời gian dài, liên quan đến quá trình biệt hóa tế bào.
Đáp án: C
Câu 47:
Nhận định dưới đây đúng hay sai?
Một đoạn ADN có một gen bị bất hoạt do methyl hóa, sau khi diễn ra quá trình nhân đôi ADN, gen bị bất hoạt trên ở ADN con chuyển sang trạng thái hoạt động.
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin đoạn đọc.
Lời giải
Một gen khi đã bị methyl hóa thì trạng thái methyl hóa sẽ được truyền lại cho các thế hệ tế bào con. -> Một phân tử ADN có một gen bị bất hoạt do methyl hóa, sau khi diễn ra quá trình nhân đôi ADN, gen bị bất hoạt trên ở ADN con vẫn ở trạng thái bật hoạt, hiện tượng này gọi là hiện tượng in vết hệ gen.
Đáp án: Sai
Câu 48:
Dao động điện từ trong mạch chọn sóng của máy thu khi máy thu bắt sóng là:
 Xem đáp án
Xem đáp án
Phương pháp giải
Cả 3 câu trên đều sai
Vận dụng lí thuyết về truyền tin bằng sóng vô tuyến.
Dựa vào thông tin bài cung cấp.
Lời giải
Ta có trong mạch chọn sóng sẽ chọn lọc sóng muốn thu nhờ mạch cộng hưởng đồng nghĩa với dao động cưỡng bức có tần số bằng tần số riêng của mạch.
Vì với dao động cưỡng bức với tần số bằng với tần số riêng của mạch thì hiện tượng cộng hưởng xảy ra.
Chọn B
Câu 49:
Chọn các nhận xét đúng khi nói về nguyên tắc phát và thu sóng điện từ.
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin bài cung cấp.
Vận dụng lí thuyết đã học về truyền tin bằng sóng điện từ.
Lời giải
Ta có để thu sóng thì chúng ta cần anten.
Trong quá trình thu và phát sóng nhờ có anten ta chọn lọc được sóng cần thu. Khi phát sóng cần mắc một máy dao động điều hòa với anten (mạch biến điệu và khuếch đại).
Còn có thiết bị có thể vừa thu và phát sóng điện từ như điện thoại.
Chọn B, C, D
Câu 50:
tách sóng, chọn sóng, khuếch đại cao tần, chuyển thành sóng âm, khuếch đại âm tần, chuyển thành sóng hạ âm
Các giai đoạn thu sóng điện từ trong máy thu thanh là: _______ - _______ - _______ - _______ - _______
 Xem đáp án
Xem đáp án
Đáp án
Các giai đoạn thu sóng điện từ trong máy thu thanh là: chọn sóng - khuếch đại cao tần - tách sóng - khuếch đại âm tần - chuyển thành sóng âm
Phương pháp giải
Phân tích thông tin bài cung cấp
Lời giải
Các giai đoạn trong máy thu thanh:
+ Anten thu: thu sóng điện từ từ cao tần biến điệu
+ Chọn sóng: chọn lọc sóng muốn thu nhờ mạch cộng hưởng.
+ Tách sóng: lấy ra dao động âm tần từ cao động cao tần biến điệu.
+ Mạch khuếch đại âm tần: là mạnh dao động âm tầm rồi đưa ra loa
Từ quá trình trên ta có sắp xếp như sau:
chọn sóng – khuếch đại cao tần – tách sóng – khuếch đại âm tần – chuyển thành sóng âm
Câu 51:
Trong “máy bắn tốc độ“ xe cộ trên đường:
 Xem đáp án
Xem đáp án
Phương pháp giải
Vận dụng lí thuyết đã học về truyền tin bằng sóng vô tuyến.
Lời giải
Ta có trong “máy bắn tốc độ” xe cộ trên đường có cả máy phát và máy thu vô tuyến. Chú ý rằng, máy này hoạt động dựa trên hiệu ứng Đôp-le nên nó vừa phát ra sóng điện từ vừa phải thu sóng điện từ phản xạ trở lại.
Chọn C
Câu 52:
Tại Hà Nội, một máy đang phát sóng điện từ. Xét một phương truyền có phương thẳng đứng hướng lên. Vào thời điểm t, tại điểm M trên phương truyền, véctơ cảm ứng từ đang có độ lớn cực đại và hướng về phía Nam. Khi đó véctơ cường độ điện trường có
 Xem đáp án
Xem đáp án
Phương pháp giải
Vận dụng lí thuyết về phương, chiều của véctơ cường độ điện trường, véctơ cảm ứng từ và vận tốc truyền sóng trong điện từ trường.
Áp dụng quy tắc cái đinh ốc
Lời giải
Ta có:
+ Véctơ cường độ điện trường \(\overrightarrow E \) và véctơ cảm ứng từ \(\overrightarrow B \) luôn luôn vuông góc với nhau và vuông góc với phương truyền sóng. 3 véctơ \(\overrightarrow E \), \(\overrightarrow B \) và \(\overrightarrow v \) tại mọi điểm tạo với nhau thành một tam diện thuận.
+ Áp dụng quy tắc đinh ốc theo chiều thuận: từ \(\overrightarrow E \) → \(\overrightarrow B \), khi đó chiều tiến của đinh ốc là v
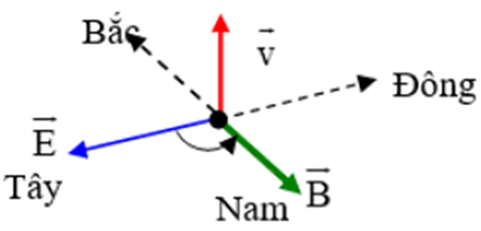
+ Do \(\overrightarrow E \), \(\overrightarrow B \) cùng pha => Khi đó véctơ cường độ điện trường có độ lớn cực đại và hướng về phía Tây
Chọn A
Câu 53:
Bước sóng điện từ mà mạch phát hoặc thu được xác định bằng công thức: \(\lambda = cT = \frac{c}{f} = 2\pi c\sqrt {LC} \). Mạch dao động của một máy thu vô tuyến gồm cuộn cảm L = 5μH và tụ xoay có điện dụng biến thiên từ \({C_1} = 10pF \to {C_2} = 250pF\). Dải sóng điện từ mà máy thu được có bước sóng là:
 Xem đáp án
Xem đáp án
Phương pháp giải
Vận dụng công thức \(\lambda = cT = \frac{c}{f} = 2\pi c\sqrt {LC} \)
Lời giải
Ta có: \(\lambda = cT = \frac{c}{f} = 2\pi c\sqrt {LC} \)
\( \Leftrightarrow 2\pi {.3.10^8}.\sqrt {{{5.10}^{ - 6}}{{.10.10}^{ - 12}}} \le \lambda \le 2\pi {.3.10^8}.\sqrt {{{5.10}^{ - 6}}{{.250.10}^{ - 12}}} \)
\( \Rightarrow 13,3 \le \lambda \le 66,6\,\,({\rm{m}})\)
Chọn B
Câu 54:
Nhận định dưới đây là đúng hay sai?
Phản ứng phân rã Uranium là một phản ứng hóa học.
 Xem đáp án
Xem đáp án
Phương pháp giải
Trong các phản ứng hóa học chỉ có lớp vỏ electron bị thay đổi.
Lời giải
Trong các phản ứng hóa học chỉ có lớp vỏ electron bị thay đổi. từ đó sinh ra chất hóa học mới chứ không sinh ra nguyên tố hóa học mới, nên phản ứng phân ra uranium không phải là một phản ứng hóa học.
Chọn B
Câu 55:
Điền số thích hợp vào chỗ trống (Lấy kết quả đến chữ số thập phân thứ hai)
Biết Uranium còn có một đồng vị nữa là 234U. Nguyên tử khối trung bình của Uranium là _______ amu.
 Xem đáp án
Xem đáp án
Đáp án: "237,98"
Phương pháp giải
- Tính phần trăm của đồng vị 234U.
- Tính nguyên tử khối trung bình của nguyên tố Uranium.
Lời giải
Phần trăm của đồng vị 234U là: 100% − 0,711% − 99,284% = 0,005%
Nguyên tử khối trung bình của nguyên tử Uranium là:
\({\bar M_U} = \frac{{234.0,041 + 235.0,711 + 238.99,284}}{{100}} = 237,98\,\,{\rm{amu}}\)
Câu 56:
Phản ứng nào dưới đây mô tả chính xác phóng xạ β?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin về phóng xạ β: Sau phóng xạ β, điện tích hạt nhân nguyên tử tăng 1 đơn vị, số khối không thay đổi.
Lời giải
Phản ứng của phóng xạ β là \(_Z^AX \to _{ - 1}^0e + _{Z + 1}^AX'\).
Chọn B
Câu 57:
Dãy nào dưới đây là kí hiệu hóa học của các hạt theo thứ tự α, β, β+?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin về các loại phóng xạ:
- Phóng xạ α: Sau phóng xạ α, điện tích hạt nhân nguyên tử giảm 2 đơn vị và số khối giảm hẳn 4 đơn vị.
- Phóng xạ β: Sau phóng xạ β, điện tích hạt nhân nguyên tử tăng 1 đơn vị, số khối không thay đổi.
- Phóng xạ β+ : Sau phóng xạ β+, điện tích hạt nhân nguyên tử giảm 1 đơn vị, số khối không thay đổi.
Lời giải
Kí hiệu của hạt α, β, β+ lần lượt là \(_2^4{\rm{He}},\,\,_{ + 1}^0e,\,\,_{ - 1}^0e\).
Chọn B
Câu 58:
Các nhận định dưới đây là đúng hay sai?
|
Phát biểu |
ĐÚNG |
SAI |
|
Khả năng đâm xuyên của các tia phóng xạ có thể sắp xếp theo thứ tự là: γ < β < α. |
||
|
Khả năng gây ion hóa của các tia phóng xạ có thể sắp xếp theo thứ tự là: γ < β < α. |
||
|
Không phải phản ứng hạt nhân nào cũng tạo ra phóng xạ γ. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Khả năng đâm xuyên của các tia phóng xạ có thể sắp xếp theo thứ tự là: γ < β < α. |
X | |
|
Khả năng gây ion hóa của các tia phóng xạ có thể sắp xếp theo thứ tự là: γ < β < α. |
X | |
|
Không phải phản ứng hạt nhân nào cũng tạo ra phóng xạ γ. |
X |
Phương pháp giải
Dựa vào đoạn thông tin trong đề bài.
Lời giải
Nhận định “Khả năng đâm xuyên của các tia phóng xạ có thể sắp xếp theo thứ tự là: γ < β < α” là sai.
Câu 59:
Nguyên tố nào được tạo ra trong phản ứng hạt nhân dưới đây?
\(_0^1n\,\, + \,\,_{92}^{235}U \to ?\,\, + \,\,_{36}^{92}Kr\,\, + \,\,3_0^1n\)
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào định luật bảo toàn điện tích hạt nhân và số khối.
Lời giải
Theo định luật bảo toàn điện tích hạt nhân và số khối, nguyên tố mới được tạo ra là \(_{56}^{141}{\rm{Ba}}\).
Chọn ACâu 60:
Phương trình \({x^3} - 3{x^2} + m = 0\) có ba nghiệm phân biệt khi và chỉ khi \(m\) thuộc khoảng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Bước 1: Tách về 1 vế đưa phương trình về dạng \(f\left( x \right) = m\)
Bước 2: Phương trình trên có 3 nghiệm phân biệt khi đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại ba điểm phân biệt.
Dấu của tam thức bậc hai
Dạng 4: Tìm điều kiện của tham số để đồ thị hàm số bậc ba cắt trục hoành
Lời giải
Ta có: \({x^3} - 3{x^2} = - m\)
Đặt \(y = f\left( x \right) = {x^3} - 3{x^2}\); ta có: \(f'\left( x \right) = 3{x^2} - 6x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 2}\end{array}} \right.\)
BBT của hàm số \(f\left( x \right) = {x^3} - 3{x^2}\)
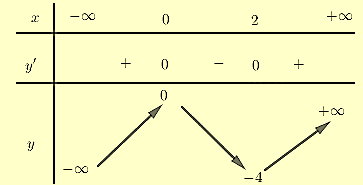
Đường thẳng \(y = - m\) cắt đồ thị hàm số \(f\left( x \right) = {x^3} - 3{x^2}\) tại ba điểm phân biệt khi \( - 4 < - m < 0 \Leftrightarrow 0 < m < 4\)
Câu 61:
 Xem đáp án
Xem đáp án
Phương pháp giải
- Xét \[f\left( x \right) + f\left( {1 - x} \right)\]
- Tính giá trị biểu thức.
Lời giải
Ta có: \(f\left( x \right) + f\left( {1 - x} \right) = \frac{{{9^{1 - x}}}}{{{9^{1 - x}} + 3}} + \frac{{{9^x}}}{{{9^x} + 3}} = \frac{9}{{9 + {{3.9}^x}}} + \frac{{{9^x}}}{{{9^x} + 3}}\)
\( = \frac{3}{{3 + {9^x}}} + \frac{{{9^x}}}{{{9^x} + 3}} = 1\)
Ta thấy \(\frac{1}{{2022}} + \frac{{2021}}{{2022}} = 1 \Rightarrow f\left( {\frac{1}{{2022}}} \right) + f\left( {\frac{{2021}}{{2022}}} \right) = 1\)
Tương tự có: \(f\left( {\frac{2}{{2022}}} \right) + f\left( {\frac{{2020}}{{2022}}} \right) = 1; \ldots \)
Vậy có tất cả là 1010 cặp số và thừa \(f\left( {\frac{{1011}}{{2022}}} \right) = \frac{1}{2}\)
\( \Rightarrow f\left( {\frac{1}{{2022}}} \right) + f\left( {\frac{2}{{2022}}} \right) + \cdots + f\left( {\frac{{2021}}{{2022}}} \right) = 1.1010 + \frac{1}{2} = \frac{{2021}}{2}\)
Chọn A
Câu 62:
 Xem đáp án
Xem đáp án
Phương pháp giải
Đặt \({x^3} - 2x + 1 = t\), đổi cận và tính tích phân.
Dạng 1: Tính tích phân bằng phương pháp đổi biến \({\rm{t}} = {\rm{u}}\left( {\rm{x}} \right)\)
Lời giải
Đặt \({x^3} - 2x + 1 = t \Rightarrow \left( {3{x^2} - 2} \right)dx = dt \Leftrightarrow \left( {9{x^2} - 6} \right)dx = 3dt\)
Đổi cận: \(\left\{ {\begin{array}{*{20}{l}}{x = 0 \Leftrightarrow t = 1}\\{x = 1 \Leftrightarrow t = 0}\end{array}} \right.\)
Ta có: \(\int\limits_0^1 {f\left( x \right)} = \int\limits_1^0 {{e^t}.3dt} = \left. {3.{e^t}} \right|_1^0 = 3 - 3e\)
Chọn B
Câu 63:
 Xem đáp án
Xem đáp án
Phương pháp giải
- Tìm \(z\) và \(\overline z \)
- Tìm \(w\)
Dạng 1: Tìm điểm biểu diễn số phức thỏa mãn điều kiện cho trước
Lời giải
Ta có: \(z = 4 - i \Rightarrow w = 1 - \overline z = 1 - \left( {4 + i} \right) = - 3 - i\)
=> Điểm biểu diễn số phức w là điểm D(-3;-1)
ÑNhiều em có thể nhầm \(w = 1 - z = 1 - \left( {4 - i} \right) = - 3 + i\) mà chọn A
Chọn C
Câu 64:
Bạn A có 4 lego và 3 hộp bút để trang trí bàn học. Bạn A muốn xếp chúng thành 1 hàng ngang thẳng hàng sao cho lego và hộp bút xen kẽ nhau.
Hỏi bạn A có bao nhiêu cách xếp?
Đáp án: _______
 Xem đáp án
Xem đáp án
Đáp án: "144"
Phương pháp giải
Sử dụng quy tắc nhân và hoán vị.
Lời giải
Số cách xếp là 3!.4!=144 cách xếp.
Câu 65:
Giá trị của tổng \(S = 1 + 11 + 111 + \ldots + \underbrace {111...1}_{n\,\,s\`e \,\,1}\) là
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Ta có: \(9S = 9 + 99 + 999 + \ldots + \underbrace {999...9}_{n\,\,s\`e \,\,9}\)
\(\begin{array}{l} = (10 - 1) + (100 - 1) + \ldots + \left( {{{10}^n} - 1} \right)\\ = \left( {10 + {{10}^2} + \ldots + {{10}^n}} \right) - n\\ = \frac{{10\left( {{{10}^n} - 1} \right)}}{{10 - 1}} - n = \frac{{10\left( {{{10}^n} - 1} \right)}}{9} - n\end{array}\)
\( \Rightarrow S = \frac{{10}}{{81}}\left( {{{10}^n} - 1} \right) - \frac{n}{9}.\)
Chọn B
Câu 66:
Điền số thích hợp vào chỗ trống:có tất cả
Số 70560 có tất cả _______ ước nguyên dương.
 Xem đáp án
Xem đáp án
Đáp án: "108"
Phương pháp giải
Phân tích thành tích các thừa số nguyên tố.
Lời giải
\(70560 = {2^5}{.3^2}{.5.7^2}\) nên nó có tất cả 6.3.2.3 \( = 108\) ước nguyên dương.
Câu 67:
 Xem đáp án
Xem đáp án
Phương pháp giải
Xét \[f\prime \left( x \right) > 0\]
Lời giải
Ta có : \(f'\left( x \right) > 0 \Leftrightarrow x > 2\)
=>Hàm số đồng biến trên khoảng \(\left( {2; + \infty } \right)\)
Chọn C
Câu 68:
 Xem đáp án
Xem đáp án
Phương pháp giải
Hàm số \(y = \frac{{ax + b}}{{cx + d}}\) nghịch biến trên \(\left( {\alpha ;\beta } \right)\) khi và chỉ khi \(\left\{ {\begin{array}{*{20}{l}}{y' < 0}\\{ - \frac{d}{c} \notin \left( {\alpha ;\beta } \right)}\end{array}} \right.\)
Tìm m để hàm phân thức bậc nhất trên bậc nhất đồng biến, nghịch biến trên một khoảng
Lời giải
TXĐ: \(D = \mathbb{R}\backslash \left\{ { - m} \right\}\).
Ta có \(y = \frac{{mx + 4}}{{x + m}} \Rightarrow y' = \frac{{{m^2} - 4}}{{{{(x + m)}^2}}}\).
Để hàm số nghịch biến trên khoảng \(\left( { - 1;1} \right)\) thì
\(\left\{ {\begin{array}{*{20}{l}}{y' < 0}\\{ - m \notin \left( { - 1;1} \right)}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{m^2} - 4 < 0}\\{\left[ {\begin{array}{*{20}{c}}{ - m \le - 1}\\{ - m \ge 1}\end{array}} \right.}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 2 < m < 2}\\{\left[ {\begin{array}{*{20}{c}}{m \ge 1}\\{m \le - 1}\end{array}} \right.}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{1 \le m < 2}\\{ - 2 < m \le - 1}\end{array}} \right.} \right.} \right.} \right.\).
Lại có \(m \in \mathbb{Z} \Rightarrow m = \pm 1\)
Vậy có 2 giá trị của m thỏa mãn yêu cầu bài toán.
Chọn B
Câu 69:
 Xem đáp án
Xem đáp án
Phương pháp giải
Bước 1: Tìm \(\mathop {{\rm{min}}}\limits_{{\rm{[}} - 1;3]} y;\mathop {{\rm{max}}}\limits_{a[ - 1;3]} y\)
Bước 2: Để \(f\left( a \right),f\left( b \right),f\left( c \right)\) là độ dài ba cạnh của một tam giác thì \(\left\{ {\begin{array}{*{20}{l}}{f\left( a \right) > 0}\\{f\left( a \right) + f\left( b \right) > f\left( c \right)}\end{array}} \right.\)
Lời giải
Ta có: \(y' = 3{x^2} - 3 = 0 \Leftrightarrow x = \pm 1 \in \left[ { - 1;3} \right]\).
Ta có \(y\left( { - 1} \right) = 2 - m;y\left( 1 \right) = - 2 - m;y\left( 3 \right) = 18 - m\)
\( \Rightarrow \mathop {{\rm{min}}}\limits_{\left[ { - 1;3} \right]} y = - 2 - m;\,\,\mathop {{\rm{max}}}\limits_{a\left[ { - 1;3} \right]} y = 18 - m\).
Không mất tính tổng quát, ta giả sử \(f\left( a \right) \le f\left( b \right) \le f\left( c \right)\).
Vì \(a,b,c \in \left[ { - 1;3} \right]\) nên \( - 2 - m \le f\left( a \right) \le f\left( b \right) \le f\left( c \right) \le 18 - m\).
Để \(f\left( a \right),f\left( b \right),f\left( c \right)\) là độ dài ba cạnh của một tam giác thì \(\left\{ {\begin{array}{*{20}{l}}{f\left( a \right) > 0}\\{f\left( a \right) + f\left( b \right) > f\left( c \right)}\end{array}\left( {\rm{*}} \right)} \right.\).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{ - 2 - m \le f\left( a \right)}\\{ - 2 - m \le f\left( b \right)}\end{array} \Rightarrow f\left( a \right) + f\left( b \right) \ge - 4 - 2m} \right.\).
Do đó (*) luôn đúng khi và chỉ khi \(\left\{ {\begin{array}{*{20}{l}}{ - 2 - m > 0}\\{ - 4 - 2m \ge 18 - m}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m < - 2}\\{m \le - 22}\end{array} \Leftrightarrow m \le - 22} \right.} \right.\).
Chọn A
Câu 70:
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng quy tắc nhân và quy tắc cộng trong xác suất.
Tính chất
Quy tắc nhân xác suất
Lời giải
Gọi \({\rm{A}}\) và \({\rm{B}}\) lần lượt là biến cố người thứ nhất và người thứ hai có bóng vào lỗ.
Vì vậy nên \(\overline A \) và \(\overline B \) sẽ lần lượt là các biến cố người thứ nhất và người thứ hai không có bóng vào lỗ.
Kết hợp với đề bài, ta tính được: \(P\left( {\overline A } \right) = 100{\rm{\% }} - P\left( A \right) = 46{\rm{\% }}\), \(P\left( {\overline B } \right) = 100{\rm{\% }} - P\left( B \right) = 55{\rm{\% }}\)
Xác suất để chỉ có một người chơi có bóng trong lỗ là :
\(P\left( {A.\overline B } \right) + P\left( {\overline A .B} \right) = P\left( A \right).P\left( {\overline B } \right) + P\left( B \right).P\left( {\overline A } \right) = 54{\rm{\% }}.55{\rm{\% }} + 45{\rm{\% }}.46{\rm{\% }} = 50,4{\rm{\% }}\)
Chọn B
Câu 71:
 Xem đáp án
Xem đáp án
Phương pháp giải
- Xác định thiết diện của mặt phẳng (P) tạo với khối chóp S.ABCD
- Tính tỉ số thể tích khối đa diện dựa trên công thức tính nhanh
Lời giải
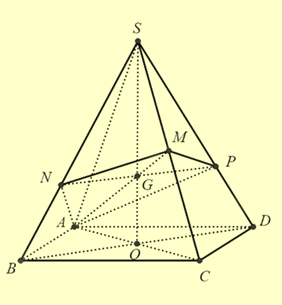
Giả sử (P) cắt SB tại N, cắt SD tại P
Ta có thiết diện là ANMP
Gọi G là giao điểm của AM và SO
Xét : Do AM và SO là các trung tuyến nên G là trọng tâm
Xét
\( \Rightarrow \frac{{SN}}{{SB}} = \frac{{SP}}{{SD}} = \frac{{SG}}{{SO}} = \frac{2}{3}\)
Giả sử thể tich khối chóp S.ABCD là V
Ta có: \(\frac{{{V_{S.ANMP}}}}{{{V_{S.ABCD}}}} = \frac{{\frac{{SB}}{{SN}} + \frac{{SD}}{{SP}} + \frac{{SC}}{{SM}} + 1}}{{4.\frac{{SB}}{{SN}}.\frac{{SD}}{{SP}}.\frac{{SC}}{{SM}}.1}} = \frac{{\frac{3}{2} + \frac{3}{2} + 2 + 1}}{{4.\frac{3}{2}.\frac{3}{2}.2.1}} = \frac{1}{3}\)
Hay \(\frac{{{V_1}}}{V} = \frac{1}{3}\)
Mà \({V_1} + {V_2} = V\)
\( \Rightarrow \frac{{{V_1}}}{{{V_2}}} = \frac{1}{2}\). Chọn C
Chọn C
Câu 72:
Cho tam giác ABC đều cạnh a nội tiếp đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối nón xoay được tạo thành khi cho phần tô đậm quay quanh đường thẳng AD bằng:
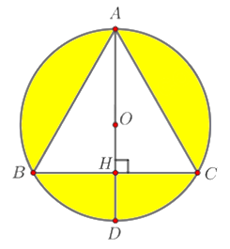
 Xem đáp án
Xem đáp án
Phương pháp giải
Bước 1: Bán kính đường tròn ngoại tiếp tam giác \(ABC\) là R.
Khi quay quanh đường thẳng \(AD\) thì thể tích hình cầu tạo thành: \({V_1} = \frac{4}{3}\pi {R^3} = \frac{{4\pi \sqrt 3 {a^3}}}{{27}}\)
Bước 2: Khi quay quanh đường thẳng \(AD\) thì thể tích khối nón tạo thành:\({V_2} = \frac{1}{3}\pi .B{H^2}.AH = \frac{{\pi \sqrt 3 {a^3}}}{{24}}\)
Bước 3: Thể tích của khối nón xoay được tạo thành khi cho phần tô đậm quay quanh đường thẳng
\(AD\) bằng: \({V_1} - {V_2} = \frac{{23\pi \sqrt 3 {a^3}}}{{216}}\).
Công thức tính diện tích mặt cầu, thể tích khối cầu
Lời giải
Bán kính đường tròn ngoại tiếp tam giác \(ABC\) là \(R = \frac{{BC}}{{2{\rm{sin}}A}} = \frac{a}{{2{\rm{sin}}{{60}^ \circ }}} = \frac{{a\sqrt 3 }}{3}\)
Khi quay quanh đường thẳng \(AD\) thì thể tích hình cầu tạo thành: \({V_1} = \frac{4}{3}\pi {R^3} = \frac{{4\pi \sqrt 3 {a^3}}}{{27}}\)
Khi quay quanh đường thẳng \(AD\) thì thể tích khối nón tạo thành:\({V_2} = \frac{1}{3}\pi .B{H^2}.AH = \frac{{\pi \sqrt 3 {a^3}}}{{24}}\)
Thể tích của khối nón xoay được tạo thành khi cho phần tô đậm quay quanh đường
thẳng \(AD\) bằng: \({V_1} - {V_2} = \frac{{23\pi \sqrt 3 {a^3}}}{{216}}\).
Chọn D
Câu 73:
 Xem đáp án
Xem đáp án
Phương pháp giải
Bước 1: Gọi điểm \(M\left( {1 - t;1 + t;2t} \right) \in {d_2}\). Suy ra \(\overrightarrow {AM} = \left( { - t;t - 1;2t - 4} \right)\).
Bước 2: Tìm vecto chỉ phương đường thẳng \({d_1}\)
Bước 3: \(AM \bot {d_1}\left( {AM \equiv {\rm{\Delta }}} \right)\) nên tìm được \(t\)
Bước 4: Lập phương trình cần tìm bằng cách thay \(t\) đã rìm được vào \(\overrightarrow {AM} = \left( { - t;t - 1;2t - 4} \right)\).
Lời giải
Gọi \(M\left( {1 - t;1 + t;2t} \right) \in {d_2}\). Ta có: \(\overrightarrow {AM} = \left( { - t;t - 1;2t - 4} \right)\).
Đường thẳng \({d_1}\) có một vectơ chỉ phương là \({\vec u_1} = \left( {1;1;1} \right)\).
Do \(AM \bot {d_1}\left( {AM \equiv {\rm{\Delta }}} \right)\) nên \(\overrightarrow {AM} .{\vec u_1} = 0 \Leftrightarrow 2t - 5 = 0 \Leftrightarrow t = \frac{5}{2}\).
Đường thẳng \({\rm{\Delta }}\) qua \(A\left( {1;2;4} \right)\) và có một vectơ chỉ phương là \(\overrightarrow {AM} = \left( { - \frac{5}{2};\frac{3}{2};1} \right) = \frac{1}{2}\left( { - 5;3;2} \right)\), có phương trình là \({\rm{\Delta }}:\frac{{x - 1}}{{ - 5}} = \frac{{y - 2}}{3} = \frac{{z - 4}}{2}\).
Chọn D
Câu 74:
Số học sinh khối 12 của một trường học là một số có ba chữ số và khi yêu cầu các em học sinh này xếp thành 16 hàng, 20 hàng hoặc 24 hàng đều nhau thì vừa đủ.
Số học sinh khối 12 của trường đó có thể là số nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án
B. 240
C. 480
Phương pháp giải
- Gọi x là số học sinh khối 12.
- Khi đó x chia hết cho 16,20 và 24.
Lời giải
Gọi \(x\) là số học sinh khối 12.
Khi đó \(x\) chia hết cho 16,20 và 24.
\( \Rightarrow x \in BC\left( {16;20;24} \right)\)
\(16 = {2^4};\,\,20 = {2^2}.5;\,\,24 = {2^3}.3\)
\( \Rightarrow BCNN\left( {16;20;24} \right) = 240\)
\( \Rightarrow BC\left( {16;20;24} \right) = \left\{ {240k\mid k \in {\mathbb{N}^{\rm{*}}}} \right\}\)
\( \Rightarrow x = 240k\)
Số học sinh khối 12 của trường đó có thể là 240 hoặc 480.
Chọn B, C
Câu 75:
 Xem đáp án
Xem đáp án
Phương pháp giải
Bước 1: Tìm tọa độ các điểm \({M_1},{M_2},{M_3}\) lần lượt là hình chiếu của điểm \(M\left( {3;1;4} \right)\) lên các trục tọa độ \(Ox,Oy,Oz\).
Bước 2: Viết phương trình mặt phẳng \(\left( P \right)\) và kết luận.
Lời giải
Hình chiếu của điểm \(M\left( {3;1;4} \right)\) lên trục \(Ox\) là \({M_1}\left( {3;0;0} \right)\).
Hình chiếu của điểm \(M\left( {3;1;4} \right)\) lên trục \(Oy\) là \({M_2}\left( {0;1;0} \right)\).
Hình chiếu của điểm \(M\left( {3;1;4} \right)\) lên trục \(Oz\) là \({M_3}\left( {0;0;4} \right)\).
Mặt phẳng \(\left( P \right)\) đi qua ba điểm \({M_1}\left( {3;0;0} \right),{M_2}\left( {0;1;0} \right),{M_3}\left( {0;0;4} \right)\) có phương trình là: \(\frac{x}{3} + \frac{y}{1} + \frac{z}{4} = 1 \Leftrightarrow 4x + 12y + 3z - 12 = 0\).
Chọn D
Câu 76:
 Xem đáp án
Xem đáp án
Phương pháp giải
Tính 55, sau đó tìm số dư khi chia cho 6.
Lời giải
\({5^5} = 3125\), chia cho 6 dư 5 nên \({5^5} \equiv 5\left( {{\rm{mod}}\,\,6} \right)\)
Chọn C
Câu 77:
Đánh số trang của một quyển sách từ trang 1 đến trang 2023.
Cần dùng _______ chữ số để đánh số trang của quyển sách đó.
 Xem đáp án
Xem đáp án
Đáp án: "6985"
Phương pháp giải
Tính số trang có 1, 2, 3, 4 chữ số.
Lời giải
Số trang có 1 chữ số: 9 trang.
Số trang có 2 chữ số: 90 trang.
Số trang có 3 chữ số: 900 trang.
Số trang có 4 chữ số: 9000 trang.
Ta có: 2023 = 9+90+900+1024
Số chữ số để đánh số trang là: 9.1+90.2+900.3+1024.4 = 6985
Câu 78:
Một sợi dây kim loại dài 60 cm được cắt thành 2 đoạn. Đoạn thứ nhất uốn thành hình vuông cạnh a, đoạn thứ hai uốn thành đường tròn bán kính r. Để tổng diện tích hình vuông và hình tròn là nhỏ nhất thì tỉ số \(\frac{a}{r}\) bằng
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Gọi x là độ dài của đoạn dây cuộn thành hình tròn \((0 < x < 60)\).
Suy ra chiều dài đoạn còn lại là \(60 - x\).
Chu vi đường tròn: \(2\pi r = x \Rightarrow r = \frac{x}{{2\pi }}\)
\({S_1} = \pi .{r^2} = \frac{{{x^2}}}{{4\pi }}\)
Diện tích hình vuông: \({S_2} = {\left( {\frac{{60 - x}}{4}} \right)^2}\).
Tổng diện tích hai hình: \(S = \frac{{{x^2}}}{{4\pi }} + {\left( {\frac{{60 - x}}{4}} \right)^2}\)
\( = \frac{{\left( {4 + \pi } \right).{x^2} - 120\pi x + 3600\pi }}{{16\pi }}\)
Đạo hàm: \(S' = \frac{{\left( {4 + \pi } \right).x - 60\pi }}{{8\pi }};S' = 0\)
\( \Leftrightarrow x = \frac{{60\pi }}{{4 + \pi }};S'' = \frac{{4 + \pi }}{{8\pi }} > 0\)
Suy ra hàm \({\rm{S}}\) chỉ có một cực trị và là cực tiểu tại \(x = \frac{{60\pi }}{{4 + \pi }}\)
Do đó \({\rm{S}}\) đạt giá trị nhỏ nhất tại \(x = \frac{{60\pi }}{{4 + \pi }}\)
Với \(x = \frac{{60\pi }}{{4 + \pi }}\)
\( \to r = \frac{{30}}{{\left( {4 + \pi } \right)}}\)
\( \to a = \frac{{60 - x}}{4} = \frac{{60}}{{\left( {4 + \pi } \right)}}\)
\( \to \frac{a}{r} = 2\)
Chọn D
Câu 79:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dạng 2: Tìm tập hợp điểm biểu diễn số phức
Lời giải
Gọi \(z = x + yi \Rightarrow 3\left| {x + yi + i} \right| = \left| {2\left( {x - yi} \right) - \left( {x + yi} \right) + 3i} \right|\)
\( \Leftrightarrow 3\left| {x + \left( {y + 1} \right)i\left| = \right|x - \left( {3y - 3} \right)i} \right| \Leftrightarrow 9{x^2} + 9{(y + 1)^2} = {x^2} + 9{(y - 1)^2}\)
\( \Leftrightarrow 8{x^2} + 18y = 0 \Leftrightarrow y = - \frac{4}{9}{x^2}\) là phương trình một parabol.
Chọn B
Câu 80:
Có 13 học sinh của một trường THPT đạt danh hiệu học sinh xuất sắc, trong đó khối 12 có 8 học sinh nam và 3 học sinh nữ, khối 11 có 2 học sinh nam. Chọn ngẫu nhiên 3 bạn bất kì lên trao thưởng. Xác suất để 3 học sinh được chọn có cả nam và nữ đồng thời có cả khối 11 và khối 12 là
 Xem đáp án
Xem đáp án
Phương pháp giải
Biến cố và xác suất của biến cố
Lời giải
Không gian mẫu là số cách chọn ngẫu nhiên 3 học sinh từ 13 học sinh.
Suy ra số phần tử của không gian mẫu là \(\left| {\rm{\Omega }} \right| = C_{13}^3 = 286\).
Gọi \(A\) là biến cố " 3 học sinh được chọn có cả nam và nữ đồng thời có cả khối 11 và khối 12 ".
Ta có các trường hợp thuận lợi cho biến cố \(A\) là:
- TH1: Chọn 1 học sinh khối 11; 1 học sinh nam khối 12 và 1 học sinh nữ khối 12 nên có \(C_2^1C_8^1C_3^1 = 48\) cách.
- TH2: Chọn 1 học sinh khối 11;2 học sinh nữ khối 12 có \(C_2^1C_3^2 = 6\) cách.
- TH3: Chọn 2 học sinh khối 11; 1 học sinh nữ khối 12 có \(C_2^2C_3^1 = 3\) cách.
Suy ra số phần tử của biến cố \(A\) là \(\left| {{{\rm{\Omega }}_A}} \right| = 48 + 6 + 3 = 57\).
Vậy xác suất cần tính \(P\left( A \right) = \frac{{\left| {{{\rm{\Omega }}_A}} \right|}}{{\left| {\rm{\Omega }} \right|}} = \frac{{57}}{{286}}\).
Chọn A
Câu 81:
Cho một đồng hồ cát như hình bên dưới (gồm 2 hình nón chung đỉnh ghép lại), trong đó đường sinh bất kì của hình nón hợp với đáy một góc 600.
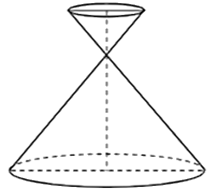
Biết rằng chiều cao của đồng hồ là 30 cm và tỉ lệ thể tích giữa phần lớn và phần nhỏ bằng 8. Thể tích cát (lấy gần đúng đến hàng đơn vị) để đổ đầy phần nhỏ của đồng hồ cát bằng
 Xem đáp án
Xem đáp án
Phương pháp giải
Diện tích hình nón, thể tích khối nón (Đọc thêm)
Lời giải
Gọi \(I\) là đỉnh chung, \(O,O'\) lần lượt là tâm đường tròn đáy của khối nón lớn và nhỏ.
Gọi \(M,M'\) là hai điểm nằm trên đường tròn đáy của khối nón lớn và nhỏ.
Gọi \(x\) là chiều cao khối nón nhỏ thì \(30 - x\) là chiều cao khối nón lớn
Ta có: \(OM = OI.{\rm{cot}}{60^ \circ } = \frac{{\sqrt 3 }}{3}\left( {30 - x} \right);O'M' = O'I.{\rm{cot}}{60^ \circ } = \frac{{\sqrt 3 }}{3}x\).
Từ tỉ số thể tích, ta có: \(\frac{{OI.O{M^2}}}{{O'I.O'M{'^2}}} = 8 \Rightarrow {(30 - x)^3} = 8{x^3} \Leftrightarrow x = 10\)
Thể tích khối nón nhỏ là: \(V = \frac{1}{9}\pi {x^3} = \frac{{1000\pi }}{9} \approx 349\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Chọn B
Câu 82:
Trong không gian \(Oxyz\), cho đường thẳng \(d:\frac{{x - 2}}{2} = \frac{{y + 1}}{1} = \frac{{z - 1}}{2}\) và mặt cầu \(\left( S \right):{(x - 3)^2} + {(y - 1)^2} + {(z + 1)^2} = 4\). Hai mặt phẳng \(\left( P \right),\left( Q \right)\) chứa đường thẳng \(d\) và tiếp xúc với mặt cầu \(\left( S \right)\) lần lượt tại các tiếp điểm \(M,N\). Độ dài đoạn thẳng \(MN\) biểu diễn dưới dạng \(\frac{{a\sqrt b }}{3}\).
Những khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án
B. \(a\) và \(b\) nguyên tố cùng nhau.
D. Một trong hai số là số chính phương.
Phương pháp giải
- Xác định tâm và bán kính mặt cầu.
- Chứng minh d(I,d) = IH và tính d(I,d).
- Gọi O là trung điểm của MN.
- Tính MN.
Lời giải
Mặt cầu \(\left( S \right)\) có tâm \(I\left( {3;1; - 1} \right)\), bán kính \(R = 2\).
Đường thẳng \(d\) đi qua điểm \(A\left( {2; - 1;1} \right)\) và có một vectơ chỉ phương là \(\overrightarrow {{u_d}} = \left( {2;1;2} \right)\)
Xét mặt phẳng thiết diện đi qua tâm \(I\), điểm \(M,N\) và cắt \(d\) tại \(H\).
Khi đó \(d\left( {I,d} \right) = IH\).
Ta có: \(\overrightarrow {IA} = \left( { - 1; - 2;2} \right)\).
\(\overrightarrow {{u_d}} = \left( {2;1;2} \right) \Rightarrow \left[ {\overrightarrow {IA} ,\overrightarrow {{u_d}} } \right] = \left( { - 6;6;3} \right)\)
\( \Rightarrow d\left( {I,d} \right) = IH = \frac{{\left[ {\overrightarrow {IA} ,\overline {{u_d}} } \right]}}{{\left| {\overrightarrow {{u_d}} } \right|}} = \frac{{\sqrt {{{( - 6)}^2} + {6^2} + {3^2}} }}{{\sqrt {{2^2} + {1^2} + {2^2}} }} = 3\)
\( \Rightarrow IH = 3,IM = IN = R = 2 \Rightarrow MH = \sqrt {{3^2} - {2^2}} = \sqrt {I{H^2} - I{M^2}} = \sqrt 5 \)
Gọi \(O\) là trung điểm của \(MN\). Khi đó:
\(MO = \frac{{MH.IM}}{{IH}} = \frac{{2\sqrt 5 }}{3} \Rightarrow MN = 2MO = \frac{{4\sqrt 5 }}{3}\)
Chọn B, D
Câu 83:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Xét tích phân \(\int\limits_0^{\frac{\pi }{4}} {f\left( {{\rm{tan}}x} \right)dx = 4} \).
Đặt \({\rm{t}} = {\rm{tan}}x \Rightarrow {\rm{dt}} = \frac{1}{{{\rm{co}}{{\rm{s}}^2}x}}{\rm{\;d}}x = \left( {{\rm{ta}}{{\rm{n}}^2}x + 1} \right){\rm{d}}x \Rightarrow {\rm{d}}x = \frac{{{\rm{dt}}}}{{1 + {{\rm{t}}^2}}}\)
Đổi cận: \(\left\{ {\begin{array}{*{20}{l}}{x = 0 \to t = 0}\\{x = \frac{\pi }{4} \to t = 1}\end{array}} \right.\)
\( \Rightarrow 4 = \int\limits_0^{\frac{\pi }{4}} {f\left( {{\rm{tan}}x} \right)dx} = \int\limits_0^1 {\frac{{f\left( t \right)}}{{{t^2} + 1}}dt} = \int\limits_0^1 {\frac{{f\left( x \right)}}{{{x^2} + 1}}dx} \)
Từ đó suy ra \(I = \int\limits_0^1 {f\left( x \right)dx} = \int\limits_0^1 {\frac{{f\left( x \right)}}{{{x^2} + 1}}} {\rm{\;d}}x + \int\limits_0^1 {\frac{{{x^2}f\left( x \right)}}{{{x^2} + 1}}} {\rm{\;d}}x = 4 + 2 = 6\)
Chọn C
Câu 84:
Một cái cổng hình parabol có dạng \(y = - \frac{1}{2}{x^2}\) có chiều rộng \(d = 4m\).
Tính chiều cao \(h\) của cổng (xem hình minh họa)
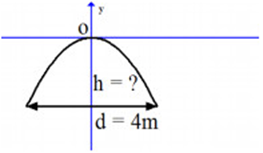
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng tính đối xứng của parabol.
Lời giải
Gọi hai điểm chân cổng là \(A\left( {{x_A};{y_A}} \right)\) và \(B\left( {{x_B};{y_B}} \right)\) thì ta có \({y_A} = {y_B}\) và \(\left| {{x_A}} \right| = \left| {{x_B}} \right|\).
Vì \(d = 4\) nên \(\left| {{x_A}} \right| = \left| {{x_B}} \right| = 2\).
Vậy \(h = \left| {{y_A}} \right| = \left| { - \frac{1}{2}x_A^2} \right| = \left| { - \frac{1}{2}{{.2}^2}} \right| = 2\,\,\left( m \right)\).
Chọn B
Câu 85:
 Xem đáp án
Xem đáp án
Phương pháp giải
\(F\left( x \right) = \mathop \smallint \nolimits^ f\left( x \right)dx = \mathop \smallint \nolimits^ ax + \frac{b}{{{x^2}}}dx\)
\( = \frac{{a{x^2}}}{2} - \frac{b}{x} + c\)
Lời giải
Ta có:
\(F\left( x \right) = \mathop \smallint \nolimits^ f\left( x \right)dx = \mathop \smallint \nolimits^ ax + \frac{b}{{{x^2}}}dx\)
\( = \frac{{a{x^2}}}{2} - \frac{b}{x} + c\)
\(\begin{array}{l}F( - 1) = 2 \Rightarrow \frac{a}{2} + b + c = 2\\F(1) = 14 \Rightarrow \frac{a}{2} - b + c = 14\end{array}\)
\(F(2) = 14 \Rightarrow 2a - \frac{b}{2} + c = 14\)
\( \Rightarrow a = 2,b = - 6,c = 7\)
\(F(x) = \frac{{a{x^2}}}{2} - \frac{b}{x} + c = {x^2} + \frac{6}{x} + 7\)
Chọn B
