30 câu hỏi trắc nghiệm thuộc Hệ tọa độ trong không gian

Câu 1:

Trong không gian với hệ tọa độ Oxyz cho điểm A(1;−2;4). Hình chiếu vuông góc của A trên trục Oy là điểm

A.P(0;0;4)

B.Q(1;0;0)

C.N(0;−2;0)

D.M(0;−2;4)

Xem đáp án

Hình chiếu vuông góc của A(1;−2;4) trên trục Oy là điểm N(0;−2;0).

Đáp án cần chọn là: C

Câu 2:

Điểm M(x;y;z) nếu và chỉ nếu:

A. $\vec{O M} = x . \vec{i} + y . \vec{j} + z . \vec{k}$

B. $\vec{O M} = z . \vec{i} + y . \vec{j} + x . \vec{k}$

C. $\vec{O M} = x . \vec{j} + y . k + z . \vec{i}$

D.

\vec{O M} = x . \vec{k} + y . \vec{j} + z . \vec{i}

Xem đáp án

Điểm $M (x; y; z) \Leftrightarrow \vec{O M} = x . \vec{i} + y . \vec{j} + z . \vec{k}$

Đáp án cần chọn là: A

Câu 3:

Điểm N là hình chiếu của M(x;y;z) trên trục tọa độ OzOz thì:

A.N(x;y;z)

B.N(x;y;0)

C.N(0;0;z)

D.N(0;0;1)

Xem đáp án

Chiếu M lên trục Oz thì $x = 0; y = 0$ và giữ nguyên z nên N(0;0;z).

Đáp án cần chọn là: C

Câu 4:

Hình chiếu của điểm M(1;−1;0) lên trục Oz là:

A.N(−1;−1;0)

B.N(1;−1;0)

C.N(−1;1;0)

D.N(0;0;0)

Xem đáp án

Vì chiếu điểm M lên trục Oz nên giữ nguyên z và cho $x = y = 0$ . Do đó ta được hình chiếu của điểm M(1;−1;0) lên trục Oz là N(0;0;0)

Đáp án cần chọn là: D

Câu 5:

Khi chiếu điểm M(−4;3;−2) lên trục Ox được điểm N thì:

A. $\bar{O N} = - 4$

B. $\bar{O N} = 3$

C. $\bar{O N} = 4$

D.

\bar{O N} = 2

Xem đáp án

Khi chiếu điểm M(−4;3;−2) lên trục Ox được điểm N có tọa độ N(−4;0;0) nên $\bar{O N} = - 4$

Đáp án cần chọn là: A

Câu 6:

Điểm $M \in (O x y)$ thì tọa độ của M là:

A.M(x;y;0)

B.M(0;x;y)

C.M(0;0;z)

D.M(0;0;1)

Xem đáp án

Điểm $M \in (O x y)$ thì cao độ $z = 0$ . Do đó M(x;y;0).

Đáp án cần chọn là: A

Câu 7:

Hình chiếu của điểm M(2;2;−1) lên mặt phẳng (Oyz) là:

A.N(0;2;−1)

B.N(2;0;0)

C.N(0;2;0)

D.N(0;2;1)

Xem đáp án

Hình chiếu của điểm M(2;2;−1) lên mặt phẳng (Oyz) là N(0;2;−1).

Đáp án cần chọn là: A

Câu 8:

Tọa độ điểm M là trung điểm đoạn thẳng AB là:

A. $M (\frac{- x_{A} + x_{B}}{2}; \frac{- y_{A} + y_{B}}{2}; \frac{- z_{A} + z_{B}}{2})$

B. $M (\frac{x_{A} + x_{B}}{3}; \frac{y_{A} + y_{B}}{3}; \frac{z_{A} + z_{B}}{3})$

C. $M (\frac{x_{A} - x_{B}}{2}; \frac{y_{A} - y_{B}}{2}; \frac{z_{A} - z_{B}}{2})$

D.

M (\frac{x_{A} + x_{B}}{2}; \frac{y_{A} + y_{B}}{2}; \frac{z_{A} + z_{B}}{2})

Xem đáp án

Điểm M là trung điểm đoạn thẳng AB nếu và chỉ nếu

$M (\frac{x_{A} + x_{B}}{2}; \frac{y_{A} + y_{B}}{2}; \frac{z_{A} + z_{B}}{2})$

Đáp án cần chọn là: D

Câu 9:

Tọa độ trọng tâm tam giác ABC là:

A. $G (\frac{x_{A} + x_{B} + x_{C}}{3}; \frac{y_{A} + y_{B} + y_{C}}{3}; \frac{z_{A} + z_{B} + z_{C}}{3})$

B. $G (\frac{x_{A} + x_{B} + x_{C}}{4}; \frac{y_{A} + y_{B} + y_{C}}{4}; \frac{z_{A} + z_{B} + z_{C}}{4})$

C. $G (\frac{x_{A} - x_{B} + x_{C}}{3}; \frac{y_{A} - y_{B} + y_{C}}{3}; \frac{z_{A} - z_{B} + z_{C}}{3})$

D.

G (\frac{x_{A} - x_{B} - x_{C}}{3}; \frac{y_{A} - y_{B} - y_{C}}{3}; \frac{z_{A} - z_{B} - z_{C}}{3})

Xem đáp án

Công thức tọa độ trọng tâm tam giác

$G (\frac{x_{A} + x_{B} + x_{C}}{3}; \frac{y_{A} + y_{B} + y_{C}}{3}; \frac{z_{A} + z_{B} + z_{C}}{3})$

Đáp án cần chọn là: A

Câu 10:

Cho hai véc tơ $\vec{u} = (a; 0; 1), \vec{v} = (- 2; 0; c)$ . Biết $\vec{u} = \vec{v}$ khi đó:

A.a=0

B.c=1

C.a=−1

D.a=c

Xem đáp án

$\vec{u} = \vec{v} \Leftrightarrow \{\begin{matrix} a = - 2 \\ 0 = 0 \\ 1 = c \end{matrix}$

Đáp án cần chọn là: B

Câu 11:

Công thức tính độ dài véc tơ

\vec{u} = (a; b; c)

là:

A. $|\vec{u}| = \sqrt{a + b + c}$

B. $|\vec{u}| = \sqrt{a^{2} + b^{2} + c^{2}}$

C. $|\vec{u}| = a^{2} + b^{2} + c^{2}$

D.

|\vec{u}| = {(\sqrt{a + b + c})}^{2}

Xem đáp án

Ta có: $|\vec{u}| = \sqrt{{\vec{u}}^{2}} = \sqrt{a^{2} + b^{2} + c^{2}}$

Đáp án cần chọn là: B

Câu 12:

Cho các véc tơ $\vec{u_{1}} (x_{1}; y_{1}; z_{1})$ và $\vec{u_{2}} (x_{2}; y_{2}; z_{2}),$ , khi đó cô sin góc hợp bởi hai véc tơ $\vec{u_{1}}, \vec{u_{2}}$ là:

A. $\frac{\vec{u_{1}} . \vec{u_{2}}}{|\vec{u_{1}}| . |\vec{u_{2}}|}$

B. $\frac{|x_{1} x_{2} + y_{1} y_{2} + z_{1} z_{2}|}{\sqrt{x_{1}^{2} + y_{1}^{2} + z_{1}^{2}} . \sqrt{x_{2}^{2} + y_{2}^{2} + z_{2}^{2}}}$

C. $\frac{x_{1} x_{2} + y_{1} y_{2} + z_{1} z_{2}}{{(\sqrt{x_{1}^{2} + y_{1}^{2} + z_{1}^{2}} . \sqrt{x_{2}^{2} + y_{2}^{2} + z_{2}^{2}})}^{2}}$

D.

\frac{|\vec{u_{1}}| . |\vec{u_{2}}|}{\vec{u_{1}} . \vec{u_{2}}}

Xem đáp án

Cô sin của góc hợp bởi hai véc tơ $\vec{u_{1}}, \vec{u_{2}}$ là:

$\cos (\vec{u_{1}}, \vec{u_{2}}) = \frac{\vec{u_{1}} . \vec{u_{2}}}{|\vec{u_{1}}| . |\vec{u_{2}}|} = \frac{x_{1} x_{2} + y_{1} y_{2} + z_{1} z_{2}}{\sqrt{x_{1}^{2} + y_{1}^{2} + z_{1}^{2}} . \sqrt{x_{2}^{2} + y_{2}^{2} + z_{2}^{2}}}$

Đáp án cần chọn là: A

Câu 13:

Cho hai véc tơ $\vec{u} = (- 1; - 1; - 1), \vec{v} = (2; 1; 0)$ , khi đó cô sin của góc hợp bởi hai véc tơ đó là:

A. $- \frac{\sqrt{15}}{5}$

B. $\frac{3}{\sqrt{15}}$

C. $- \frac{\sqrt{5}}{\sqrt{3}}$

D.

\frac{4}{\sqrt{15}}

Xem đáp án

Ta có:

$\cos (\vec{u}, \vec{v}) = \frac{- 1.2 - 1.1 - 1.0}{\sqrt{{(- 1)}^{2} + {(- 1)}^{2} + {(- 1)}^{2}} . \sqrt{2^{2} + 1^{2} + 0^{2}}} = - \frac{3}{\sqrt{15}} = - \frac{3 \sqrt{15}}{15} = - \frac{\sqrt{15}}{5}$

Đáp án cần chọn là: A

Câu 14:

Tung độ của điểm M thỏa mãn $\vec{O M} = 2 \vec{j} - \vec{i} + \vec{k}$ là:

A.−1

B.1

C.2

D.−2

Xem đáp án

$\vec{O M} = 2 \vec{j} - \vec{i} + \vec{k} = - \vec{i} + 2 \vec{j} + \vec{k} \Rightarrow M (- 1; 2; 1)$ .Do đó tung độ của M bằng 2.

Đáp án cần chọn là: C

Câu 15:

Hình chiếu của điểm M(0;2;1) trên mặt phẳng (Oxy) thuộc:

A.trục Ox

B.trục Oy

C.trục Oz

D.trùng điểm O

Xem đáp án

Hình chiếu của M(0;2;1) lên mặt phẳng (Oxy) là N(0;2;0).

Do đó N nằm trên trục Oy.

Đáp án cần chọn là: B

Câu 16:

Cho hai điểm A(−3;1;2),B(1;1;0), tọa độ trung điểm đoạn thẳng AB là:

A.M(−1;1;1)

B.M(−2;2;2)

C.M(−2;0;1)

D.M(−1;2;1)

Xem đáp án

Điểm M là trung điểm đoạn thẳng AB nên

$\{\begin{matrix} x_{M} = \frac{x_{A} + x_{B}}{2} = \frac{- 3 + 1}{2} = - 1 \\ y_{M} = \frac{y_{A} + y_{B}}{2} = \frac{1 + 1}{2} = 1 \\ z_{M} = \frac{z_{A} + z_{B}}{2} = \frac{2 + 0}{2} = 1 \end{matrix} \Rightarrow M (- 1; 1; 1)$

Đáp án cần chọn là: A

Câu 17:

Cho tam giác ABC có A(2;1;0),B(−1;0;3),C(1;2;3). Tọa độ trọng tâm tam giác là:

A. $G (2; 1; 3)$

B. $G (\frac{2}{3}; 1; 2)$

C. $G (\frac{2}{3}; \frac{1}{3}; - 2)$

D.

G (1; 1; 2)

Xem đáp án

Trọng tâm G của tam giác ABC có tọa độ thỏa mãn:

$\{\begin{matrix} x_{G} = \frac{x_{A} + x_{B} + x_{C}}{3} = \frac{2 - 1 + 1}{3} = \frac{2}{3} \\ y_{G} = \frac{y_{A} + y_{B} + y_{C}}{3} = \frac{1 + 0 + 2}{3} = 1 \\ z_{G} = \frac{z_{A} + z_{B} + z_{C}}{3} = \frac{0 + 3 + 3}{3} = 2 \end{matrix} \Rightarrow G (\frac{2}{3}; 1; 2)$

Đáp án cần chọn là: B

Câu 18:

Gọi G(4;−1;3) là tọa độ trọng tâm tam giác ABC với A(0;2;−1),B(−1;3;2). Tìm tọa độ điểm C.

A.C(−1;3;2)

B.C(11;−2;10)

C.C(5;−6;2)

D.C(13;−8;8)

Xem đáp án

Điểm G là trọng tâm tam giác ABC nếu:

$\begin{array}{l} \{\begin{matrix} x_{G} = \frac{x_{A} + x_{B} + x_{C}}{3} \\ y_{G} = \frac{y_{A} + y_{B} + y_{C}}{3} \\ z_{G} = \frac{z_{A} + z_{B} + z_{C}}{3} \end{matrix} \\ \Rightarrow \{\begin{matrix} x_{C} = 3 x_{G} - x_{A} - x_{B} = 3.4 - 0 - (- 1) = 13 \\ y_{C} = 3 y_{G} - y_{A} - y_{B} = 3. (- 1) - 2 - 3 = - 8 \\ z_{C} = 3 z_{G} - z_{A} - z_{B} = 3.3 - (- 1) - 2 = 8 \end{matrix} \end{array}$

$\Rightarrow C (13; - 8; 8)$

Đáp án cần chọn là: D

Câu 19:

Tọa độ trọng tâm tứ diện ABCD là:

A. $G (\frac{x_{A} + x_{B} + x_{C} + x_{D}}{3}; \frac{y_{A} + y_{B} + y_{C} + y_{D}}{3}; \frac{z_{A} + z_{B} + z_{C} + z_{D}}{3})$

B. $G (\frac{x_{A} + x_{B} + x_{C} + x_{D}}{4}; \frac{y_{A} + y_{B} + y_{C} + y_{D}}{4}; \frac{z_{A} + z_{B} + z_{C} + z_{D}}{4})$

C. $G (\frac{x_{A} + x_{B} + x_{C} + x_{D}}{2}; \frac{y_{A} + y_{B} + y_{C} + y_{D}}{2}; \frac{z_{A} + z_{B} + z_{C} + z_{D}}{2})$

D.

G (\frac{x_{A} + x_{B} - x_{C} + x_{D}}{4}; \frac{y_{A} + y_{B} - y_{C} + y_{D}}{4}; \frac{z_{A} - z_{B} + z_{C} + z_{D}}{4})

Xem đáp án

Tọa độ trọng tâm tứ diện ABCD là

$G (\frac{x_{A} + x_{B} + x_{C} + x_{D}}{4}; \frac{y_{A} + y_{B} + y_{C} + y_{D}}{4}; \frac{z_{A} + z_{B} + z_{C} + z_{D}}{4})$

Đáp án cần chọn là: B

Câu 20:

Cho tứ diện ABCD có A(1;0;0),B(0;1;1),C(−1;2;0),D(0;0;3). Tọa độ trọng tâm tứ diện G là:

A. $G (0; \frac{3}{4}; 1)$

B. $G (0; 3; 4)$

C. $G (\frac{1}{2}; - \frac{1}{2}; - \frac{1}{2})$

D.

G (0; \frac{3}{2}; 2)

Xem đáp án

Điểm G là trọng tâm tứ diện ABCD nếu tọa độ điểm G thỏa mãn:\

$\{\begin{matrix} x_{G} = \frac{x_{A} + x_{B} + x_{C} + x_{D}}{4} = \frac{1 + 0 - 1 + 0}{4} = 0 \\ y_{G} = \frac{y_{A} + y_{B} + y_{C} + y_{D}}{4} = \frac{0 + 1 + 2 + 0}{4} = \frac{3}{4} \\ z_{G} = \frac{z_{A} + z_{B} + z_{C} + z_{D}}{4} = \frac{0 + 1 + 0 + 3}{4} = 1 \end{matrix}$

$\Rightarrow G (0; \frac{3}{4}; 1)$

Đáp án cần chọn là: A

Câu 21:

Cho hai véc tơ $\vec{O A} = (- 1; 2; - 3), \vec{O B} = (2; - 1; 0)$ , khi đó tổng hai véc tơ $\vec{O A}, \vec{O B}$ là:

A.(1;1;−3)

B.(−3;3;−3)

C.(1;3;−3)

D.(1;−1;3)

Xem đáp án

Ta có:

$\vec{O A} = (- 1; 2; - 3), \vec{O B} = (2; - 1; 0) \Rightarrow \vec{O A} + \vec{O B} = (1; 1; - 3)$

Đáp án cần chọn là: A

Câu 22:

Cho hai véc tơ $\vec{u} = (- 2; 3; 1)$ và $\vec{v} = (1; 1; 1)$ . Khi đó số thực $m = \vec{u} . \vec{v}$ thỏa mãn:

A. $m = 0$

B. $m \in (0; 2)$

C. $m \in (- 2; 0)$

D.

m \in (1; 3)

Xem đáp án

Ta có: $m = \vec{u} . \vec{v} = - 2.1 + 3.1 + 1.1 = 2 \Rightarrow m \in (1; 3)$

Đáp án cần chọn là: D

Câu 23:

Trong không gian với hệ tọa độ Oxyz, cho ba vecto $\vec{a} = (2; 3; - 5); \vec{b} = (0; - 3; 4); \vec{c} = (1; - 2; 3)$ . Tọa độ vector $\vec{n} = 3 \vec{a} + 2 \vec{b} - \vec{c}$ là:

A. $\vec{n} = (5; 1; - 10)$

B. $\vec{n} = (7; 1; - 4)$

C. $\vec{n} = (5; 5; - 10)$

D.

\vec{n} = (5; - 5; - 10)

Xem đáp án

$\vec{n} = 3 (2; 3; - 5) + 2 (0; - 3; 4) - (1; - 2; 3) = (5; 5; - 10)$

Đáp án cần chọn là: C

Câu 24:

Cho hai véc tơ $\vec{u} = (2; 1; - 3), \vec{v} = (0; b; 1)$ , nếu $\vec{u} ⊥ \vec{v}$ thì:

A.b=2

B.b=−3

C.b=3

D.b=1

Xem đáp án

Ta có: $\vec{u} ⊥ \vec{v} \Leftrightarrow \vec{u} . \vec{v} = 2.0 + 1. b + (- 3) .1 = 0 \Leftrightarrow b = 3$

Đáp án cần chọn là: C

Câu 25:

Cho hai điểm A(5;3;1),B(1;3;5). Độ dài véc tơ $\vec{A B}$ là:

A. $(- 4; 0; 4)$

B. $4 \sqrt{2}$

C. 0

D.

6 \sqrt{3}

Xem đáp án

Ta có: $\vec{A B} = (- 4; 0; 4) \Rightarrow |\vec{A B}| = \sqrt{{(- 4)}^{2} + 0^{2} + 4^{2}} = 4 \sqrt{2}$

Đáp án cần chọn là: B

Câu 26:

Độ dài đoạn thẳng AB với A(2;1;0),B(4;−1;1) là một số:

A.nguyên âm

B.vô tỉ

C.nguyên dương

D.bằng 0

Xem đáp án

Ta có: $A B = \sqrt{{(x_{B} - x_{A})}^{2} + {(y_{B} - y_{A})}^{2} + {(z_{B} - z_{A})}^{2}}$

$= \sqrt{{(4 - 2)}^{2} + {(- 1 - 1)}^{2} + {(1 - 0)}^{2}} = \sqrt{9} = 3$

Do đó độ dài đoạn thẳng là một số nguyên dương.

Đáp án cần chọn là: C

Câu 27:

Cho hai vectơ $\vec{a} = (1; 1; - 2), \vec{b} = (1; 0; m)$ . Góc giữa chúng bằng 45⁰ khi:

A. $m = 2 + \sqrt{5}$

B. $m = 2 \pm \sqrt{6}$

C. $m = 2 - \sqrt{6}$

D.

m = 2 + \sqrt{6}

Xem đáp án

Góc giữa $\vec{u}; \vec{v}$ bằng 45⁰ khi $\cos (\vec{u}; \vec{v}) = \cos 45^{0}$

Mà $\cos (\vec{u}; \vec{v}) = \frac{\vec{u} . \vec{v}}{|\vec{u}| . |\vec{v}|}$

$\Rightarrow c o s 45^{0} = \frac{1.1 + 1.0 - 2. m}{\sqrt{1^{2} + 1^{2} + {(- 2)}^{2}} . \sqrt{1^{2} + 0^{2} + m^{2}}}$

$\Leftrightarrow \frac{1}{\sqrt{2}} = \frac{1 - 2 m}{\sqrt{6} . \sqrt{1 + m^{2}}}$

$\Leftrightarrow \sqrt{6 (1 + m^{2})} = \sqrt{2} (1 - 2 m)$

$\begin{array}{l} \Leftrightarrow \{\begin{matrix} 6 (1 + m^{2}) = 2 {(1 - 2 m)}^{2} \\ 1 - 2 m \geq 0 \end{matrix} \\ \Leftrightarrow \{\begin{matrix} 6 + 6 m^{2} = 2 (1 - 4 m + 4 m^{2}) \\ m \leq \frac{1}{2} \end{matrix} \end{array}$

$\Leftrightarrow \{\begin{matrix} 6 + 6 m^{2} = 2 - 8 m + 8 m^{2} \\ m \leq \frac{1}{2} \end{matrix}$

$\Leftrightarrow \{\begin{matrix} 2 m^{2} - 8 m - 4 = 0 \\ m \leq \frac{1}{2} \end{matrix}$

$\Leftrightarrow \{\begin{matrix} m = 2 \pm \sqrt{6} \\ m \leq \frac{1}{2} \end{matrix} \Leftrightarrow m = 2 - \sqrt{6}$

Đáp án cần chọn là: C

Câu 28:

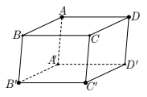
Trong không gian Oxyz, cho hình hộp ABCD.A’B’C’D’ có A(0;0;1), B’(1;0;0), C’(1;1;0). Tìm tọa độ điểm D.

Media VietJack

A.D(0;1;1)

B.D(0;-1;1)

C.D(0;1;0)

D.D(1;1;1)

Xem đáp án

Ta có AD // B’C’, AD = B’C’ nên AB’C’D là hình bình hành, do đó AB’ // DC’ và AB’ = DC’.

$\Rightarrow \vec{A B'} = \vec{D C'}$

$\begin{array}{l} \Rightarrow \{\begin{matrix} 1 - 0 = 1 - x_{D} \\ 0 - 0 = 1 - y_{D} \\ 0 - 1 = 0 - z_{D} \end{matrix} \\ \Rightarrow \{\begin{matrix} x_{D} = 0 \\ y_{D} = 1 \\ z_{D} = 1 \end{matrix} \end{array}$

Vậy D(0;1;1).

Đáp án cần chọn là: A

Câu 29:

Cho 3 điểm A(0;0;1), B(1;0;0); C(1;1;0). Tính bán kính đường tròn ngoại tiếp tam giác ABC.

A. $\frac{\sqrt{3}}{2}$

B. $\frac{\sqrt{3}}{4}$

C. $\sqrt{3}$

D.

\frac{\sqrt{3}}{3}

Xem đáp án

Bước 1: Tính độ dài cạnh AB, BC, CA.

Ta có:

$\begin{array}{l} A B = \sqrt{1^{2} + 0^{2} + {(- 1)}^{2}} = \sqrt{2} \\ B C = \sqrt{0^{2} + 1^{2} + 0^{2}} = 1 \\ C A = \sqrt{1^{2} + 1^{2} + {(- 1)}^{2}} = \sqrt{3} \end{array}$

$\Rightarrow Δ A B C$ là tam giác vuông tại B.

Bước 2: Tính bán kính đường tròn ngoại tiếp tam giác ABC.

Ta có $R = \frac{A C}{2} = \frac{\sqrt{3}}{2}$

Đáp án cần chọn là: A

Câu 30:

Trong không gian Oxyz, cho điểm A(1;1;1),B(4;1;1),C(1;1;5). Tìm tọa độ điểm II là tâm đường tròn nội tiếp tam giác ABC

A.I(−2;1;−2)

B.I(2;1;2)

C.I(2;1;−2)

D.I(−2;−1;−2)

Xem đáp án

Bước 1:

Gọi I(a;b;c) là tâm đường tròn nội tiếp tam giác ABC

Khi đó $B C \cdot \vec{I A} + C A \cdot \vec{I B} + A B \cdot \vec{I C} = \vec{0}$

Bước 2: Thay tọa độ I vào công thức, tìm a, b, c.

Áp dụng, với $I (a; b; c) A B = 3; B C = 5; A C = 4$ ta có:

$5 \vec{I A} + 4 \vec{I B} + 3 \vec{I C} = \vec{0} \Leftrightarrow 12 \vec{I A} = 4 \vec{B A} + 3 \vec{C A}$

$\Leftrightarrow 12 \vec{I A} = (- 12; 0; - 12) \Leftrightarrow \vec{I A} = (- 1; 0; - 1)$

$\Leftrightarrow \{\begin{matrix} 1 - a = - 1 \\ 1 - b = 0 \\ 1 - c = - 1 \end{matrix} \Leftrightarrow \{\begin{matrix} a = 2 \\ b = 1 \\ c = 2 \end{matrix} \Leftrightarrow I (2; 1; 2)$