Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 8)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 8)
-
233 lượt thi
-
96 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
Phần tư duy đọc hiểu
Nội dung chính của văn bản trên là gì?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung bài đọc, xác định cụ thể nội dung của từng đoạn.
Lời giải
- Nội dung chính của văn bản trên là: Tình trạng ô nhiễm và lời kêu gọi bảo vệ đại dương.
- Đọc văn bản có thể nhận thấy nhan đề chính là một gợi ý cho một phần nội dung “Đã đến lúc phải trả ơn đại dương” tức văn bản sẽ có phần kêu gọi sự chung tay, giúp sức của con người để bảo vệ đại dương. Song, văn bản dưới hình thức một văn bản thông tin có phần sapo chính là phần nêu nội dung tóm tắt của bài. Phần này đã cho thấy văn bản ngoài là lời kêu gọi còn phản ánh tình trạng ô nhiễm môi trường toàn cầu đã ảnh hưởng lên đại dương. Đại dương đang hứng chịu những vấn đề đó và bảo vệ con người khỏi chúng. Bởi vậy, văn bản sẽ có thêm một nội dung là tình trạng ô nhiễm đại dương.
Chọn B
Câu 2:
Dựa vào đoạn [1], điền từ không quá hai tiếng có trong bài đọc vào hai chỗ trống.
Rất nhiều thập kỉ qua, đại dương đã giúp ổn định _______ của bề mặt đất liền bằng cách hấp thụ một phần tư lượng khí CO2 ô nhiễm và hơn 90% nhiệt lượng dư thừa từ hiện tượng nóng lên toàn cầu, nhờ đó mà con người trên Trái đất mới có thể _______.
 Xem đáp án
Xem đáp án
Đáp án đúng là:
Rất nhiều thập kỉ qua, đại dương đã giúp ổn định nhiệt độ của bề mặt đất liền bằng cách hấp thụ một phần tư lượng khí CO2 ô nhiễm và hơn 90% nhiệt lượng dư thừa từ hiện tượng nóng lên toàn cầu, nhờ đó mà con người trên Trái đất mới có thể sống được
Phương pháp giải
Căn cứ vào nội dung đoạn số [1].
Lời giải
- Đoạn [1] có trình bày: “Hàng thập kỉ qua, bằng cách hấp thụ một phần tư lượng khí CO2 ô nhiễm và hơn 90% nhiệt lượng dư thừa từ hiện tượng nóng lên toàn cầu, các đại dương đã giữ cho nhiệt độ bề mặt đất liền của Trái đất ở mức có thể sống được”. Với các chi tiết được in đậm, có thể thấy từ khóa còn thiếu là “nhiệt độ” và “sống được”.
Câu 3:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Theo thông tin ở đoạn số [1], đại dương hút CO2 và hấp thụ nhiệt cho khí hậu bớt nóng lên.
Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn số [1].
Lời giải
Theo nội dung ở đoạn [1] thì thông tin ở đề bài hoàn toàn trùng khớp với thông tin “hấp thụ một phần tư lượng khí CO2 ô nhiễm và hơn 90% nhiệt lượng dư thừa từ hiện tượng nóng lên toàn cầu”. Vậy nên thông tin ở đề bài là chính xác.
Chọn A
Câu 4:
Dựa vào đoạn [2], hãy hoàn thành các nội dung sau bằng cách kéo thả các cụm từ vào đúng vị trí.
hóa chất, đánh bắt, độc hại, nhựa, rác
Con người đã đổ xuống biển một lượng rác thải _______ quá lớn và đầu độc bờ biển bằng các _______ nguy hiểm.
Trữ lượng cá tự nhiên bị suy giảm nghiêm trọng, chỉ còn dưới 10% đại dương là được bảo vệ do việc _______ quá mức của con người.
 Xem đáp án
Xem đáp án
Đáp án
Con người đã đổ xuống biển một lượng rác thải nhựa quá lớn và đầu độc bờ biển bằng các hóa chất nguy hiểm.
Trữ lượng cá tự nhiên bị suy giảm nghiêm trọng, chỉ còn dưới 10% đại dương là được bảo vệ do việc đánh bắt quá mức của con người.
Phương pháp giải
Căn cứ vào nội dung đoạn số [2].
Lời giải
- Theo đoạn số [2], “để đáp lại “tấm thịnh tình” ấy, con người lại đổ hàng núi rác thải nhựa xuống biển và đầu độc bờ biển bằng các hóa chất độc hại và những dòng nước công nghiệp”, tức là con người đã đổ xuống biển rác thải “nhựa” và đầu độc biển bằng “hóa chất” độc hại.
=> [vị trí thả 1]: nhựa
[vị trí thả 2]: hóa chất
- Thêm nữa, “Ít nhất một phần ba trữ lượng cá tự nhiên đã bị đánh bắt quá mức, và chỉ còn dưới 10% đại dương là được bảo vệ” đã cho chúng ta biết việc “đánh bắt” quá mức của con người cũng ảnh hưởng nặng nề tới thiên nhiên.
=> [vị trí thả 3]: đánh bắt
Dựa vào nội dung đoạn trên cùng cách sử dụng từ ngữ trong bài đọc, ta có các từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: nhựa
- Vị trí thả 2: hóa chất
- Vị trí thả 3: đánh bắt
Câu 5:
Phương tiện phi ngôn ngữ được sử dụng trong bài viết có tác dụng gì?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung bài đọc, cụ thể ở nhan đề.
Lời giải
Phương tiện phi ngôn ngữ chính là những hình ảnh xuất hiện trong văn bản. Cả văn bản chỉ có một bức ảnh ở đầu với nội dung phản ánh ô nhiễm nặng nề do nhựa gây ra trên các đại dương. Từ đó, phương tiện phi ngôn ngữ này có tác dụng thể hiện một cách trực quan tình trạng ô nhiễm môi trường.
Chọn B
Câu 6:
Qua bài viết, tác giả KHÔNG thể hiện thái độ nào?
(Chọn 2 đáp án đúng)
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung bài đọc.
Lời giải
Qua đoạn trích, tác giả KHÔNG thể hiện thái độ:
- Thất vọng vì tình trạng khí hậu và đại dương ngày càng xấu đi, khiến con người phải đối mặt với sự nguy hiểm
→ Vì đứng trước tình trạng ô nhiễm môi trường, người viết bày tỏ cảm xúc lo âu thay vì thất vọng, vì trong đoạn trích, tác giả dùng từ “lo ngại” trong đoạn số [5]. Cảm xúc thất vọng không phù hợp vì nó dành cho việc mong muốn một điều gì đó mà không được như ý nguyện. Ở đây phải là lo âu vì đó là tình trạng môi trường đáng cảnh báo.
- Tin tưởng, lạc quan vì tình trạng ô nhiễm của đại dương đang ngày càng được cải thiện, có kết quả tích cực
→ Vì trước tình trạng ô nhiễm và việc chưa tìm được cách giải quyết triệt để, các nhà khoa học không bày tỏ cảm xúc tích cực như lạc quan, tin tưởng.
=> Trong đoạn văn, tác giả có nói về những nỗ lực của các tổ chức chính phủ trong việc tạo ra các chương trình nghị sự, dù chưa có nhiều giải pháp nhưng đó là một dấu hiệu của hi vọng mà các nhà khoa học đặt vào tương lai.
Chọn A, B
Câu 7:
Dựa vào đoạn [4], điền cụm từ không quá ba tiếng có trong bài đọc vào chỗ trống.
Nguồn dinh dưỡng từ biển đảm bảo được tính bền vững và công bằng được gọi là __________.
 Xem đáp án
Xem đáp án
Đáp án
Nguồn dinh dưỡng từ biển đảm bảo được tính bền vững và công bằng được gọi là thực phẩm xanh.
Phương pháp giải
Căn cứ vào nội dung đoạn số [4].
Lời giải
Theo đoạn [4], một nội dung có trong chương trình nghị sự chính là “Và khẩu hiệu mới được đặt ra ở đây là “thực phẩm xanh” – nguồn dinh dưỡng từ biển đảm bảo được tính bền vững và công bằng”. Từ đó, có thể nhận thấy “nguồn dinh dưỡng từ biển đảm bảo được tính bền vững và công bằng” là thực phẩm xanh.
Câu 8:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Giải pháp mà thế giới đang nỗ lực thực hiện để giải cứu đại dương là?
|
|
ĐÚNG |
SAI |
|
Có những quy định để nghề đánh bắt cá tự nhiên trở nên bền vững hơn. |
||
|
Thúc đẩy mạnh mẽ sự phát triển của ngành nuôi trồng thủy sản. |
||
|
Đưa ra khẩu hiệu mới về “thực phẩm xanh”. |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Có những quy định để nghề đánh bắt cá tự nhiên trở nên bền vững hơn. |
X | |
|
Thúc đẩy mạnh mẽ sự phát triển của ngành nuôi trồng thủy sản. |
X | |
|
Đưa ra khẩu hiệu mới về “thực phẩm xanh”. |
X |
Phương pháp giải
Căn cứ vào nội dung bài đọc, cụ thể ở nhan đề.
Lời giải
- Có những quy định để nghề đánh bắt cá tự nhiên trở nên bền vững hơn.
→ Ý kiến trên: ĐÚNG
Theo đoạn số [4], “Câu hỏi làm thế nào để nghề đánh bắt cá tự nhiên, từ những con tàu chế biến cá của vùng Đông Á cho đến những chiếc thuyền đánh cá dọc theo bờ biển nhiệt đới, trở nên bền vững hơn cũng là một nội dung quan trọng trong chương trình nghị sự của Lisbon”, những từ khóa được in đậm đã cho thấy thông tin đầu tiên là chính xác.
- Thúc đẩy mạnh mẽ sự phát triển của ngành nuôi trồng thủy sản.
→ Ý kiến trên: SAI
Theo đoạn văn [4] “Ngành nuôi trồng thủy sản đang phát triển bùng nổ cũng cần phải được theo dõi chặt chẽ” chứ không phải “thúc đẩy phát triển”.
- Đưa ra khẩu hiệu mới về “thực phẩm xanh”.
→ Ý kiến trên: ĐÚNG
Thông tin này liên quan tới nội dung “Và khẩu hiệu mới được đặt ra ở đây là “thực phẩm xanh” – nguồn dinh dưỡng từ biển đảm bảo được tính bền vững và công bằng” là chính xác.
Câu 9:
Con người đã hành động như thế nào để đối phó với “tương lai đáng sợ” do chính mình gây ra?
(Chọn 2 đáp án đúng)
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn số [3] và đoạn [5].
Lời giải
- Như tiêu đề ở đoạn số [5], có thể thấy việc làm mạnh mẽ nhất của các tổ chức chính phủ ở thời điểm mức độ ô nhiễm cảnh báo là tổ chức các chương trình nghị sự giữa các quốc gia để cùng nhau tìm hướng giải quyết, khắc phục bền vững. Đã có một số chương trình diễn ra, mang đến một số giải pháp như Hội nghị Đại dương Liên Hợp Quốc, Cuộc đàm phán về khí hậu của Liên Hợp Quốc COP27 và cuộc đàm phán về đa dạng sinh học COP15.
- Trong đó, bài viết cũng không kêu gọi từng cá nhân thực hiện nhặt rác hay yêu cầu các tàu cá tạo ra “thực phẩm xanh”.
Chọn A, D
Câu 10:
thành công, thất bại, ổn định, trung bình
Các đại dương sẽ thoát khỏi sự tổn thương nghiêm trọng khi nồng độ khí nhà kính được giữ ở mức __________. Nếu đại dương an toàn, cuộc chiến chống lại hiện tượng nóng lên toàn cầu cũng sẽ __________.
 Xem đáp án
Xem đáp án
Đáp án
Các đại dương sẽ thoát khỏi sự tổn thương nghiêm trọng khi nồng độ khí nhà kính được giữ ở mức ổn định. Nếu đại dương an toàn, cuộc chiến chống lại hiện tượng nóng lên toàn cầu cũng sẽ thành công.
Phương pháp giải
Căn cứ vào nội dung đoạn số [6].
Lời giải
Theo đoạn [6], “các đại dương sẽ tiếp tục chịu ảnh hưởng trừ khi nồng độ khí nhà kính được giữ ở mức ổn định”. Có thể thấy, đại dương chịu ảnh hưởng nghiêm trọng bởi nồng độ khí nhà kính, khi nào điều này đạt mức “ổn định” thì khi đó đại dương sẽ thoát khỏi sự tổn hại.
=> [vị trí thả 1]: ổn định
Theo đoạn [6], “cuộc chiến chống lại hiện tượng nóng lên toàn cầu cũng sẽ thất bại nếu các đại dương mất khả năng hút CO2 và hấp thụ nhiệt”. Tức là khi đại dương không thực hiện được khả năng của mình nữa thì cuộc chiến chống lại hiện tượng nóng lên toàn cầu sẽ “thất bại”, và ngược lại, đại dương an toàn thì quá trình chiến đấu sẽ thành công.
=> [vị trí thả 2]: thành công
Dựa vào nội dung đoạn trên cùng cách sử dụng từ ngữ trong bài đọc, ta có các từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: ổn định
- Vị trí thả 2: thành công
Câu 11:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Hoàn cảnh của nhân vật Hộ trong đoạn trích là?
|
|
ĐÚNG |
SAI |
|
Sống một mình, chỉ chuyên sáng tác văn chương |
||
|
Có vợ, con, nhưng con cái quanh năm ốm đau, khóc mếu suốt ngày đêm |
||
|
Hộ vẫn luôn có thể lo lắng cho cuộc sống gia đình dư giả |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Sống một mình, chỉ chuyên sáng tác văn chương |
X | |
|
Có vợ, con, nhưng con cái quanh năm ốm đau, khóc mếu suốt ngày đêm |
X | |
|
Hộ vẫn luôn có thể lo lắng cho cuộc sống gia đình dư giả |
X |
Phương pháp giải
Căn cứ vào nội dung đoạn văn [6].
Lời giải
- Từ đoạn số [6] có thể thấy, Hộ đã có vợ, có con. -> Ý số 1 “sống một mình” là sai.
- Từ đoạn số [6], văn bản có viết “Từ khi đứa con này chưa kịp lớn lên, đứa con khác đã vội ra, mà đứa con nào cũng nhiều đẹn, nhiều sài, quấy rức, khóc mếu suốt ngày đêm và quanh năm uống thuốc” đã cho thấy Hộ có vợ, có con nhưng con cái thường xuyên ốm đau, khóc mếu suốt ngày. -> Ý số 2 là đúng.
- Từ chi tiết “Hộ điên người lên vì phải xoay tiền” ở đoạn số [6] có thể thấy gia đình Hộ không dư giả, thậm chí còn rất nghèo và cái nghèo khiến Hộ tức giận. -> Ý số 3 là sai.
Câu 12:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung bài đọc, kiến thức về đề tài.
Lời giải
- Theo văn bản, nhân vật chính – Hộ là một văn sĩ (tức là nhà văn), trong xã hội xưa nhà văn thuộc tầng lớp trí thức. Bi kịch của Hộ chính là bi kịch của những trí thức cùng thời lúc bấy giờ.
- Đặc biệt, để biết đề tài của văn bản là gì, HS trả lời câu hỏi: Văn bản viết về ai? Cái gì? Vậy nên đề tài của văn bản này là viết về người trí thức.
Chọn A
Câu 13:
Những biểu hiện nào dưới đây thể hiện cho sự “cẩu thả trong văn chương” trong suy nghĩ của Hộ?
Chọn hai đáp án đúng.
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn văn số [2] và [3]
Lời giải
Từ đoạn [2] và [3] có thể thấy:
- Đáp án A đúng vì nó xuất hiện trong 2 chi tiết “Hắn phải cho in nhiều cuốn văn viết vội vàng” và “Hắn đã viết những gì? Toàn những cái vô vị, nhạt nhẽo, gợi những tình cảm rất nhẹ, rất nông”.
- Đáp án B sai vì đây là tiêu chí, điều cần thiết của văn chương nhưng lại là điểm mà Hộ không thể làm đượC.
- Đáp án C đúng vì xuất hiện tại chi tiết “Hắn phải viết những bài báo để người ta đọc rồi quên ngay sau lúc đọc”.
- Đáp án D sai vì vế thứ nhất là biểu hiện của sự “cẩu thả trong văn chương”: “Toàn những cái vô vị, nhạt nhẽo, gợi những tình cảm rất nhẹ, rất nông, diễn một vài ý rất thông thường quấy loãng trong một thứ văn bằng phẳng và quá ư dễ dãi”. Tuy nhiên vế thứ hai thì không chính xác vì trong văn bản viết “Hắn chẳng đem một chút mới lạ gì đến văn chương” chứ không phải có đêm một chút mới lạ.
Chọn A, C
Câu 14:
dằn vặt, cuộc đời thừa, văn sĩ, khốn khổ, hoài bão
Hộ là một _______ nghèo mang trong mình nhiều _______. Anh là người có lí tưởng sống rất cao đẹp. Là một nhà văn, anh đã từng ước mơ có những tác phẩm lớn, có giá trị vượt thời gian. Nhưng từ khi cứu vớt cuộc đời Từ, cưới Từ về làm vợ, anh phải lo cho cuộc sống của cả gia đình chỉ với những đồng tiền ít ỏi của nghề viết văn. Hộ đã rơi vào tình trạng _______. Tạm gác ước mơ để nuôi gia đình, nhưng nỗi locơm áo và những _______ lương tâm của một nhà văn đã khiến Hộ rơi vào cái vòng luẩn qẩn, không lối thoát, sống một _______ vô vị, tẻ nhạt.
 Xem đáp án
Xem đáp án
Đáp án
Hộ là một văn sĩ nghèo mang trong mình nhiều hoài bão. Anh là người có lí tưởng sống rất cao đẹp. Là một nhà văn, anh đã từng ước mơ có những tác phẩm lớn, có giá trị vượt thời gian. Nhưng từ khi cứu vớt cuộc đời Từ, cưới Từ về làm vợ, anh phải lo cho cuộc sống của cả gia đình chỉ với những đồng tiền ít ỏi của nghề viết văn. Hộ đã rơi vào tình trạng khốn khổ. Tạm gác ước mơ để nuôi gia đình, nhưng nỗi lo cơm áo và những dằn vặt lương tâm của một nhà văn đã khiến Hộ rơi vào cái vòng luẩn qẩn, không lối thoát, sống một cuộc đời thừa vô vị, tẻ nhạt.
Phương pháp giải
Căn cứ vào nội dung bài đọc.
Lời giải
Vị trí thả 1 là phần giới thiệu nhân vật Hộ, tương đương với câu đầu tiên của văn bản “Hộ vốn nghèo. Hắn là một nhà văn…”. Câu văn cung cấp thông tin Hộ là nhà văn nghèo hay còn có thể gọi là văn sĩ nghèo.
=> [vị trí thả 1]: văn sĩ
Vị trí thả 2 nhắc đến điều mà Hộ ấp ủ trong lòng, có thể nhìn thấy ở câu văn “Lòng hắn đẹp. Ðầu hắn mang một hoài bão lớn”. Có thể thấy, mang trong mình nhiều ở đây chính là “hoài bão”, tức là Hộ nuôi dưỡng rất nhiều khát khao đẹp đẽ.
=> [vị trí thả 2]: hoài bão
Vị trí thả 3 đã nói đến hoàn cảnh của nhân vật Hộ vì phía trước chính là liệt kê nguyên nhân. Trong tất cả các đáp án chỉ có 1 đáp án là tính từ nói về hoàn cảnh của con người “khốn khổ”. Vì vậy có thể nhận thấy Hộ sau khi lấy vợ với gánh nặng áo cơm đã rơi vào tình trạng khốn khổ.
=> [vị trí thả 3]: khốn khổ
Vị trí thứ 4 khi nói về lương tâm tức là phải kể đến việc Hộ viết những thứ văn chương khốn nạn và bực bội, cáu gắt với vợ con. Những sai lầm, xấu xa của mình, khi tự nhìn lại, khiến Hộ cảm thấy “dằn vặt” lương tâm.
=> [vị trí thả 4]: dằn vặt
Vị trí thứ 5 là câu chốt lại cuộc đời của Hộ, chỉ có một từ phù hợp là “cuộc đời thừa”.
=> [vị trí thả 5]: cuộc đời thừa
Dựa vào nội dung đoạn trên cùng cách sử dụng từ ngữ trong bài đọc, ta có các từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: văn sĩ
- Vị trí thả 2: hoài bão
- Vị trí thả 3: khốn khổ
- Vị trí thả 4: dằn vặt
- Vị trí thả 5: cuộc đời thừa
Câu 15:
Quan niệm sáng tác văn chương, Quan niệm lương tâm người người cầm bút, Quan niệm về lựa chọn nghề nghiệp, Quan niệm về lẽ sống Hộ
_____________________________: Sự cẩu thả trong bất cứ nghề gì cũng là một sự bất lương rồi. Nhưng sự cẩu thả trong văn chương thật là đê tiện.
_____________________________ : Kẻ mạnh không phải là kẻ giẫm lên vai kẻ khác để thỏa mãn lòng ích kỷ. Kẻ mạnh chính là kẻ giúp đỡ kẻ khác trên đôi vai mình.
_____________________________: Văn chương chỉ dung nạp những người biết đào sâu, biết tìm tòi, khơi những nguồn chưa ai khơi, và sáng tạo những cái gì chưa có.
 Xem đáp án
Xem đáp án
Đáp án
Quan niệm về lương tâm của người cầm bút: Sự cẩu thả trong bất cứ nghề gì cũng là một sự bất lương rồi. Nhưng sự cẩu thả trong văn chương thật là đê tiện.
Quan niệm về lẽ sống của Hộ: Kẻ mạnh không phải là kẻ giẫm lên vai kẻ khác để thỏa mãn lòng ích kỷ. Kẻ mạnh chính là kẻ giúp đỡ kẻ khác trên đôi vai mình.
Quan niệm về sáng tác văn chương: Văn chương chỉ dung nạp những người biết đào sâu, biết tìm tòi, khơi những nguồn chưa ai khơi, và sáng tạo những cái gì chưa có.
Phương pháp giải
Căn cứ vào nội dung đoạn số [3] và [5].
Lời giải
Quan niệm ở vị trí thả 1 xuất hiện ở đoạn số 3 khi Hộ đang tự trách mình vì việc viết văn, viết báo vội vàng, nông cạn của mình, tự chất vấn mình vì đã cẩu thả trong văn chương. Vậy nên, câu nói đầu tiên với những từ “bất lương”, “đê tiện” tức là đang nói về quan niệm về lương tâm của người cầm bút.
=> [vị trí thả 1]: Quan niệm về lương tâm của người cầm bút
Quan niệm số hai xuất hiện ở đoạn số 5 khi Hộ đang nói về lòng thương đối với Từ và sự tầm thường của chính mình, đây là quan niệm Hộ nói về cách sống Hộ theo đuổi là “nâng người khác trên đôi vai của mình” tức là lẽ sống của Hộ.
=> [vị trí thả 2]: Quan niệm về lẽ sống của Hộ
Quan niệm thứ ba bắt đầu bằng từ “văn chương”, đặt ra các tiêu chí cho một tác phẩm văn chương đích thực.
Câu 16:
Dựa vào đoạn [1], điền các từ không quá hai tiếng có trong bài đọc vào chỗ trống.
Hộ là một nhà văn sống có lý tưởng và luôn mang một hoài bão lớn. Hắn khinh thường những lo lắng tầm thường về mặt ____________. Hắn chỉ lo rèn luyện, bồi đắp cho _________ của mình ngày càng thêm nảy nở. Đối với hắn, thứ quan trọng nhất, đáng quan tâm nhất chính là _______.
 Xem đáp án
Xem đáp án
Đáp án:
Hộ là một nhà văn sống có lý tưởng và luôn mang một hoài bão lớn. Hắn khinh thường những lo lắng tầm thường về mặt vật chất. Hắn chỉ lo rèn luyện, bồi đắp cho cái tài của mình ngày càng thêm nảy nở. Đối với hắn, thứ quan trọng nhất, đáng quan tâm nhất chính là nghệ thuật.
Phương pháp giải
Căn cứ vào nội dung đoạn số [1].
Lời giải
- Đọc kĩ đoạn số [1] có thể nhận ra đoạn văn ở đề bài đang nói về lý tưởng của văn sĩ Hộ trước khi lấy vợ. Đây là thời điểm Hộ có khát vọng lớn trở nên hơn người. Thông tin còn thiếu trong văn bản được thể hiện bằng cách diễn đạt khác đi với các từ đồng nghĩa được in đậm “Hắn khinh những lo lắng tủn mủn về vật chất. Hắn chỉ lo vun trồng cho cái tài của hắn ngày mỗi ngày một thêm nảy nở”. Vậy nên ô trống thứ nhất điền từ “vật chất”, ô trống thứ hai điền từ “cái tài”. Ô trống thứ ba có liên quan đến câu văn “Ðối với hắn lúc ấy, nghệ thuật là tất cả; ngoài nghệ thuật không còn gì đáng quan tâm nữa”, nên có thể thấy “nghệ thuật” sẽ là từ còn thiếu số 3.
- Hoàn thiện câu văn: Hộ là một nhà văn sống có lý tưởng và luôn mang một hoài bão lớn. Hắn khinh thường những lo lắng tầm thường về mặt vật chất. Hắn chỉ lo rèn luyện, bồi đắp cho cái tài của mình ngày càng thêm nảy nở. Đối với hắn, thứ quan trọng nhất, đáng quan tâm nhất chính là nghệ thuật.
Câu 17:
Dòng nào dưới đây nêu không đúng bi kịch của nhà văn Hộ?
(Chọn 2 đáp án đúng)
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung bài đọc.
Lời giải
- Đáp án A không được lựa chọn vì Hộ có hoài bão “Hắn băn khoăn nghĩ đến một tác phẩm nó sẽ làm mờ hết các tác phẩm khác cùng ra một thời” nhưng vì gia đình, miếng cơm manh áo mà phải viết những thứ văn tủn mủn, đáng khinh nên đau khổ của Hộ là không được sống hết mình với đam mê và hoài bão của mình.
- Đáp án B nêu không đúng về bi kịch của Hộ vì Hộ không sống trong cảnh mất tự do, tác phẩm không đề cập tới nỗi đau này.
- Đáp án C không được lựa chọn vì Hộ phải viết những thứ văn vô vị, nhạt nhẽo, với Hộ là nhục nhã nên hắn tự thấy mình không xứng đáng là một nhà văn. Thêm nữa, hắn vì gánh nặng vật chất mà chửi bới, cáu gắt với vợ con là chưa làm tròn trách nhiệm của người chồng, người cha.
- Đáp án D nêu không đúng về bi kịch của Hộ vì Hộ đã lấy Từ, cô gái mà Hộ cảm thấy thương xót, Hộ không rơi vào bi kịch tình yêu.
Chọn B, D
Câu 18:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Chi tiết “Hộ điên người lên vì phải xoay tiền. Hắn còn điên lên vì con khóc, nhà không lúc nào được yên tĩnh để cho hắn viết hay đọc sách. Hắn thấy mình khổ quá, bực bội quá. Hắn trở nên cau có và gắt gỏng. Hắn gắt gỏng với con, với vợ, với bất cứ ai, với chính mình” đã thể hiện Hộ gặp nhiều ngăn cản từ vợ con nên không thể viết văn, đọc sách.
Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn số [6].
Lời giải
Có thể thấy đoạn số [6] đã thể hiện được hiện thực mâu thuẫn với khát vọng của Hộ. Nếu đoạn [5] Hộ bày tỏ khát vọng sống yêu thương, là người nâng giấc, giúp đỡ kẻ yếu thì đoạn [6] chính là hiện thực nghiệt ngã ngược lại. Hộ khi bị áo cơm ghì sát đất, vật chất đè nặng đã đi ngược lại với lẽ sống yêu thương của mình. Vì vậy chi tiết ở đề bài không phải thể hiện sự ngăn cản của vợ con mà thể hiện sự thay đổi, xung đột, mâu thuẫn của chính Hộ.
=> Nhận định trên là sai.
Chọn B
Câu 19:
Đâu KHÔNG PHẢI là đặc sắc nghệ thuật xuất hiện trong đoạn trích trên?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung bài đọc, kiến thức về nghệ thuật của tác phẩm văn học.
Lời giải
- Đáp án A là nghệ thuật của đoạn trích vì văn bản đã xây dựng được tâm lý rất phức tạp với nhiều mâu thuẫn của nhân vật Hộ: khi dâng trào khát vọng, khi thất vọng, khi hối hận, lo lắng,…
- Đáp án B là nghệ thuật của đoạn trích vì tác giả hoàn toàn sử dụng cách kể chuyện rất bình dị, nhẹ nhàng, không có những câu từ lớn lao hay sử dụng nhiều từ Hán Việt, không có những sự kiện gượng ép mà diễn ra hoàn toàn tự nhiên theo nét tâm lí và hành động của nhân vật.
- Đáp án C là nghệ thuật của đoạn trích vì tác giả đã xây dựng được cốt truyện với rất nhiều những mâu thuẫn, xung đột gay gắt, éo le, những xung đột này đẩy nhân vật tới bước cần giải quyết nên đây là một cốt truyện gay cấn, kịch tính.
- Đáp án D không phải là nghệ thuật xuất hiện trong đoạn trích vì đây là tác phẩm văn học hiện thực, không sử dụng bút pháp lãng mạn.
Chọn D
Câu 20:
Dựa vào văn bản, điền một từ không quá hai tiếng có trong bài đọc vào chỗ trống.
Tác phẩm “Đời thừa” của Nam Cao thuộc chủ nghĩa ____________ .
 Xem đáp án
Xem đáp án
Đáp án: “hiện thực”
Phương pháp giải
Căn cứ vào nội dung bài đọc, cụ thể ở nhan đề.
Lời giải
Văn học Việt Nam hiện đại có hai chủ nghĩa lớn là chủ nghĩa hiện thực và chủ nghĩa lãng mạn. Trong đó:
- Chủ nghĩa lãng mạn thường viết về những đề tài mà ở đó con người vượt lên trên hoàn cảnh, hy vọng về việc con người chiến thắng hoàn cảnh.
- Chủ nghĩa hiện thực thường viết về con người chịu sự tác động, ảnh hưởng mạnh mẽ của hoàn cảnh, thậm chí bị hoàn cảnh làm cho tha hóa.
=> Với nội dung của tác phẩm “Đời thừa”, nhân vật Hộ đang dần đánh mất chính mình và tha hóa bởi hoàn cảnh nên đây là tác phẩm thuộc chủ nghĩa hiện thực.
Câu 21:
Phần tư duy khoa học / giải quyết vấn đề
Biến được kiểm soát là biến được giữ không đổi. Các biến kiểm soát trong thử nghiệm 4,5, 6 là:
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích số liệu trong bảng 1
Lời giải
Ta có biến được kiểm soát là biến được giữa không đổi trong các lần thử nghiệm.
Trong các thử 4 – 5 – 6 thì các biến được giữ không đổi là: mp; Mb và k
Chọn A, B, D
Câu 22:
Động lượng của viên đạn trong Thử nghiệm 3, trước khi va chạm, có giống như động lượng của viên đạn trong Thử nghiệm 1, trước khi va chạm không?
 Xem đáp án
Xem đáp án
Phương pháp giải
Động lượng của vật được xác định bằng: p = mv2
Dựa vào số liệu bảng 1 cung cấp
Lời giải
Ta có công thức tính động lượng: p = mv2
Ta thấy khối lượng của viên đạn ban đầu của lần 1 và 3 là khác nhau nên chúng sẽ không có cùng động lượng trước va chạm
Chọn B
Câu 23:
Trước va chạm cơ năng của cả hệ ( gồm đạn và lò xo ) bằng Động năng của viên đạn. Sau va chạm thì lò xo nén tối đa thì cơ bằng thế năng đàn hồi. Dựa vào bảng 1 cho biết hệ đã được nhận thêm hay mất đi năng lượng do va chạm.
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích số liệu từ bảng 1
Lời giải
Từ đề ta có: \[\left\{ {\begin{array}{*{20}{c}}{{{\rm{W}}_{{\rm{truoc }}}} = {{\rm{W}}_d}}\\{\;{{\rm{W}}_{{\rm{sau }}}} = {{\rm{W}}_t}\,\,}\end{array}} \right.\]
Từ bảng 1 ta luôn thấy Wd > Wt với mọi trường hợp. Đều đó có nghĩa cơ năng ( năng lượng ) của hệ sau va chạm đã mất đi một phần.
Chọn C
Câu 24:
lớn, bé, đàn hồi, hấp dẫn
Khi lò xo nén càng nhiều thì khi đó thế năng _______ dữ trữ trong lò xo càng _______
 Xem đáp án
Xem đáp án
Đáp án
Khi lò xo nén càng nhiều thì khi đó thế năng đàn hồi dữ trữ trong lò xo càng lớn
Phương pháp giải
Phân tích số liệu bảng 1 cung cấp
Vận dụng công thức tính thế năng của lò xo: \({{\rm{W}}_t} = \frac{1}{2}k{x^2}\)
Lời giải
Ta có thế năng đàn hồi được xác định bằng: \({{\rm{W}}_t} = \frac{1}{2}k{x^2}\)
=> độ biến dạng của lò xo càng lớn thì thế năng đàn hồi của lò xo sẽ càng lớn.
Câu 25:
Giả sử ban đầu viên đạn có khối lượng là 0,5kg chuyển động với vận tốc đầu là 10m/s, lò xo đang ở vị trí chọn mốc thế năng. Khi đó năng lượng của cả hệ có giá trị:
 Xem đáp án
Xem đáp án
Phương pháp giải
Áp dụng công thức tính động năng: \({{\rm{W}}_d} = \frac{1}{2}m{v^2}\)
Sử dụng lí thuyết về năng lượng đã học
Lời giải
Tại thời điểm ban đầu, lò xo đang ở vị trí mốc thế năng nên năng lượng (cơ năng) của hệ chính bằng động năng của chuyển động từ viên đạn.
=> động năng ban đầu của hệ là: \({{\rm{W}}_d} = \frac{1}{2}m{v^2} = \frac{1}{2}.0,{5.10^2} = 25\;{\rm{J}}\)
Chọn B
Câu 26:
Dựa vào kết quả của Thí nghiệm 1 và 3, chiều dài XY của cuộn dây điện từ ở Thí nghiệm 1 có khả năng là:
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin và số liệu bảng 3
Lời giải
Theo Bảng 3, khi chiều dài cuộn dây XY giảm thì trọng lượng sẽ tăng và thay đổi khi đặt điện áp 8,00 V vào mạch.
Trong Thí nghiệm 1, trọng lượng ở điện áp 8,00 V là 5,0095 N, nhỏ hơn các trọng lượng trong Bảng 3.
Vì trọng lượng này nhỏ hơn nên cuộn dây điện từ trong Thí nghiệm 1 phải có chiều dài lớn hơn bất kỳ cuộn dây nào được liệt kê trong Thí nghiệm 3 hay có nghĩa là lớn hơn 9,50 cm
Chọn D
Câu 27:
Điền đáp án thích hợp vào chỗ trống:
Dựa trên kết quả thí nghiệm 3, lực do từ trường tác dụng lên thanh nam châm _________ khi chiều dài XY cuộn dây giảm.
 Xem đáp án
Xem đáp án
Đáp án: “tăng”
Phương pháp giải
Phân tích thông tin và bảng số liệu
Lời giải
Theo Bảng 3, khi chiều dài cuộn dây XY giảm thì trọng lượng sẽ tăng khi iện áp không bị thay đổi.
=> lực do từ trường tác dụng lên thanh nam châm tăng khi chiều dài XY cuộn dây giảm.
Câu 28:
Trong thí nghiệm 1 và 2, việc thay đổi chiều của thanh nam châm so với cuộn dây điện từ xác định điều gì sau đây?
|
|
ĐÚNG |
SAI |
|
Chiều dài điện từ XY |
||
|
Hướng của lực do cuộn dây tác dụng lên thanh nam châm |
||
|
Cường độ từ trường của cuộn dây |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Chiều dài điện từ XY |
X | |
|
Hướng của lực do cuộn dây tác dụng lên thanh nam châm |
X | |
|
Cường độ từ trường của cuộn dây |
X |
Phương pháp giải
Phân tích thông tin bài cung cấp
Vận dụng lí thuyết đã học về lực điện từ
Lời giải
Thí nghiệm 2 đảo ngược 2 cực của thanh nam châm trong Thí nghiệm 1.
Dựa trên lí thuyết đã học về lực điện từ thì việc đổi cực của nam châm sẽ dẫn đến việc thay đổi hướng của lực điện từ tác dụng lên nam châm
Câu 29:
Giả sử các nhà khoa giữ nguyên chiều 2 cực nam châm giống nhau trong Thí nghiệm 3 như trong Thí nghiệm 2. Dựa trên kết quả của Thí nghiệm 1 và 2, với chiều dài nam châm XY bằng 9,50 cm, trọng lượng trên cân rất có thể là:
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin trong thí nghiệm 2 và 3
Lời giải
Trong thí nghiệm 3 được được xét ở điện áp 8,00 V.
So sánh giá trị 8,00 V trong Thí nghiệm 1 và 2 ta có:
+ Trong Thí nghiệm 1, trọng lượng ở 8,00 V là 5,0095 N
+ Trong Thí nghiệm 2, trọng lượng ở 8,00 V là 4,9905 N
=> Chênh lệch về trọng lượng là 0,019 N.
=>Do đó, nếu hướng của nam châm khớp với hướng của Thí nghiệm 2 thì trọng lượng phải nhỏ hơn khoảng 0,019 N so với giá trị 5,0105N
Vậy 4.9895N là giá trị cần tìm
Chọn C
Câu 30:
Điền đáp án thích hợp vào chỗ trống:
Trước tất cả các thử nghiệm, thang treo đã được hiệu chỉnh để đọc chính xác 0 N khi không có gì được gắn vào. Sau khi thanh nam châm được gắn vào, các nhà khoa học đã điều chỉnh để số chỉ trên cân ____________ một khoảng là ____________ N
 Xem đáp án
Xem đáp án
Đáp án
Trước tất cả các thử nghiệm, thang treo đã được hiệu chỉnh để đọc chính xác 0 N khi không có gì được gắn vào. Sau khi thanh nam châm được gắn vào, các nhà khoa học đã điều chỉnh để số chỉ trên cân tăng lên | tăng thêmmột khoảng là 0,3 | 0.3 N
Phương pháp giải
Phân tích thông tin được cung cấp trong bài
Lời giải
Câu 31:
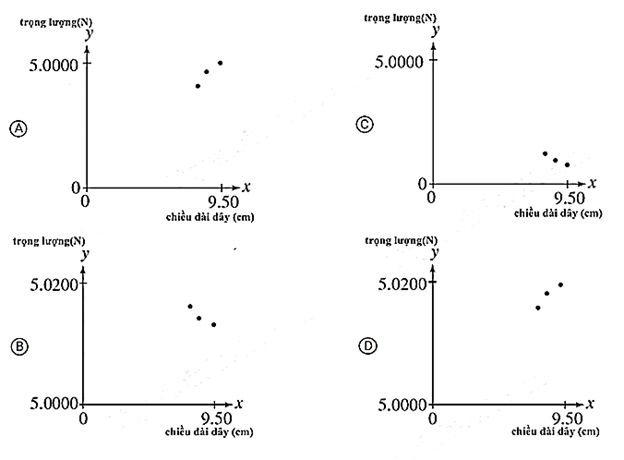
Đồ thị nào sau đây mô tả đúng nhất kết quả của Thí nghiệm 3?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào kết quả thí nghiệm 3
Lời giải
Theo Bảng 3, khi chiều dài điện từ của XY giảm thì trọng lượng sẽ tăng.
Khi đó, các trọng số trong Bảng 3 gần với 5,0200 N hơn là 0 N, do đó hình B sẽ là hình biểu diễn chính xác.
Chọn B
Câu 32:
Cả hai lý thuyết về nguồn gốc của các phân tử hữu cơ đều dựa trên giả định rằng các phân tử đó
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đã cho trong đầu bài.
Lời giải
Dựa vào thông tin “Các nhà khoa học tin rằng, trước khi có các sinh vật sống trên bề mặt Trái đất nguyên thuỷ, các phân tử hữu cơ đơn giản ban đầu được hình thành từ các phân tử vô cơ”, đây chính là giả định cơ bản để các nhà khoa học phát triển hai lý thuyết trong bài.
Chọn D
Câu 33:
Điền số thích hợp vào chỗ trống:
Theo lý thuyết "Nồi súp nguyên thuỷ", trong bầu khí quyển nguyên thuỷ có ________ chất khí là thành phần chính.
 Xem đáp án
Xem đáp án
Đáp án “4”
Phương pháp giải
Đọc lại thành phần bầu khí quyển nguyên thuỷ được đề cập đến trong lý thuyết “Nồi súp nguyên tử”.
Lời giải
Trong bầu khí quyển nguyên thuỷ được cho là có các chất khí: nước (H2O), metan (CH4), amoniac (NH3), hiđro (H2). Như vậy có 4 khí trong thí nghiệm giả định.
Câu 34:
Kéo thả ô tương ứng vào vị trí thích hợp
tụ điện, bình cầu lơn, bẫy hóa học, bình cầu nhỏ
Trong thí nghiệm “Nồi súp nguyên thuỷ” của Miller – Uray, các phân tử hợp chất hữu cơ đã được tạo ra ở bộ phận ____________ của hệ thống thí nghiệm.
 Xem đáp án
Xem đáp án
Đáp án
Trong thí nghiệm “Nồi súp nguyên thuỷ” của Miller – Uray, các phân tử hợp chất hữu cơ đã được tạo ra ở bộ phận bình cầu lớn của hệ thống thí nghiệm.
Phương pháp giải
Quan sát hình 1 về thí nghiệm “Nồi súp nguyên thuỷ”.
Lời giải
Hợp chất hữu cơ được tạo ra trong bình cầu lớn, nơi được tạo ra môi trường mô phỏng bầu khí quyển nguyên thuỷ, các khí đơn giản và có các điện tích chuyển động liên tục mô phỏng tia sét.
Câu 35:
Dựa trên lý thuyết “Lỗ phun thuỷ nhiệt”, nhận định dưới đây là đúng hay sai?
Khoảng nhiệt độ tối ưu cho sự hình thành phân tử hữu cơ là từ 0oC đến 4oC.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa theo lý thuyết “Lỗ phun thuỷ nhiệt” về quá trình hình thành các phân tử hữu cơ dưới đại dương.
Lời giải
Trong lý thuyết “Lỗ phun thuỷ nhiệt” có nhắc đến sự biến đổi nhiệt độ dần dần từ 300oC tại miệng lỗ phun thuỷ nhiệt đến 4oC khi lên trên bề mặt đại dương. Sự biến đổi nhiệt độ dần dần là từ 300oC đến 4oC sẽ có khoảng tối ưu để tạo ra các hợp chất hữu cơ ổn định. Như vậy có thể thấy, cứ nhiệt độ thấp hơn 300oC sẽ là điều kiện tối ưu để tạo ra các hợp chất hữu cơ. Còn khoảng từ 0oC đến 4oC không được nhắc đến trong bài nên không có đủ căn cứ để khẳng định đây là khẳng định đúng về khoảng nhiệt độ tối ưu tạo ra hợp chất hữu cơ dưới đáy đại dương.
Chọn B
Câu 36:
Tuyên bố nào sau đây sẽ được ủng hộ nhiều nhất bởi các nhà khoa học của hai lý thuyết trên?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào điểm chung của cả hai lý thuyết để tìm ra tuyên bố có nhắc tới điểm chung đó. Đó sẽ là tuyên bố được ủng hộ nhiều nhất.
Lời giải
Đặc điểm chung của cả hai lý thuyết đều là vai trò không thể thiếu của nước trong sự phát triển của các hợp chất hữu cơ trên Trái đất. Lý thuyết “Nồi súp nguyên thuỷ” đã xác định nước là một trong bốn thành phần chính của bầu khí quyển Trái đất nguyên thuỷ. Còn lý thuyết “Lỗ phun thuỷ nhiệt” xác định môi trường nước biển sâu chính là nơi hình thành nên các hợp chất hữu cơ.
Chọn C
Câu 37:
Tại sao các nhà khoa học lại tin rằng nguồn gốc của hợp chất hữu cơ có thể bắt nguồn từ lỗ phun thuỷ nhiệt dưới đại dương sâu?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ lý thuyết "Lỗ phun thuỷ nhiệt".
Lời giải
Theo thuyết "Lỗ phun nguyên thuỷ", cho rằng các phân tử hữu cơ ban đầu được hình thành ở các đại dương sâu sử dụng năng lượng từ bên trong Trái đất, tập trung vào sự tồn tại của các lỗ phun thuỷ nhiệt. Bằng chứng cho lý thuyết này bao gồm thực tế là hệ sinh thái của các sinh vật đa dạng đã được tìm thấy tồn tại xung quanh các lỗ phun thuỷ nhiệt trong đại dương sâu.
Chọn C
Câu 38:
Nguồn năng lượng cụ thể được sử dụng để hình thành các hợp chất hữu cơ đơn giản
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đã cho của hai lý thuyết.
Lời giải
Hai lý thuyết đều không thống nhất về nguồn năng lượng được sử dụng để cung cấp năng lượng cho các phản ứng ban đầu tạo ra các hợp chất hữu cơ. Lý thuyết “Nồi súp nguyên thuỷ” xác định sét trong khí quyển là nguồn năng lượng chính để tạo ra các hợp chất hữu cơ từ các hợp chất vô cơ đơn giản nhất, còn trong lý thuyết “Lỗ phun thuỷ nhiệt” lại cho rằng năng lượng để tạo ra các hợp chất hữu cơ đến từ bên trong Trái đất.
Chọn C
Câu 39:
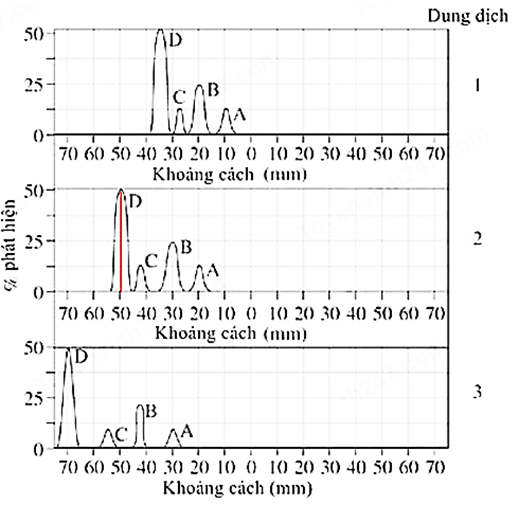
Trong thí nghiệm 2, khi dung môi 2 được sử dụng, phần lớn axit amin D đã di chuyển một khoảng cách từ điểm xuất phát là
 Xem đáp án
Xem đáp án
Phương pháp giải
Quan sát hình 2 và dung môi 2, đỉnh của amino axit D tại đâu thì đó là khoảng cách cần tìm.
Lời giải
Nhìn vào hình 2, thí nghiệm thực hiện với dung môi 2 của amino axit D có đỉnh cực đại tại 50 mm.
Câu 40:
Giả sử thí nghiệm 1 được lặp lại sử dụng dung môi có độ pH là 8,4. Khoảng cách di chuyển chuyển của axit amin A rất có thể sẽ đạt cực đại tại khoảng cách
 Xem đáp án
Xem đáp án
Phương pháp giải
Dữ liệu trong Bảng 1 kết hợp với kết quả được thể hiện trong Hình 2.
Lời giải
Dữ liệu trong Bảng 1 kết hợp với kết quả được thể hiện trong Hình 2 chứng minh rằng khi độ pH của dung môi giảm, khoảng di chuyển của amino axit A cũng giảm đi. Đối với Dung môi 1 (độ pH 8.9), amino axit A di chuyển khoảng 10 mm. Dung môi có độ pH là 8.4 ít hơn so với Dung môi 1. Do đó, dự kiến amino axit A sẽ di chuyển ít hơn so với khi sử dụng Dung môi 1
Chọn A
Câu 41:
 Xem đáp án
Xem đáp án
Đáp án
Amino axit L có điểm đẳng điện (pI) là 6,6. Kết quả của thí nghiệm 1 và thí nghiệm 2 sẽ giống nhất với các kết quả thu được trước đó được thể hiện trong hình 1 và hình 2 khi axit amin L được thay thế cho amino axit .
Phương pháp giải
Để thu được kết quả tương tự giống thí nghiệm 1 và 2, amino axit L phải có pI gần giống với amino axit mà nó thay thế. Vậy dựa vào dữ liệu Bảng 1.
Lời giải
Câu 42:
Độ phân giải của phương pháp điện di gel sẽ giảm khi tổng khoảng cách giữa các đỉnh trên đồ thị giảm đi. Dựa trên kết quả của thí nghiệm 1 và thí nghiệm 2, hãy chọn các điều kiện sẽ cho kết quả hình ảnh có độ phân thấp nhất ứng với mỗi thí nghiệm trong các điều kiện dưới đây:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào Hình 1 và Hình 2, dung môi nào có tổng khoảng cách giữa các đỉnh bé nhất thì dung môi đấy sẽ cho hình có độ phân giải thấp nhất.
Lời giải
Trong Hình 1 và Hình 2, dung môi 1 đều thể hiện có các đỉnh của các amino axit rất gần nhau nên sẽ có độ phân giải thấp nhất.
Chọn A, D
Câu 43:
Trong thí nghiệm 2, đối với dung môi 2, khi amino axit quay trở về 0% được phát hiện, thì amino axit A di chuyển được một đoạn là bao nhiêu?
 Xem đáp án
Xem đáp án
Phương pháp giải
Quan sát Hình 3.
Lời giải
Trong Hình 3, khi amino axit B quay trở về 0% được phát hiện, tức là chưa được điện di, thì amino axit A cũng chưa được điện di, tức là di chuyển một khoảng 0 mm.
Chọn A
Câu 44:
Nhận định dưới đây đúng hay sai?
Để tách các amino axit ra khỏi hỗn hợp tốt nhất nên chọn dung môi có pH lớn hơn 10.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào khoảng cách của các đỉnh trong các dung môi có môi trường pH khác nhau. Dung môi nào điện di có các đỉnh càng xa thì sử dụng dung môi đấy càng dễ tách amino axit.
Lời giải
Nhận thấy, pH tăng dần từ dung môi 1 đến dung môi 3, và trong cả thí nghiệm 1 và thí nghiệm 2 thì khoảng cách giữa các đỉnh ngày càng xa theo thứ tự điện di từ dung môi 1 đến 3. pH lớn hơn 10 là pH tương đương với pH của dung môi 3 có các đỉnh xa dần nên sẽ dễ tách amino axit ra khỏi hỗn hợp của chúng.
Chọn A
Câu 45:
Kéo thả các đáp án chính xác vào chỗ trống
có lợi, bị hại
Khi xét mối quan hệ giữa các loài khác nhau trong quần xã, thấy rằng có hai dạng quan hệ sau: mối quan hệ hỗ trợ là mối quan hệ trong đó ít nhất 1 loài _______, mối quan hệ đối kháng là mối quan hệ trong đó ít nhất 1 loài _______
 Xem đáp án
Xem đáp án
Đáp án
Khi xét mối quan hệ giữa các loài khác nhau trong quần xã, thấy rằng có hai dạng quan hệ sau: mối quan hệ hỗ trợ là mối quan hệ trong đó ít nhất 1 loài có lợi, mối quan hệ đối kháng là mối quan hệ trong đó ít nhất 1 loài bị hại
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Khi xét mối quan hệ giữa các loài khác nhau trong quần xã, thấy rằng có hai dạng quan hệ sau: mối quan hệ hỗ trợ là mối quan hệ trong đó ít nhất 1 loài có lợi, mối quan hệ đối kháng là mối quan hệ trong đó ít nhất 1 loài bị hại
Câu 46:
Nhận định dưới đây là đúng hay sai?
Mối quan hệ hợp tác mang đến lợi ích cho cả hai loài và mối quan hệ này cần thiết cho sự tồn tại và phát triển của cả hai.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Nhận định Sai vì mối quan hệ hợp tác không nhất thiết cần cho sự tồn tại và phát triển của hai loài.
Chọn B
Câu 47:
Trong quần xã sinh vật, kiểu quan hệ giữa hai loài, trong đó một loài có lợi còn loài kia không có lợi cũng không có hại là
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Trong quần xã sinh vật, kiểu quan hệ giữa hai loài, trong đó một loài có lợi còn loài kia không có lợi cũng không có hại là quan hệ hội sinh.
Các quan hệ còn lại được nhắc đến thuộc quan hệ đối kháng.
Chọn B
Câu 48:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Trong các mối quan hệ sau đây, mối quan hệ nào có vai trò thúc đẩy sự tiến hóa của cả hai loài là "Quan hệ vật ăn thịt – con mồi" vì vật ăn thịt luôn tìm cách săn mồi. Quá trình săn mồi sẽ loại bỏ những cá thể có sức sống yếu kém nên quần thể vật ăn thịt là nhân tố chọn lọc những kiểu gen thích nghi đối với quần thể con mồi. Ngược lại, các cá thể con mồi luôn luôn tìm cách chạy trốn khỏi vật ăn thịt nên chỉ có những vật ăn thịt khỏe thì mới săn bắt được con mồi, những vật ăn thịt ốm yếu thì không săn được mồi
Chọn D
Câu 49:
Xét các mối quan hệ sinh thái:
(1) Cộng sinh.
(2) Vật kí sinh và vật chủ.
(3) Hội sinh.
(4) Hợp tác.
(5) Vật ăn thịt và con mồi.
Hãy xếp theo thứ tự tăng cường tính đối kháng của các mối quan hệ trên?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Cộng sinh thì không có đối kháng, hợp tác bắt đầu có sự đối kháng, hội sinh thì một loài có lợi còn một loài trung tính nên tính đối kháng bắt đầu xuất hiện. Vật kí sinh – vật chủ có tính đối kháng thấp hơn so với vật ăn thịt và con mồi vì vật kí sinh thường không tiêu diệt vật chủ, trong khi vật ăn thịt thì luôn tìm cách tiêu diệt con mồi.
Chọn B
Câu 50:
Khi nói về mối quan hệ sinh vật chủ - sinh vật kí sinh và mối quan hệ con mồi – sinh vật ăn thịt, các phát biểu dưới đây là Đúng?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
- A sai. vì sinh vật ăn thịt có số lượng ít hơn số lượng con mồi thì con mồi mới cung cấp đủ thức ăn cho sinh vật ăn thịt.
- B sai. vì mối quan hệ vật chủ - sinh vật kí sinh, vật ăn thịt – con mồi là các nhân tố gây ra hiện tượng khống chế sinh học
- C đúng . vì vật kí sinh luôn có kích thước cơ thể nhỏ hơn vật chủ
- D sai. vì trên 1 vật chủ thường có rất nhiều vật kí sinh
Chọn C
Câu 51:
Điền từ thích hợp vào chỗ trống
Virus cúm có hệ gen là RNA, các chủng virus cúm khác nhau phân biệt dựa vào _______ bề mặt.
 Xem đáp án
Xem đáp án
Đáp án “kháng nguyên”
Phương pháp giải
Đọc kĩ thông tin cung cấp
Lời giải
Virus cúm có hệ gen là RNA, các chủng virus cúm khác nhau phân biệt dựa vào kháng nguyên bề mặt
Câu 52:
Điền từ thích hợp vào chỗ trống
Virus cúm A lây nhiễm vào tế bào chủ theo cơ chế _______ khi xâm nhập vào tế bào chủ, virus tiến hành cởi vỏ để giải phóng vật chất di truyền.
 Xem đáp án
Xem đáp án
Đáp án: “nhập bào”
Phương pháp giải
Đọc kĩ thông tin cung cấp
Lời giải
Virus cúm A lây nhiễm vào tế bào chủ theo cơ chế nhập bào khi xâm nhập vào tế bào chủ, virus tiến hành cởi vỏ để giải phóng vật chất di truyền
Câu 53:
Trong quá trình virus xâm nhập vào tế bào chủ, điều gì đã làm vỏ capsid của virus bị phá hủy và genome virus được giải phóng bên trong tế bào chủ?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin bài đọc
Lời giải
Xâm nhập: tạo thành túi nhập (endosome) bào đưa virus vào bên trong tế bào, túi nhập bào mang virus được dung hợp với túi nội bào chứa các enzyme trong lysosome, làm giảm pH trong túi khiến màng túi nhập bào và vỏ capsid của virus bị phá vỡ, virus được “cởi vỏ” giải phóng vật chất di truyền.
=> Chọn C.
Câu 54:
Nhận định sau đây đúng hay sai?
Các chủng virus cúm có tốc độ biến đổ nhanh là do có hệ genome phân mảnh gồm nhiều chuỗi RNA.
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin cung cấp
Lời giải
Các chủng virus cúm có tốc độ biến đổ nhanh là do có hệ genome phân mảnh gồm nhiều chuỗi RNA
=> Đáp án Đúng
=> Hệ gen gồm nhiều đoạn RNA nên có tần số đột biến cao, dễ biến đổi
Chọn B
Câu 55:
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin đã cung cấp
Lời giải
Gai glycoprotein trên bề mặt virus cúm có nguồn gốc từ màng sinh chất của tế bào chủ.
Chọn B
Câu 56:
NH4Cl có hiệu quả ức chế sự nhân lên của virus cúm dựa vào cơ chế
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin
Lời giải
NH4Cl có hiệu quả ức chế sự nhân lên của virus cúm dựa vào cơ chế ngăn virus cởi vỏ để giải phóng vật chất di truyền
Chọn C
Câu 57:
Chọn các nhận định Đúng
Virus gây cúm gia cầm dễ dàng truyền sang chim nhưng hiếm khi truyền sang người. Tương tự, virus gây cúm ở người rất dễ truyền sang người khác, nhưng chưa bao giờ phát hiện truyền sang chim.
Nguyên nhân nào sau đây là Đúng khi giải thích hiện tượng trên?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin được cung cấp
Lời giải
(1) Các chủng virus cúm gây nhiễm trên người và gia cầm là khác nhau
=> Đúng: do mỗi chủng có kháng nguyên bề mặt khác nhau, tương thích với thụ thể bề mặt của TB chủ
(2) Kháng nguyên bề mặt (hemagglutinin) trên màng virus cúm gia cầm không tương thích với tế bào người
=> Đúng: do kháng nguyên loại H sẽ khớp tương ứng cới thụ thể bề mặt của TB chủ
(3) Khi virus cúm gia cầm xâm nhập và tế bào người thì tế bào người không cho phép giải phóng virus
=> Sai. Virus cúm gia cầm không xâm nhập được vào TB người
(4) Chủng virus cúm lây nhiễm trên gia cầm và trên người giống nhau về các kháng nguyên bề mặt
=> Sai. Các chủng virus trên đối tượng vật chủ khác nhau có kháng nguyên bề mặt khác nhau
Chọn A, BCâu 58:
Công thức tính diện tích toàn phần hình nón có bán kính đáy r, độ dài đường cao h và độ dài đường sinh l là:
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng công thức tính diện tích toàn phần hình nón:
Stp = Sxq + Sd
Diện tích hình nón, thể tích khối nón (Đọc thêm)
Lời giải
Công thức tính diện tích toàn phần hình nón có bán kính đáy r và độ dài đường sinh l là:
Stp = πrl + πr2
Một số em sẽ chọn nhầm đáp án C vì nhớ nhầm công thức.
Câu 59:
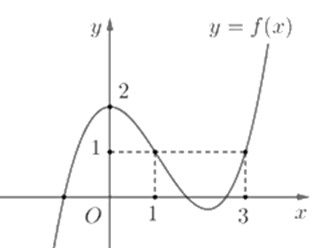
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Giá trị cực đại của hàm số là
 Xem đáp án
Xem đáp án
Quan sát đồ thị, giá trị cực đại của hàm số là giá trị y tại điểm cực đại trên đồ thị.
Tìm cực trị của hàm số
Lời giải
Quan sát đồ thị ta thấy tại x = 0 thì đồ thị đi lên rồi đi xuống nên giá trị cực đại của hàm số là f(0)=2
Câu 60:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(3;2;−1),B(5;4;3). M là điểm thuộc tia đối của tia BA sao cho . Tìm tọa độ của điểm M.
 Xem đáp án
Xem đáp án
Chỉ ra B là trung điểm AM.
Tìm tọa độ điểm thỏa mãn điều kiện cho trước \[\frac{{AM}}{{BM}} = 2\]
Lời giải
M là điểm thuộc tia đối của tia BA sao cho \[\frac{{AM}}{{BM}} = 2\] nên B là trung điểm AM.
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{5 = \frac{{3 + {x_M}}}{2}}\\{4 = \frac{{2 + {y_M}}}{2}}\\{3 = \frac{{ - 1 + {z_M}}}{2}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_M} = 7}\\{{y_M} = 6}\\{{z_M} = 7}\end{array} \Rightarrow M(7;6;7)} \right.} \right..\)
Câu 61:
Cho cấp số cộng \(\left( {{u_n}} \right)\) thỏa mãn \(\left\{ {\begin{array}{*{20}{l}}{{u_1} + {u_7} = 26}\\{u_2^2 + u_6^2 = 466}\end{array}} \right.\). Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Sử dụng công thức số hạng tổng quát của CSC \[{u_n} = {u_1} + (n - 1)d\]
Lời giải
Ta có \(\left\{ {\begin{array}{*{20}{l}}{2{u_1} + 6d = 26}\\{{{({u_1} + d)}^2} + {{({u_1} + 5d)}^2} = 466}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{u_1} = 13 - 3d}\\{{{(13 - 2d)}^2} + {{(13 + 2d)}^2} = 466}\end{array}} \right.} \right.\)
\( \Rightarrow \left[ {\begin{array}{*{20}{l}}{d = 4 \Rightarrow {u_1} = 1}\\{d = - 4 \Rightarrow {u_1} = 25}\end{array}} \right.\) .
Câu 62:
Điền số tự nhiên vào chỗ trống:
Cho hai số phức z1 = 2 − i và z2 = −3+5i. Điểm biểu diễn số phức có hoành độ bằng....?
 Xem đáp án
Xem đáp án
Đáp án: “1”
Phương pháp giải
Sử dụng các công thức biến đổi số phức.
Lời giải
Ta có .
Câu 63:
Viết phương trình mặt phẳng (α) đi qua M(0;1;2), N(2;0;1) và vuông góc với (P): 2x+3y−z+1=0
 Xem đáp án
Xem đáp án
Vì \(\left\{ {\begin{array}{*{20}{l}}{M,N \in (\alpha )}\\{(\alpha ) \bot (P)}\end{array} \Rightarrow \overrightarrow {{n_\alpha }} = \left[ {\overrightarrow {MN} .\overrightarrow {{n_P}} } \right]} \right.\)
Viết phương trình mặt phẳng
Lời giải
Ta có: \(\overrightarrow {MN} = (2; - 1; - 1);\overrightarrow {{n_P}} = (2;3; - 1)\)
Vì \(\left\{ {\begin{array}{*{20}{l}}{M,N \in (\alpha )}\\{(\alpha ) \bot (P)}\end{array} \Rightarrow \overrightarrow {{n_\alpha }} = \left[ {\overrightarrow {MN} .\overrightarrow {{n_P}} } \right] = (4;0;8)} \right.\) là vectơ pháp tuyến của mặt phẳng \((\alpha )\). \(M(0;1;2) \in (\alpha )\)
Suy ra phương trình mặt phẳng (α) là:
\(4(x - 0) + 0(y - 1) + 8(z - 2) = 0 \Leftrightarrow 4x + 8z - 16 = 0 \Leftrightarrow x + 2z - 4 = 0.\)
Câu 64:
Trong không gian \({\rm{Ox}}yz\), cho các mặt phẳng \((P):x - y + 2z + 1 = 0\), \((Q):2x + y + z - 1 = 0\). Gọi \((S)\) là mặt cầu có tâm thuộc trục hoành, đồng thời \((S)\) cắt mặt phẳng \((P)\) theo giao tuyến là một đường tròn có bán kính 2 và \((S)\) cắt mặt phẳng \((Q)\) theo giao tuyến là một đường tròn có bán kính \(r\). Để chỉ có đúng 1 mặt cầu \((S)\) thỏa mãn yêu cầu thì giá trị của \(r\) là
 Xem đáp án
Xem đáp án
Phương pháp giải
- Gọi I là tâm mặt cầu (S). Ta có I(a;0;0)
- Sử dụng các tính chất về vị trí tương đối giữa mặt cầu và mặt phẳng.
Lời giải
- Gọi \(I\) là tâm mặt cầu \((S)\). Ta có \(I(a;0;0)\)
- Sử dụng các tính chất về vị trí tương đối giữa mặt cầu và mặt phẳng.
Lời giải
Gọi \(I\) là tâm mặt cầu \((S)\). Ta có \(I(a;0;0)\)
Do \((S)\) cắt \((P)\) theo giao tuyến là đường tròn bán kính 2 nên ta có:
\(4 = {R^2} - {[d(I,(P))]^2} \Leftrightarrow 4 = {R^2} - \frac{{{{(a + 1)}^2}}}{6} \Rightarrow {R^2} = 4 + \frac{{{{(a + 1)}^2}}}{6}\)
Do \((S)\) cắt \((Q)\) theo giao tuyến là đường tròn bán kính \(r\) nên ta có:
\({r^2} = {R^2} - {[d(I,(Q))]^2} \Leftrightarrow {r^2} = {R^2} - \frac{{{{(2a - 1)}^2}}}{6}(2)\)
Từ (1) và (2) ta có \({r^2} = 4 + \frac{{{{(a + 1)}^2}}}{6} - \frac{{{{(2a - 1)}^2}}}{6} \Leftrightarrow - {a^2} + 2a + 8 - 2{r^2} = 0\) (3)
Để có duy nhất một mặt cầu (S) thỏa mãn thì phương trình (3) phải có duy nhất 1 nghiệm (S)
\( \Rightarrow \Delta ' = 9 - 2{r^2} = 0 \Rightarrow r = \frac{{3\sqrt 2 }}{2}\).
Câu 65:
Người ta cần tạo một ống bơ sữa đặc kín 2 đầu hình trụ có đáy là hình tròn với thể tích là 16πcm3. Tính diện tích tối ưu của phần vật liệu cần sử dụng.
 Xem đáp án
Xem đáp án
- Đặt ẩn, khảo sát giá trị của hàm số
- Công thức thể tích hình trụ \(V = \pi {r^2}h\)
- Diện tích toàn phần hình trụ \(S = 2\pi rh + 2\pi {r^2}\)
Thể tích khối hộp, khối lăng trụ
Lời giải
Gọi phần diện tích vật liệu cần dùng là \(S\) chiều cao hình trụ là \(h\) và bán kính đáy là \(r\) ta có:
\(16\pi = \pi {r^2}h \Leftrightarrow h = \frac{{16}}{{{r^2}}}\) ta lại có \(S = 2\pi rh + 2\pi {r^2}\)
Vậy \(S = \frac{{32\pi }}{r} + 2\pi {r^2} \Leftrightarrow S_{(r)}^\prime = 4\pi r - \frac{{32\pi }}{{{r^2}}} = 0 \Leftrightarrow r = 2(\;{\rm{cm}}) \Rightarrow S = 24\pi \left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Câu 66:
Cắt hình trụ (T) bằng một mặt phẳng song song với trục và cách trục 2m được thiết diện là một hình vuông có diện tích bằng 16m2. Tính thể tích của khối trụ (T).
 Xem đáp án
Xem đáp án
Xác định các yếu tố còn thiếu để tính thể tích của hình trụ.
Dựa vào khoảng cách trong không gian.
Diện tích hình trụ, thể tích khối trụ
Lời giải
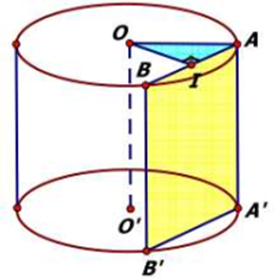
Gọi thiết diện đã cho là AA′B′B (như hình vẽ) và I là trung điểm AB . Hình vuông AA′B′B có diện tích bằng 16(cm2)⇒ cạnh hình vuông bằng AA′ = 4cm .
Mặt phẳng song song với trục và cách trục một khoảng bằng 2cm suy ra OI = 2(cm).
Ta có bán kính đáy của hình trụ là \(r = \sqrt {O{I^2} + {{\left( {\frac{{AB}}{2}} \right)}^2}} = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 \).
Thể tích của khối trụ (T) là \(V = \pi {r^2}h = \pi {(2\sqrt 2 )^2}.4 = 32\pi \left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Câu 67:
Trong không gian Oxyz, cho điểm \(A(1;2;4)\) và hai đường thẳng \({d_1}:\frac{x}{1} = \frac{y}{1} = \frac{z}{1}\), \({d_2}:\left\{ {\begin{array}{*{20}{l}}{x = 1 - t}\\{y = 1 + t{\rm{. }}}\\{z = 2t}\end{array}} \right.\)Đường thẳng Δ qua A, vuông góc với d1 và cắt d2 có phương trình là
 Xem đáp án
Xem đáp án
Bước 1: Gọi điểm \(M(1 - t;1 + t;2t) \in {d_2}\). Suy ra \(\overrightarrow {AM} = ( - t;t - 1;2t - 4)\).
Bước 2: Tìm vecto chỉ phương đường thẳng \({d_1}\)
Bước 3: \(AM \bot {d_1}(AM \equiv \Delta )\) nên tìm được \({\rm{t}}\)
Bước 4: Lập phương trình cần tìm bằng cách thay \(t\) đã rìm được vào
\(\overrightarrow {AM} = ( - t;t - 1;2t - 4){\rm{. }}\)
Lời giải
Gọi \(M(1 - t;1 + t;2t) \in {d_2}\). Ta có: \(\overrightarrow {AM} = ( - t;t - 1;2t - 4)\).
Đường thẳng \({d_1}\) có một vectơ chỉ phương là \({\vec u_1} = (1;1;1)\).
Do \(AM \bot {d_1}(AM \equiv \Delta )\) nên \(\overrightarrow {AM} .{\vec u_1} = 0 \Leftrightarrow 2t - 5 = 0 \Leftrightarrow t = \frac{5}{2}\).
Đường thẳng \(\Delta \) qua \(A(1;2;4)\) và có một vectơ chỉ phương là
\(\overrightarrow {AM} = \left( { - \frac{5}{2};\frac{3}{2};1} \right) = \frac{1}{2}( - 5;3;2)\), có phương trình là \(\Delta :\frac{{x - 1}}{{ - 5}} = \frac{{y - 2}}{3} = \frac{{z - 4}}{2}\).
Câu 68:
Trong không gian Oxyz, tọa độ điểm \(A'\) là hình chiếu vuông góc của điểm \(A( - 1;4;0)\) lên mặt phẳng \((\alpha ):x - 2y + 4z + 10 = 0\) là
 Xem đáp án
Xem đáp án
Bước 1: Viết phương trình tham số đường thắng \(\Delta \) đi qua \(A( - 1;4;0)\) và vuông góc với \((\alpha )\).
Bước 2: Tìm tọa độ \(A'\) là giao điểm của \(\Delta \) và \((\alpha )\).
Lời giải
Ta có \({\vec n_{(\alpha )}} = (1; - 2;4)\).
Gọi \(\Delta \) là đường thẳng đi qua \(A( - 1;4;0)\) và vuông góc với mặt phẳng \((\alpha )\).
Khi đó \(A'\) là giao điểm của \(\Delta \) và \((\alpha )\).
Vì \(\Delta \bot (\alpha )\) nên \(\Delta \) nhận \({\vec n_{(\alpha )}} = (1; - 2;4)\) làm vectơ chỉ phương.
Suy ra phương trình tham số của \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = - 1 + t}\\{y = 4 - 2t}\\{z = 4t}\end{array}} \right.\)
Ta có \(A' \in \Delta \Rightarrow \) tọa độ \(A'( - 1 + t;4 - 2t;4t)\).
Lại có \(A' \in (\alpha )\).
\( \Rightarrow - 1 + t - 2(4 - 2t) + 4.4t + 10 = 0\)
\( \Leftrightarrow t = - \frac{1}{{21}}.\)
Suy ra tọa độ \(A'\left( { - \frac{{22}}{{21}};\frac{{86}}{{21}}; - \frac{4}{{21}}} \right)\).
Vậy ta chọn phương án D.
Câu 69:
Một công ti bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 2 000 000 đồng một tháng thì mọi căn hộ đều có người thuê, và cứ mỗi lần tăng giá cho thuê mỗi căn hộ thêm 100 000 đồng một tháng thì có thêm 2 căn hộ bị bỏ trống. Hỏi để có thu nhập cao nhất, công ti đó phải cho thuê mỗi căn hộ với giá tiền là bao nhiêu một tháng? (đồng/tháng)
 Xem đáp án
Xem đáp án
Gọi \(x\) (đồng/tháng) là số tiền tăng thêm của giá cho thuê mỗi căn hộ \((x \ge 0)\)
Khi đó số căn hộ bỏ trống là \(\frac{{2x}}{{100000}}\) (căn)
Số tiền thu được là:
\(T(x) = (2000000 + x)\left( {50 - \frac{{2x}}{{100000}}} \right) = 100000000 + 10x - \frac{{{x^2}}}{{50000}}\)
Khảo sát hàm số trên \([0; + \infty )\) ta được: \(\mathop {\max }\limits_{x \ge 0} T(x) = T(250000)\)
Vậy để có thu nhập cao nhất thì số tiền cho thuê mỗi căn hộ là 2 250 000 đồng/tháng.
Câu 70:
Cho tập hợp A={1;2;3;4;5;6;7}. Các khẳng định sau đúng hay sai?
|
|
ĐÚNG |
SAI |
|
Có thể lập được 5040 số tự nhiên có 7 chữ số khác nhau từ các chữ số trong tập A. |
¡ |
¡ |
|
Có thể lập được 360 số tự nhiên có 7 chữ số khác nhau và chữ số 1 là hàng chục nghìn từ các chữ số trong tập A. |
¡ |
¡ |
|
Có thể lập được 4230 số tự nhiên có 7 chữ số khác nhau và chữ số 2 không ở hàng đơn vị từ các chữ số trong tập A. |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
Có thể lập được 5040 số tự nhiên có 7 chữ số khác nhau từ các chữ số trong tập A. |
¤ |
¡ |
|
Có thể lập được 360 số tự nhiên có 7 chữ số khác nhau và chữ số 1 là hàng chục nghìn từ các chữ số trong tập A. |
¡ |
¤ |
|
Có thể lập được 4230 số tự nhiên có 7 chữ số khác nhau và chữ số 2 không ở hàng đơn vị từ các chữ số trong tập A. |
¡ |
¤ |
Phương pháp giải
Lời giải
a) Mỗi cách lập một số tự nhiên có 7 chữ số khác nhau là một hoán vị của các phần tử của A. Khi đó số các hoán vị là 7!=5040
b) Với số 1 ở vị trí hàng chục nghìn thì còn 6 số chưa cố định nên có 6!=720 số.
c) Số cách lập 1 số tự nhiên có 7 chữ số khác nhau và chữ số 2 ở hàng đơn vị là 6! cách. Khi đó số cách lập 1 số tự nhiên có 7 chữ số khác nhau và chữ số 2 KHÔNG ở hàng đơn vị là 7!−6!=4320 số.
Câu 71:
Cho tam giác ABC vuông tại \(A\) có \(AB = 6\;{\rm{cm}},AC = 8\;{\rm{cm}}\). Thể tích khối tròn xoay thu được khi quay tam giác ABC quanh trục BC là
 Xem đáp án
Xem đáp án
Kẻ \(AH \bot BC\). Áp dụng hệ thức lượng trong tam giác vuông ta có \(AH = 4,8(\;{\rm{cm}})\).
Áp dụng định lý Pytago \(BC = \sqrt {A{B^2} + A{C^2}} = 10(\;{\rm{cm}})\)
Ta có \(V = \frac{1}{3}\pi A{H^2}.BH + \frac{1}{3}\pi A{H^2}.CH = \frac{1}{3}\pi .A{H^2}.BC = \frac{{384}}{5}\pi \)
Câu 72:
Cho hai số phức \({z_1},{z_2}\) thỏa mãn đồng thời hai điều kiện sau \(|z - 1| = \sqrt {34} ,|z + 1 + mi| = |z + m + 2i|\) (trong đó \(m\) là số thực) và sao cho \(\left| {{z_1} - {z_2}} \right|\) là lớn nhất. Khi đó giá trị \(\left| {{z_1} + {z_2}} \right|\) bằng
 Xem đáp án
Xem đáp án
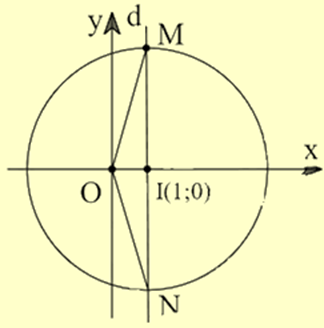
Gọi M, N lần lượt là điểm biểu diễn của số phức \({z_1},{z_2}\)
Gọi \(z = x + iy,(x,y \in \mathbb{R})\)
Ta có \(|z - 1| = \sqrt {34} \Rightarrow M,N\) thuộc đường tròn \((C)\) có tâm \(I(1;0)\), bán kính \(R = \sqrt {34} \)
Mà \(|z + 1 + mi| = |z + m + 2i| \Leftrightarrow |x + yi + 1 + mi| = |x + yi + m + 2i|\)
\( \Leftrightarrow \sqrt {{{(x + 1)}^2} + {{(y + m)}^2}} = \sqrt {{{(x + m)}^2} + {{(y + 2)}^2}} \)
\( \Leftrightarrow 2(1 - m)x + 2(m - 2)y - 3 = 0\)
Suy ra M, N thuộc đường thẳng \(d:2(1 - m)x + 2(m - 2)y - 3 = 0\)
Do đó M, N là giao điểm của đường thẳng \(d\) và đường tròn \((C)\)
Ta có \(\left| {{z_1} - {z_2}} \right| = MN\) nên \(\left| {{z_1} - {z_2}} \right|\) lớn nhất khi và chỉ khi MN lớn nhất
\( \Leftrightarrow MN\) là đường kính của \((C)\). Khi đó \(\left| {{z_1} + {z_2}} \right| = 2OI = 2\)
Câu 73:
Điểm đối xứng của điểm M(−2;3;4) qua mặt phẳng (Oxy) là điểm M′ có cao độ bằng ?
 Xem đáp án
Xem đáp án
Đáp án: “-4”
Phương pháp giải
Điểm đối xứng của điểm M(x0;y0;z0) qua mặt phẳng (Oxy) là điểm M′(x0;y0;−z0)
Lời giải
Điểm đối xứng của điểm M(−2;3;4) qua mặt phẳng (Oxy) là điểm M′(−2;3;−4)
Câu 74:
Cho hình chóp S.ABCD có đáy \({\rm{ABCD}}\) là hình bình hành. Trên các cạnh \({\rm{SA}},{\rm{SB}},{\rm{SC}}\) lần lượt lấy các điểm \({A^\prime },{B^\prime },{C^\prime }\) sao cho \(SA = 2S{A^\prime };SB = 3S{B^\prime };SC = 4S{C^\prime }\), mặt phẳng \(\left( {{A^\prime }{B^\prime }{C^\prime }} \right)\) cắt cạnh \({\rm{SD}}\) tại \({D^\prime }\). Gọi \({V_1},{V_2}\) lần lượt là thể tích của hai khối chóp \(S.{A^\prime }{B^\prime }{C^\prime }{D^\prime }\) và S.ABCD. Khi đó tỉ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng:
 Xem đáp án
Xem đáp án
VS.A′B′C′D′ = VS.A′B′C′ + VS.A′C′D′
Lời giải
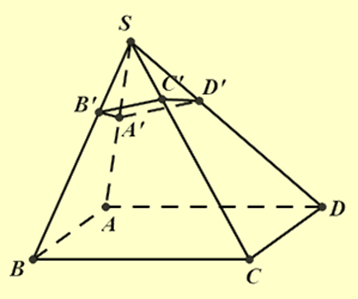
\(\frac{{SA}}{{S{A^\prime }}} + \frac{{SC}}{{S{C^\prime }}} = \frac{{SB}}{{S{B^\prime }}} + \frac{{SD}}{{S{D^\prime }}} \Rightarrow 2 + 4 = 3 + \frac{{SD}}{{S{D^\prime }}} \Rightarrow \frac{{SD}}{{S{D^\prime }}} = 3 \Rightarrow SD = 3S{D^\prime }\)
\(\frac{{{V_{S.{A^\prime }{B^\prime }{C^\prime }}}}}{{{V_{S.ABC}}}} = \frac{{S{A^\prime }}}{{SA}}.\frac{{S{B^\prime }}}{{SB}}.\frac{{S{C^\prime }}}{{SC}} = \frac{1}{2}.\frac{1}{3}.\frac{1}{4} = \frac{1}{{24}} \Rightarrow {V_{S.{A^\prime }{B^\prime }{C^\prime }}} = \frac{1}{{24}}{S_{S.ABC}}\)
\(\frac{{{V_{S.{A^\prime }{C^\prime }{D^\prime }}}}}{{{V_{S.ACD}}}} = \frac{{S{A^\prime }}}{{SA}}.\frac{{S{D^\prime }}}{{SD}}.\frac{{S{C^\prime }}}{{SC}} = \frac{1}{2}.\frac{1}{3}.\frac{1}{4} = \frac{1}{{24}} \Rightarrow {V_{S.{A^\prime }{C^\prime }{D^\prime }}} = \frac{1}{{24}}{S_{S.ACD}}\)
\( \Rightarrow {V_{S.{A^\prime }{B^\prime }{C^\prime }{D^\prime }}} = {V_{S.{A^\prime }{B^\prime }{C^\prime }}} + {V_{S.{A^\prime }{C^\prime }{D^\prime }}} = \frac{{{V_{S.ABC}} + {V_{S.ACD}}}}{{24}} \Rightarrow \frac{{{V_{S.{A^\prime }{B^\prime }{C^\prime }{D^\prime }}}}}{{{V_{S.ABCD}}}} = \frac{1}{{24}}\)
Câu 75:
Cho tam giác ABC đều cạnh bằng 4. Gọi M, N lần lượt là trung điểm AB, AC. Diện tích đa giác thu được khi lấy đối xứng tam giác ABC qua trục MN là \[a\sqrt b \;(a,b \in Z).\] Trong các phát biểu sau, phát biểu nào đúng?
a chia hết cho b.
a − 2b = 1
a + 2b chia hết cho 5.
a + b là số chính phương.
 Xem đáp án
Xem đáp án
a chia hết cho b. - ĐÚNG
a − 2b = 1
a + 2b chia hết cho 5.
a + b là số chính phương. - ĐÚNG
Phương pháp giải
Lời giải
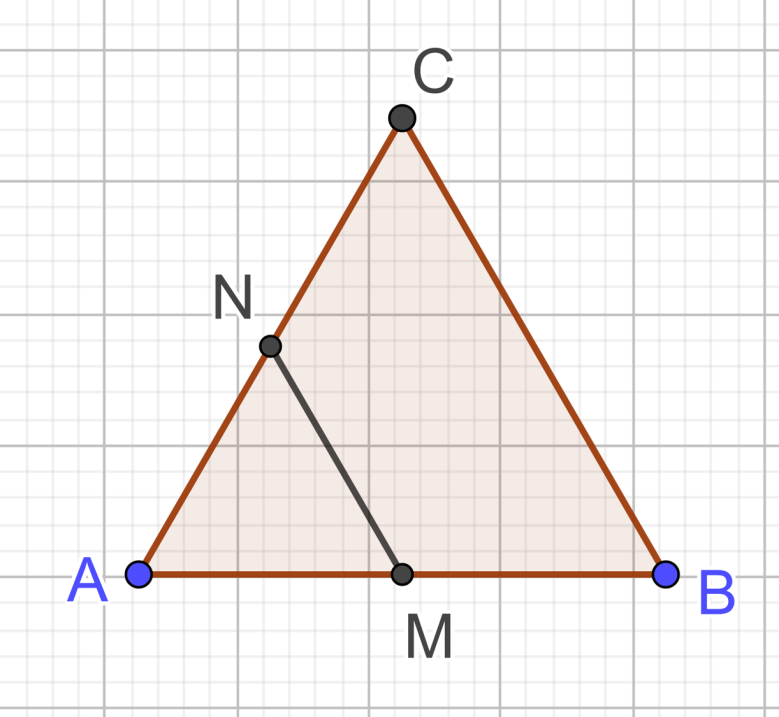
Ta có diện tích tam giác AMN bằng 1/4 diện tích tam giác ABC
Nên diện tích tứ giác MNCB bằng 3/4 diện tích tam giác ABC.
Mà diện tích cần tìm gấp 2 lần diện tích MNCB nên:
Ta được: \(S = \frac{3}{2}{S_{ABC}} = \frac{3}{2}.\frac{{{4^2}\sqrt 3 }}{4} = 6\sqrt 3 \Rightarrow a = 6;b = 3\)
Câu 76:
Cho các mệnh đề sau:
I/ Số cạnh của một khối đa diện lồi luôn lớn hơn hoặc bằng 6.
II/ Số mặt của khối đa diện lồi luôn lớn hơn hoặc bằng 5.
III/ Số đỉnh của khối đa diện lồi luôn lớn hơn 4.
Trong các mệnh đề trên, những mệnh đề nào là mệnh đề đúng?
 Xem đáp án
Xem đáp án
- Sử dụng lý thuyết về khối đa diện lồi.
Khái niệm về khối đa diện
Lời giải
Mệnh đề II sai vì khối tứ diện là khối đa diện lồi có số mặt nhỏ hơn 5.
Mệnh đề III sai vì khối tứ diện là khối đa diện lồi có 4 đỉnh.
Câu 77:
Ta gọi số nguyên bé nhất không nhỏ hơn x là phần nguyên trên của x, kí hiệu ⌈x⌉. Chẳng hạn \(\left\lceil { - 2,5} \right\rceil = - 2;\,\,\,\left\lceil {\frac{{19}}{6}} \right\rceil = 4\).
Tổng phần nguyên trên của tất cả các số có dạng \(\frac{k}{3}\) với k nguyên lấy giá trị từ −5 đến 5 bằng ?
 Xem đáp án
Xem đáp án
Đáp án: “4”
Phương pháp giải
Lời giải
Lập bảng giá trị, ta được tổng các phần nguyên trên là:
(−1) + (−1) + (−1) + 0 + 0 + 0 + 1 + 1 + 1 + 2 + 2 = 4.
Câu 78:
Một hộp chứa 5 viên bi màu trắng, 15 viên bi màu xanh và 35 viên bi màu đỏ. Lấy ngẫu nhiên từ hộp ra 7 viên bi. Xác suất để trong số 7 viên bi được lấy ra có ít nhất 1 viên bi màu đỏ là:
 Xem đáp án
Xem đáp án
- Tính số cách chọn 7 trong 20 viên bi.
- Tính số cách chọn mà trong số 7 viên bi không có viên nào màu đỏ.
- Tính xác suất \(P(\bar A) \Rightarrow P(A) = 1 - P(\bar A)\).
Biến cố và xác suất của biến cố
Lời giải
Gọi A là biến cố: “trong số 7 viên bi được lấy ra có ít nhất 1 viên bi màu đỏ.”
- Số phần tử của không gian mẫu là: Số cách chọn 7trong 55 viên bi. Có \(C_{55}^7\) cách.
- \(\bar A\) là biến cố: “trong số 7 viên bi được lấy ra không có viên bi màu đỏ nào”. Có 20 viên bi không phải màu đỏ.
\(\begin{array}{l} \Rightarrow n(\bar A) = C_{20}^7.\\ \Rightarrow n(A) = \Omega - n(\bar A) = C_{55}^7 - C_{20}^7.\end{array}\)
\( \Rightarrow P(A) = \frac{{C_{55}^7 - C_{20}^7}}{{C_{55}^7}}.\)
Câu 79:
Biết hàm số f(x) nghịch biến trên khoảng (0;+∞).
Các khẳng định sau là đúng hay sai?
|
|
ĐÚNG |
SAI |
|
\[f\left( 2 \right) < f\left( 3 \right)\] |
¡ |
¡ |
|
Với mọi \({x_1},{x_2} \in (0; + \infty ),{x_1} < {x_2}\) ta có \(\frac{{f\left( {{x_1}} \right) - f\left( {{x_2}} \right)}}{{{x_1} - {x_2}}} < 0\) |
¡ |
¡ |
|
\[f\left( {\frac{3}{4}} \right) > f\left( {\frac{2}{3}} \right)\] |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
\[f\left( 2 \right) < f\left( 3 \right)\] |
¡ |
¤ |
|
Với mọi \({x_1},{x_2} \in (0; + \infty ),{x_1} < {x_2}\) ta có \(\frac{{f\left( {{x_1}} \right) - f\left( {{x_2}} \right)}}{{{x_1} - {x_2}}} < 0\) |
¤ |
¡ |
|
\[f\left( {\frac{3}{4}} \right) > f\left( {\frac{2}{3}} \right)\] |
¡ |
¤ |
Phương pháp giải
Lời giải
Hàm số \(f(x)\) đồng biến trên khoảng \((0; + \infty )\) nên
Do \(2 < 3 = > f(2) > f(3)\)
Với mọi \({x_1},{x_2} \in (0; + \infty ),{x_1} < {x_2}\) ta có \(\frac{{f\left( {{x_1}} \right) - f\left( {{x_2}} \right)}}{{{x_1} - {x_2}}} < 0\)
Vì \(\frac{3}{4} > \frac{2}{3}\) nên \(f\left( {\frac{3}{4}} \right) < f\left( {\frac{2}{3}} \right)\)
Câu 80:
Gọi \({z_1},{z_2}\) là nghiệm của phương trình \({z^2} + 4z + 5 = 0\). Tính giá trị của biểu thức \(P = \frac{{z_1^2}}{{{z_2}}} + \frac{{z_2^2}}{{{z_1}}}\).
 Xem đáp án
Xem đáp án
Bước 1: Tìm nghiệm z1, z2 của phương trình đã cho.
Bước 2: Tính giá trị của biểu thức P và kết luận.
Giải phương trình bậc hai
Lời giải
Ta có \({z^2} + 4z + 5 = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{z_1} = - 2 + i}\\{{z_2} = - 2 - i}\end{array}} \right.\)
Khi đó \(P = \frac{{z_1^2}}{{{z_2}}} + \frac{{z_2^2}}{{{z_1}}} = \frac{{{{( - 2 + i)}^2}}}{{ - 2 - i}} + \frac{{{{( - 2 - i)}^2}}}{{ - 2 + i}} = - \frac{4}{5}\).
Câu 81:
Một vận động viên đang luyện tập chạy đường dài, dự định buổi tập hôm nay sẽ chạy trong 50 phút. Trong vòng 15 phút đầu tiên người vận động viên chạy với vận tốc 10km/h, do có sự suy giảm thể lực nên mỗi 10 phút tiếp theo vận tốc của người vận động viên giảm so với trước đó 1km/h. Hỏi đến khi hoàn thành buổi tập thì người vận động viên đã chạy được quãng đường là bao nhiêu?
 Xem đáp án
Xem đáp án
+) Tính vận tốc và quãng đường trong từng mốc thời gian di chuyển
+) s = v.t với s là quãng đường, v là vận tốc, t thời gian
Lời giải
Quãng đường di chuyển được trong 15 phút đầu với vận tốc 10km/h là \(10.\frac{1}{4} = 2,5\) (km)
Quãng đường di chuyển được trong 10 phút lần 1với vận tốc 9km/h là \(9.\frac{1}{6} = 1,5\) (km)
Quãng đường di chuyển được trong 10 phút lần 2 với vận tốc 8km/h là \({\rm{ 8}}{\rm{.}}\frac{1}{6} = \frac{4}{3}\) (km)
Quãng đường di chuyển được trong 10 phút lần 3 với vận tốc 7km/h là \({\rm{ 7}}{\rm{.}}\frac{1}{6} = \frac{7}{6}\) (km)
Quãng đường di chuyển được trong 5 phút cuối với vận tốc 6km/h là \(6.\frac{1}{{12}} = \frac{1}{2}\) (km)
Tổng quãng đường đi được là \(2,5 + 1,5 + \frac{4}{3} + \frac{7}{6} + 0,5 = 7\) (km)
Câu 82:
Số tam giác xác định bởi các đỉnh của một đa giác đều 10 cạnh là:
 Xem đáp án
Xem đáp án
Mỗi tam giác được tạo thành ứng với một cách chọn 3 trong 10 điểm.
Bài toán đếm trong hình học - hình học không gian
Lời giải
Cứ ba đỉnh của đa giác sẽ tạo thành một tam giác.
Chọn 3 trong 10 đỉnh của đa giác, có .
Vậy có 120 tam giác xác định bởi các đỉnh của đa giác 10 cạnh.
Câu 83:
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
|
|
ĐÚNG |
SAI |
|
Hàm số \(y = \frac{{\tan x + 3}}{{2\sin x - 3}}\) xác định với mọi \(x \in \mathbb{R}\). |
¡ |
¡ |
|
Các nghiệm của phương trình 2cosx − 1 = 0 được biểu diễn bởi 2 điểm trên đường tròn lượng giác. |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
Hàm số \(y = \frac{{\tan x + 3}}{{2\sin x - 3}}\) xác định với mọi \(x \in \mathbb{R}\). |
¡ |
¤ |
|
Các nghiệm của phương trình 2cosx − 1 = 0 được biểu diễn bởi 2 điểm trên đường tròn lượng giác. |
¤ |
¡ |
Phương pháp giải
Lời giải
Mệnh đề 1: Hàm số \(y = \frac{{\tan x + 3}}{{2\sin x - 3}}\) xác định khi cosx ≠ 0.
Mệnh đề 2: \(2\cos x - 1 = 0 \Leftrightarrow \cos x = \frac{1}{2} \Leftrightarrow x = \pm \frac{\pi }{3} + k2\pi \,\,(k \in \mathbb{Z})\) ứng với 2 điểm trên đường tròn.
Câu 84:
Khai triển nhị thức \({(x + 2)^{n + 5}}\quad (n \in \mathbb{N})\) có tất cả 2019 số hạng. Tìm n.
 Xem đáp án
Xem đáp án
Khai triển nhị thức \({(a + b)^n}\quad (n \in \mathbb{N})\) có tất cả n + 1 số hạng.
Nhị thức Niu - tơn
Lời giải
Khai triển nhị thức \({(x + 2)^{n + 5}}\quad (n \in \mathbb{N})\) có tất cả 2019 số hạng nên n + 5 + 1 = 2019 ⇔ n = 2013.
Câu 85:
Gọi S là tổng các nghiệm của phương trình \({9^{\frac{x}{2}}} + 9.{\left( {\frac{1}{{\sqrt 3 }}} \right)^{2x + 2}} - 4 = 0\). Khi đó S thuộc những khoảng nào trong các khoảng dưới đây?
(−1;1).
(0;2).
\(\left( { - \frac{1}{2};\frac{3}{2}} \right)\).
(−2;0).
 Xem đáp án
Xem đáp án
(−1;1).
(0;2). - ĐÚNG
\(\left( { - \frac{1}{2};\frac{3}{2}} \right)\). - ĐÚNG
(−2;0).
Phương pháp giải
Lời giải
\({9^{\frac{x}{2}}} + 9.{\left( {\frac{1}{{\sqrt 3 }}} \right)^{2x + 2}} - 4 = 0 \Leftrightarrow {3^x} + 3.\frac{1}{{{3^x}}} - 4 = 0 \Leftrightarrow {3^{2x}} - {4.3^x} + 3 = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{3^x} = 1}\\{{3^x} = 3}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 1}\end{array} \Rightarrow S = 0 + 1 = 1.} \right.} \right.\)
Câu 86:
Dãy số Phi-bô-na-xi là dãy số (un) được xác định như sau: \({u_1} = {u_2} = 1;\,\,{u_n} = {u_{n - 1}} + {u_{n - 2}}\) với n ≥ 3. Số hạng thứ 11 của dãy số Phi-bô-na-xi là
 Xem đáp án
Xem đáp án
Phương pháp giải
Lập dãy số.
Lời giải
Ta có: u11 = 89
Câu 87:
Cho tứ diện ABCD có thể tích \(V\) với M, N lần lượt là trung điểm AB, CD. Gọi \({V_1},{V_2}\) lần lượt là thể tích của MNBC và MNDA. Tỉ lệ \(\frac{{{V_1} + {V_2}}}{V}\) bằng
 Xem đáp án
Xem đáp án
Tính tỉ lệ thể tích các khối chóp.
Lời giải
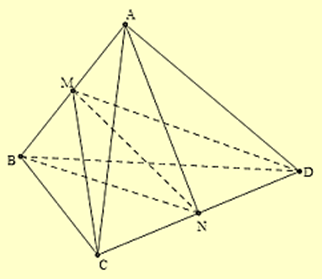
Vì M, N lần lượt là trung điểm AB, CD nên ta có:
d(A,(MCD)) = d(B,(MCD)); d(C,(NAB)) = d(D,(NAB)), do đó:
\({V_{A.MCD}} = {V_{B.MCD}} = \frac{V}{2};{V_1} = {V_{MNBC}} = {V_{C.MNB}} = {V_{D.MNB}} = \frac{{{V_{B.MCD}}}}{2} = \frac{V}{4};\)
\({V_2} = {V_{MNAD}} = {V_{D.MNA}} = {V_{C.MNA}} = \frac{{{V_{A.MCD}}}}{2} = \frac{V}{4}.\)
\( \Rightarrow \frac{{{V_1} + {V_2}}}{V} = \frac{{\frac{V}{4} + \frac{V}{4}}}{V} = \frac{1}{2}.\)
Câu 88:
Cho hàm số \(y = \left| {{x^4} - 2m{x^2} + 2m - 1} \right|\) với m là tham số thực. Số giá trị nguyên trong khoảng [−2;2] của m để hàm số đã cho có 3 điểm cực trị là
 Xem đáp án
Xem đáp án
- Đặt \(f(x) = {x^4} - 2m{x^2} + 2m - 1\)
- Xét các trường hợp:
+ Trường hợp 1: hàm số có một cực trị
+ Trường hợp 2: hàm số có ba cực trị
Lời giải
Đặt \(f(x) = {x^4} - 2m{x^2} + 2m - 1,{f^\prime }(x) = 4{x^3} - 4mx,f'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{{x^2} = m}\end{array}} \right.\)
+ Trường hợp 1: hàm số có một cực trị \( \Rightarrow m \in [ - 2;0]\).
Đồ thị hàm số \(y = f(x)\) có một điểm cực trị là \(A(0;2m - 1)\).
Do \(m \in [ - 2;0] \Rightarrow {y_A} = 2m - 1 < 0\) nên đồ thị hàm số \(y = f(x)\) cắt trục hoành tại 2 điểm phân biệt nên hàm số \(y = |f(x)|\) có 3 cực trị \( \Rightarrow \) có 3 giá trị nguyên của \(m\) thỏa ycbt.
+ Trường hợp 2: hàm số có ba cực trị \( \Rightarrow m \in (0;2]\).
Khi đó đồ thị hàm số có 3 điểm cực trị là \(A(0;2m - 1),B\left( {\sqrt m ; - {m^2} + 2m - 1} \right)\), \(C\left( { - \sqrt m ; - {m^2} + 2m - 1} \right)\).
Do \(a = 1 > 0\) nên hàm số \(y = |f(x)|\) có 3 điểm cực trị khi hàm số \(y = f(x)\) có \({y_B} = {y_C} \ge 0\)
\( \Leftrightarrow - {m^2} + 2m - 1 \ge 0 \Leftrightarrow m = 1\).
Nếu \({y_B} = {y_C} < 0\) (trong bài toán này không xảy ra) thì hàm số có ít nhất 5 điểm cực trị.
Vậy có 4 giá trị của \(m\) thỏa ycbt.
Câu 89:
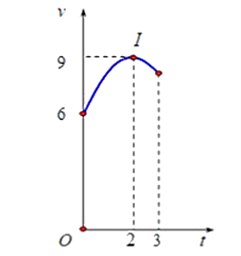
Một vật chuyển động trong 3 giờ với vận tốc v(km/h) phụ thuộc vào thời gian t(h) có đồ thị là một phần của đường parabol có đỉnh I(2;9) và trục đối xứng song song với trục tung như hình bên. Quãng đường s(km) mà vật di chuyển được trong 3 giờ là
 Xem đáp án
Xem đáp án
- Gọi \(v(t) = a{t^2} + bt + c.\)
- Tìm hàm số.
- Sử dụng tích phân tính quãng đường.
Lời giải
Gọi \(v(t) = a{t^2} + bt + c.\) Do parabol có đỉnh I(2;9) và đi qua điểm A(0;6) nên ta có hệ
\(\left\{ {\begin{array}{*{20}{l}}{\frac{{ - b}}{{2a}} = 2}\\{a{{.2}^2} + b.2 + c = 9}\\{a{{.0}^2} + b.0 + c = 6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = \frac{{ - 3}}{4}}\\{b = 3}\\{c = 6}\end{array} \Rightarrow v(t) = - \frac{3}{4}{t^2} + 3t + 6} \right.} \right.\)
Vậy \(s = \int\limits_0^3 {\left( { - \frac{3}{4}{t^2} + 3t + 6} \right)dt} = 24,75\) (km)
Câu 90:
Hàm số \(y = {x^4} - 2{x^2} + 1\) nghịch biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Bước 1: Tính đạo hàm và giải y′ = 0
Bước 2: Lập bảng biến thiên để xét tính đơn điệu của hàm số
Bước 3: Dựa vào bảng biến thiên ta tìm được khoảng nghịch biến
Lời giải
Ta có: \(y' = 4{x^3} - 4x,\,\,y' = 0 \Rightarrow 4{x^3} - 4x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 1}\\{x = - 1}\end{array}.} \right.\) .
Bảng biến thiên
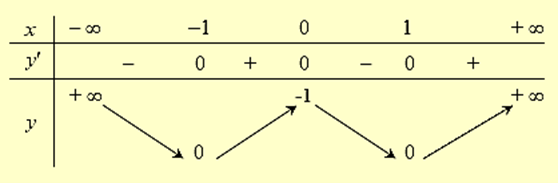
Dựa vào bảng biến thiên ta thấy hàm số nghịch biến trên khoảng (−∞;−1).
Câu 91:
Đồ thị hàm số \(y = \frac{{5x - 1 - \sqrt {{x^2} - 2} }}{{x - 4}}\) có bao nhiêu đường tiệm cận đứng và ngang?
 Xem đáp án
Xem đáp án
- Áp dụng định nghĩa đường tiệm cận đứng và ngang của đồ thị hàm số.
- Tính các giới hạn \(\mathop {\lim }\limits_{x \to > + \infty } f(x),\mathop {\lim }\limits_{x \to - \infty } f(x),\mathop {\lim }\limits_{x \to {a^ + }} f(x),\mathop {\lim }\limits_{x \to a - } f(x)\)
Tìm tiệm cận ngang của đồ thị hàm số
Tìm tiệm cận đứng của đồ thị hàm số
Lời giải
TXĐ: \(D = ( - \infty , - \sqrt 2 ) \cup (\sqrt 2 , + \infty )\)
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{5x - 1 - \sqrt {{x^2} - 2} }}{{x - 4}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{5 - \frac{1}{x} - \sqrt {1 - \frac{2}{{{x^2}}}} }}{{1 - \frac{4}{x}}} = 4\)
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{5x - 1 - \sqrt {{x^2} - 2} }}{{x - 4}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{5 - \frac{1}{x} - \sqrt {1 - \frac{2}{{{x^2}}}} }}{{1 - \frac{4}{x}}} = 6\)
=> Đồ thị hàm số có 2 đường TCN: \(\left\{ {\begin{array}{*{20}{l}}{y = 4}\\{y = 6}\end{array}} \right.\)
\(\mathop {\lim }\limits_{x \to {4^ + }} \frac{{5x - 1 - \sqrt {{x^2} - 2} }}{{x - 4}} = + \infty \) =>Đồ thị hàm số có 1 đường TCĐ: x = 4
=> Đồ thị hàm số có 3 đường tiệm cận. =>Chọn C
Câu 92:
Cho hàm số \(y = \frac{1}{3}{x^3} - (m - 1){x^2} + (m - 3)x + \frac{9}{2}\) (m là tham số thực). Có bao nhiêu giá trị nguyên của m thuộc [-5;5] để hàm số đã cho cắt đường thẳng \(y = - 3x + \frac{9}{2}\) tại 3 điểm phân biệt?
 Xem đáp án
Xem đáp án
Xét phương trình hoành độ giao điểm của 2 hàm số đã cho
Biện luận m để phương trình có 3 nghiệm phân biệt
Lời giải
Ta có phương trình hoành độ giao điểm:
\(\frac{1}{3}{x^3} - (m - 1){x^2} + (m - 3)x + \frac{9}{2} = - 3x + \frac{9}{2}\) (∗)
\( \Leftrightarrow \frac{1}{3}{x^3} - (m - 1){x^2} + mx = 0\)
\( \Leftrightarrow x\left[ {{x^2} - 3(m - 1)x + 3m} \right] = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{{x^2} - 3(m - 1)x + 3m = 0\,\,\,(1)}\end{array}} \right.\)
Để đồ thị hàm số \(y = \frac{1}{3}{x^3} - (m - 1){x^2} + (m - 3)x + \frac{9}{2}\) cắt đường thẳng \(y = - 3x + \frac{9}{2}\) tại 3 điểm phân biệt thì phương trình (*) phải có 3 nghiệm phân biệt
⇔Phương trình (*) có 2 nghiệm phân biệt \({x_1},{x_2} \ne 0\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{f_{(0)}} = 3m \ne 0}\\{\Delta = 9{{(m - 1)}^2} - 12m > 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m \ne 0}\\{\left[ {\begin{array}{*{20}{l}}{m < \frac{1}{3}}\\{m > 3}\end{array}} \right.}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m < \frac{1}{3}}\\{m > 3}\end{array},m \ne 0} \right.} \right.} \right.\)
Mà m ∈ Z, m ∈ [-5;5] ⇒ m ∈ {−5;−4;−3;−2;−1;4;5}
Có 7 giá trị của m thỏa mãn. Chọn B
Câu 93:
A,B là hai số tự nhiên liên tiếp thỏa mãn \(A < \frac{{{2^{2021}}}}{{{3^{1273}}}} < B\). Giá trị \(A + B\) là
 Xem đáp án
Xem đáp án
Bước 1: Áp dụng logarit hóa để đưa \(A < \frac{{{2^{2021}}}}{{{3^{1273}}}} < B\) về phương trình hàm logarit
Bước 2: A,B là hai số tự nhiên liên tiếp nên ta dễ dàng xác định giá trị A,B
Lời giải
Ta có: \(A < \frac{{{2^{2021}}}}{{{3^{1273}}}} < B \Leftrightarrow \log A < 2021.\log 2 - 1273.\log 3 < \log B\) (logarit hóa)
Mà 2021.log2 − 1273.log3 ≈ 1,006 ⇒ logA < 1,006 < logB ⇒ A < 101,006 < B ⇒ A < 10,145 < B
2021.log2 − 1273.log3 ≈ 1,006 ⇒ logA < 1,006 < logB ⇒ A < 101,006 < B ⇒ A < 10,145 < B
Do A, B là hai số tự nhiên liên tiếp nên A = 10, B = 11 ⇒ A + B = 21.
Câu 94:
Mệnh đề nào sau đây là sai?
 Xem đáp án
Xem đáp án
- Ta sử dụng định lý về nguyên hàm:
(1) Nếu \(F(x)\) là một nguyên hàm của hàm số \(f(x)\) trên \({\rm{K}}\) thì với mỗi hằng số \(C\), hàm số \(G(x) = F(x) + C\) cũng là một nguyên hàm của hàm số \(f(x)\) trên K .
(2) Ngược lại, nếu \(F(x)\) là một nguyên hàm của hàm số \(f(x)\) trên \({\rm{K}}\) thì mọi nguyên hàm của \(f(x)\) trên \({\rm{K}}\) đều có dạng \(F(x) + C\) với C là một hằng số tùy ý.
Lời giải
Ta có:
\(\int f (x)dx = F(x) + {C_1}\)
\(\int f (x)dx = G(x) + {C_2}\)
Nếu \({C_1} \ne {C_2} \Rightarrow F(x) \ne G(x)\).
Câu 95:
Kết quả của phép tính tích phân \(\int\limits_2^{{e^2}} {ln(x)dx = {e^a} - a\ln a + b} \) . Tính \({a^3} + b\).
 Xem đáp án
Xem đáp án
Sử dụng phương pháp tích phân từng phần.
Tích phân có chứa hàm số logarit
Lời giải
Ta có: \(\int_2^{{e^2}} {\ln } (x)dx = \left. {x\ln x} \right|_2^{{e^2}} - \int_2^{{e^2}} x .\frac{1}{x}dx = {e^2}\ln \left( {{e^2}} \right) - 2\ln 2 - \left( {{e^2} - 2} \right)\)
\( = {e^2} - 2\ln 2 + 2\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b = 2}\end{array} \Rightarrow {a^3} + b = 10} \right.\)
Câu 96:
Cho \(({\rm{H}})\) là hình phẳng giới hạn bởi parabol \({\rm{y}} = \sqrt 3 {{\rm{x}}^2}\), cung tròn có phương trình \({\rm{y}} = \sqrt {4 - {{\rm{x}}^2}} \) (với \(0 \le x \le 2\) ) và trục hoành (phần tô đậm trong hình vẽ).
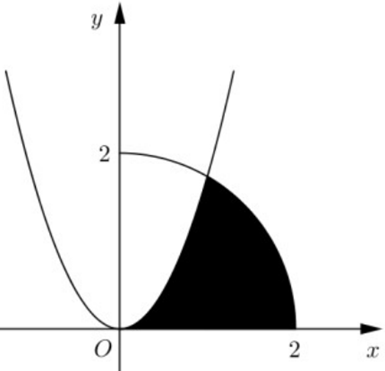
Diện tích của (H) bằng
 Xem đáp án
Xem đáp án
Phương pháp giải
- Tìm hoành độ giao điểm của hai đồ thị
- Sử dụng phương pháp đổi biến để tính diện tích.
Tính diện tích hình phẳng khi biết hai đường giới hạn
Lời giải
Phương trình hoành độ giao điểm giữa parabol và cung tròn ta được
\(\sqrt 3 {x^2} = \sqrt 4 - {x^2} \Leftrightarrow x = \pm 1\) với \(0 \le x \le 2\) nên ta có \(x = 1\)
Ta có diện tích:
\(S = \int_0^1 {\sqrt 3 } {x^2}dx + \int_1^2 {\sqrt {4 - {x^2}} } dx = \left. {\frac{{\sqrt 3 }}{3}{x^3}} \right|_0^1 + \int_1^2 {\sqrt {4 - {x^2}} } dx = \frac{{\sqrt 3 }}{3} + \int_1^2 {\sqrt {4 - {x^2}} } dx\)
Đặt: \(x = 2\sin t \Rightarrow dx = 2\cos tdt;\,\,x = 1 \Rightarrow t = \frac{\pi }{6};x = 2 \Rightarrow t = \frac{\pi }{2}\)
\( \Rightarrow S = \frac{{\sqrt 3 }}{3} + \left. {2\left( {t + \frac{1}{2}\sin 2t} \right)} \right|_{\frac{\pi }{6}}^{\frac{\pi }{2}} = \frac{{4\pi - \sqrt 3 }}{6}\)
