Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 23)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 23)
-
383 lượt thi
-
86 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Giải thích
Đọc nội dung nhan đề và đoạn [1] của văn bản, chú ý một số từ khóa: “cảm hứng”, “tạo động lực”, “nâng cao giá trị”, “bứt phá nền kinh tế”, từ đó có thể thấy, bài viết tập trung thể hiện kết quả mà các doanh nghiệp đạt được sau khi được truyền cảm hứng từ khẩu hiệu “Make in Viet Nam”. → Chọn C.
Câu 2:
Theo đoạn [1], để đạt được mục tiêu phát triển “Top 20 nền kinh tế thế giới” vai trò trung tâm thuộc về Chính phủ số là đúng hay sai?
 Xem đáp án
Xem đáp án
Giải thích
Căn cứ vào nội dung của đoạn [1] xác định các thông tin quan trọng: Quá trình chuyển đổi số diễn ra trên nhiều lĩnh vực (Chính phủ số, kinh tế số và xã hội số), nhưng vai trò trung tâm là “các doanh nghiệp ICT”.
Chọn B
Câu 3:
Để hoàn thành được mục tiêu: đưa Việt Nam bứt phá với nền kinh tế số giữ vai trò chủ đạo thì trách nhiệm lớn nhất thuộc về đơn vị nào?
 Xem đáp án
Xem đáp án
Căn cứ vào cụm từ “bứt phá với nền kinh tế số” xác định thông tin cần tìm nằm trong đoạn [1]. Trong bài viết có nhắc tới: “các doanh nghiệp ICT (công nghệ thông tin và truyền thông) được đặt vào vai trò trung tâm” nên Từ khóa là C.
Chọn C
Câu 4:
mục đích, phát triển, nâng cao, sản xuất, yêu cầu
Khẩu hiệu “Make in Viet Nam” cổ vũ cộng đồng doanh nghiệp _______ trong công cuộc chuyển đổi số và _______ giá trị đất nước trong chuỗi giá trị toàn cầu với _______: Nghiên cứu tại Việt Nam, sáng tạo tại Việt Nam và sản xuất tại Việt Nam.
 Xem đáp án
Xem đáp án
Đáp án
Khẩu hiệu “Make in Viet Nam” cổ vũ cộng đồng doanh nghiệp phát triển trong công cuộc chuyển đổi số và nâng cao giá trị đất nước trong chuỗi giá trị toàn cầu với yêu cầu: Nghiên cứu tại Việt Nam, sáng tạo tại Việt Nam và sản xuất tại Việt Nam.
Giải thích
Căn cứ vào từ khóa “nghiên cứu tại Việt Nam, sáng tạo tại Việt Nam và sản xuất tại Việt Nam” xác định nội dung cần tìm ở đoạn [2]: “số lượng doanh nghiệp số, sản phẩm/ứng dụng số Make in Viet Nam lần lượt ra đời” là sự “phát triển” của các doanh nghiệp; “Không “Make in Viet Nam” thì Việt Nam không thể trở thành nước phát triển. Không “Make in Viet Nam” thì Việt Nam không thể hùng cường thịnh vượng” cho thấy việc “nâng cao giá trị đất nước”; “xác định rõ nội hàm khái niệm cho các sản phẩm công nghệ số phải hướng tới là…” tương đương với “yêu cầu”.
Câu 5:
Dựa vào bài viết, hãy tìm một cụm từ không quá năm tiếng để hoàn thành nhận định sau:
Theo Bộ trưởng Nguyễn Mạnh Hùng, trong năm 2020, hiệu quả của khẩu hiệu “Make in Viet Nam” đã được thể hiện qua (1) ________ và sản phẩm/ứng dụng số.
 Xem đáp án
Xem đáp án
Đáp án
Dựa vào bài viết, hãy tìm một cụm từ không quá năm tiếng để hoàn thành nhận định sau:
Theo Bộ trưởng Nguyễn Mạnh Hùng, trong năm 2020, hiệu quả của khẩu hiệu “Make in Viet Nam” đã được thể hiện qua (1) số lượng doanh nghiệp số và sản phẩm/ứng dụng số.
Giải thích
HS đọc lướt để tìm từ khoá tên riêng, xác định các đoạn [2] xuất hiện lời nói của Bộ trưởng Nguyễn Mạnh Hùng. Trong đó, thông tin cần sử dụng nằm ở câu cuối cùng của đoạn [2]: “Do đó, “Make in Viet Nam” đã không dừng lại ở khẩu hiệu mà thể hiện bằng chính số lượng doanh nghiệp số, sản phẩm/ứng dụng số Make in Viet Nam lần lượt ra đời””. Như vậy, các từ được điền vào chỗ trống là: “Số lượng doanh nghiệp số”.
Câu 6:
Theo đoạn [3], những số liệu đưa ra có ý nghĩa gì?
 Xem đáp án
Xem đáp án
Đọc đoạn [3] và xác định thông tin quan trọng: “từ khi “Make in Viet Nam” ra đời, số lượng doanh nghiệp số Việt Nam đã tăng trưởng cả về lượng và chất”; “tăng hơn 11,4 tỷ USD so với năm 2020”; “tăng trưởng trên 10% so với năm 2021”. Các số liệu đưa ra đều thể hiện sự tăng trưởng của các doanh nghiệp số từ khi “Make in Viet Nam” ra đời. Vậy Từ khóa đúng là D.
Chọn D
Câu 7:
Theo đoạn [4], chỉ tiêu số lượng doanh nghiệp công nghệ số vào năm 2025 tại Việt Nam đã hoàn thành sớm theo Nghị quyết số 52/2019. Đúng hay sai?
 Xem đáp án
Xem đáp án
Đọc đoạn [4] và xác định thông tin: “mục tiêu phát triển 100.000 doanh nghiệp công nghệ số Việt Nam theo Nghị quyết số 52/2019… đang dần trở thành hiện thực”; “Mục tiêu 100.000 doanh nghiệp công nghệ số vào năm 2030 hoàn toàn có thể đạt được trước năm 2025”. Chỉ tiêu đề ra đang dần được hoàn thành chứ chưa đạt được tại thời điểm hiện tại. Vậy nhận xét trên chưa chính xác.
Chọn B
Câu 8:
Theo lời phát biểu của Bộ trưởng Nguyễn Mạnh Hùng, yếu tố then chốt để Nghị quyết số 52/20219 của Bộ chính trị hoàn thành là gì?
 Xem đáp án
Xem đáp án
Căn cứ vào thông tin của đoạn [4], bộ trưởng Nguyễn Mạnh Hùng có chia sẻ: “những nhà quản lí đã không đánh giá hết sức mạnh của dân Việt Nam”, chọn A.
Câu 9:
Nhận định nào KHÔNG đúng với thông tin được nêu trong đoạn [5], [6]?
 Xem đáp án
Xem đáp án
HS đọc đoạn [5], [6], đọc các câu chủ đề nằm ở đầu đoạn: “Năm 2014, Thủ tướng Ấn Độ khởi xướng chính sách “Make in India” với hy vọng biến nước này trở thành công xưởng thứ 2 của thế giới sau Trung Quốc.” và “Trước đó, từ thập niên 1980, Trung Quốc đã cải cách mạnh mẽ và nhanh chóng vươn lên trở thành công xưởng của thế giới ở nhiều lĩnh vực.”, như vậy, Từ khóa A phù hợp với thông tin được nêu do thời điểm Trung Quốc bắt đầu cải cách được tính là “Trước đó” – trước Ấn Độ. Thành tựu của hai nước được đề cập trong câu: “thu hút được một lượng lớn vốn FDI” và “nhanh chóng vươn lên” nên Từ khóa B tương ứng với nội dung 2 đoạn. Căn cứ vào thông tin trong đoạn [6]: “…chương trình “Make in India” đã thu hút được một lượng lớn vốn FDI, trong đó có cả các nhà đầu tư đến từ đối thủ Trung Quốc (năm 2015, các nhà đầu tư Trung Quốc đã đầu tư vào Ấn Độ tăng gấp sáu lần so với năm 2014…)”, suy ra các Trung Quốc đã đầu tư vào Ấn Độ trong cả 2 năm 2014 và 2015, Từ khóa C tương ứng với nội dung trong bài. Như vậy, Từ khóa đúng trong câu là D.
Chọn D
Câu 10:
 Xem đáp án
Xem đáp án
HS đọc kĩ nội dung đoạn [6] và kết hợp với thông tin từ các câu hỏi để lựa chọn câu trả lời đúng: “Make in Viet Nam” - “trở thành động lực”, “trở thành nguồn cảm hứng”; Cộng đồng các doanh nghiệp số - “đưa hoạt động của người dân và doanh nghiệp lên môi trường số”, “thúc đẩy Chính phủ số, kinh tế số, xã hội số”, “trở thành trụ cột gánh vác nền kinh tế”. Xác định Từ khóa đúng là A, do khẩu hiệu – phong trào “Make in Viet Nam” đem lại hiệu quả về kinh tế, phát triển đất nước, từ đó, nhấn mạnh vai trò của các doanh nghiệp số.
Chọn A
Câu 11:
 Xem đáp án
Xem đáp án
Đọc nội dung nhan đề và phần Sapo đoạn [0], xác định nội dung “bất bình đẳng giới trở thành vấn đề nan giải, làm suy giảm lợi ích và là một dạng bất công trong xã hội”. Vậy mục đích của bài viết là trình bày ảnh hưởng của bất bình đẳng giới lên nền kinh tế.
Chọn A
Câu 12:
Hãy điền một cụm từ không quá ba tiếng để hoàn thành câu sau:
Để thúc đẩy kinh tế Việt Nam tăng trưởng, không chỉ dừng lại ở việc xây dựng các chiến lược, kế hoạch vĩ mô mà còn cần chú trọng tới vấn đề bình đẳng giới, đảm bảo tính (1) ______ trong mọi khía cạnh của đời sống xã hội.
 Xem đáp án
Xem đáp án
Đáp án
Để thúc đẩy kinh tế Việt Nam tăng trưởng, không chỉ dừng lại ở việc xây dựng các chiến lược, kế hoạch vĩ mô mà còn cần chú trọng tới vấn đề bình đẳng giới, đảm bảo tính (1) công bằng trong mọi khía cạnh của đời sống xã hội.
Giải thích
Căn cứ vào từ khóa “thúc đẩy kinh tế Việt Nam tăng trưởng” xác định nội dung cần tìm ở đoạn [1]: “bình đẳng giới vừa là mục tiêu, vừa là cơ sở thúc đẩy tăng trưởng kinh tế, xây dựng xã hội ổn định”. Xác định từ cần điền tương đương với “bình đẳng” là “công bằng”.
Câu 13:
 Xem đáp án
Xem đáp án
Đọc lại nội dung văn bản, kết hợp với phương pháp loại trừ, chú ý các thông tin quan trọng: “đạt mức tăng trưởng khá và ổn định”, “chuyển vị trí từ nhóm nước nghèo nhất sang nhóm nước có thu nhập trung bình thấp”, chọn A.
Câu 14:
 Xem đáp án
Xem đáp án
Đọc lại nội dung văn bản để xác định đúng ý nghĩa của từ: “nữ giới có xu hướng đầu tư cao hơn trong y tế và giáo dục cho con cái, tăng vốn nhân lực cho thế hệ tiếp theo và thúc đẩy tăng trưởng kinh tế”, từ đó cho thấy xu hướng: gia tăng các khoản đầu tư (tiền bạc, giáo dục chất lượng cao, kĩ năng…) vào con cái khi phụ nữ có thu nhập tốt hơn, chọn B.
Việc đầu tư phát triển cho con cái không đồng nhất với việc tìm kiếm cơ hội cạnh tranh trên thị trường lao động trong tương lai nên C, D không đúng.
Chọn B
Câu 15:
 Xem đáp án
Xem đáp án
Căn cứ vào từ khóa “mô hình kinh tế”, “phát triển bền vững và lâu dài” xác định nội dung cần tìm ở đoạn [3] và [4]: “bất bình đẳng giới còn liên quan tới vấn đề thu nhập của lao động”, “cần lưu tâm tới vấn đề tăng trưởng tức thời và sự phát triển bền vững, lâu dài”, “khoảng cách ở khía cạnh này sẽ dẫn tới khoảng cách giới ở một khía cạnh, lĩnh vực khác như một hệ quả kéo theo”. Để giúp nền kinh tế phát triển bền vững, lâu dài cần có giải pháp đồng bộ, chọn C.
Câu 16:
Theo đoạn [4] và [5], khoảng cách giới trong giáo dục có thể được giải quyết bằng cách tăng thu nhập cho nữ giới. Đúng hay sai?
 Xem đáp án
Xem đáp án
Đọc đoạn [4] xác định thông tin: “Khi tồn tại… khoảng cách thu nhập”, “có thể dẫn tới việc giảm nhu cầu đối với giáo dục cho nữ giới”, “dẫn tới khoảng cách về giới trong giáo dục”. Vậy thu nhập tác động đến khoảng cách giáo dục. Đoạn [5] có thông tin: “mức tăng trưởng về thu nhập thu hút nữ giới tham gia vào lực lượng lao động, giảm thiểu những rủi ro liên quan tới vấn đề chênh lệch giáo dục”. Việc tăng thu nhập cho nữ giới chỉ giúp giảm thiểu rủi ro chứ không giải quyết được vấn đề một cách triệt để. Nhận định trên không chính xác.
Chọn B
Câu 17:
Hãy điền một cụm từ không quá hai tiếng để hoàn thành nhận định sau:
Một trong những phương pháp để thúc đẩy kinh tế phát triển chính là đảm bảo yếu tố bình đẳng trong phân phối (1) _______, tạo động lực thu hút nữ giới tham gia vào thị trường lao động.
 Xem đáp án
Xem đáp án
Đáp án
Một trong những phương pháp để thúc đẩy kinh tế phát triển chính là đảm bảo yếu tố bình đẳng trong phân phối (1) thu nhập, tạo động lực thu hút nữ giới tham gia vào thị trường lao động.
Giải thích
Căn cứ vào từ khóa “thu hút nữ giới tham gia vào thị trường lao động” xác định nội dung cần tìm ở đoạn [5]: “mức tăng trưởng về thu nhập thu hút nữ giới tham gia vào lực lượng lao động”. Xác định được từ cần điền là “thu nhập” hoặc “tiền lương”.
Câu 18:
Hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí:
pháp luật, ổn định, văn hóa, tương trưởng, công bằng
Trong những nghiên cứu về _______ kinh tế, các mô hình đều chỉ ra vai trò của việc đảm bảo tính _______ trong xã hội, bất bình đẳng giới và những quan điểm _______ có thể trở thành rào cản cho sự phát triển chung của Quốc gia.
 Xem đáp án
Xem đáp án
Đáp án
Trong những nghiên cứu về tăng trưởng kinh tế, các mô hình đều chỉ ra vai trò của việc đảm bảo tính công bằng trong xã hội, bất bình đẳng giới và những quan điểm văn hóa có thể trở thành rào cản cho sự phát triển chung của Quốc gia.
Giải thích
Đọc lại nội dung văn bản, chú ý các thông tin quan trọng để xác định từ chính xác: “những công trình nghiên cứu vĩ mô chỉ ra rằng khoảng cách giới trong giáo dục tại Việt Nam có tác động đến tăng trưởng kinh tế”, “Những định kiến xã hội liên quan tới giới là yếu tố quan trọng”, “Cần tiếp tục đẩy mạnh việc bình đẳng giới”. Chú ý “công bằng” tương đương với “bình đẳng”; “quan điểm văn hóa” tương đương với “định kiến xã hội”.
Câu hoàn chỉnh: Trong những nghiên cứu về [tăng trưởng] kinh tế, các mô hình đều chỉ ra vai trò của việc đảm bảo tính [công bằng] trong xã hội, bất bình đẳng giới và những quan điểm [văn hóa] có thể trở thành rào cản cho sự phát triển chung của Quốc gia.
Câu 19:
Những quan điểm tiêu cực về nữ giới có thể gây ảnh hưởng đến hiệu quả lao động trong quá trình sản xuất. Đúng hay sai?
 Xem đáp án
Xem đáp án
Căn cứ vào từ khóa “những quan điểm tiêu cực về nữ giới” tương đương với “những định kiến xã hội liên quan tới giới” và “ảnh hưởng đến hiệu quả lao động” tương đương với “giảm năng suất” xác định được nội dung cần tìm ở đoạn [6]. Vậy nhận định trên là đúng.
Chọn BCâu 20:
Phần tư duy khoa học / giải quyết vấn đề
Phát biểu sau đây đúng hay sai?
Hai thí nghiệm trên, vi khuẩn đều được nuôi cấy trong môi trường nuôi cấy liên tục.
 Xem đáp án
Xem đáp án
Sai. Vì môi trường nuôi cấy liên tục phải luôn được bổ sung chất dinh dưỡng, đồng thời lấy đi lượng dịch nuôi cấy tương đương. Mà trong hai thí nghiệm trên thì không có sự bổ sung dinh dưỡng, cũng không lấy ra lượng dịch nuôi cấy nào, quần thể vi khuẩn phát triển trên môi trường dinh dưỡng ban đầu, cho đến khi sử dụng hết chất dinh dưỡng – đây là dạng nuôi cấy không liên tục.
Chọn B
Câu 21:
 Xem đáp án
Xem đáp án
Theo đoạn thông tin: “..., biết rằng độ đục càng tăng thì lượng vi khuẩn phát triển càng mạnh và giá trị đo được càng lớn.”
Chọn C
Câu 22:
 Xem đáp án
Xem đáp án
Nhóm 1 thí nghiệm trong điều kiện: pH = 6 với các nhiệt độ khác nhau.
Nhóm 2 thí nghiệm trong điều kiện: nhiệt độ 37℃ với độ pH khác nhau.
→ Nhóm vi khuẩn được nuôi cấy trong cùng điều kiện là có độ pH = 6 và nhiệt độ 37℃.
Chọn B
Câu 23:
Điền từ/cụm từ vào chỗ trống sau đây:
Khi cạn kiệt chất dinh dưỡng, vi khuẩn sẽ bắt đầu pha (1) ________.
 Xem đáp án
Xem đáp án
Đáp án
Điền từ/cụm từ vào chỗ trống sau đây:
Khi cạn kiệt chất dinh dưỡng, vi khuẩn sẽ bắt đầu pha (1) suy vong.
Giải thích
Trong môi trường nuôi cấy không liên tục, quần thể vi khuẩn sẽ trải qua 4 pha: tiềm phát, lũy thừa, cân bằng, suy vong. Khi cạn kiệt chất dinh dưỡng, vi khuẩn sẽ bắt đầu pha suy vong, làm cho số lượng vi khuẩn giảm xuống nhanh chóng.
Câu 24:
Ở giá trị pH nào quần thể vi khuẩn S. Aureus KHÔNG có sự sinh trưởng?
 Xem đáp án
Xem đáp án
Nhìn vào số liệu bảng 2, ta thấy tại môi trường dinh dưỡng có độ pH = 3 và pH = 9 thì không thấy sự thay đổi của giá trị độ đục ↔ không có sự sinh trưởng của quần thể vi khuẩn.
Chọn C
Câu 25:
 Xem đáp án
Xem đáp án
Nhìn vào số liệu bảng 1, ta thấy S. Aureus phát triển nhanh nhất để đạt độ đục cao nhất tại 37℃ (0,800) cao hơn nhiều so với các nhóm khác nên tại 37℃ chủng vi khuẩn này phát triển tối ưu.
Chọn B
Câu 26:
Phát biểu sau đây đúng hay sai?
Trong thí nghiệm của nhóm 1, ở nhiệt độ 37℃, pha cân bằng có thể bắt đầu sau 10 giờ kể từ khi nuôi cấy.
 Xem đáp án
Xem đáp án
Đúng. Nhìn vào số liệu bảng 1 ở nhiệt độ 37℃, ta thấy ở giai đoạn 600 phút (= 10 giờ) trở đi thì số lượng vi khuẩn có xu hướng chững lại, không tăng (duy trì ở mức cân bằng). Do lượng dinh dưỡng bắt đầu cạn kiệt, chất độc hại tích lũy nhiều, tỉ lệ vi khuẩn sinh ra cân bằng với tỉ lệ vi khuẩn chết đi.
Chọn A
Câu 27:
 Xem đáp án
Xem đáp án
Theo phần dẫn, ta có: Nước có thể tích xác định là do lực tương tác giữa các phân tử nước là lực hút.
Chọn B
Câu 28:
Khẳng định nào sau đây là đúng nhất về sự thay đổi được thể hiện trên đồ thị?
 Xem đáp án
Xem đáp án
Theo đồ thị, ta thấy tại nhiệt độ T1, mẫu (1) có động năng lớn hơn mẫu (2) nên mẫu (1) có số phân tử chuyển động nhiều hơn mẫu (2).
Chọn B
Câu 29:
Từ đồ thị có thể thấy, với các mẫu tại nhiệt độ T1 và T2 thì động năng cao nhất là ở nhiệt độ T2, đúng hay sai?
 Xem đáp án
Xem đáp án
Theo hình vẽ, tại nhiệt độ T1 thì ta thu được chỉ số động năng là cao nhất.
Chọn B
Câu 30:
Khi nhiệt độ trong nước tăng lên đến một giới hạn nào đó thì sẽ xảy ra quá trình chuyển pha từ chất lỏng sang (1) _______.
 Xem đáp án
Xem đáp án
Đáp án
Khi nhiệt độ trong nước tăng lên đến một giới hạn nào đó thì sẽ xảy ra quá trình chuyển pha từ chất lỏng sang (1) chất khí.
Giải thích
Theo đoạn thứ hai của phần dẫn: Khi nhiệt độ trong nước tăng lên thì lực liên kết giữa các phân tử giảm dẫn đến một số phân tử sẽ bay hơi và thoát khỏi dưới dạng khí.
Câu 31:
Các hạt (nguyên tử hoặc phân tử) của chất lỏng (1) ________ không ngừng. Vận tốc của một hạt là thước đo động năng của nó. Các phân tử (2) _______ càng nhanh thì động năng càng lớn.
 Xem đáp án
Xem đáp án
Đáp án
Các hạt (nguyên tử hoặc phân tử) của chất lỏng (1) chuyển động không ngừng. Vận tốc của một hạt là thước đo động năng của nó. Các phân tử (2) chuyển động càng nhanh thì động năng càng lớn.
Giải thích
Các hạt (nguyên tử hoặc phân tử) của chất lỏng chuyển động không ngừng. Vận tốc của một hạt là thước đo động năng của nó. Vận tốc càng nhanh thì động năng càng lớn.
Câu 32:
 Xem đáp án
Xem đáp án
Khi nước xảy ra quá trình chuyển pha từ thể lỏng sang thể khí thì:
+ khi nhiệt độ tăng dẫn đến động năng tăng.
+ Động năng tăng lên làm suy yếu lực hấp dẫn liên phân tử trong nước
+ Một số phân tử thoát ra khỏi chất lỏng dưới dạng khí.
Từ thông tin trên, ta thấy Từ khóa B,C và D sai
Chọn A
Câu 33:
 Xem đáp án
Xem đáp án
Ánh sáng khả kiến là các bức xạ điện từ có bước sóng nằm trong vùng quang phổ nhìn thấy được bằng mắt thường của con người.
Chọn D
Câu 34:
Dựa vào hình 1, cho biết bước sóng nào sau đây của ánh sáng khả kiến sẽ được hấp thụ để thúc đẩy hoạt động quang hợp mạnh nhất ở cây xanh?
 Xem đáp án
Xem đáp án
Nhìn vào hình 1, ta thấy ở bước sóng 440 nm, có sự hấp thụ lớn đối với cả 3 sắc tố quang hợp.
Chọn B
Câu 35:
Dựa vào thông tin được cung cấp trong hình 1 và bảng 1, cho biết phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Nhìn vào hình 1, ta thấy diệp lục a và diệp lục b có độ hấp thụ thấp nhất ở phần quang phổ từ 525 đến 625 nm, tương ứng với độ phản xạ lớn nhất.
Chọn C
Câu 36:
Điền từ thích hợp vào chỗ trống dưới đây
Sắc tố có độ hấp thụ cao nhất trong vùng ánh sáng đỏ của quang phổ là (1) ________.
 Xem đáp án
Xem đáp án
Đáp án
Sắc tố có độ hấp thụ cao nhất trong vùng ánh sáng đỏ của quang phổ là (1) chlorophyll a.
Giải thích
Ánh sáng đỏ có bước sóng 620 – 750 nm, nhìn vào hình 1, trong phạm vi bước sóng đó, diệp lục a có độ hấp thụ cao nhất.
Câu 37:
 Xem đáp án
Xem đáp án
Nhìn vào hình 1, ta thấy quang hợp xảy ra ở miền ánh sáng đỏ và miền ánh sáng xanh tím.
Chọn A
Câu 38:
Phát biểu sau đây đúng hay sai?
Màu xanh của lá cây mà mắt người có thể nhìn thấy được là vì diệp lục có khả năng hấp thụ tốt ánh sáng màu xanh lá của quang phổ khả kiến, đồng thời phản xạ lại môi trường ánh sáng đỏ và tím.
 Xem đáp án
Xem đáp án
Mắt người có khả năng nhìn thấy màu xanh của diệp lục vì ở vùng ánh sáng màu xanh lá của quang phổ khả kiến, diệp lục gần như không hấp thụ chúng và phản xạ toàn bộ lại môi trường, phản lại mắt ta khiến ta nhìn thấy lá có màu xanh.
Chọn B
Câu 39:
Phát biểu sau đây đúng hay sai?
Phản ứng với dung dịch NaOH chứng minh nhóm chức -OH phenol có lực axit mạnh hơn nhóm chức -OH ancol.
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 40:
Phát biểu sau đây đúng hay sai?
Salbutamol có tính chất hoá học của một phenol đơn chức.
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 41:
Salbutamol thể hiện tính bazơ của nhóm amin bậc 2 bằng phản ứng với (1) ________.
 Xem đáp án
Xem đáp án
Salbutamol thể hiện tính bazơ của nhóm amin bậc 2 bằng phản ứng với (1) axit HBr.
Câu 42:
Phát biểu sau đây đúng hay sai?
Cả ba nhóm -OH của salbutamol có những tính chất hoá học tương tự nhau.
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 43:
Một vận động viên thể thao có cân nặng 80 kg thì trong vòng 24 h chỉ được sử dụng liều tối đa là bao nhiêu μg salbutamol?
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 44:
Khi cho salbutamol tác dụng với HBr dư thu được hợp chất có công thức phân tử là
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 45:
Các phát biểu sau đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Salbutamol vừa có tính chất hoá học của một axit vừa có tính chất hoá học của một bazơ. |
||
|
Salbutamol tác dụng với NaOH theo tỷ lệ mol 1:3. |
||
|
Salbutamol tác dụng với Na theo tỷ lệ mol 1:3. |
||
|
Sản phẩm sau khi đã kiềm hoá (tác dụng với NaOH) của salbutamol sẽ phản ứng với HBr dư theo tỷ lệ mol 1:5. |
||
|
Hoạt tính sinh học của salbutamol được quyết định bởi nhóm chức amino. |
 Xem đáp án
Xem đáp án
|
Phát biểu |
Đúng |
Sai |
|
Salbutamol vừa có tính chất hoá học của một axit vừa có tính chất hoá học của một bazơ. |
X | |
|
Salbutamol tác dụng với NaOH theo tỷ lệ mol 1:3. |
X | |
|
Salbutamol tác dụng với Na theo tỷ lệ mol 1:3. |
X | |
|
Sản phẩm sau khi đã kiềm hoá (tác dụng với NaOH) của salbutamol sẽ phản ứng với HBr dư theo tỷ lệ mol 1:5. |
X | |
|
Hoạt tính sinh học của salbutamol được quyết định bởi nhóm chức amino. |
X |
Câu 46:
 Xem đáp án
Xem đáp án
Theo bảng màu cung cấp những dịch có môi trường acid (pH < 7) làm nước bắp cải tím chuyển sang màu đỏ, hồng hay tím. Đối chiếu với kết quả màu sắc trong bảng thì thấy có 3 mẫu dịch lỏng có môi trường acid là: giấm ăn, sữa, nước sprite.
Chọn A
Câu 47:
Dịch dạ dày có giá trị pH trong khoảng 1,0 – 2,0. Vậy nếu cho nước bắp cải tím vào dịch dạ dày thì dung dịch sẽ chuyển sang màu xanh. Kết luận trên là đúng hay sai?
 Xem đáp án
Xem đáp án
Dựa vào hình ở trên, với pH = 1,0 - 2,0 nước bắp cải tím sẽ chuyển sang màu đỏ. Do đó kết luận là sai.
Chọn B
Câu 48:
Bắp cải tím là chất chỉ thị acid – base tự nhiên vì trong dịch chiết bắp cải tím có chứa hợp chất (1) _______.
 Xem đáp án
Xem đáp án
Đáp án
Bắp cải tím là chất chỉ thị acid – base tự nhiên vì trong dịch chiết bắp cải tím có chứa hợp chất (1) Anthocyanin.
Giải thích
Học sinh tìm thấy thông tin ở dòng 9 của văn bản dẫn.
Câu 49:
nước lau bếp, giấm ăn, bakinh soda, nước sprite, nước tinh khiết, sữa
_______ > _______ > _______ > _______ > _______ > _______
 Xem đáp án
Xem đáp án
Đáp án
Nước lau bếp > Baking soda > Nước tinh khiết > Sữa > Nước sprite > Giấm ăn
Giải thích
Dựa vào thông tin trong bảng và hình ta có khoảng giá trị pH của các dịch lỏng: Nước lau bếp: pH = 10 - 12; Baking soda: pH = 8 - 9; Nước tinh khiết: pH = 7; Sữa: pH = 6; Nước sprite: pH = 4; Giấm ăn: pH = 2 - 3.
Câu 50:
Trộn 10,0 mL dung dịch HCl 0,05M với 10,0 mL dung dịch NaOH 0,03M thu được dung dịch A. Cho nước bắp cải tím vào dung dịch A thì dung dịch có màu (1) ______ do dung dịch A có pH bằng (2) _______.
 Xem đáp án
Xem đáp án
Đáp án
Trộn 10,0 mL dung dịch HCl 0,05M với 10,0 mL dung dịch NaOH 0,03M thu được dung dịch A. Cho nước bắp cải tím vào dung dịch A thì dung dịch có màu (1) _Đỏ_ do dung dịch A có pH bằng (2) _2_ .
Giải thích
Lý do lựa chọn phương án:
Số mol HCl = 0,5 mmol; số mol NaOH là 0,3 mmol;
HCl + NaOH = NaCl + H2O
Sau phản ứng HCl dư 0,2mmol; nồng độ HCl = 0,01M; pH = 2 do đó khi cho bắp cải tím vào dung dịch A dung dịch sẽ có màu đỏ.
Câu 51:
Phản ứng trung hòa là phản ứng giữa các dung dịch acid với các dung dịch base, dung dịch thu được chứa muối và nước và không còn tính acid, base. Trộn các cặp dịch lỏng: giấm ăn với baking soda; giấm ăn với nước sprite; giấm ăn với nước tinh khiết; giấm ăn với nước lau bếp. Giả sử nếu xảy ra phản ứng vừa đủ giữa các chất có tính acid và base trong dung dịch đem trộn thì số cặp dung dịch lỏng trung hòa được nhau là
 Xem đáp án
Xem đáp án
- Giấm ăn có môi trường acid sẽ có phản ứng trung hòa với những dung dịch có tính base.
- Dung dịch baking soda và nước lau bếp có môi trường base, nên sẽ xảy ra phản ứng trung hòa với giấm ăn.
- Nước sprite có môi trường acid nên không phản ứng với giấm ăn.
- Nước tinh khiết có môi trường trung tính không phản ứng với giấm ăn.
Chọn B
Câu 52:
tăng, tím hồng, đỏ, xanh lá cây, giảm, xanh nươc biển
Cho nước bắp cải tím vào dung dịch baking soda được dung dịch X có màu _______. Cho từ từ dung dịch giấm ăn vào dung dịch X thì màu của dung dịch X sẽ nhạt dần do xảy ra phản ứng trung hòa, giá trị pH của dung dịch _______ dần. Đến khi dư giấm ăn thì màu của dung dịch sẽ chuyển sang màu _______.
 Xem đáp án
Xem đáp án
Đáp án
Cho nước bắp cải tím vào dung dịch baking soda được dung dịch X có màu xanh nước biển. Cho từ từ dung dịch giấm ăn vào dung dịch X thì màu của dung dịch X sẽ nhạt dần do xảy ra phản ứng trung hòa, giá trị pH của dung dịch giảm dần. Đến khi dư giấm ăn thì màu của dung dịch sẽ chuyển sang màu đỏ.
Câu 53:
Virus nhận ra các tế bào chủ của nó theo nguyên tắc “chìa và khóa” nghĩa là
 Xem đáp án
Xem đáp án
Theo đoạn thông tin: “Virus nhận ra các tế bào chủ của nó theo nguyên tắc “chìa và khóa” giữa các protein bề mặt của virus với các phân tử thụ thể đặc hiệu trên bề mặt ngoài của tế bào chủ”, tức là không phải virus nào cũng xâm nhập được vào hết các loại tế bào, mà cần có sự liên kết đặc hiệu với tùy từng loại thụ thể trên bề mặt tế bào.
Chọn B
Câu 54:
lắp ráp, hấp thụ, xâm nhập, giải phóng, sinh tổng hợp
_______→ _______ → _______ → _______ → _______.
 Xem đáp án
Xem đáp án
Đáp án
Hấp phụ → Xâm nhập → Sinh tổng hợp → Lắp ráp → Giải phóng.
Giải thích
Theo đoạn thông tin, ta có thể sơ đồ hóa lại quá trình nhân lên của virus theo trình tự: Hấp phụ → Xâm nhập → Sinh tổng hợp → Lắp ráp → Giải phóng.
Câu 55:
Điều nào sau đây không đúng khi nói về virus?
 Xem đáp án
Xem đáp án
Theo bài: “Chúng là các dạng sống ký sinh nội bào bắt buộc”, sử dụng hệ enzyme của vật chủ để nhân lên, nên dù ở trong hay ngoài vật chủ thì virus đều không có sự sinh trưởng.
Chọn D
Câu 56:
Các virus cần tự mã hóa một số enzyme nhất định vì
 Xem đáp án
Xem đáp án
Virus cần tự mã hóa một số loại enzyme nhất định phục vụ cho nhu cầu nhân lên của chúng, do tế bào chủ không cần thiết phải có những enzyme đó trong quá trình hoạt động của mình.
Chọn A
Câu 57:
Điền số thích hợp vào chỗ trống
Cho các phương thức sau:
(1) Ức chế hoà màng/xâm nhập.
(2) Ức chế enzyme sao chép ngược.
(3) Ức chế protease.
(4) Ức chế sự tích hợp vật chất di truyền của virus.
Có (1) ______ phương thức phù hợp với việc sản xuất các loại thuốc để ức chế sự nhân lên của virus HIV.
 Xem đáp án
Xem đáp án
Đáp án: “4”
Giải thích
4 phương thức trên đều phù hợp:
Ức chế hòa màng/xâm nhập: ngăn chặn virus xâm nhập vào tế bào.
Ức chế enzyme sao chép ngược: không tạo đủ vật chất di truyền cho các thế hệ virus.
Ức chế protease: ức chế sự tổng hợp protein, lắp ráp các vật chất virus.
Ức chế sự tích hợp vật chất di truyền của virus: ngăn chặn virus gắn hệ gene vào hệ gene tế bào.
Câu 58:
Phát biểu sau đây đúng hay sai?
Thụ thể CD4 là thụ thể của virus HIV. Nếu đưa hồng cầu có thụ thể CD4 vào bệnh nhân HIV thì bệnh nhân sẽ thiếu máu nghiêm trọng vì virus sẽ xâm nhập và phá hủy tế bào.
 Xem đáp án
Xem đáp án
Thụ thể CD4 đặc hiệu với protein bề mặt của virus. Nếu đưa hồng cầu có thụ thể CD4 vào bệnh nhân HIV thì virus sẽ xâm nhập vào nhưng không nhân lên được do hồng cầu không có nhân, không có bộ máy sao chép nucleic acid.
Chọn B
Câu 59:
Các phát biểu sau đây đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Virus bám được vào tế bào chủ là nhờ các thụ thể thích hợp có sẵn trên bề mặt tế bào chủ. |
||
|
Kết quả của quá trình nhân lên là từ một virus ban đầu tạo ra vô số virus mới có độc tính tăng gấp nhiều lần. |
||
|
Virus sử dụng nguyên liệu của tế bào chủ trong quá trình nhân lên của mình. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Virus bám được vào tế bào chủ là nhờ các thụ thể thích hợp có sẵn trên bề mặt tế bào chủ. |
X | |
|
Kết quả của quá trình nhân lên là từ một virus ban đầu tạo ra vô số virus mới có độc tính tăng gấp nhiều lần. |
X | |
|
Virus sử dụng nguyên liệu của tế bào chủ trong quá trình nhân lên của mình. |
X |
Giải thích
(1), (3) đúng.
(2) sai vì kết quả của quá trình nhân lên là từ một virus ban đầu tạo ra vô số virus mới giống hệt nhau và giống virus ban đầu.
Câu 60:
 Xem đáp án
Xem đáp án
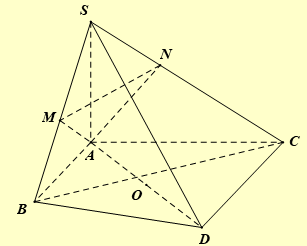
Kẻ đường kính \(AD\) của đường tròn ngoại tiếp tam giác \(ABC\) ta có \(\widehat {ABD} = \widehat {ACD} = {90^ \circ }\).
Khi đó \(\left\{ {\begin{array}{*{20}{l}}{BD \bot AB}\\{BD \bot SA}\end{array} \Rightarrow BD \bot \left( {SAB} \right)} \right.\) hay \(BD \bot AM\) và \(AM \bot SB\), từ đó ta có \(AM \bot \left( {SBD} \right) \Rightarrow AM \bot SD\).
Chứng minh tương tự ta có \(AN \bot SD\). Từ đó suy ra \(SD \bot \left( {AMN} \right)\), mà \(SA \bot \left( {ABC} \right)\).
Suy ra \(\left( {\left( {ABC} \right),\left( {AMN} \right)} \right) = \left( {SA,SD} \right) = \widehat {DSA}\).
Ta có \(BC = 2R{\rm{sin}}A = AD.\frac{{\sqrt 3 }}{2} \Rightarrow SA = 2BC = AD\sqrt 3 \).
Vậy tan \(\widehat {ASD} = \frac{{AD}}{{SA}} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {ASD} = {30^ \circ }\).
Chọn C
Câu 61:
Một bình chứa 75 viên bi gồm 35 viên bi màu xanh trong đó 25 viên bi đã từng được sử dụng và còn lại là bi đỏ trong đó có 30 viên bi đã từng được sử dụng.
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Có 190 cách chọn 2 viên bi khác màu chưa qua sử dụng. |
||
|
Có 30325 cách chọn 3 viên bi khác màu và có cả viên bi chưa sử dụng và đã qua sử dụng. |
||
|
Để xác suất chọn được một viên bi chưa qua sử dụng là \(\frac{2}{7}\) thì cần thêm vào bình 2 viên bi đã qua sử dụng. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Có 190 cách chọn 2 viên bi khác màu chưa qua sử dụng. |
X | |
|
Có 30325 cách chọn 3 viên bi khác màu và có cả viên bi chưa sử dụng và đã qua sử dụng. |
X | |
|
Để xác suất chọn được một viên bi chưa qua sử dụng là \(\frac{2}{7}\) thì cần thêm vào bình 2 viên bi đã qua sử dụng. |
X |
Số bi đỏ trong bình là \(75 - 35 = 40\) (viên bi) trong đó có \(40 - 30 = 10\) (viên bi) chưa qua sử dụng.
Số bi xanh trong bình chưa qua sử dụng là \(35 - 25 = 10\) (viên bi)
Vậy có \(C_{10}^1\).\(C_{10}^1 = 100\) cách chọn 2 viên bi khác màu chưa qua sử dụng.
Để chọn được 3 viên bi khác màu, ta xét các trường hợp sau:
TH1. 3 viên bi được chọn gồm 2 viên bi xanh và 1 viên bi đỏ có \(C_{35}^2.C_{40}^1\) cách chọn.
- Có \(C_{10}^2\).\(C_{10}^1\) cách chọn 3 viên bi gồm 2 viên bi xanh và 1 viên bi đỏ đều chưa qua sử dụng.
- Có \(C_{25}^2\).\(C_{30}^1\) cách chọn 3 viên bi gồm 2 viên bi xanh và 1 viên bi đỏ đều đã qua sử dụng.
\( \Rightarrow \) Có \(C_{35}^2.C_{40}^1 - \left( {C_{10}^2.C_{10}^1 + C_{25}^2.C_{30}^1} \right) = 14350\) cách chọn 3 viên bi (gồm 2 viên bi xanh, 1 viên bi đỏ) và có cả viên bi chưa sử dụng và đã qua sử dụng.
TH2. 3 viên bi được chọn gồm 1 viên bi xanh và 2 viên bi đỏ có \(C_{35}^1.C_{40}^2\) cách chọn.
- Có \(C_{10}^1\).\(C_{10}^2\) cách chọn 3 viên bi gồm 1 viên bi xanh và 2 viên bi đỏ đều chưa qua sử dụng.
- Có \(C_{25}^1\).\(C_{30}^2\) cách chọn 3 viên bi gồm 1 viên bi xanh và 2 viên bi đỏ đều đã qua sử dụng.
\( \Rightarrow \) Có \(C_{35}^1.C_{40}^2 - \left( {C_{10}^1.C_{10}^2 + C_{25}^1.C_{30}^2} \right) = 15975\) cách chọn 3 viên bi (gồm 1 viên bi xanh, 2 viên bi đỏ) và có cả viên bi chưa sử dụng và đã qua sử dụng.
Vậy có \(14350 + 15975 = 30325\) cách chọn 3 viên bi khác màu và có cả viên bi chưa sử dụng và đã qua sử dụng.
Khi thêm 2 viên bi đã qua sử dụng vào bình thì xác suất để chọn được một viên bi chưa qua sử dụng là: \(P = \frac{{C_{10}^1 + 10}}{{C_{75}^1 + 2}} = \frac{{20}}{{77}} \ne \frac{2}{7}\).
Câu 62:
Hai số \({2^{2023}}\) và \({5^{2023}}\) viết liền nhau tạo thành một số có (1) ______ chữ số.
 Xem đáp án
Xem đáp án
Đáp số: “2024”
Giải thích
Giả sử \({2^{2023}}\) có \(m\) chữ số và \({5^{2023}}\) có \(n\) chữ số. Khi đó hai số \({2^{2023}}\) và \({5^{2023}}\) viết liền nhau tạo thành một số có \(m + n\) chữ số.
Vì \({2^{2023}}\) có \(m\) chữ số nên \({10^{m - 1}} < {2^{2023}} < {10^m}\left( 1 \right)\).
Vì \({5^{2023}}\) có \(n\) chữ số nên \({10^{n - 1}} < {5^{2023}} < {10^n}\left( 2 \right)\).
Nhân từng vế của (1) và (2) ta được: \({10^{m + n - 2}} < {10^{2023}} < {10^{m + n}} \Leftrightarrow m + n - 2 < 2023 < m + n\)
Mà \(m,n \in \mathbb{N}\) nên \(m + n - 1 = 2023 \Leftrightarrow m + n = 2024\).
Câu 63:
Khi đường kính khối cầu giảm đi 2 lần thì thể tích khối cầu giảm đi (1) _______ lần.
 Xem đáp án
Xem đáp án
Đáp án: “8”
Giải thích
Gọi bán kính khối cầu là \(r\) thì đường kính khối cầu là \(2r\).
Thể tích ban đầu của khối cầu là \(V = \frac{4}{3}\pi {r^3}\).
Khi đường kính khối cầu giảm đi 2 lần thì bán kính khối cầu là \(\frac{r}{2}\).
Thể tích của khối cầu sau khi giảm là \(V' = \frac{4}{3}\pi {\left( {\frac{r}{2}} \right)^3} = \frac{1}{8}.\frac{4}{3}\pi {r^2} = \frac{1}{8}V\).
Vậy thể tích khối cầu giảm đi 8 lần.
Câu 64:
Cho một cấp số nhân có 3 số hạng đầu tiên theo thứ tự là \(x + 4;6;x - 5\) (với \(x < 6\)).

Giá trị của \(x\) bằng _______.
Số hạng thứ 8 của cấp số nhân trên là _______.
Tổng của 10 số hạng đầu của cấp số nhân trên bằng _______.
 Xem đáp án
Xem đáp án
Đáp án
Giá trị của \(x\) bằng -7.
Số hạng thứ 8 của cấp số nhân trên là 384.
Tổng của 10 số hạng đầu của cấp số nhân trên bằng 1023.
Giải thích
Ba số \(x + 4;6;x - 5\) theo thứ tự lập thành một cấp số nhân
\( \Leftrightarrow \left( {x + 4} \right)\left( {x - 5} \right) = {6^2} \Leftrightarrow {x^2} - x - 56 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 8\left( L \right)}\\{x = - 7\left( {tm} \right)}\end{array}} \right.\)
Vậy 3 số hạng đầu tiên của cấp số nhân là \( - 3;6; - 12\), công bội là \(q = 6:\left( { - 3} \right) = - 2\).
Số hạng thứ 8 là \({u_8} = {u_1}.{q^7} = \left( { - 3} \right).{( - 2)^7} = 384\).
Tổng 10 số hạng đầu là \({S_{10}} = \frac{{{u_1}\left( {1 - {q^{10}}} \right)}}{{1 - q}} = \frac{{ - 3.\left( {1 - {{( - 2)}^{10}}} \right)}}{{1 - \left( { - 2} \right)}} = 1023\).
Câu 65:
 Xem đáp án
Xem đáp án
Giải thích
Phương trình đã cho tương đương với:
\(\left( {m - 1} \right){\rm{log}}_3^2\left( {x - 1} \right) + m{\rm{lo}}{{\rm{g}}_3}\left( {x - 1} \right) - 5m + 3 = 0\) (1).
Đặt \({\rm{lo}}{{\rm{g}}_3}\left( {x - 1} \right) = t\). Do \(x \in \left[ {10;82} \right]\) suy ra \(t \in \left[ {2;4} \right]\).
Phương trình (1) trở thành: \(\left( {m - 1} \right){t^2} + mt - 5m + 3 = 0,t \in \left[ {2;4} \right]\) (2)
\( \Leftrightarrow m = \frac{{{t^2} - 3}}{{{t^2} + t - 5}} = f\left( t \right)\left( {} \right.\) vì \(t \in \left[ {2;4} \right]\) nên \(\left. {{t^2} + t - 5 \ne 0} \right)\)
\(f'\left( t \right) = \frac{{{t^2} - 4t + 3}}{{{{\left( {{t^2} + t - 5} \right)}^2}}},f'\left( t \right) = 0 \Leftrightarrow \frac{{{t^2} - 4t + 3}}{{{{\left( {{t^2} + t - 5} \right)}^2}}} = 0 \Leftrightarrow t = 3(\)vì \(t \in \left[ {2;4} \right]\)).
\(f\left( t \right)\) luôn xác định với mọi \(t \in \left[ {2;4} \right]\).
Ta có: \(f\left( 2 \right) = 1,f\left( 3 \right) = \frac{6}{7},f\left( 4 \right) = \frac{{13}}{{15}}\).
Do đó \(\mathop {{\rm{min}}}\limits_{\left[ {2;4} \right]} f\left( t \right) = f\left( 3 \right) = \frac{6}{7},\mathop {{\rm{max}}}\limits_{\left[ {2;4} \right]} f\left( t \right) = f\left( 2 \right) = 1\).
Phương trình đã cho có nghiệm thuộc đoạn \(\left[ {10;82} \right]\) khi phương trình (2) có nghiệm \(t \in \left[ {2;4} \right]\) nên với
\(m \in \left[ {\frac{6}{7};1} \right]\) thì phương trình đã cho có nghiệm thuộc đoạn \(\left[ {10;82} \right]\). Mà \(m\) là số nguyên nên \(m = 1\).
Chọn D
Câu 66:
Hải có một tấm bìa hình tròn như hình vẽ, Hải muốn biến hình tròn đó thành một hình cái phễu hình nón. Khi đó Hải phải cắt bỏ hình quạt tròn \(AOB\) rồi dán hai bán kính \(OA\) và \(OB\) lại với nhau (diện tích mép dán không đáng kể). Gọi \(x\) là góc ở tâm hình quạt tròn dùng làm phễu. Để thể tích phễu lớn nhất thì \(x\) gần bằng (1) ________o (kết quả làm tròn đến hàng đơn vị).
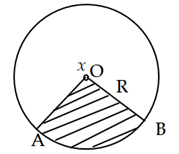
 Xem đáp án
Xem đáp án
Đáp án: “294”
Giải thích
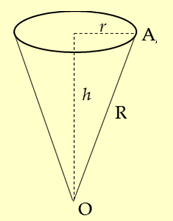
Bán kính \(R\) của hình tròn ban đầu chính là đường sinh của hình nón.
Độ dài cung lớn \(AB\) chính là chu vi của đường tròn đáy hình nón và bằng . Vậy bán kính đáy của hình nón là .
Khi đó thể tích phễu hình nón là
\(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi \frac{{{R^2}{x^2}}}{{{{360}^2}}}\sqrt {{R^2} - {{\left( {\frac{{Rx}}{{360}}} \right)}^2}} = \frac{{{R^3}{x^2}\pi }}{{{{3.360}^3}}}\sqrt {{{360}^2} - {x^2}} \).
Yêu cầu bài toán trở thành tìm giá trị lớn nhất của \(V\) với \(x \in \left( {0;360} \right)\).
Ta có \(V = \frac{{{R^3}{x^2}\pi }}{{{{3.360}^3}}}\sqrt {{{360}^2} - {x^2}} = \frac{{{R^3}\pi }}{{3\sqrt 2 {{.360}^3}}}\sqrt {{x^4}\left( {{{2.360}^2} - 2{x^2}} \right)} \).
Áp dụng bất đẳng thức Cauchy: \({x^2}{x^2}\left( {{{2.360}^2} - 2{x^2}} \right) \le {\left( {\frac{{{x^2} + {x^2} + {{2.360}^2} - 2{x^2}}}{3}} \right)^3} = \frac{{{{8.360}^6}}}{{27}}\).
Suy ra \(V \le \frac{{{R^3}\pi }}{{3\sqrt 2 {{.360}^3}}}.\frac{{2\sqrt 2 }}{{3\sqrt 3 }}{360^3} = \frac{{2\sqrt 3 {R^3}\pi }}{{27}}\).
Dấu bằng xảy ra khi \({x^2} = {2.360^2} - 2{x^2} \Leftrightarrow x = \frac{{360\sqrt 6 }}{3} \approx {294^ \circ }\).
Câu 67:
 Xem đáp án
Xem đáp án
Giải thích
Số các số thuộc \(M\) là \(A_5^3 + A_5^4 + A_5^5 = 300\).
Các tập con của \(E\) có tổng các phần tử bằng 10 gồm \({E_1} = \left\{ {1;2;3;4} \right\},{E_2} = \left\{ {2;3;5} \right\},{E_3} = \left\{ {1;4;5} \right\}\).
Gọi \(A\) là tập con của \(M\) sao cho mỗi số thuộc \(A\) có tổng các chữ số bằng 10 .
Từ \({E_1}\) lập được số các số thuộc \(A\) là 4!.
Từ mỗi tập \({E_2}\) và \({E_3}\) lập được các số thuộc \(A\) là 3!.
Suy ra số phần tử của \(A\) là \(4! + 2.3! = 36\).
Xác suất cần tìm là \(P = \frac{{36}}{{300}} = \frac{3}{{25}}\).
Chọn B
Câu 68:
 Xem đáp án
Xem đáp án
Giải thích
Gọi \(I\left( {x;y;z} \right)\) là tâm mặt cầu \(\left( S \right)\) đi qua 3 điểm \(A,B,C\).
Ta có: \[IA = IB = IC \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{I{A^2} = I{B^2}}\\{I{B^2} = I{C^2}}\end{array}} \right.\]
\( \Leftrightarrow \left\{ \begin{array}{l}{(x - 1)^2} + {y^2} + {z^2} = {(x - 2)^2} + {y^2} + {(z - 1)^2}\\{(x - 2)^2} + {y^2} + {(z - 1)^2} = {(x - 1)^2} + {(y - 1)^2} + {(z - 1)^2}\end{array} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 2x + 1 = - 4x + 4 - 2z + 1}\\{ - 4x + 4 = - 2x + 1 - 2y + 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x + z = 2}\\{x - y = 1}\end{array}} \right.} \right.\)
Vì \(I \in \left( P \right)\) nên ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{r}}{x + z = 2}\\{x - y = 1}\\{x + y + z - 6 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 5}\\{y = 4}\\{z = - 3}\end{array} \Rightarrow I\left( {5;4; - 3} \right)} \right.} \right.\)
Bán kính của mặt cầu \(\left( S \right)\) là \(R = IA = \sqrt {41} \)
\( \Rightarrow \left( S \right):{(x - 5)^2} + {(y - 4)^2} + {(z + 3)^2} = 41\).
Chọn B
Câu 69:
 Xem đáp án
Xem đáp án
Giải thích
Ta có \(f'\left( x \right) = {x^3}{(x - 1)^2}\left( {x - 2} \right)\) do đó \(f'\left( x \right) = 0\) tại các điểm \(x = 0\) (nghiệm bội ba), \(x = 1\) (nghiệm bội hai) và \(x = 2\) (nghiệm đơn).
Ta có bảng xét dấu:

Chọn A
Câu 70:
 Xem đáp án
Xem đáp án
Giải thích
Tổng số điểm vừa lấy bằng: \(3 + 4 + 5 + 6 = 18\) (điểm).
Mỗi cách chọn ra 3 điểm không nằm trên một cạnh cho ta một tam giác.
Số cách chọn 3 điểm từ 18 điểm là: \(C_{18}^3 = 816\) (cách chọn).
Số cách chọn 3 điểm cùng nằm trên một cạnh là: \(C_3^3 + C_4^3 + C_5^3 + C_6^3 = 35\) (cách chọn).
Vậy số tam giác cần tìm bằng: \(816 - 35 = 781\) (tam giác).
Chọn D
Câu 71:
Cho khối nón \(\left( S \right)\) có bán kính đáy bằng 3 . Cắt hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác vuông cân.
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
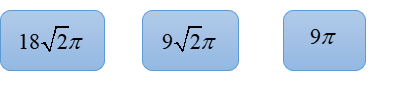
Diện tích xung quanh của hình nón \(\left( S \right)\) bằng ______.
Thể tích của khối nón \(\left( S \right)\) bằng ______.
 Xem đáp án
Xem đáp án
Đáp án
Diện tích xung quanh của hình nón \(\left( S \right)\) bằng \(9\sqrt 2 \pi \).
Thể tích của khối nón \(\left( S \right)\) bằng \(9\pi \).
Giải thích
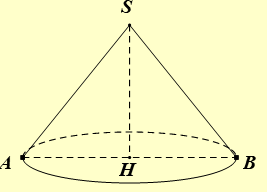
Giả sử ta có khối nón \(\left( S \right)\) như hình vẽ.
Vì vuông cân nên
+)\(h = SH = HA = HB = R = 3\);
+),\(l = SA = SB = \frac{{AB}}{{\sqrt 2 }} = \frac{{2R}}{{\sqrt 2 }} = 3\sqrt 2 \).
Vậy:
+) Diện tích xung quanh của hình nón \(\left( S \right)\) là: \({S_{xq}} = \pi Rl = 9\sqrt 2 \pi \).
+) Thể tích của khối nón \(\left( S \right)\) là: \(V = \frac{1}{3}\pi {R^2}h = 9\pi \).
Câu 72:
 Xem đáp án
Xem đáp án
Giải thích
Ta có: \({x^2} + 2{y^2} - 1 = {\rm{ln}}\left( {\frac{{1 - {y^2}}}{{{x^2} + {y^2}}}} \right)\)
\( \Leftrightarrow {\rm{ln}}\left( {1 - {y^2}} \right) + \left( {1 - {y^2}} \right) = {\rm{ln}}\left( {{x^2} + {y^2}} \right) + \left( {{x^2} + {y^2}} \right)\left( 1 \right)\)
Xét hàm số \(f\left( x \right) = {\rm{ln}}x + x{\rm{\;}}(x > 0)\).
Ta có: \(f'\left( x \right) = \frac{1}{x} + 1 > 0,\forall x > 0 \Rightarrow f\left( x \right)\) luôn đồng biến trên \(\left( {0; + \infty } \right)\) (2).
Theo (1) ta có: \(f\left( {1 - {y^2}} \right) = f\left( {{x^2} + {y^2}} \right)\) kết hợp với (2) suy ra \(1 - {y^2} = {x^2} + {y^2} \Leftrightarrow {x^2} + 2{y^2} = 1\).
Sử dụng bất đẳng thức \({\rm{AM}} - {\rm{GM}}\) đối với các số dương, ta có:
\(\frac{{{x^4}}}{{{x^2}.{y^2}.{y^2}}} \ge \frac{{{x^4}}}{{\frac{{{{\left( {{x^2} + {y^2} + {y^2}} \right)}^3}}}{{27}}}} = \frac{{{x^4}}}{{\frac{1}{{27}}}} \Rightarrow \frac{{{x^2}}}{{{y^4}}} \ge 27{x^4} \Rightarrow \frac{x}{{{y^2}}} \ge 3\sqrt 3 {x^2}\).
\(\frac{{16{y^4}}}{{2{y^2}.\left( {{x^2} + {y^2}} \right).\left( {{x^2} + {y^2}} \right)}} \ge \frac{{16{y^4}}}{{\frac{{{{\left( {2{y^2} + {x^2} + {x^2} + {y^2} + {y^2}} \right)}^3}}}{{27}}}} = \frac{{16{y^4}}}{{\frac{{{2^3}}}{{27}}}} \Rightarrow \frac{{16{y^2}}}{{{{\left( {{x^2} + {y^2}} \right)}^2}}} \ge 54{y^4} \Rightarrow \frac{{4y}}{{{x^2} + {y^2}}} \ge 3\sqrt 6 {y^2}\)
\( \Rightarrow \frac{x}{{{y^2}}} + \sqrt 2 .\frac{{4y}}{{{x^2} + {y^2}}} \ge 3\sqrt 3 {x^2} + 6\sqrt 3 {y^2}\)
\( \Leftrightarrow P \ge 3\sqrt 3 \left( {{x^2} + 2{y^2}} \right) = 3\sqrt 3 = 1.\sqrt {27} \).
Vậy có 2 bộ số \(\left( {m;n} \right)\) thỏa mãn.
Chọn C
Câu 73:
 Xem đáp án
Xem đáp án
Giải thích
Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y = \frac{{1 - m{\rm{sin}}x}}{{{\rm{cos}}x + 2}} \Leftrightarrow y{\rm{cos}}x + m{\rm{sin}}x = 1 - 2y\).
Phương trình có nghiệm khi và chỉ khi: \({y^2} + {m^2} \ge 1 - 4y + 4{y^2} \Leftrightarrow 3{y^2} - 4y + 1 - {m^2} \le 0\)
\( \Leftrightarrow \frac{{2 - \sqrt {1 + 3{m^2}} }}{3} \le y \le \frac{{2 + \sqrt {1 + 3{m^2}} }}{3}\).
Theo đề bài, ta có: \[\left\{ {\begin{array}{*{20}{l}}{\mathop {\min }\limits_{x \in \mathbb{R}} y = \frac{{2 - \sqrt {1 + 3{m^2}} }}{3} < - 2}\\{m \in [0;10]}\\{m \in \mathbb{Z}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\sqrt {1 + 3{m^2}} > 8}\\{m \in [0;10]}\\{m \in \mathbb{Z}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3{m^2} > 63}\\{m \in [0;10]}\\{m \in \mathbb{Z}}\end{array}} \right.} \right.} \right.\]
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{m^2} > 21}\\{m \in [0;10]}\\{m \in \mathbb{Z}}\end{array}} \right.\)
\( \Leftrightarrow m \in \left\{ {5,6,7,8,9,10} \right\}\).
Vậy có 6 giá trị nguyên của tham số \(m\) thỏa mãn yêu cầu bài toán.
Chọn D
Câu 74:
 Xem đáp án
Xem đáp án
Giải thích
Gọi \(x\) là số hạng thứ ba của cấp số cộng đã cho với công sai \(d\) khác 0 .
Theo đề bài ta có: \(x - 2d,x,x - d\) theo thứ tự lập thành một cấp số nhân có công bội \(q\).
\( \Rightarrow {x^2} = \left( {x - d} \right)\left( {x - 2d} \right) \Leftrightarrow 3dx - 2{d^2} = 0 \Leftrightarrow d\left( {3x - 2d} \right) = 0 \Leftrightarrow d = \frac{3}{2}x\) (vì \(d \ne 0\))
Mặt khác: \(x = \left( {x - 2d} \right).q \Leftrightarrow x = \left( {x - 3x} \right).q \Leftrightarrow x = - 2xq \Leftrightarrow q = - \frac{1}{2}\).
Chọn B
Câu 75:
Cho một lưới ô vuông \(4 \times 4\). Điền vào mỗi ô vuông một trong hai số 1 hoặc -1 sao cho tổng các số trong mỗi hàng và tổng các số trong mỗi cột đều bằng 0 . Có (1) ________ cách điền như vậy.
 Xem đáp án
Xem đáp án
Đáp án: “90”
Giải thích
Để tổng các số trong mỗi hàng và tổng các số trong mỗi cột đều bằng 0 thì trên mỗi hàng, mỗi cột phải có hai số 1 và hai số -1 .
Ta sẽ xếp theo hàng.
Ta có các khả năng của các hàng như sau:
(1) \(1,1, - 1, - 1\)
(2) \( - 1, - 1,1,1\)
(3) \(1, - 1, - 1,1\)
(4) \( - 1,1,1, - 1\)
(5) \( - 1,1, - 1,1\)
(6) \(1, - 1,1, - 1\)
Hàng 1 ta điền một hàng bất kì, giả sử hàng 1 ta điền bộ (1). Ta có các trường hợp sau:
TH1. Hàng 2 điền bộ (1), khi đó hàng 3 , hàng 4 ta phải điền bộ (2).
TH2. Hàng 2 điền bộ để tổng 2 số trong tất cả các cột của hàng 1 và 2 bằng 0 , khi đó ta điền bộ (2). Hàng 3 và hàng 4 khi đó cũng phải điền sao cho tổng các cột trong hai hàng bằng 0 . Ta có \(6.1 = 6\) cách điền như vậy.
TH3. Hàng 2 điền bộ để tổng 2 cột trong 4 cột của hàng 1 và 2 bằng 0 . Ta có 4 cách điền (trừ bộ (1), (2)). Khi đó điền hàng 3 có 2 cách, điền hàng 4 có 1 cách.
Vậy có \(6.\left( {1 + 6 + 4.2.1} \right) = 90\) cách.
Câu 76:
 Xem đáp án
Xem đáp án
Giải thích
Điều kiện \(x > 0\).
\({\rm{lo}}{{\rm{g}}_2}\left( {{3^{{\rm{lo}}{{\rm{g}}_6}x}} + x} \right) = \frac{1}{2}{\rm{lo}}{{\rm{g}}_6}{x^2}\)
\( \Leftrightarrow {\rm{lo}}{{\rm{g}}_2}\left( {{3^{{\rm{lo}}{{\rm{g}}_6}x}} + x} \right) = {\rm{lo}}{{\rm{g}}_6}x\).
Đặt \(t = {\rm{lo}}{{\rm{g}}_6}x \Rightarrow x = {6^t}\) ta được phương trình
\({\rm{lo}}{{\rm{g}}_2}\left( {{3^t} + {6^t}} \right) = t \Leftrightarrow {3^t} + {6^t} = {2^t} \Leftrightarrow {\left( {\frac{3}{2}} \right)^t} + {3^t} = 1{\rm{\;}}\left( {\rm{*}} \right)\).
Xét hàm số \(f\left( t \right) = {\left( {\frac{3}{2}} \right)^t} + {3^t}\)
\(f'\left( t \right) = {\left( {\frac{3}{2}} \right)^t}{\rm{ln}}\frac{3}{2} + {3^t}{\rm{ln}}3 > 0\forall t \in \mathbb{R} \Rightarrow f\left( t \right)\) đồng biến trên \(\mathbb{R}\)
Phương trình \(\left( {\rm{*}} \right)\) trở thành \(f\left( t \right) = f\left( { - 1} \right)\) mà \(f\left( t \right)\) đồng biến trên \(\mathbb{R}\) nên \(\left( {\rm{*}} \right)\) có nghiệm duy nhất \(t = - 1\).
Suy ra phương trình đã cho có nghiệm \(x = {6^{ - 1}} = \frac{1}{6}\).
Chọn B
Câu 77:
 Xem đáp án
Xem đáp án
Giải thích
Đạo hàm hai vế \(f\left( x \right)\) ta có:
\(3n{(1 + 3x)^{n - 1}} = {a_1} + 2{a_2}x + \ldots + n{a_n}{x^{n - 1}}\)
\( \Rightarrow f'\left( 1 \right) = 3n{.4^{n - 1}} = {a_1} + 2{a_2} + \cdots + n{a_n} = 49152n \Rightarrow {4^{n - 1}} = 16384 \Leftrightarrow n = 8\)
Số hạng tổng quát thứ \(k + 1\) trong khai triển thành đa thức của \({(1 + 3x)^8}\) là \({T_{k + 1}} = C_8^k{3^k}{x^k}\)
\( \Rightarrow {a_3} = C_8^3{3^3} = 1512\).
Chọn D
Câu 78:
Một du khách vào hội chợ và chơi trò chơi ném vòng trúng thưởng. Lần đầu du khách mua 1 lượt ném vòng với giá 1000 đồng, kể từ lần sau tiền mua số lượt ném vòng gấp đôi số tiền lần trước. Người đó thua 10 lần liên tiếp và thắng ở 2 lần cuối. Biết mỗi lần thắng, giá trị phần thưởng của người chơi nhận được gấp đôi số tiền mua ban đầu (không kể số tiền đã đặt). Giá trị phần thưởng cuối cùng người đó nhận được là (1) ________ đồng.
 Xem đáp án
Xem đáp án
Đáp án: “5121000”
Giải thích
Số tiền mỗi lần du khách mua số lượt ném vòng là một số hạng của một cấp số nhân có \({u_1} = 1000\) và công bội \(q = 2\).
Du khách thua trong 10 lần đầu tiên nên tổng số tiền du khách đã bỏ ra mua lượt ném vòng là
\({S_{10}} = {u_1} + {u_2} + \ldots + {u_{10}} = \frac{{{u_1}\left( {1 - {q^{10}}} \right)}}{{1 - q}} = 1023000\) (đồng).
Giá trị phần thưởng mà du khách thắng trong 2 lần cuối (lần thứ 11 và 12) là
\(2{u_{11}} + 2{u_{12}} = 2{u_1}\left( {{q^{10}} + {q^{11}}} \right) = 6144000\) (đồng).
Ta có \(2{u_{11}} + 2{u_{12}} - {S_{10}} = 5121000\) nên du khách nhận được 5121000 đồng.
Câu 79:
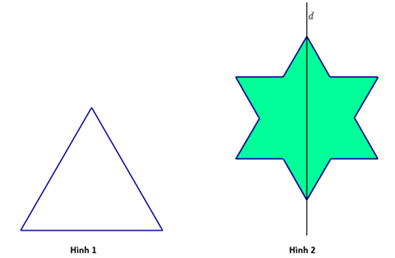
Cho một tam giác đều cạnh bằng 3 (hình 1). Chia mỗi cạnh của tam giác thành 3 đoạn bằng nhau và thay mỗi đoạn ở giữa bằng hai đoạn bằng nó sao cho chúng tạo với đoạn bỏ đi một tam giác đều về phía bên ngoài ta được hình 2.
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau
Diện tích của hình 2 bằng _______.
Thể tích khối tròn xoay khi quay hình 2 xung quanh trục \(d\) là _______ \(\pi \).
 Xem đáp án
Xem đáp án
Đáp án
Diện tích của hình 2 bằng \(3\sqrt 3 \).
Thể tích khối tròn xoay khi quay hình 2 xung quanh trục \(d\) là \(\frac{{5\sqrt 3 }}{3}\)\(\pi \).
Giải thích
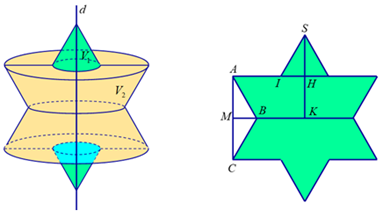
Diện tích của hình 2 bằng tổng diện tích của tam giác đều (hình 1) và 3 tam giác đều cạnh bằng 1 được vẽ thêm. \( \Rightarrow \) Diện tích hình 2 bằng: \(S = \frac{{{3^2}\sqrt 3 }}{4} + 3.\frac{{{1^2}\sqrt 3 }}{4} = 3\sqrt 3 \).
Ta có thể tích khối tròn xoay tạo thành bằng 2 lần thể tích nửa trên khi cho hình \(SIABK\) quay quanh trục \(SK\).
Tam giác \(SIH\) quay quanh trục \(SK\) tạo thành khối nón có \({r_1} = IH = \frac{1}{2};{h_1} = SH = \frac{{\sqrt 3 }}{2}\).
Thể tích khối nón này bằng \({V_1} = \frac{1}{3}\pi {r_1}{\;^2}{h_1} = \frac{1}{3}\pi .\frac{1}{4}.\frac{{\sqrt 3 }}{2} = \frac{{\sqrt 3 \pi }}{{24}}\)
Hình thang vuông \(HABK\) quay quanh trục \(HK\) tạo thành hình nón cụt có \(R = AH = \frac{3}{2};r = BK = 1\);
\(h = HK = SH = \frac{{\sqrt 3 }}{2}\).
Thể tích khối nón cụt này bằng \({V_2} = \frac{{\pi h}}{3}.\left( {{R^2} + {r^2} + R.r} \right) = \frac{\pi }{3}.\frac{{\sqrt 3 }}{2}\left( {\frac{9}{4} + 1 + \frac{3}{2}} \right) = \frac{{19\pi \sqrt 3 }}{{24}}\).
Suy ra thể tích khối tròn xoay đã cho bằng \(V = 2\left( {{V_1} + {V_2}} \right) = \frac{{5\sqrt 3 \pi }}{3}\).
Câu 80:
 Xem đáp án
Xem đáp án
Giải thích
Cách 1:
Từ giả thiết suy ra \(f\left( {1 - x} \right) + \frac{2}{{{x^2}}}f\left( {\frac{{2x - 2}}{x}} \right) = \frac{{ - {x^4} + {x^3} + 4x - 4}}{{{x^3}}}\)
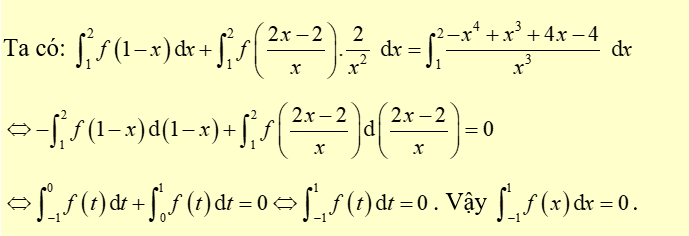
Cách 2:
Ta có: \({x^2}f\left( {1 - x} \right) + 2f\left( {\frac{{2x - 2}}{x}} \right) = \frac{{ - {x^4} + {x^3} + 4x - 4}}{x},\forall x \ne 0,x \ne 1\)
\( \Leftrightarrow {x^2}f\left( {1 - x} \right) + 2f\left( {\frac{{2x - 2}}{x}} \right) = \frac{{ - {x^4} + {x^3}}}{x} + \frac{{4x - 4}}{x},\forall x \ne 0,x \ne 1\)
\( \Leftrightarrow {x^2}f\left( {1 - x} \right) + 2f\left( {\frac{{2x - 2}}{x}} \right) = {x^2}\left( {1 - x} \right) + 2\left( {\frac{{2x - 2}}{x}} \right),\forall x \ne 0,x \ne 1\)
Chọn
Chọn D
Câu 81:
Một nhà máy cần thiết kế một chiếc bể đựng nước hình trụ bằng tôn có nắp, có thể tích là 64π (m3).
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
ĐÚNG |
SAI |
|
Bán kính đáy của hình trụ là \(\sqrt[3]{{32}}m\) thì bể nước được làm ra tốn ít nguyên liệu nhất. |
||
|
Nếu giá nguyên liệu \(1{m^2}\) tôn làm bể là 105000 đồng thì chi phí tối thiểu để mua nguyên liệu làm bể nước trên là 18 triệu 949 nghìn đồng (kết quả làm tròn đến nghìn đồng). |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Bán kính đáy của hình trụ là \(\sqrt[3]{{32}}m\) thì bể nước được làm ra tốn ít nguyên liệu nhất. |
X | |
|
Nếu giá nguyên liệu \(1{m^2}\) tôn làm bể là 105000 đồng thì chi phí tối thiểu để mua nguyên liệu làm bể nước trên là 18 triệu 949 nghìn đồng (kết quả làm tròn đến nghìn đồng). |
X |
Giải thích
Gọi hình trụ có chiều cao \(h\), bán kính đáy \(r\).
Ta có: \(V = \pi {r^2}h \Rightarrow h = \frac{{64\pi }}{{\pi {r^2}}} = \frac{{64}}{{{r^2}}}\).
Để tốn ít nguyên liệu nhất thì diện tích toàn phần của hình trụ nhỏ nhất.
Ta có: \({S_{tp}} = 2\pi {r^2} + 2\pi rh = 2\pi {r^2} + 2\pi r.\frac{{64}}{{{r^2}}} = 2\pi {r^2} + \frac{{128\pi }}{r}\)
\( = 2\pi {r^2} + \frac{{64\pi }}{r} + \frac{{64\pi }}{r} \ge 3\sqrt[3]{{2\pi {r^2}.\frac{{64\pi }}{r}.\frac{{64\pi }}{r}}} \approx 189,99\).
Số tiền nguyên liệu tối thiểu cần dùng là \(T \approx 189,99.105000 \approx 19949000\) (đồng).
Câu 82:
 Xem đáp án
Xem đáp án
Giải thích
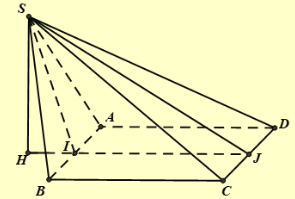
Gọi \(I,J\) lần lượt là trung điểm của \(AB\) và \(CD\).
Kẻ \(SH \bot IJ\). Ta có \(SH \bot \left( {ABCD} \right);IJ = a;SI = \frac{{a\sqrt 3 }}{2};SJ = \sqrt {S{C^2} - C{J^2}} = \frac{{a\sqrt {11} }}{2}\).
Theo định lí \({\rm{cos}}:{\rm{cos}}\widehat {SJI} = \frac{{3\sqrt {11} }}{{11}}\) suy ra \({\rm{sin}}\widehat {SJI} = \frac{{\sqrt {22} }}{{11}}\).
Suy ra \(SH = \frac{{a\sqrt 2 }}{2}\). Vậy \({V_{S.ABCD}} = \frac{{{a^3}\sqrt 2 }}{6}\).
Chọn D
Câu 83:
Ta gọi số nguyên bé nhất không nhỏ hơn x là phần nguyên trên của x , ký hiệu \(\left\lceil x \right\rceil \)
Chẳng hạn \(\left\lceil { - 2,5} \right\rceil = - 2,\left\lceil {\frac{{19}}{6}} \right\rceil = 4\)
Tổng phần nguyên trên của tất cả các số có dạng \(\frac{{\rm{k}}}{2}\) với \({\rm{k}}\) nguyên lấy giá trị từ -4 đến 4 bằng
 Xem đáp án
Xem đáp án
Chọn A
Câu 84:
 Xem đáp án
Xem đáp án
Giải thích
Điều kiện: \(\left\{ {\begin{array}{*{20}{l}}{x > 0}\\{y > 0}\\{x - 4y - 1 > 0}\end{array}} \right.\)
Ta có \({\rm{log}}_2^2\left( {xy} \right) = {\rm{lo}}{{\rm{g}}_2}\left( {\frac{x}{4}} \right){\rm{lo}}{{\rm{g}}_2}\left( {4y} \right) \Leftrightarrow {\left( {{\rm{lo}}{{\rm{g}}_2}x + {\rm{lo}}{{\rm{g}}_2}y} \right)^2} = \left( {{\rm{lo}}{{\rm{g}}_2}x - 2} \right)\left( {{\rm{lo}}{{\rm{g}}_2}y + 2} \right){\rm{\;}}\) (1).
Đặt \({\rm{lo}}{{\rm{g}}_2}x = a;{\rm{lo}}{{\rm{g}}_2}y = b\), ta có (1) trở thành :
\({(a + b)^2} = \left( {a - 2} \right)\left( {b + 2} \right) \Leftrightarrow {a^2} + ab - 2a + {b^2} + 2b + 4 = 0\)
\( \Leftrightarrow 2{a^2} + 2ab - 4a + 2{b^2} + 4b + 8 = 0 \Leftrightarrow {(a + b)^2} + {(a - 2)^2} + {(b + 2)^2} = 0\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a + b = 0}\\{a - 2 = 0}\\{b + 2 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b = - 2}\end{array}} \right.} \right.\)
Với \(\left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b = - 2}\end{array}} \right.\), ta có \(\left\{ {\begin{array}{*{20}{l}}{{\rm{lo}}{{\rm{g}}_2}x = 2}\\{{\rm{lo}}{{\rm{g}}_2}y = - 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 4}\\{y = \frac{1}{4}}\end{array}} \right.} \right.\) (thỏa mãn điều kiện).
Khi đó \(P = {\rm{lo}}{{\rm{g}}_3}\left( {4 + 4.\frac{1}{4} + 4} \right) + {\rm{lo}}{{\rm{g}}_2}\left( {4 - 4.\frac{1}{4} - 1} \right) = 3\).
Chọn A
Câu 85:
 Xem đáp án
Xem đáp án
Giải thích
Số đường thẳng đi qua 2 điểm bất kì từ \(n\) đỉnh của đa giác là \(C_n^2\).
Mà đa giác có \(n\) cạnh nên số đường chéo của đa giác là: \(C_n^2 - n\).
Theo bài ra ta có: \(C_n^2 - n = n \Leftrightarrow \frac{{n\left( {n - 1} \right)}}{2} = 2n \Leftrightarrow {n^2} - 5n = 0 \Leftrightarrow n = 5\).
Vậy đa giác có 5 cạnh.
Giao điểm của 2 đường chéo trong đa giác lồi là giao điểm của 2 đường chéo trong tứ giác mà 4 đỉnh của nó là 4 đỉnh của đa giác lồi.
Khi đó, số giao điểm của các đường chéo bằng số tứ giác với các đỉnh là các đỉnh của đa giác lồi \(n\) cạnh.
Vậy số giao điểm cần tìm là \(C_n^4 = C_5^4 = 5\).
Chọn B
Câu 86:
Cổng trường Đại học Bách Khoa Hà Nội có hình dạng Parabol, chiều rộng \(8m\), chiều cao 12,5 m. Diện tích của cổng là (1) ________\({m^2}\).
 Xem đáp án
Xem đáp án
Đáp án: “200/3”
Giải thích
Xét hệ trục tọa độ như hình vẽ với trục đối xứng của Parabol trùng với trục tung, trục hoành trùng với đường tiếp đất của cổng.
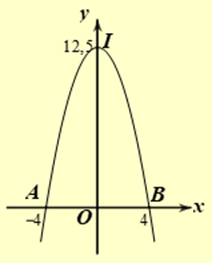
Khi đó Parabol có phương trình dạng \(y = a{x^2} + c\).
Vì \(\left( P \right)\) đi qua đỉnh \(I\left( {0;12,5} \right)\) nên ta có \(c = 12,5\).
\(\left( P \right)\) cắt trục hoành tại hai điểm \(A\left( { - 4;0} \right)\) và \(B\left( {4;0} \right)\) nên ta có \(0 = 16a + c \Rightarrow a = \frac{{ - c}}{{16}} = - \frac{{25}}{{32}}\).
Do đó \(\left( P \right):y = - \frac{{25}}{{32}}{x^2} + 12,5\).
Diện tích của cổng là: \(S = \int\limits_{ - 4}^4 {\left( { - \frac{{25}}{{32}}{x^2} + 12,5} \right)dx = \frac{{200}}{3}\left( {{m^2}} \right)} \).
