Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 11)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 11)
-
423 lượt thi
-
96 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
Phần tư duy đọc hiểu
Mục đích chính của tác giả trong bài đọc này là gì?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung toàn bài đọc.
Lời giải
- Mục đích chính của tác giả trong đoạn trích này là bác bỏ suy nghĩ cho rằng khoa học khô khan, lạnh lùng. Tác giả đã đưa ra các lập luận, dẫn chứng để cho người đọc thấy khoa học không khô khan, lạnh lùng mà khoa học vẫn hướng về những vẻ đẹp nhất định.
- Phân tích, loại trừ: Đáp án A, C, D sai vì bài đọc không nhắc tới những nội dung này.
Chọn B
Câu 2:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Theo bài đọc, mục đích đầu tiên khiến tác giả nghiên cứu khoa học là đem lại sự hiểu biết cho mọi người về thế giới. Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [1]
Lời giải
→ Ý kiến trên: Sai
- Phần cuối đoạn [1] có đề cập: Đối với tôi, niềm đam mê nghiên cứu thực tại, không nghi ngờ gì nữa, được thúc đẩy trước tiên bởi sự cảm nhận cái đẹp của thế giới.
=> Đối với tác giả, mục đích khiến đầu tiên khích lệ ông nghiên cứu khoa học là nhận thức về vẻ đẹp của thế giới chứ không phải là đem lại sự hiểu biết cho mọi người về thế giới.
Chọn B
Câu 3:
Điền những từ ngữ không quá hai tiếng có trong bài đọc vào chỗ trống.
Nhà khoa học cũng là con người, và họ thường phải cân nhắc giữa _______ và _______ trong quá trình nghiên cứu. Họ cố gắng để lý giải, đo lường và hiểu rõ các hiện tượng tự nhiên dựa trên dữ liệu và kiến thức khoa học, nhưng đôi khi cảm xúc và đạo đức có thể ảnh hưởng đến quá trình nghiên cứu và ra quyết định.
 Xem đáp án
Xem đáp án
Đáp án đúng là:
Nhà khoa học cũng là con người, và họ thường phải cân nhắc giữa tình cảm và lí trí | lý trí trong quá trình nghiên cứu. Họ cố gắng để lý giải, đo lường và hiểu rõ các hiện tượng tự nhiên dựa trên dữ liệu và kiến thức khoa học, nhưng đôi khi cảm xúc và đạo đức có thể ảnh hưởng đến quá trình nghiên cứu và ra quyết định.
Phương pháp giải
Căn cứ vào nội dung đoạn [1]
Lời giải
- Nhà khoa học cũng là con người, và họ thường phải cân nhắc giữa tình cảm và lí trí trong quá trình nghiên cứu. Họ cố gắng để lý giải, đo lường và hiểu rõ các hiện tượng tự nhiên dựa trên dữ liệu và kiến thức khoa học, nhưng đôi khi cảm xúc và đạo đức có thể ảnh hưởng đến quá trình nghiên cứu và ra quyết định.
- Phân tích, suy luận:
Đoạn 1 có trình bày: Con người luôn có lí trí và tình cảm, và nhà khoa học, cũng như bất kì ai, không thể tách rời những cảm xúc của mình ra khỏi lí trí khi tìm cách đối thoại với tự nhiên.
→ Đáp án cần điền là: tình cảm/ lí trí
Câu 4:
vẻ đẹp, tính đúng đắn, phát triển, hiểu biết, hình thành
Sự khẳng định về _______ khoa học trong bài đọc đã cho thấy tác giả vô cùng thán phục trước sự phức tạp và tinh tế của tự nhiên. Sự _______ về vẻ đẹp trong khoa học không chỉ giúp tạo ra một tinh thần thánh thiện, mà còn có thể thúc đẩy lòng đam mê trongviệc nghiên cứu và hiểu sâu hơn về thế giới xung quanh chúng ta. Nó có thể kích thích trí tò mò và khao khát tìm hiểu sâu hơn, từ đó đóng góp vào tiến bộ của khoa học và sự _______ của con người.
 Xem đáp án
Xem đáp án
Đáp án
Sự khẳng định về vẻ đẹp khoa học trong bài đọc đã cho thấy tác giả vô cùng thán phục trước sự phức tạp và tinh tế của tự nhiên. Sự hiểu biết về vẻ đẹp trong khoa học không chỉ giúp tạo ra một tinh thần thánh thiện, mà còn có thể thúc đẩy lòng đam mê trongviệc nghiên cứu và hiểu sâu hơn về thế giới xung quanh chúng ta. Nó có thể kích thích trí tò mò và khao khát tìm hiểu sâu hơn, từ đó đóng góp vào tiến bộ của khoa học và sự phát triển của con người.
Phương pháp giải
Căn cứ vào nội dung của toàn bài đọc
Lời giải
Phân tích, suy luận, loại trừ:
- Sự khẳng định về _____ khoa học trong bài đọc đã cho thấy tác giả vô cùng thán phục trước sự phức tạp và tinh tế của tự nhiên.
→ Đáp án đúng là: vẻ đẹp
Vì đoạn này đã trình bày: Vậy cái đẹp trong khoa học là gì? Trước hết đó chính là vẻ đẹp vật chất của thế giới, nó đập ngay vào mắt chúng ta và làm chúng ta choáng ngợp. -> Tác giả đề cập đến vẻ đẹp của tự nhiên.
- Sự _____ về vẻ đẹp trong khoa học không chỉ giúp tạo ra một tinh thần thánh thiện, mà còn có thể thúc đẩy lòng đam mê trong việc nghiên cứu và hiểu sâu hơn về thế giới xung quanh chúng ta.
→ Đáp án đúng là: hiểu biết
Vì bài đọc có trình bày: Chẳng hạn, nhà toán học người Pháp Henri Poincaré đã nói: “Nhà khoa học không nghiên cứu tự nhiên vì mục đích vụ lợi. Anh ta nghiên cứu nó vì tìm thấy ở đó niềm vui sướng; và anh ta tìm thấy niềm vui sướng bởi vì tự nhiên rất đẹp. Nếu tự nhiên không đẹp, nó sẽ không đáng để nghiên cứu, và cuộc đời cũng sẽ không đáng sống.” Tôi hoàn toàn tán thành ý kiến này.
- Nó có thể kích thích trí tò mò và khao khát tìm hiểu sâu hơn, từ đó đóng góp vào tiến bộ của khoa học và sự _____ của con người.
→ Đáp án đúng là: phát triển
Vì tác giả đã trình bày ý kiến của mình: Đối với tôi, niềm đam mê nghiên cứu thực tại, không nghi ngờ gì nữa, được thúc đẩy trước tiên bởi sự cảm nhận cái đẹp của thế giới.
Dựa vào nội dung đoạn trên cùng cách phân tích và suy luận, ta có các cụm từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: vẻ đẹp
- Vị trí thả 2: hiểu biết
- Vị trí thả 3: phát triển
Câu 5:
Điền từ ngữ không quá hai tiếng có trong bài đọc vào chỗ trống.
Tự nhiên không ngừng tự __________ và đổi mới thông qua các quá trình tự nhiên, tiến hóa, và tương tác phức tạp giữa các yếu tố khác nhau. Điều này đã cung cấp cơ hội cho nghiên cứu và phát triển khoa học, từ tìm hiểu về sinh học đến hiểu biết về khí hậu và môi trường.
 Xem đáp án
Xem đáp án
Đáp án đúng là “sáng tạo”
Phương pháp giải
Căn cứ vào nội dung đoạn [3]
Lời giải
- Căn cứ vào nội dung đoạn [3] có trình bày: Chúng ta sống trong một thế giới cực kì phong phú và đa dạng, với một thiên nhiên không ngừng tự do sáng tạo và đổi mới.
- Phân tích, suy luận:
Từ câu văn trên, ta có từ khoá “sáng tạo” phù hợp để điền vào chỗ trống của đề bài.
→ Đáp án cần điền là: sáng tạo
Tự nhiên không ngừng tự sáng tạo và đổi mới thông qua các quá trình tự nhiên, tiến hóa, và tương tác phức tạp giữa các yếu tố khác nhau. Điều này đã cung cấp cơ hội cho nghiên cứu và phát triển khoa học, từ tìm hiểu về sinh học đến hiểu biết về khí hậu và môi trường.
Câu 6:
bằng chứng, bác bỏ, chứng minh, mỹ học, thế giới
Bằng thao tác lập luận _______, tác giả đã phủ định ý kiến cho rằng khoa học là khô khan, lạnh lùng và đưa ra những lập luận thuyết phục để chứng minh khoa học có sự giao thoa với _______. Khoa học đẹp bởi vì thế giới thực sự đẹp từ trong bản chất của nó. Và khoa học đã phát hiện ra những vẻ đẹp của _______ thế giới qua sự khám phá, nghiên cứu, tìm tòi.
 Xem đáp án
Xem đáp án
Đáp án
Bằng thao tác lập luận bác bỏ, tác giả đã phủ định ý kiến cho rằng khoa học là khô khan, lạnh lùng và đưa ra những lập luận thuyết phục để chứng minh khoa học có sự giao thoa với mỹ học. Khoa học đẹp bởi vì thế giới thực sự đẹp từ trong bản chất của nó. Và khoa học đã phát hiện ra những vẻ đẹp của thế giới thế giới qua sự khám phá, nghiên cứu, tìm tòi.
Phương pháp giải
Căn cứ vào nội dung của toàn văn bản.
Lời giải
Phân tích, suy luận, loại trừ:
- Bằng thao tác lập luận _____, tác giả đã phủ định ý kiến cho rằng khoa học là khô khan, lạnh lùng
→ Đáp án đúng là: bác bỏ
Vì phía sau chỗ trống có đề cập từ “phủ định”, đây là từ ngữ chỉ thao tác lập luận bác bỏ.
- và đưa ra những lập luận thuyết phục để chứng minh khoa học có sự giao thoa với _____.
→ Đáp án đúng là: mỹ học.
Vì bài đọc có đề cập “Vậy cái đẹp trong khoa học là gì? Trước hết đó chính là vẻ đẹp vật chất của thế giới, nó đập ngay vào mắt chúng ta và làm chúng ta choáng ngợp.” (bài đọc khẳng định khoa học có sự giao thoa với cái đẹp, cái đẹp còn được hiểu là mỹ học).
- Và khoa học đã phát hiện ra những vẻ đẹp của [vị trí thả 3] qua sự khám phá, nghiên cứu, tìm tòi.
→ Đáp án đúng là: thế giới.
Vì bài đọc có đề cập “Vậy cái đẹp trong khoa học là gì? Trước hết đó chính là vẻ đẹp vật chất của thế giới, nó đập ngay vào mắt chúng ta và làm chúng ta choáng ngợp.”
Dựa vào nội dung đoạn trên cùng cách phân tích và suy luận, ta có các từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: bác bỏ
- Vị trí thả 2: mỹ học
- Vị trí thả 3: thế giới
Câu 7:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nghĩa của từ
Lời giải
- Để làm được câu này, trước tiên phải đi cắt nghĩa từ “duy lí”. Duy lí được hiểu là một học thuyết dựa trên bằng chứng, tư duy để nhìn nhận vấn đề.
- Tìm hiểu nghĩa của các phương án đã cho:
+ Duy cảm: là học thuyết khẳng định rằng mọi thứ đều tồn tại bên trong tinh thần và thuộc về ý thứC.
+ Duy ý chí: là học thuyết khẳng định rằng mọi thứ đều tồn tại ở ý chí con người.
+ Duy vật: là học thuyết khẳng định rằng mọi thứ đều tồn tại bên trong vật chất.
+ Duy thực: là học thuyết khẳng định rằng mọi thứ đều tồn tại ở hiện thực.
- Phân tích, loại trừ:
+ Đáp án A đúng vì “tinh thần” và “ý thức” đối lập với “bằng chứng” và “tư duy”. (một bên thiên về cảm tính, một bên thiên về lý trí, kiến thức).
+ Đáp án B sai vì “ý chí” không đối lập với “bằng chứng” và “tư duy”.
+ Đáp án C sai vì “vật chất” không đối lập với “bằng chứng” và “tư duy”.
+ Đáp án D sai vì “hiện thực” không đối lập với “bằng chứng” và “tư duy”.
Chọn A
Câu 8:
Tác giả đã dùng đối tượng nào dưới đây để chứng minh cho vẻ đẹp của khoa học trong tự nhiên?
Chọn các đáp án đúng.
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [3]
Lời giải
- Phân tích, suy luận:
+ Đáp án A đúng vì đoạn [3] có trình bày “Chúng ta sống trong một thế giới đầy những kì quan quang học, và bầu trời là mặt bức tranh hoành tráng nơi màu sắc và ánh sáng tác động và phô diễn một cách bất ngờ nhất.” -> Câu văn ca ngợi bầu trời là một bức tranh hoành tráng.
+ Đáp án B đúng vì đoạn [3] có trình bày “Bạn không thể không ấn tượng với cầu vồng - cái vòng cung đa sắc khổng lồ xuất hiện giữa những giọt nước mưa ở cuối một trận mưa dông, sự hài hòa về sắc màu và sự hoàn hảo của các cung tròn đã tạo nên cây cầu nối giữa hai bờ thơ ca và khoa học, khiến người ta phải khâm phục và sùng kính.” -> Câu văn ca ngợi vẻ đẹp của cầu vồng sau mưa.
+ Đáp án C sai vì đoạn [3] có trình bày “Bạn không thể không ấn tượng với cầu vồng - cái vòng cung đa sắc khổng lồ xuất hiện giữa những giọt nước mưa ở cuối một trận mưa dông, sự hài hòa về sắc màu và sự hoàn hảo của các cung tròn đã tạo nên cây cầu nối giữa hai bờ thơ ca và khoa học, khiến người ta phải khâm phục và sùng kính.” -> Câu văn ca ngợi vẻ đẹp của cầu vồng, và những giọt nước mưa chỉ là nhân tố xuất hiện để tôn lên vẻ đẹp của cầu vồng mà tác giả nhắc đến trong câu văn. Có thể giọt nước mưa cũng là một vẻ đẹp của tự nhiên nhưng trong bài đọc này, tác giả không có câu văn nào nói về vẻ đẹp của nó.
+ Đáp án D đúng vì đoạn [3] có trình bày “Rồi cảnh hoàng hôn, một lễ hội của sắc vàng, cam và đỏ chiếu rọi bầu trời ngay trước khi vầng dương biến mất dưới chân trời.” -> Câu văn ca ngợi vẻ đẹp của hoàng hôn.
=> A, B, D là đáp án đúng
Câu 9:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
|
|
ĐÚNG |
SAI |
|
- Khoa học là một lĩnh vực hoàn toàn duy lí. |
||
|
- Thao tác lập luận chính trong đoạn [2] là giải thích. |
||
|
- Thiên nhiên có thể giúp con người cân bằng trạng thái cảm xúc. |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
- Khoa học là một lĩnh vực hoàn toàn duy lí. |
X | |
|
- Thao tác lập luận chính trong đoạn [2] là giải thích. |
X | |
|
- Thiên nhiên có thể giúp con người cân bằng trạng thái cảm xúc. |
X |
Phương pháp giải
Căn cứ vào 3 đoạn [1], [2], [3]
Lời giải
Phân tích, suy luận:
- Khoa học là một lĩnh vực hoàn toàn duy lí.
→ Ý kiến trên: SAI
Vì đoạn [1] nói rằng “Ý nghĩ cho rằng công việc của một nhà khoa học hoàn toàn không có xúc cảm là hết sức sai lầm.” (Tác giả đã bác bỏ ý kiến cho rằng khoa học là một lĩnh vực hoàn toàn duy lí).
- Thao tác lập luận chính trong đoạn [2] là giải thích.
→ Ý kiến trên: ĐÚNG
Vì đoạn [2] cắt nghĩa cái đẹp trong khoa học: “Vậy cái đẹp trong khoa học là gì? Trước hết đó chính là vẻ đẹp vật chất của thế giới, nó đập ngay vào mắt chúng ta và làm chúng ta choáng ngợp.” (Những câu văn sau đó, tác giả đã dùng Mặt Trời để minh hoạ cho định nghĩa trên).
- Thiên nhiên có thể giúp con người cân bằng trạng thái cảm xúc.
→ Ý kiến trên: ĐÚNG
Vì đoạn [3] nói rằng “Khi chúng ta buồn, đôi khi chỉ cần nhìn bầu trời xanh, đầy nắng không một gợn mây cũng đủ để vơi bớt nỗi muộn phiền.”.
Câu 10:
Thông tin nào được suy ra từ đoạn trích trên?
Chọn các đáp án đúng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung của toàn đoạn trích
Lời giải
Phân tích, suy luận:
- Khoa học có tác dụng điều hoà cảm xúc của con người.
→ Ý kiến trên không được suy ra từ văn bản.
Vì văn bản không đề cập đến tác dụng này của khoa học.
- Khoa học vật lí không quan tâm đến việc thưởng ngoạn cái đẹp.
→ Ý kiến trên không được suy ra từ văn bản.
Vì bài đọc đã phản bác ý kiến này: Trong ý nghĩ của công chúng, hoạt động khoa học thường được coi là một việc làm hoàn toàn duy lí, chỉ dựa trên logic thuần túy và tước bỏ mọi cảm xúc, và vật lí cũng là một môn khoa học nên hoàn toàn không biết đến thưởng ngoạn cái đẹp… Ý nghĩ cho rằng công việc của một nhà khoa học hoàn toàn không có xúc cảm là hết sức sai lầm.
- Cái đẹp nằm trong khoa học.
→ Ý kiến trên được suy ra từ văn bản.
Vì bài đọc có trình bày: Các nhà bác học vĩ đại nhất cũng đều đưa ra ý kiến rõ ràng về vai trò của cái đẹp đối với khoa học.
- Các nhà khoa học nghiên cứu tự nhiên vì cảm thấy thiên nhiên đẹp.
→ Ý kiến trên được suy ra từ văn bản.
Vì bài đọc có trình bày: Nhà khoa học không nghiên cứu tự nhiên vì mục đích vụ lợi. Anh ta nghiên cứu nó vì tìm thấy ở đó niềm vui sướng; và anh ta tìm thấy niềm vui sướng bởi vì tự nhiên rất đẹp.
Chọn C, D
Câu 11:
Xác định nhân vật trung tâm trong truyện.
Nhân vật trung tâm trong đoạn trích trên là _______.
 Xem đáp án
Xem đáp án
Đáp án đúng là “dì Mây | Mây”
Phương pháp giải
Căn cứ vào các nhân vật xuất hiện trong truyện
Lời giải
- Nhân vật trung tâm trong đoạn trích trên là dì Mây.
Câu 12:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Ngày dì Mây về làng, chú San đi lấy vợ do dì Mây đã biệt tích nhiều năm, không có thông tin nào về dì.
Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung câu chuyện
Lời giải
→ Ý kiến trên: Sai
- “Ngày dì Mây khoác ba lô về làng, chú San đi lấy vợ” (do tưởng Mây đã hi sinh, gia đình đã nhận giấy báo tử). Vì bài đọc có trình bày: Ông gỡ tấm ảnh dì Mây viền đen trong khung kính và bằng Tổ quốc ghi công cất vào tủ. (Chi tiết này cho thấy gia đình đã nhận được giấy báo tử nên cất ảnh thờ và bằng Tổ quốc ghi công của dì Mây lên bàn thờ)
=> Vì vậy, khẳng định “do dì Mây đã biệt tích nhiều năm” là không đúng.
Chọn B
Câu 13:
tủi hờn, nghẹn ngào, ngổn ngang, xót xa, hờn giận
- Tâm trạng của dì Mây khi được trở về quê hương, gặp lại bố ở bến sông: _______
- Tâm trạng của dì Mây khi nói chuyện với chú San: _______
- Tâm trạng của dì Mây sau khi đỡ đẻ cho cô Thanh: _______
 Xem đáp án
Xem đáp án
Đáp án
- Tâm trạng của dì Mây khi được trở về quê hương, gặp lại bố ở bến sông: nghẹn ngào
- Tâm trạng của dì Mây khi nói chuyện với chú San: ngổn ngang
- Tâm trạng của dì Mây sau khi đỡ đẻ cho cô Thanh: tủi hờn
Phương pháp giải
Căn cứ vào nội dung của câu chuyện
Lời giải
Phân tích, suy luận, loại trừ:
- Tâm trạng của dì Mây khi được trở về quê hương, gặp lại bố ở bến sông: nghẹn ngào.
→ Vì đoạn [1] trình bày “Dì đứng ở bờ đê xóm Bãi gọi ông. Giọng dì nghèn nghẹn lẫn trong ráng chiều lúc hiện lên rất rõ, lúc nhoè đi.” Từ ngữ “nghèn nghẹn” khi dì Mây gọi bố diễn tả trạng thái xúc động mạnh của nhân vật dẫn đến sự nghẹn ứ trong cổ họng không nói thành lời. Đó chính là tâm trạng nghẹn ngào (xúc động mạnh, bị nghẹn lời).
- Tâm trạng của dì Mây khi thấy nhà chú San đang có đám cưới: ngổn ngang.
→ Vì đoạn [3] tái hiện lại cuộc nói chuyện riêng của dì Mây và chú Sang với bao tâm trạng, ý nghĩ chồng chất: ban đầu tâm trạng dì Mây đau khổ, uất ức (nuốt nước mắt vào trong); tiếp đó là nỗi tức tưởi, trách móc (Hôm nay là ngày gì? Anh nhớ không. Có ngờ đâu ngày ấy tiễn anh đi cũng là ngày li biệt); rồi tình cảm yêu thương, sâu nặng bùng lên da diết (Dì Mây lặng đi, người rũ ra, mềm oặt. Dì từ từ khuỵu xuống.); cuối cùng là thái độ tỉnh táo, đưa ra quyết định dứt khoát (Thôi! Thôi! Lỡ rồi! Đằng nào cũng chỉ một người đàn bà khổ. Anh về đi). Những cảm xúc lộn xộn, chồng chất, không thoát ra được của nhân vật được gọi là tâm trạng ngổn ngang.
- Tâm trạng của dì Mây sau khi đỡ đẻ cho cô Thanh: tủi hờn.
→ Vì bài đọc trình bày “Ở trong, dì Mây gục luôn xuống bàn đỡ đẻ khóc tức tưởi. “Ơ cái con này!”. Thím Ba ngạc nhiên. Dì Mây càng khóc to hơn. Tiếng khóc của dì hoà lẫn tiếng oe oe của đứa bé. Nghe xót xa, tủi hờn, xen lẫn niềm ao ước, chờ mong và vui buồn lẫn lộn.” Điều này cho thấy dì Mây cảm thấy xót xa, tủi hờn vì dì cũng khao khát có con, có mái ấm gia đình như mẹ con người phụ nữ dì vừa đỡ đẻ.
Dựa vào nội dung đoạn trên cùng cách phân tích và suy luận, ta có các từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: nghẹn ngào
- Vị trí thả 2: ngổn ngang
- Vị trí thả 3: tủi hờn
Câu 14:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
|
|
ĐÚNG |
SAI |
|
- Chú San muốn từ bỏ cô dâu mới để quay về với dì Mây. |
||
|
- Người vợ mới của chú San hận dì Mây nhưng sau khi được dì đỡ đẻ, đã biết ơn dì. |
||
|
- Truyện viết về những gian khổ, hi sinh của nữ chiến binh nơi chiến trinh lửa đạn. |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
- Chú San muốn từ bỏ cô dâu mới để quay về với dì Mây. |
X | |
|
- Người vợ mới của chú San hận dì Mây nhưng sau khi được dì đỡ đẻ, đã biết ơn dì. |
X | |
|
- Truyện viết về những gian khổ, hi sinh của nữ chiến binh nơi chiến trinh lửa đạn. |
X |
Phương pháp giải
Căn cứ vào nội dung câu chuyện
Lời giải
Phân tích, suy luận:
- Chú San muốn từ bỏ cô dâu mới để quay về với dì Mây.
→ Ý kiến trên: ĐÚNG
Vì bài đọc có trình bày “Chú San đột nhiên vung tay đấm rung cành bưởi: “Mây! Chúng ta sẽ làm lại”. “San! Anh nói gì thế???”. “Anh sẽ từ bỏ tất cả. Chúng ta về sống với nhau”.”
- Người vợ mới của chú San hận dì Mây nhưng sau khi được dì đỡ đẻ, đã biết ơn dì.
→ Ý kiến trên: SAI
Vì bài đọc không đề cập đến chi tiết nào chứng minh vợ của chú San hận dì Mây. Bài đọc khắc hoạ các chi tiết cô Thanh biết ơn dì Mây vì đã cao thượng từ bỏ để gia đình cô được hạnh phúc và biết ơn dì Mây hơn nữa khi dì Mây đỡ đẻ thành công cho cô Thanh (Cô Thanh sướt mướt: “Nhà em ơn chị đời đời”).
- Truyện viết về những gian khổ, hi sinh của nữ chiến binh nơi chiến trinh lửa đạn.
→ Ý kiến trên: SAI
Vì bài đọc không viết về chiến tranh, bom đạn; không viết về những gian khổ, hi sinh nơi chiến trường mà truyện tập trung kể về sự hi sinh thầm lặng, bản lĩnh phi thường, phẩm chất tốt đẹp của người nữ thương binh giữa đời thường.
Câu 15:
Câu chuyện đã diễn ra trong những không gian nào?
Chọn các đáp án đúng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung câu chuyện
Lời giải
- Theo dõi toàn câu chuyện, ta thấy câu chuyện diễn ra tại hai không gian chính:
+ Không gian sinh hoạt gia đình (nhà ông ngoại và nhà chú San) được tái hiện trong các bối cảnh ngày dì Mây về làng và ngày dì Mây đỡ đẻ cho cô Thanh.
+ Không gian sông nước (bến sông - lều cỏ) được tái hiện qua cảnh dì Mây trở về gặp bố, dì Mây chèo đò đưa lũ trẻ đi học, dì Mây ngồi nhớ lại kỉ niệm xưa.
- Phân tích, loại trừ: đáp án B, D sai vì các không gian này không được nhắc đến trong văn bản.
Chọn A, C
Câu 16:
Điền một từ không quá hai tiếng có trong bài đọc vào chỗ trống.
Truyện ngắn đặc sắc một phần nhờ những hình ảnh giàu giá trị biểu tượng. Trong đó, _______ gợi lên ý nghĩa về dòng đời bí ẩn, nhiều biến động, sóng gió (như tình yêu của dì Mây và chú San); nhiều trớ trêu, đau khổ (như cuộc đời dì Mây, thím Ba); nhiều đổi thay xoay vần (những vẻ đẹp thời trẻ của dì Mây bị mất đi khi tham gia chiến tranh và sự hồi sinh vẻ đẹp đó ngày dì gắn bó với quê hương).
 Xem đáp án
Xem đáp án
Đáp án đúng là "sông Châu"
Phương pháp giải
Căn cứ vào nội dung toàn câu chuyện
Lời giải
- Truyện ngắn đặc sắc một phần nhờ những hình ảnh giàu giá trị biểu tượng. Trong đó, sông Châu gợi lên ý nghĩa về dòng đời bí ẩn, nhiều biến động, sóng gió (như tình yêu của dì Mây và chú San); nhiều trớ trêu, đau khổ (như cuộc đời dì Mây, thím Ba); nhiều đổi thay xoay vần (những vẻ đẹp thời trẻ của dì Mây bị mất đi khi tham gia chiến tranh và sự hồi sinh vẻ đẹp đó ngày dì gắn bó với quê hương).
- Đây là từ ngữ phù hợp nhất để điền vào chỗ trống vì sông Châu là hình ảnh biểu tượng giàu ý nghĩa, mang trọn vẹn những ý đã được nhắc ở đề bài.
Câu 17:
khó khăn, lòng nhân hậu, cổ vũ, khuyến khích, sự kiên cường
Bản lĩnh và _______ của nhân vật dì Mây thật đáng ngưỡng mộ. Cuộc sống hôm nay, tuy không còn chiến tranh, bom đạn, nhưng bản lĩnh, nghị lực phi thường và lòng nhân hậu của nhân vật dì Mây có sức mạnh _______ chúng ta sống bản lĩnh, can đảm đối mặt và sẵn sàng vượt qua những tình huống _______, nan giải trong cuộc sống, có ý chí vươn lên làm người tốt, sống có ích giữa cuộc đời.
 Xem đáp án
Xem đáp án
Đáp án
Bản lĩnh và lòng nhân hậu của nhân vật dì Mây thật đáng ngưỡng mộ. Cuộc sống hôm nay, tuy không còn chiến tranh, bom đạn, nhưng bản lĩnh, nghị lực phi thường và lòng nhân hậu của nhân vật dì Mây có sức mạnh cổ vũ chúng ta sống bản lĩnh, can đảm đối mặt và sẵn sàng vượt qua những tình huống khó khăn, nan giải trong cuộc sống, có ý chí vươn lên làm người tốt, sống có ích giữa cuộc đời.
Phương pháp giải
Căn cứ vào nội dung của câu chuyện
Lời giải
Phân tích, suy luận, loại trừ:
- Bản lĩnh và _____ của nhân vật dì Mây thật đáng ngưỡng mộ
→ Đáp án đúng là: lòng nhân hậu
Vì bài đọc đã khắc họa nhân vật dì Mây sau trận chiến trở về đã đối diện với tất cả nỗi đau (thương tật, mẹ mất, hạnh phúc dở dang) bằng bản lĩnh phi thường và tấm lòng nhân ái, bao dung (rút lui để người yêu có cuộc sống êm ấm, đỡ đẻ cho vợ người yêu cũ). Tất cả những điều này làm toát lên sự bản lĩnh + nhân hậu trong con người dì Mây.
- bản lĩnh, nghị lực phi thường và lòng nhân hậu của nhân vật dì Mây có sức mạnh _____ chúng ta sống bản lĩnh, can đảm đối mặt và sẵn sàng vượt qua những tình huống _____, nan giải
→ Đáp án đúng là: cổ vũ / khó khăn
Vì những phẩm chất đẹp của dì Mây đem lại ý nghĩa cao đẹp. Những phẩm chất đẹp đẽ ấy có ý nghĩa cổ vũ chúng ta sống đẹp hơn và để can đảm đối diện với những khó khăn trong cuộc sống.
Dựa vào nội dung câu chuyện cùng cách phân tích và suy luận, ta có các từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: lòng nhân hậu
- Vị trí thả 2: cổ vũ
- Vị trí thả 3: khó khăn
Câu 18:
Từ “đãi bôi” (in đậm, gạch chân) trong đoạn [3] được hiểu là gì?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nghĩa của từ
Lời giải
- Từ “đãi bôi” (in đậm, gạch chân) trong đoạn [3] được hiểu là: niềm nở bề ngoài, không thật tình.
- Đây là nghĩa chuẩn xác của từ đồng thời cũng rất phù hợp khi để vào ngữ cảnh của đoạn văn (gia đình dì Mây tỏ ra niềm nở với chú San nhưng thực chất không thật tình).
Chọn A
Câu 19:
Nhân vật dì Mây nổi bật với những phẩm chất gì?
Chọn các đáp án đúng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung của văn bản
Lời giải
- Theo văn bản, nhân vật dì Mây nổi bật với những phẩm chất:
+ Có bản lĩnh vững vàng và nhân hậu, bao dung: dì Mây dù rất đau đớn, xót xa vì người yêu lấy vợ và lòng còn rất thương người cũ nhưng dì đã dùng lí trí và lòng bao dung để chịu một mình tổn thương, hạnh phúc nhường lại cho người khác; bản lĩnh vững vàng, nhân hậu bao dung còn được thể hiện rõ khi trong hoàn cảnh khó khăn, cô Thanh sinh khó nhưng dì Mây vẫn lấy hết can đảm để cứu hai mẹ con cô Thanh.
+ Dũng cảm, gan dạ: thể hiện qua chi tiết đỡ đẻ cho cô Thanh. Trong tình huống mưa gió, đêm hôm, thai ngôi ngược, suýt chết, dì Mây không toan tính ích kỉ chỉ biết nghĩ cho bản thân mà can đảm, tự tin, tận tâm vì mạng sống của người khác, dù người đó chính là vợ người yêu cũ của mình.
- Phân tích, loại trừ: phẩm chất hoạt bát, vui vẻ không được thể hiện rõ trong đoạn trích trên.
Chọn A, B, D
Câu 20:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung bài đọc và chọn nội dung phù hợp
Lời giải
Phân tích, suy luận:
- Tình yêu chân chính đáng được trân trọng, tôn vinh
→ Đây là một nội dung được suy ra từ câu chuyện vì dì Mây trong câu chuyện đã yêu hết mình (chèo đò chở người yêu đi du học, mạnh mẽ sống sót qua chiến tranh để trở về với người yêu và cũng bao dung chịu phần thiệt thòi về mình để người yêu bên hạnh phúc mới). -> Đây là tình yêu cao thượng, chân chính và là một nội dung được suy ra từ bài đọc.
- Gia đình luôn là bến đỗ bình yên sau những thăng trầm.
→ Đây là một nội dung được suy ra từ câu chuyện vì bài đọc nói về những đau đớn của dì Mây đều được chị gái, người bố và cô cháu gái động viên, an ủi, cảm thông. Đó chính là bến đỗ bình yên của dì Mây và là nội dung được suy ra từ câu chuyện.
- Nỗi đau của đạn bom là thứ không dễ gì bù đắp.
→ Đây là một nội dung được suy ra từ câu chuyện vì dì Mây trong câu chuyện vì tham gia chiến tranh mà thương tật, mất mẹ, hạnh phúc dở dang để rồi ngày trở về dù chiến tranh có kết thúc nhưng nỗi đau về hình hài không trọn vẹn, nỗi đau về tình yêu không thành và nỗi đau về gia đình thiếu vắng bóng mẹ mãi không thể bù đắp được.
- Lý tưởng có vai trò dẫn lối, soi sáng mọi quyết định của con người.
→ Đây là một nội dung KHÔNG được suy ra từ câu chuyện vì bài đọc không nói về lý tưởng hay mục đích của con người, bài đọc chỉ nói về thân phận con người sau chiến tranh với nhiều điều suy ngẫm.
Chọn DCâu 21:
Phần tư duy khoa học / giải quyết vấn đề
Điều nào sau đây giải thích đúng nhất tại sao học sinh tắt đèn trong phòng?
 Xem đáp án
Xem đáp án
Phương pháp giải
Vận dụng kiến thức đã học và phân tích thông tin từ bài đọc
Lời giải
Học sinh làm thí nghiệm để so sánh độ sáng của ánh sáng do Đèn 1 và 2 trong nhiều điều kiện khác nhau.
Ánh sáng từ các nguồn khác ngoài mạch 1 và 2 có thể đã đưa sai số vào phép đo L.
Đèn trong phòng tắt để tất cả ánh sáng trên các khối phát ra từ các bóng đèn trong Mạch 1 và 2. Vì vậy, A là câu trả lời đúng nhất.
Chọn A
Câu 22:
Trong Thí nghiệm 2, giả sử học sinh thay thế Vật cố định 1 bằng một vật cố định mới. Thiết bị cố định mới chứa 6 bóng đèn, mỗi bóng giống hệt với Bóng đèn F. Khi tất cả 6 bóng đèn trong thiết bị mới được thắp sáng và các khối parafin trông sáng như nhau, L có thể gần với:
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích nội dung câu hỏi
Vận dụng các thông tin và số liệu bài cho
Lời giải
Theo Bảng 2, khi số lượng bóng đèn thắp sáng trong Vật cố định 1 tăng từ 2 lên 5 thì L tăng lên. => nếu sử dụng thiết bị cố định mới, tăng số lượng bóng đèn thắp sáng từ 5 lên 6, thì L sẽ lớn hơn giá trị của L cho trong Bảng 2 đối với 5 bóng đèn thắp sáng là 0,446 m.
=> Giá trị L > 0,446m là 0,490 m hay D là đáp án chính xác.
Chọn D
Câu 23:
Cho các nhận xét về mục đích chính của Thí nghiệm 1, nhận xét nào đúng, nhận xét nào sai?
|
|
ĐÚNG |
SAI |
|
Hiệu chỉnh đồng hồ đo. |
||
|
Xác định mối quan hệ giữa L và số bóng đèn thắp sáng. |
||
|
Xác định xem L có phụ thuộc vào vị trí của bóng đèn trong Vật cố định 1 hay không. |
||
|
Tìm độ sáng của bóng đèn F. |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Hiệu chỉnh đồng hồ đo. |
X | |
|
Xác định mối quan hệ giữa L và số bóng đèn thắp sáng. |
X | |
|
Xác định xem L có phụ thuộc vào vị trí của bóng đèn trong Vật cố định 1 hay không. |
X | |
|
Tìm độ sáng của bóng đèn F. |
X |
Phương pháp giải
Phân tích thông tin từ bài đọc
Lời giải
Trong Thí nghiệm 1 ta thấy mỗi lần một bóng đèn được thắp sáng trong Vật cố định 1, nhưng vị trí của bóng đèn sáng trong Vật cố định 1 đã thay đổi.
=> Do đó, mục đích chính của Thí nghiệm 1 phải là xác định ảnh hưởng, nếu có, của vị trí của bóng đèn đối với giá trị của L. Hay xác định xem L có phụ thuộc vào vị trí của bóng đèn trong Vật cố định 1 hay không.
Câu 24:
Giả sử rằng tất cả các bóng đèn trong Vật cố định 1 đã được thay thế bằng một bóng đèn duy nhất. Dựa vào thí nghiệm 1 và 2, nếu 2 khối parafin sáng như nhau khi vật 2 cách lá nhôm 0,200 m và L= 0,446 m thì độ sáng của bóng đèn mới rất có thể là:
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin và bảng số liệu bài cung cấp.
Lời giải
Theo Bảng 2, 2 khối parafin phát sáng như nhau khi cả 5 bóng đèn trong Vật cố định 1 đều sáng và L là 0,446 m , giống như L thu được với bóng đèn mới.
Như vậy, độ sáng của bóng đèn mới sẽ phải bằng tổng độ sáng của 5 bóng đèn ban đầu. Vì mỗi bóng đèn trong số 5 bóng đèn ban đầu có cùng độ sáng nên bóng đèn mới sẽ phải sáng gấp 5 lần bóng đèn ban đầu.
=> đáp án C là đáp án phù hợp với kết luận trên.
Chọn C
Câu 25:
Trong Thí nghiệm 2, giả sử học sinh đã thay Bóng đèn F bằng một bóng đèn sáng hơn nhiều, Bóng đèn G. So với L khi sử dụng Bóng đèn F, L khi sử dụng Bóng đèn G sẽ là:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa trên thông tin và số liệu bài cung cấp
Lời giải
Bởi vì Bóng đèn G sáng hơn Bóng đèn F và cách lá nhôm một khoảng (0,200 m) giống như Bóng đèn F
=> khối parafin ở gần Bóng đèn G sẽ phát sáng hơn so với khi sử dụng Bóng đèn F.
Do đó, đối với mỗi sự kết hợp của các bóng đèn trong Vật cố định 1, để làm cho 2 khối phát sáng với độ sáng bằng nhau, thì Vật cố định 1 sẽ phải ở gần các khối hơn so với khi sử dụng Bóng đèn F. Nghĩa là, khi sử dụng Bóng đèn G, L cho mỗi tổ hợp bóng đèn sáng trong Vật cố định 1 sẽ phải nhỏ hơn so với khi sử dụng Bóng đèn F để 2 khối phát sáng với độ sáng bằng nhau.
Chọn B
Câu 26:
Điền số thích hợp vào chỗ trống:
Khi hai khối parafin phát sáng như nhau và khoảng cách L khoảng 0,3m thì khi đó có _______ bóng đèn bật sáng, trừ bóng đèn F
 Xem đáp án
Xem đáp án
Đáp án đúng là “3”
Phương pháp giải
Dựa trên thông tin bảng số liệu cung cấp
Lời giải
Từ bảng kết quả thí nghiệm ta có khi hai khối parafin phát sáng như nhau và khoảng cách L khoảng 0,3m thì sẽ có 3 bóng đèn bật sáng.
Câu 27:
Khi xác định thế năng hấp dẫn của các vật thể khác nhau trên Trái đất, biến nào sẽ được coi là hằng số?
 Xem đáp án
Xem đáp án
Phương pháp giải
Áp dụng công thức xác định thế năng: Wt = mgh
Lời giải
Ta có công thức tính thế năng: Wt = mgh
trong công thức trên có khối lượng m, chiều cao ( hay chính là vị trí đặt vật ) h và gia tốc trọng trường g thì đại lượng không thay đổi được đó chính là gia tốc trọng trường g.
Chọn C
Câu 28:
Điền từ thích hợp vào chỗ trống:
Theo công thức được cung cấp trong đoạn văn, khi độ cao của vật đưa cao lên 2 lần thì thế năng của vật _______ 2 lần
 Xem đáp án
Xem đáp án
Đáp án đúng là “tăng | tăng lên”
Phương pháp giải
Áp dụng công thức xác định thế năng: Wt = mgh
Dựa vào thông tin bài cung cấp
Lời giải
Ta có công thức tính thế năng: Wt = mgh
khi đưa vật lên cao gấp 2 lần so với ban đầu thì: Wt′ = 2mgh = 2Wt
hay thế năng sẽ tăng 2 lần
Câu 29:
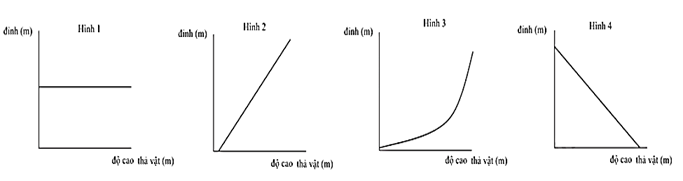
Đồ thị nào sau đây thể hiện rõ nhất mối quan hệ giữa vị trí thả vật và đỉnh đạt được trong Thí nghiệm 1?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào số liệu bảng 2
Lời giải
Từ bảng 2 ta có: Khi chiều cao thả tăng, chiều cao của đỉnh vật đạt được cũng tăng
=> đồ thị thể hiện đúng sẽ là hình 2
Chọn B
Câu 30:
Kéo thả từ thích hợp vào chỗ trống:
cao, thấp, lực ma sát, trọng lực, thế năng, động năng
Dữ liệu trong Bảng 2 ta thấy rằng nếu quãng đường đi theo phương ngang càng dài thì vật sẽ lên đến độ cao càng _______ do ảnh hưởng từ _______ khiến _______ dữ trự của vật giảm đi, khi đó năng lượng đã biến thành nhiệt và âm thanh.
 Xem đáp án
Xem đáp án
Đáp án
Dữ liệu trong Bảng 2 ta thấy rằng nếu quãng đường đi theo phương ngang càng dài thì vật sẽ lên đến độ cao càng thấp do ảnh hưởng từ lực ma sát khiến động năng dữ trự của vật giảm đi, khi đó năng lượng đã biến thành nhiệt và âm thanh.
Phương pháp giải
Phân tích thông tin từ bài đọc
Sử dụng lí thuyết đã học về năng lượng
Lời giải
Năng lượng tiêu hao do ma sát sẽ được xác định bằng: A = Fmsd
=> quãng đường đi càng dài thì năng lượng tiêu hao càng lớn hay phần năng lượng mất đi càng nhiều
Kết quả trên được thể hiện trong bảng 2 ta thấy rằng: khi thả cùng tại một vị trí, quãng đường đi được theo phương ngang càng lớn thì viên bi sẽ lên được độ cao càng thấp do phần động năng của vật đã tiêu hao nhiều.
=>các từ cần kéo thả: thấp / lực ma sát / động năng
Câu 31:
 Xem đáp án
Xem đáp án
Phương pháp giải
Vận dụng lí thuyết về biến độc lập và biến phụ thuộc
Phân tích các thông tin bài cung cấp
Lời giải
Ta có biến phụ thuộc sẽ là những chỉ tiêu đo đạc và bị ảnh hưởng trong suốt quá trình thí nghiệm, hay có thể nói kết quả đo đạc phụ thuộc vào sự thay đổi của biến độc lập.
Trong Thí nghiệm 1, chiều cao thả rơi là biến độc lập. Học sinh thay đổi độ cao thả để xác định ảnh hưởng của độ cao của đỉnh. Trong Thí nghiệm 2, độ cao thả rơi được giữ không đổi để xác định ảnh hưởng của khoảng cách ngang đến độ cao của đỉnh. Cả hai thí nghiệm đều không đo chiều cao rơi làm biến phụ thuộc.
Chọn D
Câu 32:
Sự biến đổi năng lượng nào sau đây không được thể hiện bởi tàu lượn siêu tốc bằng đá cẩm thạch trong Thí nghiệm 1 hoặc Thí nghiệm 2?
 Xem đáp án
Xem đáp án
Phương pháp giải
Thế năng thành động năng
Lời giải
Ta có cơ năng của vật bằng tổng động năng và thế năng, liên quan đến chuyển động và vị trí của vật. Trong các thí nghiệm tàu lượn siêu tốc, cơ năng được biến đổi giữa dạng thế năng và động năng. Sự tiêu tán ma sát cũng làm cho cơ năng chuyển hóa thành nhiệt năng (nhiệt) và âm thanh. Không có sự chuyển đổi năng lượng hóa học xảy ra.
Chọn C
Câu 33:
Khi thử pH dịch vị của người bình thường bằng giấy chỉ thị pH thì có thể có những màu nào sau đây?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đề bài đã cho về pH của dạ dày và hình 1 để tìm ra màu của chỉ thị pH tương ứng.
Lời giải
pH dịch vị dạ dày người bình thường là từ 2 - 4. Vậy màu của chỉ thị pH có thể là màu 3 và 4.
Chọn B, C
Câu 34:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào dữ kiện đầu bài cho.
Lời giải
Theo dữ kiện trong đầu bài, cây khoai lang phù hợp để trồng trong khoảng pH từ 5,5 - 6,8.
Chọn D
Câu 35:
Một mảnh đất có nồng độ ion H+: [H+] = 10-5,3 - 10-5,6. Mảnh đất này phù hợp trồng những loại cây nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Từ nồng độ ion H+ đã cho suy ra pH của mảnh đất. Từ đó tìm ra loại cây trồng phù hợp với pH của mảnh đất đấy.
Lời giải
Một mảnh đất có nồng độ ion H+: [H+] = 10-5,3 - 10-5,6 nên pH của mảnh đất này nằm trong khoảng từ 5,3 - 5,6.
Tại pH trong khoảng từ 5,3 - 5,6 thích hợp trồng khoai tây và khoai lang.
Chọn C, D
Câu 36:
Nhận định dưới đây là đúng hay sai?
Người ta có thể trồng cả khoai lang và cà chua trên cùng một mảnh đất.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào pH cần cho cây cà chua và cây khoai lang, nếu hai loại cây này có trùng khoảng pH thì hai loại cây này có thể được trồng trên cùng một mảnh đất.
Lời giải
- Cà chua cần trồng trên mảnh đất có pH trong khoảng 6,0 - 7,0.
- Khoai lang cần trồng trên mảnh đất có pH trong khoảng từ 5,5 - 6,8.
Cả hai loại cây này có trùng khoảng pH là từ 6,0 - 6,8.
Vậy hai loại cây này có thể trồng trên cùng một mảnh đất có độ pH từ 6,0 - 6,8.
Chọn A
Câu 37:
Nhận định dưới đây là đúng hay sai?
Việc thiếu acid trong dạ dày là một nguyên nhân gây nên bệnh nhiễm khuẩn đường tiêu hoá.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đã cung cấp trong đề bài.
Lời giải
Thiếu axit trong dạ dày tức là thiếu HCl. Vì nhiệm vụ của HCl là sát khuẩn, tiêu diệt vi khuẩn có trong thức ăn nên nếu thiếu HCl sẽ gây ra nhiễm khuẩn đường tiêu hoá.
Chọn A
Câu 38:
Trong môi trường acid, diệp lục có màu từ vàng đến đỏ, còn trong môi trường kiềm diệp lục có màu xanh. Hoàn thành nhận định dưới đây:
màu xanh, màu đỏ, màu vàng, axit hơn, kiềm hơn
Khi vắt chanh vào nước luộc rau muống thì màu của nước luộc rau sẽ chuyển từ _______ thành _______ do sau khi vắt chanh đã làm thay đổi môi trường nước luộc rau _______ vì vậy làm cho diệp lục trong nước rau cũng đổi màu theo trong nước rau cũng đổi màu theo.
 Xem đáp án
Xem đáp án
Đáp án
Khi vắt chanh vào nước luộc rau muống thì màu của nước luộc rau sẽ chuyển từ màu xanh thành màu vàng do sau khi vắt chanh đã làm thay đổi môi trường nước luộc rau axit hơn vì vậy làm cho diệp lục trong nước rau cũng đổi màu theo trong nước rau cũng đổi màu theo.
Phương pháp giải
Dựa vào quá trình đổi màu của diệp lục.
Lời giải
Khi vắt nước chanh là cung cấp thêm axit cho nước rau, vì vậy diệp lục đổi màu theo tính axit của nước rau.
Câu 39:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào pH của đất trồng khoai để suy ra môi trường đất tương ứng.
Lời giải
Khoai tây trồng trong đất có pH từ 5,0 - 6,0, khoai lang trồng trong đất có pH từ 5,5 - 6,8 là môi trường axit nhẹ vì pH < 7.
Chọn B
Câu 40:
Đất có nhiều tế bào sống trên mỗi mm3 thường tiêu thụ nhiều oxi hơn đất có ít tế bào sống hơn. Đất của trang trại nào sẽ tiêu thụ nhiều oxi hơn?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào dữ liệu bảng 3, nông trại nào nhiều tế bào sống trên 1 mm3 sẽ tiêu thụ nhiều oxi nhất.
Lời giải
Dựa vào dữ liệu bảng 3, nông trại 5 có nhiều tế bào sống nhất nên tiêu thụ nhiều oxi nhất.
Chọn C
Câu 41:
Trong nghiên cứu 2, nếu trước và sau khi nung mẫu đất ở nhiệt độ 500oC trong 20 phút và loại bỏ tro, khối lượng của mẫu gần như nhau, kết luận nào sau đây đúng?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào mục đích của việc nung mẫu đất đến 500oC trong 20 phút được cho ở trong đoạn thông tin.
Lời giải
Đất đã bị loại bỏ hết nước trước khi được nung nóng đến 500oC vì vậy lựa chọn (A) và (B) đều không đúng. Lý do các nhà khoa học làm nóng đất đến 500oC trong 20 phút là đốt cháy hết chất hữu cơ. Nói cách khác, khoáng chất vẫn còn và chất hữu cơ biến mất. Vì vậy, nếu có ít hoặc không có chất hữu cơ thì khối lượng của đất sẽ ít hoặc không có sự thay đổi.
Chọn C
Câu 42:
Trong nghiên cứu 2, trước khi nung mẫu đến 500oC, các nhà khoa học cần làm khô mẫu đất để đảm bảo rằng
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc đoạn ngữ liệu và tìm ra mục đích của việc làm khô mẫu đất trước khi nung.
Lời giải
Khối lượng chất hữu cơ được xác định bằng cách nung mẫu đến 500oC, loại bỏ tro và tính chênh lệch khối lượng trước và sau khi nung. Nếu có nước, nó sẽ bay hơi và khối lượng nước của nó sẽ được tính vào khối lượng chất hữu cơ. Việc đưa nước vào trọng lượng ban đầu sẽ khiến ước tính trọng lượng của chất hữu cơ cao một cách không hợp lí.
Chọn D
Câu 43:
Nhận định dưới đây là đúng hay sai?
Dựa trên nghiên cứu 2, nếu các nhà khoa học lấy mẫu đất từ một trang trại khác và số lượng tế bào sống trên mỗi mm3 được xác định là 2,100 thì % chất hữu cơ trong đất đó rất có thể sẽ là giữa 4,8% và 6,6%.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào mục đích của việc nung mẫu đất đến 500oC trong 20 phút được cho ở trong đoạn thông tin.
Lời giải
Trong bảng 3, lưu ý rằng khi % chất hữu cơ tăng lên thì số lượng tế bào sống trên mỗi tế bào sống trên mỗi mm3. Với 2,100 tế bào sống trên mỗi mm3, mẫu giả định sẽ nằm ở khoảng giữa nông trại 3 và 4. Do đó, % chất hữu cơ cũng sẽ nằm ở giữa nông trại 3 và 4, hoặc từ 4,8% đến 6,6%.
Chọn A
Câu 44:
Điền số thích hợp vào chỗ trống:
Đậu phát triển nhanh nhất ở đất có hàm lượng nitơ và sắt cao. Nếu tất cả điều kiện khác đều bằng nhau thì dựa trên kết quả của nghiên cứu 1, nông trại _______ sẽ sản xuất ra loại đậu phát triển nhanh nhất?
 Xem đáp án
Xem đáp án
Đáp án đúng là “5”
Phương pháp giải
Dựa vào dữ liệu bảng 5, nông trại nào có hàm lượng nitơ và sắt cao nhất thì đậu sẽ phát triển tốt nhất.
Lời giải
Nhìn vào hàm lượng nitơ và sắt trong bảng 2 thấy rằng hàm lượng trong đất của nông trại 5 (lần lượt là 210 và 165) là cao nhất.
Câu 45:
Mối quạn hệ giữa hàm lượng chất hữu cơ và tế bào sống trong đất là _______ với nhau.
 Xem đáp án
Xem đáp án
Đáp án
Mối quạn hệ giữa hàm lượng chất hữu cơ và tế bào sống trong đất là tỉ lệ thuận với nhau.
Phương pháp giải
Dựa vào dữ liệu bảng 3.
Lời giải
Dựa vào bảng 3, phần trăm chất hữu cơ và lượng tế bào sống trong đất tỉ lệ thuận với nhau.
Câu 46:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào dữ liệu bảng 1 và bảng 2.
Lời giải
Nông trại 4 có hàm lượng P là 94% so với nồng độ lý tưởng. Vậy nồng độ P của nông trại 4 là: 14.94% = 13,16 ppm.
Chọn B
Câu 47:
Điền từ thích hợp vào chỗ trống
Đơn phân cấu tạo nên nucleic acid là nucleotide. Các nucleotide liên kết với nhau bằng liên kết _______ theo chiều 5’ – 3’ tạo thành mạch polynucleotide được gọi là cấu trúc bậc 1 của DNA.
 Xem đáp án
Xem đáp án
Đáp án đúng là “cộng hóa trị”
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Đơn phân cấu tạo nên nucleic acid là nucleotide. Các nucleotide liên kết với nhau bằng liên kết cộng hóa trị theo chiều 5’ – 3’ tạo thành mạch polynucleotide được gọi là cấu trúc bậc 1 của DNA.
Đáp án: cộng hóa trị
Câu 48:
Nhận định dưới đây là đúng hay sai?
Do tính chất bổ sung giữa các cặp nitrogenous base nên số lượng các loại nucleotide A = T, G = C.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Khi Erwin Chargaff và cộng sự phân tích thành phần DNA của nhiều sinh vật khác nhau, họ thấy rằng nồng độ của thymine luôn bằng nồng độ của adenine và nồng độ của cytosine luôn bằng với nồng độ của guanine. Trên cơ sở đó, họ đã đưa ra kết luận: số lượng A = T, G = C
Đáp án: A
Câu 49:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Thành phần cấu tạo của đơn phân nucleotide gồm
(1) một phân tử photphoric acid
(2) một phân tử đường 5C (pentose): deoxyribose (C5H10O4) ở DNA và ribose (C5H10O5) ở RNA
(3) một trong các loại nitrogenous bases (A, G, T, C).
--> Bốn loại nuclêôtit trong cấu trúc phân tử DNA phân biệt nhau ở thành phần: Nitrogenous bases
Chọn A
Câu 50:
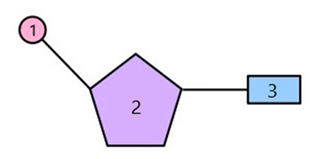
Hình ảnh sau mô tả cấu trúc một đơn phân nucleotit của phân trử AND. Hãy cho biết các thành phần cấu tạo tương ứng trong một nucleotit?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Chú thích đúng là: 1- axit phosphoric, 2- đường deoxyribose, 3-base nitơ
Chọn C
Câu 51:
Đoạn mạch thứ nhất của gen có trình tự các các nuclêôtit là 3'ATGTAXXGTAGG-5'. Trình tự các các nuclêôtit của đoạn mạch thứ hai là
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
- Áp dụng theo nguyên tắc bổ sung: A liên kết với T bằng 2 liên kết H, G liên kết với X bằng 3 liên kết H và ngược lại
- Các nucleotit trên hai mạch liên kết ngược chiều
Đoạn mạch thứ nhất của gen có trình tự các các nuclêôtit là 3'ATGTAXXGTAGG-5'
--> Trình tự các các nuclêôtit của đoạn mạch thứ hai là 5’-TAXATGGXATXX-3’.
Chọn D
Câu 52:
Có 2 loài vi khuẩn được tìm thấy ở 2 môi trường sống khác nhau là môi trường suối nước nóng và môi trường bình thường. Khi phân tích ADN, các nhà khoa học thấy loài 1 có tỉ lệ (A+T)/(G+X) = 1,3; loài 2 có tỉ lệ này = 0,4. Hãy dự đoán môi trường sống của 2 loài này?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
- Tỷ lệ (A+T) / (G+ X) phản ánh số lượng liên kết Hidro trong phân tử ADN. Theo nguyên tắc bổ sung (A liên kết với T bằng 2 liên kết H, G liên kết với X bằng 3 liên kết H và ngược lại), tỷ lệ (A+T) / (G+ X) tỷ lệ nghịch với số lượng liên kết H trong phân tử.
- Số lượng liên kết H tỷ lệ thuận với khả năng chịu nhiệt của phân tử ADN (
+, Loài 1 có tỉ lệ (A+T)/(G+X) = 1,3 => có ít liên kết H hơn => sống ở MT bình thường
+ Loài 2 có tỉ lệ (A+T)/(G+X) = 0,4 => có nhiều liên kết H hơn => sống ở MT suối nước nóng
Chọn B
Câu 53:
Điền các đáp án chính xác vào chỗ trống
Khi phân tích vật chất di truyền của một số loài, người ta thu được kết quả sau đây:
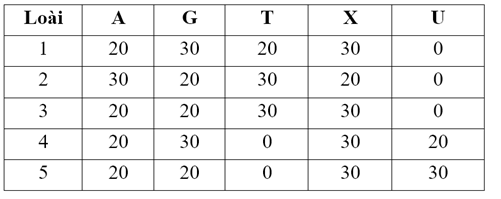
Loài 1: ADN mạch _______
Loài 2: ADN mạch _______
Loài 3: ADN mạch _______
 Xem đáp án
Xem đáp án
Đáp án đúng là:
Loài 1: ADN mạch kép
Loài 2: ADN mạch kép
Loài 3: ADN mạch đơn
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
1 – B: Vật chất DT gồm 4 loại đơn phân: A, T, G, X chứng tỏ là ADN. Số Nu loại A = T, G = X theo nguyên tắc bổ sung chứng tỏ là mạch ADN kép
2 – B: Vật chất DT gồm 4 loại đơn phân: A, T, G, X chứng tỏ là ADN. Số Nu loại A = T, G = X theo nguyên tắc bổ sung chứng tỏ là mạch ADN kép
3 – A: Vật chất DT gồm 4 loại đơn phân: A, T, G, X chứng tỏ là ADN. Số Nu loại A ≠ T, G ≠ X theo nguyên tắc bổ sung chứng tỏ là mạch ADN đơn
4 – C: Vật chất DT gồm 4 loại đơn phân: A, T, G, U chứng tỏ là ARN
5 – C: Vật chất DT gồm 4 loại đơn phân: A, T, G, U chứng tỏ là ARN
Câu 54:
Điền từ thích hợp vào chỗ trống
Sâu bột (Tenebrio molitor) có vòng đời phát triển qua biến thái _______ gồm các giai đoạn: trứng; ấu trùng; nhộng và bọ trưởng thành.
 Xem đáp án
Xem đáp án
Đáp án đúng là “hoàn toàn”
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Sâu bột (Tenebrio molitor) có vòng đời phát triển qua biến thái hoàn toàn gồm các giai đoạn: trứng; ấu trùng; nhộng và bọ trưởng thành
Câu 55:
Nhận định dưới đây là đúng hay sai?
Trong suốt vòng đời của sâu bột, giai đoạn ấu trùng tồn tại trong thời gian lâu nhất.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Gian đoạn ấu trùng của sâu bôt tồn tại khoảng 45 ngày, là giai đoạn tồn tại lâu nhất.
Đáp án: A
Câu 56:
Nhận định dưới đây là đúng hay sai?
Trong thí nghiệm thứ hai, mỗi nhóm được cho ăn 4 loại thức ăn?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Trong thí nghiệm hai, các sinh viên chia sâu bột ra làm 4 nhóm, mỗi nhóm chỉ cho ăn một loại thức ăn.
Đáp án: B
Câu 57:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Nhóm sâu bột ăn lúa mì có chiều dài trung bình con trưởng thành lớn nhất: 21,3mm
Chọn D
Câu 58:
Theo bảng kết quả thí nghiệm 2, yếu tố nào sau đây không ảnh hưởng đến kích thước trưởng thành của con bọ cánh cứng Tenebrio molitor?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Kích thước ấu trùng ở 4 nhóm ăn 4 loại thức ăn khác nhau là không có sự khác biệt đáng kể: 25,8 – 24,5 – 24,9 – 25,3
=> Theo bảng kết quả thí nghiệm 2, kích thước ấu trùng không ảnh hưởng đến kích thước trưởng thành của con bọ cánh cứng Tenebrio molitor
Chọn A
Câu 59:
Ở thí nghiệm 2, nhóm sâu bột được nuôi bằng lúa mì có thời gian trung bình của giai đoạn ấu trùng là bao nhiêu ngày?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Ở thí nghiệm 2, nhóm sâu bột được nuôi bằng lúa mì có thời gian trung bình của giai đoạn ấu trùng là 57,2 ngày
Chọn D
Câu 60:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn đọc
Lời giải
Dựa vào hình 2, ta dễ dàng nhận thấy trong vòng đời phát triển, Tenebrio molitor phải trải qua ít nhất 20 ngàyCâu 61:
 Xem đáp án
Xem đáp án
Phương pháp giải
Tính trung bình 12 tháng.
Lời giải
Lương trung bình hàng tháng của anh ấy trong 12 tháng là
Câu 62:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dự đoán quy luật.
Lời giải
Ta thấy 8 = 3 + 5, tức là u1 = 3; u2 = u1 + 3 + 2
14 = 8 + 6, u3 = 14 = u2 + 3 + 3
21 = 14 + 7, u4 = 21 = u3 + 3 + 4
29 = 21+8, u5 = 21 = u4 + 3 + 5
=> Suy đoán dãy này là un+1 = un + 3 + n
Khi đó u6 = 29 + 3 + 6 = 38. Chọn D
Câu 63:
 Xem đáp án
Xem đáp án
Phương pháp giải
Chứng minh các số có đúng 3 ước là các số chính phương.
Lời giải
Ta có: 4=1.2.2
k là số có đúng 3 ước nên k là hợp số.
Mà k luôn có 2 ước là 1 và k
=> Khi phân tích ra thừa số nguyên tố thì chỉ có 1 thừa số nguyên tố p. Tức là k = pn.
Thật vậy, giả sử k = pm.qn với m ≠ n; p ≠ q thì số ước của k lớn hơn 3=> Loại.
Khi đó k = p2 với p là số nguyên tố gần 2 nhất.
⇒ p = 3
Vậy tổng của 3 ước số của k là: 1 + 3 + 9 = 13. Chọn A
Câu 64:
 Xem đáp án
Xem đáp án
Phương pháp giải
- Gọi số cần tìm là x ∈ N*
- Lập phương trình giải x.
Lời giải
Gọi số cần tìm là x ∈ N*
Khi đó 4x − 7 = (x − 7).11. Chọn A
Câu 65:
Mật khẩu cho hệ thống máy tính yêu cầu chính xác 6 ký tự. Mỗi ký tự có thể là một trong 26 chữ cái từ A đến Z hoặc một trong mười chữ số từ 0 đến 9. Ký tự đầu tiên phải là một chữ cái và ký tự cuối cùng phải là một chữ số. Có bao nhiêu mật khẩu khác nhau có thể có?
 Xem đáp án
Xem đáp án
Phương pháp giải
Quy tắc nhân
Lời giải
Vì kí tự đầu tiên phải là một chữ nên kí tự đầu tiên có 26 cách chọn.
Kí tự cuối cùng phải là một chữ số nên kí tự cuối cùng có 10 cách chọn.
4 kí tự ở giữa không bị giới hạn nên ở mỗi kí tự sẽ có (26+10)=36 cách chọn.
Vậy số mật khẩu khác nhau là: 26.10.364 = 9360 mật khẩu. Chọn C
Câu 66:
 Xem đáp án
Xem đáp án
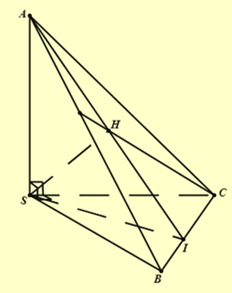
Ta có:
\(\left. {\begin{array}{*{20}{l}}{SA \bot SB}\\{SA \bot SC}\end{array}} \right\} \Rightarrow SA \bot (SBC).\)
\(\left. {\begin{array}{*{20}{l}}{BC \bot SA}\\{BC \bot SH}\end{array}} \right\} \Rightarrow BC \bot (SAH) \Rightarrow BC \bot AH\,\,(1)\)
Tương tự, ta có:
\(\left. {\begin{array}{*{20}{l}}{SC \bot SA}\\{SC \bot SB}\end{array}} \right\} \Rightarrow SC \bot (SAB)\)
\(\left. {\begin{array}{*{20}{l}}{AB \bot SC}\\{AB \bot SH}\end{array}} \right\} \Rightarrow AB \bot (SCH) \Rightarrow AB \bot CH\,\,(2)\)
Từ (1) và (2) suy ra H là trực tâm tam giác ABC. Chọn A
Câu 67:
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng công thức tính thể tích V = π.r2.h rồi rút ra chiều cao h
Lời giải
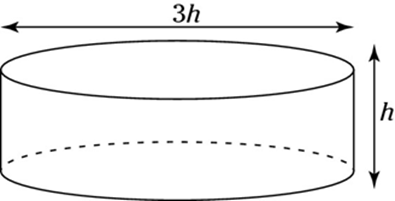
Thể tích của bể là: \(V = \pi .{r^2}.h = \pi .{\left( {\frac{{3h}}{2}} \right)^2}.h = \frac{{9\pi }}{4}.{h^3} = 231,5\)
⇒ h ≈ 3,2m. Chọn B
Câu 68:
 Xem đáp án
Xem đáp án
Phương pháp giải
- Gọi x, y, z lần lượt là số tiền mà Minh, Quyên và Vân quyên góp. (x, y, z > 0)
- Lập hệ phương trình từ đề bài.
Lời giải
Gọi x, y, z lần lượt là số tiền mà Minh, Quyên và Vân quyên góp. (x, y, z > 0)
Từ giả thiết ta có: \(\left\{ {\begin{array}{*{20}{l}}{x = y + z}\\{3y - x = 40}\\{z - 20 = \frac{x}{2}}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 200}\\{y = 80}\\{z = 120}\end{array}} \right.\)
Vậy Minh đã quyên góp 200 đô la. Chọn D
Câu 69:
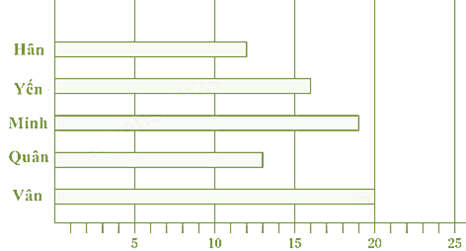
Cho biểu đồ cung cấp thông tin về số lượng khách hàng mới mà năm nhân viên bán hàng đã đăng ký vào tháng trước.
Điền các số thích hợp vào chỗ trống:
Yến đã đăng ký _____________ phần trăm khách hàng mới. Giả sử rằng tháng tới Vân đăng ký số lượng khách hàng gấp đôi so với tháng này và mỗi người trong số bốn nhân viên bán hàng còn lại đăng ký số lượng khách hàng bằng với số lượng khách hàng mà họ đã đăng ký trong tháng này. Trong trường hợp này, Vân sẽ đăng ký ___________ phần trăm khách hàng.
 Xem đáp án
Xem đáp án
Đáp án đúng là:
Yến đã đăng ký 20 phần trăm khách hàng mới. Giả sử rằng tháng tới Vân đăng ký số lượng khách hàng gấp đôi so với tháng này và mỗi người trong số bốn nhân viên bán hàng còn lại đăng ký số lượng khách hàng bằng với số lượng khách hàng mà họ đã đăng ký trong tháng này. Trong trường hợp này, Vân sẽ đăng ký 40 phần trăm khách hàng.
Phương pháp giải
- Lấy số khách mà Yến đã đăng ký chia cho tổng khách rồi nhân với 100%.
- Xác định lượng khách mà Vân đã đăng kí trong tháng này.
Lời giải
a) Tổng số lượng khách mà cả 5 nhân viên đăng kí là: 12 + 16 + 19 + 13 + 20 = 80
Yến đã đăng ký 16 khách hàng mới và chiếm phần trăm là: \(\frac{{16}}{{80}}.100\% = 20\% \)
b)
Vân đã đăng kí 20 khách trong tháng này. Khi đó số khách mà Vân đăng kí trong tháng sau là: 40 khách.
Tổng số lượng khách mà cả 5 nhân viên đăng kí tháng tới là: 12 + 16 + 19 + 13 + 20.2 = 100
Câu 70:
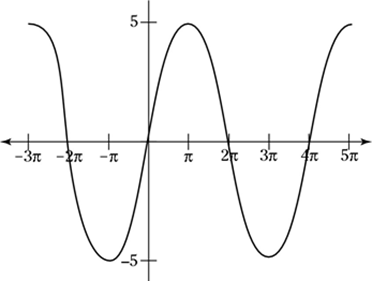
Cho đồ thị của hàm số hàm số \(y = a\sin kx\), với \(a,k > 0\)
Kéo thả đáp án vào ô trống thích hợp: 2π, 4π, 5/2, 10, -5, 5
Từ đồ thị ta thấy chu kì của hàm số là _____
Giá trị của a là _____
Giá trị của biểu thức \(\frac{a}{k}\) là _____
 Xem đáp án
Xem đáp án
Đáp án
Từ đồ thị ta thấy chu kì của hàm số là 4π
Giá trị của a là 5
Giá trị của biểu thức \(\frac{a}{k}\) là 10
Phương pháp giải
\(y = a\sin kx\) có chu kì là \(\frac{{2\pi }}{{|k|}}\)
Lời giải
Từ đồ thị ta thấy cứ đi được một khoảng 4π thì đồ thị lại lặp lại một lần nên chu kì của hàm số là 4π.
\(y = a\sin kx\) có chu kì là \(\frac{{2\pi }}{{|k|}}\)
Nên \(k = \frac{1}{2}\)
Giá trị lớn nhất của hàm số là 5 nên a = 5
\(\frac{a}{k} = \frac{5}{{\frac{1}{2}}} = 10\)
Câu 71:
 Xem đáp án
Xem đáp án
Phương pháp giải
Đồ thị \(y = f(x + p)\) thu được bằng cách tịnh tiến đồ thị \(y = f(x)\) sang trái p đơn vị
Lời giải
Đồ thị \(y = f(x + 2)\) thu được bằng cách tịnh tiến đồ thị \(y = f(x)\) sang trái 2 đơn vị
Chọn A
Câu 72:
Cho đồ thị hàm số \(y = f'(x)\) như hình vẽ
![Cho đồ thị hàm số \(y = f'(x)\) như hình vẽ Hàm số \(y = f(x)\) đạt giá trị lớn nhất trên khoảng [1;3] tại x0. Khi đó giá trị của \(x_0^2 - 2{x_0} + 2019\) bằng bao nhiêu? A. 2018 B. 2019 C. 2021 D. 2022 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid6-1729650225.png)
Hàm số \(y = f(x)\) đạt giá trị lớn nhất trên khoảng [1;3] tại x0. Khi đó giá trị của \(x_0^2 - 2{x_0} + 2019\) bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Dựa vào đồ thị của hàm số \(y = f'(x)\) ta có bảng biến thiên như sau
![Cho đồ thị hàm số \(y = f'(x)\) như hình vẽ Hàm số \(y = f(x)\) đạt giá trị lớn nhất trên khoảng [1;3] tại x0. Khi đó giá trị của \(x_0^2 - 2{x_0} + 2019\) bằng bao nhiêu? A. 2018 B. 2019 C. 2021 D. 2022 (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid5-1729650209.png)
Dựa vào bảng biến thiên suy ra hàm số \(y = f(x)\) đạt giá trị lớn nhất trên khoảng [1; 3] tại x0 = 2.
Vậy \(x_0^2 - 2{x_0} + 2019 = 2019\). Chọn B
Câu 73:
 Xem đáp án
Xem đáp án
Đáp án
A. Giá trị cực đại của hàm số \(y = f(x)\) luôn lớn hơn giá trị cực tiểu của nó.
B. Hàm số \(y = a{x^4} + bx + c(a \ne 0)\) luôn có ít nhất một cực trị.
C. Giá trị cực đại của hàm số \(y = f(x)\) luôn lớn hơn mọi giá trị của hàm số đó trên tập xác định.
D. Hàm số \(y = \frac{{ax + b}}{{cx + d}}\,\,(c \ne 0,ad - bc \ne 0)\) không có cực trị.
Phương pháp giải
Lời giải
A Sai vì nếu ta xét hàm số \(y = \frac{{{x^2} - x + 1}}{{x - 1}}\) thì ta có giá trị cực đại tại x = 0 là −1 , giá trị cực tiểu tại x=2 là 3.
B Đúng vì khi đạo hàm của hàm số bậc hai, ta luôn đưa về phương trình bậc nhất luôn có một nghiệm.
C Sai vì Giá trị lớn nhất của hàm số luôn lớn hơn hoặc bằng mọi giá trị khác của hàm số đó chứ không phải là giá trị cực đại.
D Đúng vì hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có đạo hàm luôn bé hơn hoặc lớn hơn không.
Chọn B, D
Câu 74:
 Xem đáp án
Xem đáp án
Phương pháp giải
Tính đạo hàm của \(y = \left( {a{x^2} + bx} \right){e^{ - cx}}\) rồi đồng nhất hệ số và số mũ.
Lời giải
Ta có:
\(y' = (2ax + b).{e^{ - cx}} + ( - c).\left( {a{x^2} + bx} \right){e^{ - cx}}\)
\( = \left[ { - ac{x^2} + (2a - bc)x + b} \right]{e^{ - cx}}\)
Khi đó \(\left[ { - ac{x^2} + (2a - bc)x + b} \right]{e^{ - cx}} = \left( { - {x^2} + 2} \right){e^{ - x}}\)
Đồng nhất hệ số ta được:
\(\left\{ {\begin{array}{*{20}{l}}{c = 1}\\{ac = 1}\\{2a - bc = 0}\\{b = 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{c = 1}\\{a = 1}\\{b = 2}\end{array}} \right.} \right.\)
Vậy \[a + b + c = 4\].
Chọn D
Câu 75:
Cho hàm số \(y = f(x)\) liên tục trên R và có bảng xét dấu \(y = f'(x)\) như sau

Mệnh đề nào sau đây sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Từ bảng xét dấu ta thấy hàm số \(y = f(x)\) có đúng 2 điểm cực trị.
\(y = f(x)\) đạt cực đại tại x = −2 và cực tiểu tại x = 5
Vậy C là mệnh đề sai.
Chọn C
Câu 76:
 Xem đáp án
Xem đáp án
Phương pháp giải
Tính y′; y′′.
Đồng nhất hệ số để tìm m.
Lời giải
\(y' = 3.{e^{3x}}\sin 5x + {e^{3x}}.5.\cos 5x = {e^{3x}}.(3\sin 5x + 5\cos 5x)\)
\(y'' = 3.{e^{3x}}.(3\sin 5x + 5\cos 5x) + {e^{3x}}.(15\cos 5x - 25\sin 5x)\)
\( = {e^{3x}}.(9\sin 5x + 15\cos 5x + 15\cos 5x - 25\sin 5x)\)
\( = {e^{3x}}.(30\cos 5x - 16\sin 5x)\)
\(6y' - y'' + my = 0\)
\( \Leftrightarrow 6.\left( {3.{e^{3x}}.\sin 5x + {e^{3x}}.5.\cos 5x} \right) - {e^{3x}}.(30\cos 5x - 16\sin 5x) + m{e^{3x}}.\sin 5x = 0\)
\( \Leftrightarrow {e^{3x}}.(34 + m)\sin 5x = 0\)
\( \Leftrightarrow m = - 34\)
Chọn B
Câu 77:
Cho đồ thị của hàm số \(y = 2{\cos ^2}x\) và đường thắng \(y = \frac{1}{2}\) sau:
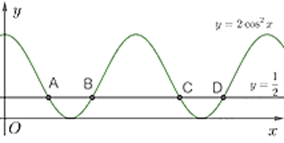
Tính \({x_D} - {x_A}\)
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Xét hoành độ giao điểm của đồ thị hàm số \(y = 2{\cos ^2}x\) và đường thẳng \(y = \frac{1}{2}\)
\(2{\cos ^2}x = \frac{1}{2} \Leftrightarrow \cos 2x = \frac{{ - 1}}{2}\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2x = \frac{{2\pi }}{3} + k2\pi }\\{2x = - \frac{{2\pi }}{3} + k2\pi }\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{3} + k\pi }\\{x = - \frac{\pi }{3} + k\pi }\end{array}} \right.} \right.\)
Xét \(x = \frac{\pi }{3} + k\pi \)
Với \(x \ge 0\) thì \(\frac{\pi }{3} + k\pi \ge 0 \Rightarrow x = \frac{\pi }{3};x = \frac{{4\pi }}{3};x = \frac{{7\pi }}{3}; \ldots \)
Xét \(x = - \frac{\pi }{3} + k\pi \)
Với \(x \ge 0\) thì \( - \frac{\pi }{3} + k\pi \ge 0 \Rightarrow x = \frac{{2\pi }}{3};x = \frac{{5\pi }}{3};x = \frac{{8\pi }}{3}; \ldots \)
Khi đó: \({x_D} = \frac{{5\pi }}{3};{x_A} = \frac{\pi }{3}\)
Vậy \({x_D} - {x_A} = \frac{{4\pi }}{3}\)
Chọn A
Câu 78:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
\({S_n} = \frac{{3{n^2} - 19n}}{4} = \frac{{n\left[ {2{u_1} + (n - 1)d} \right]}}{2}\)
\( = \frac{{\left( {2{u_1} - d} \right)}}{2}.n + \frac{d}{2}.{n^2}\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{{2{u_1} - d}}{2} = - \frac{{19}}{4}}\\{\frac{d}{2} = \frac{3}{4}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{u_1} = - 4}\\{d = \frac{3}{2}}\end{array}} \right.} \right.\)
Chọn B
Câu 79:
 Xem đáp án
Xem đáp án
Phương pháp giải
Bài toán này yêu cầu các em ghi nhớ công thức khoảng cách từ một điểm đến một đường thẳng.
Khoảng cách từ điểm \(M\left( {{x_0};{y_0}} \right)\) đến đường thẳng d: \(ax + by + c = 0\) là: \(d = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}.\)
Lời giải
Ta có \(x = 1 \Rightarrow y = 0;{f^\prime }(1) = 8 - 6 = 2\). Do đó phương trình tiếp tuyến là \[y = 2(x - 1)\,\,(d).\]
Do đó d: \(2x - y - 2 = 0\) suy ra \(d(O;d) = \frac{{| - 2|}}{{\sqrt 5 }}\).
Chọn A
Câu 80:
Một lớp học 40 học sinh gồm có 15 học sinh nam giỏi toán và 8 học sinh nữ giỏi. Chọn ngẫu nhiên một học sinh. Gọi A là biến cố chọn một nam sinh giỏi toán và B là biến cố chọn một nữ sinh giỏi lý.
a) A và B là hai biến cố _______
b) Xác suất để chọn được một nam sinh giỏi toán hay một nữ sinh giỏi lý là _______
 Xem đáp án
Xem đáp án
b) Xác suất để chọn được một nam sinh giỏi toán hay một nữ sinh giỏi lý là 23/40
Phương pháp giải
Lời giải
Ta có A∪B là biến cố chọn một nam sinh giỏi toán hay một nữ sinh giỏi lý.
Ta có \(P(A) = \frac{{15}}{{40}} = \frac{3}{8}{\rm{ v\`a }}P(B) = \frac{8}{{40}} = \frac{1}{5}\) A và B là hai biến cố xung khắc nên
\(P(A \cup B) = P(A) + P(B) = \frac{3}{8} + \frac{1}{5} = \frac{{23}}{{40}}\)
Câu 81:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Theo bài cho, tổng số viên bi có trong hộp là: n + 8 (n ∈ N*).
Lấy ngẫu nhiên 3 viên bi từ hộp. Số kết quả có thể xảy ra là: \(n(\Omega ) = C_{n + 8}^3\).
Gọi \(A\) là biến cố: "3 viên bi lấy được có đủ ba màu". Số kết quả thuận lợi cho \(A\) là:
\(n(A) = C_5^1.C_3^1.C_n^1 = 15n{\rm{. }}\)
\( \Rightarrow \) Xác suất để trong 3 viên bi lấy được có đủ ba màu là:
\(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{15n}}{{C_{n + 8}^3}} = \frac{{90n}}{{(n + 6)(n + 7)(n + 8)}}\)
Theo bài, ta có: \(P(A) = \frac{{45}}{{182}}\) nên ta được phương trình:
\(\frac{{90n}}{{(n + 6)(n + 7)(n + 8)}} = \frac{{45}}{{182}} \Leftrightarrow 364n = (n + 6)(n + 7)(n + 8)\)
\( \Leftrightarrow {n^3} + 21{n^2} - 218n + 336 = 0.\)
Giải phương trình trên với điều kiện \(n\) là số nguyên dương, ta được \(n = 6\).
Do đó, trong hộp có tất cả 14 viên bi và \(n(\Omega ) = C_{14}^3\).
Gọi \(B\) là biến cố: "3 viên bi lấy được có nhiều nhất hai viên bi đỏ". Suy ra, \(\bar B\) là biến cố: "3 viên bi lấy được đều là bi đỏ". Số kết quả thuận lợi cho \(\bar B\) là: \(n(\bar B) = C_5^3\).
Khi đó, xác suất \(P\) để trong 3 viên bi lấy được có nhiều nhất 2 viên bi đỏ là:
\(P = P(B) = 1 - P(\bar B) = 1 - \frac{{n(\bar B)}}{{n(\Omega )}} = 1 - \frac{{C_5^3}}{{C_{14}^3}} = \frac{{177}}{{182}}\).
Chọn B
Câu 82:
Cho hình hộp ABCD.A′B′C′D′ có các mặt là các hình vuông. Tính các góc (AA′,CD), (A′C′,BD), (AC,DC′).
Kéo thả các đáp án vào ô trống thích hợp: 90o, 60o, 90o, 30o, 30o, 45o
Góc (AA′,CD) là ____
Góc (A′C′,BD) là ____
Góc (AC,DC′) là ____
 Xem đáp án
Xem đáp án
Đáp án
Góc (AA′,CD) là 90o
Góc (A′C′,BD) là 90o
Góc (AC,DC′) là 60o
Phương pháp giải
Lời giải
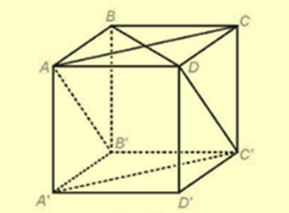
+) Vì CD // AB nên \(\left( {A\widehat {A',C}D} \right) = \left( {A\widehat {A',A}B} \right) = {90^^\circ }\) .
+) Tứ giác ACC′A′ có các cặp cạnh đối bằng nhau nên nó là một hình bình hành. Do đó, A′C′//AC. Vậy \[\widehat {\left( {A\prime C\prime ,BD} \right)} = \widehat {\left( {AC,BD} \right)} = {90^ \circ }.\]
+) Tương tự, DC′ // AB′DC′ // AB′. Vậy \[\widehat {\left( {AC,DC\prime } \right)} = \widehat {\left( {AC,AB\prime } \right)}\] . Tam giác AB′C có ba cạnh bằng nhau (vì là các đường chéo của các hình vuông có độ dài cạnh bằng nhau) nên nó là một tam giác đều.
Từ đó, \[\widehat {\left( {AC,DC\prime } \right)} = \widehat {\left( {AC,AB\prime } \right)} = {60^ \circ }\].
Câu 83:
Cho tứ diện ABCD có ba cạnh AB, AC, AD đôi một vuông góc.
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
Hình chiếu vuông góc của đỉnh Alên mặt phẳng (BCD) trùng với trọng tâm của tam giác BCD |
||
|
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} + \frac{1}{{A{D^2}}}\) |
||
|
Tam giác BCD có đúng 2 góc nhọn |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Hình chiếu vuông góc của đỉnh Alên mặt phẳng (BCD) trùng với trọng tâm của tam giác BCD |
|
x |
|
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} + \frac{1}{{A{D^2}}}\) |
x |
|
|
Tam giác BCD có đúng 2 góc nhọn |
|
x |
Phương pháp giải
a) Gọi H là hình chiếu vuông góc của điểm A trên mặt phẳng (BCD)
Chứng minh H là trực tâm của tam giác BCD
b) Gọi \(E = DH \cap BC\). Chứng minh \(\frac{1}{{A{E^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}\)
c) Đặt \(AB = x;\,\,AC = y{\rm{ v\`a }}AD = z\). Sử dụng định lí cos.
Lời giải
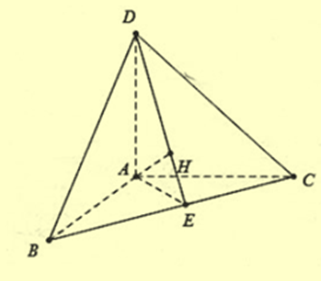
a) Gọi \(H\) là hình chiếu vuông góc của điểm \(A\) trên mặt phẳng \((BCD)\) thì \(AH \bot (BCD)\).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{AD \bot AB}\\{AD \bot AC}\end{array} \Rightarrow AD \bot (ABC) \Rightarrow AD \bot BC} \right.\).
Mặt khác \(AH \bot BC \Rightarrow BC \bot (ADH) \Rightarrow BC \bot DH\)
Tương tự chứng minh trên ta có: \(BH \bot CD\)
Do đó \(H\) là trực tâm của tam giác BCD.
=> Mệnh đề 1 sai
b) Gọi \(E = DH \cap BC\), do \(BC \bot (ADH) \Rightarrow BC \bot AE\).
Xét vuông tại \(A\) có đường cao \({\rm{AE}}\) ta có:
\(\frac{1}{{A{E^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}{\rm{. }}\)
Lại có: \(\frac{1}{{A{H^2}}} = \frac{1}{{A{D^2}}} + \frac{1}{{A{E^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} + \frac{1}{{A{D^2}}}\) (đpcm).
=> Mệnh đề 2 đúng.
c) Đặt \(AB = x;AC = y\) và \(AD = z\). Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BC = \sqrt {{x^2} + {y^2}} }\\{BD = \sqrt {{x^2} + {z^2}} }\\{CD = \sqrt {{y^2} + {z^2}} }\end{array}} \right.\)
Khi đó \(\cos B = \frac{{B{C^2} + B{D^2} - C{D^2}}}{{2.BC.BD}} = \frac{{{x^2}}}{{BC.BD}} > 0 \Rightarrow \widehat {CBD} < {90^^\circ }\)
Tương tự chứng minh trên ta cũng có \(\left\{ {\begin{array}{*{20}{l}}{\widehat {BDC} < {{90}^o}}\\{\widehat {BCD} < {{90}^o}}\end{array}} \right. \Rightarrow \) tam giác BCD có 3 góc nhọn.
=> Mệnh đề 3 sai
Câu 84:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
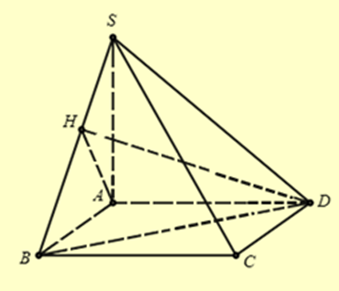
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{(SAB) \cap (SAD) = SA}\\{(SAB) \bot (ABCD)}\\{(SAD) \bot (ABCD)}\end{array}} \right. \Rightarrow SA \bot (ABCD)\)
Gọi H là hình chiếu của A trên SB ⇒AH ⊥ SB.
Dễ thấy AD ⊥ (SAB) ⇒ AD ⊥ SB.
Do đó: SB ⊥ (AHD) ⇒ SB ⊥ HD.
Khi đó ta có:
\(\left\{ {\begin{array}{*{20}{l}}{(SAB) \cap (SBD) = SB}\\{AH \bot SB;HD \bot SB}\\{AH \subset (SAB);HD \subset (SBD)}\end{array}} \right. \Rightarrow ((SAB);(SBD)) = \widehat {AHD} = {45^^\circ }\) .
Hay ΔAHD vuông cân tại A ⇒ AH = AD = a.
ΔSAB vuông tại A: \(\frac{1}{{S{A^2}}} = \frac{1}{{A{H^2}}} - \frac{1}{{A{B^2}}} = \frac{1}{{{a^2}}} - \frac{1}{{4{a^2}}} = \frac{3}{{4{a^2}}} \Rightarrow SA = \frac{{2a}}{{\sqrt 3 }}.\)
Suy ra \(V = {V_{S.ABC}} = \frac{1}{3}SA.{S_{ABCD}} = \frac{1}{3}.\frac{{2a}}{{\sqrt 3 }}.2{a^2} = \frac{{4{a^3}}}{{3\sqrt 3 }}\). Vậy \(\frac{V}{{{a^3}}} = \frac{4}{{3\sqrt 3 }} \approx 0,77\).
Chọn C
Câu 85:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Gọi cạnh hình lập phương là a. Ta có: \(6{a^2} = 96 \Leftrightarrow a = 4 \Rightarrow V = {a^3} = 64\)
Chọn C
Câu 86:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Ta \(L = \mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {2{x^2} - 7x + 12} }}{{3|x| - 17}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {{x^2}\left( {2 - \frac{7}{x} + \frac{{12}}{{{x^2}}}} \right)} }}{{3|x| - 17}}\)
\( = \mathop {\lim }\limits_{x \to - \infty } \frac{{|x|\sqrt {2 - \frac{7}{x} + \frac{{12}}{{{x^2}}}} }}{{3|x| - 17}}\)
\( = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - x\sqrt {2 - \frac{7}{x} + \frac{{12}}{{{x^2}}}} }}{{ - 3x - 17}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{\sqrt {2 - \frac{7}{x} + \frac{{12}}{{{x^2}}}} }}{{3 + \frac{{17}}{x}}} = \frac{{\sqrt 2 }}{3} = \frac{{\sqrt a }}{b} \to \left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b = 3}\end{array}} \right.\)
Chọn D
Câu 87:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
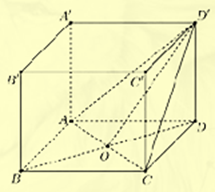
Giả sử cạnh của hình lập phương có độ dài là x.
Ta có \(AC = x\sqrt 2 ,OD' = \sqrt {O{D^2} + A'{A^2}} = \frac{{x\sqrt 6 }}{2}\)
\({S_{ACD'}} = \frac{1}{2}OD'.AC = \frac{1}{2}x\sqrt 2 .\frac{{x\sqrt 6 }}{2} = \frac{{{x^2}\sqrt 3 }}{2}\)
\( \Rightarrow {a^2}\sqrt 3 = \frac{{{x^2}\sqrt 3 }}{2}\)
\( \Leftrightarrow {a^2} = \frac{{{x^2}}}{2} \Leftrightarrow x = a\sqrt 2 \)
\( \Rightarrow V = {x^3} = 2{a^3}\sqrt 2 \)
Chọn B
Câu 88:
Cho hình chóp S.ABCD có đáy ABCD là một hình vuông, SA ⊥ (ABCD). Kẻ AH vuông góc với SC (H thuộc SC), BM vuông góc với SC (M thuộc SC).
Kéo thả các đáp án vào ô trống thích hợp: vuông goc, song song, nằm trênKhi đó SC _______ với (MBD).
AH ________ với (MBD).
 Xem đáp án
Xem đáp án
Đáp án
Khi đó SC vuông góc với (MBD).
AH song song với (MBD).
Phương pháp giải
Đặt O là trung điểm của AB, E là trung điểm của CD, N là trung điểm của BC.
Kẻ BD. Ta có MBD là tam giác vuông tại M.
Lời giải
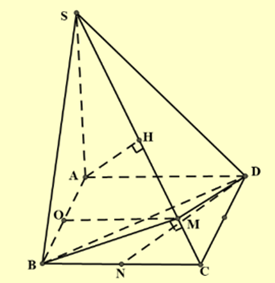
Đặt \(O\) là trung điểm của \({\rm{AB}}\), E là trung điểm của \({\rm{CD}},{\rm{N}}\) là trung điểm của \({\rm{BC}}\).
Ta có \(OM//ND\) vì \(OM//AB\) và \(ND//AB\). Do đó, .
Ta có \(SA//BC\) vì \({\rm{ABCD}}\) là hình vuông nên \(AH = \frac{1}{{\sqrt 2 }}SC,BM = \frac{1}{2}SC\), và \(MN = \frac{1}{2}BC = \frac{1}{2}SA\).
Kẻ BD. Ta có MBD là tam giác vuông tại \(M\).
Vì \(AH = \frac{1}{{\sqrt 2 }}SC\) và \(\frac{{OM}}{{MB}} = \frac{1}{2}\) nên \(\Delta OMB\) và \(\Delta AHS,\,\,\Delta OMB\) và \(\Delta AHS\) đồng dạng.
Vậy \(\widehat {AHS} = \widehat {OMB}\).
Tương tự, \(\Delta NDB\) và \(\Delta ASC\) đồng dạng nên \(\widehat {SCN} = \widehat {NDB}\).
Suy ra, \(\widehat {MBD} = \widehat {AHS} = \widehat {OMB}\) và \(SC \bot BD\). Do đó, \(SC \bot (MBD)\) và \(AH//(MBD)\).
Câu 89:
Người ta cần trang trí một kim tự tháp hình chóp tứ giác đều S.ABCD cạnh bên bằng 200m, góc ASB = 15o bằng đường gấp khúc dây đèn led vòng quanh kim tự tháp AEFGHIJKLS. Trong đó điểm L cố định và LS = 40 m (tham khảo hình vẽ). Hỏi khi đó cần dung ít nhất bao nhiêu mét dây đèn led để trang trí?
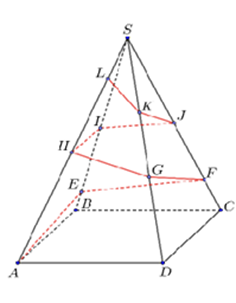
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Ta sử dụng phương pháp trải đa diện:
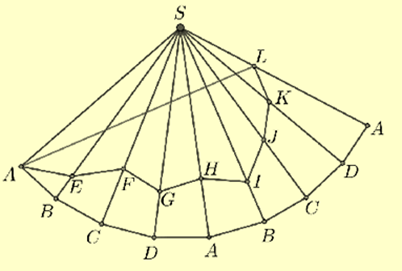
Cắt hình chóp theo cạnh bên SA rồi trải ra mặt phẳng hai lần như hình vẽ trên. Từ đó suy ra chiều dài dây đèn led ngắn nhất là bằng AL + LS.
Từ giả thiết về hình chóp đều S.ABCD ta có \[\widehat {ASL} = {120^o}\].
Ta có \[A{L^2} = S{A^2} + S{L^2} - 2SA.SL.\cos \widehat {ASL}\] \( = {200^2} + {40^2} - 2.200.40.\cos {120^^\circ } = 49600.\)
Nên \(AL = \sqrt {49600} = 40\sqrt {31} .\)
Vậy, chiều dài dây đèn led cần ít nhất là \(40\sqrt {31} + 40\) mét.
Chọn C
Câu 90:
 Xem đáp án
Xem đáp án
Phương pháp giải
Diện tích hình nón, thể tích khối nón (Đọc thêm)
Lời giải
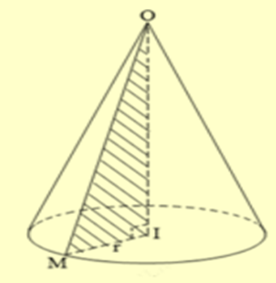
Ta có \(V = \frac{1}{3}\pi {r^2}h \Rightarrow 36\pi {a^3} = \frac{1}{3}\pi .9{a^2}h \Leftrightarrow h = 12a.\)
Chọn B
Câu 91:
Một khối cầu bằng thủy tinh có bán kính 4dm, người ta muốn cắt bỏ một chỏm cầu có diện tích mặt cắt là 15π(dm2) để lấy phần còn lại làm bể nuôi cá.
Hỏi thể tích nước tối đa mà bể cá này có thể chứa là bao nhiêu dm3?
(Làm tròn đến chữ số thập phân thứ hai)
Đáp án: _______
 Xem đáp án
Xem đáp án
Đáp án đúng là “183,26 | 183.26”
Phương pháp giải
Lời giải
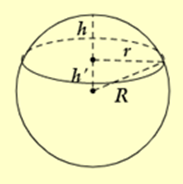
Gọi V, VC, VCh lần lượt là thể tích tối đa của bể nuôi cá có thể chứa, thể tích khối cầu bằng thủy tinh và thể tích chỏm cầu bị cắt bỏ.
Khi đó: \(V = {V_C} - {V_{Ch}} = \frac{4}{3}\pi {R^3} - \pi {h^2}\left( {R - \frac{h}{3}} \right)\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{R = 4\,\,(dm)}\\{S = 4\pi {r^2} = 15\pi \,\,\left( {d{m^2}} \right) \Rightarrow {r^2} = 15}\end{array}} \right.\)
Khi đó: \(h' = \sqrt {{R^2} - {r^2}} = \sqrt {{4^2} - 15} = 1 \Rightarrow h = R - h' = 3\,\,(dm)\)
Vậy thể tích nước tối đa mà bề cá này có thể chứa là:
\(V = \frac{4}{3}\pi {.4^3} - \pi {.3^2}\left( {4 - \frac{3}{3}} \right) = \frac{{175}}{3}\pi \,\,\left( {d{m^3}} \right)\)
Câu 92:
 Xem đáp án
Xem đáp án
Phương pháp giải
Hàm số logarit
Lời giải
Ta có: \(y' = \frac{1}{2}.\frac{{2x}}{{{x^2} + 4}} - m = \frac{x}{{{x^2} + 4}} - m\)
Hàm số \(y = \frac{1}{2}\ln \left( {{x^2} + 4} \right) - mx + 3\) nghịch biến trên \(\mathbb{R}\)
\( \Leftrightarrow \frac{x}{{{x^2} + 4}} - m \le 0\forall x \in \mathbb{R}\)
\( \Leftrightarrow m \ge \frac{x}{{{x^2} + 4}}\forall x \in \mathbb{R}\)
Xét hàm số \(g(x) = \frac{x}{{{x^2} + 4}}\) trên \(\mathbb{R}\)
Ta có: \(g'(x) = \frac{{1.\left( {{x^2} + 4} \right) - 2x.x}}{{{{\left( {{x^2} + 4} \right)}^2}}} = \frac{{4 - {x^2}}}{{{{\left( {{x^2} + 4} \right)}^2}}}\)
\(\begin{array}{l}g'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 2}\\{x = - 2}\end{array}} \right.\\\min g(x) = \frac{{ - 1}}{4};\max g(x) = \frac{1}{4}\\m \ge \frac{x}{{{x^2} + 4}}\forall x \in \mathbb{R} \Leftrightarrow m \ge \max g(x) = \frac{1}{4}\end{array}\)
Chọn B
Câu 93:
Gọi \(S\) là tổng các nghiệm của phương trình \({9^{\frac{x}{2}}} + 9.{\left( {\frac{1}{{\sqrt 3 }}} \right)^{2x + 2}} - 4 = 0\). Khi đó \(S\) thuộc những khoảng nào trong các khoảng dưới đây?
 Xem đáp án
Xem đáp án
Đáp án
A. \(\left( { - 1;1} \right)\)
B. \(\left( {0;2} \right)\)
C. \(\left( { - \frac{1}{2};\frac{3}{2}} \right)\)
D. \(\left( { - 2;0} \right)\)
Phương pháp giải
Lời giải
\({9^{\frac{x}{2}}} + 9.{\left( {\frac{1}{{\sqrt 3 }}} \right)^{2x + 2}} - 4 = 0 \Leftrightarrow {3^x} + 3.\frac{1}{{{3^x}}} - 4 = 0 \Leftrightarrow {3^{2x}} - {4.3^x} + 3 = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{3^x} = 1}\\{{3^x} = 3}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 1}\end{array} \Rightarrow S = 0 + 1 = 1.} \right.} \right.\)
Chon B, C
Câu 94:
 Xem đáp án
Xem đáp án
Phương pháp giải
- Đặt \(t = {\log _a}b\), biến đổi x, y và \(P\) theo \(t\).
- Sử dụng bất đẳng thức Cauchy.
Lời giải
Đặt \(t = {\log _a}b\). Vì \(a,b > 1\) nên \(t > 0\).
Ta có: \({a^x} = \sqrt {ab} \Rightarrow x = {\log _a}\sqrt {ab} = \frac{1}{2}\left( {1 + {{\log }_a}b} \right) = \frac{1}{2}(1 + t)\).
\({b^y} = \sqrt {ab} \Rightarrow y = {\log _b}\sqrt {ab} = \frac{1}{2}\left( {1 + {{\log }_b}a} \right) = \frac{1}{2}\left( {1 + \frac{1}{t}} \right)\).
Vậy \(P = x + 2y = \frac{1}{2}(1 + t) + 1 + \frac{1}{t} = \frac{3}{2} + \frac{t}{2} + \frac{1}{t} \ge \frac{3}{2} + \sqrt 2 \).
Dấu đắng thức xảy ra khi và chỉ khi \(\frac{t}{2} = \frac{1}{t} \Leftrightarrow b = {a^{\sqrt 2 }}\).
Giá trị nhỏ nhất của biểu thức \(P = x + 2y\) bằng \(\frac{3}{2} + \sqrt 2 \) thuộc nửa khoảng \(\left[ {\frac{5}{2};3} \right)\).
Chọn D
Câu 95:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Ta có 9 số có một chữ số, 90 số có hai chữ số (từ 10 đến 99 ) và 900 số có ba chữ số (từ 100 đến 999 ) nên ta phải dùng 9 + 90.2 + 900.3 = 2889 chữ số để viết tất cả các số có một, hai, ba chữ số. Vì 2889 < 3897 nên số trang của cuốn sách là một số có 4 chữ số.
Số các số có 4 chữ số đã viết là : (3897 − 2889) : 4 = 1008 : 4 = 252.
Số thứ 252 có 4 chữ số là số: 1000 + 252 − 1 = 1251.
Vậy quyển sách có 1251 trang.
Chọn B
Câu 96:
 Xem đáp án
Xem đáp án
\(\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {a{x^2} + x + 1} - \sqrt {{x^2} + bx - 2} } \right) = \mathop {\lim }\limits_{x \to - \infty } \frac{{(a - 1).{x^2} + (1 - b).x + 3}}{{\sqrt {a{x^2} + x + 1} + \sqrt {{x^2} + bx - 2} }}\)
\( = \mathop {\lim }\limits_{x \to - \infty } \frac{{(a - 1).x + 1 - b + \frac{3}{x}}}{{ - \sqrt {a + \frac{1}{x} + \frac{1}{{{x^2}}}} - \sqrt {1 + \frac{b}{x} - \frac{2}{{{x^2}}}} }}\)
\( = 1\,\,{\rm{khi}}\left\{ {\begin{array}{*{20}{l}}{a - 1 = 0}\\{1 - b}\\{ - \sqrt a - 1}\end{array} = 1 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = 3}\end{array} \Rightarrow a.b = 3} \right.} \right.\)
Chọn A
