Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 9)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 9)
-
140 lượt thi
-
100 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
Phần tư duy đọc hiểu
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung toàn văn bản.
Lời giải
- Ý chính của bài viết: văn bản trình bày những nghiên cứu về thực phẩm chức năng và đưa ra lời khuyên về sức khỏe. Từ đoạn [1] đến đoạn [5] trình bày những nghiên cứu về thực phẩm chức năng; từ đoạn [6] đến đoạn [8] đưa ra những lời khuyên về sức khỏe.
- Phân tích, suy luận:
+ Đáp án A sai vì chưa nêu ra được lời khuyên sức khỏe mà bài đọc có đề cập.
+ Đáp án C sai vì chưa nêu ra được lời khuyên sức khỏe mà bài đọc có đề cập.
+ Đáp án D sai vì chưa nêu ra những nghiên cứu về thực phẩm chức năng và chưa nêu ra được lời khuyên sức khỏe mà bài đọc có đề cập.
Chọn B
Câu 2:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Theo bài đọc, thị trường thực phẩm chức năng toàn cầu dự kiến sẽ tăng về quy mô từ 180,58 tỷ USD vào năm 2021 lên 243,83 tỷ USD vào năm 2026 với tốc độ tăng trưởng kép hàng năm là 6,2%.
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [1]
Lời giải
- Ý kiến trên: Đúng
- Đoạn [1] văn bản có đề cập: Theo Báo cáo thị trường toàn cầu năm 2022 về thực phẩm chức năng do The Business Reserch thực hiện, quy mô thị trường thực phẩm chức năng toàn cầu dự kiến sẽ tăng từ 180,58 tỷ USD vào năm 2021 lên 191,68 tỷ USD trong năm 2022 với tốc độ tăng trưởng kép hàng năm (CAGR) là 6,1%; dự kiến sẽ tăng lên 243,83 tỷ USD vào năm 2026 với tốc độ CAGR là 6,2%
Chọn A
Câu 3:
Điền một cụm từ không quá hai tiếng có trong bài đọc vào chỗ trống.
Nhiều người chọn sử dụng thực phẩm chức năng, nguyên nhân chủ yếu vì nghĩ cho _______ của mình và muốn đảm bảo dinh dưỡng hàng ngày.
 Xem đáp án
Xem đáp án
Đáp án: “sức khỏe”
Phương pháp giải
Căn cứ vào nội dung đoạn [2]
Lời giải
- Nhiều người chọn sử dụng thực phẩm chức năng, nguyên nhân chủ yếu vì nghĩ cho sức khỏe của mình và muốn đảm bảo dinh dưỡng hàng ngày.
- Phân tích, suy luận:
Đoạn 2 có trình bày: Lý do phổ biến nhất được mọi người đưa ra khi sử dụng thực phẩm chức năng là vì sức khỏe nói chung cũng như để lấp đầy khoảng trống về chất dinh dưỡng trong chế độ ăn uống.
→ Đáp án cần điền là: sức khỏe.
Câu 4:
Đoạn [2], Đoạn [4], Đoạn [5], Đoạn [8]
_______ đưa ra lời khuyên trong cách chọn thực phẩm chức năng.
_______ trình bày tác dụng phụ của việc bổ sung vitamin quá mức.
_______ trình bày lí do thúc đẩy mọi người sử dụng thực phẩm chức năng.
 Xem đáp án
Xem đáp án
Đáp án
Đoạn [8] đưa ra lời khuyên trong cách chọn thực phẩm chức năng.
Đoạn [5] trình bày tác dụng phụ của việc bổ sung vitamin quá mức.
Đoạn [2] trình bày lí do thúc đẩy mọi người sử dụng thực phẩm chức năng.
Phương pháp giải
Căn cứ vào nội dung của các đoạn trích [3], [4], [5], [8].
Lời giải
- Đưa ra lời khuyên trong cách chọn thực phẩm chức năng.
→ Đáp án đúng là: Đoạn [8]
Vì đoạn này đã đưa ra lời khuyên về một số đối tượng cần chọn thực phẩm chức năng cho phù hợp: Phụ nữ mang thai nên bổ sung 0,4-0,8 miligam axit folic/ngày; người cao tuổi có thể cần bổ sung thêm vitamin B12, vitamin B6 và vitamin D.
- Trình bày tác dụng phụ của việc bổ sung vitamin quá mức.
→ Đáp án đúng là: Đoạn [5]
Vì đoạn này trình bày một số tác dụng không mong muốn của việc bổ sung vitamin quá mức: sử dụng quá mức vitamin A có thể làm giảm mật độ khoáng của xương, ở liều cao có thể gây độc cho gan hoặc gây quái thai; Vitamin D có những tác hại tiềm ẩn khi dùng liều cao, chẳng hạn như nguy cơ tăng canxi trong máu và sỏi thận.
- Lí do thúc đẩy mọi người sử dụng thực phẩm chức năng.
→ Đáp án đúng là: Đoạn [2]
Vì đoạn này đã nêu ra rất rõ ràng: lý do phổ biến nhất được mọi người đưa ra khi sử dụng thực phẩm chức năng là vì sức khỏe nói chung cũng như để lấp đầy khoảng trống về chất dinh dưỡng trong chế độ ăn uống.
Dựa vào nội dung đoạn trên cùng cách phân tích và suy luận, ta có các cụm từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: Đoạn [8]
- Vị trí thả 2: Đoạn [5]
- Vị trí thả 3: Đoạn [2]
Câu 5:
Điền những cụm từ không quá hai tiếng có trong bài đọc vào chỗ trống.
USPSTF đã khẳng định rằng _______ bằng chứng để chứng minh lợi ích về việc tăng cường sức khỏe hay kéo dài tuổi thọ của một người bình thường khi dùng bổ sung các vitamin: E, D, A, B3, B6, C; canxi; beta carotene và selen và hoàn toàn _______ bằng chứng để khuyến cáo không nên sử dụng các chất bổ sung beta carotene.
 Xem đáp án
Xem đáp án
Đáp án:
USPSTF đã khẳng định rằng không đủ bằng chứng để chứng minh lợi ích về việc tăng cường sức khỏe hay kéo dài tuổi thọ của một người bình thường khi dùng bổ sung các vitamin: E, D, A, B3, B6, C; canxi; beta carotene và selen và hoàn toàn có đủ bằng chứng để khuyến cáo không nên sử dụng các chất bổ sung beta carotene.
Phương pháp giải
Căn cứ vào nội dung đoạn [3]
Lời giải
- Căn cứ vào nội dung đoạn [3] có trình bày: USPSTF đã từng thực hiện một nghiên cứu tương tự vào năm 2014. Kết luận không có gì thay đổi. Đó là: không đủ bằng chứng để chứng minh bất kỳ lợi ích nào về việc tăng cường sức khỏe hay kéo dài tuổi thọ của một người bình thường khi dùng bổ sung các vitamin: E, D, A, B3, B6, C; canxi; beta carotene và selen. Tuy nhiên, USPSTF cho biết, có đủ bằng chứng để khuyến cáo không nên sử dụng các chất bổ sung beta carotene.
- Phân tích, suy luận:
Từ các câu văn trên, ta có từ khoá “không đủ” và “có đủ” phù hợp để điền vào những chỗ trống của đề bài.
→ Đáp án cần điền là: không đủ/ có đủ.
USPSTF đã khẳng định rằng không đủ bằng chứng để chứng minh lợi ích về việc tăng cường sức khỏe hay kéo dài tuổi thọ của một người bình thường khi dùng bổ sung các vitamin: E, D, A, B3, B6, C; canxi; beta carotene và selen và hoàn toàn có đủ bằng chứng để khuyến cáo không nên sử dụng các chất bổ sung beta carotene.
Câu 6:
bằng chứng, hiểm nghèo, nghiên cứu, mạn tính, tài liệu
Các _______ đã chỉ ra rằng nhiều người chi tiền cho thực phẩm chức năng trong khi có ít _______ chứng minh lợi ích của chúng.Tiến sĩ Jeffrey Linder đưa ra lời khuyên về một lối sống lành mạnh với chế độ ăn cân bằng có nhiều trái cây, rau quả và hoạt động thể chất sẽ giúp ngăn ngừa các bệnh _______
 Xem đáp án
Xem đáp án
Đáp án
Các nghiên cứu đã chỉ ra rằng nhiều người chi tiền cho thực phẩm chức năng trong khi có ít bằng chứng chứng minh lợi ích của chúng.Tiến sĩ Jeffrey Linder đưa ra lời khuyên về một lối sống lành mạnh với chế độ ăn cân bằng có nhiều trái cây, rau quả và hoạt động thể chất sẽ giúp ngăn ngừa các bệnh mạn tính
Phương pháp giải
Căn cứ vào nội dung của toàn văn bản.
Lời giải
Phân tích, suy luận, loại trừ:
- Các _____ đã chỉ ra rằng nhiều người chi tiền cho thực phẩm chức năng trong khi có ít _____ chứng minh lợi ích của chúng.
→ Đáp án đúng là: nghiên cứu/ bằng chứng
+ Vì để chỉ ra những kết luận về khoa học phải dựa vào quá trình nghiên cứu, nghiền ngẫm kĩ lưỡng của các nhà khoa học, có cơ sở, có độ tin cậy cao vì vậy ở vị trí thả 1 điền từ “nghiên cứu” là hợp lý nhất (nghiên cứu được hiểu là xem xét, tìm hiểu kĩ để nắm vững vấn đề, giải quyết vấn đề hay để rút ra những hiểu biết mới).
+ Để chứng minh một điều gì đó người ta cần chứng cứ xác đáng, cụ thể, sinh động bởi vậy từ ngữ thích hợp nhất điền vào vị trí thả 2 là “bằng chứng”. Vì bằng chứng chính là thứ dùng để chứng minh tính chân thật của đối tượng.
- Tiến sĩ Jeffrey Linder đưa ra lời khuyên về một lối sống lành mạnh với chế độ ăn cân bằng có nhiều trái cây, rau quả và hoạt động thể chất sẽ giúp ngăn ngừa các căn bệnh _____.
→ Đáp án đúng là: mạn tính.
Vì bài đọc có đề cập “TS Jeffrey Linder (Trưởng Khoa Nội tổng hợp, Trường Đại học Feinberg - Đại học Northwestern, Hoa Kỳ) cho biết: một lối sống lành mạnh sẽ giúp ngăn ngừa các căn bệnh mãn tính” (bệnh mãn tính hay còn gọi là mạn tính).
Dựa vào nội dung đoạn trên cùng cách phân tích và suy luận, ta có các từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: nghiên cứu
- Vị trí thả 2: bằng chứng
- Vị trí thả 3: mạn tính
Câu 7:
Đâu là nội dung không được suy ra từ đoạn [4]?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [4]
Lời giải
- Nội dung không được suy ra từ đoạn [4] là: Dầu cá có thể ngăn chặn các bệnh nguy hiểm về tim.
- Phân tích, suy luận:
+ Đáp án A sai vì đoạn [4] có trình bày “Kết quả cho thấy, mọi thứ là “không thay đổi” khi bạn sử dụng vitamin hay giả dược.” -> Đáp án A có xuất hiện trong đoạn [4].
+ Đáp án B đúng vì đoạn [4] có trình bày “Theo PGS.TS Pieter Cohen: “Không có dữ liệu thuyết phục nào cho thấy bổ sung omega-3 có thể ngăn ngừa các cơn đau tim đối với những người có nguy cơ”.” (omega-3 chính là thành phần chính của dầu cá. Đoạn trích này khẳng định không có bằng chứng chứng minh dầu cá có tác dụng ngăn ngừa các cơn đau tim). -> Đáp án B không xuất hiện trong đoạn [4].
+ Đáp án C sai vì vì đoạn [4] có trình bày “Nhiều người tin rằng, những viên nang màu hổ phách chứa axit béo omega-3 DHA và EPA này có thể làm dịu chứng viêm, giúp ngăn ngừa cục máu đông.” (viên nang màu hổ phách chứa axit béo omega-3 DHA và EPA chính là dầu cá). -> Đáp án C có xuất hiện trong đoạn [4].
+ Đáp án D sai vì vì đoạn [4] có trình bày “Các đánh giá này dựa trên 22 nghiên cứu thử nghiệm so sánh vitamin với giả dược.” -> Đáp án D có xuất hiện trong đoạn [4].
Chọn B
Câu 8:
Đâu là nội dung đúng khi nói về các nghiên cứu về thực phẩm chức năng?
Chọn các đáp án đúng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung cả bài đọc.
Lời giải
- Phân tích, suy luận:
+ Đáp án A đúng vì đoạn [1] có trình bày “quy mô thị trường thực phẩm chức năng toàn cầu dự kiến sẽ tăng từ 180,58 tỷ USD vào năm 2021 lên 191,68 tỷ USD trong năm 2022 với tốc độ tăng trưởng kép hàng năm (CAGR) là 6,1%; dự kiến sẽ tăng lên 243,83 tỷ USD vào năm 2026 với tốc độ CAGR là 6,2%.” -> Con số tăng lên qua từng năm.
+ Đáp án B sai vì đoạn [1] có trình bày “Tính đến năm 2021, châu Á Thái Bình Dương là khu vực lớn nhất, Tây Âu là khu vực lớn thứ hai về thị trường thực phẩm chức năng.” -> Tây Âu là khu vực lớn thứ hai chứ không phải Đông Âu.
+ Đáp án C sai vì đoạn [3] có trình bày “Nhiều phụ nữ sau mãn kinh bổ sung vitamin D với hy vọng giảm gãy xương, nhưng USPSTF tuyên bố vitamin D kết hợp với canxi không ảnh hưởng đến tỷ lệ gãy xương ở phụ nữ mãn kinh.” -> Bài đọc khẳng định vitamin D kết hợp với canxi không ảnh hưởng đến tỷ lệ gãy xương.
+ Đáp án D đúng vì đoạn [5] có trình bày “Vitamin D có những tác hại tiềm ẩn khi dùng liều cao, chẳng hạn như nguy cơ tăng canxi trong máu và sỏi thận.”
Chọn A, D
Câu 9:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
|
|
ĐÚNG |
SAI |
|
Các khuyến nghị từ USPSTF không áp dụng cho người đang mang thai. |
||
|
Chế độ ăn Địa Trung Hải và chế độ ăn DASH đều hướng đến lối ăn thuần chay. |
||
|
Chế độ ăn cân bằng và các hoạt động thể dục thể thao giúp ngăn ngừa các bệnh mãn tính. |
||
|
Dầu cá là chất bổ sung phổ biến hàng đầu tại Mỹ. |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Các khuyến nghị từ USPSTF không áp dụng cho người đang mang thai. |
X | |
|
Chế độ ăn Địa Trung Hải và chế độ ăn DASH đều hướng đến lối ăn thuần chay. |
X | |
|
Chế độ ăn cân bằng và các hoạt động thể dục thể thao giúp ngăn ngừa các bệnh mãn tính. |
X | |
|
Dầu cá là chất bổ sung phổ biến hàng đầu tại Mỹ. |
X |
Phương pháp giải
Căn cứ vào 3 đoạn [4], [6], [7]
Lời giải
- Các khuyến nghị từ USPSTF không áp dụng cho người đang mang thai.
→ Ý kiến trên: ĐÚNG
Vì đoạn [6] nói rằng “Mặc dù vậy, nên lưu ý rằng, những khuyến nghị của USPSTF áp dụng cho những người không mang thai và những người bị mắc các căn bệnh về thiếu hụt dinh dưỡng.” (Những khuyến nghị đó không áp dụng cho người mang thai).
- Chế độ ăn Địa Trung Hải và chế độ ăn DASH đều hướng đến lối ăn thuần chay.
→ Ý kiến trên: SAI
Vì đoạn [7] nói rằng “Cả 2 chế độ ăn Địa Trung Hải và DASH đều tránh thực phẩm chế biến sẵn và tập trung vào trái cây, rau, đậu, ngũ cốc nguyên hạt” và hạn chế các loại thịt chứ không phải là lối ăn thuần chay.
- Chế độ ăn cân bằng và các hoạt động thể dục thể thao giúp ngăn ngừa các bệnh mãn tính.
→ Ý kiến trên: ĐÚNG
Vì đoạn [7] nói rằng “TS Jeffrey Linder (Trưởng Khoa Nội tổng hợp, Trường Đại học Feinberg - Đại học Northwestern, Hoa Kỳ) cho biết: một lối sống lành mạnh sẽ giúp ngăn ngừa các căn bệnh mãn tính”.
- Dầu cá là chất bổ sung phổ biến hàng đầu tại Mỹ.
→ Ý kiến trên: SAI
Vì đoạn [4] nói rằng “Sau vitamin và khoáng chất, dầu cá là chất bổ sung phổ biến thứ hai tại Hoa Kỳ và đang được khoảng 19 triệu người sử dụng.”
Câu 10:
Thông tin nào được suy ra từ đoạn trích trên?
Chọn các đáp án đúng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung của đoạn trích
Lời giải
Phân tích, suy luận:
- Thực phẩm chức năng không có tác dụng đối với người bình thường.
→ Ý kiến trên không được suy ra từ văn bản.
Vì đoạn 3 có trình bày “USPSTF cho biết, có đủ bằng chứng để khuyến cáo không nên sử dụng các chất bổ sung beta carotene (chất mà cơ thể chuyển hóa thành vitamin A), để ngăn ngừa bệnh tim mạch hoặc ung thư vì “có thể tăng nguy cơ tử vong do tim mạch và ung thư phổi”.”
- Không nên mua thực phẩm chức năng một cách tùy tiện.
→ Ý kiến trên được suy ra từ văn bản.
Vì bài đọc đã trình bày những nghiên cứu để bác bỏ tác dụng thần thánh của thực phẩm chức năng và khuyến cáo người tiêu dùng nên sử dụng một cách thông minh, tránh lạm dụng nó với hàng loạt lời nhắn nhủ: Tác dụng chưa rõ ràng và “lợi bất cập hại”; Thông điệp trên từ USPSTF có lẽ sẽ khiến chúng ta suy nghĩ kỹ hơn khi chi tiền cho việc mua thực phẩm chức năng.
- Một chế độ ăn uống cân bằng và lối sống lành mạnh sẽ tốt hơn việc dùng các thực phẩm chức năng.
→ Ý kiến trên được suy ra từ văn bản.
Vì bài đọc có trình bày: Kết quả cho thấy, mọi thứ là “không thay đổi” khi bạn sử dụng vitamin hay giả dược; một lối sống lành mạnh sẽ giúp ngăn ngừa các căn bệnh mãn tính, bao gồm chế độ ăn cân bằng có nhiều trái cây, rau quả và hoạt động thể chất.
- Phụ nữ mang thai và người già cần bổ sung nhiều vitamin để tránh thiếu hụt các chất trong cơ thể.
→ Ý kiến trên không được suy ra từ văn bản.
Vì đoạn cuối có trình bày: Phụ nữ mang thai nên bổ sung 0,4-0,8 miligam axit folic/ngày để ngăn ngừa dị tật bẩm sinh ống thần kinh cho thai nhi.[...] Bên cạnh đó, người cao tuổi thường ít tiếp xúc với ánh nắng mặt trời hơn so với những người trẻ tuổi. Họ có thể cần bổ sung vitamin D, nhưng liều lượng cần được bác sĩ kê đơn, vì các nghiên cứu cho thấy bổ sung quá nhiều vitamin D có thể gây hại cho cơ thể. -> Phụ nữ mang thai và người già cần bổ sung theo liều lượng nhất định và được bác sĩ kê đơn chứ không phải bổ sung nhiều vitamin là tốt.
Chọn B, C
Câu 11:
Truyện được kể theo ngôi kể nào?
Truyện được kể theo _______
 Xem đáp án
Xem đáp án
Đáp án: “ngôi thứ ba”
Phương pháp giải
Căn cứ vào cách xưng hô và các nhân vật trong câu chuyện
Lời giải
- Truyện được kể theo ngôi thứ ba.
- Nhân vật giấu mình, gọi tên của các nhân vật xuất hiện trong truyện: nó, mẹ nó, bố, cô Út,...
Câu 12:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Nhân vật “nó” trong truyện là đứa trẻ đáng thương, từ nhỏ đã mồ côi mẹ và luôn sống trong sự lạnh nhạt của cha.
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung câu chuyện
Lời giải
- Ý kiến trên: Sai
- Vì nhân vật “nó” là đứa trẻ đáng thương, mồ côi mẹ nhưng phần đầu truyện đã liệt kê những chi tiết thể hiện sự quan tâm, yêu thương của người cha dành cho con gái (đẽo voi cho con gái chơi, bế con ra vườn ru ngủ,...) mãi sau này khi có vợ mới, có thêm con, người bố mới lạnh nhạt với con gái.
=> Vì vậy, khẳng định “luôn sống trong sự lạnh nhạt của cha” là không đúng.
Chọn B
Câu 13:
tủi hờn, đau khổ, phấn khích, cảm động, sợ hãi
Tâm trạng của nhân vật “nó” khi được người lạ ngợi khen: _______
Tâm trạng của nhân vật “nó” mỗi khi bố đi làm về: _______
Tâm trạng của nhân vật “nó” từ khi bố mẹ có em bé: _______
 Xem đáp án
Xem đáp án
Đáp án
Tâm trạng của nhân vật “nó” khi được người lạ ngợi khen: sợ hãi
Tâm trạng của nhân vật “nó” mỗi khi bố đi làm về: phấn khích
Tâm trạng của nhân vật “nó” từ khi bố mẹ có em bé: tủi hờn
Phương pháp giải
Căn cứ vào nội dung của câu chuyện
Lời giải
Phân tích, suy luận, loại trừ:
- Tâm trạng của nhân vật “nó” khi được người lạ ngợi khen: sợ hãi.
→ Vì bài đọc nói rằng “Nó sợ những lời khen đó. Vì sau những lời khen người ta lại tỏ ra thương hại.” Điều này cho thấy “nó” không muốn nghe những lời khen, luôn sợ hãi khi ai đó khen mình, vì sau những lời khen là những sự ái ngại về hoàn cảnh của cô bé.
- Tâm trạng của nhân vật “nó” mỗi khi bố đi làm về: phấn khích.
→ Vì bài đọc nói rằng “Bao giờ ông cũng gọi từ cổng “Con ơi...” Chỉ chờ có vậy, nó chạy ra nhảy tót lên người bố, khúc khích cười.” Điều này cho thấy “nó” cảm thấy vô cùng phấn khích khi sau một ngày dài, bố trở về nhà với nó.
- Tâm trạng của nhân vật “nó” từ khi bố mẹ có em bé: tủi hờn.
→ Vì bài đọc nói rằng “Nó biết thân phận mình, nhưng trong lòng nó đắng cay vì bố đã quên nó rồi, dù nó đang sống cùng một nhà với ông. Ông quên rằng ông còn một đứa con gái bé bỏng, tội nghiệp.” Điều này cho thấy “nó” cảm thấy buồn bã, xót xa cho thân phận mình và có ý như oán trách người bố đã quên đi đứa con gái tội nghiệp.
Dựa vào nội dung đoạn trên cùng cách phân tích và suy luận, ta có các từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: sợ hãi
- Vị trí thả 2: phấn khích
- Vị trí thả 3: tủi hờn
Câu 14:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
|
|
ĐÚNG |
SAI |
|
Bố luôn bên cạnh chăm sóc “nó” kể từ khi mẹ mất |
||
|
Bố hát rất hay và thường ru “nó” vào mỗi tối |
||
|
Từ khi có em trai, bố cưng chiều em trai và không còn quan tâm đến “nó” |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Bố luôn bên cạnh chăm sóc “nó” kể từ khi mẹ mất |
X | |
|
Bố hát rất hay và thường ru “nó” vào mỗi tối |
X | |
|
Từ khi có em trai, bố cưng chiều em trai và không còn quan tâm đến “nó” |
X |
Phương pháp giải
Căn cứ vào nội dung câu chuyện
Lời giải
Phân tích, suy luận:
- Bố luôn bên cạnh chăm sóc “nó” kể từ khi mẹ mất.
→ Ý kiến trên: SAI
Vì bài đọc có trình bày các chi tiết người bố đi làm, cô bé phải ở nhà một mình, tự chơi các trò chơi quen thuộc, tự múa trước bàn thờ của mẹ, ngủ trên nền xi măng lạnh ngắt của nhà người hàng xóm khi bố đi công tác xa. Điều này cho thấy bố cô bé rất bận rộn và thường phải để con ở nhà một mình để đi làm nên ý “luôn bên cạnh chăm sóc” là không đúng.
- Bố hát rất hay và thường ru “nó” vào mỗi tối.
→ Ý kiến trên: ĐÚNG
Vì bài đọc nói rằng “Đêm đêm bố thường bế nó ra vườn, ru nó ngủ. Bố hát hay lắm.” Điều này cho thấy bố hát hay và thường ru con gái ngủ vào mỗi tối.
- Từ khi có em trai, bố cưng chiều em trai và không còn quan tâm đến “nó”.
→ Ý kiến trên: ĐÚNG
Vì bài đọc nói rằng “Từ khi có mẹ, có em bố gần như chẳng còn nhìn đến nó. Còn nó, luôn nhìn bố bằng ánh mắt chờ đợi. Nó biết thân phận mình, nhưng trong lòng nó đắng cay vì bố đã quên nó rồi, dù nó đang sống cùng một nhà với ông.” Điều này cho thấy từ khi có con trai và vợ mới, bố đã vô tình quên mất cô con gái tội nghiệp của mình.
Câu 15:
Theo đoạn [1], “nó” thường lặp lại những trò chơi quen thuộc, vì sao?
Chọn các đáp án đúng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung câu chuyện
Lời giải
- Theo đoạn [1], “nó” thường lặp lại những trò chơi quen thuộc, vì:
+ Bố quên mua đồ chơi mới cho nó (“Nó thích một con búp bê hơn. Bố hứa sẽ mua cho nó nhưng hai năm rồi nó chẳng thấy đâu.”).
+ Nó không có ai chơi cùng (bài đọc có khẳng định “Hình như nó không biết cười mà cũng không biết khóc, vì suốt ngày thui thủi trong nhà một mình thì khóc và cười với ai đây?” và phần đầu truyện có bày các chi tiết người bố đi làm, cô bé phải ở nhà một mình, tự ăn cơm trong lồng bàn bố để lại, tự chơi các trò chơi quen thuộc, tự múa trước bàn thờ của mẹ rồi nhìn sang nhà hàng xóm và ước ao được đi học giống những đứa trẻ hàng xóm).
- Phân tích, loại trừ:
+ Đáp án A sai vì bài đọc có đề cập “Nó thích một con búp bê hơn.”, cô bé thường lặp lại những trò chơi quen thuộc không phải vì thích mà vì trong nhà cô bé chỉ có những trò chơi này thôi, từ lâu rồi bố không mua thêm đồ chơi cho cô.
+ Đáp án D sai vì trong bài đọc không đề cập đến chi tiết này. Bài đọc chỉ đề cập chi tiết cô bé nhớ và khao khát mẹ khi bị bố gửi nhờ sang nhà hàng xóm để bố đi công tác xa.
Chọn B, C
Câu 16:
Điền một cụm từ không quá một tiếng có trong bài đọc vào chỗ trống.
Cuộc sống buồn tủi, cô đơn khiến cho cô bé trong câu chuyện quên đi những cảm xúc cơ bản của một con người. Nhưng có đôi khi cô bé vẫn khóc, cô bé khóc mỗi khi bị ______________ và cười vào lúc cô nhìn thấy hình ảnh của ________________
 Xem đáp án
Xem đáp án
Đáp án:
Cuộc sống buồn tủi, cô đơn khiến cho cô bé trong câu chuyện quên đi những cảm xúc cơ bản của một con người. Nhưng có đôi khi cô bé vẫn khóc, cô bé khóc mỗi khi bị ốm và cười vào lúc cô nhìn thấy hình ảnh của mẹ
Phương pháp giải
Căn cứ vào nội dung đoạn [4]
Lời giải
- Cuộc sống buồn tủi, cô đơn khiến cho “nó” quên đi những cảm xúc cơ bản của một con người. Nhưng có đôi khi cô bé vẫn khóc, cô bé khóc mỗi khi bị ốm và cười vào lúc cô nhìn thấy hình ảnh của mẹ.
- Lưu ý: Trong truyện có viết: Hình như nó không biết cười mà cũng không biết khóc, vì suốt ngày thui thủi trong nhà một mình thì khóc và cười với ai đây? Nó nhớ lại. Có chứ! Thỉnh thoảng nó cũng khóc mỗi khi nó ốm. Những lúc nó ốm, có một ông thầy thuốc già luôn đến tiêm thuốc cho nó, rất đau. Nó cũng biết cười, nhưng là cười với mẹ qua bức ảnh to bố đặt trên bàn thờ.
Câu 17:
nỏng nảy, bận rộn, xa xỉ, mỉm cười
Số phận không _______ với cô bé trong câu chuyện. Cô mồ côi mẹ, bản thân lại mang bệnh tật và sống cùng người cha _______.Cô bé có những điều ước vô cùng nhỏ bé nhưng đối với em lại quá _______: thèm được đến trường mẫu giáo, đợi được bố mua cho một con búp bê, ước có mẹ để được yêu thương, bảo vệ.
 Xem đáp án
Xem đáp án
Đáp án
Số phận không mỉm cười với cô bé trong câu chuyện. Cô mồ côi mẹ, bản thân lại mang bệnh tật và sống cùng người cha bận rộn.Cô bé có những điều ước vô cùng nhỏ bé nhưng đối với em lại quá xa xỉ: thèm được đến trường mẫu giáo, đợi được bố mua cho một con búp bê, ước có mẹ để được yêu thương, bảo vệ.
Phương pháp giải
Căn cứ vào nội dung của câu chuyện
Lời giải
Phân tích, suy luận, loại trừ:
- Số phận không _____ với cô bé trong câu chuyện.
→ Đáp án đúng là: mỉm cười
Vì bài đọc đã khắc họa nhân vật cô bé rơi vào hoàn cảnh mồ côi mẹ, lại mang bệnh tật (hen suyễn) và thường phải ở trong nhà một mình, tự ăn, tự chơi mà không được người lớn bế bồng, chăm bẵm. Điều này cho thấy số phận đã không mỉm cười khi để cô bé chịu quá nhiều thiệt thòi.
- Cô mồ côi mẹ, bản thân lại mang bệnh tật và sống cùng người cha _____.
→ Đáp án đúng là: bận rộn
Vì bài đọc khắc họa các chi tiết cô bé tự ở nhà, tự ăn, tự chơi để bố đi làm cả ngày. Có những lần công tác xa bố còn gửi nhờ nhà hàng xóm trông hộ con gái mình. Khiến cho cô bé luôn trong trạng thái nhớ nhung, mong ngóng chỉ đợi tiếng “Con ơi” là lao ra nhảy tót lên người bố.
- Cô bé có những điều ước vô cùng nhỏ bé nhưng đối với em lại quá _____: thèm được đến trường mẫu giáo, đợi được bố mua cho một con búp bê, ước có mẹ để được yêu thương, bảo vệ.
→ Đáp án đúng là: xa xỉ
Vì những mong muốn, khát khao của cô bé tuy nhỏ nhoi nhưng mãi không thành hiện thực bởi vậy nó xa xỉ đến mức cô bé không bao giờ có thể có được. Từ nhỏ, em đã không được đi học mẫu giáo, thèm một con búp bê nhưng bố mãi không mua nên đành chấp nhận chơi đồ chơi cũ, ước có mẹ để được yêu thương nhưng mẹ kế chỉ quan tâm em trai còn mẹ ruột của em không thể sống lại được.
Dựa vào nội dung câu chuyện cùng cách phân tích và suy luận, ta có các từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: mỉm cười
- Vị trí thả 2: bận rộn
- Vị trí thả 3: xa xỉ
Câu 18:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung câu chuyện
Lời giải
Nội dung không được suy ra từ câu chuyện là: Đấu tranh giữa cái ác và cái thiện, cái đẹp và cái xấu
Phân tích, suy luận:
- Tình cảm gia đình thiêng liêng.
→ Đây là một nội dung được suy ra từ câu chuyện vì cô bé trong truyện luôn khao khát tình mẹ cha, ước được giống nhà hàng xóm có cuộc sống bình dị đầy đủ các thành viên, ước có mẹ để được vỗ về. Những lúc một mình hay khi bị gửi nhờ ở nhà hàng xóm, cô bé cũng luôn khao khát hơi ấm của mẹ, của cha. Tất cả các chi tiết này đã khiến ta liên tưởng đến tình cảm gia đình thiêng liêng, quý giá.
- Trân trọng những mơ ước của trẻ thơ.
→ Đây là một nội dung được suy ra từ câu chuyện vì bài đọc nói về những mong ước của cô bé: thèm được đến trường mẫu giáo, đợi được bố mua cho một con búp bê, ước có mẹ để được yêu thương, bảo vệ. Những ước mơ tưởng chừng nhỏ bé và đôi khi người lớn không để tâm đến nhưng đối với trẻ thơ, chúng vô cùng quan trọng.
- Phân biệt đối xử trong gia đình sẽ khiến con cái dễ bị trầm cảm.
→ Đây là một nội dung được suy ra từ câu chuyện vì bài đọc có chi tiết từ khi bố mẹ có em bé mới, mọi người đã lãng quên cô bé, khiến cho cô bé “buồn bã”, “đắng cay”, “gương mặt đầy ưu tư, lặng lẽ”, “Ai nhìn nó cũng ái ngại”. Đó là những biểu hiện trầm cảm của một đứa trẻ không được gia đình quan tâm đủ đầy.
- Đấu tranh giữa các ác và cái thiện, cái đẹp và cái xấu:
→ Đây là một nội dung không được suy ra từ câu chuyện vì bài đọc không nói về sự đối lập hay xung đột giữa các giá trị hay nhân vật. Bài đọc chỉ nói về thân phận của cô bé đáng thương khi sống thiếu thốn tình cảm của cha mẹ.
Chọn D
Câu 19:
Theo văn bản, nhân vật “nó” hiện lên với những phẩm chất gì?
Chọn các đáp án đúng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung của văn bản
Lời giải
- Theo văn bản, nhân vật “nó” hiện lên với những phẩm chất:
+ Ngoan ngoãn, nhân hậu: ngoan ngoãn ở nhà một mình tự chơi, tự ăn, tự ngủ để bố đi làm; thích đồ chơi nhưng đợi 2 năm bố chưa mua vẫn không vòi vĩnh; bố nấu gì cũng chịu ăn; ở nhà hàng xóm phải nằm nền đất nhưng không dám than thở vì sợ bố buồn; buồn vì bố mẹ không quan tâm nhưng vẫn cố làm vui cho bố mẹ yên lòng; sung sướng khi có mẹ mới.
+ Siêng năng, tháo vát: ngoài giờ học, tranh thủ chơi với em và làm việc nhà; nghỉ hè sang nhà cô Út may vá và phụ việc nhà giúp cô.
- Phân tích, loại trừ:
+ Đáp án B sai vì bài đọc không đề cập đến tình hình hay kết quả học tập của nhân vật “nó”.
+ Đáp án C sai vì nhân vật “nó” trong bài đọc luôn ở trong trạng thái một mình, buồn bã, đắng cay; những khoảnh khắc vui vẻ ít ỏi trong văn bản chỉ thoáng qua và chủ yếu để làm hài lòng cha mẹ.
Chọn A, D
Câu 20:
Đâu là giọng điệu nổi bật trong văn bản trên?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung bài đọc và chọn giọng điệu phù hợp nhất.
Lời giải
- Văn bản trên nổi bật với giọng điệu nhẹ nhàng nhưng buồn thương day dứt. Cả bài đọc giống như một bản nhạc buồn, lặng lẽ về hoàn cảnh cô đơn, buồn bã của cô bé mồ côi mẹ, luôn khao khát tình yêu thương. Để rồi cái kết để lại cho người đọc sự thương cảm, day dứt và suy ngẫm về thân phận của những trẻ em thiếu thốn tình yêu thương.
- Phân tích, loại trừ:
+ Đáp án B sai vì ấm áp, chân tình là giọng điệu không xuất hiện trong văn bản trên. Đáp án này cũng không đề cập đến giọng điệu buồn thương xuất hiện xuyên suốt câu chuyện.
+ Đáp án C sai vì đằm thắm là giọng điệu không xuất hiện trong văn bản trên. Đáp án này cũng không đề cập đến giọng điệu buồn thương xuất hiện xuyên suốt câu chuyện.
+ Đáp án D sai vì văn bản trên không gợi ra những rung động êm dịu tinh tế. Đáp án này cũng không đề cập đến giọng điệu buồn thương xuất hiện xuyên suốt câu chuyện.
Chọn ACâu 21:
Phần tư duy khoa học / giải quyết vấn đề
Nhận xét nào sau đây về mối liên hệ giữa U, I và R là đúng?
Khi đặt cùng một hiệu điện thế vào hai đầu R1; R2 thì cường độ dòng điện chạy qua hai vật dẫn là:
|
|
ĐÚNG |
SAI |
|
bằng nhau |
||
|
khác nhau |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
bằng nhau |
X | |
|
khác nhau |
X |
Phương pháp giải
Phân tích thông tin và số liệu từ bảng
Vận dụng công thức định luật Ohm đã học: \(I = \frac{U}{R}\)
Lời giải
Ta có công thức định luật Ohm: \(I = \frac{U}{R}\)
Khi sử dụng cùng một hiệu điện thế thì giá trị của cường độ dòng điện qua các vật dẫn có điện trở khác nhau thì sẽ khác nhau
Câu 22:
Điền từ thích hợp vào chỗ trống:
Trong hình 1, ampe kế được mắc _______ với vật dẫn để đo cường độ dòng điện , vôn kế được mắc _______ với vật để đo hiệu điện thế giữa hai đầu vật dẫn.
 Xem đáp án
Xem đáp án
Đáp án đúng là:
Trong hình 1, ampe kế được mắc nối tiếp với vật dẫn để đo cường độ dòng điện , vôn kế được mắc song song với vật để đo hiệu điện thế giữa hai đầu vật dẫn.
Phương pháp giải
Quan sát hình ảnh bài cho
Vận dụng lí thuyết đã học về cách mắc các dụng cụ
Lời giải
Cách mắc ampe kế vào mạch : mắc nối tiếp sao cho chốt dương nối với cực dương chốt âm nối với cực âm
Cách mắc vôn kế vào mạch: mắc song song sao cho chốt dương nối với cực dương chốt âm nối với cực âm
=> Từ cần điền: nối tiếp, song song
Câu 23:
Hiệu điện thế của nguồn đo được qua vôn kế là 6V, khi đó cường độ dòng điện qua R2 là bao nhiêu?
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng thông tin từ bảng số liệu
Lời giải
Từ bảng 1 ta có hiệu điện thế của nguồn đo được qua vôn kế là 6V, khi đó cường độ dòng điện qua R2 là 1,31V
Chọn B
Câu 24:
Khi cường độ dòng điện qua vật 1 có giá trị xấp xỉ bằng 4,58mA thì hiệu điện thế của nguồn khi đó có thế là:
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng thông tin từ bảng số liệu
Vận dụng công thức \(I = \frac{U}{R}\)
Lời giải
Ta có công thức từ định luật Ohm: \(I = \frac{U}{R}\)
Ta thấy rằng với cùng giá trị của điện trở R thì khi giá trị cường độ dòng điện tăng sẽ ứng với hiệu điện thế tăng theo
=> để có thể có I xấp xỉ 4,68mA > giá trị cực đại tron bảng 3,45mA thì \(U > {U_{\max }} = 8\;{\rm{V}} \Rightarrow U = 9\;{\rm{V}}\)
Chọn D
Câu 25:
Khi mắc nối tiếp hai vật dẫn, khi đó điện trở của mạch điện được xác định bằng biểu thức nào sau đây?
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng lí thuyết đã học về điện trở tương đương của mạch
Lời giải
Khi mắc nối nối tiếp 2 điện trở ta có điện trở tổng của mạch sẽ được xác định bằng công thức: \[R = {R_1} + {R_2}\]
Chọn A
Câu 26:
Khi ghép song song hai vật dẫn rồi thay vào vị trí R1 và lặp lại các bước thí nghiệm. Khi vôn kế chỉ 8V thì ampe kế sẽ chỉ:
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng số liệu bài cho
Áp dụng công thức định luật Ohm: \(R = \frac{U}{I}\)
Áp dụng công thức tính điện trở khi mắc song song: \(R = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\)
Lời giải
Ta có khi vôn kế chỉ 8V thì:
\({R_1} = \frac{U}{{{I_1}}} = \frac{8}{{3,45}} \approx 2,32\Omega \)
\({R_2} = \frac{U}{{{I_2}}} = \frac{8}{{1,75}} \approx 4,57\Omega \)
Khi mắc song song 2 điện trở thì điện trở tương đương của mạch là:
\(R = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{{2,32.4,57}}{{2,32 + 4,57}} \approx 20,9\Omega \)
Cường độ dòng điện khi đó là: \(I = \frac{U}{R} = \frac{8}{{20,9}} \equiv 0,38A\)
Chọn C
Câu 27:
Đồ thị thể hiện mối quan hệ thể hiện đường đặc trưng U-I của vật rắn có nhiệt độ không đổi là:
|
|
ĐÚNG |
SAI |
|
đường parabol |
||
|
đường thẳng đi qua gốc toạ độ |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
đường parabol |
X | |
|
đường thẳng đi qua gốc toạ độ |
X |
Phương pháp giải
Sử dụng số liệu bài cho
Áp dụng công thức định luật Ohm: \(R = \frac{U}{I}\)
Lời giải
Khi nhiệt độ không đổi thì khi đó điện trở sẽ được xác định qua định luật Ohm: \(R = \frac{U}{I}\)
hay U = R.I có dạng tương tự hàm số y = ax
=> đồ thị sẽ là đường thẳng đi qua gốc toạ độ
Câu 28:
Dẫn nhiệt có thể xảy ra trong môi trường nào:
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc và phân tích thông tin bài đọc
Lời giải
Từ thông tin ta có:
Dẫn nhiệt: là quá trình truyền nhiệt năng khi có sự tiếp xúc trực tiếp giữa các vật (hoặc các phần của vật) có nhiệt độ khác nhau.
Từ đó ta có thể nhận định rằng dẫn nhiệt có thể xảy ra ở cả môi trường rắn, lỏng và khí
Chọn D
Câu 29:
Phát biểu sau đây đúng hay sai:
Vật càng đen thì hấp thụ tia bức xạ càng nhiều.
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin từ bài đọc cung cấp
Lời giải
Ta có Vật có bề mặt càng xù xì và màu càng sẫm thì hấp thụ tia nhiệt càng nhiều.
Vậy nên phát biểu trên là chính xác
Chọn A
Câu 30:
Số phát biểu đúng là:
(1) - Dẫn nhiệt thường xảy ra tốt nhất trong vật rắn
(2) - Đối lưu chỉ có thể xảy ra trong môi trường chất lỏng và chất khí
(3) - Mọi vật có nhiệt độ đều phát ra tia bức xạ
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin bài cung cấp
Lời giải
Ta có chất rắn là chất dẫn nhiệt tốt nhất => Dẫn nhiệt thường xảy ra tốt nhất trong vật rắn là đúng
Đối lưu nhiệt là quá trình trao đổi nhiệt xảy ra khi có sự dịch chuyển của khối chất lỏng hoặc chất khí
Tất cả các vật chất với nhiệt độ lớn hơn độ không tuyệt đối (0 K) đều phát ra bức xạ nhiệt.
=> cả 3 phát biểu trên đều đúng
Chọn B
Câu 31:
Quan sát hình ảnh dưới đây:
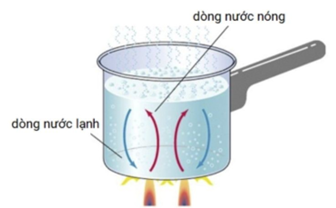
Phương pháp truyền nhiệt được thể hiện là _______
 Xem đáp án
Xem đáp án
Đáp án đúng là “đối lưu | đối lưu nhiệt”
Phương pháp giải
Phân tích thông tin từ bài đọc cung cấp
Lời giải
Ta thấy sự truyền nhiệt của dòng nước được thể hiện trong hình sẽ là phương pháp truyền nhiệt đối lưu
Câu 32:
Nhận xét sau đúng hay sai?
Có thể xảy ra đồng thời cả ba cách truyền nhiệt
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin bài cung cấp
Lời giải
Nhận xét trên là chính xác. Một ví dụ cụ thể nhất mô phỏng cho nhận xét trên đó là trường hợp ta đun nấu. Quá trình đun nấu được thể hiện qua hình ảnh sau đây.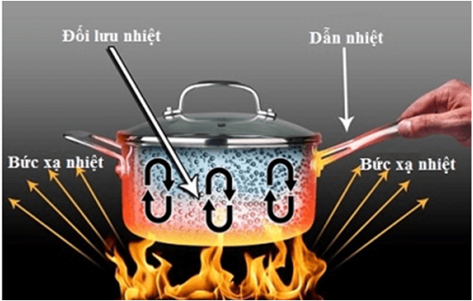
Câu 33:
Ở những nơi có mùa đông giá lạnh, khi làm cửa sổ người ta thường làm cửa sổ có hai hay ba lớp kính? Lý do là vì:
 Xem đáp án
Xem đáp án
Phương pháp giải
Vận dụng thông tin bài cung cấp
Lời giải
Người ta làm như thế là để ngăn cách quá trình truyền nhiệt từ trong nhà ra ngoài thông qua cửa sổ. Lớp không khí ở giữa được dùng như một lớp cách nhiệt.
Chọn B
Câu 34:
Cho các vật liệu sau đây: gỗ, nước biển, thép, bạc, nhôm. Thứ tự sắp xếp nào sau đây là đúng với khả năng dẫn nhiệt theo quy luật tăng dần?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa trên thông tin bài cung cấp
Vận dụng lí thuyế đã học
Lời giải
- Trong các vật liệu thì kim loại dẫn nhiệt rất tốt, nước dẫn nhiệt tốt và gỗ dẫn nhiệt kém.
- Vì vậy thứ tự sắp xếp là Gỗ, nước biển, thép.
Chọn A
Câu 35:
Dựa vào bảng 1, nếu đo lượng Fe2O3 được tạo ra trong ngày thứ 9 ở trong dung dịch nước muối thì giá trị thu được có thể là
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào số liệu bảng 1, nhận thấy khối lượng Fe2O3 được tạo ra trong môi các môi trường tăng lên theo thời gian. Vậy khối lượng Fe2O3 được tạo ra trong dung dịch nước muối của ngày thứ 9 sẽ phải nhiều hơn ngày thứ 8.
Lời giải
Tại ngày thứ 8, trong dung dịch nước muối, lượng Fe2O3 được tạo ra 1,84 g. Vậy sang ngày thứ 9, khối lượng Fe2O3 được tạo ra sẽ nhiều hơn 1,84 g.
Chọn D
Câu 36:
Thí nghiệm được thể hiện ở trong hình 1 và bảng 1, bằng cách đo tốc độ hình thành Fe2O3 mỗi ngày, những người thực hiện thí nghiệm cũng có thể đo được tốc độ của
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào phương trình hoá học và điều kiện môi trường của phản ứng xảy ra.
Lời giải
Phương trình hoá học cho thấy ngoài sự hình thành Fe2O3 còn một sản phẩm nữa được tạo ra là H2 cũng có thể đo được tốc độ tạo thành.
Chọn A
Câu 37:
Dựa vào bảng 1, lượng Fe2O3 được tạo ra bởi dung dịch nước đường tính từ ngày 6 đến ngày 8 là bao nhiêu?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào bảng 1, tìm lượng gỉ sắt được tạo ra ở ngày 6 và ngày 8 trong dung dịch nước đường.
Lời giải
Trong dung dịch nước đường:
- Lượng gỉ sắt được tạo ra ở ngày 6 là 0,11 g.
- Lượng gỉ sắt được tạo ra ở ngày 8 là 0,19 g.
Lượng Fe2O3 được tạo ra bởi dung dịch nước đường tính từ ngày 6 đến ngày 8 là: 0,19 – 0,11 = 0,08 g.
Chọn A
Câu 38:
Xem xét lượng Fe2O3 được tạo ra bởi dung dịch muối trong ngày 2. Dựa vào bảng 1 và hình 1, tại nước có đệm pH = 10 sẽ tạo ra một lượng Fe2O3 tương ứng như trên vào ngày thứ bao nhiêu?
 Xem đáp án
Xem đáp án
Phương pháp giải
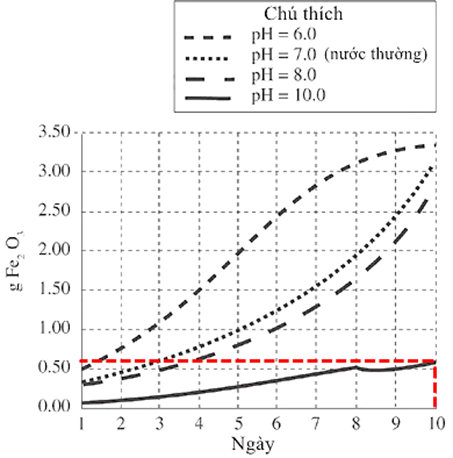
Tìm khối lượng Fe2O3 được tạo ra bởi dung dịch muối trong ngày thứ 2. Trong hình 1, ứng với đường biểu diễn pH = 10 và khối lượng gỉ sắt được tạo ra.
Lời giải
- Khối lượng gỉ sét được tạo ra bởi dung dịch muối trong ngày thứ 2 là 0,56 g.
- Trong môi trường nước cất có pH = 10, để tạo ra được một lượng Fe2O3xấp xi 0,56 g, cần đến ngày thứ 10.
Câu 39:
Dựa vào bảng 1, đồ thị nào thể hiện tốt nhất lượng Fe2O3 được tạo ra trong dung dịch nước đường theo thời gian?
 Xem đáp án
Xem đáp án
Phương pháp giải
Quan sát bảng 1 để rút ra sự thay đổi lượng Fe2O3 giữa các ngày để từ đó chọn được đồ thị phù hợp.
Lời giải
- Bảng 1 cho thấy trong dung dịch đường có 0,00 g Fe2O3 vào ngày thứ 2 nên loại đồ thị ở đáp án B và D.
- Các ngày sau đó theo số liệu thu thập được thì thấy mức tăng của Fe2O3 là đều đặn và ổn định trong những ngày tiếp theo. Đồ thị ở đáp án C cho thấy mức tăng lớn nhất của Fe2O3 giữa ngày 2 và ngày 6, sau đó tăng ít giữa ngày 6 và ngày 8. Bảng 1 cho thấy mức tăng lớn nhất của Fe2O3 là giữa Ngày 6 và Ngày 8, 0,08 g, vì vậy đồ thị đáp án C không thể đúng.
Chọn C
Câu 40:
Điền từ phù hợp vào chỗ trống để hoàn thành nhận định sau:
Trong dung dịch nước _______ thì tốc độ tạo thành gỉ sét là lớn nhất.
 Xem đáp án
Xem đáp án
Đáp án đúng là “muối”
Phương pháp giải
Nhìn vào bảng 1 để so sánh khối lượng gỉ sét được tạo ra trong ba dung dịch. Ở dung dịch nào tạo ra được khối lượng Fe2O3 nhiều nhất thì dung dịch đó tạo gỉ sét tốt nhất.
Lời giải
Trong 3 dung dịch, khối lượng ở Fe2O3 được tạo ra trong dung dịch muối là lớn nhất ở tất cả các ngày nên dung dịch muối tạo gỉ sét tốt nhất.
Câu 41:
Những nhận định sau là đúng hay sai?
|
|
ĐÚNG |
SAI |
|
pH càng lớn thì quá trình tạo thành gỉ sét càng tốt. |
¡ |
¡ |
|
Trong đời sống và sản xuất người ta mong muốn đẩy mạnh quá trình tạo thành gỉ sét. |
¡ |
¡ |
|
Quá trình tạo thành gỉ sét thực chất là phản ứng oxi hoá - khử. |
¡ |
¡ |
|
Nếu thực hiện thí nghiệm trên với dung dịch bao gồm 20 mL rượu nguyên chẩt pha với 100 mL nước thì quá trình tạo thành gỉ sét sẽ là nhanh nhất. |
¡ |
¡ |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
pH càng lớn thì quá trình tạo thành gỉ sét càng tốt. |
X | |
|
Trong đời sống và sản xuất người ta mong muốn đẩy mạnh quá trình tạo thành gỉ sét. |
X | |
|
Quá trình tạo thành gỉ sét thực chất là phản ứng oxi hoá - khử. |
X | |
|
Nếu thực hiện thí nghiệm trên với dung dịch bao gồm 20 mL rượu nguyên chẩt pha với 100 mL nước thì quá trình tạo thành gỉ sét sẽ là nhanh nhất. |
X |
Phương pháp giải
Dựa vào đồ thị trong hình 1 và kiến thức thực tế.
Lời giải
- Nhận định "pH càng lớn thì quá trình tạo thành gỉ sét càng tốt" là nhận định SAI. Dựa vào đồ thị hình 1, ta thấy pH càng lớn thì quá trình tạo thành gỉ sét càng kém.
- Nhận định "Trong đời sống và sản xuất người ta mong muốn đẩy mạnh quá trình hình thành gỉ sét" là nhận định SAI. Quá trình hình thành gỉ sét gây tổn thất rất lớn trong đời sống và sản xuất, làm hỏng hóc máy móc, nhà cửa,... và người ta làm mọi cách để ngăn chặn quá trình này.
- Nhận định "Quá trình tạo thành gỉ sét thực chất là phản ứng oxi hoá - khử" là nhận định ĐÚNG. Trong phản ứng: 2Fe + 3H2O → Fe2O3 + 3H2 thì Fe là chất khử, H2O là chất oxi hoá.
- Nhận đinh "Nếu thực hiện thí nghiệm trên với dung dịch bao gồm 20 mL rượu nguyên chẩt pha với 100 mL nước thì quá trình tạo thành gỉ sét sẽ là nhanh nhất" là nhận định SAI vì dung dịch rượu loãng không phải là dung dịch điện li tốt như dung dịch nước muối nên không thể có tốc độ tạo thành gỉ sét nhanh nhất.
Câu 42:
Trong thí nghiệm 1, nếu bổ sung thêm một mẫu thí nghiệm và đưa lên 40oC với khối lượng riêng là 1,018 g/mL, khối lượng dung dịch mong muốn trong ống đong là bao nhiêu?
 Xem đáp án
Xem đáp án
Phương pháp giải
Khối lượng riêng của dung dịch trong ống đong được tính theo công thức: khối lượng dung dịch (gam)/150 mL dung dịch trong ống đong. Từ khối lượng riêng đã được cho sẵn và thể tích dung dịch trong ống đong đã được cố định là 150 mL sẽ tính ra được khối lượng của mẫu thử giả thuyết.
Lời giải
Khối lượng dung dịch của mẫu thử là: 150.1,018 = 152,7 g.
Chọn C
Câu 43:
Dựa vào bảng 2, đâu là giá trị khối lượng riêng gần nhất của nước ở 10oC và độ mặn 2,50%?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào bảng 2 có thể thấy khối lượng riêng của dung dịch giảm dần theo sự giảm dần độ mặn tại cùng một nhiệt độ. Vậy dựa vào bảng 2 có thể thấy khối lượng riêng của dung dịch có độ mặn 2,50% sẽ nhỏ hơn khối lượng riêng của dung dịch có độ mặn 2,65% và lớn hơn khối lượng riêng của dung dịch có độ mặn 2,35% tại cùng một nhiệt độ là 10oC.
Lời giải
Khối lượng riêng của mẫu dung dịch có độ mặn 2,60% tại 10oC là 1,020 g/mL.
Khối lượng riêng của mẫu dung dịch có độ mặn 2,35% tại 10oC là 1,018 g/mL.
Vậy trong các giá trị đáp án cho, chỉ có giá trị 1,019 g/mL là phù hợp với mẫu dung dịch có độ mặn 2,50%.
Chọn A
Câu 44:
Một kĩ sư khẳng định rằng mẫu thử nghiệm U3 thích hợp hơn X2 trong việc thu thập dữ liệu mặt nước ở môi trường 10oC và độ mặn 2,35%. Kết quả thu thập được từ thí nghiệm có ủng hộ khẳng định này không?
 Xem đáp án
Xem đáp án
Phương pháp giải
Điều kiện môi trường nước 10oC và 2,35% tương ứng với mẫu nước số VII. Để thu thập dữ liệu mặt nước, công cụ thử nghiệm phải nổi trên mặt nước. Vậy dựa vào kết quả của bảng 3, tại mẫu thử số VII dụng cụ nào nổi thì sẽ thích hợp hơn trong việc thu thập dữ liệu mặt nước.
Lời giải
Trong bảng 3, tại mẫu nước VII, dụng cụ thử nghiệm U3 chìm còn dụng cụ thử nghiệm X2 nổi. Như vậy để thu thập dữ liệu mặt nước thì dụng cụ U3 không phù hợp. Vậy kết quả thí nghiệm không ủng hộ khẳng định của kỹ sư.
Chọn C
Câu 45:
Một dụng cụ thử nghiệm mới được kiểm tra với mẫu nước từ IV đến VII với một quy trình tương tự như trong thí nghiệm 3. Kết quả nào dưới đây không thể xảy ra?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào kết quả của bảng 3, xét khả năng chìm/nổi của một dụng cụ thử nghiệm với các mẫu dung dịch từ IV đến VII để nhận xét.
Lời giải
Ta thấy dựa vào kết quả thí nghiệm ở bảng 3, tất cả các mẫu thử nghiệm đều nổi ở các mẫu dung dịch nước ở trên và chìm ở các dung dịch nước phía dưới. Như vậy, không có dụng cụ thử nghiệm nào chìm ở dung dịch phía trên rồi lại nổi ở dung dịch dưới. Do đó kết quả ở đáp án D là không phù hợp.
Chọn D
Câu 46:
Trong thí nghiệm 1, dung dịch được chuyển sang ống đong để đo lường chính xác hơn về
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin trong thí nghiệm 1.
Lời giải
Theo mô tả của thí nghiệm 1, ống đong chia vạch dùng để lấy chính xác 150 mL dung dịch từ đó tính được khối lượng riêng của hợp chất.
Không chọn đáp án A vì muốn đo khối lượng thì phải dùng cân điện tử.
Không chọn đáp án B vì muốn đo độ mặn thường đo gián tiếp thông qua độ dẫn điện.
Không chọn đáp án D vì muốn đo nhiệt độ thường phải đo bằng nhiệt kế.
Chọn C
Câu 47:
Trong mẫu phân tích sau đó, khối lượng riêng của dụng cụ thử nghiệm U3 được tính một cách thủ công. Giá trị nào dưới đây phù hợp với kết quả thu được từ thí nghiệm 1 đến 3?
 Xem đáp án
Xem đáp án
Phương pháp giải
Để tính khối lượng riêng của dụng cụ thử nghiệm U3 phải dựa vào kết quả của bảng thí nghiệm 3 và điều kiện để một vật nổi được trong một dung dịch: khối lượng riêng của vật đó phải nhỏ hơn khối lượng riêng của dung dịch và ngược lại.
Lời giải
Trong thí nghiệm 3, dụng cụ thử nghiệm U3 nổi trong dung dịch mẫu thử số V nhưng lại chìm trong dung dịch mẫu VI. Như vậy, khối lượng riêng của mẫu thử nghiệm U3 phải nhỏ hơn khối lượng riêng của dung dịch VI.
Ta có khối lượng riêng của dung dịch V là 1,022 g/mL, của dung dịch VI là 1,020 g/mL. Vậy giá trị 1,021 g/mL là phù hợp với giá trị khối lượng riêng của dụng cụ thử nghiệm U3.
Chọn A
Câu 48:
Điền đáp án thích hợp vào chỗ trống
Theo kết quả của cả 3 thí nghiệm, dụng cụ thử nghiệm có khối lượng riêng lớn nhất là _______.
 Xem đáp án
Xem đáp án
Đáp án đúng là “R5”
Phương pháp giải
Thu thập kết quả khối lượng riêng của các dung dịch từ I đến X, sau đó dựa vào thí nghiệm 3, so sánh sự chìm, nổi của các dụng cụ thử nghiệm. Dụng cụ nào chìm ở dung dịch có khối lượng riêng càng lớn thì khối lượng riêng của dụng cụ đó càng lớn.
Lời giải
Trong 10 dung dịch thử nghiệm, dung dịch số I có khối lượng riêng lớn nhất và giảm dần ở các dung dịch phía sau. Dụng cụ thử nghiệm R5 là dụng cụ chìm sớm nhất khi chìm ở dung dịch số III. Vậy dụng cụ R5 có khối lượng riêng lớn nhất.
Câu 49:
Kéo thả đáp án chính xác vào chỗ trống
Vi khuẩn Gram âm, Vi khuẩn Gram dương
Xác định vi khuẩn (1) và (2) được mô tả trong hình 1
Vi khuẩn (1): ___________ Vi khuẩn (2): _____________
 Xem đáp án
Xem đáp án
Đáp án
Vi khuẩn (1): Vi khuẩn Gram dương Vi khuẩn (2): Vi khuẩn Gram âm
Phương pháp giải
Đọc kĩ thông tin
Lời giải
Vi khuẩn (1) – Vi khuẩn Gram dương à vì có màu tím sau khi nhuộm.
Vi khuẩn (2) – Vi khuẩn Gram âm à vì có màu hồng sau khi nhuộm.
Câu 50:
Điền từ thích hợp vào chỗ trống
Cấu trúc __________ trong thành tế bào vi khuẩn có vai trò giữ màu thuốc nhuộm tím của vi khuẩn gram trong quá trình nhuộm gram
 Xem đáp án
Xem đáp án
Đáp án đúng là “peptidoglycan”
Phương pháp giải
Đọc kĩ thông tin
Lời giải
Cấu trúc peptidoglycan trong thành tế bào vi khuẩn có vai trò giữ màu thuốc nhuộm tím của vi khuẩn gram trong quá trình nhuộm gram.
Câu 51:
Neisseria meningitidis (cầu khuẩn màng não) là một vi khuẩn gram âm, nhận định nào sau đây chính xác khi tiến hành nhuộm gram Neisseria meningitidis?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin
Lời giải
Cầu khuẩn màng não có màu hồng vì vi khuẩn Gram âm có màu hồng sau khi nhuộm gram
Chọn B
Câu 52:
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc thông tin được cung cấp
Lời giải
Vì vi khuẩn gram âm có thành peptidoglycan mỏng nên các đáp án 1, 3, 4 là hợp lý.
Chọn B
Câu 53:
Cầu khuẩn Staphylococcus aereus là một vi khuẩn có thể gây ra các bệnh nhiễm trùng da, viêm phổi, viêm nội tâm mạc, viêm khớp nhiễm trùng, viêm tủy xương và áp xe. Khi nhuộm gram, Cầu khuẩn Staphylococcus aereus bắt màu thuốc nhuộm tím. Theo em, loài vi khuẩn này có thể tương ứng với loài nào trong bảng 1?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin
Lời giải
vì cầu khuẩn bắt màu thuốc nhuộm màu tím à nó là vi khuẩn gram dương à có thành peptidoglycan dày à tương ứng với loài 2.
Chọn B
Câu 54:
Penicillin là một nhóm thuốc kháng khuẩn có thể tấn công và tiêu diệt nhiều loại vi khuẩn bằng cách phá vỡ thành peptidoglycan. Theo em, loại thuốc kháng sinh này có tác dụng ức chế hiệu quả trên loài vi khuẩn nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin
Lời giải
Vì Penicillin tiêu diệt vi khuẩn bằng cách phá vỡ thành peptidoglycan à penicillin sẽ có hiệu quả khi tiêu diệt vi khuẩn có thành peptidoglycan dày à tương ứng với loài 2
Chọn B
Câu 55:
Điền từ thích hợp vào chỗ trống
Phương pháp kháng sinh đồ được sử dụng để tăng hiệu quả điều trị và giảm thiểu nguy cơ kháng _______ trong điều trị nhiễm khuẩn
 Xem đáp án
Xem đáp án
Đáp án đúng là “kháng sinh”
Phương pháp giải
Đọc kĩ thông tin được cung cấp
Lời giải
Phương pháp kháng sinh đồ được sử dụng để tăng hiệu quả điều trị và giảm thiểu nguy cơ kháng kháng sinh trong điều trị nhiễm khuẩn
Câu 56:
Nhận định dưới đây là đúng hay sai?
Kháng sinh đồ là phương pháp để xác định loại vi khuẩn gây bệnh
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin
Lời giải
kháng sinh đồ là phương pháp xác định hiệu quả của thuốc kháng sinh với mỗi loại vi khuẩn
=> Đáp án; Sai
Chọn B
Câu 57:
Nhận định dưới đây là đúng hay sai?
Vi khuẩn nuôi cấy trong thí nghiệm được lấy từ mẫu bệnh phẩm của bệnh nhân?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin
Lời giải
Vi khuẩn nuôi cấy trong thí nghiệm được lấy từ mẫu bệnh phẩm của bệnh nhân.
=> Đáp án: Đúng.
Chọn A
Câu 58:
Trong thí nghiệm, sau khi đặt giấy thấm các loại kháng sinh với nồng độ xác định lên đĩa thạch đang nuôi cấy vi khuẩn, vi khuẩn được nuôi trong tủ ấm trong khoảng :
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tín
Lời giải
Trong thí nghiệm, sau khi đặt giấy thấm các loại kháng sinh với nồng độ xác định lên đĩa thạch đang nuôi cấy vi khuẩn, vi khuẩn được nuôi trong tủ ấm trong khoảng : 24-48h
Chọn C
Câu 59:
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin
Lời giải
- kháng sinh E có đường kính vòng vô khuẩn lớn nhất => kháng sinh E có hiệu quả điều trị cao nhất
Chọn D
Câu 60:
Trong thực hiện thí nghiệm, các sai sót ngẫu nhiên là không thể tránh khỏi. Trong bảng số liệu trên, số liệu nào là bất thường?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin
Lời giải
Số liệu về kháng sinh C ở đĩa thạch 3 có giá trị lệch khá xa mức trung bình.
Chọn DCâu 61:
Bánh xe của người đi xe đạp quay được 11 vòng trong 5 giây. Biết rằng đường kính bánh xe đạp là 600mm. Quãng đường mà người đi xe đã đi được trong 30 giây là bao nhiêu mét? (Kết quả làm tròn đến hàng đơn vị).
Đáp án: ? (m)
 Xem đáp án
Xem đáp án
Đáp án đúng là “124”
Phương pháp giải
- Tính số vòng
- Quãng đường = số vòng.chu vi
Lời giải
Trong 30 giây bánh xe quay được \(30.\frac{{11}}{5} = 66\) (vòng)
Chu vi của bánh xe là 600π(mm)
Quãng đường mà người đi xe đạp đã đi được trong 30 giây là
600π.66 = 39600π (mm) = 39,6π(m) ≈ 124(m)
Câu 62:
Huyết áp của mỗi người thay đổi trong ngày. Giả sử huyết áp tâm trương (tức là áp lực máu lên thành động mạch khi tim giãn ra) của một người nào đó ở trạng thái nghỉ ngơi tại thời điểm t được cho bởi công thức: \(B(t) = 80 + 7\sin \frac{{t\pi }}{{12}}\) (mmHg), trong đó t là số giờ tính từ lúc nửa đêm (0 giờ 00 phút) và B(t) tính bằng mmHg (milimét thủy ngân).
a) Huyết áp tâm trương của người này vào 10 giờ 30 phút sáng là ______ (mmHg)
b) Huyết áp tâm trương của người này vào 12 giờ trưa là _______ (mmHg)
c) Huyết áp của người đó đạt cao nhất tại thời điểm sớm nhất trong ngày là lúc _______ (giờ)
 Xem đáp án
Xem đáp án
a) Huyết áp tâm trương của người này vào 10 giờ 30 phút sáng là __82,68___ (mmHg)
b) Huyết áp tâm trương của người này vào 12 giờ trưa là __80___ (mmHg)
c) Huyết áp của người đó đạt cao nhất tại thời điểm sớm nhất trong ngày là lúc ___6___ (giờ)
Phương pháp giải
a) Thay t = 10,5
b) Thay t = 12
c) Đánh giá B(t)
Lời giải
a) Thời điểm 10 giờ 30 phút sáng, tức t = 10,5, khi đó \(B(10,5) = 80 + 7\sin \frac{{10,5\pi }}{{12}} \approx 82,68\)
Vậy huyết áp tâm trương của người đó vào lúc 10 giờ 30 phút sáng xấp xỉ 82,68 mmHg.
b) Thời điểm 12 giờ trưa, tức t = 12, khi đó \(B(12) = 80 + 7\sin \frac{{12\pi }}{{12}} = 80\)
Vậy huyết áp tâm trương của người đó vào lúc 12 giờ trưa là 80 mmHg.
c) Ta có:
\(B(t) = 80 + 7\sin \frac{{t\pi }}{{12}} \ge 80 + 7 \Leftrightarrow \sin \frac{{t\pi }}{{12}} = 1\)
\( \Leftrightarrow \frac{{t\pi }}{{12}} = \frac{\pi }{2} \Leftrightarrow t = 6\)
Vậy huyết áp tâm trương của người đó vào lúc 6 giờ sáng là 87 mmHg
Câu 63:
Cho hàm số \(y = \cos x + \sin x\)
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
|
|
ĐÚNG |
SAI |
|
Hàm số đã cho tuần hoàn với chu kì \(T = \frac{\pi }{2}\) |
¡ |
¡ |
|
Hàm số đã cho là hàm số chẵn |
¡ |
¡ |
|
Số điểm biểu diễn của phương trình \(y = \frac{{\sqrt 2 }}{2}\) trên đường tròn lượng giác là 1 |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
Hàm số đã cho tuần hoàn với chu kì \(T = \frac{\pi }{2}\) |
¡ |
¤ |
|
Hàm số đã cho là hàm số chẵn |
¡ |
¤ |
|
Số điểm biểu diễn của phương trình \(y = \frac{{\sqrt 2 }}{2}\) trên đường tròn lượng giác là 1 |
¡ |
¤ |
Phương pháp giải
Xét từng đáp án
Tìm chu kì của hàm số lượng giác
Lời giải
\(y = \cos x + \sin x = \sqrt 2 .\sin \left( {x + \frac{\pi }{4}} \right)\)
\( \Rightarrow \) Chu kì \(T = 2\pi \Rightarrow \) Phát biểu 1 sai
Hàm số \(y = \cos x + \sin x\) là hàm số không chẵn không lẻ=> Phát biểu 2 sai
Xét \(y = \frac{{\sqrt 2 }}{2} \Leftrightarrow \sqrt 2 .\sin \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\)
\( \Leftrightarrow \sin \left( {x + \frac{\pi }{4}} \right) = \frac{1}{2}\)
\( \Rightarrow \) Có 2 điểm biểu diễn trên đường tròn lượng giác \( \Rightarrow \) Phát biểu 3 sai.Câu 64:
Cho hai đường thẳng a và b song song với nhau và mặt phẳng (P). Xét các mệnh đề sau
(I) Nếu (P)//a thì (P)//b .
(II) Nếu (P)//a thì (P) chứa đường thẳng b.
(III) Nếu (P) cắt a thì (P) cắt b.
(IV) Nếu (P)//a thì (P) song song hoặc chứa đường thẳng b.
Số mệnh đề sai trong các mệnh đề trên là
 Xem đáp án
Xem đáp án
Lời giải
Nếu (P) //a mà a//b thì (P) có thể song song hoặc chứa b
=> Mệnh đề (I) và (II) sai, mệnh đề (IV) đúng.
Nếu (P) cắt a thì (P) cắt b=> Mệnh đề (III) đúng
Vậy có 2 mệnh đề sai.
Câu 65:
Sau khoảng thời gian từ 0 giờ đến 3 giờ thì kim giây đồng hồ sẽ quay được một góc có số đo bằng:
 Xem đáp án
Xem đáp án
-Tính số đo trong 1 phút.
- Tính số đo trong 3 giờ.
Lời giải
Cứ 1 phút thì kim giây quay được 1 vòng tức là 360o
3 giờ thì kim giây quay được: 3.60.360 = 64800o
Câu 66:
Có bao nhiêu số nguyên m để phương trình \(\sin 3x = \sqrt {2m - 1} + 1\) có nghiệm?
 Xem đáp án
Xem đáp án
- Biện luận m
Lời giải
Ta có: \(\sin 3x = \sqrt {2m - 1} + 1 \ge 1\)
=>Phương trình có nghiệm khi và chỉ khi \(\sqrt {2m - 1} + 1 = 1 \Leftrightarrow m = \frac{1}{2} \notin \mathbb{Z}\)
Vậy không tồn tại số nguyên m để phương trình có nghiệm.
Câu 67:
Phương trình \(\sin 2x = {m^2} - 2m + 2\) có tối đa bao nhiêu nghiệm trên khoảng (0;2π)?
 Xem đáp án
Xem đáp án
Tìm điều kiện để phương trình có nghiệm => sinx ≤ 1
Lời giải
\(\sin 2x = {m^2} - 2m + 2 = {(m - 1)^2} + 1\)
=> Phương trình có nghiệm khi và chỉ khi \[m - 1 = 0\]
Khi đó \(\sin 2x = 1 \Leftrightarrow 2x = \frac{\pi }{2} + k2\pi \Leftrightarrow x = \frac{\pi }{4} + k\pi \)
Vì \(x \in (0;2\pi )\) nên \(0 < \frac{\pi }{4} + k\pi < 2\pi \Leftrightarrow - \frac{1}{4} < k < \frac{7}{4} \Rightarrow k \in \{ 0;1\} \)
\( = > \) Phương trình \(\sin 2x = {m^2} - 2m + 2\) có tối đa 2 nghiệm trên khoảng \((0;2\pi )\)
Câu 68:
Cho hàm số \(y = f(x) = a\sin (bx + c),(a,b,c \in \mathbb{R})\) có đồ thị như hình vẽ.
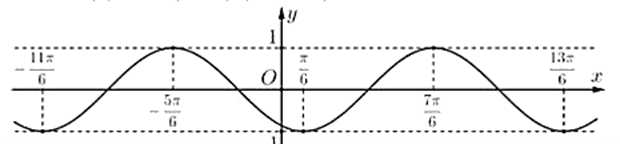
Điền đáp án vào các ô trống sau:
a) Chu kì của hàm số là T = kπ. Giá trị của k là: _______
b) Giá trị của |b| là _______
 Xem đáp án
Xem đáp án
a) Chu kì của hàm số là T = kπ. Giá trị của k là: 2
b) Giá trị của |b| là 1
Phương pháp giải
a) Quan sát đồ thị tìm chu kì.
b) Hàm số \(y = k.\sin (ax + b),y = k.\cos (ax + b)\) tuần hoàn với chu kỳ \(T = \frac{{2\pi }}{{|a|}}\).
Lời giải
a) Quan sát đồ thị ta thấy chu kì của hàm số là T = 2π
b) Chu kì của hàm số là \(T = \frac{{2\pi }}{{|b|}} \Rightarrow |b| = 1\)
Câu 69:
Cho hàm số \(y = a{x^2} + bx + c\) có đồ thị như hình bên.
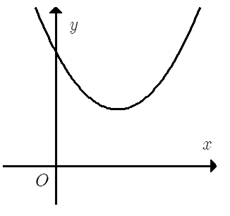
Khẳng định nào sau đây đúng ?
 Xem đáp án
Xem đáp án
Cách giải:
Bề lõm hướng lên nên a > 0.
Hoành độ đỉnh parabol \(x = - \frac{b}{{2a}} > 0\) nên b < 0.
Parabol cắt trục tung tại điểm có tung độ dương nên c > 0.
Câu 70:
Gọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) để giá trị nhỏ nhất của hàm số \(y = f(x) = 4{x^2} - 4mx + {m^2} - 2m\) trên đoạn \([ - 2;0]\) bằng 3 . Tính tổng \(T\) các phần tử của \(S\).
 Xem đáp án
Xem đáp án
Parabol có hệ số theo \({x^2}\) là \(4 > 0\) nên bề lõm hướng lên. Hoành độ đỉnh \({x_I} = \frac{m}{2}\).
Nếu \(\frac{m}{2} < - 2 \Leftrightarrow m < - 4\) thì \({x_I} < - 2 < 0\). Suy ra \(f(x)\) đồng biến trên đoạn \([ - 2;0]\).
Do đó \(\mathop {\min }\limits_{[ - 2;0]} f(x) = f( - 2) = {m^2} + 6m + 16\).
Theo yêu cầu bài toán: \({m^2} + 6m + 16 = 3\) (vô nghiệm).
Nếu \( - 2 \le \frac{m}{2} \le 0 \Leftrightarrow - 4 \le m \le 0\) thì \({x_I} \in [0;2]\).
Suy ra \(f(x)\) đạt giá trị nhỏ nhất tại đỉnh. Do đó \(\mathop {\min }\limits_{[ - 2;0]} f(x) = f\left( {\frac{m}{2}} \right) = - 2m\).
Theo yêu cầu bài toán \( - 2m = 3 \Leftrightarrow m = - \frac{3}{2}\) (thỏa mãn \( - 4 \le m \le 0\) ).
Nếu \(\frac{m}{2} > 0 \Leftrightarrow m > 0\) thì \({x_I} > 0 > - 2\). Suy ra \(f(x)\) nghịch biến trên đoạn \([ - 2;0]\).
Do đó \(\mathop {\min }\limits_{[ - 2;0]} f(x) = f(0) = {m^2} - 2m\).
Theo yêu cầu bài toán: \({m^2} - 2m = 3 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = - 1\,\,\,\left( l \right){\rm{ }}}\\{m = 3\quad \left( {tm} \right){\rm{ }}}\end{array}} \right.\)
Vậy tổng giá trị của m là \(\frac{3}{2}\).
Câu 71:
Với giá trị nào của m thì hàm số \(y = \frac{{2x + 1}}{{{x^2} - 2x - 3 - m}}\) xác định trên \(\mathbb{R}\).
 Xem đáp án
Xem đáp án
Lời giải
Hàm số \(y = \frac{{2x + 1}}{{{x^2} - 2x - 3 - m}}\) xác định trên \(\mathbb{R}\) khi phương trình \({x^2} - 2x - 3 - m = 0\) vô nghiệm
Hay Δ′ = m + 4 < 0 ⇔ m < −4.
Câu 72:
Cho hàm số \(f(x) = {x^2} - |x|\). Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đại cương về hàm số
Lời giải
Ta có tập xác định của hàm số \(f(x) = {x^2} - |x|\) là \(D = \mathbb{R}\).
Dễ thấy \(f(x) = f( - x)\) nên \(f(x) = {x^2} - |x|\) là hàm số chẵn.
Câu 73:
Cho tập hợp A = {1,2,3,4,.,20}. Chọn ngẫu nhiên 3 số trong tập hợp A. Tính xác suất để ba số được chọn không có 2 số tự nhiên liên tiếp.
 Xem đáp án
Xem đáp án
Số cách chọn ba số đôi một khác nhau từ A: \(n(\Omega ) = C_{20}^3\).
TH1: Ta chọn số có 3 chữ số tự nhiên liên tiếp
TH2: Chọn ba số có đúng hai chữ số liên tiếp
Lời giải
Số cách chọn ba số đôi một khác nhau từ A: \(n(\Omega ) = C_{20}^3\).
TH1 : Ta chọn số có 3 chữ số tự nhiên liên tiếp :
Chọn phần tử bất kì trong A∖{19;20} : 18 cách chọn.
Với mỗi phần tử được chọn, ta lấy hai phần tử liền kề bên phải : 1 cách chọn.
Vậy có 18 cách chọn 3 phần tử liên tiếp nhau.
TH2 : Chọn ba số có đúng hai chữ số liên tiếp :
Chọn 1 trong hai phần tử {1;19}: 2 cách.
Với mỗi cách chọn phần tử trên, ta có 1 cách chọn phần tử liền sau đó.
Chọn phần tử thứ ba không liên tiếp với 2 phần tử đã chọn : 17 cách.
Chọn 1 phần tử trong tập {2;3;4;.;18} : 17 cách.
Với mỗi cách chọn trên, ta có 1 cách chọn phần tử thứ hai liền sau nó.
Để chọn phần tử thứ 3 không liên tiếp, cứ 1 cặp 2 phần từ đã chọn ở trên thì ta có: 16 cách chọn phần tử thứ 3.
Vậy có 17.2+17.16 cách chọn 3 phần tử có đúng hai chữ số liên tiếp.
\(P = \frac{{C_{20}^3 - 18 - 17.2 - 17.16}}{{C_{20}^3}} = \frac{{68}}{{95}}\)
Câu 74:
Trong 1 cái hộp có 3 bi đỏ, 4 bi vàng, 5 bi xanh cùng chất, cùng kích thước. Một người lấy ngẫu nhiên cùng lúc 4 viên bi. Tính xác suất để số bi đỏ mà người đó lấy được không lớn hơn 2.
 Xem đáp án
Xem đáp án
Lời giải
Lấy ngẫu nhiên, cùng lúc 4 viên bi trong hộp có 3 bi đỏ, 4 bi vàng và 5 bi xanh nên có số phần tử của không gian mẫu là: \(n(\Omega ) = C_{12}^4\).
Gọi A: “Biến cố trong 4 bi lẫy ngẫu nhiên có 3 bi màu đỏ”.
\(n(A) = C_3^3.C_9^1\)
Xác suất của biến cố A là: \(P(A) = \frac{{C_3^3.C_9^1}}{{C_{12}^4}} = \frac{1}{{55}}\)
Vậy xác suất để số bi đỏ mà người đó lấy được không lớn hơn 2 là \(1 - P(A) = 1 - \frac{1}{{55}} = \frac{{54}}{{55}}\).
Câu 75:
Người ta quy định mật khẩu của chương trình máy tính gồm 3 kí tự.
Điền các số nguyên vào các ô trống thích hợp:
a) Nếu mỗi kí tự là một chữ số. Hỏi có thể tạo được số mật khẩu khác nhau là: _______
b) Theo quy định mới, nếu mật khẩu vẫn gồm 3 kí tự, nhưng kí tự đầu tiên phải là một chữ cái in hoa trong bảng chữ cái tiếng Anh gồm 26 chữ (từ A đến Z) và 2 kí tự sau là các chữ số (từ 0 đến 9). Theo quy định mới, số mật khẩu tạo được nhiều hơn theo quy định cũ là _______ Xem đáp án
Xem đáp án
a) Nếu mỗi kí tự là một chữ số. Hỏi có thể tạo được số mật khẩu khác nhau là: 1000
b) Theo quy định mới, nếu mật khẩu vẫn gồm 3 kí tự, nhưng kí tự đầu tiên phải là một chữ cái in hoa trong bảng chữ cái tiếng Anh gồm 26 chữ (từ A đến Z) và 2 kí tự sau là các chữ số (từ 0 đến 9). Theo quy định mới, số mật khẩu tạo được nhiều hơn theo quy định cũ là 1600
Phương pháp giải
a) Giả sử mật khẩu của máy tính gồm 3 ký tự, mỗi ký tự là một chữ số. Sử dụng quy tắc nhân.
b) Giả sử mật khẩu mới của máy tính gồm 3 ký tự , ký tự đầu là một chữ cái in hoa, 2 ký tự sau là một chữ số.
Chọn ký tự đầu tiên là một chữ cái in hoa trong bảng chữ cái tiếng Anh.
Chọn ký tự thứ hai là các chữ số (từ 0 đến 9)
Chọn ký tự thứ ba là các chữ số (từ 0 đến 9)
Lời giải
a) Giả sử mật khẩu của máy tính gồm 3 ký tự, mỗi ký tự là một chữ số.
Chọn ký tự đầu tiên: Có 10 cách chọn.
Chọn ký tự thứ hai: Có 10 cách chọn.
Chọn ký tự thứ ba: Có 10 cách chọn.
Vậy có thể tạo được 10.10.10=1000 mật khẩu khác nhau thỏa mãn bài toán.
b) Giả sử mật khẩu mới của máy tính gồm 3 ký tự , ký tự đầu là một chữ cái in hoa, 2 ký tự sau là một chữ số.
Chọn ký tự đầu tiên là một chữ cái in hoa trong bảng chữ cái tiếng Anh gồm 26 chữ (từ A đến Z): Có 26 cách chọn.
Chọn ký tự thứ hai là các chữ số (từ 0 đến 9): Có 10 cách chọn.
Chọn ký tự thứ ba là các chữ số (từ 0 đến 9): Có 10 cách chọn.
Vậy có thể tạo được 26.10.10 = 2600 mật khẩu khác nhau thỏa mãn bài toán.
Do đó quy định mới có thể tạo được nhiều hơn quy định cũ số mật khẩu khác nhau là:
2600 − 1000 = 1600 (mật khẩu).
Câu 76:
Trong một giải cờ vua gồm nam và nữ vận động viên. Mỗi vận động viên phải chơi hai ván với mỗi động viên còn lại. Cho biết có 2 vận động viên nữ và cho biết số ván các vận động viên chơi nam chơi với nhau hơn số ván họ chơi với hai vận động viên nữ là 84. Hỏi số ván tất cả các vận động viên đã chơi?
 Xem đáp án
Xem đáp án
Gọi số vận động viên nam là n.
Số ván các vận động viên nam chơi với nhau là \(2.C_n^2 = n(n - 1)\)
Số ván các vận động viên nam chơi với các vận động viên nữ là 2.2.n = 4n
Vậy ta có \(n(n - 1) - 4n = 84 \Rightarrow n = 12\)
Số vận động viên nam và nữ là 14.
Vậy số ván các vận động viên chơi là \(2C_{14}^2 = 182\).
Câu 77:
Giá trị của n ∈ N* thỏa mãn đẳng thức \(C_n^6 + 3C_n^7 + 3C_n^8 + C_n^9 = 2C_{n + 2}^8\) là
 Xem đáp án
Xem đáp án
PP sử dụng máy tính để chọn đáp số đúng:
+ Nhập PT vào máy tính: \(C_n^6 + 3C_n^7 + 3C_n^8 + C_n^9 - 2C_{n + 2}^8 = 0\)

+ Tính (CALC) lần lượt với X = 18 (không thoả); với X = 16 (không thoả); với X = 15 (thoả), với X = 14 (không thoả)

Câu 78:
Cho khai triển \({\left( {\frac{1}{{\sqrt 2 }} + 3} \right)^n}.\)
Khẳng định nào đúng trong các khẳng định sau?
Số các số hạng trong khai triển là n + 1
Với n = 4 thì có 4 số hạng hữu tỉ
Số nguyên lẻ trong khai triển là 3n
Tỉ số giữa số hạng thứ tư và thứ ba bằng \(3\sqrt 2 \) thì n = 6
 Xem đáp án
Xem đáp án
Số các số hạng trong khai triển là n + 1 - ĐÚNG
Với n = 4 thì có 4 số hạng hữu tỉ
Số nguyên lẻ trong khai triển là 3n - ĐÚNG
Tỉ số giữa số hạng thứ tư và thứ ba bằng \(3\sqrt 2 \) thì n = 6
Phương pháp giải
Xét từng mệnh đề.
Lời giải
a) Số các số hạng trong khai triển là n + 1
b) Với n = 4 thì \({\left( {\frac{1}{{\sqrt 2 }} + 3} \right)^4} = \sum\limits_{k = 0}^4 {C_4^k} {.3^k}.{\left( {{2^{\frac{{ - 1}}{2}}}} \right)^{4 - k}}\)
\( = \sum\limits_{k = 0}^4 {C_4^k} {.3^k}{.2^{\frac{{k - 4}}{2}}}\)
Số hạng hữu tỉ khi và chỉ khi \(\frac{{k - 4}}{2} \in \mathbb{Z}\) mà \( - 4 \le k - 4 \le 0\)
\( \Rightarrow k - 4 \in \{ 0; - 2; - 4\} \Leftrightarrow k \in \{ 0;2;4\} \)
Vậy có 3 số hạng hữu tỉ.
c) Số nguyên duy nhất trong khai triển nhị thức là 3n và đây là một số lẻ.
d) Ta có \({\left( {\frac{1}{{\sqrt 2 }} + 3} \right)^n} = {\left( {3 + {2^{\frac{{ - 1}}{2}}}} \right)^n} = \sum\limits_{k = 0}^n {C_n^k} {.3^k}.{\left( {{2^{\frac{{ - 1}}{2}}}} \right)^{n - k}}\)
Bài ra thì \(\frac{{C_n^4{{.3}^4}.{{\left( {{2^{\frac{{ - 1}}{2}}}} \right)}^{n - 4}}}}{{C_n^3{{.3}^3}.{{\left( {{2^{\frac{{ - 1}}{2}}}} \right)}^{n - 3}}}} = 3\sqrt 2 \Rightarrow \frac{{\frac{{3.n!}}{{(n - 4)!.4!}}}}{{\frac{{n!}}{{(n - 3)!.3!}}}}.{\left( {{2^{\frac{{ - 1}}{2}}}} \right)^{ - 1}} = 3\sqrt 2 \)
\( \Rightarrow \frac{{3(n - 3)}}{4}.\sqrt 2 = 3\sqrt 2 \Rightarrow n = 7\)Câu 79:
Để trang trí cho quán trà sữa sắp mở cửa của mình, bạn Việt quyết định tô màu một mảng tường hình vuông cạnh bằng 1 m. Phần tô màu dự kiến là các hình vuông nhỏ được đánh số lần lượt là 1,2,3…n,…, trong đó cạnh của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó như hình vẽ. Giả sử quá trình tô màu của Việt có thể diễn ra nhiều giờ. Hỏi bạn Việt tô màu đến hình vuông thứ mấy thì diện tích của hình vuông được tô bắt đầu nhỏ hơn \(\frac{1}{{1000}}\left( {{m^2}} \right)\)?
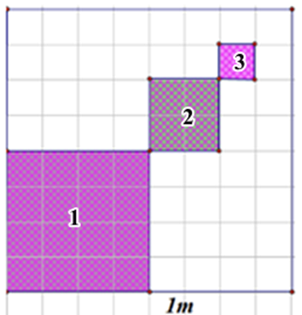
 Xem đáp án
Xem đáp án
Diện tích của hình vuông lập thành cấp số nhân với số hạng đầu tiên là \({u_1} = \frac{1}{4},q = \frac{1}{4}\).
Do đó số hạng tổng quát là \({u_n} = \frac{1}{4}.{\left( {\frac{1}{4}} \right)^{n - 1}} = \frac{1}{{{4^n}}}\,\,(n \ge 1)\). Để diện tích của hình vuông tô màu nhỏ hơn \(\frac{1}{{1000}} \Leftrightarrow \frac{1}{{{4^n}}} < \frac{1}{{1000}} \Leftrightarrow {4^n} > 1000 \Rightarrow n \ge 5\). Vậy tô màu từ hình vuông thứ 5 thỏa mãn yêu cầu bài toán.
Câu 80:
Cho cấp số cộng (un) có u1 = 3 và công sai d = 2, và cấp số cộng (vn) có v1 = 2 và công sai d′ = 3. Gọi X, Y là tập hợp chứa 1000 số hạng đầu tiên của mỗi cấp số cộng. Chọn ngẫu nhiên 2 phần tử bất kỳ trong tập hợp X ∪ Y. Xác suất để chọn được 2 phần tử bằng nhau gần với số nào nhất trong các số dưới đây?
 Xem đáp án
Xem đáp án
Chọn ngẫu nhiên 2 phần tử bất kỳ trong tập hợp \(X \cup Y\) ta có \(C_{2000}^2\) cách chọn.
Gọi 2 phần tử bằng nhau trong X, Y là uk và vl.
Do \({u_k} = {v_l} \Rightarrow 3 + 2(k - 1) = 2 + 3(l - 1) \Rightarrow k = \frac{{3l}}{2} - 1\)
Do \(1 \le k \le 1000 \Rightarrow 1 \le l \le 667\). Mặt khác \(l = 2x \Rightarrow \frac{1}{2} \le x \le 333,5\) ⇒ có 333 số
Vậy xác suât để chọn được 2 phần tử bằng nhau là: \(\frac{{333}}{{C_{2000}^2}} \approx 1,{665832916.10^{ - 4}}\).
Câu 81:
Cho dãy số \(\left( {{u_n}} \right)\) với \(\left\{ {\begin{array}{*{20}{l}}{{u_1} = 1}\\{{u_{n + 1}} = {u_n} + {{( - 1)}^{2n}}}\end{array}} \right.\) . Số hạng tổng quát \({u_n}\) của dãy số là số hạng nào dưới đây?
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \({u_{n + 1}} = {u_n} + {( - 1)^{2n}} = {u_n} + 1 \Rightarrow {u_2} = 2;{u_3} = 3;{u_4} = 4; \ldots \) Dễ dàng dự đoán được \({u_n} = n\).
Thật vậy, ta chứng minh được \({u_n} = n\,\,(*)\) bằng phương pháp quy nạp như sau:
+ Với \(n = 1 \Rightarrow {u_1} = 1\). Vậy (*) đúng với \(n = 1\)
+ Giả sử (*) đúng với mọi \(n = k\left( {k \in {\mathbb{N}^*}} \right)\), ta có: \({u_k} = k\). Ta đi chứng minh (*) cũng đúng với \(n = k + 1\), tức là: \({u_{k + 1}} = k + 1\)
+ Thật vậy, từ hệ thức xác định dãy số \(\left( {{u_n}} \right)\) ta có: \({u_{k + 1}} = {u_k} + {( - 1)^{2k}} = k + 1\). Vậy \((*)\) đúng với mọi \(n \in {\mathbb{N}^*}\).
Câu 82:
Tổng n số hạng đầu tiên của cấp số cộng \(\left( {{u_n}} \right)\) là \({S_n} = 2 + 4 + 6 + \ldots + 2n,\forall n \in {\mathbb{N}^*}\). Tìm S100?
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
|
|
ĐÚNG |
SAI |
|
Tổng của 10 số hạng đầu tiên của cấp số cộng \(\left( {{u_n}} \right)\) là 110
|
¡ |
¡ |
|
\({S_n} = \frac{{n(n + 1)}}{2}\) |
¡ |
¡ |
|
Số hạng tổng quát của \(\left( {{u_n}} \right)\) là \({u_n} = 2n + 1\) |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
Tổng của 10 số hạng đầu tiên của cấp số cộng \(\left( {{u_n}} \right)\) là 110
|
¤ |
¡ |
|
\({S_n} = \frac{{n(n + 1)}}{2}\) |
¡ |
¤ |
|
Số hạng tổng quát của \(\left( {{u_n}} \right)\) là \({u_n} = 2n + 1\) |
¡ |
¤ |
Phương pháp giải
- Tính tổng 10 số hạng đầu
- Tính tổng cấp số nhân
Lời giải
\(\begin{array}{l}{S_{10}} = 2 + 4 + 6 + \ldots + 2.10 = 110\\{S_n} = 2 + 4 + 6 + \ldots + 2n,\forall n \in {\mathbb{N}^*}\\2{S_n} = (2 + 2n) + (4 + 2n - 2) + \ldots + (2n + 2)\end{array}\)
\({S_n} = \frac{{n(2 + 2n)}}{2} = n(n + 1)\)
\(\begin{array}{l}{u_1} = {S_1} = 2\\{S_2} = 2 + 4 = 6\end{array}\)
\({S_2} = {u_1} + {u_2} \Rightarrow {u_2} = 4 \Rightarrow d = 2\)
Số hạng tổng quát của \(\left( {{u_n}} \right)\) là \({u_n} = {u_1} + (n - 1).d = 2 + (n - 1).2 = 2n\)
Câu 83:
Dãy số Phi – bô – na – xi là dãy số \(\left( {{u_n}} \right)\) được xác định: \(\left\{ {\begin{array}{*{20}{l}}{{u_1} = {u_2} = 1}\\{{u_n} = {u_{n - 1}} + {u_{n - 2}}}\end{array}} \right.\)với n ≥ 3. Số hạng thứ 10 của dãy số này là:
 Xem đáp án
Xem đáp án
Bấm số 1 => “=”
Bấm tiếp số 1 => “=”
Bấm Ans + ALPHA Ans => Rồi ấn “=” 8 lần
Lời giải
Bấm số 1 => “=”
Bấm tiếp số 1 => “=”
Bấm Ans + ALPHA Ans => Rồi ấn “=” 8 lần
Kết quả u10 = 55
Câu 84:
Trong các hàm số sau, hàm số nào không tồn tại giới hạn khi x→0
\(y = |x|\)
\(y = \frac{{|x|}}{x}\)
\(y = \sqrt x \)
\(y = [x]\)
 Xem đáp án
Xem đáp án
\(y = |x|\)
\(y = \frac{{|x|}}{x}\) - Đúng
\(y = \sqrt x \) - Đúng
\(y = [x]\) - Đúng
Phương pháp giải
- Sử dụng phương pháp loại trừ.
Lời giải
\(y = |x| = \left\{ {\begin{array}{*{20}{l}}{x{\rm{ khi }}x \ge 0}\\{ - x{\rm{ khi }}x < 0}\end{array}} \right.\)
\(\mathop {\lim }\limits_{x \to 0} |x| = 0\)
\(\mathop {\lim }\limits_{x \to 0} \sqrt x \) không tồn tại.
\(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{|x|}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{x}{x} = 1\)
\(\mathop {\lim }\limits_{x \to {0^ - }} \frac{{|x|}}{x} = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{ - x}}{x} = - 1\)
=> Không tồn tại giới hạn.
\(\mathop {\lim }\limits_{x \to {0^ + }} [x] = 0\)
\(\mathop {\lim }\limits_{x \to {0^ - }} [x] = - 1\)
=> Không tồn tại giới hạn.
Câu 85:
Cho dãy số có giới hạn \(\left( {{u_n}} \right)\) xác định bởi \(\left\{ {\begin{array}{*{20}{l}}{{u_1} = 1}\\{{u_{n + 1}} = \frac{1}{{2 - {u_n}}},n \ge 1}\end{array}} \right.\). Tính lim un.
 Xem đáp án
Xem đáp án
Lời giải
Giả sử \(\lim {u_n} = a\) thì ta có
\(a = \lim {u_{n + 1}} = \lim \frac{1}{{2 - {u_n}}} = \frac{1}{{2 - a}}\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a \ne 2}\\{a(2 - a) = 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a \ne 2}\\{{a^2} - 2a + 1 = 0}\end{array} \Leftrightarrow a = 1} \right.} \right..\)
Câu 86:
Cho dãy số có giới hạn \(\left( {{u_n}} \right)\) xác định bởi \(\left\{ {\begin{array}{*{20}{l}}{{u_1} = 2}\\{{u_{n + 1}} = \frac{{{u_n} + 1}}{2},n \ge 1}\end{array}} \right.\) . Tính lim un.
 Xem đáp án
Xem đáp án
Giả sử \(\lim {u_n} = a\) thì ta có
\(a = \lim {u_{n + 1}} = \lim \frac{{{u_n} + 1}}{2} = \frac{{a + 1}}{2} \Leftrightarrow a = 1.\)
Câu 87:
Tính các giới hạn sau \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{|2 - x|}}{{2{x^2} - 5x + 2}}\)
 Xem đáp án
Xem đáp án
\(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{|2 - x|}}{{2{x^2} - 5x + 2}} = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{x - 2}}{{(x - 2)(2x - 1)}} = \mathop {\lim }\limits_{x \to {2^ + }} \frac{1}{{2x - 1}} = \frac{1}{3}\)
Câu 88:
Cho \(\mathop {\lim }\limits_{x \to 3} \frac{{x - 3}}{{{x^2} + ax + b - 2}} = \frac{1}{7}\) với a ,b là các số hữu tỉ. Tính \(P = a - 3b\)
 Xem đáp án
Xem đáp án
Lời giải
Đặt \(f(x) = {x^2} + ax + b - 2\).
Vì \(\mathop {\lim }\limits_{x \to 3} \frac{{x - 3}}{{f(x)}} = \frac{1}{7} \Rightarrow f(3) = 0 \Leftrightarrow 3a + b = - 7 \Leftrightarrow b = - 3a - 7\)
Khi đó \(f(x) = {x^2} + ax - 3a - 9 = {x^2} - 9 + a(x - 3) = (x - 3)(x + a + 3)\)
Suy ra \(\mathop {\lim }\limits_{x \to 3} \frac{{x - 3}}{{f(x)}} = \mathop {\lim }\limits_{x \to 3} \frac{{x - 3}}{{(x - 3)(x + a + 3)}} = \mathop {\lim }\limits_{x \to 3} \frac{1}{{x + a + 3}} = \frac{1}{{a + 6}} = \frac{1}{7} \Rightarrow a = 1;b = - 10\)
Vậy P = 31.
Câu 89:
Cho hàm số \(f(x) = \frac{{\sqrt {1 + mx} - \sqrt {1 + m{x^2}} }}{{5x}}\). Tìm giá trị thực của tham số m để hàm số \(f(x)\) có giới hạn bằng 1 khi x dần tới 0
 Xem đáp án
Xem đáp án
Ta có \((1 + mx) - \left( {1 + m{x^2}} \right) = \left( {\sqrt {1 + mx} - \sqrt {1 + m{x^2}} } \right)\left( {\sqrt {1 + mx} + \sqrt {1 + m{x^2}} } \right)\)
Suy ra \(\sqrt {1 + mx} - \sqrt {1 + m{x^2}} = \frac{{mx - m{x^2}}}{{\sqrt {1 + mx} + \sqrt {1 + m{x^2}} }} = \frac{{mx(1 - x)}}{{\sqrt {1 + mx} + \sqrt {1 + m{x^2}} }}\)
Khi đó \(f(x) = \frac{{m(1 - x)}}{{5\left( {\sqrt {1 + mx} - \sqrt {1 + m{x^2}} } \right)}} \Rightarrow g(x) = \frac{{m(1 - x)}}{{5\left( {\sqrt {1 + mx} + \sqrt {1 + m{x^2}} } \right)}} \Rightarrow g(0) = \frac{m}{{10}}\)
Vậy giới hạn \(\mathop {\lim }\limits_{x \to 0} f(x) = g(0) = \frac{m}{{10}} = 1 \to m = 10\)
Câu 90:
Từ một tấm tôn hình vuông có cạnh 8 dm, bán Hùng cắt bỏ bốn phần như nhau ở bốn góc, sau đó bác hàn các mép lại để được một chiếc thùng (không nắp) như hình bên dưới
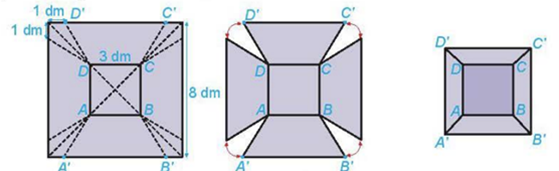
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
Chiếc thùng nhận được là hình chóp cụt |
¡ |
¡ |
|
Cạnh bên của chiếc thùng là 3 dm |
¡ |
¡ |
|
Thùng có thể chứa được nhiều nhất 42 lít nước |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
Chiếc thùng nhận được là hình chóp cụt |
¤ |
¡ |
|
Cạnh bên của chiếc thùng là 3 dm |
¡ |
¤ |
|
Thùng có thể chứa được nhiều nhất 42 lít nước |
¤ |
¡ |
Phương pháp giải
b) Cạnh bên của chiếc thùng là độ dài cạnh DD’
Kẻ DQ vuông góc với D’C’
c) Số lít nước mà thùng có thể chứa được nhiều nhất bằng thể tích của hình chóp cụt.
Gọi O và O’ lần lượt là tâm của ABCD và A’B’C’D’
Qua D kẻ DH vuông góc với O’D’
Đáy A’B’C’D’ có cạnh là 6dm
Tính:
O′D′
OD
Lời giải
a) Chiếc thùng nhận được là hình chóp cụt
AB//A'B'
=>AB//(A'B'C'D')
AD//A'D'
=>AD//(A'B'C'D')
=>(A'B'C'D')//(ABCD)
=>Chiếc thùng có dạng hình chóp cụt vì khi bác Hùng cắt bỏ bốn phần như nhau ở bốn góc của tấm tôn vuông, sẽ tạo thành bốn tam giác vuông cân
b) Cạnh bên của chiếc thùng là độ dài cạnh DD’
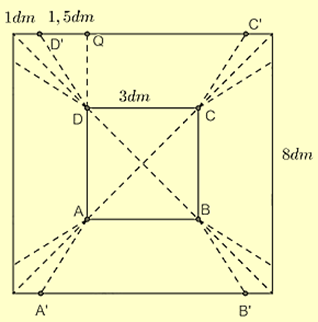
Kẻ DQ vuông góc với D’C’
Khi đó DQ=2,5dm và D’Q=1,5dm
\(D'{D^2} = D{Q^2} + D'{Q^2} = \frac{{17}}{2} \Rightarrow DD' = \frac{{\sqrt {34} }}{2}\)dm
c) Số lít nước mà thùng có thể chứa được nhiều nhất bằng thể tích của hình chóp cụt.
Gọi O và O’ lần lượt là tâm của ABCD và A’B’C’D’
Qua D kẻ DH vuông góc với O’D’
Đáy A’B’C’D’ có cạnh là 6dm
\(O'D' = \frac{6}{{\sqrt 2 }} = 3\sqrt 2 \,\,({\rm{dm}})\)
\(OD = \frac{3}{{\sqrt 2 }} = \frac{{3\sqrt 2 }}{2}\,\,({\rm{dm}})\)
Xét mặt chứa đường chéo của hình vuông, nó là hình thang cân có chiều cao bằng chiều cao của hình chóp cụt và được \(h = \sqrt {D'{D^2} - D'{H^2}} = \sqrt {\frac{{17}}{2} - {{\left( {3\sqrt 2 - \frac{{3\sqrt 2 }}{2}} \right)}^2}} = 2\,\,(dm)\)
Thể tích cần tìm là \(V = \frac{1}{3}.2.\left( {{3^2} + {6^2} + 3.6} \right) = 42\) lít.
Câu 91:
Cho ngôi nhà 4 mái dốc có kích thước như sau
Điền số thích hợp vào ô trống (Làm tròn đến chữ số thập phân thứ hai)
Chiều cao từ đỉnh cao nhất của ngôi nhà đến mặt đất là _______ m
 Xem đáp án
Xem đáp án
Đáp án đúng là “3.66 | 3,66”
Phương pháp giải
Chiều cao từ đỉnh cao nhất của ngôi nhà đến mặt đất là khoảng cách từ S đến mặt đất.
Gọi H là hình chiếu của S lên (ABNM).
Khi đó khoảng cách từ S đến mặt đất bằng tổng độ dài SH và độ dài BC.
Qua H kẻ (α) vuông góc với (ABNM), cắt BN, AM lần lượt tại E và F.
Lời giải
Chiều cao từ đỉnh cao nhất của ngôi nhà đến mặt đất là khoảng cách từ S đến mặt đất.
Gọi H là hình chiếu của S lên (ABNM)
Khi đó khoảng cách từ S đến mặt đất bằng tổng độ dài SH và độ dài BC.
Qua H kẻ (α) vuông góc với (ABNM), cắt BN, AM lần lượt tại E và F.
Khi đó EF = AB =2,5m;\(BH = \sqrt {1,{{25}^2} + 0,{5^2}} = \frac{{\sqrt {29} }}{4} \Rightarrow SH = \sqrt {1,{5^2} - \frac{{29}}{{16}}} = \frac{{\sqrt 7 }}{4}\)
Chiều cao cần tìm là \(\frac{{\sqrt 7 }}{4} + 3 \approx 3,66m\)
Câu 92:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SA \bot (ABCD)\) và \(SA = a\). Gọi F, G, H lần lượt là trung điểm của SB, SC, SD. Tính khoảng cách giữa AF và GH.
 Xem đáp án
Xem đáp án
Phương pháp tính khoảng cách giữa hai đường thẳng
Lời giải
Ta có: HG//AB ⇒ HG//(SAB)
⇒d(AF,HG) = d(HG,(SAB)) = d(H,(SAB))
\( = \frac{1}{2}d(D,(SAB)) = \frac{1}{2}DA = \frac{a}{2}\)
Câu 93:
Cho lăng trụ đứng tam giác như hình vẽ
Giá trị tan góc giữa đường thẳng CA′ và (CC′B′B)
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \(C{B^\prime } = 2\sqrt {61} \)
\({A^\prime }{B^\prime } \bot \left( {BC{C^\prime }{B^\prime }} \right) \Rightarrow \tan \widehat {\left( {C{A^\prime },\left( {C{C^\prime }{B^\prime }B} \right)} \right)} = \frac{{{A^\prime }{B^\prime }}}{{C{B^\prime }}} = \frac{4}{{2\sqrt {61} }} = \frac{2}{{\sqrt {61} }}\)
Câu 94:
Góc nhị diện [P,d,Q]
Hình gồm hai nửa mặt phẳng (P) và (Q) có chung bờ d được gọi là một góc nhị diện, kí hiệu [P,d,Q]. Từ một điểm O thuộc d, kẻ các tia Ox, Oy lần lượt thuộc hai nửa mặt phẳng (P) và (Q) và cùng vuông góc với d. Góc xOy được gọi là góc phẳng nhị diện của [P,d,Q]. Số đo của xOy được gọi là số đo của góc [P,d,Q].
Gọi A, B lần lượt là 2 điểm thuộc (P) và (Q) (A,B ∉ d). Khi đó ta coi [A,d,B] như là góc nhị diện [P,d,Q]. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AB = a, SA ⊥ (ABC), SA = \(a\sqrt 3 \).
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
Góc nhị diện [B,SA,C] là góc \[\widehat {BSC}\] |
¡ |
¡ |
|
Góc [B,SA,C] có số đo 450 |
¡ |
¡ |
|
Gọi M là trung điểm của SB. Giá trị tan của góc [M,BC,A] là \(\sqrt 3 \) |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
Góc nhị diện [B,SA,C] là góc \[\widehat {BSC}\] |
¡ |
¤ |
|
Góc [B,SA,C] có số đo 450 |
¤ |
¡ |
|
Gọi M là trung điểm của SB. Giá trị tan của góc [M,BC,A] là \(\sqrt 3 \) |
¤ |
¡ |
Phương pháp giải
Đọc kĩ giả thiết và xét từng mệnh đề.
Lời giải
+ Ta có \(SA \bot (ABC)\) nên \(SA \bot AB;SA \bot AC\)
Do đó \(\widehat {BAC}\) là góc phẳng nhị diện của [B, SA, C]
+ Tam giác ABC vuông cân tại B nên \(\widehat {BAC} = {45^^\circ }\)
+ Số đo góc [M, BC, A] bằng số đo góc [S, BC, A] do \(M \in (SBC)\)
Ta có \(SA \bot (ABC)\) nên \(SA \bot BC\). Mà \(BC \bot AB\) nên \(BC \bot (SAB)\) \( \Rightarrow BC \bot SB\)
Góc SBA là góc phẳng nhị diện của góc nhị diện [S, BC, A]
Trong tam giác vuông SAB, ta có:
\(\tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \)
Câu 95:
Cho tứ diện \({\rm{ABCD}}\). Lấy các điểm \({\rm{M}}\) và \({\rm{N}}\) lần lượt thuộc \({\rm{AD}}\) và \({\rm{BC}}\) sao cho \(\overrightarrow {AM} = 3\overrightarrow {MD} \), \(\overrightarrow {NB} = - 3\overrightarrow {NC} \). Biết \(\overrightarrow {AB} = \vec a,\overrightarrow {CD} = \vec b\). Biết \(\overrightarrow {MN} = x\vec a - y\vec b\).
Khi đó x + y = _______
 Xem đáp án
Xem đáp án
Đáp án: “1”
Phương pháp giải
Lời giải
Ta có: \(\overrightarrow {MN} = \overrightarrow {MD} + \overrightarrow {DC} + \overrightarrow {CN} \) (1)
Lại có \(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {BN} \) (2)
Lấy (2) + 3.(1) ta được: \(4\overrightarrow {MN} = \overrightarrow {AB} + 3\overrightarrow {DC} \)
Do đó \(\overrightarrow {MN} = \frac{1}{4}\vec a - \frac{3}{4}\vec b\)
Vậy \(x + y = \frac{1}{4} + \frac{3}{4} = 1\)
Câu 96:
Viết liền nhau các số tự nhiên từ 1 đến 100. Khi đó chữ số 5 được viết bao nhiêu lần?
 Xem đáp án
Xem đáp án
Ta thấy từ 1 đến 10 thì số 5 được viết 1 lần.
Xét các số có 2 chữ số. Ta chia các số làm 2 trường hợp:
TH1: Số có dạng \(\overline {a5} \) với a ≠ 5. Khi đó a ∈ {1;2;3;4;6;7;8;9} => Có 8 số, mỗi số có 1 chữ số 5.
TH2: Số có dạng \(\overline {5b} \), khi đó thì b ∈ {0;1;2;3;4;5;6;7;8;9}
=> Có 10 số, trong đó 9 số có 1 chữ số 5, 1 số có 2 chữ số 5 (số 55).
=> Số 5 được viết 11 lần.
Vậy tổng cộng có 1+8+11=20 chữ số 5.
Câu 97:
Hàm Euler của một số nguyên dương N được định nghĩa là số các số nguyên dương nhỏ hơn hoặc bằng N và nguyên tố cùng nhau với N, kì hiệu là ϕ(N). Hai số nguyên dương a và b được gọi là nguyên tố cùng nhau nếu ƯCLN(a,b)=1.
Chọn các khẳng định đúng:
ϕ(1) = 1
ϕ(4) = 3
ϕ(9) = 6
ϕ(10) = 3
 Xem đáp án
Xem đáp án
ϕ(1) = 1 - ĐÚNG
ϕ(4) = 3
ϕ(9) = 6 - ĐÚNG
ϕ(10) = 3
Phương pháp giải
Tìm các số nguyên nhỏ hơn hoặc bằng n và nguyên tố cùng nhau với n.
Lời giải
Số các số nguyên dương nguyên tố cùng nhau với 1 là 1.
Khi đó ϕ(1) = 1
Với N = 4 thì các số nguyên tố cùng nhau với 4 là 1;3
Khi đó ϕ(4)=2
Với N = 9 thì các số nguyên tố cùng nhau với 9 là: 1;2;4;5;7;8 => ϕ(9) = 6
Với N = 10 thì các số nguyên tố cùng nhau với 10 là 1;3;7;9 => ϕ(10) = 4
Câu 98:
Cho n là số tự nhiên nhỏ nhất khi chia cho 7, 5, 3, 11 có cùng số dư là 1.
Khi đó n = _______
 Xem đáp án
Xem đáp án
Đáp án: “1156”
Phương pháp giải
Đưa về (n − 1)
Lời giải
n chia cho 7 dư 1 nên (n - 1) chia hết cho 7
n chia cho 5 dư 1 nên (n - 1) chia hết cho 5
n chia cho 3 dư 1 nên (n - 1) chia hết cho 3
n chia cho 11 dư 1 nên (n - 1) chia hết cho 11
Khi đó n − 1 là bội chung nhỏ nhất của 7;5;3;11
Do đó n − 1 = 3.5.7.11 = 1155
Vậy n = 1156
Câu 99:
Chữ số tận cùng của 1520 là
 Xem đáp án
Xem đáp án
Lời giải
Ta thấy 5.5=25 nên chữ số tận cùng của 1520 là 5.
Câu 100:
Cho \[ - 5 \le a \le 5\] . Giá trị của \[\sum\limits_{a = - 5}^5 {\left[ {\frac{a}{3}} \right]} \] là:
 Xem đáp án
Xem đáp án
Ta có: \[ - 5 \le a \le 5\] nên \(\frac{{ - 5}}{3} \le \frac{a}{3} \le \frac{5}{3}\)
Khi đó:

\( \Rightarrow \sum\limits_{a = - 5}^5 {\left[ {\frac{a}{3}} \right]} = ( - 2).2 + ( - 1).3 + 0.3 + 1.3 = - 4\)
