Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 2)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 2)
-
397 lượt thi
-
99 câu hỏi
-
148 phút
Danh sách câu hỏi
Câu 1:
Phần tư duy đọc hiểu
Ý chính của bài viết là gì?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn trích, cụ thể ở nhan đề.
Lời giải
Ý chính của bài viết là: Trình bày phương pháp phân tích mẫu máu muỗi để tìm bằng chứng nhiễm bệnh ở người và động vật.
Câu 2:
Virus sông Ross là một bệnh do muỗi lây truyền có thể gây suy nhược, đặc thù ở Úc và các đảo nam Thái Bình Dương.
Từ hiểu biết của mình, hãy cho biết Virus này thuộc về họ nào sau đây?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ nội dung đoạn [4] của đoạn trích và hiểu biết của bản thân
Lời giải
Virus sông Ross là một bệnh do muỗi lây truyền có thể gây suy nhược, đặc thù ở Úc và các đảo nam Thái Bình Dương. Virus này thuộc Họ Togaviridae.
Giải thích:
Virus sông Ross là một bệnh do muỗi lây truyền có thể gây suy nhược, đặc thù ở Úc và các đảo nam Thái Bình Dương. Virus này thuộc về họ Togaviridae, cùng với các virus khác như virus Đông ngựa và virus ngựa phương Tây.
Virus sông Ross được phát hiện lần đầu tiên ở Queensland, Úc vào năm 1959. Nó được đặt tên theo sông Ross, nơi mà nhiều trường hợp nhiễm bệnh được ghi nhận.
Virus sông Ross có thể gây ra các triệu chứng như sốt, đau khớp, phù nề và phát ban. Triệu chứng thường xuất hiện từ 3 đến 11 ngày sau khi bị muỗi cắn. Hầu hết các trường hợp nhiễm virus sông Ross sẽ tự khỏi trong vòng một tuần, nhưng một số người có thể có các biến chứng như viêm khớp mãn tính hoặc viêm não.
Chọn A
Câu 3:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Phương pháp sáng tạo, phân tích mẫu máu muỗi hút lần cuối để tìm bằng chứng nhiễm bệnh có thể hỗ trợ việc phát hiện sớm ở động vật và người những căn bệnh như Ebola, SARS-CoV-2. Ngoài ra, nó còn giúp các nhà khoa học xác định động vật nào là vật chủ của một loại virus mới.
Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ nội dung đoạn [2] của đoạn trích
Lời giải
→ Ý kiến trên: SAI
Trong bài viết đã đề cập:
Phương pháp này cũng có thể hỗ trợ việc phát hiện sớm ở động vật những căn bệnh như Ebola và SARS-CoV-2 và nó có thể giúp các nhà khoa học xác định động vật nào là vật chủ của một loại virus mới.
-> Bài viết đề cập đến việc phát hiện bệnh ở động vật chứ không phải ở người như ý kiến trên. Do đó, ý kiến trên sai.
Chọn B
Câu 4:
 Xem đáp án
Xem đáp án
Đáp án
Các nghiên cứu đã sử dụng phương pháp xét nghiệm máu để tìm kháng thể và phát hiện dấu hiệu nhiễm bệnh trong quá khứ từ các vật chủ cụ thể. Nhà sinh thái học bệnh tật Carla Vieirra tại Viện Nghiên cứu Y khoa QIMR Berghofer ở Brisbane, Úc đã sử dụng phương pháp này để phát hiện trong máu từ một loạt động vật và người.
Phương pháp giải
Căn cứ vào nội dung đoạn [3]
Lời giải
Căn cứ vào nội dung đoạn 3:
Các nghiên cứu trước đã phát hiện việc tiếp xúc với mầm bệnh trước đây bằng cách xét nghiệm máu để tìm kháng thể, những dấu hiệu nhiễm bệnh trong quá khứ có thể tuần hoàn trong máu hàng tháng tới hàng năm trời, từ các vật chủ cụ thể. Phương pháp này từng được nhà sinh thái học bệnh tật Carla Vieirra tại Viện Nghiên cứu Y khoa QIMR Berghofer ở Brisbane, Úc sử dụng, nó có thể phát hiện kháng thể trong máu từ một loạt động vật và người.
Dựa vào nội dung đoạn trên cùng cách sử dụng từ ngữ trong bài đọc, ta có các từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: sử dụng
- Vị trí thả 2: phát hiện
- Vị trí thả 3: quá khứ
- Vị trí thả 4: sinh thái học
Câu 5:
Thông tin nào dưới đây xuất hiện trong đoạn 5 và đoạn 7?
Chọn hai đáp án đúng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ nội dung đoạn [5] và đoạn [7] của đoạn trích
Lời giải
- Đoạn [5] trình bày: Từ những con muỗi vừa hút máu, họ vắt ra vài mililit máu và xét nghiệm nó để tìm kháng thể có thể liên kết với virus sông Ross. (đáp án A)
- Đoạn [7] trình bày: Trong một nghiên cứu riêng biệt được đăng vào tháng Một, Verhulst cùng đồng nghiệp đã phát hiện các kháng thể với SARS-CoV-2 và ký sinh trùng Toxoplasma gondii trong máu mà muỗi hút từ động vật, bao gồm cả lạc đà không bướu và mèo. (đáp án D)
=> Thông tin xuất hiện trong đoạn 5 và đoạn 7 là: A và D
Câu 6:
Hãy tìm một cụm từ không quá hai tiếng trong văn bản để hoàn thành nhận định sau:
Theo lý luận, phương pháp này có thể áp dụng “cho hầu như bất kỳ loại bệnh nào gây ra sự ________________ của hệ thống miễn dịch trong cơ thể chủ”, chuyên gia côn trùng học và ký sinh trùng Carl Lowenberger tại Trường Đại học Simon Fraser ở Vancouver, Canada, nói.
 Xem đáp án
Xem đáp án
Đáp án: “phản ứng”
Phương pháp giải
Căn cứ vào nội dung đoạn [8]
Lời giải
Căn cứ vào nội dung đoạn 8:
Về lý thuyết, phương pháp này có thể được dùng “đối với hầu hết mọi mầm bệnh gây ra phản ứng miễn dịch trong vật chủ”, nhà côn trùng học và ký sinh trùng Carl Lowenberger tại Đại học Simon Fraser ở Vancouver, Canada, cho biết.
-> Như vậy, từ phù hợp nhất để điền vào chỗ trống là: phản ứng
Câu 7:
Cụm từ “kỹ thuật này” (in đậm, gạch chân) trong đoạn 9 đang nói đến:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [9]
Lời giải
Trong đoạn [9], cụm từ "kỹ thuật này" được sử dụng để nói đến phương pháp phân tích mẫu máu muỗi để tìm kiếm bằng chứng nhiễm bệnh ở người hay động vật đã tiếp xúc với các mầm bệnh. Đây là kỹ thuật được nhà sinh thái học bệnh tật Eloise Skinner tại Đại học Griffith ở Gold Coast đề cập và ông ta nhận xét rằng kỹ thuật này rất thú vị và có thể giúp các nhà khoa học nghiên cứu một số bệnh mà chúng ta chưa hiểu rõ, chẳng hạn bệnh viêm não Nhật Bản ở Úc.
Chọn C
Câu 8:
Hãy tìm một cụm từ không quá hai tiếng trong văn bản để hoàn thành nhận định sau:
Phương pháp phân tích mẫu máu muỗi cũng có những hạn chế, bao gồm việc không thể làm rõ tỷ lệ mẫu máu chứa kháng thể phản ánh tỷ lệ người nhiễm bệnh chính xác thế nào. Ngoài ra, cần lưu ý rằng nhiều con muỗi có thể đã cắn cùng một người, điều này hạn chế sử dụng kỹ thuật này để giám sát bệnh ____________.
 Xem đáp án
Xem đáp án
Đáp án: “bùng phát”
Phương pháp giải
Căn cứ vào nội dung đoạn [10] và đoạn [11]
Lời giải
Căn cứ vào nội dung đoạn 10 và đoạn 11:
Một nhược điểm khác của kỹ thuật này là nó không làm rõ tỷ lệ mẫu máu chứa kháng thể phản ánh tỷ lệ người nhiễm bệnh chính xác thế nào, nhà dịch tễ học y tế David Harley tại Đại học Queensland ở Brisbane, cho biết. Nhiều con muỗi có thể đã cắn cùng một người.
Cũng rất khó bắt được những con muỗi đã hút no máu, điều này hạn chế việc sử dụng kỹ thuật này để giám sát bệnh bùng phát.
-> Như vậy, từ phù hợp nhất để điền vào chỗ trống là: bùng phát.
Câu 9:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Đoạn 11 đề cập đến cách mà nhà nghiên cứu Niels Verhulst và đồng nghiệp tạo ra một hỗn hợp từ mật mía để bắt được nhiều muỗi hút máu hơn. Hỗn hợp này được sản xuất bằng cách lên men mật mía để tạo ra khí CO2 thu hút muỗi. Nhà nghiên cứu hy vọng sẽ sớm có thể thử nghiệm phương pháp này ngoài phòng thí nghiệm.
Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [11] văn bản.
Lời giải
-> Ý kiến trên là: ĐÚNG
Căn cứ vào nội dung đoạn 11:
Dựa trên việc muỗi bị thu hút bởi khí carbon dioxide, Verhulst và đồng nghiệp đã tạo ra một hỗn hợp được sản xuất bằng cách lên men mật mía để bắt được nhiều muỗi đã hút máu hơn so với khi không dùng hỗn hợp này. Họ hy vọng sẽ sớm có thể thử nghiệm phương pháp này ngoài phòng thí nghiệm.
- Khí carbon dioxide chính là khí CO2 và các nội dung khác đúng với đoạn trích. Do đó, ý kiến trên đúng.
Chọn A
Câu 10:
Theo bài đọc, một trong những lợi ích của kỹ thuật phân tích máu muỗi là gì?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn trích, chủ yếu ở đoạn [2].
Lời giải
Theo bài đọc, một trong những lợi ích của kỹ thuật phân tích máu muỗi là: Tránh được các vấn đề đạo đức và thực tiễn khi xét nghiệm trực tiếp.
- Phân tích, loại trừ:
+ Đáp án A không đúng vì kỹ thuật này không giảm thiểu rủi ro lây nhiễm virus cho người và động vật, mà chỉ phát hiện sự tiếp xúc với virus trong quá khứ.
+ Đáp án B đúng vì bài đọc có nói rằng “các nhà khoa học cho biết có thể dùng phương pháp này để nghiên cứu trước đây người và động vật đã tiếp xúc với những mầm bệnh nào, đồng thời tránh được các vấn đề đạo đức và thực tiễn khi xét nghiệm trực tiếp”.
+ Đáp án C không đúng vì kỹ thuật này rất khó bắt được những con muỗi đã hút no máu, điều này hạn chế việc sử dụng kỹ thuật này để giám sát bệnh bùng phát.
+ Đáp án D không đúng vì kỹ thuật này không làm rõ tỷ lệ mẫu máu chứa kháng thể phản ánh tỷ lệ người nhiễm bệnh chính xác thế nào. Một nguyên nhân có thể gây ra hiện tượng này là nhiều con muỗi có thể đã cắn cùng một người.
Chọn B
Câu 11:
Đâu là lý do mà từ lâu nay người ta lại định giết mực?
Chọn đáp án đúng nhất:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [1]
Lời giải
Lý do mà từ lâu nay người ta lại định giết mực vì: Mực có nhiều nết xấu như tục ăn, nhiều vắt và sủa như gà gáy
Phương pháp suy luận, loại trừ:
Đáp án A -> sai: vì trong truyện không có nói rằng Mực rất ngon và béo. Người ta định giết Mực không phải vì thèm ăn mà vì ghét nó. Đáp án A cũng không thể hiện được sự tàn bạo và vô cảm của con người đối với loài vật mà tác giả muốn chỉ trích.
Đáp án B -> đúng: vì trong truyện có nói rằng Mực có nhiều nết xấu như tục ăn, nhiều vắt và sủa như gà gáy. Đây là những lý do mà người ta định giết Mực. Đáp án B cũng thể hiện được sự tàn bạo và vô cảm của con người đối với loài vật mà tác giả muốn chỉ trích.
Đáp án C -> sai: vì trong truyện không có nói rằng Mực hay cắn càn và làm phiền người ta. Ngược lại, Mực chỉ sủa như gà gáy và tục ăn. Đáp án C cũng không thể hiện được sự tàn bạo và vô cảm của con người đối với loài vật mà tác giả muốn chỉ trích.
Câu 12:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Người ta không thể nào tha thứ cho Mực vì Mực tham lam và bẩn thỉu.
Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [1]
Lời giải
→ Ý kiến trên: SAI
Căn cứ vào nội dung đoạn 1:
Nó tục ăn: đó là thường. Nó nhiều vắt: cái ấy đủ khổ cho nó. Nó cắn càn ấy là cái khổ của bọn ăn mày. Nhưng nó lại sủa như một con gà gáy: cái này thì không thể nào tha thứ được.
Câu 13:
Từ thông tin của câu chuyện, hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí.
run run, nghẹn ngào, vui mừng, thương hại, hào hứng, buồn bã
- Cảm xúc của Du khi trở về nhà sau một thời gian xa xôi: _________
- Cảm xúc của Du khi gặp lại Mực - người bạn lặng lẽ bên chàng những năm xưa, nay già nua và bẩn thỉu: __________
- Cảm xúc của Du khi hét lên bảo mọi người phải đè thật chặt cái Mực: __________
- Cảm xúc của Du khi thấy Mực bị Hoa úp thúng, trói chân và buộc mõm: ______
 Xem đáp án
Xem đáp án
Đáp án
- Cảm xúc của Du khi trở về nhà sau một thời gian xa xôi: vui mừng
- Cảm xúc của Du khi gặp lại Mực - người bạn lặng lẽ bên chàng những năm xưa, nay già nua và bẩn thỉu: thương hại
- Cảm xúc của Du khi hét lên bảo mọi người phải đè thật chặt cái Mực: run run
- Cảm xúc của Du khi thấy Mực bị Hoa úp thúng, trói chân và buộc mõm: nghẹn ngào
Phương pháp giải
Căn cứ vào nội dung của cả câu chuyện
Lời giải
Phân tích, suy luận, loại trừ:
Cảm xúc của Du khi trở về nhà sau một thời gian xa xôi
→ Đáp án đúng là: vui mừng. Vì câu chuyện nói rằng "Chiều hôm qua con người phóng đãng ấy đã khệ nệ xách cái vali rất nặng bước vào sân, miệng mỉm cười và mặt đỏ." Đây là những dấu hiệu của sự vui mừng khi gặp lại gia đình.
Cảm xúc của Du khi gặp lại Mực - người bạn lặng lẽ bên chàng những năm xưa nay già nua và bẩn thỉu:
→ Đáp án đúng là: thương hại. Vì câu chuyện nói rằng "Du thương hại: đó là người bạn lặng lẽ thui thủi bên chàng những năm xưa khi đêm vắng, chàng ngồi nhìn trăng mà mơ mộng." Đây là cảm xúc khi bạn thấy ai đó đang gặp khó khăn hoặc đau khổ và bạn muốn giúp đỡ họ.
→ Đáp án bỡ ngỡ là sai vì đã nhận ra Mực là con chó của mình. Đáp án nghẹn ngào là sai vì Du không khóc hay than khóc khi gặp Mực. Đáp án buồn bã là sai vì Du không có biểu hiện nào của sự buồn bã khi gặp Mực.
Cảm xúc của Du khi hét lên bảo mọi người phải đè thật chặt cái Mực:
→ Đáp án đúng là: run run. Vì câu chuyện nói rằng "Du kêu lên như thế nhưng tiếng chàng đã hơi run run." Đây là cảm xúc khi bạn sợ hãi hoặc lo lắng cho ai đó hoặc cho chính mình.
→ Đáp án lo lắng là sai vì Du không chỉ lo lắng cho Mực mà còn sợ hãi cho chính mình. Đáp án tức giận là sai vì Du không có lý do gì để tức giận với Mực. Đáp án sợ hãi là sai vì Du không chỉ sợ hãi cho Mực mà còn lo lắng cho chính mình.
Cảm xúc của Du khi thấy Mực bị Hoa úp thúng, trói chân và buộc mõm:
→ Đáp án đúng là: nghẹn ngào. Vì câu chuyện nói rằng "Du nghẹn ngào nén khóc…" Đây là cảm xúc khi bạn cảm thấy đau khổ hoặc xúc động quá mức và không thể nói ra lời nào.
→ Đáp án thương hại là sai vì Du không chỉ thương hại cho Mực mà còn cảm thấy đau khổ và xúc động. Đáp án buồn bã là sai vì Du không chỉ buồn bã mà còn nghẹn ngào và nén khóc. Đáp án cảm động là sai vì Du không chỉ cảm động mà còn đau khổ và nghẹn ngào.
Dựa vào nội dung đoạn trên cùng cách phân tích và suy luận, ta có các từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: vui mừng
- Vị trí thả 2: thương hại
- Vị trí thả 3: run run
Câu 14:
Đọc đoạn 5 và trả lời câu hỏi, tại sao Du thấy lòng nằng nặng?
Chọn đáp án đúng nhất:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [5]
Lời giải
Căn cứ vào nội dung đoạn 5:
Du thương hại: đó là người bạn lặng lẽ thui thủi bên chàng những năm xưa khi đêm vắng, chàng ngồi nhìn trăng mà mơ mộng. Chàng muốn cúi xuống vuốt ve. Nhưng nó bẩn ghê gớm quá, lông rụng từng mảng, thịt trắng lộ ra có nơi sần mụn nữa. Dáng điệu thì già nua, có vẻ buồn và len lén như phòng bị một cách yếu ớt. Không còn những cái vẫy đuôi mạnh dạn những cái nhìn rất bạn bè và những cái hít chân vồ vập như khi một con chó đã vui và không ngờ vực. Du thấy lòng nằng nặng.
→ Du thấy lòng nằng nặng: Vì anh cảm thấy mất mát - con chó đã già đi và không còn như ngày xưa nữa.
Con chó - người bạn năm xưa của anh giờ không còn khoẻ mạnh và vui vẻ như trước, thay vào đó là một con chó bẩn thỉu, yếu ớt, buồn bã. Anh cảm thấy thương hại cho nó.
Câu 15:
Hãy chọn một trong hai từ sau điền vào chỗ trống đề hoàn thành câu sau: vui mừng, háo hức
Bà mẹ rất ________________ và cả khóc lẫn cười khi người con trai về, bà thấy như tìm được một vật quý bị rơi vậy.
 Xem đáp án
Xem đáp án
Đáp án: "vui mừng"
Phương pháp giải
Căn cứ vào nội dung đoạn [3]
Lời giải
Căn cứ vào nội dung đoạn 3:
Chiều hôm qua con người phóng đãng ấy đã khệ nệ xách cái vali rất nặng bước vào sân, miệng mỉm cười và mặt đỏ. Cái nhà tranh, mấy cây cau hình như vừa đứng thẳng hơn lên để chào chàng. Rồi đến lũ em ầm ỹ đẩy mành chạy oà ra, và bà mẹ mừng quá cười và khóc.
Câu 16:
Từ nội dung của đoạn 6, hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Con chó vẫy đuôi mạnh hơn khi Du đưa chân chạm khẽ vào người nó. Nhưng nó lại len lén lánh ra vì nó sợ.
Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [6]
Lời giải
→ Ý kiến trên: Đúng.
- Căn cứ vào nội dung ở đoạn 6:
Con chó vẫy đuôi mạnh hơn khi Du đưa chân chạm khẽ vào người nó, nhưng nó lại len lén lánh ra vì nó sợ Du. Đoạn văn đã miêu tả rõ ràng như vậy:
-> Con chó vẫy đuôi mạnh hơn nhưng len lén lánh ra: dáng điệu một kẻ sợ hãi cố cười với người nó sợ.
- Các lý do khiến Mực sợ là:
+ Nó đã bị người nhà đối xử tàn nhẫn và bị đe dọa giết thịt nhiều lần, nên nó không còn tin tưởng vào con người. Nó cảm thấy mình là kẻ bị ruồng bỏ và không có ai yêu thương.
+ Một lý do khác là nó đã già yếu và bệnh tật, nên nó không còn sức mạnh để chống lại hay bảo vệ mình. Nó biết rằng mình sẽ chết sớm hay muộn, nên nó chỉ còn biết chấp nhận số phận.
+ Một lý do nữa là nó không nhận ra được tình cảm của Du dành cho nó, và chỉ cảm nhận được sự khác biệt giữa Du và những người khác trong nhà. Nó sợ rằng Du cũng sẽ đối xử với nó như những kẻ khác. Do đó, nó sợ hãi và lén tránh ra khi được Du chạm chân vào người.
Câu 17:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai từ nội dung đoạn 1.
Cái chết của con Mực là cái chết của tâm hồn người lao động.
Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [7] và đoạn [8]
Lời giải
→ Ý kiến trên: SAI
Căn cứ vào nội dung đoạn 7 và đoạn 8:
Nhưng mà không thể được: dịu dàng quá là yếu tâm hồn, và ai hiểu được rằng mình lại có thể yêu thương một con chó bẩn ghê gớm như thế được?
Sau cùng thì chàng bực mình: chàng nhận ra rằng một con chó đã làm mất sự bình tĩnh của tâm hồn chàng. Và đột nhiên chàng muốn giết con Mực lắm. Chàng muốn có đủ can đảm để giết người. Phải dám giết mà không run tay khi cần phải giết. Còn làm được trò gì nữa nếu chỉ giết một con chó mà tim cũng đập?
-> Cái chết của con Mực là cái chết của tâm hồn người trí thức không phải cái chết của tâm hồn người lao động.
Khi con Mực bị giết, Du cũng mất đi phần tốt đẹp nhất trong mình và trở nên vô cảm, tuyệt vọng. Qua cái chết của Mực, Nam Cao gián tiếp đặt ra những vấn đề nhân cách tha hoá, tâm hồn mòn gỉ hay sự bất lực của con người trước sự chi phối của hoàn cảnh xã hội.
Với Nam Cao, hơn cả sự đau đớn của cái chết thể xác là bi kịch của “cái chết tinh thần” - “chết ngay trong lúc sống”, đó là sự vô cảm, thờ ơ trước nỗi đau của người khác, bản chất, bản tính tự nhiên tốt đẹp của con người tạm thời biến đổi hay bị che lấp bởi hoàn cảnh xã hội.
Câu 18:
Từ nội dung của câu chuyện, hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
|
|
ĐÚNG |
SAI |
|
Mực 3 lần thoát được cái chết đã được mọi người định sẵn. |
||
|
Du luôn tỏ ra thân thiết với Mực sau một thời gian dài gặp lại người bạn cũ. |
||
|
Mực cảm thấy tủi thân và sợ hãi khi bị mọi người ghét bỏ và đối xử tàn nhẫn. |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Mực 3 lần thoát được cái chết đã được mọi người định sẵn. |
X | |
|
Du luôn tỏ ra thân thiết với Mực sau một thời gian dài gặp lại người bạn cũ. |
X | |
|
Mực cảm thấy tủi thân và sợ hãi khi bị mọi người ghét bỏ và đối xử tàn nhẫn. |
X |
Phương pháp giải
Căn cứ vào nội dung câu chuyện
Lời giải
Phân tích, lý giải:
Mực 3 lần thoát được cái chết đã được mọi người định sẵn.
→ Ý kiến trên: Đúng
- Tại vì: Trong truyện, có ba lần người ta định giết Mực nhưng nó đều may mắn thoát được vì có những lý do khác nhau:
+ Lần đầu tiên là vào dịp Thanh Minh, nhưng may cho nó hôm ấy bà chủ nhà bị ốm.
+ Lần thứ hai là vào Tết tháng năm, nhưng may cho nó lúc ấy bà chủ nhà phải kiêng để lấy sữa cho con út.
+ Lần thứ ba là vào rằm tháng bảy, nhưng may cho nó lúc ấy Du về thăm nhà nên cả nhà quyết định đợi Du về mới làm thịt Mực.
Du luôn tỏ ra thân thiết với Mực sau một thời gian dài gặp lại người bạn cũ.
→ Ý kiến trên: Sai
- Tại vì: Trong truyện, Du chỉ có một lần muốn cúi xuống vuốt ve Mực khi gặp lại nó, nhưng nó bẩn ghê gớm quá nên chàng không dám. Sau đó, chàng cũng không dám gọi nó vào kẹp nó vào giữa hai bàn chân và vừa ăn vừa vẩy cho nó miếng cơm vì sợ bị mọi người chê cười. Chàng cũng không can thiệp khi Mực bị Hoa bắt và giết để làm thịt cho Tết. Chỉ có khi Mực đã chết rồi, Du mới nghẹn ngào nén khóc.
Mực cảm thấy tủi thân và sợ hãi khi bị mọi người ghét bỏ và đối xử tàn nhẫn.
→ Ý kiến trên: Đúng
- Tại vì: Trong truyện, Mực được miêu tả là một con chó già nua, bẩn và sủa nhiều. Nó bị mọi người trong nhà ghét bỏ và đối xử tàn nhẫn vì nó không có giá trị gì trong gia đình.
Sự tủi thân của Mực được thể hiện qua các chi tiết:
+ "Nó đứng lặng vẫy đuôi, đầu cúi xuống, hai mắt nhèm ươn ướt nhìn đất như tủi phận."
+ "Nó không có bạn bè và không được sống tự do. Nó cảm thấy cô đơn và bất lực trước số phận bi thảm của mình."
+ "Lòng đen ươn ướt cứ đờ dần rồi ngược lên lần một nửa vào mí trên. Lòng trắng đã hơi đục."
Sự sợ hãi của Mực được thể hiện qua những đoạn văn sau:
+ "Nó vẫy đuôi mạnh hơn nhưng len lén lánh ra: dáng điệu một kẻ sợ hãi cố cười với người nó sợ."
+ "Nó lấm lét lảng dần cũng không dám chạy một cách thẳng thắn để đi trốn nữa."
Câu 19:
Xuyên suốt câu chuyện, đâu là những cảm xúc của Du khi gặp lại Mực?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung câu chuyện
Lời giải
Phân tích, suy luận:
- Thương hại: Du thương hại Mực khi thấy nó già nua và bẩn thỉu, và nó né tránh sự chạm vào của anh. Anh cũng nhớ lại tình bạn của họ trong quá khứ. Anh muốn vuốt ve nó nhưng không thể.
-Bực mình: Du bực mình với Mực khi nó làm phiền giấc ngủ của anh bằng tiếng sủa. Anh cũng cảm thấy Mực đã làm mất sự bình tĩnh của tâm hồn anh. Anh đột nhiên muốn giết nó nhưng không đủ can đảm.
- Nghẹn ngào: Du nghẹn ngào khi thấy Mực bị Hoa úp thúng và trói chặt. Anh muốn khóc nhưng không thể.
Câu 20:
Từ thông tin của câu chuyện, hãy sắp xếp lại thứ tự các sự kiện quan trọng trong truyện theo đúng trình tự xảy ra bằng cách kéo thả các từ vào đúng vị trí.
Du về thăm nhà, Mực bị bắt và giết để làm thịt Tết, Mực bị đá vào sườn, Mực thoát được cái chết vào rằm tháng bảy, Mực thoát được cái chết vào Tết tháng năm, Mực bị bà chủ nhà bắt
 Xem đáp án
Xem đáp án
Đáp án:
Mực thoát được cái chết vào Tết tháng năm, Mực thoát được cái chết vào rằm tháng bảy, Du về thăm nhà, Mực bị bắt và giết để làm thịt Tết
Phương pháp giải
Căn cứ vào nội dung câu chuyện
Lời giải
- Phân tích, suy luận:
Sự kiện thứ năm xảy ra trước sự kiện thứ tư vì trong truyện có nói: "Rồi thì là Tết tháng năm. Bỗng nhiên đứa con út của bà ươn mình: bà phải kiêng để lấy sữa lành cho con bú. Sau cùng người ta nhất định thịt nó vào rằm tháng bảy ai ốm mặc."
Có nghĩa là Mực phải thoát chết ở Tết tháng năm thì mới thoát được qua tháng bảy. Do đó, sự kiện thứ năm xảy ra đầu tiên, sau đó đến sự kiện thứ tư.
Sự kiện thứ tư xảy ra trước sự kiện thứ nhất vì trong truyện có nói: "Nhưng lần nầy Mực vẫn còn thoát nạn là vì nhờ có Du. Người con cả xa xôi ấy vừa viết thư báo chẳng bao lâu sẽ về."
Sự kiện thứ nhất xảy ra trước sự kiện thứ hai vì trong truyện có nói: "Chiều hôm qua con người phóng đãng ấy đã khệ nệ xách cái vali rất nặng bước vào sân, miệng mỉm cười và mặt đỏ." và "Nhưng trời gần sáng chàng còn đương mơ mộng, thì đã nghe tiếng Hoa gọi cuống cuồng lên. Con vật khốn nạn không biết mỏi mệt thế nào mà ngủ quên đi ngay ở giữa sân để đến nỗi bị Hoa úp được."
Sự kiện thứ ba không đúng vì Mực bị đá vào sườn là một chi tiết trong truyện, không phải là một sự kiện quan trọng. Nó không ảnh hưởng đến số phận của Mực hay tình cảm của Du.
Sự kiện thứ sáu không đúng vì Mực không bị bà chủ nhà bắt, mà bị Hoa, một người khác trong nhà, úp thúng và trói chặt. Bà chủ nhà chỉ là người quyết định ngày chết cho Mực, nhưng không thực hiện hành động bắt nó.
Từ nội dung trên, ta có các từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: Mực thoát được cái chết vào Tết tháng năm
- Vị trí thả 2: Mực thoát được cái chết vào rằm tháng bảy
- Vị trí thả 3: Du về thăm nhà
Câu 21:
Phần tư duy khoa học/ giải quyết vấn đề
Dựa vào kết quả thí nghiệm 3, nếu tăng áp suất của một lượng khí lên gấp đôi, giữ nguyên thể tích và thể tích của khí trong xi lanh thì nhiệt độ sẽ như thế nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích bảng số liệu
Lời giải
Câu 22:
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích bảng số liệu
Lời giải
Từ bảng 1, có thể thấy rằng 'Áp suất × Thể tích' không đổi khi áp suất tăng. Chỉ có lựa chọn trả lời (D) hiển thị 'Áp suất × Thể tích' không đổi khi 'Áp suất' tăng lên.
Câu 23:
Dựa vào kết quả của thí nghiệm 2, hãy cho biết thể tích khí trong xi lanh sẽ là bao nhiêu nếu nung nóng xi lanh đến 350K?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích bảng số liệu
Lời giải
Từ bảng 2, có thể thấy rằng tỷ lệ thể tích và nhiệt độ là không đổi.
Câu 24:
Thí nghiệm nào sau đây sẽ giúp nhà khoa học nghiên cứu tốt nhất mối quan hệ giữa thể tích khí (tính bằng ml) và lượng khí (tính bằng mol)?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin từ bài đọc và đáp án
Vận dụng kiến thức đã học về các quá trình biến đổi trạng thái của chất
Lời giải
Để nghiên cứu mối quan hệ giữa thể tích của một chất khí và lượng của chất khí đó, nhà khoa học nên thiết lập một thí nghiệm trong đó chỉ có hai yếu tố đó thay đổi, còn tất cả các yếu tố khác không đổi. Thí nghiệm C là một thí nghiệm như vậy.
Thí nghiệm A sẽ không thực hiện được vì cần phải giữ cả nhiệt độ và áp suất không đổi, nhưng như đã mô tả, chỉ có nhiệt độ được giữ không đổi. Thí nghiệm A cũng không làm thay đổi tương đối số mol. Thí nghiệm B sẽ không hoạt động vì âm lượng được giữ không đổi. Cần phải biến thiên thể tích để nghiên cứu mối quan hệ giữa thể tích và lượng khí. Thí nghiệm D sẽ không thực hiện được vì áp suất không được giữ cố định.
Chọn C
Câu 25:
Dựa vào kết quả của thí nghiệm 2, nếu một nhà khoa học thổi không khí vào một quả bóng bay cho đến khi đường kính của quả bóng bay đạt 20 cm rồi tiếp tục hơ quả bóng bay trên ngọn lửa đèn Bunsen thì các nhận xét sau đây đúng hay sai với quả bóng bay khi nó được nung nóng?
|
|
ĐÚNG |
SAI |
|
Nhiệt độ của quả bóng sẽ giữ nguyên. |
||
|
Thể tích của quả bóng sẽ giảm. |
||
|
Thể tích của quả bóng sẽ tăng lên. |
||
|
Nhiệt độ của quả bóng sẽ giảm. |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Nhiệt độ của quả bóng sẽ giữ nguyên. |
X | |
|
Thể tích của quả bóng sẽ giảm. |
X | |
|
Thể tích của quả bóng sẽ tăng lên. |
X | |
|
Nhiệt độ của quả bóng sẽ giảm. |
X |
Phương pháp giải
Phân tích thông tin từ bài đọc và kết quả của thí nghiệm 2
Lời giải
Từ thí nghiệm 2, có thể thấy rằng khi nhiệt độ tăng thì thể tích cũng tăng. Do đó nhận xét cho rằng khi quả bóng được làm nóng, thể tích của quả bóng sẽ tăng lênlà chính xác
Câu 26:
Nhìn vào kết quả của các thí nghiệm 1, 2 và 3, bạn cho biết điều gì sẽ xảy ra với thể tích khí trong một xi lanh nếu cả áp suất và nhiệt độ của khí đều tăng gấp đôi và tất cả các yếu tố khác được giữ không đổi?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin từ bài đọc và các số liệu từ kết quả thí nghiệm
Lời giải
Từ thí nghiệm 1 có thể thấy thể tích tỉ lệ nghịch với áp suất; khi áp suất tăng, thể tích giảm. Từ thí nghiệm 2, có thể thấy thể tích tỉ lệ thuận với nhiệt độ; khi nhiệt độ tăng, thể tích tăng. Vì thể tích tỷ lệ thuận với nhiệt độ và tỷ lệ nghịch với áp suất, nên việc tăng gấp đôi nhiệt độ của khí sẽ bù đắp tác động của việc tăng gấp đôi áp suất.
Chọn B
Câu 27:
Từ kết quả của thí nghiệm 3, ta có đồ thị nhiệt độ - áp suất có dạng là đường thẳng song song với trục hoành, đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin từ bài đọc và các số liệu từ kết quả thí nghiệm
Lời giải
Tử bảng 3, ta xác định định đồ thị của P-T là đường thẳng đi qua gốc tọa độ
Chọn B
Câu 28:
Trong một thí nghiệm, một thanh sắt không có từ tính được nung nóng và để nguội, được đặt theo hướng Bắc - Nam với từ trường của Trái đất. Sau khi nguội, thanh sắt được phát hiện có từ tính. Nhà khoa học 1 rất có thể sẽ giải thích kết quả này bằng cách nói điều nào sau đây?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích nghiên cứu của nhà khoa học 1
Lời giải
Nhà khoa học 1 tuyên bố rằng từ tính xảy ra khi các miền từ tính trong vật liệu thẳng hàng.
Vì ban đầu thanh sắt không có từ tính nên chúng ta có thể giả định rằng các miền từ tính của nó ban đầu được định hướng ngẫu nhiên và nó không có cực từ.
Đồng thời, thanh sắt trở nên có từ tính sau khi được nung nóng và làm mát, nên quá trình nung nóng và làm mát có thể đã định hướng lại các miền từ tính trong thanh sắt để chúng trở nên thẳng hàng hơn, tạo ra hai cực từ.
=> Kết luận đúng là: Thí nghiệm cho phép các miền từ tính của thanh thẳng hàng, làm cho thanh có từ tính.
Chọn C
Câu 29:
Khi đặt hai dây dẫn có dòng điện gần nhau, người ta 2 dây hút nhau với một lực khá nhỏ. Điều này có thể được nhà khoa học 3 rất có thể sẽ giải thích như thế nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích nghiên cứu của nhà khoa học 3
Vận dụng kiến thức đã học về từ trường và điện trường
Lời giải
Nhà khoa học 3 cho rằng rằng một dòng điện có thể tạo ra một từ trường xung quanh nó. Vì vậy, khi có hai dây dẫn mang dòng điện, nhà khoa học cho rằng cả hai dây dẫn đều tạo ra từ trường. Vì khi hai dây bị hút vào nhau, nên từ trường cũng có khả năng hút lẫn nhau.
Cuối cùng, Nhà khoa học 3 cũng tuyên bố rằng từ trường do dòng điện tạo ra tồn tại vuông góc với hướng dòng điện chạy qua. Vì vậy, các từ trường được định hướng vuông góc với các dây tạo ra chúng.
Chọn C
Câu 30:
Trong một chiếc la bàn, một chiếc kim quay để căn chỉnh hướng Bắc-Nam, theo từ trường của Trái đất. Giả sử đặt một chiếc la bàn gần dây dẫn có dòng điện chạy qua, người ta quan sát thấy kim la bàn không còn thẳng hàng với hướng Bắc-Nam. Từ đó kết quả nghiên cứu của nhà khoa học 2 và 3 có ảnh hưởng. Các nhận xét sau đây về sự ảnh hưởng về kết quả nghiên cứu là đúng hay sai?
|
|
ĐÚNG |
SAI |
|
Nó sẽ củng cố lập luận của Nhà khoa học 2 và nó sẽ làm suy yếu lập luận của Nhà khoa học 3. |
||
|
Nó sẽ làm suy yếu lập luận của Nhà khoa học 2 và nó sẽ củng cố lập luận của Nhà khoa học 3. |
||
|
Nó sẽ củng cố lập lập của cả 2 Nhà khoa học |
||
|
Nó sẽ không ảnh hưởng gì đến lập luận của Nhà khoa học 2 và nó sẽ củng cố lập luận của Nhà khoa học 3. |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Nó sẽ củng cố lập luận của Nhà khoa học 2 và nó sẽ làm suy yếu lập luận của Nhà khoa học 3. |
X | |
|
Nó sẽ làm suy yếu lập luận của Nhà khoa học 2 và nó sẽ củng cố lập luận của Nhà khoa học 3. |
X | |
|
Nó sẽ củng cố lập lập của cả 2 Nhà khoa học |
X | |
|
Nó sẽ không ảnh hưởng gì đến lập luận của Nhà khoa học 2 và nó sẽ củng cố lập luận của Nhà khoa học 3. |
X |
Phương pháp giải
Phân tích nghiên cứu của nhà khoa học 2 và 3
Vận dụng kiến thức đã học về từ trường và điện trường
Lời giải
Ở đây, vì la bàn (từ tính) không còn thẳng hàng với hướng Bắc-Nam khi nó ở gần dây, điều này ngụ ý rằng có một loại từ trường nào đó gần dây đang cản trở la bàn. Điều này hỗ trợ những gì Nhà khoa học 3 nói trong đoạn đầu tiên của lời giải thích của cô ấy: rằng một dòng điện có thể tạo ra một từ trường xung quanh nó.
Tuy nhiên, nhà khoa học 2 không đề cập đến loại cảm ứng điện từ này trong lời giải thích của mình; tuy nhiên, anh ấy cũng không nói rằng điều đó là không thể. Lời giải thích của ông chủ yếu là về cách các cực từ giống và khác với các điện tích tĩnh. Vì vậy, lập luận của ông không bị ảnh hưởng bởi quan sát cho rằng dòng điện gây ra từ trường.
Câu 31:
Cho rằng tất cả những nhận xét sau đây đều đúng, điều nào sau đây, nếu được tìm thấy sẽ có thể chống lại giả thuyết của Nhà khoa học 1?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin bài đọc
Vận dụng kiến thức đã học về điện trường và từ trường
Lời giải
Nhà khoa học 1 cho rằng rằng điện và từ là những hiện tượng hoàn toàn riêng biệt; tuy nhiên, nếu một dây dẫn mang dòng điện tác dụng lực hút lên một cực của nam châm và lực đẩy lên cực kia của nam châm thì phải có sự tương tác giữa dòng điện chạy qua dây dẫn và nam châm. Cụ thể, như dòng điện chạy qua dây dẫn đang tạo ra từ trường riêng của nó, từ trường này hút một cực của nam châm và đẩy cực kia.
Chọn C
Câu 32:
Theo Nhà khoa học 2, điều nào sau đây sẽ là một ví dụ về điện tích tĩnh?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin bài đọc và kết quả của nhà khoa học 2
Lời giải
Nhà khoa học 2 cho rằng điện tích tĩnh xảy ra khi một vật thể có quá nhiều điện tích dương hoặc âm. Theo Nhà khoa học 2, điện tích tĩnh cũng không liên quan đến điện tích chuyển động. Vì vậy, một ví dụ về điện tích tĩnh là một quả bóng bay đã hút các electron thừa: nó thừa điện tích âm, nhưng điện tích không chuyển động.
Chọn D
Câu 33:
Nhà khoa học 3 cho rằng __________ có thể tạo ra _________
Khi cuộn dây quay giữa các cực của nam châm thì trong cuộn dây sinh ra dòng điện. Kết quả này đã _________ lập luận của Nhà khoa học 3
 Xem đáp án
Xem đáp án
Đáp án
Nhà khoa học 3 cho rằng từ trường có thể tạo ra dòng điện
Khi cuộn dây quay giữa các cực của nam châm thì trong cuộn dây sinh ra dòng điện. Kết quả này đã ủng hộ lập luận của Nhà khoa học 3
Phương pháp giải
Phân tích thông tin bài cung cấp
Lời giải
Nhà khoa học 3 cho rằng từ trường có thể tạo ra dòng điện. Cụ thể đó là việc di chuyển một sợi dây qua từ trường có thể tạo ra dòng điện trong dây.
Khi cuộn dây quay giữa các cực của nam châm thì trong cuộn dây sinh ra dòng điện. Kết quả này đã ủng hộ lập luận của Nhà khoa học 3
Câu 34:
Điều nào sau đây sẽ là một ví dụ về điện theo Nhà khoa học 2, nhưng không phải theo Nhà khoa học 1?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin từ bài đọc
Vận dụng kiến thức đã học về tương tác tính điện
Lời giải
Theo Nhà khoa học 2, điện có thể có hai dạng: tĩnh điện và dòng điện. Nhà khoa học 2 phát biểu rằng trong khi dòng điện bao gồm một điện tích chuyển động, thì tĩnh điện không bao gồm một điện tích chuyển động. Nhà khoa học 2 cho rằng tĩnh điện có thể khiến hai vật thể đẩy hoặc hút lẫn nhau. Ngược lại, Nhà khoa học 1 định nghĩa điện là điện tích chuyển động - ông nói rằng điện phải liên quan đến dòng điện tích.
Vì vậy, một tình huống không có dòng điện tích - trong đó hai vật thể đẩy nhau do tĩnh điện sẽ được Nhà khoa học 2 coi là một ví dụ về điện, chứ không phải bởi Nhà khoa học 1.
Chọn A
Câu 35:
Ốc bươu vàng (Ampullariidea) thuộc ngành động vật _________
 Xem đáp án
Xem đáp án
Đáp án “thân mềm”
Phương pháp giải
Đọc kĩ đoạn trích
Lời giải
Ốc bươu vàng(Ampullariidea) thuộc ngành động vật thân mềm.
Đáp án: thân mềm.
Câu 36:
Đặc điểm nào sau đây xuất hiện ở ốc bươu vàng(Ampullariidea)?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ đoạn trích
Lời giải
C đúng.
Các loài ốc thuộc Họ Ampullariidae có tỷ lệ giới tính không đều, ốc cái chiếm tỷ lệ cao hơn ốc đực trong quần đàn, quần thể càng già thì tỷ lệ con cái càng tăng => A sai.
Ốc đực và ốc cái phát triển giới tính riêng biệt, sau khi bắt cặp giao phối thì quá trình thụ tinh diễn ra trong buồng chứa tinh của con cái => B sai.
Con cái có kích thước lớn hơn con đực các loài ốc thuộc họ Ampullariidae. => D sai.
Chọn C
Câu 37:
Chọn đáp án chính xác nhất
Hoạt động sinh sản của ốc bươu vàng (Ampullariidae) tập trung vào mùa nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ đoạn trích
Lời giải
Hoạt động sinh sản tập trung vào mùa mưa sau thời kỳ vùi mình dưới đất.
Đáp án: mùa mưa.
Chọn A
Câu 38:
Nhận định dưới đây đúng hay sai?
Trứng ốc khi được đẻ ra ngoài là trứng chưa được thụ tinh, sau một thời gian trứng mới được con đực thụ tinh trong môi trường nước.
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ đoạn trích
Lời giải
Sau khi bắt cặp giao phối thì quá trình thụ tinh diễn ra trong buồng chứa tinh của con cái => Trứng ốc khi được đẻ ra ngoài là trứng đã được thụ tinh.
Đáp án: B
Câu 39:
Thành tế bào vi khuẩn được cấu tạo bởi lớp _________
 Xem đáp án
Xem đáp án
Đáp án “peptidoglican”
Phương pháp giải
Đọc kĩ đoạn thông tin
Lời giải
Thành tế bào vi khuẩn có độ dày từ 10-20nm và được cấu tạo bởi lớp peptidoglican (bao gồm polisaccarit liên kết với peptit).
Câu 40:
Nhận định dưới đây đúng hay sai?
Vi khuẩn gram âm có thành tế bào gồm một lớp mỏng peptidoglycan và màng ngoài có lipopolysaccharide (thành phần này không có ở vi khuẩn gram dương).
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ đoạn thông tin
Lời giải
Điểm khác nhau chủ yếu để phân biệt vi khuẩn gram âm và vi khuẩn gram dương liên quan đến thành phần thành tế bào của chúng.
Vi khuẩn gram dương có thành tế bào được cấu tạo chủ yếu từ một lớp được gọi là peptidoglycan. Các vi khuẩn này sẽ có màu tím sau khi nhuộm gram.
Vi khuẩn gram âm có thành tế bào gồm một lớp mỏng peptidoglycan và màng ngoài có lipopolysaccharide (thành phần này không có ở vi khuẩn gram dương). Vi khuẩn gram âm có màu đỏ hoặc hồng sau khi nhuộm gram.
Đáp án: A
Câu 41:
Chọn đáp án chính xác nhất
Khi nghiên cứu 1 loài vi khuẩn Pseudomonas aeruginosa(trực khuẩn mủ xanh), gây các bệnh: nhiễm trùng vết thương, viêm tai ngoài, viêm kết mạc, viêm giác mạc, viêm phổi, nhiễm trùng tiểu, nhiễm trùng huyết,…, các nhà khoa học thực hiện nhuộm gram. Kết quả như hình dưới, theo em, vi khuẩn Pseudomonas aeruginosa thuộc loại vi khuẩn nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ đoạn thông tin
Lời giải
Kết quả cho thấy vi khuẩn được nghiên cứu bắt màu thuốc nhuộm
Câu 42:
Cấu trúc nào dưới đây không có ở vi khuẩn gram âm?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ đoạn thông tin
Lời giải
Chuỗi axit teichoic chỉ có ở vi khuẩn gram dương, Axit teichoic giúp một số vi khuẩn gram dương xâm nhập vào tế bào và gây bệnh.
=> Chọn B
Câu 43:
Chọn đáp án chính xác nhất.
Cơ thể vi khuẩn được cấu tạo từ dạng tế bào nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin được cung cấp
Lời giải
Tế bào nhân sơ (Procaryota) cấu tạo nên cơ thể vi khuẩn
=> Đáp án: Procaryota.
Chọn B
Câu 44:
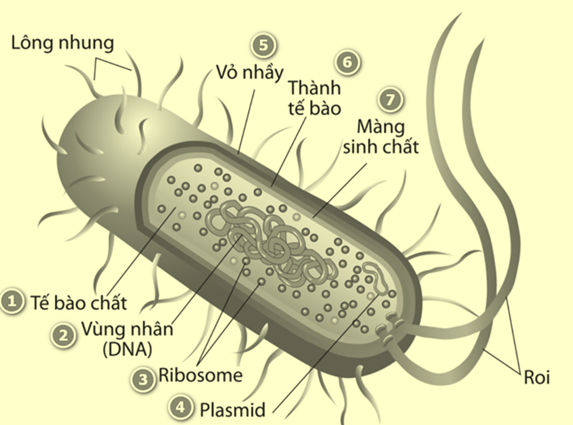
Chú thích chính xác đối với hình 1 là?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin được cung cấp
Lời giải
Chú thích chính xác đối với hình 1 là:
(1) Tế bào chất; (2) Vùng nhân; (3) Ribosome; (4) Plasmid; (5) Màng nhầy; (6) Thành tế bào; (7) Màng sinh chất.
 Chọn C
Chọn CCâu 45:
Vùng nhân của tế bào vi khuẩn có đặc điểm
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào hình ảnh
Lời giải
Vùng nhân của tế bào vi khuẩn chứa một phân tử ADN dạng vòng, đơn
=> Chọn B
Câu 46:
Nhận định dưới đây, đúng hay sai?
Khi vi khuẩn mất đi thành tế bào, chúng vẫn có thể sống được một thời gian dài sau đó.
 Xem đáp án
Xem đáp án
Phương pháp giải
Thành tế bào
- Đặc điểm cấu tạo : có thành phần chính là peptiđôglican.
- Chức năng : quy định hình dạng của tế bào.
Lời giải
Thành tế bào có chức năng duy trì hình thái, áp suất thẩm thấu bên trong tế bào, bảo vệ tế bào trước những tác nhân vật lý hóa học và thực hiện việc tích điện ở bề mặt tế bào.
Khi bị mất thành tế bào dẫn tới vi khuẩn mất khả năng chống lại sức trương nước làm vỡ tế bào.
=> Khi bị mất thành tế bào vi khuẩn thường bị chết.
Câu 47:
Khối lượng muối carbonate đã dùng trong thí nghiệm 1 là
 Xem đáp án
Xem đáp án
Phương pháp giải
Khối lượng muối carbonate đã dùng trong thí nghiệm 1 = Khối lượng ống nghiệm ở bước 2 - khối lượng ống nghiệm bước 1
Lời giải
Câu 48:
Khi phản ứng phân hủy xảy ra hoàn toàn khối lượng của CO2 thoát ra ở thí nghiệm 1 là
 Xem đáp án
Xem đáp án
Phương pháp giải
Khối lượng khí CO2 đã thoát ra = Khối lượng ống nghiệm bước 2 - Khối lượng ống nghiệm bước 5.
Lời giải
Sau khi nung lần 4, lần 5, khối lượng của ống nghiệm không đổi nên tại bước 5 muối carbonate đã được nhiệt phân hoàn toàn.
Vậy khối lượng ống nghiệm giảm đi so với trước khi nung chính là khối lượng của khí CO2 thoát ra.
Câu 49:
Phát biểu sau đây đúng hay sai?
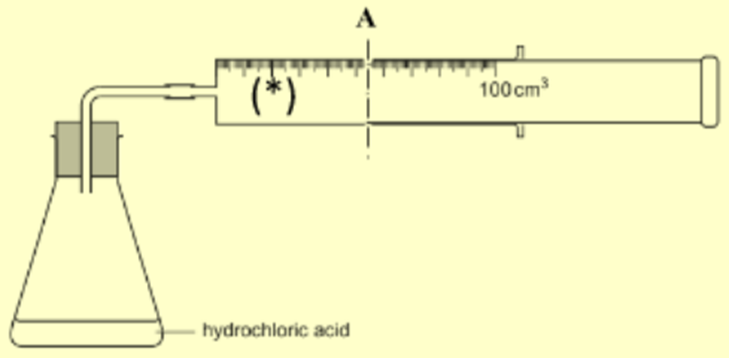
Thể tích khí CO2 thu được khi kết thúc phản ứng ở thí nghiệm 2 là 54 mL.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào hình vẽ
Lời giải
Thể tích khí CO2 thu được khi kết thúc phản ứng là 54 ml (tương ứng đường A)
Câu 50:
Ở điều kiện đang xét thể tích mol của chất khí là 24 lít. Giá trị m (khối lượng muối carbonate được lấy ban đầu là
 Xem đáp án
Xem đáp án
Phương pháp giải
Áp dụng công thức m = n.M
Lời giải
Số mol của chất khí là 54/24000 = 2,25.10-3 mol
=> Khối lượng muối carbonate là 2,25.10-3.(24 + 12 + 3.16) = 0,189 gam
Chọn A
Câu 51:
Các sinh viên khác cũng làm tương tự thí nghiệm này nhưng thấy rằng các kết quả có thể khác nhau. Lý do nào dưới đây không hợp lý để giải thích sự khác nhau ở trên?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thực nghiệm
Lời giải
Đáp án C sai vì số mol HCl ở các thí nghiệm là như nhau thì lượng khí CO2 thu được cũng phải giống nhau, chứ không phải do nồng độ mol và thể tích của HCl khác nhau gây nên lượng khí thu được giữa các thí nghiệm là khác nhau.
Chọn C
Câu 52:
Kim loại hóa trị II đang xét là _______
 Xem đáp án
Xem đáp án
Đáp án “Mg”
Phương pháp giải
Viết PTHH. Tính toán theo PTHH
Lời giải
Số mol CO2 phản ứng là 2,2/40 = 0,05 mol
Từ PTHH => Số mol của RCO3 là 0,05 mol
Câu 53:
Trong thí nghiệm trên, bạn học sinh đã thực hiện nung muối carbonate của kim loại ba lần. Theo em, nhận định dưới đây là đúng hay sai?
Bạn học sinh nung muối carbonate của kim loại ba lần để chắc chắn rằng phản ứng xảy ra hoàn toàn.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào kỹ năng làm thí nghiệm.
Lời giải
Nhận thấy sau khi nung lần 2 và lần 3 thì khối lượng của ống nghiệm và muối carbonate sau khi nung là giống nhau => Phản ứng xảy ra hoàn toàn.
Chọn A
Câu 54:
Điều nào sau đây là đúng với cả ba lý thuyết acid - base đã nêu? Em hãy chọn Đúng/Sai phù hợp cho mỗi ý kiến.
|
|
ĐÚNG |
SAI |
|
Phản ứng giữa acid và base tạo ra nước và muối. |
||
|
Phản ứng giữa acid và base có thể tạo ra nước. |
||
|
Phản ứng giữa acid và base mất ít nhất vài giờ. |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Phản ứng giữa acid và base tạo ra nước và muối. |
X | |
|
Phản ứng giữa acid và base có thể tạo ra nước. |
X | |
|
Phản ứng giữa acid và base mất ít nhất vài giờ. |
X |
Phương pháp giải
Dựa vào các lý thuyết acid - base đã nêu trong bài.
Lời giải
- Phản ứng acid - base the thuyết Lewis không đề cập đến việc sau phản ứng sản phẩm tạo ra có nước nên nhận định 1 và 2 sai.
- Không có bất kỳ lý thuyết nào trao đổi về tốc độ phản ứng của acid - base nên nhận định 3 là sai.
Câu 55:
Điền số thích hợp vào chỗ trống:
Nếu xác định một chất là acid hoặc base theo lý thuyết __________ thì số lượng chất được coi là acid, base phù hợp với thuyết này sẽ là lớn nhất.
 Xem đáp án
Xem đáp án
Đáp án: “3”
Phương pháp giải
Dựa vào cách định nghĩa thế nào là acid - base trong mỗi thuyết.
Lời giải
Câu 56:
Giả sử có một khám phá mới phát hiện ra rằng các phản ứng acid - base không thực sự đảo ngược. Khám phá này sẽ bác bỏ hoàn toàn khái niệm nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào nội dung 3 thuyết.
Lời giải
Như đã nêu trong đề bài, ý tưởng về các cặp acid - base liên hợp trong lý thuyết Bronsted - Lowry là dựa trên phản ứng thuận nghịch của các chất acid - base. Các câu trả lời khác không dựa vào điều này và sẽ không bị ảnh hưởng ở mức độ tương tự như các cặp liên hợp.
Chọn A
Câu 57:
Lý thuyết nào ủng hộ khái niệm rằng các phản ứng acid - base dựa trên sự cho - nhận giữa acid và base?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn văn.
Lời giải
Cả lý thuyết 2 và lý thuyết 3 đều dựa trên định nghĩa của họ về các phản ứng acid - base dựa trên khái niệm cho - nhận. Lý thuyết 2 liên quan đến sự cho các ion H+từ acid sang base, trong khi lý thuyết 3 liên quan đến sự cho các cặp electron từ base sang acid. Lý thuyết 1 không thảo luận về sự cho - nhận bất kì yếu tố gì.
Chọn B
Câu 58:
Lý thuyết nào sẽ coi BF3 là một axit?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn văn
Lời giải
BF3 không có H trong hợp chất và do đó không thể phân ly ra H+ trong nước hoặc nhường H+ cho base. Nó chỉ có thể là một phần của phản ứng acid - base thông qua việc nhận một cặp electron, vì vậy chỉ có thuyết 3 mới coi nó là một acid.
Chọn C
Câu 59:
Giả sử lý thuyết 2 được chứng minh là đúng và lý thuyết 1 và 3 bị bác bỏ. Điều nào sau đây sẽ là kết quả của điều này?
|
|
ĐÚNG |
SAI |
|
Phản ứng acid - base sẽ không còn được coi là một phần của hóa học |
||
|
Phản ứng acid - base không có ion H+ sẽ bị bỏ qua. |
||
|
Phản ứng acid - base chỉ xảy ra trong dung dịch. |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Phản ứng acid - base sẽ không còn được coi là một phần của hóa học |
X | |
|
Phản ứng acid - base không có ion H+ sẽ bị bỏ qua. |
X | |
|
Phản ứng acid - base chỉ xảy ra trong dung dịch. |
X |
Phương pháp giải
Dựa vào đoạn thông tin đề bài cho
Lời giải
Lý thuyết 2 yêu cầu sự cho H+ để xảy ra phản ứng acid - base. Nếu Lý thuyết 2 được chứng minh là hoàn toàn đúng thì phản ứng giữa các chất không có sự cho ion H+sẽ không được coi là phản ứng acid - base. Nếu chỉ có lý thuyết 1 được chứng minh là đúng, thì chỉ những phản ứng liên quan đến sự thay đổi nồng độ của các ion H+và/hoặc ion OH- trong nước mới được coi là phản ứng acid - base. Phản ứng acid - base vẫn sẽ là một phần của hóa học.
Câu 60:
Theo thuyết 2, đâu được coi là dạng base liên hợp của HCl trong phản ứng sau?
\({{\rm{H}}_2}{\rm{O}} + {\rm{HCl}} \to {{\rm{H}}_3}{{\rm{O}}^ + } + {\rm{C}}{{\rm{l}}^ - }\)
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào nội dung lý thuyết 2.
Lời giải
Câu 61:
Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống. Hình minh hoạ quỹ đạo của quả bóng là một phần của cung parabol trong mặt phẳng toạ độ Oth, trong đó t là thời gian (tính bằng giây) kể từ khi quả bóng được đá lên và h là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá từ mặt đất. Sau khoảng 2s, quả bóng lên đến vị trí cao nhất là 8m.

Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
Hàm số bậc hai biểu thị độ cao h theo thời gian t và có phần đồ thị trùng với quỹ đạo của quả bóng trong tình huống này là \[f(t) = - 2{t^2} + 4t\]. |
¡ |
¡ |
|
Độ cao của quả bóng sau khi đá lên được 3s là 6m |
¡ |
¡ |
|
Sau 4 giây thì quả bóng chạm đất kể từ khi đá lên |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
Hàm số bậc hai biểu thị độ cao h theo thời gian t và có phần đồ thị trùng với quỹ đạo của quả bóng trong tình huống này là \[f(t) = - 2{t^2} + 4t\]. |
¡ |
¤ |
|
Độ cao của quả bóng sau khi đá lên được 3s là 6m |
¤ |
¡ |
|
Sau 4 giây thì quả bóng chạm đất kể từ khi đá lên |
¤ |
¡ |
Phương pháp giải
- Tìm hàm số bậc hai biểu thị độ cao h theo thời gian tvà có phần đồ thị trùng với quỹ đạo của quả bóng.
- Tính độ cao của quả bóng sau khi đá lên được 3s.
- Cho h = 0 rồi tìm t.
Lời giải
a) Gọi hàm số bậc hai biểu thị độ cao \(h(m)\) theo thời gian \(t(s)\) là:
\(h = f(t) = a{t^2} + bt + c(a < 0)\). Theo giả thiết, quả bóng được đá lên từ mặt đất, nghĩa là \(f(0) = c = 0\), do đó \(f(t) = a{t^2} + bt\). Sau 2s, quả bóng lên đến vị trí cao nhất là 8m nên
\(\left\{ {\begin{array}{*{20}{l}}{ - \frac{b}{{2a}} = 2}\\{f(2) = 8}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b = - 4a}\\{4a + 2b = 8}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b = - 4a}\\{ - 4a = 8}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = - 2}\\{b = 8.}\end{array}} \right.} \right.} \right.} \right.\)
Vậy \(f(t) = - 2{t^2} + 8t\).
b) Độ cao của quả bóng sau khi đá lên được 3s là:
\(h = f(3) = - {2.3^2} + 8.3 = 6(m){\rm{. }}\)
c) Cách 1. Quả bóng chạm đất (trở lại) khi độ cao h = 0, tức là:
Vì thế sau 4s quả bóng sẽ chạm đất kể từ khi đá lên.
Cách 2. Quỹ đạo chuyển động của quả bóng là một phần của cung parabol có trục đối xứng là đường thẳng . Điểm xuất phát và điểm quả bóng chạm đất (trở lại) đối xứng nhau qua đường thẳng . Vì thế sau quả bóng sẽ chạm đất kể từ khi đá lên.
Câu 62:
Cho hai hàm số \(f(x)\) và \(g(x)\) cùng đồng biến trên khoảng \((a;b)\). Có thể kết luận gì về chiều biến thiên của hàm số \(y = f(x) + g(x)\) trên khoảng \((a;b)\)?
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Ta có hàm số \(y = f(x) + g(x)\) đồng biến trên khoảng \((a;b)\).
Câu 63:
Tìm tất cả các giá trị của \(m\) để hàm số \(y = \sqrt { - 2x + 3m + 2} + \frac{{x + 1}}{{x + 2m - 4}}\) xác định trên \(( - \infty ; - 2)\).
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Hàm số xác định \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 2x + 3m + 2 \ge 0}\\{x + 2m - 4 \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \le \frac{{3m + 2}}{2}}\\{x \ne 4 - 2m}\end{array}} \right.} \right.\).
Hàm số xác định trên
\(( - \infty ; - 2) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 2 \le \frac{{3m + 2}}{2}}\\{4 - 2m \notin ( - \infty ; - 2)}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 4 \le 3m + 2}\\{4 - 2m \ge - 2}\end{array}} \right.} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m \ge - 2}\\{m \le 3}\end{array} \Leftrightarrow - 2 \le m \le 3} \right.\).
Câu 64:
Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua vào một chiếc là 27 (triệu đồng) và bán ra với giá là 31 triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm 1 triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ tăng thêm 200 chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu để sau khi đã thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất.
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Gọi \(x\) (triệu) đồng là số tiền mà doanh nghiệp \(A\) dự định giảm giá; \((0 \le x \le 4)\).
Khi đó:
Lợi nhuận thu được khi bán một chiếc xe là \(31 - x - 27 = 4 - x\) (triệu đồng).
Số xe mà doanh nghiệp sẽ bán được trong một năm là \(600 + 200x\) (chiếc).
Lợi nhuận mà doanh nghiệp thu được trong một năm là
\(f(x) = (4 - x)(600 + 200x) = - 200{x^2} + 200x + 2400.{\rm{ }}\)
Lợi nhuật thu được lớn nhất khi \(x = - \frac{b}{{2a}} = - \frac{{200}}{{ - 400}} = 0,5\) triệu đồng.
Khi đó giá bán mới là \(31 - 0,5 = 30,5\) triệu đồng.
Câu 65:
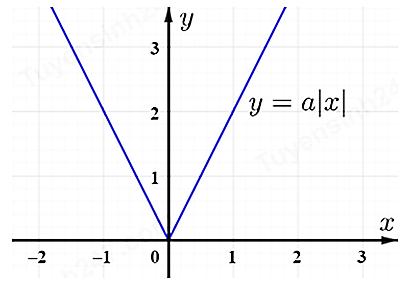
Cho đồ thị hàm số \[y = a|x|\]
 Xem đáp án
Xem đáp án
Đáp án: “2”
Phương pháp giải
Thay x = 1 tìm y
Lời giải
Ta có: với x = 1 thì y = 2 => a = 2
Câu 66:
Tìm giá trị thực của tham số m ≠ 0 để hàm số y = mx2 − 2mx − 3m − 2 có giá trị nhỏ nhất bằng -10 trên \(\mathbb{R}\).
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Ta có \(x = - \frac{b}{{2a}} = \frac{{2m}}{{2m}} = 1,\)suy ra \(y = - 4m - 2\).
Để hàm số có giá trị nhỏ nhất bằng -10 khi và chỉ khi
\(\left\{ {\begin{array}{*{20}{l}}{m > 0}\\{ - 4m - 2 = - 10}\end{array} \Leftrightarrow m = 2.} \right.\)
Câu 67:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số \(y = 2\cos 2x + 5,x \in \left[ {0;\frac{\pi }{6}} \right]\) lần lượt là ....và ....
 Xem đáp án
Xem đáp án
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số \(y = 2\cos 2x + 5,x \in \left[ {0;\frac{\pi }{6}} \right]\) lần lượt là 7 và 6
Phương pháp giải
- Sử dụng đường tròn lượng giác.
Lời giải
Ta có: \(x \in \left[ {0;\frac{\pi }{6}} \right] \Leftrightarrow 2x \in \left[ {0;\frac{\pi }{3}} \right].\)
Sử dụng đường tròn lượng giác:
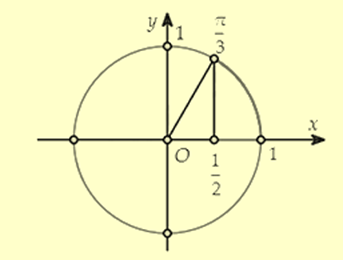
Ta có: \(\forall x \in \left[ {0;\frac{\pi }{6}} \right] \Leftrightarrow 2x \in \left[ {0;\frac{\pi }{3}} \right]:\frac{1}{2} \le \cos 2x \le 1\)
\( \Leftrightarrow 1 \le 2\cos 2x \le 2\)
\( \Leftrightarrow 6 \le 2\cos 2x + 5 \le 7\)
Vậy \(\mathop {\max }\limits_{x \in \left[ {0;\frac{\pi }{6}} \right]} y = 7\) đạt được khi \(\cos 2x = 1 \Leftrightarrow x = 0 \in \left[ {0;\frac{\pi }{6}} \right]\) ;
\(\mathop {\min }\limits_{x \in \left[ {0;\frac{\pi }{6}} \right]} y = 6\)
\( \Leftrightarrow \cos 2x = \frac{1}{2} \Leftrightarrow x = \frac{\pi }{6} \in \left[ {0;\frac{\pi }{6}} \right]\)
Câu 68:
Tìm tập giá trị \(T\) của hàm số \(y = \sqrt {7{{\sin }^2}2x + 9} \)
 Xem đáp án
Xem đáp án
Phương pháp giải
Đánh giá dựa trên kết quả: \(0 \le {\sin ^2}2x \le 1\)
Lời giải
Ta có: \(\forall x \in \mathbb{R}:0 \le {\sin ^2}2x \le 1 \Leftrightarrow 9 \le 7{\sin ^2}2x + 9 \le 16 \Leftrightarrow 3 \le \sqrt {7{{\sin }^2}2x + 9} \le 4.\)
\(\mathop {\min }\limits_\mathbb{R} y = 4\) đạt được khi \({\sin ^2}2x = 1\)
\(\begin{array}{l} \Leftrightarrow \cos 2x = 0\\ \Leftrightarrow 2x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\\ \Leftrightarrow x = \frac{\pi }{4} + \frac{{k\pi }}{2},k \in \mathbb{Z}\end{array}\)
\(\mathop {\min }\limits_\mathbb{R} y = 3\) đạt được khi \(\sin 2x = 0 \Leftrightarrow x = \frac{{k\pi }}{2},k \in \mathbb{Z}{\rm{. }}\)
Vậy tập giá trị của hàm số là T = [3;4].
Câu 69:
Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước trong kênh được tính tại thời điểm t (giờ) trong một ngày bởi công thức \(h = 3\cos \left( {\frac{{\pi t}}{8} + \frac{\pi }{4}} \right) + 12\). Mực nước của con kênh cao nhất khi
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Mực nước của con kênh cao nhất khi h lớn nhất
\( \Leftrightarrow \cos \left( {\frac{{\pi t}}{8} + \frac{\pi }{4}} \right) = 1 \Leftrightarrow \frac{{\pi t}}{8} + \frac{\pi }{4} = k2\pi \)
\( \Rightarrow t = 16k - 2{\rm{ }}\)với \(0 < t \le 24\) (*)
\( \Leftrightarrow k > \frac{1}{8},k \in \mathbb{Z}\)
+ Với k = 1 ⇒ t = 14
+ Với k ≥ 2 ⇒ t > 24 => Loại
Vậy mực nước của con kênh cao nhất khi t = 14 (giờ).
Câu 70:
Hàm số nào sau đây là hàm số lẻ trên \(\mathbb{R}\)?
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Xét hàm số \(y = x\cos x\).
Tập xác định: \(D = \mathbb{R}\).
+) \(\forall x \in D \Rightarrow - x \in D.{\rm{ }}\)
+) \(\forall x \in D:y( - x) = ( - x)\cos ( - x) = - x\cos x = - y(x){\rm{.}}\)
Vậy hàm số \(y = x\cos x\) là hàm số lẻ trên \(\mathbb{R}\).
Hàm số \(y = {\tan ^2}x\sin x;\,\,y = {\tan ^3}x\) là hàm số lẻ trên tập xác định \(D\) của nó với \(D \ne \mathbb{R}\).
Câu 71:
Cho cấp số nhân (un) có u1 = 2, u3 = 4. Tìm số hạng thứ 5 của cấp số nhân đã cho.
 Xem đáp án
Xem đáp án
Lời giải
Ta có: \({q^2} = \frac{{{u_3}}}{{{u_1}}} = 2\)
\({u_5} = {q^4}.{u_1} = {2.2^2} = 8\)
Câu 72:
Cho cấp số cộng (un) có u1 = 4; u2 = 1. Giá trị của u10bằng
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
\(d = {u_2} - {u_1} = - 3 \Rightarrow {u_{10}} = 4 + 9.( - 3) = - 23\)
Câu 73:
Gọi S là tập hợp tất cả các giá trị \(x \in (0;10\pi )\) và \(\frac{{\sin x}}{2};\sqrt 3 \cos x;\tan x\) theo thứ tự là một cấp số nhân, tính tổng các phần tử của S.
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
ĐK: \(x \ne \frac{\pi }{2} + k\pi \)
\(\frac{{\sin x}}{2};\sqrt 3 \cos x;\,\,\tan x\) theo thứ tự là một cấp số nhân nên ta có:
\(\frac{{\sin x}}{2}.\tan x = {(\sqrt 3 \cos x)^2}\)
\( \Leftrightarrow \frac{{{{\sin }^2}x}}{{2\cos x}} = 3{\cos ^2}x\)
\( \Leftrightarrow {\sin ^2}x = 6{\cos ^3}x\)
\( \Leftrightarrow 1 - {\cos ^2}x = 6{\cos ^3}x\)
\( \Leftrightarrow \cos x = \frac{1}{2} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{3} + k2\pi }\\{x = - \frac{\pi }{3} + k2\pi }\end{array}} \right.\)
Với \(x = \frac{\pi }{3} + k2\pi \)
\(0 < \frac{\pi }{3} + k2\pi < 10\pi \Leftrightarrow - \frac{\pi }{3} < k2\pi < \frac{{29\pi }}{3} \Leftrightarrow \frac{{ - 1}}{6} < k < \frac{{29}}{6}\)
\( \Rightarrow x \in \left\{ {\frac{\pi }{3};\frac{{7\pi }}{3};\frac{{13\pi }}{3};\frac{{19\pi }}{3};\frac{{25\pi }}{3}} \right\}\)
Với \(x = - \frac{\pi }{3} + k2\pi \)
\(0 < - \frac{\pi }{3} + k2\pi < 10\pi \Leftrightarrow \frac{\pi }{3} < k2\pi < \frac{{31\pi }}{3} \Leftrightarrow \frac{1}{6} < k < \frac{{31}}{6}\)
\( \Rightarrow x \in \left\{ {\frac{{5\pi }}{3};\frac{{11\pi }}{3};\frac{{17\pi }}{3};\frac{{23\pi }}{3};\frac{{29\pi }}{3}} \right\}\)
Tổng các phần tử của S là 50π.
Câu 74:
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 2\) và \(d = - 3\). Trên mặt phẳng tọa độ Oxy lấy các điểm \({A_1},{A_2}, \ldots \) sao cho với mỗi số nguyên dương \(n\), điểm \({A_n}\) có tọa độ \(\left( {n;{u_n}} \right)\). Biết rằng khi đó tất cả các điểm \({A_1},{A_2}, \ldots {A_n}, \ldots \) cùng nằm trên một đường thẳng. Viết phương trình đường thẳng đó.
 Xem đáp án
Xem đáp án
Phương pháp giải
- Tìm số hạng tổng quát của cấp số cộng
- Liên hệ mối quan hệ giữa n và un và các điểm
Lời giải
Số hạng tổng quát của cấp số cộng (un) là un = −3n + 5
Ta thấy tọa độ của các điểm An đều thỏa mãn phương trình y = −3x + 5 nên phương trình đường thẳng đi qua các điểm A1, A2,…An,… là y = −3x + 5
Câu 75:
Cho dãy số (un) có \[{u_n} = {n^2} - 2n + 2\] , dãy có bao nhiêu số hạng là số chính phương
 Xem đáp án
Xem đáp án
Phương pháp giải
- Với n = 1 tìm un.
- Với n ≥ 2 chứng minh không tồn tại số chính phương thỏa mãn bài toán.
Lời giải
Ta có: un = n2 − 2n + 2
Với n = 1 ta có un = 1 là số chính phương
Với n ≥ 2 ta thấy u2 = 2
Nếu un = (n − 1)2 + 1 là số chính phương thì (n−1)2 và un là 2 số chính phương liên tiếp
Khi đó n − 1 = 0 ⇔ n = 1
Vậy có đúng 1 số chính phương thỏa mãn bài toán.
Câu 76:
Cho hàm số \(f(x)\) xác định trên [a;b]. Tìm mệnh đề đúng.
 Xem đáp án
Xem đáp án
Phương pháp giải
- Xét từng đáp án.
Lời giải
Xét đáp án C:
Vì \(f(a)f(b) > 0\) nên \(f(a)\) và \(f(b)\) cùng dương hoặc cùng âm. Mà \(f(x)\) liên tục, tăng trên [a;b] nên đồ thị hàm \(f(x)\) nằm trên hoặc nằm dưới trục hoành trên [a;b] hay phương trình \(f(x) = 0\) không có nghiệm trong khoảng \((a;b)\).
Câu 77:
Cho \({u_n} = \frac{{{{5.6}^{n + 1}} + {2^n}}}{{{{4.6}^n} + {3^{n + 2}}}}\). Biết \(\lim {u_n} = \frac{a}{b}\) với \(a,b \in {\mathbb{N}^*}\) và \(\frac{a}{b}\) là phân số tối giản. Đặt \(S = a + b\), mệnh đề nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Ta có \(\lim {u_n} = \frac{{5.6 + {{\left( {\frac{2}{6}} \right)}^n}}}{{4 + 9.{{\left( {\frac{3}{6}} \right)}^n}}} = \frac{{5.6}}{4} = \frac{{15}}{2} \Rightarrow S = 17\).
Câu 78:
Cho dãy số \(\left( {{u_n}} \right)\) được xác định bởi: \(\left\{ {\begin{array}{*{20}{l}}{{u_1} = 1}\\{{u_{n + 1}} = {u_n} + \frac{1}{{{2^n}}}\,\,(n \ge 1)}\end{array}} \right.\)
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
Đặt \({v_n} = {u_{n + 1}} - {u_n}\). Khi đó \({v_1} + {v_2} + \ldots + {v_n} = 1 - \frac{1}{{{2^{n + 1}}}}\) |
¡ |
¡ |
|
\({u_n} = 2 - \frac{1}{{{2^{n - 1}}}}\) |
¡ |
¡ |
|
\(\lim {u_n} = 3\). |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
Đặt \({v_n} = {u_{n + 1}} - {u_n}\). Khi đó \({v_1} + {v_2} + \ldots + {v_n} = 1 - \frac{1}{{{2^{n + 1}}}}\) |
¡ |
¤ |
|
\({u_n} = 2 - \frac{1}{{{2^{n - 1}}}}\) |
¤ |
¡ |
|
\(\lim {u_n} = 3\). |
¡ |
¤ |
Phương pháp giải
a)
- Biểu diễn vn theo n.
- Tính \(A - \frac{A}{2}\) từ đó biểu diễn A theo n.
b) Biểu diễn A theo n và un
Lời giải
a) Ta có \({v_n} = {u_{n + 1}} - {u_n} = \left( {{u_n} + \frac{1}{{{2^n}}}} \right) - {u_n} = \frac{1}{{{2^n}}}\)
Khi đó \(A = {v_1} + {v_2} + \ldots + {v_n} = \frac{1}{2} + \frac{1}{{{2^2}}} + \ldots + \frac{1}{{{2^n}}}\)
\( \Rightarrow \frac{A}{2} = \frac{1}{2}\left( {\frac{1}{2} + \frac{1}{{{2^2}}} + \ldots + \frac{1}{{{2^n}}}} \right)\)
\( \Rightarrow A - \frac{A}{2} = \left( {\frac{1}{2} + \frac{1}{{{2^2}}} + \ldots + \frac{1}{{{2^n}}}} \right) - \left( {\frac{1}{{{2^2}}} + \frac{1}{{{2^3}}} + \ldots + \frac{1}{{{2^{n + 1}}}}} \right) = \frac{1}{2} - \frac{1}{{{2^{n + 1}}}}\)
\( \Rightarrow A = 1 - \frac{1}{{{2^n}}}\)
b) Từ câu a, suy ra \(A = {v_1} + {v_2} + \ldots + {v_n} = {u_2} - {u_1} + {u_3} - {u_2} + \ldots + {u_n} - {u_{n - 1}} + {u_{n + 1}} - {u_n}\)
\( \Leftrightarrow A = \sum\limits_{i = 1}^n {{v_i}} = {u_{n + 1}} - {u_1} = {u_{n + 1}} - 1 = {u_n} + \frac{1}{{{2^n}}} - 1 \Rightarrow 1 - \frac{1}{{{2^n}}} = {u_n} + \frac{1}{{{2^n}}} - 1\)
\( \Rightarrow {u_n} = 2 - \frac{1}{{{2^{n - 1}}}}\)
c) \(\lim {u_n} = \lim \left( {2 - \frac{1}{{{2^{n - 1}}}}} \right) = 2\)
Câu 79:
Số thập phân vô hạn tuần hoàn 0,5111… được biểu diễn bởi phân số tối giản \(\frac{a}{b}\). Tính a + b
 Xem đáp án
Xem đáp án
Phương pháp giải
Cách 1: Tách thành tổng của cấp số nhân lùi vô hạn
Cách 2: Sử dụng máy tính.
Dãy số có giới hạn hữu hạn
Lời giải
Ta có:
0,5111… = 0,5 + 0,01 + 0,001 + ...
\( = 0,5 + \frac{1}{{{{10}^2}}} + \frac{1}{{{{10}^3}}} + \ldots \)
\( = 0,5 + \frac{{\frac{1}{{{{10}^2}}}}}{{1 - \frac{1}{{10}}}} = \frac{{23}}{{45}}\)
Cách 2: Bấm máy tính
0,5 + ALPHA (dấu căn bậc hai) + ấn số 1 + dấu =
Câu 80:
Cho \(\mathop {\lim }\limits_{x \to 2} \frac{{\sqrt {2x + 5} - 3}}{{x - 2}} = \frac{a}{b}\), trong đó a, b là các số nguyên dương và phân số \(\frac{a}{b}\) tối giản. Tính giá trị biểu thức \(P = 1984{a^2} + 4{b^2}\).
 Xem đáp án
Xem đáp án
Lời giải
Ta có:
\(\mathop {\lim }\limits_{x \to 2} \frac{{\sqrt {2x + 5} - 3}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{(2x + 5) - 9}}{{(x - 2)(\sqrt {2x + 5} + 3)}}\)
\( = \mathop {\lim }\limits_{x \to 2} \frac{{2(x - 2)}}{{(x - 2)(\sqrt {2x + 5} + 3)}} = \mathop {\lim }\limits_{x \to 2} \frac{2}{{\sqrt {2x + 5} + 3}} = \frac{2}{6} = \frac{1}{3}\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = 3}\end{array}} \right..\)
Vậy \(P = {1984.1^2} + {4.3^2} = 2020\).
Câu 81:
Cho a, b là hai số nguyên thỏa mãn \(2a - 5b = - 8\) và \(\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt[3]{{ax + 1}} - \sqrt {1 - bx} }}{x} = 4\). Mệnh đề nào dưới đây sai?
 Xem đáp án
Xem đáp án
Lời giải
\(\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt[3]{{ax + 1}} - \sqrt {1 - bx} }}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{\sqrt[3]{{ax + 1}} - 1 + 1 - \sqrt {1 - bx} }}{x}\)
\( = \mathop {\lim }\limits_{x \to 0} \left( {\frac{{\sqrt[3]{{ax + 1}} - 1}}{x} + \frac{{1 - \sqrt {1 - bx} }}{x}} \right)\)
\( = \mathop {\lim }\limits_{x \to 0} \left( {\frac{{ax + 1 - 1}}{{x\left[ {{{(\sqrt[3]{{ax + 1}})}^2} + \sqrt[3]{{ax + 1}} + 1} \right]}} + \frac{{1 - (1 - bx)}}{{x(1 + \sqrt {1 - bx} )}}} \right)\)
\( = \mathop {\lim }\limits_{x \to 0} \left( {\frac{a}{{{{(\sqrt[3]{{ax + 1}})}^2} + \sqrt[3]{{ax + 1}} + 1}} + \frac{b}{{1 + \sqrt {1 - bx} }}} \right) = \frac{a}{3} + \frac{b}{2}\)
Theo giả thiết \(\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt[3]{{ax + 1}} - \sqrt {1 - bx} }}{x} = 4 \Rightarrow \frac{a}{3} + \frac{b}{2} = 4 \Leftrightarrow 2a + 3b = 24\)
Ta có hệ \(\left\{ {\begin{array}{*{20}{l}}{2a - 5b = - 8}\\{2a + 3b = 24}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 6}\\{b = 4}\end{array}} \right.} \right.\) nên \(|a| \le 5\) là sai.
Câu 82:
Điền số thích hợp vào chỗ trống:
Số A = 1078000 có ___________ ước.
 Xem đáp án
Xem đáp án
Đáp án “120”
Phương pháp giải
Phân tích X về thừa số nguyên tố giả sử: \(X = {A^a}{B^b}{C^c}{D^d}{E^e}\) (A, B, C, D, E là các số nguyên tố). Tổng tất cả các ước số của X là \((a + 1)(b + 1)(c + 1)(d + 1)(e + 1)\)
Lời giải
Sử dụng máy tính để phân tích 1078000 thành thừa số nguyên tố như sau:
Bước 1: Bấm số 1078000 rồi ấn dấu “=”
Bước 2: Ấn SHIFT + FACT
Khi đó ta được: \(1078000 = {2^4}{.5^3}{.7^2}.11\)
Số ước là 5.4.3.2=120 ước.
Câu 83:
Giả sử từ tỉnh A đến tỉnh B có thể đi bằng các phương tiện: ô tô, tàu hỏa, tàu thủy hoặc máy bay. Mỗi ngày có 10 chuyến ô tô, 5 chuyến tàu hỏa, 3 chuyến tàu thủy và 2 chuyến máy bay. Hỏi có bao nhiêu cách đi từ tỉnh A đến tỉnh B?
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng quy tắc cộng.
Lời giải
Số cách đi từ A đến B là: 10 + 5 + 3 + 2 = 20
Câu 84:
Số phần tử của S là ...
 Xem đáp án
Xem đáp án
Đáp án: “3600”
Phương pháp giải
- Dùng 7 chữ số đã cho, ta lập được 7! số có 7 chữ số.
- Trong các số trên có những số có 2 số chẵn liền nhau là {2,4}
Các trường hợp hai chữ số 2, 4 đứng kề nhau:
Dán hai chữ số 2 và 4 thành chữ số X.
Lời giải
- Dùng 7 chữ số đã cho, ta lập được 7! số có 7 chữ số.
- Trong các số trên có những số có 2 số chẵn liền nhau là {2,4}
Các trường hợp hai chữ số 2, 4 đứng kề nhau:
Dán hai chữ số 2 và 4 thành chữ số X.
Bước 1: Sắp xếp X và 5 chữ số còn lại có 6! cách.
Bước 2: Ứng với mỗi cách xếp ở bước 1, có 2! cách xếp 2 phần tử trong X.
Vậy có 6!.2! = 1440 số mà 2 chữ số 2 và 4 đứng kề nhau.
Kết luận có 7! – 1440 = 3600 số thỏa yêu cầu.
Câu 85:
Có bao nhiêu số tự nhiên có ba chữ số dạng \(\overline {abc} \) với a,b,c ∈ {1;2;3;4;5;6} sao cho a < b < c.
 Xem đáp án
Xem đáp án
Lời giải
Vì số tự nhiên có ba chữ số dạng \(\overline {abc} \) với a,b,c ∈{1;2;3;4;5;6} sao cho a < b < c nên a, b,c ∈ {1;2;3;4;5;6}. Suy ra số các số có dạng \(\overline {abc} \) là \(C_6^3 = 20\).
Câu 86:
Bạn A có 12 bi đỏ, 5 bi xanh và 10 bi vàng. Sau đó bạn A lại cho thêm một số bi đỏ vào. Bạn A lấy ngẫu nhiên 1 viên bi. Xác suất để lấy được bi đỏ là 1/2.
Số viên bi đỏ bạn A đã cho thêm là ....
 Xem đáp án
Xem đáp án
Đáp án “3”
Phương pháp giải
- Gọi x là số bi đỏ bạn A thêm vào.
- Tính số phần tử không gian mẫu theo x.
- Tính số cách lấy 1 viên bi đỏ theo x.
- Lập phương trình tìm x.
Lời giải
Gọi x là số bi đỏ bạn A thêm vào.
Khi đó ta có:
Số cách lấy bi đỏ là \(|\Omega | = 12 + 10 + 5 + x = x + 27\)
Xác suất lấy được viên bi đỏ là: \(\frac{{x + 12}}{{x + 27}}\)
Khi đó \(\frac{{x + 12}}{{x + 27}} = \frac{1}{2} \Leftrightarrow x = 3\)
Câu 87:
Tìm số hạng không chứa \(x\) trong khai triển \({\left( {{x^2} + \frac{2}{x}} \right)^6}\).
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
\({\left( {{x^2} + \frac{2}{x}} \right)^6} = \sum\limits_{k = 0}^6 {C_6^k} {x^{2(6 - k)}}.{\left( {\frac{2}{x}} \right)^k}\)
\( = \sum\limits_{k = 0}^6 {C_6^k} {x^{12 - 3k}}{.2^k}\)
Số hạng không chứa \(x\) là số hạng có \(12 - 3k = 0 \Leftrightarrow k = 4\)
Vậy số hạng không chứa \(x\) là \(C_6^4{.2^4} = C_6^2{.2^4}\) vì \(C_6^4 = C_6^2\)
Câu 88:
Cho hình lập phương ABCD.A′B′C′D′ (tham khảo hình vẽ).
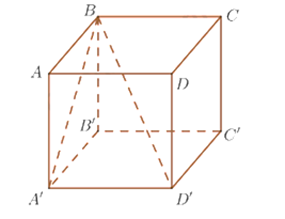
Tính cosin góc giữa hai đường thẳng AD và B D’ là
 Xem đáp án
Xem đáp án
Phương pháp giải
Tính góc giữa hai đường thẳng
Lời giải
Ta có .\(\frac{{\sqrt 2 }}{{\sqrt 3 }}.\)
Mặt khác \(BA' = a\sqrt 2 ,BD' = a\sqrt 3 \).
Do đó \(\cos \widehat {BD'A'} = \frac{{D'{B^2} + D'A{'^2} - BA{'^2}}}{{2.D'B.D'A}} = \frac{{{{(a\sqrt 3 )}^2} + {a^2} - {{(a\sqrt 2 )}^2}}}{{2.a\sqrt 3 .a}} = \frac{{\sqrt 3 }}{3}.\)
Câu 89:
Cho hai mặt phẳng (P),(Q) vuông góc với nhau. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Góc giữa hai mặt phẳng là 90∘.
(2) Mọi đường thẳng trong (P) đều vuông góc với (Q).
(3) Tồn tại đường thẳng trong (Q) vuông góc với (P).
(4) Nếu (R) vuông góc với (Q) thì (R) song song với (P).
(5) Nếu mặt phẳng (R) vuông góc với (P),(R) vuông góc với (Q) thì (R) vuông góc với giao tuyến của (P) và (Q).
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Mệnh đề thứ nhất đúng theo định nghĩa về góc.
Mệnh đề thứ hai sai và mệnh đề thứ ba đúng theo định nghĩa hai mặt phẳng vuông góc.
Mệnh đề thứ tư sai vì (R) có thể trùng với (P)
Mệnh đề thứ năm đúng theo tính chất hai mặt phẳng cắt nhau cùng vuông góc với mặt phẳng thứ 3 thì giao tuyến của chúng sẽ vuông góc với mặt phẳng ấy.
Câu 90:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi có cạnh bằng 2a và \[\widehat {DAB} = {120^ \circ }.\] Biết hình chiếu vuông góc của đỉnh S xuống mặt phẳng đáy trùng với trung điểm H của cạnh AD và tam giác SAD đều.
Số đo của góc giữa đường thẳng SH và mặt phẳng (SBD) là ....... (Làm tròn đến hàng đơn vị)
 Xem đáp án
Xem đáp án
Đáp án “16”
Phương pháp giải
- Trong mặt phẳng (HBD), từ H kẻ HK ⊥ BD tại K. ( K là trung điểm của cạnh DO )
Trong mặt phẳng (SHK), từ H kẻ HI ⊥ SK tại I.
- Chứng minh HI ⊥ (SBD).
- Xét tam giác SHK vuông tại H, tính góc.
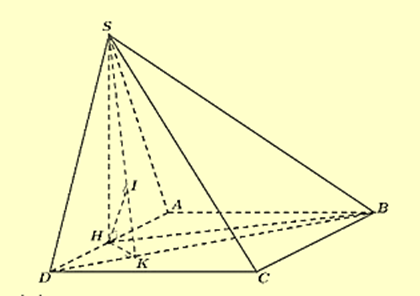
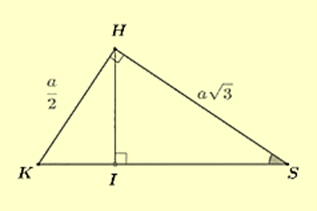
Ta có: \(SA \cap (SBC) = \{ S\} \).
Trong mặt phẳng \((HBD)\), từ \(H\) kẻ \(HK \bot BD\) tại \(K\). (\(K\) là trung điểm của cạnh \(DO)\) Trong mặt phẳng \((SHK)\), từ \(H\) kẻ \(HI \bot SK\) tại \(I\).
Khi đó: \(\left\{ {\begin{array}{*{20}{l}}{BD \bot HK}\\{BD \bot SH}\end{array} \Rightarrow BD \bot (SHK) \Rightarrow BD \bot HI} \right.\). Mà
\(HI \bot SK\) nên \(HI \bot (SBD)\).
Hay SI là hình chiếu vuông góc của SH lên mặt phẳng \((SBD)\).
Suy ra \((SH,(SBD)) = (SH,SI) = \widehat {ISH} = \widehat {KSH}\).
Xét tam giác SHK vuông tại \(H\), ta có:
\(\tan \widehat {KSH} = \frac{{HK}}{{SH}} = \frac{{\frac{a}{2}}}{{a\sqrt 3 }} = \frac{{\sqrt 3 }}{6} \Rightarrow \widehat {KSH} = \arctan \frac{{\sqrt 3 }}{6}\)
Vậy \((SH,(SBD)) = \arctan \frac{{\sqrt 3 }}{6}\).
Câu 91:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại \(A,\)\(\widehat {ABC} = {30^^\circ }\), tam giác SBC là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ điểm \(C\) đến mặt phẳng \((SAB)\) bằng?
 Xem đáp án
Xem đáp án
Phương pháp giải
- Chứng minh SH ⊥ (ABC)
- Trong (SHE), kẻ HK ⊥ SE, (K ∈ SE) (1)
- Tính HK
Tính khoảng cách từ một điểm đến một mặt phẳng
Lời giải
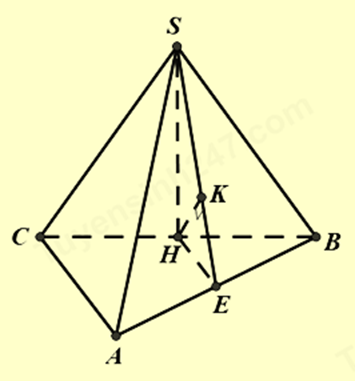
Gọi \(H\) là trung điểm của BC
Vì \(\left\{ {\begin{array}{*{20}{l}}{(SBC) \bot (ABC)}\\{(SBC) \cap (ABC) = BC \Rightarrow SH \bot (ABC)}\\{(SBC) \supset SH \bot BC}\end{array}} \right.\)
\({\rm{V\`i }}CH \cap (SAB) = B \Rightarrow \frac{{d(C,(SAB))}}{{d(H,(SAB))}} = \frac{{CB}}{{HB}} = 2\)
\( \Rightarrow d(C,(SAB)) = 2d(H,(SAB))\)
Gọi \(E\) là trung điểm của \(AB \Rightarrow HE//AC \Rightarrow HE \bot AB\)
Trong (SHE), kẻ \(HK \bot SE,(K \in SE)(1)\)
Vì \(\left\{ {\begin{array}{*{20}{l}}{AB \bot HE}\\{AB \bot SH}\end{array} \Rightarrow AB \bot (SHE) \Rightarrow AB \bot HK} \right.\)
Từ (1) và (2) \( \Rightarrow HK \bot (SAB) \Rightarrow d(H,(SAB)) = HK\)
Ta có:\({\rm{ }}\left\{ {\begin{array}{*{20}{l}}{SH = \frac{{a\sqrt 3 }}{2}}\\{HE = \frac{{AC}}{2} = \frac{{BC.\sin \widehat {ABC}}}{2} = \frac{a}{4}}\end{array}} \right.\)
Xét \(\Delta SHE\) vuông tại \(H\) có đường cao HK, ta có \(HK = \frac{{SH.HE}}{{\sqrt {S{H^2} + H{E^2}} }} = \frac{{a\sqrt {39} }}{{26}}\).
Vậy \(d(C,(SAB)) = 2d(H,(SAB)) = 2HK = \frac{{a\sqrt {39} }}{{13}}\).
Câu 92:
Cho hình chóp S.ABCD có mặt bên \((SAB)\) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy, ABCD là hình chữ nhật với \(AB = a,BC = 2a\). Khoảng cách giữa hai đường thẳng AC và SD bằng
 Xem đáp án
Xem đáp án
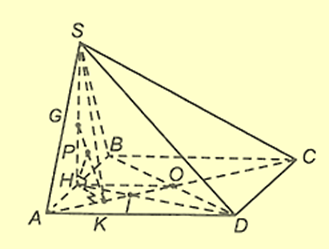
Gọi O là tâm hình chữ nhật ABCD,H là trung điểm AB.
Do \((SAB) \bot (ABCD)\) và \(SH \bot AB\) nên \(SH \bot (ABCD)\).
Gọi I là giao điểm của HD và \(AC \Rightarrow ID = 2IH\).
Gọi \(G\) là trọng tâm .
Suy ra \(IG//SD \Rightarrow SD//(AGC)\).
\( \Rightarrow d(SD;AC) = d(SD;(AGC)) = d(D;(AGC)) = 2d(H;(AGC)){\rm{. }}\)
Dựng \(HK \bot AC \Rightarrow AC \bot (GHK)\).
Dựng \(HP \bot GK \Rightarrow HP \bot (GAC)\).
Suy ra \(d(H;(GAC)) = HP\).
Ta có \(AH = \frac{{AB}}{2} = \frac{a}{2};HO = \frac{{BC}}{2} = a;SH = \frac{{a\sqrt 3 }}{2} \Rightarrow HG = \frac{1}{3}SH = \frac{{a\sqrt 3 }}{6}\).
Xét tam giác GHK vuông tại \(H\):
\(\frac{1}{{H{P^2}}} = \frac{1}{{H{K^2}}} + \frac{1}{{H{G^2}}} = \frac{1}{{H{A^2}}} + \frac{1}{{H{O^2}}} + \frac{1}{{H{G^2}}} = \frac{{17}}{{{a^2}}}{\rm{. }}\)
Suy ra \(HP = \frac{{\sqrt {17} a}}{{17}}\).
Vậy \(d(SD;AC) = \frac{{2\sqrt {17} a}}{{17}}\).
Câu 93:
Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác cân, \(AB = AC = a,\widehat {BAC} = {120^^\circ }\). Mặt phẳng \(\left( {AB'C'} \right)\) tạo với mặt đáy một góc \({60^^\circ }\). Tính khoảng cách từ đường thẳng BC đến mặt phẳng \(AB'C'\) theo \(a\).
 Xem đáp án
Xem đáp án
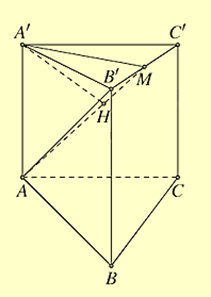
- Vì và \( \Rightarrow d\left( {BC;\left( {AB'C'} \right)} \right) = d\left( {B;\left( {AB'C'} \right)} \right)\).
- Vì trung điểm \(A'B\) nằm trong \(mp\left( {AB'C'} \right)\) nên \(d\left( {B,\left( {AB'C'} \right)} \right) = d\left( {A',\left( {AB'C'} \right)} \right)\).
- Do góc giữa \(\left( {A'B'C'} \right)\) và \(\left( {AB'C'} \right)\) bằng góc giữa \((ABC)\) và \(\left( {AB'C'} \right)\) và bằng \({60^^\circ }\).
- Gọi \(M\) là trung điểm của \(B'C'\), do \(A'B'C'\) là tam giác cân nên \(A'M \bot B'C'\).
Kẻ \(A'H \bot AM(H \in AM)\). Ta có
\(AA' \bot B'C'\left( {AA' \bot \left( {A'B'C'} \right)} \right)\) và \(A'M \bot B'C' \Rightarrow B'C' \bot \left( {AA'M} \right) \Rightarrow B'C' \bot A'H\).
Mà \(A'H \bot AM \Rightarrow A'H \bot \left( {AB'C'} \right) \Rightarrow d\left( {A';\left( {AB'C'} \right)} \right) = A'H\).
- Vì \(A'M \bot B'C'\) và \(AM \bot B'C' \Rightarrow \) góc giữa \(\left( {AB'C'} \right)\) và \(\left( {A'B'C'} \right)\) là góc \(\widehat {AMA'} = {60^^\circ }\).
- Có \(\widehat {C'A'M} = \frac{{\widehat {B'A'C'}}}{2} = {60^^\circ };A'M = A'C'.\cos \widehat {C'A'M} = \frac{a}{2}\).
- \(A'H = A'M.\sin \widehat {A'MA} = \frac{{a\sqrt 3 }}{4}\).
Câu 94:
Khi viết các số tự nhiên tăng dần từ 1, 2, 3,… liên tiếp nhau, ta nhận được một dãy các chữ số 1234567891011121314151617181920…
Chữ số thứ 191 là .....
Chữ số thứ 263 là ........
Chữ số thứ 334 là ........
 Xem đáp án
Xem đáp án
Đáp án
Chữ số thứ 191 là 0
Chữ số thứ 263 là 1
Chữ số thứ 334 là 2
Phương pháp giải
Các số có 1 chữ số: Từ 1 đến 9 => Có 9 số
Các số có 2 chữ số: Từ 10 đến 99 => Có 90 số
Các số có 3 chữ số: Từ 100 đến 999 => Có 900 số
Ta thực hiện thuật toán tách số
Chữ số thứ n = 1.a + 2.b + 3.c + r
Nếu a bằng 9 thì tách đến 2.b; nếu b=90 rồi thì tách đến c.
r là số dư khi tách đến 3.c
Trong dãy các số 1;2;3;… thì số điền cuối cùng là số thứ (a+b+c+1)
Số dư r sẽ quyết định chữ số thứ n.
Lời giải
Các số có 1 chữ số: Từ 1 đến 9 => Có 9 số
Các số có 2 chữ số: Từ 10 đến 99 => Có 90 số
Các số có 3 chữ số: Từ 100 đến 999 => Có 900 số
+) Chữ số thứ 191
191=1.9+2.90+2
=> Ta cần viết đến số tự nhiên thứ (9+90)+1=100
=> Chữ số thứ 191 là chữ số hàng chục của 100, và là số 0
+) Chữ số thứ 263
263=1.9+2.90+3.24+2
=> Ta cần viết đến số tự nhiên thứ 9+90+24+1=124
Chữ số thứ 263 là chữ số hàng chục của 124, và là số 2
+) Chữ số thứ 334
334=1.9+2.90+3.48+1
=> Ta cần viết đến số tự nhiên thứ 9+90+48+1=148
Chữ số thứ 334 là chữ số hàng trăm của 148, và là số 1
Câu 95:
Số chính phương hay còn gọi là số hình vuông là số tự nhiên có căn bậc hai là một số tự nhiên, hay nói cách khác, số chính phương bằng bình phương của một số nguyên.
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
Số 529 không là số chính phương |
¡ |
¡ |
|
Số \[C = \underbrace {11 \ldots 1}_{2024} + \underbrace {44 \ldots 4}_{1012} + 1\] là số chính phương |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
Số 529 không là số chính phương |
¡ |
¤ |
|
Số \[C = \underbrace {11 \ldots 1}_{2024} + \underbrace {44 \ldots 4}_{1012} + 1\] là số chính phương |
¤ |
¡ |
Phương pháp giải
Khi biến đổi một số trong đó có nhiêu chữ số giống nhau thành một số chính phương ta nên đặt 11…1 = a và như vậy 99…9 + 1 = 10n = 9a + 1.
Lời giải
+) Ta có: 529 = 232 nên 529 là số chính phương=> Mệnh đề 1 sai.
+) Xét số tổng quát \[C = \underbrace {11 \ldots 1}_{2n} + \underbrace {44 \ldots 4}_n + 1\]
Ta có: \[C = \underbrace {11 \ldots 100 \ldots 0}_n + \underbrace {11 \ldots 1}_n + \underbrace {44 \ldots 4}_n + 1\]
Đặt a = 11…1 thì 9a = 99…9. Do đó 99…9 + 1 = 10n = 9a + 1
C = a.10n + a + 4a +1 = a9a + 1 + 5a + 1
→ C − 9a2 + 6a + 1 − 3a − 12 ⇒ C = 33…342
Vậy C là một số chính phương.
Câu 96:
Tìm số tự nhiên n sao cho \(\frac{{{n^3} - 1}}{9}\) là số nguyên tố.
Giá trị của n là .....
 Xem đáp án
Xem đáp án
Đáp án: “4”
Phương pháp giải
- Đặt \(n = 3k + 1\,\,(k \in N){\rm{.}}\)
Lời giải
\({n^3} - 1:9 \Rightarrow {n^3} - 1:3 \Rightarrow n\) chia cho 3 dư 1 (vì nếu n chia cho 3 dư 0 hoặc 2 thì n3 chia hết cho 3 dư 0 hoặc 2). Đặt \(n = 3k + 1\,\,(k \in N)\). Ta có
\(\frac{{{n^3} - 1}}{9} = \frac{{{{(3k + 1)}^3} - 1}}{9} = \frac{{27{k^3} + 27{k^2} + 9k}}{9} = 3{k^3} + 3{k^2} + k = k\left( {3{k^2} + 3k + 1} \right)\)
Để \(\frac{{{n^3} - 1}}{9}\) là số nguyên tố, phải có k = 1. Khi đó n = 4 và \(\frac{{{n^3} - 1}}{9} = \frac{{64 - 1}}{9} = 7\), là số nguyên tố.
Câu 97:
Cho số nguyên tố p sao cho 43p + 1 là lập phương của một số tự nhiên.
Số nguyên tố p là ....
 Xem đáp án
Xem đáp án
Đáp án “5”
Phương pháp giải
Đặt \(43p + 1 = {n^3}(n \in N)\)
Lời giải
Đặt \(43p + 1 = {n^3}(n \in N)\) thì \(43p = (n - 1)\left( {{n^2} + n + 1} \right)\)
Số 43p có bốn ước nguyên dương là 1,43, p, 43p
a) \(\left\{ {\begin{array}{*{20}{c}}{n - 1 = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\{{n^2} + n + 1 = 43p}\end{array}} \right.\) khi đó n = 2 và \(43p = {2^2} + 2 + 1 = 7\), loại.
b) \(\left\{ {\begin{array}{*{20}{c}}{n - 1 = 43\,\,\,\,\,\,}\\{{n^2} + n + 1 = p}\end{array}} \right.\) khi đó n = 44 và \(p = {44^2} + 44 + 1 = 1981:7\), loại.
c) \(\left\{ {\begin{array}{*{20}{c}}{{n^2} + n + 1 = 43}\\{n - 1 = p\,\,\,\,\,\,\,\,\,}\end{array}} \right.\) khi đó n(n + 1) = 42 ⇒ n = 6, p = 5 (là số nguyên tố).
Đáp số p = 5.
Câu 98:
Trên bảng viết các số \(\frac{1}{{2015}},\frac{2}{{2015}}, \ldots ,\frac{{2014}}{{2015}},\frac{{2015}}{{2016}}\). Mỗi lần biến đổi, xóa đi hai số \({\rm{a}},{\rm{b}}\) bất kì và thay bằng số \(a + b - 5ab\). Sau 2014 lần thực hiện phép biến đổi trên bảng còn lại một phân số \(\frac{m}{n}\). (tối giản)
Tổng m + n = ?
 Xem đáp án
Xem đáp án
Đáp án: “6”
Phương pháp giải
Áp dụng nguyên lý bất biến trong giải toán:
Cho a, b, c là những số thực ta xét tổng S = a + b + c . Nếu ta đổi chỗ a cho b, b cho c, c cho a, thì tổng S luôn luôn chỉ là một (không đổi). Tổng này không thay đổi đối với thứ tự phép cộng. Dù a, b, c có thay đổi thứ tự như thế nào chăng nữa S vẫn không thay đổi, nghĩa là S bất biến đối với việc thay đổi các biến khác.
Thông thường ta sẽ dựa vào kinh nghiệm dự đoán số bất biến trong dãy.
Lời giải
Nhận xét: c = a + b − 5ab là một tổng mà vai trò của a và b như nhau. Cứ xóa 2 số a, b bất kì và xóa 2014 theo bất kì cách nào thì luôn ra một số duy nhất, nên ta có thể dự đoán: khi xóa đến một số nào đó thì số c là không đổi. Giả sử xóa đến số a0 thì được số co = ao + b1 − 5a0b1
Xóa tiếp số co và b2 thì vẫn được co, tức là: co = co + b2 − 5cob2 ⇔ co = \(\frac{1}{5}\)
Thử lại ta thấy:
Trong dãy số trên có số \(\frac{{403}}{{2015}} = \frac{1}{5}\)
Nếu xóa hai số a và b bất kì và thay bằng số mới là c = a + b − 5ab, như vậy sau mỗi lần xóa dãy trên giảm đi một số. Như vậy sau 2014 lần xóa trên bảng còn lại đúng 1 số.
Ta cứ xóa đến một lúc nào đó ta sẽ xóa \(\frac{{403}}{{2015}}\) và được thay bằng \(c = \frac{1}{5} + b - 5.\frac{1}{5}b = \frac{1}{5}\)
Như vậy cứ xóa số \(\frac{1}{5}\) và một số b bất kì thì lại viết được c = \(\frac{1}{5}\)
Vậy số cuối cùng còn lại là \(\frac{1}{5}\)
Câu 99:
 Xem đáp án
Xem đáp án
Phương pháp giải
- Chứng minh y là số lẻ
- Đặt \(y = 2k + 1\) (với k nguyên).
- Nhận xét tính chẵn lẻ của x rồi tìm hai số x,y
Lời giải
Ta có \({y^2} - 2{x^2} = 1 \Rightarrow {y^2} = 2{x^2} + 1 \Rightarrow y\) là số lẻ
Đặt \(y = 2k + 1\) (với knguyên). Ta có: \({(2k + 1)^2} = 2{x^2} + 1\)
\( \Leftrightarrow {x^2} = 2{k^2} + 2k \Rightarrow x\) chẵn, mà \(x\) nguyên tố \( \Rightarrow x = 2,y = 3\)
Vậy nghiệm của phương trình là \((x,y) = (2,3)\)
Cách khác: Thử các số vào.
