Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 6)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 6)
-
286 lượt thi
-
99 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Giải thích
Đọc nội dung đoạn đầu tiên của văn bản, xác định các thông tin quan trọng: “viên cảnh sát”, “trông anh ta có vẻ gì nghiêm trọng”, “mạnh khỏe và rất tích cực trong công việc” để chọn đáp án B.
Câu 2:
Vì sao viên cảnh sát lại đứng nói chuyện với người đàn ông đứng bên đường?
 Xem đáp án
Xem đáp án
Giải thích
Câu 3:
Việc quay trở về và thực hiện lời hẹn với người bạn của mình thể hiện điều gì ở nhân vật?
 Xem đáp án
Xem đáp án
Giải thích
Câu 4:
 Xem đáp án
Xem đáp án
Giải thích
Đọc nội dung cuộc hội thoại của hai nhân vật có thể thấy rằng: người đàn ông đang chia sẻ với viên cảnh sát về lý do mà mình đứng ở ngoài đường vào lúc khuya nhưng đã bị “ngắt lời” và thông báo về việc nhà hàng đã đóng cửa; viên cảnh sát dường như mất kiên nhẫn và chờ đợi để xác nhận điều gì đó nên mới “đứng sát vào gã đàn ông và nhìn kỹ vào mặt gã”.
Câu 5:
Theo Bob, quãng thời gian 20 năm đủ để con người có thể biết được thân thế, sự nghiệp và cả tương lai của bản thân là đúng hay sai?
 Xem đáp án
Xem đáp án
Giải thích
Câu 6:
Từ nội dung trong văn bản, hãy tìm một từ không quá hai tiếng để hoàn thành câu văn sau:
Sau quãng thời gian 20 năm, Bob đã mong muốn có thể gặp lại Jimmy Wells để kiểm chứng về tình bạn của mình, để chia sẻ những câu chuyện mà anh ta đã trải qua trong suốt quãng thời gian ở (1) ________; và để thực hiện điều ấy, Bob đã vượt qua hàng ngàn cây số để có thể trở về đúng hẹn.
 Xem đáp án
Xem đáp án
Đáp án
Từ nội dung trong văn bản, hãy tìm một từ không quá hai tiếng để hoàn thành câu văn sau:
Sau quãng thời gian 20 năm, Bob đã mong muốn có thể gặp lại Jimmy Wells để kiểm chứng về tình bạn của mình, để chia sẻ những câu chuyện mà anh ta đã trải qua trong suốt quãng thời gian ở (1) miền Tây; và để thực hiện điều ấy, Bob đã vượt qua hàng ngàn cây số để có thể trở về đúng hẹn.
Giải thích
Câu 7:
Trong cuộc trò chuyện với viên cảnh sát, Bob đã thể hiện mong muốn gì về người bạn của mình?
 Xem đáp án
Xem đáp án
Giải thích
Câu 8:
 Xem đáp án
Xem đáp án
Giải thích
Câu 9:
 Xem đáp án
Xem đáp án
Giải thích
Câu 10:
 Xem đáp án
Xem đáp án
Giải thích
Câu 11:
Theo Canalys, sự sụt giảm tốc độ tăng trưởng của chi tiêu toàn cầu cho dịch vụ đám mây chủ yếu là do:
 Xem đáp án
Xem đáp án
Giải thích
Câu 12:
 Xem đáp án
Xem đáp án
Giải thích
Câu 13:
Hãy điền một cụm từ không quá bốn tiếng vào chỗ trống để hoàn thành nhận định sau:
Đối tượng nghiên cứu của Canalys trong báo cáo này là (1) _________ và các nhà cung cấp đám mây hàng đầu quốc tế.
 Xem đáp án
Xem đáp án
Đáp án
Hãy điền một cụm từ không quá bốn tiếng vào chỗ trống để hoàn thành nhận định sau:
Đối tượng nghiên cứu của Canalys trong báo cáo này là (1) khách hàng doanh nghiệp và các nhà cung cấp đám mây hàng đầu quốc tế.
Giải thích
Câu 14:
Nghiên cứu của Canalys KHÔNG làm rõ yếu tố nào liên quan đến việc giảm nhu cầu sử dụng dịch vụ đám mây trên toàn cầu?
 Xem đáp án
Xem đáp án
Giải thích
Đọc đoạn [2] đến [7], xác định nội dung chính được đề cập trong các đoạn này:
Đoạn [2]: Nguyên nhân dẫn đết sự sụt giảm nhu cầu sử dụng dịch vụ đám mây.
Đoạn [3]: Xu hướng sử dụng dịch vụ đám mây của các doanh nghiệp.
Đoạn [4] - [7]: Thực trạng và tác động của việc sử dụng dịch vụ đám mây của các doanh nghiệm.
Như vậy, yếu tố không được làm rõ trong bài là các giải pháp khắc phục việc giảm thiểu nhu cầu sử dụng dịch vụ đám mây. Từ khóa đúng là C.
Câu 15:
Thông tin từ nhà phân tích nghiên cứu của Canalys liên quan tới trường hợp của công ty nào?
 Xem đáp án
Xem đáp án
Giải thích
Câu 16:
Đầu tư máy chủ và thiết bị mạng, Đầu tư cộng đồng đối tác kênh, Đầu tư vào trí tuệ nhân tạo, Đầu tư vào hệ sinh thái kênh
Bị ảnh hưởng bởi các điều kiện kinh tế vĩ mô và suy thoái kinh tế, các nhà cung cấp đám mây hàng đầu quốc tế đã lựa chọn định hướng về động lực phát triển khác nhau:
Amazon Cloud Technology: _____.
Microsoft Azure: ______.
Google Cloud: ______.
 Xem đáp án
Xem đáp án
Đáp án
Bị ảnh hưởng bởi các điều kiện kinh tế vĩ mô và suy thoái kinh tế, các nhà cung cấp đám mây hàng đầu quốc tế đã lựa chọn định hướng về động lực phát triển khác nhau:
Amazon Cloud Technology: Đầu tư vào hệ sinh thái kênh.
Microsoft Azure: Đầu tư vào trí tuệ nhân tạo.
Google Cloud: Đầu tư vào cộng đồng đối tác kênh.
Giải thích
Để trả lời được câu hỏi, HS cần tìm kiếm các thông tin liên quan trong đoạn[8] - [10] và thực hiện kéo thả nội dung tương ứng với tên công ty. Lần lượt kéo thả như sau:
[vị trí thả 1] : Đầu tư vào hệ sinh thái kênh
[vị trí thả 2]: Đầu tư vào trí tuệ nhân tạo
[vị trí thả 3]: Đầu tư vào cộng đồng đối tác kênh
Câu 17:
Tốc độ tăng trưởng tiêu thụ của Microsoft Azure vào quý 4 năm 2023 đạt ngưỡng dưới 36%. Đúng hay Sai?
 Xem đáp án
Xem đáp án
Đáp án
B. Sai.
Giải thích
Câu 18:
 Xem đáp án
Xem đáp án
Giải thích
Câu 19:
Dòng nào dưới đây nhận xét đúng về tình trạng của 3 công ty lớn khi chi tiêu toàn cầu cho dịch vụ đám mây giảm?
 Xem đáp án
Xem đáp án
Giải thích
Câu 20:
Trường hợp của Microsoft, Amazon và Google chứng minh tốc độ tăng trưởng của dịch vụ đám mây đã chững lại trong năm 2021 và 2022. Đúng hay Sai?
 Xem đáp án
Xem đáp án
Đáp án
B. Sai
Giải thích
Câu 21:
Phần tư duy khoa học/ giải quyết vấn đề
Phát biểu sau đây đúng hay sai?
Môi trường nuôi thủy hải sản có sự thay đổi lớn về pH: thấp nhất vào lúc sáng sớm, đạt cực đại vào khoảng sau giữa trưa và giảm dần cho đến tối.
 Xem đáp án
Xem đáp án
Đáp án
A. Đúng
Giải thích
Câu 22:
Một nhóm học sinh dự định nghiên cứu sự thay đổi pH của ao nuôi thủy hải sản trong ngày, học sinh cần phải thu thập các thông tin sau:
- Loại dữ liệu: _______ của nước trong ao nuôi.
- Vị trí lấy mẫu nước: tại _______ trong các lần lấy mẫu khác nhau.
- Thời gian lấy mẫu: ít nhất _______ trong ngày.
 Xem đáp án
Xem đáp án
Đáp án
Một nhóm học sinh dự định nghiên cứu sự thay đổi pH của ao nuôi thủy hải sản trong ngày, học sinh cần phải thu thập các thông tin sau:
- Loại dữ liệu: pH của nước trong ao nuôi.
- Vị trí lấy mẫu nước: tại cùng 1 vị trí trong các lần lấy mẫu khác nhau.
- Thời gian lấy mẫu: ít nhất 3 lần trong ngày.
Giải thích
Để nghiên cứu sự thay đổi pH của ao nuôi thủy hải sản trong ngày, học sinh cần phải thu thập các thông tin sau:
- Loại dữ liệu: pH của nước trong ao nuôi.
- Vị trí lấy mẫu nước: tại cùng 1 vị trí trong các lần lấy mẫu khác nhau.
Câu 23:
Điền từ/cụm từ thích hợp vào chỗ trống.
Nguyên nhân chính của sự giảm độ kiềm trong ao nuôi thủy hải sản là do quá trình oxy hóa ammonia thành nitrate với sản phẩm trung gian là nitrite trong điều kiện có oxygen gọi là quá trình (1) __________.
 Xem đáp án
Xem đáp án
Đáp án
Điền từ/cụm từ thích hợp vào chỗ trống.
Nguyên nhân chính của sự giảm độ kiềm trong ao nuôi thủy hải sản là do quá trình oxy hóa ammonia thành nitrate với sản phẩm trung gian là nitrite trong điều kiện có oxygen gọi là quá trình (1) nitrate hóa.
Giải thích
Nguyên nhân chính của sự giảm độ kiềm trong ao nuôi thủy hải sản là do quá trình nitrate hóa. Ammonia (NH3) là chất thải chính có chứa nitrogen của động vật thủy hải sản dễ dàng bị oxy hóa thành nitrite bởi nhóm vi khuẩn nitrite hóa. Sau đó, nitrite chuyển hóa thành nitrate bởi nhóm vi khuẩn nitrate hóa. Kết quả là H+ sẽ làm trung hòa độ kiềm và làm giảm độ kiềm vào buổi sáng.Câu 24:
 Xem đáp án
Xem đáp án
Giải thích
Câu 25:
 Xem đáp án
Xem đáp án
Giải thích
Độ kiềm trong nước do 3 ion chính tạo ra, gồm bicarbonate (HCO3−), carbonate (CO32−) và hydroxide (OH–).
Câu 26:
Một nhóm học sinh tiến hành khảo sát pH nước trong ao nuôi tại các thời điểm khác nhau và thu được kết quả như sau:
|
Ngày/Giờ |
6h |
8h |
10h |
12h |
13h |
14h |
16h |
18h |
20h |
22h |
|
1 |
7,4 |
7,5 |
7,7 |
7,9 |
8,0 |
7,9 |
7,7 |
7,6 |
7,5 |
7,4 |
|
2 |
7,6 |
7,7 |
7,9 |
8,1 |
8,2 |
8,1 |
7,9 |
7,8 |
7,7 |
7,6 |
|
3 |
7,5 |
7,6 |
7,8 |
8,0 |
8,1 |
8,0 |
7,8 |
7,7 |
7,6 |
7,5 |
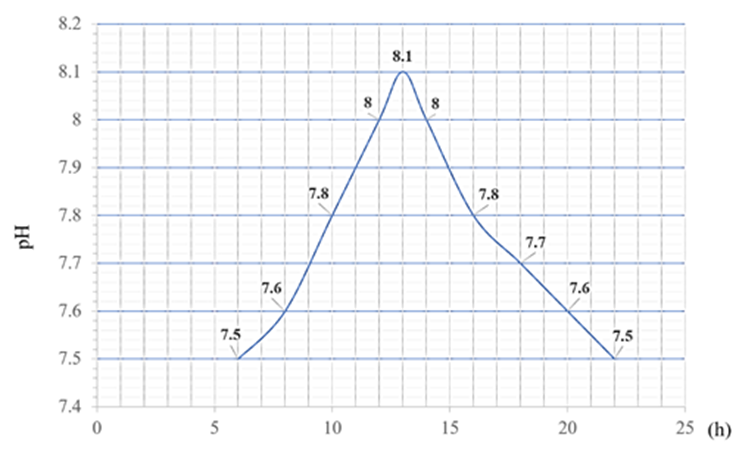
Biểu đồ biểu diễn số liệu nhóm học sinh thu thập được là
 Xem đáp án
Xem đáp án
Giải thích
Tính giá trị trung bình pH trong 3 ngày:
|
Ngày/Giờ |
6h |
8h |
10h |
12h |
13h |
14h |
16h |
18h |
20h |
22h |
|
1 |
7,4 |
7,5 |
7,7 |
7,9 |
8,0 |
7,9 |
7,7 |
7,6 |
7,5 |
7,4 |
|
2 |
7,6 |
7,7 |
7,9 |
8,1 |
8,2 |
8,1 |
7,9 |
7,8 |
7,7 |
7,6 |
|
3 |
7,5 |
7,6 |
7,8 |
8,0 |
8,1 |
8,0 |
7,8 |
7,7 |
7,6 |
7,5 |
|
Trung bình |
7,5 |
7,6 |
7,8 |
8,0 |
8,1 |
8,0 |
7,8 |
7,7 |
7,6 |
7,5 |
Sau đó biểu diễn trên đồ thị:
Câu 27:
Lượng năng lượng được sóng âm truyền qua một đơn vị diện tích đặt vuông góc với phương truyền âm trong một đơn vị thời gian gọi là (1) _______.
 Xem đáp án
Xem đáp án
Đáp án
Câu 28:
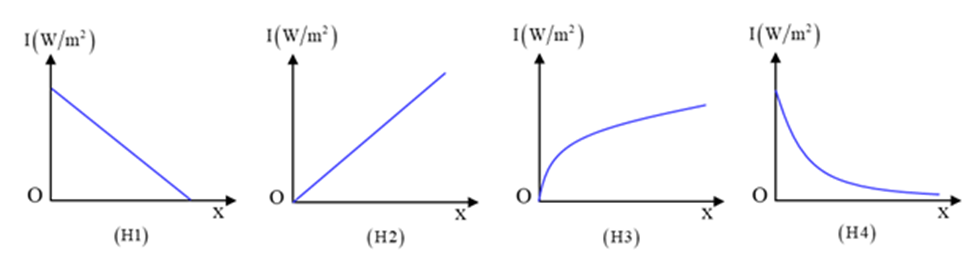
Trên trục Ox, một nguồn âm điểm có công suất không đổi, phát âm đẳng hướng ra môi trường. Hình nào sau đây có thể mô tả đúng sự phụ thuộc của cường độ âm I tại những điểm trên trục Ox theo tọa độ x.
 Xem đáp án
Xem đáp án
Giải thích
Ta có: \[I = \frac{P}{{4\pi {r^2}}} = \frac{P}{{4\pi {x^2}}} \Rightarrow I\~\frac{1}{{{x^2}}}\]
Câu 29:
Một máy bay khi bay ở độ cao 3200 m gây ra ở mặt đất phía dưới tiếng ồn có mức cường độ âm là 100 dB. Giả thiết máy bay là nguồn điểm, môi trường không hấp thụ âm. Cho biết ngưỡng nghe trung bình của tai người có thính giác bình thường là 130 dB. Ở độ cao bao nhiêu thì tiếng ồn của máy bay bắt đầu gây ra cảm giác nhức nhối cho tai người?
 Xem đáp án
Xem đáp án
Giải thích
Cường độ âm tại: \(I = \frac{P}{{4\pi {r^2}}} \to I\~\frac{1}{{{r^2}}}\)
Câu 30:
Những âm thanh vượt quá ngưỡng đau là những âm thanh mà tai của con người không nghe được, đúng hay sai?
 Xem đáp án
Xem đáp án
Đáp án
B. Sai
Giải thích
Câu 31:
Công suất âm thanh cực đại của một máy nghe nhạc gia đình là 10 W. Cho rằng cứ truyền trên khoảng cách 1 m, năng lượng âm bị giảm 5% so với lần đầu so sự hấp thụ âm của môi trường. Biết I0 = 10-12 W/m2. Nếu mở to hết mức thì cường độ âm ở khoảng cách 6 m gần nhất với giá trị nào sau đây?
 Xem đáp án
Xem đáp án
Giải thích
Đây là bài toán mà trong quá trình truyền âm có sự hấp thụ âm. Vì có sự hấp thụ âm nên năng lượng âm giảm dần trong quá trình truyền âm. Để giải được bài toán này, chúng ta phải nắm được mối liên hệ giữa năng lượng âm và công suất âm: \({\rm{A}} = {\rm{P}}.{\rm{t}}\)
Cường độ âm phát đi từ nguồn điểm: \(I = \frac{P}{S} = \frac{P}{{4\pi {r^2}}}\)
Năng lượng âm giảm nên công suất giảm theo quan hệ: \(P = \frac{A}{t}\), cứ 1 m thì giảm 5%, hay:
\(\frac{{{A_0} - {A_1}}}{{{A_0}}} = 0,05 \Rightarrow \frac{{{A_1}}}{{{A_0}}} = 0,95\)
Ở khoảng cách 6 m, ta có: \(\frac{{{A_6}}}{{{A_0}}} = 0,{95^6} \Rightarrow {P_6} = {P_0}.0,{95^6}\)
Mức cường độ âm tại vị trí cách nguồn âm 6 m là:
Câu 32:
Phát biểu sau đây đúng hay sai?
Từ đồ thị cho biết các chất NaCl, Ba(NO3)2, Na2HAsO4 có độ tan tăng khi nhiệt độ tăng.
 Xem đáp án
Xem đáp án
Đáp án
A. Đúng
Giải thích
Câu 33:
Phát biểu sau đây đúng hay sai?
Khi tăng nhiệt độ thì độ tan của chất rắn trong nước tăng.
 Xem đáp án
Xem đáp án
Đáp án
B. Sai
Giải thích
Câu 34:
Điền từ/cụm từ thích hợp vào chỗ trống.
Độ tan của Ba(NO3)2 ở 60∘C là (1) ______.
 Xem đáp án
Xem đáp án
Đáp án
Điền từ/cụm từ thích hợp vào chỗ trống.
Độ tan của Ba(NO3)2 ở 60∘C là (1) 20 gam.
Giải thích
Câu 35:
 Xem đáp án
Xem đáp án
Giải thích
Câu 36:
 Xem đáp án
Xem đáp án
Giải thích
Câu 37:
 Xem đáp án
Xem đáp án
Giải thích
Câu 38:
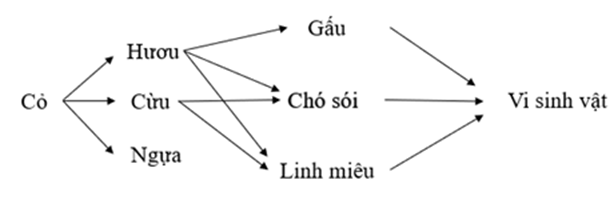
Sinh vật nào có mức năng lượng lớn nhất trong lưới thức ăn sau đây?
 Xem đáp án
Xem đáp án
Giải thích
Câu 39:
Hai nhà khoa học đều đồng ý với quan điểm việc phá vỡ chuỗi/lưới thức ăn làm mất cân bằng hệ sinh thái.
 Xem đáp án
Xem đáp án
Đáp án
A. Đúng.
Giải thích
Câu 40:
Kéo các ô vuông thả vào vị trí thích hợp:
theo nhóm, đồng đều, ngẫu nhiên
“Sự phân bố của hươu trong quần thể hươu núi Kaibab trước khi loại bỏ các sinh vật cạnh tranh thì chúng có xu hướng phân bố _______”.
 Xem đáp án
Xem đáp án
Đáp án
“Sự phân bố của hươu trong quần thể hươu núi Kaibab trước khi loại bỏ các sinh vật cạnh tranh thì chúng có xu hướng phân bố theo nhóm”.
Giải thích
Câu 41:
 Xem đáp án
Xem đáp án
Giải thích
Câu 42:
 Xem đáp án
Xem đáp án
Giải thích
Câu 43:
Trứng muỗi chỉ nở thành ấu trùng nếu được cung cấp đủ nước.
 Xem đáp án
Xem đáp án
Đáp án
A. Đúng.
Giải thích
Câu 44:
Giai đoạn bọ gậy trong sự biến thái hoàn toàn của muỗi tương ứngvới giai đoạn (1) ________ trong hình 1.
 Xem đáp án
Xem đáp án
Đáp án
Giai đoạn bọ gậy trong sự biến thái hoàn toàn của muỗi tương ứngvới giai đoạn (1) ấu trùng trong hình 1.
Giải thích
Câu 45:
 Xem đáp án
Xem đáp án
Giải thích
Các phương pháp nhằm xác định bệnh do virus:
Xét nghiệm huyết thanh học: phát hiện kháng thể đặc hiệu với virus gây bệnh.
Xét nghiệm PCR: nhằm phát hiện vật chất di truyền RNA của virus.
Câu 46:
Chu kì dao động T là thời gian vật thực hiện được một dao động. Hệ thức nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Giải thích
Câu 47:
Phát biểu nào sau đây là đúng hoặc sai?
|
Phát biểu |
Đúng |
Sai |
|
Tần số dao động có đơn vị là Hertz (Hz). |
||
|
SHM có thể được mô tả bằng tần số dao động. |
||
|
Con lắc trong Thí nghiệm 1 có tần số dao động phụ thuộc vào khối lượng của vật nặng. |
||
|
Con lắc trong Thí nghiệm 2 có tần số dao động phụ thuộc vào chiều dài của dây treo. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Tần số dao động có đơn vị là Hertz (Hz). |
X | |
|
SHM có thể được mô tả bằng tần số dao động. |
X | |
|
Con lắc trong Thí nghiệm 1 có tần số dao động phụ thuộc vào khối lượng của vật nặng. |
X | |
|
Con lắc trong Thí nghiệm 2 có tần số dao động phụ thuộc vào chiều dài của dây treo. |
X |
Giải thích
1. Đúng. Theo phần dẫn thì tần số dao động được đo bằng số dao động vật thực hiện được trong mỗi giây hoặc Hertz (Hz).
2. Đúng. Theo phần dẫn thì dao động điều hòa đơn giản (SHM – Simple Harmonic Motion) là dao động tuần hoàn, hoặc một loại chuyển động lặp đi lặp lại, có tính chu kỳ và có thể được mô tả bằng tần số dao động.
3. Sai. Theo Hình 1, con lắc trong Thí nghiệm 1 có tần số dao động phụ thuộc vào chiều dài dây treo của con lắc.
Câu 48:
Trong các thí nghiệm trên, tại thời điểm buông nhẹ để vật nặng dao động thì tốc độ của vật nặng khi đó là
 Xem đáp án
Xem đáp án
Giải thích
Câu 49:
Điền từ/cụm từ thích hợp vào chỗ trống.
Hệ con lắc lò xo A – vật nặng có khối lượng 200 g dao động điều hòa với tần số 0,5 Hz. Số dao động vật thực hiện trong 2 s là (1) ____________.
 Xem đáp án
Xem đáp án
Đáp án
Điền từ/cụm từ thích hợp vào chỗ trống.
Hệ con lắc lò xo A – vật nặng có khối lượng 200 g dao động điều hòa với tần số 0,5 Hz. Số dao động vật thực hiện trong 2 s là (1) ____1_____.
Giải thích
Theo phần dẫn của Thí nghiệm 1, Tần số dao động được đo bằng số dao động vật thực hiện được trong mỗi giây.
→ Hệ con lắc lò xo B – vật nặng có khối lượng 200 g dao động điều hòa với tần số 0,5 Hz tương ứng với vật thực hiện 0,5 dao động trong mỗi giây.
Câu 50:
 Xem đáp án
Xem đáp án
Giải thích
Dựa vào và chú ý trong Hình 3, các đường được vẽ cho lò xo B, C và D giao nhau ở một vị trí có khối lượng như nhau.
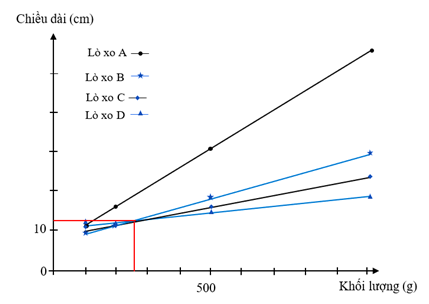
→ Từ Hình 3, ta thấy giá trị khối lượng của vật nặng phù hợp nhất là 270 g. Chọn B
Câu 51:
Một học sinh đã đưa ra giả thuyết rằng độ dài dây của con lắc trong Sơ đồ 1 tăng lên thì tần số dao động của con lắc trong SHM sẽ giảm. Giả thuyết của học sinh trên là đúng hay sai?
 Xem đáp án
Xem đáp án
Đáp án
A. Đúng
Giải thích
Câu 52:
Điền từ/cụm từ thích hợp vào chỗ trống
Ở thí nghiệm 2, sau khi buông nhẹ cho lò xo dao động thì con lắc dao động chậm nhất trong 4 con lắc A, B, C, D là con lắc (1) _____________.
 Xem đáp án
Xem đáp án
Đáp án
Điền từ/cụm từ thích hợp vào chỗ trống
Ở thí nghiệm 2, sau khi buông nhẹ cho là xo dao động thì con lắc dao động chậm nhất trong 4 con lắc A, B, C, D là con lắc (1) _____A______.
Giải thích
Ta có: tần số dao động được đo bằng số dao động mỗi giây. Con lắc dao động càng nhanh thì số dao động trong mỗi giây càng lớn nên tần số dao động càng cao. Do đó, con lắc ứng với lò xo A có tần số dao động thấp nhất nên dao động chậm nhất.
Câu 53:
Thí nghiệm 2 được lặp lại bằng cách sử dụng lò xo thứ năm – lò xo E. Treo vật nặng có khối lượng 100 g vào đầu dưới lò xo E, sau đó kích thích cho hệ lò xo – vật nặng dao động. Khi đó, tần số dao động của lò xo là 1,4 Hz. Dựa trên kết quả của Thí nghiệm 2, sắp xếp theo tần số giảm dần trong dao động của 5 lò xo với vật nặng có khối lượng 100 g được treo vào đầu dưới của lò xo nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Giải thích:
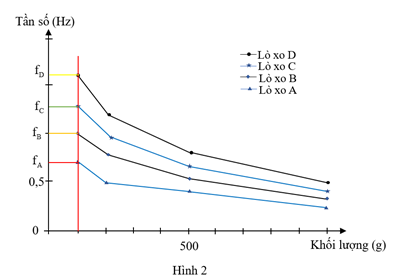
Theo Hình 2, hệ lò xo – vật nặng có khối lượng 100 g có tần số dao động được sắp xếp theo thứ tự giảm dần là: \[{f_D} > {\rm{ }}{f_C} > {\rm{ }}{f_B} > {f_A}\]
Mặt khác, từ Hình 2, thấy rằng tần số dao động của hệ lò xo C - vật nặng và hệ lò xo D – vật nặng là:
\[\left\{ {\begin{array}{*{20}{l}}{{f_C} \approx 1,25\;{\rm{Hz}}}\\{{f_D} \approx 1,6\;{\rm{Hz}}}\end{array}} \right.\]
Theo dữ kiện đề bài, hệ lò xo E – vật nặng dao động với tần số: \[{f_E} = 1,4\;{\rm{Hz}}\]
Câu 54:
 Xem đáp án
Xem đáp án
Giải thích
Câu 55:
 Xem đáp án
Xem đáp án
Giải thích
Câu 56:
 Xem đáp án
Xem đáp án
Giải thích
Câu 57:
Những phát biểu sau đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Trong một cây phát sinh loại, loài đã tuyệt chủng được gọi là đơn vị phân loại còn tồn tại. |
||
|
Tổ tiên chung gần gũi nhất với cả năm loài kể trên sẽ thuộc bộ Carnivora. |
||
|
Con người không được sắp xếp vào bất kì hệ thống phân loại sinh vật nào do là động vật bậc cao. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Trong một cây phát sinh loại, loài đã tuyệt chủng được gọi là đơn vị phân loại còn tồn tại. |
X | |
|
Tổ tiên chung gần gũi nhất với cả năm loài kể trên sẽ thuộc bộ Carnivora. |
X | |
|
Con người không được sắp xếp vào bất kì hệ thống phân loại sinh vật nào do là động vật bậc cao. |
X |
Giải thích
(1) Sai. Theo đoạn thông tin: “...Trong một cây phân loại, các loài hiện đang sống được gọi là phân loại còn tồn tại”.
(2) Đúng. Nhìn vào bảng 1 ta thấy cả 5 loài trên đều mới bắt đầu phân li từ bộ Carnivora thành các họ tương ứng. Có nghĩa là tổ tiên gần gũi nhất với chúng sẽ thuộc đơn vị phân loại Carnivora.
Câu 58:
Cho phân loại khoa học của loài linh miêu Á – Âu như sau:
|
Giới |
Ngành |
Lớp |
Bộ |
Họ |
Chi |
Loài |
|
Động vật (Animalia) |
Dây sống (Chordata) |
Thú (Mammalia) |
Ăn thịt (Carnivora) |
Mèo (Felidae) |
Lynx |
lynx |
Loài linh miêu này sẽ có họ hàng gần nhất với loài nào trong năm loài được kể trên?
 Xem đáp án
Xem đáp án
Giải thích
Câu 59:
Điền từ/cụm từ thích hợp vào chỗ trống dưới đây.
Tên khoa học của loài báo hoa mai là (1) ___________.
 Xem đáp án
Xem đáp án
Đáp án
Điền từ/cụm từ thích hợp vào chỗ trống dưới đây.
Tên khoa học của loài báo hoa mai là (1) Panthera pardus.
Giải thích
Câu 60:
Gieo con xúc xắc 100 lần, kết quả thu được ghi ở bảng sau:
|
Số chấm |
Số lần xuất hiện |
|
1 |
14 |
|
2 |
18 |
|
3 |
30 |
|
4 |
12 |
|
5 |
14 |
|
6 |
12 |
Xác suất của biến cố mặt lẻ chấm xuất hiện bằng
 Xem đáp án
Xem đáp án
Số lần xuất hiện mặt lẻ chấm là 14 + 30 + 14 = 58.
⇒ Xác suất của biến cố là: \(\frac{{58}}{{100}} = \frac{{29}}{{50}}\).
Câu 61:
Trong mặt phẳng tọa độ Oxy, gọi \((H)\) là tập hợp điểm biểu diễn số phức \(w = (1 + \sqrt 3 i)z + 2\) thỏa mãn \(|z - 1| \le 2\). Tính diện tích của hình \((H)\).
 Xem đáp án
Xem đáp án
Ta có \(w = (1 + \sqrt 3 i)z + 2 \Leftrightarrow w - 3 - \sqrt 3 i = (1 + \sqrt 3 i)(z - 1)\).
\( \Leftrightarrow |w - 3 - \sqrt 3 i| = |1 + \sqrt 3 i||z - 1| \le 4\).
Vậy điểm biểu diễn số phức \(w\) nằm trên hình tròn có bán kính \(r = 4\).
Diện tích hình \((H)\) là \(S = \pi {r^2} = 16\pi \).
Câu 62:
Cho hình nón có thiết diện qua trục là tam giác đều. Gọi V1, V2 lần lượt là thể tích của khối cầu ngoại tiếp và nội tiếp hình nón đã cho. Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\).
 Xem đáp án
Xem đáp án
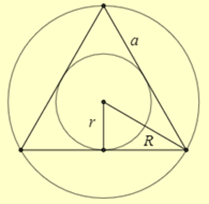
Giả sử hình nón đã cho có đường sinh \(l = a\)
Ta có khối cầu ngoại tiếp và khối cầu nội tiếp hình nón có bán kính lần lượt là \(R = \frac{{a\sqrt 3 }}{3}\) và \(r = \frac{{a\sqrt 3 }}{6}\). Gọi \({V_1},{V_2}\) lần lượt là thể tích của khối cầu ngoại tiếp và nội tiếp hình nón.
Ta có: \(\frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{4}{3}\pi {R^3}}}{{\frac{4}{3}\pi {r^3}}} = 8\).
Câu 63:
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng \(a\) và \(SA \bot (ABCD)\). Biết \(SA = \frac{{a\sqrt 6 }}{3}\).
Tính góc giữa SC và \((ABCD)\).
 Xem đáp án
Xem đáp án
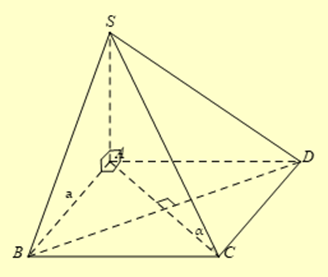
Ta có: \(SA \bot (ABCD) \Rightarrow (\widehat {SC;(ABCD)}) = \widehat {SCA} = \alpha \)
Mà ABCD là hình vuông cạnh \(a \Rightarrow AC = a\sqrt 2 \)
vuông tại \(A\) có: 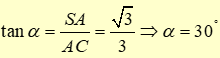
Câu 64:
Cho hàm số \(y = f(x)\) xác định và có đạo hàm trên \(\mathbb{R}\), biết \(f(4) = 5\) và \({f^\prime }(4) = 2\). Giới hạn \(\mathop {\lim }\limits_{x \to 4} \frac{{{f^2}(x) + f(x) - 30}}{{\sqrt x - 2}}\) bằng (1) _________.
 Xem đáp án
Xem đáp án
Cho hàm số \(y = f(x)\) xác định và có đạo hàm trên \(\mathbb{R}\), biết \(f(4) = 5\) và \({f^\prime }(4) = 2\). Giới hạn \(\mathop {\lim }\limits_{x \to 4} \frac{{{f^2}(x) + f(x) - 30}}{{\sqrt x - 2}}\) bằng (1) __ 88 __.
Giải thích
Ta có: \(\mathop {\lim }\limits_{x \to 4} \frac{{{f^2}(x) + f(x) - 30}}{{\sqrt x - 2}} = \mathop {\lim }\limits_{x \to 4} \frac{{(f(x) - 5)(f(x) + 6)}}{{\sqrt x - 2}}\)
\( = \mathop {\lim }\limits_{x \to 4} \left[ {\frac{{f(x) - f(4)}}{{x - 4}}.(\sqrt x + 2).(f(x) + 6)} \right] = {f^\prime }(4).(\sqrt 4 + 2).(f(4) + 6) = 88\) (vì
\[{f^\prime }\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {\frac{{f(x) - f\left( {{x_0}} \right)}}{{x - {x_0}}}} \right)\]
Câu 65:
Theo thống kê tại một nhà máy Z, nếu áp dụng tuần làm việc 40 giờ thì mỗi tuần có 100 công nhân đi làm và mỗi công nhân làm được 120 sản phẩm trong một giờ. Nếu tăng thời gian làm việc thêm 2 giờ mỗi tuần thì sẽ có 1 công nhân nghỉ việc và năng suất lao động giảm 5 sản phẩm/1 công nhân/1 giờ. Ngoài ra, số phế phẩm mỗi tuần ước tính là \(P(x) = \frac{{95{x^2} + 120x}}{4}\), với x là thời gian làm việc trong một tuần. Nhà máy cần áp dụng thời gian làm việc mỗi tuần (1) _______ giờ để số lượng sản phẩm thu được mỗi tuần là lớn nhất.
 Xem đáp án
Xem đáp án
Theo thống kê tại một nhà máy Z, nếu áp dụng tuần làm việc 40 giờ thì mỗi tuần có 100 công nhân đi làm và mỗi công nhân làm được 120 sản phẩm trong một giờ. Nếu tăng thời gian làm việc thêm 2 giờ mỗi tuần thì sẽ có 1 công nhân nghỉ việc và năng suất lao động giảm 5 sản phẩm/1 công nhân/1 giờ. Ngoài ra, số phế phẩm mỗi tuần ước tính là \(P(x) = \frac{{95{x^2} + 120x}}{4}\), với x là thời gian làm việc trong một tuần. Nhà máy cần áp dụng thời gian làm việc mỗi tuần (1) __ 36 __ giờ để số lượng sản phẩm thu được mỗi tuần là lớn nhất.
Giải thích
Gọi \(t\) là số giờ làm tăng thêm mỗi tuần, \(t \in \mathbb{R}\)
\( \Rightarrow \) số công nhân bỏ việc là \(\frac{t}{2}\) nên số công nhân làm việc là \(100 - \frac{t}{2}\) người.
Năng suất của công nhân còn \(120 - \frac{{5t}}{2}\) sản phẩm một giờ.
Số thời gian làm việc một tuần là \(40 + t\) giờ.
Để nhà máy hoạt động được thì \(\left\{ {\begin{array}{*{20}{l}}{40 + t > 0}\\{120 - \frac{{5t}}{2} > 0 \Rightarrow t \in ( - 40;48){\rm{. }}}\\{100 - \frac{t}{2} > 0}\end{array}} \right.\)
Số sản phẩm trong một tuần làm được: \(S = \left( {100 - \frac{t}{2}} \right)\left( {120 - \frac{{5t}}{2}} \right)(40 + t)\).
Số sản phẩm thu được là
\(f(t) = \left( {100 - \frac{t}{2}} \right)\left( {120 - \frac{{5t}}{2}} \right)(40 + t) - \frac{{95{{(40 + t)}^2} + 120(40 + t)}}{4} = \frac{5}{4}{t^3} - \frac{{1135}}{4}{t^2} - 2330t + 440800.\)
\( \Rightarrow {f^\prime }(t) = = \frac{{15}}{4}{t^2} - \frac{{1135}}{2}t - 2330.\)
\({f^\prime }(t) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = - 4\,\,\,\,\,\,\,\,\,\,\,}\\{t = \frac{{466}}{3}\,\,(\;{\rm{L}})}\end{array}} \right.\)
Ta có BBT như sau
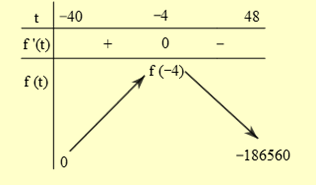
Vậy số lượng sản phẩm thu được mỗi tuần lớn nhất khi x = 36.
Câu 66:
Trong không gian Oxyz, cho ba điểm \(A(1;0;0),B(2;0;1),C(1;1;1)\) và mặt phẳng \((P):x + y + z - 6 = 0\). Gọi \((S)\) là mặt cầu đi qua ba điểm A, B, C và có tâm thuộc mặt phẳng \((P)\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Bán kính mặt cầu (S) bằng _______.
Tâm mặt cầu (S) có tung độ bằng _______; cao độ bằng _______.
 Xem đáp án
Xem đáp án
Trong không gian Oxyz, cho ba điểm \(A(1;0;0),B(2;0;1),C(1;1;1)\) và mặt phẳng \((P):x + y + z - 6 = 0\). Gọi \((S)\) là mặt cầu đi qua ba điểm A, B, C và có tâm thuộc mặt phẳng \((P)\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
Bán kính mặt cầu (S) bằng \(\sqrt {41} \).
Tâm mặt cầu (S) có tung độ bằng 4; cao độ bằng -3.
Giải thích
Gọi \(I(x;y;z)\) là tâm mặt cầu \((S)\) đi qua 3 điểm A, B, C.
Ta có: \(IA = IB = IC \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{I{A^2} = I{B^2}}\\{I{B^2} = I{C^2}}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{{(x - 1)}^2} + {y^2} + {z^2} = {{(x - 2)}^2} + {y^2} + {{(z - 1)}^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\{{{(x - 2)}^2} + {y^2} + {{(z - 1)}^2} = {{(x - 1)}^2} + {{(y - 1)}^2} + {{(z - 1)}^2}}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 2x + 1 = - 4x + 4 - 2z + 1}\\{ - 4x + 4 = - 2x + 1 - 2y + 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x + z = 2}\\{x - y = 1}\end{array}} \right.} \right.\)
Vì \(I \in (P)\) nên ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{r}}{x + z = 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\{x - y = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\{x + y + z - 6 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 5}\\{y = 4}\\{z = - 3}\end{array} \Rightarrow I(5;4; - 3)} \right.} \right.\)
Bán kính của mặt cầu \((S)\) là \(R = IA = \sqrt {41} \)
\( \Rightarrow (S):{(x - 5)^2} + {(y - 4)^2} + {(z + 3)^2} = 41.{\rm{ }}\)
Câu 67:
Phần nguyên của số thực x là số nguyên lớn nhất không vượt quá x, kí hiệu là [x]. Chẳng hạn [1,2]=1; [-2;7]= -3.
Tổng các phần nguyên của số \(\sqrt k \) với k là số tự nhiên và k ∈ [1;24] bằng
 Xem đáp án
Xem đáp án
Ta có:
\(S = \sum\limits_{k = 1}^{24} {[\sqrt k ] = [\sqrt 1 ] + [\sqrt 2 ] + [\sqrt 3 ] + [\sqrt 4 ] + \ldots + [\sqrt 8 ] + [\sqrt 9 ] + \ldots + [\sqrt {15} ] + [\sqrt {16} ] + \ldots } {\rm{ + [}}\sqrt {23} {\rm{] + [}}\sqrt {24} {\rm{]}}\)
\( \Leftrightarrow S = 1 + 1 + 1 + 2 + \ldots + 2 + 3 + \ldots + 3 + 4 + \ldots + 4 + 4\)
\( \Leftrightarrow S = 3.1 + 5.2 + 7.3 + 9.4 = 70\)
Câu 68:
Tìm tham số thực \(m\) để hàm số \(y = f(x) = \left\{ {\begin{array}{*{20}{l}}{\frac{{{x^2} + x - 12}}{{x + 4}}}&{{\rm{khi }}x \ne - 4}\\{mx + 1}&{{\rm{khi }}x = - 4}\end{array}} \right.\) liên tục tại điểm \({x_0} = - 4\).
 Xem đáp án
Xem đáp án
Tập xác định: \(D = \mathbb{R}\).
Ta có:
+\(\mathop {\lim }\limits_{x \to - 4} f(x) = \mathop {\lim }\limits_{x \to - 4} \frac{{{x^2} + x - 12}}{{x + 4}} = \mathop {\lim }\limits_{x \to - 4} \frac{{(x - 3)(x + 4)}}{{x + 4}} = \mathop {\lim }\limits_{x \to - 4} (x - 3) = - 7.\)
+ \(f( - 4) = - 4m + 1.\)
Hàm số \(f(x)\) liên tục tại điểm \({x_0} = - 4 \Leftrightarrow \mathop {\lim }\limits_{x \to - 4} f(x) = f( - 4) \Leftrightarrow - 4m + 1 = - 7 \Leftrightarrow m = 2\).
Câu 69:
Có 4 hành khách bước lên một đoàn tàu gồm 4 toa. Mỗi hành khách độc lập với nhau và chọn ngẫu nhiên một toa. Tính xác suất để 1 toa có 3 người, 1 toa có 1 người, 2 toa còn lại không có ai.
 Xem đáp án
Xem đáp án
Không gian mẫu là số cách sắp xếp 4 hành khách lên 4 toa tàu. Vì mỗi hành khách có 4 cách chọn toa nên có 44 cách xếp.
Suy ra số phần tử của không gian mẫu là n(Ω) = 44.
Gọi A là biến cố: “1 toa có 3 người, 1 toa có 1 người, 2 toa còn lại không có ai”. Để tìm số phần tử của A, ta chia làm hai giai đoạn như sau:
Giai đoạn thứ nhất: Chọn 3 hành khách trong 4 hành khách, chọn 1 toa trong 4 toa và xếp lên toa đó 3 hành khách vừa chọn có \(C_4^3.C_4^1\) cách.
Giai đoạn thứ hai: Chọn 1 toa trong 3 toa còn lại và xếp lên toa đó 1 một hành khách còn lại có \(C_3^1\) cách.
Suy ra số phần tử của biến cố A là \(n(A) = C_4^3.C_4^1.C_3^1.\)
Vậy xác suất cần tính là: \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{3}{{16}}\).
Câu 70:
Trong không gian Oxyz, cho mặt cầu \((S):{(x - 3)^2} + {(y - 1)^2} + {(z - 1)^2} = 4\) và ba điểm \(A( - 1;2; - 3),B(5;2;3),C(1;2;3)\). Gọi \(S\) là điểm thay đổi trên mặt cầu \((S)\). Giá trị lớn nhất của thể tích khối chóp S.ABC là (1) _________.
 Xem đáp án
Xem đáp án
Trong không gian Oxyz, cho mặt cầu \((S):{(x - 3)^2} + {(y - 1)^2} + {(z - 1)^2} = 4\) và ba điểm \(A( - 1;2; - 3),B(5;2;3),C(1;2;3)\). Gọi \(S\) là điểm thay đổi trên mặt cầu \((S)\). Giá trị lớn nhất của thể tích khối chóp S.ABC là (1) __ 12 __ .
Giải thích
Mặt cầu (S) có tâm \(I(3;1;1)\) và bán kính \(R = 2\)
Phương trình mặt phẳng \((ABC)\) là: \(y - 2 = 0\).
Ta có thể tích S.ABC đạt giá trị lớn nhất khi \(d(S;(ABC))\) đạt giá trị lớn nhất.
\({\rm{M\`a }}d(I;(ABC)) = 1 < R = 2\)
\( \Rightarrow d{(S;(ABC))_{\max }} = R + d(I;(ABC)) = 3.\)
\({V_{S.AB{C_{\max }}}} = \frac{1}{3}{S_{ABC}}.d{(S;(ABC))_{\max }} = \frac{1}{3}.12.3 = 12\).
Câu 71:
Cho hình nón tròn xoay ngoại tiếp tứ diện đều cạnh a.
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Bán kính đáy của hình nón bằng \(\frac{{a\sqrt 3 }}{2}\) . |
¡ |
¡ |
|
Diện tích xung quanh hình nón đã cho bằng \(\frac{{\pi {a^2}\sqrt 3 }}{3}\). |
¡ |
¡ |
|
Thể tích của khối nón đã cho bằng \(\frac{{{a^3}\sqrt 6 }}{9}\). |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
Đúng |
Sai |
|
Bán kính đáy của hình nón bằng \(\frac{{a\sqrt 3 }}{2}\) . |
¡ |
¤ |
|
Diện tích xung quanh hình nón đã cho bằng \(\frac{{\pi {a^2}\sqrt 3 }}{3}\). |
¤ |
¡ |
|
Thể tích của khối nón đã cho bằng \(\frac{{{a^3}\sqrt 6 }}{9}\). |
¡ |
¤ |
Giải thích
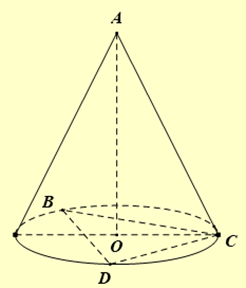
Giả sử hình nón ngợi tiếp tứ diện đều ABCD cạnh \(a\) như hình vẽ trên. Ta có:
+) Bán kính đáy \(R = OC = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\).
+) Độ dài đường sinh \(l = AC = a\).
+) Chiều cao của khối chóp là \(h = AO = \sqrt {{{\left. {A{B^2} - \frac{{BC\sqrt 3 }}{3}} \right)}^2}} = \frac{{a\sqrt 6 }}{3}\)
Vậy:
+) Diện tích xung quanh hình nón là: \({S_{xq}} = \pi Rl = \pi .\frac{{a\sqrt 3 }}{3}a = \frac{{\pi {a^2}\sqrt 3 }}{3}\).
+) Thể tích của khối nón là: \(V = \frac{1}{3}\pi {R^2}h = \frac{{{a^3}\sqrt 6 }}{{27}}\)
Câu 72:
Cho hàm số \(f(x) = \frac{{x - m}}{{x + 4}}\). Tổng tất cả các giá trị của m để \(\mathop {\min }\limits_{[ - 3;3]} f(x) = 2\) là
 Xem đáp án
Xem đáp án
Ta có \({f^\prime }(x) = \frac{{4 + m}}{{{{(x + 4)}^2}}},\forall x \ne - 4\) và phương trình tiệm cận đứng \(x = - 4\).
TH1. Với \(m + 4 > 0 \Leftrightarrow m > - 4\) thì \({f^\prime }(x) > 0,\forall x \in [ - 3;3]\) nên
\(\mathop {\min }\limits_{[ - 3;3]} f(x) = 2 \Leftrightarrow f( - 3) = 2 \Leftrightarrow \frac{{ - 3 - m}}{1} = 2 \Rightarrow m = - 5\) (loại).
TH2. Với \(m + 4 < 0 \Leftrightarrow m < - 4\) thì \({f^\prime }(x) < 0,\forall x \in [ - 3;3]\) nên
\(\mathop {\min }\limits_{[ - 3;3]} f(x) = 2 \Leftrightarrow f(3) = 2 \Leftrightarrow \frac{{3 - m}}{7} = 2 \Rightarrow m = - 11\) (thỏa mãn).
Vậy tổng các giá trị \(m\) thỏa mãn yêu cầu bài toán là -11 .Câu 73:
Tích phân \(I = \int\limits_1^2 {\frac{1}{{2x - 1}}} \;{\rm{d}}x\) bằng
 Xem đáp án
Xem đáp án
Cách 1.
\(I = \int\limits_1^2 {\frac{1}{{2x - 1}}} \;{\rm{d}}x = \left. {\frac{1}{2}\ln |2x - 1|} \right|_1^2\)
\( = \frac{1}{2}(\ln 3 - \ln 1) = \frac{1}{2}\ln 3 = \ln \sqrt 3 .\)
Câu 74:
Cho \(\log _2^2(xy) = {\log _2}\left( {\frac{x}{4}} \right){\log _2}(4y)\). Biểu thức \(P = {\log _3}(x + 4y + 4) + {\log _2}(x - 4y - 1)\) có giá trị bằng
 Xem đáp án
Xem đáp án
Điều kiện: \(\left\{ {\begin{array}{*{20}{c}}{x > 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\{y > 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\{x - 4y - 1 > 0}\end{array}} \right.\).
Ta có \(\log _2^2(xy) = {\log _2}\left( {\frac{x}{4}} \right){\log _2}(4y) \Leftrightarrow {\left( {{{\log }_2}x + {{\log }_2}y} \right)^2} = \left( {{{\log }_2}x - 2} \right)\left( {{{\log }_2}y + 2} \right)\,\,\,\left( 1 \right)\) .
Đặt \({\log _2}x = a;{\log _2}y = b\), ta có (1) trở thành :
\({(a + b)^2} = (a - 2)(b + 2) \Leftrightarrow {a^2} + ab - 2a + {b^2} + 2b + 4 = 0\)
\( \Leftrightarrow 2{a^2} + 2ab - 4a + 2{b^2} + 4b + 8 = 0 \Leftrightarrow {(a + b)^2} + {(a - 2)^2} + {(b + 2)^2} = 0\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a + b = 0}\\{a - 2 = 0}\\{b + 2 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 2}\\{b = - 2}\end{array}} \right.} \right.\).
Với \(\left\{ {\begin{array}{*{20}{c}}{a = 2\,\,}\\{b = - 2}\end{array}} \right.\) , ta có \(\left\{ {\begin{array}{*{20}{c}}{ log{ _2}x = 2\,\,\,}\\{ log{ _2}y = - 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 4}\\{y = \frac{1}{4}}\end{array}} \right.} \right.\) (thỏa mãn điều kiện).
Khi đó \(P = {\log _3}\left( {4 + 4.\frac{1}{4} + 4} \right) + {\log _2}\left( {4 - 4.\frac{1}{4} - 1} \right) = 3\).
Câu 75:
Cho hình phẳng (H) giới hạn bởi đồ thị hai hàm số \(y = 2{x^2}\) và \(y = x\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Đồ thị hai hàm số cắt nhau tại điểm có hoành độ bằng _______.
Diện tích hình phẳng (H) bằng _______.
 Xem đáp án
Xem đáp án
Cho hình phẳng (H) giới hạn bởi đồ thị hai hàm số \(y = 2{x^2}\) và \(y = x\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
Đồ thị hai hàm số cắt nhau tại điểm có hoành độ bằng \(\frac{1}{2}\).
Diện tích hình phẳng (H) bằng \(\frac{1}{{24}}\).
Giải thích
Xét phương trình hoành độ điểm chung của hai đồ thị ta có: \(2{x^2} - x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = \frac{1}{2}}\end{array}} \right.\).
Diện tích hình phẳng (H) là \(S = \int\limits_0^{\frac{1}{2}} {\left| {2{x^2} - x} \right|} dx = \frac{1}{{24}}{\rm{. }}\)
Câu 76:
Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \({f^\prime }(x) = {x^2}(x + 2)(x - 3)\).
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Hàm số \(f(x)\) có 3 điểm cực trị. |
¡ |
¡ |
|
Hàm số \(f(x)\) nghịch biến trên (-2;3). |
¡ |
¡ |
|
Hàm số \(f(x)\) có điểm cực đại là x = 2. |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
Đúng |
Sai |
|
Hàm số \(f(x)\) có 3 điểm cực trị. |
¡ |
¤ |
|
Hàm số \(f(x)\) nghịch biến trên (-2;3). |
¡ |
¤ |
|
Hàm số \(f(x)\) có điểm cực đại là x = 2. |
¤ |
¡ |
Giải thích
Ta có: \(f'\left( x \right) = 0 \Leftrightarrow \)\(\begin{array}{l}x = 0\\x = - 2\\x = 3.\end{array}\).
Bảng xét dấu của hàm số \(f'\left( x \right)\):

Vậy hàm số có 2 điểm cực trị: x = −2 là điểm cực đại và x = 3 là điểm cực tiểu.
Câu 77:
Có bao nhiêu số tự nhiên có 3 chữ số có dạng \(\overline {abc} \) thỏa mãn \(a,\,\,b,\,\,c\) là độ dài 3 cạnh của một tam giác cân?
 Xem đáp án
Xem đáp án
Gọi độ dài cạnh bên và cạnh đáy của tam giác cân là x, y (thỏa mãn x, y là các chữ số)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{1 \le x \le 9}\\{1 \le y \le 9}\\{1 \le y < 2x}\end{array}} \right.\)
TH1: \[\left\{ {\begin{array}{*{20}{l}}{1 \le y \le 9}\\{5 \le x \le 9}\end{array} \Rightarrow {\rm{ c\'o }}9.5 = 45} \right.\] cặp số \((x;y)\).
TH2: \(\left\{ {\begin{array}{*{20}{l}}{1 \le x \le 4}\\{x = i}\\{1 \le y \le 2i - 1}\end{array}} \right.\)
Với mỗi giá trị của i có 2i − 1 cặp số thỏa mãn, do đó ta có:
\[(2.1 - 1) + (2.2 - 1) + (2.3 - 1) + (2.4 - 1) = 16\] cặp số \((x;y)\)
Suy ra có 61 cặp số \((x;y)\) mà với mỗi cặp, ta có thể viết số có 3 chữ số trong đó có 2 chữ số \(x\) và 1 chữ số \(y\). Trong 61 cặp số này có:
+ 9 cặp \(x = y\) thì viết được 9 số.
+ 52 cặp \(x \ne y\) thì mỗi cặp viết được 3 số \((\overline {xxy} ,\overline {xyx} ,\overline {yxx} )\) nên có \(52.3 = 156\) số.
Vậy tất cả viết được 165 số.
Câu 78:
Trong không gian, cho bốn mặt cầu có bán kính lần lượt là 2,3,3,2 tiếp xúc ngoài với nhau. Mặt cầu nhỏ nhất tiếp xúc ngoài với cả bốn mặt cầu nói trên có bán kính bằng
 Xem đáp án
Xem đáp án
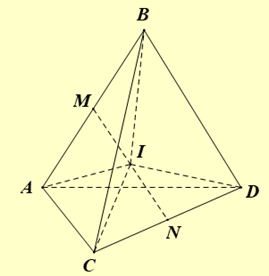
Gọi A, B là tâm mặt cầu bán kính bằng 2 ; C, D là tâm mặt cầu bán kính bằng 3 ; I là tâm mặt cầu nhỏ nhất có bán kính \(x\) tiếp xúc ngoài với cả bốn mặt cầu trên.
Mặt cầu \((I)\) tiếp xúc ngoài với 4 mặt cầu tâm A, B, C, D nên \(IA = IB = x + 2,IC = ID = x + 3\).
Gọi \((P),(Q)\) lần lượt là các mặt phẳng trung trực đoạn AB và CD.
\(\left\{ {\begin{array}{*{20}{l}}{IA = IB \Rightarrow I \in (P)}\\{IC = ID \Rightarrow I \in (Q)}\end{array} \Rightarrow I \in (P) \cap (Q)\,\,(1).} \right.\)
Gọi M, N lần lượt là trung điểm cạnh AB, CD.
Tứ diện ABCD có \(DA = DB = CA = CB = 5\) suy ra MN là đường vuông góc chung của AB và CD, suy ra \(MN = (P) \cap (Q)\,\,(2)\).
Từ (1) và (2) suy ra \(I \in MN\)
Tam giác IAM có \(IM = \sqrt {I{A^2} - A{M^2}} = \sqrt {{{(x + 2)}^2} - 4} \).
Tam giác CIN có \(IN = \sqrt {I{C^2} - C{N^2}} = \sqrt {{{(x + 3)}^2} - 9} \).
Tam giác AMN có \(NM = \sqrt {N{A^2} - A{M^2}} = \sqrt {12} \).
Suy ra \(\sqrt {{{(x + 3)}^2} - 9} + \sqrt {{{(x + 2)}^2} - 4} = \sqrt {12} \Rightarrow x = \frac{6}{{11}}\).
Câu 79:
Để in một quyển tạp chí, người ta cần sử dụng 1 tờ giấy bìa cứng và 25 tờ giấy in cùng với mực in. Một tập giấy in gồm 500 tờ và một tập giấy bìa cứng gồm 60 tờ, có giá gấp đôi giá của một tập giấy in. Mỗi hộp mực in được 130 tờ giấy in hoặc giấy bìa cứng. Một tập giấy in có giá 50 nghìn đồng. Hộp mực có giá 900 nghìn đồng mỗi hộp.
Với ngân sách là 60 triệu đồng, có tối đa (1) ______ tạp chí hoàn chỉnh có thể được in.
 Xem đáp án
Xem đáp án
Để in một quyển tạp chí, người ta cần sử dụng 1 tờ giấy bìa cứng và 25 tờ giấy in cùng với mực in. Một tập giấy in gồm 500 tờ và một tập giấy bìa cứng gồm 60 tờ, có giá gấp đôi giá của một tập giấy in. Mỗi hộp mực in được 130 tờ giấy in hoặc giấy bìa cứng. Một tập giấy in có giá 50 nghìn đồng. Hộp mực có giá 900 nghìn đồng mỗi hộp.
Với ngân sách là 60 triệu đồng, có tối đa (1) __ 325 __ tạp chí hoàn chỉnh có thể được in.
Giải thích
Mỗi tập giấy in có 500 tờ và mỗi quyển tạp chí cần 25 tờ giấy in nên có 500 : 25 = 20 quyển tạp chí có thể được in. Mỗi tập giấy in có giá 50 nghìn đồng.
Mỗi tập giấy bìa cứng có 60 tờ và mỗi quyển tạp chí cần 1 tờ giấy bìa nên có 60 tạp chí có thể được in. Mỗi tập giấy bìa cứng có giá 50 × 2 = 100 (nghìn đồng).
Mỗi hộp mực in được 130 tờ giấy in hoặc giấy bìa cứng nên có 130 : (25 + 1) = 5 quyển tạp chí có thể được in. Mỗi hộp mực in có giá 900 nghìn đồng.
Số lượng tạp chí tối đa có thể in để tận dụng hết giấy in, giấy bìa và mực in là bội chung nhỏ nhất của 20, 60, 5 và bằng 60.
Khi đó, 60 quyển tạp chí cần 3 tập giấy in, 1 tập giấy bìa cứng và 12 hộp mực.
Vậy tổng chi phí in 60 quyển tạp chí là:
3 × 50 + 1 × 100 + 12 × 900 = 11050 (nghìn đồng) =11 triệu 50 nghìn đồng.
Ta có: 60 : 11,050 = 5 dư 4,75.
Với 4,75 triệu đồng còn dư ta mua được x tập giấy in, y hộp mực in và 1 tập giấy bìa cứng thỏa mãn \(1 \le x \le 3;\,\,1 \le y \le 12;\,\,x,y \in \mathbb{N}\).
⇒Tổng chi phí in là: \(50x + 100 + 900y \le 4750 \Leftrightarrow x + 18y \le 93 \Rightarrow y \le \frac{{93 - x}}{{18}}\).
Ứng với x tập giấy in ta có 20x quyển tạp chí.
Ứng với y hộp mực in ta có 5y quyển tạp chí.
Ứng với 1 tập giấy bìa cứng ta có 60 quyển tạp chí.
Khi đó ứng với 4,75 triệu đồng còn dư, số tạp chí tối đa có thể in là
min{20x; 5y;60} = min{20x; 5y}.
⇒Số tạp chí tối đa có thể in ứng với 4,75 triệu đồng là giá trị lớn nhất của min{20x; 5y}.
Ta có bảng sau:
|
x |
1 |
2 |
3 |
|
ymax |
5 |
5 |
5 |
|
20x |
20 |
40 |
60 |
|
5y |
25 |
25 |
25 |
|
min{20x; 5y} |
20 |
25 (Chọn) |
25 (Chọn) |
Vậy với ngân sách là 60 triệu đồng, số tạp chí hoàn chỉnh có thể được in là:
60 × 5 + 25 = 325 (tạp chí).
Câu 80:
 Xem đáp án
Xem đáp án
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = 3\sin x + 4\cos x + 1\) bằng (1) __ 2 __.
Giải thích
Ta có \(\frac{y}{5} = \frac{3}{5}\sin x + \frac{4}{5}\cos x + \frac{1}{5} = \sin (x + \alpha ) + \frac{1}{5}\) với \(\cos \alpha = \frac{3}{5}\) và \(\sin \alpha = \frac{4}{5}\).
Mà \( - 1 \le \sin (x + \alpha ) \le 1 \Leftrightarrow \frac{{ - 4}}{5} \le \sin (x + \alpha ) + \frac{1}{5} \le \frac{6}{5}\) hay \(\frac{{ - 4}}{5} \le \frac{y}{5} \le \frac{6}{5}\) suy ra \( - 4 \le y \le 6\).
Vậy \(\min y = - 4;\max y = 6\).
Câu 81:
Xét các số thực dương \(a,b\) thoả mãn \({\log _2}\frac{{1 - ab}}{{a + b}} = 2ab + a + b - 3\). Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
\[a + b = 1 - ab\]. |
¡ |
¡ |
|
\[P = a + b\] đạt giá trị nhỏ nhất tại \(a = 2 - b = \frac{{1 - \sqrt 5 }}{2}\). |
¡ |
¡ |
|
Giá trị nhỏ nhất của \[P = a + b\] bằng \( - 1 + \sqrt 5 \). |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
Đúng |
Sai |
|
\[a + b = 1 - ab\]. |
¡ |
¤ |
|
\[P = a + b\] đạt giá trị nhỏ nhất tại \(a = 2 - b = \frac{{1 - \sqrt 5 }}{2}\). |
¡ |
¤ |
|
Giá trị nhỏ nhất của \[P = a + b\] bằng \( - 1 + \sqrt 5 \). |
¤ |
¡ |
Giải thích
Điều kiện \(1 - ab > 0 \Leftrightarrow ab < 1\).
Ta có \({\log _2}\frac{{1 - ab}}{{a + b}} = 2ab + a + b - 3 \Leftrightarrow {\log _2}\left( {1 - ab} \right) - {\log _2}\left( {a + b} \right) = \left( {a + b} \right) - 2\left( {1 - ab} \right) - 1\)
\[ \Leftrightarrow {\log _2}\left( {1 - ab} \right) + 1 + 2\left( {1 - ab} \right) = {\log _2}\left( {a + b} \right) + \left( {a + b} \right)\]
\( \Leftrightarrow {\log _2}2\left( {1 - ab} \right) + 2\left( {1 - ab} \right) = {\log _2}\left( {a + b} \right) + \left( {a + b} \right).\,\,\left( 1 \right)\).
Xét hàm số \(f\left( t \right) = {\log _2}t + t\) với \(t > 0\) có \({f^\prime }\left( t \right) = \frac{1}{{t.\ln 2}} + 1 > 0,\forall t > 0\) nên hàm số \(f\left( t \right) = {\log _2}t + t\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\).
Ta có (1)\( \Leftrightarrow f2\left( {1 - ab} \right) = f\left( {a + b} \right) \Leftrightarrow 2\left( {1 - ab} \right) = a + b \Leftrightarrow 2 - a = b\left( {2a + 1} \right) \Leftrightarrow b = \frac{{2 - a}}{{2a + 1}}\).
Do \(a,b > 0 \Rightarrow \frac{{2 - a}}{{2a + 1}} > 0 \Leftrightarrow 0 < a < 2\).
Khi đó \(P = a + b = a + \frac{{2 - a}}{{2a + 1}} = \frac{{2{a^2} + 2}}{{2a + 1}}\)
Xét hàm \(g\left( a \right) = \frac{{2{a^2} + 2}}{{2a + 1}} \Rightarrow g'\left( a \right) = \frac{{4{a^2} + 4a - 4}}{{2a + 1{)^2}}} \Rightarrow g'\left( a \right) = 0 \Leftrightarrow a = \frac{{ - 1 \pm \sqrt 5 }}{2}.\)
Bảng biến thiên
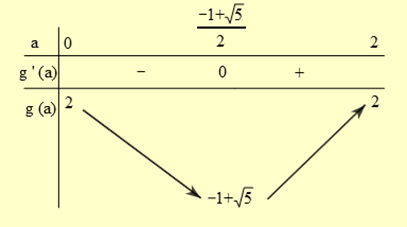
Vậy \[{P_{min}} = {\rm{ }} - 1 + \sqrt 5 \].
Câu 82:
Một vật đang chuyển động đều với vận tốc v0(m/s) thì bắt đầu tăng tốc với phương trình gia tốc \(a(t) = {v_0}t + {t^2}\left( {{\rm{m}}/{{\rm{s}}^2}} \right)\) trong đó t là khoảng thời gian được tính bằng giây kể từ thời điểm vật bắt đầu tăng tốc. Biết quãng đường vật đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng tốc là 100 m. Khi đó, vận tốc ban đầu v0 của vật bằng bao nhiêu (làm tròn đến chữ số thập phân thứ 3)?
 Xem đáp án
Xem đáp án
Phương trình vận tốc \(v(t) = \int a (t){\rm{d}}t = \int {\left( {{v_0}t + {t^2}} \right)} dt = {v_0}\frac{{{t^2}}}{2} + \frac{{{t^3}}}{3} + C\)
Tại thời điểm \(t = 0 \Rightarrow v(t) = {v_0} \Rightarrow C = {v_0}\)
Vì quãng đường vật đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng tốc là 100 m nên
\(S = 100 = \int\limits_0^3 {v(t)} {\rm{d}}t = \int\limits_0^3 {\left( {{v_0}\frac{{{t^2}}}{2} + \frac{{{t^3}}}{3} + {v_0}} \right)} {\rm{d}}t = 3{v_0} + \frac{9}{2}{v_0} + \frac{{27}}{4} \Rightarrow {v_0} = 12,433\) m/s.
Câu 83:
Cho hình lăng trụ tam giác \(ABC.A'B'C'\) có cạnh bên bằng \(a\sqrt 2 \), đáy ABC là tam giác vuông tại \(B,BC = a\sqrt 3 ,AB = a\). Biết hình chiếu vuông góc của đỉnh \(A'\) lên mặt đáy là điểm \(M\) thoả mãn \(3\overrightarrow {AM} = \overrightarrow {AC} \). Thể tích lăng trụ tam giác \(ABC.A'B'C'\) bằng
 Xem đáp án
Xem đáp án
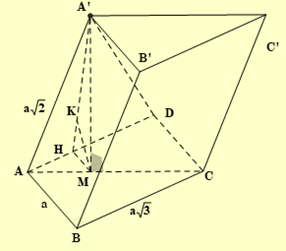
Trong tam giác ABC ta có
\(AC = \sqrt {A{B^2} + B{C^2}} = 2a \Rightarrow AM = \frac{1}{3}AC = \frac{{2a}}{3} \Rightarrow {A^\prime }M = \sqrt {{A^\prime }{A^2} - A{M^2}} = \frac{{a\sqrt {14} }}{3}{\rm{. }}\)
Tính thể tích lăng trụ tam giác \(ABC.{A^\prime }{B^\prime }{C^\prime }\) là:
\({V_{ABC.{A^\prime }{B^\prime }{C^\prime }}} = A'M.{S_{ABC}} = \frac{{a\sqrt {14} }}{3}.\frac{1}{2}.a.a\sqrt 3 = \frac{{{a^3}\sqrt {42} }}{6}.\)
Câu 84:
Mỗi phát biểu sau là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Tổng của hai số nguyên dương là một số nguyên dương. |
¡ |
¡ |
|
Tích của hai số nguyên âm là một số nguyên âm. |
¡ |
¡ |
|
Tích của hai số nguyên bằng 0 khi và chỉ khi ít nhất một trong hai số nguyên đó bằng 0. |
¡ |
¡ |
|
Hiệu là một số nguyên âm nếu a dương và b dương. |
¡ |
¡ |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Tổng của hai số nguyên dương là một số nguyên dương. |
¤ |
¡ |
|
Tích của hai số nguyên âm là một số nguyên âm. |
¡ |
¤ |
|
Tích của hai số nguyên bằng 0 khi và chỉ khi ít nhất một trong hai số nguyên đó bằng 0. |
¤ |
¡ |
|
Hiệu là một số nguyên âm nếu a dương và b dương. |
¡ |
¤ |
Giải thích
Khẳng định sai là:
+, “Tích của hai số nguyên âm là một số nguyên âm”. Ví dụ: (−1).(−3) = 3 > 0.
+, “Hiệu là một số nguyên âm nếu a dương và b dương”. Ví dụ: 3 − 2 = 1 > 0.
Câu 85:
Cho số phức z thỏa mãn \({z^2} + z.\bar z - 1 = 0\).
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Điểm biểu diễn số phức z có tọa độ \(\left( {\frac{{\sqrt 2 }}{2}; - \frac{{\sqrt 2 }}{2}} \right)\) |
¡ |
¡ |
|
z là số thuần ảo |
¡ |
¡ |
|
\(\left| z \right| = \frac{{\sqrt 2 }}{2}\) |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
Đúng |
Sai |
|
Điểm biểu diễn số phức z có tọa độ \(\left( {\frac{{\sqrt 2 }}{2}; - \frac{{\sqrt 2 }}{2}} \right)\) |
¡ |
¤ |
|
z là số thuần ảo |
¡ |
¤ |
|
\(\left| z \right| = \frac{{\sqrt 2 }}{2}\) |
¤ |
¡ |
Giải thích
Gọi \(z = x + yix,\left( {y \in \mathbb{R}} \right)\).
Ta có: \({z^2} + z.\bar z - 1 = 0\)
\[ \Leftrightarrow {\left( {x + yi} \right)^2} + \left( {x + yi} \right)\left( {x - yi} \right) - 1 = 0\]
\( \Leftrightarrow {x^2} - {y^2} + 2xyi + {x^2} + {y^2} - 1 = 0\)
\( \Leftrightarrow 2{x^2} - 1 + 2xyi = 0\)
\( \Leftrightarrow \left\{ \begin{array}{l}2{x^2} - 1 = 0\\2xy = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \pm \frac{1}{{\sqrt 2 }}\\y = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{z_1} = - \frac{1}{{\sqrt 2 }}\\{z_2} = \frac{1}{{\sqrt 2 }}\end{array} \right. \Rightarrow \left| {{z_1}} \right| = \frac{{\sqrt 2 }}{2}\)
⇒ Điểm biểu diễn số phức z có tọa độ \(\left( {\frac{{\sqrt 2 }}{2};0} \right)\) và \(\left( { - \frac{{\sqrt 2 }}{2};0} \right)\).
Câu 86:
Hai chất điểm \(M\) và \(N\) chuyển động thẳng đều trên trục Ox và Oy vuông góc với nhau (như hình vẽ):
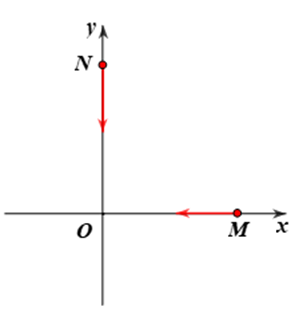
Tại thời điểm t = 0 chất điểm \(M\) đang cách gốc tọa độ \(O\) một đoạn 10 mét; chất điểm \(N\) cách gốc tọa độ \(O\) một đoạn \(12\;{\rm{m}}\). Hai chất điểm cùng chuyển động hướng về \(O\) với các tốc độ tương ứng là 0,4 m/s và 0,3 m/s. Khoảng cách nhỏ nhất giữa 2 chất điểm bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Tam giác OMN vuông tại \(O\) nên ta có \(O{M^2} + O{N^2} = M{N^2} = {S^2}\) với \(S\) là khoảng cách giữa hai chất điểm.
Tại thời điểm \(t = {t_0}\) thì khoảng cách đạt giá trị nhỏ nhất \({S_{\min }}\), khi đó ta có:
- Quãng đường mà chất điểm \(M\) đi được là \(0,4.{t_0} \Rightarrow OM = 10 - 0,4{t_0}\)
- Quãng đường mà chất điểm \(N\) đi được là \(0,3.{t_0} \Rightarrow ON = 12 - 0,3{t_0}\)
Vậy \({S_{\min }} = \sqrt {{{\left( {10 - 0,4{t_0}} \right)}^2} + {{\left( {12 - 0,3{t_0}} \right)}^2}} \)
Xét \(f(t) = {(10 - 0,4t)^2} + {(12 - 0,3t)^2}\)
Ta có \({f^\prime }(t) = 2(10 - 0,4t)\).\(( - 0,4) + 2(12 - 0,3t)( - 0,3)\)
\( = - 8 + 0,32t - 7,2 + 0,18t\)
\( = - 15,2 + 0,5t\)
\({f^\prime }(t) = 0 \Leftrightarrow t = 30,4(s)\)
Ta có \(f(0) = 224;f(30,4) = 12,96;\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \)
Vậy \(f(x)\) đạt giá trị nhỏ nhất khi \(t = 30,4(s)\)
Khoảng cách nhỏ nhất là \({S_{\min }} = \sqrt {{{(10 - 0,4.30,4)}^2} + {{(12 - 0,3.30,4)}^2}} = 3,6\,\,({\rm{m}})\).
Câu 87:
Một quả bóng được ném theo phương ngang xác định bởi phương trình \(s = \frac{2}{3}{t^3} - \frac{5}{2}{t^2} - 3t + 2\), trong đó \(t\) tính bằng giây, \(s\) tính bằng mét. Tính gia tốc của quả bóng tại thời điểm vận tốc triệt tiêu.
 Xem đáp án
Xem đáp án
Vận tốc của quả bóng tại thời điểm \(t\) là \(v(t) = s'(t) = 2{t^2} - 5t - 3\)
Thời điểm vận tốc triệt tiêu là \(v(t) = 0 \Leftrightarrow 2{t^2} - 5t - 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = 3\,\,({\rm{tm}})\,\,\,\,\,\,\,\,}\\{t = - \frac{1}{2}\,\,({\rm{ktm}})}\end{array}} \right.\)
Phương trình gia tốc của quả bóng là \(a(t) = v'(t) = 4t - 5 \Rightarrow a(3) = 7\,\,\left( {{\rm{m}}/{{\rm{s}}^2}} \right)\)
Câu 88:
Cho tứ diện đều cạnh \(a\) và điểm \(I\) bất kì nằm trong tứ diện. Tổng khoảng cách từ \(I\) đến các mặt của tứ diện bằng
 Xem đáp án
Xem đáp án
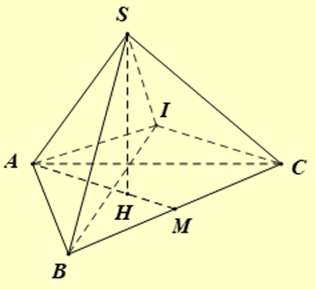
Giả sử ta có tứ diện đều như hình vẽ.
Ta có \(AH = \frac{2}{3}AM = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}.\)
\(SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {{a^2} - \frac{{{a^2}}}{3}} = \frac{{a\sqrt 6 }}{3}\).
Ta có \({V_{SABC}} = \frac{1}{3}{S_{ABC}}.SH = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{4}.\frac{{a\sqrt 6 }}{3} = \frac{{{a^3}\sqrt 2 }}{{12}}\) .
Mặt khác, \[{V_{SABC}} = {V_{ISAB}} + {V_{IABC}} + {V_{ISAC}} + {V_{ISBC}}\]
\( = \frac{1}{3}{S_{ABC}}.[d(I;(SAB)) + d(I;(ABC)) + d(I;(SAC)) + d(I;(SBC))]\)
\( \Leftrightarrow d(I;(SAB)) + d(I;(ABC)) + d(I;(SAC)) + d(I;(SBC)) = \frac{{3{V_{SABC}}}}{{{S_{ABC}}}} = \frac{{3.\frac{{{a^3}\sqrt 2 }}{{12}}}}{{\frac{{{a^2}\sqrt 3 }}{4}}} = \frac{{a\sqrt 6 }}{3}.\)
Câu 89:
Một loại nút chai rượu được sản xuất bằng cách cắt bỏ đi một góc của khúc gỗ hình trụ có chiều cao 3 cm, đường kính đáy 1,6 cm bằng một mặt phẳng như hình vẽ, biết AB = 0,8 cm. Sau đó bề mặt cắt sẽ được sơn bằng một loại sơn không độc hại. Nếu sản xuất 100 000 nút chai rượu như thế thì cần bao nhiêu lít sơn không độc hại kể trên (biết rằng 1 lít sơn được 5cm2)?
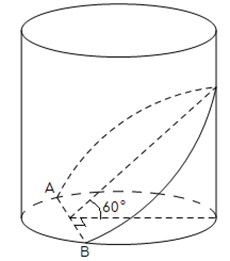
 Xem đáp án
Xem đáp án
Gọi S là diện tích mặt cắt, S′ là diện tích của hình chiếu mặt cắt xuống đáy hình trụ.
Theo công thức hình chiếu ta có: S′ = S.cos60o
Đặt mặt phẳng đáy vào hệ trục tọa độ như sau với S′ là phần hình tròn không bị gạch chéo:
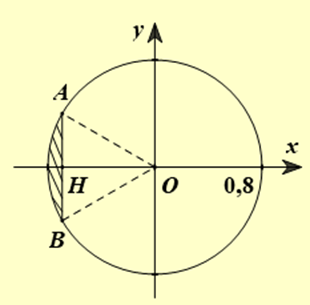
Ta có \(OA = OB = AB = 0,8 \Rightarrow \Delta ABO\) đều \( \Rightarrow OH = \frac{{0,8\sqrt 3 }}{2} = 0,4\sqrt 3 \)
Phương trình đường tròn đáy là \({x^2} + {y^2} = 0,{8^2} \Rightarrow y = \pm \sqrt {0,64 - {x^2}} \)
\( \Rightarrow S' = 2\int\limits_{0,4\sqrt 3 }^{0,8} {\sqrt {0,64 - {x^2}} } dx \approx 1,95 \Rightarrow S = \frac{{S'}}{{\cos {{60}^0}}} = 3,9\)
Tổng diện tích cần sơn cho 100 000 nút chai rượu là 3,9.100000 = 390000 (cm2) = 39 (m2)
Vậy lượng sơn cần dùng là 39 : 5 = 7,8 (l).
Câu 90:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng \({d_1}:\left\{ {\begin{array}{*{20}{l}}{x = 3 - t}\\{y = t}\\{z = 7}\end{array}} \right.\) và \({d_2}:\left\{ {\begin{array}{*{20}{l}}{x = 6 + t}\\{y = 9 - mt}\\{z = 1 - (m + 1)t}\end{array}} \right.\). Giá trị của tham số m để hai đường thẳng d1 và d2 vuông góc với nhau là
 Xem đáp án
Xem đáp án
Để \({d_1} \bot {d_2} \Leftrightarrow \overrightarrow {{u_1}} \bot \overrightarrow {{u_2}} \Leftrightarrow - 1.1 + 1.( - m) + 0.[ - (m + 1)] = 0 \Leftrightarrow m = - 1\).
Câu 91:
Cho dãy số \(\left( {{u_n}} \right):\left\{ {\begin{array}{*{20}{c}}{{u_1} = 2}\\{{u_{n + 1}} + 4{u_n} = 4 - 5n}\end{array}} \right.\) với \(n \ge 1\). Giá trị của \({u_{2023}} - 2{u_{2022}}\) bằng
 Xem đáp án
Xem đáp án
Ta có \({u_{n + 1}} + 4{u_n} = 4 - 5n \Leftrightarrow {u_{n + 1}} = - 4{u_n} - 5n + 4 \Leftrightarrow {u_{n + 1}} + n = - 4\left( {{u_n} + n - 1} \right)\,\,(*)\).
Đặt \({v_{n + 1}} = {u_{n + 1}} + n\) suy ra \({v_n} = {u_n} + n - 1\), khi đó \((*) \Leftrightarrow {v_{n + 1}} = - 4{v_n}\)
Do đó \({v_n}\) là cấp số nhân với công bội \(q = - 4 \Rightarrow {v_n} = {( - 4)^{n - 1}}{v_1}\).
Mà \({v_1} = {u_1} = 2\) nên suy ra \({v_n} = 2\).\({( - 4)^{n - 1}} \Rightarrow {u_n} = 2.{( - 4)^{n - 1}} - n + 1\).
Vậy \(S = {u_{2023}} - 2{u_{2022}} = 2.{( - 4)^{2022}} - 2022 - 2\left[ {2.{{( - 4)}^{2021}} - 2021} \right] = 2020 + {.4^{2023}}\).
Câu 92:
Một công ty du lịch đầu tư xây dựng 24 nhà chòi trong khu du lịch sinh thái. Mô hình thiết kế như hình vẽ, mái nhà có hình dạng là mặt xung quanh của hình nón với bán kính đáy là 3m và chiều cao của mái nhà là 4m. Chi phí làm mái là 2 triệu đồng/m2, chi phí làm hệ thống cột, khung nhà và nền nhà là 100 triệu đồng/nhà chòi. Công ty chỉ trả được 30% tổng chi phí xây dựng 24 nhà chòi đó. Số tiền còn thiếu, công ty phải vay ngân hàng với lãi suất 10%/năm (với thể thức lãi kép, lãi suất không thay đổi trong thời gian vay). Sau đúng 5 năm, công ty trả nợ ngân hàng cả gốc và lãi với số tiền là (làm tròn đến hàng ngàn)
 Xem đáp án
Xem đáp án
Gọi r, h, l lần lượt là bán kính đáy, chiều cao và độ dài đường sinh của mái nhà chòi.
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{r = 3\;{\rm{m}}}\\{h = 4\;{\rm{m}}}\end{array} \Rightarrow l = \sqrt {{r^2} + {h^2}} = \sqrt {{3^2} + {4^2}} = 5\;{\rm{m}}} \right.{\rm{.}}\)
\( \Rightarrow \) Diện tích xung quanh của mái một nhà chòi là \({S_{xq}} = \pi rl = \pi .3.5 = 15\pi \,\,\left( {{{\rm{m}}^2}} \right)\).
\( \Rightarrow \) Tổng chi phí xây dựng 24 căn nhà chòi là
\(P = 24.\left( {2.{S_{xq}} + 100} \right){.10^6} = 24.(2.15\pi + 100){.10^6} = (72\pi + 240){.10^7}\) (đồng).
\( \Rightarrow \) Số tiền công ty còn thiếu là \({A_0} = 70\% .P = (504\pi + 1680){.10^6}\) (đồng).
Sau năm thứ nhất, số tiền công ty nợ ngân hàng là
\({S_1} = {A_0} + {A_0}.10\% = {A_0}(1 + 10\% )\)
Sau năm thứ hai, số tiền công ty nợ ngân hàng là
\({S_2} = {S_1} + {S_1}.10\% = {S_1}(1 + 10\% ) = {A_0}(1 + 10\% )(1 + 10\% ) = {A_0}{(1 + 10\% )^2}{\rm{. }}\)
...
Sau 5 năm, số tiền công ty phải trả nợ ngân hàng cả gốc lẫn lãi là
\({S_5} = {A_0}{(1 + 10\% )^5} = (504\pi + 1680).{(1 + 10\% )^5}{.10^6} \approx 5255678000\) (đồng).
Câu 93:
Phương trình \({\log _2}\left( {{3^{{{\log }_6}x}} + x} \right) = \frac{1}{2}{\log _6}{x^2}\) có bao nhiêu nghiệm?
 Xem đáp án
Xem đáp án
Điều kiện \(x > 0\).
\({\log _2}\left( {{3^{{{\log }_6}x}} + x} \right) = \frac{1}{2}{\log _6}{x^2}\)
\( \Leftrightarrow {\log _2}\left( {{3^{{{\log }_6}x}} + x} \right) = {\log _6}x.\)
Đặt \(t = {\log _6}x \Rightarrow x = {6^t}\) ta được phương trình
\({\log _2}\left( {{3^t} + {6^t}} \right) = t \Leftrightarrow {3^t} + {6^t} = {2^t} \Leftrightarrow {\left( {\frac{3}{2}} \right)^t} + {3^t} = 1\,\,\,\left( * \right)\).
Xét hàm số \(f(t) = {\left( {\frac{3}{2}} \right)^t} + {3^t}\)
\({f^\prime }(t) = {\left( {\frac{3}{2}} \right)^t}\ln \frac{3}{2} + {3^t}\ln 3 > 0\,\,\forall t \in \mathbb{R} \Rightarrow f(t)\) đồng biến trên \(\mathbb{R}\)
Phương trình \((*)\) trở thành \(f(t) = f( - 1)\) mà \(f(t)\) đồng biến trên \(\mathbb{R}\) nên \((*)\) có nghiệm duy nhất \(t = - 1\).
Suy ra phương trình đã cho có nghiệm \(x = {6^{ - 1}} = \frac{1}{6}\).
Câu 94:
Với số nguyên dương \(n\), gọi \({a_{3n - 3}}\) là hệ số của \({x^{3n - 3}}\) trong khai triển thành đa thức của \({\left( {{x^2} + 1} \right)^n}{(x + 2)^n}\). Tìm \(n\) để \({a_{3n - 3}} = 26n\).
 Xem đáp án
Xem đáp án
Ta có:
\({\left( {{x^2} + 1} \right)^n} = C_n^0{x^{2n}} + C_n^1{x^{2n - 2}} + C_n^2{x^{2n - 4}} + \ldots + C_n^n\)
\({(x + 2)^n} = C_n^0{x^n} + 2C_n^1{x^{n - 1}} + {2^2}C_n^2{x^{n - 2}} + \ldots + {2^n}C_n^n\)
Ta thấy \[n = 1,n = 2\] không thoả mãn điều kiện bài toán.
Với \(n \ge 3\) ta có: \({x^{3n - 3}} = {x^{2n}}.{x^{n - 3}} = {x^{2n - 2}}.{x^{n - 1}}\)
Do đó hệ số của \({x^{3n - 3}}\) trong khai triển thành đa thức của \({\left( {{x^2} + 1} \right)^n}{(x + 2)^n}\).
\({a_{3n - 3}} = {2^3}.C_n^0.C_n^3 + 2.C_n^1.C_n^1\).
\( \Rightarrow {a_{3n - 3}} = 26n \Leftrightarrow \frac{{2n\left( {2{n^2} - 3n + 4} \right)}}{3} = 26n \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{n = 0\,\,(L)\,\,\,\,\,}\\{n = - \frac{7}{2}\,\,(L).}\\{n = 5\,\,(t/m)}\end{array}} \right.\)
Vậy n = 5 là giá trị cần tìm.Câu 95:
Cho hàm số \(y = f(x)\) xác định trên \(\mathbb{R}\backslash \{ - 1;2\} \), liên tục trên các khoảng xác định của nó và có bảng biến thiên như sau:
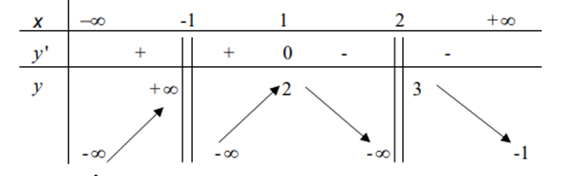
Chọn các khẳng định đúng.
Đồ thị hàm số \(y = \frac{1}{{f(x) - 2}}\) có
o 3 đường tiệm cận ngang.
o 5 đường tiệm cận.
o 2 đường tiệm cận ngang.
o 2 đường tiệm cận đứng.
 Xem đáp án
Xem đáp án
5 đường tiệm cận. - ĐÚNG
2 đường tiệm cận ngang. - ĐÚNG
Giải thích
Dựa vào bảng biến thiên, phương trình \(f(x) - 2 = 0\) (hay \(f(x) = 2\)) có 3 nghiệm \({x_1},{x_2},{x_3}\) thỏa \({x_1} \in ( - \infty ; - 1),{x_2} = 1,{x_3} \in (2; + \infty )\). Suy ra đồ thị hàm số \(y = \frac{1}{{f(x) - 2}}\) có 3 tiệm cận đứng là \(x = {x_1},\,\,x = {x_2},\,\,x = {x_3}\).
Vì \(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{f(x) - 2}} = 0\) nên \(y = 0\) là tiệm cận ngang của đồ thị hàm số \(y = \frac{1}{{f(x) - 2}}\).
Vì \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{f(x) - 2}} = \frac{{ - 1}}{3}\) nên \(y = \frac{{ - 1}}{3}\) là tiệm cận ngang của đồ thị hàm số \(y = \frac{1}{{f(x) - 2}}\).
Do đó đồ thị hàm số \(y = \frac{1}{{f(x) - 2}}\) có 2 tiệm cận ngang là \(y = 0,y = \frac{{ - 1}}{3}\).
Vậy tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y = \frac{1}{{f(x) - 2}}\) là 5.
Câu 96:
Cho số phức \(z\) thỏa mãn \(|z - 6| + |z + 6| = 20\). Gọi M, n lần lượt là môđun lớn nhất và nhỏ nhất của z. Tính \(M - n\).
 Xem đáp án
Xem đáp án
Gọi \(z = x + yi\,\,(x,y \in \mathbb{R})\). Theo giả thiết, ta có \(|z - 6| + |z + 6| = 20\).
\( \Leftrightarrow |x - 6 + yi| + |x + 6 + yi| = 20 \Leftrightarrow \sqrt {{{(x - 6)}^2} + {y^2}} + \sqrt {{{(x + 6)}^2} + {y^2}} = 20\,\,{\rm{ (*)}}{\rm{. }}\)
Gọi \(M(x;y),\,\,{F_1}(6;0)\) và \({F_2}( - 6;0)\).
Khi đó \((*) \Leftrightarrow M{F_1} + M{F_2} = 20 > {F_1}{F_2} = 12\) nên tập hợp các điểm \(M\) là đường elip \((E)\) có hai tiêu điểm \({F_1}\) và \({F_2}\). Và độ dài trục lớn bằng 20 .
Ta có: \(c = 6;\,\,2a = 20 \Leftrightarrow a = 10{\rm{ v\`a }}{b^2} = {a^2} - {c^2} = 64 \Rightarrow b = 8.{\rm{ }}\)
Do đó, phương trình chính tắc của \((E)\) là \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\).
Suy ra \(max|z| = OA = OA' = 10\) khi \(z = \pm 10\) và \(min|z| = OB = OB' = 8\) khi \(z = \pm 8i\).
Vậy \(M - n = 2\).
Câu 97:
Một cốc nước dạng hình trụ có chiều cao 15 cm, đường kính đáy 4 cm, lượng nước trong cốc cao 10 cm. Thả vào cốc nước 3 viên đá hình cầu có đường kính 2 cm. (Bỏ qua độ dày của cốc).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Nước trong cốc dâng thêm _______ cm.
Nước dâng cao cách mép cốc _______ cm.
 Xem đáp án
Xem đáp án
Một cốc nước dạng hình trụ có chiều cao 15 cm, đường kính đáy 4 cm, lượng nước trong cốc cao 10 cm. Thả vào cốc nước 3 viên đá hình cầu có đường kính 2 cm. (Bỏ qua độ dày của cốc).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
Nước trong cốc dâng thêm 1 cm.
Nước dâng cao cách mép cốc 4 cm.
Giải thích
Lượng nước dâng lên chính là tổng thể tích của 3 viên đá thả vào và bằng \({V_b} = 3.\frac{4}{3}\pi {r_b}^3 = 4\pi \,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
Ta có phần nước dâng lên là khối trụ có đáy bằng với đáy cốc nước và thể tích là \(4\pi \,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Chiều cao của phần nước dâng lên là \({h_d}\) thỏa mãn: \(4\pi = \pi {r^2}{h_d} \Leftrightarrow {h_d} = 1\,\,({\rm{cm}}).\)
Vậy nước dâng cao cách mép cốc là 15 − 10 − 1 = 4 (cm).
Câu 98:
Bà chủ quán trà sữa X muốn trang trí quán cho đẹp nên quyết định thuê nhân công xây một bức tường bằng gạch với xi măng (như hình vẽ bên dưới), biết hàng dưới cùng có 500 viên, mỗi hàng tiếp theo đều có ít hơn hàng trước 1 viên và hàng trên cùng có 1 viên. Hỏi số gạch cần dùng để hoàn thành bức tường trên là bao nhiêu viên?
 Xem đáp án
Xem đáp án
Ta có số gạch ở mỗi hàng là các số hạng của 1 cấp số cộng: 500, 499, 498,…, 2, 1.
⇒ Tổng số gạch cần dùng là tổng của cấp số cộng trên và bằng
\({S_{500}} = \frac{{500(500 + 1)}}{2} = 250.501 = 125250\) (viên).
Câu 99:
Cho khối lăng trụ đứng \(ABC.{A^\prime }{B^\prime }{C^\prime }\) có \(B{B^\prime } = a\), đáy ABC là tam giác vuông cân tại \(B\) và \(AC = a\sqrt 2 \). Tính thể tích \(V\) của khối lăng trụ đã cho.
 Xem đáp án
Xem đáp án
Ta có: \(A{C^2} = B{A^2} + B{C^2} \Leftrightarrow 2{a^2} = 2A{B^2} \Leftrightarrow A{B^2} = {a^2}\) .
\( \Rightarrow {V_{ABC.A'B'C'}} = BB'.{S_{\Delta ABC}} = a.\frac{1}{2}.{a^2} = \frac{{{a^3}}}{2}\).