33 câu hỏi trắc nghiệm thuộc Phương trình lượng giác thường gặp

Câu 1:

\sin 2 x + 3 \sin 4 x = 0

có nghiệm là:

A. $[\begin{matrix} x = \frac{k π}{2} \\ x = \pm \frac{1}{2} \arccos (- \frac{1}{6}) + k π \end{matrix} (k \in Z)$

B. $[\begin{matrix} x = \frac{k π}{2} \\ x = \pm \frac{5}{2} \arccos (- \frac{1}{6}) + k π \end{matrix} (k \in Z)$

C. $[\begin{matrix} x = \frac{k π}{2} \\ x = \pm \frac{1}{2} \arccos (- \frac{1}{3}) + k π \end{matrix} (k \in Z)$

D. $[\begin{matrix} x = \frac{k π}{2} \\ x = \pm \frac{1}{3} \arccos (- \frac{1}{6}) + k π \end{matrix} (k \in Z)$

Xem đáp án

$\sin 2 x + 3 \sin 4 x = 0$

$\Leftrightarrow \sin 2 x + 6 \sin 2 x \cos 2 x = 0$

$\Leftrightarrow \sin 2 x (1 + 6 \cos 2 x) = 0$

$\Leftrightarrow [\begin{matrix} \sin 2 x = 0 \\ 1 + 6 \cos 2 x = 0 \end{matrix}$

$\Leftrightarrow [\begin{matrix} \sin 2 x = 0 \\ \cos 2 x = - \frac{1}{6} \end{matrix}$

$\Leftrightarrow [\begin{matrix} 2 x = k π \\ 2 x = \pm \arccos (- \frac{1}{6}) + k 2 π \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = \frac{k π}{2} \\ x = \pm \frac{1}{2} \arccos (- \frac{1}{6}) + k π \end{matrix} (k \in Z)$

Đáp án cần chọn là: A

Câu 2:

Phương trình $\frac{\cos 2 x}{1 - \sin 2 x} = 0$ có nghiệm là:

A. $x = \frac{π}{4} + k π (k \in Z)$

B. $x = \frac{π}{4} + \frac{k π}{2} (k \in Z)$

C. $x = \frac{3 π}{4} + 2 k π (k \in Z)$

D. $x = \frac{3 π}{4} + k π (k \in Z)$

Xem đáp án

Bước 1:

Điều kiện: $1 - \sin 2 x \neq 0$

$\Leftrightarrow \sin 2 x \neq 1$

$\Leftrightarrow 2 x \neq \frac{π}{2} + k 2 π$

$\Leftrightarrow x \neq \frac{π}{4} + k π (k \in Z)$

Bước 2:

$\frac{\cos 2 x}{1 - \sin 2 x} = 0$

$\Leftrightarrow \cos 2 x = 0$

$\Leftrightarrow \cos^{2} 2 x = 0$

$\Leftrightarrow 1 - s i n^{2} 2 x = 0$

$\Leftrightarrow s i n^{2} 2 x = 1$

$\Leftrightarrow s i n 2 x = - 1 (d o \sin 2 x \neq 1)$

$\Leftrightarrow 2 x = - \frac{π}{2} + k 2 π$

$\Leftrightarrow x = - \frac{π}{4} + k π$

Đặt k = l + 1 ta được:

$- \frac{π}{4} + k π = - \frac{π}{4} + l π + π = \frac{3 π}{4} + l π (l \in Z)$

Vậy $[\begin{matrix} x = \frac{3 π}{4} + l π (l \in Z) \\ x = \frac{3 π}{4} + k π (k \in Z) \end{matrix}$

Đáp án cần chọn là: D

Câu 3:

Phương trình $\sqrt{3} \cot^{2} x - 4 \cot x + \sqrt{3} = 0$ có nghiệm là:

A. $[\begin{matrix} x = \frac{π}{3} + k π \\ x = \frac{π}{6} + k π \end{matrix} (k \in Z)$

B. $[\begin{matrix} x = \frac{π}{3} + k 2 π \\ x = \frac{π}{6} + k 2 π \end{matrix} (k \in Z)$

C. $[\begin{matrix} x = - \frac{π}{3} + k π \\ x = - \frac{π}{6} + k π \end{matrix} (k \in Z)$

D. $[\begin{matrix} x = - \frac{π}{3} + k 2 π \\ x = \frac{π}{6} + k π \end{matrix} (k \in Z)$

Xem đáp án

ĐK: $\sin x \neq 0 \Leftrightarrow x \neq k π (k \in Z)$

$\sqrt{3} \cot^{2} x - 4 \cot x + \sqrt{3} = 0$

Đặt cos x = t khi đó phương trình có dạng:

$\sqrt{3} t^{2} - 4 t + \sqrt{3} = 0$

$\Leftrightarrow [\begin{matrix} t = \frac{1}{\sqrt{3}} \\ t = \sqrt{3} \end{matrix}$

$\Rightarrow [\begin{matrix} \cot x = \frac{1}{\sqrt{3}} \\ \cot x = \sqrt{3} \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = \frac{π}{3} + k π \\ x = \frac{π}{6} + k π \end{matrix} (k \in Z) (t m)$

Đáp án cần chọn là: A

Câu 4:

Nghiệm của phương trình $4 \sin^{2} 2 x + 8 \cos^{2} x - 9 = 0$ là:

A. $x = \pm \frac{π}{6} + k π (k \in Z)$

B. $x = \pm \frac{π}{6} + k 2 π (k \in Z)$

C. $x = \pm \frac{π}{3} + k π (k \in Z)$

D. $[\begin{matrix} x = \frac{π}{6} + k π (k \in Z) \\ x = \frac{π}{3} + k π (k \in Z) \end{matrix}$

Xem đáp án

Bước 1:

$4 \sin^{2} 2 x + 8 \cos^{2} x - 9 = 0$

$\Leftrightarrow 4 (1 - \cos^{2} 2 x) + 8. \frac{1 + \cos 2 x}{2} - 9 = 0$

$\Leftrightarrow 4 (1 - \cos^{2} 2 x) + 4. (1 + \cos 2 x) - 9 = 0$

$\Leftrightarrow 4 (1 - \cos^{2} 2 x) + 4 + 4 \cos 2 x - 9 = 0$

$\Leftrightarrow 4 - 4 \cos^{2} 2 x + 4 \cos 2 x - 5 = 0$

$\Leftrightarrow - 4 \cos^{2} 2 x + 4 \cos 2 x - 1 = 0$

Bước 2:

Đặt $\cos 2 x = t (- 1 \leq t \leq 1)$ . Khi đó phương trình có dạng:

$- 4 t^{2} + 4 t - 1 = 0$

$\Leftrightarrow - (4 t^{2} - 4 t + 1) = 0$

$\Leftrightarrow - {(2 t - 1)}^{2} = 0$

$\Leftrightarrow t = \frac{1}{2} (t m)$

$\Leftrightarrow \cos 2 x = \frac{1}{2}$

$\Leftrightarrow \cos 2 x = \cos \frac{π}{3}$

$\Leftrightarrow 2 x = \pm \frac{π}{3} + k 2 π$

$\Leftrightarrow x = \pm \frac{π}{6} + k π (k \in Z)$

Đáp án cần chọn là: A

Câu 5:

Số vị trí biểu diễn các nghiệm của phương trình 4sin² x − 4sinx – 3 = 0 trên đường tròn lượng giác là:

A. 0

B. 1

C. 2

D. 4

Xem đáp án

4sin² x − 4sinx – 3 = 0

Đặt sinx = t (−1 ≤ t ≤ 1) khi đó phương trình có dạng:

$4 t^{2} - 4 t - 3 = 0$

$\Leftrightarrow [\begin{matrix} t = \frac{3}{2} (k t m) \\ t = - \frac{1}{2} (t m) \end{matrix}$

$t = - \frac{1}{2} \Leftrightarrow \sin x = - \frac{1}{2}$

$\Leftrightarrow [\begin{matrix} x = - \frac{π}{6} + k 2 π \\ x = \frac{7 π}{6} + k 2 π \end{matrix} (k \in Z)$

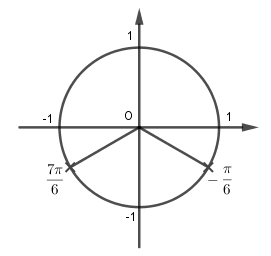
Vây số vị trí biểu diễn các nghiệm của phương trình 4sin² x − 4sinx – 3 = 0 trên đường tròn lượng giác là 2 điểm như hình trên.

Đáp án cần chọn là: C

Câu 6:

Phương trình

\sqrt{3} \sin 2 x - \cos 2 x + 1 = 0

có nghiệm là:

A. $[\begin{matrix} x = k π \\ x = \frac{π}{3} + k π \end{matrix} (k \in Z)$

B. $[\begin{matrix} x = k π \\ x = \frac{2 π}{3} + k 2 π \end{matrix} (k \in Z)$

C. $[\begin{matrix} x = k 2 π \\ x = \frac{2 π}{3} + k 2 π \end{matrix} (k \in Z)$

D. $[\begin{matrix} x = k π \\ x = \frac{2 π}{3} + k π \end{matrix} (k \in Z)$

Xem đáp án

$\sqrt{3} \sin 2 x - \cos 2 x + 1 = 0$

$\Leftrightarrow \frac{\sqrt{3}}{2} \sin 2 x - \frac{1}{2} \cos 2 x + \frac{1}{2} = 0$

$\Leftrightarrow \sin 2 x . \cos \frac{π}{6} - \cos 2 x . \sin \frac{π}{6} + \frac{1}{2} = - \frac{1}{2}$

$\Leftrightarrow \sin (2 x - \frac{π}{6}) - \sin (- \frac{π}{6})$

$\Leftrightarrow [\begin{matrix} 2 x - \frac{π}{6} = - \frac{π}{6} + k 2 π \\ 2 x - \frac{π}{6} = \frac{7 π}{6} + k 2 π \end{matrix}$

$\Leftrightarrow [\begin{matrix} 2 x = k 2 π \\ 2 x = \frac{4 π}{3} + k 2 π \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = k π \\ x = \frac{2 π}{3} + k π \end{matrix} (k \in Z)$

Đáp án cần chọn là: D

Câu 7:

Phương trình $\sin x + \sqrt{3} \cos x = \sqrt{2}$ có hai họ nghiệm có dạng $x = α + k 2 π, x = β + k 2 π, (- \frac{π}{2} < α < β < \frac{π}{2})$ . Khi đó α, β là:

A. $- \frac{5 π^{2}}{12}$

B. $- \frac{5 π^{2}}{144}$

C. $\frac{5 π^{2}}{144}$

D. $\frac{π^{2}}{12}$

Xem đáp án

Bước 1:

$\sin x + \sqrt{3} \cos x = \sqrt{2}$

$\Leftrightarrow \frac{1}{2} \sin x + \frac{\sqrt{3}}{2} \cos x = \frac{\sqrt{2}}{2}$

$\Leftrightarrow \sin x \cos \frac{π}{3} + \cos x \sin \frac{π}{3} = \frac{\sqrt{2}}{2}$

$\Leftrightarrow \sin (x + \frac{π}{3}) = \sin \frac{π}{4}$

Bước 2:

$\Leftrightarrow [\begin{matrix} x + \frac{π}{3} = \frac{π}{4} + k 2 π \\ x + \frac{π}{3} = \frac{3 π}{4} + k 2 π \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = - \frac{π}{12} + k 2 π \\ x = \frac{5 π}{12} + k 2 π \end{matrix} (k \in Z)$

$\Rightarrow [\begin{matrix} α = - \frac{π}{12} \\ β = \frac{5 π}{12} \end{matrix}$

( Vì $- \frac{π}{12}$ và $\frac{5 π}{12}$ đều thỏa mãn điều kiện đề bài)

$\Rightarrow α . β = \frac{- 5 π^{2}}{144}$

Đáp án cần chọn là: B

Câu 8:

Giải phương trình

\sin 18 x \cos 13 x = \sin 9 x \cos 4 x

A. $x = \frac{k π}{18}; x = \frac{k π}{22} (k \in Z)$

B. $x = \frac{k π}{9}; x = \frac{π}{44} + \frac{k π}{22} (k \in Z)$

C. $x = \frac{π}{3} + \frac{k π}{18}; x = \frac{π}{22} + \frac{k π}{22} (k \in Z)$

D. $x = \frac{k π}{3}; x = \frac{π}{44} + \frac{k π}{44} (k \in Z)$

Xem đáp án

$\sin 18 x \cos 13 x = \sin 9 x \cos 4 x$

$\Leftrightarrow \frac{1}{2} (\sin 31 x + \sin 5 x) = \frac{1}{2} (\sin 13 x + \sin 5 x)$

$\Leftrightarrow \sin 31 x + \sin 5 x = \sin 13 x + \sin 5 x$

$\Leftrightarrow \sin 31 x = \sin 13 x$

$\Leftrightarrow [\begin{matrix} 31 x = 13 x + k 2 π \\ 31 x = π - 13 x + k 2 π \end{matrix}$

$\Leftrightarrow [\begin{matrix} 18 x = k 2 π \\ 44 x = π + k 2 π \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = \frac{k π}{9} \\ x = \frac{π}{44} + \frac{k π}{22} \end{matrix} (k \in Z)$

Vậy nghiệm của phương trình là:

$x = \frac{k π}{9}; x = \frac{π}{44} + \frac{k π}{22} (k \in Z)$

Đáp án cần chọn là: B

Câu 9:

Để phương trình $\frac{a^{2}}{1 - \tan^{2} x} = \frac{\sin^{2} x + a^{2} - 2}{\cos 2 x}$ có nghiệm, tham số a thỏa mãn điều kiện:

A. $|a| \geq 1$

B. $|a| > 1$

C. $|a| = 1$

D. $|a| \neq 1$

Xem đáp án

Điều kiện: $\{\begin{matrix} 1 - \tan^{2} x \neq 0 \\ \cos 2 x \neq 0 \\ \cos x \neq 0 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} \frac{\cos^{2} x - \sin^{2} x}{\cos^{2} x} \neq 0 \\ \cos 2 x \neq 0 \\ \cos x \neq 0 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} \cos 2 x \neq 0 \\ \cos x \neq 0 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} 2 x \neq \frac{π}{2} + k π \\ x \neq \frac{π}{2} + k π \end{matrix}$

$\Leftrightarrow \{\begin{matrix} x \neq \frac{π}{4} + \frac{k π}{2} \\ x \neq \frac{π}{2} + k π \end{matrix} (k \in Z)$

Ta có: $\frac{a^{2}}{1 - \tan^{2} x} = \frac{\sin^{2} x + a^{2} - 2}{\cos 2 x}$

$\Leftrightarrow \frac{a^{2}}{\frac{\cos^{2} x - \sin^{2} x}{\cos^{2} x}} = \frac{\sin^{2} x + a^{2} - 2}{\cos 2 x}$

$\Leftrightarrow \frac{a^{2} \cos^{2} x}{\cos 2 x} = \frac{\sin^{2} x + a^{2} - 2}{\cos 2 x}$

$\Leftrightarrow a^{2} \cos^{2} x = \sin^{2} x + a^{2} - 2$

$\Leftrightarrow a^{2} \cos^{2} x = 1 - \cos^{2} x + a^{2} - 2$

$\Leftrightarrow (a^{2} + 1) \cos^{2} x = a^{2} - 1$

$\Leftrightarrow \cos^{2} x = \frac{a^{2} - 1}{a^{2} + 1} < 1$

Vì: $\cos x \neq 0$

$\Rightarrow 0 < \cos^{2} x \leq 1$

$\Leftrightarrow \cos^{2} x > 0$

$\Leftrightarrow a^{2} - 1 > 0$

$\Rightarrow |a > 1|$

Đáp án cần chọn là: B

Câu 10:

Giải hệ phương trình $\{\begin{matrix} x - y = \frac{π}{3} \\ \cos x - \cos y = - 1 \end{matrix}$

A. $\{\begin{matrix} x = \frac{π}{6} + k 2 π \\ y = - \frac{π}{6} + k 2 π \end{matrix} (k \in Z)$

B. $\{\begin{matrix} x = \frac{2 π}{3} + k 2 π \\ y = \frac{π}{3} - k 2 π \end{matrix} (k \in Z)$

C. $\{\begin{matrix} x = \frac{2 π}{3} + k 2 π \\ y = \frac{π}{3} + k 2 π \end{matrix} (k \in Z)$

D. $\{\begin{matrix} x = \frac{π}{2} + k 2 π \\ y = \frac{π}{6} + k 2 π \end{matrix} (k \in Z)$

Xem đáp án

Bước 1:

$\{\begin{matrix} x - y = \frac{π}{3} \\ \cos x - \cos y = - 1 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} x = y + \frac{π}{3} \\ \cos (y + \frac{π}{3}) - \cos y = - 1 (*) \end{matrix}$

Bước 2:

$(*) \Leftrightarrow - 2 \sin (y + \frac{π}{6}) . \sin \frac{π}{6} = - 1$

$\Leftrightarrow - 2 \sin (y + \frac{π}{6}) . \frac{1}{2} = - 1$

$\Leftrightarrow \sin (y + \frac{π}{6}) = 1$

Bước 3:

$\Leftrightarrow y + \frac{π}{6} = \frac{π}{2} + k 2 π$

$\Leftrightarrow y = \frac{π}{3} + k 2 π (k \in Z)$
$\Rightarrow x = y + \frac{π}{3} = \frac{2 π}{3} + k 2 π (k \in Z)$

Vậy nghiệm của hệ phương trình là:

$(x; y) = (\frac{2 π}{3} + k 2 π; \frac{π}{3} + k 2 π) (k \in Z)$

Đáp án cần chọn là: C

Câu 11:

Phương trình

\sin^{2} 3 x + (m^{2} - 3) \sin 3 x + m^{2} - 4 = 0

khi m = 1 có nghiệm là:

A. $x = - \frac{π}{6} + k 2 π (k \in Z)$

B. $x = \frac{π}{6} + \frac{k 2 π}{3} (k \in Z)$

C. $x = - \frac{π}{6} + \frac{k 2 π}{3} (k \in Z)$

D. $x = \pm \frac{π}{6} + \frac{k 2 π}{3} (k \in Z)$

Xem đáp án

Khi m = 1 phương trình có dạng:

$\sin^{2} 3 x - 2 \sin 3 x + - 3 = 0$

Đặt $\sin 3 x = t (- 1 \leq t \leq 1)$ khi đó phương trình có dạng:

$t^{2} - 2 t - 3 = 0$

$\Leftrightarrow [\begin{matrix} t = - 1 (t m) \\ t = 3 (k t m) \end{matrix}$

$t = - 1 \Leftrightarrow \sin 3 x = - 1$

$\Leftrightarrow 3 x = - \frac{π}{2} + k 2 π$

$\Leftrightarrow x = - \frac{π}{6} + \frac{k 2 π}{3} (k \in Z)$

Đáp án cần chọn là: C

Câu 12:

Khẳng định nào đúng về phương trình

2 \sqrt{2} (\sin x + \cos x) \cos x = 3 + \cos 2 x

A. Có 1 họ nghiệm

B. Có 2 họ nghiệm

C. Vô nghiệm

D. Có 1 nghiệm duy nhất

Xem đáp án

$2 \sqrt{2} (\sin x + \cos x) \cos x = 3 + \cos 2 x$

$\Leftrightarrow 2 \sqrt{2} \sin x \cos x + 2 \sqrt{2} \cos^{2} x = 3 + \cos 2 x$

$\Leftrightarrow \sqrt{2} \sin x + \sqrt{2} (1 + \cos 2 x) = 3 + \cos 2 x$

$\Leftrightarrow \sqrt{2} \sin x + (\sqrt{2} - 1) \cos 2 x = 3 - \sqrt{2}$

Ta có: $\{\begin{matrix} a = \sqrt{2} \\ b = \sqrt{2} - 1 \\ c = 3 - \sqrt{2} \end{matrix}$

$\Rightarrow a^{2} + b^{2} - c^{2} = 2 + {(\sqrt{2} - 1)}^{2} - {(3 - \sqrt{2})}^{2}$

$\Rightarrow a^{2} + b^{2} - c^{2} = 2 + 3 - 2 \sqrt{2} - 11 + 6 \sqrt{2}$

$\Rightarrow a^{2} + b^{2} - c^{2} = - 6 + 4 \sqrt{2}$

$\Rightarrow a^{2} + b^{2} - c^{2} < 0$

$\Rightarrow a^{2} + b^{2} < c^{2}$

Vậy phương trình vô nghiệm

Đáp án cần chọn là: C

Câu 13:

Số vị trí biểu diễn nghiệm của phương trình $\sin x + (\sqrt{3} - 2) \cos x = 1$ trên đường tròn lượng giác là:

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Bước 1:

Với $a = 1; b = \sqrt{3} - 2; c = 1$ ta có:

$\sin x + (\sqrt{3} - 2) \cos x = 1$

$\Leftrightarrow \frac{1}{\sqrt{8 - 4 \sqrt{3}}} \sin x + \frac{\sqrt{3} - 2}{\sqrt{8 - 4 \sqrt{3}}} \cos x = \frac{1}{\sqrt{8 - 4 \sqrt{3}}}$

Đặt $\frac{1}{\sqrt{8 - 4 \sqrt{3}}} = \cos α$

$\Rightarrow \frac{\sqrt{3} - 2}{\sqrt{8 - 4 \sqrt{3}}} = \sin α$

Khi đó phương trình tương đương:

$\sin x \cos α + \cos x \sin α = \cos α$

Bước 2:

$\Leftrightarrow \sin (x + α) = \sin (\frac{π}{2} - α)$

$\Leftrightarrow [\begin{matrix} x + α = \frac{π}{2} - α + k 2 π \\ x + α = \frac{π}{2} + α + k 2 π \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = \frac{π}{2} - 2 α + k 2 π \\ x = \frac{π}{2} + k 2 π \end{matrix}$

Vì $α \neq 0 \Rightarrow$ có 2 vị trí biểu diễn nghiệm của phương trình.

Đáp án cần chọn là: C

Câu 14:

Tổng các nghiệm thuộc đoạn $[0; \frac{π}{2}]$ của phương trình $2 \sqrt{3} \cos^{2} \frac{5 x}{2} + \sin 5 x = 1 + \sqrt{3}$ là:

A. $\frac{3 π}{5}$

B. $\frac{29 π}{30}$

C. $\frac{5 π}{6}$

D. $\frac{23 π}{30}$

Xem đáp án

$2 \sqrt{3} \cos^{2} \frac{5 x}{2} + \sin 5 x = 1 + \sqrt{3}$

$\Leftrightarrow \sqrt{3} (1 + \cos 5 x) + \sin 5 x = 1 + \sqrt{3}$

$\Leftrightarrow \sin 5 x + \sqrt{3} \cos 5 x = 1$

$\Leftrightarrow \frac{1}{2} \sin 5 x + \frac{\sqrt{3}}{2} \cos 5 x = \frac{1}{2}$

$\Leftrightarrow \sin 5 x \cos \frac{π}{3} + \cos 5 x \sin \frac{π}{3} = \frac{1}{2}$

$\Leftrightarrow \sin (5 x + \frac{π}{3}) = \sin \frac{π}{6}$

$\Leftrightarrow [\begin{matrix} 5 x + \frac{π}{3} = \frac{π}{6} + k 2 π \\ 5 x + \frac{π}{3} = \frac{5 π}{6} + k 2 π \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = - \frac{π}{30} + \frac{k 2 π}{5} \\ x = \frac{π}{10} + \frac{k 2 π}{5} \end{matrix} (k \in Z)$

Với họ nghiệm $x = - \frac{π}{30} + \frac{k 2 π}{5} (k \in Z)$ , ta được:

$0 \leq - \frac{π}{30} + \frac{k 2 π}{5} \leq \frac{π}{2}$

$\Leftrightarrow 0 \leq - \frac{1}{30} + \frac{2 k}{5} \leq \frac{1}{2}$

$\Leftrightarrow \{\begin{matrix} \frac{1}{12} \leq k \leq \frac{4}{3} \\ k \in Z \end{matrix}$

$\Rightarrow k = 1$

$\Rightarrow x = - \frac{π}{30} + \frac{2 π}{5} = \frac{11 π}{30}$

Với họ nghiệm $x = \frac{π}{10} + \frac{k 2 π}{5} (k \in Z)$ , ta được:

$0 \leq - \frac{π}{10} + \frac{k 2 π}{5} \leq \frac{π}{2}$

$\Leftrightarrow 0 \leq \frac{1}{10} + \frac{2 k}{5} \leq \frac{1}{2}$

$\Leftrightarrow \{\begin{matrix} - \frac{1}{4} \leq k \leq 1 \\ k \in Z \end{matrix}$

$\Rightarrow \{\begin{matrix} k = 0 \\ k = 1 \end{matrix}$

$\Rightarrow \{\begin{matrix} x = \frac{π}{10} \\ x = \frac{π}{10} + \frac{2 π}{5} = \frac{π}{2} \end{matrix}$

Vậy tổng các nghiệm thuộc đoạn $[0; \frac{π}{2}]$ là:

$\frac{11 π}{30} + \frac{π}{10} + \frac{π}{2} = \frac{29 π}{30}$

Đáp án cần chọn là: B

Câu 15:

Phương trình

\sin^{3} x + \cos^{3} x = \sin x - \cos x

có nghiệm là:

A. $x = k π (k \in Z)$

B. $x = \frac{π}{2} + k π (k \in Z)$

C. $x = \frac{π}{6} + k 2 π (k \in Z)$

D. Tất cả đều đúng

Xem đáp án

Bước 1:

$\sin^{3} x + \cos^{3} x = \sin x - \cos x$

$\Leftrightarrow \cos^{3} x + \cos x = \sin x - \sin^{3} x$

$\Leftrightarrow \cos x (\cos^{2} x + 1) = \sin x (1 - \sin^{2} x)$

$\Leftrightarrow \cos x (\frac{1 + \cos 2 x}{2} + 1) = \sin x . \cos^{2} x$

$\Leftrightarrow \cos x (\frac{1 + \cos 2 x}{2} + 1 - \sin x \cos x) = 0$

$\Leftrightarrow \cos x . \frac{1 + \cos 2 x + 2 - \sin 2 x}{2} = 0$

$\Leftrightarrow \cos x . (1 + \cos 2 x + 2 - \sin 2 x) = 0$

$\Leftrightarrow \cos x . (- \sin 2 x + \cos 2 x + 3) = 0$

$\Leftrightarrow [\begin{matrix} \cos x = 0 (1) \\ - \sin 2 x + \cos 2 x + 3 = 0 (2) \end{matrix}$

Bước 2:

$(1) \Leftrightarrow x = \frac{π}{2} + k π (k \in Z)$

Xét (2) ta có: $\{\begin{matrix} a = - 1 \\ b = 1 \\ c = - 3 \end{matrix} \Rightarrow a^{2} + b^{2} < c^{2}$

⇒ phương trình (2) vô nghiệm.

Vậy nghiệm của phương trình là: $\Rightarrow x = \frac{π}{2} + k π (k \in Z)$

Đáp án cần chọn là: B

Câu 16:

Phương trình

6 \sin^{2} x + 7 \sqrt{3} \sin 2 x - 8 \cos^{2} x = 6

có nghiệm là:

A. $\Leftrightarrow [\begin{matrix} x = \frac{π}{2} + k π \\ x = \frac{π}{6} + k π \end{matrix} (k \in Z)$

B. $[\begin{matrix} x = \frac{π}{4} + k π \\ x = \frac{π}{3} + k π \end{matrix} (k \in Z)$

C. $[\begin{matrix} x = \frac{π}{8} + k 2 π \\ x = \frac{π}{12} + k 2 π \end{matrix} (k \in Z)$

D. $[\begin{matrix} x = \frac{π}{8} + k π \\ x = \frac{π}{12} + k π \end{matrix} (k \in Z)$

Xem đáp án

$6 \sin^{2} x + 7 \sqrt{3} \sin 2 x - 8 \cos^{2} x = 6$

$\Leftrightarrow 6 \sin^{2} x + 14 \sqrt{3} \sin x - 8 \cos^{2} x = 6 (*)$

Trường hợp 1: $\cos x = 0 \Leftrightarrow x = \frac{π}{2} + k π (k \in Z)$ .

Khi đó: $\sin^{2} x = 1$

Thay vào phương trình (*) ta có: 6.1 + 14.0 − 8.0 = 6 ⇔ 6 = 6 (luôn đúng)

Trường hợp 2: $\cos x \neq 0 \Leftrightarrow x \neq \frac{π}{2} + k π (k \in Z)$ . Chia cả 2 vế của phương trình (*) cho cos²x ta được:

$6 \frac{\sin^{2} x}{\cos^{2} x} + 14 \sqrt{3} \frac{\sin x}{\cos x} - 8 = \frac{6}{\cos^{2} x}$

$\Leftrightarrow 6 \tan^{2} x + 14 \sqrt{3} \tan x - 8 = 6 (1 + \tan^{2} x)$

$\Leftrightarrow 14 \sqrt{3} \tan x - 14 = 0$

$\Leftrightarrow \sqrt{3} \tan x - 1 = 0$

$\Leftrightarrow \tan x = \frac{1}{\sqrt{3}}$

$\Leftrightarrow x = \frac{π}{6} + k π (k \in Z)$

Kết hợp 2 trường hợp ta có nghiệm của phương trình là:

$[\begin{matrix} x = \frac{π}{2} + k π \\ x = \frac{π}{6} + k π \end{matrix} (k \in Z)$

Đáp án cần chọn là: A

Câu 17:

Trong khoảng $(0; \frac{π}{2})$ phương trình $\sin^{2} 4 x + 3 \sin 4 x \cos 4 x - 4 \cos^{2} 4 x = 0$ có:

A. Ba nghiệm

B. Một nghiệm

C. Hai nghiệm

D. Bốn nghiệm

Xem đáp án

Trường hợp 1: $\cos 4 x = 0$

$\Leftrightarrow 4 x = \frac{π}{2} + k π$

$\Leftrightarrow x = \frac{π}{8} + \frac{k π}{4} (k \in Z)$

Khi đó, $\sin^{2} 4 x = 1$

Thay vào phương trình ta có: 1 + 3.0 – 4.0 = 0 ↔ 1 = 0 (vô lí)

$\Leftrightarrow x = \frac{π}{8} + \frac{k π}{4} (k \in Z)$ không là nghiệm của phương trình.

Trường hợp 2: $\cos 4 x \neq 0$

$\Leftrightarrow x \neq \frac{π}{8} + \frac{k π}{4} (k \in Z)$

Chia cả 2 vế của phương trình cho cos²4x ta được:

$\frac{\sin^{2} 4 x}{\cos^{2} 4 x} + 3 \frac{\sin 4 x}{\cos 4 x} - 4 = 0$

$\Leftrightarrow \tan^{2} 4 x + 3 \tan 4 x - 4 = 0$

Đặt tan 4x = t. Khi đó phương trình trở thành:

$t^{2} + 3 t - 4 = 0$

$\Leftrightarrow [\begin{matrix} t = 1 \\ t = - 4 \end{matrix}$

$\Leftrightarrow [\begin{matrix} \tan 4 x = 1 \\ \tan 4 x = - 4 \end{matrix}$

$\Leftrightarrow [\begin{matrix} 4 x = \frac{π}{4} + k π \\ 4 x = \arctan (- 4) + k π \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = \frac{π}{16} + \frac{k π}{4} \\ x = \frac{1}{4} \arctan (- 4) + \frac{k π}{4} \end{matrix} (k \in Z)$

Xét nghiệm $x = \frac{π}{16} + \frac{k π}{4} (k \in Z), x \in (0; \frac{π}{2})$

$\Leftrightarrow \{\begin{matrix} 0 < \frac{π}{16} + \frac{k π}{4} < \frac{π}{2} \\ k \in Z \end{matrix}$

$\Leftrightarrow \{\begin{matrix} 0 < \frac{1}{16} + \frac{k}{4} < \frac{1}{2} \\ k \in Z \end{matrix}$

$\Leftrightarrow \{\begin{matrix} - \frac{1}{4} < k < \frac{7}{4} \\ k \in Z \end{matrix}$

$\Leftrightarrow \{\begin{matrix} k = 0 \\ k = 1 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} x = \frac{π}{16} \\ x = \frac{5 π}{16} \end{matrix}$

Xét nghiệm $x = \frac{1}{4} \arctan (- 4) + \frac{k π}{4} (k \in Z), x \in (0; \frac{π}{2})$

$\Leftrightarrow \{\begin{matrix} 0 < \frac{1}{4} \arctan (- 4) + \frac{k π}{4} < \frac{π}{2} \\ k \in Z \end{matrix}$

$\Leftrightarrow \{\begin{matrix} - \frac{1}{4} \arctan (- 4) < \frac{k π}{4} < \frac{π}{2} - \frac{1}{4} \arctan (- 4) \\ k \in Z \end{matrix}$

$\Leftrightarrow \{\begin{matrix} 0, 42 < k < 2, 42 \\ k \in Z \end{matrix}$

$\Leftrightarrow \{\begin{matrix} k = 1 \\ k = 2 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} x = \frac{1}{4} \arctan (- 4) + \frac{π}{4} \\ x = \frac{1}{4} \arctan (- 4) + \frac{π}{2} \end{matrix}$

Vậy phương trình có nghiệm thuộc khoảng $(0; \frac{π}{2})$

Đáp án cần chọn là: D

Câu 18:

Giải phương trình

\sqrt{3} \cos 5 x - 2 \sin 3 x \cos 2 x - \sin x = 0

ta được nghiệm:

A. $x = \frac{π}{9} + \frac{k 2 π}{3}; (k \in Z)$

B. $x = \frac{π}{18} + \frac{k π}{6}; (k \in Z)$

C. $x = \pm \frac{π}{6} + \frac{k π}{2}; (k \in Z)$

D. $x = \frac{π}{18} + \frac{k π}{3}; x = - \frac{π}{6} + \frac{k π}{2}; (k \in Z)$

Xem đáp án

$\sqrt{3} \cos 5 x - 2 \sin 3 x \cos 2 x - \sin x = 0$

$\Leftrightarrow \sqrt{3} \cos 5 x - (\sin 5 x + \sin x) - \sin x = 0$

$\Leftrightarrow \sqrt{3} \cos 5 x - \sin 5 x = 2 \sin x$

$\Leftrightarrow \frac{\sqrt{3}}{2} \cos 5 x - \frac{1}{2} \sin 5 x = \sin x$

$\Leftrightarrow \sin \frac{π}{3} \cos 5 x - \cos \frac{π}{3} \sin 5 x = \sin x$

$\Leftrightarrow \sin (\frac{π}{3} - 5 x) = \sin x$

$\Leftrightarrow [\begin{matrix} \frac{π}{3} - 5 x = x + k 2 π \\ \frac{π}{3} - 5 x = π - x + k 2 π \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = \frac{π}{18} + \frac{k π}{3} \\ x = - \frac{π}{6} + \frac{k π}{2} \end{matrix} (k \in Z)$

Vậy nghiệm của phương trình là:

$x = \frac{π}{18} + \frac{k π}{3}; x = - \frac{π}{6} + \frac{k π}{2} (k \in Z)$

Đáp án cần chọn là: D

Câu 19:

Giải phương trình

\cos x \cos \frac{x}{2} \cos \frac{3 x}{2} - \sin x \sin \frac{x}{2} \sin \frac{3 x}{2} = \frac{1}{2}

A. $x = - \frac{π}{4} + k π; x = \frac{π}{6} + k 2 π; x = \frac{5 π}{6} + k 2 π; x = - \frac{π}{2} + k 2 π (k \in Z)$

B. $x = \frac{π}{4} + k 2 π; x = - \frac{π}{6} + k 2 π; x = \frac{5 π}{6} + k π; x = - \frac{π}{2} + k π (k \in Z)$

C. $x = \pm \frac{π}{6} + k 2 π; x = \frac{5 π}{6} + k 2 π; x = - \frac{π}{2} + k 2 π (k \in Z)$

D. $x = - \frac{π}{8} + k π; x = \frac{π}{6} + k π; x = - \frac{5 π}{6} + \frac{k π}{6}; x = - \frac{π}{2} + \frac{k π}{6} (k \in Z)$

Xem đáp án

$\cos x \cos \frac{x}{2} \cos \frac{3 x}{2} - \sin x \sin \frac{x}{2} \sin \frac{3 x}{2} = \frac{1}{2}$

$\Leftrightarrow \frac{1}{2} \cos x (\cos 2 x + \cos x) + \frac{1}{2} \sin x (\cos 2 x - \cos x) = \frac{1}{2}$

$\Leftrightarrow \cos x \cos 2 x + \cos^{2} x + \sin x \cos 2 x - \sin x \cos x = 1$

$\Leftrightarrow \cos 2 x (\sin x + \cos x) - \sin x \cos x + \cos^{2} x - 1 = 0$

$\Leftrightarrow \cos 2 x (\sin x + \cos x) - \sin x \cos x - s i n^{2} x = 0$

$\Leftrightarrow \cos 2 x (\sin x + \cos x) - \sin x (\sin x + \cos x) = 0$

$\Leftrightarrow (\sin x + \cos x) (\cos 2 x - \sin x) = 0$

$\Leftrightarrow [\begin{matrix} \sin x + \cos x = 0 \\ \cos 2 x - \sin x = 0 \end{matrix}$

$\Leftrightarrow [\begin{matrix} \sin x = - \cos x \\ 1 - 2 \sin^{2} x - \sin x = 0 \end{matrix}$

$\Leftrightarrow [\begin{matrix} \tan x = - 1 \\ \sin x = \frac{1}{2} \\ \sin x = - 1 \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = - \frac{π}{4} + k π \\ x = \frac{π}{6} + k 2 π \\ x = \frac{5 π}{6} + k 2 π \\ x = - \frac{π}{2} + k 2 π \end{matrix} (k \in Z)$

Vậy nghiệm của phương trình đã cho là:

$x = - \frac{π}{4} + k π; x = \frac{π}{6} + k 2 π; x = \frac{5 π}{6} + k 2 π; x = - \frac{π}{2} + k 2 π (k \in Z)$

Đáp án cần chọn là: A

Câu 20:

Giải phương trình

8 \sin x = \frac{\sqrt{3}}{\cos x} + \frac{1}{\sin x}

A. $x = - \frac{π}{6} + \frac{k π}{2}; x = \frac{π}{12} + \frac{k π}{2} (k \in Z)$

B. $x = \frac{π}{12} + \frac{k π}{4} (k \in Z)$

C. $x = \pm \frac{π}{6} + k π; x = - \frac{π}{12} + \frac{k π}{2} (k \in Z)$

D. $x = \frac{π}{6} + k π; x = - \frac{π}{12} + \frac{k π}{2} (k \in Z)$

Xem đáp án

ĐKXĐ: $\{\begin{matrix} \sin x \neq 0 \\ \cos x \neq 0 \end{matrix} \Leftrightarrow \sin 2 x \neq 0 \Leftrightarrow x \neq \frac{k π}{2}$

$8 \sin x = \frac{\sqrt{3}}{\cos x} + \frac{1}{\sin x}$

$\Leftrightarrow 8 \sin^{2} x \cos x = \sqrt{3} \sin x + \cos x$

$\Leftrightarrow 4 \sin^{2} x \cos x = \sqrt{3} \sin x + \cos x$

$\Leftrightarrow - 2 (\cos 3 x - \cos x) = \sqrt{3} \sin x + \cos x$

$\Leftrightarrow - 2 \cos 3 x + 2 \cos x = \sqrt{3} \sin x + \cos x$

$\Leftrightarrow \cos x - \sqrt{3} \sin x = 2 \cos 3 x$

$\Leftrightarrow \frac{1}{2} \cos x - \frac{\sqrt{3}}{2} \sin x = \cos 3 x$

$\Leftrightarrow \cos x \cos \frac{π}{3} - \sin x \sin \frac{π}{3} = \cos 3 x$

$\Leftrightarrow \cos (x + \frac{π}{3}) = \cos 3 x$

$\Leftrightarrow [\begin{matrix} x + \frac{π}{3} = 3 x + k 2 π \\ x + \frac{π}{3} = - 3 x + k 2 π \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = \frac{π}{6} + k π \\ x = - \frac{π}{12} + \frac{k π}{2} \end{matrix} (k \in Z) (t m)$

Vậy nghiệm của phương trình đã cho là:

$x = \frac{π}{6} + k π; x = - \frac{π}{12} + \frac{k π}{2} (k \in Z)$

Đáp án cần chọn là: D

Câu 21:

Giải phương trình

\sin 3 x - \frac{2}{\sqrt{3}} \sin^{2} x = 2 \sin x \cos 2 x

A. $x = \pm \frac{π}{3} + k 2 π; x = \frac{2 π}{3} + k 2 π (k \in Z)$

B. $x = \frac{π}{4} + k π; x = \frac{π}{6} + k π (k \in Z)$

C. $x = k π; x = \frac{π}{3} + k 2 π; x = \frac{2 π}{3} + k 2 π (k \in Z)$

D. $x = \frac{π}{2} + k π; x = \frac{π}{6} + \frac{k π}{3} (k \in Z)$

Xem đáp án

$\sin 3 x - \frac{2}{\sqrt{3}} \sin^{2} x = 2 \sin x \cos 2 x$

$\Leftrightarrow \sqrt{3} \sin 3 x - 2 \sin^{2} x = \sqrt{3} (\sin 3 x - \sin x)$

$\Leftrightarrow \sqrt{3} \sin 3 x - 2 \sin^{2} x = \sqrt{3} \sin 3 x - \sqrt{3} \sin x$

$\Leftrightarrow 2 \sin^{2} x - \sqrt{3} \sin x = 0$

$\Leftrightarrow \sin x (2 \sin x - \sqrt{3})$

$\Leftrightarrow [\begin{matrix} \sin x = 0 \\ \sin x = \frac{\sqrt{3}}{2} \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = k π \\ x = \frac{π}{3} + k 2 π \\ x = \frac{2 π}{3} + k 2 π \end{matrix} (k \in Z)$

Vậy nghiệm của phương trình đã cho là:

$x = k π; x = \frac{π}{3} + k 2 π; x = \frac{2 π}{3} + k 2 π (k \in Z)$

Đáp án cần chọn là: C

Câu 22:

Giải phương trình

(\sin x + \sqrt{3} \cos x) . \sin 3 x = 2

A. $x = \frac{π}{6} + k π, k \in Z$

B. $x = - \frac{π}{12} + \frac{k π}{2}, k \in Z$

C. $x = \frac{2 π}{3} + k π, k \in Z$

D. $x = \frac{k π}{12}; x = \frac{2 π}{3} + k π, k \in Z$

Xem đáp án

$(\sin x + \sqrt{3} \cos x) . \sin 3 x = 2$

$\Leftrightarrow (\frac{1}{2} \sin x + \frac{\sqrt{3}}{2} \cos x) . \sin 3 x = 1$

$\Leftrightarrow (\sin x \cos \frac{π}{3} + \cos x \sin \frac{π}{3}) . \sin 3 x = 1$

$\Leftrightarrow \sin (x + \frac{π}{3}) . \sin 3 x = 1$

$\Leftrightarrow - \frac{1}{2} [\cos (4 x + \frac{π}{3}) - \cos (2 x - \frac{π}{3})] = 1$

$\Leftrightarrow \cos (4 x + \frac{π}{3}) - \cos (2 x - \frac{π}{3}) = - 2$

Do $- 1 \leq \cos (4 x + \frac{π}{3}), \cos (2 x - \frac{π}{3}) \leq 1$ nên:

$\{\begin{matrix} \cos (4 x + \frac{π}{3}) = - 1 \\ \cos (2 x - \frac{π}{3}) = 1 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} 4 x + \frac{π}{3} = π + k 2 π \\ 2 x - \frac{π}{3} = k 2 π \end{matrix}$

$\Leftrightarrow \{\begin{matrix} 4 x = \frac{2 π}{3} + k 2 π \\ 2 x = \frac{π}{3} + k 2 π \end{matrix}$

$\Leftrightarrow \{\begin{matrix} x = \frac{π}{6} + \frac{k π}{2} \\ x = \frac{π}{6} + k π \end{matrix} (k \in Z)$

$\Rightarrow x = \frac{π}{6} + k π$

Vậy phương trình đã cho có họ nghiệm là $x = \frac{π}{6} + k π$

Đáp án cần chọn là: A

Câu 23:

Giải phương trình $1 + \sin x + \cos 3 x = \cos x + \sin 2 x + \cos 2 x$

A. $x = k π; x = \frac{π}{6} + \frac{k π}{3}, x = \frac{π}{12} + k π, x = \frac{5 π}{7} + k π$

B. $x = k 2 π; x = \frac{π}{3} + \frac{k 2 π}{3}, x = - \frac{π}{6} + k 2 π, x = \frac{7 π}{6} + k 2 π$

C. $x = k π; x = \frac{π}{3} + \frac{k 2 π}{3}, x = - \frac{π}{12} + k π, x = \frac{5 π}{12} + k π$

D. $x = k 2 π; x = \frac{π}{6} + \frac{k 2 π}{3}, x = \frac{π}{12} + k π, x = \frac{7 π}{12} + k π$

Xem đáp án

1 + sinx + cos3x = cosx + sin2x + cos2x

⇔ (1 − cos2x) + (sinx − sin2x) + (cos3x − cosx) = 0

⇔2sin ²x + (sinx − sin2x) − 2sin2xsinx = 0

⇔ 2sinx(sinx − sin2x) + (sinx − sin2x) = 0

⇔ (sinx − sin2x)(2sinx + 1) = 0

$\Leftrightarrow [\begin{matrix} \sin 2 x = \sin x \\ \sin x = - \frac{1}{2} \end{matrix}$

$\Leftrightarrow [\begin{matrix} 2 x = x + k 2 π \\ 2 x = π - x + k 2 π \\ x = - \frac{π}{6} + k 2 π \\ x = \frac{7 π}{6} + k 2 π \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = k 2 π \\ x = \frac{π}{3} + \frac{k 2 π}{3} \\ x = - \frac{π}{6} + k 2 π \\ x = \frac{7 π}{6} + k 2 π \end{matrix}$

Vậy nghiệm của phương trình là:

$x = k 2 π; x = \frac{π}{3} + \frac{k 2 π}{3}, x = - \frac{π}{6} + k 2 π, x = \frac{7 π}{6} + k 2 π$

Đáp án cần chọn là: B

Câu 24:

Giải phương trình

\cos x + \cos 3 x + 2 \cos 5 x = 0

A. $x = \frac{π}{2} + k π, x = \pm \frac{1}{5} \arccos \frac{1 + \sqrt{17}}{8} + k π, x = \pm \frac{1}{5} \arccos \frac{1 - \sqrt{17}}{8} + k π$

B. $x = \pm \frac{π}{6} + k π$

C. $x = \pm \frac{1}{2} \arccos \frac{1 + \sqrt{15}}{7} + k π, x = \pm \frac{1}{2} \arccos \frac{1 - \sqrt{15}}{7} + k π$

D. $x = \frac{π}{2} + k π, x = \pm \frac{1}{2} \arccos \frac{1 + \sqrt{17}}{8} + k π, x = \pm \frac{1}{2} \arccos \frac{1 - \sqrt{17}}{8} + k π$

Xem đáp án

cosx + cos3x + 2cos5x = 0

⇔ cosx + cos3x + cos5x + cos5x = 0

⇔ (cosx + cos5x) + (cos3x + cos5x) = 0

⇔ 2cos3xcos2x + 2cos4xcosx = 0
⇔ 2(4cos³ x − 3cosx)cos2x + 2cos4xcosx = 0

⇔2cosx(4cos² x − 3)cos2x + 2cos4xcosx = 0

⇔ 2cosx[(4cos² x − 3)cos2x + cos4x] = 0

⇔ 2cosx[[2(1 + cos2x) − 3]cos2x + 2cos² 2x − 1] = 0

⇔ 2cosx[(2cos2x − 1)cos2x + 2cos² 2x − 1] = 0

⇔ 2cosx[4cos² 2x − cos2x − 1] = 0

$\Leftrightarrow [\begin{matrix} \cos x = 0 \\ \cos 2 x = \frac{1 + \sqrt{17}}{8} \\ \cos 2 x = \frac{1 - \sqrt{17}}{8} \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = \frac{π}{2} + k π \\ 2 x = \pm \arccos \frac{1 + \sqrt{17}}{8} + k 2 π \\ 2 x = \pm \arccos \frac{1 - \sqrt{17}}{8} + k 2 π \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = \frac{π}{2} + k π \\ x = \pm \frac{1}{2} \arccos \frac{1 + \sqrt{17}}{8} + k π \\ x = \pm \frac{1}{2} \arccos \frac{1 - \sqrt{17}}{8} + k π \end{matrix}$

Vậy nghiệm của phương trình là: $x = \frac{π}{2} + k π, x = \pm \frac{1}{2} \arccos \frac{1 + \sqrt{17}}{8} + k π, x = \pm \frac{1}{2} \arccos \frac{1 - \sqrt{17}}{8} + k π$

Đáp án cần chọn là: D

Câu 25:

Giải phương trình

\sin 3 x - \sin x + \sin 2 x = 0

A. $x = k π, x = \frac{π}{3} + \frac{k 2 π}{3}$

B. $x = \pm \frac{π}{3} + \frac{k 2 π}{3}$

C. $x = \frac{π}{2} + k π, x = - \frac{π}{3} + \frac{k 2 π}{3}$

D. $x = 2 k π, x = \frac{π}{2} + \frac{k π}{3}$

Xem đáp án

$\sin 3 x - \sin x + \sin 2 x = 0$

$\Leftrightarrow 2 c o s 2 x \sin x + 2 \sin x \cos x = 0$

$\Leftrightarrow 2 \sin x (c o s 2 x + \cos x) = 0$

$\Leftrightarrow [\begin{matrix} \sin x = 0 \\ c o s 2 x = - \cos x = \cos (π - x) \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = k π \\ 2 x = π - x + k 2 π \\ 2 x = x - π + k 2 π \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = k π \\ x = \frac{π}{3} + \frac{k 2 π}{3} \\ x = - π + k 2 π \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = k π \\ x = \frac{π}{3} + \frac{k 2 π}{3} \end{matrix} (k \in Z)$

Vậy nghiệm của phương trình là: $x = \frac{π}{3} + \frac{k 2 π}{3}$

Đáp án cần chọn là: A

Câu 26:

Có bao nhiêu giá trị m nguyên để phương trình: $\sin^{2} x - m \sin x \cos x - 3 \cos^{2} x = 2 m$ có nghiệm?

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Trường hợp 1: $\cos x = 0 \Leftrightarrow x = \frac{π}{2} + k π (k \in Z)$

Khi đó $\sin^{2} x = 1$

Thay vào phương trình ta có:

1 − m.0 − 3.0 = 2m

⇔ 2m = 1

$\Leftrightarrow m = \frac{1}{2} \notin Z$

⇒ loại

Trường hợp 2: $\cos x \neq 0$

$\Leftrightarrow x \neq \frac{π}{2} + k π (k \in Z)$

Chia cả 2 vế của phương trình cho $\cos^{2} x$ ta được:

$\frac{s i n^{2} x}{\cos^{2} x} - m \frac{\sin x}{\cos x} - 3 = \frac{2 m}{\cos^{2} x}$

$\Leftrightarrow \tan^{2} x - m \tan x - 3 = 2 m (1 + \tan^{2} x)$

$\Leftrightarrow (2 m - 1) \tan^{2} x + m \tan x + 2 m + 3 = 0$

Đặt tanx = t khi đó phương trình có dạng:

$(2 m - 1) t^{2} + m t + 2 m + 3 = 0$

$m = \frac{1}{2} \notin Z \Rightarrow$ Loại

$m \neq \frac{1}{2}$ ta có:

$Δ = m^{2} - 4 (2 m - 1) (2 m + 3)$

$= m^{2} - 16 m^{2} - 16 m + 12$

$= - 15 m^{2} - 16 m + 12$

Để phương trình có nghiệm thì: $Δ \geq 0$

$\Leftrightarrow \frac{- 8 - 2 \sqrt{61}}{15} \leq m \leq \frac{- 8 + 2 \sqrt{61}}{15}$

Mà $m \in Z \Rightarrow \{\begin{matrix} m = - 1 \\ m = 0 \end{matrix}$

Đáp án cần chọn là: C

Câu 27:

Các giá trị nguyên dương nhỏ hơn 5 của m để phương trình $\tan x + \cot x = m$ có nghiệm $x \in (0; \frac{π}{2})$ có tổng là:

A. 9

B. 3

C. 6

D. 7

Xem đáp án

Với $x \in (0; \frac{π}{2})$ ta có:

$\{\begin{matrix} \sin x > 0 \\ \cos x > 0 \end{matrix} \Rightarrow \{\begin{matrix} \tan x > 0 \\ \cot x > 0 \end{matrix}$

Ta có:

$\tan x + \cot x = \tan x + \frac{1}{\tan x} \geq 2 \sqrt{\tan x . \frac{1}{\tan x}} = 2$ (BĐT Cauchy)

Phương trình có nghiệm ⇔ m ≥ 2

Kết hợp điều kiện ta có: $\{\begin{matrix} 2 \leq m < 5 \\ m \in Z^{+} \end{matrix} \Rightarrow m \in (2; 3; 4)$

Vậy tổng các giá trị của m thỏa mãn là 2 + 3 + 4 = 9

Đáp án cần chọn là: A

Câu 28:

Với giá trị nào của m thì phương trình $(1 - m) \tan^{2} x - \frac{2}{\cos x} + 1 + 3 m = 0$ có nhiều hơn 1 nghiệm trên $(0; \frac{π}{2})$ ?

A. $m \neq \frac{1}{2}$

B. $m = \frac{1}{2}$

C. $\{\begin{matrix} \frac{1}{3} < m < 1 \\ m \neq \frac{1}{2} \end{matrix}$

D. $\frac{1}{3} < m < 1$

Xem đáp án

$(1 - m) \tan^{2} x - \frac{2}{\cos x} + 1 + 3 m = 0$

$\Leftrightarrow (1 - m) \frac{\sin^{2} x}{\cos^{2} x} - \frac{2}{\cos x} + 1 + 3 m = 0$

$\Leftrightarrow (1 - m) \sin^{2} x - 2 \cos x + (1 + 3 m) \cos^{2} x = 0$

$\Leftrightarrow (1 - m) (1 - \cos^{2} x) - 2 \cos x + (1 + 3 m) \cos^{2} x = 0$

$\Leftrightarrow 4 m \cos^{2} x - 2 \cos x + 1 - m = 0$

Đặt t = cos x

Vì $(0; \frac{π}{2}) \Rightarrow t \in (0; 1)$ khi đó phương trình trở thành:

$4 m t^{2} - 2 t + 1 - m = 0$ (1)

$\Leftrightarrow m (4 t^{2} - 1) - (2 t - 1) = 0$

$\Leftrightarrow m (2 t + 1) (2 t - 1) - (2 t - 1) = 0$

$\Leftrightarrow (2 t - 1) (2 m t + m - 1) = 0$

$\Leftrightarrow [\begin{matrix} t = \frac{1}{2} \in (0; 1) \\ 2 m t = 1 - m (2) \end{matrix}$

Để phương trình ban đầu có nhiều hơn 1 nghiệm thuộc $(0; \frac{π}{2})$ thì phương trình (1) có nhiều hơn 1 nghiệm thuộc (0; 1). Khi đó phương trình (2) có nghiệm thuộc $(0; 1)$ \ $\{\frac{1}{2}\}$

Khi m = 0 ta có 0t = 1 (vô nghiệm)

Khi $m \neq 0$ thì $2 \Leftrightarrow t = \frac{1 - m}{2 m}$

Để phương trình (2) có nghiệm thuộc $(0; 1)$ \ $\{\frac{1}{2}\}$ thì:

$\{\begin{matrix} m \neq 0 \\ 0 < \frac{1 - m}{2 m} < 1 \\ \frac{1 - m}{2 m} \neq \frac{1}{2} \end{matrix}$ $\Leftrightarrow \{\begin{matrix} m \neq 0 \\ \frac{1 - m}{2 m} > 0 \\ \frac{1 - m}{2 m} < 1 \\ 2 (1 - m) \neq 2 m \end{matrix}$

$\Leftrightarrow \{\begin{matrix} m \neq 0 \\ \frac{1 - m}{2 m} > 0 \\ \frac{1 - 3 m}{2 m} < 0 \\ 4 m \neq 2 \end{matrix} \Leftrightarrow \Leftrightarrow \{\begin{matrix} m \neq 0 \\ 0 < m < 1 \\ [\begin{matrix} m < 0 \\ m > \frac{1}{3} \end{matrix} \\ m \neq \frac{1}{2} \end{matrix}$

$\Leftrightarrow \{\begin{matrix} \frac{1}{3} < m < 1 \\ m \neq \frac{1}{2} \end{matrix}$

Đáp án cần chọn là: C

Câu 29:

Giải phương trình $\cos 2 x + \cos 4 x + \cos 6 x = \cos x \cos 2 x \cos 3 x + 2$

A. $x = k π (k \in Z)$

B. $x = \frac{2 π}{3} + 2 k π (k \in Z)$

C. $x = \frac{π}{3} + 2 k π (k \in Z)$

D. $x = \frac{k π}{3} (k \in Z)$

Xem đáp án

$\cos 2 x + \cos 4 x + \cos 6 x = \cos x \cos 2 x \cos 3 x + 2$

$\Leftrightarrow 2 \cos 4 x \cos 2 x + \cos 4 x = \frac{1}{2} \cos 2 x (\cos 4 x + \cos 2 x) + 2$

$\Leftrightarrow 2 \cos 4 x \cos 2 x + \cos 4 x = \frac{1}{2} \cos 2 x \cos 4 x + \frac{1}{2} \cos^{2} 2 x + 2$

$\Leftrightarrow \frac{3}{2} \cos 4 x \cos 2 x + \cos 4 x = \frac{1}{2} \cos^{2} 2 x + 2$

$\Leftrightarrow 3 \cos 4 x \cos 2 x + 2 \cos 4 x = \cos^{2} 2 x + 4$

$\Leftrightarrow 3 (2 \cos^{2} 2 x - 1) \cos 2 x + 2 (2 \cos^{2} 2 x - 1) = \cos^{2} 2 x + 4$

$\Leftrightarrow 6 \cos^{3} 2 x - 3 \cos 2 x + 4 \cos^{2} 2 x - 2 = \cos^{2} 2 x + 4$

$\Leftrightarrow 6 \cos^{3} 2 x + 3 \cos^{2} 2 x - 3 \cos 2 x - 6 = 0$

$\Leftrightarrow 2 \cos^{3} 2 x + \cos^{2} 2 x - \cos 2 x - 2 = 0$

$\Leftrightarrow 2 (\cos^{3} 2 x - 1) + \cos 2 x (\cos 2 x - 1) = 0$

$\Leftrightarrow 2 (\cos 2 x - 1) (\cos^{2} 2 x + \cos 2 x + 1) + \cos 2 x (\cos 2 x - 1) = 0$

$\Leftrightarrow (\cos 2 x - 1) (2 \cos^{2} 2 x + 2 \cos 2 x + 2 + \cos 2 x) = 0$

$\Leftrightarrow (\cos 2 x - 1) (2 \cos^{2} 2 x + 3 \cos 2 x + 2) = 0$

$\Leftrightarrow \cos 2 x = 1$

$\Leftrightarrow 2 x = k 2 π$

$\Leftrightarrow x = k π (k \in z)$

Vậy nghiệm của phương trình đã cho là: x = kπ (k ∈ Z).

Đáp án cần chọn là: A

Câu 30:

Giải phương trình

4 \sin x \sin (x + \frac{π}{3}) \sin (x + \frac{2 π}{3}) + \cos 3 x = 1

A. Vô nghiệm

B. $x = \frac{π}{6} + \frac{k 2 π}{3} (k \in Z)$ hoặc $x = \frac{k 2 π}{3} (k \in Z)$

C. $x = \frac{π}{6} + k 2 π (k \in Z)$

D. $x = \frac{π}{6} + \frac{k π}{3} (k \in Z)$

Xem đáp án

$4 \sin x \sin (x + \frac{π}{3}) \sin (x + \frac{2 π}{3}) + \cos 3 x = 1$

$\Leftrightarrow 4 \sin x . (- \frac{1}{2}) [\cos (2 x + π) - \cos (- \frac{π}{3})] + \cos 3 x = 1$

$\Leftrightarrow - 2 \sin x (- \cos 2 x - \frac{1}{2}) + \cos 3 x = 1$

⇔ 2sinxcos2x + sinx + cos3x = 1

⇔ sin3x – sinx + sinx + cos3x = 1

⇔ sin3x + cos3x = 1

$\Leftrightarrow \frac{1}{\sqrt{2}} \sin 3 x + \frac{1}{\sqrt{2}} \cos 3 x = \frac{1}{\sqrt{2}}$

$\Leftrightarrow \sin (3 x + \frac{π}{4}) = \sin \frac{π}{4}$

$\Leftrightarrow [\begin{matrix} 3 x + \frac{π}{4} = \frac{π}{4} + k 2 π \\ 3 x + \frac{π}{4} = \frac{3 π}{4} + k 2 π \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = \frac{k 2 π}{3} \\ x = \frac{π}{6} + \frac{k 2 π}{3} \end{matrix} (k \in Z)$

Vậy phương trình có nghiệm là:

$\Leftrightarrow [\begin{matrix} x = \frac{k 2 π}{3} \\ x = \frac{π}{6} + \frac{k 2 π}{3} \end{matrix} (k \in Z)$

Đáp án cần chọn là: B

Câu 31:

Giải phương trình $\cos 3 x \tan 5 x = \sin 7 x$

A. $x = \frac{n π}{2}; x = \frac{π}{20} + \frac{k π}{13} (k, n \in Z)$

B. $x = n π; x = \frac{π}{20} + \frac{k π}{10} (k, n \in Z)$

C. $x = n π; x = \frac{3 π}{5} + \frac{2 k π}{7} (k, n \in Z)$

D. $x = n π; x = \frac{3 π}{5} + \frac{7 k π}{13} (k, n \in Z)$

Xem đáp án

ĐKXĐ: $\cos 5 x \neq 0$

$\Leftrightarrow 5 x \neq \frac{π}{2} + m π$

$\Leftrightarrow x \neq \frac{π}{10} + \frac{m π}{5} (m \in Z)$

$\cos 3 x \tan 5 x = \sin 7 x$

$\Leftrightarrow \cos 3 x \sin 5 x = \sin 7 x \cos 5 x$

$\Leftrightarrow \frac{1}{2} (\sin 8 x + \sin 2 x) = \frac{1}{2} (\sin 12 x + \sin 2 x)$

$\Leftrightarrow \sin 8 x + \sin 2 x = \sin 12 x + \sin 2 x$

$\Leftrightarrow \sin 12 x = \sin 8 x$

$\Leftrightarrow [\begin{matrix} 12 x = 8 x + k 2 π \\ 12 x = π - 8 x + k 2 π \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = \frac{k π}{2} \\ x = \frac{π}{20} + \frac{k π}{10} \end{matrix} (k \in Z)$

Đối chiếu điều kiện ta có:

$\frac{k π}{2} \neq \frac{π}{10} + \frac{m π}{5} (k, m \in Z)$

$\Leftrightarrow 5 k \neq 1 + 2 m$

$\Leftrightarrow k \neq \frac{1 + 2 m}{5}$

Do kϵZ nên: $k = \frac{1 + 2 m}{5} \Leftrightarrow \frac{1 + 2 m}{5}$ là số nguyên.

Mà 1 + 2m luôn lẻ nên $\frac{1 + 2 m}{5}$ không chia hết cho 2 với mọi m.

Do đó, nếu $k \neq \frac{1 + 2 m}{5}$ thì k phải là số nguyên chẵn.

⇒k chẵn, đặt k = 2n, khi đó ta có $x = \frac{2 n π}{2} = n π (n \in Z)$

$\frac{π}{20} + \frac{k π}{10} \neq \frac{π}{10} + \frac{m π}{5} (k, m \in Z)$

$\Leftrightarrow 1 + 2 k \neq 2 + 4 m$

Vì 1 + 2k lẻ, 2 + 4m chẵn nên 1 + 2k ≠ 2 + 4m luôn đúng với mọi k, m ∈ Z.

Vậy nghiệm của phương trình đã cho là:

$x = n π; x = \frac{π}{20} + \frac{k π}{10} (k, n \in Z)$

Đáp án cần chọn là: B

Câu 32:

Số nghiệm của phương trình

\sin 5 x + \sqrt{3} \cos 5 x = 2 \sin 7 x

trên khoảng

(0; \frac{π}{2})

là:

A. 2

B. 3

C. 1

D. 4

Xem đáp án

Phương trình:

$\Leftrightarrow \frac{1}{2} \sin 5 x + \frac{\sqrt{3}}{2} \cos 5 x = \sin 7 x$

$\Leftrightarrow \sin (5 x + \frac{π}{3}) = \sin 7 x$

$\Leftrightarrow \sin 7 x = \sin (5 x + \frac{π}{3})$

$\Leftrightarrow [\begin{matrix} 7 x = 5 x + \frac{π}{3} + k 2 π \\ 7 x = π - (5 x + \frac{π}{3}) + k 2 π \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = \frac{π}{6} + k π \\ x = \frac{π}{18} + \frac{k π}{6} \end{matrix} (k \in Z)$

Xét khoảng $(0; \frac{π}{2})$ :

+) $0 < \frac{π}{6} + k π < \frac{π}{2}$

$\Leftrightarrow - \frac{1}{6} < k < \frac{1}{3}$

$\overset{k \in Z}{\to} k = 0 \Rightarrow x = \frac{π}{6}$

+) $0 < \frac{π}{18} + k \frac{π}{6} < \frac{π}{2}$

$\Leftrightarrow - \frac{1}{3} < k < \frac{8}{3}$

$\overset{k \in Z}{\to} [\begin{matrix} k = 0 \Rightarrow x = \frac{π}{18} \\ k = 1 \Rightarrow x = \frac{2 π}{9} \\ k = 2 \Rightarrow x = \frac{7 π}{18} \end{matrix}$

Vậy phương trình có 4 nghiệm thỏa mãn yêu cầu bài toán

Đáp án cần chọn là: D

Câu 33:

Gọi m, M lần lượt là GTNN và GTLN của hàm số $y = \frac{\sin x + 3}{\sin x + \cos x + 2}$ . Khi đó giá trị của biểu thức m + M bằng

A. $\frac{24}{5}$

B. $\frac{28}{5}$

C. 5

D. $\frac{25}{8}$

Xem đáp án

Ta có: $y = \frac{\sin x + 3}{\sin x + \cos x + 2}$

⇔ y(sinx + cosx + 2) = sinx + 3

⇔y.cosx + (y − 1).sinx = 3 − 2y
Phương trình trên có nghiệm

⇔ y²+ (y − 1)²≥ (3 − 2y)²

⇔ 2y²− 2y + 1 ≥ 9 − 12y + 4y²

⇔ 2y²− 10y + 8 ≤ 0

⇔ 1 ≤ y ≤ 4

=> Min y = 1, Max y = 4

Đáp án cần chọn là: C