Trắc nghiệm Toán 6 KNTT Các dạng toán về phép nhân, chia số nguyên, bội và ước của một số nguyên (tiếp) có đáp án (Phần 2)
Trắc nghiệm Toán 6 KNTT Bài 23. Các dạng toán về phép nhân, chia số nguyên, bội và ước của một số nguyên (tiếp) có đáp án
-
496 lượt thi
-
21 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Trả lời:
\[\begin{array}{l}( - 5).125.( - 8).20.( - 2)\\ = [125.( - 8)].[( - 5).20].( - 2)\\ = - (125.8).[ - (5.20)].( - 2)\\ = ( - 1000).( - 100).( - 2)\\ = 100000.( - 2)\\ = - 200000\end{array}\]
Đáp án cần chọn là: A
Câu 2:
Giá trị biểu thức \[M = \left( { - 192873} \right).\left( { - 2345} \right).{\left( { - 4} \right)^5}.0\;\] là
 Xem đáp án
Xem đáp án
Trả lời:
Vì trong tích có một thừa số bằng 0 nên \[M = 0\]
Đáp án cần chọn là: C
Câu 3:
 Xem đáp án
Xem đáp án
Trả lời:
\[\begin{array}{l}A = - 43.18 - 82.43 - 43.100\\A = 43.( - 18 - 82 - 100)\\A = 43.[ - (18 + 82 + 100)]\\A = 43.( - 200)\\A = - 8600\end{array}\]
Đáp án cần chọn là: C
Câu 4:
 Xem đáp án
Xem đáp án
Trả lời:
\[\begin{array}{l}Q = - 135.17 - 121.17 - 256.( - 17)\\Q = - 135.17 - 121.17 + 256.17\\Q = 17.( - 135 - 121 + 256)\\Q = 17.( - 256 + 256)\\Q = 17.0\\Q = 0\end{array}\]
Đáp án cần chọn là: B
Câu 5:
Tìm \[x \in Z\;\] biết \[(x + 1) + (x + 2) + ... + (x + 99) + (x + 100) = 0\]
 Xem đáp án
Xem đáp án
Trả lời:
\[\begin{array}{l}(x + 1) + (x + 2) + ... + (x + 99) + (x + 100) = 0\\(x + x + .... + x) + (1 + 2 + ... + 100) = 0\\100x + (100 + 1).100:2 = 0\end{array}\]
\[\begin{array}{l}100x + 5050 = 0\\100x = - 5050\\x = - 50,5\end{array}\]
Mà \[x \in Z\] nên không có x thỏa mãn.
Đáp án cần chọn là: B
Câu 6:
 Xem đáp án
Xem đáp án
Trả lời:
Có 88 ước tự nhiên của 24 là: 1;2;3;4;6;8;12;24
Có 88 ước nguyên âm của 24 là: −1;−2;−3;−4;−6;−8;−12;−24
Vậy có \[8.2 = 16\] ước của 24 nên cũng có 16 ước của −24.
Đáp án cần chọn là: D
Câu 7:
 Xem đáp án
Xem đáp án
Trả lời:
Tập hợp ước của 12 là: \[A = \{ \pm 1; \pm 2; \pm 3; \pm 4; \pm 6; \pm 12\} \]
Vì x < -2 nên \[x \in \left\{ { - 3; - 4; - 6; - 12} \right\}\]
Đáp án cần chọn là: B
Câu 8:
Giá trị lớn nhất của aa thỏa mãn \[a + 4\;\] là ước của 9 là:
 Xem đáp án
Xem đáp án
Trả lời:
\[a + 4\;\] là ước của 9
\[ \Rightarrow (a + 4) \in U\left( 9 \right) = \left\{ { \pm 1; \pm 3; \pm 9} \right\}\;\]
Ta có bảng giá trị như sau:

Vậy giá trị lớn nhất của a là \[a = 5\]
Đáp án cần chọn là: A
Câu 9:
Tìm x biết \[25.x = - 225\]
 Xem đáp án
Xem đáp án
Trả lời:
\[\begin{array}{l}25.x = - 225\\x = - 225:25\\x = - 9\end{array}\]
Đáp án cần chọn là: C
Câu 10:
Cho \(x \in \mathbb{Z}\) và \[( - 154 + x) \vdots 3\] thì:
 Xem đáp án
Xem đáp án
Trả lời:
Ta có:
\[\begin{array}{l}\left( { - 154 + x} \right)\, \vdots \,3\\( - 153 - 1 + x) \vdots 3\end{array}\]
Suy ra \[\left( {x - 1} \right)\, \vdots \,3\] (do \[ - 153\, \vdots \,3\] )
Do đó \[x - 1 = 3k \Rightarrow x = 3k + 1\]
Vậy x chia cho 3 dư 1.
Đáp án cần chọn là: A
Câu 11:
Giá trị nào dưới đây của x thỏa mãn \[ - 6(x + 7) = 96\] ?
 Xem đáp án
Xem đáp án
Trả lời:
\[\begin{array}{l} - 6(x + 7) = 96\\x + 7 = 96:( - 6)\\x + 7 = - 16\\x = - 16 - 7\\x = - 23\end{array}\]
Đáp án cần chọn là: C
Câu 12:
Tìm \(n \in {\rm Z}\) biết \[\left( {n + 5} \right) \vdots \left( {n + 1} \right)\]
 Xem đáp án
Xem đáp án
Trả lời:
\[\left( {n + 5} \right) \vdots \left( {n + 1} \right) \Rightarrow (n + 1) + 4 \vdots (n + 1)\]
Vì \[n + 1\, \vdots \,n + 1\] và \[n \in Z\] nên để \[n + 5\, \vdots \,n + 1\]thì \[4\, \vdots \,n + 1\]
Hay \[n + 1 \in U\left( 4 \right) = \left\{ { \pm 1; \pm 2; \pm 4} \right\}\]
Ta có bảng:

Vậy \[n \in \left\{ { - 5; - 3; - 2;0;1;3} \right\}\]
Đáp án cần chọn là: B
Câu 13:
Có bao nhiêu số nguyên a < 5 biết: 10 là bội của (2a+5)
 Xem đáp án
Xem đáp án
Trả lời:
Vì 10 là bội của \[2a + 5\;\] nên \[2a + 5\] là ước của 10
\[U(10) = \{ \pm 1; \pm 2; \pm 5; \pm 10\} \]
Ta có bảng:

Mà \[a < 5\;\] nên \[a \in \left\{ { - 3; - 2;0; - 5} \right\}\]
Vậy có 4 giá trị nguyên của a thỏa mãn bài toán.
Đáp án cần chọn là: A
Câu 14:
Có bao nhiêu cặp số (x;y) nguyên biết: \[(x - 1)(y + 1) = 3\] ?
 Xem đáp án
Xem đáp án
Trả lời:
Ta có: \[3 = 1.3 = 3.1 = ( - 1).( - 3) = ( - 3).( - 1)\]
Ta có bảng:
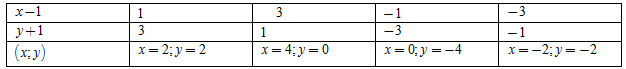
Vậy có 4 cặp số (x;y) thỏa mãn là: \[(2;2),(4;0),(0; - 4),( - 2; - 2)\]
Đáp án cần chọn là: D
Câu 15:
 Xem đáp án
Xem đáp án
Trả lời:
\[\begin{array}{*{20}{l}}{{{\left( { - 9} \right)}^2}.x = 150 + 12.13x}\\{81x = 150 + 156x}\\{81x - 156x = 150}\\{ - 75x = 150}\\{x = 150:\left( { - 75} \right)}\\{x = - 2}\end{array}\]
Đáp án cần chọn là: B
Câu 16:
Cho a và b là hai số nguyên khác 0. Biết \(a \vdots b\) và \(b \vdots a\) . Khi đó
 Xem đáp án
Xem đáp án
Trả lời:
Ta có
\[\begin{array}{l}a \vdots b \Rightarrow a = b.{q_1}({q_1} \in Z)\\b \vdots a \Rightarrow b = a.{q_2}({q_2} \in Z)\end{array}\]
Suy ra \[a = b.{q_1} = \left( {a.{q_2}} \right).{q_1} = a.\left( {{q_1}{q_2}} \right)\]
Vì \[a \ne 0\] nên \[a = a\left( {{q_1}{q_2}} \right) \Rightarrow 1 = {q_1}{q_2}\]
Mà \[{q_1},{q_2} \in Z\] nên \[{q_1} = {q_2} = 1\] hoặc \[{q_1} = {q_2} = - 1\]
Do đó \(a = b\) hoặc \(a = - b\)
Đáp án cần chọn là: D
Câu 17:
Gọi A là tập hợp các giá trị \[n \in Z\] để \[({n^2} - 7)\;\] là bội của \[(n + 3)\] .Tổng các phần tử của A bằng:
 Xem đáp án
Xem đáp án
Trả lời:
Ta có \[{n^2} - 7 = {n^2} + 3n - 3n - 9 + 2 = n\left( {n + 3} \right) - 3\left( {n + 3} \right) + 2\]
\[ = (n - 3)(n + 3) + 2\]
Vì \[n \in Z\] nên để \[{n^2} - 7\] là bội của \[(n + 3)\]thì 2 là bội của \(n + 3\) hay \(n + 3\) là ước của 2
Ư\[\left( 2 \right) = \left\{ { \pm 1; \pm 2} \right\}\] nên \[n + 3 \in \{ \pm 1; \pm 2\} \]
Ta có bảng:
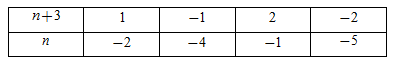
Vậy \[n \in A = \{ - 5; - 4; - 2; - 1\} \]
Do đó tổng các phần tử của A là\[( - 5) + ( - 4) + ( - 2) + ( - 1) = - 12\]
Đáp án cần chọn là: A
Câu 18:
Cho \[x;y \in \mathbb{Z}\] . Nếu \[5x + 46y\;\] chia hết cho 16 thì \[x + 6y\;\] chia hết cho
 Xem đáp án
Xem đáp án
Trả lời:
Ta có
\[\begin{array}{l}5x + 46y = 5x + 30y + 16y\\ = (5x + 30y) + 16y\\ = 5(x + 6y) + 16y\end{array}\]
Vì \[5x + 46y\] chia hết cho 16 và 16y chia hết cho 16 nên suy ra \[5\left( {x + 6y} \right)\] chia hết cho 16.
Mà 5 không chia hết cho 16 nên suy ra \[x + 6y\] chia hết cho 16
Vậy nếu \[5x + 46y\] chia hết cho 16 thì \[x + 6y\] cũng chia hết cho 16.
Đáp án cần chọn là: C
Câu 19:
Có bao nhiêu số nguyên n thỏa mãn \[(n - 1)\;\] là bội của \[(n + 5)\;\] và \[(n + 5)\;\] là bội của \[(n - 1)?\;\]
 Xem đáp án
Xem đáp án
Trả lời:
Vì \[\left( {n - 1} \right)\] là bội của \[\left( {n + 5} \right)\] và \[\left( {n + 5} \right)\] là bội của \[n - 1\] ,
Nên \[n - 1\] khác 0 và \[n + 5\] khác 0
Nên \[n + 5,n - 1\] là hai số đối nhau
Do đó:
\[\begin{array}{l}(n + 5) + (n - 1) = 0\\2n + 5 - 1 = 0\\2n + 4 = 0\\2n = - 4\\n = - 2\end{array}\]
Vậy có 1 số nguyên n thỏa mãn bài toán.
Đáp án cần chọn là: C
Câu 20:
Trong các phát biểu sau đây, phát biểu nào đúng?
 Xem đáp án
Xem đáp án
Trả lời:
Ta có: \[ - 18 = \left( { - 6} \right).3\;\] nên −18 chia hết cho −6 => C đúng
Đáp án cần chọn là: C
Câu 21:
Có bao nhiêu cách phân tích số 21 thành tích của hai số nguyên
 Xem đáp án
Xem đáp án
Trả lời:
Ta có hai cách phân tích 21 thành tích hai số nguyên dương là: \[21 = 3.7 = 1.21\]
Từ đó suy ra các 2 cách phân tích khác nhờ đổi dấu hai thừa số:
\[21 = \left( { - 3} \right).\left( { - 7} \right) = \left( { - 1} \right).\left( { - 21} \right)\]
Vậy ta có bốn cách phân tích.
Đáp án cần chọn là: C
