Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 12)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 12)
-
377 lượt thi
-
98 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Mục đích chính của văn bản là chỉ ra những rào cản ảnh hưởng đến hành vi tìm kiếm hỗ trợ của phụ nữ bị trầm cảm sau sinh:
Đoạn [1], [2] : Rào cản từ bản thân người phụ nữ.
Đoạn [3], [4] : Rào cản từ phía gia đình.
Đoạn [5], [6] : Rào cản từ phía nhân viên y tế.
Đoạn [7] : Rào cản từ truyền thống văn hóa, xã hội.
Chọn C
Câu 2:
Theo đoạn [1] và [2], đâu là một trong những lí do khiến người phụ nữ không tìm kiếm sự giúp đỡ khi có dấu hiệu trầm cảm sau sinh?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Từ đoạn [2] có thông tin:
Một số bà mẹ có biểu hiện một số triệu chứng của trầm cảm sau sinh như: tức ngực, nhức đầu, rối loạn giấc ngủ, mệt mỏi và lo âu ...nhưng vì thiếu kiến thức về vấn đề này nên họ không biết mình bị trầm cảm sau sinh.
=> Chọn Không nhận thức được rõ bản thân đang có các biểu hiện của trầm cảm sau sinh.
- Ý Chủ động tìm kiếm sự giúp đỡ khi có dấu hiệu trầm cảm nhưng không được phản hồi sai vì theo đoạn [1], nhiều phụ nữ không chủ động tìm kiếm sự giúp đỡ khi có dấu hiệu trầm cảm mặc dù họ thường xuyên liên hệ với các chuyên gia y tế trong thời kỳ hậu sản.
- Ý Họ tuyệt đối không tham khảo ý kiến của chuyên gia y tế sai vì theo đoạn [1], vẫn có khoảng 25% tham khảo ý kiến của chuyên gia y tế.
- Ý Tất cả phụ nữ đều biết rõ nơi mình cần tìm đến để nhận được sự hỗ trợ nhưng vì mặc cảm nên không tới sai vì theo đoạn [1] thì Nhiều bà mẹ đã chia sẻ không biết đến đâu để nhận được sự hỗ trợ hoặc là không biết về khả năng điều trị.
Chọn B
Câu 3:
nhận ra, biểu lộ, đưa ra, nhận thức
Một số phụ nữ _______ họ không sẵn sàng chia sẻ về cảm xúc của mình với chồng, người thân, bạn bè và chuyên gia y tế. Để che giấu triệu chứng trầm cảm, họ cố gắng ______ cảm xúc bình thường. Không chỉ vậy, việc thiếu _______ cũng là một nguyên nhân khiến một số bà mẹ bị trầm cảm đã tìm cách từ chối điều trị.
 Xem đáp án
Xem đáp án
Đáp án đúng:
Kéo thả cụm từ phù hợp vào mỗi chỗ trống để hoàn thành thông tin về đoạn [3]:
Một số phụ nữ nhận ra họ không sẵn sàng chia sẻ về cảm xúc của mình với chồng, người thân, bạn bè và chuyên gia y tế. Để che giấu triệu chứng trầm cảm, họ cố gắng biểu lộ cảm xúc bình thường. Không chỉ vậy, việc thiếu nhận thức cũng là một nguyên nhân khiến một số bà mẹ bị trầm cảm đã tìm cách từ chối điều trị.
(Kéo thả hoặc click vào để điền)
Câu 4:
Theo đoạn [4], phụ nữ luôn gặp khó khăn khi chia sẻ về vấn đề trầm cảm sau sinh, đúng hay sai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Sai, vì theo đoạn [4], phụ nữ đã nói chuyện một cách thoải mái trong bệnh viện về vấn đề trầm cảm sau sinh, nghĩa là họ có thể chia sẻ thoải mái với những người có cùng tình trạng với mình.
Họ gặp khó khăn khi chia sẻ với những đối tượng còn lại trong gia đình và xã hội: đó là người thân, bạn bè hoặc thậm chí là nhân viên y tế.
Chọn B
Câu 5:
Điền một cụm từ không quá hai tiếng từ đoạn [4] để hoàn thành nhận định sau:
Việc các triệu chứng trầm cảm không được _________ hoặc không muốn chia sẻ về những khó khăn của họ với người ngoài gia đình vì sợ bị kỳ thị là một trong những lí do khiến các thành viên trong gia đình còn ngăn cản người phụ nữ tìm kiếm sự giúp đỡ.
 Xem đáp án
Xem đáp án
Đáp án đúng:
Điền một cụm từ không quá hai tiếng từ đoạn [4] để hoàn thành nhận định sau:
Việc các triệu chứng trầm cảm không được thừa nhận hoặc không muốn chia sẻ về những khó khăn của họ với người ngoài gia đình vì sợ bị kỳ thị là một trong những lí do khiến các thành viên trong gia đình còn ngăn cản người phụ nữ tìm kiếm sự giúp đỡ.
Hướng dẫn giải:
Từ đoạn [2], có thông tin: Trong một số nền văn hóa, các thành viên trong gia đình của họ còn ngăn cản người phụ nữ tìm kiếm sự giúp đỡ, vì họ không thừa nhận triệu chứng trầm cảm hoặc không muốn chia sẻ về những khó khăn của họ với người ngoài gia đình vì sợ bị kỳ thị.
=> Điền từ "thừa nhận".
Câu 6:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Từ đoạn 5 có thông tin: phụ nữ sau sinh bị trầm cảm đã tìm kiếm sự trợ giúp từ nhân viên y tế, cán bộ tâm lý nhưng họ cảm thấy thất vọng khi tiếp xúc vì nhân viên y tế tỏ thái độ không tôn trọng, không quan tâm tới cảm xúc, tâm trạng, dấu hiệu trầm cảm của họ.
=> Việc nhân viên y tế không tôn trọng và quan tâm đúng mức tới tình trạng của bệnh nhân đã thể hiện rằng họ thờ ơ, vô cảm với người bệnh của mình. Đây chính là một trong những lí do cản trở việc tìm kiếm giúp đỡ của phụ nữ có dấu hiệu trầm cảm sau sinh.
Chọn C
Câu 7:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Từ đoạn [6] có thông tin: Nhân viên y tế thường ưu tiên kê đơn thuốc hơn là tư vấn trị liệu tâm lý.
Trầm cảm là một bệnh tâm lí nên để chữa trị cần có sự sẻ chia, đồng cảm và giúp họ tháo gỡ được các vấn đề về tâm lí nên không thể chỉ đơn thuần sử dụng thuốc là có thể chữa trị. Thế nhưng các nhân viên y tế thường ưu tiên kê đơn thuốc hơn là tư vấn trị liệu tâm lý. Từ đó cho thấy, việc chia sẻ và giúp bệnh nhân tháo gỡ các vấn đề về tâm lí chưa được chú trọng.
Chọn D
Câu 8:
Điền một cụm từ không quá bốn tiếng có trong văn bản vào chỗ trống:
Các _________ chưa phát huy được vai trò của mình trong việc giúp phụ nữ mắc trầm cảm sau sinh vì việc tư vấn, khám bệnh và kiểm tra vẫn chưa được thực hiện đúng cách.
 Xem đáp án
Xem đáp án
Đáp án đúng:
Điền một cụm từ không quá bốn tiếng có trong văn bản vào chỗ trống:
Các nhân viên y tế chưa phát huy được vai trò của mình trong việc giúp phụ nữ mắc trầm cảm sau sinh vì việc tư vấn, khám bệnh và kiểm tra vẫn chưa được thực hiện đúng cách.
Hướng dẫn giải:
Điền nhân viên y tế hoặc cán bộ tâm lí.
Đây là 2 cụm từ được sử dụng để nói đến các đối tượng có chuyên môn, tư vấn, thăm khám và kê đơn thuốc cho các bệnh nhân. Tuy nhiên, theo đoạn thì họ chưa phát huy được vai trò của mình do không có đủ thời gian để tham vấn cho bệnh nhân; bệnh nhân không được khám bệnh một cách nghiêm túc; không được kiểm tra đúng cách.
Câu 9:
chuẩn mực, tiêu chuẩn, tiết lộ, e ngại, dự đoán
Một trong những lí do tác động đến việc người phụ nữ mắc chứng trầm cảm sau sinh có quyết định tìm kiếm dịch vụ hỗ trợ hay không đó là những _______ văn hóa xã hội đặt ra cho phụ nữ. Và ở Hoa Kỳ, quan niệm về "người mẹ tốt" khiến người phụ nữ không _______ lí do bị trầm cảm do họ ________ sẽ bị kỳ thị do chính bệnh tâm thần của họ.
 Xem đáp án
Xem đáp án
Đáp án đúng:
Kéo thả các từ phù hợp vào mỗi ô trống.
Một trong những lí do tác động đến việc người phụ nữ mắc chứng trầm cảm sau sinh có quyết định tìm kiếm dịch vụ hỗ trợ hay không đó là những chuẩn mực văn hóa xã hội đặt ra cho phụ nữ. Và ở Hoa Kỳ, quan niệm về "người mẹ tốt" khiến người phụ nữ không tiết lộ lí do bị trầm cảm do họ e ngại sẽ bị kỳ thị do chính bệnh tâm thần của họ.
(Kéo thả hoặc click vào để điền)
Câu 10:
Theo đoạn [7], người phụ nữ cảm nhận xã hội dành cho họ cách đối xử thế nào khiến họ cố gắng giấu diếm tình trạng bệnh của mình?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Theo đoạn [6], với một người phụ nữ bị trầm cảm sau sinh ví dụ ở Hoa Kỳ - 1 trong những đất nước tiên tiến và phát triển bậc nhất thế giới cũng vấp phải vấn đề bị kỳ thị và gặp phải định kiến, phân biệt đối xử. Không chỉ vậy, họ còn cảm nhận xã hội sẽ đánh giá họ là "bà mẹ xấu”.
=> Người phụ nữ mắc chứng trầm cảm sau sinh cảm nhận xã hội dành cho họ kì thị, phân biệt đối xử và cách đánh giá đầy định kiến khiến họ cố gắng giấu diếm tình trạng bệnh của mình.
Chọn A
Câu 11:
Thông tin nào sau đây KHÔNG được đề cập đến trong văn bản?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đoạn [2] và [3] có nhắc đến tác động của STKT đối với các doanh nghiệp, cụ thể là về quá trình tiêu thụ sản phẩm và tổng tài sản/tổng nguồn vốn của doanh nghiệp. Trong bài viết không nói đến “STKT ảnh hưởng nghiêm trọng đến doanh thu của các doanh nghiệp.”.
Chọn B
Câu 12:
Điền một từ không quá hai tiếng từ đoạn [6] để hoàn thành nhận định sau:
Để các khoản đầu tư cốt yếu được _______ trong hiện tại và tương lai, doanh nghiệp cần giảm chi phí sản xuất.
 Xem đáp án
Xem đáp án
Đáp án đúng:
Điền một từ không quá hai tiếng từ đoạn [6] để hoàn thành nhận định sau:
Để các khoản đầu tư cốt yếu được đảm bảo trong hiện tại và tương lai, doanh nghiệp cần giảm chi phí sản xuất.
Hướng dẫn giải:
Chú ý vào đoạn văn:
Tuy nhiên, DN cần chắc chắn rằng việc giảm chi phí này chỉ là đối với những chi phí không hiệu quả và đảm bảo cho các khoản đầu tư cốt yếu trong cả hiện tại và tương lai của DN.
--> Từ cần điền là “đảm bảo”.
Câu 13:
Ở đoạn [3], theo kết quả điều tra có tới 61% doanh nghiệp ở các tỉnh miền Bắc chịu áp lực rất lớn về giá bán. Đúng hay sai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Theo kết quả điều tra, có tới 35/57, chiếm 61% DN điều tra chịu áp lực rất lớn về giá bán.
Con số 61% là kết quả điều tra của 57 doanh nghiệp, chứ không phải là tất các doanh nghiệp ở các tỉnh miền Bắc.
Chọn B
Câu 14:
Dòng nào là thông tin chính xác được đề cập trong văn bản?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
- Đoạn [3]: Trong đó, tỷ lệ doanh nghiệp chế biến (DNCB) chịu áp lực về giá là lớn nhất với khoảng 75%. Con số này của doanh nghiệp sản xuất (DNSX) và doanh nghiệp dịch vụ (DNDV) lần lượt là 70% và 48%.
--> Đáp án “Doanh nghiệp sản xuất chịu áp lực về giá thấp nhất với khoảng 48%.” là sai.
- Đoạn [4]: STKT có ảnh hưởng lớn tới thu nhập của người tiêu dùng, do vậy ảnh hưởng không nhỏ đến thị trường tiêu thụ sản phẩm của DN.
--> Đáp án “Thị trường tiêu thụ sản phẩm của doanh nghiệp bị ảnh hưởng là vì nguồn nhân lực không đạt yêu cầu.” là sai.
- Đoạn [3]: Trong thời kỳ suy thoái, DN gặp nhiều khó khăn nhưng theo kết quả điều tra, có tới gần 58% DN cho rằng khó khăn quan trọng nhất đó là sức mua của thị trường giảm sút một cách nghiêm trọng. Điều này đã làm giảm lượng cầu gây khó khăn cho vấn đề giải quyết đầu ra của DN.
--> Đáp án “Khoảng 58% doanh nghiệp khẳng định khó khăn lớn nhất là mở rộng thị trường trong thời kỳ STKT.” là sai.
- Đoạn [2], tác giả có viết: Kết quả nghiên cứu cho thấy có khoảng 1/3 số DN được điều tra gặp những khó khăn về vốn trong thời kỳ STKT. Sự khó khăn này là do tồn kho và các khoản phải thu của DN tăng lên đáng kể so với thời kỳ không suy thoái.
--> Đáp án “Trong thời kỳ STKT, có 1/3 doanh nghiệp được điều tra gặp khó khăn về vốn do tồn kho và các khoản phải thu tăng lên đáng kể.” là đúng.
Chọn B
Câu 15:
nhân lực, doanh nghiệp, kế hoạch
Trong thời kỳ suy thoái kinh tế, doanh nghiệp cần nâng cao chất lượng nguồn _______. Những chính sách hợp lí sẽ giúp _______ thu hút, giữ chân lao động có chuyên môn, kĩ thuật cao. Bên cạnh đó, để có _______ tuyển dụng và sử dụng hợp lý, doanh nghiệp cần rà soát lại đội ngũ nhân sự.
 Xem đáp án
Xem đáp án
Đáp án đúng:
Chọn kéo cụm từ phù hợp vào mỗi chỗ trống:
Trong thời kỳ suy thoái kinh tế, doanh nghiệp cần nâng cao chất lượng nguồn nhân lực. Những chính sách hợp lí sẽ giúp doanh nghiệp thu hút, giữ chân lao động có chuyên môn, kĩ thuật cao. Bên cạnh đó, để có kế hoạch tuyển dụng và sử dụng hợp lý, doanh nghiệp cần rà soát lại đội ngũ nhân sự.
Hướng dẫn giải:
Đọc kĩ đoạn [5] kết hợp với hiểu nghĩa của các từ ngữ.
- Vị trí (1) điền từ “nhân lực”: sức người, về mặt sử dụng trong lao động sản xuất (nguồn nhân lực).
- Vị trí (2) điền từ “doanh nghiệp”: đơn vị hoạt động kinh doanh.
- Vị trí (3) điền từ “kế hoạch”: toàn bộ những điều vạch ra một cách có hệ thống và cụ thể về cách thức, trình tự, thời hạn tiến hành những công việc dự định làm trong một thời gian nhất định, với mục tiêu nhất định.
Câu 16:
Mục đích chính của đoạn [4], [5], [6], [7] là gì?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Lần lượt xem xét các đoạn:
- Đoạn [4]: Tác giả chỉ ra cụ thể một số giải pháp đối với thị trường đầu ra: DN cần tiếp tục và mở rộng chính sách giá linh hoạt đối với các sản phẩm và dịch vụ để thu hút thêm khách hàng; Thực hiện niêm yết giá mới mỗi khi có sự thay đổi giá sản phẩm và dịch vụ.
- Đoạn [5]: Tác giả chỉ ra giải pháp trong việc sử dụng/ quản lí nhân lực:
+ Có các chính sách hợp lý nhằm thu hút, giữ chân lao động có trình độ chuyên môn, kỹ thuật cao, nâng cao năng suất lao động, chất lượng sản phẩm thông qua đào tạo và phát triển nguồn nhân lực nhằm giảm bớt áp lực về việc làm trong thời kỳ STKT.
+ Áp dụng các hình thức tiền lương linh hoạt, tiền lương được trả theo đóng góp lao động, hiệu quả sản xuất - kinh doanh của DN và theo quan hệ thị trường để nâng cao tính kích thích, cạnh tranh của tiền lương.
- Đoạn [6]: Tác giả chỉ ra giải pháp trong tổ chức sản xuất:
+ Rà soát nhằm giảm bớt các khoản mục chi phí không cần thiết nhằm giảm giá thành sản phẩm bằng cách tổ chức hợp lý các quá trình sản xuất, lược bớt những khâu không mang lại hiệu quả.
- Đoạn [7]: Tác giả chỉ ra giải pháp đảm bảo đầu vào cho sản xuất
+ Giữ vững các nhà cung cấp hiện có và tìm kiếm thêm các nhà cung ứng mới có uy tín, chủ động đàm phán lại với các nhà cung ứng về giá đầu vào,...
+ Tận dụng tối đa chính sách hỗ trợ lãi suất của Chính phủ, thực hiện vay vốn ngân hàng để đảm bảo vốn cho sản xuất - kinh doanh.
--> Mục đích chính của đoạn [4], [5], [6], [7] là “Chỉ ra một số giải pháp nhằm hạn chế tác động tiêu cực của STKT tới sản xuất kinh doanh của doanh nghiệp.”
Chọn B
Câu 17:
Theo tác giả, giải pháp nào là ưu tiên số một của doanh nghiệp trong thời kỳ suy thoái?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đọc kĩ đoạn [6]: Giảm chi phí sản xuất là cách ứng phó quan trọng và là ưu tiên số một của DN trong thời kỳ suy thoái. Tuy nhiên, DN cần chắc chắn rằng việc giảm chi phí này chỉ là đối với những chi phí không hiệu quả và đảm bảo cho các khoản đầu tư cốt yếu trong cả hiện tại và tương lai của DN. Vì vậy, DN phải rà soát nhằm giảm bớt các khoản mục chi phí không cần thiết nhằm giảm giá thành sản phẩm bằng cách tổ chức hợp lý các quá trình sản xuất, lược bớt những khâu không mang lại hiệu quả.
--> Đáp án đúng là “Giảm chi phí không hiệu quả.”.
Chọn C
Câu 18:
Ở đoạn [2], theo thống kê, trong giai đoạn 2006 – 2009, tốc độ tăng trưởng giảm liên tục còn xấp xỉ 4%. Điều này cho thấy rõ tình hình tài sản/nguồn vốn của doanh nghiệp có những biến động rõ rệt. Đúng hay sai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Trong giai đoạn 2006 – 2009, tốc độ tăng trưởng giảm so với thời kỳ nền kinh tế không bị suy thoái. Tốc độ tăng trưởng bình quân mỗi năm đạt 7,36%. Tuy nhiên, con số này lại không đều qua các năm. Năm 2007 có tốc độ tăng trưởng cao nhất với gần 11%, năm 2009 là thấp nhất với xấp xỉ 4%.
Vậy nghĩa là tốc độ tăng trưởng không giảm liên tục.
Chọn B
Câu 19:
Điền một cụm từ không quá bốn tiếng từ đoạn [2] để hoàn thành nhận định sau:
So với thời kỳ không suy thoái, để thu toàn bộ tiền hàng từ khách hàng và nhà phân phối cũng như các khoản hoàn ứng của nhân viên, doanh nghiệp phải mất _______ dài hơn.
 Xem đáp án
Xem đáp án
Đáp án đúng:
Điền một cụm từ không quá bốn tiếng từ đoạn [2] để hoàn thành nhận định sau:
So với thời kỳ không suy thoái, để thu toàn bộ tiền hàng từ khách hàng và nhà phân phối cũng như các khoản hoàn ứng của nhân viên, doanh nghiệp phải mất thời gian trung bình dài hơn.
Hướng dẫn giải:
Chú ý vào đoạn văn: Trong thời kỳ suy thoái, thời gian trung bình để thu toàn bộ tiền hàng từ khách hàng và nhà phân phối cũng như các khoản hoàn ứng của nhân viên là dài hơn.
--> Cụm từ cần điền là “thời gian trung bình”.
Câu 20:
Nội dung chính của đoạn [3] là gì?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đoạn [3] đề cập rất rõ:
- Trong thời kỳ suy thoái, DN gặp nhiều khó khăn nhưng theo kết quả điều tra, có tới gần 58% DN cho rằng khó khăn quan trọng nhất đó là sức mua của thị trường giảm sút một cách nghiêm trọng. Điều này đã làm giảm lượng cầu gây khó khăn cho vấn đề giải quyết đầu ra của DN.
- Theo kết quả điều tra, có tới 35/57, chiếm 61% DN điều tra chịu áp lực rất lớn về giá bán.
- Đối với DN, vì giá đầu vào tăng lên gần 20%, để đảm bảo lợi nhuận cho các nhà đầu tư và cho cả quá trình tái sản xuất mở rộng, DN phải chịu áp lực không nhỏ là phải tăng giá bán.
- Đối với khách hàng, trong thời kỳ kinh tế khó khăn, với nguồn ngân quỹ tăng lên với tốc độ giảm hoặc thấp hơn so với thời kỳ trước. Vì vậy, để có thể bán được hàng hóa, DN phải giảm giá, đây là một áp lực rất lớn.
--> Nội dung chính của đoạn [3] là “Tác động của STKT tới quá trình tiêu thụ sản phẩm.”
Chọn ACâu 21:
Phần tư duy khoa học / giải quyết vấn đề
 Xem đáp án
Xem đáp án
Chọn đáp án C
Câu 24:
từ cực, nam châm, lực đẩy và lực hút, điện trường, hút hoặc đẩy, từ trường
Nguyên lí hoạt động của tàu đệm từ: Khi dòng điện chạy qua cuộn dây dẫn điện, nó sẽ sinh ra một ________ trong các vòng dây. Sau đó các vòng dây này sẽ bị từ hóa và tạo ra ________ . Với từ trường này nó có thể _________ một vật có từ tính khác nằm trong từ trường của nó. Từ trường này có tính chất tương đương với từ trường của _________. Vì vậy khi dòng điện trong các cuộn dây dẫn liên tục đổi chiều, thì các nam châm điện cũng liên tục thay đổi _______, làm đoàn tàu di chuyển về phía trước nhờ vào ________ giữa các nam châm với nhau.
(Kéo thả hoặc click vào để điền)
 Xem đáp án
Xem đáp án
Đáp án đúng:
Điền từ còn thiếu vào chỗ trống.
Nguyên lí hoạt động của tàu đệm từ: Khi dòng điện chạy qua cuộn dây dẫn điện, nó sẽ sinh ra một điện trường trong các vòng dây. Sau đó các vòng dây này sẽ bị từ hóa và tạo ra từ trường. Với từ trường này nó có thể hút hoặc đẩy một vật có từ tính khác nằm trong từ trường của nó. Từ trường này có tính chất tương đương với từ trường của nam châm. Vì vậy khi dòng điện trong các cuộn dây dẫn liên tục đổi chiều, thì các nam châm điện cũng liên tục thay đổi từ cực, làm đoàn tàu di chuyển về phía trước nhờ vào lực đẩy và lực hút giữa các nam châm với nhau.
(Kéo thả hoặc click vào để điền)
Câu 25:
Nam châm siêu dẫn đã tạo ra từ trường mạnh để giúp tàu đệm từ di chuyển với tốc độ cao. Hiện tượng siêu dẫn là hiện tượng gì?
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 26:
Một đầu tàu đệm từ nặng 19 tấn chạy ổn định với vận tốc 540 km/h. Biết lực cản của không khí được tính theo biểu thức: F = k.v2 với k = 0,5. Hỏi lực từ tổng hợp tác dụng lên đầu tàu là bao nhiêu?
Trả lời: _______ N.
(Kết quả làm tròn đến số nguyên gần nhất)
 Xem đáp án
Xem đáp án
Đáp án đúng “190332”:
Hướng dẫn giải:
\({F_{{\rm{nang }}}} = P = mg = 19000.10 = 190000N\)
Khi tàu chạy ổn định thì: \({F_{day}} = {F_{can}} = k{v^2} = 0,{5.150^2} = 11250N\)
\(F = \sqrt {F_{{\rm{nang }}}^2 + F_{{\rm{day }}}^2} = 190333\;{\rm{N}}\)
Câu 27:
 Xem đáp án
Xem đáp án
Chọn đáp án B
Câu 28:
Điền từ thích hợp vào chỗ trống.
không từ lực, hai đám mây, đám mây và mặt đất, từ lực
Sét là quá trình phóng điện _________ .
Sấm là tiếng nổ khi có sự phóng điện giữa __________.
Sét là tiếng nổ khi có sự phóng điện giữa __________.
(Kéo thả hoặc click vào để điền)
 Xem đáp án
Xem đáp án
Đáp án đúng:
Điền từ thích hợp vào chỗ trống.
Sét là quá trình phóng điện tự lực .
Sấm là tiếng nổ khi có sự phóng điện giữa hai đám mây.
Sét là tiếng nổ khi có sự phóng điện giữa đám mây và mặt đất.
(Kéo thả hoặc click vào để điền)
Câu 30:
Cho các ảnh hưởng của sét lên đời sống như sau:
(1) Sét phá hủy các công trình cao tầng và gây các đám cháy rừng lớn.
(2) Khi có chớp (tia lửa điện) sẽ tạo điều kiện cho nitơ hoạt động.
(3) Sét đánh thẳng vào nhà cửa, công trình hoặc bồn nước kim loại hay trụ anten nằm trên công trình đó, đánh vào cây cối, đánh vào người đang di chuyển khi đang có dông.
(4) Khi có sấm chớp tạo ra một lượng nhỏ khí ozon (O3) có tác dụng sát khuẩn trong không khí và hấp thụ các tia tử ngoại để bảo vệ sự sống trên Trái Đất.
(5) Tia lửa điện từ sét giúp nitơ và oxy trong không khí kết hợp lại thành NO2 theo nước mưa thành phân đạm cho đất.
Những lợi ích của sét là
 Xem đáp án
Xem đáp án
Chọn đáp án A
Câu 31:
Một dòng điện được tạo ra trong một ống chứa khí hidro. Khi có một hiệu điện thế đủ cao giữa hai điện cực của ống, chất khí bị ion hoá và các electron chuyển động về cực dương, các ion dương về cực âm. Khi có 4,2.1018 electron và 2,2.1018 proton chuyển động qua tiết diện của ống trong mỗi giây thì cường độ và chiều của dòng điện chạy qua ống khí này là
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Chiều dòng điện trong ống phóng điện là từ cực dương sang cực âm của ống. Cường độ dòng điện qua ống:
\(I = \frac{q}{t} = \frac{{\left( {{n_e} + {n_p}} \right).|e|}}{t} = \frac{{4,{{2.10}^{18}} + 2,{{2.10}^{18}}.1,{{6.10}^{ - 19}}}}{1} = 1,024\;{\rm{A}}\)
Chọn D
Câu 34:
Một máy biến áp có số vòng dây cuộn sơ cấp lớn hơn số vòng dây của cuộn thứ cấp. Máy biến áp này có tác dụng
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Cuộn sơ cấp có số vòng là N1, cuộn thứ cấp có số vòng là N2.
Ta có: \(\frac{{{N_1}}}{{{N_2}}} = \frac{{{U_1}}}{{{U_2}}} = \frac{{{I_2}}}{{{I_1}}}\)
\({N_1} > {N_2} \Rightarrow {U_1} > {U_2};{I_1} < {I_2}\)
Chọn B
Câu 35:
Muốn làm giảm hao phí do tỏa nhiệt của dòng fuco gây trên khối kim loại người ta thường
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Muốn làm giảm hao phí do tỏa nhiệt của dòng fuco gây trên khối kim loại người ta thường chia khối kim loại thành nhiều lá kim loại mỏng ghép cách điện nhau. Khi đó dòng fuco chỉ chạy trong từng lá mỏng, vì từng lá đơn lẻ có kích thước nhỏ nên có điện trở lớn, cường độ dòng điện fuco trong các lá sẽ giảm đi nhiều so với cường độ dòng điện fuco trong cả khối lớn.
Chọn B
Câu 36:
Bằng đường dây truyền tải một pha, điện năng từ một nhà máy phát điện nhỏ được đưa đến một khu tái định cư. Các kĩ sư tính toán được rằng: nếu tăng điện áp truyền đi từ U lên 2U thì số hộ dân được nhà máy cung cấp đủ điện năng tăng từ 36 lên 144. Biết rằng chỉ có hao phí trên đường dây là đáng kể; các hộ dân tiêu thụ điện năng như nhau. Điện áp truyền đi là 3U, nhà máy này cung cấp đủ điện năng cho bao nhiêu hộ dân?
Trả lời: _______ hộ dân.
 Xem đáp án
Xem đáp án
Đáp án đúng: “164”
Hướng dẫn giải:
Công suất điện của nhà máy: P
Công suất tiêu thụ của mỗi hộ dân là P0
Điện trở đường dây tải là R
n là số hộ dân được cung cấp điện khi điện áp truyền đi là 3U
Công suất hao phí trên đường dây: \(\Delta P = \frac{{{P^2}R}}{{{U^2}}}\)
Theo bài ta có:
\(P = 36{P_0} + \frac{{{P^2}R}}{{{U^2}}}\) (1)
\(P = 144{P_0} + \frac{{{P^2}R}}{{4{U^2}}}\) (2)
\(P = n{P_0} + \frac{{{P^2}R}}{{9{U^2}}}\) (3)
Giải các phương trình trên ta tìm được n = 164
Câu 37:
Phương trình phản ứng điều chế este vinyl axetat là
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Không thể điều chế trực tiếp vinyl axetat từ axit axetic và ancol vinylic vì ancol này không bền, do đó phải thực hiện phản ứng giữa axit axetic và axetilen.
Chọn A
Câu 38:
Thực hiện phản ứng điều chế isoamyl axetat (dầu chuối) theo trình tự sau:
- Bước 1: Cho 2 ml ancol isomylic, 2 ml axit axetic nguyên chất và 2 giọt axit sunfuric đặc vào ống nghiệm khô.
- Bước 2: Lắc đều, đun cách thuỷ hỗn hợp 8-10 phút trong nồi nước sôi.
- Bước 3: Để nguội, rồi rót hỗn hợp sản phẩm và ống nghiệm chứa 3-4 ml nước lạnh.
Phát biểu nào sau đây đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
(1) Từ hỗn hợp thu được sau bước 3, tách lấy isoamyl axetat bằng phương pháp chiết.
Đúng. Do este thu được không tan trong nước, nổi lên trên, nên có thể sử dụng phương pháp chiết để tách este (chiết là phương pháp dùng để tách hai chất lỏng không hoà tan vào nhau).
(2) Sau bước 3, hỗn hợp thu được tách thành 3 lớp.
Sai. Hỗn hợp bị tách thành 2 lớp, trong đó lớp este bên trên, lớp bên dưới chứa ancol dư, axit dư, nước.
(3) Phản ứng este hoá giữa ancol isoamylic với axit axetic là phản ứng một chiều.
Sai. Phản ứng este hoá là phản ứng thuận nghịch.
(4) Việc cho hỗn hợp sản phẩm vào nước lạnh ở bước 3 nhằm tránh sự thuỷ phân của isoamyl axetat.
Sai. Thêm nước lạnh để tăng tỉ khối của hỗn hợp giúp tách este ra dễ dàng hơn.
Chọn C
Câu 39:
Tiến hành thí nghiệm theo các bước sau:
- Bước 1: Cho vào hai ống nghiệm mỗi ống 2 ml etyl axetat.
- Bước 2: Thêm 2 ml dung dịch H2SO4 20% vào ống thứ nhất; 4 ml dung dịch NaOH 30% vào ống thứ hai.
- Bước 3: Lắc đều cả hai ống nghiệm, lắp ống sinh hàn, đun sôi nhẹ trong khoảng 5 phút, để nguội.
Cho các phát biểu sau:
(a) Sau bước 2, chất lỏng trong cả hai ống nghiệm đều phân thành hai lớp.
(b) Sau bước 3, chất lỏng trong cả hai ống nghiệm đều đồng nhất.
(c) Sau bước 3, ở hai ống nghiệm đều thu được sản phẩm giống nhau.
(d) Ở bước 3, có thể thay việc đun sôi nhẹ bằng đun cách thuỷ (ngâm trong nước nóng).
(e) Ống sinh hàn có tác dụng hạn chế sự thất thoát của các chất lỏng trong ống nghiệm.
Số phát biểu đúng là
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
(a) Sau bước 2, chất lỏng trong cả hai ống nghiệm đều phân thành hai lớp.
Đúng. Do este không tan trong nước.
(b) Sau bước 3, chất lỏng trong cả hai ống nghiệm đều đồng nhất.
Sai. Do phản ứng thuỷ phân este trong môi trường axit là phản ứng không hoàn toàn, nên ống nghiệm thứ nhất hỗn hợp bị tách thành hai lớp.
(c) Sau bước 3, ở hai ống nghiệm đều thu được sản phẩm giống nhau.
Sai. Ống 1 thu được CH3COOH và C2H5OH, cùng với CH3COOC2H5 dư. Ống 2 thu được CH3COONa và C2H5OH.
(d) Ở bước 3, có thể thay việc đun sôi nhẹ bằng đun cách thuỷ (ngâm trong nước nóng).
Đúng. Cả hai cách đều cung cấp nhiệt độ cho phản ứng ở mức 50 - 70 độ C.
(e) Ống sinh hàn có tác dụng hạn chế sự thất thoát của các chất lỏng trong ống nghiệm.
Đúng. Trong ống sinh hàn, những chất bay hơi khi gặp lạnh sẽ ngưng tụ và chảy ngược trở lại ống nghiệm.
Chọn B
Câu 40:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đất chua là đất có dư axit (ion H+), do đó sẽ không dùng axit để khử chua đất trồng.
Chọn C
Câu 41:
Phát biểu sau đây đúng hay sai? Hiện nay, công nghệ CaSO4 là công nghệ được áp dụng phổ biến nhất để chế tạo axit sunfuric.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Sai, công nghệ tiếp xúc.
Chọn B
Câu 42:
Ở Mỹ, nguyên liệu chính được sử dụng để sản xuất axit sunfuric là _______.
 Xem đáp án
Xem đáp án
Đáp án đúng:
Ở Mỹ, nguyên liệu chính được sử dụng để sản xuất axit sunfuric là lưu huỳnh.
Hướng dẫn giải:
Lưu huỳnh.
Câu 43:
Cho sơ đồ điều chế axit sunfuric: A → SO2 → B → H2SO4.
A và B lần lượt là
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
(1) 4FeS2 + 11O2 → 2Fe2O3 + 8SO2
(2) 2SO2 + O2 → 2SO3
(3) SO3 + H2O → H2SO4
Chọn B
Câu 44:
Có một loại quặng pirit chứa 96% FeS2. Nếu mỗi ngày, nhà máy sản xuất 100 tấn axit sunfuric 98% thì tiêu thụ bao nhiêu tấn quặng pirit đó? Biết hiệu suất của quá trình sản xuất là 90%.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Ta có sơ đồ: FeS2 → 2H2SO4
1 mol → 2 mol
120 gam → 196 gam
60 tấn ← 98 tấn
Khối lượng FeS2 lý thuyết để sản xuất được 98 tấn H2SO4 là 60 tấn.
→ Khối lượng FeS2 thực tế là: \(\frac{{60}}{{90\% }} = 66,67\) (tấn)
Quặng pirit chứa 96% FeS2 → Khối lượng quặng là: \(\frac{{66,67}}{{96\% }} = 69,44\) (tấn)
Chọn B
Câu 45:
Giả sử lưới thức ăn của một quần xã sinh vật gồm các loài sinh vật được kí hiệu là A, B, C, D, E, F, G và H. Cho biết loài A và loài C là sinh vật sản xuất, các loài còn lại đều là sinh vật tiêu thụ. Trong lưới thức ăn này, nếu loại bỏ loài C ra khỏi quần xã thì chỉ có loài D và loài F mất đi. Sơ đồ lưới thức ăn nào dưới đây đúng với các thông tin đã cho?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Sơ đồ I, nếu loại bỏ C thì mất đi 3 loài là B, D và F.
Sơ đồ II, nếu loại bỏ C thì chỉ mất đi loài B.
Sơ đồ III, nếu loại bỏ C thì mất đi 2 loài là G và F.
Sơ đồ IV, nếu loại bỏ C thì mất đi 2 loài là D và F.
Chọn B
Câu 46:
Chuỗi thức ăn dài nhất có _______ bậc dinh dưỡng.
 Xem đáp án
Xem đáp án
Đáp án đúng:
Chuỗi thức ăn dài nhất có 5 bậc dinh dưỡng.
Hướng dẫn giải:
Các chuỗi thức ăn có 5 bậc dinh dưỡng bao gồm:
A → B → E → C → D
A → G → E → C → D
A → B → E → H → D
A → G → E → H → D
Câu 47:
Theo lí thuyết, lưới thức ăn trên có tổng số _______ chuỗi thức ăn.
 Xem đáp án
Xem đáp án
Đáp án đúng:
Theo lí thuyết, lưới thức ăn trên có tổng số 11 chuỗi thức ăn.
Hướng dẫn giải:
Lưới thức ăn trên có tổng số 11 chuỗi thức ăn.
|
A → B → E → C → D A → G → E → C → D A → B → E → D A → E → D A → E → H → D A → G → E → D |
A → B → E → H → D A → G → E → H → D A → G → H → D A → B → C → D A → E → C → D |
Câu 48:
Nếu loài C bị nhiễm độc ở nồng độ thấp thì loài _______ sẽ bị nhiễm độc ở nồng độ cao hơn so với loài C.
 Xem đáp án
Xem đáp án
Đáp án đúng:
Nếu loài C bị nhiễm độc ở nồng độ thấp thì loài D sẽ bị nhiễm độc ở nồng độ cao hơn so với loài C.
Hướng dẫn giải:
Loài D sử dụng loài C làm thức ăn nên loài D sẽ bị nhiễm độc ở nồng độ cao hơn nếu như loài C bị nhiễm độc.
Câu 49:
Loại đột biến nào dưới đây không phải đột biến nhiễm sắc thể?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đột biến cấu trúc nhiễm sắc thể là những biến đổi trong cấu trúc nhiễm sắc thể; bao gồm: mất đoạn, lặp đoạn, đảo đoạn, chuyển đoạn.
Đột biến số lượng nhiễm sắc thể là những đột biến làm thay đổi về số lượng nhiễm sắc thể trong tế bào; bao gồm: đột biến lệch bội (dị bội) và đột biến đa bội.
Chọn D
Câu 50:
Loại đột biến nào dưới đây dẫn đến sự trao đổi hoặc thay thế cặp bazơ nitric theo kiểu thay thế đồng hoán?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Kiểu thay thế đồng hoán là đột biến thay thế nucleotit xảy ra trong mỗi nhóm purin hoặc pirimidin.
Nhóm purin gồm A và G.
Nhóm pirimidin gồm T và X.
Chọn A
Câu 51:
Khi nói về đột biến điểm, phát biểu nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
- Đột biến điểm bao gồm: mất một cặp nucleotit, thêm một cặp nucleotit và thay thế một cặp nucleotit.
→ Khi mất và thêm một cặp nucleotit thì tổng số nucleotit sẽ thay đổi.
- Nếu đột biến xảy ra ở vùng điều hòa thì có thể không làm thay đổi cấu trúc của chuỗi nhưng có thể làm tăng số lượng chuỗi.
→ Đột biến vẫn có thể gây hại.
- Vì là đột biến điểm và không làm thay đổi tổng liên kết hiđro.
→ Dạng thay A - T bằng T - A hoặc thay G - X bằng X - G.
→ Tổng nucleotit không đổi.
→ Chiều dài của gen không đổi.
Chọn C
Câu 52:
Tính trạng thân xám (A), cánh dài (B) ở ruồi giấm là trội hoàn toàn so với thân đen (a), cánh cụt (b); 2 gen quy định tính trạng trên cùng nằm trên một cặp nhiễm sắc thể thường. Gen D quy định màu mắt đỏ là trội hoàn toàn so với d quy định mắt trắng nằm trên vùng không tương đồng của nhiễm sắc thể giới tính X. Thế hệ P cho giao phối ruồi cái \(\frac{{Ab}}{{aB}}{X^D}{X^d}\) với ruồi đực \(\frac{{AB}}{{ab}}{X^d}Y\) được F1 gồm 160 cá thể trong đó có 6 ruồi cái thân đen, cánh dài, mắt trắng. Cho rằng tất cả các trứng tạo ra đều tham gia vào quá trình thụ tinh và hiệu suất thụ tinh của trứng là 80%; 100% trứng được thụ tinh phát triển thành cá thể. Có bao nhiêu tế bào sinh trứng của ruồi giấm nói trên không xảy ra hoán vị gen trong quá trình tạo giao tử?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đối tượng của câu hỏi là ruồi giấm → Hoán vị gen chỉ xảy ra ở giới cái, không xảy ra ở giới đực.
Ta có: \(aa{B_ - }{X^d}{X^d} = 6:160 = 3,75\% {\rm{.}}\)
\( \to aaB = 15\% \left( {{X^D}{X^d} \times {X^d}Y \to 1/4{X^d}{X^d}} \right)\)
Mặt khác ở ruồi giấm, hoán vị gen chỉ xảy ra ở con cái.
→ Con đực cho ra giao tử ab = 1/2.
→ Ở con cái giao tử aB = 30%.
→ Tần số hoán vị gen là 40%.
Số trứng tham gia thụ tinh: 160 : 80% = 200.
→ Số trứng xảy ra hoán vị: 200 x 40% = 80.
→ Số tế bào xảy ra hoán vị: 80 x 2 = 160 (do 1 tế bào cho 1 trứng).
Tế bào xảy ra hoán vị cho 1/2 giao tử hoán vị và 1/2 giao tử liên kết.
→ Số tế bào không hoán vị: 200 - 160 = 40 tế bào.
Chọn A
Câu 53:
Ở ruồi giấm có bộ nhiễm sắc thể lưỡng bội 2n = 8. Xét hai tế bào sinh dục sơ khai ở vùng sinh sản đều nguyên phân liên tiếp 11 đợt. 1,5625% tế bào con trải qua giảm phân. Số lượng nhiễm sắc thể đơn môi trường cần cung cấp cho qua trình giảm phân là bao nhiêu?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Bộ NST lưỡng bội của loài 2n = 8.
Hai tế bào sinh dục sơ khai nguyên phân 11 đợt tạo ra 2 x 211 = 4096 tế bào.
Số tế bào tham gia giảm phân là 4096 x 0,015625 = 64 tế bào.
Số NST đơn môi trường cung cấp cho giảm phân là 64 x 8 = 512 NST.
Chọn D
Câu 54:
Quá trình tổng hợp của vi sinh vật được ứng dụng trong những quá trình sản xuất nào dưới đây?
I. Sản xuất rượu, tương, cà muối.
II. Sản xuất chất xúc tác sinh học, gôm.
III. Sản xuất protein đơn bào.
IV. Sản xuất nem chua, nước mắm.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Việc sản xuất rượu, tương, cà muối, nem chua và nước mắm dựa trên quá trình phân giải vi sinh vật.
Chọn A
Câu 55:
Trong quá trình nhân lên của virut, giai đoạn nào xảy ra sự liên kết giữa các thụ thể của virut với thụ thể của tế bào chủ?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Giai đoạn hấp phụ: virut bám vào tế bào chủ nhờ các gai glycoprotein hoặc protein bề mặt của virut (đối với virut không có vỏ ngoài) tương tác đặc hiệu với các thụ thể trên bề mặt của tế bào chủ (như chìa khóa và ổ khóa).
Chọn B
Câu 56:
Các con đực của nhiều loài ruồi Drosophila khác nhau sống trên cùng một vùng của quần đảo Hawaii có các trình tự giao hoan tinh tế bao gồm cả việc đánh đuổi các con đực khác và các kiểu di chuyển đặc trưng nhằm thu hút các con cái. Sự hình thành các con ruồi trên là ví dụ minh hoạ cho con đường hình thành loài bằng kiểu cách li sinh sản nào?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Cách li tập tính: Các cá thể của các loài khác nhau có thể có những tập tính giao phối riêng nên giữa chúng thường không giao phối với nhau.
Chọn D
Câu 57:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Cơ quan thoái hoá cũng là các cơ quan tương đồng vì chúng được bắt nguồn từ một cơ quan ở một loài tổ tiên nhưng nay không còn chức năng hoặc chức năng bị tiêu giảm.
Xương cùng, ruột thừa và răng khôn ở người được xem là cơ quan thoái hoá.
Chọn D
Câu 58:
Giả sử trong một hồ tự nhiên, tảo là thức ăn của giáp xác; cá mương sử dụng giáp xác làm thức ăn đồng thời lại làm mồi cho cá quả. Cá quả tích luỹ được 1152 × 103 kcal, tương đương với 10% năng lượng tích luỹ ở bậc dinh dưỡng thấp hơn liền kề với nó. Cá mương tích luỹ được một lượng năng lượng tương đương với 8% năng lượng tích luỹ ở giáp xác. Tảo tích luỹ được 12 × 108 kcal. Hiệu suất sinh thái giữa bậc dinh dưỡng cấp 2 và bậc dinh dưỡng cấp 1 là bao nhiêu?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
- Bậc dinh dưỡng cấp 2 là giáp xác.
- Bậc dinh dưỡng cấp 1 là tảo, tích luỹ được 12 × 108 kcal.
- Cá quả tích luỹ được 1152 × 103 kcal = 10% năng lượng tích luỹ ở cá mương.
→ Số năng lượng cá mương tích luỹ được là: 1152 × 104 kcal.
- Cá mương tích luỹ được một lượng năng lượng tương đương với 8% năng lượng tích luỹ ở giáp xác.
→ Số năng lượng tích luỹ ở giáp xác là: 144 × 106 kcal.
- Hiệu suất sinh thái giữa bậc dinh dưỡng cấp 2 và bậc dinh dưỡng cấp 1 là
(144 × 106) : (12 × 108) = 12%.
Chọn A
Câu 59:
Hiện tượng nào dưới đây phản ánh dạng biến động số lượng của quần thể sinh vật không theo chu kì?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
- Ở đồng rêu phương Bắc, cứ 3 - 4 năm, số lượng cáo lại tăng lên gấp 100 lần và sau đó lại giảm.
→ Biến động theo chu kì, cứ 3 - 4 năm lại lặp lại.
- Ở Việt Nam, vào mùa xuân khí hậu ấm áp, sâu hại thường xuất hiện nhiều.
→ Biến động theo chu kì, ở nước ta thì mùa xuân năm nào cũng ấm áp.
- Ở miền Bắc Việt Nam, số lượng ếch và nhái giảm vào những năm có mùa động giá rét, nhiệt độ xuống dưới 8oC.
→ Không xác định được những năm có mùa đông giá rét có lặp đi lặp lại được hay không.
→ Biến động không theo chu kì.
- Ở Việt Nam, hàng năm vào mùa thu hoạch lúa và ngô, chim cu gáy thường xuất hiện nhiều.
→ Biến động theo chu kì, có từ "hàng năm" tức là có sự lặp đi lặp lại.
Chọn C
Câu 60:
Khi nói về hình thức sinh sản trinh sinh, phát biểu nào dưới đây sai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Trinh sinh là một hình thức sinh sản vô tính mà trứng không thụ tinh phát triển thành cá thể mới có bộ nhiễm sắc thể đơn bội (n).
Câu 61:
Phần tư duy toán học
Mô đun của z là ___________ .
 Xem đáp án
Xem đáp án
Đáp án đúng: 13
Gọi z là số phức liên hợp của 5 − 12i.Mô đun của z là .
Hướng dẫn giải:
Từ giả thiết, ta có z = 5 + 12i.
\(\left| z \right| = \sqrt {{5^2} + {{12}^2}} = 13\).
Câu 62:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
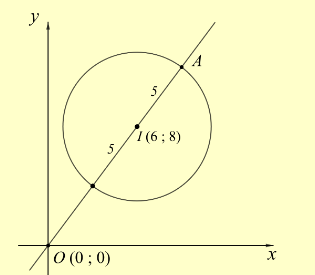
Tập hợp điểm z là đường tròn tâm I(6;8) bán kính R = 5.
Dựa vào hình minh hoạ, ta thấy số phức z có modul lớn nhất có điểm biểu diễn là điểm A ở trên hình vẽ.
Vậy max∣z∣ = OI + IA = OI + R = 10 + 5 = 15.
Chọn B
Câu 63:
Lan mua một máy tính xách tay tại một cửa hàng với giá niêm yết đã giảm 20% so với giá ban đầu. Tổng số tiền Lan phải trả là 10 triệu đồng, bao gồm 8% thuế giá trị gia tăng (VAT) trên giá niêm yết. Mỗi khẳng định sau đúng hay sai?
|
Đúng |
Sai |
|
|
Giá ban đầu của máy tính trên là 11 574 074 đồng. |
||
|
Nếu giá ban đầu của máy tính là x đồng (x > 0) thì tiền thuế VAT là 8%x đồng. |
||
|
Nếu giá ban đầu của máy tính là x đồng (x > 0) thì tiền thuế VAT là 0,64x đồng. |
 Xem đáp án
Xem đáp án
Đáp án đúng:
|
Đúng |
Sai |
|
|
Giá ban đầu của máy tính trên là 11 574 074 đồng. |
X | |
|
Nếu giá ban đầu của máy tính là x đồng (x > 0) thì tiền thuế VAT là 8%x đồng. |
X | |
|
Nếu giá ban đầu của máy tính là x đồng (x > 0) thì tiền thuế VAT là 0,64x đồng. |
X |
Hướng dẫn giải:
Gọi giá ban đầu của máy tính trên là x đồng (x > 0).
Giá tiền niêm yết máy tính trên là (100% − 20%)x = 80%x
Tiền thuế giá trị gia tăng của máy tính trên là \[80\% x.8\% = \frac{{64}}{{1000}}x\]
Theo bài ra ta có : \(\frac{{80}}{{100}}x + \frac{{64}}{{1000}}x = 10000000 \Leftrightarrow x = 11574074\) đồng.
Vậy giá ban đầu của máy tính trên là 11 574 074 đồng.
Câu 64:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đặt \(\left\{ \begin{array}{l}u = \ln x\\dv = x\end{array} \right.\), ta có \(\left\{ \begin{array}{l}du = \frac{{dx}}{x}\\v = \frac{{{x^2}}}{2}\end{array} \right.\)
\[F\left( x \right) = \smallint xlnxdx\]
\( = \frac{1}{2}{x^2}\ln x - \int {\frac{x}{2}dx} = \frac{1}{2}{x^2}\ln x - \frac{{{x^2}}}{4} + C.\)
Chọn B
Câu 65:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Hàm số y = f(x) xác định trên tập R.
Hàm số f(x) liên tục tại điểm x = 0 khi và chỉ khi \(\mathop {\lim }\limits_{x \to {0^ + }} f(x) = \mathop {\lim }\limits_{x \to {0^ - }} f(x) = f(0)\)
\( \Leftrightarrow \mathop {\lim }\limits_{x \to {0^ + }} \left( {{x^2} + x + 1} \right) = \mathop {\lim }\limits_{x \to {0^ - }} (x + 2a) = {0^2} + 0 + 1\)
\( \Leftrightarrow 0 + 2a = 1\)
\( \Leftrightarrow a = \frac{1}{2}.\)
Chọn A
Câu 66:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Do \(\int\limits_a^b {f(x){\rm{d}}x} = \int\limits_a^c {f(x){\rm{d}}x} + \int\limits_c^b {f(x){\rm{d}}x} \)
\(\begin{array}{l}{I_1} = {I_2} + I\\ \Leftrightarrow I = {I_1} - {I_2}\\ \Leftrightarrow I = m - n\end{array}\)
Chọn B
Câu 67:
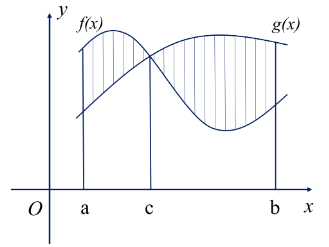
Kí hiệu S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số y = f(x), y = g(x) và hai đường thẳng x = a, x = b như hình vẽ bên. Khẳng định nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Gọi \({S_1}\) là diện tích hình phẳng được giới hạn bởi \(y = f(x),y = g(x)\) và hai đường thẳng \(x = a;x = c \Rightarrow {S_1} = \int\limits_a^c {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} \)
Gọi \({S_2}\) là diện tích hình phẳng được giới hạn bởi \(y = f(x),y = g(x)\) và hai đường thẳng \(x = c;x = b \Rightarrow {S_2} = \int\limits_c^b {\left[ {g\left( x \right) - f\left( x \right)} \right]} dx\)
Vậy \(S = {S_1} + {S_2} = \int\limits_a^c {[f(x) - g(x)]{\rm{d}}x} + \int\limits_c^b {[g(x) - f(x)]{\rm{d}}x} {\rm{.}}\)
Chọn A
Câu 68:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Ta có: \(y' = 3{x^2} - 27a = 0 \Leftrightarrow {x^2} = 9a\)
Để hàm số có cực đại, cực tiểu ⇔ phương trình y′ = 0 có 2 nghiệm phân biệt ⇔ a > 0
Khi đó, phương trình y′ = 0 có 2 nghiệm phân biệt.
\(\left[ \begin{array}{l}x = 3\sqrt a \Rightarrow y = - 54a\sqrt a \Rightarrow A(3\sqrt a ; - 54a\sqrt a )\\x = - 3\sqrt a \Rightarrow y = 54a\sqrt a \Rightarrow B( - 3\sqrt a ;54a\sqrt a )\end{array} \right.\)
⇒ Phương trình đường thẳng đi qua cực đại, cực tiểu là
\(\frac{{x + 3\sqrt a }}{{3\sqrt a + 3\sqrt a }} = \frac{{y - 54a\sqrt a }}{{ - 54a\sqrt a - 54a\sqrt a }}\)
\( \Leftrightarrow \frac{{x + 3\sqrt a }}{{6\sqrt a }} = \frac{{y - 54a\sqrt a }}{{ - 108a\sqrt a }}\)
\( \Leftrightarrow 18a(x + 3\sqrt a ) = - y + 54a\sqrt a \)
\( \Leftrightarrow 18ax + y = 0\,\,(d).\)
Ta thấy đường thẳng d luôn đi qua gốc tọa độ với mọi a > 0.
Chọn B
Câu 69:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
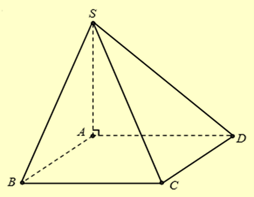
Thể tích khối chóp \({V_{S.ABCD}} = \frac{1}{3}{S_{ABCD}}.SA = \frac{1}{3}.{a^2}.3a\sqrt 2 = {a^3}\sqrt 2 \).
Chọn B
Câu 70:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đường thẳng \(\Delta \) có VTCP \(\vec u = (1;2; - 2)\)
Mặt phẳng \((P)\) có VTPT \(\vec n = (2; - 1;2)\)
\(\sin \alpha = \frac{{|\vec u.\vec n|}}{{|\vec u|.|\vec n|}} = \frac{{|1.2 + 2.( - 1) + ( - 2).2|}}{{\sqrt {{1^2} + {2^2} + {2^2}} .\sqrt {{2^2} + {1^2} + {2^2}} }} = \frac{4}{9}\)
Chọn A
Câu 71:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Ta viết lại phương trình đường thẳng \(d:\frac{{x - 2}}{{ - 1}} = \frac{{y - 1}}{2} = \frac{{z - 3}}{1}\).
Câu 72:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Số mặt đối xứng của lăng trụ đứng tam giác bằng số trục đối xứng của đáy + 1.
Lăng trụ đứng tam giác đều sẽ có 3 + 1 = 4 mặt đối xứng, đó là:
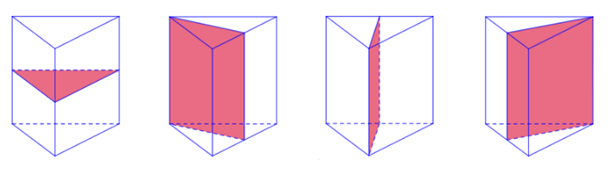
Chọn B
Câu 73:
Trong không gian Oxyz, cho hình chữ nhật ABCD có AB = 1, AD = 2. Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật ABCD xung quanh trục MN ta được một hình trụ.
Độ dài đường sinh của hình trụ bằng ____.
Diện tích toàn phần của hình trụ bằng ____.
 Xem đáp án
Xem đáp án
Đáp án đúng
Trong không gian Oxyz, cho hình chữ nhật ABCD có AB = 1, AD = 2. Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật ABCD xung quanh trục MN ta được một hình trụ.
Độ dài đường sinh của hình trụ bằng 1 .
Diện tích toàn phần của hình trụ bằng 4π .
Hướng dẫn giải:
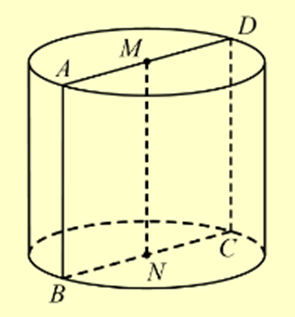
Ta có \(r = \frac{{AD}}{2} = 1;\,\,l = AB = 1\).
Vậy diện tích toàn phẩn của hình trụ : \(S = 2\pi rl + 2\pi {r^2} = 2\pi .1.1 + 2.\pi {.1^2} = 4\pi \).
Câu 74:
Bạn Hải lấy một cặp số tự nhiên phân biệt rồi tính số dư khi chia tổng lập phương của hai số cho tổng các chữ số của số lớn trong hai số đó. Nếu làm theo đúng quy tắc của bạn Hải với cặp số (31;175) ta thu được kết quả bằng ____.
 Xem đáp án
Xem đáp án
Đáp án “3”
Hướng dẫn giải:
Theo quy tắc ta có: (313 + 1753) chia (1 + 7 + 5) được 414551 dư 3.
Vậy kết quả là 3.
Câu 75:
Cho đa giác đều 20 đỉnh nội tiếp trong đường tròn tâm O. Chọn ngẫu nhiên 4 đỉnh của đa giác. Xác suất để 4 đỉnh được chọn là 4 đỉnh của một hình chữ nhật bằng
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Số cách chọn 4 đỉnh của đa giác là \(C_{20}^4\) nên \(|\Omega | = C_{20}^4\).
Do hình chữ nhật nội tiếp trong đường tròn tâm \(O\) có hai đường chéo đi qua tâm \(O\) nên mỗi hình chữ nhật có 4 đỉnh là 4 đỉnh của đa giác ứng với 1 cách chọn hai đường chéo đi qua tâm \(O\) của đa giác.
Mà đa giác có 10 đường chéo đi qua tâm \(O\) nên có \(C_{10}^2\) hình chữ nhật.
Gọi \(A\) là biến cố: "4 đỉnh được chọn là 4 đỉnh của một hình chữ nhật" \( \Rightarrow \left| {{\Omega _A}} \right| = C_{10}^2\).
Vậy xác suất để 4 đỉnh được chọn là 4 đỉnh của một hình chữ nhật là \(P(A) = \frac{{\left| {{\Omega _A}} \right|}}{{|\Omega |}} = \frac{{C_{10}^2}}{{C_{20}^4}} = \frac{3}{{323}}\).
Chọn D
Câu 76:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Dãy Tribonacci gồm các số hạng là: 0, 0, 1, 2, 3, 6, 11, 20, 37, 68, 123, ...
Chọn D
Câu 77:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đường tròn \(\left( {{C_1}} \right)\) có bán kính \({R_1} = {I_1}A = R\) và \({S_1} = \pi {R^2}\).
Đường tròn \(\left( {{C_2}} \right)\) có bán kính \({R_2} = {I_2}A = \frac{{{I_1}A}}{2} = \frac{R}{2}\) và \({S_2} = \pi R_2^2 = \pi {\left( {\frac{R}{2}} \right)^2} = \frac{{\pi R}}{4} = \frac{{{S_1}}}{4}\).
Đường tròn \(\left( {{C_3}} \right)\) có bán kính \({R_3} = {I_3}A = \frac{{{I_2}A}}{2} = \frac{R}{4}\) và \({S_3} = \pi R_3^2 = \pi {\left( {\frac{R}{4}} \right)^2} = \pi \frac{{{R^2}}}{{16}} = \frac{{{S_2}}}{4}\).
Đường tròn \(\left( {{C_n}} \right)\) có bán kính \({R_n} = {I_n}A = \frac{{{I_{n - 1}}A}}{2} = \frac{R}{{{2^{n - 1}}}}\) và \({S_n} = \pi R_n^2 = \pi {\left( {\frac{R}{{{2^{n - 1}}}}} \right)^2} = \pi \frac{{{R^2}}}{{{2^{2(n - 1)}}}} = \frac{{{S_{n - 1}}}}{4}\).
Vậy các đường tròn \(\left( {{C_1}} \right),\left( {{C_2}} \right),\left( {{C_3}} \right), \ldots ,\left( {{C_n}} \right), \ldots \) có diện tích \({S_1},{S_2},{S_3}, \ldots ,\left( {{S_n}} \right), \ldots \) lập thành một cấp số nhân với \({u_1} = {S_1} = \pi {R^2} = \pi {.86^2} \approx 23235\;{\rm{c}}{{\rm{m}}^2}\), công bội \(q = \frac{1}{4}\).
Vậy \(S = {S_1} + {S_2} + \ldots + {S_6} = \frac{{{u_1}\left( {{q^6} - 1} \right)}}{{q - 1}} = \frac{{23235\left( {{{\left( {\frac{1}{4}} \right)}^6} - 1} \right)}}{{\frac{1}{4} - 1}} \approx 30973\,\,\;{\rm{c}}{{\rm{m}}^2}\).
Chọn C
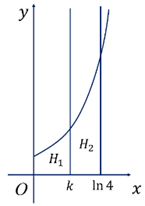
Câu 78:
Kí hiệu \((H)\) là hình phẳng giới hạn bởi đường cong \(y = {e^x}\), trục hoành, trục tung và đường thẳng \(x = \ln 4\). Đường thẳng \(x = k(0 < k < \ln 4)\) chia \((H)\) thành hai phần \({H_1},{H_2}\) như hình vẽ bên. Khi quay \({H_1},\,\,{H_2}\) quanh trục hoành ta được hai khối tròn xoay có thể tích tương ứng là \({V_1},{V_2}\). Giá trị của \(k\) bằng bao nhiêu để \({V_1} = 2{V_2}\)?
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Ta có:
\({V_1} = \pi \int\limits_0^k {{{\left( {{e^x}} \right)}^2}\;{\rm{d}}x} ;\,\,{V_2} = \pi \int\limits_k^{\ln 4} {{{\left( {{e^x}} \right)}^2}\;{\rm{d}}x} \)
\({V_1} = 2{V_2} \Leftrightarrow \pi \int\limits_0^k {{e^{2x}}\;{\rm{d}}x} = \left. {2\pi \int\limits_k^{\ln 4} {{e^{2x}}\;{\rm{d}}x} \Leftrightarrow \frac{1}{2}{e^{2x}}} \right|_0^k = \left. {2.\frac{1}{2}{e^{2x}}} \right|_k^{\ln 4}\)
\( \Leftrightarrow {e^{2k}} - {e^0} = 2.{e^{2\ln 4}} - 2{e^{2k}}\)
\( \Leftrightarrow 3{e^{2k}} = 33\)
\( \Leftrightarrow {e^{2k}} = \frac{{33}}{3} \Leftrightarrow 2k = \ln 11 \Leftrightarrow k = \frac{1}{2}\ln 11\)
Chọn C
Câu 79:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Tập xác định: D = R\{−m}
Ta có: \(y' = \frac{{m - 4}}{{{{(x + m)}^2}}}\)
Hàm số đã cho đồng biến trên khoảng \(( - \infty ; - 7) \Leftrightarrow {y^\prime } > 0,\forall x \in ( - \infty ; - 7) \Leftrightarrow \left\{ \begin{array}{l}m - 4 > 0\\ - m \notin ( - \infty ; - 7)\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m > 4\\ - m \ge - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 4\\m \le 7\end{array} \right. \Leftrightarrow 4 < m \le 7.\)
Chọn B
Câu 80:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Ta có \(\frac{{36}}{{{2^{x - 2}}}} = 10 + {4^{\frac{x}{2}}} \Leftrightarrow \frac{{36}}{{{2^{x - 2}}}} = 10 + {2^{\frac{{2x}}{2}}} \Leftrightarrow \frac{{36}}{{{2^{x - 2}}}} = 10 + {2^x}\)
\( \Leftrightarrow \frac{{144}}{{{2^x}}} = 10 + {2^x}\) (∗)
Đặt \({2^x} = t\,\,(t > 0)\), khi đó phương trình (∗)\( \Leftrightarrow \frac{{144}}{t} = 10 + t \Leftrightarrow 144 = 10t + {t^2} \Leftrightarrow {t^2} + 10t - 144 = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}t = 8\,\,(TM)\\t = - 18\,\,(L)\end{array} \right.\)
Với \(t = 8 \Rightarrow {2^x} = 8 \Leftrightarrow x = 3\).
Vậy phương trình đã cho có 1 nghiệm.
Chọn A
Câu 81:
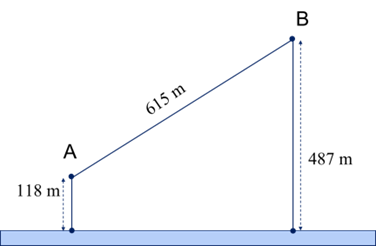
Cho hai vị trí A, B cách nhau 615 m, cùng nằm về một phía bờ sông như hình vẽ. Khoảng cách từ A và từ B đến bờ sông lần lượt là 118 m và 487 m. Một người đi từ A đến bờ sông để lấy nước mang về B. Đoạn đường ngắn nhất mà người đó có thể đi là
(Kết quả được làm tròn đến hàng đơn vị).
 Xem đáp án
Xem đáp án
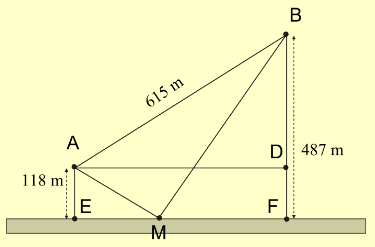
Giả sử người đó đi từ A đến M để lấy nước và đi từ M về B. Dễ dàng tính được BD = 369, EF = 492. Ta đặt EM = x, khi đó:
\(MF = 492 - x,AM = \sqrt {{x^2} + {{118}^2}} ,BM = \sqrt {{{(492 - x)}^2} + {{487}^2}} .\)
Như vậy ta có hàm số f(x) được xác định bằng tổng quãng đường AM và MB :
\(f(x) = \sqrt {{x^2} + {{118}^2}} + \sqrt {{{(492 - x)}^2} + {{487}^2}} \) với \(x \in [0;492]\)
Ta cần tìm giá trị nhỏ nhất của f(x) để có quãng đường ngắn nhất và từ đó xác định được vị trí điểm M.
\(f'(x) = \frac{x}{{\sqrt {{x^2} + {{118}^2}} }} - \frac{{492 - x}}{{\sqrt {{{(492 - x)}^2} + {{487}^2}} }}\)
\(f'(x) = 0 \Leftrightarrow \frac{x}{{\sqrt {{x^2} + {{118}^2}} }} - \frac{{492 - x}}{{\sqrt {{{(492 - x)}^2} + {{487}^2}} }} = 0\)
\( \Leftrightarrow \frac{x}{{\sqrt {{x^2} + {{118}^2}} }} = \frac{{492 - x}}{{\sqrt {{{(492 - x)}^2} + {{487}^2}} }}\)
\( \Leftrightarrow x\sqrt {{{(492 - x)}^2} + {{487}^2}} = (492 - x)\sqrt {{x^2} + {{118}^2}} \)
\( \Leftrightarrow \left\{ \begin{array}{l}{x^2}\left[ {{{(492 - x)}^2} + {{487}^2}} \right] = {\left( {492 - x} \right)^2}\left( {{x^2} + {{118}^2}} \right)\\0 \le x \le 492\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{(487x)^2} = {(58056 - 118x)^2}\\0 \le x \le 492\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{58056}}{{605}}{\rm{ hay }}x = - \frac{{58056}}{{369}}\\0 \le x \le 492\end{array} \right.\)
\( \Leftrightarrow x = \frac{{58056}}{{605}}\)
Hàm số \(f(x)\) liên tục trên đoạn [0; 492]. So sánh các giá trị của \(f(0),f\left( {\frac{{58056}}{{605}}} \right),f(492)\) ta có giá trị nhỏ nhất là \(f\left( {\frac{{58056}}{{605}}} \right) \approx 779,8\;{\rm{m}}\).
Chọn B
Câu 82:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
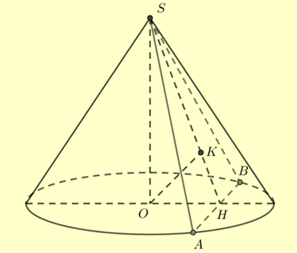
Gọi thiết diện qua đỉnh là tam giác vuông cân SAB và gọi \(H\) là trung điểm AB.
Kẻ \(OK \bot SH \Rightarrow d(O,(SAB)) = OK = \frac{a}{3}\) và ta có \(\frac{1}{{O{K^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{H^2}}} \Rightarrow OH = \frac{{a\sqrt 2 }}{4}\).
Do tam giác SAB vuông cân tại \(S \Rightarrow AH = SH = SH = \sqrt {S{O^2} + O{H^2}} = \frac{{3a\sqrt 2 }}{4}\).
\( \Rightarrow OA = \sqrt {O{H^2} + A{H^2}} = \frac{{a\sqrt 5 }}{2} \Rightarrow V = \frac{1}{3}\pi .O{A^2}.SO = \frac{1}{3}\pi {\left( {\frac{{a\sqrt 5 }}{2}} \right)^2}.a = \frac{{5\pi {a^3}}}{{12}}\).
Vậy thể tích của khối nón được giới hạn bởi hình nón đã cho bằng \(\frac{{5\pi {a^3}}}{{12}}\).
Chọn B
Câu 83:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
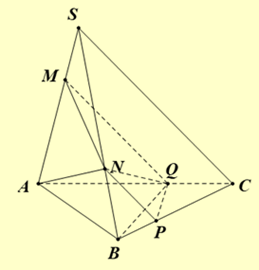
Mặt phẳng (α) qua MN và song song với SC cắt BC và AC lần lượt tại P và Q thỏa mãn MQ//SC và NP//SC.
Áp dụng định lí Ta - lét, ta suy ra:
CP = 2BP; AQ = 2QC; AM = 2MS; SN = 2NB.
Gọi V là thể tích của khối tứ diện SABC.
Xét \({V_2} = {V_{MNABPQ}} = {V_{N.ABPQ}} + {V_{Q.AMN}}\).
\(\frac{{{V_2}}}{V} = \frac{{{V_{N.ABPQ}}}}{V} + \frac{{{V_{Q.AMN}}}}{V}\)
\(\frac{{{V_{N.ABPQ}}}}{V} = \left( {1 - \frac{{CQ}}{{CA}}.\frac{{CP}}{{CB}}} \right).\frac{{BN}}{{BS}} = \left( {1 - \frac{1}{3}.\frac{2}{3}} \right).\frac{1}{3} = \frac{7}{{27}}\)
\(\frac{{{V_{Q.AMN}}}}{V} = \frac{2}{3}.\frac{2}{3}.\frac{2}{3} = \frac{8}{{27}}\)
Vậy \(\frac{{{V_2}}}{V} = \frac{5}{9} \Rightarrow \frac{{{V_1}}}{{{V_2}}} = \frac{4}{5}\).
Chọn A
Câu 84:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Gọi O là tâm hình vuông ABCD.
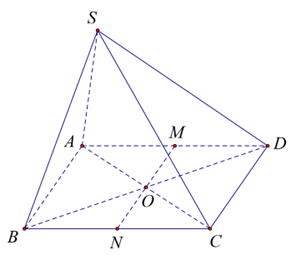
Ta có O là trung điểm của MN và O = MN ∩ (SBD).
Do đó \(\frac{{d(M,(SBD))}}{{d(N,(SBD))}} = \frac{{OM}}{{ON}} = 1\)
\( \Rightarrow d(M,(SBD)) = d(N,(SBD)) = \frac{{6a}}{7}\).
Chọn B
Câu 85:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Ta có: \[{\left( {2x + \frac{1}{{{x^2}}}} \right)^6} = \sum\limits_{k = 0}^6 {C_6^k.{{(2x)}^{6 - k}}.{{\left( {\frac{1}{{{x^2}}}} \right)}^k}} = \sum\limits_{k = 0}^6 {C_6^k{{.2}^{6 - k}}.{x^{6 - 3k}}} \]
Số hạng không chứa x trong khai triển ứng với: \(6 - 3k = 0 \Leftrightarrow k = 2\)
Số hạng đó là \(C_6^2{.2^4} = 240\).
Chọn A
Câu 86:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
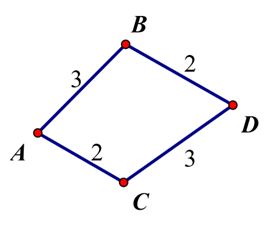
Số cách đi từ A đến D bằng cách đi từ A đến B rồi đến D là 3.2 = 6.
Số cách đi từ A đến D bằng cách đi từ A đến C rồi đến D là 2.3 = 6.
Câu 87:
Xét những tờ giấy hình chữ nhật, kẻ ca-rô cỡ m × n ô vuông, một cách phân chia “tốt” được xác định khi ta chỉ dùng những dòng kẻ có sẵn chia tờ giấy thành những phần bằng nhau sao cho mỗi phần đều là những hình vuông cỡ p × p (p ≥ 2) ô. Chẳng hạn, ở hình dưới, bằng những dòng kẻ được tô màu xanh, ta xác định một cách phân chia “tốt” với m = 9, n = 12, p = 3.
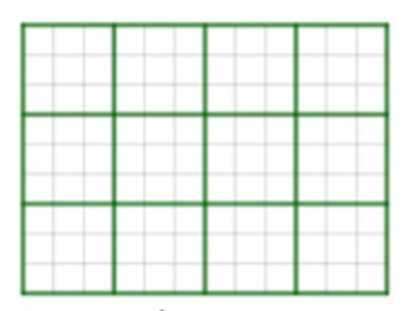
Số cách phân chia “tốt” đối với một tờ giấy ca-rô cỡ 120 × 300 là
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Ta có 300 = 3.52.22 ; 120 = 3.23.5.
Ta có ước chung lớn nhất của 300 và 120 là 3.22.5;
Số cách phân chia “tốt” đối với một tờ giấy ca-rô cỡ 120 × 300 là số ước tự nhiên của số 3.22.5.
Gọi 3x.2y.5z, (x, y, z là các số tự nhiên; 0 ≤ x ≤ 1, 0 ≤ y ≤ 2, 0 ≤ z ≤ 1) là ước của số 3.22.5.
Số cách chọn x là: 2 cách;
Số cách chọn y là: 3 cách;
Số cách chọn z là: 2 cách;
Do đó số ước tự nhiên là: 2.3.2 = 12;
Vậy có 12 cách phân chia “tốt” đối với một tờ giấy ca-rô cỡ 120 × 300.
Chọn A
Câu 88:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
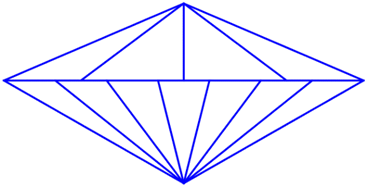
Mỗi tam giác ở phần trên được tạo thành bởi cạnh đáy (cạnh ngang) và hai trong năm cạnh.
Do đó số tam giác ở phần trên là \(C_5^2 = 10\).
Mỗi tam giác ở phần dưới được tạo thành bởi cạnh đáy (cạnh ngang) và hai trong tám cạnh.
Do đó số tam giác ở phần dưới là \(C_8^2 = 28\).
Vậy số tam giác trong hình là 38.
Chọn D
Câu 89:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Vì \(f(x + \pi ) = \sin [2(x + \pi )] + \tan (x + \pi ) = \sin (2x + 2\pi ) + \tan (x) = \sin 2x + \tan x = f(x)\) nên hàm số đã cho có chu kì là \(\pi \).
Chọn D
Câu 90:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đặt \({z_1} = {a_1} + {b_1}i,\,\,{z_2} = {a_2} + {b_2}i\,\,\left( {{a_1},{a_2},{b_1},{b_2} \in \mathbb{R}} \right)\). Ta có:
\(\left| {{z_1}} \right| = \left| {{z_2}} \right| = 2 \Leftrightarrow a_1^2 + b_1^2 = a_2^2 + b_2^2 = 4\)
\(\left| {{z_1} + {z_2}} \right| = 4 \Rightarrow {\left( {{a_1} + {a_2}} \right)^2} + {\left( {{b_1} + {b_2}} \right)^2} = 4\)
\( \Leftrightarrow a_1^2 + a_2^2 + 2{a_1}{a_2} + b_1^2 + b_2^2 + 2{b_1}{b_2} = 4\)
\( \Rightarrow {a_1}{a_2} + {b_1}{b_2} = - 2\)
Do đó \({z_1} - {z_2} = \left( {{a_1} - {a_2}} \right) + \left( {{b_1} - {b_2}} \right)i\)
\(\left| {{z_1} - {z_2}} \right| = \sqrt {{{\left( {{a_1} - {a_2}} \right)}^2} + {{\left( {{b_1} - {b_2}} \right)}^2}} \)
\(\sqrt {\left( {a_1^2 + b_1^2} \right) + \left( {a_2^2 + b_2^2} \right) - 2\left( {{a_1}{a_2} + {b_1}{b_2}} \right)} = \sqrt {4 + 4 - 2.( - 2)} = 2\sqrt 3 \).
Chọn A
Câu 91:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
ĐK: \(\left\{ \begin{array}{l}3 - \sqrt {4 - x} > 0\\3 - \sqrt {4 - x} \ne 1\\x \ge 0\\x + 12 \ge 0\\4 - x \ge 0\end{array} \right. \Leftrightarrow 0 \le x \le 4\).
Nhận xét: \(3 - \sqrt {4 - x} > 3 - \sqrt {4 - 0} = 1 \Rightarrow {\log _{3 - \sqrt {4 - x} }}3 > {\log _{3 - \sqrt {4 - x} }}1 = 0\).
\(m{\log _{3 - \sqrt {4 - x} }}3 \ge x\sqrt x + \sqrt {x + 12} \Leftrightarrow m \ge \frac{{x\sqrt x + \sqrt {x + 12} }}{{{{\log }_{3 - \sqrt {4 - x} }}3}} \Leftrightarrow m \ge \left( {x\sqrt x + \sqrt {x + 12} } \right).{\log _3}\left( {3 - \sqrt {4 - x} } \right)\)
Đặt \(f(x) = \left( {x\sqrt x + \sqrt {x + 12} } \right).{\log _3}\left( {3 - \sqrt {4 - x} } \right)\)
\({f^\prime }(x) = \left( {\frac{3}{2}\sqrt x + \frac{2}{{2\sqrt {x + 12} }}} \right){\log _3}\left( {3 - \sqrt {4 - x} } \right) + \left( {x\sqrt x + \sqrt {x + 12} } \right).\frac{1}{{\left( {3 - \sqrt {4 - x} } \right)\ln 3.2\sqrt {4 - x} }}\)
Vì \(f'(x) > 0,\forall x \in (0;4) \Rightarrow f(x)\) tăng trên (0;4) ⇒ tập giá trị của f(x) là (0;12).
Vậy bất phương trình có nghiệm khi và chỉ khi m > 0.
Chọn C
Câu 92:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Ta có: \((4xy + 7y)(2x - 1)\left( {{e^{2xy}} - {e^{4x + y + 7}}} \right) = \left[ {2x(2 - y) + y + 7} \right]{e^y}\)
\(\left. { \Leftrightarrow (4x + 7)(2xy - y)\left( {{e^{2xy - y}} - {e^{4x + 7}}} \right) = 2x(2 - y) + y + 7{\rm{ (v\`i }}{e^y} > 0\,\,\forall y} \right)\)
\( \Leftrightarrow (4x + 7)(2xy - y).\left( {{e^{2xy - y}} - {e^{4x + 7}}} \right) = (4x + 7) - (2xy - y)\)
\( \Leftrightarrow (4x + 7).\left[ {(2xy - y){e^{2xy - y}} - 1} \right] = (2xy - y)\left[ {(4x + 7){e^{4x + 7}} - 1} \right]\)
\( \Rightarrow \frac{{(2xy - y){e^{2xy - y}} - 1}}{{2xy - y}} = \frac{{(4x + 7){e^{4x + 7}} - 1}}{{4x + 7}}\) với \(x \ne - \frac{7}{4};x \ne \frac{1}{2};y \ne 0\).
\( \Leftrightarrow {e^{2xy - y}} - \frac{1}{{2xy - y}} = {e^{4x + 7}} - \frac{1}{{4x + 7}}\)
Xét\(f(t) = {e^t} - \frac{1}{t}\,\,(t \ne 0)\)
\( \Rightarrow f'(t) = {e^t} + \frac{1}{{{t^2}}} > 0\,\,\forall t \ne 0\)
⇒ f(t) đồng biến trên các khoảng xác định
⇒ f(2xy − y) = f(4x + 7)
TH1: (2xy − y). (4x + 7) < 0
Giả sử 2xy − y < 0 và 4x + 7 > 0. Do x, y ∈ Z nên 2xy − y ≤ −1 và 4x + 7 ≥ 1.
\( \Rightarrow \left\{ \begin{array}{l}f(2xy - y) \le f( - 1) = 1 - \frac{1}{e} < 1\\f(4x + 7) \ge f(1) = e - 1 > 1\end{array} \right.\).Do đó, \(f(2xy - y) \ne f(4x + 7)\).
TH2: (2xy − y).(4x + 7) > 0
f(2xy − y) = f(4x + 7)
⇔2xy − y = 4x + 7
\( \Rightarrow y = \frac{{4x + 7}}{{2x - 1}} = 2 + \frac{9}{{2x - 1}}\).
Theo bài, \(y \in \mathbb{Z}\) nên 2x − 1 ∈ {±1; ±3; ±9} ⇒ x ∈ {−4;−1;0;1;2;5}.
Chọn C
Câu 93:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Do \(m > 0\) nên đồ thị hàm số \(f(x) = - {x^4} + 4{x^2} + m\) thu được do tịnh tiến đồ thị hàm số \(f(x) = - {x^4} + 4{x^2}\) lên trên \(m\) đơn vị.
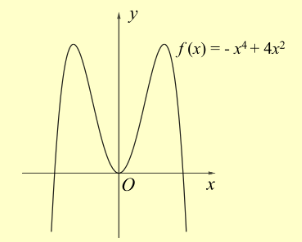
Để đường thẳng y = 8 cắt đồ thị hàm số y = ∣f(x)∣ tại 4 điểm phân biệt thì đường thẳng y = 8 phải đi qua hai điểm cực đại của hàm số y = f(x), hay xcđ là nghiệm của phương trình f(x) = 8. (∗)
Ta có: \[f\prime (x) = - 4{x^3} + 8x\]
\[f'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - \sqrt 2 }\\{x = 0}\\{x = \sqrt 2 }\end{array}} \right.\]
Vậy xcđ = ±\(\sqrt 2 \).
f(xcđ) = 4 + m.
Từ (∗) suy ra 4 + m = 8 ⇔ m = 4.
Chọn B
Câu 94:
Kéo thả hoặc click vào để điền: 2t - 2, t - 2, 6, 7,25, t - 1, 4
Một vật bắt đầu chuyển động thẳng có vận tốc được xác định theo phương trình \(v(t) = {t^2} - 2t + 5\), trong đó tt tính bằng giây và v(t) tính bằng m/s.
Gia tốc chuyển động của vật là _______ m/s2;
Vật có gia tốc tức thời tại thời điểm t = 4 (s) là _______ m/s2;
 Xem đáp án
Xem đáp án
Đáp án đúng:
Một vật bắt đầu chuyển động thẳng có vận tốc được xác định theo phương trình \(v(t) = {t^2} - 2t + 5\), trong đó t tính bằng giây và v(t) tính bằng m/s.
Gia tốc chuyển động của vật là 2t - 2 m/s2;
Vật có gia tốc tức thời tại thời điểm t = 4 (s) là 6 m/s2;
(Kéo thả hoặc click vào để điền)
Hướng dẫn giải:
Gia tốc chuyển động của vật là \(a(t) = v'(t) = \left( {{t^2} - 2t + 5} \right)' = 2t - 2.\)
Gia tốc tức thời của vật tại thời điểm t = 4 s là \(a(4) = 2.4 - 2 = 6\;\,\,{\rm{m/}}{{\rm{s}}^2}{\rm{. }}\)
Câu 95:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
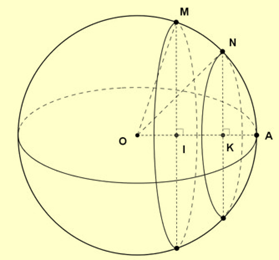
Bán kính mặt cầu (S) là R = 6 cm nên OA = 6cm ⇒ OI = IK = KA = 2 cm nên OK = 4cm.
Gọi một giao điểm của các mặt phẳng (P), (Q) với mặt cầu (S) là M, N ⇒ \(\left\{ \begin{array}{l}IM = {r_1},IN = {r_2}\\OM = ON = 6\end{array} \right.\).
Do đó, ta có
\(\left\{ \begin{array}{l}{r_1} = \sqrt {O{M^2} - O{I^2}} = \sqrt {{6^2} - {2^2}} = 4\sqrt 2 \\{r_2} = \sqrt {O{N^2} - O{K^2}} = \sqrt {{6^2} - {4^2}} = 2\sqrt 5 \end{array} \right. \Rightarrow \frac{{{r_1}}}{{{r_2}}} = \frac{{4\sqrt 2 }}{{2\sqrt 5 }} = \frac{4}{{\sqrt {10} }}\).
Chọn B
Câu 96:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Theo tính chất của phép vị tự thì phép vị tự tỉ số k biến đường tròn có bán kính R thành đường tròn có bán kính ∣k∣ R.
Đường tròn (C) có bán kính \[R = \sqrt 9 = 3\;\] nên đường tròn (C′) có bán kính là ∣−2∣.3 = 6.
Chọn C
Câu 97:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Hình chiếu của điểm (a;b;c) lên mặt phẳng (Oxz) là (a;0;c) (tọa độ y bị triệt tiêu).
Hình chiếu của điểm M(−1;2;−3) lên mặt phẳng (Oxz) là: H(−1;0;−3).
Chọn D
Câu 98:
Kéo thả hoặc click vào để điền

Từ một nhóm có 8 học sinh nam và 10 học sinh nữ, số cách chọn ra:
3 học sinh nam là: _______.
5 học sinh trong đó có 3 học sinh nam và 2 học sinh nữ là _______.
 Xem đáp án
Xem đáp án
Đáp án đúng:
Từ một nhóm có 8 học sinh nam và 10 học sinh nữ, số cách chọn ra:
3 học sinh nam là: \(C_8^3\) .
5 học sinh trong đó có 3 học sinh nam và 2 học sinh nữ là \(C_8^3.C_{10}^2\).
Hướng dẫn giải:
Số cách chọn ra 3 học sinh nam là \(C_8^3\).
Số cách chọn ra 2 học sinh nữ từ 10 học sinh nữ là: \(C_{10}^2\).
Vậy số cách chọn thỏa yêu cầu là: \(C_8^3.C_{10}^2\).
