Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 30)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 30)
-
127 lượt thi
-
97 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
Tại Việt Nam, minh chứng về tai nạn do selfie là sự việc xảy ra trong khu công nghiệp tại Hưng Yên vào năm 2016. Đúng hay sai?
 Xem đáp án
Xem đáp án
Đọc kĩ thông tin được cung cấp trong đoạn [3] của văn bản: “Tháng 7/2016, hai công nhân làm việc tại một khu công nghiệp ở huyện Văn Lâm, Hưng Yên khi đi trên đường dân sinh cắt qua đường sắt ở thị trấn Như Quỳnh đã dừng lại selfie trên đường ray bằng điện thoại mà không để ý là đoàn tàu đã tới quá gần.”. Sự việc xảy ra khi 2 người này đang đi trên đường dân sinh và chụp ảnh trên đường ray trong khi đoàn tàu đang tới gần, không phải là sự việc xảy ra trong khu công nghiệp. Mệnh đề trên là “Sai”.
Chọn B
Câu 2:
 Xem đáp án
Xem đáp án
Xét từ trong ngữ cảnh được sử dụng: “Nhưng tại sao, giữa vô vàn các tình huống đột sinh trong cuộc sống, con người lại chủ động đặt thêm mình vào rủi ro, trong nhiều trường hợp là toàn bộ cuộc đời mình, với một cú chạm trên điện thoại để mong có một bức ảnh hoàn hảo?”. Nhận thấy quan hệ từ “nhưng” đánh dấu sự đối lập trong nội dung giữa các vế của câu, “các tình huống đột sinh” được đặt trong đối lập với “con người chủ động”. Như vậy, cụm từ “phát sinh đột ngột” phù hợp để làm rõ những tình huống mà con người bị động trong việc tiếp nhận, trái ngược với chủ động lựa chọn hành động selfie dù biết trước rủi ro. Từ khóa đúng là A.
Chọn A
Câu 3:
Từ đoạn [5], dòng nào dưới đây nhận xét đúng về việc nghiên cứu về hành vi chụp ảnh selfie?
 Xem đáp án
Xem đáp án
Đọc và phân tích nội dung được cung cấp trong đoạn [5]. Câu chủ đề được đặt ở đầu đoạn: “Để đi tìm nguyên nhân sâu xa đằng sau hành vi chụp ảnh selfie, chúng ta hãy thử vẽ chân dung phổ biến của những người thích chụp ảnh selfie.”, từ “chân dung phổ biến” được làm rõ ở câu sau đó: “Các nhà nghiên cứu quốc tế đã “khoanh vùng” được những đặc điểm của họ”. Như vậy, Từ khóa đúng là C.
Chọn C
Câu 4:
Nghiên cứu về hành vi selfie tại Việt Nam không nhiều và đa số nghiên cứu khảo sát đối tượng là nữ giới. Đúng hay Sai?
 Xem đáp án
Xem đáp án
Xác định mệnh đề được đưa ra có 2 thông tin về nghiên cứu hành vi selfie tại Việt Nam: Một là số lượng không nhiều và hai là tập trung ở nữ giới. Đọc đoạn [6], thông tin cần sử dụng nằm ở đầu đoạn: “Ở Việt Nam chưa có nhiều nghiên cứu về hành vi selfie của con người nhưng có một khảo sát quy mô nhỏ về xu hướng selfie ở phụ nữ do công ty nghiên cứu thị trường Q&Me thực hiện vào tháng 1/2017 với 300 người độ tuổi 16 – 34.”, theo đó, thông tin về đối tượng khảo sát là nữ giới trong các nghiên cứu ở mệnh đề không tương ứng với thông tin trong bài “có một khảo sát quy mô nhỏ về xu hướng selfie ở phụ nữ” nên mệnh đề “Sai”.
Chọn B
Câu 5:
 Xem đáp án
Xem đáp án
Đọc đoạn [8] và [9] trong bài, xác định các thông tin trong văn bản: “selfie là hành vi “tự tôn” của những người bình thường trong xã hội. Mỗi bức ảnh là một khía cạnh về bản sắc cá nhân…”, “Giờ đây, chiếc máy ảnh hoặc điện thoại thông minh trao quyền để họ tự do thể hiện chính mình trong một trạng thái cảm xúc mà mình mong muốn bộc lộ”, “những người độ tuổi ngoài 20 và tuổi teen đang ở giai đoạn xây dựng bản sắc cá nhân và cac bức ảnh này đem lại cho họ một sự nhận diện mới, một dấu ấn nào đó trong xã hội”.... Dáp án D là Từ khóa chính xác.
Chọn D
Câu 6:
Hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí:
văn hóa đại chúng, bản chất xã hội, bản sắc cá nhân, công nghệ
Người ta cho rằng selfie là một hiện tượng liên quan chặt chẽ với sự phát triển của _______ nhưng qua việc liên kết với sự phát triển của văn hóa, GS Claus-Christian Carbon cho rằng, hành vi này và việc vẽ tranh tự họa đều là hình thức thể hiện _______ và cho thấy _______ của con người.
 Xem đáp án
Xem đáp án
Đáp án
Người ta cho rằng selfie là một hiện tượng liên quan chặt chẽ với sự phát triển của công nghệ nhưng qua việc liên kết với sự phát triển của văn hóa, GS Claus-Christian Carbon cho rằng, hành vi này và việc vẽ tranh tự họa đều là hình thức thể hiện bản sắc cá nhân và cho thấy bản chất xã hội của con người.
Giải thích
Căn cứ vào nội dung của đoạn văn số [13] và [14], lần lượt xác định vị trí thả của các từ trong danh sách. Sau đây là một số dẫn chứng cần thiết: “Nếu nhìn vào xu hướng selfie hiện nay, người ta có thể đi đến kết luận đây là một hiện tượng văn hóa đại chúng của thế kỷ 21, liên quan trực tiếp đến sự phát triển và chiếm ưu thế của điện thoại thông minh tích hợp camera”, “ Tuy nhiên, GS. Claus-Christian Carbon cho rằng về cơ bản, hai hình thức thể hiện bản sắc cá nhân này đều dựa trên ý tưởng hoặc mong muốn ghi lại một lát cắt đầy biến động nhưng quan trọng trong cuộc sống của mình và trưng bày cái tôi của mình”, “chân dung tự họa cũng là một cách thể hiện bản chất xã hội của con người nói chung”. Các từ tương ứng với vị trí thả từ 1 đến 3 lần lượt là: “công nghệ”, “bản sắc cá nhân”, “bản chất xã hội”.
Câu 7:
 Xem đáp án
Xem đáp án
Đọc đoạn [15], xác định thông tin liên quan đến câu hỏi: “Nếu vậy thì họ không biết rằng sự xuất hiện của các bức tự họa gần gũi với quá trình những phát minh và tiên tiến công nghệ xuất hiện ví dụ như kỹ thuật làm ra những tấm gương chất lượng cao đầu tiên..”. Từ khóa đúng là A. Việc sản xuất gương chỉ là một ví dụ của sự tiên tiến trong công nghệ - điều thúc đẩy các bức tự họa nên loại Từ khóa B. Từ khóa C và D không tương ứng với nội dung trong đoạn.
Chọn A
Câu 8:
Mối liên hệ giữa hiện tượng selfie và một trạng thái tâm lý bất thường vẫn chưa được kết luận cụ thể. Đúng hay sai?
 Xem đáp án
Xem đáp án
Theo đoạn [7], “một trạng thái tâm lý bất thường” ở đây chỉ “tính ái kỷ (Narcissism)” trong câu: “Nhiều người cho rằng, những người quá đắm chìm vào thế giới ảo và selfie thường liên quan đến tính ái kỷ (Narcissism) nhưng cũng có người cho rằng không hẳn như vậy…”, mối liên hệ này được đánh giá trong câu đầu tiên của đoạn: “Có nhiều bàn cãi xung quanh hiện tượng này.”. Như vậy, mệnh đề được đưa ra trong đề bài “Đúng”.
Chọn A
Câu 9:
 Xem đáp án
Xem đáp án
Đọc phần “Mặt trái của selfie”, trong đoạn [18] và [19] của bài viết, các mặt trái của selfie đã được đề cập: “việc đưa các bức ảnh “sống ảo”, “tự sướng” trên mạng xã hội khiến con người dễ bị tổn thương hơn bởi những lời bình luận ác ý về hình thức”, “selfie trên mạng xã hội có liên quan đến những suy nghĩ tiêu cực về hình ảnh cơ thể ở các cô gái. Đó là một hệ quả xấu khác của selfie, bên cạnh sự rủi ro tính mạng mà chúng ta đã thấy.”. Việc gợi ý con người suy nghĩ về bản thân nhiều hơn là do môi trường của mạng xã hội (thông tin trong đoạn [19]) nên Từ khóa đúng là D.
Chọn D
Câu 10:
 Xem đáp án
Xem đáp án
Đọc lại nội dung của đoạn [1], xác định các thông tin quan trọng liên quan tới hậu quả của tình trạng tắc nghẽn giao thông: “lãng phí thời gian, tiêu hao nhiên liệu và ô nhiễm môi trường”; từ các thông tin trong bài viết cần đưa ra suy luận để tiến hành loại trừ Từ khóa: việc lãng phí thời gian và tiền bạc sẽ làm mất đi cơ hội phát triển của con người, tiêu hao nhiên liệu và ô nhiễm môi trường sẽ gây ra hậu quả về sức khỏe và việc khai thác chất đốt trong tự nhiên; Từ khóa đúng là C.
Chọn C
Câu 11:
Từ thông tin của đoạn [1] hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí:
ứng dụng, xây dựng, thiết kế, áp dụng
Theo đánh giá từ Viện chiến lược và phát triển Giao thông vận tải, tình trạng tắc nghẽn giao thông đang gây ảnh hưởng nghiêm trọng tới đời sống, vậy nên, các cơ quan tổ chức đang _______ nhiều biện pháp và _______ khoa học máy tính vào việc _______ các hệ thống thu thập và xử lý dữ liệu.
 Xem đáp án
Xem đáp án
Đáp án
Theo đánh giá từ Viện chiến lược và phát triển Giao thông vận tải, tình trạng tắc nghẽn giao thông đang gây ảnh hưởng nghiêm trọng tới đời sống, vậy nên, các cơ quan tổ chức đang áp dụng nhiều biện pháp và ứng dụng khoa học máy tính vào việc thiết kế các hệ thống thu thập và xử lý dữ liệu.
Giải thích
Đọc lại thông tin trong đoạn [1] để tìm ra được một số từ khóa quan trọng: “nhiều các biện pháp được nghiên cứu và áp dụng”, “ứng dụng khoa học máy tính càng được chú ý”, “thiết kế hệ thống thị giác máy tính thu thập và xử lý dữ liệu”. Câu văn đầy đủ là: “Theo đánh giá từ Viện chiến lược và phát triển Giao thông vận tải, tình trạng tắc nghẽn giao thông đang gây ảnh hưởng nghiêm trọng tới đời sống, vậy nên, các cơ quan tổ chức đang [áp dụng] nhiều biện pháp và [ứng dụng] khoa học máy tính vào việc [thiết kế] các hệ thống thu thập và xử lý dữ liệu.”
Câu 12:
Mục đích của nhóm nghiên cứu khi tìm kiếm giải pháp phân loại phương tiện giao thông là gì?
 Xem đáp án
Xem đáp án
Đọc lại nội dung của đoạn [1]: Khi triển khai nghiên cứu giải pháp từ việc thu thập dữ liệu của camera giao thông để “xác định số lượng phương tiện lưu thông trên đường và tính toán mật độ lưu lượng phương tiện tham gia giao thông trong một khoảng thời gian xác định”; vậy mục tiêu cốt lõi sẽ là dự báo về tình trạng giao thông để giảm thiểu tình trạng tắc nghẽn.
Chọn D
Câu 13:
Yolov4 là phiên bản nâng cấp, có cơ chế hoạt động của mô hình mạng dùng cho việc phát hiện, nhận dạng, phân loại đối tượng; phân chia và xử lý hình ảnh sau đó đưa ra các dự đoán theo một yêu cầu xác định là đúng hay sai?
 Xem đáp án
Xem đáp án
Đọc lại nội dung đoạn [2] để tìm hiểu định nghĩa về Yolo: “mô hình mạng dùng cho việc phát hiện, nhận dạng, phân lại đối tượng”, “dự đoán xem trong mỗi ô liệu có đối tượng (object) mà điểm trung tâm rơi vào ô đó không, dự đoán điểm trung tâm, kích thước của đối tượng và xác suất là đối tượng nào trong số các đối tượng cần xác định”; chú ý câu “phiên bản đang được sử dụng là thế hệ thứ 4, gọi là Yolov4”.
Chọn A
Câu 14:
Theo đoạn [3], Tracking-by-dectection là:
 Xem đáp án
Xem đáp án
Đọc kĩ nội dung của đoạn [3], cần phân biệt Sort và Tracking-by-detection; trong đó, Tracking-by-dectection là thuật toán để giải quyết từng đối tượng (xác định, dự đoán) còn Sort là “sự phát triển của khung theo dõi nhiều đối tượng”.
Chọn B
Câu 15:
 Xem đáp án
Xem đáp án
Đọc nội dung của đoạn [4] xác định thông tin: “… từ đó gán địa chỉ nhận dạng ID cho từng phương tiện lưu thông và phân loại chúng… xe ô tô, xe tải, xe buýt, xe máy và xe đạp”; cần lưu ý xe đạp không phải xe cơ giới nên chọn Từ khóa B.
Chọn B
Câu 16:
Theo nội dung của bài viết, tỉ lệ chính xác của mô hình phụ thuộc nhiều nhất vào yếu tố nào?
 Xem đáp án
Xem đáp án
Căn cứ vào từ khóa “tỷ lệ chính xác” để tìm thông tin trong đoạn [5]: “với xe ô tô, xe tải và xe buýt thì tỉ lệ chính xác tương đối cao và ổn định do đặc điểm kích thước và nhận dạng của chúng”; trong đoạn có nhắc tới yếu tố góc quan sát của camera, thời tiết, ánh sáng… nhưng đó không phải yếu tố quan trọng nhất.
Chọn A
Câu 17:
Đọc đoạn [5] và tìm từ không quá ba tiếng để hoàn thành câu văn sau:
Ở Việt Nam, phương tiện di chuyển chủ yếu là (1) _________, mật độ lưu thông cao nên để xây dựng được thuật toán ổn định và chính xác là rất phức tạp, cần thời gian dài để có thể hoàn thiện mô hình.
 Xem đáp án
Xem đáp án
Đáp án
Ở Việt Nam, phương tiện di chuyển chủ yếu là (1) xe máy, mật độ lưu thông cao nên để xây dựng được thuật toán ổn định và chính xác là rất phức tạp, cần thời gian dài để có thể hoàn thiện mô hình.
Giải thích
Đọc thông tin trong đoạn [5] xác định từ cần điền là: “xe máy” vì có thông tin “tại Việt Nam, giao thông với đặc thù lượng xe máy lớn và mật độ lưu thông cao…”.
Câu 18:
Sau quá trình thử nghiệm tại các thành phố lớn, nhóm nghiên cứu đã thấy kết quả phân loại và kiểm đếm:
 Xem đáp án
Xem đáp án
Căn cứ vào từ khóa “kết quả phân loại và kiểm đếm” để đọc lại nội dung của đoạn [6] và xác định thông tin: “nhóm nghiên cứu nhận thấy khi mật độ lưu thông thấp, thuật toán cho kết quả phân loại và kiểm đếm tương đối chính xác. Với mật độ lưu thông trung bình và cao, kết quả bắt đầu có độ chênh lệch và mất định hơn ở loại phương tiện và xe đạp và xe máy”.
Chọn B
Câu 19:
Phần tư duy khoa học / giải quyết vấn đê
Các thiên thạch khi nằm trong phạm vi 50 km từ bề mặt Trái Đất thì chúng sẽ
 Xem đáp án
Xem đáp án
Theo phần thứ nhất của đoạn văn, ta có: Hầu hết các thiên thạch bốc hơi hoàn toàn trước khi chúng nằm trong phạm vi 50 km từ bề mặt Trái Đất.
Chọn C
Câu 20:
Phát biểu sau đây là đúng hay sai?
Các Sao chổi ở vị trí cách bề mặt Trái Đất khoảng 50 đến 85 km sẽ ma sát với không khí khiến chúng phát sáng và có thể nhìn thấy được.
 Xem đáp án
Xem đáp án
Theo phần thứ nhất của đoạn dẫn: Khi Sao chổi bị lực hấp dẫn kéo vào khí quyển Trái Đất thì có thể tạo thành hiện tượng sao băng, tức là có thể nhìn thấy từ bề mặt Trái Đất. Khi tiếp xúc với khí quyển, Sao chổi bắt đầu sáng lên do sự ma sát, thường xảy ra ở độ cao từ 50 đến 85 km so với bề mặt Trái Đất.
Chọn B
Câu 21:
Nhà khoa học 1 có thể sẽ đề xuất sử dụng các thiết bị công nghệ cao để chụp ảnh các vật thể trong khí quyển nhằm nghiên cứu và tìm kiếm các sao chổi nhỏ trong khu vực nào sau đây?
 Xem đáp án
Xem đáp án
Theo lập luận của Nhà khoa học 1: Khoảng 30000 Sao chổi nhỏ đi vào từ quyển của Trái Đất mỗi ngày. Các đốm tối và vệt sẫm màu trên ảnh UVA và VIS xảy ra khi các Sao chổi nhỏ bắt đầu bốc hơi trong từ quyển, giải phóng krypton, argon và tạo ra khí H2O tương tác với các gốc hydroxyl, OH−. Các hình ảnh được chụp bởi các thiết bị này tại các thời điểm khác nhau cho thấy các đốm tối và vệt sẫm ở cùng một tần số, đồng thời đưa ra bằng chứng thuyết phục ủng hộ giả thuyết Sao chổi nhỏ.
Theo giả thuyết này, các thiết bị công nghệ cao có thể chụp ảnh từ quyển mới hữu ích cho việc quan sát các Sao chổi nhỏ.
→ Các thiết bị công nghệ cao có thể ghi dữ liệu cách mặt nước biển lớn hơn 600 km để chụp ảnh các vật thể trong khí quyển nhằm nghiên cứu và tìm kiếm các sao chổi nhỏ mới đem lại hiệu quả cao nhất.
Chọn D
Câu 22:
Đa phần các Sao chổi hiện nay trên có quỹ đạo là hình _______.
 Xem đáp án
Xem đáp án
Đáp án
Đa phần các Sao chổi hiện nay trên có quỹ đạo là hình elip.
Giải thích
Theo phần dẫn, ta có: Hầu hết các Sao chổi có quỹ đạo hình elip (hình bầu dục), nó khác biệt so với các vật thể khác trong Hệ Mặt Trời.
Câu 23:
Giả sử một nghiên cứu về các đốm tối và vệt sẫm trong hình ảnh UVA và VIS cho thấy mức độ krypton trong khí quyển cao gấp 500 lần so với mức bình thường. Những kết quả của nghiên cứu này sẽ ảnh hưởng đến quan điểm của các nhà khoa học như thế nào?
 Xem đáp án
Xem đáp án
Theo lập luận của Nhà khoa học 1: Các hình ảnh được chụp bởi các thiết bị này tại các thời điểm khác nhau cho thấy các đốm tối và vệt sẫm ở cùng một tần số, đồng thời đưa ra bằng chứng thuyết phục ủng hộ giả thuyết Sao chổi nhỏ. Nếu các đốm tối và vệt sẫm là do sự nhiễu công nghệ ngẫu nhiên, thì tần suất xuất hiện của chúng sẽ dao động.
→ Nhà Khoa học 1 cho rằng sự thay đổi trong điều kiện khí quyển xung quanh những đốm tối và vệt sẫm này sẽ hỗ trợ cho quan điểm đó. Nhà khoa học 1 cũng cho rằng: Sao chổi giải phóng krypton khi chúng bốc cháy, vì vậy việc phát hiện ra krypton xung quanh các đốm tối và vệt sẫm ủng hộ quan điểm của Nhà khoa học 1.
Chọn A
Câu 24:
Khẳng định nào sau đây về Sao chổi nhỏ là phù hợp nhất với quan điểm của Nhà khoa học 1?
 Xem đáp án
Xem đáp án
Nhà khoa học 1 cho rằng: Sao chổi nhỏ quá nhỏ để trở thành sao băng. Nhà khoa học 1 cũng cho rằng các Sao chổi nhỏ bốc cháy trong từ quyển, nhưng phần dẫn đề cập các sao băng bốc cháy ở độ cao từ 50 đến 85 km trên bề mặt Trái Đất, nghĩa là trong tầng trung lưu.
→ Không có Sao chổi nhỏ nào từng trở thành sao băng.
Chọn A
Câu 25:
Cho elip có phương trình \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), với các tiêu điểm \({F_1}( - c;0),\,\,{F_2}(c;0);\,\,\left( {c = \sqrt {{a^2} - {b^2}} } \right)\). Với điểm M(x;y) thuộc elip, ta có bán kính qua tiêu của M là MF1, MF2 trong đó: \(M{F_1} = a + \frac{c}{a}x,\) \(M{F_2} = a - \frac{c}{a}x\) và tâm sai \(e = \frac{c}{a} < 1\).
Sao chổi Halley là sao chổi nổi tiếng nhất trong các sao chổi theo chu kỳ. Quỹ đạo chuyển động của sao chổi Halley là một elip, nhận tâm Mặt Trời là một tiêu điểm, có tâm sai bằng 0,967. Biết khoảng cách gần nhất từ sao chổi Halley đến tâm Mặt Trời là khoảng 88.106 km. Khoảng cách xa nhất từ sao chổi Halley đến tâm Mặt Trời là (1) _____ triệu km. (làm tròn đến chữ số thập phân thứ nhất).
 Xem đáp án
Xem đáp án
Đáp án
Sao chổi Halley là sao chổi nổi tiếng nhất trong các sao chổi theo chu kỳ. Quỹ đạo chuyển động của sao chổi Halley là một elip, nhận tâm Mặt Trời là một tiêu điểm, có tâm sai bằng 0,967. Biết khoảng cách gần nhất từ sao chổi Halley đến tâm Mặt Trời là khoảng 88.106 km. Khoảng cách xa nhất từ sao chổi Halley đến tâm Mặt Trời là (1) 5245,3 triệu km. (làm tròn đến chữ số thập phân thứ nhất).
Giải thích
Chọn hệ trục toạ độ sao cho tâm Mặt Trời trùng với tiêu điểm F1 của elip, đơn vị trên các trục là triệu km.
Phương trình chính tắc của quỹ đạo elip này là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\,\,(a > b > 0)\)
Gọi toạ độ của sao chổi Halley là M(x; y).
Khoảng cách giữa sao chổi Halley và tâm Mặt Trời là MF1
\({\rm{M}}{{\rm{F}}_1} = {\rm{a}} + \frac{c}{a}{\rm{x}}\), vì \( - {\rm{a}} \le {\rm{x}} \le {\rm{a}}\) nên \({\rm{a}} - {\rm{c}} \le {\rm{M}}{{\rm{F}}_1} \le {\rm{a}} + {\rm{c}}\)
→ Khoảng cách gần nhất từ sao chổi Halley đến tâm Mặt Trời là a − c
Theo đề bài, ta có:
Khoảng cách gần nhất từ sao chổi Halley đến tâm Mặt Trời là khoảng 88.106 km
→ a − c = 88.
Mặt khác, elip có tâm sai bằng 0,967
\( \to \frac{c}{a} = 0,967 \to \frac{a}{1} = \frac{c}{{0,967}} = \frac{{a - c}}{{1 - 0,967}} = \frac{{88}}{{1 - 0,967}} = \frac{{8000}}{3} \to \left\{ {\begin{array}{*{20}{l}}{a = \frac{{8000}}{3}}\\{c = \frac{{7736}}{3}}\end{array}} \right.\)
→ Khoảng cách xa nhất từ sao chổi Halley đến tâm Mặt Trời là:
\(a + c = \frac{{15736}}{3} \approx 5245,3\) (triệu km).
Vậy khoảng cách xa nhất từ sao chổi Halley đến tâm Mặt Trời là khoảng 5245,3 triệu km.
Câu 26:
 Xem đáp án
Xem đáp án
Đột biến chuyển đoạn NST là sự trao đổi những đoạn NST không tương đồng, làm thay đổi nhóm gen liên kết, ví dụ như ở đây NST số 21 được gắn với NST số 14.
Chọn B
Câu 27:
Nhận định nào sau đây là đúng khi nói về cha mẹ của người mắc hội chứng Down sơ cấp?
 Xem đáp án
Xem đáp án
Hội chứng Down sơ cấp không mang tính di truyền, nguyên nhân từ sự phân li bất thường của NST trong quá trình hình thành trứng. Vì vậy trong gia đình có con bị mắc bệnh Down, cha mẹ của người đó đều có kiểu hình bình thường, và trong tế bào sinh dưỡng có chứa 46 NST.
Chọn D
Câu 28:
Điền số thích hợp vào chỗ trống dưới đây
Người mắc hội chứng Down sơ cấp có (1) ______ nhiễm sắc thể.
Người mắc hội chứng Down thứ cấp có (2) _____ nhiễm sắc thể.
 Xem đáp án
Xem đáp án
Đáp án
Người mắc hội chứng Down sơ cấp có (1) __47_ _ nhiễm sắc thể.
Người mắc hội chứng Down thứ cấp có (2) __46_ _ nhiễm sắc thể.
Giải thích
Người mắc hội chứng Down sơ cấp có 3 NST số 21.
Người mắc hội chứng Down thứ cấp có 46 NST nhưng dư một phần NST số 21.
Câu 29:
Anh A bình thường sinh một người con trai mắc hội chứng Down. Chị của anh A bình thường nhưng sinh một người con gái mắc hội chứng Down. Anh trai của anh A bị Down. Biết rằng trong phân bào, quá trình phân ly NST diễn ra bình thường và không xuất hiện đột biến mới, vợ của anh A bình thường, không mang NST đảo đoạn 14 – 21. Phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Do quá trình phân ly NST diễn ra bình thường, không xuất hiện đột biến; mà anh A và chị của anh A bình thường đều sinh con mắc hội chứng Down → hội chứng Down thứ cấp do di truyền.
Người mắc hội chứng Down thứ cấp do di truyền vẫn có 46 NST, trong đó có 1 NST chuyển đoạn 14 – 21, nên con trai của anh A có 46 NST.
Anh A di truyền lại cho con NST số 14 – 21 mà anh A lại có kiểu hình bình thường, nên anh A có 45 NST.
Chọn C
Câu 30:
Một người đàn ông bình thường có 45 NST với 1 NST mang đột biến chuyển đoạn 14 – 21 kết hôn với người phụ nữ bình thường. Nếu tất cả các tế bào sinh tinh đều giảm phân theo cách 1 và không xuất hiện đột biến mới thì nội dung nào sau đây đúng?
 Xem đáp án
Xem đáp án
Do tế bào sinh tinh giảm phân theo cách 1 nên con của người đàn ông này có khả năng sẽ mang nhiễm sắc thể chuyển đoạn 14 – 21. Trong trường hợp này cháu của ông ta sẽ có khả năng mắc hội chứng Down. Nếu người con không mang NST chuyển đoạn thì bộ NST của người con sẽ bình thường, gồm 46 NST.
Chọn D
Câu 31:
Phát biểu sau đây đúng hay sai?
Một giao tử bình thường, kết hợp với một trong hai giao tử trong trường hợp phân li số 3, thì có khả năng tạo ra hợp tử không mang NST số 14 nào.
 Xem đáp án
Xem đáp án
Giao tử bình thường luôn chứa NST số 14, nên cho dù kết hợp với giao tử không chứa NST số 14 ở trường hợp phân li thứ 3, thì vẫn tạo ra được hợp tử chứa 1 NST số 14.
Chọn B
Câu 32:
Phát biểu sau đúng hay sai?
Nếu Thí nghiệm 3 được lặp lại ở 80°C, độ dẫn điện của các dung dịch đều tăng, ngoại trừ hydrogen chloride giảm; nước tinh khiết và sucrose không thay đổi (do nước tinh khiết và sucrose không dẫn điện).
 Xem đáp án
Xem đáp án
Dựa vào kết quả của Thí nghiệm 2 và 3, ta thấy khi tăng nhiệt độ thì độ dẫn điện của các dung dịch đều tăng, ngoại trừ HCl giảm (từ 11,4 xuống 1,7); nước tinh khiết và sucrose không thay đổi (do nước tinh khiết và sucrose không dẫn điện).
Chọn A
Câu 33:
Các phát biểu sau đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Khả năng dẫn điện của nước vôi trong (dung dịch Ca(OH)2 trong nước) khi để trong không khí giảm dần theo thời gian. |
||
|
Nước tinh khiết được thử nghiệm trong cả ba thí nghiệm để chứng minh nước tinh khiết là một chất dẫn điện tốt. |
||
|
Dung dịch NaF dẫn được điện, còn NaF nóng chảy và NaF rắn, khan không có khả năng dẫn điện. |
||
|
Từ Thí nghiệm 1 và 2, kết quả thí nghiệm của dung dịch HCl không ủng hộ giả thuyết: việc tăng lượng chất tan sẽ làm tăng độ dẫn điện của dung dịch. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Khả năng dẫn điện của nước vôi trong (dung dịch Ca(OH)2 trong nước) khi để trong không khí giảm dần theo thời gian. |
X | |
|
Nước tinh khiết được thử nghiệm trong cả ba thí nghiệm để chứng minh nước tinh khiết là một chất dẫn điện tốt. |
X | |
|
Dung dịch NaF dẫn được điện, còn NaF nóng chảy và NaF rắn, khan không có khả năng dẫn điện. |
X | |
|
Từ Thí nghiệm 1 và 2, kết quả thí nghiệm của dung dịch HCl không ủng hộ giả thuyết: việc tăng lượng chất tan sẽ làm tăng độ dẫn điện của dung dịch. |
X |
Giải thích
1. Đúng, vì: Vì Ca(OH)2 phản ứng với CO2 trong không khí tạo thành kết tủa CaCO3 và H2O làm giảm nồng độ các ion trong dung dịch:
Ca2+ + 2OH– + CO2 → CaCO3 + H2O
2. Sai, vì: H2O được thử nghiệm trong cả 3 thí nghiệm nhằm xác định độ dẫn điện của dung dịch được đóng góp bởi dung môi.
3. Sai, vì: Dung dịch NaF và NaF nóng chảy dẫn được điện, còn NaF rắn, khan không có khả năng dẫn điện.
4. Sai, vì: Theo Bảng 1 và 2, ta thấy khi tăng lượng chất tan thì độ dẫn điện của các dung dịch đều tăng, ngoại trừ nước và sucrose (C12H22O11) không thay đổi (do nước và sucrose không dẫn điện).
Câu 34:
|
magnesium acetate |
potassium chloride |
sodium fluoride |
|
hydrogen chloride |
sucrose |
Từ kết quả của thí nghiệm 1 và 2, khả năng dẫn điện của các dung dịch (ngoại trừ nước tinh khiết) được sắp xếp theo thứ tự giảm dần là:
_______, _______, ______ , _______, _______.
 Xem đáp án
Xem đáp án
Đáp án
Từ kết quả của thí nghiệm 1 và 2, khả năng dẫn điện của các dung dịch (ngoại trừ nước tinh khiết) được sắp xếp theo thứ tự giảm dần là:
hydrogen chloride, sodium fluoride, potassium chloride, magnesium acetate, sucrose.
Giải thích
Theo Bảng 1 và 2, khả năng dẫn điện của các dung dịch (ngoại trừ nước tinh khiết) được sắp xếp theo thứ tự giảm dần là: hydrogen chloride, sodium fluoride, potassium chloride, magnesium acetate, sucrose.
Câu 35:
Điền số vào chỗ trống
Dựa vào Thí nghiệm 2 và 3, nếu hòa tan 20 g C12H22O11 và (1) ____ g KCl trong 100 ml H2O ở (2) ____°C, giá trị của ampe kế đọc được khoảng 7,4 mA.
 Xem đáp án
Xem đáp án
Đáp án
Dựa vào Thí nghiệm 2 và 3, nếu hòa tan 20 g C12H22O11 và (1) __10__ g KCl trong 100 ml H2O ở (2) __50__ °C, giá trị của ampe kế đọc được khoảng 7,4 mA.
Giải thích
Thí nghiệm 2 và 3, lượng chất tan thử nghiệm là 10 g và nhiệt độ thử nghiệm là 50°C.
Mà C12H22O11 không dẫn điện nên khi hòa tan 10 g C12H22O11 và 10 g KCl trong 100 ml H2O ở 50°C, giá trị của ampe kế đọc được khoảng 7,4 mA.
Câu 36:
Trong dung dịch CH3COOH 4,3.10–2 M, người ta xác định được nồng độ H+ bằng 8,6.10–4 M. Hỏi có bao nhiêu phần trăm phân tử CH3COOH trong dung dịch này phân li ra ion?
 Xem đáp án
Xem đáp án
\({\rm{C}}{{\rm{H}}_3}{\rm{COOH}} \mathbin{\lower.3ex\hbox{$\buildrel\textstyle\rightarrow\over{\smash{\leftarrow}\vphantom{_{\vbox to.5ex{\vss}}}}$}} {\rm{C}}{{\rm{H}}_3}{\rm{CO}}{{\rm{O}}^ - } + {{\rm{H}}^ + }\)
Nồng độ ban đầu: 4,3.10–2 ……….0…… 0 (M)
Nồng độ cân bằng: (4,3.10–2 – 8,6.10–4) ← 8,6.10–4 ← 8,6.10–4 (M)
Phần trăm phân tử CH3COOH trong dung dịch này phân li ra ion: \(\frac{{8,{{6.10}^{ - 4}}}}{{4,{{3.10}^{ - 2}}}}.100\% = 2\% \)
CHọn B
Câu 37:
Theo kết quả của cả 3 thí nghiệm, dung dịch chứa chất tan Mg(C2H3O2)2 trong trường hợpnào sau đây có khả năng dẫn điện tốt nhất?
 Xem đáp án
Xem đáp án
Từ kết quả của Thí nghiệm 1 và 2, ta thấy khi tăng lượng chất tan Mg(C2H3O2)2 trong 100 ml nước thì độ dẫn điện của dung dịch tăng.
Từ kết quả của Thí nghiệm 2 và 3, ta thấy khi tăng nhiệt độ từ 20°C lên 50°C, độ dẫn điện của dung dịch cũng tăng.
Do đó, phương án có nhiệt độ cao nhất và lượng chất tan cao nhất là phù hợp.
Chọn C
Câu 38:
Trên cơ sở kết quả của các thí nghiệm, thử nghiệm tiếp theo nào sau đây là phù hợp để có thêm thông tin về độ dẫn điện của dung dịch?
 Xem đáp án
Xem đáp án
Ta thấy, Thí nghiệm 1, 2 và 3 đã thử nghiệm về ảnh hưởng của lượng chất tan và ảnh hưởng của nhiệt độ đến khả năng dẫn điện của dung dịch → A sai.
Màu sắc của dung dịch và nước không ảnh hưởng đến khả năng dẫn điện của dung dịch→ B và C sai.
Do đó, để có thêm thông tin về độ dẫn điện của dung dịch, ta có thể thử nghiệm về ảnh hưởng của các dung môi khác nhau đến độ dẫn điện.
Chọn D
Câu 39:
 Xem đáp án
Xem đáp án
Theo phần dẫn, ta có:
Hành tinh thứ chín trong Hệ Mặt Trời của chúng ta, Sao Diêm Vương, được phát hiện vào năm 1930.
Chọn C
Câu 40:
Điền số thích hợp vào chỗ trống.
Sao Diêm Vương có thể được coi là hành tinh nhỏ nhất trong Hệ Mặt Trời với diện tích bề mặt nhỏ hơn Trái Đất hơn (1) ________ lần.
 Xem đáp án
Xem đáp án
Đáp án
Sao Diêm Vương có thể được coi là hành tinh nhỏ nhất trong Hệ Mặt Trời với diện tích bề mặt nhỏ hơn Trái Đất hơn (1) _300_ lần.
Giải thích
Theo phần dẫn, ta có: Sao Diêm Vương là hành tinh nhỏ nhất trong Hệ Mặt Trời, với diện tích bề mặt nhỏ hơn Trái Đất hơn 300 lần.
Câu 41:
Kéo thả từ hoặc cụm từ vào vị trí thích hợp:
Cấu tạo, Quỹ đạo, Diện tích bề mặt
Cả hai nhà khoa học rất có thể đồng ý với phát biểu: _______ của sao Diêm Vương khác với tất cả các hành tinh khác trong Hệ Mặt Trời.
 Xem đáp án
Xem đáp án
Đáp án
Cả hai nhà khoa học rất có thể đồng ý với phát biểu: Quỹ đạo của sao Diêm Vương khác với tất cả các hành tinh khác trong Hệ Mặt Trời.
Giải thích
Cả hai nhà khoa học đều đề cập đến sự bất thường trong quỹ đạo của Sao Diêm Vương trong các lập luận:
+ Nhà khoa học 1 cho rằng: "Quỹ đạo của Sao Diêm Vương không đều so với các hành tinh khác trong Hệ Mặt Trời”
+ Nhà khoa học 2 cho rằng: độ lệch tâm của quỹ đạo Sao Diêm Vương.
Câu 42:
 Xem đáp án
Xem đáp án
Theo Nhà khoa học 2, Sao Diêm Vương không đủ tiêu chí là một hành tinh
→ Sao Diêm Vương không thuộc Hệ Mặt Trời.
Chọn B
Câu 43:
Phát biểu nào sau đây là đúng hoặc sai?
|
Phát biểu |
Đúng |
Sai |
|
Sao Diêm Vương có đuôi bụi và khí. |
||
|
Sao Diêm Vương là hành tinh nhỏ nhất trong hệ Mặt Trời |
||
|
Bốn hành tinh bên trong Hệ Mặt Trời bao gồm Sao Thủy, Sao Kim, Trái Đất và Sao Hỏa là những hành tinh khí. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Sao Diêm Vương có đuôi bụi và khí. |
X | |
|
Sao Diêm Vương là hành tinh nhỏ nhất trong hệ Mặt Trời |
X | |
|
Bốn hành tinh bên trong Hệ Mặt Trời bao gồm Sao Thủy, Sao Kim, Trái Đất và Sao Hỏa là những hành tinh khí. |
X |
Giải thích
(1) - Sai
(2) – Đúng
(3) - Sai
Theo Nhà Khoa học 1 thì: Sao Diêm Vương lớn hơn gần 1000 lần so với một sao chổi trung bình và nó không có đuôi bụi và khí như sao chổi.
Dựa trên lập luận của Nhà khoa học 2: Bốn hành tinh bên trong, Sao Thủy, Sao Kim, Trái Đất và Sao Hỏa là những hành tinh đá; Sao Mộc, Sao Thổ, Sao Thiên Vương và Sao Hải Vương đều là hành tinh khí.
Câu 44:
Các chỏm băng ở hai cực trên bề mặt Sao Diêm Vương tan chảy một lần trong mỗi quỹ đạo 249 năm của nó, để lộ ra bề mặt đá thực sự của Sao Diêm Vương, tương tự như bề mặt của Sao Hỏa. Dựa trên thông tin được cung cấp, phát hiện này, nếu đúng, rất có thể sẽ làm suy yếu lập luận của Nhà khoa học nào?
 Xem đáp án
Xem đáp án
Nhà khoa học 2 cho rằng Sao Diêm Vương không giống các hành tinh khác do bề mặt băng của nó. Nếu băng tan chảy và tiết lộ rằng bề mặt của Sao Diêm Vương tương tự như Sao Hỏa, lập luận của Nhà khoa học 2 sẽ yếu đi đáng kể.
Chọn B
Câu 45:
Quan điểm của nhà khoa học 1 chỉ ra rằng Sao Diêm Vương khác với các tiểu hành tinh và sao chổi ở tất cả các điểm, ngoại trừ Sao Diêm Vương có thể tạo ra nhiệt thông qua phản ứng phân hạch hạt nhân.
 Xem đáp án
Xem đáp án
Theo đoạn dẫn, ta có: Sao Diêm Vương không tạo ra nhiệt bằng phản ứng phân hạch hạt nhân, giúp phân biệt nó với một ngôi sao. Nó đủ lớn để bị lực hấp dẫn của chính nó kéo thành hình cầu, giúp phân biệt nó với sao chổi hoặc tiểu hành tinh.
→ Sao Diêm Vương, tiểu hành tinh và sao chổi đều không thể tạo ra nhiệt thông qua phản ứng phân hạch hạt nhân.
Chọn B
Câu 46:
Bụi hoa hồng nào sau đây được dùng làm đối chứng trong thí nghiệm 1?
 Xem đáp án
Xem đáp án
Bụi hoa hồng không được xử lý thuốc trừ sâu mới được sử dụng làm đối chứng, các bụi hoa trồng trên đất xử lý thuốc trừ sâu nhằm xác định ảnh hưởng của thuốc trừ sâu lên số lượng cánh hoa.
Chọn A
Câu 47:
Dựa vào kết quả thí nghiệm 2, với cùng một nồng độ thuốc trừ sâu thì khối lượng bụi hoa thấp nhất trong điều kiện nào sau đây?
 Xem đáp án
Xem đáp án
Nhìn vào bảng 2, ta thấy cùng điều kiện nồng độ thuốc trừ sâu, bụi hoa sử dụng loại đất 1, thuốc trừ sâu A luôn có khối lượng nhỏ hơn (so sánh theo chiều ngang).
Chọn B
Câu 48:
Phát biểu sau đây đúng hay sai?
Với nồng độ thuốc trừ sâu 35 ppm thì không nên trồng hoa hồng ở loại đất 1 và sử dụng thuốc trừ sâu A vì bụi hoa sẽ nhỏ và hoa ít cánh.
 Xem đáp án
Xem đáp án
Kết hợp bảng 1 và bảng 2, ta thấy nếu trồng hoa hồng ở đất loại 1, với nồng độ thuốc trừ sâu A là 35 ppm thì khối lượng trung bình của hoa là 19,7 oz và hoa chỉ có khoảng 5 cánh.
Chọn A
Câu 49:
Giả sử có một mối tương quan trực tiếp giữa trọng lượng cây và số lượng cánh hoa, thì trường hợp bụi hoa hồng được trồng trên đất loại 2, số lượng cánh hoa sẽ nhỏ nhất với điều kiện nào sau đây?
 Xem đáp án
Xem đáp án
Ta thấy trọng lượng cây càng thấp thì số lượng cánh hoa cũng càng ít. Nên với lô đất 2, ở điều kiện sử dụng thuốc trừ sâu A ở mức 35 ppm thì trọng lượng cây và số lượng cánh hoa ít nhất.
Chọn B
Câu 50:
Tại sao thuốc trừ sâu ở trên được bón vào đất thay vì phun trực tiếp lên bụi hoa hồng?
 Xem đáp án
Xem đáp án
Lí do quan trọng nhất khi bón thuốc trừ sâu vào đất thay vì phun trực tiếp lên bụi hoa hồng là tránh làm cho bụi hoa hồng bị héo và chết.
Chọn C
Câu 51:
Phát biểu sau đây đúng hay sai?
Mối quan hệ giữa rệp và cây hoa hồng là mối quan hệ kí sinh.
 Xem đáp án
Xem đáp án
Do rệp ăn thực vật (cây hoa hồng) nên đây là mối quan hệ sinh vật này ăn sinh vật khác.
Chọn B
Câu 52:
Phát biểu sau đúng hay sai?
Một sinh viên dự đoán rằng khi nickel hydroxide monohydrate rắn được thu hồi bằng phương pháp lọc thông thường, CNF trong thời gian phản ứng 3 ngày sẽ lớn hơn so với thời gian phản ứng 10 phút.
 Xem đáp án
Xem đáp án
Cách 1: nhìn nhanh các giá trị CNF trong Bảng 1, ta thấy ở cả 2 thí nghiệm, CNF ở thời gian phản ứng 3 ngày đều cao hơn CNF ở thời gian phản ứng 10 phút.
Cách 2:
Thí nghiệm 1 sử dụng phương pháp lọc thông thường.
Theo Bảng 1, khi thời gian phản ứng là 3 ngày thì CNF là 39 mg/kg (thử nghiệm 2) và khi thời gian phản ứng là 10 phút thì CNF là 6 mg/kg (thử nghiệm 1).
→ CNF trong 3 ngày sẽ lớn hơn so với 10 phút (bằng phương pháp lọc thông thường).
Chọn A
Câu 53:
Tóm tắt các bước tiến hành trong 2 thí nghiệm trên như sau:
(1) Đo CNF.
(2) Trộn dung dịch Ni2+ và dung dịch OH–.
(3) Thu hồi chất rắn bằng cách lọc.
Tiến trình thí nghiệm đúng là
 Xem đáp án
Xem đáp án
Đầu tiên, các dung dịch OH– và Ni2+ được trộn với nhau và khuấy đều. Sau đó thu hồi chất rắn bằng cách lọc (lọc thông thường hoặc lọc chân không) và cuối cùng là đo CNF.
Chọn C
Câu 54:
Phương pháp lọc chân không cho CNF cao hơn phương pháp lọc thông thường, đúng hay sai?
 Xem đáp án
Xem đáp án
Đúng. Vì: Từ kết quả trong Bảng 1, CNF trong thí nghiệm 2 (phương pháp lọc chân không) cao hơn thí nghiệm 1 (phương pháp lọc thông thường).
Chọn A
Câu 55:
Có (1) _______ trong số 6 thử nghiệm mà nickel hydroxide monohydrate được thu hồi bằng phương pháp lọc thông thường sau thời gian phản ứng ít nhất 3 ngày.
 Xem đáp án
Xem đáp án
Đáp án
Có (1) __2__ trong số 6 thử nghiệm mà nickel hydroxide monohydrate được thu hồi bằng phương pháp lọc thông thường sau thời gian phản ứng ít nhất 3 ngày.
Giải thích
Theo thông tin trong bài, các thử nghiệm 1, 2 và 3 sử dụng phương pháp lọc thông thường. Trong đó, thử nghiệm 1 có thời gian phản ứng là 10 phút; thử nghiệm 2 có thời gian phản ứng là 3 ngày và thử nghiệm 3 có thời gian phản ứng là 7 ngày.
Do đó, chỉ có thử nghiệm 2 và thử nghiệm 3 là chất rắn được thu hồi bằng phương pháp lọc thông thường sau thời gian phản ứng ít nhất 3 ngày.
Câu 56:
Dựa trên kết quả của thí nghiệm 1 và 2, sự kết hợp giữa thời gian phản ứng và phương pháp lọc nào làm cho nồng độ Ni2+ trong dịch lọc là cao nhất?
 Xem đáp án
Xem đáp án
Theo Bảng 1, nồng độ Ni2+ trong dịch lọc cao nhất ở thử nghiệm 6 – phương pháp lọc chân không, trong thời gian phản ứng là 7 ngày.
Chọn B
Câu 57:
Lực tác dụng lên hỗn hợp trong phễu lớn hơn trong thử nghiệm 3 hay trong thử nghiệm 6?
 Xem đáp án
Xem đáp án
Lực tác dụng lên hỗn hợp khi sử dụng phương pháp lọc chân không lớn hơn khi sử dụng phương pháp lọc thông thường.
Thử nghiệm 3 sử dụng phương pháp lọc thông thường → Loại A và B.
Thử nghiệm 6 sử dụng phương pháp lọc chân không → Chọn C.
Chọn C
Câu 58:
Dựa trên kết quả của thí nghiệm 1 và 2, sự kết hợp giữa thời gian phản ứng và phương pháp lọc nào làm cho nồng độ Ni2+ trong dịch lọc là thấp nhất?
 Xem đáp án
Xem đáp án
Theo Bảng 1, nồng độ Ni2+ trong dịch lọc thấp nhất ở thử nghiệm 1 – phương pháp lọc thông thường, trong thời gian phản ứng là 10 phút.
Chọn A
Câu 59:
Trong không gian \(Oxyz\), cho phương trình \({x^2} + {y^2} + {z^2} - 2\left( {m + 2} \right)x + 4my - 2mz + 5{m^2} + 9 = 0\). Điều kiện của tham số \(m\) để phương trình đó là phương trình của một mặt cầu là
 Xem đáp án
Xem đáp án
Ta có \({x^2} + {y^2} + {z^2} - 2\left( {m + 2} \right)x + 4my - 2mz + 5{m^2} + 9 = 0\,\,\left( * \right)\).
\(\left( * \right) \Leftrightarrow {(x - m - 2)^2} + {(y + 2m)^2} + {(z - m)^2} = {m^2} + 4m - 5\).
Do đó phương trình (*) là phương trình mặt cầu khi \({m^2} + 4m - 5 > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m > 1}\\{m < - 5}\end{array}} \right.\).
Câu 60:
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên đoạn \(\left[ { - 1;3} \right]\) và có đồ thị là đường cong trong hình vẽ bên. Tập hợp \(T\) là tập tất cả các giá trị thực của tham số \(m\) để phương trình \(f\left( x \right) = m\) có 3 nghiệm phân biệt thuộc đoạn \(\left[ { - 1;3} \right]\).
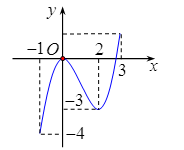
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Giá trị nguyên nhỏ nhất của tập là _______.
Giá trị nguyên lớn nhất của tập là _______.
 Xem đáp án
Xem đáp án
Giá trị nguyên nhỏ nhất của tập \(T\) là -2 .
Giá trị nguyên lớn nhất của tập \(T\) là -1 .
Giải thích
Dựa vào đồ thị hàm số đã cho, phương trình \(f\left( x \right) = m\) có 3 nghiệm phân biệt thuộc đoạn \(\left[ { - 1;3} \right]\) thì \( - 3 < m < 0\) hay \(S = \left( { - 3;0} \right)\).
Vậy giá trị nguyên nhỏ nhất của tập \(T\) là -2 , giá trị nguyên lớn nhất của tập \(T\) là -1.
Câu 61:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với đáy. Gọi \(J\) là trung điểm \(SD\).
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
ĐÚNG |
SAI |
|
Thể tích khối chóp \(S.ABCD\) bằng \(\frac{{{a^3}\sqrt 3 }}{6}\). |
¡ |
¡ |
|
Thể tích khối tứ diện \(ACDJ\) bằng \(\frac{{{a^3}\sqrt 3 }}{{36}}\). |
¡ |
¡ |
|
Khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {ACJ} \right)\) bằng \(\frac{{2a}}{{\sqrt {21} }}\). |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Thể tích khối chóp \(S.ABCD\) bằng \(\frac{{{a^3}\sqrt 3 }}{6}\). |
¤ |
¡ |
|
Thể tích khối tứ diện \(ACDJ\) bằng \(\frac{{{a^3}\sqrt 3 }}{{36}}\). |
¡ |
¤ |
|
Khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {ACJ} \right)\) bằng \(\frac{{2a}}{{\sqrt {21} }}\). |
¡ |
¤ |
Giải thích
Gọi \(I\) là trung điểm cạnh \(AB\).
Vì tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với đáy nên \(SI \bot \left( {ABCD} \right)\).
\( \Rightarrow SI = \frac{{a\sqrt 3 }}{2} \Rightarrow {V_{S.ABCD}} = \frac{1}{3}SI.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt 3 }}{2}.{a^2} = \frac{{{a^3}\sqrt 3 }}{6}\)
Ta có: \(\frac{{d\left( {J;\left( {ACD} \right)} \right)}}{{d\left( {S;\left( {ABCD} \right)} \right)}} = \frac{1}{2}\) và \({S_{ACD}} = \frac{1}{2}{S_{ABCD}}\).
\( \Rightarrow {V_{ACDJ}} = \frac{1}{2}.\frac{1}{2}.{V_{S.ABCD}} = \frac{1}{4}{V_{S.ABCD}} = \frac{{{a^3}\sqrt 3 }}{{24}}\).
Ta có: \(d\left( {D;\left( {ACJ} \right)} \right) = \frac{{3{V_{ACDJ}}}}{{{S_{ACJ}}}}\).
\({\rm{\Delta }}BCI\) vuông tại \(B\) có: \(C{I^2} = C{B^2} + B{I^2} = {a^2} + {\left( {\frac{a}{2}} \right)^2} = \frac{{5{a^2}}}{4}\).
\({\rm{\Delta }}SIC\) vuông tại \(I\) có: \(S{C^2} = S{I^2} + I{C^2} = \frac{{3{a^2}}}{4} + \frac{{5{a^2}}}{4} = 2{a^2}\).
\({\rm{\Delta }}SID\) vuông tại \(I\) có: \(S{D^2} = S{I^2} + I{D^2} = 2{a^2}\).
\({\rm{\Delta }}SCD\) có \(CJ\) là đường trung tuyến nên \(C{J^2} = \frac{{S{C^2} + C{D^2}}}{2} - \frac{{S{D^2}}}{4} = {a^2}\).
\({\rm{\Delta }}SAD\) cân tại \(A\left( {do\,\,SA = AD = a} \right)\) nên \(AJ\) vừa là đường trung tuyến vừa là đường cao.
\( \Rightarrow A{J^2} = A{D^2} - D{J^2} = A{D^2} - {\left( {\frac{{SD}}{2}} \right)^2} = \frac{{{a^2}}}{2}\)
Xét có \({\rm{cos}}A = \frac{{A{J^2} + A{C^2} - C{J^2}}}{{2AJ.AC}} = \frac{3}{4}\).
\( \Rightarrow {\rm{sin}}\widehat {JAC} = \frac{{\sqrt 7 }}{4} \Rightarrow {S_{AJC}} = \frac{1}{2}AJ.AC.{\rm{sin}}\widehat {JAC} = \frac{{{a^2}\sqrt 7 }}{8}\).
\( \Rightarrow d\left( {D;\left( {ACJ} \right)} \right) = \frac{{a\sqrt {21} }}{7}\).
Câu 62:
Cho hình chóp \(S.ABC\) có \(AB = BC = CA = a,SA = SB = SC = a\sqrt 3 ,M\) là điểm bất kì trong không gian. Gọi \(d\) là tổng khoảng cách từ \(M\) đến tất cả các đường thẳng \(AB,BC,CA,SA\),\(SB,SC\). Giá trị nhỏ nhất của \(d\) bằng
 Xem đáp án
Xem đáp án
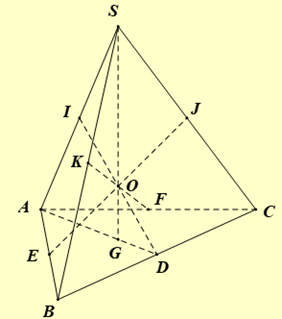
Ta có khối chóp \(S.ABC\) là khối chóp tam giác đều.
Gọi \(G\) là trọng tâm tam giác \(ABC\). Khi đó \(SG\) là chiều cao của khối chóp \(S.ABC\).
Gọi \(D,E,F\) lần lượt là trung điểm của \(BC,AB,CA\) và \(I,J,K\) lần lượt là hình chiếu của \(D,E,F\) trên \(SA,SC,SB\).
Khi đó \(DI,EJ,FK\) tương ứng là các đường vuông góc chung của các cặp cạnh \(SA\) và \(BC,SC\) và \(AB,SB\) và \(CA\).
Ta có \(DI = EJ = FK\). Do đó \({\rm{\Delta }}SID = {\rm{\Delta }}SJE\) nên \(SI = SJ\).
Suy ra \(ED//IJ\) (cùng song song với \(AC\)). Do đó bốn điểm \(D,E,I,J\) đồng phẳng.
Tương tự ta có bộ bốn điểm \(D,F,I,K\) và \(E,F,J,K\) đồng phẳng.
Ba mặt phẳng \(\left( {DEIJ} \right),\left( {DFIK} \right),\left( {EFJK} \right)\) đôi một cắt nhau theo ba giao tuyến \(DI,EJ,FK\).
Suy ra \(DI,EJ,FK\) đồng quy tại điểm \(O\) thuộc \(SG\).
Xét điểm \(M\) bất kì trong không gian.
Ta có \(\left\{ {\begin{array}{*{20}{r}}{d\left( {M,SA} \right) + d\left( {M,BC} \right)}&{ \ge DI}\\{d\left( {M,SC} \right) + d\left( {M,AB} \right)}&{ \ge EJ}\\{d\left( {M,SB} \right) + d\left( {M,AC} \right)}&{ \ge FK}\end{array} \Rightarrow d \ge DI + EJ + FK} \right.\).
Do đó \(d\) nhỏ nhất bằng \(DI + EJ + FK = 3DI\) khi \(M \equiv O\).
Ta có \(AD = \frac{{a\sqrt 3 }}{2},AG = \frac{2}{3}AD = \frac{{a\sqrt 3 }}{3},SG = \sqrt {S{A^2} - A{G^2}} = \frac{{2a\sqrt 6 }}{3}\), \(\sin \widehat {SAG} = \frac{{SG}}{{SA}} = \frac{{2\sqrt 2 }}{3}\).
Suy ra \(DI = AD.\sin \widehat {SAD} = \frac{{a\sqrt 3 }}{2}.\frac{{2\sqrt 2 }}{3} = \frac{{a\sqrt 6 }}{3}\).
Vậy giá trị nhỏ nhất cần tìm là \(3DI = 3\frac{{a\sqrt 6 }}{3} = a\sqrt 6 \).
Câu 63:
Cho khối chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M,N\) là hai điểm nằm trên hai cạnh \(SC,SD\) sao cho \(\frac{{SM}}{{SC}} = \frac{1}{2},\frac{{SN}}{{ND}} = 2\), biết G là trọng tâm tam giác \(SAB\). Tỉ số thể tích \(\frac{{{V_{G.MND}}}}{{{V_{S.ABCD}}}} = \frac{m}{n}\), \(m,n\) là các số nguyên dương và \(\left( {m,n} \right) = 1\). Giá trị của \(m + n\) bằng (1) ____
 Xem đáp án
Xem đáp án
Đáp án: “19”
Giải thích
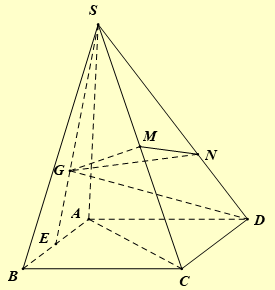
Ta có:
Gọi E là trung điểm của \(AB\).
\( \Rightarrow d\left( {G,\left( {DMN} \right)} \right) = \frac{2}{3}d\left( {{\rm{E}},\left( {DMN} \right)} \right) = \frac{2}{3}d\left( {{\rm{A}},\left( {DMN} \right)} \right) = \frac{2}{3}d\left( {{\rm{A}},\left( {SCD} \right)} \right)\)
\( \Rightarrow {V_{G.MND}} = \frac{1}{3}.{S_{{\rm{\Delta }}DMN}}.d\left( {G,\left( {DMN} \right)} \right)\)
\( \Rightarrow \frac{{{V_{G.MND}}}}{{{V_{S.ABCD}}}} = \frac{1}{{18}} \Rightarrow m + n = 19\).
Câu 64:
Cho số thực \(a\) và hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{2x}&{{\rm{khi\;}}x \le 1}\\{a\left( {x - 2{x^2}} \right)}&{{\rm{khi\;}}x > 1}\end{array}} \right.\) liên tục trên \(\mathbb{R}\). Tính \(\int\limits_0^2 {f\left( x \right){\rm{dx}}} \).
 Xem đáp án
Xem đáp án
Vì hàm số liên tục trên \(\mathbb{R}\) nên \(\mathop {{\rm{lim}}}\limits_{x \to {1^ + }} f\left( x \right) = \mathop {{\rm{lim}}}\limits_{x \to {1^ - }} f\left( x \right) = f\left( 1 \right)\).
\( \Leftrightarrow \mathop {{\rm{lim}}}\limits_{x \to {1^ + }} \left[ {a\left( {x - 2{x^2}} \right)} \right] = \mathop {{\rm{lim}}}\limits_{x \to {1^ - }} \left( {2x} \right) \Leftrightarrow a = - 2\).
Ta có
![]()
Câu 65:
Vào sinh nhật lần thứ 18 của mình (ngày 05 tháng 02 năm 2024), Hằng dự định tiết kiệm trong vòng 1 năm để mua một chiếc xe máy giá 40 500 000 đồng để làm quà sinh nhật cho chính mình vào năm sau bằng cách bắt đầu bỏ 1000 đồng vào ống heo từ ngày này. Trong các ngày tiếp theo, Hằng đều bỏ vào ống nhiều hơn ngày liền trước 1000 đồng. Đến ngày sinh nhật năm sau của mình, Hằng có đủ tiền mua xe không (biết rằng bạn dừng bỏ ống heo từ ngay trước ngày sinh nhật)? Nếu có đủ tiền mua thì có dư tiền không và dư bao nhiêu tiền?
 Xem đáp án
Xem đáp án
Số tiền bỏ heo của Hằng mỗi ngày tạo thành một cấp số cộng có số hạng đầu \({u_1} = 1000\) (đồng),
công sai \(d = 1000\) (đồng).
Tính đến hết ngày 04 tháng 02 năm 2025 (là ngày thứ 366 do 2024 là năm nhuận có ngày 29 tháng 2) tổng số tiền bỏ heo là
\({S_{366}} = \frac{{366\left[ {2.1000 + \left( {366 - 1} \right).1000} \right]}}{2} = 67161000 = 40500000 + 26661000\) (đồng).
Vậy sau 1 năm Hằng đã đủ tiền mua xe và còn dư 26661000 đồng.
Câu 66:
Trong các dãy số sau, dãy số nào là dãy số giảm?
 Xem đáp án
Xem đáp án
\(\forall n \in {\mathbb{N}^{\rm{*}}}\) ta có:
+ Với \({u_n} = {n^2}\) thì \({n^2} < {(n + 1)^2} \Leftrightarrow {u_n} < {u_{n + 1}} \Rightarrow {u_n} = {n^2}\) không là dãy số giảm.
+ Với \({u_n} = 2n\) thì \(2n < 2\left( {n + 1} \right) \Leftrightarrow {u_n} < {u_{n + 1}} \Rightarrow {u_n} = 2n\) không là dãy số giảm.
+ Với \({u_n} = {n^3} - 1\) thì \({n^3} - 1 < {(n + 1)^3} - 1 \Leftrightarrow {u_n} < {u_{n + 1}} \Rightarrow {u_n} = {n^3} - 1\) không là dãy số giảm.
+ Với \({u_n} = \frac{{2n + 1}}{{n - 1}}\) thì \({u_{n + 1}} - {u_n} = \frac{{ - 3}}{{\left( {n - 1} \right).n}} < 0\) nên dãy \({u_n} = \frac{{2n + 1}}{{n - 1}}\) là dãy số giảm.
Câu 67:
Điền số tự nhiên vào chỗ trống
Cho đa giác lồi có 10 cạnh. Biết rằng không có ba đường chéo nào đồng quy, số giao điểm của các đường chéo là (1) _______.
 Xem đáp án
Xem đáp án
Đáp án: “595”
Giải thích
Số đường chéo của đa giác là: \(C_{10}^2 - 10 = 35\).
Cứ hai đường chéo cho ta một giao điểm, hơn nữa không có ba đường chéo nào đồng quy nên số giao điểm của các đường chéo là \(C_{35}^2 = 595\).
Câu 68:
Cho dãy số \(\left( {{u_n}} \right)\) được xác định bởi \[\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1,{u_2} = 3}\\{{u_{n + 2}} + {u_n} = 2\left( {{u_{n + 1}} + 1} \right),n \in {\mathbb{N}^{\rm{*}}}}\end{array}} \right.\] . Giới hạn \[\mathop {{\rm{lim}}}\limits_{n \to + \infty } \frac{{{u_n}}}{{{n^2}}}\]bằng (1) _______.
 Xem đáp án
Xem đáp án
Đáp án: “1”
Giải thích
\(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1,{u_2} = 3\,\,\left( 1 \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\{{u_{n + 2}} + {u_n} = 2\left( {{u_{n + 1}} + 1} \right)\,\,\left( 2 \right)}\end{array}} \right.\) \(\left( {n \ge 1} \right)\).
Đặt \({v_n} = {u_{n + 1}} - {u_n}\).
Ta có \(\left( 2 \right) \Leftrightarrow {u_{n + 2}} - {u_{n + 1}} = {u_{n + 1}} - {u_n} + 2 \Leftrightarrow {v_{n + 1}} = {v_n} + 2\).
Suy ra \(\left( {{v_n}} \right)\) lập thành một cấp số cộng có số hạng đầu \({v_1} = 2\) và công sai \(d = 2\).
Nên \({v_n} = 2 + \left( {n - 1} \right).2 = 2n\).
Khi đó: \({u_n} = \left( {{u_n} - {u_{n - 1}}} \right) + \left( {{u_{n - 1}} - {u_{n - 2}}} \right) + \ldots + \left( {{u_2} - {u_1}} \right) + {u_1}\)
\( = {v_{n - 1}} + {v_{n - 2}} + \ldots + {v_1} + {u_1} = 2\left( {\left( {n - 1} \right) + \left( {n - 2} \right) + \ldots + 1} \right) + 1\)
\( = 2\frac{{n\left( {n - 1} \right)}}{2} + 1 = n\left( {n - 1} \right) + 1\).
Do đó: \(\mathop {{\rm{lim}}}\limits_{n \to + \infty } \frac{{{u_n}}}{{{n^2}}} = \mathop {{\rm{lim}}}\limits_{n \to + \infty } \frac{{n\left( {n - 1} \right) + 1}}{{{n^2}}} = \mathop {{\rm{lim}}}\limits_{n \to + \infty } \frac{{{n^2} - n + 1}}{{{n^2}}} = 1\).
Vậy \(\mathop {{\rm{lim}}}\limits_{n \to + \infty } \frac{{{u_n}}}{{{n^2}}} = 1\).
Câu 69:
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông cân tại \(C\), cạnh bên \(SA\) vuông góc với mặt đáy. Biết \(AB = 2a,SC = \sqrt 3 a\). Thể tích \(V\) của khối chóp \(S.ABC\) bằng
 Xem đáp án
Xem đáp án
Tam giác ABC vuông cân tại \(C\), có \(AB = 2a\) nên \(AC = CB = a\sqrt 2 \).
SA vuông góc với mặt đáy nên \(SA \bot AC\) nên tam giác SAC vuông tại \(A\).
Do đó \(SA = \sqrt {S{C^2} - A{C^2}} = a\).
Thể tích khối chóp \(S.ABC\) là: \(V = \frac{1}{3}.SA.{S_{ABC}} = \frac{1}{3}.a.\frac{1}{2}{(a\sqrt 2 )^2} = \frac{{{a^3}}}{3}\).
Câu 70:
Cho hàm số \(y = a{x^4} + b{x^2} + c\) có đồ thị như hình vẽ bên.
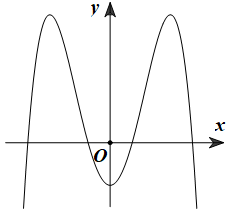
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
ĐÚNG |
SAI |
|
a > 0. |
¡ |
¡ |
|
b > 0. |
¡ |
¡ |
|
c < 0. |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
a > 0. |
¡ |
¤ |
|
b > 0. |
¤ |
¡ |
|
c < 0. |
¤ |
¡ |
Giải thích
Từ đồ thị ta có \(\mathop {{\rm{lim}}}\limits_{x \to + \infty } y = - \infty ;\mathop {{\rm{lim}}}\limits_{x \to - \infty } y = - \infty \) nên \(a < 0\).
Đồ thị hàm số có 3 điểm cực trị nên \(\frac{b}{a} < 0\) do đó \(b > 0\).
Đồ thị hàm cắt trục \(Oy\) tại điểm có tung độ âm nên \(c < 0\).
Câu 71:
Cho tứ diện đều ABCD có cạnh bằng 4 và hình trụ (T) có đường tròn đáy là đường tròn nội tiếp tam giác BCD và có chiều cao bằng chiều cao của tứ diện đều ABCD.
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
ĐÚNG |
SAI |
|
Thể tích khối tứ diện đều \(ABCD\) bằng \(\frac{{8\sqrt 2 }}{3}\). |
¡ |
¡ |
|
Bán kính đáy của hình trụ \(\left( T \right)\) bằng \(\frac{{\sqrt 3 }}{3}\). |
¡ |
¡ |
|
Diện tích xung quanh của hình trụ \(\left( T \right)\) bằng \(\frac{{16\sqrt 2 }}{3}\pi \). |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Thể tích khối tứ diện đều \(ABCD\) bằng \(\frac{{8\sqrt 2 }}{3}\). |
¡ |
¤ |
|
Bán kính đáy của hình trụ \(\left( T \right)\) bằng \(\frac{{\sqrt 3 }}{3}\). |
¡ |
¤ |
|
Diện tích xung quanh của hình trụ \(\left( T \right)\) bằng \(\frac{{16\sqrt 2 }}{3}\pi \). |
¤ |
¡ |
Giải thích
Thể tích khối tứ diện \(ABCD\) là: \(V = \frac{{{4^3}\sqrt 2 }}{{12}} = \frac{{16\sqrt 2 }}{3}\)
Gọi \(I\) là trọng tâm tam giác \(BCD\).
Tam giác \(BCD\) đều cạnh bằng 4 nên \(I\) là tâm đường tròn nội tiếp tam giác \(BCD\) và
\(BM = \frac{{4\sqrt 3 }}{2} = 2\sqrt 3 \Rightarrow \left\{ {\begin{array}{*{20}{c}}{BI = \frac{2}{3}BM = \frac{{4\sqrt 3 }}{3}}\\{r = IM = \frac{1}{3}BM = \frac{{2\sqrt 3 }}{3}}\end{array}} \right.\)
Vì \(AI\) là đường cao của tứ diện đều \(ABCD\) nên \(AI = \sqrt {A{B^2} - I{B^2}} = \frac{{4\sqrt 6 }}{3}\)
Vậy diện tích xung quanh hình trụ \({S_{xq}} = 2\pi rh = \frac{{16\sqrt 2 }}{3}\pi \).
Câu 72:
Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 2x + 4y - 4z - 27 = 0\). Bán kính \(R\) của mặt cầu \(\left( S \right)\) bằng (1) ________.
 Xem đáp án
Xem đáp án
Đáp án: “6”
Giải thích
Mặt cầu \(\left( S \right):{(x - 1)^2} + {(y + 2)^2} + {(z - 2)^2} = 36\).
Khi đó \(\left( S \right)\) có tâm \(I\left( {1; - 2;2} \right)\), bán kính \(R = 6\).
Câu 73:
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Lấy hai điểm \(M\) và \(N\) theo thứ tự di động trên \(AC\) và \(A'B\) sao cho \(AM = A'N = t\,\,\left( {0 \le t \le a\sqrt 2 } \right)\). Giá trị nhỏ nhất của \(MN\) bằng _______, khi đo góc (MN, AC) bằng _______.
 Xem đáp án
Xem đáp án
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Lấy hai điểm \(M\) và \(N\) theo thứ tự di động trên \(AC\) và \(A'B\) sao cho \(AM = A'N = t\,\,\left( {0 \le t \le a\sqrt 2 } \right)\). Giá trị nhỏ nhất của \(MN\) bằng \(\frac{a}{{\sqrt 2 }}\), khi đo góc (MN, AC) bằng 60o.
Giải thích
Kẻ \(MJ \bot AB\) suy ra \(AJ = \frac{t}{{\sqrt 2 }}\). Kẻ \(JI \bot A'B'\). Dễ thấy \(J,N,I\) thẳng hàng.
Ta có:
\(M{N^2} = M{J^2} + J{N^2} = \frac{{{t^2}}}{2} + {\left( {a - \frac{t}{{\sqrt 2 }}} \right)^2} = {t^2} - a\sqrt 2 t + {a^2} = {\left( {t - \frac{a}{{\sqrt 2 }}} \right)^2} + \frac{{{a^2}}}{2} \ge \frac{{{a^2}}}{2}\)
Suy ra \(MN \ge \frac{a}{{\sqrt 2 }}\). Dấu "=" xảy ra khi \(t = \frac{a}{{\sqrt 2 }}\). Khi đó \({M_s}N\) lần lượt là trung điểm của \(AC\) và \(A'B\).
Vộy giá trị nhỏ nhất của \(MN\) là \(\frac{a}{{\sqrt 2 }}\).
Dễ thấy khi đó \(MN//B'C\left( {//A'D} \right)\) nên \(\left( {MN,AC} \right) = \left( {B'C,AC} \right) = \widehat {B'CA}\).
Mà ta có tam giác \(AB'C\) đều nên \(\widehat {B'CA} = {60^ \circ }\).
Do đó \(\left( {MN,AC} \right) = {60^ \circ }\).
Câu 74:
Cho hình phẳng \(\left( H \right)\) giới hạn bởi đồ thị hai hàm số \(y = 2{x^2}\) và \(y = x\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
Đồ thị hai hàm số cắt nhau tại điểm có hoành độ bằng _______.
Diện tích hình phẳng \(\left( H \right)\) bằng _______.
 Xem đáp án
Xem đáp án
Đồ thị hai hàm số cắt nhau tại điểm có hoành độ bằng \(\frac{1}{2}\).
Diện tích hình phẳng \(\left( H \right)\) bằng \(\frac{1}{{24}}\).
Giải thích
Xét phương trình hoành độ điểm chung của hai đồ thị ta có: \(2{x^2} - x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = \frac{1}{2}}\end{array}} \right.\).
Diện tích hình phẳng \(\left( H \right)\) là \(S = \int\limits_0^{\frac{1}{2}} {\left| {2{x^2} - x} \right|dx = \frac{1}{{24}}} \).
Câu 75:
Trong không gian \(Oxyz\), cho ba điểm \(A\left( { - 1;6; - 1} \right),B\left( {2; - 1;3} \right),C\left( { - 3;5;1} \right)\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
Để tứ giác \(ABCD\) là hình bình hành thì hoành độ điểm \(D\) là _______.
Chân đường cao \(H\) hạ từ đỉnh \(A\) của có tọa độ là (_______; _______;_______)
 Xem đáp án
Xem đáp án
Để tứ giác \(ABCD\) là hình bình hành thì hoành độ điểm \(D\) là -6 .
Chân đường cao \(H\) hạ từ đỉnh \(A\) của có tọa độ là (-3 ; 5 ;1 )
Giải thích
Ta có: \(\overrightarrow {BC} = \left( { - 5;6; - 2} \right)\)
Để tứ giác \(ABCD\) là hình bình hành thì \(\overrightarrow {AD} = \overrightarrow {BC} \)
\( \Leftrightarrow \left( {{x_D} + 1;{y_D} - 6;{z_D} + 1} \right) = \left( { - 5;6; - 2} \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x_D} + 1 = - 5}\\{{y_D} - 6 = 6}\\{{z_D} + 1 = - 2}\end{array} \Rightarrow D\left( { - 6;12; - 3} \right)} \right.\).
Đường thẳng BC đi qua \(B(2; - 1;3)\) và nhận \(\overrightarrow {BC} = ( - 5;6; - 2)\) làm một vecto chỉ phương có phương trình: \(\left\{ {\begin{array}{*{20}{c}}{x = 2 - 5t}\\{y = - 1 + 6t}\\{z = 3 - 2t}\end{array}} \right.\)
Vì \(H \in BC\) nên \(H(2 - 5t; - 1 + 6t;3 - 2t) \Rightarrow \overrightarrow {AH} (3 - 5t; - 7 + 6t;4 - 2t)\).
Vì \(H\) là chân đường cao hạ từ đỉnh \(A\) của nên \(AH \bot BC\).
\( \Leftrightarrow \overrightarrow {AH} .\overrightarrow {BC} = 0 \Leftrightarrow - 5(3 - 5t) + 6( - 7 + 6t) - 2(4 - 2t) = 0 \Leftrightarrow t = 1\)
\( \Rightarrow H( - 3;5;1)\)
Câu 76:
Trong không gian \({\rm{Ox}}yz\), cho ba điểm \(M\left( {1;1;1} \right),N\left( { - 1; - 1;0} \right),P\left( {3;1; - 1} \right)\). Xác định tọa độ điểm \(I\) thuộc mặt phẳng \(\left( {Oxy} \right)\) sao cho \(I\) cách đều ba điểm \(M,N,P\).
 Xem đáp án
Xem đáp án
Gọi tọa độ điểm \(I\left( {a;b;0} \right)\).Ta có:
\(\overrightarrow {IM} \left( {1 - a;1 - b;1} \right),\overrightarrow {IN} \left( { - 1 - a; - 1 - b;0} \right),\overrightarrow {IP} \left( {3 - a;1 - b; - 1} \right)\).
Theo giả thiết có: \(IM = IN = IP\).
\( \Leftrightarrow \left( {\begin{array}{*{20}{l}}{IM = IN}\\{IM = IP}\end{array}} \right)\). Khi đó ta có hệ:
\[\left( {\begin{array}{*{20}{c}}{{{(1 - a)}^2} + {{(1 - b)}^2} + 1 = {{(1 + a)}^2} + {{(1 + b)}^2}}\\{{{(1 - a)}^2} + {{(1 - b)}^2} + 1 = {{(3 - a)}^2} + {{(1 - b)}^2} + 1}\end{array}} \right) \Leftrightarrow \left( {\begin{array}{*{20}{c}}{4a + 4b = 1}\\{4a = 8}\end{array}} \right) \Leftrightarrow \left( {\begin{array}{*{20}{c}}{a = 2}\\{b = - \frac{7}{4}}\end{array}} \right).\]
Vậy tọa độ điểm \(I\left( {2; - \frac{7}{4};0} \right)\).
Câu 77:
Cho hàm số \(y = {x^2}.{{\rm{e}}^{ - x}}\). Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
ĐÚNG |
SAI |
|
Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất. |
¡ |
¡ |
|
Hàm số đạt cực đại tại \(x = 0\) và đạt cực tiểu tại \(x = 2\). |
¡ |
¡ |
|
Giá trị nhỏ nhất của hàm số bằng 0 . |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất. |
¤ |
¡ |
|
Hàm số đạt cực đại tại \(x = 0\) và đạt cực tiểu tại \(x = 2\). |
¡ |
¤ |
|
Giá trị nhỏ nhất của hàm số bằng 0 . |
¤ |
¡ |
Giải thích
TXĐ: \(\mathbb{R}\).
Ta có: \(y' = x{{\rm{e}}^{ - x}}\left. {\left( {2 - x} \right.} \right);y' = 0 \Leftrightarrow \left\{ \begin{array}{l}x = 0\\x = 2\end{array} \right.\).
Bảng biến thiên
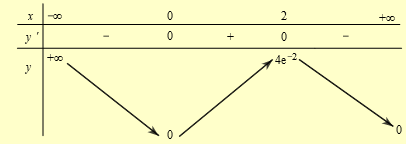
Hàm số đạt cực tiểu tại \(x = 0\) và đạt cực đại tại \(x = 2\).
Hàm số đạt giá trị nhỏ nhất bằng 0 tại \(x = 0\).
Câu 78:
Cho khai triển \(P\left( x \right) = \left( {1 + 2x} \right){(3 + x)^{11}}\).
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
ĐÚNG |
SAI |
|
Khai triển \(P\left( x \right)\) có 12 số hạng. |
¡ |
¡ |
|
Hệ số của \({x^9}\) trong khai triển là 9045 . |
¡ |
¡ |
|
Hệ số tự do trong khai triển là 531441. |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Khai triển \(P\left( x \right)\) có 12 số hạng. |
¡ |
¤ |
|
Hệ số của \({x^9}\) trong khai triển là 9045 . |
¤ |
¡ |
|
Hệ số tự do trong khai triển là 531441. |
¡ |
¤ |
Giải thích
Ta có: \(P(x) = (1 + 2x){(3 + x)^{11}} = {(3 + x)^{11}} + 2x{(3 + x)^{11}}\)
\( = \sum\limits_{k = 0}^{11} {C_{11}^k} {.3^{11 - k}}.{x^k} + 2x\sum\limits_{m = 0}^{11} {C_{11}^m} {.3^{11 - m}}.{x^m}\)
\( = \sum\limits_{k = 0}^{11} {C_{11}^k} {.3^{11 - k}}.{x^k} + \sum\limits_{m = 0}^{11} {C_{11}^m} {.2.3^{11 - m}}.{x^{m + 1}}\)
Khi đó:
+, Khai triển \(P\left( x \right)\) có 13 số hạng.
+, Hệ số của \({x^9}\) trong khai triển là: \(C_{11}^9{.3^2} + C_{11}^8{.2.3^3} = 9045\) (với \(k = 9,m = 8\)).
+, Hệ số tự do trong khai triển là: \(C_{11}^0{.3^{11}} = 177147\)
Câu 79:
Trong không gian \(Oxyz\), cho ba vecto \(\vec a = \left( {1;2; - 3} \right),\vec b = \left( {2; - 1;0} \right),\vec c = \left( {m; - 2;3} \right)\). Giá trị của \(m\) để ba vectơ \(\vec a,\vec b,\vec c\) đồng phẳng là
 Xem đáp án
Xem đáp án
Để ba vectơ \(\vec a,\vec b,\vec c\) đồng phẳng thì \(\left[ {\vec a,\vec b} \right].\vec c = 0\).
Ta có: \(\left[ {\vec a,\vec b} \right] = \left( { - 3; - 6; - 5} \right)\).
\(\left[ {\vec a,\vec b} \right].\vec c = \left( { - 3; - 6; - 5} \right).\left( {m; - 2;3} \right) = - 3m + 12 - 15 = - 3m - 3\)
\(\left[ {\vec a,\vec b} \right].\vec c = 0\) suy ra \( - 3m - 3 = 0\) hay \(m = - 1\).
Câu 80:
Cho khai triển \(P(x) = \left( {x + \frac{1}{2}} \right)\left( {x + \frac{1}{{{2^2}}}} \right) \ldots \left( {x + \frac{1}{{{2^{9999}}}}} \right) = {x^{9999}} + {A_1}{x^{9998}} + {A_2}{x^{9997}} + \ldots + {A_{9999}}.\)
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Hệ số A1 bằng _______ .
Hệ số A2 bằng _______ .
 Xem đáp án
Xem đáp án
Hệ số A1 bằng \(1 - \frac{1}{{{2^{9999}}}}\) .
Hệ số A2 bằng \[\frac{{{4^{9999}} - {{3.2}^{9999}} + 2}}{{{{3.4}^{9999}}}}\] .
Giải thích
Hệ số của \[{x^{9998}}\] là: \[{A_1} = \frac{1}{2} + \frac{1}{{{2^2}}} + \ldots + \frac{1}{{{2^{9999}}}} = \frac{1}{2}.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^{9999}}}}{{1 - \frac{1}{2}}} = 1 - \frac{1}{{{2^{9999}}}}\] .
Hệ số của \[{x^{9997}}\] là \[{A_2} = \frac{1}{2}.\frac{1}{{{2^2}}} + \frac{1}{{{2^2}}}.\frac{1}{{{2^3}}} + \ldots + \frac{1}{{{2^{9998}}}}.\frac{1}{{{2^{9999}}}}\]
Ta có: \[A_1^2 = {\left( {\frac{1}{2} + \frac{1}{{{2^2}}} + \ldots + \frac{1}{{{2^{9999}}}}} \right)^2}\]
\[ \Leftrightarrow {\left( {1 - \frac{1}{{{2^{9999}}}}} \right)^2} = \frac{1}{4} + \frac{1}{{{4^2}}} + \ldots + \frac{1}{{{4^{9999}}}} + 2.\frac{1}{2}.\frac{1}{{{2^2}}} + 2.\frac{1}{{{2^2}}}.\frac{1}{{{2^3}}} + \ldots + 2.\frac{1}{{{2^{9998}}}}.\frac{1}{{{2^{9999}}}}\]
\[ \Leftrightarrow 1 - 2.1.\frac{1}{{{2^{9999}}}} + \frac{1}{{{4^{9999}}}} = \frac{1}{4}.\frac{{1 - {{\left( {\frac{1}{4}} \right)}^{9999}}}}{{1 - \frac{1}{4}}} + 2B\]
\[ \Leftrightarrow 1 - 2.1.\frac{1}{{{2^{9999}}}} + \frac{1}{{{4^{9999}}}} = \frac{1}{4}.\frac{{1 - {{\left( {\frac{1}{4}} \right)}^{9999}}}}{{1 - \frac{1}{4}}} + 2B\]
\[ \Leftrightarrow 1 - \frac{1}{{{2^{9998}}}} + \frac{1}{{{4^{9999}}}} = \frac{1}{3}.\left( {1 - \frac{1}{{{4^{9999}}}}} \right) + 2B\]
\[ \Leftrightarrow B = \frac{{{4^{9999}} - {{3.2}^{9999}} + 2}}{{{{3.4}^{9999}}}}\]
Câu 81:
Cho mặt phẳng \(\left( P \right):2x - 2y + z + 1 = 0\) và hai điểm \(A\left( {0;2;1} \right),B\left( {\frac{7}{9};\frac{2}{9};\frac{{17}}{9}} \right)\).
Mỗi phát biểu sau là đúng hay sai?
|
Phát biểu |
ĐÚNG |
SAI |
|
Hai điểm \(A\) và \(B\) nằm cùng phía nhau đối với mặt phẳng \(\left( P \right)\). |
¡ |
¡ |
|
Điểm \(M \in \left( P \right)\) sao cho \(\left| {MA - MB} \right|\) đạt giá trị lớn nhất là \(\left( {1;2;1} \right)\). |
¡ |
¡ |
|
Điểm \(N \in \left( P \right)\) sao cho \(NA + NB\) đạt giá trị nhỏ nhất là \(\left( { - 2; - 1;1} \right)\). |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Hai điểm \(A\) và \(B\) nằm cùng phía nhau đối với mặt phẳng \(\left( P \right)\). |
¡ |
¤ |
|
Điểm \(M \in \left( P \right)\) sao cho \(\left| {MA - MB} \right|\) đạt giá trị lớn nhất là \(\left( {1;2;1} \right)\). |
¤ |
¡ |
|
Điểm \(N \in \left( P \right)\) sao cho \(NA + NB\) đạt giá trị nhỏ nhất là \(\left( { - 2; - 1;1} \right)\). |
¡ |
¤ |
Giải thích
Ta có \(\left( {2.0 - 2.2 - 1 + 1} \right)\left( {2.\frac{7}{9} - 2.\frac{2}{9} + \frac{{17}}{9} + 1} \right) < 0\) nên hai điểm \(A\) và \(B\) nằm khác phía đối với \(\left( P \right)\).
* Tìm \(M\).
Lấy điểm \(B'\left( {{x_{B'}};{y_{B'}};{z_{B'}}} \right)\) đối xứng với \(B\) qua \(\left( P \right)\).
Hạ \(BH \bot \left( P \right)\) suy ra \(\overrightarrow {{u_{BH}}} = \overrightarrow {{n_{\left( P \right)}}} = \left( {2; - 2;1} \right)\) nên phương trình đường thẳng \(BH\) là \(\left\{ \begin{array}{l}x = \frac{7}{9} + 2t\\y = \frac{2}{9} - 2t\,\,\left( {t \in \mathbb{R}} \right)\\z = \frac{{17}}{9} + t\end{array} \right.\).
Gọi tọa độ điểm \(H\) là \(H\left( {\frac{7}{9} + 2h;\frac{2}{9} - 2h;\frac{{17}}{9} + h} \right)\). Vì \(H \in \left( P \right)\) nên
\(2\left( {\frac{7}{9} + 2h} \right) - 2\left( {\frac{2}{9} - 2h} \right) + \left( {\frac{{17}}{9} + h} \right) + 1 = 0 \Leftrightarrow h = - \frac{4}{9}\) do đó \(H\left( {\frac{{ - 1}}{9};\frac{{10}}{9};\frac{{13}}{9}} \right)\).
\(B'\) đối xứng với \(B\) qua \(\left( P \right)\) nên \(H\) là trung điểm của \(BB'\).
Do đó \(\left\{ \begin{array}{l}{x_{B'}} + \frac{7}{9} = 2.\frac{{ - 1}}{9}\\{y_{B'}} + \frac{2}{9} = 2.\frac{{10}}{9} \Leftrightarrow \left\{ \begin{array}{l}{x_{B'}} = - 1\\{y_{B'}} = 2\\{z_{B'}} = 1\end{array} \right.\\{z_{B'}} + \frac{{17}}{9} = 2.\frac{{13}}{9}\end{array} \right.\) suy ra \(\left. {B'( - 1;2;1} \right)\).
Khi đó \(\left| {MA - MB} \right| = \left| {MA - MB'} \right| \le AB'\).
Dấu "=" xảy ra khi \(M\) là giao điểm của đường thẳng \(AB'\) và \(\left( P \right)\).
Có \(d\left( {A,\left( P \right)} \right) = \frac{2}{3},d\left( {B',\left( P \right)} \right) = \frac{4}{3}\) nên \(d\left( {B',\left( P \right)} \right) = 2d\left( {A,\left( P \right)} \right)\) do đó \(A\) là trung điểm của đoạn thẳng \(B'M\) suy ra \(M\left( {1;2;1} \right)\).
* Tìm \(N\).
\(NA + NB \ge AB\)
Dấu “=" xảy ra khi \(N\) là giao điểm của đường thẳng \(AB\) và \(\left( P \right)\).
Có \(d\left( {A,\left( P \right)} \right) = \frac{2}{3},d\left( {B,\left( P \right)} \right) = \frac{4}{3}\) nên \(d\left( {B,\left( P \right)} \right) = 2d\left( {A,\left( P \right)} \right)\) do đó \(\overrightarrow {AB} = 3\overrightarrow {AN} \) nên \(N\left( {\frac{7}{{27}};\frac{{38}}{{27}};\frac{{35}}{{27}}} \right)\).
Câu 82:
Đường kính ngoài của quả bóng rỗng ruột là 10 cm. Quả bóng được làm từ cao su dày 0,4 cm. Tính khối lượng cao su cần dùng để làm quả bóng biết khối lượng riêng của cao su là \(913{\rm{\;kg}}/{{\rm{m}}^3}\). (Kết quả làm tròn đến chữ số thập phân thứ ba).
 Xem đáp án
Xem đáp án
Đổi \(913{\rm{\;kg/}}{{\rm{m}}^3} = 0,913{\rm{\;g/c}}{{\rm{m}}^3}\).
Thể tích cao su để làm quả bóng là: \(\frac{4}{3}\pi {.5^3} - \frac{4}{3}\pi .4,{6^3} = \frac{{13832\pi }}{{375}}\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Khối lượng cao su cần dùng để làm quả bóng là: \(0,913.\frac{{13832\pi }}{{375}} \approx 105,797\) (gam).
Câu 83:
Cho mặt cầu có diện tích là \(100\pi \). Thể tích của khối cầu được giới hạn bởi mặt cầu đã cho là \(\frac{{k\pi }}{3}\). Giá trị của \(k\) bằng (1) _________.
 Xem đáp án
Xem đáp án
Đáp án: “500”
Giải thích
Gọi \(r\) là bán kính mặt cầu.
Diện tích mặt cầu là \(S = 4\pi {r^2} \Leftrightarrow 4\pi {r^2} = 100\pi \Leftrightarrow r = 5\).
Thể tích của khối cầu là \(V = \frac{4}{3}\pi {r^3} = \frac{4}{3}\pi {.5^3} = \frac{{500\pi }}{3}\).
Vậy \(k = 500\).
Câu 84:
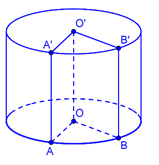
Nga làm thạch rau câu có dạng khối trụ với đường kính \(20{\rm{\;cm}}\) và chiều cao bằng \(9{\rm{\;cm}}\). Nga cắt dọc theo đường sinh một miếng từ khối thạch này (như hình vẽ) biết \(O,O'\) là tâm của hai đường tròn đáy, đoạn thẳng \(AB = 6{\rm{\;cm}}\). Thể tích của miếng thạch cắt ra gần bằng với giá trị nào sau đây?
 Xem đáp án
Xem đáp án
Ta có: \({\rm{cos}}\widehat {AOB} = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2OA.OB}} = \frac{{{{10}^2} + {{10}^2} - {6^2}}}{{2.10.10}} = \frac{{41}}{{50}} \Rightarrow \widehat {AOB} = \alpha \approx 0,609\left( {{\rm{rad}}} \right)\)
\( \Rightarrow \) số đo cung nhỏ là: \(\alpha = 0,609\left( {{\rm{rad}}} \right)\)
Diện tích hình quạt chắn bởi cung nhỏ là: \(S = \frac{{{R^2}\alpha }}{2} \approx \frac{{{{10}^2}.0,609}}{2} = 30,45\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Thể tích miếng thạch là \(V = OO'.S \approx 9.30,45 = 274,05\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right) \approx 274\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Câu 85:
Hàm số \(y = f\left( x \right) = \frac{{{x^3}}}{3} + a{x^2} + bx + c\) có bảng biến thiên được cho như hình vẽ.
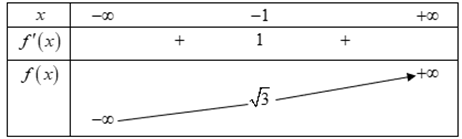
Có bao nhiêu số âm trong các hệ số a, b, c?
 Xem đáp án
Xem đáp án
Dựa vào bảng biến thiên, ta suy ra \(f\left( 0 \right) > f\left( { - 1} \right) \Leftrightarrow c > \sqrt 3 \Rightarrow c > 0\).
Ta có \(y' = f'\left( x \right) = {x^2} + 2ax + b,{{\rm{\Delta '}}_{y'}} = {a^2} - b\).
Vì \(f'\left( x \right) > 0,\forall x \in \mathbb{R}\) nên phương trình \(f'\left( x \right) = 0\) vô nghiệm.
\( \Rightarrow {\rm{\Delta '}}{\;_{y'}} < 0 \Leftrightarrow {a^2} - b < 0 \Leftrightarrow {a^2} < b \Rightarrow b > 0\).
Mặt khác \(f'\left( { - 1} \right) = 1 \Leftrightarrow 1 - 2a + b = 1 \Leftrightarrow b = 2a \Rightarrow a > 0\).
Câu 86:
Cho hàm số có đồ thị như hình vẽ.
\(y = f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x + 3{\rm{\;khi\;}}x \le 0}\\{3{\rm{\;\;khi\;}}x > 0}\end{array}} \right.\)
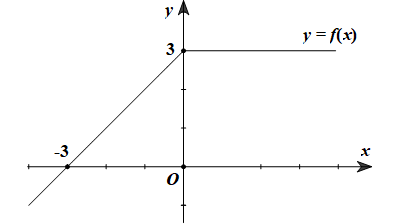
 Xem đáp án
Xem đáp án
Nhận xét: Hàm số y=f(x) liên tục trên .
Câu 87:
Trong không gian \(Oxyz\), cho điểm \(I\left( {1;2; - 2} \right)\) và mặt phẳng \(\left( P \right):2x + 2y + z + 5 = 0\). Mặt cầu \(\left( S \right)\) có tâm \(I\) cắt mặt phẳng \(\left( P \right)\) theo một đường tròn có chu vi bằng \(8\pi \).
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
ĐÚNG |
SAI |
|
Bán kính mặt cầu \(\left( S \right)\) bằng 3. |
¡ |
¡ |
|
Mặt cầu \(\left( S \right)\) tiếp xúc với mặt phẳng có phương trình \(2x + 2y + z + 11 = 0\). |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Bán kính mặt cầu \(\left( S \right)\) bằng 3. |
¡ |
¤ |
|
Mặt cầu \(\left( S \right)\) tiếp xúc với mặt phẳng có phương trình \(2x + 2y + z + 11 = 0\). |
¤ |
¡ |
Giải thích
Gọi \(H\) là hình chiếu của \(I\) trên mặt phẳng \(\left( P \right)\).
Ta có \(IH = d\left( {I,\left( P \right)} \right) = \frac{{\left| {2.1 + 2.2 + 1.\left( { - 2} \right) + 5} \right|}}{{\sqrt {{2^2} + {2^2} + {1^2}} }} = 3\).
Gọi \(r\) là bán kính đường tròn và \(R\) là bán kính mặt cầu.
Ta có chu vi đường tròn là \(2\pi r = 8\pi \Rightarrow r = 4\).
Bán kính mặt cầu là \(R = \sqrt {I{H^2} + {r^2}} = \sqrt {{3^2} + {4^2}} = 5\).
Gọi \(\left( \alpha \right):2x + 2y + z + 11 = 0\).
Ta có \(d\left( {I,\left( \alpha \right)} \right) = \frac{{\left| {2.1 + 2.2 + 1.\left( { - 2} \right) + 11} \right|}}{{\sqrt {{2^2} + {2^2} + {1^2}} }} = 5 = R\).
\( \Rightarrow \left( S \right)\) tiếp xúc với \(\left( \alpha \right)\).
Câu 88:
Phần nguyên của số thực \(x\) là số nguyên lớn nhất không vượt quá \(x\), kí hiệu là \(\left[ x \right]\). Chẳng hạn \(\left[ {1,2\left] { = 1;} \right[ - 2,7} \right] = - 3\).
Tổng các phần nguyên của số \(\sqrt k \) với \(k\) là số tự nhiên và \(k \in \left[ {1;24} \right]\) bằng
 Xem đáp án
Xem đáp án
Ta có:
\(S = \sum\limits_{k = 1}^{24} {[\sqrt k ] = [\sqrt 1 ] + [\sqrt 2 ] + [\sqrt 3 ] + [\sqrt 4 ] + \ldots + [\sqrt 8 ] + [\sqrt 9 ] + \ldots + [\sqrt {15} ] + [\sqrt {16} ] + \ldots + [\sqrt {23} ] + [\sqrt {24} ]} \)
\( \Leftrightarrow S = 1 + 1 + 1 + 2 + \ldots + 2 + 3 + \ldots + 3 + 4 + \ldots + 4 + 4\)
\( \Leftrightarrow S = 3.1 + 5.2 + 7.3 + 9.4 = 70\)
Câu 89:
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
![]()
Để tìm số các chữ số của một số tự nhiên \(A\) khi viết trong hệ thập phân, ta có công thức là:
\(\left[ {{\rm{log}}A} \right] + 1\).
Số nguyên tố dạng \({M_p} = {2^p} - 1\), trong đó \(p\) là một số nguyên tố được gọi là số nguyên tố Mec-xen (M. Mersenne, 1588 - 1648, người Pháp).
Ơ-le phát hiện \({M_{31}}\) có _______ chữ số năm 1750.
Luy-ca (E. Lucas, 1842 - 1891, người Pháp) phát hiện \({M_{127}}\) có _______ chữ số năm 1876.
\({M_{1398269}}\) được phát hiện có _______ chữ số năm 1996.
 Xem đáp án
Xem đáp án
Ơ-le phát hiện \({M_{31}}\) có 10 chữ số năm 1750.
Luy-ca (E. Lucas, 1842 - 1891, người Pháp) phát hiện \({M_{127}}\) có 39 chữ số năm 1876.
\({M_{1398269}}\) được phát hiện có 420921 chữ số năm 1996.
Giải thích
Áp dụng công thức \(\left[ {{\rm{log}}A} \right] + 1\) để tìm các chữ số của số \(A\).
Ta có: \({\rm{log}}\left( {{M_p} + 1} \right) = {\rm{log}}{2^p} = p{\rm{log}}2\).
+ Với \(p = 31 \Rightarrow {\rm{log}}\left( {{M_{31}} + 1} \right) = 31.{\rm{log}}2 \approx 9,33\)
\( \Rightarrow {M_{31}}\) có 10 chữ số.
+ Với \(p = 127 \Rightarrow {\rm{log}}\left( {{M_{127}} + 1} \right) = 127.{\rm{log}}2 \approx 38,23\)
\( \Rightarrow {M_{127}}\) có 39 chữ số.
+ Với \(p = 1398269 \Rightarrow {\rm{log}}\left( {{M_{1398269}} + 1} \right) = 1398269.{\rm{log}}2 \approx 420920,911\)
\( \Rightarrow {M_{1398269}}\) có 420921 chữ số.
Câu 90:
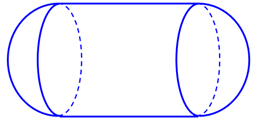
Một cái bồn chứa nước gồm hai nửa hình cầu và một hình trụ (như hình vẽ). Đường sinh của hình trụ bằng hai lần đường kính của hình cầu. Biết thể tích của bồn chứa nước là \(\frac{{128\pi }}{3}\left( {{{\rm{m}}^3}} \right)\). Diện tích xung quanh của cái bồn chứa nước bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Gọi \(4x\,\,\left( {\rm{m}} \right)\) là độ dài đường sinh hình trụ \((x > 0)\).
\( \Rightarrow \) Đường tròn đáy hình trụ và mặt cầu có bán kính là \(x\,\,\left( {\rm{m}} \right)\).
Thể tích bồn chứa nước này chính là thể tích của khối trụ có bán kính đáy \(R = x\), đường sinh \(l = h = 4x\) và thể tích khối cầu có bán kính \(R = x\).
Do đó: \(\pi \left( {{x^2}.4x + \frac{4}{3}{x^3}} \right) = \frac{{128\pi }}{3} \Leftrightarrow x = 2\,\,\left( {\rm{m}} \right)\).
Vậy diện tích xung quanh bồn nước là: \(S = \pi \left( {4{x^2} + 2.x.4x} \right) = 48\pi \,\,\left( {{{\rm{m}}^2}} \right)\).
Câu 91:
Cho cấp số nhân \(\left( {{u_n}} \right)\) công bội là \(q = - 4\) và \({u_5} = - 512\). Tổng của 8 số hạng đầu tiên của \(\left( {{u_n}} \right)\) là
 Xem đáp án
Xem đáp án
Ta có: \({u_5} = {u_1}.{q^4} \Leftrightarrow - 512 = {u_1}.{( - 4)^4} \Leftrightarrow {u_1} = - 2\).
Tổng của 8 số hạng đầu tiên của \(\left( {{u_n}} \right)\) là \({S_8} = {u_1}.\frac{{{q^8} - 1}}{{q - 1}} = 26214\).
Câu 92:
Biết \[\mathop {{\rm{lim}}}\limits_{x \to - 1} \frac{{{x^2} + \left( {2a - 1} \right)x + b}}{{{x^3} + 1}} = 2\]. Giá trị của a = (1) ______ và b = (2) ______ với \(a,b\) là các phân số tối giản (nếu có).
 Xem đáp án
Xem đáp án
Đáp án
Biết \[\mathop {{\rm{lim}}}\limits_{x \to - 1} \frac{{{x^2} + \left( {2a - 1} \right)x + b}}{{{x^3} + 1}} = 2\]. Giá trị của a = (1) ___9/2___ và b = (2) ___7___ với \(a,b\) là các phân số tối giản (nếu có).
Giải thích
Vì \[\mathop {{\rm{lim}}}\limits_{x \to - 1} \frac{{{x^2} + \left( {2a - 1} \right)x + b}}{{{x^3} + 1}} = 2\] nên \(x = - 1\) là nghiệm của phương trình \({x^2} + \left( {2a - 1} \right)x + b = 0\).
\( \Leftrightarrow {( - 1)^2} - \left( {2a - 1} \right) + b = 0 \Leftrightarrow b = 2a - 2\).
Khi đó, \(\mathop {{\rm{lim}}}\limits_{x \to - 1} \frac{{{x^2} + \left( {2a - 1} \right)x + b}}{{{x^3} + 1}} = 2 \Leftrightarrow \mathop {{\rm{lim}}}\limits_{x \to - 1} \frac{{{x^2} + \left( {2a - 1} \right)x + 2a - 2}}{{{x^3} + 1}} = 2\)
\( \Leftrightarrow \mathop {{\rm{lim}}}\limits_{x \to - 1} \frac{{\left( {x + 1} \right)\left( {x + 2a - 2} \right)}}{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} = 2\)
\( \Leftrightarrow \mathop {{\rm{lim}}}\limits_{x \to - 1} \frac{{x + 2a - 2}}{{{x^2} - x + 1}} = 2\)
\( \Leftrightarrow \frac{{ - 1 + 2a - 2}}{{{{( - 1)}^2} - \left( { - 1} \right) + 1}} = 2 \Leftrightarrow a = \frac{9}{2}\)
\( \Rightarrow b = 2.\frac{9}{2} - 2 = 7\)
Câu 93:
Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right)\) có tâm \(I\left( {2; - 1;3} \right)\). Từ điểm \(M\left( {4;1;1} \right)\) nằm ngoài mặt cầu \(\left( S \right)\), kẻ ba tiếp tuyến \(MA,MB,MC\) với mặt cầu \(\left( S \right)\) sao cho \(MA = MB = MC\). Biết \(\widehat {AMB} = {60^ \circ },\widehat {BMC} = {90^ \circ },\widehat {CMA} = {120^ \circ }\). Bán kính mặt cầu \(\left( S \right)\) bằng (1) _______.
 Xem đáp án
Xem đáp án
Đáp án: “3”
Giải thích
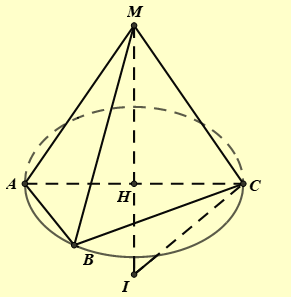
Đặt \(MA = MB = MC = a > 0\).
Áp dụng định lí \({\rm{cos}}\) cho tam giác \(MAB\) ta có:
\(A{B^2} = M{A^2} + M{B^2} - 2MA.MB.{\rm{cos}}\widehat {AMB} = {a^2} + {a^2} - 2a.a.{\rm{cos}}{60^ \circ } = {a^2}\). Suy ra \(AB = a\).
Tương tự, ta cũng tính được \(BC = \sqrt 2 a,CA = \sqrt 3 a\).
Xét tam giác \(ABC\) có: \(C{A^2} = B{C^2} + A{B^2}\) suy ra tam giác \(ABC\) vuông tại \(B\) (định lí Pythagore đảo). Do đó trung điểm \(H\) của \(AC\) là tâm đường tròn ngoại tiếp tam giác \(ABC\). Suy ra \(M,H,I\) thẳng hàng.
Xét tam giác \(MCI\) vuông tại \(C\) đường cao \(CH\):
\(IC.MC = CH.MI\) suy ra \(IC = \frac{{CH.MI}}{{MC}} = \frac{{\frac{{\sqrt 3 a}}{2}.2\sqrt 3 }}{a} = 3\).
Câu 94:
Cho phương trình \({\rm{lo}}{{\rm{g}}_4}{(x + 1)^2} + 2 = {\rm{lo}}{{\rm{g}}_{\sqrt 2 }}\sqrt {4 - x} + {\rm{lo}}{{\rm{g}}_8}{(4 + x)^3}\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Số nghiệm của phương trình đã cho là _______.
Tổng của các nghiệm của phương trình đã cho là _______.
 Xem đáp án
Xem đáp án
Số nghiệm của phương trình đã cho là 2 .
Tổng của các nghiệm của phương trình đã cho là \(4 - 2\sqrt 6 \).
Giải thích
Điều kiện : \( - 4 < x < 4\) và \(x \ne - 1\).
Ta có \({\rm{lo}}{{\rm{g}}_4}{(x + 1)^2} + 2 = {\rm{lo}}{{\rm{g}}_{\sqrt 2 }}\sqrt {4 - x} + {\rm{lo}}{{\rm{g}}_8}{(4 + x)^3}\)
\( \Leftrightarrow {\rm{lo}}{{\rm{g}}_2}\left( {4\left| {x + 1} \right|} \right) = {\rm{lo}}{{\rm{g}}_2}\left[ {\left( {4 - x} \right)\left( {4 + x} \right)} \right]\)
\( \Leftrightarrow 4\left| {x + 1} \right| = 16 - {x^2} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{4\left( {x + 1} \right) = 16 - {x^2}}\\{4\left( {x + 1} \right) = {x^2} - 16}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{x^2} + 4x - 12 = 0}\\{{x^2} - 4x - 20 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 2}\\{x = - 6}\\{x = 2 + 2\sqrt 6 }\\{x = 2 - 2\sqrt 6 }\end{array}} \right.} \right.\)
Đối chiếu điều kiện, phương trình đã cho có hai nghiệm \(x = 2\) và \(x = 2 - 2\sqrt 6 \).Câu 95:
Gọi S là tập hợp các số tự nhiên có năm chữ số chia hết cho 5. Chọn ngẫu nhiên một số từ tập S.
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
ĐÚNG |
SAI |
|
Số phần tử của tập hợp \(S\) là 6043 . |
¡ |
¡ |
|
Xác suất để số được chọn chia hết cho 3 là \(\frac{1}{3}\). |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Số phần tử của tập hợp \(S\) là 6043 . |
¡ |
¤ |
|
Xác suất để số được chọn chia hết cho 3 là \(\frac{1}{3}\). |
¤ |
¡ |
Giải thích
Giả sử số có năm chữ số có dạng \(\overline {abcde} \).
Vì số cần tìm chia hết cho 5 nên \(e\) có hai cách chọn là chữ số 0 và 5 .
Khi đó, \(a\) có chín cách chọn vì \(a \ne 0\); các vị trí \(b,c,d\) mỗi vị trí có mười cách chọn.
Suy số phần tử tập \(S\) là \({2.9.10^3} = 18000\) phần tử \( \Rightarrow n\left( {\rm{\Omega }} \right) = 18000\).
Số có năm chữ số bé nhất chia hết cho 5 là 10000 và lớn nhất là 99995 .
Gọi \(B\) là biến cố: "một số lấy từ tập \(S\) và chia hết cho 3 ", khi đó số được lấy này phải chia hết cho 15.
Số có năm chữ số bé nhất chia hết cho 15 là 10005 và lớn nhất là 99990 .
Vì chia hết cho 15 nên các số trong tập \(B\) này có thể xem như một cấp số cộng với
\({u_1} = 10005,{u_n} = 99990,d = 15 \Rightarrow n = \frac{{99990 - 10005}}{{15}} + 1 = 6000\)
Hay \(n\left( B \right) = 6000\). Vậy \({P_B} = \frac{{n\left( B \right)}}{{n\left( {\rm{\Omega }} \right)}} = \frac{{6000}}{{18000}} = \frac{1}{3}\).
Câu 96:
Số lượng ghế của một rạp hát nhiều hơn 320 và ít hơn 330 ghế. Biết mỗi hàng có 18 ghế. Số lượng ghế của rạp hát là (1) ______.
 Xem đáp án
Xem đáp án
Đáp án: “324”
Giải thích
Gọi \(x\) là số ghế của rạp hát \(\left. {\left( {x \in {\mathbb{N}^{\rm{*}}};\,\,320 < x < 330;\,\,x} \right. \vdots 18} \right)\)
Ta thấy \(\frac{{320}}{{18}} < \frac{x}{{18}} < \frac{{330}}{{18}} \Leftrightarrow 17,78 < \frac{x}{{18}} < 18,33 \Rightarrow \frac{x}{{18}} = 18 \Leftrightarrow x = 324\).
Câu 97:
Hai bạn \(A\) và \(B\) chơi một trò chơi: hai bạn sẽ tung hai con xúc xắc luân phiên, để giành chiến thắng thì tổng số chấm xuất hiện trên hai con xúc xắc phải bằng 8 . Biết bạn \({\rm{A}}\) là người chơi trước, xác suất giành chiến thắng của bạn \({\rm{A}}\) bằng (1) __________.
 Xem đáp án
Xem đáp án
Đáp án: “36/67”
Giải thích
Bước 1. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc bằng 8 .
Số phần tử không gian mẫu \(n\left( {\rm{\Omega }} \right) = 36\).
Để tổng số chấm xuất hiện trên hai con xúc xắc bằng 8 thì số chấm trên hai con xúc xắc là một trong các trường hợp sau \(\left( {2;6} \right),\left( {3;5} \right),\left( {4;4} \right),\left( {5;3} \right),\left( {6;2} \right)\).
Vậy xác suất để tổng số chấm xuất hiện trên hai con xúc xắc bằng 8 là \(\frac{5}{{36}}\).
Bước 2. Tính xác suất thắng của mỗi bạn.
\(A\) là biến cố bạn \({\rm{A}}\) là người chiến thắng.
\(P\left( A \right) = \left( {\frac{5}{{36}}} \right) + \left( {\frac{{31}}{{36}}.\frac{{31}}{{36}}.\frac{5}{{36}}} \right) + \left( {\frac{{31}}{{36}}.\frac{{31}}{{36}}.\frac{{31}}{{36}}.\frac{{31}}{{36}}.\frac{5}{{36}}} \right) + \ldots \)
\( = \frac{5}{{36}}\left[ {1 + {{\left( {\frac{{31}}{{36}}} \right)}^2} + {{\left( {\frac{{31}}{{36}}} \right)}^4} + \ldots } \right]\)
\( = \frac{5}{{36}}.\frac{1}{{1 - {{\left( {\frac{{31}}{{36}}} \right)}^2}}} = \frac{{36}}{{67}}\)
