Thi Online Đề thi Đánh giá tư duy tốc chiến Đại học Bách khoa năm 2023-2024 có đáp án (Đề 3)
Thi Online Đề thi Đánh giá tư duy tốc chiến Đại học Bách khoa năm 2023-2024 có đáp án (Đề 3)
-
269 lượt thi
-
62 câu hỏi
-
120 phút
Danh sách câu hỏi
Câu 1:
Ý nào sau đây thể hiện rõ nhất nội dung chính của bài đọc trên?
 Xem đáp án
Xem đáp án
Ý chính của các đoạn trong bài:
Đoạn 1-4: Vì sao cần nghiên cứu chế tạo pin năng lượng mặt trời trong suốt.
Đoạn 5: Lí do các nhà khoa học vẫn chưa chế tạo được pin năng lượng mặt trời trong suốt.
Đoạn 6: Các đặc điểm của TiO2.
Đoạn 7: Các đặc điểm của NiO.
Đoạn 8-10: Kết quả thử nghiệm vật liệu mới trong chế tạo pin mặt trời trong suốt.
Đoạn 11-12: Nhận định của các nhà khoa học về kết quả của nghiên cứu.
Tổng hợp các ý trên, ta có ý chính của toàn bài là: “Con đường hướng tới pin năng lượng mặt trời trong suốt.”
Chọn C
Câu 2:
Theo đoạn 2 (dòng 5-7), năng lượng mặt trời được giới khoa học kì vọng cao vì lí do nào sau đây?
 Xem đáp án
Xem đáp án
Câu 3:
Dựa vào đoạn 3 (dòng 8-11), ta có thể đưa ra kết luận nào sau đây?
 Xem đáp án
Xem đáp án
B. Pin năng lượng mặt trời truyền thống đòi hỏi chi phí lắp đặt cao. → Sai, đoạn trích không đề cập thông tin này.
C. Pin năng lượng mặt trời truyền thống chỉ có thể lắp đặt trên mái nhà. → Sai, pin truyền thống có thể được lắp trên mái nhà hoặc ở các trang trại năng lượng ở xa.
D. Pin năng lượng mặt trời truyền thống chỉ có thể được sử dụng ở quy mô nhỏ. → Sai, đoạn trích không đề cập thông tin này.
Câu 4:
Theo đoạn 5 (dòng 17-20), vai trò của chất bán dẫn trong pin mặt trời là gì?
 Xem đáp án
Xem đáp án
Câu 5:
 Xem đáp án
Xem đáp án
Câu 6:
Dựa vào đoạn 9 (dòng 33-36), chúng ta có thể nhận định như thế nào về kết quả của nghiên cứu?
 Xem đáp án
Xem đáp án
Câu 7:
Tại đoạn 9 (dòng 33-36), vì sao các nhà khoa học đánh giá tỉ lệ chuyển đổi năng lượng 2,1% là mức tương đối cao?
 Xem đáp án
Xem đáp án
Câu 8:
GS Joondong Kim cho biết định hướng phát triển tiếp theo của nghiên cứu là gì?
 Xem đáp án
Xem đáp án
Câu 9:
Ý nào sau đây thể hiện rõ nhất nội dung chính của bài đọc trên?
 Xem đáp án
Xem đáp án
Đoạn 1: Đặt vấn đề nghiên cứu.
Đoạn 2-4: Đặc điểm giấc ngủ của chim.
Đoạn 5-7: Giải thích cơ chế đậu tự động.
Đoạn 8: Một trường hợp ngoại lệ không sử dụng cơ chế đậu tự động.
Đoạn 9-10: Những khó khăn khi tiến hành nghiên cứu giấc ngủ của chim.
Tổng hợp các ý trên, ta có ý chính của toàn bài là: “Tại sao chim không rơi khỏi cành cây khi ngủ?”
Câu 10:
Dựa vào thông tin trong đoạn trích, điều nào sau đây đúng với giấc ngủ của các loài chim?
 Xem đáp án
Xem đáp án
Câu 11:
 Xem đáp án
Xem đáp án
Câu 12:
Theo đoạn 6 (dòng 22-30), trình tự các bước thực hiện cơ chế khóa tự động ở chân chim là
 Xem đáp án
Xem đáp án
Câu 13:
Từ “Nó” ở dòng 28 được dùng để chỉ:
 Xem đáp án
Xem đáp án
Chọn A
Câu 14:
Việc nhắc đến loài vẹt ở đoạn 7 (dòng 31-34) nhằm mục đích gì?
 Xem đáp án
Xem đáp án
Câu 15:
Theo đoạn 8 (dòng 35-41), thông tin nào sau đây về loài chim sáo châu Âu là KHÔNG chính xác?
 Xem đáp án
Xem đáp án
Thông tin tại dòng 37-38: chim chỉ hơi cong chân, không đủ khiến móng gập lại để bám vào cành cây.
Chọn B
Câu 16:
 Xem đáp án
Xem đáp án
Câu 17:
Ý nào sau đây thể hiện rõ nhất nội dung chính của bài đọc trên?
 Xem đáp án
Xem đáp án
Đoạn 1: Tính cấp thiết của việc tái chế rác thải xây dựng.
Đoạn 2: Một số phương pháp được đề xuất để tái chế chất thải xây dựng.
Đoạn 3-5: Giới thiệu và những ưu điểm chính của phương pháp tái chế chất thải xây dựng thành hạt cốt liệu nung rỗng.
Đoạn 6-9: Quá trình thực hiện nghiên cứu chế tạo bê tông cách nhiệt chịu lực từ chất thải xây dựng.
Đoạn 10-11: Những khó khăn trong quá trình thực hiện nghiên cứu và đề xuất phương án giải quyết.
Tổng hợp các ý trên, ta có ý chính của toàn bài là: “Chế tạo bê tông nhẹ có khả năng cách nhiệt và chịu lực từ chất thải xây dựng”
Câu 18:
Theo đoạn trích, giải pháp chủ yếu đang được sử dụng để xử lí rác thải xây dựng ở Việt Nam hiện này là gì?
 Xem đáp án
Xem đáp án
Câu 19:
Theo đoạn 2 (dòng 8-13), phương án nào sau đây là thành phẩm trực tiếp của máy nghiền tái chế vật liệu xây dựng?
 Xem đáp án
Xem đáp án
Câu 20:
Theo PGS.TS. Nguyễn Hùng Phong, ưu điểm chính của bê tông nhẹ là gì?
 Xem đáp án
Xem đáp án
Câu 21:
Tại đoạn 5 (dòng 25-28), câu văn “Việc dùng phế thải xây dựng làm đầu vào để sản xuất hạt cốt liệu cũng giúp giảm gánh nặng chôn lấp phế thải và bảo vệ môi trường, đồng thời mở ra hướng nghiên cứu để chế tạo vật liệu bê tông mà không cần sử dụng, khai thác mới các nguồn tài nguyên tự nhiên như đá, cát, sỏi.” minh họa rõ nhất cho ý nào sau đây?
 Xem đáp án
Xem đáp án
Câu 22:
Theo đoạn 6 (dòng 29-32), ta có thể rút ra kết luận gì về công trình nghiên cứu được đề cập đến trong bài?
 Xem đáp án
Xem đáp án
Câu 23:
Theo đoạn trích, các loại hạt cốt liệu chất lượng thấp sẽ được sử dụng để
 Xem đáp án
Xem đáp án
Câu 24:
Cụm từ “những hạt vật liệu này” ở dòng 45 được dùng để chỉ
 Xem đáp án
Xem đáp án
Câu 25:
Ý chính của đoạn 10 (dòng 48-54) là
 Xem đáp án
Xem đáp án
Câu 26:
Theo đoạn cuối, phương án nào sau đây KHÔNG phải là một trong những phương hướng hoàn thiện quy trình sản xuất hạt cốt liệu nhẹ?
 Xem đáp án
Xem đáp án
Câu 27:
Ý nào sau đây thể hiện rõ nhất nội dung chính của bài đọc trên?
 Xem đáp án
Xem đáp án
Đoạn 1: Giới thiệu dự án phát triển công nghệ nuôi tôm hùm thương phẩm trong bể trên bờ quy mô hàng hóa.
Đoạn 2-3: Thực trạng ô nhiễm môi trường do nghề nuôi tôm hùm.
Đoạn 4: Những khó khăn khi triển khai nuôi tôm hùm trong bể trên bờ.
Đoạn 5-7: Quy trình xử lý của RAS giúp triển khai dự án nuôi tôm hùm trong bể trên bờ.
Đoạn 8-9: Kết quả của dự án.
Đoạn 10-11: Lần đầu sử dụng thức ăn công nghiệp để nuôi tôm hùm.
Tổng hợp các ý trên, ta có ý chính của toàn bài là: “Việt Nam phát triển công nghệ nuôi tôm hùm thương phẩm trong bể.”
Câu 28:
Cụm từ “lưu thông thường xuyên” tại dòng 8 được dùng để miêu tả điều kiện nào sau đây?
 Xem đáp án
Xem đáp án
Cụm từ “lưu thông thường xuyên” chỉ lồng tôm hùm cần được đặt trong vùng nước có các luồng nước di chuyển nhằm đảm bảo nước được thay mới liên tục, tôm hùm không bị sống vùng nước tù đọng.
Chọn C
Câu 29:
Tại đoạn 3 (dòng 12-17), chị Trần Thị Lưu đã thể hiện thái độ gì?
 Xem đáp án
Xem đáp án
Câu 30:
Dựa vào đoạn 4 (dòng 18-21), ta có thể rút ra điều gì?
 Xem đáp án
Xem đáp án
Câu 31:
 Xem đáp án
Xem đáp án
Chọn D
Thông tin tại dòng 24-25: “...giúp kiểm soát được môi trường nuôi, kiểm soát dịch bệnh, không bị ảnh hưởng thời tiết, dễ dàng trong quá trình vận hành chăm sóc”. Đoạn trích không cung cấp thông tin so sánh chi phí giữa hai phương pháp nuôi.
Câu 32:
Theo đoạn 7 (dòng 33-40), trong quy trình xử lý RAS nước sẽ lưu chuyển tuần hoàn qua các thiết bị theo thứ tự nào sau đây?
 Xem đáp án
Xem đáp án
Câu 33:
Tại đoạn 9 (dòng 45-49), câu văn “Nếu như nuôi lồng ngoài biển nặng nhọc, chỉ đàn ông mới làm được, do hàng ngày phải lặn sâu xuống nước để kiểm tra, cho ăn, thì với mô hình nuôi trên bờ, ai cũng có thể đảm nhận công việc này” minh họa tốt nhất cho ý nào sau đây?
 Xem đáp án
Xem đáp án
Chọn A
A. Nuôi tôm hùm trong bể giúp giảm công sức chăm sóc tôm. → Đúng, văn bản cho biết ai cũng có thể làm công việc này (do yêu cầu đơn giản hơn).
B. Mô hình nuôi tôm hùm trên bờ khiến số việc làm cho nam giới giảm sút. → Sai, nam giới vẫn có thể tham gia cho nuôi tôm trong mô hình nuôi trên bờ.
C. Nuôi tôm hùm trên biển là mô hình có thể dễ dàng nhân rộng. → Sai, do cần lao động nặng nhọc và khó nên việc nhân rộng là không dễ dàng.
D. Tôm hùm được nuôi trong trên bờ ít cần sự giám sát của con người hơn. → Sai, văn bản không đề cập.
Câu 34:
 Xem đáp án
Xem đáp án
Chọn A
Thông tin tại dòng 50-51: thức ăn công nghiệp lần đầu được ứng dụng → chưa phổ biến.
Câu 35:
Theo đoạn 11 (dòng 55-60), nhóm nghiên cứu đánh giá thức ăn công nghiệp cho tôm hùm
 Xem đáp án
Xem đáp án
Chọn C
Thông tin tại dòng 57-58: “...việc đưa thức ăn viên trong môi trường biển tự nhiên khó khả thi...”.
Câu 36:
Cho hàm số y = f(x) có đồ thị hàm số y = f'(x) như hình bên dưới. Tìm số điểm cực trị của hàm số
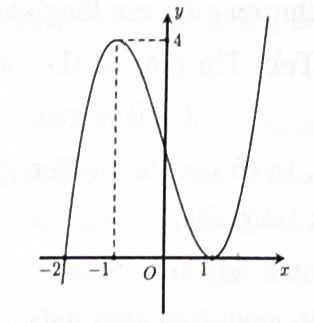
 Xem đáp án
Xem đáp án
Ta có
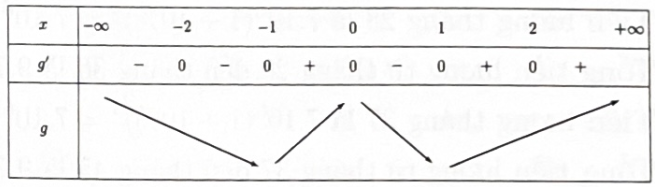
Dựa vào bảng biến thiên ta thấy hàm số có 3 điểm cực trị.
Câu 37:
Lưu lượng xe ô tô vào đường hầm được cho bởi công thức (xe/giây), trong đó u(km/h) là vận tốc trung bình của các xe ô tô khi vào đường hầm. Gọi v0 vận tốc trung bình của các xe ô tô khi vào đường hầm sao cho lưu lượng xe là lớn nhất. Giá trị của v0 xấp xỉ giá trị nào sau đây nhất?
 Xem đáp án
Xem đáp án
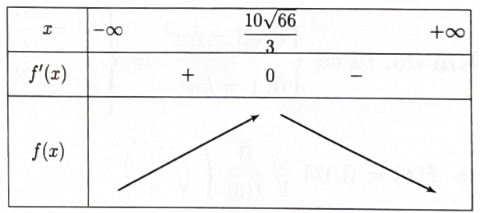
Dựa vào bảng biến thiên ta có Vậy lưu lượng xe lớn nhất khi
Câu 38:
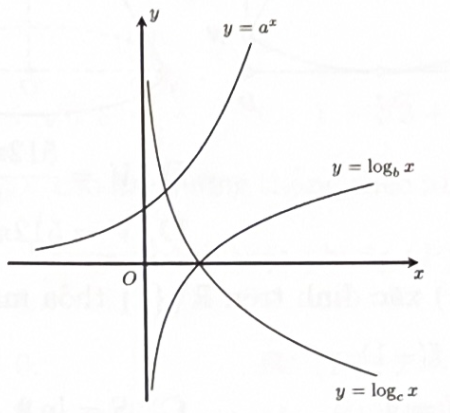
 Xem đáp án
Xem đáp án
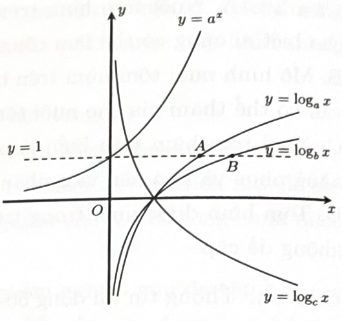
Mặt khác, là hàm số nghịch biến nên
Vẽ đồ thị hàm số bằng cách lấy đối xứng đồ thị hàm số qua đường thẳng
Kẻ đường thẳng cắt hai đồ thị hàm số và lần lượt tại hai điểm A và B. Khi đó, và Từ đồ thị hàm số ta thấy Vậy a<b
Câu 39:
Một kĩ sư mới ra trường làm việc với mức lương khởi điểm là 7 triệu đồng/tháng. Cứ sau 9 tháng làm việc, mức lương của kĩ sư đó lại được tăng thêm 10%. Hỏi sau 4 năm làm việc, tổng số tiền lương kĩ sư đó nhận được là bao nhiêu?
 Xem đáp án
Xem đáp án
Tiền lương tháng 10 là đồng.
Tổng tiền lương từ tháng 10 đến tháng 18 là đồng.
Tiền lương tháng 19 là đồng.
Tổng tiền lương từ tháng 19 đến tháng 27 là đồng.
Tiền lương tháng 28 là đồng.
Tổng tiền lương từ tháng 28 đến tháng 36 là đồng.
Tiền lương tháng 37 là đồng.
Tổng tiền lương từ tháng 37 đến tháng 45 là đồng.
Tiền lương tháng 46 là đồng.
Tổng tiền lương từ tháng 46 đến tháng 48 là đồng.
Tổng tiền lương sau 4 năm (từ tháng 1 đến tháng 48) là 418 442 010 đồng.
Câu 40:
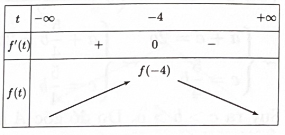
Các nhà khoa học nghiên cứu đã chỉ ra rằng giả sử nhiệt độ trung bình của năm lấy làm mốc là t0, khi nhiệt độ trung bình Trái Đất tăng lên so với to là t°C thì nước biển dâng lên so với lúc đầu là
f(t) = kat (m), trong đó k, a là các hằng số dương. Biết khi nhiệt độ trung bình tăng 2°C so với t0 thì nước biển dâng 0,03m, khi nhiệt độ trung bình tăng 5°C so với to thì nước biển dâng 0, 1 m. Hỏi khi nhiệt độ trung bình Trái Đất tăng thêm bao nhiêu độ C so với t0 thì mực nước biển dâng lên 0, 15 m? (lấy gần đúng)
 Xem đáp án
Xem đáp án
Khi đó, ta có
Khi nước biển dâng lên 0,15m thì ta có
Vậy khi nhiệt độ trung bình trái đất tăng thêm 6,01°C so với thì mực nước biển dâng lên 0,15m.
Câu 41:
Cho hình chữ nhật ABCD có AB = 2BC = 2a. Tính thể tích khối tròn xoay khi quay hình phẳng ABCD quanh trục AB.
 Xem đáp án
Xem đáp án
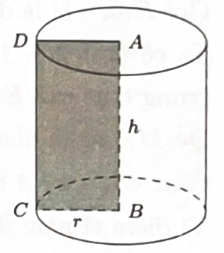
Độ dài đường cao là
Thể tích khối trụ là
Câu 42:
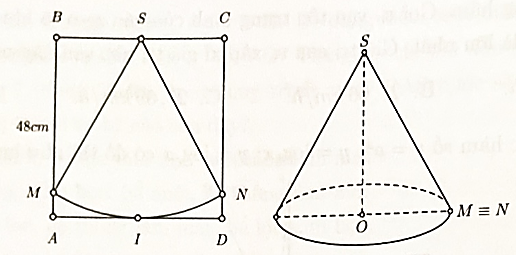
Cho một tấm bìa hình vuông ABCD cạnh 48 cm. Gọi S, I lần lượt là trung điểm của BC, AD. Dùng compa vạch cung tròn MN có tâm là S và bán kính SI (như hình vẽ) rồi cắt tấm bìa theo cung tròn đó. Dán phần hình quạt sao cho cạnh SM và SN trùng nhau thành một cái mũ hình nón không đáy với đỉnh S (giả sử phần mép dán không đáng kể). Tính thể tích V của cái mũ đó.
 Xem đáp án
Xem đáp án
Chu vi đường tròn đáy của cái mũ chính là chiều dài x của dây cung MN.
Mặt khác số đo cung MN bằng số đo nên
Gọi r là bán kính của đường tròn đáy của cái mũ, ta có
Chiều cao của cái mũ
Vậy thể tích cái mū
Câu 43:
Cho hàm số y = f(x) xác định trên ℝ\{1} thỏa mãn f(0) = 2017, f(2) = 2018. Tính S = f(3) – f(−1)..
 Xem đáp án
Xem đáp án
Mà
+) Trên khoảng ta có
Mà
Vậy
Câu 44:
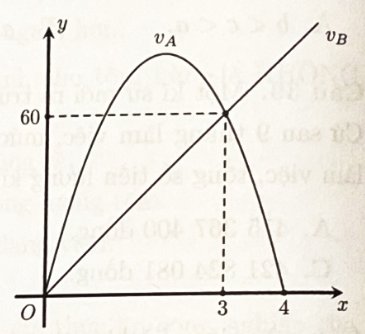
Cho đồ thị biểu diễn vận tốc của hai xe A và B khởi hành cùng một lúc và cùng vạch xuất phát, đi cùng chiều trên một con đường. Biết đồ thị biểu diễn vận tốc của xe A là một đường parabol và đồ thị biểu diễn vận tốc của xe B là một đường thẳng như hình vẽ bên. Hỏi sau 5 giây kể từ lúc xuất phát thì khoảng cách giữa hai xe là bao nhiêu mét? (Biết rằng xe A sẽ dừng lại khi vận tốc bằng 0).
 Xem đáp án
Xem đáp án
Biểu thức biểu diễn vận tốc của xe B là đường thẳng đi qua diểm
Ta có nên xe A dừng lại sau giầy thứ 4.
Do đó quãng đường xe A đi được sau 4 giây là
Quãng đường xe B đi được sau 5 giây đầu là
Khoảng cách giữa hai xe sau 5 giây kể từ lúc xuất phát là
Câu 45:
Cho số phức z thỏa mãn (1 + 2i)z = 5(1+i)2. Tổng bình phương phần thực và phần ảo của số phức bằng
 Xem đáp án
Xem đáp án
Suy ra
Vậy số phức w có phần thực bằng 2 , phần ảo bằng 2. Suy ra
Câu 46:
Trong mặt phẳng phức Oxy, các số phức z thỏa mãn |z + 2 – 1| = |z + i|. Tìm số phức z được biểu diễn bởi điểm M sao cho MA ngắn nhất với A(1,3).
 Xem đáp án
Xem đáp án
Gọi là điểm biểu diễn số phức
Gọi là điểm biểu diễn số phức
Gọi là điểm biểu diễn số phức
Ta có Tập hợp điểm biểu diễn số phức z là đường trung trực của
Để MA ngắn nhất thì tại
Chọn A
Câu 47:
Trong không gian Oxyz, cho mặt cầu (S) có tâm là điểm I(−1;2; –3) và tiếp xúc với trục Ox. Phương trình của (S) là
 Xem đáp án
Xem đáp án
Vì điểm A nằm trên mặt cầu nên bán kính của mặt cầu là
Phương trình mặt cầu S tâm và bán kính là
Câu 48:
 Xem đáp án
Xem đáp án
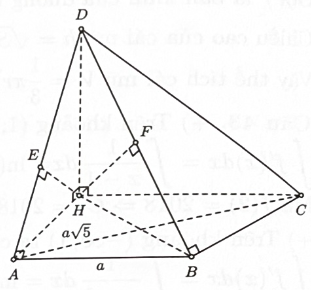
Ta co
Tương tự
Tam giác AHB có
vuông cân tại
Áp dụng định lý cosin, ta có
Vậy
Dựng và
Suy ra và tam giác HEF vuông tại E.
Đặt khi đó
Suy ra
Vậy
Câu 49:
Cho hình nón chứa bốn mặt cầu cùng có bán kính là trong đó ba mặt cầu tiếp xúc với đáy, tiếp xúc lẫn nhau và tiếp xúc với mặt xung quanh của hình nón. Mặt cầu thứ tư tiếp xúc với ba mặt cầu kia và tiếp xúc với mặt xung quanh của hình nón. Tính bán kính đáy của hình nón.
 Xem đáp án
Xem đáp án
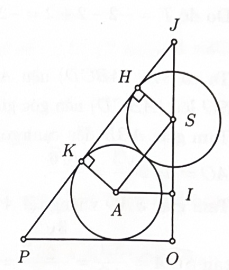
Xét trường hợp tổng quát là bốn mặt cầu có bán kính r.
Gọi tâm các mặt cầu là S, A, B, C, trong đó S là tâm của mặt cầu trền cùng. Do các mặt cầu tiếp xúc ngoài nhau nên S.ABC là chóp đều cạnh 2r.
Gọi I là tâm của tam giác ABC, khi đó SI vuông góc với mặt phẳng và
Tam giác SAI$ vuông tại I, có
Kẻ đường sinh JP của hình nón tiếp xúc với hai mặt cầu tâm S và tâm A lần lượt tại H, K.
Ta có (g-g) nên
Chiều cao của khối nón là
Bán kính khối nón là
Áp dụng với ta được
Chọn C
Câu 50:
Trong không gian Oxyz, cho hai đường thẳng chéo nhau và Phương trình mặt phẳng (P) chứa và song song với đường thẳng là
 Xem đáp án
Xem đáp án
Đường thẳng có một vectơ chỉ phương
Gọi là một vectơ pháp tuyến của mặt phẳng Do mặt phẳng chứa và song song với đường thẳng nên
Vậy phương trình mặt phẳng đi qua và có một vectơ pháp tuyến là
Câu 51:
 Xem đáp án
Xem đáp án
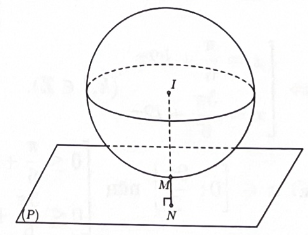
Vậy điểm M thuộc mặt cầu tầm bán kính
Vậy MN nhỏ nhất khi M, N thuộc đường thẳng đi qua tâm I và vuông góc với mặt phẳng (P). Gọi (d) là đường thẳng đi qua tâm I và vuông góc với mặt phẳng (P)
Khi đó
Tọa độ điểm N là nghiệm của hệ phương trình
Do đó
Câu 52:
 Xem đáp án
Xem đáp án
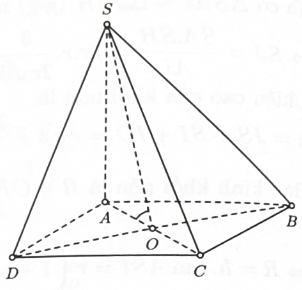
Tam giác ABD đều cạnh nên
Vậy góc giữa đường thẳng SO và mặt phẳng (ABCD) bằng 60°.
Câu 53:
 Xem đáp án
Xem đáp án
Ta có
Khi đó góc giữa hai mặt phẳng và là góc có
Ta có
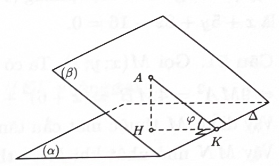
Câu 54:
 Xem đáp án
Xem đáp án
Vì nên
Vậy phương trình có 5 nghiệm.
Câu 55:
Có 5 nhà Toán học nam, 3 nhà Toán học nữ và 4 nhà Vật lý học nam. Người ta chọn trong số người này ra 3 người để lập một đoàn đi công tác, trong đó phải có cả nam lẫn nữ và phải có cả nhà Toán học lẫn nhà Vật lý. Số cách thành lập đoàn này là
 Xem đáp án
Xem đáp án
TH1: 1 nhà Vật lý nam, 2 nhà Toán học nữ có cách.
TH2: 1 nhà Vật lý nam, 1 nhà Toán học nam, 1 nhà toán học nữ có cách.
TH3: 2 nhà Vật lý nam, 1 nhà Toán học nữ có cách.
Vậy có cách.
Câu 56:
Một công ty nhận được 50 hồ sơ xin việc của 50 người khác nhau muốn xin việc vào công ty, trong đó có 20 người biết tiếng Anh, 17 người biết tiếng Pháp và 18 người không biết cả tiếng Anh và tiếng Pháp. Công ty cần tuyển 5 người biết ít nhất một thứ tiếng Anh hoặc Pháp. Tính xác suất để trong 5 người được chọn có đúng 3 người biết cả tiếng Anh và tiếng Pháp.
 Xem đáp án
Xem đáp án
Số người biết cả tiếng Anh và tiếng Pháp là:
Số phần tử của không gian mẫu là số cách chọn 5 người trong 32 người biết tiếng Anh hoặc tiếng Pháp. Suy ra
Gọi A là biến cố "trong 5 người được chọn có đúng 3 người biết cả tiếng Anh và tiếng Pháp". Chọn 3 người biết cả tiếng Anh và tiếng Pháp có cách.
Ứng với mỗi cách chọn 3 người nói trên, có cách chọn 2 người còn lại.
Suy ra,
Vậy xác suất của biến cố A là
Câu 57:
Cho cấp số nhân (un) với u2 = 2 và u4 = 18. Công bội của cấp số nhân đã cho bằng
 Xem đáp án
Xem đáp án
Do là cấp số nhân nên với suy ra
Chọn A
Câu 58:
Cho tam giác ABC có độ dài ba cạnh là a; b; c. Gọi p là nửa chu vi của tam giác. Biết dãy số a; b; c; p theo thứ tự lập thành một cấp số cộng. Tìm cosin của góc nhỏ nhất trong tam giác đó.
 Xem đáp án
Xem đáp án
Suy ra . Do đó góc A là góc nhỏ nhất.
Từ đó ta có
Câu 59:
 Xem đáp án
Xem đáp án
Tam giác có bán kính đường tròn ngoại tiếp là
Tam giác có bán kính đường tròn ngoại tiếp là
...........................................................................
Tam giác có bán kính đường tròn ngoại tiếp là
Suy ra S là tổng của cấp số nhân lùi vô hạn, có công bội
Vậy
Câu 60:
Theo thống kê tại một nhà máy Z, nếu áp dụng tuần làm việc 40 giờ thì mỗi tuần có 100 công nhân đi làm và mỗi công nhân làm được 120 sản phẩm trong một giờ. Nếu tăng thời gian làm việc thêm 2 giờ mỗi tuần thì sẽ có 1 công nhân nghỉ việc và năng suất lao động giảm 5 sản phẩm/1 công nhân/1 giờ. Ngoài ra, số phế phẩm mỗi tuần ước tính là với x là thời gian làm việc trong một tuần. Nhà máy cần áp dụng thời gian làm việc mỗi tuần mấy giờ để số lượng sản phẩm thu được mỗi tuần là lớn nhất?
 Xem đáp án
Xem đáp án
=> số công nhân bỏ việc là nên số công nhân làm việc là người.
Năng suất của công nhân còn sản phẩm một giờ.
Số thời gian làm việc một tuần là giờ.
Để nhà máy hoạt động được thì
Số sản phẩm trong một tuần làm được:
Số sản phẩm thu được là
Ta có
Dựa vào bảng biến thiên ta có số lượng sản phẳm thu được mỗi tuẳn lớn nhất khi
Câu 61:
Cho 2 bình: bình 1 dựng 6 viên bi xanh và 4 viên bi vàng; bình 2 đựng 3 viên bị xanh và 6 viên bi vàng. An và Bình cùng nhau chơi trò gieo súc sắc như sau: Gieo hai con súc sắc xanh và đỏ. Gọi x, y lần lượt là kết quả số chấm xuất hiện của hai con súc sắc đó. Nếu x + y > 5 thì lấy ra 2 viên bi từ bình 1, còn nếu 2 + y < 5 thì lấy ra 2 viên bị từ bình 2. Tính xác suất để lấy được ít nhất một viên bi xanh.
 Xem đáp án
Xem đáp án
=> Số phần tử của không gian mẫu là
Ta thấy trong 36 bộ số của không gian mẫu chỉ có 6 cặp có tổng nhỏ hơn 5.
Đó là
Vậy xác suất để là
Xác suát để là
Bình 1 đựng 6 viên bi xanh và 4 viến bi vàng
=> Xác suất lấy cả 2 viên bi vàng từ bình 1 là
=> Xác suất lấy được ít nhất 1 viên bi xanh từ bình 1 là
Bình 2 đựng 3 viên bi xanh và 6 viên bi vàng
=> Xác suất lấy cả 2 viên bi vàng từ bình 2 là
=> Xác suất lấy được ít nhất 1 viên bi xanh từ bình 2 là
Do đó xác suất để lấy được ít nhất 1 bi xanh trong trò chơi là
Câu 62:
Nhân viên của một quán cafe cần làm 7 li sinh tố bơ. Biết li thủy tinh đựng sinh tố có dạng hình trụ, chiều cao gấp hai lần đường kính đáy. Mỗi li sinh tố khách hàng yêu cầu thả ba viên đá, các viên đá của quán đều có dạng hình lập phương, cạnh của hình lập phương bằng một nửa bán kính đáy li. Biết mỗi quả bơ có thể làm được 2 li sinh tố (không chứa đá) có thể tích bằng thể tích li. Hỏi để làm được 7 li sinh tố theo yêu cầu của khách hàng thì nhân viên cần dùng tối thiểu bao nhiêu quả bơ? Biết thể tích sinh tố trong li đều bằng thể tích li.
 Xem đáp án
Xem đáp án
Khi đó, chiều cao của li là cạnh của viên đá là
=> thể tích của li là
Thể tích của một viên đá là
Để làm được 7 li sinh tố cần viên đá.
Khi đó, thể tích các viên đá bằng
Vì mỗi quả bơ có thể làm được 2 li sinh tố (không chứa đá) có thể tích bằng thể tích li nên thể tích sinh tố bơ được làm từ một quả bơ là
Thể tích sinh tố bơ được làm từ n quả bơ là
Tổng thể tích bơ và đá để làm 7 li sinh tố là
Theo đề bài ra ta có
Vậy cần tối thiểu 4 quả bơ để làm được 7 li sinh tố như yêu cầu.
