20 câu trắc nghiệm Toán 11 KNTT Bài 15. Giới hạn của dãy số có đáp án
-
64 lượt thi
-
20 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Kết quả của giới hạn \[\mathop {{\rm{lim}}}\limits_{} \left( {\frac{{{\rm{sin5n}}}}{{{\rm{3n}}}} - {\rm{2}}} \right)\] bằng:
 Xem đáp án
Xem đáp án
Ta có \[{\rm{0}} \le \left| {\frac{{{\rm{sin5n}}}}{{{\rm{3n}}}}} \right| \le \frac{{\rm{1}}}{{\rm{n}}}\] mà \[\lim \frac{1}{{\rm{n}}} = 0\]
Nên theo nguyên lý kẹp có: \[{\mathop{\rm li}\nolimits} {\rm{m}}\,\frac{{{\rm{sin5n}}}}{{{\rm{3n}}}}{\rm{ = 0}}\] do đó \[\mathop {\lim }\limits_{} \left( {\frac{{{\rm{sin5n}}}}{{{\rm{3n}}}} - 2} \right) = - 2\]
Đáp án cần chọn là: A
Câu 5:
Kết quả của giới hạn 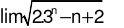 bằng:
bằng:
 Xem đáp án
Xem đáp án
Ta có \[{\rm{C}}_{\rm{n}}^{\rm{2}}{\rm{ < }}{{\rm{2}}^{\rm{n}}}\]
Khi \[{\rm{n}} \to \infty \Rightarrow {2^{\rm{n}}} < {3^{\rm{n}}}\] do đó \[{\rm{C}}_{\rm{n}}^{\rm{2}}{\rm{ < }}{{\rm{3}}^{\rm{n}}} \Rightarrow \frac{{{\rm{n}}\left( {{\rm{n}} - {\rm{1}}} \right)}}{{\rm{2}}}{\rm{ < }}{{\rm{3}}^{\rm{n}}}\]
Ta có
\[ \Rightarrow \lim \sqrt {{{2.3}^{\rm{n}}} - {\rm{n}} + 2} = + \infty \]
Đáp án cần chọn là: D
Câu 6:
Kết quả của giới hạn\[\lim \frac{{3\sin {\rm{n}} + 4\cos {\rm{n}}}}{{{\rm{n}} + 1}}\]bằng:
 Xem đáp án
Xem đáp án
Ta có\[0 \le \left| {\frac{{3\sin {\rm{n}} + 4\cos {\rm{n}}}}{{{\rm{n}} + 1}}} \right| \le \left| {\frac{{\left( {{3^2} + {4^2}} \right).\left( {{{\sin }^2}{\rm{n}} + {{\cos }^2}{\rm{n}}} \right)}}{{{\rm{n}} + 1}}} \right| = \frac{5}{{{\rm{n}} + 1}} \to 0\]
Theo nguyên lý kẹp ta suy ra\[\lim \frac{{3\sin {\rm{n}} + 4\cos {\rm{n}}}}{{{\rm{n}} + 1}} = 0\]
Đáp án cần chọn là: B
Câu 7:
Chọn khẳng định đúng:
 Xem đáp án
Xem đáp án
Định nghĩa 1\[\lim {{\rm{u}}_{\rm{n}}}{\rm{ = 0}}\]nếu \[\left| {{{\rm{u}}_{\rm{n}}}} \right|\]có thể nhỏ hơn môt số dương bé tùy ý, kể từ một số hạng nào đó trở đi
Đáp án cần chọn là: A
Câu 8:
Cho dãy số (un) với 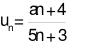 trong đó a là tham số thực. Để dãy số có giới hạn bằng 2, giá trị của a là
trong đó a là tham số thực. Để dãy số có giới hạn bằng 2, giá trị của a là
 Xem đáp án
Xem đáp án
Ta có 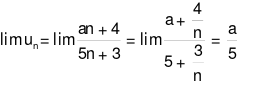

Đáp án cần chọn là: A
Câu 9:
Cho dãy số (un) với 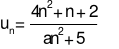 trong đó a là tham số thực. Để dãy số có giới hạn bằng 2, giá trị của a là
trong đó a là tham số thực. Để dãy số có giới hạn bằng 2, giá trị của a là
 Xem đáp án
Xem đáp án

Đáp án cần chọn là:
DCâu 11:
Có bao nhiêu giá trị nguyên của tham số thuộc khoảng (−10; 10) để
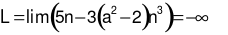
 Xem đáp án
Xem đáp án
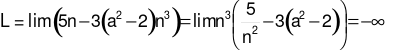
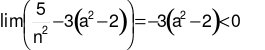

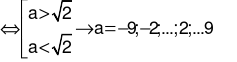
Đáp án cần chọn là: B
Câu 14:
Giá trị của giới hạn  là:
là:
 Xem đáp án
Xem đáp án
Đây là một cấp số nhân lùi vô hạn có 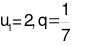
Do đó 
Đáp án cần chọn là: B
Câu 17:
Cho dãy số (un) với 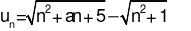 , trong đó a là tham số thực. Tìm a để
, trong đó a là tham số thực. Tìm a để 
 Xem đáp án
Xem đáp án
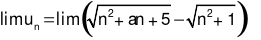
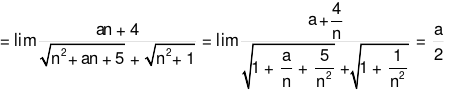
Để
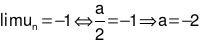
Đáp án cần chọn là: C
Câu 18:
Rút gọn \[{\rm{S}} = 1 + {\cos ^2}{\rm{x}} + {\cos ^4}{\rm{x}} + {\cos ^6}{\rm{x}} + .... + {\cos ^{2{\rm{n}}}}{\rm{x}} + ...\]với\[\cos {\rm{x}} \ne \pm 1\]
 Xem đáp án
Xem đáp án
Vì \[ - 1 \le \cos {\rm{x}} \le 1,\,\cos {\rm{x}} \ne \pm 1 \Rightarrow - 1 < \cos {\rm{x}} < 1\]
Do đó \[1,\,{\cos ^2}{\rm{x}},{\cos ^4}{\rm{x}},{\cos ^6}{\rm{x}},....,{\cos ^{2{\rm{n}}}}{\rm{x}},...\]là cấp số nhân lùi vô hạn với công bội \[{\cos ^2}{\rm{x}}.\].
Do đó:
\[{\rm{S}} = 1 + {\cos ^2}{\rm{x}} + {\cos ^4}{\rm{x}} + {\cos ^6}{\rm{x}} + .... + {\cos ^{2{\rm{n}}}}{\rm{x}} + ... = \frac{1}{{1 - {{\cos }^2}{\rm{x}}}} = \frac{1}{{{{\sin }^2}{\rm{x}}}}\]
Đáp án cần chọn là: C
Câu 19:
Số thập phân vô hạn tuần hoàn 0,5111… được biểu diễn bởi phân số tối giản  . Tính tổng
. Tính tổng 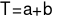
 Xem đáp án
Xem đáp án
Ta có 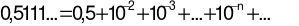
Dãy số 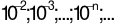 là một cấp số nhân lùi vô hạn có số hạng đầu bằng
là một cấp số nhân lùi vô hạn có số hạng đầu bằng 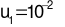 , công bội
, công bội 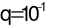 nên
nên 
Vậy 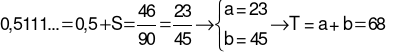
Đáp án cần chọn là: B
Câu 20:
Bạn An thả một quả bóng cao su từ độ cao 9 m so với mặt đất. Mỗi lần chạm đất quả bóng nảy lên độ cao bằng  độ cao của lần rơi trước. Giả sử quả bóng luôn chuyển động vuông góc với mặt đất. Tổng quãng đường bóng đã di chuyển (từ lúc bắt đầu thả đến lúc bóng không di chuyển nữa) gần nhất với kết quả nào sau đây?
độ cao của lần rơi trước. Giả sử quả bóng luôn chuyển động vuông góc với mặt đất. Tổng quãng đường bóng đã di chuyển (từ lúc bắt đầu thả đến lúc bóng không di chuyển nữa) gần nhất với kết quả nào sau đây?
 Xem đáp án
Xem đáp án
Ta coi độ cao nảy lên lần thứ nhất là 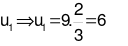
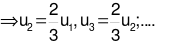
⇒Đây là cấp số nhân lùi vô hạn với 
Vì mỗi quả bóng sau khi nảy lên lại tiếp tục rơi xuống nên tổng quãng đường bóng di chuyển là: 
Đáp án cần chọn là: C

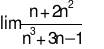 bằng:
bằng:
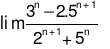 bằng:
bằng:
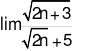 bằng:
bằng: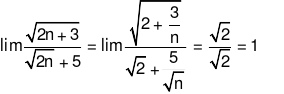 Đáp án cần chọn là:
Đáp án cần chọn là: 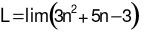
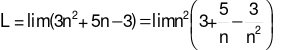
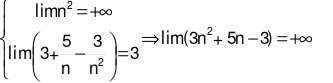
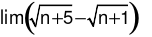 bằng
bằng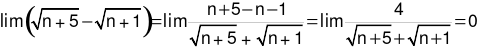
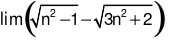 bằng
bằng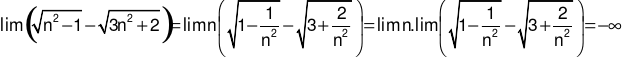
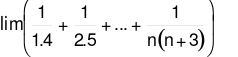 là:
là: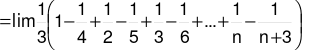
 bằng:
bằng: