Bài tập chuyên đề toán 11 Bài 3: Đường thẳng song song với mặt phẳng có đáp án
Dạng 1: Chứng minh đường thẳng song song với mặt phẳng có đáp án
-
1250 lượt thi
-
22 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
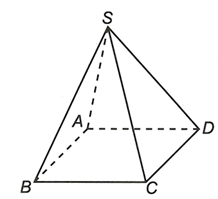
Câu 2:
 Xem đáp án
Xem đáp án
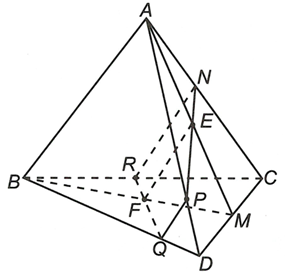
a) Ta có EF là đường trung bình của tam giác ABM suy ra
Do nên và nên
Câu 3:
 Xem đáp án
Xem đáp án
b) Kéo dài NE cắt AD tại P.
Do EF // (ABD) nên kẻ Px // AB và cắt BD tại Q.
Kẻ QF cắt BC tại R.
Khi đó hình thang NPQR là thiết diện của mặt phẳng (NEF) với tứ diện ABCD.
Câu 4:
 Xem đáp án
Xem đáp án

Gọi I là trung điểm của AD.
Ta có G là trọng tâm khi đó
Mặt khác, và
Từ đó suy ra
Áp dụng định lý Ta-lét đảo suy ra
Mà nênCâu 5:
 Xem đáp án
Xem đáp án
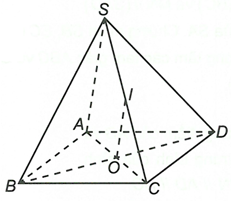
Ta có IO là đường trung bình của tam giác SAC suy ra IO // SA
Do và từ đó suy ra vàCâu 6:
 Xem đáp án
Xem đáp án
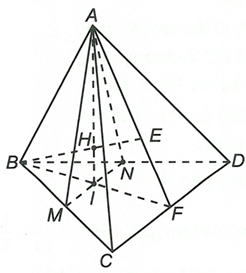
a) Vì M, N lần lượt là trung điểm của BC, BD nên MN //CD
Câu 7:
 Xem đáp án
Xem đáp án
b) Trong gọi
Ta có
Xét và có
Trong có
Suy ra
Trong gọi Suy ra
Câu 8:
 Xem đáp án
Xem đáp án
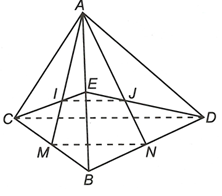
Gọi M, N lần lượt là trung điểm của BC và BD.
Khi đó
Suy ra
Mà
Câu 9:
 Xem đáp án
Xem đáp án
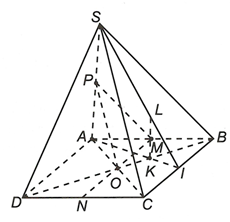
a) Do M, N lần lượt là trung điểm của AB và CD nên MN là đường trung bình của hình bình hành ABCD nên
Từ đó suy ra vàCâu 10:
 Xem đáp án
Xem đáp án
b) Gọi O là tâm hình bình hành ABCD. Ta có PM là đường trung bình của tam giác SAB suy ra nên
Do MN là đường trung bình của hình bình hành ABCD suy ra
Xét tam giác SAC có P, O lần lượt là trung điểm của SA và AC nên PO là đường trung bình của tam giác SAC suy ra
Từ đó suy ra do
Câu 11:
 Xem đáp án
Xem đáp án
c) Gọi I là trung điểm của BC.
Do K là trọng tâm của tam giác ABC
Tương tự L là trọng tâm của tam giác SBC
Từ đó ta có nên
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án B
Nếu a, b là hai đường thẳng chéo nhau thì chỉ có một mặt phẳng chứa a và song song với b nên mệnh đề 4 sai.
Câu 13:
Cho các mệnh đề:
1.
2. với và
3. Nếu hai mặt phẳng cắt nhau cùng song song với một đường thẳng thì giao tuyến của chúng cũng song song với đường thẳng đó.
4. Nếu a, b là hai đường thẳng chéo nhau thì có vô số mặt phẳng chứa a và song song với b.
Số mệnh đề đúng là:
 Xem đáp án
Xem đáp án
Câu 14:
 Xem đáp án
Xem đáp án
Đáp án B
Câu 15:
 Xem đáp án
Xem đáp án
Đáp án D
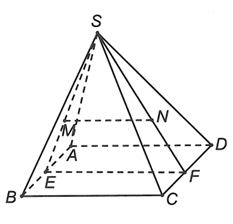
Gọi E và F lần lượt là trung điểm của AB và CD.
Do M; N là trọng tâm tam giác SAB, SCD nên S, M, E thẳng hàng;
S, N, F thẳng hàng.
Xét có nên theo định lý Ta-lét ta có MN // EFMà nên MN // (ABCD)
Câu 16:
 Xem đáp án
Xem đáp án
Đáp án C
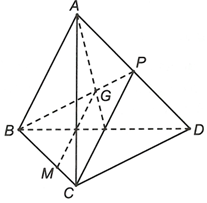
Gọi P là trung điểm của AD.
Ta có nên GM // PC mà
VậyCâu 17:
 Xem đáp án
Xem đáp án
Đáp án B
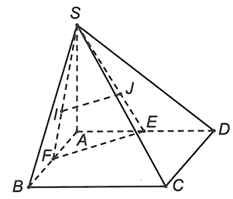
Vì I; J lần lượt là trọng tâm các tam giác SAD và SAB nên
Do nên IJ // (ABD)Câu 18:
Đường thẳng a // (P) nếu
 Xem đáp án
Xem đáp án
Câu A sai vì a có thể nằm trong (P). Câu B vì đường thẳng song song với mặt phẳng khi đường thẳng và mặt phẳng không có điểm chung. Câu C sai vì a và (P) không có điểm chung.
Câu 19:
 Xem đáp án
Xem đáp án
Đáp án A
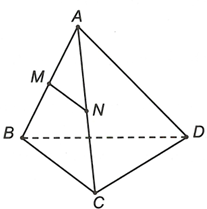
Câu 20:
 Xem đáp án
Xem đáp án
Đáp án D
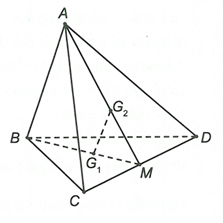
Vì A đúng.
Vì C đúng.
Ba đường đồng quy tại M => B đúng.Câu 21:
 Xem đáp án
Xem đáp án
Đáp án C
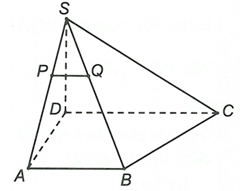
Câu 22:
 Xem đáp án
Xem đáp án
Đáp án B
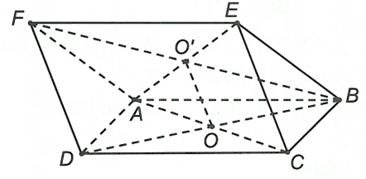
Có O là trung điểm của BD; O' là trung điểm của BF nên
Vì nên