Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 1)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 1)
-
430 lượt thi
-
92 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
Phần tư duy đọc hiểu
Ý chính của bài viết là gì?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn trích
Lời giải
Ý chính của bài viết là: Cách giảm chi phí logistics cho doanh nghiệp xuất nhập khẩu.
Phương pháp suy luận, loại trừ:
Đáp án A -> sai: vì nó chỉ nói về một phần của bài viết. Bài viết không chỉ phân tích những nguyên nhân và hạn chế của chi phí logistics cao ở Việt Nam, mà còn đưa ra những cách thức để giải quyết vấn đề này.
Đáp án B -> sai: vì nó không phản ánh được ý chính của bài viết. Bài viết không tập trung vào đánh giá hiệu quả của các phương thức vận chuyển và dịch vụ logistics, mà chỉ đề cập đến một số giải pháp để tối ưu hóa chúng.
Đáp án C -> đúng: vì nó tóm tắt được ý chính của bài viết. Bài viết giới thiệu những cách thức được khuyến nghị để giảm chi phí logistics cho doanh nghiệp xuất nhập khẩu trong bối cảnh hiện nay, như thay đổi điều kiện bán và mua hàng, thỏa thuận với các hãng vận chuyển, kiểm soát các phụ phí, sử dụng tích hợp chuỗi dịch vụ...
Câu 2:
Đọc đoạn 1 và chỉ ra ngành logistics tại Việt Nam có những đóng góp nào sau đây?
Chọn hai đáp án đúng:
 Xem đáp án
Xem đáp án
Căn cứ vào nội dung đoạn [1]
Lời giải
Ngành logistics tại Việt Nam có những đóng góp là: Đóng góp vào GDP 4-5% và Đứng thứ 4 tại khu vực Đông Nam Á về chỉ số logistics thị trường mới nổi
Phân tích, loại trừ:
- Đáp án A -> đúng: Theo nội dung trên, ngành logistics tại Việt Nam đóng góp vào GDP 4-5%. Đây là một đóng góp quan trọng của ngành này cho nền kinh tế quốc dân.
- Đáp án B -> sai: Theo nội dung trên, ngành logistics tại Việt Nam là một trong những ngành tăng trưởng nhanh và ổn định nhất, không phải là ngành tăng trưởng ổn định nhất trong khu vực. Đây là một sự phóng đại không chính xác về tình hình ngành logistics tại Việt Nam.
- Đáp án C -> đúng: Theo nội dung trên, Việt Nam đứng thứ 4 tại khu vực Đông Nam Á về chỉ số logistics thị trường mới nổi do Agility công bố. Đây là một chỉ số quan trọng để đánh giá tiềm năng và hiệu quả của ngành logistics tại các quốc gia mới nổi.
Câu 3:
Từ thông tin của đoạn 2, hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí.
giao thương, giao thông, trường hợp, giao lưu, yếu tố, doanh nghiệp, đất nước, đường bộ
Hiện nay, khi _____________ với toàn cầu nói chung và với châu Âu – châu Mỹ nói riêng, ___________ Việt Nam gặp rất nhiều trở ngại và thử thách, bao gồm các vấn đề về cơ sở hạ tầng thiếu đồng bộ, nhất là cơ sở hạ tầng ___________ và logistics như kho bãi, trung tâm logistics; các doanh nghiệp logistics không có đủ thông tin; thiếu liên kết, ứng dụng công nghệ thấp kém...Đây là những _________ khiến chi phí logistics của Việt Nam rất cao, trở thành gánh nặng cho doanh nghiệp.
 Xem đáp án
Xem đáp án
Đáp án
Hiện nay, khi giao thương với toàn cầu nói chung và với châu Âu – châu Mỹ nói riêng, doanh nghiệp Việt Nam gặp rất nhiều trở ngại và thử thách, bao gồm các vấn đề về cơ sở hạ tầng thiếu đồng bộ, nhất là cơ sở hạ tầng giao thông và logistics như kho bãi, trung tâm logistics; các doanh nghiệp logistics không có đủ thông tin; thiếu liên kết, ứng dụng công nghệ thấp kém...Đây là những yếu tố khiến chi phí logistics của Việt Nam rất cao, trở thành gánh nặng cho doanh nghiệp.
Phương pháp giải
Căn cứ vào nội dung đoạn [2]
Lời giải
Căn cứ vào nội dung đoạn 2:
Tuy nhiên, trong bối cảnh hiện nay, doanh nghiệp (DN) Việt Nam khi trao đổi thương mại với thế giới nói chung và với khu vực châu Âu – châu Mỹ vẫn phải đối mặt với rất nhiều khó khăn, thách thức, trong đó phải kể đến các vấn đề như, cơ sở hạ tầng hạn chế, thiếu đồng bộ, đặc biệt là hạ tầng giao thông và hạ tầng logistics như kho bãi, trung tâm logistics; các DN logistics còn thiếu thông tin; thiếu liên kết, ứng dụng công nghệ lạc hậu... Đây là những hạn chế rất lớn khiến chi phí logistics của Việt Nam luôn ở mức rất cao, được xem là gánh nặng đối với DN.
Suy luận, phân tích và loại trừ:
+ giao thương: Đây là đáp án đúng. Theo nội dung trên, doanh nghiệp Việt Nam khi trao đổi thương mại với thế giới nói chung và với khu vực châu Âu – châu Mỹ phải đối mặt với rất nhiều khó khăn, thách thức. Giao thương là một từ đồng nghĩa với trao đổi thương mại, có nghĩa là hoạt động buôn bán hàng hoá giữa các quốc gia hoặc các đơn vị kinh tế.
+ doanh nghiệp: Đây là đáp án đúng. Theo nội dung trên, doanh nghiệp Việt Nam khi trao đổi thương mại với thế giới nói chung và với khu vực châu Âu – châu Mỹ phải đối mặt với rất nhiều khó khăn, thách thức. Doanh nghiệp là một từ chỉ các tổ chức kinh tế có mục tiêu sinh lời từ việc sản xuất và kinh doanh hàng hoá, dịch vụ.
+ giao thông: Đây là đáp án đúng. Theo nội dung trên, doanh nghiệp Việt Nam phải đối mặt với rất nhiều khó khăn, thách thức, trong đó phải kể đến các vấn đề như cơ sở hạ tầng hạn chế, thiếu đồng bộ, đặc biệt là hạ tầng giao thông và hạ tầng logistics như kho bãi, trung tâm logistics. Giao thông là một từ chỉ sự đi lại của người và phương tiện trên các tuyến đường bộ, đường sắt, đường thuỷ, đường hàng không.
+ yếu tố: Đây là đáp án đúng. Theo nội dung trên, cơ sở hạ tầng hạn chế, thiếu đồng bộ, thiếu thông tin, liên kết và ứng dụng công nghệ lạc hậu... là những yếu tố khiến chi phí logistics của Việt Nam luôn ở mức rất cao, được xem là gánh nặng đối với doanh nghiệp. Yếu tố là một từ chỉ một thành phần hoặc một nguyên nhân ảnh hưởng đến một hiện tượng hoặc một kết quả nào đó.
Dựa vào nội dung đoạn trên cùng cách phân tích và suy luận, ta có các từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: giao thương
- Vị trí thả 2: doanh nghiệp
- Vị trí thả 3: giao thông
Câu 4:
Từ nội dung của đoạn 3, hãy hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Khu vực Cái Mép có 8 cảng container với tổng chiều dài các bến là 5.470m. Các bến cảng được phân tán ra nhiều nơi, tương đối cách xa nhau và đều có chiều dài cầu tàu khá ngắn (trung bình 600m bến/cảng)
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [3]
Lời giải
→ Ý kiến trên: Đúng
- Căn cứ vào nội dung ở đoạn 3:
Trong khi đó, theo ông Trương Tấn Lộc - Giám đốc Marketing Tổng Công ty Tân cảng Sài Gòn, tổng chiều dài các bến cảng container khu vực Cái Mép khoảng 5.470m, được chia thành 8 cảng. Các bến cảng được phân bổ rải rác và hầu hết đều hạn chế về chiều dài cầu tàu (trung bình 600m bến/cảng) trong khi kích cỡ tàu cập cảng ngày càng tăng, chiều dài tàu lên tới 400m nên tại mỗi thời điểm, mỗi cảng chỉ có thể tiếp nhận được 1 tàu mẹ.
+ Phân bố rải rác chính là phân tán ra nhiều nơi, tương đối cách xa nhau.
Câu 5:
Hãy tìm một cụm từ không quá hai tiếng để hoàn thành nhận định sau từ nội dung của đoạn 4:
Việt Nam chủ yếu xuất FOB và nhập CIF có nghĩa là các DN Việt Nam phải chịu trách nhiệm về hàng hoá cho đến khi nó được giao cho ______________ tại cảng xuất phát và phải trả tiền cho phụ phí cảng biển tại cảng đích đến.
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [4] và hiểu biết về FOB, CIF
Lời giải
Để điền được từ còn thiếu, ta phải hiểu được ý nghĩa của các điều kiện bán hàng FOB và CIF.
- FOB (Free On Board) có nghĩa là người bán chịu trách nhiệm về hàng hoá cho đến khi nó được giao cho chủ tàu tại cảng xuất phát. Sau đó, người mua sẽ chịu trách nhiệm về chi phí vận chuyển và bảo hiểm hàng hoá.
Ví dụ: Nếu bạn mua một lô hàng từ Trung Quốc với điều kiện FOB Thượng Hải, bạn sẽ phải trả tiền cho chi phí vận chuyển từ Thượng Hải đến Việt Nam và chi phí bảo hiểm cho hàng hoá trong quá trình vận chuyển. Người bán chỉ có trách nhiệm giao hàng cho chủ tàu tại Thượng Hải.
- CIF (Cost, Insurance and Freight) có nghĩa là người bán chịu trách nhiệm về chi phí vận chuyển và bảo hiểm hàng hoá cho đến khi nó được giao tại cảng đích đến. Sau đó, người mua sẽ phải trả các phụ phí cảng biển do các chủ tàu nước ngoài áp đặt.
Ví dụ: Nếu bạn mua một lô hàng từ Mỹ với điều kiện CIF Hồ Chí Minh, bạn sẽ không phải trả tiền cho chi phí vận chuyển từ Mỹ đến Việt Nam và chi phí bảo hiểm cho hàng hoá trong quá trình vận chuyển. Người bán sẽ có trách nhiệm giao hàng cho bạn tại Hồ Chí Minh. Tuy nhiên, bạn sẽ phải trả các phụ phí cảng biển như thuế nhập khẩu, lệ phí xử lý container, lệ phí xếp dỡ hàng hoá... do các chủ tàu nước ngoài áp đặt.
Câu 6:
Từ nội dung của đoạn 2 và đoạn 4, hãy chỉ ra đâu là nguyên nhân khiến chi phí logistics của Việt Nam luôn ở mức cao?
Chọn 3 đáp án đúng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [2] và đoạn [4].
Lời giải
Nguyên nhân khiến chi phí logistics của Việt Nam luôn ở mức cao là: Cơ sở hạ tầng hạn chế, thiếu đồng bộ, Chi phí vận tải hàng hoá bằng đường bộ quá cao so với đường thuỷ hay đường sắt và Phụ phí tại cảng biển mà chủ tàu container nước ngoài đang thu của chủ hàng Việt Nam
- Phân tích, loại trừ:
+ Lựa chọn A: Cơ sở hạ tầng hạn chế, thiếu đồng bộ. Đây là đáp án đúng và thuộc đoạn [2] của văn bản: "Tuy nhiên, trong bối cảnh hiện nay, doanh nghiệp (DN) Việt Nam khi trao đổi thương mại với thế giới nói chung và với khu vực châu Âu – châu Mỹ vẫn phải đối mặt với rất nhiều khó khăn, thách thức, trong đó phải kể đến các vấn đề như, cơ sở hạ tầng hạn chế, thiếu đồng bộ, đặc biệt là hạ tầng giao thông và hạ tầng logistics như kho bãi, trung tâm logistics..."
+ Lựa chọn B: Chi phí vận tải hàng hoá bằng đường không quá cao so với đường bộ hay đường sắt. Đây là đáp án sai và gây nhiễu và không thuộc bất kỳ đoạn nào của văn bản. Văn bản trên không nói gì về chi phí vận tải hàng hoá bằng đường không, mà chỉ nói về đường bộ và đường thuỷ.
+ Lựa chọn C: Chi phí vận tải hàng hoá bằng đường bộ quá cao so với đường thuỷ hay đường sắt. Đây là đáp án đúng và thuộc đoạn [4] của văn bản: "Phân tích các yếu tố làm tăng chi phí logistics, ông Kha cho biết, có 5 yếu tố bao gồm: Phụ phí vận tải cảng biển mà chủ tàu container nước ngoài đang thu chủ hàng Việt Nam, thời gian thông quan hàng hoá, kiểm tra chuyên môn còn bị kéo dài gây tăng chi phí, chi phí vận tải hàng hoá bằng đường bộ quá cao, tính kết nối và hạ tầng các phương tiện vận tải chưa cao, năng lực cạnh tranh của DN cung cấp dịch vụ logistics thấp."
Câu 7:
Hãy điền một từ có trong đoạn 5 vào chỗ trống để hoàn thành nhận định sau.
Cơ chế "cảng mở" là một giải pháp để ____________ chi phí logistics cho hàng hoá xuất nhập khẩu thông qua khu vực Cái Mép - Thị Vải.
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [5] để điền từ thích hợp vào chỗ trống.
Lời giải
Căn cứ vào nội dung đoạn 5, từ cần điền vào chỗ trống là: giảm
Đây là cụm từ có trong đoạn 5 của văn bản: "Giải quyết được các hạn chế về cầu bến như hiện nay sẽ giảm chi phí logistics cho hàng hoá xuất nhập khẩu thông qua khu vực này."
Đây là cụm từ phù hợp với ý nghĩa của nhận định, vì cơ chế "cảng mở" là một giải pháp để tối ưu hóa công suất khai thác và tận dụng tối đa cầu bến của nhau, từ đó giảm chi phí logistics cho hàng hoá xuất nhập khẩu.
Câu 8:
Từ nội dung của đoạn 7, hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Tiến sĩ KC Chang khuyên doanh nghiệp nên dùng dịch vụ hải quan của những nhà cung cấp có uy tín, chuyên nghiệp và có trình độ để giảm chi phí vận chuyển hàng hoá.
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [7]
Lời giải
→ Ý kiến trên: Đúng.
- Căn cứ vào nội dung ở đoạn 7:
Theo Tiến sĩ KC Chang - chuyên gia thủ tục hải quan kiêm pháp chế thương mại khu vực châu Á - Thái Bình Dương thuộc GEODIS Logistics, khi nhập khẩu hàng hoá vào Hoa Kỳ, DN phải tuân thủ quy định của mọi pháp luật đặc biệt có thể áp dụng đối với hàng hoá; tìm hiểu kỹ các quy định về đóng gói và dán nhãn tại Hoa Kỳ trước khi xuất khẩu; phải xin giấy phép nhập khẩu để được nhập khẩu các mặt hàng được kiểm soát… Do đó, nên sử dụng nhà cung cấp dịch vụ hải quan có giấy phép và đủ trình độ để vận chuyển hàng hoá nhằm tiết giảm chi phí.
Câu 9:
Theo các chuyên gia tại Diễn đàn Logistics với khu vực châu Âu - châu Mỹ 2022, DN XNK nên thay đổi điều kiện bán hàng, mua hàng sang giá CIF thay vì FOB nhằm mục đích gì?
Chọn đáp án không đúng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [8,9,10]
Lời giải
Điều kiện bán hàng CIF (Cost, Insurance and Freight) có nghĩa là người bán phải chịu trách nhiệm về chi phí, bảo hiểm và vận chuyển hàng hóa đến cảng đích. Điều kiện bán hàng FOB (Free On Board) có nghĩa là người bán chỉ chịu trách nhiệm về chi phí và vận chuyển hàng hóa đến cảng xuất phát.
Do đó, khi DN XNK thay đổi điều kiện bán hàng, mua hàng sang giá CIF thay vì FOB, họ sẽ có những lợi ích sau:
- Chủ động hơn trong việc sử dụng các lịch vận chuyển phù hợp: Họ có thể lựa chọn các hãng vận tải uy tín và tin cậy, không phụ thuộc vào người bán.
- Tìm kiếm nguồn cung cấp cạnh tranh uy tín nhằm tiết kiệm chi phí cước tàu: Họ có thể so sánh giá cả và chất lượng của các nguồn cung cấp khác nhau, không bị ép buộc mua hàng từ người bán.
- Giảm thiểu các rủi ro trong quá trình vận chuyển: Họ có thể bảo hiểm hàng hóa và được bồi thường nếu có sự cố xảy ra trong quá trình vận chuyển.
- Tuy nhiên, khi DN XNK thay đổi điều kiện bán hàng, mua hàng sang giá CIF thay vì FOB, họ không nhất thiết tăng cường khả năng cạnh tranh với các DN XNK khác. Đó là vì giá CIF thường cao hơn giá FOB do bao gồm chi phí vận chuyển và bảo hiểm. Do đó, DN XNK có thể gặp khó khăn khi bán hàng cho các khách hàng nhạy cảm với giá.
Câu 10:
Đâu là lý do mà từ lâu nay người ta lại định giết mực?
Chọn đáp án đúng nhất:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [1]
Lời giải
Lý do mà từ lâu nay người ta lại định giết mực vì: Mực có nhiều nết xấu như tục ăn, nhiều vắt và sủa như gà gáy
Phương pháp suy luận, loại trừ:
Đáp án A -> sai: vì trong truyện không có nói rằng Mực rất ngon và béo. Người ta định giết Mực không phải vì thèm ăn mà vì ghét nó. Đáp án A cũng không thể hiện được sự tàn bạo và vô cảm của con người đối với loài vật mà tác giả muốn chỉ trích.
Đáp án B -> đúng: vì trong truyện có nói rằng Mực có nhiều nết xấu như tục ăn, nhiều vắt và sủa như gà gáy. Đây là những lý do mà người ta định giết Mực. Đáp án B cũng thể hiện được sự tàn bạo và vô cảm của con người đối với loài vật mà tác giả muốn chỉ trích.
Đáp án C -> sai: vì trong truyện không có nói rằng Mực hay cắn càn và làm phiền người ta. Ngược lại, Mực chỉ sủa như gà gáy và tục ăn. Đáp án C cũng không thể hiện được sự tàn bạo và vô cảm của con người đối với loài vật mà tác giả muốn chỉ trích.
Câu 11:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Người ta không thể nào tha thứ cho Mực vì Mực tham lam và bẩn thỉu.
Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [1]
Lời giải
→ Ý kiến trên: SAI
Căn cứ vào nội dung đoạn 1:
Nó tục ăn: đó là thường. Nó nhiều vắt: cái ấy đủ khổ cho nó. Nó cắn càn ấy là cái khổ của bọn ăn mày. Nhưng nó lại sủa như một con gà gáy: cái này thì không thể nào tha thứ được.
Câu 12:
Từ thông tin của câu chuyện, hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí.
run run, nghẹn ngào, vui mừng, thương hại, hào hứng, buồn bã
- Cảm xúc của Du khi trở về nhà sau một thời gian xa xôi: _________
- Cảm xúc của Du khi gặp lại Mực - người bạn lặng lẽ bên chàng những năm xưa, nay già nua và bẩn thỉu: __________
- Cảm xúc của Du khi hét lên bảo mọi người phải đè thật chặt cái Mực: __________
- Cảm xúc của Du khi thấy Mực bị Hoa úp thúng, trói chân và buộc mõm: ______
 Xem đáp án
Xem đáp án
Đáp án
- Cảm xúc của Du khi trở về nhà sau một thời gian xa xôi: vui mừng
- Cảm xúc của Du khi gặp lại Mực - người bạn lặng lẽ bên chàng những năm xưa, nay già nua và bẩn thỉu: thương hại
- Cảm xúc của Du khi hét lên bảo mọi người phải đè thật chặt cái Mực: run run
- Cảm xúc của Du khi thấy Mực bị Hoa úp thúng, trói chân và buộc mõm: nghẹn ngào
Phương pháp giải
Căn cứ vào nội dung của cả câu chuyện
Lời giải
Phân tích, suy luận, loại trừ:
Cảm xúc của Du khi trở về nhà sau một thời gian xa xôi
→ Đáp án đúng là: vui mừng. Vì câu chuyện nói rằng "Chiều hôm qua con người phóng đãng ấy đã khệ nệ xách cái vali rất nặng bước vào sân, miệng mỉm cười và mặt đỏ." Đây là những dấu hiệu của sự vui mừng khi gặp lại gia đình.
Cảm xúc của Du khi gặp lại Mực - người bạn lặng lẽ bên chàng những năm xưa nay già nua và bẩn thỉu:
→ Đáp án đúng là: thương hại. Vì câu chuyện nói rằng "Du thương hại: đó là người bạn lặng lẽ thui thủi bên chàng những năm xưa khi đêm vắng, chàng ngồi nhìn trăng mà mơ mộng." Đây là cảm xúc khi bạn thấy ai đó đang gặp khó khăn hoặc đau khổ và bạn muốn giúp đỡ họ.
→ Đáp án bỡ ngỡ là sai vì đã nhận ra Mực là con chó của mình. Đáp án nghẹn ngào là sai vì Du không khóc hay than khóc khi gặp Mực. Đáp án buồn bã là sai vì Du không có biểu hiện nào của sự buồn bã khi gặp Mực.
Cảm xúc của Du khi hét lên bảo mọi người phải đè thật chặt cái Mực:
→ Đáp án đúng là: run run. Vì câu chuyện nói rằng "Du kêu lên như thế nhưng tiếng chàng đã hơi run run." Đây là cảm xúc khi bạn sợ hãi hoặc lo lắng cho ai đó hoặc cho chính mình.
→ Đáp án lo lắng là sai vì Du không chỉ lo lắng cho Mực mà còn sợ hãi cho chính mình. Đáp án tức giận là sai vì Du không có lý do gì để tức giận với Mực. Đáp án sợ hãi là sai vì Du không chỉ sợ hãi cho Mực mà còn lo lắng cho chính mình.
Cảm xúc của Du khi thấy Mực bị Hoa úp thúng, trói chân và buộc mõm:
→ Đáp án đúng là: nghẹn ngào. Vì câu chuyện nói rằng "Du nghẹn ngào nén khóc…" Đây là cảm xúc khi bạn cảm thấy đau khổ hoặc xúc động quá mức và không thể nói ra lời nào.
→ Đáp án thương hại là sai vì Du không chỉ thương hại cho Mực mà còn cảm thấy đau khổ và xúc động. Đáp án buồn bã là sai vì Du không chỉ buồn bã mà còn nghẹn ngào và nén khóc. Đáp án cảm động là sai vì Du không chỉ cảm động mà còn đau khổ và nghẹn ngào.
Dựa vào nội dung đoạn trên cùng cách phân tích và suy luận, ta có các từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: vui mừng
- Vị trí thả 2: thương hại
- Vị trí thả 3: run run
Câu 13:
Đọc đoạn 5 và trả lời câu hỏi, tại sao Du thấy lòng nằng nặng?
Chọn đáp án đúng nhất:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [5]
Lời giải
Căn cứ vào nội dung đoạn 5:
Du thương hại: đó là người bạn lặng lẽ thui thủi bên chàng những năm xưa khi đêm vắng, chàng ngồi nhìn trăng mà mơ mộng. Chàng muốn cúi xuống vuốt ve. Nhưng nó bẩn ghê gớm quá, lông rụng từng mảng, thịt trắng lộ ra có nơi sần mụn nữa. Dáng điệu thì già nua, có vẻ buồn và len lén như phòng bị một cách yếu ớt. Không còn những cái vẫy đuôi mạnh dạn những cái nhìn rất bạn bè và những cái hít chân vồ vập như khi một con chó đã vui và không ngờ vực. Du thấy lòng nằng nặng.
→ Du thấy lòng nằng nặng: Vì anh cảm thấy mất mát - con chó đã già đi và không còn như ngày xưa nữa.
Con chó - người bạn năm xưa của anh giờ không còn khoẻ mạnh và vui vẻ như trước, thay vào đó là một con chó bẩn thỉu, yếu ớt, buồn bã. Anh cảm thấy thương hại cho nó.
Câu 14:
Hãy chọn một trong hai từ sau điền vào chỗ trống đề hoàn thành câu sau: vui mừng, háo hức
Bà mẹ rất ________________ và cả khóc lẫn cười khi người con trai về, bà thấy như tìm được một vật quý bị rơi vậy.
 Xem đáp án
Xem đáp án
Đáp án: "vui mừng"
Phương pháp giải
Căn cứ vào nội dung đoạn [3]
Lời giải
Căn cứ vào nội dung đoạn 3:
Chiều hôm qua con người phóng đãng ấy đã khệ nệ xách cái vali rất nặng bước vào sân, miệng mỉm cười và mặt đỏ. Cái nhà tranh, mấy cây cau hình như vừa đứng thẳng hơn lên để chào chàng. Rồi đến lũ em ầm ỹ đẩy mành chạy oà ra, và bà mẹ mừng quá cười và khóc.
Câu 15:
Từ nội dung của đoạn 6, hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Con chó vẫy đuôi mạnh hơn khi Du đưa chân chạm khẽ vào người nó. Nhưng nó lại len lén lánh ra vì nó sợ.
Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [6]
Lời giải
→ Ý kiến trên: Đúng.
- Căn cứ vào nội dung ở đoạn 6:
Con chó vẫy đuôi mạnh hơn khi Du đưa chân chạm khẽ vào người nó, nhưng nó lại len lén lánh ra vì nó sợ Du. Đoạn văn đã miêu tả rõ ràng như vậy:
-> Con chó vẫy đuôi mạnh hơn nhưng len lén lánh ra: dáng điệu một kẻ sợ hãi cố cười với người nó sợ.
- Các lý do khiến Mực sợ là:
+ Nó đã bị người nhà đối xử tàn nhẫn và bị đe dọa giết thịt nhiều lần, nên nó không còn tin tưởng vào con người. Nó cảm thấy mình là kẻ bị ruồng bỏ và không có ai yêu thương.
+ Một lý do khác là nó đã già yếu và bệnh tật, nên nó không còn sức mạnh để chống lại hay bảo vệ mình. Nó biết rằng mình sẽ chết sớm hay muộn, nên nó chỉ còn biết chấp nhận số phận.
+ Một lý do nữa là nó không nhận ra được tình cảm của Du dành cho nó, và chỉ cảm nhận được sự khác biệt giữa Du và những người khác trong nhà. Nó sợ rằng Du cũng sẽ đối xử với nó như những kẻ khác. Do đó, nó sợ hãi và lén tránh ra khi được Du chạm chân vào người.
Câu 16:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai từ nội dung đoạn 1.
Cái chết của con Mực là cái chết của tâm hồn người lao động.
Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [7] và đoạn [8]
Lời giải
→ Ý kiến trên: SAI
Căn cứ vào nội dung đoạn 7 và đoạn 8:
Nhưng mà không thể được: dịu dàng quá là yếu tâm hồn, và ai hiểu được rằng mình lại có thể yêu thương một con chó bẩn ghê gớm như thế được?
Sau cùng thì chàng bực mình: chàng nhận ra rằng một con chó đã làm mất sự bình tĩnh của tâm hồn chàng. Và đột nhiên chàng muốn giết con Mực lắm. Chàng muốn có đủ can đảm để giết người. Phải dám giết mà không run tay khi cần phải giết. Còn làm được trò gì nữa nếu chỉ giết một con chó mà tim cũng đập?
-> Cái chết của con Mực là cái chết của tâm hồn người trí thức không phải cái chết của tâm hồn người lao động.
Khi con Mực bị giết, Du cũng mất đi phần tốt đẹp nhất trong mình và trở nên vô cảm, tuyệt vọng. Qua cái chết của Mực, Nam Cao gián tiếp đặt ra những vấn đề nhân cách tha hoá, tâm hồn mòn gỉ hay sự bất lực của con người trước sự chi phối của hoàn cảnh xã hội.
Với Nam Cao, hơn cả sự đau đớn của cái chết thể xác là bi kịch của “cái chết tinh thần” - “chết ngay trong lúc sống”, đó là sự vô cảm, thờ ơ trước nỗi đau của người khác, bản chất, bản tính tự nhiên tốt đẹp của con người tạm thời biến đổi hay bị che lấp bởi hoàn cảnh xã hội.
Câu 17:
Xuyên suốt câu chuyện, đâu là những cảm xúc của Du khi gặp lại Mực? Chọn 3 đáp án Đúng
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung câu chuyện
Lời giải
Phân tích, suy luận:
- Thương hại: Du thương hại Mực khi thấy nó già nua và bẩn thỉu, và nó né tránh sự chạm vào của anh. Anh cũng nhớ lại tình bạn của họ trong quá khứ. Anh muốn vuốt ve nó nhưng không thể.
-Bực mình: Du bực mình với Mực khi nó làm phiền giấc ngủ của anh bằng tiếng sủa. Anh cũng cảm thấy Mực đã làm mất sự bình tĩnh của tâm hồn anh. Anh đột nhiên muốn giết nó nhưng không đủ can đảm.
- Nghẹn ngào: Du nghẹn ngào khi thấy Mực bị Hoa úp thúng và trói chặt. Anh muốn khóc nhưng không thể.
Câu 18:
Nếu Thí nghiệm 1 được lặp lại cho dụng cụ nấu ăn nhãn hiệu B với vật có khối lượng 200 gam, thì lực trung bình cần thiết để vật chuyển động sẽ gần nhất với:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa trên bảng số liệu bài cung cấp
Lời giải
Với nhãn hiệu B ta có:
- nếu vật có khối lượng 150g thì lực kéo vật chuyển động sẽ là 0,09N
- nếu vật có khối lượng 250g thì lực kéo vật chuyển động sẽ là 0,147N
⇒khi khối lượng vật là 200g thì lực để làm vật chuyển động sẽ ở khoảng
0,09 (N) < F < 0,147 (N)
Câu 19:
Dựa vào kết quả của thí nghiệm 1 và 2, hãy cho biết sự kết hợp nào sau đây sẽ tạo ra bề mặt có hệ số ma sát nghỉ nhỏ nhất?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa trên bảng số liệu bài cung cấp
Lời giải
Kết quả bảng 1 cho thấy dụng cụ nấu bếp hiệu C có hệ số ma sát nghỉ nhỏ nhất.
Kết quả từ bảng 2 cho thấy bình xịt nấu ăn nhãn hiệu Y có hệ số ma sát nghỉ nhỏ nhất.
Câu 20:
Các nhận xét sau đây về thí nghiệm 2 là chính xác?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa trên bảng số liệu bài cung cấp
Lời giải
Trong bảng 2 ta thấy rằng:
Nhãn hiệu dầu Y tạo ra hệ số ma sát lớn nhất
Nhãn hiệu dầu Z được thực hiện thí nghiệm với 2 vật nặng khác nhauCâu 21:
Người hướng dẫn sinh viên đưa cho họ một dụng cụ nấu chống dính và yêu cầu họ xác định thương hiệu. Các học sinh lặp lại quy trình trong Thí nghiệm 1 và thu được lực trung bình là 0,088 N đối với vật 150 gam và 0,149 N đối với vật 250 gam. Thương hiệu nào sau đây rất có thể đã tạo ra những kết quả này?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa trên bảng số liệu bài cung cấp
Lời giải
Theo Bảng 1, dụng cụ nấu nướng nhãn hiệu B có lực trung bình là 0,090 N đối với khối lượng 150 g và 0,147 N đối với khối lượng 250 g. Những kết quả này gần nhất với kết quả mà các sinh viên thu được khi người hướng dẫn đưa cho họ dụng cụ nấu chống dính mới.
Đối chiếu với bảng 1 ta có với nhãn hiệu B khi :
\[\bar F = 0,09N \leftrightarrow m = 150g\]
\[\bar F = 0,147N \leftrightarrow m = 250g\]
Câu 22:
Theo đoạn văn, để học sinh đo chính xác hệ số ma sát tĩnh thì lực cần xác định đó là:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa trên bảng số liệu bài cung cấp
Lời giải
Câu 23:
Trong thí nghiệm 1 học sinh dùng thêm chảo D, lực trung bình để kéo một vật nặng 200g trên chảo D là 0,02N. Khi đó ta có thể xác định được hệ số ma sát của chảo là bao nhiêu? Lấy g = 9,8m/s2
 Xem đáp án
Xem đáp án
Phương pháp giải
Vận dụng công thức xác định lực ma sát đã học: Fms = μN
Lời giải
Ta có công thức xác định lực ma sát giữa bề mặt chảo vào vật như sau Fms = μN (1)
Phân tích quá trình chuyển động của vật và áp dụng định luật II và III Newton ta có:
N = P = mg = 0,2.9,8 = 1,96N (2)
Và Fms = F = 0,02N (3)
Từ (1) (2) và (3) ta có: \[\mu = \frac{{{F_{ms}}}}{N} = \frac{{1,96}}{{0,02}} \approx 0,01\]Câu 24:
Dựa vào dữ liệu trong Thí nghiệm 1, biểu thức nào sau đây mô tả đúng nhất mối quan hệ giữa cường độ dòng điện, hiệu điện thế và điện trở? Cường độ dòng điện:
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích đồ thị và bảng số liệu
Áp dụng định luật Ohm
Lời giải
Ta có công thức của định luật Ohm: \(I = \frac{U}{R}\)
Từ công thức trên ta thấy cường độ dòng điện tỉ lệ thuận với điện áp (hiệu điện thế) và tỉ lệ nghịch với điện trở của dây dẫn
Câu 25:
Trong một thí nghiệm bổ sung, các học sinh mắc một mạch điện tương tự như thí nghiệm 1, chỉ khác là sử dụng một pin 2V và một điện trở 5Ω, thì thấy cường độ dòng điện đo được trong mạch này là 0,400 A. Cường độ dòng điện phải là bao nhiêu, nếu học sinh mong đợi để họ tăng gấp đôi cả điện áp và điện trở?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích đồ thị và bảng số liệu
Áp dụng định luật Ohm
Lời giải
Ta có công thức của định luật Ohm: \(I = \frac{U}{R}\)
Khi tăng gấp đôi điện trở dây dẫn và điện áp ta có:
\(I' = \frac{{2U}}{{2R}} = \frac{U}{R} = I\)
Câu 26:
Bạc dẫn điện tốt hơn đồng một chút. Xem xét dữ liệu từ Thí nghiệm 3, giá trị nào sau đây có thể là điện trở của cuộn dây bạc dài 1 m?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích đồ thị và bảng số liệu
Áp dụng định luật Ohm
Lời giải
Ta có điện trở đặc trưng cho mức độ cản trở dòng điện chạy trong mạch
Đồng thời có biểu thức của định luật Ohm \(I = \frac{U}{R}\)
⇒điện trở càng lớn thì càng độ dòng điện càng nhỏ và ngược lại
Bạc dẫn điện tốt hơn đồng có nghĩa là cường độ dòng điện qua dây dẫn bằng bạc sẽ lớn hơn hay điện trở của dây bạc sẽ nhỏ hơn của dây đồng
Câu 27:
Điều gì sẽ xảy ra với dòng điện trong mạch nếu cuộn dây niken dài 2 m trong Thí nghiệm 2 được sử dụng để thay thế điện trở trong mạch Thử nghiệm 1 trong Thí nghiệm 1?
|
|
ĐÚNG |
SAI |
|
Cường độ dòng điện giảm vì điện trở trong mạch tăng. |
||
|
Cường độ dòng điện giảm vì điện trở trong mạch giảm. |
||
|
Cường độ dòng điện tăng vì điện trở trong mạch giảm. |
||
|
Cường độ dòng điện tăng vì điện trở trong mạch tăng. |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Cường độ dòng điện giảm vì điện trở trong mạch tăng. |
X | |
|
Cường độ dòng điện giảm vì điện trở trong mạch giảm. |
X | |
|
Cường độ dòng điện tăng vì điện trở trong mạch giảm. |
X | |
|
Cường độ dòng điện tăng vì điện trở trong mạch tăng. |
X |
Phương pháp giải
Phân tích đồ thị và bảng số liệu
Áp dụng định luật Ohm
Lời giải
Với dây nike dài 2m thì ta có RNi ≈ 0,18Ω
So sánh với điện trở dây dẫn ở lần 1 trong thí nghiệm 1 thì ta thấy RNi ≪ R1
Ta có công thức định luật Ohm: \(I = \frac{U}{R}\)
⇒ khi điện trở tăng lên thì cường độ dòng điện chạy trong mạch sẽ giảm đi và ngược lại
Câu 28:
Điện trở của chiều dài dây phụ thuộc vào độ dẫn điện của vật liệu: vật liệu có độ dẫn điện cao cung cấp điện trở thấp hơn vật liệu có độ dẫn điện thấp. Dựa vào dữ kiện ở thí nghiệm 2 và 3, hãy cho biết dãy nào sau đây sắp xếp các kim loại theo thứ tự độ dẫn điện tăng dần?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích đồ thị và bảng số liệu
Áp dụng định luật Ohm
Lời giải
Ta có độ dẫn điện càng cao thì điện trở của dây dẫn càng thấp
Từ hình 2 và bảng 3 ta có với cùng dây dẫn dài 1m thì điện trở của các loại dây dẫn như sau:
RNi = 0,08Ω; RCu = 0,0214Ω; Rvonrfam = 0,0672Ω; RAl = 0,0338Ω
⇒ RNi > Rvonrfam > RAl > RCu
Câu 29:
Các thí nghiệm 1-3 được hoàn thành trong phòng học ở nhiệt độ 20°C. Trong năm học trước, điều hòa không khí bị hỏng nên phòng thí nghiệm tương tự đã được hoàn thành ở nhiệt độ 28°C. Được biết, độ dẫn điện của kim loại giảm khi nhiệt độ tăng. Nhiệt độ lớp học cao hơn sẽ ảnh hưởng như thế nào đến điện áp cần thiết để đạt được 1 A trong Thí nghiệm 2?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích đồ thị và bảng số liệu
Áp dụng định luật Ohm
Lời giải
Ta có độ dẫn điện giảm khi nhiệt độ tăng và điện trở sẽ tăng khi đó.
Câu 30:
Cho điện trở suất của đồng là ρ = 1,68.10−8 (Ω.m). Dây đồng trong thí nghiệm 3 sẽ có tiết diện là :
 Xem đáp án
Xem đáp án
Phương pháp giải
Áp dụng công thức tính điện trở đối với dây dẫn dài: \(R = \rho \frac{l}{S}\)
Dựa trên số liệu và đồ thị bài cung cấp
Lời giải
Ta có công thức tính điện trở của dây dẫn dài là \(R = \rho \frac{l}{S}\)
Ta có dây đồng có: \(l = 1m;R = 0,0214\Omega ;\,\,\rho = 1,{68.10^{ - 8}}(\Omega .m)\)
Câu 31:
Hạt được tổng hợp từ thành phần nào có kích thước bé nhất?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào dữ liệu trong bảng.
Lời giải
Câu 32:
Nhận định sau đây là đúng hay sai?
Nếu thời gian trộn tối thiểu để tạo ra các hạt siêu nhỏ là 5 giây thì có thể tạo ra các hạt siêu nhỏ có kích thước giống nhau.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào số liệu trong bảng.
Lời giải
Kích thước hạt lớn nhất mà thành phần D tổng hợp được là 45,8 nm tại thời điểm 5 giây, trong khi kích thước hạt nhỏ nhất mà thành phần A có thể đạt được là 63,1nm tại thời điểm 20 giây, 30 giây hoặc 60 giây (không có sự khác biệt đáng kể về kích thước hạt sau 20 giây). Kích thước nhỏ nhất của thành phần A lớn hơn rất nhiều so với kích thước lớn nhất có thể của thành phần D; do đó, mục tiêu của nhà khoa học về tổng hợp các hạt có kích thước đồng đều là không thể đạt được.
Chọn B
Câu 33:
Có thể suy ra điều gì về ảnh hưởng của thời gian trộn đối với kích thước hạt nano?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào dữ liệu trong bảng.
Lời giải
Câu 34:
Chọn nhận định đúng trong những nhận định dưới đây:
Sau khi nhà khoa học thực hiện xong thí nghiệm, cô ấy đã lựa chọn được điều kiện tối ưu nhất để tổng hợp ra hạt có kích thước siêu nhỏ trong những thí nghiệm tiếp theo, với mục đích là tổng hợp được hạt có kích thước càng nhỏ càng tốt. Đó là:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào bảng dữ liệu và thông tin đề bài cung cấp.
Lời giải
Câu 35:
Thí nghiệm nào sau đây có thể giải quyết cuộc tranh luận giữa hai giáo sư?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn văn
Lời giải
Tranh luận chính giữa hai giáo sư là xem phương trình nào- Van der Waals' hay Định luật khí lý tưởng- là cách thích hợp nhất để ước tính dữ liệu thực nghiệm.
Câu 36:
Phát biểu sau đúng hay sai?
Giáo sư 2 sẽ đồng ý với phát biểu: “Luật khí lý tưởng phản ánh gần nhất các tương tác khí xảy ra trong tự nhiên”
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin về quan điểm của giáo sư 2
Lời giải
Giáo sư 2 tuyên bố "Dữ liệu thực nghiệm liên quan đến nước ở dạng khí phù hợp nhất được tìm thấy bằng cách sử dụng Định luật khí lý tưởng" vì vậy câu trả lời đúng là "Luật khí lý tưởng phản ánh gần nhất các tương tác khí xảy ra trong tự nhiên."
Ngoài ra, "Phương trình Van der Waals phản ánh gần nhất các tương tác khí xảy ra trong tự nhiên." và "Trạng thái của nước phụ thuộc vào cường độ của lực nội phân tử và năng lượng nhiệt có trong hệ." đều là những tuyên bố phù hợp với tuyên bố của giáo sư đầu tiên. Cuối cùng, giáo sư 2 tuyên bố "Nhiệt độ càng cao, nước càng có khả năng ở dạng khí" chứ không phải "Ở nhiệt độ thấp, nước ở dạng khí."
Câu 37:
Cả hai giáo sư đều đồng ý với phát biểu nào sau đây?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin về quan điểm của 2 giáo sư
Lời giải
Câu 38:
Cả hai giáo sư sẽ đồng ý với tuyên bố nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin về quan điểm của 2 giáo sư
Lời giải
Câu 39:
Phát biểu nào của giáo sư 2 không mâu thuẫn với giáo sư 1?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin quan điểm của 2 giáo sư
Lời giải
Câu 40:
Dựa trên kết quả 2 thí nghiệm, thức ăn nào cho kết quả tăng trọng nhiều nhất?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào kết quả 2 thí nghiệm
Lời giải
Chuột có trọng lượng cao nhất trong cả 2 thí nghiệm là 98g, tương ứng với thức ăn V
Câu 41:
Điền đáp án thích hợp vào chỗ trống
Theo kết quả của thí nghiệm 1, chuột lang trong nhóm được cho ăn thức ăn làm từ ngũ cốc có bổ sung vitamin tăng trung bình ____________ g trong mỗi tuần của thí nghiệm.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào kết quả thí nghiệm 1
Lời giải
Theo kết quả của thí nghiệm 1, chuột lang trong nhóm được cho ăn thức ăn làm từ ngũ cốc có bổ sung vitamin sau 8 tuần đạt trọng lượng là 80g
=> Trọng lượng tăng trung bình trong mỗi tuần là 80/8 = 10g
Câu 42:
Điền đáp án thích hợp vào chỗ trống
Theo kết quả của thí nghiệm 2, chuột lang trong nhóm được cho ăn thức ăn giàu protein cộng với trái cây và rau quả tăng trung bình _________ g trong mỗi tuần của thí nghiệm.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào kết quả thí nghiệm 2
Lời giải
Theo kết quả của thí nghiệm 2, chuột lang trong nhóm được cho ăn thức ăn giàu protein cộng với trái cây và rau quả sau 8 tuần đạt trọng lượng là 96g
=> Trọng lượng tăng trung bình trong mỗi tuần là 96/8 = 12g
Câu 43:
Dựa vào kết quả của cả hai thí nghiệm, thành phần nào của thức ăn làm cho chuột lang phát triển tốt nhất?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào kết quả thí nghiệm 2
Lời giải
Dựa vào thí nghiệm 1, ta nhận thấy nhóm chuột lang được cho ăn thức ăn chứa protein phát triển tốt nhất. Và ở thí nghiệm 2, nhóm chuột lang được cho ăn thức ăn chứa protein và trái cây, rau phát triển tốt nhất
=> Thành phần thức ăn làm cho chuột lang phát triển tốt nhất là protein.
Câu 44:
Điền đáp án thích hợp vào chỗ trống
Theo đoạn văn, chuột lang trong nhóm ________ có tốc độ tăng trưởng tổng thể kém nhất.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào kết quả 2 thí nghiệm
Lời giải
Theo đoạn văn, chuột lang trong nhóm 8 có tốc độ tăng trưởng tổng thể kém nhất (74g và 23.25cm).
Câu 45:
Nhận định nào sau đây chính xác về mối quan hệ giữa trọng lượng và chiều dài của những con chuột lang được nghiên cứu?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào kết quả 2 thí nghiệm
Lời giải
Ta dễ dàng nhận thấy khi trọng lượng của những con chuột lang lớn thì chiều dài cơ thể của chúng cũng lớn. Và trọng lượng của những con chuột lang nhỏ hơn thì chiều dài cơ thể của chúng cũng nhỏ hơn.
Câu 46:
Một con chuột lang chọn ngẫu nhiên từ những con chuột được nghiên cứu, người ta đo các chỉ số của con chuột này có kết quả là 90g và 30cm. Con chuột này có thể thuộc nhóm?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào kết quả 2 thí nghiệm
Lời giải
Con chuột có trọng lượng là 91g => Có thể thuộc nhóm 1 hoặc 6
Nhưng con chuột có chiều dài cơ thể là 30cm => Nhóm 6 phù hợp hơn
Câu 47:
Điền từ thích hợp vào chỗ trống
Theo thí nghiệm 1, ở nồng độ 10nM, thuốc ________ diệt khuẩn hiệu quả nhất.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thí nghiệm 1
Lời giải
Theo bảng 1, tại nồng độ thuốc là 10 mM, Thuốc R có ít khuẩn lạc vi khuẩn nhất (26), có nghĩa là Thuốc R có hiệu quả nhất trong việc tiêu diệt vi khuẩn nhất.
Câu 48:
Điền từ thích hợp vào chỗ trống
Theo thí nghiệm 1, ở nồng độ ________ nM, các loại thuốc trong nghiên cứu diệt khuẩn tốt nhất
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thí nghiệm 1
Lời giải
Theo bảng 1, tại nồng độ thuốc là 25 mM, các loại thuốc có ít khuẩn lạc vi khuẩn nhất, có nghĩa là tại nồng độ này các lại thuốc diệt khuẩn hiệu quả nhất.
Câu 49:
Nhận định dưới đây đúng hay sai?
Theo kết quả thí nghiệm 3, thuốc R xâm nhập vào tế bào vi khuẩn nhanh nhất
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thí nghiệm 3
Lời giải
Thí nghiệm 3 cho biết: “Hệ số thấm càng lớn thì thuốc có khả năng chuyển qua màng càng nhanh”. Thuốc có hệ số thấm lớn nhất, theo Bảng 3, là Thuốc R.
Câu 50:
Nếu Thí nghiệm 2 được lặp lại với Thuốc U và thời gian ủ là 3 giờ, số lượng khuẩn lạc đếm được rất có thể là:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thí nghiệm 2
Lời giải
Theo Bảng 2, Thuốc U có 41 khuẩn lạc trong thời gian ủ là 1 giờ và 18 khuẩn lạc trong thời gian ủ là 6 giờ. Ở thời gian ủ là 3 giờ (trong khoảng từ 1 đến 6 giờ), số lượng khuẩn lạc đếm được rất có thể nằm trong khoảng từ 18 đến 41 khuẩn lạc.
Câu 51:
Phát biểu nào sau đây mô tả đúng nhất mối quan hệ giữa khối lượng phân tử và hệ số thấm của thuốc, trong Thí nghiệm 3?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thí nghiệm 3
Lời giải
Theo bảng 3, khi khối lượng phân tử tăng thì hệ số thấm giảm. Do đó, khi khối lượng phân tử giảm thì hệ số thấm tăng.
Có thể loại đáp án C và D vì hệ số thấm không đổi khi khối lượng phân tử thay đổi
Câu 52:
Phát biểu nào sau đây mô tả đúng nhất mối quan hệ giữa thời gian ủ và số lượng vi khuẩn sống trong Thí nghiệm 2?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thí nghiệm 2
Lời giải
Theo Bảng 2, khi thời gian ủ tăng lên, số lượng khuẩn lạc giảm. Điều này có nghĩa là khi thời gian trôi qua, sẽ có ít vi khuẩn sống sót hơn.
Câu 53:
Trong thí nghiệm 1, mối quan hệ giữa nồng độ thuốc và hiệu quả của thuốc trong việc tiêu diệt vi khuẩn kháng penicillin là gì?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thí nghiệm 1
Lời giải
Bảng 1 thể hiện kết quả của thí nghiệm 1.
Trong bảng 1, khi nồng độ thuốc tăng lên thì số khuẩn lạc của mỗi loại thuốc giảm đi, điều đó có nghĩa là hiệu lực của thuốc tăng lên.
=> Cả 5 loại thuốc đều đạt hiệu quả cao nhất ở nồng độ cao.
Câu 54:
Hàm số nào sau đây nghịch biến trong khoảng (−∞;0)?
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng tính đơn điệu của hàm số bậc hai.
- Nếu a > 0 thì hàm số đồng biến trên \(\left( { - \frac{b}{{2a}}; + \infty } \right)\), nghịch biến trên \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\), đạt được GTNN trên \(R\) tại \(x = - \frac{b}{{2a}}\).
- Nếu \(a < 0\) thì hàm số nghịch biến trên \(\left( { - \frac{b}{{2a}}; + \infty } \right)\), đồng biến trên \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\), đạt được GTLN trên \(R\) tại \(x = - \frac{b}{{2a}}\).
Sự biến thiên của hàm số bậc hai
Lời giải
Đáp án \({\rm{A}}:a = \sqrt 2 > 0\) và \( - \frac{b}{{2a}} = 0\) nên hàm số nghịch biến trên \(( - \infty ;0)\)
Đáp án \({\rm{B}}:a = - \sqrt 2 < 0\) và \( - \frac{b}{{2a}} = 0\) nên hàm số đồng biến trên \(( - \infty ;0)\)
Đáp án C: \(y = \sqrt 2 \left( {{x^2} + 2x + 1} \right) = \sqrt 2 {x^2} + 2\sqrt 2 x + \sqrt 2 \) có \(a = \sqrt 2 > 0\) và \( - \frac{b}{{2a}} = - 1\) nên hàm số nghịch biến trên \(( - \infty ; - 1)\) nhưng \(( - \infty ;0)\not \subset ( - \infty ; - 1)\) nên hàm số không nghịch biến trên \(( - \infty ;0)\)
Đáp án \({\rm{D}}:y = - \sqrt 2 \left( {{x^2} + 2x + 1} \right) = - \sqrt 2 {x^2} - 2\sqrt 2 x - \sqrt 2 \) có \(a = - \sqrt 2 < 0\) và \( - \frac{b}{{2a}} = - 1\) nên hàm số nghịch biến trên \(( - 1; + \infty )\)
Câu 55:
Xác định Parabol \((P):y = a{x^2} + bx + 2\) biết rằng Parabol đi qua hai điểm \(M(1;5)\) và \(N(2; - 2)\).
 Xem đáp án
Xem đáp án
Phương pháp giải
Thay tọa độ các M, N vào phương trình parabol.
Phương pháp giải các bài toán về hàm số bậc hai
Lời giải
Vì M, N ∈ (P) nên tọa độ của hai điểm M, N phải thỏa mãn phương trình của (P).
Do đó, ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{5 = a + b + 2}\\{ - 2 = 4a + 2b + 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = - 5}\\{b = 8}\end{array}} \right.} \right.\) .
Vậy phương trình của (P) là: \(y = - 5{x^2} + 8x + 2\).
Câu 56:
Kéo biểu thức ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Hàm số \(y = \cot x\) không xác định với mọi x có dạng ...... (\(k \in \mathbb{Z}\)).
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Hàm số \(y = \sin x + 5\) tuần hoàn với chu kì 2π
\(y = \cot x = \frac{{\cos x}}{{\sin x}}\) không xác định khi x = kπ
Câu 57:
Tập hợp các giá trị của tham số \(m\) để hàm số \(y = {x^2} + (2m + 1)x - m + 3\) nghịch biến trên khoảng \(( - \infty ;2)\) là
 Xem đáp án
Xem đáp án
Phương pháp giải
Bước 1: Tìm khoảng đồng biến của hàm số đã cho bằng cách sử dụng kiến thức: Hàm số \(y = a{x^2} + bx + c\,\,(a > 0)\) đồng biến trên khoảng \(\left( { - \frac{b}{{2a}}; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\).
Bước 2: Tìm \(m\) bằng cách sử dụng kiến thức: Để hàm số đã cho nghịch biến trên khoảng \(( - \infty ;2)\) thì \(( - \infty ;2) \subset \left( { - \infty ; - \frac{b}{{2a}}} \right)\). Tức là, \(2 \le - \frac{b}{{2a}}\).
Bước 3: Kết luận.
Lời giải
Ta có \( - \frac{b}{{2a}} = - \frac{{2m + 1}}{{2.1}} = - \frac{{2m + 1}}{2}\).
Suy ra hàm số \(y = {x^2} + (2m + 1)x - m + 3\) nghịch biến trên khoảng \(\left( { - \infty ; - \frac{{2m + 1}}{2}} \right)\).
Hàm số đã cho nghịch biến trên khoảng \(( - \infty ;2)\) khi và chỉ khi
\(( - \infty ;2) \subset \left( { - \infty ; - \frac{{2m + 1}}{2}} \right){\rm{. }}\)
Tức là, \(2 \le - \frac{{2m + 1}}{2} \Leftrightarrow \frac{{2m + 1}}{2} \le - 2 \Leftrightarrow 2m + 1 \le - 4 \Leftrightarrow 2m \le - 5 \Leftrightarrow m \le - \frac{5}{2}\)
Vậy \(m \in \left( { - \infty ; - \frac{5}{2}} \right]\) thỏa mãn yêu cầu bài toán.
Câu 58:
Phương trình \(m{x^2} - 2mx + 4 = 0\) vô nghiệm khi và chỉ khi
 Xem đáp án
Xem đáp án
Phương pháp giải
Xét 2 trường hợp m = 0 và m ≠ 0.
Lời giải
Xét phương trình \(m{x^2} - 2mx + 4 = 0\) (*)
TH1: Với m = 0, khi đó phương trình (∗) ⇔ 4 = 0 (Vô lý)
Suy ra với m = 0 thì phương trình (*) vô nghiệm.
TH2: Với m ≠ 0, khi đó để phương trình (*) vô nghiệm ⇔ Δ′ < 0
⇔ m2 − 4m < 0 ⇔ m(m − 4) ⇔ 0 < m < 4
Kết hợp 2 điều kiện ta được 0 ≤ m < 4.
Câu 59:
Một công ty chuyên sản xuất đĩa CD với chi phí mỗi đĩa là 40 (nghìn đồng). Theo nghiên cứu nếu mỗi đĩa bán với giá x (nghìn đồng) thì số lượng đĩa bán được sẽ là q(x) = 120 − x, (x ∈ N*). Hãy xác định giá bán của mỗi đĩa sao cho lợi nhuận mà công ty thu được là cao nhất?
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Chi phí mà công ty này bỏ ra để sản xuất đĩa là :
\(q(x).40 = (120 - x).40 = 4800 - 40x\) (nghìn đồng).
Số tiền mà công ty này thu về từ việc bán đĩa là :
\(x.q(x) = x.(120 - x) = 120x - {x^2}\)(nghìn đồng).
Lợi nhuận của công ty này thu được từ việc bán đĩa là :
\(f(x) = \left( {120x - {x^2}} \right) - (4800 - 40x) = - {x^2} + 160x - 4800\)(nghìn đồng).
Bài toán trở thành tìm giá trị lớn nhất của hàm số \(f(x)\) trên \((0;120)\).
Nhận thấy rằng đây là hàm số dạng \(a{x^2} + bx + c\) với \(a < 0\) nên nó đạt giá trị lớn nhất trên \(\mathbb{R}\) khi \(x = - \frac{b}{{2a}}\). Suy ra khi \(x = - \frac{{160}}{{2.( - 1)}} = 80\) thì hàm số \(f(x) = - {x^2} + 160x - 4800\) đạt giá trị lớn nhất trên \(\mathbb{R}\), mà \(0 < 80 < 120\) nên \(x = 80\) thì hàm số \(f(x) = - {x^2} + 160x - 4800\) đạt giá trị lớn nhất trên \((0;120)\).
Câu 60:
Quỹ đạo của một vật được ném lên từ gốc O (được chọn là điểm ném) trong mặt phẳng toạ độ Oxy là một parabol có phương trình \(y = - \frac{1}{{10}}{x^2} + x\), trong đó x (mét) là khoảng cách theo phương ngang trên mặt đất từ vị trí của vật đến gốc O, y (mét) là độ cao của vật so với mặt đất (tham khảo hình vẽ). Tính khoảng cách từ điểm chạm đất sau khi bay của vật đến gốc O (khoảng cách này được gọi là tầm xa của quỹ đạo).
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Vật chạm đất khi độ cao bằng 0
\( \Leftrightarrow - \frac{1}{{10}}{x^2} + x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 10}\end{array}} \right.\)
Vậy khoảng cách từ điểm chạm đất sau khi bay của vật đến gốc O bằng 10 mét)
Câu 61:
Số liệu thống kê tình hình đỗ đại học của học sinh trường THPT X trong hai năm 2018 và 2019 như sau:
Đơn vị: người
|
STT |
Trường Đại học |
Khóa tốt nghiệp 2018 |
Khóa tốt nghiệp 2019 |
||
|
Nữ |
Nam |
Nữ |
Nam |
||
|
1 |
Khoa học Tự nhiên |
15 |
50 |
20 |
45 |
|
2 |
Bách khoa |
20 |
43 |
15 |
32 |
|
3 |
Kinh tế |
5 |
20 |
10 |
55 |
|
4 |
Ngoại thương |
10 |
34 |
5 |
12 |
Kéo biểu thức ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Trong số học sinh nữ đỗ đại học khóa tốt nghiệp 2018, tỉ lệ phần trăm đỗ Đại học Khoa học Tự nhiên là .....
Tính cả hai khóa tốt nghiệp 2018 và 2019, số học sinh đỗ Đại học Bách khoa nhiều hơn số học sinh đỗ Đại học Ngoại thương khoảng ......
 Xem đáp án
Xem đáp án
Đáp án
Trong số học sinh nữ đỗ đại học khóa tốt nghiệp 2018, tỉ lệ phần trăm đỗ Đại học Khoa học Tự nhiên là 30%
Tính cả hai khóa tốt nghiệp 2018 và 2019, số học sinh đỗ Đại học Bách khoa nhiều hơn số học sinh đỗ Đại học Ngoại thương khoảng 80,3%
Phương pháp giải
- Tính tỉ lệ phần trăm.
- Phần trăm A nhiều hơn B là \(\frac{{A - B}}{B}.100\% \)
Lời giải
1) Ta có: Số học sinh nữ đỗ đại học khóa 2018 là 15+20+5+10=50 (người)
Số học sinh nữ đỗ Đại học Khoa học Tự nhiên là 15 (người)
Tỉ lệ phần trăm đỗ Đại học Khoa học Tự nhiên là \[\frac{{15}}{{50}}.100{\rm{\% }} = 30{\rm{\% }}\]
2) Tổng số học sinh đỗ Đại học Bách khoa cả 2 năm là 20+43+15+32=110 (người)
Tổng số học sinh đỗ Đại học Ngoại thương là 10+34+5+12=61
Số học sinh đỗ Đại học Bách khoa nhiều hơn số học sinh đỗ Đại học Ngoại thương khoảng:
\[\frac{{110 - 61}}{{61}}.100{\rm{\% }} \approx 80,3{\rm{\% }}\]
Câu 62:
Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ta lập được bao nhiêu số tự nhiên có 6 chữ số (các chữ số đôi một khác nhau), mà luôn có mặt nhiều hơn một chữ số lẻ và đồng thời trong đó hai chữ số kề nhau không cùng là số lẻ?
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Gọi số cần tìm có dạng \[m = \overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}} \] với \({a_i} \in \{ 0;1;2;3;4;5;6;7;8;9\} ,\,\,{a_1} \ne 0\) và \(i \in \{ 1;2;3;4;5;6\} \).
Vì các chữ số \({a_1},{a_2},{a_3},{a_4},{a_5},{a_6}\) là đôi một khác nhau, có nhiều hơn một chữ số lẻ và đồng thời trong đó có hai chữ số kề nhau không cùng là số lẻ nên ta xét hai trường hợp sau:
1. Trường hợp 1. Có 4 chữ số chẵn và 2 chữ số lẻ.
- Chữ số 0 đứng ở vị trí bất kì.
- Lấy 4 chữ số chẵn và 2 chữ số lẻ có \(C_5^4.C_5^2\).
- Xếp 4 chữ số chẵn có 4!.
- Xếp 2 chữ số lẻ có \(A_5^2\).
Vậy trường hợp này có \(C_5^4.C_5^2.4!.A_5^2 = 24000\) số.
- Chữ số a1 = 0.
- Lấy thêm 3 chữ số chẵn; 2 chữ số lẻ có \(C_4^3.C_5^2\).
- Xếp 3 chữ số chẵn có 3!.
- Xếp 2 chữ số lẻ có \(A_4^2\).
Vậy trường hợp này có \(C_4^3.C_5^2.3!.A_4^2 = 2880\).
2. Trường hợp 2 . Có 3 chữ số chẵn và 3 chữ số lẻ.
- Chữ số 0 dứng ở vị trí bất kì.
- Lấy 3 chữ số chẵn và 3 chữ số lẻ có \(C_5^3.C_5^3\).
- Xếp 3 chữ số chẵn có 3!.
- Xếp 3 chữ số lẻ có \(A_4^3\).
Vậy trường hợp này có \(C_5^3.C_5^3.3!.A_4^3 = 14400\) số.
- Chữ số a1 = 0.
- Lấy thêm 2 chữ số chẵn; 3 chữ số lẻ có \(C_4^2.C_5^3\).
- Xếp 2 chữ số chẵn có 2!.
- Xếp 3 chữ số lẻ có \(A_3^3 = 3!\).
Vậy trường hợp này có \(C_4^2.C_5^3.2!.3! = 720\).
Vậy có (24000 − 2880) + (14400 − 720) = 34800 số thỏa mãn yêu cầu bài toán.
Câu 63:
Trong không gian cho điểm A và mặt phẳng (P). Mệnh đề nào đưới đây đúng ?
 Xem đáp án
Xem đáp án
Phương pháp giải
Hai mặt phẳng vuông góc
Lời giải
Có vô số mặt phẳng qua A và vuông góc với (P).
Câu 64:
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh \(a\sqrt 2 \), biết các cạnh bên tạo với đáy một góc \({60^^\circ }\). Giá trị lượng giác tang của góc giữa hai mặt phẳng \((SAC)\) và \((SCD)\) bằng
 Xem đáp án
Xem đáp án
Phương pháp giải
Góc giữa hai mặt phẳng
Lời giải
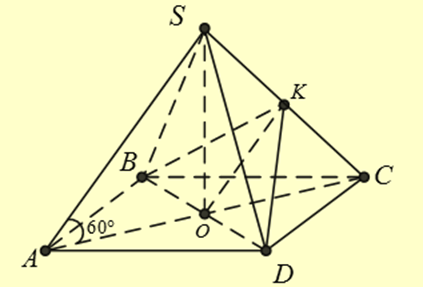
Kẻ \(OK \bot SC\). Do S.ABCD là hình chóp đều và ABCD là hình vuông nên \(SO \bot (ABCD)\); \(BD \bot (SAC) \Rightarrow SC \bot BD\). Suy ra \(SC \bot (BKD) \Rightarrow KD \bot SC\).
Vậy góc giữa hai mặt phẳng \((SAC)\) và \((SCD)\) là \(\widehat {OKD}\) và \(\tan \widehat {OKD} = \frac{{OD}}{{OK}}\) (do \(\Delta KOD\) vuông ở \(O\)) : ABCD là hình vuông cạnh \(a\sqrt 2 \) nên \(AC = 2a \Rightarrow OA = OC = OD = a\).
Trong hình chóp đều S.ABCD, cạnh bên tạo với đáy một góc \({60^^\circ }\) nên \(\widehat {SAC} = {60^^\circ }\) \( \Rightarrow SO = OA.\tan {60^^\circ } = a\sqrt 3 \).
Ta có \(\frac{1}{{O{K^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{C^2}}} \Rightarrow OK = \frac{{a\sqrt 3 }}{2} \Rightarrow \tan \widehat {OKD} = \frac{{OD}}{{OK}} = \frac{2}{{\sqrt 3 }} = \frac{{2\sqrt 3 }}{3}\).
Câu 65:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với \(AB = a,AD = a\sqrt 3 \). Hình chiếu vuông góc \(H\) của \(S\) trên mặt đáy trùng với trọng tâm tam giác ABC và \(SH = \frac{a}{2}\). Gọi M, N lần lượt là trung điểm các cạnh BC và SC. Gọi \(\alpha \) là góc giữa đường thẳng MN với mặt đáy \((ABCD)\). Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng các mối quan hệ hình học đã biết kết hợp với cách xác định góc giữa đường thẳng và mặt phẳng để tìm góc giữa MN với mặt đáy (ABCD).
Góc giữa đường thẳng và mặt phẳng
Lời giải
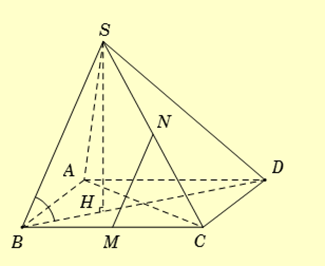
Ta có . Do đó \(\widehat {MN,(ABCD)} = \widehat {SB,(ABCD)}\)
Do SH ⊥ (ABCD) nên \(\widehat {MN,(ABCD)} = \widehat {SB,(ABCD)} = \widehat {SB,HB} = \widehat {SBH}\).
Ta có \(BD = \sqrt {A{B^2} + A{D^2}} = 2a;BH = \frac{{BD}}{3} = \frac{{2a}}{3}{\rm{. }}\)
Tam giác SHB, có \(\tan \widehat {SBH} = \frac{{SH}}{{BH}} = \frac{3}{4}\) .
Câu 66:
Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = {( - 1)^n}{.5^{2n + 3}}\). Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dãy số bị chặn
Lời giải
Nếu n chẵn thì \({u_n} = {5^{2n + 1}} > 0\) tăng lên vô hạn (dương vô cùng) khi n tăng lên vô hạn nên dãy \(\left( {{u_n}} \right)\) không bị chặn trên.
Nếu n lẻ thì \({u_n} = - {5^{2n + 1}} < 0\) giảm xuống vô hạn (âm vô cùng) khi n tăng lên vô hạn nên dãy \(\left( {{u_n}} \right)\) không bị chặn dưới.
Vậy dãy số đã cho không bị chặn.
Câu 67:
Một người muốn mua một thanh gỗ đủ để cắt ra làm các thanh ngang của một cái thang. Biết rằng chiều dài các thanh ngang của cái thang đó (từ bậc dưới cùng) lần lượt là 45 cm, 43 cm , 41 cm,…,31 cm

Khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
Cái thang đó có 8 bậc |
¡ |
¡ |
|
Chiều dài thanh gỗ mà người đó cần mua là 304 cm, giả sử chiều dài các mối nối (phần gỗ bị cắt thành mùn cưa) là không đáng kể |
¡ |
¡ |
 Xem đáp án
Xem đáp án
Đáp án
|
|
ĐÚNG |
SAI |
|
Cái thang đó có 8 bậc |
¤ |
¡ |
|
Chiều dài thanh gỗ mà người đó cần mua là 304 cm, giả sử chiều dài các mối nối (phần gỗ bị cắt thành mùn cưa) là không đáng kể |
¤ |
¡ |
Phương pháp giải
- Tìm số hạng đầu và công sai
- Sử dụng công thức số hạng tổng quát tìm n
- Sử dụng công thức tính tổng n số hạng đầu tiên
Lời giải
a) Chiều dài các thanh ngang là dãy cấp số cộng có số hạng đầu là 45, công sai là −2
số hạng tổng quát là: un = 45 − 2(n − 1) = 47 − 2n
khi un = 31 ⇒ n = 8
Vậy cái thang có 8 bậc
b) \({S_8} = \frac{{8.(45 + 31)}}{2} = 304\)
Vậy chiều dài thanh gỗ là 304cm.
Câu 68:
Với hình vuông A1B1C1D1 như hình vẽ bên, cách tô màu như phần gạch sọc được gọi là cách tô màu “đẹp”. Một nhà thiết kế tiến hành tô màu cho một hình vuông như hình bên, theo quy định sau:
Bước 1: Tô màu "đẹp" cho hình vuông A1B1C1D1.
Bước 2: Tô màu "đẹp" cho hình vuông A2B2C2D2 là hình vuông ở chính giữa khi chia hình vuông A1B1C1D1 thành 9 phần bằng nhau như hình vẽ.
Bước 3: Tô màu "đẹp" cho hình vuông A3B3C3D3 là hình vuông ở chính giữa khi chia hình vuông A2B2C2D2 thành 9 phần bằng nhau. Cứ tiếp tục như vậy. Hỏi cần đúng bao nhiêu bước để tổng diện tích phần được tô màu chiếm \(\frac{{40}}{{81}}\) phần diện tích hình vuông ban đầu?
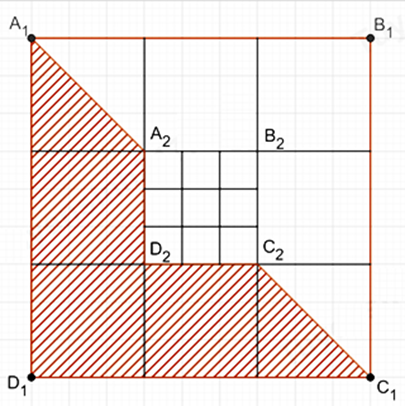
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Gọi diện tích được tô màu ở mỗi bước là \({u_n},n \in {\mathbb{N}^*}\). Dễ thấy dãy các giá trị \({u_n}\) là một cấp số nhân với số hạng đầu \({u_1} = \frac{4}{9}\) và công bội \(q = \frac{1}{9}\).
Gọi \({S_k}\) là tổng của \(k\) số hạng đầu trong cấp số nhân đang xét thì \({S_k} = \frac{{{u_1}\left( {{q^k} - 1} \right)}}{{q - 1}}\). Để tổng diện tích phần được tô màu chiếm \(\frac{{40}}{{81}}\) phần diện tích hình vuông ban đầu thì \(\frac{{{u_1}\left( {{q^k} - 1} \right)}}{{q - 1}} = \frac{{40}}{{81}} \Leftrightarrow k = 2\).
Vậy cần đúng 2 bước.
Câu 69:
Giới hạn \(L = \lim \frac{{3n - 1}}{{n + 2}}\) bằng
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng máy tính cầm tay
Lời giải
Sử dụng máy tính cầm tay ta được:
\(L = \lim \frac{{3n - 1}}{{n + 2}} = 3\)
Câu 70:
Từ khai triển biểu thức \({(x + 1)^{2023}}\) thành đa thức. Tổng các hệ số của đa thức là
 Xem đáp án
Xem đáp án
Phương pháp giải
Nhị thức Niu - tơn
Lời giải
Ta có \({(x + 1)^{2023}} = \sum\limits_{k = 0}^{2023} {C_{2023}^k} {x^k}\)
Tổng các hệ số của đa thức là: \(\sum\limits_{k = 0}^{2023} {C_{2023}^k} = \sum\limits_{k = 0}^{2023} {C_{2023}^k} {1^k} = {(1 + 1)^{2023}} = {2^{2023}}\)
Câu 71:
Xếp 6 người A, B, C, D, E, F vào ghế dài có 6 chỗ.
Kéo các ô sau thả vào vị trí thích hợp để được khẳng định đúng:
![]()
1) Có .... cách xếp sao cho A và F ngồi ở hai đầu ghế.
2) Có .... cách xếp sao cho A và F ngồi cạnh nhau.
3) Có ...... cách xếp sao cho A và F không ngồi cạnh nhau.
 Xem đáp án
Xem đáp án
1) Có 48 cách xếp sao cho A và F ngồi ở hai đầu ghế.
2) Có 240 cách xếp sao cho A và F ngồi cạnh nhau.
3) Có 480 cách xếp sao cho A và F không ngồi cạnh nhau.
Phương pháp giải
1) Ưu tiên xếp A và F trước
2) Xếp A và F ngồi cạnh nhau ta ghép A và F thành 1 "bó" trước.
3) Đếm số cách xếp 6 người bất kì rồi đếm số cách xếp sao cho A và F ngồi cạnh nhau
Lời giải
1) Xếp A và F ở hai đầu ghế: có 2! cách xếp A và F
Các vị trí ở giữa: có 4! cách xếp
Vậy có 2!.4! = 48 cách xếp sao cho A và F ở hai đầu ghế.
2) Xếp A và F ngồi cạnh nhau ta ghép A và F thành 1 "bó": có 2 ! cách sắp xếp vị trí bên trong "bó"
Rồi mang sắp xếp 4 người còn lại và 1 "bó" trên ghế dài: ta được 5 ! cách xếp.
Vậy có 2!. 5! = 240 cách xếp sao cho A và F ngồi cạnh nhau.
3) Số cách xếp 6 người bất kì là 6! cách
Số cách xếp sao cho A và F ngồi cạnh nhau là 240 cách.
Vậy có 6! − 240 = 480 cách xếp sao cho A và F không ngồi cạnh nhau.
Câu 72:
Trong mặt phẳng Oxy, cho hình chữ nhật OMNP với \(M(0;10),N(100;10),P(100;0)\). Gọi \(S\) là tập hợp tất cả các điểm \(A(x;y)\,\,(x;y \in \mathbb{Z})\) nằm bên trong (kể cả trên cạnh) của OMNP. Lấy ngẫu nhiên một điểm \(A \in S\). Xác suất để \(x + y \le 90\) là
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Số điểm có tọa độ nguyên trong hình chữ nhật OMNPlà tích số số điểm chiều dài với số điểm chiều rộng và bằng 101.11 điểm.
Nhận thấy các điểm cần tìm nằm trên đường thẳng \(y = m\), với \(m = \overline {0,10} \)
Dễ thấy trên các đường y = 0; y = 1;...; y = 10 có lần lượt 91, 90, …, 81 điểm
Vậy xác xuất cần tìm là \(P = \frac{{91 + 90 + \ldots + 81}}{{11.101}} = \frac{{86}}{{101}}\)
Câu 73:
Giả sử có 12 viên bi khác màu nhau và 3 cái hộp, ta chia đều bi vào các hộp.
Kéo các ô sau thả vào vị trí thích hợp để được khẳng định đúng:

Số cách xếp 12 viên vào 3 hộp giống nhau là ....
 Xem đáp án
Xem đáp án
Số cách xếp 12 viên vào 3 hộp khác nhau là 34650
Số cách xếp 12 viên vào 3 hộp giống nhau là 5775
Phương pháp giải
+ Xếp 12 viên bi vào 3 hộp khác nhau:
- Xếp 4 viên bi vào hộp thứ nhất
- Xếp 4 viên bi vào hộp thứ 2
- Còn lại vào hộp thứ 3
+ Xếp 12 viên bi vào 3 hộp giống nhau = Số cách xếp vào 3 hộp khác : 3!
Lời giải
+ Xếp 12 viên bi vào 3 hộp khác nhau:
Xếp 4 viên bi vào hộp số 1: \(C_{12}^4 = 495\)
Xếp 4 viên bi vào hộp số 2: \(C_8^4 = 70\)
Số cách xếp 12 viên bi vào 3 hộp khác nhau: 495.70 = 34650
+ Số cách xếp 12 viên vào 3 hộp giống nhau là \(\frac{{34650}}{{3!}} = 5775\)
Câu 74:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(SA \bot (ABCD)\) và \(SA = a\sqrt 2 \). Khoảng cách giữa hai đường thẳng chéo nhau \({\rm{AC}}\) và \({\rm{SB}}\) bằng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Kẻ đường thẳng d qua B và song song với AC.
Gọi M là hình chiếu vuông góc của A lên d.
H là hình chiếu của A lên SM.
Chứng minh d(AC;SB) = d(A;(SBM)) = AH.
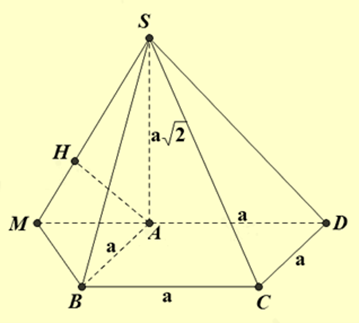
Kẻ đường thẳng d qua B và song song với AC.
Gọi M là hình chiếu vuông góc của A lên d.
H là hình chiếu của A lên SM.
Ta có: \(\left. {\begin{array}{*{20}{l}}{SA \bot BM}\\{AM \bot BM}\end{array}} \right\} \Rightarrow BM \bot (SAM)\)
⇒ BM ⊥ AH mà AH ⊥ SM
⇒ AH ⊥ (SBM)
Do đó: d(AC;SB) = d(A;(SBM)) = AH
Xét ΔSAM vuông tại A, đường cao AH:
\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{M^2}}} = \frac{5}{{2{a^2}}} \Rightarrow AH = \frac{{a\sqrt {10} }}{5}.\)
Câu 75:
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(A\) với \(AB = a,AC = 2a\). Mặt phẳng \((SBC)\) vuông góc với mặt phắng \((ABC)\). Mặt phẳng \((SAB),(SAC)\) cùng tạo với mặt phẳng \((ABC)\) một góc bằng \({60^^\circ }\). Gọi \(\alpha \) là góc giữa hai mặt phẳng \((SAB)\) và \((SBC)\). Tính \(\tan \alpha \).
 Xem đáp án
Xem đáp án
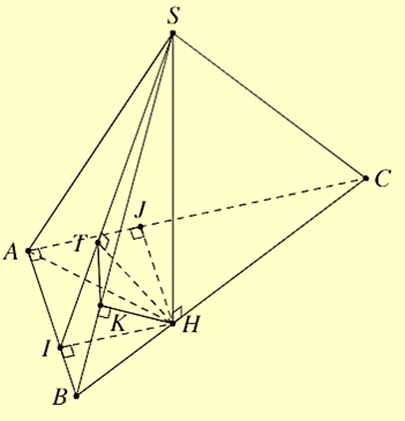
Kẻ \(HI \bot AB(I \in AB),HJ \bot AC(J \in AC)\). Dễ thấy và (vì \(\Delta ABC\) vuông tại \(A\)) nên AlHJ là hình bình hành.
Có \(HI \bot AB\) và \(SH \bot AB\) (vì \(SH \bot (ABC))\) nên \(AB \bot (SHI)\)
\( \Rightarrow \) góc giữa \((SAB)\) và \((ABC)\) là góc \(\widehat {SIH} = {60^^\circ }\).
Tương tự thì \(\widehat {SJH} = {60^^\circ }\).
Kẻ \(HK \bot SB(K \in SB)\) và \(HT \bot SI(I \in SI)\).
Ta có \(HT \bot AB\) và \(HT \bot SI \Rightarrow HT \bot (SAB) \Rightarrow HT \bot SB\) và \(HK \bot SB \Rightarrow \) góc giữa \((SAB)\) và \((SBC)\) là góc \(\widehat {HKT}\).
Ta có \(HI = SH\cot \widehat {SHH} = SH\cot {60^^\circ }\) và \(HJ = SH\cot \widehat {SJH} = SH\cot {60^^\circ }\)
\( \Rightarrow HI = HJ \Rightarrow AIHJ\) là hình thoi \( \Rightarrow AH\) là phân giác \(\widehat {BAC}\).
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt 5 a,\frac{{BH}}{{HC}} = \frac{{AB}}{{AC}} = \frac{1}{2} \Rightarrow BH = \frac{{\sqrt 5 }}{3}a,CH = \frac{{2\sqrt 5 }}{3}a.\)
\(\frac{{BH}}{{BC}} = \frac{{HI}}{{AC}} \Rightarrow HI = HJ = \frac{2}{3}a,\,\,SH = HI\tan \widehat {SIH} = HI\tan {60^^\circ } = \frac{{2\sqrt 3 }}{3}a,\)
\(HT = HI\sin \widehat {SIH} = HI\sin {60^^\circ } = \frac{{2\sqrt 3 }}{6}a\).
Tam giác SHB vuông tại \(H(SH \bot (ABC))\) có đường cao HK
\( \Rightarrow \frac{1}{{H{K^2}}} = \frac{1}{{H{B^2}}} + \frac{1}{{S{H^2}}} \Rightarrow HK = \frac{{10}}{{\sqrt {255} }}a\).
Vì \(HT \bot (SAB)\) nên \(HT \bot TK\) từ đó \(TK = \sqrt {H{K^2} - H{T^2}} = \frac{1}{{\sqrt {17} }}a\)
\( \Rightarrow \tan \widehat {HKT} = \frac{{HT}}{{TK}} = \frac{{\sqrt {51} }}{3}\).
Câu 76:
Khối chóp \(S.ABCD\)có \(SA \bot (ABC)\), tam giác ABC vuông tại \(B,AB = a,BC = a\sqrt 3 \), \(SA = 2a\sqrt 3 \)
Kéo biểu thức ở các ô thả vào vị trí thích hợp:
![]()
Độ dài cạnh AC bằng ....
Góc giữa SC và mặt phẳng (ABC) bằng .....
 Xem đáp án
Xem đáp án
Độ dài cạnh AC bằng 2a
Góc giữa SC và mặt phẳng (ABC) bằng
Phương pháp giải
- Xác định hình chiếu của SC xuống mặt phẳng (ABC).
- Tính AC
- Tính góc giữa SC và mặt phẳng ABC
Lời giải
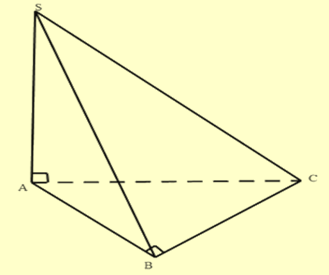
Ta có: \(SA \bot (ABC) \Rightarrow AC\) là hình chiếu của \({\rm{SC}}\) xuống mặt phẳng \((ABC)\).
Tam giác \({\rm{ABC}}\) vuông tại \(B\) nên \(AC = \sqrt {A{B^2} + B{C^2}} = 2a\).
Khi đó, góc giữa \({\rm{SC}}\) và mặt phẳng \({\rm{ABC}}\) là góc \(\widehat {SCA}\).
Xét tam giác vuông SCA có: \(\tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{{2a\sqrt 3 }}{{2a}} = \sqrt 3 \Rightarrow \widehat {SCA} = {60^^\circ }\).
Câu 77:
Một bộ ba số Pythagoras (còn gọi là bộ ba số Pytago hay bộ ba số Pythagore) gồm ba số nguyên dương a, b và c, sao cho \({a^2} + {b^2} = {c^2}\). Khi đó ta viết bộ ba đó là (a;b;c). Một bộ ba số Pythagoras được gọi là bộ ba số Pythagoras nguyên tố nếu a, b và c là các số nguyên tố cùng nhau.
Khẳng định nào sau đây đúng hay sai?
|
|
ĐÚNG |
SAI |
|
Bộ ba số (3;4;5) là bộ ba số Pytago nguyên tố |
¡ |
¡ |
|
Hai số 153 và 185 có cùng thuộc 1 bộ ba số Pytago |
¡ |
¡ |
|
Nếu (a, b, c) là bộ ba số Pytago, thì cả bộ ba (ka, kb, kc) với số nguyên k bất kỳ cũng là Pytago |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
Bộ ba số (3;4;5) là bộ ba số Pytago nguyên tố |
¤ |
¡ |
|
Hai số 153 và 185 có cùng thuộc 1 bộ ba số Pytago |
¤ |
¡ |
|
Nếu (a, b, c) là bộ ba số Pytago, thì cả bộ ba (ka, kb, kc) với số nguyên k bất kỳ cũng là Pytago |
¡ |
¤ |
Phương pháp giải
- Kiểm tra bộ ba có là số nguyên tố không
- Kiểm tra bộ ba số có nguyên tố cùng nhau không.
- Các số nguyên a;b;c được gọi là nguyên tố cùng nhau nếu ước chung lớn nhất của chúng bằng 1.
Lời giải
a) Ta thấy 52 = 32 + 42
Nên (3;4;5) là bộ ba số Pytago
Mà 3;4;5 có ước chung lớn nhất là 1 nên 3;4;5 là các số nguyên tố cùng nhau.
b)
TH1: Cả 2 số là các cạnh góc vuông
1532 + 1852 = 57634
Mà 57634 không là số chính phương nên loại
TH2: Có 1 số lớn nhất là cạnh huyền
1852 − 1532 = 1042
=> Thỏa mãn.
Hai số 153 và 185 có cùng thuộc 1 bộ ba số Pytago
c) Mệnh đề 3 sai vì với k = 0 thì (ka;kb;kc) không là bộ ba số Pytago.
Câu 78:
Kéo các ô sau thả vào vị trí thích hợp để được khẳng định đúng:
![]()
Số dư khi chia 15325 − 1 cho 9 là ....
Số dư khi chia 20162018 + 2 cho 5 là .........
 Xem đáp án
Xem đáp án
Số dư khi chia 15325 − 1 cho 9 là 4
Số dư khi chia 20162018 + 2 cho 5 là 3
Phương pháp giải
Nếu \(a \equiv b\,\,(\bmod \,\,m) \Rightarrow {a^n} \equiv {b^n}\,\,(\bmod \,\,m)\)
Lời giải
a) Ta có \(1532 = 9.170 + 2 \equiv 2\,\,(\bmod \,\,9)\)
Do đó \({1532^5} \equiv {2^5}\,\,(\bmod \,\,9) \Rightarrow {1532^5} - 1 \equiv {2^5} - 1\,\,(\bmod \,\,9)\).
Mà \({2^5} - 1 = 31 \equiv 4\,\,(\bmod \,\,9)\).
Do đó \({1532^5} - 1 \equiv 4\,\,(\bmod \,\,9)\).
Vậy số dư cần tìm là 4 .
b) Ta có \(2016 \equiv 1\,\,(\bmod \,\,5)\) do đó \({2016^{2018}} \equiv {1^{2018}}\,\,(\bmod \,\,5) \Rightarrow \) \({2016^{2018}} + 2 \equiv {1^{2018}} + 2\,\,(\bmod \,\,5)\).
Mà \(1 + 2 = 3 \equiv 3\,\,(\bmod \,\,5)\). Do đó \({2016^{2018}} + 2 \equiv 3\,\,(\bmod \,\,5)\).
Vậy số dư cần tìm là 3 .
Câu 79:
Hàm số nào sau đây là một hàm số tuần hoàn
 Xem đáp án
Xem đáp án
Phương pháp giải
Hàm số tuần hoàn
Lời giải
Hàm số \(y = 2.\sin x + 3.\cos x\) là hàm số tuần hoàn.
Giả sử hàm số \(y = x.\sin x\) là hàm số tuần hoàn
Nghĩa là tồn tại T > 0 sao cho \(f(x + T) = f(x)\,\,\forall x \in \mathbb{R}\)
Do đó
\((x + T).\sin (x + T) = x.\sin x\,\,\forall x \in \mathbb{R}\)
\(x = 0 \Rightarrow T.\sin T = 0 \Rightarrow \sin T = 0\)
\(x = \frac{\pi }{2} \Rightarrow \left( {T + \frac{\pi }{2}} \right).\sin \left( {T + \frac{\pi }{2}} \right) = \frac{\pi }{2}.1\)
\( \Rightarrow \sin \left( {T + \frac{\pi }{2}} \right) = \frac{{\frac{\pi }{2}}}{{\frac{\pi }{2} + T}} = \cos T\)
\( \Rightarrow \cos T = 1(T > 0)\)
\( \Rightarrow \frac{{\frac{\pi }{2}}}{{\frac{\pi }{2} + T}} \Rightarrow T = 0\)
Xét hàm số \(y = \sin {x^2}\)
Giả sử hàm số tuần hoàn chu kì T
\( \Rightarrow \sin {x^2} = \sin {(x + T)^2}\forall x \in \mathbb{R}\)
Với \(x = 0 \Rightarrow \sin {T^2} = 0 \Rightarrow {T^2} = k\pi \)
Giả sử \(k = {m_o} \ge 1,{m_o} \in {\mathbb{N}^*}\) vì \({\rm{T}} > 0\)
Với \(x = \sqrt {\frac{\pi }{2}} \Rightarrow \sin {\left( {\sqrt {\frac{\pi }{2}} + \sqrt {{m_o}\pi } } \right)^2} = 1\)
\( \Rightarrow \sin \left( {\frac{\pi }{2} + {m_o}\pi + 2\sqrt {\frac{\pi }{2}.{m_o}\pi } } \right) = 1\)
\( \Rightarrow \cos \left( {{m_o}\pi + 2\sqrt {\frac{\pi }{2}.{m_o}\pi } } \right) = 1\)
\( \Rightarrow \sin \left( {{m_o}\pi + 2\sqrt {\frac{\pi }{2}.{m_o}\pi } } \right) = 0\)
\(\begin{array}{l} \Rightarrow \sin \left( {{m_o}\pi + \pi \sqrt {2{m_o}} } \right) = 0\\ \Rightarrow \sin \left( {{m_o} + \sqrt {2{m_o}} } \right)\pi = 0\\ \Rightarrow \sqrt {2{m_o}} \in {\mathbb{N}^*}\end{array}\)
Với \(x = \sqrt \pi \)
\(\begin{array}{l} \Rightarrow \sin {\left( {\sqrt \pi + \sqrt {{m_o}\pi } } \right)^2} = 0\\ \Rightarrow \sin {\left( {1 + \sqrt {{m_o}} } \right)^2}\pi = 0\\ \Rightarrow 2\sqrt {{m_o}} \in {\mathbb{N}^*} \Rightarrow \sqrt {{m_o}} \in {\mathbb{N}^*}\\ \Rightarrow \sqrt {{m_o}} + \sqrt {2{m_o}} \in {\mathbb{N}^*}\end{array}\)
Vì \(\sqrt {{m_o}} \in {\mathbb{N}^*} \Rightarrow 1 + \sqrt 2 \in {\mathbb{N}^*}\) (Vô lí)
Câu 80:
Một cầu thang đường lên cổng trời của một điểm giải trí ở công viên tỉnh X được hàn bằng sắt có hình dáng các bậc thang đều là hình chữ nhật với cùng chiều rộng là 35cm và chiều dài của nó theo thứ tự mỗi bậc đều giảm dần đi 7cm. Biết rằng bậc đầu tiên của cầu thang là hình chữ nhật có chiều dài 189cm và bậc cuối cùng cầu thang là hình chữ nhật có chiều dài 63cm. Hỏi giá thành làm cầu thang đó gần với số nào dưới đây nếu giá thành làm một mét vuông cầu thang đó là 1250 000 đồng trên một mét vuông?
 Xem đáp án
Xem đáp án
Phương pháp giải
Cấp số cộng
Lời giải
Ta có chiều dài của mỗi mặt cầu thang theo thứ tự lập thành một cấp số cộng với số hạng đầu tiên là \({u_1} = 189\), công sai \(d = - 7\) và số hạng cuối cùng là \({u_n} = 63\).
Khi đó áp dụng công thức tính số hạng tồng quát ta có:
\({u_n} = {u_1} + (n - 1)d \Leftrightarrow 63 = 189 - 7(n - 1) \Leftrightarrow n = 19\)
Tổng chiều dài của 19 hình chữ nhật đó là: .
Diện tích của 19 bậc thang là:
Tổng số tiền để làm cầu thang đó là: đồng.\({S_{19}} = 19.\frac{{{u_1} + {u_{19}}}}{2} = 2394\)
Câu 81:
Có bao nhiêu giá trị thực của tham số m để phương trình \[(x - 1)(x - 3)(x - m) = 0\] có 3 nghiệm phân biệt lập thành cấp số nhân tăng?
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Ta có: \((x - 1)(x - 3)(x - m) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = 3}\\{x = m}\end{array}} \right.\).
Để phương trình có 3 nghiệm phân biệt thì: \(m \notin \{ 1;3\} \).
Trường hợp 1: \(m < 1 < 3\).
Để 3 số m ; 1; 3 lập thành cấp số nhân tăng thì: \(m.3 = {1^2} \Leftrightarrow m = \frac{1}{3}\)
Cấp số nhân tăng đó là: \(\frac{1}{3};1;3\)
Trường hợp 2: \(1 < m < 3\).
Để 3 số 1; m; 3 lập thành cấp số nhân tăng thì: \(1.3 = {m^2} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = \sqrt 3 }\\{m = - \sqrt 3 }\end{array}} \right.\)
Đối chiếu điều kiện \(1 < m < 3\) ta chọn \(m = \sqrt 3 \).
Cấp số nhân tăng đó là: \(1;\sqrt 3 ;3\)
Trường hợp 3 : \(1 < 3 < m\).
Để 3 số 1; 3; m lập thành cấp số nhân tăng thì: \(1.m = {3^2} \Leftrightarrow m = 9\)
Cấp số nhân tăng đó là: 1; 3; 9
Vậy \(m \in \left\{ {\frac{1}{3};\sqrt 3 ;9} \right\}\) thì phương trình \((x - 1)(x - 3)(x - m) = 0\) có 3 nghiệm phân lập thành cấp số nhân tăng.
Câu 82:
Phương trình \(\frac{{4{{\cos }^2}x + 2\sin x - 5}}{{\tan x + \sqrt 3 }} = 0\) có bao nhiêu nghiệm?
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
PT tương đương với \(\frac{{4{{\cos }^2}x + 2\sin x - 5}}{{\tan x + \sqrt 3 }} = 0\)
\( \Leftrightarrow \frac{{4 - 4{{\sin }^2}x + 2\sin x - 5}}{{\tan x + \sqrt 3 }} = 0\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4{{\sin }^2}x - 2\sin x + 1 = 0}\\{\tan x \ne - \sqrt 3 ;\cos x \ne 0}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3{{\sin }^2}x + {{(\sin x - 1)}^2} = 0}\\{\tan x \ne - \sqrt 3 ;\cos x \ne 0}\end{array} \Leftrightarrow x \in \emptyset } \right.\)Câu 83:
Tổng các nghiệm trên khoảng \((0;\pi )\) của phương trình lượng giác
\(4{\sin ^2}\frac{x}{2} - \sqrt 3 \cos 2x = 1 + 2{\cos ^2}\left( {x - \frac{{3\pi }}{4}} \right)\) là:
 Xem đáp án
Xem đáp án
Phương pháp giải
- Sử dụng công thức hạ bậc:
\(2{\cos ^2}x = 1 + \cos 2x\)
\(2{\sin ^2}x = 1 - \cos 2x.\)
Lời giải
Ta có:
\(4{\sin ^2}\frac{x}{2} - \sqrt 3 \cos 2x = 1 + 2{\cos ^2}\left( {x - \frac{{3\pi }}{4}} \right)\)
\( \Leftrightarrow 2(1 - \cos x) - \sqrt 3 \cos 2x = 1 + 1 + \cos \left( {2x - \frac{{3\pi }}{2}} \right)\)
\( \Leftrightarrow - 2\cos x = \sqrt 3 \cos 2x - \sin 2x\)
\( \Leftrightarrow - \cos x = \frac{{\sqrt 3 }}{2}\cos 2x - \frac{1}{2}\sin 2x\)
\( \Leftrightarrow \cos (\pi - x) = \cos \left( {2x + \frac{\pi }{6}} \right)\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\pi - x = 2x + \frac{\pi }{6} + k2\pi }\\{\pi - x = - 2x - \frac{\pi }{6} + k2\pi }\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{{5\pi }}{{18}} - \frac{{k2\pi }}{3}}\\{x = \frac{{ - 7\pi }}{6} + k2\pi }\end{array},k \in \mathbb{Z}.} \right.\)
Vì \(x \in (0;\pi )\) nên ta chỉ chọn \(x = \frac{{5\pi }}{{18}},x = \frac{{17\pi }}{{18}},x = \frac{{5\pi }}{6}\)
Vậy tổng các nghiệm trên khoảng \((0;\pi )\) của phương trình lượng giác là \(\frac{{37\pi }}{{18}}\).
Câu 84:
Chọn mệnh đề đúng trong các mệnh đề sau:
 Xem đáp án
Xem đáp án
Phương pháp giải
-Dựa vào định nghĩa đạo hàm.
Khái niệm đạo hàm
Lời giải
A: \(y = \cos x \Rightarrow y' = - \sin x\) xác định với \(\forall x \in \mathbb{R}\).
B: \(y = \tan x\)
TXĐ: \(\cos x \ne 0\)
\(y' = \frac{1}{{{{\cos }^2}x}}{\rm{ c\'o }}D = \cos x \ne 0.{\rm{ }}\)
C: \(y = \cot x\)
ТХĐ: \(\sin x \ne 0\)
\(y' = - \frac{1}{{{{\sin }^2}x}}{\rm{ c\'o }}D = \sin x \ne 0.{\rm{ }}\)
D:\(y = \frac{1}{{\sin x}} \Rightarrow y' = \frac{{ - \cos x}}{{{{\sin }^2}x}}\) có \(D = \sin x \ne 0\).
Câu 85:
Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là\(f(t) = 30{t^2} - {t^3},\,\,t = 0;1;2;3; \ldots ;20\)
Nếu xem f′(t) là tốc độ truyền bệnh (người/ngày) tại thời điểm t.
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
Tốc độ truyền bệnh vào ngày thứ 4 là 272 (người/ngày) |
¡ |
¡ |
|
Tốc độ truyền bệnh sẽ lớn nhất vào ngày thứ 10 |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
Tốc độ truyền bệnh vào ngày thứ 4 là 272 (người/ngày) |
¡ |
¤ |
|
Tốc độ truyền bệnh sẽ lớn nhất vào ngày thứ 10 |
¤ |
¡ |
Phương pháp giải
a) Tính đạo hàm và thay t = 4 vào
b) Tìm giá trị lớn nhất của f′(t)
Lời giải
Ta có: \(f'(x) = 60t - 3{t^2}\)
a) \(f'(4) = 60.4 - {3.4^2} = 240 - 48 = 192\)
b) Vì tốc độ truyền bệnh tại thời điểm \({\rm{t}}\) là \(f'(x) = 60t - 3{t^2}\)
Nên tốc độ truyện bệnh lớn nhất là giá trị lớn nhất của \(f'(t)\) trên [0;20]
Ta có \( - \frac{b}{{2a}} = - \frac{{60}}{{2.( - 3)}} = 10 \in [0;20]\) nên tốc độ truyền bệnh lớn nhất là:
\(f'(10) = 60.10 - {3.10^2} = 300\) (người/ngày)
Câu 86:
Cho số nguyên tố p để 13p + 1 bằng một số lập phương của số nguyên dương.
Số giá trị của p bằng: ....
 Xem đáp án
Xem đáp án
Phương pháp giải
- Giả sử tồn tại n là số tự nhiên thỏa mãn: 13p + 1 = n3
- Vì 13 và p là số nguyên tố mà và
Lời giải
Giả sử tồn tại n là số tự nhiên thỏa mãn:
Vì 13 và p là số nguyên tố mà và
Nên \(n - 1 > 1\)
Với \(n - 1 = 13 \Rightarrow n = 14 \Rightarrow 13p = 2743 \Rightarrow p = 211\)
Với \(n - 1 = p \Rightarrow 13 = {n^2} + n + 1 \Rightarrow n = 3 \Rightarrow p = 2\)
Vậy có 2 giá trị của p thỏa mãn bài toán.
Câu 87:
Tìm \(n \in {N^*}\) để: \({n^{2003}} + {n^{2002}} + 1\) là số nguyên tố.
Giá trị của n là ....
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng tính chất: \({a^n} - 1 \vdots (a - 1)\,\,\forall n \in {\mathbb{N}^*}\)
Lời giải
Ta có: \({n^{2003}} + {n^{2002}} + 1 = {n^2}\left( {{n^{2001}} - 1} \right) + n\left( {{n^{2001}} - 1} \right) + {n^2} + n + 1\).
Với \(n > 1\) ta có :
\({n^{2001}} - 1 = {\left( {{n^3}} \right)^{667}} - 1\) chia hết cho \({n^3} - 1\) nên chia hết cho \({n^2} + n + 1\)
Do đó : \({n^{2003}} + {n^{2002}} + 1:{n^2} + n + 1\) và \({n^2} + n + 1 > 1\) nên \({n^{2003}} + {n^{2002}} + 1\) là hợp số.
Với \(n = 1\) thì \({n^{2003}} + {n^{2002}} + 1 = 3\) là số nguyên tố.
Câu 88:
Một vật chuyển động với quãng đường \(s(t) = - {t^3} + 12{t^2}\), với t là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s là quãng đường vật di chuyển được trong khoảng thời gian t. Hỏi trong khoảng thời gian 10 giây kể từ khi bắt đầu chuyển động, vật đạt được vận tốc lớn nhất bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Phương pháp giải
Bước 1: Tìm hàm v(t) = s′(t).
Bước 2: Tìm hàm v′(t).
Bước 3: Tìm nghiệm của phương trình v′(t) = 0.
Bước 4: Lập bảng biến thiên của hàm v(t), tính \(\mathop {\max }\limits_{[0;10]} v(t)\) và kết luận.
Lời giải
Ta có v(t) = s′(t) = −3t2 + 24t và v′(t) = −6t+24
Cho v′(t) = 0 ⇔ −6t + 24 = 0 ⇔ t = 4.
Bảng biến thiên:
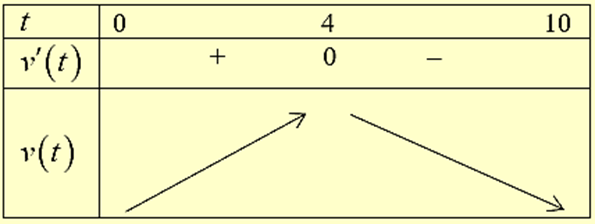
Quan sát bảng biến thiên, ta thấy \(\mathop {\max }\limits_{[0;10]} v(t) = v\left( 4 \right) = 48\).
Vậy vật đạt được vận tốc lớn nhất bằng 48 m/s.
Do đó ta chọn phương án C.
Câu 89:
Cho dãy số \(\left( {{u_n}} \right)\) được xác định bởi \(\left\{ {\begin{array}{*{20}{l}}{{u_1} = 1,{u_2} = 3}\\{{u_{n + 2}} = 2{u_{n + 1}} - {u_n} + 1,\forall n \in {\mathbb{N}^*}}\end{array}} \right.\). Khi đó giá trị của \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{n^2}}}\) được viết dưới dạng \(\frac{a}{b}\,\,(a,b \in \mathbb{Z},b \ne 0)\) và \(\frac{a}{b}\) tối giản.
Tổng a+b bằng
 Xem đáp án
Xem đáp án
Phương pháp giải
Biểu diễn un − u1 theo n.
Lời giải
Ta có: \({u_{n + 2}} - {u_{n + 1}} = {u_{n + 1}} - {u_n} + 1,\,\,n = 1,2,3, \ldots \)
\( \Rightarrow {u_{n + 2}} - {u_{n + 1}} = {u_{n + 1}} - {u_n} + 1 = {u_n} - {u_{n - 1}} + 2 = \ldots = {u_2} - {u_1} + n\)
Do đó
\({u_n} - {u_1} = \left( {{u_n} - {u_{n - 1}}} \right) + \left( {{u_{n - 1}} - {u_{n - 2}}} \right) + \ldots + \left( {{u_2} - {u_1}} \right) = (n) + (n - 1) + \ldots + (2)\)
\( \Rightarrow {u_n} = 1 + 2 + \ldots + n = \frac{{n(n + 1)}}{2} \Rightarrow \mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{n} = \mathop {\lim }\limits_{n \to + \infty } \frac{{n(n + 1)}}{{2{n^2}}} = \frac{1}{2}\)
Vậy \(a + b = 3\)
Câu 90:
Giới hạn \(I = \mathop {\lim }\limits_{x \to + \infty } \sqrt {{x^6} + 5x - 1} \) bằng
 Xem đáp án
Xem đáp án
Đáp án
Giới hạn \(I = \mathop {\lim }\limits_{x \to + \infty } \sqrt {{x^6} + 5x - 1} \) bằng
Phương pháp giải
Lời giải
\(I = \mathop {\lim }\limits_{x \to + \infty } \sqrt {{x^6} + 5x - 1} = \mathop {\lim }\limits_{x \to + \infty } \left| {{x^3}} \right|\sqrt {1 + \frac{5}{{{x^5}}} - \frac{1}{{{x^6}}}} = \mathop {\lim }\limits_{x \to + \infty } {x^3}\sqrt {1 + \frac{5}{{{x^5}}} - \frac{1}{{{x^6}}}} = + \infty \)
Câu 91:
Chọn đáp án thích hợp:
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
251 − 1 không chia hết cho 7. |
¡ |
¡ |
|
Số dư khi chia 2100 cho 9 là 7 |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
251 − 1 không chia hết cho 7. |
¡ |
¤ |
|
Số dư khi chia 2100 cho 9 là 7 |
¤ |
¡ |
Phương pháp giải
Sử dụng tính chất \({a^n} - {b^n} \vdots a - b\).
Lời giải
a) Ta có \({2^{51}} - 1 = {\left( {{2^3}} \right)^{17}} - 1 \vdots {2^3} - 1 = 7\)
b) Ta có \({2^{100}} = {2.2^{99}} = 2{\left( {{2^3}} \right)^{33}} = 2{(9 - 1)^{33}} = 2.(B(9) - 1) = 2.B(9) - 2 = B(9) + 7.\)
Câu 92:
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
|
|
ĐÚNG |
SAI |
|
Chữ số tận cùng của \({4^{{3^2}}}\)là 4. |
¡ |
¡ |
|
Số dư của 250 + 4165 khi chia cho 7 là 5. |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
|
ĐÚNG |
SAI |
|
Chữ số tận cùng của \({4^{{3^2}}}\)là 4. |
¤ |
¡ |
|
Số dư của 250 + 4165 khi chia cho 7 là 5. |
¡ |
¤ |
Phương pháp giải
Áp dụng công thức
\(a \equiv b\,\,(\bmod \,\,m) \Rightarrow {a^n} \equiv {b^n}\,\,(\bmod \,\,m)\)
Lời giải
a) Vì \({4^2} \equiv 6\,\,(\bmod \,\,10)\) nên \({4^{{3^2}}} = {4^9} = {\left( {{4^2}} \right)^4}.4 \equiv 6.4 \equiv 4\,\,(\bmod \,\,10)\)
=> chữ số tận cùng là 4.
b)
\({2^3} \equiv 1\,\,(\bmod \,\,7) \Rightarrow {2^{50}} = {\left( {{2^3}} \right)^{16}}.4 \equiv 4\,\,(\bmod \,\,7)\)
\(41 \equiv - 1\,\,(\bmod \,\,7) \Rightarrow {41^{65}} = {( - 1)^{16}} \equiv - 1\,\,(\bmod \,\,7)\)
\( \Rightarrow {2^{50}} + {41^{65}} \equiv 4 - 1 \equiv 3\,\,(\bmod \,\,7)\)
