Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 14)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 14)
-
434 lượt thi
-
84 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
Theo bài viết, vì sao nhà dân tộc học người Pháp Condominas lại có nhiều công trình nghiên cứu và thành tựu liên quan tới Tây Nguyên?
 Xem đáp án
Xem đáp án
Giải thích
Xác định thông tin cần tìm nằm trong đoạn [0]: “nơi đây níu chân Condominas suốt từ năm 1948 bởi vẻ hoang sơ đầy ma mị.”; cụm từ “hoang sơ và ma mị” có ý diễn giải đây là vùng đất chưa có nhiều người biết tới và Condominas đã dành nhiều thời gian để tìm hiểu về nơi này.
Chọn A
Câu 2:
 Xem đáp án
Xem đáp án
Giải thích
Đọc và xác định thông tin trong đoạn [1] của văn bản, cần phân biệt đặc điểm của ngôi nhà và không gian sống mà tác giả cảm nhận được khi tới nơi đây: “được làm bằng gỗ, cất sát mặt đất, khác với những ngôi nhà “cao cẳng”, phía dưới có gầm trống chăn nuôi gia súc của người Bana Chăm (Chăm - H’roi) vùng núi Phú Yên”
Chọn B
Câu 3:
 Xem đáp án
Xem đáp án
Giải thích
Đọc và xác định thông tin trong đoạn [2] của bài viết, cần chú ý phân biệt tục của người K’Ho và người Việt (người Kinh): “Đêm đầu tiên, Người đưa tin dặn tôi không được nằm quay chân ra cửa. Trong bụng nghĩ thầm, cha này đúng là nhiễu sự! Nằm quay chân hay đầu vào đâu có khác gì nhau! Sự thật không phải lúc nào cũng như vậy. Người Việt có tập tục không được nằm quay chân vào bàn thờ.”
Chọn A
Câu 4:
 Xem đáp án
Xem đáp án
Giải thích
Đọc và xác định thông tin trong đoạn [3] của bài viết: “Thần linh chẳng hề trú ngụ bên trong các di tượng, không có một hình tướng cụ thể nào để tạm trú hay tạm vắng sau nghi thức hành lễ, kể cả Yang, vị chúa tể có quyền uy bao trùm đời sống tinh thần cũng chỉ ẩn hiện trong cõi vô hình”; từ đó có thể thấy, với con người Tây Nguyên, các vị thần tồn tại trong ý niệm và tưởng tượng, không có một hình dáng cụ thể.
Chọn B
Câu 5:
Ở Tây Nguyên, mỗi vị thần đều bắt nguồn và tồn tại, biến đổi trong tâm thức con người vừa bằng niềm tin vào sức mạnh vừa bằng nỗi sợ vô hình là đúng hay sai?
 Xem đáp án
Xem đáp án
Đáp án
A. Đúng.
Giải thích
Đọc và xác định thông tin trong đoạn [3] của bài viết: “Yang không thuần túy là một đơn vị thần, mà tập hợp nhiều thần linh, có lúc là Yang Bri (thần rừng), Yang Bnơm (thần núi), Yang hiu (thần nhà) hay Yang mat tơngai (thần mặt trời)… Tất cả các vị thần này đều có chung một đặc điểm: không hiện hữu”; từ đó có thể thấy, các vị thần đều gắn với những ước mơ và nỗi sợ của con người và sự kì bí của thiên nhiên.
Câu 6:
 Xem đáp án
Xem đáp án
Giải thích
Đọc và xác định thông tin trong đoạn [4] của văn bản: Bài học đầu tiên về kỹ năng lắng nghe qua màn nghi thức vô cùng giản dị. Rồi già tắm cho trẻ, lấy rượu đổ từ trên đầu xuống, những thành viên khác bắt đầu tấu chiêng, thổi M’buốt nhằm truyền đi thứ âm thanh linh diệu vào tai đứa bé. Cần chú ý nghi thức Thổi tai chính là nghi thức đầu tiên mà con người tham gia.
Chọn C
Câu 7:
 Xem đáp án
Xem đáp án
Giải thích
Đọc và xác định thông tin trong đoạn [4] của bài viết: Ẩn hiện qua lớp màn tập quán sinh hoạt cộng đồng, lễ hội là những dạng thức văn hóa tập thể, chan chứa nét hồn nhiên, cộng cảm để từ đó, các vị thần bước ra; từ đó có thể thấy việc thực hiện các nghi thức, nghi lễ chính là cách để con người đặt niềm tin vào thần linh, dựng nên nền tảng về thế giới thần linh luôn hiện hữu.
Chọn A
Câu 8:
Trong nghi lễ Thổi tai của người Stiêng, người già đọc lời cúng trước khi thực hiện nghi thức đổ rượu qua đầu đứa trẻ là đúng hay sai?
 Xem đáp án
Xem đáp án
Đáp án
B. Sai.
Giải thích
Đọc lại thông tin trong đoạn [4] của bài viết: già làng (người có chức sắc, được coi là linh hồn của làng) mới là người thực hiện nghi thức. Chú ý phân biệt “người già” và “già làng”.
Câu 9:
Tìm một từ thích hợp (không quá hai tiếng) để hoàn thành câu văn sau:
Trong nghi thức thách cưới của người Stiêng, nhà trai mang đến nhà gái những lễ vật tượng ứng cho rượu, heo, trâu...; đó là những sính lễ chứa đựng (1) ______ của mỗi người và nhờ đó con người chạm vào cõi vô hình, thế giới nơi thần linh trú ngụ.
 Xem đáp án
Xem đáp án
Đáp án
Tìm một từ thích hợp (không quá hai tiếng) để hoàn thành câu văn sau:
Trong nghi thức thách cưới của người Stiêng, nhà trai mang đến nhà gái những lễ vật tượng ứng cho rượu, heo, trâu...; đó là những sính lễ chứa đựng (1) niềm tin của mỗi người và nhờ đó con người chạm vào cõi vô hình, thế giới nơi thần linh trú ngụ.
Giải thích
Đọc và xác định thông tin trong đoạn [5] của bài viết: “Tất cả chỉ mang ý nghĩa tượng trưng, căn cứ vào số lượng que, nhà trai sẽ mang đến cho nhà gái những lễ vật tương ứng với rượu, heo, trâu… Và giá trị thực của món quà nhận được còn tùy thuộc vào niềm tin trong tâm hồn mỗi người. Nhờ vậy, người ta đã chạm vào cõi vô hình, tạo tiền đề dựng nên miền huyễn tưởng, thế giới cho thần linh trú ngụ.”
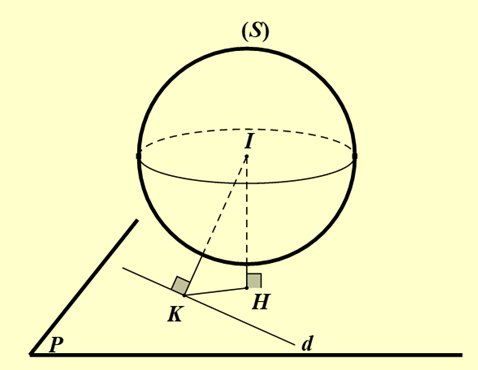
Câu 10:
 Xem đáp án
Xem đáp án
Giải thích
Nội dung chính của bài viết là cuộc hành trình của người viết (tác giả) đến vùng Tây Nguyên, nơi ông/ông bắt đầu khám phá và tìm hiểu về nền văn hóa và tâm linh của người dân địa phương, đặc biệt là nghi thức thách cưới của người Stiêng. Bài viết tập trung vào việc trình bày và mô tả những trải nghiệm và quan sát của tác giả trong cuộc hành trình này, đồng thời thảo luận về ý nghĩa của các nghi thức và tín ngưỡng tâm linh trong văn hóa của người dân Tây Nguyên.
Chọn B
Câu 11:
Theo đoạn [1], công ti khởi nghiệp muốn biến carbon dioxide thành protein vì không thể loại bỏ lượng khí thải đó trong bầu khí quyển. Đúng hay sai?
 Xem đáp án
Xem đáp án
Đáp án
B. Sai
Giải thích
Đọc lại nội dung đoạn [1] xác định nội dung quan trọng: “bơm carbon dioxide vào bầu khí quyển”, “cơ hội có lợi nhuận khá thấp”, “biến carbon dioxide thành protein”. Nội dung đoạn [1] có nêu lên vấn đề: nhiều công ti/doanh nghiệp đưa ra giải pháp loại bỏ carbon dioxide nhưng sự khác biệt khi biến carbon dioxide thành protein chính là “lợi nhuận”.
Câu 12:
Dựa vào đoạn [2], hãy điền một cụm từ không quá hai tiếng để hoàn thành nhận định sau:
Đẩy mạnh những tiến bộ về (1) _____, công ti NovoNutrients đầu tư trang thiết bị kĩ thuật cao, tìm ra cơ sở trong quá trình trao đổi chất của vi khuẩn, sử dụng khí thải làm năng lượng.
 Xem đáp án
Xem đáp án
Đáp án
Dựa vào đoạn [2], hãy điền một cụm từ không quá hai tiếng để hoàn thành nhận định sau:
Đẩy mạnh những tiến bộ về (1) công nghệ, công ti NovoNutrients đầu tư trang thiết bị kĩ thuật cao, tìm ra cơ sở trong quá trình trao đổi chất của vi khuẩn, sử dụng khí thải làm năng lượng.
Giải thích
Đọc lại đoạn [2] và xác định thông tin, chú ý nội dung: “dựa vào vi khuẩn để làm công việc bẩn thỉu. Công ti đã khảo sát các tài liệu khoa học để tìm ra những loài có thể sử dụng carbon dioxide trong quá trình trao đổi chất của chúng, cho phép chúng sử dụng khí thải làm năng lượng” và “công nghiệp hóa quá trình trao đổi chất” nên từ cần điền là “công nghệ”.
Câu 13:
 Xem đáp án
Xem đáp án
Giải thích
Đọc kĩ đoạn [2] để hiểu được: “công việc bẩn thỉu” do vi khuẩn thực hiện: “NovoNutrients dựa vào vi khuẩn để làm công việc bẩn thỉu”, “sử dụng carbon dioxide trong quá trình trao đổi chất của chúng, cho phép chúng sử dụng khí thải làm năng lượng”.
Chọn D
Câu 14:
Hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí:
hoạt đồng, đậm đặc, tái tạo, chế tạo
Việc phát triển các lò phản ứng sinh học trở thành yêu cầu cấp thiết và nguyên liệu chính là cacbon dioxide _______- sản phẩm từ bất kì _______ gây ô nhiễm nào trong đời sống và từ đó _______ thành nhiều sản phẩm khác nhau.
 Xem đáp án
Xem đáp án
Đáp án
Việc phát triển các lò phản ứng sinh học trở thành yêu cầu cấp thiết và nguyên liệu chính là cacbon dioxide đậm đặc - sản phẩm từ bất kì hoạt động gây ô nhiễm nào trong đời sống và từ đó tái tạo thành nhiều sản phẩm khác nhau.
Giải thích
Căn cứ vào từ khoá “lò phản ứng sinh học”, đọc lại nội dung đoạn [3] và tìm thông tin thích hợp: “Nguồn gốc của carbon dioxide có thể là bất kì hoạt động nào đang gây ô nhiễm ngày nay, cho dù đó là hoạt động dầu khí, nhà máy hóa chất, nhà máy phân bón hay nhà máy xi măng. Tất cả những gì cần thiết là cung cấp đủ carbon dioxide đậm đặc. Mặt khác, các nhà máy của NovoNutrients sẽ sản xuất một loại bột khô có thể được tinh chế thành một số sản phẩm khác nhau, bao gồm chất bổ sung protein cho người, động vật và cá nuôi”.
Việc phát triển các lò phản ứng sinh học trở thành yêu cầu cấp thiết và nguyên liệu chính là cacbon dioxide [đậm đặc] - sản phẩm từ bất kì [hoạt động] gây ô nhiễm nào trong đời sống và từ đó [tái tạo] thành nhiều sản phẩm khác nhau.
Câu 15:
 Xem đáp án
Xem đáp án
Giải thích
Căn cứ vào từ khóa “cải thiện hiệu suất” xác định được nội dung cần tìm nằm ở đoạn [4]: “Một cách khác mà công ti khởi nghiệp có thể tăng sản lượng là sử dụng nhiều chủng khác nhau trong một bể”. Chú ý “công ti khởi nghiệp” chính là NovoNutrients và “chủng” ở đây là các chủng vi khuẩn.
Chọn C
Câu 16:
Hãy điền một cụm từ không quá ba tiếng để hoàn thành nhận định sau:
Bên cạnh các mục tiêu thương mại, NovoNutrients hướng tới việc cung cấp (1) _____ cho các doanh nghiệp và đào tạo quy trình hoạt động cho những cơ sở có nhu cầu sử dụng công nghệ này.
 Xem đáp án
Xem đáp án
Đáp án
Hãy điền một cụm từ không quá ba tiếng để hoàn thành nhận định sau:
Bên cạnh các mục tiêu thương mại, NovoNutrients hướng tới việc cung cấp (1) giải pháp cho các doanh nghiệp và đào tạo quy trình hoạt động cho những cơ sở có nhu cầu sử dụng công nghệ này.
Giải thích
Đọc lại nội dung đoạn [5] xác định: “bán các vi khuẩn để duy trì hoạt động của mọi thứ”, “lấy tiền bản quyền giấy phép công nghệ”, “cung cấp toàn bộ gói công nghệ”, “đào tạo nhân viên điều hành và sẽ sẵn sàng hỗ trợ.”. Mục tiêu của doanh nghiệp ngoài kinh doanh chính là cung cấp các giải pháp cho doanh nghiệp cần tới công nghệ.
Câu 17:
 Xem đáp án
Xem đáp án
Giải thích
Căn cứ vào từ khóa “cung cấp”, “đối tác” để xác định nội dung cần tìm nằm ở đoạn [5]: “Và tất nhiên, chúng tôi sẽ cung cấp toàn bộ gói công nghệ - cả sinh học và phần cứng” (đáp án A); “làm việc với các công ti xây dựng mua sắm kĩ thuật, do đối tác được cấp phép của chúng tôi lựa chọn để xây dựng công trình đó” (đáp án D); “Chúng tôi sẽ đào tạo nhân viên điều hành” (đáp án B).
Sử dụng phương pháp loại trừ, chọn đáp án C. Thông tin trong đoạn là “công ti đối tác sẽ quyết định sản phẩm nào họ muốn sản xuất” chứ không phải do NovoNutrients quyết định.
Chọn C
Câu 18:
Hãy hoàn thành các câu sau đây bằng cách kéo thả các từ vào đúng vị trí:
công nghệ, thu mua, cung cấp, tiêu dùng
Công ti NovoNutrients lấy _______ làm trung tâm và cấp phép cho công nghệ cốt lõi của mình. Với vai trò là một công ti _______ dịch vụ, NovoNutrients tư vấn cho các công ti đối tác về quy trình xây dựng, vận hành và hỗ trợ tiếp cận người _______.
 Xem đáp án
Xem đáp án
Đáp án
Hãy hoàn thành các câu sau đây bằng cách kéo thả các từ vào đúng vị trí:
Công ti NovoNutrients lấy công nghệ làm trung tâm và cấp phép cho công nghệ cốt lõi của mình. Với vai trò là một công ti cung cấp dịch vụ, NovoNutrients tư vấn cho các công ti đối tác về quy trình xây dựng, vận hành và hỗ trợ tiếp cận người tiêu dùng.
Câu 19:
 Xem đáp án
Xem đáp án
Giải thích
Đọc kĩ đoạn [6] để xác định nội dung chính: “Cách tiếp cận cấp phép và dịch vụ có thể hạn chế tăng doanh thu cuối cùng, nhưng nó chắc chắn hạn chế rủi ro vốn” cho thấy, các doanh nghiệp gặp thất bại do sự kì vọng tạo nên chuỗi cung ứng toàn bộ, thiếu sự hợp tác chiến lược, chọn A.
Câu 20:
 Xem đáp án
Xem đáp án
Giải thích
Đọc nội dung nhan đề và đoạn [1] xác định mục đích chính của bài viết: “dành một thế kỉ rưỡi qua để bơm carbon dioxide vào bầu khí quyển”, “dành những thập kỉ tới để loại bỏ một phần đáng kể lượng đó”, “Nhưng sau đó chúng ta sẽ làm gì với tất cả?” và “Một công ti khởi nghiệp nghĩ rằng câu trả lời là biến carbon dioxide thành protein.” nên Từ khóa đúng là C.
Chọn C
Câu 21:
Phần tư duy khoa học, giải quyết vấn đề
Phát biểu sau đây đúng hay sai?
Hai thí nghiệm trên, vi khuẩn đều được nuôi cấy trong môi trường nuôi cấy liên tục.
 Xem đáp án
Xem đáp án
Đáp án
B. Sai
Giải thích
Sai. Vì môi trường nuôi cấy liên tục phải luôn được bổ sung chất dinh dưỡng, đồng thời lấy đi lượng dịch nuôi cấy tương đương. Mà trong hai thí nghiệm trên thì không có sự bổ sung dinh dưỡng, cũng không lấy ra lượng dịch nuôi cấy nào, quần thể vi khuẩn phát triển trên môi trường dinh dưỡng ban đầu, cho đến khi sử dụng hết chất dinh dưỡng – đây là dạng nuôi cấy không liên tục.
Câu 22:
 Xem đáp án
Xem đáp án
Giải thích
Theo đoạn thông tin: “..., biết rằng độ đục càng tăng thì lượng vi khuẩn phát triển càng mạnh và giá trị đo được càng lớn.”
Chọn C
Câu 23:
 Xem đáp án
Xem đáp án
Giải thích
Nhóm 1 thí nghiệm trong điều kiện: pH = 6 với các nhiệt độ khác nhau.
Nhóm 2 thí nghiệm trong điều kiện: nhiệt độ 37℃ với độ pH khác nhau.
→ Nhóm vi khuẩn được nuôi cấy trong cùng điều kiện là có độ pH = 6 và nhiệt độ 37℃.
Chọn B
Câu 24:
Điền từ/cụm từ vào chỗ trống sau đây:
Khi cạn kiệt chất dinh dưỡng, vi khuẩn sẽ bắt đầu pha (1) ________.
 Xem đáp án
Xem đáp án
Đáp án
Điền từ/cụm từ vào chỗ trống sau đây:
Khi cạn kiệt chất dinh dưỡng, vi khuẩn sẽ bắt đầu pha (1) suy vong.
Giải thích
Trong môi trường nuôi cấy không liên tục, quần thể vi khuẩn sẽ trải qua 4 pha: tiềm phát, lũy thừa, cân bằng, suy vong. Khi cạn kiệt chất dinh dưỡng, vi khuẩn sẽ bắt đầu pha suy vong, làm cho số lượng vi khuẩn giảm xuống nhanh chóng.
Câu 25:
 Xem đáp án
Xem đáp án
Giải thích
Nhìn vào số liệu bảng 2, ta thấy tại môi trường dinh dưỡng có độ pH = 3 và pH = 9 thì không thấy sự thay đổi của giá trị độ đục ↔ không có sự sinh trưởng của quần thể vi khuẩn.
Chọn C
Câu 26:
 Xem đáp án
Xem đáp án
Giải thích
Nhìn vào số liệu bảng 1, ta thấy S. Aureus phát triển nhanh nhất để đạt độ đục cao nhất tại 37℃ (0,800) cao hơn nhiều so với các nhóm khác nên tại 37℃ chủng vi khuẩn này phát triển tối ưu.
Chọn B
Câu 27:
Phát biểu sau đây đúng hay sai?
Trong thí nghiệm của nhóm 1, ở nhiệt độ 37℃, pha cân bằng có thể bắt đầu sau 10 giờ kể từ khi nuôi cấy.
 Xem đáp án
Xem đáp án
Đáp án
A. Đúng
Giải thích
Đúng. Nhìn vào số liệu bảng 1 ở nhiệt độ 37℃, ta thấy ở giai đoạn 600 phút (= 10 giờ) trở đi thì số lượng vi khuẩn có xu hướng chững lại, không tăng (duy trì ở mức cân bằng). Do lượng dinh dưỡng bắt đầu cạn kiệt, chất độc hại tích lũy nhiều, tỉ lệ vi khuẩn sinh ra cân bằng với tỉ lệ vi khuẩn chết đi.
Câu 28:
 Xem đáp án
Xem đáp án
Giải thích
Theo phần dẫn ta có, để đặc trưng cho mức độ làm việc của động cơ nhiệt là hiệu suất nhiệt: \(e = \frac{{\left| A \right|}}{{\left| {{Q_1}} \right|}}\)
→ Khi Q1 không đổi, để e càng lớn thì A càng lớn, hay nói cách khác Mục đích của một động cơ nhiệt là càng nhiều nhiệt lượng nhận từ nguồn nhiệt Q1 chuyển thành công càng tốt.
Chọn A
Câu 29:
Phát biểu nào sau đây là đúng hoặc sai?
|
Phát biểu |
Đúng |
Sai |
|
Nhiệt kế rượu được sử dụng để ghi lại sự thay đổi nhiệt độ của không khí trong các thử nghiệm. |
||
|
Khi thiết bị làm mát được đặt ở chế độ để làm mát nước đến nhiệt độ 10°C thì nhiệt độ của nước thay đổi nhanh nhất trong khoảng thời gian từ 0 – 100 phút. |
||
|
Trong các thử nghiệm, nhiệt độ thay đổi chậm lúc đầu và nhanh hơn theo thời gian. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Nhiệt kế rượu được sử dụng để ghi lại sự thay đổi nhiệt độ của không khí trong các thử nghiệm. |
X | |
|
Khi thiết bị làm mát được đặt ở chế độ để làm mát nước đến nhiệt độ 10°C thì nhiệt độ của nước thay đổi nhanh nhất trong khoảng thời gian từ 0 – 100 phút. |
X | |
|
Trong các thử nghiệm, nhiệt độ thay đổi chậm lúc đầu và nhanh hơn theo thời gian. |
X |
Giải thích
Trong đoạn thứ ba của phần dẫn, ta thấy rằng sự thay đổi nhiệt độ được đo bằng nhiệt kế thủy ngân → (1) sai.
Trong mọi cài đặt nhiệt độ của các thử nghiệm, nhiệt độ thay đổi nhanh nhất lúc đầu và chậm hơn theo thời gian. Theo Hình 2, đối với thử nghiệm làm mát nước mặn ở xuống nhiệt độ 10°C thì từ 0 - 100 phút, nhiệt độ nước mặn giảm từ 50°C lên khoảng 31°C, thay đổi 19°C → (2) đúng, (3) sai
Câu 30:
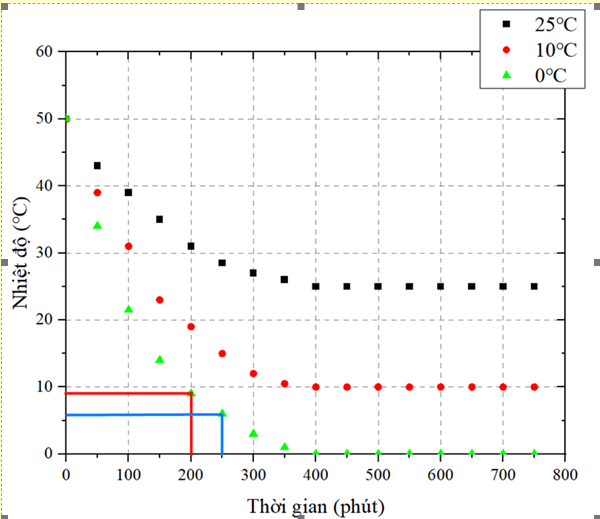
Trong thử nghiệm làm mát nước mặn, khi bộ làm mát của máy lạnh được đặt ở chế độ để làm mát nước đến nhiệt độ 0℃ thì trong 220 phút nhiệt độ của nước là
 Xem đáp án
Xem đáp án
Kết quả trong các thử nghiệm làm mát nước mặn được thể hiện trong Hình 2.
Từ đồ thị, ta thấy sau 200 phút, nhiệt độ nước mặn là khoảng 9℃, và ở 250 phút nhiệt độ khoảng 6℃. Do đó, ở 220 phút, nhiệt độ của nước nằm trong khoảng từ 5°C đến 8°C. Chọn D
Câu 31:
phòng cần làm lạnh, không khí bên ngoài, motor của máy lạnh
Trong máy điều hòa không khí, nguồn nhiệt độ thấp là ______, nguồn nhiệt độ cao là ______ và công là do ______ thực hiện.
 Xem đáp án
Xem đáp án
Đáp án
Trong máy điều hòa không khí, nguồn nhiệt độ thấp là phòng cần làm lạnh, nguồn nhiệt độ cao là không khí bên ngoài và công là do motor của máy lạnh thực hiện.
Câu 32:
Kéo thả từ/cụm từ vào vị trí thích hợp:
thấp, cao
Trong tủ lạnh của gia đình, nguồn nhiệt độ _______ là buồng chứa thực phẩm, nguồn có nhiệt độ _______ là phòng, nơi đặt tủ lạnh.
 Xem đáp án
Xem đáp án
Đáp án
Trong tủ lạnh của gia đình, nguồn nhiệt độ thấp là buồng chứa thực phẩm, nguồn có nhiệt độ cao là phòng, nơi đặt tủ lạnh.
Câu 33:
Tủ lạnh của gia đình bạn Hoa có hiệu suất K là 4,7. Tủ lạnh lấy nhiệt từ buồng lạnh với tốc độ 250 J trong mỗi chu trình. Công mà hệ thực hiện được trong một chu trình để nó hoạt động có độ lớn là (1) ________J. (Làm tròn đến chữ số thập phân thứ nhất)
 Xem đáp án
Xem đáp án
Đáp án
Tủ lạnh của gia đình bạn Hoa có hiệu suất K là 4,7. Tủ lạnh lấy nhiệt từ buồng lạnh với tốc độ 250 J trong mỗi chu trình. Công mà hệ thực hiện được trong một chu trình để nó hoạt động có độ lớn là (1) __ 53,2 __ J. (Làm tròn đến chữ số thập phân thứ nhất)
Giải thích
Từ khóa: 53,2 J
Ta có: \[K = \frac{{\left| {{Q_2}} \right|}}{{|A|}} = \frac{{250}}{{4,7}} = 53,2J\]
→ Công mà hệ thực hiện được trong một chu trình để nó hoạt động có độ lớn là 53,2 J.
Câu 34:
Một động cơ ô tô có hiệu suất nhiệt là 22% chuyển động được 95 chu trình trong thời gian một giây và thực hiện một công là 120 HP. Biết rằng 1HP = 746W. Phát biểu nào sau đây là đúng hoặc sai?
|
Phát biểu |
Đúng |
Sai |
|
Công thực hiện trong mỗi chu trình là 942 J. |
||
|
Động cơ nhận năng lượng 3340 J trong mỗi chu trình. |
||
|
Năng lượng mà động cơ thải ra lớn gấp 3,6 lần năng lượng biến thành có ích. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Công thực hiện trong mỗi chu trình là 942 J. |
X | |
|
Động cơ nhận năng lượng 3340 J trong mỗi chu trình. |
X | |
|
Năng lượng mà động cơ thải ra lớn gấp 3,6 lần năng lượng biến thành có ích. |
X |
Giải thích
Công thực hiện trong mỗi chu trình là: \(A = \frac{P}{t} = \frac{{120.746}}{{95}} = 942,32J\)
Năng lượng mà động cơ nhận được ở nguồn nóng: \({Q_1} = \frac{A}{e} = \frac{{942,32}}{{0,22}} = 4283,3J\)
Mặt khác, ta có: \(\left| {{Q_2}} \right| = \left| {{Q_1}} \right| - |A| = 4283,3 - 942,32 = 3340,98\;{\rm{J}}\)
→ Nhiệt thải ra khỏi động cơ là: \({Q_2} = - 3340,98\;{\rm{J}}\)
Năng lượng mà động cơ thải ra gấp \(\frac{{3340,98}}{{942,32}} \approx 3,55\) lần năng lượng biến thành năng lượng có ích.
Câu 35:
Phát biểu sau đúng hay sai?
Theo quan điểm của học sinh 3, mẫu A và B được tạo thành từ cùng một chất.
 Xem đáp án
Xem đáp án
Đáp án
A. Đúng
Giải thích
Văn bản đã cung cấp thông tin về quan điểm của học sinh 3: “Nếu hai mẫu có cùng khối lượng, thể tích, khối lượng riêng thì chúng được tạo thành từ cùng một chất”. So sánh dữ liệu ở Bảng 1, mẫu A và B có cùng khối lượng, thể tích, khối lượng riêng, do đó theo quan điểm của học sinh 3, mẫu A và B được tạo thành từ cùng một chất.
Câu 36:
Điền số thích hợp vào chỗ trống
Các số liệu về khối lượng, thể tích và khối lượng riêng của các mẫu A – H trong Bảng 1 được xác định tại nhiệt độ (1) ________ oC.
 Xem đáp án
Xem đáp án
Đáp án
Điền số thích hợp vào chỗ trống
Các số liệu về khối lượng, thể tích và khối lượng riêng của các mẫu A – H trong Bảng 1 được xác định tại nhiệt độ (1) __ 20 __ oC.
Giải thích
Văn bản đã cung cấp thông tin: “Khối lượng, thể tích và khối lượng riêng được xác định ở 20oC”.
Câu 37:
 Xem đáp án
Xem đáp án
Giải thích
Dựa vào Bảng 1, nhận thấy mẫu B và C chỉ giống nhau ở khối lượng riêng.
Chọn A
Câu 38:
Điền từ/cụm từ thích hợp vào chỗ trống
Giả sử nhiệt độ của mẫu D tăng lên 890°C ở áp suất 1 atm, lúc này mẫu D sẽ chuyển sang thể khí. Khối lượng riêng của mẫu sẽ (1) ________ so với ở 20°C và 1 atm.
 Xem đáp án
Xem đáp án
Đáp án
Điền từ/cụm từ thích hợp vào chỗ trống
Giả sử nhiệt độ của mẫu D tăng lên 890°C ở áp suất 1 atm, lúc này mẫu D sẽ chuyển sang thể khí. Khối lượng riêng của mẫu sẽ (1) thấp hơn so với ở 20°C và 1 atm.
Giải thích
Tại nhiệt độ 890℃, mẫu D sẽ là chất khí và tại nhiệt độ 20℃, mẫu D là chất rắn (do điểm nóng chảy của D là 885℃). Chất khí nhẹ hơn chất rắn, do đó câu trả lời là “thấp hơn”.
Câu 39:
 Xem đáp án
Xem đáp án
Giải thích
Văn bản đã cung cấp thông tin về quan điểm của học sinh 1: “Nếu 2 mẫu có cùng giá trị về cả 5 tính chất thì chúng được tạo thành bởi cùng một chất”. So sánh dữ liệu ở Bảng 1, mẫu C và D giống nhau ở cả 5 tính chất, do đó đáp án đúng là C.
Câu 40:
Cho quan điểm sau: “Hai mẫu có cùng khối lượng, thể tích, khối lượng riêng và điểm sôi được tạo thành từ cùng một chất, ngay cả khi chúng có điểm nóng chảy khác nhau”. Học sinh nào trong số học sinh 2 và 4 sẽ có khả năng đồng ý với ý kiến này?
 Xem đáp án
Xem đáp án
Giải thích
Theo quan điểm của học sinh 2, các mẫu phải giống nhau ở 3 tính chất bất kỳ thì mới được cấu tạo từ cùng một chất. Do đó, học sinh 2 sẽ đồng ý với quan điểm trên.
Theo quan điểm của học sinh 4, các mẫu có khối lượng riêng, nhiệt độ nóng chảy và nhiệt độ sôi giống nhau thì chúng được dự đoán tạo thành từ cùng một chất. Nếu bất kỳ tính chất nào trong số các tính chất này khác nhau, thì các mẫu không được tạo thành từ cùng một chất.
Chọn A
Câu 41:
 Xem đáp án
Xem đáp án
Dựa vào đoạn thông tin “...các tế bào của chúng có gen mã hóa beta lactamasecó vai trò giúp vi khuẩn kháng penicillin”.
Chọn A
Câu 42:
Saccharose và lactose thuộc nhóm (1) _________.
 Xem đáp án
Xem đáp án
Đáp án
Saccharose và lactose thuộc nhóm (1) disaccharide.
Giải thích
Saccharose và lactose thuộc nhóm đường đôi (disaccharide).
Câu 43:
 Xem đáp án
Xem đáp án
Giải thích
Nhìn vào bảng kết quả 1, ta thấy tại môi trường chứa lactose vi khuẩn dạng dại không tồn tại và sinh trưởng được, còn ở môi trường chứa glucose và saccharose thì vi khuẩn dạng dại sinh trưởng bình thường tạo ra các thế hệ mới → vi khuẩn dạng dại có khả năng chuyển hóa glucose và saccharose để cung cấp nguồn carbon cần thiết.
Nhìn vào bảng kết quả 2, ta thấy tại môi trường chứa kháng sinh (penicillin và tetracyclin), chủng vi khuẩn dạng dại đều không tồn tại và sinh trưởng nên chúng không có khả năng kháng kháng sinh.
Chọn C
Câu 44:
 Xem đáp án
Xem đáp án
Giải thích
Nước thịt là nguồn hợp chất cung cấp nitrogen hữu cơ cho quần thể vi khuẩn sinh trưởng.
Chọn C
Câu 45:
Điền từ/cụm từ thích hợp vào chỗ trống sau đây:
Sự (1) ________ của quần thể vi sinh vật là sự tăng số lượng tế bào trong quần thể.
 Xem đáp án
Xem đáp án
Đáp án
Điền từ/cụm từ thích hợp vào chỗ trống sau đây:
Sự (1) sinh trưởng của quần thể vi sinh vật là sự tăng số lượng tế bào trong quần thể.
Giải thích
Sự sinh trưởng của quần thể vi sinh vật (vi khuẩn) được định nghĩa là sự tăng lên về số lượng tế bào trong quần thể.
Câu 46:
Kết luận nào dưới đây có thể rút ra từ kết quả thí nghiệm ở bảng 2?
 Xem đáp án
Xem đáp án
Giải thích
Nhìn vào bảng kết quả thí nghiệm 2, ta thấy chủng vi khuẩn dạng dại không sinh trưởng được trên môi trường chứa penicillin, nhưng khi gây nhiễm bởi phage I thì lại có khả năng sinh trưởng, chính vì vậy mà kết luận đúng nhất trong câu trên là phage I mang gen mã hóa cho beta lactamase, làm cho vi khuẩn có khả năng kháng penicillin, để có thể tồn tại và sinh trưởng bình thường trên môi trường chứa penicillin.
Chọn C
Câu 47:
Phát biểu sau đây đúng hay sai?
Tế bào vi khuẩn dạng dại trong tự nhiên không có khả năng kháng lại cả tetracyclin và penicillin.
 Xem đáp án
Xem đáp án
Đáp án
A. Đúng
Giải thích
Đúng. Theo như kết quả ở bảng 2, ta có thể thấy ở trên đĩa chứa tetracyclin và penicillin thì đều không thấy sự sinh trưởng của vi khuẩn dạng dại.
Câu 48:
Phát biểu sau đúng hay sai?
Phương trình phản ứng xảy ra trong thí nghiệm 2 là: 2H2+O2→2H2O.
 Xem đáp án
Xem đáp án
Đáp án
B. Sai
Giải thích
Phương trình: 2H2 + O2 → 2H2O là phương trình xảy ra trong thí nghiệm 1.
Phương trình phản ứng xảy ra trong thí nghiệm 2 là: H2 + CuO Cu + H2O. Chọn B
Câu 49:
Phát biểu sau đúng hay sai?
Sử dụng CuO bị lẫn tạp chất không làm ảnh hưởng đến kết quả của thí nghiệm 2.
 Xem đáp án
Xem đáp án
Đáp án
B. Sai
Giải thích
Nếu CuO bị lẫn tạp chất có phản ứng với H2 thì việc xác định lượng CuO đã phản ứng không còn chính xác, ngoài ra chúng có thể tạo ra các sản phẩm khác mà CaCl2 có thể hấp thụ, ảnh hưởng đến khối lượng cuối cùng của CaCl2 hay khối lượng H2O tạo thành.
Câu 50:
Điền từ/cụm từ thích hợp vào chỗ trống.
Trong thí nghiệm 2, nếu CuO phản ứng với H2 để tạo ra các sản phẩm không phải là H2O thì (1) _______ dùng thí nghiệm này để xác định tính đúng đắn của phản ứng: H2 + CuO Cu + H2O.
 Xem đáp án
Xem đáp án
Đáp án
Điền từ/cụm từ thích hợp vào chỗ trống.
Trong thí nghiệm 2, nếu CuO phản ứng với H2 để tạo ra các sản phẩm không phải là H2O thì (1) không thể dùng thí nghiệm này để xác định tính đúng đắn của phản ứng: H2 + CuO Cu + H2O.
Giải thích
Trong thí nghiệm 2, nếu CuO phản ứng với H2 để tạo ra các sản phẩm không phải là H2O thì không thể dùng thí nghiệm này để xác định tính đúng đắn của phản ứng: H2 + CuO Cu + H2O. Người ta không thể xác định được liệu sự tăng khối lượng của CaCl2 có phải chỉ do H2O gây ra hay không.
Câu 52:
Phát biểu nào sau đây là đúng về phản ứng hóa học trong thí nghiệm 2?
 Xem đáp án
Xem đáp án
Giải thích
A và D sai, vì H2 và O2 không được sử dụng trong thí nghiệm 2.
Phản ứng giữa CuO và H2 chỉ xảy ra khi CuO được nung nóng.
CaCl2 được sử dụng để hấp thụ H2O sinh ra từ phản ứng H2 + CuO Cu + H2O. Từ đó, xác định được khối lượng H2O tạo thành.
Chọn B
Câu 53:
Kéo thả vào vị trí thích hợp:
25ml, 25ml, 0ml, 50ml
Nếu thể tích ban đầu của H2 và O2 lần lượt là 50 ml và 50 ml thì thể tích cuối cùng của O2 sau khi phản ứng xảy ra hoàn toàn là _______.
 Xem đáp án
Xem đáp án
Đáp án
Nếu thể tích ban đầu của H2 và O2 lần lượt là 50 ml và 50 ml thì thể tích cuối cùng của O2 sau khi phản ứng xảy ra hoàn toàn là 25 ml.
Giải thích
Từ phương trình phản ứng và dữ liệu trong Bảng 1 cho thấy H2 và O2 phản ứng theo tỷ lệ 2:1 để tạo thành H2O.
Nếu 50 ml H2 phản ứng với 50 ml O2, thì tất cả 50 ml H2 đều phản ứng, nhưng chỉ có 25 ml O2 phản ứng. Do đó, thể tích O2 còn lại trong ống bơm sẽ là 25 ml.
Câu 54:
Phát biểu sau đúng hay sai?
Hợp chất hữu cơ X có phần trăm khối lượng của các nguyên tố như sau: %C = 45,80%; %H = 10,57%; %N = 13,24%, còn lại là O. Biết MC =12,01 g/mol, MH = 1,008 g/mol và MO = 16,00 g/mol. Công thức kinh nghiệm của X là C4H10NO2.
 Xem đáp án
Xem đáp án
Đáp án
B. Sai
Giải thích
Tỉ số mol nguyên tử, cũng chính là tỉ số nguyên tử của C, H, N và O trong phân tử hợp chất X là:
\[{\rm{nC}}:{\rm{nH}}:{\rm{nN}}:{\rm{nO}} = \frac{{45,80}}{{12,01}}:\frac{{10,57}}{{1,008}}:\frac{{13,24}}{{14,01}}:\frac{{30,39}}{{16,00}} = 3,813:10,49:0,945:1,899\]
Tỉ số nguyên tử được quy về tỉ số của các số nguyên tối giản, bằng cách chia cho số nhỏ nhất trong chúng (0,945), ta thu được công thức kinh nghiệm.
\({\rm{nC}}:{\rm{nH}}:{\rm{nN}}:{\rm{nO}} = \frac{{3,813}}{{0,945}}:\frac{{10,49}}{{0,945}}:\frac{{0,945}}{{0,945}}:\frac{{1,899}}{{0,945}} = 4,03:11,1:1,00:2,01 = 4:11:1:2\)
Công thức kinh nghiệm là C4H11NO2.
Câu 55:
Các phát biểu sau đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Công thức phân tử của methyl formate và glucose lần lượt là C2H4O2 và C6H12O6. Công thức kinh nghiệm của hai chất này là CH2O. |
||
|
Người ta thường xác định tỉ khối của một chất khí X (chưa biết phân tử khối) so với không khí (dX/kk) rồi tính phân tử khối của X theo công thức: MX =26.dX/kk. |
||
|
Trong phương pháp phổ khối lượng, đối với các hợp chất đơn giản, thường mảnh có giá trị m/z lớn nhất ứng với mảnh ion phân tử [M+] và giá trị này bằng giá trị nguyên tử khối của chất nghiên cứu. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Công thức phân tử của methyl formate và glucose lần lượt là C2H4O2 và C6H12O6. Công thức kinh nghiệm của hai chất này là CH2O. |
X | |
|
Người ta thường xác định tỉ khối của một chất khí X (chưa biết phân tử khối) so với không khí (dX/kk) rồi tính phân tử khối của X theo công thức: MX =26.dX/kk. |
X | |
|
Trong phương pháp phổ khối lượng, đối với các hợp chất đơn giản, thường mảnh có giá trị m/z lớn nhất ứng với mảnh ion phân tử [M+] và giá trị này bằng giá trị nguyên tử khối của chất nghiên cứu. |
X |
Giải thích
1. Đúng, vì: (CH2O)2 tương đương với C2H4O2 và (CH2O)6 tương đương với C6H12O6.
Do đó, methyl formate và glucose có cùng công thức kinh nghiệm là CH2O.
2. Sai, vì: người ta thường xác định tỉ khối của một chất khí X (chưa biết phân tử khối) so với không khí (dX/kk) rồi tính phân tử khối của X theo công thức: MX =29.dX/kk.
3. Sai, vì: trong phương pháp phổ khối lượng, đối với các hợp chất đơn giản, thường mảnh có giá trị m/z lớn nhất ứng với mảnh ion phân tử [M+] và giá trị này bằng giá trị phân tử khối của chất nghiên cứu.
Câu 56:
Điền số thích hợp vào chỗ trống
Cho biết nước có nhiệt độ sôi là 100°C và hằng số nghiệm sôi K là 0,51 (℃.g/mol). Hoà tan 18 g glucose vào 150 g nước thì thu được một dung dịch sôi ở 100,34°C. Khối lượng phân tử của glucose là (1) ______ (g/mol).
 Xem đáp án
Xem đáp án
Đáp án
Điền số thích hợp vào chỗ trống
Cho biết nước có nhiệt độ sôi là 100°C và hằng số nghiệm sôi K là 0,51 (℃.g/mol). Hoà tan 18 g glucose vào 150 g nước thì thu được một dung dịch sôi ở 100,34°C. Khối lượng phân tử của glucose là (1) __ 180 __ (g/mol).
Giải thích
\({{\rm{M}}_{{\rm{glucose }}}} = 0,51.\frac{{18.1000}}{{150.(100,34 - 100)}} = 180\) (g/mol)
Câu 57:
Kéo thả các ô vuông vào vị trí thích hợp:
H, HCl, CuSO4 khan, H2O, AgNO3, CO2, C, Cl2O7
Khi đốt cháy hoàn toàn hợp chất hữu cơ thì ______ chuyển thành CO2, ______ chuyển thành ______, Cl chuyển thành ______. Người ta nhận ra trong sản phẩm cháy có ______ nhờ nước vôi trong, nhận ra sự có mặt của H2O nhờ ______, nhận ra HCl nhờ dung dịch ______.
 Xem đáp án
Xem đáp án
Đáp án
Khi đốt cháy hoàn toàn hợp chất hữu cơ thì C chuyển thành CO2, H chuyển thành H2O, Cl chuyển thành HCl. Người ta nhận ra trong sản phẩm cháy có CO2 nhờ nước vôi trong, nhận ra sự có mặt của H2O nhờ CuSO4 khan, nhận ra HCl nhờ dung dịch AgNO3.
Giải thích
Khi đốt cháy hoàn toàn hợp chất hữu cơ thì C chuyển thành CO2, H chuyển thành H2O, Cl chuyển thành HCl. Người ta nhận ra trong sản phẩm cháy có CO2 nhờ nước vôi trong, nhận ra sự có mặt của H2O nhờ CuSO4 khan, nhận ra HCl nhờ dung dịch AgNO3.
Câu 58:
Hoà tan 1,00 mg một protein vào nước thu được 1,00 ml dung dịch rồi đo áp suất thẩm thấu ở 25°C thì được giá trị π = 1,12 mmHg. Phân tử khối của protein đã cho là
 Xem đáp án
Xem đáp án
Giải thích
Ta có:
\(\pi = \frac{{1,12{\rm{mmHg}}}}{{760{\rm{mmHg}}}} = 1,{47.10^{ - 3}}\) atm
→ Phân tử khối của protein đã cho là:
\({\rm{M}} = \frac{{{\rm{mRT}}}}{{\pi .{\rm{V}}}} = \frac{{{{1.10}^{ - 3}}.0,08206.(273 + 25)}}{{1,{{47.10}^{ - 3}}{{.1.10}^{ - 3}}}} \approx 1,{66.10^4}\) (g/mol).
Chọn C
Câu 59:
Cho biết benzene có nhiệt độ đông đặc là 5,5°C và hằng số nghiệm lạnh K là 5,12 (℃.g/mol). Xác định phân tử khối của hormone thyroxine? (Biết rằng dung dịch chứa 0,546 g thyroxine trong 15 g benzene đông đặc ở 5,26°C).
 Xem đáp án
Xem đáp án
Giải thích
Ta có độ hạ băng điểm của dung dịch là: Δt = 5,50 − 5,26 = 0,24°C
→ Phân tử khối của hormone thyroxine là:
\({{\rm{M}}_{{\rm{thyroxine }}}} = 5,12.\frac{{0,546.1000}}{{15.0,24}} \approx 777\) (g/mol).
Chọn B
Câu 60:
Lindane là một hóa chất được sử dụng làm thuốc trừ sâu trong nông nghiệp và làm dược phẩm điều trị bệnh ghẻ, diệt chấy,.... Tiếp xúc với một lượng lớn lindane có thể gây hại cho hệ thần kinh, gây ra một loạt các triệu chứng như đau đầu, chóng mặt dẫn đến co giật và hiếm gặp hơn là tử vong. Thành phần phần trăm khối lượng của các nguyên tố có trong lindane là: 24,78% C; 2,08% H và 73,14% Cl. Dựa vào phổ khối lượng, xác định được phân tử khối của lindane là 288 (ứng với 35Cl) hoặc 300 (ứng với 37Cl). Trong tự nhiên, 35Cl chiếm 75,77% số lượng nguyên tử còn 37Cl chiếm 24,23% số lượng nguyên tử. Công thức phân tử của lindane là
 Xem đáp án
Xem đáp án
Giải thích
Nguyên tử khối trung bình của chlorine là:
\(\frac{{(75,77.35) + (24,23.37)}}{{100}} = 35,5\)
Tỉ lệ về số nguyên tử carbon : hydrogen : chlorine có trong phân tử lindane là:
\({\rm{nC}}:{\rm{nH}}:{{\rm{n}}_{{\rm{Cl}}}} = \frac{{24,78}}{{12}}:\frac{{2,08}}{1}:\frac{{73,14}}{{35,5}} = 1:1:1\)
→ Công thức thực nghiệm của lindane là CHCl.
Tính với 35Cl, lindane có phân tử khối 288: (CHCl)n = 288 hay 48n = 288 → n = 6.
Tương tự, với 37Cl, lindane có phân từ khối 300: (CHCl)n = 300 hay 50n = 300 →n = 6. Vậy công thức phân tử của lindane là C6H6Cl6.
Chọn DCâu 61:
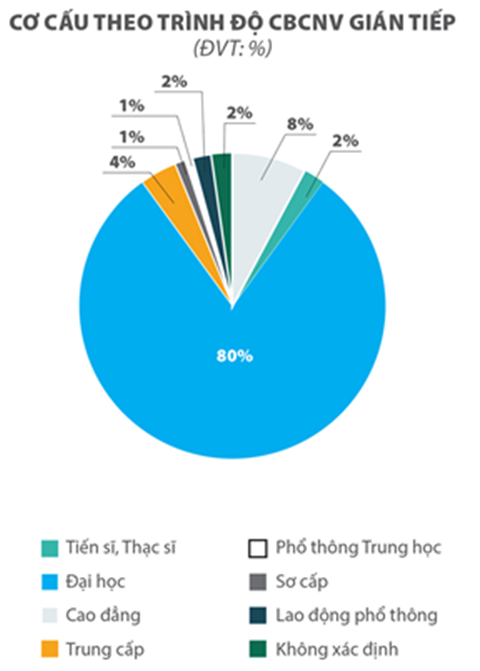
Trong một hội thảo của công ty A gồm 100 người có cơ cấu theo trình độ cán bộ công nhân viên (CBCNV) như biểu đồ dưới đây:
Chọn ra 20 người để nhận phần quà may mắn từ diễn giả của hội thảo. Xác suất để trong 20 người có \(\frac{3}{4}\) số người có trình độ là Đại học là bao nhiêu? (Kết quả làm tròn đến chữ số thập phân thứ hai)
 Xem đáp án
Xem đáp án
Giải thích
Trong hội nghị có 100 người nên \[n\left( \Omega \right) = C_{100}^{20}\]
+ Số người có trình độ là Đại học là: 100.80 (người).
Trong 20 người được nhận quà của diễn giả: có \(\frac{3}{4}\) số người có trình độ là Đại học và còn lại là các trình độ khác nên số cách chọn 20 người lên nhận quà là: \(n(A) = C_{80}^{15}.C_{20}^5\).
Xác suất cần tìm của đề bài là: \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{C_{80}^{15}.C_{20}^5}}{{C_{100}^{20}}} \approx 0,19.\)
Chọn A
Câu 62:
Cho M là điểm biểu diễn số phức z và N là điểm biểu diễn số phức \(w = - 4 - 3i\). Biết \(MN = 3\).

Độ dài đoạn thẳng ON bằng _____.
Tập hợp điểm biểu diễn số phức z là đường tròn có tọa độ tâm là (_____; _____) và bán kính bằng _____.
 Xem đáp án
Xem đáp án
Đáp án
Độ dài đoạn thẳng ON bằng 5 .
Tập hợp điểm biểu diễn số phức z là đường tròn có tọa độ tâm là (-4 ; -3 ) và bán kính bằng 3 .
Giải thích
Ta có: \(N( - 4; - 3) \Rightarrow ON = \sqrt {{{( - 4)}^2} + {{( - 3)}^2}} = 5\).
Gọi \(z = x + yi\,\,(x;y \in \mathbb{R})\).
\(MN = 3 \Leftrightarrow \sqrt {{{(x + 4)}^2} + {{(y + 3)}^2}} = 3 \Leftrightarrow {(x + 4)^2} + {(y + 3)^2} = 9\)
Vậy tập hợp điểm biểu diễn số phức \(z\) là đường tròn có tâm là \(N( - 4; - 3)\), bán kính \(r = 3\).
Câu 63:
 Xem đáp án
Xem đáp án
Giải thích
Để chia thành 4 phần quà mà mỗi phần có ít nhất 3 hộp bánh ta làm như sau:
+ Chia mỗi phần là 2 hộp bánh.
+ Còn lại 12 hộp bánh. Khi đó bài toán trở thành. Có bao nhiêu cách chia 12 hộp bánh thành 4 phần quà sao cho mỗi phần có ít nhất 1 hộp bánh. Để làm bài toán này ta xếp 12 hộp bánh thành hàng ngang, khi đó có 11 khoảng trống. Chọn 3 trong 11 khoảng trống để đặt vách ngăn. Khi đó ta có \[C_{11}^3 = 165\] cách chia.
Chọn D
Câu 64:
 Xem đáp án
Xem đáp án
Giải thích
Ta có:
\({1^1} + {2^2} + {3^3} + \ldots + {n^n} < {n^1} + {n^2} + {n^3} + \ldots + {n^n} < {n^n} + {n^n} + {n^n} + \ldots + {n^n} = n.{n^n} = {n^{n + 1}},\forall n \in \mathbb{N},n \ge 2\)
Vậy \(c = {1^1} + {2^2} + {3^3} + \ldots + {1000^{1000}} < {1000^{1001}} = a\) hay \(c < a\) (1).
Mặt khác
\(\log a = 3003\)
\(\log b = {2^{64}}.\log 2 = {2^{10}}{.2^{50}}{.2^4}.\log 2 = \left( {1024.\log {2^{16}}} \right){.2^{50}} > 3003 = \log a\). Vậy \(b > a\) (2).
Từ (1) và (2) suy ra \[c < a < b\].
Chọn A
Câu 65:
 Xem đáp án
Xem đáp án
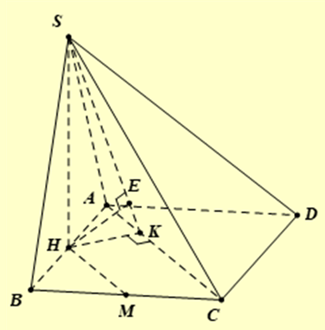
Kẻ \(SH \bot AB \Rightarrow H\) là trung điểm của AB.
Do \((SAB) \bot (ABCD)\) và \((SAB) \cap (ABCD) = AB\) nên từ \(SH \bot AB\) ta được \(SH \bot (ABCD)\).
Mặt khác ta có \(B\dot A \cap (SAC) = \{ A\} \) và \(H\) là trung điểm của AB nên ta có \(d(B,(SAC)) = 2d(H,(SAC))\).
Trong \((ABCD)\) kẻ \(HK \bot AC\,\,(K \in AC)\) và trong \((SHK)\) kẻ \(HE \bot SK(E \in SK)\).
Ta có: \(SH \bot (ABCD) \Rightarrow SH \bot AC\). Kết hợp với \(HK \bot AC\) ta được \(AC \bot (SHK) \Rightarrow AC \bot HE\).
Hơn nữa \(HE \bot SK\) nên \(HE \bot (SAC)\).
Vậy \(d(H,(SAC)) = HE \Rightarrow d(B,(SAC)) = 2HE\).
Trong \((ABCD)\) ta có .
Mặt khác do \(\Delta SAB\) đều nên \(SH = \frac{{8\sqrt 3 }}{2} = 4\sqrt 3 \). Áp dụng hệ thức lượng trong \(\Delta SHK\) ta có
\(\frac{1}{{H{E^2}}} = \frac{1}{{H{K^2}}} + \frac{1}{{S{H^2}}} \Rightarrow HE = \frac{{4\sqrt {21} }}{7} \Rightarrow d(B,(SAC)) = \frac{{8\sqrt {21} }}{7}\). Suy ra \(a = 8,b = 21,c = 7\).
Vậy \(a + {b^2} - {c^3} = 106\).
Chọn C
Câu 66:
 Xem đáp án
Xem đáp án
Điều kiện: \(\left\{ {\begin{array}{*{20}{l}}{x > 0}\\{y > 0}\\{x - 4y - 1 > 0}\end{array}} \right.\)
Ta có \(\log _2^2(xy) = {\log _2}\left( {\frac{x}{4}} \right){\log _2}(4y) \Leftrightarrow {\left( {{{\log }_2}x + {{\log }_2}y} \right)^2} = \left( {{{\log }_2}x - 2} \right)\left( {{{\log }_2}y + 2} \right)\)(1)
Đặt \({\log _2}x = a;{\log _2}y = b\), ta có (1) trở thành :
\({(a + b)^2} = (a - 2)(b + 2) \Leftrightarrow {a^2} + ab - 2a + {b^2} + 2b + 4 = 0\)
\( \Leftrightarrow 2{a^2} + 2ab - 4a + 2{b^2} + 4b + 8 = 0 \Leftrightarrow {(a + b)^2} + {(a - 2)^2} + {(b + 2)^2} = 0\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a + b = 0}\\{a - 2 = 0}\\{b + 2 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b = - 2}\end{array}} \right.} \right.\)
Với \(\left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b = - 2}\end{array}} \right.\), ta có \(\left\{ {\begin{array}{*{20}{l}}{{{\log }_2}x = 2}\\{{{\log }_2}y = - 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 4}\\{y = \frac{1}{4}}\end{array}} \right.} \right.\) (thỏa mãn điều kiện).
Khi đó \(P = {\log _3}\left( {4 + 4.\frac{1}{4} + 4} \right) + {\log _2}\left( {4 - 4.\frac{1}{4} - 1} \right) = 3\).
Chọn A
Câu 67:
 Xem đáp án
Xem đáp án
Ta có \({f^\prime }(x) = \frac{{4 + m}}{{{{(x + 4)}^2}}},\forall x \ne - 4\) và phương trình tiệm cận đứng \(x = - 4\).
TH1. Với \(m + 4 > 0 \Leftrightarrow m > - 4\) thì \({f^\prime }(x) > 0,\forall x \in [ - 3;3]\) nên
\(\mathop {\min }\limits_{[ - 3;3]} f(x) = 2 \Leftrightarrow f( - 3) = 2 \Leftrightarrow \frac{{ - 3 - m}}{1} = 2 \Rightarrow m = - 5\) (loại).
TH2. Với \(m + 4 < 0 \Leftrightarrow m < - 4\) thì \({f^\prime }(x) < 0,\forall x \in [ - 3;3]\) nên
\(\mathop {\min }\limits_{[ - 3;3]} f(x) = 2 \Leftrightarrow f(3) = 2 \Leftrightarrow \frac{{3 - m}}{7} = 2 \Rightarrow m = - 11\) (thỏa mãn).
Vậy tổng các giá trị \(m\) thỏa mãn yêu cầu bài toán là -11 .
Chọn B
Câu 68:
Trong buổi sáng thứ sáu có 150 người đến phòng khám An Tâm kiểm tra sức khoẻ. Kết quả xét nghiệm nhóm máu của 150 người đó được thể hiện qua biểu đồ dưới đây.
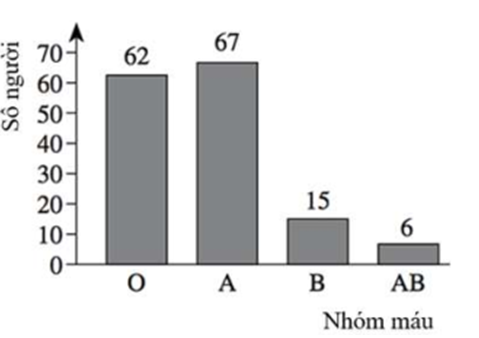
Chọn ngẫu nhiên một trong 150 người đã kiểm tra sức khoẻ. Xác suất để người này có nhóm máu A hoặc AB là
 Xem đáp án
Xem đáp án
Chọn A
Câu 69:
 Xem đáp án
Xem đáp án
Giải thích
Ta có: \(\int\limits_{ - 1}^1 {f(x){\rm{d}}x = 7} \Leftrightarrow \int\limits_{ - 1}^0 { - 2(x + 1){\rm{d}}x} + \int\limits_0^1 {m\left( {1 - {x^2}} \right)} {\rm{d}}x = 7 \Leftrightarrow - 1 + \frac{2}{3}m = 7 \Leftrightarrow m = 12.\)
Chọn A
Câu 70:
 Xem đáp án
Xem đáp án
Giải thích
Điều kiện: \(\left\{ {\begin{array}{*{20}{l}}{{x^2} - x - m > 0}\\{x - 2 > 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x^2} - x - m > 0}\\{x > 2}\end{array}} \right.} \right.\)
Với điều kiện trên bất phương trình đã cho tương đương với
\({\log _4}\left( {{x^2} - x - m} \right) \ge {\log _2}(x - 2) \Leftrightarrow {\log _2}\left( {{x^2} - x - m} \right) \ge {\log _2}{(x - 2)^2}\)
\( \Leftrightarrow {x^2} - x - m \ge {x^2} - 4x + 4 \Leftrightarrow m \le 3x - 4\) (∗∗).
Khi đó \({x^2} - x - m > 0 \Leftrightarrow {x^2} - x - m \ge {x^2} - x - 3x + 4 = {x^2} - 4x + 4 = {(x - 2)^2} > 0\) (vì x > 2).
Vậy bất phương trình đã cho có nghiệm với mọi giá trị x thuộc tập xác định khi (∗∗) có nghiệm với mọi giá trị x thuộc tập xác định \( \Leftrightarrow m \le \mathop {\min }\limits_{(2; + \infty )} (3x - 4) \Rightarrow m \le 2\).
Chọn D
Câu 71:
 Xem đáp án
Xem đáp án
Giải thích
Ta có: \({u_2} + {u_{22}} = 40 \Leftrightarrow {u_1} + d + {u_1} + 21d = 40 \Leftrightarrow 2{u_1} + 22d = 40\)
Mà \({S_{23}} = \frac{{23}}{2}\left( {2{u_1} + 22d} \right) = \frac{{23}}{2}.40 = 460\).
Chọn D
Câu 72:

Khoảng cách từ tâm mặt cầu (S) đến đường thẳng d bằng _______.
Mặt phẳng (P) chứa đường thẳng d và có khoảng cách từ tâm mặt cầu (S) tới mặt phẳng là lớn nhất có phương trình \[ax + by + cz = 18\] với a = _______ ; b = _______; c = _______.
 Xem đáp án
Xem đáp án
Đáp án
Khoảng cách từ tâm mặt cầu (S) đến đường thẳng d bằng \(\sqrt 5 \) .
Mặt phẳng (P) chứa đường thẳng d và có khoảng cách từ tâm mặt cầu (S) tới mặt phẳng là lớn nhất có phương trình \[ax + by + cz = 18\] với a = 5 ; b = 2 ; c = 4 .
Giải thích
Mặt cầu \((S)\) có tâm \(I(1; - 1;0)\), bán kính \(R = 2\).
Đường thẳng \(d\) có vecto chỉ phương \(\vec u = ( - 2;1;2)\) và điểm \(M(4; - 1;0) \in d\).
\(\overrightarrow {IM} = (3;0;0) \Rightarrow [\overrightarrow {IM} ;\vec u] = (0; - 6;3) \Rightarrow d(I;d) = \frac{{\left| {\left[ {\overrightarrow {IM} ;\vec u} \right]} \right|}}{{|\vec u|}} = \sqrt 5 \)
Gọi H, K lần lượt là hình chiếu của \(I\) trên mặt phẳng \((P)\) và đường thẳng \(d\).
Khi đó, \(IH \le IK \Rightarrow I{H_{\max }} = IK = d(I;d) = \sqrt 5 \).
Mặt phẳng \((\alpha )\) đi qua điểm \(I(1; - 1;0)\) và nhận \(\vec u = ( - 2;1;2)\) làm vecto pháp tuyến có phương trình: \( - 2(x - 1) + (y + 1) + 2z = 0 \Leftrightarrow 2x - y - 2z - 3 = 0\).
\( \Rightarrow K = d \cap (\alpha ) \Rightarrow \) Tọa độ điểm \(K\) thỏa mãn hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{\frac{{x - 4}}{{ - 2}} = \frac{{y + 1}}{1} = \frac{z}{2}}\\{2x - y - 2z - 3 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = \frac{8}{3}}\\{y = - \frac{1}{3}}\\{z = \frac{4}{3}}\end{array}} \right.} \right.\) \( \Rightarrow K\left( {\frac{8}{3}; - \frac{1}{3};\frac{4}{3}} \right) \Rightarrow \overrightarrow {IK} = \left( {\frac{5}{3};\frac{2}{3};\frac{4}{3}} \right)\).
Mặt phẳng \((P)\) đi qua điểm \(M(4; - 1;0)\) và nhận vecto \(\vec n(5;2;4)\) làm vecto pháp tuyến có phương trình: \(5(x - 4) + 2(y + 1) + 4z = 0 \Leftrightarrow 5x + 2y + 4z - 18 = 0\).
Câu 73:
 Xem đáp án
Xem đáp án
Giải thích
Ta có: \({V_0} = \frac{4}{3}\pi {R^3}\). Khi thể tích của khối cầu giảm 8 lần thì bán kính của mặt cầu giảm 2 lần.
Vì diện tích mặt cầu là \({S_0} = 4\pi {R^2}\) nên diện tích của mặt cầu giảm 4 lần.
Chọn C
Câu 74:
Bạn Xuân là thành viên trong một nhóm gồm 15 người.
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Chọn ngẫu nhiên 3 người từ nhóm để lập một ban đại diện. Xác suất để Xuân là 1 trong 3 người được chọn là 0,2. |
||
|
Chọn ngẫu nhiên 2 người từ nhóm để làm nhóm trưởng và nhóm phó. Xác suất để Xuân không làm nhóm trưởng cũng như nhóm phó nhỏ hơn 0,8. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Chọn ngẫu nhiên 3 người từ nhóm để lập một ban đại diện. Xác suất để Xuân là 1 trong 3 người được chọn là 0,2. |
X | |
|
Chọn ngẫu nhiên 2 người từ nhóm để làm nhóm trưởng và nhóm phó. Xác suất để Xuân không làm nhóm trưởng cũng như nhóm phó nhỏ hơn 0,8. |
X |
Giải thích
+) Chọn ngẫu nhiên 3 người từ nhóm để lập một ban đại diện thì số phần tử của không gian mẫu là \(n(\Omega ) = C_{15}^3 = 455\).
Gọi A là biến cố: “Xuân là một trong ba người được chọn”.
Có 1 cách chọn Xuân trong nhóm 15 người.
Có \(C_{14}^2\) cách chọn 2 người trong 14 người còn lại.
Suy ra \(n(A) = 1.C_{14}^2 = 91\).
Xác suất cần tìm là \(P(A) = \frac{{91}}{{455}} = 0,2\).
+) Chọn ngẫu nhiên 2 người từ nhóm để làm nhóm trưởng và nhóm phó thì số phần tử của không gian mẫu là \[n\left( \Omega \right) = 15.14 = 210\].
Gọi A là biến cố: “Xuân không làm nhóm trưởng cũng như nhóm phó”.
Trong 14 người còn lại, chọn nhóm trưởng có 14 cách, chọn nhóm phó có 13 cách.
Suy ra \[n\left( A \right) = 14.13 = 182\].
Xác suất cần tìm là \(P(A) = \frac{{182}}{{210}} = \frac{{13}}{{15}} \approx 0,87 > 0,8\).
Câu 75:
Cho 5 đoạn thẳng có độ dài là 1; 2; 3; 4; 5. Lấy ngẫu nhiên ba đoạn thẳng. Xác suất để độ dài ba đoạn thẳng này là độ dài ba cạnh của một tam giác là (1) _______.
 Xem đáp án
Xem đáp án
Đáp án
Cho 5 đoạn thẳng có độ dài là 1; 2; 3; 4; 5. Lấy ngẫu nhiên ba đoạn thẳng. Xác suất để độ dài ba đoạn thẳng này là độ dài ba cạnh của một tam giác là (1) __ 3/10 __ .
Giải thích
Số phần tử của không gian mẫu là: \(n(\Omega ) = C_5^3 = 10\).
Để độ dài ba đoạn thẳng là độ dài ba cạnh của tam giác thì tổng độ dài hai cạnh lớn hơn độ dài cạnh còn lại.
Do đó, các khả năng xảy ra là bộ các độ dài {(2;3;4), (2;4;5), (3;4;5)}.
Vậy xác suất cần tìm là: \(P = \frac{3}{{10}}\).
Câu 76:
Xét các số thực a, b thỏa mãn điều kiện \({\log _5}\left( {{5^a}{{.125}^b}} \right) = {\log _{25}}5\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau
Nếu \(b = \frac{1}{2}\) thì giá trị của số thực a bằng _______.
Mối liên hệ giữa a và b là \(2a + 6b = \) _______.
Nếu a là số nguyên âm thuộc [−10;−5] thì có _______ giá trị nguyên dương của b Xem đáp án
Xem đáp án
Đáp án
Nếu \(b = \frac{1}{2}\) thì giá trị của số thực a bằng -1 .
Mối liên hệ giữa a và b là \(2a + 6b = \) 1 .
Nếu a là số nguyên âm thuộc [−10;−5] thì có 0 giá trị nguyên dương của b .
Giải thích
Ta có: \({\log _5}\left( {{5^a}{{.125}^b}} \right) = {\log _{25}}5 \Leftrightarrow {\log _5}{5^a} + {\log _5}{5^{3b}} = {\log _{{5^2}}}5\)
\( \Leftrightarrow a{\log _5}5 + 3b{\log _5}5 = \frac{1}{2}{\log _5}5 \Leftrightarrow a + 3b = \frac{1}{2} \Leftrightarrow 2a + 6b = 1\).
Nếu \(b = \frac{1}{2}\) thì \(2a + 6.\frac{1}{2} = 1 \Leftrightarrow a = - 1\).
Vì a là số nguyên âm thuộc [−10;−5] nên ta có bảng sau:
|
a |
−10 |
−9 |
−8 |
−7 |
−6 |
−5 |
|
b |
\(\frac{7}{2}\) |
\(\frac{{19}}{6}\) |
\(\frac{{17}}{6}\) |
\(\frac{5}{2}\) |
\(\frac{{13}}{6}\) |
\(\frac{{11}}{6}\) |
Vậy không có giá trị nguyên dương của b thỏa mãn.
Câu 77:
 Xem đáp án
Xem đáp án
Chọn C
Câu 78:
 Xem đáp án
Xem đáp án
Giải thích
Ta có: \(\overrightarrow {AB} = (2; - 1;3)\) và \(\overrightarrow {{n_{(Q)}}} = (3;2;1)\) là vectơ pháp tuyến của mặt phẳng \((Q)\).
Mặt phẳng \((P)\) chứa hai điểm A, B và vuông góc với mặt phẳng \((Q)\) nên vectơ pháp tuyến của mặt phẳng \((P)\) là: \(\overrightarrow {{n_{(P)}}} = \left[ {\overrightarrow {AB} ,\overrightarrow {{n_{(Q)}}} } \right] = ( - 7;7;7)\).
Mặt phẳng \((P)\) đi qua điểm \(A( - 1;1;1)\) và có vectơ pháp tuyến \(\overrightarrow {{n_{(P)}}} = ( - 7;7;7)\) nên có phương trình là: \( - 7(x + 1) + 7(y - 1) + 7(z - 1) = 0\) hay \(x - y - z + 3 = 0\).
\( \Rightarrow a = 1;b = c = - 1 \Rightarrow a + 2b - 3c = 2.\)
Chọn C
Câu 79:
 Xem đáp án
Xem đáp án
Giải thích
Ta có: \(S = \int\limits_1^2 {\left| {{{(x - 2)}^2} - 1} \right|} {\rm{d}}x = \int\limits_1^2 {\left| {{x^2} - 4x + 3} \right|} {\rm{d}}x = \left. {\left( {\frac{{{x^3}}}{3} - 2{x^2} + 3x} \right)} \right|_1^2 = \frac{2}{3}\)
Chọn D
Câu 80:
![Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau Một chiếc ô tô đang đi trên đường với vận tốc \(v(t) = 3t - 15\,\,(t \ge 3)\,\,\left( {m/s} \right)\), trong đó t là khoảng thời gian tính bằng giây. Quãng đường ô tô đi được trong 10 giây bắt đầu từ thời điểm t = 3 là: ______(m). Khi ô tô đạt vận tốc 30 m/s thì người lái xe phát hiện có hàng rào chắn ngang đường ở phía trước cách xe 100 m (tính từ đầu xe tới hàng rào) nên người lái đạp phanh. Từ thời điểm đó, xe chuyển động chậm dần đều với vận tốc \[v\left( t \right) = - 5t + 100\,\,\left( {m/s} \right)\]. Từ lúc đạp phanh đến khi dừng hẳn ô tô còn di chuyển ______ (m). Khi xe dừng hẳn, khoảng cách từ xe đến hàng rào là ______ (m). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid16-1729673090.png)
Một chiếc ô tô đang đi trên đường với vận tốc \(v(t) = 3t - 15\,\,(t \ge 3)\,\,\left( {m/s} \right)\), trong đó t là khoảng thời gian tính bằng giây. Quãng đường ô tô đi được trong 10 giây bắt đầu từ thời điểm t = 3 là: ______(m).
Khi ô tô đạt vận tốc 30 m/s thì người lái xe phát hiện có hàng rào chắn ngang đường ở phía trước cách xe 100 m (tính từ đầu xe tới hàng rào) nên người lái đạp phanh. Từ thời điểm đó, xe chuyển động chậm dần đều với vận tốc \[v\left( t \right) = - 5t + 100\,\,\left( {m/s} \right)\]. Từ lúc đạp phanh đến khi dừng hẳn ô tô còn di chuyển ______ (m).
Khi xe dừng hẳn, khoảng cách từ xe đến hàng rào là ______ (m).
 Xem đáp án
Xem đáp án
Đáp án
Một chiếc ô tô đang đi trên đường với vận tốc \(v(t) = 3t - 15\,\,(t \ge 3)\,\,\left( {m/s} \right)\), trong đó t là khoảng thời gian tính bằng giây. Quãng đường ô tô đi được trong 10 giây bắt đầu từ thời điểm t = 3 là: 90(m).
Khi ô tô đạt vận tốc 30 m/s thì người lái xe phát hiện có hàng rào chắn ngang đường ở phía trước cách xe 100 m (tính từ đầu xe tới hàng rào) nên người lái đạp phanh. Từ thời điểm đó, xe chuyển động chậm dần đều với vận tốc \[v\left( t \right) = - 5t + 100\,\,\left( {m/s} \right)\]. Từ lúc đạp phanh đến khi dừng hẳn ô tô còn di chuyển 62,5 (m).
Khi xe dừng hẳn, khoảng cách từ xe đến hàng rào là 37,5 (m).
Giải thích
Quãng đường ô tô đi được trong 15 giây từ thời điểm \(t = 3\) là: \({S_1} = \int\limits_3^{13} {(3t - 15)} dt = 90\,\,(m)\).
Khi xe đạt vận tốc 30 m/s thì xe đã đi được \(\frac{{30 + 15}}{3} = 15\) (giây).
Xe dừng lại khi \(v(t) = 0 \Leftrightarrow - 5t + 100 = 0 \Leftrightarrow t = 20\,\,(s)\).
Quãng đường xe đi được kể từ lúc đạp phanh đến khi dừng lại là:
\(s(t) = \int\limits_{15}^{20} {v(t)dt} = \int\limits_{15}^{20} {( - 5t + 100)} dt = \left. {\left( {100t - \frac{{5{t^2}}}{2}} \right)} \right|_{15}^{20} = 62,5\,\,(m)\) .
Khi xe dừng hẳn, khoảng cách từ xe đến hàng rào là 100 − 62,5 = 37,5 (m).
Câu 81:
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = 3\sin x + 4\cos x + 1\) bằng (1) ______.
 Xem đáp án
Xem đáp án
Đáp án
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = 3\sin x + 4\cos x + 1\) bằng (1) __ 2 __ .
Giải thích
Ta có \(\frac{y}{5} = \frac{3}{5}\sin x + \frac{4}{5}\cos x + \frac{1}{5} = \sin (x + \alpha ) + \frac{1}{5}\) với \(\cos \alpha = \frac{3}{5}\) và \(\sin \alpha = \frac{4}{5}\).
Mà \( - 1 \le \sin (x + \alpha ) \le 1 \Leftrightarrow \frac{{ - 4}}{5} \le \sin (x + \alpha ) + \frac{1}{5} \le \frac{6}{5}\) hay \(\frac{{ - 4}}{5} \le \frac{y}{5} \le \frac{6}{5}\) suy ra \( - 4 \le y \le 6\).
Vậy \[\min y = - 4;\;\max y = 6\].
Câu 82:
Định luật làm mát của Newton phát biểu rằng tốc độ làm mát của một vật tỉ lệ thuận với chênh lệch nhiệt độ giữa vật đó và môi trường xung quanh, với điều kiện là chênh lệch này không quá lớn. Giả sử T(t) là nhiệt độ của vật thể (đơn vị: độ C) tại thời điểm t (đơn vị: phút) và Ts là nhiệt độ của môi trường xung quanh, chênh lệch giữa nhiệt độ của vật thể và môi trường xung quanh là \(y(t) = T(t) - {T_s}\) thì \(\frac{{y'(t)}}{{y(t)}} = k\) với k là hằng số.
Một cốc nước đang ở nhiệt độ phòng là 22∘C được đưa vào ngăn mát tủ lạnh có nhiệt độ là 5∘C . Sau 30 phút, nhiệt độ của cốc nước được đo lại là 16∘C. Giả sử T (t) là nhiệt độ của cốc nước, y (t) là nhiệt độ chênh lệch giữa cốc nước và nhiệt độ ngăn mát tủ lạnh sau khoảng thời gian t.
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Nhiệt độ của chênh lệch giữa cốc nước và nhiệt độ ngăn mát tủ lạnh sau khoảng thời gian t là hàm số có dạng \(y(t) = y(0){e^{kt}}\). |
||
|
Kết quả làm tròn đến chữ số thập phân thứ tư của k là −0,0145. |
||
|
Sau 60 phút trong tủ lạnh, nhiệt độ của cốc nước khoảng 10∘C (Kết quả làm tròn đến chữ số hàng đơn vị). |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Nhiệt độ của chênh lệch giữa cốc nước và nhiệt độ ngăn mát tủ lạnh sau khoảng thời gian t là hàm số có dạng \(y(t) = y(0){e^{kt}}\). |
X | |
|
Kết quả làm tròn đến chữ số thập phân thứ tư của k là −0,0145. |
X | |
|
Sau 60 phút trong tủ lạnh, nhiệt độ của cốc nước khoảng 10∘C (Kết quả làm tròn đến chữ số hàng đơn vị). |
X |
Giải thích
|
Lí do lựa chọn phương án |
1) |
Đúng vì: Do \(\frac{{y'(t)}}{{y(t)}} = k\) với k là hằng số. Lấy tích phân với cận từ 0 đến t hai vế. Ta được \(\int_0^t {\frac{{y'(t)}}{{y(t)}}} dt = \int_0^t k dt\) Kéo theo \(\ln \frac{{y(t)}}{{y(0)}} = kt\), hay \(y(t) = y(0).{e^{kt}}\). |
|
2) |
Đúng vì: Tính được \[y(0) = T(0) - {T_s} = 22 - 5 = 17\]. Ta có \(T(t) = {T_s} + y(t) = 5 + 17{e^{kt}}\). Thay t = 30 ta được \(T(30) = 5 + 17{e^{30k}}\). Mà \(T(30) = 16\) nên \(k = \ln \left( {\frac{{11}}{{17}}} \right):30 \approx - 0,0145\). |
|
|
3) |
Sai vì: Tính \(T(60) \approx 12\) (Kết quả làm tròn đến chữ số hàng đơn vị). |
Câu 83:
 Xem đáp án
Xem đáp án
Giải thích
Gọi chiều cao của hình nón là \(h\) và đường kính đáy của hình nón là \(4r\,\,(h,r > 0)\).
\( \Rightarrow \) Chiều cao của hình trụ là 2h và đường kính đáy của hình trụ là 2r.
Thể tích của khối nón \((N)\) là: \({V_1} = \frac{1}{3}\pi {(2r)^2}h = \frac{4}{3}\pi {r^2}h\).
Thể tích của khối nón \((T)\) là: \({V_2} = \pi {r^2}.2h = 2\pi {r^2}h\).
\( \Rightarrow \frac{{{V_2}}}{{{V_1}}} = \frac{{2\pi {r^2}h}}{{\frac{4}{3}\pi {r^2}h}} = \frac{3}{2}\)
Chọn A
