Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 15)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 15)
-
117 lượt thi
-
93 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
Phần tư duy đọc hiểu
Ý chính của bài viết là gì?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn trích
Lời giải
Ý chính của bài viết là: Cách giảm chi phí logistics cho doanh nghiệp xuất nhập khẩu.
Phương pháp suy luận, loại trừ:
Đáp án A -> sai: vì nó chỉ nói về một phần của bài viết. Bài viết không chỉ phân tích những nguyên nhân và hạn chế của chi phí logistics cao ở Việt Nam, mà còn đưa ra những cách thức để giải quyết vấn đề này.
Đáp án B -> sai: vì nó không phản ánh được ý chính của bài viết. Bài viết không tập trung vào đánh giá hiệu quả của các phương thức vận chuyển và dịch vụ logistics, mà chỉ đề cập đến một số giải pháp để tối ưu hóa chúng.
Đáp án C -> đúng: vì nó tóm tắt được ý chính của bài viết. Bài viết giới thiệu những cách thức được khuyến nghị để giảm chi phí logistics cho doanh nghiệp xuất nhập khẩu trong bối cảnh hiện nay, như thay đổi điều kiện bán và mua hàng, thỏa thuận với các hãng vận chuyển, kiểm soát các phụ phí, sử dụng tích hợp chuỗi dịch vụ...
Đáp án D -> sai: vì nó không liên quan đến bài viết. Bài viết không có so sánh chi phí logistics của Việt Nam và các nước khác, mà chỉ nói về tình hình và giải pháp cho chi phí logistics của Việt Nam.
Chọn C
Câu 2:
Đọc đoạn 1 và chỉ ra ngành logistics tại Việt Nam có những đóng góp nào sau đây?
Chọn hai đáp án đúng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [1]
Lời giải
Ngành logistics tại Việt Nam có những đóng góp là: Đóng góp vào GDP 4-5% và Đứng thứ 4 tại khu vực Đông Nam Á về chỉ số logistics thị trường mới nổi
Phân tích, loại trừ:
- Đáp án A -> đúng: Theo nội dung trên, ngành logistics tại Việt Nam đóng góp vào GDP 4-5%. Đây là một đóng góp quan trọng của ngành này cho nền kinh tế quốc dân.
- Đáp án B -> sai: Theo nội dung trên, ngành logistics tại Việt Nam là một trong những ngành tăng trưởng nhanh và ổn định nhất, không phải là ngành tăng trưởng ổn định nhất trong khu vựC. Đây là một sự phóng đại không chính xác về tình hình ngành logistics tại Việt Nam.
- Đáp án C -> đúng: Theo nội dung trên, Việt Nam đứng thứ 4 tại khu vực Đông Nam Á về chỉ số logistics thị trường mới nổi do Agility công bố. Đây là một chỉ số quan trọng để đánh giá tiềm năng và hiệu quả của ngành logistics tại các quốc gia mới nổi.
- Đáp án D -> sai: Theo nội dung trên, Việt Nam không đứng thứ 2 tại khu vực Đông Nam Á về doanh thu ngành logistics, mà là đứng thứ 11 trong top 50 quốc gia đứng đầu thị trường logistics mới nổi. Đây là một sự nhầm lẫn giữa hai chỉ số khác nhau và cũng không chính xác về thực tế.
Chọn A, C
Câu 3:
giao thương, giao thông, trường hợp, giao lưu, yếu tố, doanh nghiệp, đất nươc, đường bộ
Hiện nay, khi _________ với toàn cầu nói chung và với châu Âu – châu Mỹ nói riêng, _________ Việt Nam gặp rất nhiều trở ngại và thử thách, bao gồm các vấn đề về cơ sở hạ tầng thiếu đồng bộ, nhất là cơ sở hạ tầng _________ và logistics như kho bãi, trung tâm logistics; các doanh nghiệp logistics không có đủ thông tin; thiếu liên kết, ứng dụng công nghệ thấp kém...Đây là những _________ khiến chi phí logistics của Việt Nam rất cao, trở thành gánh nặng cho doanh nghiệp.
 Xem đáp án
Xem đáp án
Đáp án
Hiện nay, khi giao thương với toàn cầu nói chung và với châu Âu – châu Mỹ nói riêng, doanh nghiệp Việt Nam gặp rất nhiều trở ngại và thử thách, bao gồm các vấn đề về cơ sở hạ tầng thiếu đồng bộ, nhất là cơ sở hạ tầng giao thông và logistics như kho bãi, trung tâm logistics; các doanh nghiệp logistics không có đủ thông tin; thiếu liên kết, ứng dụng công nghệ thấp kém...Đây là những yếu tố khiến chi phí logistics của Việt Nam rất cao, trở thành gánh nặng cho doanh nghiệp.
Phương pháp giải
Căn cứ vào nội dung đoạn [2]
Lời giải
Căn cứ vào nội dung đoạn 2:
Tuy nhiên, trong bối cảnh hiện nay, doanh nghiệp (DN) Việt Nam khi trao đổi thương mại với thế giới nói chung và với khu vực châu Âu – châu Mỹ vẫn phải đối mặt với rất nhiều khó khăn, thách thức, trong đó phải kể đến các vấn đề như, cơ sở hạ tầng hạn chế, thiếu đồng bộ, đặc biệt là hạ tầng giao thông và hạ tầng logistics như kho bãi, trung tâm logistics; các DN logistics còn thiếu thông tin; thiếu liên kết, ứng dụng công nghệ lạc hậu... Đây là những hạn chế rất lớn khiến chi phí logistics của Việt Nam luôn ở mức rất cao, được xem là gánh nặng đối với DN.
Suy luận, phân tích và loại trừ:
+ giao thương: Đây là đáp án đúng. Theo nội dung trên, doanh nghiệp Việt Nam khi trao đổi thương mại với thế giới nói chung và với khu vực châu Âu – châu Mỹ phải đối mặt với rất nhiều khó khăn, thách thức. Giao thương là một từ đồng nghĩa với trao đổi thương mại, có nghĩa là hoạt động buôn bán hàng hoá giữa các quốc gia hoặc các đơn vị kinh tế.
+ doanh nghiệp: Đây là đáp án đúng. Theo nội dung trên, doanh nghiệp Việt Nam khi trao đổi thương mại với thế giới nói chung và với khu vực châu Âu – châu Mỹ phải đối mặt với rất nhiều khó khăn, thách thức. Doanh nghiệp là một từ chỉ các tổ chức kinh tế có mục tiêu sinh lời từ việc sản xuất và kinh doanh hàng hoá, dịch vụ.
+ giao thông: Đây là đáp án đúng. Theo nội dung trên, doanh nghiệp Việt Nam phải đối mặt với rất nhiều khó khăn, thách thức, trong đó phải kể đến các vấn đề như cơ sở hạ tầng hạn chế, thiếu đồng bộ, đặc biệt là hạ tầng giao thông và hạ tầng logistics như kho bãi, trung tâm logistics. Giao thông là một từ chỉ sự đi lại của người và phương tiện trên các tuyến đường bộ, đường sắt, đường thuỷ, đường hàng không.
+ yếu tố: Đây là đáp án đúng. Theo nội dung trên, cơ sở hạ tầng hạn chế, thiếu đồng bộ, thiếu thông tin, liên kết và ứng dụng công nghệ lạc hậu... là những yếu tố khiến chi phí logistics của Việt Nam luôn ở mức rất cao, được xem là gánh nặng đối với doanh nghiệp. Yếu tố là một từ chỉ một thành phần hoặc một nguyên nhân ảnh hưởng đến một hiện tượng hoặc một kết quả nào đó.
Dựa vào nội dung đoạn trên cùng cách phân tích và suy luận, ta có các từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: giao thương
- Vị trí thả 2: doanh nghiệp
- Vị trí thả 3: giao thông
- Vị trí thả 4: yếu tố
Câu 4:
Từ nội dung của đoạn 3, hãy hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Khu vực Cái Mép có 8 cảng container với tổng chiều dài các bến là 5.470m. Các bến cảng được phân tán ra nhiều nơi, tương đối cách xa nhau và đều có chiều dài cầu tàu khá ngắn (trung bình 600m bến/cảng)
Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [3]
Lời giải
→ Ý kiến trên: Đúng
- Căn cứ vào nội dung ở đoạn 3:
Trong khi đó, theo ông Trương Tấn Lộc - Giám đốc Marketing Tổng Công ty Tân cảng Sài Gòn, tổng chiều dài các bến cảng container khu vực Cái Mép khoảng 5.470m, được chia thành 8 cảng. Các bến cảng được phân bổ rải rác và hầu hết đều hạn chế về chiều dài cầu tàu (trung bình 600m bến/cảng) trong khi kích cỡ tàu cập cảng ngày càng tăng, chiều dài tàu lên tới 400m nên tại mỗi thời điểm, mỗi cảng chỉ có thể tiếp nhận được 1 tàu mẹ.
+ Phân bố rải rác chính là phân tán ra nhiều nơi, tương đối cách xa nhau.
→ Ý kiến trên trùng khớp với nội dung của đoạn 3. Do đó, ý kiến trên đúng
Chọn A
Câu 5:
Hãy tìm một cụm từ không quá hai tiếng để hoàn thành nhận định sau từ nội dung của đoạn 4:
Việt Nam chủ yếu xuất FOB và nhập CIF có nghĩa là các DN Việt Nam phải chịu trách nhiệm về hàng hoá cho đến khi nó được giao cho ___________ tại cảng xuất phát và phải trả tiền cho phụ phí cảng biển tại cảng đích đến.
 Xem đáp án
Xem đáp án
Đáp án: "chủ tàu"
Phương pháp giải
Căn cứ vào nội dung đoạn [4] và hiểu biết về FOB, CIF
Lời giải
Để điền được từ còn thiếu, ta phải hiểu được ý nghĩa của các điều kiện bán hàng FOB và CIF.
- FOB (Free On Board) có nghĩa là người bán chịu trách nhiệm về hàng hoá cho đến khi nó được giao cho chủ tàu tại cảng xuất phát. Sau đó, người mua sẽ chịu trách nhiệm về chi phí vận chuyển và bảo hiểm hàng hoá.
Ví dụ: Nếu bạn mua một lô hàng từ Trung Quốc với điều kiện FOB Thượng Hải, bạn sẽ phải trả tiền cho chi phí vận chuyển từ Thượng Hải đến Việt Nam và chi phí bảo hiểm cho hàng hoá trong quá trình vận chuyển. Người bán chỉ có trách nhiệm giao hàng cho chủ tàu tại Thượng Hải.
- CIF (Cost, Insurance and Freight) có nghĩa là người bán chịu trách nhiệm về chi phí vận chuyển và bảo hiểm hàng hoá cho đến khi nó được giao tại cảng đích đến. Sau đó, người mua sẽ phải trả các phụ phí cảng biển do các chủ tàu nước ngoài áp đặt.
Ví dụ: Nếu bạn mua một lô hàng từ Mỹ với điều kiện CIF Hồ Chí Minh, bạn sẽ không phải trả tiền cho chi phí vận chuyển từ Mỹ đến Việt Nam và chi phí bảo hiểm cho hàng hoá trong quá trình vận chuyển. Người bán sẽ có trách nhiệm giao hàng cho bạn tại Hồ Chí Minh. Tuy nhiên, bạn sẽ phải trả các phụ phí cảng biển như thuế nhập khẩu, lệ phí xử lý container, lệ phí xếp dỡ hàng hoá... do các chủ tàu nước ngoài áp đặt.
-> Như vậy, từ phù hợp nhất để điền vào chỗ trống là: chủ tàu
Câu 6:
Từ nội dung của đoạn 2 và đoạn 4, hãy chỉ ra đâu là nguyên nhân khiến chi phí logistics của Việt Nam luôn ở mức cao?
Chọn 3 đáp án đúng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [2] và đoạn [4].
Lời giải
Nguyên nhân khiến chi phí logistics của Việt Nam luôn ở mức cao là: Cơ sở hạ tầng hạn chế, thiếu đồng bộ, Chi phí vận tải hàng hoá bằng đường bộ quá cao so với đường thuỷ hay đường sắt và Phụ phí tại cảng biển mà chủ tàu container nước ngoài đang thu của chủ hàng Việt Nam
- Phân tích, loại trừ:
+ Lựa chọn A: Cơ sở hạ tầng hạn chế, thiếu đồng bộ. Đây là đáp án đúng và thuộc đoạn [2] của văn bản: "Tuy nhiên, trong bối cảnh hiện nay, doanh nghiệp (DN) Việt Nam khi trao đổi thương mại với thế giới nói chung và với khu vực châu Âu – châu Mỹ vẫn phải đối mặt với rất nhiều khó khăn, thách thức, trong đó phải kể đến các vấn đề như, cơ sở hạ tầng hạn chế, thiếu đồng bộ, đặc biệt là hạ tầng giao thông và hạ tầng logistics như kho bãi, trung tâm logistics..."
+ Lựa chọn B: Chi phí vận tải hàng hoá bằng đường không quá cao so với đường bộ hay đường sắt. Đây là đáp án sai và gây nhiễu và không thuộc bất kỳ đoạn nào của văn bản. Văn bản trên không nói gì về chi phí vận tải hàng hoá bằng đường không, mà chỉ nói về đường bộ và đường thuỷ.
+ Lựa chọn C: Chi phí vận tải hàng hoá bằng đường bộ quá cao so với đường thuỷ hay đường sắt. Đây là đáp án đúng và thuộc đoạn [4] của văn bản: "Phân tích các yếu tố làm tăng chi phí logistics, ông Kha cho biết, có 5 yếu tố bao gồm: Phụ phí vận tải cảng biển mà chủ tàu container nước ngoài đang thu chủ hàng Việt Nam, thời gian thông quan hàng hoá, kiểm tra chuyên môn còn bị kéo dài gây tăng chi phí, chi phí vận tải hàng hoá bằng đường bộ quá cao, tính kết nối và hạ tầng các phương tiện vận tải chưa cao, năng lực cạnh tranh của DN cung cấp dịch vụ logistics thấp."
+ Lựa chọn D: Phụ phí tại cảng biển mà chủ tàu container nước ngoài đang thu của chủ hàng Việt Nam. Đây là đáp án đúng và thuộc đoạn [4] của văn bản: "Phân tích các yếu tố làm tăng chi phí logistics, ông Kha cho biết, có 5 yếu tố bao gồm: Phụ phí vận tải cảng biển mà chủ tàu container nước ngoài đang thu chủ hàng Việt Nam, thời gian thông quan hàng hoá, kiểm tra chuyên môn còn bị kéo dài gây tăng chi phí, chi phí vận tải hàng hoá bằng đường bộ quá cao, tính kết nối và hạ tầng các phương tiện vận tải chưa cao, năng lực cạnh tranh của DN cung cấp dịch vụ logistics thấp."
Chọn A, C, D
Câu 7:
vận tải hàng hóa, đường bộ, đề xuất, Đứng sau, vận chuyển hàng hóa, dduowgf thủy, đứng trước, khuyến khích
Theo Bộ Công thương, đường bộ là phương thức _______ được sử dụng nhiều nhất hiện nay, chiếm gần 73% tổng lượng hàng hoá vận chuyển. _______đường bộ là đường thuỷ nội địa với hơn 21%. Tuy nhiên, _______ là phương thức có chi phí cao hơn rất nhiều so với _______. Để giảm chi phí logistics, ông Lộc _______ các DN nên chuyển sang sử dụng đường thuỷ nội địa hơn.Để làm được điều này, cần có các bến sà lan ở khu vực Đồng Nai, Bình Dương.
 Xem đáp án
Xem đáp án
Đáp án
Theo Bộ Công thương, đường bộ là phương thức vận tải hàng hoá được sử dụng nhiều nhất hiện nay, chiếm gần 73% tổng lượng hàng hoá vận chuyển. Đứng sau đường bộ là đường thuỷ nội địa với hơn 21%. Tuy nhiên, đường bộ là phương thức có chi phí cao hơn rất nhiều so với đường thuỷ. Để giảm chi phí logistics, ông Lộc khuyến khích các DN nên chuyển sang sử dụng đường thuỷ nội địa hơn.Để làm được điều này, cần có các bến sà lan ở khu vực Đồng Nai, Bình Dương.
Phương pháp giải
Căn cứ vào nội dung đoạn [6]
Lời giải
Căn cứ vào nội dung đoạn 6:
Về phương thức vận chuyển, theo báo cáo của Bộ Công thương, đường bộ vẫn là phương thức vận tải phổ biến nhất hiện nay, chiếm 72,93% tổng lượng hàng hoá được vận chuyển đứng thứ hai là đường thuỷ nội địa với 21,73%. Trong khi đó, đây là phương thức có phí vận chuyển cao hơn hẳn đường thuỷ. Nhiều giải pháp kéo giảm chi phí logistics hữu hiệu ‘‘DN cần tăng cường thay đổi phương thức vận tải nội địa từ đường bộ sang đường thuỷ nội địa. Để làm được điều này, cần đầu tư xây dựng các bến sà lan tại khu vực Đồng Nai, Bình Dương’’ – ông Lộc khuyến nghị.
Phân tích, loại trừ:
Chọn “vận tải hàng hoá”: Vì trong đoạn văn ban đầu, có nói về "phương thức vận tải" và "tổng lượng hàng hoá được vận chuyển". Vì vậy, từ phù hợp nhất ở đây là "vận tải hàng hoá".
Chọn “đứng sau” vì trong đoạn văn có nói "đứng thứ hai là đường thuỷ nội địa". Vì vậy, từ phù hợp nhất ở đây là "đứng sau".
Chọn “đường bộ” vì trong đoạn văn có nói "đây là phương thức có phí vận chuyển cao hơn hẳn đường thuỷ". Vì vậy, từ phù hợp nhất ở đây là "đường bộ".
Chọn “đường thuỷ” vì đoạn văn có nói, đường bộ là phương thức có chi phí cao nhất, thì phương thức còn lại là đường thuỷ sẽ có chi phí thấp hơn. Vì vậy, từ phù hợp nhất ở đây là "đường thuỷ".
Chọn “khuyến khích” vì:
+ Từ khuyến khích có nghĩa là thúc đẩy, gợi ý, động viên ai làm gì. Từ này thể hiện sự tích cực, quan tâm và hỗ trợ của người nói đối với người nghe.
Từ đề xuất có nghĩa là nêu ra, trình bày một ý kiến, một kế hoạch cho ai xem xét và quyết định. Từ này thể hiện sự trung lập, chủ quan và chờ đợi của người nói đối với người nghe.
Trong đoạn văn ban đầu, ông Lộc là một chuyên gia về logistics, và ông ta muốn các DN chuyển sang sử dụng đường thuỷ nội địa hơn để giảm chi phí và tăng hiệu quả. Vì vậy, ông ta không chỉ trình bày một ý kiến mà còn thúc đẩy, gợi ý và động viên các DN làm theo. Do đó, từ khuyến khích phù hợp hơn là từ đề xuất trong trường hợp này.
Từ sự phân tích và suy luận trên, ta có các từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: vận tải hàng hoá
- Vị trí thả 2: đứng sau
- Vị trí thả 3: đường bộ
- Vị trí thả 4: đường thuỷ
- Vị trí thả 5: khuyến khích
Câu 8:
Từ nội dung của đoạn 7, hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Tiến sĩ KC Chang khuyên doanh nghiệp nên dùng dịch vụ hải quan của những nhà cung cấp có uy tín, chuyên nghiệp và có trình độ để giảm chi phí vận chuyển hàng hoá.
Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [7]
Lời giải
→ Ý kiến trên: Đúng.
- Căn cứ vào nội dung ở đoạn 7:
Theo Tiến sĩ KC Chang - chuyên gia thủ tục hải quan kiêm pháp chế thương mại khu vực châu Á - Thái Bình Dương thuộc GEODIS Logistics, khi nhập khẩu hàng hoá vào Hoa Kỳ, DN phải tuân thủ quy định của mọi pháp luật đặc biệt có thể áp dụng đối với hàng hoá; tìm hiểu kỹ các quy định về đóng gói và dán nhãn tại Hoa Kỳ trước khi xuất khẩu; phải xin giấy phép nhập khẩu để được nhập khẩu các mặt hàng được kiểm soát… Do đó, nên sử dụng nhà cung cấp dịch vụ hải quan có giấy phép và đủ trình độ để vận chuyển hàng hoá nhằm tiết giảm chi phí.
→ Ý kiến trên hoàn toàn phù hợp với nội dung của đoạn văn. Do đó, ý kiến trên đúng.
Chọn A
Câu 9:
Theo các chuyên gia tại Diễn đàn Logistics với khu vực châu Âu - châu Mỹ 2022, DN XNK nên thay đổi điều kiện bán hàng, mua hàng sang giá CIF thay vì FOB nhằm mục đích gì?
Chọn đáp án không đúng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn [8,9,10]
Lời giải
Điều kiện bán hàng CIF (Cost, Insurance and Freight) có nghĩa là người bán phải chịu trách nhiệm về chi phí, bảo hiểm và vận chuyển hàng hóa đến cảng đích. Điều kiện bán hàng FOB (Free On Board) có nghĩa là người bán chỉ chịu trách nhiệm về chi phí và vận chuyển hàng hóa đến cảng xuất phát.
Do đó, khi DN XNK thay đổi điều kiện bán hàng, mua hàng sang giá CIF thay vì FOB, họ sẽ có những lợi ích sau:
- Chủ động hơn trong việc sử dụng các lịch vận chuyển phù hợp: Họ có thể lựa chọn các hãng vận tải uy tín và tin cậy, không phụ thuộc vào người bán.
- Tìm kiếm nguồn cung cấp cạnh tranh uy tín nhằm tiết kiệm chi phí cước tàu: Họ có thể so sánh giá cả và chất lượng của các nguồn cung cấp khác nhau, không bị ép buộc mua hàng từ người bán.
- Giảm thiểu các rủi ro trong quá trình vận chuyển: Họ có thể bảo hiểm hàng hóa và được bồi thường nếu có sự cố xảy ra trong quá trình vận chuyển.
- Tuy nhiên, khi DN XNK thay đổi điều kiện bán hàng, mua hàng sang giá CIF thay vì FOB, họ không nhất thiết tăng cường khả năng cạnh tranh với các DN XNK kháC. Đó là vì giá CIF thường cao hơn giá FOB do bao gồm chi phí vận chuyển và bảo hiểm. Do đó, DN XNK có thể gặp khó khăn khi bán hàng cho các khách hàng nhạy cảm với giá.
Vậy nên, đáp án không đúng là B. Tăng cường khả năng cạnh tranh với các DN XNK khác.
Chọn B
Câu 10:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Đoạn trích trên được kể theo ngôi thứ nhất và ngôi thứ ba, người kể chuyện là tía của An.
Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung câu chuyện.
Lời giải
Ý kiến trên: Sai
- Đoạn trích trên được trích từ truyện “Người đàn ông cô độc giữa rừng”, thuộc tiểu thuyết “Đất rừng phương Nam” của nhà văn Đoàn Giỏi.
- Người kể lại câu chuyện trong đoạn trích trên kể theo ngôi thứ ba. Đến phần cuối đoạn trích, tác giả lại chuyển về kể theo ngôi thứ nhất (xưng “tôi”). Ngôi kể ở đoạn trích này có tác dụng khắc hoạ chân dung Võ Tòng một cách khách quan, sinh động hơn, giúp người đọc nhìn nhận từ nhiều phía khác nhau,...
- Ngoài ra, người kể chuyện là An, không phải là tía của An.
Chọn B
Câu 11:
Đoạn trích tập trung khắc hoạ nhân vật Võ Tòng từ các phương diện nào sau đây?
Chọn 2 đáp án đúng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung cả đoạn trích để chỉ ra các phương diện khi khắc hoạ nhân vật Võ Tòng
Lời giải
Đoạn trích tập trung khắc hoạ nhân vật Võ Tòng từ các phương diện: xuất thân và hành động
- Xuất thân (lai lịch): Đoạn trích kể lại quá khứ của Võ Tòng, từ khi ông bị bắt tội giết địa chủ, ngồi tù mười năm, trở về quê nhưng mất hết gia đình, rồi bỏ đi giang hồ.
- Hành động: Đoạn trích cũng mô tả những hành động của Võ Tòng, như giết hổ, đánh trả địa chủ, sẵn sàng nhận tội, đi tù, trở về và bỏ vào rừng sống một mình,...
- Đoạn trích không thể hiện rõ ngôn ngữ và suy nghĩ của nhân vật.
Chọn A, C
Câu 12:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn trích
Lời giải
- Chuyện Võ Tòng giết hổ hé mở về cuộc đời nhân vật là một: Cuộc đời gian truân, éo le.
- Cuộc đời ông phải chịu nhiều bất hạnh và đau khổ, từ việc bị tù oan, mất vợ con, đến việc phải sống đơn độc trong rừng. Cuộc đời của ông không có nhiều an nhàn, sung sướng mà chỉ toàn những gian nan, vất vả.
Chọn B
Câu 13:
Hãy điền một cụm từ không quá hai tiếng vào chỗ trống để hoàn thành nhận định sau.
Câu văn "đánh lên đầu là nơi thờ phụng ông bà" là nhằm bảo vệ _______ của bản thân và gia đình Võ Tòng.
 Xem đáp án
Xem đáp án
Đáp án: "danh dự"
Phương pháp giải
Căn cứ vào nội dung đoạn trích và hiểu biết về truyền thống dân gian người Việt.
Lời giải
- Câu "đánh lên đầu là nơi thờ phụng ông bà" là nhằm bảo vệ danh dự của bản thân và gia đình. Đó là một cách thể hiện sự tôn trọng và kính trọng đối với tổ tiên và cha mẹ, cũng như sự tự trọng và kiêu hãnh của con người.
- “Đánh lên đầu là nơi thờ phụng ông bà” là một câu nói dân gian của người Việt Nam, thể hiện sự tôn kính và hiếu thảo đối với tổ tiên và cha mẹ. Đầu là nơi trí tuệ, linh hồn và danh dự của con người, không được xúc phạm hay tổn thương. Đánh lên đầu là hành vi xúc phạm nặng nề nhất, coi như là phỉ báng và xúc phạm đến tổ tiên và cha mẹ của người bị đánh. Người Việt Nam coi trọng việc thờ cúng ông bà tổ tiên cho rằng họ luôn bảo vệ và ban phước cho con cháu. Vì vậy, khi bị đánh lên đầu, người ta thường nói “đánh đâu thì còn nhịn được, chứ đánh lên đầu là nơi thờ phụng ông bà...thì số mày tới rồi!” để bày tỏ sự phẫn nộ và quyết tâm trả thù.
- Trong đoạn trích trên, câu nói này được dùng để miêu tả tâm trạng của Võ Tòng khi bị tên địa chủ quyền thế nhất xã vung ba toong đánh lên đầu . Võ Tòng là một người có võ nghệ cao cường, thích hành hiệp trượng nghĩa, không chịu nhục nhã trước kẻ ác. Khi bị xúc phạm đến danh dự và tổ tiên của mình, ông đã dùng dao chém trả vào mặt tên địa chủ. Đây là một hành động dũng cảm nhưng cũng gây ra hậu quả nghiêm trọng cho cuộc đời của ông.
=> Đáp án cần điền là: danh dự
Câu 14:
Hoàn thành câu hỏi bằng cách điền những từ ngữ có trong bài đọc vào chỗ trống.
Nhân vật Võ Tòng xuất hiện với lai lịch bí ẩn, vẻ ngoài khác lạ nhưng lại có một tấm lòng hào hiệp, trượng nghĩa. Trước khi đi tù, anh là người _______, yêu thương vợ, cương trực, khẳng khái. Sau khi đi tù về và vào rừng ở, anh trở thành người đàn ông _______; anh giỏi võ nghệ, chất phác, thật thà, hào hiệp, sẵn sàng giúp đỡ mọi người. Võ Tòng mang những phẩm chất đáng quý của con người Nam Bộ.
 Xem đáp án
Xem đáp án
Đáp án:
Nhân vật Võ Tòng xuất hiện với lai lịch bí ẩn, vẻ ngoài khác lạ nhưng lại có một tấm lòng hào hiệp, trượng nghĩa. Trước khi đi tù, anh là người hiền lành, yêu thương vợ, cương trực, khẳng khái. Sau khi đi tù về và vào rừng ở, anh trở thành người đàn ông cô độc; anh giỏi võ nghệ, chất phác, thật thà, hào hiệp, sẵn sàng giúp đỡ mọi người. Võ Tòng mang những phẩm chất đáng quý của con người Nam Bộ.
Phương pháp giải
Căn cứ vào nội dung đoạn trích
Lời giải
Phân tích, suy luận:
- Trước khi đi tù, anh là người _____, yêu thương vợ, cương trực, khẳng khái.
-> Câu văn trên trình bày những phẩm chất của Võ Tòng trước khi đi tù. Từ cần điền vào chỗ trống phải đáp ứng các yêu cầu sau:
+ Từ này có trong đoạn trích.
+ Là một từ ngữ chỉ phẩm chất, tính cách con người.
=> Từ cần điền là hiền lành. Vì đoạn trích có câu: “Gã đàn ông hiền lành, quý vợ rất mực ấy bèn liều xách dao đến bụi tre đình làng xẳn một mụt măng”.
- Sau khi đi tù về và vào rừng ở, anh trở thành người đàn ông _____; anh giỏi võ nghệ, chất phác, thật thà, hào hiệp, sẵn sàng giúp đỡ mọi người.
-> Câu văn trên trình bày hoàn cảnh và các đặc điểm của Võ Tòng sau khi ra tù. Từ cần điền vào chỗ trống phải đáp ứng các yêu cầu sau:
+ Từ này có trong đoạn trích.
+ Là một từ ngữ chỉ hoàn cảnh của Võ Tòng.
=> Từ cần điền là cô độc. Vì đoạn trích có câu: “Hơn mười năm sống trơ trọi giữa rừng, mặc dầu, cũng có nhiều người đánh tiếng mối mai cho gã, nhưng tuyệt nhiên Võ Tòng không để mắt tới một người đàn bà nào nữa”. Câu văn này nói lên hoàn cảnh cô đơn của Võ Tòng và trong nhan đề đoạn trích có dòng “Người đàn ông cô độc”. Từ ngữ “cô độc” là từ ngữ chính xác nhất để điền vào vị trí trên.
- Đoạn văn hoàn thiện: Nhân vật Võ Tòng xuất hiện với lai lịch bí ẩn, vẻ ngoài khác lạ nhưng lại có một tấm lòng hào hiệp, trượng nghĩa. Trước khi đi tù, anh là người hiền lành, yêu thương vợ, cương trực, khẳng khái. Sau khi đi tù về và vào rừng ở, anh trở thành người đàn ông cô độc, giỏi võ nghệ, chất phác, thật thà, hào hiệp, sẵn sàng giúp đỡ mọi người. Võ Tòng mang những phẩm chất đáng quý của con người Nam Bộ.
Câu 15:
Hành vi chống trả tên địa chủ ngang ngược với việc đánh hổ của Võ Tòng có điểm gì giống nhau?
Chọn đáp án không đúng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Căn cứ vào nội dung đoạn trích
Lời giải
Hành vi chống trả tên địa chủ ngang ngược với việc đánh hổ của Võ Tòng có điểm giống nhau là: cái ác đều tự tìm đến với nhân vật, đều là hành động chính đáng bảo vệ bản thân, và nhân vật Võ Tòng đều thể hiện sự mạnh mẽ chống trả cái ác tới cùng.
- Phân tích, loại trừ:
+ Câu A: Cái ác đều tự tìm đến với nhân vật. Điểm giống nhau là cả hai trường hợp đều là do cái ác (hổ và tên địa chủ) chủ động tấn công Võ Tòng mà không có lý do chính đáng. Võ Tòng không có ý định gây hấn hay xung đột với cái ác mà chỉ là nạn nhân bị hại.
+ Câu B: Đều là hành động chính đáng bảo vệ bản thân. Điểm giống nhau là cả hai trường hợp đều là do Võ Tòng không chịu nhục nhã hay để bản thân bị tổn thương trước cái ác. Võ Tòng coi trọng sự tôn trọng và công bằng cho bản thân và gia đình. Võ Tòng cũng không để cho cái ác xâm phạm hay hủy hoại cuộc sống của mình và người thân.
+ Câu C: Nhân vật Võ Tòng mạnh mẽ chống trả cái ác. Cả hai trường hợp gặp hổ tấn công và bị tên địa chủ bắt nạt, Võ Tòng đều không chịu khuất phục mà mạnh mẽ chống lại cái ác đến cùng để bảo vệ bản thân và danh dự của bản thân, gia đình.
+ Câu D: Kết quả chung là cái ác đều bị tiêu diệt. Đây là điểm khác của hai sự việc vì “tiêu diệt” được hiểu là “chết” nhưng trong hai trường hợp trên, con hổ thì bị giết chết còn tên địa chủ thì vẫn sống, sau này hắn còn lấy vợ của Võ Tòng khi Võ Tòng đang ngồi trong khám lạnh.
=> Đáp án không đúng là: Kết quả chung là cái ác đều bị tiêu diệt.
Chọn D
Câu 16:
Từ thông tin của đoạn trích, hãy hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí để sắp xếp lại các sự kiện theo thứ tự xảy ra trong nội dung.
Võ Tòng bị tù đày, Võ Tòng lấy vợ, Võ Tòng chém tên địa phủ, Võ Tòng giết con hổ chúa, Võ Tòng bỏ làng ra đi, Võ Tòng chết.
Các sự kiện được sắp xếp theo thứ tự xảy ra trong cuộc đời Võ Tòng là: __________, __________, __________, __________, __________.
 Xem đáp án
Xem đáp án
Đáp án
Các sự kiện được sắp xếp theo thứ tự xảy ra trong cuộc đời Võ Tòng là: Võ Tòng lấy vợ Võ Tòng chém tên địa chủ Võ Tòng bị tù đày Võ Tòng bỏ làng ra đi Võ Tòng giết con hổ chúa
Phương pháp giải
Căn cứ vào nội dung đoạn trích
Lời giải
Suy luận, phân tích:
- Võ Tòng lấy vợ: Đây là sự kiện đầu tiên xảy ra trong cuộc đời Võ Tòng. Võ Tòng có một gia đình đàng hoàng như ai. Vợ gã là một người đàn bà trông cũng xinh mắt. Chị ấy, lúc có chửa đứa đầu lòng, cứ kêu thèm ăn măng.
- Võ Tòng chém tên địa chủ: Đây là sự kiện thứ hai xảy ra trong cuộc đời Võ Tòng. Vì muốn làm vừa lòng vợ, Võ Tòng liều xách dao đến bụi tre đình làng xẳn một mụt măng. Khi về qua ngang bờ tre nhà tên địa chủ, tên này bắt gã bỏ mụt măng xuống và vu cho gã lấy trộm măng tre của hắn. Gã một mực cãi lại, nhưng tên địa chủ quyền thế nhất xã ấy cứ vung ba toong đánh lên đầu gã. “Đánh đâu thì còn nhịn được, chứ đánh lên đầu là nơi thờ phụng ông bà…. thì số mày tới rồi!”. Lưỡi dao trên tay gã không cho phép tên địa chủ ngang ngược kia giơ tay đánh ba toong lên đầu gã đến cái thứ hai. Nhát dao chém trả vào mặt đã gí tên bóc lột và hống hách này nằm gục xuống vũng máu.
- Võ Tòng bị tù đày: Đây là sự kiện thứ ba xảy ra trong nội dung. Sau khi giết tên địa chủ, Võ Tòng không trốn chạy. Gã đường hoàng xách dao đến ném trước nhà việc, bỏ tay chịu tội. Sau mười năm tù đày, gã trở về làng cũ.
- Võ Tòng bỏ làng ra đi: Đây là sự kiện thứ tư xảy ra trong nội dung. Khi trở về làng cũ, Võ Tòng nghe tin vợ đã làm lẽ tên địa chủ kia, và đứa con trai độc nhất mà gã chưa biết mặt thì đã chết từ khi gã còn ngồi trong khám lạnh. Người trong xã vốn ghét tên địa chủ hống hách, khấp khởi chờ xem cuộc rửa thù bằng máu lần thứ hai. Nhưng họ đã thất vọng. Gã chỉ kêu trời một tiếng rồi cười nhạt bỏ làng ra đi.
- Võ Tòng giết con hổ chúa: Đây là sự kiện cuối cùng xảy ra trong nội dung. Sau khi bỏ làng ra đi, Võ Tòng sống trơ trọi giữa rừng. Một buổi trưa, gã đang ngủ trong lều, có con hổ chúa mò vào, từ ngoài sân phóng một cái phủ lên người gã. Bất thần gã tỉnh dậy. Gã vớ luôn cái mác bên người, cũng không kịp ngồi dậy nữa, cử nằm ngửa thế mà xóc mũi mác lên đâm thẳng một nhát vào hàm dưới con hổ chúa, hai chân gã đá thốc lên bụng nó, không cho con ác thú kịp chụp xuống người. Con hổ chúa lộn vòng, rơi xuống đất. Lưỡi mác đâm từ hàm dưới thấu lên tận óc, làm nó không hả họng được, nhưng vẫn còn cố vớt cái tát cuối cùng, để lại trên mặt gã một hàng sẹo khủng khiếp chạy từ thái dương xuống cổ. Không biết có phải do đấy mà gã mang tên “Võ Tòng” hay không?
Dựa vào nội dung đoạn trên cùng cách phân tích và suy luận, ta có các từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: Võ Tòng lấy vợ
- Vị trí thả 2: Võ Tòng chém tên địa chủ
- Vị trí thả 3: Võ Tòng bị tù đày
- Vị trí thả 4: Võ Tòng bỏ làng ra đi
- Vị trí thả 5: Võ Tòng giết con hổ chúa.
Câu 17:
Những người trong xã vốn ghét tên địa chủ vì lý do gì?
Chọn các đáp án đúng:
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ đoạn trích và trả lời câu hỏi
Lời giải
Những người trong xã vốn ghét tên địa chủ vì: Vì tên địa chủ bóc lột và hống hách và Vì tên địa chủ lấy vợ của Võ Tòng làm vợ lẽ
Phân tích, loại trừ:
- Đáp án A, D đúng vì đoạn trích có nói rằng tên địa chủ là người bóc lột và hống hách. Gã đã vu cho Võ Tòng lấy trộm măng tre của hắn và vung ba toong đánh lên đầu Võ Tòng. Gã cũng đã lấy vợ của Võ Tòng làm vợ lẽ khi gã đi tù. Những hành động này cho thấy tên địa chủ là một người ác độc và không có lòng nhân ái.
- Đáp án B sai vì đoạn trích không nói rằng tên địa chủ lấy trộm măng tre của người dân. Gã chỉ vu cho Võ Tòng lấy trộm măng tre của hắn mà thôi. Chúng ta không biết gã có lấy trộm măng tre của người dân khác hay không.
- Đáp án C sai vì đoạn trích có nói rằng tên địa chủ quyền thế nhất xã, nhưng đó không phải là lý do khiến người trong xã ghét gã. Người trong xã ghét gã vì gã bóc lột và hống hách, chứ không phải vì gã quyền thế. Nếu gã quyền thế mà có lòng nhân ái và công bằng, người trong xã có thể không ghét gã.
Chọn A, D
Câu 18:
Hoàn thành câu hỏi bằng cách chọn đáp án Đúng hoặc Sai.
Những chữ bùa xanh lè xăm rằn rực trên người Võ Tòng là do gã có từ lúc gã đi giang hồ.
Đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ nội dung đoạn trích và trả lời câu hỏi
Lời giải
-> Ý kiến trên: SAI
Trong nội dung đoạn trích có nói rằng những chữ bùa xanh lè xăm rằn rực trên người Võ Tòng là do gã có từ lúc nào, thì có kẻ nói đó là dấu vết trong những năm gã ở tù, lại có người bảo đó là mới có từ lúc gã đi giang hồ. Điều này cho thấy không ai biết chắc chắn nguồn gốc của những chữ bùa trên người gã. Có thể là do gã có từ lúc gã ở tù, hoặc từ lúc gã đi giang hồ, hoặc từ một thời điểm kháC.
Vì vậy, không thể khẳng định rằng những chữ bùa xanh lè xăm rằn rực trên người Võ Tòng là do gã có từ lúc gã đi giang hồ.
Chọn B
Câu 19:
Từ thông tin của đoạn trích, hãy hoàn thành nhận định sau bằng cách kéo thả các từ vào đúng vị trí:
Thủy Hử, giết hổ, Tam quốc diễn nghĩa, cứu người, 108, 118
Người ta gọi nhân vật chính trong truyện là Võ Tòng dựa vào sự việc _______ của anh. Sự việc này có mối liên hệ với tác phẩm _______- một tác phẩm kinh điển của cổ điển phương Đông viết về _______ vị anh hùng Lương Sơn Bạc.
 Xem đáp án
Xem đáp án
Đáp án
Người ta gọi nhân vật chính trong truyện là Võ Tòng dựa vào sự việc giết hổ của anh. Sự việc này có mối liên hệ với tác phẩm Thủy hử - một tác phẩm kinh điển của cổ điển phương Đông viết về 108 vị anh hùng Lương Sơn Bạc.
Phương pháp giải
Căn cứ vào nội dung đoạn trích
Lời giải
Suy luận, phân tích:
- Người ta gọi nhân vật chính trong truyện là Võ Tòng vì: Anh ta giết chết một con hổ chúa hung bạo khi bị nó tấn công.
-> Vị trí 1: giết hổ
- Tên gọi này bắt nguồn từ nhân vật Võ Tòng trong Thủy hử của Thi Nại Am, đây là một hành giả võ nghệ cao cường, trượng nghĩa hào hiệp, có nhiều sự tích nổi tiếng như Võ Tòng đả hổ, Võ Tòng sát tẩu, Võ Tòng đánh Tây Môn Khánh... Anh ta là một trong 108 anh hùng Lương Sơn BạC.
-> Vị trí 2: Thủy hử
-> Vị trí 3: 108
- Đoàn Giỏi có nhắc đến Võ Tòng đánh hổ ở Cảnh Dương cương (Kiến Dương cang) trong truyện Đất rừng phương Nam:
Võ Tòng mà đả hổ
Tại Kiến Dương Cang
Gặp anh thời giữa đàng…
- Ngoài ra, trong truyện cũng nhắc đến “Không biết có phải do đấy mà gã mang tên “Võ Tòng” hay không?” khi kể đến chi tiết Võ Tòng giết hổ.
Dựa vào nội dung đoạn trên cùng cách phân tích và suy luận, ta có các từ phù hợp để kéo thả vào các vị trí là:
- Vị trí thả 1: giết hổ
- Vị trí thả 2: Thủy hử
- Vị trí thả 3: 108
Câu 20:
Phần tư duy khoa học / giải quyết vấn đề
 Xem đáp án
Xem đáp án
Phương pháp giải
Quan sát và phân tích bảng số liệu và đồ thị
Lời giải
Trong khoảng thời gian 0–2 giây, nhiệt độ của Vật liệu A tăng khoảng 20°C. Trong khoảng thời gian 2–12 giây và từ 12 – 22 giây, nhiệt độ của Vật liệu A không đổi. Trong khoảng thời gian 22–24 giây, nhiệt độ của Vật liệu A tăng khoảng 25°C.
Do thời lượng của khoảng thời gian 0 –2 giây bằng thời lượng của khoảng thời gian 22–24 giây và mức tăng nhiệt độ lớn hơn trong khoảng thời gian sau, nên nhiệt độ tăng nhanh nhất trong khoảng thời gian 22–24 giây.
Chọn D
Câu 21:
Dựa vào đoạn văn và Bảng 1, khối lượng riêng của Chất lỏng A là bao nhiêu?
 Xem đáp án
Xem đáp án
Phương pháp giải
Quan sát và phân tích bảng số liệu và đồ thị
Lời giải
Hình 1 cho thấy Vật liệu A ở thể lỏng từ Thời điểm 0 đến Thời điểm 2. Bảng 1 cho thấy Vật liệu A có thể tích 1 cm3 trong thời gian này. Theo đoạn văn, khối lượng của Vật liệu A là 1 g.
Khối lượng riêng của chất lỏng A là: \[D = \frac{m}{V} = 1\,\,g/c{m^3}\]
Chọn B
Câu 22:
Quan sát hình 1 và cho biết các nhận xét sau đây đúng hay sai?
|
PHÁT BIỂU |
ĐÚNG |
SAI |
|
Trong khoảng −100C đến 100C chất A đang ở thể lỏng |
||
|
Nhiệt độ sôi của chất A là khoảng 100C |
||
|
Trong quá trình biến đổi chất A có xảy ra hiện tượng thăng hoa |
||
|
Chất A ở trạng thái hỗn hợp trong khoảng 22s |
 Xem đáp án
Xem đáp án
Đáp án
|
PHÁT BIỂU |
ĐÚNG |
SAI |
|
Trong khoảng −100C đến 100C chất A đang ở thể lỏng |
X | |
|
Nhiệt độ sôi của chất A là khoảng 100C |
X | |
|
Trong quá trình biến đổi chất A có xảy ra hiện tượng thăng hoa |
X | |
|
Chất A ở trạng thái hỗn hợp trong khoảng 22s |
X |
Phương pháp giải
Phân tích đồ thị trong hình 1
Áp dụng các kiến thức đã học về quá trình biến đổi trạng thái của chất
Lời giải
Từ Hình 1 ta có:
Trong khoảng −100C đến 100C chất A đang ở thể lỏng.
Nhiệt độ sôi của chất A sẽ là 100C vì khi đó bắt đầu có khí và chất A chuyển hoàn toàn sang thể khí.
Quá trình thăng hoa là quá trình chất chuyển trạng thái trực tiếp từ rắn sang khí, không quá thể lỏng. Ở đây không diễn ra quá trình thăng hoa
Chất A sẽ ở trạng thái hỗn hợp khí và lỏng trong vòng 20s từ giây thứ 2 đến giây thứ 22.
Câu 23:
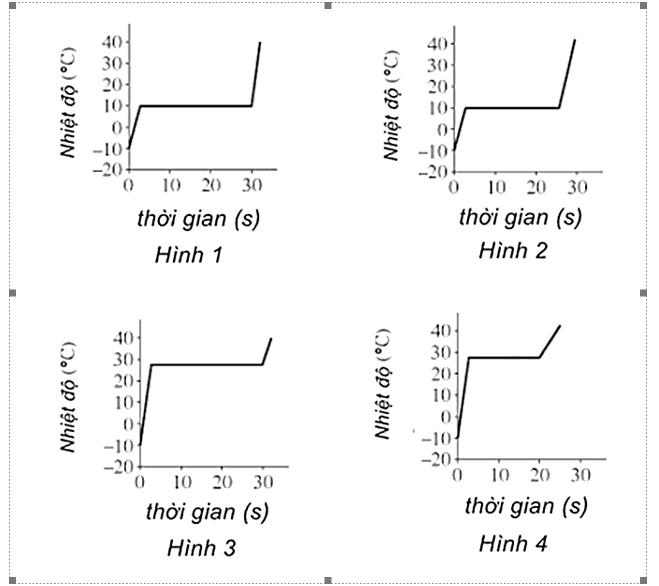
Giả sử 1 g Vật liệu D ở –10°C được nung nóng với tốc độ 10 cal/giây và giữ ở 1 atm cho đến khi toàn bộ chất lỏng hóa hơi. Dựa vào Hình 1 và Bảng 2, biểu đồ nhiệt độ của Vật liệu D theo thời gian sẽ được biểu thị tốt nhất bằng biểu đồ nào sau đây?
 Xem đáp án
Xem đáp án
Phương pháp giải
Quan sát và phân tích bảng số liệu và đồ thị
Lời giải
Theo Bảng 2, điểm sôi của Vật liệu D là 28°C. Vì vậy, phần nằm ngang của biểu đồ phải ở 28°C. Vì cần 270 cal để biến 1 g Chất lỏng D ở điểm sôi của nó thành khí, chiều rộng của phần nằm ngang của biểu đồ phải tương ứng với 270 cal nhiệt. Hệ thống sưởi xảy ra với tốc độ 10 cal/giây. Do đó, phần nằm ngang của biểu đồ phải kéo dài hơn 27 giây.
Chọn C
Câu 24:
Bảng 1 và Hình 1 hỗ trợ tốt nhất cho giả thuyết nào sau đây về nhiệt độ và thể tích của Vật liệu A? (Lưu ý: Áp suất được giả định là không đổi.)
 Xem đáp án
Xem đáp án
Phương pháp giải
Quan sát và phân tích bảng số liệu và đồ thị
Lời giải
Theo Hình 1, Vật liệu A hoàn toàn ở pha khí từ Thời gian 22 giây đến Thời gian 24 giây. Trong thời gian này, nhiệt độ của Vật liệu A tăng lên. Theo Bảng 1, trong thời gian này, khối lượng Vật liệu A cũng tăng lên.
Chọn D
Câu 25:
Giả sử 1 g mẫu Vật liệu lỏng A–D mới bắt đầu sôi. Nếu mỗi chất lỏng hấp thụ nhiệt với tốc độ 10 cal/giây trong khi giữ ở 1 atm, thì chất lỏng đầu tiên bị biến hoàn toàn thành khí là _______
 Xem đáp án
Xem đáp án
Đáp án: "chất A"
Phương pháp giải
Quan sát và phân tích bảng số liệu và đồ thị
Lời giải
Hình 1 cho thấy điểm sôi của Vật liệu A là 10°C, vì ở nhiệt độ này, Vật liệu A chuyển từ dạng lỏng hoàn toàn sang dạng khí hoàn toàn. Chất A ở nhiệt độ sôi từ thời gian 2 giây đến thời gian 22 giây. Trong 20 giây này, nó được làm nóng với tốc độ 10 cal/giây. Vì vậy, cần 200 cal để biến 1 g Chất lỏng A ở điểm sôi của nó thành khí. Lượng nhiệt cần thiết để biến chất lỏng tại điểm sôi của nó thành chất khí được đưa ra trong Bảng 2 đối với Vật liệu B, C và D. Các giá trị này lần lượt là 500 cal, 610 cal và 270 cal. Do đó, lượng nhiệt cần thiết để thực hiện quá trình chuyển đổi này là thấp nhất đối với Vật liệu A. Vì vậy, Vật liệu A sẽ hoàn toàn biến thành khí nhanh hơn các vật liệu khác.
Câu 26:
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin số liệu trong Hình 2.
Lời giải
Quan sát đồ thị hình 2 ta có: trong khoảng thời gian từ 0→30s thì điện áp trên tụ chỉ tăng.
Chọn A
Câu 27:
Dựa trên Bảng 2, bắt đầu từ thời điểm t = 0s, rất có thể phải mất bao lâu để điện tích trên tụ điện bằng 200pC trong Nghiên cứu 2?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào số liệu trong bảng 2.
Lời giải
Từ bảng 2 ta thấy: trong khoảng thời gian 5→10s thì điện tích của tụ sẽ là 240pC→150pC
⇒điện tích trong tụ là 200pC sẽ có thể là trong khoảng thời gian là 5→10s
Chọn B
Câu 28:
Điền số thích hợp vào chỗ trống:
Giả sử rằng trong Nghiên cứu 1, điện áp của pin là 10 V thay vì 4 V. Dựa trên Hình 2, khi tụ điện được sạc đầy, điện áp trên tụ điện sẽ là ______
 Xem đáp án
Xem đáp án
Đáp án: "10V | 10 V"
Phương pháp giải
Phân tích đồ thị hình 2.
Lời giải
Theo hình 2, điện áp ban đầu của pin là 4 V và điện áp tối đa mà tụ đạt tới cũng là 4 V, bằng với điện áp của pin.
⇒khi hiệu điện thế ắc quy là 10 V thì hiệu điện thế cực đại của tụ điện cũng là 10 V.
Câu 29:
Từ nghiên cứu 1:
Tại thời điểm t = 0 tụ không được tích điện, đúng hay sai?
 Xem đáp án
Xem đáp án
Phương pháp giải
Phân tích thông tin và đồ thị bài cung cấp.
Lời giải
Pin ở nghiên cứu 1 đang nạp điện cho tụ nên khi t = 0 thì tụ chưa được nạp điện.
Chọn A
Câu 30:
Dựa trên Bảng 1 và Hình 2, khi tụ điện được phóng điện trong khoảng thời gian t = 0 và t =30s trong Nghiên cứu 2, điện áp trên tụ điện:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin bảng 1 và hình 2 cung cấp.
Lời giải
Qua hình 2 và bảng 1 cho thấy khi tụ điện đang tích điện thì điện áp tăng dần và điện tích Q của tụ cũng tăng; sau đó, khi tụ phóng điện thì điện tích của tụ giảm và hiệu điện thế cũng giảm.
Chọn B
Câu 31:
Câu nào sau đây giải thích đúng nhất giá trị của I tại thời điểm t = 100s trong Hình 4? Tại thời điểm t = 100s:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào đồ thị hình 4 cung cấp.
Lời giải
Có thể thấy từ hình 4, khi t ≥ 60s ⇒ I = 0
⇒ t = 100s ⇔ I = 0
⇒ lúc này tụ điện đã phóng điện hoàn toàn.
Chọn D
Câu 32:
Những nhận định sau là đúng hay sai?
|
PHÁT BIỂU |
ĐÚNG |
SAI |
|
Mục đích thực hiện Thí nghiệm 1 và Thí nghiệm 2 giống nhau. |
||
|
Việc so sánh kết quả của các mẫu đồng xu II và IV để ủng hộ giả thuyết: Kẽm được mạ nhiều hơn khi được tiếp xúc với dung dịch bạc nitrat so với dung dịch đồng sunfat. |
 Xem đáp án
Xem đáp án
Đáp án
|
PHÁT BIỂU |
ĐÚNG |
SAI |
|
Mục đích thực hiện Thí nghiệm 1 và Thí nghiệm 2 giống nhau. |
X | |
|
Việc so sánh kết quả của các mẫu đồng xu II và IV để ủng hộ giả thuyết: Kẽm được mạ nhiều hơn khi được tiếp xúc với dung dịch bạc nitrat so với dung dịch đồng sunfat. |
X |
Phương pháp giải
Đọc cách thực hiện Thí nghiệm 1 cũng như quan sát kết quả trong bảng 1 để rút ra nhận xét.
Lời giải
- Nhận định: “Mục đích thực hiện Thí nghiệm 1 và Thí nghiệm 2 giống nhau” là SAI, vì quy trình thực hiện Thí nghiệm 1 và Thí nghiệm 2 là khác nhau. Thí nghiệm 1 có mục đích là khảo sát sự ảnh hưởng của dung dịch mạ và cường độ dòng điện tới quá trình mạ kim loại quý lên trên mẫu đồng xu, còn Thí nghiệm 2 khảo sát thời gian thực hiện quá trình mạ và diện tích tiếp xúc của đồng xu ảnh hưởng như thế nào tới kết quả cuối cùng.
- Nhận định: "Việc so sánh kết quả của các mẫu đồng xu III và IV để ủng hộ giả thuyết rằng cường độ dòng điện tăng thì khối lượng bạc mạ lên kẽm giảm." là SAI, vì cường độ dòng điện tăng thì khối lượng bạc được mạ lên kẽm tăng.
Câu 33:
Việc so sánh kết quả của các mẫu đồng xu II và IV ủng hộ giả thuyết rằng kẽm được mạ nhiều hơn khi tiếp xúc với
 Xem đáp án
Xem đáp án
Phương pháp giải
So sánh các điều kiện thực hiện mạ đồng xu II và IV và kết quả thu được để chọn đáp án đúng.
Lời giải
Ta thấy đồng xu II và IV khác nhau về dung dịch mạ. Đồng xu II được nhúng vào dung dịch AgNO3 và có độ tăng khối lượng lớn hơn so với đồng xu IV được nhúng vào dung dịch CuSO4 và có độ tăng khôi lượng ít hơn. Như vậy kẽm được mạ nhiều hơn khi tiếp xúc với dung dịch AgNO3 so với dung dịch CuSO4.
Chọn C
Câu 34:
Điền cụm từ thích hợp vào chỗ trống
Thông qua Thí nghiệm 1 và Thí nghiệm 2, từ khối lượng kim loại phủ lên đồng xu hợp kim kẽm ta thấy việc có _______ chạy qua đồng xu là cần thiết trong quá trình mạ.
 Xem đáp án
Xem đáp án
Đáp án: "dòng điện"
Phương pháp giải
Đọc các thông tin trong đề bài, dựa vào những từ ngữ trong nhận định cần hoàn thiện để điền cụm từ thích hợp vào chỗ trống.
Lời giải
từ cần điền là "dòng điện".
Câu 35:
Kéo thả đáp án thích hợp vào chỗ trống
tỉ lệ thuận, tỉ lệ nghịch, đồng, bạc
Thông qua Thí nghiệm 1, ta thấy cường độ dòng điện và khối lượng kim loại bao phủ lên bề mặt đồng xu _______ với nhau. Quá trình mạ kim loại _______ lên bề mặt đồng xu xảy ra dễ dàng hơn so với quá trình mạ kim loại _______ lên bề mặt đồng xu.
 Xem đáp án
Xem đáp án
Đáp án
Thông qua Thí nghiệm 1, ta thấy cường độ dòng điện và khối lượng kim loại bao phủ lên bề mặt đồng xu tỉ lệ thuận với nhau. Quá trình mạ kim loại bạc lên bề mặt đồng xu xảy ra dễ dàng hơn so với quá trình mạ kim loại đồng lên bề mặt đồng xu.
Phương pháp giải
Quan sát bảng 1 để đưa ra nhận xét.
Lời giải
Thông qua Thí nghiệm 1, ta thấy cường độ dòng điện và khối lượng kim loại bao phủ lên bề mặt đồng xu tỉ lệ thuận với nhau. Quá trình mạ kim loại bạc lên bề mặt đồng xu xảy ra dễ dàng hơn so với quá trình mạ kim loại đồng lên bề mặt đồng xu.
Câu 36:
Nhận định dưới đây là đúng hay sai?
Thí nghiệm 1 và 2 không nghiên cứu quá trình mạ kim loại vàng lên đồng xu kẽm.
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào quy trình thực hiện thí nghiệm 1 và thí nghiệm 2.
Lời giải
Trong thí nghiệm 1 và 2 không khảo sát quá trình mạ kim loại vàng lên đồng xu. Thí nghiệm 1 khảo sát quá trình mạ kim loại bạc và đồng, thí nghiệm 2 khảo sát quá trình mạ kim loại bạc lên mẫu đồng xu.
Chọn A
Câu 37:
Trong thí nghiệm 1, nếu nhà khoa học đưa dòng điện 1 580 mA vào một đồng xu hợp kim kẽm bán kính 1 cm trong dung dịch đồng sunfat thì sau 30 phút sẽ mạ được khoảng bao nhiêu đồng?
 Xem đáp án
Xem đáp án
Phương pháp giải
Theo kết quả trong Bảng 1, khối lượng kim loại mạ lên đồng xu sẽ tăng theo cường độ dòng điện sử dụng. Vậy khối lượng Cu mạ lên đồng Cu tại 1 580 mA sẽ lớn hơn khối lượng Cu mạ được tại cường độ dòng điện 1 000 mA và nhỏ hơn khối lượng Cu mạ được tại 2 000 mA.
Lời giải
Kết quả phù hợp là 1,9 mg.
Chọn C
Câu 38:
Nếu nhà hoá học lặp lại thí nghiệm 1 nhưng nén từng mẫu đồng xu thành bán kính 0,5 cm để giảm đi diện tích tiếp xúc với dung dịch xung quanh thì khối lượng kim loại quý được mạ lên đồng xu có khả năng bị ảnh hưởng như nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Giảm diện tích tiếp xúc sẽ làm giảm lượng kim loại bám lên trên đồng xu.
Lời giải
Khối lượng kim loại bám lên trên đồng xu sẽ giảm nếu bán kính đồng xu giảm do giảm diện tích tiếp xúc.
Chọn A
Câu 39:
Giả sử rằng bất cứ khi nào nồng độ CH4 tăng lên, nhiệt độ trung bình toàn cầu sẽ tăng lên ngay lập tức và bất cứ khi nào nồng độ CH4 giảm, nhiệt độ trung bình toàn cầu sẽ giảm ngay lập tức. Dựa trên Hình 2, biểu đồ nào sau đây thể hiện đúng nhất biểu đồ nhiệt độ trung bình toàn cầu trong 11.000 năm qua?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa trên hình 2
Lời giải
Từ hình 2 ta thấy
- từ 5000 năm trước đến hiện tại nồng độ CH4 tăng => Nhiệt độ trung bình toàn cầu sẽ tăng
- từ 5000 năm trước đó nồng độ CH4 không đổi => Nhiệt độ trung bình toàn cầu coi như không đổi
=> Đồ thị hình D phù hợp
Chọn D
Câu 40:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào hình 2
Lời giải
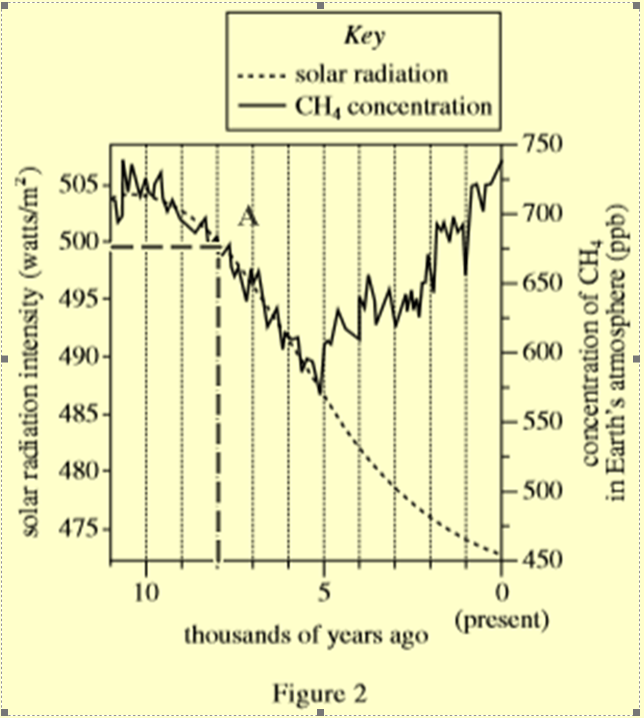
Từ trục hoành chọn mốc thời gian 8000 năm trước kẻ một đường thẳng song song với trục tung cắt đường biểu diễn tại điểm A. Từ A kẻ một đường thẳng song song với trục hoành cắt trục cường độ tại điểm cần xác định
=> Cường độ gần nhất với giá trị 500 watt/m2.
Câu 41:
Theo Hình 2, nếu xu hướng về nồng độ CH4 tiếp tục phù hợp với xu hướng về cường độ bức xạ mặt trời, thì Nồng độ CH4 hiện tại rất có thể là
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào hình 2
Lời giải
Từ hình 2 ta thấy chiều biến đổi về nồng độ CH4 cùng chiều với cường độ bức xạ mặt trời
Ở thời điểm hiện tại nồng độ CH4 gần nhất với 450 ppb thuộc khoảng dưới 550 ppb
Chọn A
Câu 42:
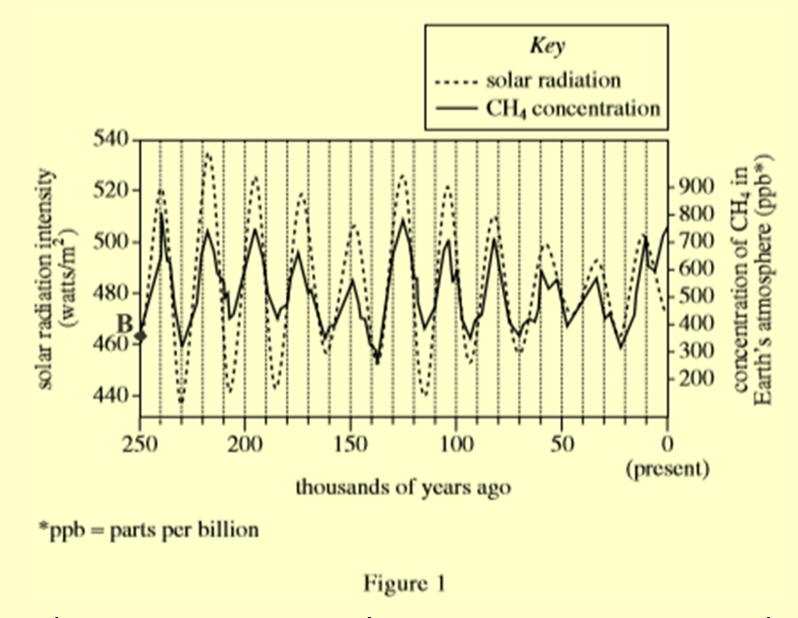
Dựa trên Hình 1, cường độ bức xạ mặt trời trung bình trong 250.000 năm qua gần nhất với giá trị nào sau đây?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào hình 1
Lời giải
Câu 43:
Điền số thích hợp vào chỗ trống:
Một chu kỳ bức xạ mặt trời là khoảng thời gian giữa cường độ bức xạ mặt trời cực đại và cường độ bức xạ mặt trời cực đại tiếp theo . Theo Hình 1, độ dài trung bình của một chu kỳ bức xạ mặt trời trong 250.000 năm qua là ______
 Xem đáp án
Xem đáp án
Đáp án: "195000 đến 220000 năm"
Phương pháp giải
Dựa vào hình 1
Lời giải
Từ hình 1 và thông tin về một chu kỳ bức xạ mặt trời trên suy ra điểm C, D
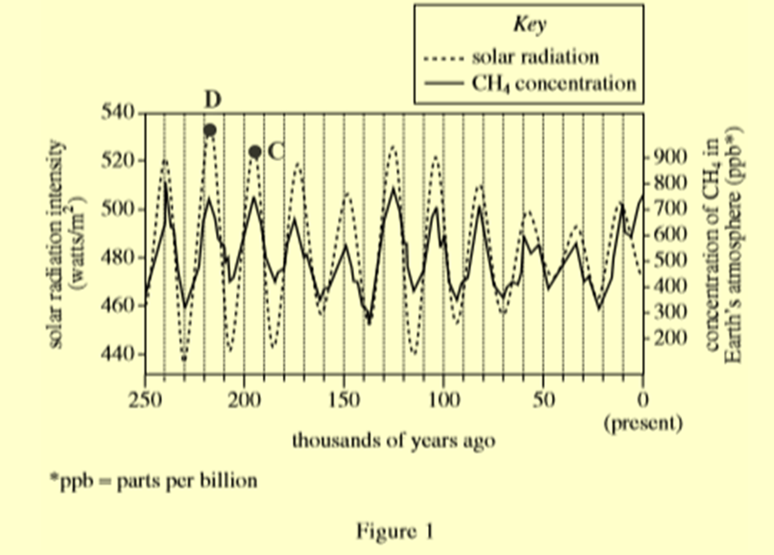
=> Khoảng thời gian phù hợp là 195000 đến 220000 năm
Câu 44:
Câu nào sau đây mô tả đúng nhất tác động chính của CH4 đối với khí hậu Trái đất?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào thông tin đoạn văn
Lời giải
Câu trả lời đúng nhất là CH4 hấp thụ nhiệt tỏa ra từ bề mặt Trái đất, làm khí hậu Trái đất nóng lên.
Chọn D
Câu 45:
CH4 thuộc hợp chất nào sau đây?
 Xem đáp án
Xem đáp án
Phương pháp giải
Dựa vào công thức chung của các hợp chất
Lời giải
Công thức chung của anken là CnH2n với n lớn hơn hoặc bằng 2
Công thức chung của ankan là CnH2n+2 với n lớn hơn hoặc bằng 1
Công thức chung của xicloankan là CnH2n+2 với n lớn hơn hoặc bằng 3
Công thức chung của ankin là CnH2n-2 với n lớn hơn hoặc bằng 2
=> CH4 thuộc hợp chất ankan
Chọn B
Câu 46:
Ở động vật, quá trình nào giúp chuyển hóa năng lượng từ glucose thành năng lượng cung cấp cho các hoạt động sống?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin bài đọc.
Lời giải
Trong chuyển hóa năng lượng, glucose là nguồn nguyên liệu quan trọng nhất trong tất cả các sinh vật để tạo ra năng lượng trong quá trình hô hấp tế bào.
Đáp án: B
Câu 47:
Theo em, tại sao glucose lại được vận chuyển vào tế bào máu bằng cơ chế khuếch tán nhờ một loại protein vận chuyển hay vận chuyển thụ động?
 Xem đáp án
Xem đáp án
Phương pháp giải
Ở tế bào động vật, glucose được vận chuyển vào máu bằng cơ chế khuếch tán nhờ một loại protein vận chuyển và được dự trữ dưới dạng glycogen trong gan.
Lời giải
Glucose không thể dễ dàng khuyếch tán qua lỗ của màng tế bào bởi trọng lượng phân tử lớn nhất có thể dễ dàng khuyếch tán qua màng khoảng 100, và glucose có trọng lượng phân tử là 180. Glucose vào được bên trong tế bào bằng cơ chế khuyếch tán nhờ một loại protein vận chuyển.
Chọn C
Câu 48:
Điền đáp án chính xác vào chỗ trống
Đối tượng thí nghiệm trên là tế bào ______ của chuột lang.
 Xem đáp án
Xem đáp án
Đáp án: "hồng cầu"
Phương pháp giải
Đọc kĩ thông tin bài đọc.
Lời giải
Các nhà khoa học đã tiến hành thí nghiệm để kiểm tra sự hấp thụ glucose vào máu phụ thuộc vào độ tuổi. Đối tượng thí nghiệm là tế bào hồng cầu của chuột lang 15 ngày tuổi và chuột lang 1 tháng tuổi.
Đáp án: hồng cầu.
Câu 49:
Chọn những nhận định chính xác
Theo kết quả thí nghiệm, những nhận định nào sau đây chính xác?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin bài đọc.
Lời giải
Theo kết quả thí nghiệm, tuổi tác của chuột lang có ảnh hưởng đến hiệu suất hấp thụ glucose của tế bào hồng cầu.
Cụ thể là:
- Chuột lang tuổi càng cao thì sự hấp thụ glucose của tế bào hồng cầu càng kém.
- Chuột lang tuổi càng thấp thì sự hấp thụ glucose của tế bào hồng cầu càng cao.
Sau 60 phút ủ, tế bào hồng cầu của chuột lang 15 tháng tuổi hấp thụ nhiều glucose hơn tế bào hồng cầu chuột lang 1 tháng tuổi.
Sau 40 phút ủ, tế bào hồng cầu của chuột lang 15 tháng tuổi hấp thụ nhiều glucose hơn tế bào hồng cầu chuột lang 1 tháng tuổi.
Đáp án: B, D, E.
Câu 50:
Theo em, khi tăng nhiệt độ thí nghiệm lên 40oC thì sự hấp thụ glucose vào tế bào máu ở chuột lang thay đổi như thế nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin bài đọc.
Lời giải
Khi tăng nhiệt độ có thể làm biến tính protein vận chuyển nên sẽ làm giảm hiệu suất làm việc của protein.
=> Khi tăng nhiệt độ lên cao hơn và 25oC thì sự hấp thụ glucose vào tế bào máu ở chuột lang có thể làm giảm hiệu suất hấp thụ.
Đáp án: B
Câu 51:
Nhận định nào sau đây đúng hay sai?
Khi thực hiện thí nghiệm tương tự trên tế bào hồng cầu của chuột lang 45 ngày tuổi thì kết quả thí nghiệm là sự hấp thụ glucose sau 10 phút ủ là cao hơn 20 (mM).
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin bài đọc.
Lời giải
Theo kết quả thí nghiệm, độ tuổi chuột lang càng cao thì sự hấp thụ glucose vào tế bào càng kém.
à Khi thực hiện thí nghiệm tương tự trên tế bào hồng cầu của chuột lang 45 ngày tuổi thì kết quả thí nghiệm là sự hấp thụ glucose sau 10 phút ủ là thấp hơn 20 (mM).
Đáp án: B
Câu 52:
Điền đáp án thích hợp vào chỗ trống
Thuốc kháng sinh là nhóm thuốc được sử dụng để chống nhiễm trùng do _______
 Xem đáp án
Xem đáp án
Đáp án: "vi khuẩn"
Phương pháp giải
Đọc kĩ thông tin đoạn đọc.
Lời giải
Thuốc kháng sinh là nhóm thuốc được sử dụng để chống nhiễm trùng do vi khuẩn.
Đáp án: vi khuẩn
Câu 53:
Thuốc kháng sinh dưới đây thuộc nhóm kháng sinh nào?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin đoạn đọc.
Lời giải
Thuốc kháng sinh trên là Ampicillin, loại thuốc này thuộc nhóm - lactams.
Đáp án: A
Câu 54:
Chọn những đáp án đúng
Để diệt những bệnh nhiễm trùng gây nên bởi vi khuẩn gram dương thì người ta cần dùng những loại thuốc kháng sinh nào dưới đây?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin đoạn đọc.
Lời giải
Theo như thông tin bài đọc, những loại thuốc có thể diệt được vi khuẩn gram dương là: Ampicillin, Azithromycin, Gatifloxacin, Trimerhoprim.
Đáp án: A, B, D, E.
Câu 55:
Đâu là cơ chế hoạt động diệt khuẩn của nhóm kháng sinh Antifolates?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin đoạn đọc.
Lời giải
Cơ chế hoạt động diệt khuẩn của nhóm kháng sinh Antifolates là: Ức chế quá trình sao chép ADN và mARN của vi khuẩn.
Đáp án: A
Câu 56:
Điền đáp án chính xác vào chỗ trống
Khi sử dụng cùng một loại thuốc kháng sinh nhưng khi sử dụng với liều lượng _______ hơn thì hiệu quả điều trị sẽ cao hơn.
 Xem đáp án
Xem đáp án
Đáp án: "cao"
Phương pháp giải
Đọc kĩ thông tin đoạn đọc.
Lời giải
Khi sử dụng cùng một loại thuốc kháng sinh nhưng khi sử dụng với liều lượng cao hơn thì hiệu quả điều trị sẽ cao hơn.
Ví dụ: Khi sử dụng thuốc Sulfamethozazole 800 mg hiệu quả điều trị cao hơn khi sử dụng thuốc Sulfamethozazole 400 mg.
Đáp án: cao.
Câu 57:
Khi kết hợp thuốc kháng sinh với hợp chất SMX thì hiệu quả điều trị bệnh _______
 Xem đáp án
Xem đáp án
Đáp án
Khi kết hợp thuốc kháng sinh với hợp chất SMX thì hiệu quả điều trị bệnh tăng lên
Phương pháp giải
Đọc kĩ thông tin đoạn đọc.
Lời giải
Khi kết hợp thuốc kháng sinh với hợp chất SMX thì hiệu quả điều trị bệnh tăng lên.
Ví dụ: khi sử dụng thuốc azithromycin 250 mg thì hiệu quả điều trị sẽ thấp hơn so với khi sử dụng SMX/azithromycin 200/250 mg.
Đáp án: tăng lên
Câu 58:
Theo em, với một bệnh nhân bị bệnh nhiễm trùng da do vi khuẩn gây ra thì nên dùng loại thuốc kháng sinh nào để đạt được hiệu quả điều trị tốt nhất?
 Xem đáp án
Xem đáp án
Phương pháp giải
Đọc kĩ thông tin đoạn đọc.
Lời giải
Theo thông tin bài đọc, ta nhận thấy, các loại thuốc kháng sinh được nhắc đến bên trên đều có khả năng diệt khuẩn trong trường hợp bị nhiễm khuẩn da.
Tuy nhiên, quan sát sơ đồ khả năng diệt khuẩn thì ta thấy thuốc Sulfamethozazole 800 mg cao nhất.
Chọn DCâu 59:
 Xem đáp án
Xem đáp án
Đáp án
B. \(\alpha = 1\).
C. \(\alpha = 2\).
Phương pháp giải
- Bước 1: Xác định số mũ α của hàm số.
- Bước 2: Nêu điều kiện để hàm số xác định.
+ α nguyên dương: D = R.
+ α nguyên âm hoặc α = 0: D = R∖{0}.
+ α không nguyên: D = (0;+∞).
- Bước 3: Giải các bất phương trình ở trên để tìm tập xác định của hàm số.
Tìm tập xác định của hàm số
Lời giải
Dễ thấy khi α nguyên thì hàm số xác định trên R.
Với α = −1 và \(\alpha = \frac{1}{{10}}\) thì hàm số không xác định trên R. Chọn B, C
Câu 60:
 Xem đáp án
Xem đáp án
Phương pháp giải
Nguyên hàm từng phần và bài toán tìm nguyên hàm
Lời giải
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{u = x}\\{{\rm{d}}v = f(x){\rm{d}}x}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{d}}u = {\rm{d}}x}\\{v = F(x)}\end{array}} \right.} \right.\\ \Rightarrow \int x f(x)dx = xF(x) - \int F (x){\rm{d}}x = xF(x) - {x^{2022}} - C.\end{array}\)
Chọn B
Câu 61:
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng tính đơn điệu của hàm số.
Định nghĩa hàm số đồng biến, nghịch biến
Lời giải
\(f'(x) < 0,\forall x \in \mathbb{R}\)
⇒ Hàm số đồng biến trên \(\mathbb{R}\).
\( \Rightarrow \frac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} < 0,\forall {x_1},{x_2} \in \mathbb{R},{x_1} \ne {x_2}\)
Chọn C
Câu 62:
 Xem đáp án
Xem đáp án
Phương pháp giải
Phương pháp đặt ẩn phụ giải phương trình logarit
Lời giải
TXĐ: \(x > 0;x \ne 1\).
\({\log _2}x - {\log _x}64 = 1 \Leftrightarrow {\log _2}x - {\log _x}{2^6} = 1\)
\( \Leftrightarrow {\log _2}x - 6{\log _x}2 = 1 \Leftrightarrow {\log _2}x - \frac{6}{{{{\log }_2}x}} = 1\)
\( \Leftrightarrow {\left( {{{\log }_2}x} \right)^2} - 6 = {\log _2}x \Leftrightarrow {\left( {{{\log }_2}x} \right)^2} - {\log _2}x - 6 = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ lo{g_2}x = - 2}\\{ lo{g_2}x = 3}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{1}{4}}\\{x = 8}\end{array}} \right.} \right.\)
Vậy phương trình có 2 nghiệm.
Chọn C
Câu 63:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dãy số tăng, dãy số giảm
Lời giải
Vì \({2^n};n\) là các dãy dương và tăng nên \(\frac{1}{{{2^n}}};\frac{1}{n}\) là các dãy giảm, do đó loại A, B
Xét đáp án C: \({u_n} = \frac{{n + 5}}{{3n + 1}} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{u_1} = \frac{3}{2}}\\{{u_2} = \frac{7}{6}}\end{array} \Leftrightarrow {u_1} > {u_2} \Rightarrow } \right.\) loại C
Xét đáp án D: \({u_n} = \frac{{2n - 1}}{{n + 1}} = 2 - \frac{3}{{n + 1}} \Rightarrow {u_{n + 1}} - {u_n} = 3\left( {\frac{1}{{n + 1}} - \frac{1}{{n + 2}}} \right) > 0\)
Chọn D
Câu 64:
 Xem đáp án
Xem đáp án
Phương pháp giải
Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn
Lời giải
+) Tập xác định của hàm số: \(D = \mathbb{R}\).
\(\begin{array}{l} + )\,\,\forall x \in D \Rightarrow - x \in D\\ + )\,\,f( - x) = | - x|\sin ( - x) = - |x|\sin x = - f(x)\end{array}\)
Vậy hàm số lẻ.
+) Tập xác định của hàm số:\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}.\)
\(\begin{array}{l} + )\,\,\forall x \in D \Rightarrow - x \in D.\\ + )\,\,f( - x) = \tan | - x| = \tan |x| = f(x)\end{array}\)
Vậy hàm số chẵn.
+) Tập xác định của hàm số: \(D = \mathbb{R}\).
Với mọi \(x \in D\) thì \( - x \in D\) nên \(D\) là tập đối xứng.
Ta có \(f( - x) = {\sin ^2}( - 2x) + \cos ( - 3x) = {\sin ^2}2x + \cos 3x = f(x),\forall x \in D\).
Do đó hàm số \(f(x)\) đã cho là hàm số chẵn.
+) Tập xác định \(D = \mathbb{R}\).
Với mọi \(x \in D \Rightarrow - x \in D\).
\(f( - x) = \sqrt {2 + \sin ( - x)} + \sqrt {2 - \sin ( - x)} = \sqrt {2 - \sin x} + \sqrt {2 + \sin x} = f(x).\)
Do đó hàm số đã cho chẵn trên \(D\).
Vậy đáp án đúng là A.
Câu 65:
Hai hàm số \[y = F\left( x \right),y = G\left( x \right)\] có đồ thị như hình vẽ bên. Đặt \[P\left( x \right) = F\left( x \right).G\left( x \right)\]. Tính \[P\prime \left( 2 \right)\]
![Hai hàm số \[y = F\left( x \right),y = G\left( x \right)\] có đồ thị như hình vẽ bên. Đặt \[P\left( x \right) = F\left( x \right).G\left( x \right)\]. Tính \[P\prime \left( 2 \right)\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid0-1729738874.png)
 Xem đáp án
Xem đáp án
Phương pháp giải
Các quy tắc tính đạo hàm
Lời giải
Ta có:
\[\begin{array}{l}P\prime \left( x \right) = F\prime \left( x \right).G\left( x \right) + F\left( x \right).G\prime \left( x \right)\\ \Rightarrow P\prime \left( 2 \right) = F\prime \left( 2 \right).G\left( 2 \right) + F\left( 2 \right).G\prime \left( 2 \right)\\ = 0.G\left( 2 \right) + 3.G\prime \left( 2 \right) = 3.G\prime \left( 2 \right)\end{array}\]
Trên [0;4] hàm số \[G\left( x \right) = ax + b\]
\[\begin{array}{*{20}{l}}{G\left( 0 \right) = 1;G\left( 4 \right) = 3 \Rightarrow a = \frac{1}{2}\; \Rightarrow G\left( x \right) = \frac{1}{2}x + 1\;\,\,{\rm{khi}}\,\,\;x \in \left[ {0;4} \right]}\\{ \Rightarrow G\prime \left( 2 \right) = \frac{1}{2}}\\{ \Rightarrow P\prime \left( 2 \right) = 3.\frac{1}{2} = \frac{3}{2}}\end{array}\]
Chọn A
Câu 66:
 Xem đáp án
Xem đáp án
Phương pháp giải
Cấp số cộng
Lời giải
Cần phải khoan sâu xuống 50m nên giá tiền khoan tăng 9 lần.
Giá tiền khoang mỗi mét (từ lúc chưa tăng đến lúc tăng lần cuối cùng) lập thành cấp số cộng (un) có u1 = 80000, d = 5000. Do cần khoang 50 mét nên tổng số tiền cần trả là
\[5.{u_1} + 5.{u_2} + \ldots + 5.{u_9} + 5.{u_{10}} = 5.\left( {{u_1} + {u_2} + \cdots + {u_{10}}} \right) = 5.{S_{10}}\]
\[ = 5.\left( {10{u_1} + \frac{{9.10}}{2}d} \right)\]
=5.(10.80000+45.5000) = 5125000 đồng.
Chọn A
Câu 67:
 Xem đáp án
Xem đáp án
Phương pháp giải
Đồ thị hàm số \(y = \frac{{ax + b}}{{cx + d}}\) nhận giao điểm của hai đường tiệm cận làm tâm đối xứng nên \(I\left( { - \frac{d}{c};\frac{a}{c}} \right)\).
Các đường tiệm cận
Lời giải
Áp dụng lý thuyết về tâm đối xứng ta thấy:
\(y = \frac{{3x - 5}}{{x - 2}}\) có tâm đối xứng là \({I_1}(2;3) \Rightarrow O{I_1} = \sqrt {{2^2} + {3^2}} = \sqrt {13} < 6 \Rightarrow \) Nằm phía trong đường tròn trên.
\(y = \frac{{3x + 9}}{{x + 5}}\) có tâm đối xứng là \({I_2}( - 5;3) \Rightarrow O{I_2} = \sqrt {{{( - 5)}^2} + {3^2}} = \sqrt {34} < 6 \Rightarrow \) Nằm phía trong đường tròn trên.
\(y = \frac{{4x - 1}}{{x + \sqrt {26} }}\) có tâm đối xứng là \({I_3}( - \sqrt {26} ;4) \Rightarrow O{I_3} = \sqrt {42} > 6 \Rightarrow \) Nằm phía ngoài đường tròn trên.
\(y = \frac{{\sqrt {21} x + 1}}{{x + \sqrt 7 }}\) có tâm đối xứng là \({I_4}( - \sqrt 7 ;\sqrt {21} ) \Rightarrow O{I_4} = \sqrt {28} < 6 \Rightarrow \) Nằm phía trong đường tròn trên.
Chọn A
Câu 68:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dạng 2: Tính tích phân bằng phương pháp đổi biến \(x = u({\rm{t}})\)
Lời giải
Đặt: \(x = {t^3} + 3t + 1 \Rightarrow dx = \left( {3{t^2} + 3} \right)dt\).
Đổi cận: \(x = 1 \to t = 0;x = 5 \to t = 1\).
\(\int_1^5 f (x)dx = \int_0^1 {\left( {3{t^2} + 3} \right)} f\left( {{t^3} + 3t + 1} \right)dt = \int_0^1 {\left( {3{t^2} + 3} \right)} (t + 3)dt = \frac{{57}}{4}\)
Chọn C
Câu 69:
 Xem đáp án
Xem đáp án
Đáp án
A. Tổng của z và \(\bar z\) luôn là một số thực.
D. Tích của z và \(\bar z\) luôn là một số ảo.
Phương pháp giải
- Giả sử \[z = a + bi,\,\,(a,b \in R)\]
- Xét từng đáp án.
Lời giải
Giả sử \(z = a + bi,(a,b \in \mathbb{R}) \Rightarrow \bar z = a - bi\)
\( \Rightarrow z + \bar z = 2a \in \mathbb{R}\) và \(z - \bar z = 2bi\) là số ảo nếu \(b \ne 0\).
Và \(z.\bar z = {a^2} + {b^2} \in \mathbb{R}\)
Chọn A, D
Câu 70:
Cho hàm số \[y = f\left( x \right)\] có đồ thị trên đoạn [−2;4] như hình vẽ. Tìm giá trị lớn nhất của hàm số \[y = \left| {f\left( x \right)} \right|\] trên đoạn [−2;4]
![Cho hàm số \[y = f\left( x \right)\] có đồ thị trên đoạn [−2;4] như hình vẽ. Tìm giá trị lớn nhất của hàm số \[y = \left| {f\left( x \right)} \right|\] trên đoạn [−2;4] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid3-1729739389.png)
 Xem đáp án
Xem đáp án
Phương pháp giải
Vẽ lại đồ thị.
Lời giải
Ta có đồ thị hàm số thấy hàm số \[y = \left| {f\left( x \right)} \right|\] trên đoạn [−2;4] như sau:
![Cho hàm số \[y = f\left( x \right)\] có đồ thị trên đoạn [−2;4] như hình vẽ. Tìm giá trị lớn nhất của hàm số \[y = \left| {f\left( x \right)} \right|\] trên đoạn [−2;4] (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid1-1729739366.png)
\[ \Rightarrow y( - 1) > y(2) > y( - 2) = y(4) > 0 \Rightarrow \mathop {\max }\limits_{[ - 2;4]} |f(x)| = y( - 1) = 3\]
Chọn C
Câu 71:
Trong các hàm số sau, hàm số nào có giới hạn bằng −1 khi x tiến tới 0?
 Xem đáp án
Xem đáp án
Đáp án
B. \(y = \sqrt {x + 1} - 2\)
C. \(y = \frac{{\sqrt {x + 1} }}{{x - 1}}\)
Phương pháp giải
- Tìm tập xác định.
- Định lý: \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L \Leftrightarrow \mathop {\lim }\limits_{x \to x_0^ + } f(x) = \mathop {\lim }\limits_{x \to x_0^ - } f(x) = L\)
Lời giải
+) \(y = \sqrt x - 1\) có tập xác định là \(D = [0; + \infty )\) nên không tồn tại giới hạn tại 0
\( \Rightarrow \) Không thỏa mãn.
+) \(y = \sqrt {x + 1} - 2\) có tập xác định là \(D = [ - 1; + \infty )\) và \(\mathop {\lim }\limits_{x \to 0} (\sqrt {x + 1} - 2) = 1 - 2 = - 1\) \( \Rightarrow \) Thỏa mãn.
+) \(y = \frac{{\sqrt {x + 1} }}{{x - 1}}\) có tập xác định là \(D = [ - 1; + \infty )\backslash \{ 1\} \) và \(\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {x + 1} }}{{x - 1}} = \frac{1}{{ - 1}} = - 1 \Rightarrow \) Thỏa mãn.
+) \(y = \frac{{\sin x}}{x}\) có tập xác định là \(D = \mathbb{R}\backslash \{ 0\} \) và có \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1 \Rightarrow \) Không thỏa mãn.
Chọn B, C
Câu 72:
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
|
PHÁT BIỂU |
ĐÚNG |
SAI |
|
Phương trình \[\left| {f\left( x \right)} \right| = 1\] có 2 nghiệm phân biệt. |
||
|
Đồ thị hàm số \[y = f\left( x \right)\] có 3 đường tiệm cận đứng. |
||
|
Số đường tiệm cận của đồ thị hàm số \(g(x) = \frac{2}{{3{\rm{f}}({\rm{x}}) - 2}}\) là 2. |
 Xem đáp án
Xem đáp án
Đáp án
|
PHÁT BIỂU |
ĐÚNG |
SAI |
|
Phương trình \[\left| {f\left( x \right)} \right| = 1\] có 2 nghiệm phân biệt. |
X | |
|
Đồ thị hàm số \[y = f\left( x \right)\] có 3 đường tiệm cận đứng. |
X | |
|
Số đường tiệm cận của đồ thị hàm số \(g(x) = \frac{2}{{3{\rm{f}}({\rm{x}}) - 2}}\) là 2. |
X |
Phương pháp giải
Giải các phương trình và áp dụng định nghĩa đường tiệm cận.
Lời giải
\(|{\rm{f}}({\rm{x}})| = 1 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{\rm{f}}({\rm{x}}) = 1}\\{{\rm{f}}({\rm{x}}) = - 1}\end{array}} \right.\)
\({\rm{f}}({\rm{x}}) = 1\) có 1 nghiệm và \({\rm{f}}({\rm{x}}) = - 1\) có 1 nghiệm.
\( \Rightarrow \) Phương trình \(|{\rm{f}}({\rm{x}})| = 1\) có 2 nghiệm phân biệt.
Ta thấy \(\mathop {\lim }\limits_{{\rm{x}} \to - {2^ - }} {\rm{f}}({\rm{x}}) = - \infty ;\mathop {\lim }\limits_{{\rm{x}} \to {2^ + }} {\rm{f}}({\rm{x}}) = + \infty \)
\( \Rightarrow \) Đồ thị hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) có 2 đường tiệm cận đứng là \({\rm{y}} = - 2;{\rm{y}} = 2\).
Dựa vào đồ thị hàm số ta có:
\(\mathop {\lim }\limits_{{\rm{x}} \to - \infty } {\rm{g}}({\rm{x}}) = \frac{2}{{3.( - 1) - 2}} = - \frac{2}{5}\)
\(\mathop {\lim }\limits_{{\rm{x}} \to + \infty } {\rm{g}}({\rm{x}}) = \frac{2}{{3.1 - 2}} = 2\)
Suy ra đồ thị hàm số đã cho có 2 đường tiệm cận ngang.
Xét phương trình \(3{\rm{f}}({\rm{x}}) - 2 = 0 \Leftrightarrow {\rm{f}}({\rm{x}}) = \frac{2}{3}\)
Dựa vào đồ thị hàm số ta thấy: phương trình \({\rm{f}}({\rm{x}}) = \frac{2}{3}\) có duy nhất một nghiệm. Vậy hàm số có 3 đường tiệm cận.
Câu 73:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Ta có \(\frac{{{{\rm{u}}_{{\rm{n}} + 1}}}}{{{{\rm{u}}_{\rm{n}}}}} = \frac{{ - \frac{{{{\rm{u}}_{\rm{n}}}}}{5}}}{{{{\rm{u}}_{\rm{n}}}}} = - \frac{1}{5}\) do đó dãy \(\left( {{{\rm{u}}_{\rm{n}}}} \right),\,\,{\rm{n}} \in \mathbb{N}*\) là một cấp số nhân lùi vô hạn có \({{\rm{u}}_1} = 3,\;{\rm{d}} = - \frac{1}{5}\).
Suy ra \(\lim {{\rm{S}}_{\rm{n}}} = \frac{{{{\rm{u}}_1}}}{{1 - {\rm{q}}}} = \frac{3}{{1 + \frac{1}{5}}} = \frac{5}{2}\).
Chọn D
Câu 74:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Đặt \(z = x + yi\left( {x,y \in \mathbb{R}} \right)\).
Theo giả thiết, \(\left| z \right| = 1 \Rightarrow z.\bar z = 1\) và \({x^2} + {y^2} = 1\).
\(P = \left| z \right|.\left| {{z^2} - 1 + 2\bar z} \right| = \left| {{z^2} - 1 + 2\bar z} \right| = \left| {{x^2} - {y^2} + 2xyi - 1 + 2x - 2yi} \right|\)
\(\; = \left| {\left( {{x^2} + 2x - {y^2} - 1} \right) + 2y\left( {x - 1} \right)i} \right| = \sqrt {{{\left( {{x^2} + 2x - {y^2} - 1} \right)}^2} + 4{y^2}{{(x - 1)}^2}} \)
\(\; = \sqrt {{{\left( {{x^2} + 2x - 1 + {x^2} - 1} \right)}^2} + 4\left( {1 - {x^2}} \right){{(x - 1)}^2}} \left( {{\rm{\;V\`i \;y\;}}{\;^2} = 1 - {x^2}} \right)\)
\( = \sqrt {16{x^3} - 4{x^2} - 16x + 8} .\)
\({\rm{V\`i \;}}{x^2} + {y^2} = 1 \Rightarrow {x^2} = 1 - {y^2} \le 1 \Rightarrow - 1 \le x \le 1.\)
Xét hàm số \({\rm{f}}\left( {\rm{x}} \right) = 16{{\rm{x}}^3} - 4{{\rm{x}}^2} - 16{\rm{x}} + 8,\,\,{\rm{x}} \in \left[ { - 1;1} \right]\).
\({\rm{f'}}\left( {\rm{x}} \right) = 48{{\rm{x}}^2} - 8{\rm{x}} - 16.{\rm{f'}}\left( {\rm{x}} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{\rm{x}} = - \frac{1}{2} \in \left[ { - 1;1} \right]}\\{{\rm{x}} = \frac{2}{3} \in \left[ { - 1;1} \right]}\end{array}.} \right.\)
\({\rm{f}}\left( { - 1} \right) = 4;{\rm{f}}\left( { - \frac{1}{2}} \right) = 13;{\rm{f}}\left( {\frac{2}{3}} \right) = \frac{8}{{27}};{\rm{f}}\left( 1 \right) = 4.\)
Vậy \({\rm{max}}P = \sqrt {13} \).
Chọn A
Câu 75:
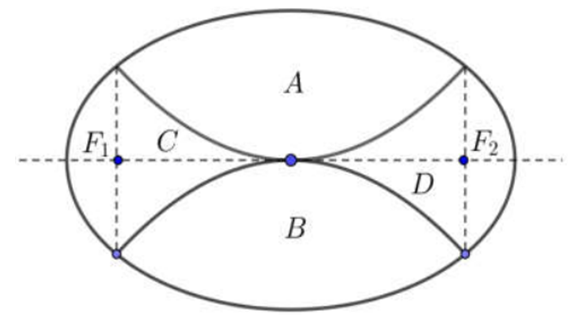
Nhà trường dự định làm một vườn hoa dạng hình elip được chia ra làm bốn phần bởi hai đường parabol có chung đinh, đối xứng với nhau qua trục của elip như hình vẽ. Biết độ dài trục lớn, trục nhỏ của elip lần lượt là 8m và 4m, F1, F2 lần lượt là hai tiêu điểm của elip. Phần A, B dùng để trồng hoa, phần C, D dùng để trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa và cỏ lần lượt là 250.000 đ và 150.000 đ. Tính tồng số tiền để hoàn thành vườn hoa trên (làm tròn đến hàng nghìn).
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Gọi SA, SB, SC, SD lần lượt là diện tích các phần A, B, C và D. Theo giả thiết ta được \[{S_A} = {S_B},\,\,{S_C} = {S_D}\].
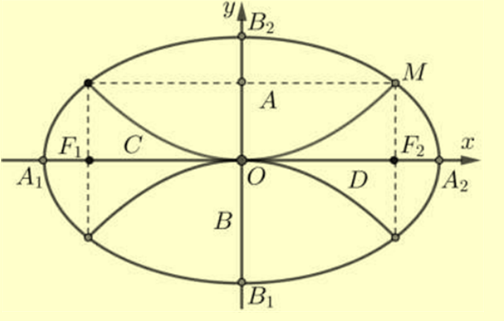
Chọn hệ tọa độ như hình vẽ. Khi đó elip \((E)\) có dạng \((E):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1,(0 < b < a)\).
Theo bài \(2a = 8 \Leftrightarrow a = 4;2b = 4 \Leftrightarrow b = 2\) suy ra phương trình của elip là
\((E):\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{4} = 1\) (1). \(c = \sqrt {{a^2} - {b^2}} = 2\sqrt 3 \) suy ra \({F_2}(2\sqrt 3 ;0)\).
Gọi \((P)\) là parabol nẳm ở phần phía trên của trục \({\rm{Ox}}\), cắt \((E)\) tại điểm \(M\) với hoành độ \({x_M} = 2\sqrt 3 \) khi đó \(M \in (E) \Rightarrow M(2\sqrt 3 ;1)\).
Theo giả thiết, parabol \((P)\) có dạng \(y = m.{x^2}\). Do \(M \in (P) \Rightarrow 1 = 12.m \Leftrightarrow m = \frac{1}{{12}}\).
Từ (1) ta được \(\frac{{{y^2}}}{4} = 1 - \frac{{{x^2}}}{{16}} \Leftrightarrow y = \pm \frac{1}{2}\sqrt {16 - {x^2}} \).
Diện tích của phần \(A\) là
\({S_A} = \int_{ - 2\sqrt 3 }^{2\sqrt 3 } {\left( {\frac{1}{2}\sqrt {16 - {x^2}} - \frac{1}{{12}}{x^2}} \right)} {\rm{d}}x = \int_{ - 2\sqrt 3 }^{2\sqrt 3 } {\frac{1}{2}} \sqrt {16 - {x^2}} \;{\rm{d}}x - \frac{1}{{12}}\int_{ - 2\sqrt 3 }^{2\sqrt 3 } {{x^2}} \;{\rm{d}}x{\rm{ hay}}\)
\({S_A} = {I_1} - \left. {\frac{1}{{36}}{x^3}} \right|_{ - 2\sqrt 3 }^{2\sqrt 3 } = {I_1} - \frac{{4\sqrt 3 }}{3}.\)
Với \({I_1} = \frac{1}{2}\int_{ - 2\sqrt 3 }^{2\sqrt 3 } {\sqrt {16 - {x^2}} } \;{\rm{d}}x\). Đặt \(x = 4\sin t \Rightarrow {\rm{d}}x = 4\cos t\;{\rm{d}}t\) với \(t \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\).
Đổi cận: Khi \(x = - 2\sqrt 3 \) ta được \(t = - \frac{\pi }{3}\); khi \(x = 2\sqrt 3 \) ta được \(t = \frac{\pi }{3}\).
Theo công thức đổi biến số, thì:
\[{I_1} = \frac{1}{2}\int\limits_{ - \frac{\pi }{3}}^{\frac{\pi }{3}} {\sqrt {16 - 16{{\sin }^2}x} } .4\cos tdt = 8\int\limits_{ - \frac{\pi }{3}}^{\frac{\pi }{3}} {{{\cos }^2}} tdt\]
Hay \({I_1} = 4\int_{ - \frac{\pi }{3}}^{\frac{\pi }{3}} {(1 + \cos 2t)} dt = \left. {4\left( {t + \frac{1}{2}\sin 2t} \right)} \right|_{ - \frac{\pi }{3}}^{\frac{\pi }{3}} = 8\left( {\frac{\pi }{3} + \frac{{\sqrt 3 }}{4}} \right)\).
Từ đó tìm được \({S_A} = \frac{{8\pi + 2\sqrt 3 }}{3}\).
Diện tích của \((E)\) là \({S_{(E)}} = \pi ab = 8\pi \).
Diện tích của phần \(C\) là \({S_C} = {S_D} = \frac{{{S_{(E)}} - 2{S_A}}}{2} = \frac{{4\pi - 2\sqrt 3 }}{3}\).
Số tiền cần sử dụng để hoàn thành khu vườn trên là:
\(\left( {2.{S_A}} \right) \times 250000 + \left( {2.{S_C}} \right) \times 150000 \approx 5676367,372\)
Chọn A
Câu 76:
Cho hàm số \(y = f(x)\) có đạo hàm liên tục trên \(\mathbb{R}\) và \(f(0) = 0;f(4) > 4\). Biết hàm \(y = {f^\prime }(x)\) có đồ thị như hình vẽ.
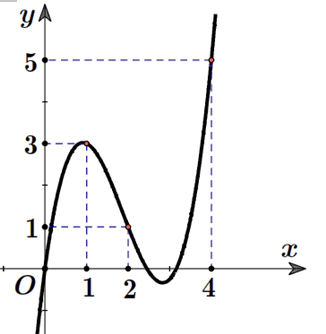
Số điểm cực trị của hàm số \(g(x) = \left| {f\left( {{x^2}} \right) - 2x} \right|\) là
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Xét hàm số \(h(x) = f\left( {{x^2}} \right) - 2x\).
Ta có: \({h^\prime }(x) = 2x{f^\prime }\left( {{x^2}} \right) - 2\).
\({h^\prime }(x) = 0 \Leftrightarrow {f^\prime }\left( {{x^2}} \right) = \frac{1}{x}\) (vô nghiệm \(\forall x \le 0\)).
Đặt \(t = {x^2} \Rightarrow x = \sqrt t ,\forall t > 0\).
Khi đó: \({f^\prime }(t) = \frac{1}{{\sqrt t }}(*)\). Nhận thấy trên khoảng \((0;1)\) thì \(w(t) = \frac{1}{{\sqrt t }}\) nghịch biến và \({f^\prime }(t)\) đồng biến, do đó \((*)\) nếu có nghiệm là duy nhất.
Mặt khác: \({h^\prime }(0).{h^\prime }(1) = - 2\left( {2{f^\prime }(1) - 2} \right) = - 8 < 0\) và \({h^\prime }(x)\) liên tục trên [0 ;1] nên \(\exists {x_0} \in (0;1):{h^\prime }\left( {{x_0}} \right) = 0\).
Vậy \({h^\prime }(x) = 0\) có nghiệm duy nhất \({x_0} \in (0;1)\) và \(h(x)\) có một điểm cực tiểu (1)
Xét phương trình: \(h(x) = 0 \Leftrightarrow f\left( {{x^2}} \right) - 2x = 0\,\,(**)\).
Ta có: \(h(0) = f(0) = 0 \Rightarrow x = 0\) là một nghiệm của \((**)\).
Mặt khác:
\(h\left( {\sqrt {{x_0}} } \right).h(2) = \left( {f\left( {{x_0}} \right) - 2\sqrt {{x_0}} } \right)(f(4) - 4) < 0 \Rightarrow \exists {x_1} \in \left( {\sqrt {{x_0}} ;2} \right):h\left( {{x_1}} \right) = 0.\)
Nên \((**)\) có nghiệm \({x_1} \in \left( {\sqrt {{x_0}} ;2} \right)\).
Vì \(h(x)\) có một điểm cực trị, nên \((**)\) có không quá 2 nghiệm.
Vậy \(h(x) = f\left( {{x^2}} \right) - 2x = 0\) có hai nghiệm phân biệt. (2)
Từ (1) và (2) ta được: hàm số \(g(x) = \left| {f\left( {{x^2}} \right) - 2x} \right|\) có 3 điểm cực trị.
Chọn D
Câu 77:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
Một đoạn thẳng được tạo thành từ hai điểm bất kì thuộc 9 điểm trên.
Vậy số đoạn thẳng cần tìm chính là số cách chọn rah ai điểm bất kì từ 9 điểm trên: \(C_9^2 = 36\).
Chọn C
Câu 78:
 Xem đáp án
Xem đáp án
Phương pháp giải
Sử dụng tính chất khối đa diện.
Khái niệm về khối đa diện
Lời giải
Phương án A: hai cạnh bất kì có thể không có điểm chung.
Phương án B: ba mặt bất kì có thể không có đỉnh chung.
Phương án C: hai mặt bất kì có thể không có điểm chung.
Trong một khối đa diện, mỗi đỉnh là đỉnh chung của ít nhất ba mặt.
Chọn D
Câu 79:
 Xem đáp án
Xem đáp án
Phương pháp giải
Lời giải
\(d\left( {B;\left( {ACC'A'} \right)} \right) = d(B;AC) = \frac{{4\sqrt 3 }}{2} = 2\sqrt 3 \).
Chọn B
Câu 80:
 Xem đáp án
Xem đáp án
Phương pháp giải
Bước 1: Áp dụng pytago tính bán kính r.
Bước 2: Áp dụng công thức Stoàn phần = Sxung quanh + Sđáy = πrl + πr2
Diện tích hình nón, thể tích khối nón
Lời giải
Bán kính \[r = \sqrt {{l^2} - {h^2}} = 8\].
Diện tích toàn phần hình nón là: Stp = π.8.10 + 64π = 144π.
=> Đáp án A.
Câu 81:
 Xem đáp án
Xem đáp án
Phương pháp giải
Tìm mối quan hệ giữa các véc tơ
Lời giải
Do \(A \in {d_1} \Rightarrow A(1 + 2a; - 3 + 4a;3a)\) và \(B \in {d_2} \Rightarrow B(b;2 + b; - 4 + 3b)\).
Ta có \(\overrightarrow {MA} = (2a - 3;4a - 9;3a - 4);\overrightarrow {MB} = (b - 4;b - 4;3b - 8)\).
Do điểm \({\rm{M}},{\rm{A}},{\rm{B}}\) thẳng hàng nên \(\exists k \ne 0\) sao cho \(\overrightarrow {MA} = k.\overrightarrow {MB} \)
Từ đó ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2a - 3 = k.(b - 4)}&{{\rm{(1) }}}\\{4a - 9 = k.(b - 4)}&{(2)}\\{3a - 4 = k.(3b - 8)}&{(3)}\end{array}} \right.\)
Từ (1), (2) \( \Rightarrow 2a - 3 = 4a - 9 \Leftrightarrow a = 3\). Thay vào (2), (3) ta có hệ \({\rm{PT}}\)
\(\left\{ {\begin{array}{*{20}{l}}{k(b - 4) = 3}\\{k(3b - 8) = 5}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b = 1}\\{k = - 1}\end{array}.} \right.} \right.\)
Từ đó suy ra \(A(7;9;9);B(1;3; - 1) \Rightarrow AB = 2\sqrt {43} \).
Chọn B
Câu 82:
 Xem đáp án
Xem đáp án
Phương pháp giải
Tính 55, sau đó tìm số dư khi chia cho 6.
Lời giải
55 = 3125, chia cho 6 dư 5 nên 55 ≡ 5 ( mod 6)
Chọn C
Câu 83:
 Xem đáp án
Xem đáp án
Phương pháp giải
Muốn tính tổng hệ số của tất cả các số hạng trong khai triển \({(ax + by)^n}\) ta cho \(x = y = 1\)
Nhị thức Niu - tơn
Lời giải
Với \(x = y = 1\), thay vào \({(x - 2y)^{18}}\), ta được: \({(1 - 2.1)^{18}} = 1\)
Chọn C
Câu 84:
 Xem đáp án
Xem đáp án
Phương pháp giải
- Tính số cách xếp 6 học sinh nam và 3 học sinh nữ thành một hàng ngang.
- Gọi A là biến cố: “để có đúng 2 học sinh nam đứng xen kẽ giữa 3 học sinh nữ”.
- Tính số cách xếp để có đúng 2 học sinh nam đứng xen kẽ giữa 3 học sinh nữ.
- Tính xác suất: \[P\left( A \right) = \frac{{\left| {{\Omega _A}} \right|}}{{\left| \Omega \right|}}\]
Biến cố và xác suất của biến cố
Lời giải
Cách xếp 6 học sinh nam và 3 học sinh nữ thành một hàng ngang là |Ω| = 9! = 362880.
Gọi A là biến cố: “để có đúng 2 học sinh nam đứng xen kẽ giữa 3 học sinh nữ”.
Xếp 3 học sinh nữ có 3! cách. Khi đó tạo ra 2 khoảng trống. Chọn 2 học sinh nam từ 6 học sinh nam cho vào 2 khoảng trống có \(A_6^2\), còn lại 4 học sinh nam có 5!cách.
Do đó: \[\left| {{\Omega _A}} \right| = A_6^2.3!.5! = 21600\].
Vậy xác suất để có đúng 2 học sinh nam đứng xen kẽ giữa 3 học sinh nữ là:
\(P(A) = \frac{{\left| {{\Omega _A}} \right|}}{{|\Omega |}} = \frac{{21600}}{{362880}} = \frac{5}{{84}}\).
Chọn B
Câu 85:
 Xem đáp án
Xem đáp án
Phương pháp giải
- Chia khối tứ diện và tính thể tích của mỗi khối theo thể tích của khối hộp ABCD.A′B′C′D′
- Tính tỷ lệ thể tích.
Tính thể tích khối lăng trụ xiên
Lời giải
Hình hộp bị chia thành 5 khối tứ diện bao gồm ACB′D′ và bốn khối tứ diện còn lại là ABCB′, ADCD′, CD′C′B′, AD′A′B′
Mỗi khối tứ diện này là hình chóp tam giác có đáy bằng \(\frac{1}{2}\) đáy hình hộp, chiều cao bằng chiều cao hình hộp nên thể tích mỗi tứ diện này bằng \(\frac{1}{6}\) thể tích hình hộp, tổng thể tích 4 tứ diện này bằng \(4.\frac{1}{6} = \frac{2}{3}\) thể tích hình hộp.
=> Thể tích của ACB′D′ bằng \(\frac{1}{3}\) thể tích hình hộp là
Vậy thể tích của ACB′D′ so với phần còn lại là \(\frac{1}{2}\).
Chọn B
Câu 86:
 Xem đáp án
Xem đáp án
Phương pháp giải
Quy bài toán hình học về hàm số rồi khảo sát hàm số đó để tìm GTLN, GTNN.
- Gọi chiều rộng của bể là x > 0, chiều cao của bể là h > 0
- Biểu diễn thể tích và diện tích theo các biến.
- Áp dụng BĐT Cô si tìm giá trị nhỏ nhất.
Thể tích khối hộp, khối lăng trụ
Lời giải
Gọi chiều rộng của bể là x > 0, chiều cao của bể là \[h > 0\; \Rightarrow V = 3{x^2}h = 1000\,\,\left( {{m^3}} \right)\] . (I)
Vì bể có dạng hình hộp chữ nhật không nắp nên diện tích mặt là:
\[S = 3{x^2} + 2xh + 6xh = 3{x^2} + 8xh\;\] (II)
Từ (I) và (II), ta có: \(S = 3{{\rm{x}}^2} + \frac{{8000}}{{3{\rm{x}}}} \ge 3\sqrt[3]{{3{{\rm{x}}^2}.\frac{{4000}}{{3{\rm{x}}}}.\frac{{4000}}{{3{\rm{x}}}}}} = 100\sqrt[3]{{144}}\) (Áp dụng BĐT Cô si).
Dấu xảy ra khi và chỉ khi \(3{{\rm{x}}^2} = \frac{{4000}}{{3{\rm{x}}}} \Leftrightarrow x = 10\sqrt[3]{{\frac{4}{9}}} > 0\)
Chọn B
Câu 87:
Kéo biểu thức ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Cho x, y là các số nguyên tố thỏa mãn \[{y^2} - 2{x^2} = 1\]. Khi đó x = ___ và y = ___
 Xem đáp án
Xem đáp án
Đáp án
Cho x, y là các số nguyên tố thỏa mãn \[{y^2} - 2{x^2} = 1\]. Khi đó x = 2 và y = 3
Phương pháp giải
- Chứng minh y là số lẻ
- Đặt \[y = 2k + 1\] (với k nguyên).
- Nhận xét tính chẵn lẻ của x rồi tìm hai số x,y
Lời giải
Ta có \({y^2} - 2{x^2} = 1 \Rightarrow {y^2} = 2{x^2} + 1 \Rightarrow y\) là số lẻ
Đặt \(y = 2k + 1\) (với k nguyên). Ta có: \({(2k + 1)^2} = 2{x^2} + 1\)
\( \Leftrightarrow {x^2} = 2{k^2} + 2k \Rightarrow x\) chẵn, mà \(x\) nguyên tố \( \Rightarrow x = 2,y = 3\)
Vậy nghiệm của phương trình là \((x,y) = (2,3)\)
Cách khác: Thử các số vào.
Câu 88:
 Xem đáp án
Xem đáp án
Phương pháp giải
- Tính bán kính khối trụ bên trong và bên ngoài.
- Tính thể tích khối trụ ngoài Vn và trong Vt
- Lượng hồ bê tông cho một ống là: V = Vn − Vt
- Số lượng bao xi măng cần mua = Lượng hồ bê tông để làm 200 ống.10
Diện tích hình trụ, thể tích khối trụ
Lời giải
Bán kính khối trụ bên trong là 0,5m
Vì độ dày của thành kính là 8cm nên ta có bán kính khối trụ ngoài là \(0,5 + 0,08 = 0,58\,\,(m)\)
Tính thể tích khối trụ ngoài bán kính \(0,6m:\,\,{V_n} = \pi {r^2}h = \pi {(0,58)^2}.2 = \frac{{841}}{{1250}}\pi \)
Tính thể tích khối trụ trong bán kính \(0,5m:\,\,{V_t} = \pi {r^2}h = \pi {(0,5)^2}.2 = \frac{1}{2}\pi \)
Lượng hồ bê tông cho một ống là: \(V = {V_n} - {V_t} = \left( {\frac{{841}}{{1250}} - \frac{1}{2}} \right)\pi \) \( = \frac{{108}}{{625}}\pi \approx 0,5429\,\,\left( {{m^3}} \right)\)
Lượng hồ bê tông để làm 200 ống là: \({V_{200}} = 200.\frac{{108}}{{625}}\pi = \frac{{864}}{{25}}\pi \approx 108,5734\,\,\left( {{{\rm{m}}^3}} \right)\)
Số lượng bao xi măng cần mua là 1086 (bao)
Chọn A
Câu 89:
 Xem đáp án
Xem đáp án
Phương pháp giải
- Tính \([\overrightarrow {AB} ,\overrightarrow {AC} ]\)
- \({\rm{A}},{\rm{B}},{\rm{C}},{\rm{D}}\) đồng phẳng khi và chỉ khi \(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AD} = 0\)
Phương pháp giải các bài toán về tọa độ điểm và véc tơ
Lời giải
Ta có: \(\overrightarrow {AB} = ( - 1; - 2;1);\overrightarrow {AC} = (4; - 6;0);\overrightarrow {AD} = (9;m + 1;1)\)
\[\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = (6;4;14),\,\,\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AD} = 4m + 72\]
Vậy A, B, C, D đồng phẳng khi và chỉ khi \(m = - 18\)
Chọn D
Câu 90:
 Xem đáp án
Xem đáp án
Phương pháp giải
- Tìm số phần tử của không gian mẫu nΩ
- Xác định biến cố, số kết quả có thể có của biến số và tính xác suất
Lời giải
Gieo 3 con xúc xắc cân đối, đồng chất ⇒ nΩ = 63 = 216
A:“Tổng số chấm xuất hiện trên mặt của 3 xúc xắc là một số chia hết cho 3”
Gọi số chấm xuất hiện trên mặt của 3 xúc xắc lần lượt là a, b, c
Ta có: a, b, c ∈ {1,2,3,4,5,6}
⇒ a + b + c ≤ 6.3 = 18
Chia tập hợp {1,2,3,4,5,6} thành 3 loại
Loại 1- Chia hết cho 3: {3;6}
Loại 2- Chia 3 dư 1: {1;4}
Loại 3- Chia 3 dư 2: {2;5}
Do (a + b + c) chia hết cho 3
⇒Trường hợp 1- cả a, b và c cùng thuộc 1 trong 3 loại trên: 3.(2.2.2) = 24
Trường hợp 2- a, b, c mỗi số thuộc một loại: 3!.2.2.2 = 48
⇒ nA = 24 + 48 = 72
\[ \Rightarrow {P_A} = \frac{{{n_A}}}{{{n_\Omega }}} = \frac{{72}}{{216}} = \frac{1}{3}\].
Chọn A
Câu 91:
 Xem đáp án
Xem đáp án
Phương pháp giải
- Gọi h là chiều cao của hình trụ, biểu diễn h theo R.
- Biểu diễn diện tích toàn phần theo R.
- Sử dụng BĐT Cauchy để tìm giá trị min.
Diện tích hình trụ, thể tích khối trụ
Lời giải
Ta có 1000 lít = 1 m3.
Gọi h là chiều cao của hình trụ ta có \(K = \pi {R^2}h = 1 \Rightarrow h = \frac{1}{{\pi {R^2}}}\).
Diện tích toàn phần là: \({S_{tp}} = 2\pi {R^2} + 2\pi Rh = 2\pi {R^2} + 2\pi R\frac{1}{{\pi {R^2}}} = 2\pi {R^2} + \frac{2}{R}\)
\( = 2\left( {\pi {R^2} + \frac{1}{{2R}} + \frac{1}{{2R}}} \right) \ge 2.3\sqrt[3]{{\pi {R^2}.\frac{1}{{2R}}.\frac{1}{{2R}}}} = 6\sqrt[3]{{\frac{\pi }{4}}}\)
Dấu "=" xảy ra khi và chỉ khi \(\pi {R^2} = \frac{1}{{2R}} \Leftrightarrow R = \sqrt[3]{{\frac{1}{{2\pi }}}}\)
Chọn C
Câu 92:
 Xem đáp án
Xem đáp án
Phương pháp giải
Bước 1: Gọi MA = MB = MC = m. Tìm AB, AB, BC.
Bước 2: Ta có: AB2 + BC2 = AC2 ⇒ ΔABC vuông tại B. Gọi H là trung điểm của AC, suy ra, H là tâm đường tròn ngoại tiếp tam giác ABC. Chứng minh M, H, I thẳng hàng .
Bước 3: Áp dụng hệ thức lượng cho tam giác ΔMAI vuông tại A, ta nhận được tính IM.
Bước 4: Tìm tọa độ M(a,b,c) sau đó tính tổng a + b + c.
Lời giải
Mặt cầu \((S)\) có tâm \(I(1;2; - 3)\), bán kính \(R = 3\sqrt 3 \).
Gọi \(MA = MB = MC = m\).
Tam giác MAB đều \( \Rightarrow AB = m\).
Tam giác MBC vuông cân tại \(M \Rightarrow BC = m\sqrt 2 \).
Tam giác MAC cân tại M, \(\widehat {CMA} = {120^o } \Rightarrow AC = m\sqrt 3 \).
Ta có: vuông tại \(B\).
Gọi \(H\) là trung điểm của AC, suy ra, \(H\) là tâm đường tròn ngoại tiếp tam giác ABC
Vì \(MA = MB = MC,IA = IB = IC\) nên M, H, I thẳng hàng .
Áp dụng hệ thức lượng cho tam giác \(\Delta MAI\) vuông tại \(A\), ta nhận được \(MI = \frac{{AI}}{{\sin {{60}^o }}} = 6\)
\(M \in d \Rightarrow M(t - 1;t - 2;t + 1) \Rightarrow \overrightarrow {IM} = (t - 2;t - 4;t + 4)\).
\(I{M^2} = 36 \Rightarrow 3{t^2} - 4t = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t = 0 \Rightarrow M( - 1; - 2;1)\quad (t/m)}\\{t = \frac{4}{3} \Rightarrow M\left( {\frac{1}{3};\frac{{ - 2}}{3};\frac{7}{3}} \right)\quad (l)}\end{array} \Rightarrow a + b + c = - 2} \right.\).
Chọn A
Câu 93:
 Xem đáp án
Xem đáp án
Phương pháp giải
Dùng phương pháp liên hợp.
Dạng vô định ∞ - ∞
Lời giải
Ta có: \(\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {9{x^2} - ax} + \sqrt[3]{{27{x^3} + b{x^2} + 5}}} \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {9{x^2} - ax} + 3x} \right) + \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt[3]{{27{x^3} + b{x^2} + 5}} - 3x} \right)\)
\( = \mathop {\lim }\limits_{x \to - \infty } \frac{{9{x^2} - ax - 9{x^2}}}{{\sqrt {9{x^2} - ax} - 3x}} + \mathop {\lim }\limits_{x \to - \infty } \frac{{27{x^3} + b{x^2} + 5 - 27{x^3}}}{{{{\left( {\sqrt[3]{{27{x^3} + b{x^2} + 5}}} \right)}^2} + \sqrt[3]{{27{x^3} + b{x^2} + 5}}.3x + 9{x^2}}}\)
\( = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - ax}}{{\sqrt {9{x^2} - ax} - 3x}} + \mathop {\lim }\limits_{x \to - \infty } \frac{{b{x^2} + 5}}{{{{\left( {\sqrt[3]{{27{x^3} + b{x^2} + 5}}} \right)}^2} + \sqrt[3]{{27{x^3} + b{x^2} + 5}}.3x + 9{x^2}}}\)
\( = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - a}}{{ - \sqrt {9 - \frac{a}{x}} - 3}} + \mathop {\lim }\limits_{x \to - \infty } \frac{{b + \frac{5}{{{x^2}}}}}{{{{\left( {\sqrt[3]{{27 + \frac{b}{x} + \frac{5}{{{x^2}}}}}} \right)}^2} + \sqrt[3]{{27 + \frac{b}{x} + \frac{5}{{{x^2}}}}}.3 + 9}}\)
\( = \frac{{ - a}}{{ - 6}} + \frac{b}{{27}} = \frac{a}{6} + \frac{b}{{27}} = \frac{{27a + 6b}}{{6.27}}\).
Mà \(\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {9{x^2} - ax} + \sqrt[3]{{27{x^3} + b{x^2} + 5}}} \right) = \frac{7}{{27}}\)
\( \Rightarrow \frac{{27a + 6b}}{{6.27}} = \frac{7}{{27}} \Leftrightarrow \frac{{27a + 6b}}{6} = 7 \Leftrightarrow 27a + 6b = 42\)
\( \Leftrightarrow b = \frac{{42 - 27a}}{6} = 7 - \frac{9}{2}a\)
Khi đó: \(ab = a.\left( {7 - \frac{9}{2}a} \right) = - \frac{1}{2}\left( {9{a^2} - 14a} \right) = - \frac{1}{2}{\left( {3a - \frac{7}{3}} \right)^2} + \frac{{49}}{{18}} \le \frac{{49}}{{18}}\)
Dấu “=” xảy ra ⇔ \(a = \frac{7}{9},b = \frac{7}{2}\). Chọn A
