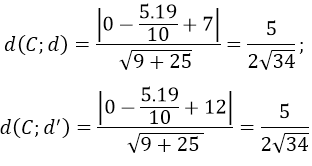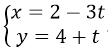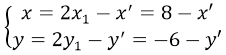19 câu hỏi trắc nghiệm thuộc Trắc nghiệm Phép đối xứng tâm có đáp án

Câu 1:

Hình có hai đường thẳng a và b song song với nhau thì có bao nhiêu phép đối xứng tâm biến a thành b?

A. Một

B. Hai

C. Ba

D. Vô số

Xem đáp án

Lấy hai điểm A, B bất kì lần lượt thuộc a, b. Trung điểm I của AB chính là tâm đối xứng của hình.

Vì A và B là 2 điểm bất kì nên có vô số điểm I thỏa mãn.

Chọn đáp án D

Câu 2:

Cho hình bình hành ABCD tâm O. Gọi E, F lần lượt là trung điểm của các cạnh BC và AD. Phép đối xứng tâm O biến.

A. $\vec{D F}$ thành $\overset{⇀}{E B}$

B. $\vec{E C}$ thành $\vec{A F}$

C. $\vec{B O}$ thành $\vec{O D}$

D. $\vec{B E}$ thành $\vec{D F}$

Xem đáp án

Phép đối xứng tâm O biến:

$Đ_{O} (B) = D; Đ_{O} (E) = F : Đ_{O} (C) = A; Đ_{O} (O) = O; Đ_{O} (D) = B$

Ba phương án A, B, C đều sai về hướng của vecto

Đáp án D

Câu 3:

Trong mặt phẳng Oxy cho điểm M(-3;7). Phép đối xứng tâm O biến M thành M’ thì tọa độ M’ là:

A. M’(-3;-7)

B. M’(3;-7)

C. M’(7;-3)

D. M’(7;3)

Xem đáp án

Phép đối xứng tâm O biến M(x;y) thành M’(-x;-y).

Áp dụng biểu thức tọa độ của phép đối xứng tâm ta có:

Chọn đáp án B

Câu 4:

Trong mặt phẳng Oxy cho điểm M(2;-6) và điểm I(1;4). Phép đối xứng tâm I biến M thành M’ thì tọa độ M’ là:

A. M’(0;14)

B. M’(14;0)

C. M’(-3/2;-2)

D. M’(-1/2;5)

Xem đáp án

Phép đối xứng tâm I biến điểm M thành điểm M' thì điểm I là trung điểm của MM'.
Do đó:

Câu 5:

Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x - 6y + 5 = 0 điểm I(2;-4). Phép đối xứng tâm I biến d thành d’ có phương trình:

A.2x - 6y - 5 = 0

B.2x - 6y - 61 = 0

C.6x - 2y + 5 = 0

D. 6x - 2y + 61 = 0

Xem đáp án

Lấy M(x;y) thuộc d, phép đối xứng tâm I (x0; y0) biến M(x; y) thành M'(x'; y') thuộc d'

Suy ra, I là trung điểm của MM'. Do đó:

(1)

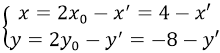
Vì điểm M(x, y) thuộc đường thẳng d nên : 2x - 6y + 5 = 0 (2)

Thay (1) vào (2) ta được :

2(4 - x') - 6(-8 - y') + 5 = 0 ⇒ 2x' - 6y' - 61 = 0

Suy ra,phương trình đường thẳng d' là: 2x - 6y - 61 = 0.

Chọn đáp án B

Câu 6:

Hình nào dưới đây vừa có tâm đối xứng vừa có trục đối xứng?

A. hình bình hành

B. hình chữ nhật

C. hình tam giác đều

D. hình tam giác cân

Xem đáp án

Hình bình hành có tâm đối xứng; hình tam giác cân và hình tam giác đều chỉ có trục đối xứng.

Đáp án B

Câu 7:

Có bao nhiêu phép đối xứng tâm biến hình chữ nhật thành chính nó?

A. một

B. hai

C. ba

D. không

Xem đáp án

Đáp án A.

Hình chữ nhật có 1 tâm đối xứng là giao điểm của 2 đường chéo

Do đó, có duy nhất một phép đối xứng tâm biến hình chữ nhật thành chính nó.

Câu 8:

Trong mặt phẳng Oxy cho điểm M(-5;9). Phép đối xứng tâm I(2; -6) biến M thành M’ thì tọa độ M’ là.

A. M'(9;-15)

B. M'(9;-3)

C.M'(9;-21)

D. M'(1;-3)

Xem đáp án

Đáp án C

Câu 9:

Trong mặt phẳng Oxy cho điểm I(2; -5). Phép đối xứng tâm I biến M(x; y) thành M'(3; 7). Tọa độ của M là:

A. M(5/2;1)

B. M(7;-3)

C. M(-1;-12)

D. M(1;-17)

Xem đáp án

Phép đối xứng tâm I biến điểm M(x;y) thành điểm M'(x'; y') nên I là trung điểm của đoạn thẳng MM '

Đáp án D

Câu 10:

Trong mặt phẳng Oxy phép đối xứng tâm I biến M(6; -9) thành M'(3;7). Tọa độ của tâm đối xứng I là:

A. I(-3/2; -8)

B. (-3;16)

C. (9/2; -1)

D. I(-3/2; -1)

Xem đáp án

Đáp án C

Câu 11:

Trong mặt phẳng Oxy cho đường thẳng d có phương trình 6x + 5y - 7 = 0; điểm I(2;-1). Phép đối xứng tâm I biến d thành d’ có phương trình:

A. 6x - 5y - 7 = 0

B. 6x + 5y - 7 = 0

C. 6x - 5y + 7 = 0

D. 6x + 5y + 7 = 0

Xem đáp án

Thay tọa độ điểm I vào phương trình đường thẳng d ta được:

6. 2 + 5. (-1) - 7 = 0

Suy ra,điểm I nằm trên đường thẳng d

Vì tâm đối xứng I thuộc d thì phép đối xứng tâm I biến d thành chính nó.

Nhận xét: lưu ý kiểm tra xem tâm có thuộc d không, cũng như với phép tịnh tiến thì kiểm tra xem vecto tịnh tiến có cùng phương với vecto chỉ phương của d không.

Đáp án B

Câu 12:

Trong mặt phẳng Oxy cho hình (H) gồm đường thẳng d có phương trình: 3x - 5y + 7 = 0; đường thẳng d’ có phương trình 3x - 5y + 12 = 0. Một tâm đối xứng của (H) là:

A. (1;2)

B. (-4;0)

C. (0;19/10)

D. (19/10;0)

Xem đáp án

Hai đường thẳng d và d’ song song.

+ Xét phương án A và B : vì điểm A(1; 2) thuộc d và điểm B(-4; 0) thuộc d’ nên A và B bị loại

+ Xét phương án C: điểm C ( 0; 19/10)

Tính khoảng cách từ C tới hai đường thẳng d, d’

⇒ d(C;d)=d(C;d')=> C là tâm đối xứng của hình

Nhận xét: nếu I là tâm đối xứng của hình gồm hai đường thẳng song song thì I cách đều hai đường thẳng song song đó.

Đáp án C

Câu 13:

Trong mặt phẳng Oxy cho hình (H) gồm đường thẳng d có phương trình 3x - 5y + 7 = 0 và đường thẳng d’ có phương trình:

Tâm đối xứng của (H) là:

A. I(-7/2;7/2)

B. I(7;-7)

C. I(7/2;7/2)

D. I(7;7)

Xem đáp án

Đường thẳng d vó vecto chỉ phương $\vec{u} = (5; 3)$ ; Đường thẳng d’ có vecto chỉ phương $\vec{v} (- 3; 1)$ nên d không song song với d’. Tâm đối xứng của hình (H) chính là giao điểm của d và d’:

Gọi I là giao điểm của d và d’.

Điểm I thuộc d’ nên tọa độ I(2- 3t; 4+ t)

Lại có, I thuộc d nên thay tọa độ điểm I vào phương trình đường thẳng d ta được:

3(2 - 3t) - 5(4 + t) + 7 = 0 ⇒ -14t = 7

$\Rightarrow t = \frac{- 1}{2} \Rightarrow I (\frac{7}{2}; \frac{7}{2})$

Đáp án C

Câu 14:

Trong mặt phẳng Oxy cho đường tròn (C) có phương trình ${(x - 2)}^{2} + {(y + 4)}^{2} = 9$ và đường tròn (C’) có phương trình ${(x - 3)}^{2} + {(y + 3)}^{2} = 9$ . Phép đối xứng tâm K biến (C) thành (C’). tọa độ của K là:

A. K(2; -4)

B. K(3; -3)

C. K(-7/2;5/2)

D. K(5/2; -7/2)

Xem đáp án

Đường tròn (C) có tâm I(2; -4), bán kính R= 3

Đường tròn (C’) có tâm J( 3; -3) và bán kính R’ = 3

Vì R= R’ nên tồn tại phép đối xứng tâm: biến đường tròn (C) thành (C’).

Khi đó; tâm đối xứng K là trung điểm IJ.

$\{\begin{matrix} x_{K} = \frac{2 + 3}{2} = \frac{5}{2} \\ y_{K} = \frac{(- 4) + (- 3)}{2} = \frac{- 7}{2} \end{matrix}$

$\Rightarrow K (\frac{5}{2}; - \frac{7}{2})$

Đáp án D

Câu 15:

Trong mặt phẳng Oxy cho đường tròn (C) có phương trình $x^{2} + y^{2} + 2 x - 6 y + 6 = 0$ ; điểm I(1;2). Phép đối xứng tâm I biến (C) thành (C’) có phương trình:

A. $x^{2} + y^{2} - 6 x - 2 y + 6 = 0$

B. $x^{2} + y^{2} - 2 x - 6 y + 6 = 0$

C. $x^{2} + y^{2} + 6 x - 2 y - 6 = 0$

D. $x^{2} + y^{2} - 6 x + 2 y + 6 = 0$

Xem đáp án

Phép đối xứng tâm I(1; 2) biến đường tròn (C) thành đường tròn (C')

và biến M(x; y) thuộc (C) thành M’(x’; y’) thuộc (C') thì:

(1)

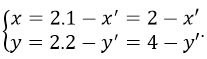
Vì điểm M(x, y) thuộc (C) nên:

$x^{2} + y^{2} + 2 x - 6 y + 6 = 0$ (2)

Thay (1) vào (2) ta được:

${(2 - x')}^{2} + {(4 - y')}^{2} + 2 (2 - x') - 6 (4 - y') + 6 = 0$

⇒ $x'^{2} + y'^{2} - 6 x' - 2 y' + 6 = 0$

Suy ra phương trình (C') $x^{2} + y^{2} - 6 x - 2 y + 6 = 0$

Đáp án A

Câu 16:

Trong mặt phẳng Oxy cho đường tròn (C) có phương trình: ${(x - 3)}^{2} + {(y - 1)}^{2} = 4$ . Phép đối xứng có tâm O là gốc tọa độ biến (C) thành (C’) có phương trình:

A. $x^{2} + y^{2} - 6 x - 2 y - 6 = 0$

B. $x^{2} + y^{2} - 2 x - 6 y + 6 = 0$

C. $x^{2} + y^{2} + 6 x - 2 y - 6 = 0$

D. $x^{2} + y^{2} + 6 x + 2 y + 6 = 0$

Xem đáp án

Đáp án D

Câu 17:

Trong mặt phẳng Oxy cho parabol (P) có phương trình $y = x^{2} - 3 x + 1$ . Phép đối xứng tâm O(0;0) biến (P) thành (P’) có phương trình:

A. $y = x^{2} + 3 x - 1$

B. $y = - x^{2} + 3 x + 1$

C. $y = - x^{2} - 3 x - 1$

D. $y = - x^{2} - 3 x + 1$

Xem đáp án

Đáp án C

Câu 18:

Trong mặt phẳng Oxy cho parabol (P) có phương trình: $y = x^{2} - 3 x + 1$ . Phép đối xứng tâm I(4; -3) biến P thành (P’) có phương trình:

A. $y = - x^{2} + 13 x - 47$

B. $y = x^{2} - 13 x + 47$

C. $y = - x^{2} - 13 x - 47$

D. $y = - x^{2} - 13 x + 47$

Xem đáp án

Phép đối xứng tâm I biến M(x; y) thành M’(x’; y’) thì:

Thay vào phương trình (P) ta được:

$- 6 - y' = {(8 - x')}^{2} - 3 (8 - x') + 1$

⇒ $- y' = x'^{2} - 13 x' + 47$ hay

$y = - x^{2} + 13 x - 47$

Đáp án A

Câu 19:

Trong mặt phẳng Oxy cho đường thẳng d có phương trình x - 2y + 2 = 0; đường thẳng d’ có phương trình x - 2y - 8 = 0. Tìm tọa độ điểm I sao cho phép đối xứng tâm I biến d thành d’ đồng thời biến trục Oy thành chính nó.

A. I(-2;0)

B. I(8;0)

C. I(-3/2;0)

D. I(0; -3/2)

Xem đáp án

Dễ thấy d // d’, ta có d ∩ Oy = A(0; 1); d’ ∩ Oy = A’(0; -4). Phép đối xứng tâm I biến Oy thành Oy thì I thuộc trục Oy; biến d thành d’ thì I là trung điểm của AA’ ⇒ I(0; -3/2).

Đáp án D