11 câu hỏi trắc nghiệm thuộc Dạng 2: Tìm giao tuyến của hai mặt phẳng có đáp án

Câu 1:

Cho tứ diện ABCD. M và N là trung điểm của AD và AC. G là trọng tâm tam giác BCD. Giao tuyến của 2 mặt phẳng (GMN) và (BCD) là đường thẳng

A. qua M và song song với AB;

B. qua N và song song với BD;

C. qua G và song song với CD;

D. qua G và song song với BC.

Xem đáp án

Đáp án đúng là: C

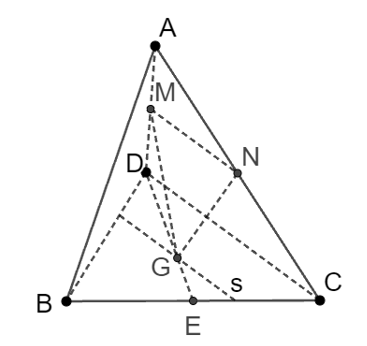
Cho tứ diện ABCD. M và N là trung điểm của AD và AC. G là trọng tâm tam giác BCD. Giao tuyến của 2 mặt phẳng (GMN) và (BCD) là đường thẳng (ảnh 1)

Ta có: $\{\begin{matrix} M N ∥ C D \\ M N \subset (G M N); C D \subset (B C D) \\ (B C D) \cap (G M N) = G \end{matrix}$

$\Rightarrow (G M N) \cap (B C D) = G s ∥ C D ∥ M N$ .

Đáp án đúng là C

Câu 2:

Cho hình chóp S. ABCD có đáy là hình thang với các cạnh đáy là AB và CD. M và N là trung điểm AD và BC. G là trọng tâm tam giác SAB. Giao tuyến của (SAB) và (MNG) là:

A. SC;

B. Đường thẳng qua S và song song với AB;

C. Đường thẳng qua G và song song với CD;

D. Đường thẳng qua G và cắt BC.

Xem đáp án

Đáp án đúng là: C

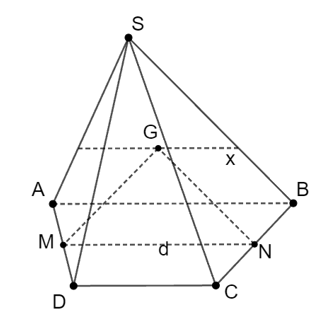
Cho hình chóp S. ABCD có đáy là hình thang với các cạnh đáy là AB và CD. M và N là trung điểm AD và BC. (ảnh 1)

Vì M và N lần lượt là trung điểm của AD và BC.

Nên MN là đường trung bình của hình thang ABCD.

Do đó MN // AB // CD.

Ta có: $\{\begin{matrix} M N ∥ A B \\ M N \subset (G M N); A B \subset (S A B) \\ G \in (S A B) \cap (G M N) \end{matrix}$

Suy ra (GMN) ∩ (SAB) = Gx // MN // AB.

Câu 3:

Cho hình bình hành ABCD và điểm S nằm ngoài (ABCD). E là một điểm bất kì thuộc cạnh SA. Giao tuyến của mặt phẳng (ECD) và (SAB) là

A. Qua E và song song với AD;

B. Qua E và song song với AB;

C. Qua E và song song với AC;

D. Qua E và song song với BD.

Xem đáp án

Đáp án đúng là: B

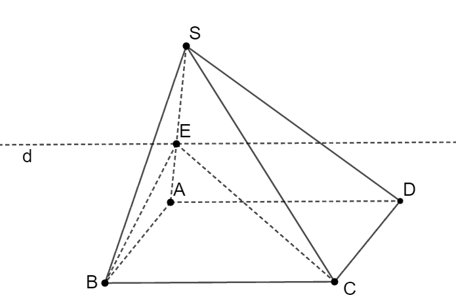
Cho hình bình hành ABCD và điểm S nằm ngoài (ABCD). E là một điểm bất kì thuộc cạnh SA. Giao tuyến của mặt phẳng (ECD) và (SAB) là (ảnh 1)

Ta có: $\{\begin{matrix} C D ∥ A B \\ C D \subset (E C D); A B \subset (S A B) \\ M \in (S A B) \cap (E C D) \end{matrix}$

Do đó (SAB) ∩ (SCD) = d, với d // AB // CD và E ∈ d.

Câu 4:

Cho hình thoi ABCD và S nằm ngoài (ABCD). O là giao điểm của AC và BD. E và F lần lượt là trung điểm của CD và AE. Giao tuyến của (SFO) và (SCD) là

A. Qua A và song song EC;

B. Qua E và song song FO;

C. Qua S và song song FO;

D. Qua O và song song EC.

Xem đáp án

Đáp án đúng là: C

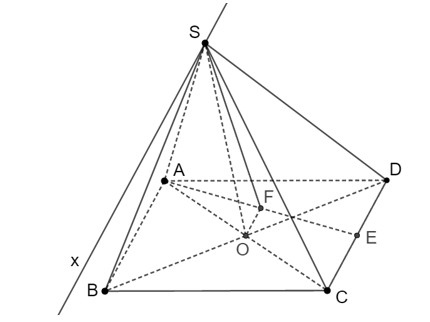
Cho hình thoi ABCD và S nằm ngoài (ABCD). O là giao điểm của AC và BD. (ảnh 1)

Vì F và O là trung điểm của AE và AC nên FO là đường trung bình của tam giác ACE.

Suy ra FO // EC.

Ta có: $\{\begin{matrix} F O ∥ E C \\ F O \subset (S F O); E C \subset (S E C) \\ S \in (S F O) \cap (S E C) \end{matrix}$ .

Do đó (SFO) ∩ (SEC) = Sx // FO // EC.

Câu 5:

Cho hình thoi ABCD và S nằm ngoài (ABCD). Lấy điểm E trên SA sao cho 2SE = EA; Lấy điểm F trên SB sao cho 2SF = FB. Điểm H nằm trên cạnh SC không trùng với S. Giao tuyến của (EFH) và (SCD) là

A. Qua A và song song AB;

B. Qua F và song song CD;

C. Qua H và song song CD;

D. Đáp án khác.

Xem đáp án

Đáp án đúng là: C

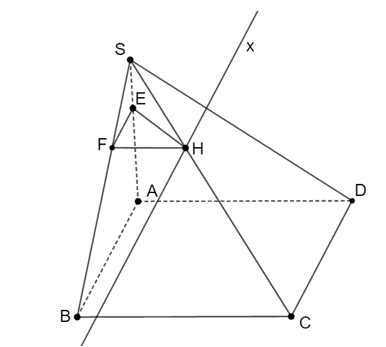
Cho hình thoi ABCD và S nằm ngoài (ABCD). Lấy điểm E trên SA sao cho 2SE = EA; Lấy điểm F trên SB sao cho 2SF = FB (ảnh 1)

Ta có: 2SE = EA và 2SF = FB nên $\frac{S E}{E A} = \frac{S F}{F B} = \frac{1}{2}$ .

Suy ra EF // AB (định lí Thalès đảo) (1)

Lại có ABCD là hình thoi nên AB // CD (2)

Từ (1) và (2) suy ra: EF // CD.

Ta có: $\{\begin{matrix} E F ∥ C D \\ E F \subset (E F H); C D \subset (S C D) \\ H \in (E F H) \cap (S C D) \end{matrix}$ .

Suy ra (EFH) ∩ (SCD) = Hx // EF // CD.

Câu 6:

Cho tứ diện ABCD và ba điểm P, Q, R lần lượt trên cạnh AB, CD và BC. Biết rằng PR // AC. Giao điểm S của mp(PQR) và cạnh AD là

A. giao điểm của đường thẳng Qx và AD với Qx // AC;

B. giao điểm của đường thẳng Px và AD với Px // BD;

C. giao điểm của đường thẳng Rx và AD với Rx // BD;

D. giao điểm của đường thẳng Qx và AD với Qx // BD.

Xem đáp án

Đáp án đúng là: A

Chọn mặt phẳng phụ chứa AD là (ACD).

Ta có: $\{\begin{matrix} P R ∥ A C \\ P R \subset (P Q R); A C \subset (A C D) \\ Q \in (P Q R) \cap (A C D) \end{matrix}$

⇒ (PQR) ∩ (ACD) = Qx // PR // AC

+ Trong mặt phẳng (ACD); Qx cắt AD tại S ta được điểm S cần tìm.

Câu 7:

Cho hình bình hành ABCD và S nằm ngoài (ABCD). Giao tuyến của hai mặt phẳng (SAB) và (SCD) là

A. Đường thẳng đi qua S song song với AB, CD;

B. Đường thẳng đi qua S;

C. Điểm S;

D. Mặt phẳng (SAD).

Xem đáp án

Đáp án đúng là: A

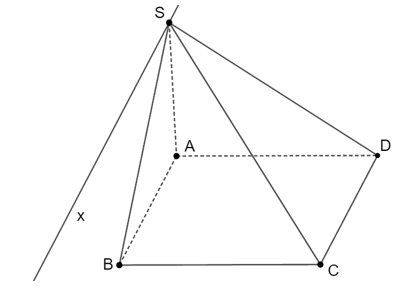
Cho hình bình hành ABCD và S nằm ngoài (ABCD). Giao tuyến của hai mặt phẳng (SAB) và (SCD) là (ảnh 1)

Ta có $\{\begin{matrix} A B ∥ C D \\ A B \subset (S A B); C D \subset (S C D) \\ S \in (S A B) \cap (S C D) \end{matrix}$ .

⇒ (SAB) ∩ (SCD) = d // AB // CD, S ∈ d.

Vậy đáp án đúng là A.

Câu 8:

Cho hình bình hành ABCD và S nằm ngoài (ABCD). Giao tuyến của hai mặt phẳng (SAB) và (SCD) là một đường thẳng song song với đường thẳng

A. AB;

B. AC;

C. BC;

D. SA.

Xem đáp án

Đáp án đúng là: A

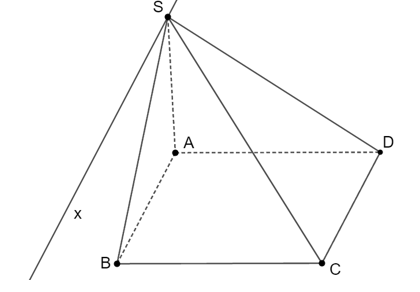
Cho hình bình hành ABCD và S nằm ngoài (ABCD). Giao tuyến của hai mặt phẳng (SAB) và (SCD) là một đường thẳng song song với đường thẳng (ảnh 1)

Ta có $\{\begin{matrix} A B ∥ C D \\ A B \subset (S A B); C D \subset (S C D) \\ S \in (S A B) \cap (S C D) \end{matrix}$

⇒ (SAB) ∩ (SCD) = Sx // AB // CD.

Vậy đáp án đúng là A.

Câu 9:

Cho tứ diện ABCD. Gọi M và N theo thứ tự là trung điểm của AD và AC, G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (GMN) và (BCD) là đường thẳng

A. qua M và song song với AB;

B. qua N và song song với BD;

C. qua G và song song với CD;

D. qua G và song song với BC.

Xem đáp án

Đáp án đúng là: C

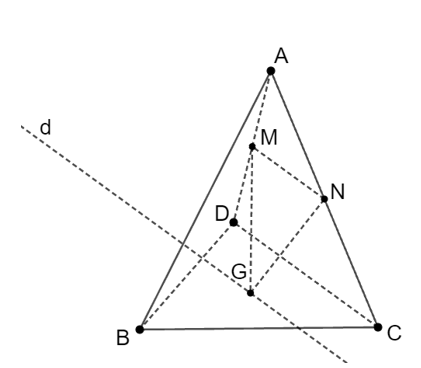
Cho tứ diện ABCD. Gọi M và N theo thứ tự là trung điểm của AD và AC, G là trọng tâm tam giác BCD (ảnh 1)

Gọi d là giao tuyến của (GMN) và (BCD).

Vì M và N là trung điểm của AD và AC nên MN là đường trung bình của tam giác ACD

Suy ra MN // CD.

Ta có: $\{\begin{matrix} M N ∥ C D \\ M N \subset (G M N); C D \subset (B C D) \\ G \in (G M N) \cap (B C D) \end{matrix}$ .

⇒ (GMN) ∩ (BCD) = d // MN // CD với d đi qua G.

Vậy đáp án đúng là C.

Câu 10:

Cho hình bình hành ABCD và S nằm ngoài (ABCD), O là giao điểm của AC và BD. M là trung điểm cạnh SC. Trong các khẳng định sau, khẳng định sai là

A. MO // SA;

B. 4 điểm M, O, S và A đồng phẳng;

C. Giao tuyến của (SAB) và (MBD) là Bx trong đó Bx // SA // MO;

D. (MBD) ∩ (SAC) = MD.

Xem đáp án

Đáp án đúng là: D

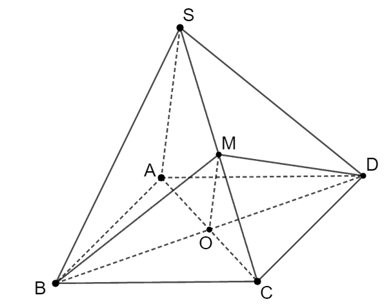
Cho hình bình hành ABCD và S nằm ngoài (ABCD), O là giao điểm của AC và BD. M là trung điểm cạnh SC (ảnh 1)

M và O là trung điểm của SC và AC nên OM là đường trung bình của tam giác SAC.

⇒ SA // MO và 4 điểm S, A, M, O đồng phẳng

⇒ A và B đúng.

Ta có: $\{\begin{matrix} M O ∥ S A \\ M O \subset (M B D); S A \subset (S A B) \\ B \in (M B D) \cap (S A B) \end{matrix}$

⇒ (MBD) ∩ (SAB) = Bx // SA // MO.

⇒ C đúng.

Vậy khẳng định sai là D.

Câu 11:

Các đường chéo của hình hộp

A. Tạo thành một tam giác đều;

B. Tạo thành một tam giác cân;

C. Tạo thành một tam giác;

D. Đồng quy tại trung điểm mỗi đường.

Xem đáp án

Đáp án đúng là: D

Các đường chéo của hình hộp đồng quy tại trung điểm mỗi đường.