10 câu hỏi trắc nghiệm thuộc Dạng 3. Bài toán thực tiễn liên quan đến phương trình lượng giác

Câu 1:

Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ 40° Bắc trong ngày thứ t của một năm không nhuận được cho bởi hàm số:

$d (t) = 3 \sin [\frac{π}{182} (t - 80)] + 12$ , với t ∈ ℤ và 0 ≤ t ≤ 365.

Thành phố A có đúng 15 giờ có ánh sáng mặt trời vào ngày nào trong năm?

A. 171;

B. 170;

C. 169;

D. 168.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Giả sử thành phố A có đúng 15 giờ có ánh sáng mặt trời vào ngày thứ t₀.

Ta có: $d (t_{0}) = 3 \sin [\frac{π}{182} (t_{0} - 80)] + 12$

Mà d(t₀) = 15 nên ta có:

$3 \sin [\frac{π}{182} (t_{0} - 80)] + 12 = 15$

⇔ $3 \sin [\frac{π}{182} (t_{0} - 80)] = 3$

⇔ $\sin [\frac{π}{182} (t_{0} - 80)] = 1$

⇔ $\frac{π}{182} (t_{0} - 80) = \frac{π}{2} + k 2 π$ , k ∈ ℤ

⇔ t₀ – 80 = 91 + 364k, k ∈ ℤ

⇔ t₀ = 364k + 171, k ∈ ℤ

Mà 0 ≤ t₀ ≤ 365

⇔ –171 ≤ 364k ≤ 194

⇔ –0,47 ≤ k ≤ 0,53

Mà k ∈ ℤ nên k = 0

Nếu k = 0 thì t₀ = 171

Vậy thành phố A có đúng 15 giờ có ánh sáng mặt trời vào ngày thứ 171.

Câu 2:

Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ 40° Bắc trong ngày thứ t của một năm không nhuận được cho bởi hàm số:

$d (t) = 3 \sin [\frac{π}{182} (t - 80)] + 12$ , với t ∈ ℤ và 0 ≤ t ≤ 365.

Vào ngày nào trong năm thì thành phố A có đúng 9 giờ có ánh sáng mặt trời?

A. 351;

B. 352;

C. 353;

D. 354.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Giả sử thành phố A có đúng 9 giờ có ánh sáng mặt trời vào ngày thứ t₀.

Ta có: $d (t_{0}) = 3 \sin [\frac{π}{182} (t_{0} - 80)] + 12$

Mà d(t₀) = 9 nên ta có:

$3 \sin [\frac{π}{182} (t_{0} - 80)] + 12 = 9$

⇔ $3 \sin [\frac{π}{182} (t_{0} - 80)] = - 3$

⇔ $\sin [\frac{π}{182} (t_{0} - 80)] = - 1$

⇔ $\frac{π}{182} (t_{0} - 80) = - \frac{π}{2} + k 2 π$ , k ∈ ℤ

⇔ t₀ – 80 = –91 + 364k , k ∈ ℤ

⇔ t₀ = 364k – 11, k ∈ ℤ

Mà 0 ≤ t₀ ≤ 365

⇔ 11 ≤ 364k ≤ 376

⇔ 0,03 ≤ k ≤ 1,03

Mà k ∈ ℤ nên k = 1

Nếu k = 1 thì t₀ = 353

Vậy thành phố A có đúng 9 giờ có ánh sáng mặt trời vào ngày thứ 353.

Câu 3:

Một quả đạn pháp được bắn khỏi nòng pháp với vận tốc ban đầu v₀ = 500 m/s hợp với phương ngang một góc α. Trong Vật lí, ta biết rằng, nếu bỏ qua sức cản của không khí và coi quả đạn pháo được bắn ra từ mặt đất thì quỹ đạo của quả đạn tuân theo phương trình $y = \frac{- g}{2 {v_{0}}^{2} \cos^{2} α} x^{2} + x \tan α$ , ở đó g = 9,8 m/s² là gia tốc trọng trường. Tìm góc bắn α để quả đạn trúng mục tiêu cách vị trí đặt khẩu pháo 22 000 m.

A. $α \approx 29 ° 47' 37''$ ;

B. $α \approx 28 ° 47' 36''$ ;

C. $α \approx 29 ° 47' 30''$ ;

D.

α \approx 29 ° 40' 36''

.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Vì v₀ = 500 m/s và g = 9,8 m/s²nên ta có phương trình quỹ đạo của quả đạn là:

$y = \frac{- 9, 8}{{2.500}^{2} \cos^{2} α} x^{2} + x \tan α = \frac{- 49}{2500000 \cos^{2} α} x^{2} + x \tan α$ \.

Quả đạn chạm đất khi y = 0, khi đó

$\frac{- 49}{2500000 \cos^{2} α} x^{2} + x \tan α = 0$

⇔ $x (\frac{- 49}{2500000 \cos^{2} α} x + \tan α) = 0$

⇔ $[\begin{array}{l} x = 0 \\ x = \frac{2500000 \cos^{2} α . \tan α}{49} \end{array}$

⇔ $[\begin{array}{l} x = 0 \\ x = \frac{2500000 \cos α . \sin α}{49} \end{array}$

⇔ $[\begin{array}{l} x = 0 \\ x = \frac{1250000 \sin 2 α}{49} \end{array}$

Loại x = 0 (đạn pháo chưa được bắn)

Vậy tầm xa mà quả đạn đạt tới là $x = \frac{1250000 \sin 2 α}{49}$ (m).

Để quả đạn trúng mục tiêu cách vị trí đặt khẩu pháp 22 000 m thì x = 22 000 m.

Khi đó: $\frac{1250000 \sin 2 α}{49} = 22000$

⇔

⇔.

Câu 4:

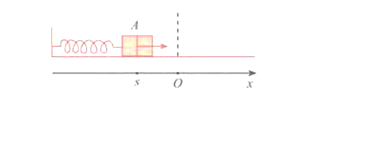
Trong hình vẽ, khi được kéo ra khỏi vị trí cân bằng ở điểm O và buông tay, lực đàn hồi của lò xo khiến vật A gắn ở đầu lò xo dao động quanh O. Tọa độ s (cm) của A trên trục Ox vào thời điểm t (giây) sau khi buông tay được xác định bởi công thức $s = 10 \sin (10 t + \frac{π}{2})$ . Vào thời điểm nào dưới dây thì s $= - 5 \sqrt{3}$ cm?

Trong hình vẽ, khi được kéo ra khỏi vị trí cân bằng ở điểm O và buông tay, lực đàn hồi của lò xo khiến (ảnh 1)

A. $\frac{- π}{3}$ ;

B. $\frac{- π}{12}$ ;

C. $\frac{- π}{6}$ ;

D.

\frac{- π}{4}

.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Khi s $= - 5 \sqrt{3}$ cm thì:

$10 \sin (10 t + \frac{π}{2}) = - 5 \sqrt{3}$

⇔ $\sin (10 t + \frac{π}{2}) = \frac{- \sqrt{3}}{2}$

⇔ $\sin (10 t + \frac{π}{2}) = \sin (\frac{- π}{3})$

⇔ $[\begin{array}{l} 10 t + \frac{π}{2} = \frac{- π}{3} + k 2 π \\ 10 t + \frac{π}{2} = \frac{4 π}{3} + k 2 π \end{array}$ , k ∈ ℤ

⇔ $[\begin{array}{l} 10 t = \frac{- 5 π}{6} + k 2 π \\ 10 t = \frac{5 π}{6} + k 2 π \end{array}$ , k ∈ ℤ

⇔ $[\begin{array}{l} t = \frac{- π}{12} + k \frac{π}{5} \\ t = \frac{π}{12} + k \frac{π}{5} \end{array}$ , k ∈ ℤ

Khi k = 0 thì t = $\frac{- π}{12}$ hoặc t = $\frac{π}{12}$ .

Câu 5:

Theo Định luật khúc xạ ánh sáng, khi một tia sáng được chiếu tới mặt phân cách giữa hai môi trường trong suốt không đồng chất thì tỉ số $\frac{\sin i}{\sin r}$ , với i là góc tới và r là góc khúc xạ, là một hằng số phụ thuộc vào chiết suất của hai môi trường. Biết rằng khi góc tới là 45° thì góc khúc xạ bằng 30°. Khi góc tới là 60° thì góc khúc xạ là bao nhiêu?

A. 30°;

B. 45°;

C. 38°;

D. 60°.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Khi góc tới là 45° thì góc khúc xạ bằng 30° nên ta có:

Tỉ số $\frac{\sin i}{\sin r}$ = $\frac{\sin 45 °}{\sin 30 °} = \sqrt{2}$

Khi góc tới là 60° thì ta có:

$\frac{\sin 60 °}{\sin r} = \sqrt{2}$

⇔ $\sin 60 ° = \sqrt{2} \sin r$

⇔ $\sqrt{2} \sin r = \frac{\sqrt{3}}{2}$

⇔ $\sin r = \frac{\sqrt{6}}{4}$

⇔ $\sin r \approx \sin (38 °)$

⇔ $[\begin{array}{l} r \approx 38 ° (T M) \\ r \approx 142 ° (K T M) \end{array}$ .

Câu 6:

Vận tốc của con lắc đơn v (cm/s) được cho bởi công thức:

$v (t) = - 4 \cos (\frac{2}{3} t + \frac{π}{4})$ .

Tại thời điểm nào dưới đây thì vận tốc của con lắc đơn bằng 2 cm/s?

A. $- \frac{5 π}{8}$ ;

B. $\frac{5 π}{3}$ ;

C. $\frac{π}{8}$ ;

D.

\frac{5 π}{8}

.

Xem đáp án

Câu 7:

Vận tốc của con lắc đơn v (cm/s) được cho bởi công thức:

$v (t) = 2 \sin (2 t + \frac{π}{6})$ .

Tại thời điểm nào dưới đây thì vận tốc của con lắc đơn bằng 2 cm/s?

A. $\frac{π}{4}$ ;

B. $\frac{π}{8}$ ;

C. $\frac{π}{6}$ ;

D.

\frac{π}{3}

.

Xem đáp án

Vận tốc của con lắc đơn v (cm/s) được cho bởi công thức: (ảnh 1)

Câu 8:

Hằng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu h (m) của mực nước trong kênh tính theo thời gian t (giờ) trong một ngày (0 ≤ t ≤ 24) cho bởi công thức $h = 3 \cos (\frac{π}{6} t) + 12$ . Một giá trị của t để độ sâu của mực nước là 15 m là

A. 0 giờ;

B. 1 giờ;

C. 2 giờ;

D. 3 giờ.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Để độ sâu của mực nước là 15 m thì

$3 \cos (\frac{π}{6} t) + 12 = 15$

$\Leftrightarrow 3 \cos (\frac{π}{6} t) = 3$

$\Leftrightarrow \cos (\frac{π}{6} t) = 1$

$\Leftrightarrow \frac{π}{6} t = k 2 π$ (k ∈ ℤ)

$\Leftrightarrow t =$ 12k (k ∈ ℤ)

Mà 0 ≤ t ≤ 24 ⇔ 0 ≤ k ≤ 2.

Với k = 0 thì t = 0.

Với k = 1 thì t = 12.

Với k = 2 thì t = 24.

Vậy tại các thời điểm 0 giờ, 12 giờ, 24 giờ thì độ sâu của mực nước là 15 m.

Câu 9:

Chiều cao h (m) của một cabin trên vòng quay vào thời điểm t giây sau khi bắt đầu chuyển động được cho bởi công thức

$h (t) = 30 + 20 \sin (\frac{π}{25} t + \frac{π}{3})$ . Cabin đạt độ cao tối đa là bao nhiêu?

A. 30 m;

B. 40 m

C. 50 m

D. 60 m.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Với mọi t > 0, ta có:

⇔ $- 1 \leq \sin (\frac{π}{25} t + \frac{π}{3}) \leq 1$

⇔ $- 20 \leq 20 \sin (\frac{π}{25} t + \frac{π}{3}) \leq 20$

⇔ $10 \leq 30 + 20 \sin (\frac{π}{25} t + \frac{π}{3}) \leq 50$

Hay 10 ≤ h(t) ≤ 50

Vậy cabin đạt độ cao tối đa là 50 (m).

Câu 10:

Chiều cao h (m) của một cabin trên vòng quay vào thời điểm t giây sau khi bắt đầu chuyển động được cho bởi công thức $h (t) = 30 + 20 \sin (\frac{π}{25} t + \frac{π}{3})$ . Sau bao nhiêu giây thì cabin đạt độ cao 40 m lần đầu tiên?

A. 48,5 giây;

B. 12,5 giây;

C. 13,48 giây;

D. 45,6 giây.

Xem đáp án