29 câu hỏi trắc nghiệm thuộc Đề kiểm tra học kì 2 Chuyên đề toán 11: Kiểm tra cuối kì có đáp án (Đề 3)

Câu 1:

Trong các mệnh đề sau đây, mệnh đề nào sai?

A. Có duy nhất một mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng cho trước.

B. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.

C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

D. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.

Xem đáp án

Chọn D

Câu 2:

Chọn mệnh đề đúng trong các mệnh đề sau?

A. Nếu

a ⊥ (P)

và

b ⊥ a

thì

b \subset (P)

.

B. Nếu $A \in (P)$ và $A \in b$ thì $b \in (P)$ .

C. Nếu

a \subset (P)

và

b ⊥ a

thì

b ⊥ (P)

.

D. Nếu

a \subset (P)

và

b ⊥ (P)

thì

b ⊥ a

.

Xem đáp án

Chọn D

Câu 3:

Đạo hàm của hàm số $f (x) = \frac{- 3 x + 4}{2 x + 1}$ tại $x = - 1$ bằng

A. $\frac{1}{5}$

B. -11

C. $- \frac{11}{9}$

D. $- \frac{11}{3}$

Xem đáp án

Chọn B

Câu 4:

Phương trình tiếp tuyến của đồ thị $(C) : y = 3 x - 4 x^{3}$ tại điểm có hoành độ $x_{0} = 0$ là

A. y=-12x

B. $y = 3 x$

C. y=0

D. $y = 3 x - 2$

Xem đáp án

Chọn B

Câu 5:

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, $S A ⊥ (A B C)$ và $S A = a \sqrt{6}$ . Gọi M là trung điểm của BC, khi đó khoảng cách từ A đến đường thẳng SM bằng

A. $a \sqrt{2}$

B. $a \sqrt{3}$

C. $a \sqrt{6}$

D. $a \sqrt{11}$

Xem đáp án

Chọn A

Câu 6:

Cho dãy số $u_{n} = n (\sqrt{n^{2} + 1} - n)$ . Khi đó $\lim u_{n}$ bằng

A. $\frac{1}{2}$

B. 0

C. 1

D. $+ \infty$

Xem đáp án

Chọn A

Câu 7:

Giới hạn $\lim_{x \to 1^{-}} \frac{2 x + 1}{x - 1}$ bằng

A. $+ \infty$

B. -1.

C.

- \infty

D. 2.

Xem đáp án

Chọn C

Câu 8:

Trong các mệnh đề sau đây, mệnh đề nào sai?

A. Nếu có

m \vec{a} + n \vec{b} + p \vec{c} = \vec{0}

và một trong ba số m, n, p khác 0 thì ba vectơ

\vec{a}, \vec{b}, \vec{c}

đồng phẳng.

B. Ba tia Ox, Oy, Oz vuông góc với nhau từng đôi một thì ba tia đó không đồng phẳng.

C. Cho hai vectơ không cùng phương $\vec{a}$ và $\vec{b}$ . Khi đó ba vectơ $\vec{a}, \vec{b}, \vec{c}$ đồng phẳng khi và chỉ khi có cặp số m, n sao cho $\vec{c} = m \vec{a} + n \vec{b}$ , ngoài ra cặp số m, n là duy nhất.

D. Ba vectơ

\vec{a}, \vec{b}, \vec{c}

đồng phẳng khi và chỉ khi ba vectơ đó có giá thuộc một mặt phẳng.

Xem đáp án

Chọn D

Câu 9:

Hệ số góc của tiếp tuyến với đồ thị hàm số $y = 2 x^{3} - 3 x^{2} + 5$ tại điểm có hoành độ -2 là

A. 36.

B. 12.

C. -12.

D. 38.

Xem đáp án

Chọn A

Câu 10:

Hãy chọn phát biểu sai trong các phát biểu sau

A. Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trên mặt phẳng này đều song song với mặt phẳng kia.

B. Nếu mặt phẳng (P) chứa hai đường thẳng cùng song song với mặt phẳng (Q) thì (P) và (Q) song song với nhau.

C. Nếu hai mặt phẳng (P) và (Q) song song với nhau thì mặt phẳng (R) đã cắt (P) đều phải cắt (Q) và các giao tuyến của chúng song song với nhau.

D. Nếu một đường thẳng cắt một trong hai mặt phẳng song song thì sẽ cắt mặt phẳng còn lại.

Xem đáp án

Chọn B

Câu 11:

Cho hàm số $f (x) = \{\begin{cases} \frac{x^{2} - 3}{x - \sqrt{3}}, x \neq \sqrt{3} \\ 2 \sqrt{3}, x = \sqrt{3} \end{cases}$ và các khẳng định

(I) $f (x)$ liên tục tại $x = \sqrt{3}$ .

(II) $f (x)$ gián đoạn tại $x = \sqrt{3}$ .

(III) $f (x)$ liên tục trên $ℝ$ .

Khẳng $f (x)$ định đúng là

A. Chỉ (I) và (II).

B. Chỉ (II) và (III).

C. Chỉ (I) và (III).

D. Cả (I), (II), (III) đều đúng.

Xem đáp án

Chọn C

Câu 12:

Giá trị của $\lim (\sqrt{n^{2} + 6 n} - n)$ bằng

A. 1.

B.

+ \infty

C.

- \infty

D. 3.

Xem đáp án

Chọn D

Câu 13:

Cho chuyển động thẳng xác định bởi phương trình

S = t^{2} - 2 t + 3

, trong đó t được tính bằng giây và s được tính bằng mét. Vận tốc của chuyển động tại thời điểm t=2s là

A. 2m/s.

B. 5 m/s.

C. 1 m/s.

D. 3 m/s.

Xem đáp án

Chọn A

Câu 14:

Cho hình chóp S.ABC có $S A ⊥ (A B C)$ và $A B ⊥ B C$ , gọi I là trung điểm BC. Góc giữa hai mặt phẳng (SBC) và (ABC) là góc nào sau đây?

A. $\hat{S I A}$

B. $\hat{S B A}$

C. $\hat{S C A}$

D. $\hat{S C B}$

Xem đáp án

Chọn B

Câu 15:

Giá trị

\lim_{x \to - 1} \frac{x^{2} + 2 x + 1}{2 x^{3} + 2}

bằng

A. $+ \infty$

B. $- \infty$

C. 0

D. $\frac{1}{2}$

Xem đáp án

Chọn C

Câu 16:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông, $S A ⊥ (A B C D)$ . Mặt phẳng qua A và vuông góc với SC cắt SB, SC, SD theo thứ tự tại H, M, K. Chọn khẳng định sai trong các khẳng định sau

A. $A K ⊥ H K$

B. $H K ⊥ A M$

C. $B D ⊥ H K$

D. $A H ⊥ S B$

Xem đáp án

Chọn A

Câu 17:

Cho hình lập phương $A B C D . A^{'} B^{'} C^{'} D^{'}$ cạnh a. Tích vô hướng $\vec{A B} . \vec{A^{'} D}$ bằng

A. 4a²

B. 2a²

C. 0

D. a²

Xem đáp án

Chọn C

Câu 18:

Xét hai khẳng định

(1) Hàm số $y = \frac{|x|}{x + 1}$ liên tục tại x=0.

(2) Hàm số $y = \frac{|x|}{x + 1}$ có đạo hàm tại x=0.

Trong hai khẳng định trên

A. Cả hai đều đúng.

B. Cả hai đều sai.

C. Chỉ có (2) đúng.

D. Chỉ có (1) đúng.

Xem đáp án

Chọn D

Câu 19:

Vi phân của hàm số $y = \frac{\tan \sqrt{x}}{\sqrt{x}}$ là

A. $d y = \frac{2 \sqrt{x}}{4 x \sqrt{x} \cos^{2} \sqrt{x}} d x$

B. $d y = \frac{\sin (2 \sqrt{x})}{4 x \sqrt{x} \cos^{2} \sqrt{x}} d x$

C. $d y = \frac{2 \sqrt{x} - \sin (2 \sqrt{x})}{4 x \sqrt{x} \cos^{2} \sqrt{x}} d x$

D. $d y = - \frac{2 \sqrt{x} - \sin (2 \sqrt{x})}{4 x \sqrt{x} \cos^{2} \sqrt{x}} d x$

Xem đáp án

Chọn C

Câu 20:

Giới hạn $\lim_{x \to + \infty} [\sqrt[n]{(x + a_{1}) (x + a_{2}) ... (x + a_{n})} - x]$ bằng

A. $- \infty$

B. $\frac{a_{1} + a_{2} + ... + a_{n}}{n}$

C. $\frac{a_{1} + a_{2} + ... + a_{n}}{2 n}$

D. $+ \infty$

Xem đáp án

Chọn B

Câu 21:

a) Tính giới hạn $\lim \frac{3^{n} - 1}{2^{n} - {2.3}^{n} + 1}$ .

Xem đáp án

a) Ta có

\lim \frac{3^{n} - 1}{2^{n} - {2.3}^{n} + 1} = \lim \frac{1 - {(\frac{1}{3})}^{n}}{{(\frac{2}{3})}^{n} - 2 + {(\frac{1}{3})}^{n}} = - \frac{1}{2}

Câu 22:

b) Tính giới hạn $\lim_{x \to 2} \frac{\sqrt{x + 2} - 2}{x - 2}$ .

Xem đáp án

b) Ta có $\lim_{x \to 2} \frac{\sqrt{x + 2} - 2}{x - 2} = \lim_{x \to 2} \frac{(\sqrt{x + 2} - 2) (\sqrt{x + 2} + 2)}{(x - 2) (\sqrt{x + 2} + 2)} = \lim_{x \to 2} \frac{x - 2}{(x - 2) (\sqrt{x + 2} + 2)}$

= \lim_{x \to 2} \frac{1}{\sqrt{x + 2} + 2} = \frac{1}{4}

. Vậy

\lim_{x \to 2} \frac{\sqrt{x + 2} - 2}{x - 2} = \frac{1}{4}

Câu 23:

c) Tính giới hạn $\lim_{x \to + \infty} \frac{1}{\sqrt{x^{2} + x + 2} - x}$

Xem đáp án

c) Ta có $\lim_{x \to + \infty} \frac{1}{\sqrt{x^{2} + x + 2} - x} = \lim_{x \to + \infty} \frac{\sqrt{x^{2} + x + 2} + x}{x^{2} + x + 2 - x^{2}} = \lim_{x \to + \infty} \frac{\sqrt{x^{2} + x + 2} + x}{x + 2}$

$= \lim_{x \to + \infty} \frac{x \sqrt{1 + \frac{1}{x} + \frac{2}{x^{2}}} + x}{x + 2} = \lim_{x \to + \infty} \frac{\sqrt{1 + \frac{1}{x} + \frac{2}{x^{2}}} + 1}{1 + \frac{2}{x}} = 2$

Câu 24:

a) Tìm giá trị thực của tham số m để hàm số $f (x) = \{\begin{cases} m^{2} x^{2} k h i x \leq 2 \\ (1 - m) x k h i x > 2 \end{cases}$ liên tục trên $ℝ$ .

Xem đáp án

a) Tập xác định $D = ℝ$ . Hàm số liên tục trên mỗi khoảng $(- \infty; 2); (2; + \infty)$

Khi đó $f (x)$ liên tục trên $ℝ \Leftrightarrow f (x)$ liên tục tại x=2

$\Leftrightarrow \lim_{x \to 2} f (x) = f (2) \Leftrightarrow \lim_{x \to 2^{+}} f (x) = \lim_{x \to 2^{-}} f (x) = f (2)$

(*)

Ta có

$\{\begin{cases} f (2) = 4 m^{2} \\ \lim_{x \to 2^{+}} f (x) = \lim_{x \to 2^{+}} [(1 - m) x] = 2 (1 - m) \\ \lim_{x \to 2^{-}} f (x) = \lim_{x \to 2^{-}} m^{2} x^{2} = 4 m^{2} \end{cases} \Rightarrow (*) \Leftrightarrow 4 m^{2} = 2 (1 - m) \Leftrightarrow [\begin{array}{l} m = - 1 \\ m = \frac{1}{2} \end{array}$

Câu 25:

b) Viết phương trình tiếp tuyến của đồ thị hàm số $y = x^{3} - 2 x + 3$ tại điểm $M (1; 2)$

Xem đáp án

b) Đạo hàm $y^{'} = 3 x^{2} - 2 \Rightarrow$ hệ số góc $k = y^{'} (1) = 1$

Ta có

\{\begin{cases} x_{0} = 1 \\ y_{0} = 2 \\ k = 1 \end{cases} \Rightarrow

phương trình tiếp tuyến

y = (x - 1) + 2 \Leftrightarrow y = x + 1

Câu 26:

c) Viết phương trình tiếp tuyến song song với trục hoành của đồ thị hàm số $y = x^{4} - 2 x^{2} + 10$

Xem đáp án

c) Xét $y^{'} = 4 x^{3} - 4 x$ . Vì tiếp tuyến song song với trục hoành nên

$k = y^{'} (x_{0}) = 0 \Leftrightarrow 4 x_{0}^{3} - 4 x_{0} = 0 \Leftrightarrow [\begin{array}{l} x_{0} = 0 \\ x_{0} = 1 \\ x_{0} = - 1 \end{array}$

Với $x_{0} = 0 \Rightarrow y_{0} = 10$ . Phương trình tiếp tuyến $y = 0 (x - 0) + 10 \Leftrightarrow y = 10$

Với $x_{0} = 1 \Rightarrow y_{0} = 9$ . Phương trình tiếp tuyến $y = 0 (x - 1) + 9 \Leftrightarrow y = 9$ .

Với $x_{0} = - 1 \Rightarrow y_{0} = 9$ . Phương trình tiếp tuyến $y = 0 (x + 1) + 9 \Leftrightarrow y = 9$

Vậy có hai tiếp tuyến cần tìm là

y = 9, y = 10

.

Câu 27:

Cho hình chóp S.ABCD đáy là hình vuông cạnh a, mặt bên (SAB), (SAD) vuông góc với đáy, các mặt bên (SBC), (SCD) cùng tạo với đáy góc 60°

a) Chứng minh rằng $\hat{S B A} = \hat{S D A} = 60 °$

Xem đáp án

Hai mặt phẳng (SAB), (SAD) cùng vuông góc với mặt đáy nên có giao tuyến SA cũng vuông góc mặt đáy.

\{\begin{cases} B C ⊥ S A (d o S A ⊥ (A B C D)) \\ B C ⊥ A B \end{cases} \Rightarrow B C ⊥ (S A B) \Rightarrow B C ⊥ S B

\{\begin{cases} C D ⊥ S A (d o S A ⊥ (A B C D)) \\ C D ⊥ A D \end{cases} \Rightarrow C D ⊥ (S A D) \Rightarrow C D ⊥ S D

a) Ta có $\{\begin{cases} (S A B) \cap (A B C D) = B C \\ S B \subset (S A B); S B ⊥ B C \\ A B \subset (A B C D); A B ⊥ B C \end{cases}$

$\Rightarrow (\hat{(S A B); (A B C D)}) = (\hat{S B, A B}) = \hat{S B A} = 60 °$

Tương tự $\{\begin{cases} (S C D) \cap (A B C D) = C D \\ D C \subset (S C D); S D ⊥ C D \\ A D \subset (A B C D); A D ⊥ C D \end{cases}$

\Rightarrow (\hat{(S A D); (A B C D)}) = (\hat{S D, A D}) = \hat{S D A} = 60 °

Câu 28:

b) Chứng minh rằng $(S A C) ⊥ (S B D)$

Xem đáp án

b) Ta có $\{\begin{cases} B D ⊥ S A (d o S A ⊥ (A B C D)) \\ B D ⊥ A C \end{cases} \Rightarrow B D ⊥ (S A C)$

Mà

B D \subset (S B D)

nên

(S B D) ⊥ (S A C)

.

Câu 29:

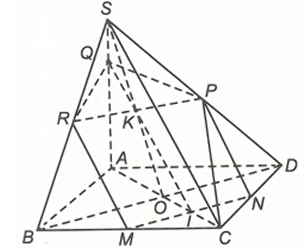
c) Gọi M, N là trung điểm BC, CD. Xác định thiết diện của hình chóp đi qua M, N và song song với SC. Tính diện tích thiết diện.

Xem đáp án

c) Gọi $\{I\} = M N \cap A C$ . Từ I kẻ đường thẳng song song với SC cắt SA tại Q.

Ta có $\{\begin{cases} I Q q u a I \in (P) \\ I Q / / S C \\ S C / / (P) \end{cases} \Rightarrow I Q \subset (P)$ hay $(P) \equiv (Q M N)$ .

Gọi $\{K\} = S O \cap Q I$ . Qua K kẻ đường thẳng song song với BD cắt SB, SD tại R, P.

Ta có $\{\begin{cases} R P q u a K \in (P) \\ R P / / M N \\ M N \subset (P) \end{cases} \Rightarrow R P \subset (P)$ hay $(P) \equiv (M N P Q R)$

Dựa vào hình vẽ ta có thiết diện cần tìm là ngũ giác MNPQR.

Ta có $S_{M N P Q R} = S_{M N P R} + S_{P Q R}$

Mặt phẳng (P) cắt (SBC) theo giao tuyến RM và (P) song song với SC nên RM // SC.

Mặt phẳng (P) cắt (SCD) theo giao tuyến NP và (P) song song với SC nên NP // SC

Vậy tứ giác MNPR là hình bình hành có $M N ⊥ N P$ (do MN // BD; NP // SC; $B D ⊥ S C$ ) nên là hình chữ nhật.

Tam giác PQR có PR // BD; $B D ⊥ (S A C)$ chứa QK nên là $Q K ⊥ P R$ .

Do QK // SC và $\frac{A I}{A C} = \frac{3}{4}$ nên

$Q I = \frac{3}{4} S C = \frac{3}{4} \sqrt{S A^{2} + A C^{2}} = \frac{3}{4} \sqrt{{(a \sqrt{3})}^{2} + {(a \sqrt{2})}^{2}} = \frac{3 a \sqrt{5}}{4}$

Suy ra $Q K = Q I - K I = Q I - \frac{S C}{2} = \frac{3 a \sqrt{5}}{4} - \frac{a \sqrt{5}}{2} = \frac{3 a \sqrt{5}}{4}$

$\Rightarrow S_{P Q R} = \frac{1}{2} P R . Q K = \frac{1}{2} . \frac{a \sqrt{2}}{2} . \frac{a \sqrt{5}}{4} = \frac{a^{2} \sqrt{10}}{16}$

Lại có $S_{M N P R} = M N . N P = \frac{B D}{2} . \frac{S C}{2} = \frac{a \sqrt{2}}{2} . \frac{a \sqrt{5}}{2} = \frac{a^{2} \sqrt{10}}{4}$

Suy ra

S_{M N P Q R} = S_{M N P R} + S_{P Q R} = \frac{a^{2} \sqrt{10}}{4} + \frac{a^{2} \sqrt{10}}{16} = \frac{5 a^{2} \sqrt{10}}{16}