Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 10)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 10)
-
208 lượt thi
-
98 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
Phần tư duy đọc hiểu
Mục đích chính của bài viết là gì?
 Xem đáp án
Xem đáp án
Giải thích
|
Lí do lựa chọn phương án |
A |
Tác giả có đề cập đến một số kỹ thuật xâm phạm bản quyền (đoạn [4][6]), nhưng chỉ là dẫn chứng cho khó khăn trong quá trình phát hiện và xử lý xâm phạm bản quyền. |
|
B |
Tác giả phân tích những khó khăn trong việc phát hiện (đoạn [2][4][5][6]) xử lý xâm phạm bản quyền (đoạn [1][2][3][4]). |
|
|
C |
Tác giả có đề cập đến quy trình pháp lý ở đoạn [2], nhưng đây chỉ là dẫn chứng cho khó khăn trong quá trình xử lý xâm phạm bản quyền. |
|
|
D |
Tác giả có đề cập đến tầm quan trọng của việc thu thập bằng chứng khi xử lý xâm phạm bản quyền ở đoạn [2] và [5], nhưng để nhằm chỉ ra khó khăn trong việc phát hiện xâm phạm bản quyền. |
Chọn B
Câu 2:
Theo đoạn [1], cơ sở gia công HT bị kết tội vi phạm bản quyền và phải bồi thường thiệt hại cho công ty T.V – F.N. Đúng hay sai?
 Xem đáp án
Xem đáp án
Đáp án
B. Sai
Giải thích
T.V – F.N bị thua kiện vì chưa đủ bằng chứng xử lý vi phạm của cơ sở H.T.
Câu 3:
Kéo thả cụm từ phù hợp vào chỗ trống để hoàn thành thông tin về đoạn [1]:
xác định, phát hiện, khám xét, bắt giữ
Vụ kiện giữa Công ty T.V – F.N và một cơ sở gia công in ấn cho thấy việc _______ và xử lý xâm phạm bản quyền là một quá trình dài và phức tạp, đặc biệt là khi cơ quan chức năng chưa _______ được chủ sở hữu và thiệt hại thương mại.
 Xem đáp án
Xem đáp án
Đáp án
Vụ kiện giữa Công ty T.V – F.N và một cơ sở gia công in ấn cho thấy việc phát hiện và xử lý xâm phạm bản quyền là một quá trình dài và phức tạp, đặc biệt là khi cơ quan chức năng chưa xác định được chủ sở hữu và thiệt hại thương mại.
Giải thích
|
Lí do lựa chọn phương án |
phát hiện |
“Quá trình phát hiện ra đối tượng xâm phạm bản quyền cho đến khi áp dụng thành công biện pháp trừng phạt luôn là một quãng đường dài.” |
|
xác định |
“Một khi cơ quan điều tra chưa xác định được ai là chủ thì chưa thể luận tội được.” |
|
|
khám xét |
Phương án nhiễu với Từ khóa “phát hiện”, có ý nghĩa khác. |
|
|
bắt giữ |
Phương án nhiễu với Từ khóa “xác định”, có ý nghĩa khác. |
Câu 4:
Điền một cụm từ không quá ba tiếng trong đoạn [2] vào chỗ trống:
Quá trình phát hiện và xử lý các vụ việc xâm phạm bản quyền hiện nay gặp nhiều khó khăn do (1) _____________ của môi trường số.
 Xem đáp án
Xem đáp án
Đáp án
Điền một cụm từ không quá ba tiếng trong đoạn [2] vào chỗ trống:
Quá trình phát hiện và xử lý các vụ việc xâm phạm bản quyền hiện nay gặp nhiều khó khăn do (1) tính linh hoạt của môi trường số.
Giải thích
|
Lí do lựa chọn phương án |
tính linh hoạt |
“Tính linh hoạt của internet khiến việc thu thập chứng cứ trở thành một bài toán khó”. Có thể hiểu khái niệm “môi trường số” trong câu hỏi là tương đương với khái niệm “Internet”. |
Câu 5:
Theo đoạn [2], nhận định nào sau đây là KHÔNG chính xác về việc thu thập chứng cứ xâm phạm bản quyền?
 Xem đáp án
Xem đáp án
Giải thích
|
Lí do lựa chọn phương án |
A |
“Tính linh hoạt của internet khiến việc thu thập chứng cứ trở thành một bài toán khó. Quá trình lập vi bằng rất tốn kém thời gian và nguồn lực”. |
|
B |
“Trên môi trường số, con đường trở nên gập ghềnh hơn rất nhiều, ngay từ những bước đầu tiên như lập vi bằng.”; “…đặc biệt là trên môi trường số, các bên vi phạm có thể nhanh chóng xóa dấu vết và lẩn trốn”. |
|
|
C |
“tính linh hoạt của internet khiến việc thu thập chứng cứ trở thành một bài toán khó”; “các bên vi phạm có thể “nhanh chóng xóa dấu vết và lẩn trốn” à nhận định C không chính xác. |
|
|
D |
“Các tài liệu này sẽ dùng để lập vi bằng, làm căn cứ để giải quyết tranh chấp, yêu cầu chấm dứt hành vi vi phạm hoặc bồi thường thiệt hại”. |
Chọn C
Câu 6:
Theo đoạn [3]. Văn phòng Luật Phan Law đã tiến hành hoạt động nào sau đây để khởi tố trang web PM.net? Chọn hai đáp án đúng:
 Xem đáp án
Xem đáp án
Giải thích
|
Lí do lựa chọn phương án |
A |
Họ đã hoàn thiện và gửi tài liệu chứng cứ vi phạm, đề nghị cơ quan điều tra vào cuộc. |
|
B |
Công việc thu thập bằng chứng được tiến hành trong 5 năm kể từ năm 2014, nhưng không đề cập đến việc thu thập từ dữ liệu người dùng trang web. |
|
|
C |
Họ đã thu thập chứng cứ từ năm 2014 dưới sự ủy quyền từ các bên sở hữu quyền phân phối phim. |
|
|
D |
Các tổ chức đã vào cuộc trong quá trình phát hiện và xử lý vi phạm của trang web, nhưng không có thông tin là do họ đề nghị. |
Chọn A, B
Câu 7:
Theo thiếu tá Lê Hồng Giang, nhận định nào sau đây về hoạt động né tránh phát hiện và xử lý xâm phạm bản quyền là chính xác? Chọn hai đáp án đúng.
 Xem đáp án
Xem đáp án
Giải thích
|
Lí do lựa chọn phương án |
A |
Đoạn [4] nhắc tới việc các đối tượng đăng tải nội dung xâm bản quyền trên các website, ứng dụng quốc tế, nhưng không đề cập tới khả năng giám sát, kiểm duyệt các nền tảng này. |
|
B |
Nhiều đối tượng tái phạm trên các website, ứng dụng di động tại thị trường quốc tế nhưng chủ động chặn IP truy cập từ người dùng Việt Nam. |
|
|
C |
Các đối tượng xâm phạm còn ứng dụng nhiều kỹ thuật để tránh sự theo dõi của các cơ quan chức năng. |
|
|
D |
Đoạn [4] nhắc tới việc các đối tượng chủ động chặn người dùng Việt Nam truy cập các nền tảng chứa nội dung xâm phạm bản quyền, nhưng không đề cập đến việc Việt Nam làm điều tương tự tới các nền tảng trong nước. |
Chọn B, C
Câu 8:
Điền một cụm từ không quá hai tiếng trong đoạn [4] vào chỗ trống:
Mặc dù cơ quan chức năng ở Việt Nam đã có biện pháp xử lý các hành vi xâm phạm quyền tác giả, nhiều đối tượng vẫn (1) ____________ trên các nền tảng số ở nước ngoài.
 Xem đáp án
Xem đáp án
Đáp án
Điền một cụm từ không quá hai tiếng trong đoạn [4] vào chỗ trống
Mặc dù cơ quan chức năng ở Việt Nam đã có biện pháp xử lý các hành vi xâm phạm quyền tác giả, nhiều đối tượng vẫn (1) tái phạm trên các nền tảng số ở nước ngoài.
Giải thích
|
Lí do lựa chọn phương án |
tái phạm |
“…nhiều đối tượng tại Việt Nam đã từng bị cơ quan chức năng xử lý vi phạm hành chính …vẫn có xu hướng tái phạm trên các website, ứng dụng di động tại thị trường quốc tế...” |
Câu 9:
Theo đoạn [5] và [6], quá trình ngăn chặn vi phạm bản quyền đang được áp dụng có những đặc điểm nào? Các nhận định sau ĐÚNG hay SAI?
|
Nhận định |
Đúng |
Sai |
|
Truy dấu hành vi xâm phạm là yếu tố quan trọng để hạn chế xâm phạm trên môi trường số. |
||
|
Cá nhân hóa nội dung đưa lên internet là phương tiện duy nhất để truy dấu hành vi xâm pham. |
||
|
Các công nghệ bảo vệ bản quyền đang gặp khó khăn trong việc chống lại các mánh lới xâm phạm. |
||
|
Chỉ có công nghệ finger printing được sử dụng để ngăn chặn đăng tải trái phép các trận bóng đá. |
 Xem đáp án
Xem đáp án
Đáp án
|
Nhận định |
Đúng |
Sai |
|
Truy dấu hành vi xâm phạm là yếu tố quan trọng để hạn chế xâm phạm trên môi trường số. |
X | |
|
Cá nhân hóa nội dung đưa lên internet là phương tiện duy nhất để truy dấu hành vi xâm pham. |
X | |
|
Các công nghệ bảo vệ bản quyền đang gặp khó khăn trong việc chống lại các mánh lới xâm phạm. |
X | |
|
Chỉ có công nghệ finger printing được sử dụng để ngăn chặn đăng tải trái phép các trận bóng đá. |
X |
Giải thích
|
Lí do lựa chọn phương án |
Nhân định 1 |
Đoạn [5]: “Một trong những yếu tố quan trọng nhất để hạn chế được xâm phạm trên môi trường số là truy dấu (tracking) được hành vi xâm phạm” |
|
Nhân định 2 |
Đoạn [5] + [6]: “Một trong những yếu tố quan trọng nhất để hạn chế được xâm phạm trên môi trường số là truy dấu … để làm được phải cá nhân hóa...” à không phải là phương tiện duy nhất. |
|
|
Nhân định 3 |
Đoạn [6]: “những công nghệ bảo vệ bản quyền như trên đang bị bỏ lại đằng sau trong cuộc đua với mánh lới xâm phạm”. |
|
|
Nhân định 4 |
Đoạn [6]: ngoài công nghệ finger printing, còn công nghệ so sánh màn hình. |
Câu 10:
Điền một cụm từ không quá hai tiếng trong đoạn [7] vào chỗ trống:
Việc bảo vệ bản quyền trong sự phát triển của môi trường kỹ thuật số là (1) __________ cho các nhà phát triển công nghệ tiếp tục nghiên cứu.
 Xem đáp án
Xem đáp án
Đáp án
Điền một cụm từ không quá hai tiếng trong đoạn [7] vào chỗ trống:
Việc bảo vệ bản quyền trong sự phát triển của môi trường kỹ thuật số là (1) thách thức cho các nhà phát triển công nghệ tiếp tục nghiên cứu.
Giải thích
|
Lí do lựa chọn phương án |
thách thức |
“Môi trường kỹ thuật số ngày càng phát triển, mở ra nhiều thách thức trong vấn đề bảo vệ bản quyền, đòi hỏi các nhà phát triển công nghệ phải liên tục nghiên cứu...”. |
Câu 11:
 Xem đáp án
Xem đáp án
Giải thích
Ý chính các đoạn trong bài.
Đoạn 1. Tính cấp thiết của việc tái chế rác thải xây dựng.
Đoạn 2. Một số phương pháp được đề xuất để tái chế chất thải xây dựng.
Đoạn 3-5. Giới thiệu và những ưu điểm chính của phương pháp tái chế chất thải xây dựng thành hạt cốt liệu nung rỗng.
Đoạn 6-9. Quá trình thực hiện nghiên cứu chế tạo bê tông cách nhiệt chịu lực từ chất thải xây dựng.
Đoạn 10-11. Những khó khăn trong quá trình thực hiện nghiên cứu và đề xuất phương án giải quyết.
Tổng hợp các ý trên, ta có ý chính của toàn câu là: “Chế tạo bê tông nhẹ có khả năng cách nhiệt và chịu lực từ chất thải xây dựng.”
Chọn A
Câu 12:
Từ thông tin trong đoạn [1] và [2], hãy điền một cụm từ không quá ba tiếng để hoàn thành đoạn sau.
Các thành phố lớn tại Việt Nam đang phải đối mặt với nguy cơ ô nhiễm môi trường do chất thải xây dựng. Một số chuyên gia đã đề xuất sử dụng (1) _______ mới, thay thế việc chôn lấp tại các khu xử lý. Trong đó, công nghệ nghiền tái chế được cho rằng sẽ tận dụng 70-100% phế thải xây dựng ngay tại công trình.
 Xem đáp án
Xem đáp án
Đáp án
Từ thông tin trong đoạn [1] và [2], hãy điền một cụm từ không quá ba tiếng để hoàn thành đoạn sau.
Các thành phố lớn tại Việt Nam đang phải đối mặt với nguy cơ ô nhiễm môi trường do chất thải xây dựng. Một số chuyên gia đã đề xuất sử dụng (1) biện pháp mới, thay thế việc chôn lấp tại các khu xử lý. Trong đó, công nghệ nghiền tái chế được cho rằng sẽ tận dụng 70-100% phế thải xây dựng ngay tại công trình.
Giải thích
Đọc đoạn [1], [2] trong văn bản, chú ý câu văn sử dụng từ “chôn lấp”. “Tuy nhiên, phần lớn các khu xử lý chất thải rắn hiện nay đều bị quá tải và chủ yếu sử dụng biện pháp chôn lấp.”. Nhận thấy đề bài đã thay thế “biện pháp chôn lấp” thành “việc chôn lấp”, kết hợp thông tin trong đoạn. “Đó là lý do khiến ngành xây dựng đang nghĩ đến cách tiếp cận mới. Tái chế chất thải xây dựng.” để suy luận. biện pháp chôn lấp không còn phù hợp, cần thay thế bằng một biện pháp mới. Từ cần điền trong đoạn là “biện pháp”.
HS cần lưu ý, trong bài đọc có sử dụng cụm từ “cách tiếp cận mới”, tuy nhiên, cụm từ này không phù hợp để kết hợp với từ “sử dụng” trong câu điền khuyết.
Câu 13:
Theo đoạn [2], phương án nào sau đây là thành phẩm trực tiếp của máy nghiền tái chế vật liệu xây dựng?
 Xem đáp án
Xem đáp án
Giải thích
Thông tin tại đoạn [2]. “máy nghiền lắp đặt ngay tại chân công trình, cho phép nghiền tại chỗ các khối bê tông, vật liệu rắn thành các hạt nhỏ 3x4cm và cát mịn mà không cần tập kết ra bãi phế liệu.”, như vậy, đáp án đúng là D. Các phương án còn lại là chế phẩm tạo ra từ vật liệu tái chế, không phải sản phẩm trực tiếp hình thành từ máy nghiền tái chế.
Chọn D
Câu 14:
 Xem đáp án
Xem đáp án
Giải thích
Từ “này” cho thấy cụm từ/đối tượng được nhắc tới trong đoạn này đã được làm rõ trước đó để người đọc biết đến. Tìm kiếm từ khóa và thông tin liên quan trong các đoạn [1], [2] → Trong đoạn [2] có đề cập thông tin như sau. “...chẳng hạn như máy nghiền lắp đặt ngay tại chân công trình, cho phép nghiền tại chỗ các khối bê tông, vật liệu rắn thành các hạn nhỏ 3x4cm và cát mịn…”, từ đó chọn đáp án đúng là A.
Câu 15:
 Xem đáp án
Xem đáp án
Giải thích
Dựa vào thông tin trong đoạn [4]. “so với gạch xây thông thường, ta có thể giảm chi phí đáng kể trong các công trình xây dựng do giảm được tải trọng tác dụng, qua đó giảm kích thước các kết cấu chịu lực và móng công trình”, chọn đáp án đúng là C.
Câu 16:
Theo đoạn [6], việc sử dụng công nghệ nung và đầu vào là phế thải xây dựng lần đầu tiên được nghiên cứu bởi một tập hợp các chuyên gia của Việt Nam. Đúng hay Sai?
 Xem đáp án
Xem đáp án
Đáp án
B. Sai
Giải thích
Thông tin tại đoạn [6] như sau. “...ở Việt Nam đây là một trong những nghiên cứu đầu tiên sử dụng công nghệ nung và sử dụng đầu vào là phế thải xây dựng. Để làm được điều đó, nhóm nghiên cứu đã tập hợp các chuyên gia từ nhiều lĩnh vực, ...”. Theo đó, nghiên cứu này chỉ là “một trong những nghiên cứu tiên” nên mệnh đề trên “Sai”.
Câu 17:
Từ thông tin trong đoạn [8], hãy điền một cụm từ không quá bốn tiếng để hoàn thành đoạn sau.
Theo đoạn trích, các loại hạt cốt liệu được phân loại dựa trên (1) ________, sau đó, có thể được ứng dụng trong nhiều ngành khác nhau.
 Xem đáp án
Xem đáp án
Đáp án
Từ thông tin trong đoạn [8], hãy điền một cụm từ không quá bốn tiếng để hoàn thành đoạn sau.
Theo đoạn trích, các loại hạt cốt liệu được phân loại dựa trên (1) khả năng chịu lực, sau đó, có thể được ứng dụng trong nhiều ngành khác nhau.
Giải thích
Căn cứ vào thông tin trong đoạn. “Do các hạt cốt liệu nhẹ chế tạo từ phế thải xây dựng nên chúng tôi không kì vọng chúng có khả năng chịu lực quá cao.”, “Bù lại, các hạt cốt liệu nhẹ có thể có nhiều ứng dụng khác nhau ...”. Như vậy, sự phân loại các hạt thành có chất lượng thấp, chất lượng tốt hơn, có cường độ tốt nhất để ứng dụng được là căn cứ vào khả năng chịu lực. Từ cần điền để hoàn thành câu là “khả năng chịu lực”.
Câu 18:
 Xem đáp án
Xem đáp án
Giải thích
Đọc đoạn [10], xác định các vấn đề được đưa ra trong đoạn. “việc nung trên cơ sở lò quay vẫn là khâu thách thức nhất”, “công nghệ chế tạo lò vẫn chưa thể nội địa hóa…chi phí vẫn còn cao”, “nhiệt lượng sử dụng khá lớn và có thể khiến tổng chi phí tăng lên”, “Một số ý kiến phản hồi …chưa đủ “xanh” cho môi trường”. Như vậy, chọn đáp án đúng là B.
Câu 19:
Theo đoạn [11], phương án nào sau đây KHÔNG phải hướng hoàn thiện quy trình sản xuất hạt cốt liệu nhẹ?
 Xem đáp án
Xem đáp án
Giải thích
Đọc đoạn [11]. “...chẳng hạn tận dụng khí gas từ chất thải hữu cơ làm năng lượng đốt lò – để giảm thiểu tác động, hoặc tạo ra một quá trình sản xuất liên tục để giảm hao phí năng lượng và chi phí vận hành. Trong tương lai, họ cũng xem xét nghiên cứu thêm cách hạ thấp nhiệt độ nung để nâng cao hiệu quả kinh tế - kỹ thuật của sản phẩm hạt nhẹ này.”, nhận thấy phương án “Tạo ra sản phẩm hạt nhẹ có giá trị kinh tế cao” không được nhắc tới trong bài nên đáp án đúng là D.
Câu 20:
Để các hạt vật liệu nhẹ đảm bảo hiệu quả về kinh tế - kỹ thuật, các chuyên gia dự định nghiên cứu việc giảm nhiệt lượng cần thiết trong quy trình nung và nội địa hóa công nghệ chế tạo lò. Đúng hay Sai?
 Xem đáp án
Xem đáp án
Đáp án
B. Sai
Giải thích
Đọc đoạn [10], [11]. Trong đoạn [10], các thông tin liên quan đến chi phí (hiệu quả kinh tế) bao gồm. “Hiện công nghệ chế tạo lò vẫn chưa thể nội địa hóa mà phải nhập khẩu, do vậy chi phí vẫn còn cao. Hơn thế nữa, quy trình đòi hỏi nhiệt độ nung phải trên 12000C – tức nhiệt lượng sử dụng khá lớn và có thể khiến tổng chi phí tăng lên.”. Tuy nhiên, trong đoạn [11], thông tin được đưa ra là. “họ cũng xem xét nghiên cứu thêm cách hạ thấp nhiệt độ nung để nâng cao hiệu quả kinh tế - kỹ thuật của sản phẩm hạt nhẹ”. Như vậy, việc nội địa hóa công nghệ chế tạo lò chưa nằm trong dự định. Mệnh đề trên là “Sai”
Câu 21:
Phần tư duy khoa học / giải quyết vấn đề
 Xem đáp án
Xem đáp án
Giải thích
Đơn vị của năng lượng liên kết là J hoặc MeV, trong đó: 1MeV=1,6.10-13J.
Chọn A, B
Câu 22:
Năng lượng liên kết riêng của hạt nhân có thể được tính theo công thức nào sau đây?
 Xem đáp án
Xem đáp án
Giải thích
Năng lượng liên kết riêng của hạt nhân, kí hiệu là ε, có giá trị bằng tỷ số giữa năng lượng liên kết và tổng số nuclôn của hạt nhân \(\varepsilon = \frac{{\Delta {\rm{W}}}}{A} = \frac{{\Delta m{c^2}}}{A}\).
Chọn A
Câu 23:
Phát biểu nào sau đây là đúng hoặc sai?
|
Phát biểu |
Đúng |
Sai |
|
Năng lượng liên kết riêng là năng lượng liên kết tính cho một nuclôn |
||
|
Hạt nhân có độ hụt khối càng lớn thì năng lượng liên kết càng lớn. |
||
|
Hạt nhân càng bền vững khi có năng lượng liên kết càng lớn. |
||
|
Năng lượng liên kết đặc trưng cho mức độ bền vững của hạt nhân |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Năng lượng liên kết riêng là năng lượng liên kết tính cho một nuclôn |
X | |
|
Hạt nhân có độ hụt khối càng lớn thì năng lượng liên kết càng lớn. |
X | |
|
Hạt nhân càng bền vững khi có năng lượng liên kết càng lớn. |
X | |
|
Năng lượng liên kết đặc trưng cho mức độ bền vững của hạt nhân |
X |
Giải thích
1. Đúng. Năng lượng liên kết riêng là năng lượng liên kết trung bình cho một nuclôn.
2. Đúng. \[\Delta {\rm{W}} = \Delta m.{c^2}\] nên \[\Delta m\] càng lớn thì ΔW càng lớn.
3. Sai. Để so sánh độ bền vững giữa các hạt nhân, cần so sánh năng lượng liên kết riêng của hạt nhân.
4. Sai. Năng lượng liên kết riêng đặc trưng cho mức độ bền vững của hạt nhân.
Câu 24:
Năng lượng liên kết riêng của hạt nhân là (1) __________ MeV/nuclôn.
 Xem đáp án
Xem đáp án
Đáp án: “8,75”
Giải thích
Từ đồ thị ta thấy:
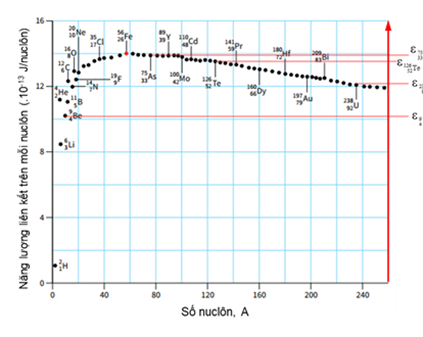
\({\varepsilon _{_{26}^{56}{\rm{Fe}}}} = {14.10^{ - 13}}\;{\rm{J/nuclon }} = \frac{{{{14.10}^{ - 13}}}}{{1,{{6.10}^{ - 13}}}} = 8,75\,\,{\rm{MeV/nuclon }}.\)
Câu 25:
Cho các hạt nhân sau: \(_4^9{\rm{Be}};\,\,_{33}^{75}{\rm{As}};\,\,_{52}^{126}{\rm{Te}};\,\,_{92}^{238}U\). Sắp xếp các hạt nhân theo thứ tự tăng dần độ bền vững của hạt nhân là
 Xem đáp án
Xem đáp án
Giải thích
Nhìn vào biểu đồ có thể thấy: \({\varepsilon _{_4^9{\rm{Be}}}} < {\varepsilon _{_{92}^{238}U}} < {\varepsilon _{_{52}^{126}Te}} < {\varepsilon _{_{33}^{75}{\rm{As}}}}\).
Câu 26:
Biết khối lượng nghỉ của protôn, nơtron, và electrôn lần lượt là 1,00728u; 1,00866u và 5,486.10-4u. Khối lượng của nguyên tử \(_7^{14}N\) có giá trị là
 Xem đáp án
Xem đáp án
Giải thích
Từ đồ thị có thể thấy \({\varepsilon _{_7^{14}N}} = {12.10^{ - 13}}\)J/nuclôn.
Mà: \(\Delta {{\rm{W}}_{_7^{14}N}} = A.{\varepsilon _{_7^{14}N}} = {14.12.10^{ - 13}} = 1,{68.10^{ - 11}}\;{\rm{J}} = 105\,\,{\rm{MeV}}\).
Mặt khác: \(\Delta {W_{_7^{14}N}} = 931,5.\Delta {m_{_7^{14}N}} \Rightarrow \Delta {m_{_7^{14}N}} = \frac{{105}}{{931,5}}u = \frac{{70}}{{621}}u\)
\(\Delta {m_{N_7^{14}}} = 7\left( {{m_n} + {m_p}} \right) - {M_{N_7^{14}}}\)
\( \Rightarrow {M_{N_7^{14}}} = 7\left( {{m_n} + {m_p}} \right) - \Delta {m_{N_7^{14}}} = 7(1,00728u + 1,00866u) - \frac{{70}}{{621}}u = 13,99886u\).
Khối lượng nguyên tử \(_7^{14}N\) là: \(m = {M_{_7^{14}N}} + 7{m_e} = 13,99886u + 7.5,{486.10^{ - 4}}u = 14,0027u\).
Chọn A
Câu 27:
20, 200, 50 < A < 80, bền vững, kém bền vững
Ngoại trừ các hạt sơ cấp riêng rẽ (như protôn, nơtrôn, êlectron), hạt nhân có năng lượng liên kết riêng càng lớn thì càng ___. Thực nghiệm cho thấy những hạt nhân có số khối lớn hơn ___ hoặc số khối nhỏ hơn ___ thì kém bền vững, còn những hạt nhân có số khối ___ thì rất bền.
 Xem đáp án
Xem đáp án
Đáp án
Ngoại trừ các hạt sơ cấp riêng rẽ (như protôn, nơtrôn, êlectron), hạt nhân có năng lượng liên kết riêng càng lớn thì càng bền vững. Thực nghiệm cho thấy những hạt nhân có số khối lớn hơn 200 hoặc số khối nhỏ hơn 20 thì kém bền vững, còn những hạt nhân có số khối 50 < A < 80 thì rất bền.
Giải thích
Từ bài đọc có thể rút ra nhận xét: Hạt nhân có năng lượng liên kết riêng càng lớn thì càng bền vững.
Từ đồ thị ta thấy:
- Khi A tăng dần từ 0 đến 20, năng lượng liên kết riêng tăng dần từ khoảng 10-13 J/nuclôn đến
13.10-13 J/nuclôn.
- Khi A tăng dần từ 200 trở đi, năng lượng liên kết riêng giảm dần từ khoảng 12,5.10-13 J/nuclôn.
⇒ Hai vùng A < 20 và A > 200 có năng lượng liên kết riêng thấp nhất nên kém bền vững nhất.
- Khi A nằm trong khoảng từ 50 đến 80, năng lượng liên kết riêng của hạt nhân có giá trị lớn nhất, vào khoảng 14.10-13 J/nuclôn. Vì vậy những hạt nhân có số khối nằm trong khoảng này là bền vững
Câu 28:
 Xem đáp án
Xem đáp án
Giải thích
Theo đoạn thông tin: “Pepsin chỉ hoạt động trong môi trường có tính acid” tức là môi trường có độ pH thấp.
Chọn B
Câu 29:
 Xem đáp án
Xem đáp án
Giải thích
Enzyme pepsin là enzyme được sản xuất trong dạ dày và là một trong những enzyme tiêu hóa chính trong hệ thống tiêu hóa của con người và nhiều loài động vật khác.
Chọn C
Câu 30:
Giải thích tại sao các ống nghiệm 3 và 4, hoạt tính của enzyme pepsin cao, trong khi ống nghiệm 5 enzyme không có hoạt tính?
 Xem đáp án
Xem đáp án
Giải thích
Ở các ống nghiệm 3, 4 và 5 đều có chung điều kiện về độ pH và nhiệt độ, khác nhau ở thành phần dung dịch tham gia:
Ống nghiệm 3: có cả casein và anserine.
Ống nghiệm 4: có casein.
Ống nghiệm 5: có anserine.
Nếu hoạt tính của enzyme pepsin phụ thuộc vào cả casein và anserine thì ống nghiệm 4 enzyme pepsin phải không hoạt động (không đúng với kết quả thí nghiệm).
Nếu hoạt tính của pepsin bị anserine ức chế hoặc anserine có khả năng phân giải pepsin thì ở ống nghiệm 3 enzyme pepsin phải không hoạt động (không đúng với kết quả thí nghiệm).
→ Enzyme pepsin có khả năng phân giải casein nhưng không có khả năng phân giải anserine.
Chọn C
Câu 31:
Enzyme pepsin giúp phân giải các protein có trong thức ăn thành các đơn vị nhỏ hơn gọi là (1) ________.
 Xem đáp án
Xem đáp án
Đáp án
Enzyme pepsin giúp phân giải các protein có trong thức ăn thành các đơn vị nhỏ hơn gọi là (1) peptide.
Giải thích
Theo thông tin bài đọc: “...Pepsin là một loại enzyme ở người có vai trò xúc tác quá trình tiêu hóa protein thành các đơn vị nhỏ hơn gọi là peptide”
Câu 32:
Pepsin có hoạt tính phân giải protein lớn nhất khi độ pH lớn hơn 4.0 và nhiệt độ khoảng 40°C.
 Xem đáp án
Xem đáp án
Đáp án
B. Sai
Giải thích
Sai. Pepsin có hoạt tính phân giải protein lớn nhất khi độ pH nhỏ hơn 4.0 và nhiệt độ khoảng 40°C.
Câu 33:
Dạng enzyme chưa hoạt động (tiền enzyme) của pepsin là (1) _________.
 Xem đáp án
Xem đáp án
Đáp án
Dạng enzyme chưa hoạt động (tiền enzyme) của pepsin là (1) pepsinogen.
Giải thích
|
peptide |
pespsinogen |
trypsin |
Pepsin được sản xuất bởi các tuyến dạ dày của dạ dày ở dạng không hoạt động được gọi là pepsinogen và có thể chuyển thành dạng hoạt động dưới tác dụng của HCl trong dạ dày.
Câu 34:
Phát biểu sau đúng hay sai?
Axit lactic vừa có tính chất của axit, vừa có tính chất của ancol.
 Xem đáp án
Xem đáp án
Đáp án
A. Đúng
Giải thích
Vì công thức cấu tạo của axit lactic có chứa nhóm chức axit (–COOH) và nhóm chức ancol (–OH) nên nó vừa có tính chất của axit, vừa có tính chất của ancol.
Câu 35:
Các phát biểu sau đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Axit lactic vừa có tính chất hoá học của một axit vừa có tính chất hoá học của một base. |
||
|
Axit lactic tác dụng với NaOH theo tỷ lệ mol 1:1. |
||
|
Axit lactic tác dụng với Na theo tỷ lệ mol 1:1. |
||
|
Có thể tổng hợp trực tiếp axit lactic từ glucozơ bằng phương pháp lên men rượu. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Axit lactic vừa có tính chất hoá học của một axit vừa có tính chất hoá học của một base. |
X | |
|
Axit lactic tác dụng với NaOH theo tỷ lệ mol 1:1. |
X | |
|
Axit lactic tác dụng với Na theo tỷ lệ mol 1:1. |
X | |
|
Có thể tổng hợp trực tiếp axit lactic từ glucozơ bằng phương pháp lên men rượu. |
X |
Giải thích
1. Axit lactic vừa có tính chất hoá học của một axit vừa có tính chất hoá học của một base.
Sai, vì axit lactic có chứa nhóm chức –OH ancol và nhóm axit carboxilic –COOH nên nó vừa có tính chất hoá học của một axit vừa có tính chất hoá học của một ancol.
2. Axit lactic tác dụng với NaOH theo tỷ lệ mol 1:1.
Đúng, vì: axit lactic có chứa 1 nhóm chức –COOH có khả năng phản ứng với NaOH nên axit lactic tác dụng với NaOH theo tỷ lệ mol 1:1. Phương trình phản ứng như sau:
CH3CH(OH)COOH + NaOH → CH3CH(OH)COONa + H2O
3. Axit lactic tác dụng với Na theo tỷ lệ mol 1:1.
Sai, vì: axit lactic có chứa 1 nhóm chức –OH ancol và 1 nhóm axit carboxilic –COOH có khả năng phản ứng với Na nên axit lactic tác dụng với Na theo tỷ lệ mol 1:2. Phương trình phản ứng như sau:
CH3CH(OH)COOH + 2Na → CH3CH(ONa)COONa + H2
4. Có thể tổng hợp trực tiếp axit lactic từ glucozơ bằng phương pháp lên men rượu.
Sai, vì: axit lactic được tổng hợp trực tiếp từ glucozơ bằng phương pháp lên men lactic:
Câu 36:
Hãy hoàn thành đoạn sau bằng cách kéo thả các từ vào đúng vị trí.
etyl lactat, ion lactat, nhiều oxi, ít oxi, yếm khí, hiếu khí
Axit lactic là sản phẩm trung gian của quá trình đường phân _______ (phân giải đường, sinh ra năng lượng trong điều kiện _______). Ngay sau khi sinh ra, nó biến đổi thành _______.
 Xem đáp án
Xem đáp án
Đáp án
Axit lactic là sản phẩm trung gian của quá trình đường phân yếm khí (phân giải đường, sinh ra năng lượng trong điều kiện ít oxi). Ngay sau khi sinh ra, nó biến đổi thành ion lactat.
Giải thích
Axit lactic là sản phẩm trung gian của quá trình đường phân yếm khí (phân giải đường, sinh ra năng lượng trong điều kiện ít oxi). Ngay sau khi sinh ra, nó biến đổi thành ion lactat.
Câu 37:
 Xem đáp án
Xem đáp án
Giải thích
Axit lactic có tính chất của axit, đó là: làm quỳ tím hóa đỏ; tác dụng với kim loại, oxide kim loại; tác dụng với muối; … và không tác dụng với phi kim.
Chọn C
Câu 38:
 Xem đáp án
Xem đáp án
Giải thích
Dựa vào thông tin ở bài đọc: “Máu gồm hai thành phần chính là các tế bào máu và huyết tương.”.
Chọn A
Câu 39:
 Xem đáp án
Xem đáp án
Giải thích
Quan sát hình 1, ta thấy người có nhóm máu AB không có kháng thể nào trong huyết thanh, chính vì vậy mà người có nhóm máu AB có khả năng nhận máu từ tất cả mọi người.
Chọn B
Câu 40:
Các phát biểu sau đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Tế bào máu gồm có hồng cầu, bạch cầu, tiểu cầu và kháng thể. |
||
|
Nên thực hiện truyền máu giữa những người cùng nhóm máu, trong trường hợp khác nhóm máu nhưng vẫn đủ điều kiện truyền máu thì nên truyền với số lượng ít (<250ml). |
||
|
Người có nhóm máu O nhận được tất cả các nhóm máu khác, người có nhóm máu AB cho được tất cả các nhóm máu khác. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Tế bào máu gồm có hồng cầu, bạch cầu, tiểu cầu và kháng thể. |
X | |
|
Nên thực hiện truyền máu giữa những người cùng nhóm máu, trong trường hợp khác nhóm máu nhưng vẫn đủ điều kiện truyền máu thì nên truyền với số lượng ít (<250ml). |
X | |
|
Người có nhóm máu O nhận được tất cả các nhóm máu khác, người có nhóm máu AB cho được tất cả các nhóm máu khác. |
X |
Giải thích
(1) Sai. Tế bào máu gồm hồng cầu, bạch cầu và tiểu cầu. Huyết tương mới có kháng thể.
(2) Đúng. Ví dụ người nhóm máu A truyền cho nhóm máu AB thì huyết thanh của người nhóm máu A có chứa kháng thể B, trong khi hồng cầu người nhóm máu AB có chứa kháng nguyên B, vẫn xảy ra sự ngưng kết, truyền ở mức < 250ml sẽ đảm bảo được an toàn, lưu ý truyền máu với tốc độ chậm.
(3) Sai. Người có nhóm máu O cho được tất cả các nhóm máu khác, người có nhóm máu AB nhận được tất cả các nhóm máu khác.
Câu 41:
Kéo thả các từ vào đúng vị trí.
nhóm máu B, nhóm máu AB, nhóm máu A
Người có _______ thì truyền được cho người có nhóm máu A.
Người có _______ thì nhận được từ người có nhóm máu _______.
 Xem đáp án
Xem đáp án
Đáp án
Người có nhóm máu A thì truyền được cho người có nhóm máu A.
Người có nhóm máu AB thì nhận được từ người có nhóm máu nhóm máu B.
Giải thích
|
nhóm máu A |
nhóm máu B |
nhóm máu AB |
Ô trống thứ 1: nhóm máu A
Ô trống thứ 2: nhóm máu AB
Ô trống thứ 3: nhóm máu B
Người có nhóm máu A thì truyền được cho người có nhóm máu A.
Người có nhóm máu AB thì nhận được từ người có nhóm máu B.
Câu 42:
(1) ________ là huyết tương được loại bỏ các chất chống đông máu và để lại các chất điện giải.
 Xem đáp án
Xem đáp án
Đáp án
(1) Huyết thanh là huyết tương được loại bỏ các chất chống đông máu và để lại các chất điện giải.
Câu 43:
Theo quan điểm của học sinh 1, vận động viên tác dụng toàn bộ trọng lực cơ thể của mình lên diện tích bề mặt nhỏ xíu của hai lưỡi dao gây ra
 Xem đáp án
Xem đáp án
Giải thích
Theo lập luận của Học sinh 1: Một vận động viên trượt băng tác dụng toàn bộ trọng lực cơ thể của mình lên diện tích bề mặt nhỏ xíu của hai lưỡi dao. Điều này dẫn đến một áp suất rất lớn, nhanh chóng làm tan chảy một lượng băng nhỏ ngay dưới các lưỡi dao giày trượt.
Chọn B
Câu 44:
Theo quan điểm của học sinh 2, nước đóng băng bắt đầu đóng băng từ bề mặt hồ do mật độ khối lượng băng (1) ______ mật độ khối lượng của nước ở trạng thái lỏng.
 Xem đáp án
Xem đáp án
Đáp án
Theo quan điểm của học sinh 2, nước đóng băng bắt đầu đóng băng từ bề mặt hồ do mật độ khối lượng băng (1) nhỏ hơn mật độ khối lượng của nước ở trạng thái lỏng.
Giải thích
Theo Học sinh 2, nước bắt đầu đóng băng từ trên bề mặt hồ vì mật độ khối lượng băng nhỏ hơn mật độ khối lượng nước ở trạng thái lỏng.
Câu 45:
 Xem đáp án
Xem đáp án
Giải thích
Dựa vào lập luận của Học sinh 2, ta thấy:
+ Mật độ khối lượng băng nhỏ hơn mật độ khối lượng nước ở trạng thái lỏng.
+ Lực ma sát càng lớn thì băng tan càng nhanh.
Chọn C
Câu 46:
Theo quan điểm của Học sinh 1, đại lượng nào sau đây đối với các phân tử nước bên dưới mặt hồ lớn hơn đối với các phân tử nước trên bề mặt?
 Xem đáp án
Xem đáp án
Giải thích
+ Đại lượng mật độ khối lượng và lực nổi là quan điểm của học sinh 2.
Theo Học sinh 1:
Dưới bề mặt, áp suất thủy tĩnh của nước làm cho điểm đóng băng của nước thấp hơn một chút so với trên bề mặt.
Chọn B
Câu 47:
Dựa trên lập luận của học sinh 2 có thể giải thích hiện tượng khinh khí cầu bay lên khỏi mặt đất là do không khí bên trong khinh khí cầu có mật độ khối lượng cao hơn không khí bên ngoài khinh khí cầu.
Nội dung trên là đúng hay sai?
 Xem đáp án
Xem đáp án
Đáp án
B. Sai
Giải thích
Theo quan điểm của Học sinh 2 thì Nước đóng băng đầu tiên trên bề mặt hồ vì mật độ khối lượng băng nhỏ hơn nước ở trạng thái lỏng. Không giống như hầu hết các chất lỏng, mật độ khối lượng của một khối lượng nước giảm khi đóng băng. Kết quả là đối với bất kỳ khối băng nào, lực nổi của nước tác dụng lên trên lớn hơn lực hấp dẫn tác dụng xuống dưới, và tất cả các hạt băng nổi lên bề mặt khi đóng băng.
→ Khinh khí cầu có thể bay lên khỏi mặt đất là do không khí bên trong khinh khí cầu có mật độ khối lượng thấp hơn không khí bên ngoài khinh khí cầu.
Câu 48:
Người ta thấy một cốc đựng ethanol đóng băng từ đáy lên trên mà không phải từ trên bề mặt trở xuống. Từ lập luận của học sinh 2 có thể giải thích hiện tượng trên là do khối lượng riêng của ethanol đóng băng
 Xem đáp án
Xem đáp án
Giải thích
Khối lượng riêng chính là mật độ khối lượng
Học sinh 2 giải thích nước bắt đầu đóng băng từ trên bề mặt hồ vì mật độ khối lượng băng nhỏ hơn mật độ khối lượng nước ở trạng thái lỏng tức là chất có khối lượng riêng nhỏ hơn sẽ nổi trên các chất có khối lượng riêng lớn hơn. Như vậy việc ethanol đóng băng từ dưới đáy lên có thể giải thích do ethanol ở trạng thái đóng băng có khối lượng riêng lớn hơn ethanol ở trạng thái lỏng.
Chọn C
Câu 49:
 Xem đáp án
Xem đáp án
Giải thích
Theo thông tin bài: “...Cấu trúc của một operon Lac gồm có vùng vận hành (operator), vùng khởi động (promoter), các gen cấu trúc Z, Y, A. Ngoài ra, còn có gen điều hòa có vai trò quan trọng trong điều hòa hoạt động gen, nhưng không nằm trong cấu trúc operon Lac.”
Chọn C
Câu 50:
 Xem đáp án
Xem đáp án
Giải thích
Nhìn vào hình 2, ta thấy được lactose đóng vai trò như là chất cảm ứng.
Chọn A
Câu 51:
 Xem đáp án
Xem đáp án
Giải thích
Theo bài đọc: “...Khi có mặt lactose trong môi trường, các phân tử lactose sẽ liên kết với protein ức chế, làm biến đổi cấu trúc không gian của protein ức chế, làm cho protein ức chế không bám được vào vùng vận hành.”
Chọn D
Câu 52:
Xét một Operon Lac, khi môi trường không có lactose nhưng enzyme chuyển hóa lactose vẫn được tạo ra. Nhận định nào sau đây là đúng?
|
Phát biểu |
Đúng |
Sai |
|
Do vùng khởi động (P) bị bất hoạt nên enzyme RNA polymerase có thể bám vào để khởi động quá trình phiên mã. |
||
|
Do gen điều hòa (R) bị đột biến nên không tạo được protein ức chế. |
||
|
Do vùng vận hành (O) bị đột biến nên không liên kết được với protein ức chế. |
||
|
Do gen cấu trúc (gen Z, Y, A) bị đột biến làm tăng khả năng biểu hiện gen. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Do vùng khởi động (P) bị bất hoạt nên enzyme RNA polymerase có thể bám vào để khởi động quá trình phiên mã. |
X | |
|
Do gen điều hòa (R) bị đột biến nên không tạo được protein ức chế. |
X | |
|
Do vùng vận hành (O) bị đột biến nên không liên kết được với protein ức chế. |
X | |
|
Do gen cấu trúc (gen Z, Y, A) bị đột biến làm tăng khả năng biểu hiện gen. |
X |
Giải thích
(2) và (3) đúng.
(1) sai vì vùng khởi động bị bất hoạt thì enzyme RNA polymerase không bám vào được.
(4) sai vì đột biến làm tăng khả năng biểu hiện gen không làm cho quá trình phiên mã được diễn ra ở trong môi trường không có lactose, protein ức chế vẫn liên kết vào vùng vận hành và ngăn cản phiên mã.
Câu 53:
Trong cơ chế điều hòa hoạt động của operon Lac, sự kiện nào sau đây diễn ra cả khi môi trường có lactose và cả khi môi trường không có lactose?
 Xem đáp án
Xem đáp án
Giải thích
Trong môi trường có hay không có lactose thì gen điều hòa vẫn tổng hợp protein ức chế.
Chọn B
Câu 54:
(1) ________ là quá trình tổng hợp RNA trên mạch khuôn DNA.
 Xem đáp án
Xem đáp án
Đáp án
(1) Phiên mã là quá trình tổng hợp RNA trên mạch khuôn DNA.
Giải thích
Phiên mã là quá trình tổng hợp RNA trên mạch khuôn DNA.
Câu 55:
Tóm tắt các bước tiến hành trong 2 thí nghiệm trên như sau:
(1) Đo CNF.
(2) Trộn dung dịch Ni2+ và dung dịch OH–.
(3) Thu hồi chất rắn bằng cách lọc.
Tiến trình thí nghiệm đúng là
 Xem đáp án
Xem đáp án
Giải thích
Đầu tiên, các dung dịch OH– và Ni2+ được trộn với nhau và khuấy đều. Sau đó thu hồi chất rắn bằng cách lọc (lọc thông thường hoặc lọc chân không) và cuối cùng là đo CNF.
Chọn C
Câu 56:
Phương pháp lọc chân không cho CNF cao hơn phương pháp lọc thông thường, đúng hay sai?
 Xem đáp án
Xem đáp án
Đáp án
A. Đúng
Giải thích
Đúng. Vì: Từ kết quả trong Bảng 1, CNF trong thí nghiệm 2 (phương pháp lọc chân không) cao hơn thí nghiệm 1 (phương pháp lọc thông thường)
Câu 57:
Có (1) ________ trong số 6 thử nghiệm mà nickel hydroxide monohydrate được thu hồi bằng phương pháp lọc thông thường sau thời gian phản ứng ít nhất 3 ngày.
 Xem đáp án
Xem đáp án
Đáp án
Có (1) __ 2 __ trong số 6 thử nghiệm mà nickel hydroxide monohydrate được thu hồi bằng phương pháp lọc thông thường sau thời gian phản ứng ít nhất 3 ngày.
Giải thích
Theo thông tin trong bài, các thử nghiệm 1, 2 và 3 sử dụng phương pháp lọc thông thường. Trong đó, thử nghiệm 1 có thời gian phản ứng là 10 phút; thử nghiệm 2 có thời gian phản ứng là 3 ngày và thử nghiệm 3 có thời gian phản ứng là 7 ngày.
Câu 58:
Dựa trên kết quả của thí nghiệm 1 và 2, sự kết hợp giữa thời gian phản ứng và phương pháp lọc nào làm cho nồng độ Ni2+ trong dịch lọc là cao nhất?
 Xem đáp án
Xem đáp án
Giải thích
Theo Bảng 1, nồng độ Ni2+ trong dịch lọc cao nhất ở thử nghiệm 6 – phương pháp lọc chân không, trong thời gian phản ứng là 7 ngày.
Chọn B
Câu 59:
Dựa trên kết quả của thí nghiệm 1 và 2, sự kết hợp giữa thời gian phản ứng và phương pháp lọc nào làm cho nồng độ Ni2+ trong dịch lọc là thấp nhất?
 Xem đáp án
Xem đáp án
Giải thích
Theo Bảng 1, nồng độ Ni2+ trong dịch lọc thấp nhất ở thử nghiệm 1 – phương pháp lọc thông thường, trong thời gian phản ứng là 10 phút.
Chọn A
Câu 60:
 Xem đáp án
Xem đáp án
Giải thích
Lực tác dụng lên hỗn hợp khi sử dụng phương pháp lọc chân không lớn hơn khi sử dụng phương pháp lọc thông thường.
Thử nghiệm 3 sử dụng phương pháp lọc thông thường → Loại A và B.
Câu 61:
Cho hàm số \(y = f(x)\) có đạo hàm \(f'(x) = {(x - 1)^2}\left( {{x^2} - 1} \right)\). Số cực trị của hàm số \(y = f(x)\) là
 Xem đáp án
Xem đáp án
Ta có: \(f'(x) = {(x - 1)^2}\left( {{x^2} - 1} \right) = 0 \Leftrightarrow {(x - 1)^3}(x + 1) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 1}\\{x = 1}\end{array}} \right.\).
Ta thấy \(x = \pm 1\) đều là các nghiệm bội lẻ nên hàm số có 2 cực trị.
Câu 62:
Cho Parabol như hình vẽ.
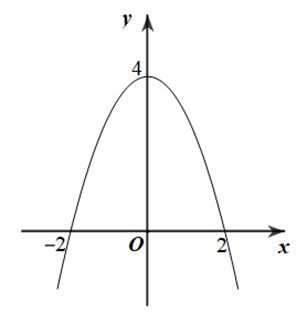
Diện tích hình phẳng giới hạn bởi Parabol và trục hoành bằng
 Xem đáp án
Xem đáp án
Dựa vào Parabol như hình vẽ, suy ra phương trình của Parabol là \((P):y = a{x^2} + 4;\) \((P)\) cắt trục hoành tại các điểm có hoành độ \( \pm 2\) nên \(a = - 1 \Rightarrow (P):y = - {x^2} + 4\).
Do đó, diện tích hình phẳng giới hạn bởi Parabol và trục hoành bằng
\(S = \int\limits_{ - 2}^2 {\left( { - {x^2} + 4} \right)} {\rm{d}}x = 2\int\limits_0^2 {\left( { - {x^2} + 4} \right)} {\rm{d}}x = \left. {2\left( { - \frac{{{x^3}}}{3} + 4x} \right)} \right|_0^2 = \frac{{32}}{3}\)
Câu 63:
Cho số phức \(z\) thỏa mãn điều kiện \(|z| = 2\). Biết tập hợp các điểm biểu diễn số phức \(w = (3 - 4i)z - 1 + i\) là một đường tròn. Tìm bán kính \(r\) của đường tròn đó.
 Xem đáp án
Xem đáp án
Ta có: \(w = (3 - 4i)z - 1 + i \Leftrightarrow w + 1 - i = (3 - 4i)z \Rightarrow |w + 1 - i| = |(3 - 4i)z|\)
\( \Rightarrow |w + 1 - i| = |3 - 4i|.|z| \Rightarrow |w + 1 - i| = 10\)
Gọi \(w = x + yi\,\,(x,y \in \mathbb{R})\).
Khi đó
\(|w + 1 - i| = 10 \Leftrightarrow |x + yi + 1 - i| = 10 \Leftrightarrow \sqrt {{{(x + 1)}^2} + {{(y - 1)}^2}} = 10 \Leftrightarrow {(x + 1)^2} + {(y - 1)^2} = 100.\)
Vậy tập hợp điểm biểu diễn số phức \(w\) là một đường tròn có tâm \(I( - 1;1)\), bán kính \(r = 10\).
Câu 64:
Một lớp học trong một trường đại học có 60 sinh viên, trong đó có 40 sinh viên học tiếng Anh, 30 sinh viên học tiếng Pháp và 20 sinh viên học cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên 2 sinh viên của lớp học này. Tính xác suất để 2 sinh viên được chọn không học ngoại ngữ. Biết rằng trường này chỉ dạy hai loại ngoại ngữ là tiếng Anh và tiếng Pháp.
 Xem đáp án
Xem đáp án
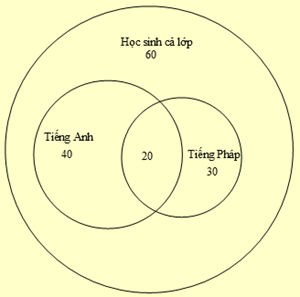
Ta có sơ đồ Ven như hình vẽ.
Số lượng sinh viên học ít nhất một môn ngoại ngữ là: 40 + 30 − 20 = 50 (học sinh).
Số lượng sinh viên không học ngoại ngữ là: 60 − 50 = 10 (học sinh).
Ta xét phép thử: Chọn 2 sinh viên bất kỳ trong số 60 sinh viên của lớp học.
⇒Số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{60}^2\).
Xét biến cố A: “Chọn ra 2 sinh viên không học ngoại ngữ”.
⇒Số phần tử của biến cố A là: \(n\left( A \right) = C_{10}^2\).
Vậy xác suất để chọn được 2 sinh viên không học ngoại ngữ là: \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{C_{10}^2}}{{C_{60}^2}} = \frac{3}{{118}}\).
Câu 65:
Anh Dũng có 36 tấm bưu thiếp từ các công viên quốc gia mà anh ấy đã đến thăm. Anh ấy muốn cất chúng vào một quyển album ảnh. Mỗi trang album chứa được tối đa 2 tấm bưu thiếp. Anh Dũng cần quyển album có tối thiểu (1) _________ tờ để cất hết toàn bộ số bưu thiếp. Biết mỗi tờ album có 2 trang.
 Xem đáp án
Xem đáp án
Đáp án “9”
Giải thích
Để cất hết toàn bộ số bưu thiếp anh Dũng cần quyển album có tối thiểu 36 : 2 : 2 = 9 (tờ).
Câu 66:
Cho tam giác ABC như hình vẽ.
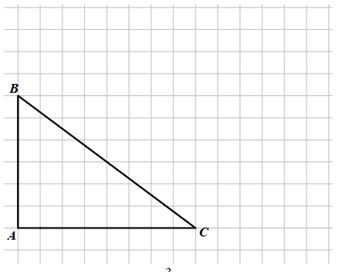
Phép vị tự tâm A tỉ số \(k = \frac{3}{2}\) biến tam giác ABC thành tam giác A′B′C′. Khi đó, diện tích tam giác A′B′C′ bằng ________ ô vuông.
 Xem đáp án
Xem đáp án
Coi mỗi cạnh của một ô vuông có độ dài bằng 1 thì AB = 6; AC = 8.
Ta có:
\({V_{\left( {A;\frac{3}{2}} \right)}}(A) = A\)
\({V_{\left( {A;\frac{3}{2}} \right)}}(B) = B' \Rightarrow AB' = \frac{3}{2}AB = 9;\)
\({V_{\left( {A;\frac{3}{2}} \right)}}(C) = C' \Rightarrow AC' = \frac{3}{2}AC = 12\)
\( \Rightarrow {S_{A'B'C'}} = {S_{AB'C'}} = \frac{1}{2}.AB'.AC' = 54\)
Câu 67:
Trong không gian Oxyz, cho điểm M(−2;−1;1). Khoảng cách từ điểm M tới trục Oy bằng
 Xem đáp án
Xem đáp án
Khoảng cách từ điểm M tới trục Oy bằng khoảng cách từ điểm M tới hình chiếu của điểm M trên trục Oy.
Ta có H(0;−1;0) ∈ Oy là hình chiếu của điểm M trên trục Oy.
\( \Rightarrow d(M;Oy) = MH = \sqrt {{{( - 2 - 0)}^2} + {{( - 1 + 1)}^2} + {{(1 - 0)}^2}} = \sqrt 5 \).
Câu 68:
Trong không gian Oxyz, cho các điểm \(A(1;0;0),B(0;1;0)\). Mặt phẳng đi qua các điểm A, B đồng thời cắt tia Oz tại \(C\) sao cho tứ diện OABC có thể tích bằng \(\frac{1}{6}\) có phương trình dạng \(x + ay + bz + c = 0\). Khi đó giá trị của biểu thức \(a + 3b - 2c\) bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Gọi điểm \(C(0;0;c)\) thuộc tia \(Oz,\,\,c > 0\).
Mặt phẳng \((P)\) đi qua các điểm A, B đồng thời cắt tia Oz tại \(C\) có dạng \(\frac{x}{1} + \frac{y}{1} + \frac{z}{c} = 1\).
Tứ diện OABC có thể tích bằng \(\frac{1}{6} \Rightarrow {V_{OABC}} = \frac{1}{6}OA.OB.OC = \frac{1}{6}\)
\( \Leftrightarrow \frac{1}{6}\).1.1.\(c = \frac{1}{6} \Leftrightarrow c = 1\).
Suy ra \((P)\) có phương trình \(\frac{x}{1} + \frac{y}{1} + \frac{z}{1} = 1 \Leftrightarrow x + y + z - 1 = 0 \Rightarrow a = 1,b = 1,c = - 1\).
Vậy \(a + 3b - 2c = 6\).
Câu 69:
Cho số thực \(a\) và hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{2x}&{{\rm{ khi }}x \le 1}\\{a\left( {x - 2{x^2}} \right)}&{{\rm{ khi }}x > 1}\end{array}} \right.\) liên tục trên \(\mathbb{R}\). Tính \(\int_0^2 f (x){\rm{dx}}\).
 Xem đáp án
Xem đáp án
Vì hàm số liên tục trên R nên \(\mathop {\lim }\limits_{x \to {1^ + }} f(x) = \mathop {\lim }\limits_{x \to {1^ - }} f(x) = f(1)\)
\( \Leftrightarrow \mathop {\lim }\limits_{x \to {1^ + }} \left[ {a\left( {x - 2{x^2}} \right)} \right] = \mathop {\lim }\limits_{x \to {1^ - }} (2x) \Leftrightarrow a = - 2.\)
Ta có \(\int\limits_0^2 {f(x){\rm{d}}x} = \int\limits_0^1 {f(x){\rm{d}}x} + \int\limits_1^2 {f(x){\rm{d}}x} = \int\limits_0^1 {2x\;{\rm{d}}x} + \int\limits_1^2 { - 2\left( {x - 2{x^2}} \right){\rm{d}}x} = \frac{{22}}{3}.\)
Câu 70:
\(\mathop {\lim }\limits_{x \to 0} \frac{{{e^x} - 1}}{x}\) bằng
 Xem đáp án
Xem đáp án
Ta có giới hạn đặc biệt: \(\mathop {\lim }\limits_{x \to 0} \frac{{{e^x} - 1}}{x} = 1\).
Câu 71:
Trong không gian Oxyz, cho ba điểm \(M(6;0;0),N(0;6;0),P(0;0;6)\). Hai mặt cầu có phương trình \(\left( {{S_1}} \right):{x^2} + {y^2} + {z^2} - 2x - 2y + 1 = 0\) và \(\left( {{S_2}} \right):{x^2} + {y^2} + {z^2} - 8x + 2y + 2z + 1 = 0\) cắt nhau theo giao tuyến là đường tròn \((C)\). Có bao nhiêu mặt cầu có tâm thuộc mặt phẳng chứa \((C)\) và tiếp xúc với ba đường thẳng MN, NP, PM?
 Xem đáp án
Xem đáp án
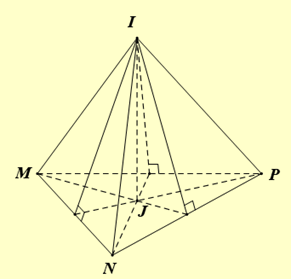
Gọi \((\alpha )\) là mặt phẳng chứa \((C)\) và \(I\) là tâm mặt cầu cần tìm.
Trừ theo vế hai phương trình mặt cầu ta được \((\alpha ):6x - 4y - 2z = 0 \Leftrightarrow 3x - 2y - z = 0\).
Mặt cầu tiếp xúc với ba cạnh của tam giác MNP suy ra tâm mặt cầu thuộc đường thẳng vuông góc với \((MNP)\) và đi qua tâm đường tròn nội tiếp hoặc bằng tiếp tam giác MNP.
Dễ thấy \((\alpha ) \bot (MNP)\) và \((\alpha )\) qua \(J(2;2;2)\) là tâm đường tròn nội tiếp tam giác đều MNP nên I thuộc đường thẳng qua \(J\) và vuông góc \((MNP)\).
Vậy có vô số mặt cầu thỏa mãn yêu cầu bài toán.
Câu 72:
Biết khai triển \({\left( {1 + 2x + 3{x^2}} \right)^{10}} = {a_0} + {a_1}x + {a_2}{x^2} + \ldots + {a_{20}}{x^{20}}\). Tính tổng \(S = {a_0} + 2{a_1} + 4{a_2} + \ldots + {2^{20}}{a_{20}}\).
 Xem đáp án
Xem đáp án
Đặt \(f(x) = {\left( {1 + 2x + 3{x^2}} \right)^{10}} = {a_0} + {a_1}x + {a_2}{x^2} + \ldots + {a_{20}}{x^{20}}\), ta có \(S = {a_0} + 2{a_1} + 4{a_2} + \ldots + {2^{20}}{a_{20}} = f(2) = {17^{10}}\).
Câu 73:
Kim tự tháp Cheops (có dạng hình chóp) là kim tự tháp cao nhất ở Ai Cập. Chiều cao của kim tự tháp này là 144 m, đáy của kim tự tháp là hình vuông có cạnh dài 230 m. Các lối đi và phòng bên trong chiếm 30% thể tích của kim tự tháp. Để xây dựng kim tự tháp, người Ai Cập cổ đại đã vận chuyển các khối đá qua những lối đi vào phòng bên trong. Biết một lần vận chuyển gồm 10 xe, mỗi xe chở 6 tấn đá, và khối lượng riêng của đá bằng 2,5.103 kg/m3. Số lần vận chuyển đá để xây dựng kim tự tháp là (1) _________
 Xem đáp án
Xem đáp án
Đáp án: “74060”
Giải thích
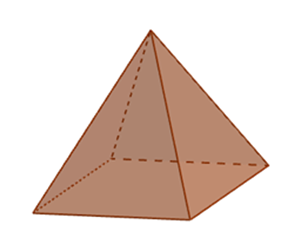
Thể tích kim tự tháp là \(V = \frac{1}{3}{.230^2}.144 = 2539200\left( {\;{{\rm{m}}^3}} \right)\).
Thể tích khối đá cần vận chuyển là \(0.7\;{\rm{V}} = 1777440\left( {\;{{\rm{m}}^3}} \right)\).
Gọi \(x\) là số lần vận chuyển.
Để đủ đá xây dựng kim tự tháp thì \(\frac{{x.10.6000}}{{2,{{5.10}^3}}} = 1777440 \Rightarrow x = 74060\).
Câu 74:
Minh và Thành đang chơi một trò chơi. Trong trò chơi, mỗi người chơi bắt đầu với 0 điểm và sau khi kết thúc trò chơi, người có nhiều điểm nhất sẽ giành chiến thắng. Biết Minh có ba lần được 5 điểm, bị trừ mất 12 điểm và sau đó được cộng 3 điểm. Thành có hai lần bị trừ mất 3 điểm, một lần trừ mất 1 điểm, một lần được cộng 6 điểm và sau đó được cộng 7 điểm.
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Sau khi kết thúc trò chơi, Minh được 6 điểm. |
¡ |
¡ |
|
Sau khi kết thúc trò chơi, Thành được 18 điểm. |
¡ |
¡ |
|
Thành là người chiến thắng. |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
Đúng |
Sai |
|
Sau khi kết thúc trò chơi, Minh được 6 điểm. |
¤ |
¡ |
|
Sau khi kết thúc trò chơi, Thành được 18 điểm. |
¡ |
¤ |
|
Thành là người chiến thắng. |
¡ |
¤ |
Giải thích
Số điểm của Minh là: 3.5 − 12 + 3 = 6.
Số điểm của Thành là: 2.(−3) − 1 + 6 + 7 = 6.
Vậy hai bạn hòa nhau.
Câu 75:
Cho tứ giác ABCD. Trên các cạnh AB, BC, CD, AD lần lượt lấy 3; 4; 5; 6 điểm phân biệt khác các điểm A, B, C, D. Số tam giác phân biệt có các đỉnh là các điểm vừa lấy là
 Xem đáp án
Xem đáp án
Tổng số điểm vừa lấy bằng: 3 + 4 + 5 + 6 = 18 (điểm).
Mỗi cách chọn ra 3 điểm không nằm trên một cạnh cho ta một tam giác.
Số cách chọn 3 điểm từ 18 điểm là: \[C_{18}^3 = 816\] (cách chọn).
Số cách chọn 3 điểm cùng nằm trên một cạnh là: \(C_3^3 + C_4^3 + C_5^3 + C_6^3 = 35\) (cách chọn).
Vậy số tam giác cần tìm bằng. 816 − 35 = 781 (tam giác).
Câu 76:
Trong các số phức sau, những số phức nào có môđun bằng 3?
 Xem đáp án
Xem đáp án
Ta có:
\(|1 - 2i| = \sqrt 5 ;\,\,|\sqrt 5 + 2i| = 3;\,\,|3| = 3;\,\,|2 - \sqrt 7 i| = \sqrt {11} \).
Câu 77:
Cho các số dương a, b, c thỏa mãn \(a \ne 1,\,\,{\log _3}a + b = 0,\,\,{\log _a}b = \frac{1}{c},\,\,\ln \frac{b}{c} = c - b\). Tổng \(S = a + b + c\) nằm trong khoảng nào cho dưới đây?
 Xem đáp án
Xem đáp án
Ta có : \(\ln \frac{b}{c} = c - b \Leftrightarrow \ln b + b = \ln c + c \Leftrightarrow b = c\) (vì hàm số \(y = \ln x + x\) đồng biến trên khoảng \((0; + \infty )\) ).
Mặt khác, \({\log _3}a + b = 0 \Leftrightarrow a = {3^{ - b}}\).
Với \(b = c\) và \(a = {3^{ - b}}\) thì \({\log _a}b = \frac{1}{c} \Leftrightarrow {\log _{{3^{ - b}}}}b = \frac{1}{b} \Leftrightarrow \frac{1}{b}{\log _{{3^{ - 1}}}}b = \frac{1}{b} \Leftrightarrow {\log _{{3^{ - 1}}}}b = 1 \Leftrightarrow b = \frac{1}{3}\).
Suy ra \(a = \frac{1}{{\sqrt[3]{3}}},b = c = \frac{1}{3}\). Vì vậy \(S = a + b + c = \frac{1}{{\sqrt[3]{3}}} + \frac{2}{3} \in \left( {\frac{6}{5};\frac{3}{2}} \right)\).
Câu 78:
Cho hàm số \(f(x) = \sin x + \cos x\). Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Hàm số \(f\left( x \right)\) tuần hoàn với chu kì \(\pi \). |
¡ |
¡ |
|
Hàm số \(f\left( x \right)\) là hàm số chẵn |
¡ |
¡ |
|
Phương trình \(f\left( x \right)\)= 0 có 2 điểm biểu diễn trên đường tròn lượng giác. |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
Đúng |
Sai |
|
Hàm số \(f\left( x \right)\) tuần hoàn với chu kì \(\pi \). |
¡ |
¤ |
|
Hàm số \(f\left( x \right)\) là hàm số chẵn |
¡ |
¤ |
|
Phương trình \(f\left( x \right)\)= 0 có 2 điểm biểu diễn trên đường tròn lượng giác. |
¤ |
¡ |
Giải thích
Hàm số \(\sin x\) và \(\cos x\) đều có chu kì tuần hoàn là \(2\pi \) nên hàm số \(f(x)\) tuần hoàn với chu kì \(2\pi \).
Ta có: \(f( - x) = \sin ( - x) + \cos ( - x) = - \sin x + \cos x\).
\( \Rightarrow \) Hàm số \(f(x)\) không chẵn, không lẻ.
Mặt khác, \(f(x) = 0 \Leftrightarrow \sin x + \cos x = 0 \Leftrightarrow \sin \left( {x + \frac{\pi }{4}} \right) = 0 \Leftrightarrow x = - \frac{\pi }{4} + k\pi (k \in \mathbb{Z})\).
Biểu diễn nghiệm trên đường tròn lượng giác ta thấy phương trình \(f(x) = 0\) có 2 điểm biểu diễn trên đường tròn lượng giác.
Câu 79:
Cho số phức z thỏa mãn \(|z - 1 - 2i| \le 1\) và \(|z - 1 + 2i| \ge |z + 3 - 2i|\). Diện tích phần mặt phẳng chứa các điểm biểu diễn của số phức z bằng (1) _______. (Lấy \(\pi \approx 3,14\) và kết quả viết dưới dạng phân số tối giản).
 Xem đáp án
Xem đáp án
Đáp án: “157/100”
Giải thích
Giả sử \(z = x + yi\,\,(x,y \in \mathbb{R})\).
Khi đó\(|z - 1 - 2i| \le 1 \Leftrightarrow |(x - 1) + (y - 2)i| \le 1\)
\( \Leftrightarrow \sqrt {{{(x - 1)}^2} + {{(y - 2)}^2}} \le 1 \Leftrightarrow {(x - 1)^2} + {(y - 2)^2} \le 1.\)
Và \(|z - 1 + 2i| \ge |z + 3 - 2i|\)
\( \Leftrightarrow \sqrt {{{(x - 1)}^2} + {{(y + 2)}^2}} \ge \sqrt {{{(x + 3)}^2} + {{(y - 2)}^2}} \)
\( \Leftrightarrow {(x - 1)^2} + {(y + 2)^2} \ge {(x + 3)^2} + {(y - 2)^2} \Leftrightarrow y \ge x + 1.\)
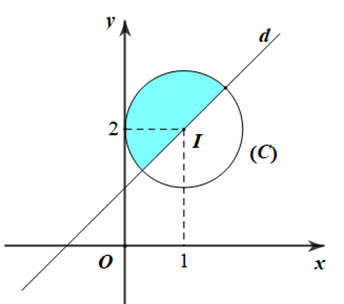
Gọi \((T)\) là nửa mặt phẳng có bờ là đường thẳng \(d:y = x + 1\), không chứa gốc tọa độ \(O(0;0)\). Khi đó tập hợp các điểm biểu diễn số phức \(z\) thỏa mãn đề là nửa hình tròn \((C)\) tâm \(I(1;2)\), bán kính \(R = 1\) và thuộc \((T)\) (phần tô màu trên hình vẽ).
Vì đường thẳng \(d\) đi qua tâm \(I(1;2)\) của hình tròn \((C)\) nên diện tích cần tìm là một nửa diện tích hình tròn \((C)\). Do đó \(S = \frac{\pi }{2} \approx \frac{{157}}{{100}}\).
Câu 80:
Giả sử hàm số \(f(x)\) liên tục trên [a; b]. Biết \(F(x),G(x)\) là hai nguyên hàm của hàm số \(f(x)\). Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
\[F(x) = G(x) + C\] với C là hằng số |
¡ |
¡ |
|
\(\int\limits_a^b {f(x){\rm{d}}x} = F(a) - F(b)\) |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
Đúng |
Sai |
|
\[F(x) = G(x) + C\] với C là hằng số |
¤ |
¡ |
|
\(\int\limits_a^b {f(x){\rm{d}}x} = F(a) - F(b)\) |
¡ |
¤ |
Giải thích
Vì \(F(x),\,\,G(x)\) là hai nguyên hàm của hàm số \(f(x)\) nên \(F(x) - G(x) = C\) với \(C\) là hằng số hay \(F(x) = G(x) + C\).
\(\int\limits_a^b {f(x){\rm{d}}x} = \left. {F(x)} \right|_a^b = F(b) - F(a).\)Câu 81:
Cho tứ diện đều SABC cạnh bằng \(a\). Gọi \(I\) là trung điểm của đoạn AB, M là điểm di động trên đoạn AI. Qua \(M\) vẽ mặt phẳng \((\alpha )\) song song với \((SIC)\). Tính chu vi của thiết diện tạo bởi \((\alpha )\) với tứ diện SABC, biết \(AM = x\).
 Xem đáp án
Xem đáp án
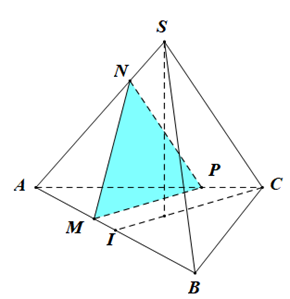
Ta thấy tam giác MNP và SIC đồng dạng với tỉ số \(\frac{{AM}}{{AI}} = \frac{{2x}}{a}\)
\( \Rightarrow \frac{{{C_{MNP}}}}{{{C_{SIC}}}} = \frac{{2x}}{a} \Leftrightarrow {C_{MNP}} = \frac{{2x}}{a}(SI + IC + SC) = \frac{{2x}}{a}\left( {\frac{{a\sqrt 3 }}{2} + \frac{{a\sqrt 3 }}{2} + a} \right) = 2x(\sqrt 3 + 1){\rm{. }}\)
Câu 82:
Kéo số ở các ô vuông thả vào vị trí thích hợp:
Một xe dịch vụ chất lượng cao đi từ Hà Giang xuống Hà Nội chở được nhiều nhất 50 hành khách trên một chuyến đi. Theo tính toán của nhà xe, nếu xe chở được k khách thì giá tiền mà mỗi khách phải trả khi đi tuyến đường này là \({\left( {180 - \frac{{3k}}{2}} \right)^2}\) trăm đồng. Tổng số tiền thu được từ hành khách nhiều nhất là _______ nghìn đồng khi xe chở _______ hành khách.
 Xem đáp án
Xem đáp án
Một xe dịch vụ chất lượng cao đi từ Hà Giang xuống Hà Nội chở được nhiều nhất 50 hành khách trên một chuyến đi. Theo tính toán của nhà xe, nếu xe chở được k khách thì giá tiền mà mỗi khách phải trả khi đi tuyến đường này là \({\left( {180 - \frac{{3k}}{2}} \right)^2}\) trăm đồng. Tổng số tiền thu được từ hành khách nhiều nhất là 57600 nghìn đồng khi xe chở 40 hành khách.
Giải thích
Số tiền thu được trên mỗi chuyến xe là \(T(k) = k{\left( {180 - \frac{{3k}}{2}} \right)^2}\) với \(k \in \mathbb{N},0 \le k \le 50\).
Xét hàm số \(T(k) = k{\left( {180 - \frac{{3k}}{2}} \right)^2}\) với \(k \in [0;50]\).
Ta có \(T'(k) = {\left( {180 - \frac{{3k}}{2}} \right)^2} + 2k\left( {180 - \frac{{3k}}{2}} \right)\left( { - \frac{3}{2}} \right) = \left( {180 - \frac{{3k}}{2}} \right)\left( {180 - \frac{{9k}}{2}} \right)\) và
\(T'(k) = 0 \Leftrightarrow \left( {180 - \frac{{3k}}{2}} \right)\left( {180 - \frac{{9k}}{2}} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{k = 120 \notin [0;50]}\\{k = 40 \in [0;50]}\end{array}} \right.\).
Ta tính được \(T(0) = 0,T(50) = 551250,T(40) = 576000\).
Do đó \(\mathop {\max }\limits_{[0;50]} T(k) = T(40) = 576000\).
Vậy số tiền thu được nhiều nhất khi xe chở 40 hành khách và số tiền đó là 57 600 000 đồng.
Câu 83:
Cho dãy số \(\left( {{u_n}} \right)\) được xác định bởi: \({u_1} = 2;{u_n} = 2{u_{n - 1}} + 3n - 1\). Công thức số hạng tổng quát của dãy số đã cho là biểu thức có dạng \(a{.2^n} + bn + c\), với a, b, c là các số nguyên, \(n \ge 2;n \in N\). Khi đó tổng \(a + b + c\) có giá trị bằng?
 Xem đáp án
Xem đáp án
Từ công thức truy hồi \({u_1} = 2;{u_n} = 2{u_{n - 1}} + 3n - 1\) ta suy ra: \(\left\{ {\begin{array}{*{20}{l}}{{u_2} = 9}\\{{u_3} = 26}\\{{u_4} = 63}\end{array}} \right.\).
Mà \({u_n} = a{.2^n} + bn + c,\,\,n \ge 2\) nên ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{4a + 2b + c = 9}\\{8a + 3b + c = 26}\\{16a + 4b + c = 63}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 5}\\{b = - 3}\\{c = - 5}\end{array}} \right.} \right.\).
Do đó \(a + b + c = - 3\).
Tải đề thi tại website Tailieuchuan.vn để được bảo hành vĩnh viễn
Câu 84:
Công ty X muốn thiết kế các hộp chứa sản phẩm dạng hình trụ có nắp với dung tích bằng 330 cm3, bán kính đáy x cm, chiều cao ℎ cm. Khi thiết kế, công ty X luôn đặt mục tiêu sao cho vật liệu làm vỏ hộp là ít nhất, nghĩa là diện tích toàn phần hình trụ là nhỏ nhất.
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau :

Để công ty X tiết kiệm được vật liệu nhất thì bán kính x bằng _______ cm và chiều cao ℎ bằng _______ cm.
(Kết quả làm tròn đến chữ số thập phân thứ ba).
 Xem đáp án
Xem đáp án
Công ty X muốn thiết kế các hộp chứa sản phẩm dạng hình trụ có nắp với dung tích bằng 330 cm3, bán kính đáy x cm, chiều cao ℎ cm. Khi thiết kế, công ty X luôn đặt mục tiêu sao cho vật liệu làm vỏ hộp là ít nhất, nghĩa là diện tích toàn phần hình trụ là nhỏ nhất.
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau :
Để công ty X tiết kiệm được vật liệu nhất thì bán kính x bằng 3,745 cm và chiều cao ℎ bằng 7,490 cm.
(Kết quả làm tròn đến chữ số thập phân thứ ba).
Giải thích
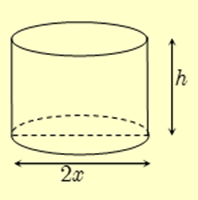
Ta có: \(V = \pi {x^2}h\).
Theo giả thiết thể tích hình trụ bằng \(330\;{\rm{c}}{{\rm{m}}^3}\) nên \(V = 330 \Leftrightarrow \pi {x^2}h = 330 \Leftrightarrow h = \frac{{330}}{{\pi {x^2}}}\)
Chi phí sản xuất là thấp nhất khi diện tích toàn phần hình trụ nhỏ nhất.
Ta có: \({S_{tp}} = {S_{xq}} + 2.{S_d} = 2\pi xh + 2\pi {x^2} = 2\pi \left( {{x^2} + \frac{{330}}{{\pi x}}} \right)\).
Áp dụng bất đẳng thức Cauchy cho 3 số dương ta có:
\({x^2} + \frac{{330}}{{\pi x}} = {x^2} + \frac{{165}}{{\pi x}} + \frac{{165}}{{\pi x}} \ge 3\sqrt[3]{{\frac{{27225.{x^2}}}{{{\pi ^2}.{x^2}}}}} = 3\sqrt[3]{{\frac{{27225}}{{{\pi ^2}}}}}\)
Dấu bằng xảy ra khi \({x^2} = \frac{{165}}{{\pi x}} \Leftrightarrow x = \sqrt[3]{{\frac{{165}}{\pi }}} \approx 3,745.\)
Để công ty X tiết kiệm được vật liệu nhất cần sản xuất hộp với kích thước \(h \approx 7,490\;{\rm{cm}}\) và \(x \approx 3,745\;{\rm{cm}}\).
Câu 85:
Một vật chuyển động trong 3 giờ với vận tốc v (km/ℎ) phụ thuộc thời gian t (ℎ) có đồ thị là một phần của đường parabol như hình vẽ.
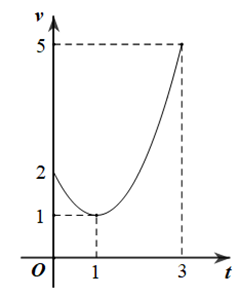
Quãng đường mà vật di chuyển được trong 3 giờ đó là (1) __________ km.
 Xem đáp án
Xem đáp án
Đáp án: “6”
Giải thích
Gọi \((P):v(t) = a.{t^2} + b.t + c\).
Vì các điểm có tọa độ (0;2);(1;1);(3;5) thuộc (P) nên ta có hệ phương trình
\(\left\{ {\begin{array}{*{20}{l}}{a.0 + b.0 + c = 2}\\{a.1 + b.1 + c = 1}\\{a.9 + b.3 + c = 5}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{c = 2\,\,\,}\\{b = - 2}\\{a = 1\,\,\,}\end{array}} \right.} \right.\). Vậy \(v(t) = 2 - 2t + {t^2}\).
Quãng đường vật di chuyển trong 3 giờ là
\(S = \int\limits_0^3 {\left( {2 - 2t + {t^2}} \right)} dt = \left. {\left( {2t - {t^2} + \frac{1}{3}{t^3}} \right)} \right|_0^3 = 6\,\,\left( {km} \right)\).
Câu 86:
Anh Nam dự tính làm một số lượng kem nhất định để phát miễn phí cho người đi đường. Sau khi tham khảo hàng trong siêu thị anh thấy một gói vỏ kem ốc quế gồm 50 cái, một hộp kem làm được 20 cái kem và một chai siro rưới được cho 40 cái kem. Biết mỗi cái kem đều phải đủ cả 3 thành phần gồm vỏ ốc quế, kem và siro. Anh Nam cần mua tối thiểu bao nhiêu hộp kem để tận dụng hết được phần vỏ, kem và siro?
 Xem đáp án
Xem đáp án
Để tận dụng hết được phần vỏ, kem và siro thì số kem làm được là bội chung nhỏ nhất của 50, 20 và 40.
Ta có: BCNN (50;20;40) = 200.
Vậy anh Nam cần mua tối thiểu 200 : 20 = 10 hộp kem.
Câu 87:
Cho hình phẳng \(D\) giới hạn bởi đồ thị các hàm số \(y = \frac{{{x^2}}}{2},y = 4\sqrt x \). Khối tròn xoay tạo thành khi quay \(D\) quanh trục hoành có thể tích \(V\) bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm \(\frac{{{x^2}}}{2} = 4\sqrt x \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ge 0}\\{\frac{{{x^4}}}{4} = 16x}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 4}\end{array}} \right.} \right.\).
Thể tích vật thể tròn xoay tạo thành là \(V = \pi \left| {\int\limits_0^4 {\left[ {{{\left( {\frac{{{x^2}}}{2}} \right)}^2} - {{(4\sqrt x )}^2}} \right]} {\rm{d}}x} \right| = \frac{{384}}{5}\pi \).
Câu 88:
Trong cuộc thi: "Thiết kế và trình diễn các trang phục dân tộc" do Đoàn trường THPT tổ chức vào tháng 3, mỗi lớp cần tham gia một tiết mục. Kết quả có 12 tiết mục đạt giải trong đó có 4 tiết mục khối 12, có 5 tiết mục khối 11 và 3 tiết mục khối 10. Ban tổ chức chọn ngẫu nhiên 5 tiết mục biểu diễn chào mừng ngày 26 tháng 3. Tính xác suất sao cho khối nào cũng có tiết mục được biểu diễn và trong đó có ít nhất 2 tiết mục của khối 12.
 Xem đáp án
Xem đáp án
Gọi không gian mẫu của phép chọn ngẫu nhiên là Ω.
Số phần tử của không gian mẫu là: \(n(\Omega ) = C_{12}^5 = 792.\)
Gọi A là biến cố : "Chọn 5 tiết mục sao cho khối nào cũng có tiết mục được biểu diễn và trong đó có ít nhất hai tiết mục của khối 12".
Chỉ có 3 khả năng xảy ra thuận lợi cho biến cố A là:
+ 2 tiết mục khối 12, hai tiết mục khối 10, một tiết mục khối 11.
+ 2 tiết mục khối 12, 1 tiết mục khối 10, 2 tiết mục khối 11.
+ 3 tiết mục khối 12, 1 tiết mục khối 10, 1 tiết mục khối 11.
Số kết quả thuận lợi cho biến cố A là: \(n(A) = C_4^2.C_3^2.C_5^1 + C_4^2.C_3^1.C_5^2 + C_4^3.C_3^1.C_5^1 = 330.\)
Xác suất cần tìm là \(P = \frac{{n(A)}}{{n(\Omega )}} = \frac{{330}}{{792}} = \frac{5}{{12}}\).
Câu 89:
Một khối lập phương có thể tích gấp 24 lần thể tích của một khối tứ diện đều. Cạnh khối lập phương gấp bao nhiêu lần cạnh của tứ diện đều?
 Xem đáp án
Xem đáp án
Gọi cạnh của khối lập phương là \(a\), cạnh của tứ diện đều là \(b\).
Thể tích của khối lập phương là: \({V_1} = {a^3}\).
Thể tích của khối tứ diện đều là: \({V_2} = \frac{{{b^3}\sqrt 2 }}{{12}}\).
Theo giả thiết khối lập phương có thể tích gấp 24 lần thể tích của khối tứ diện đều nên ta có:
\({V_1} = 24.{V_2} \Leftrightarrow {a^3} = 24.\frac{{{b^3}\sqrt 2 }}{{12}} \Leftrightarrow {a^3} = 2\sqrt 2 .{b^3} \Leftrightarrow a = \sqrt 2 .b.\)
Vậy cạnh khối lập phương gấp \(\sqrt 2 \) lần cạnh của tứ diện đều.
Câu 90:
Xác định điều kiện của tham số \(m\) để hàm số \(y = \frac{{mx - 1}}{{2x + 3}}\) luôn đồng biến trên tập xác định?
 Xem đáp án
Xem đáp án
Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - \frac{3}{2}} \right\}\).
Ta có: \(y' = \frac{{3m + 2}}{{{{(2x + 3)}^2}}}\).
Hàm số luôn đồng biến trên tập xác định \( \Leftrightarrow y' > 0,\forall x \in D\).
\( \Leftrightarrow 3m + 2 > 0 \Leftrightarrow m > - \frac{2}{3}{\rm{. }}\)
Câu 91:
Trong không gian Oxyz, cho điểm \(M(3;1; - 1)\) và mặt phẳng \((P)\) có phương trình: \(x - 2y + z - 6 = 0\)
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau :Hình chiếu của điểm M trên mặt phẳng (P) có hoành độ là _______, tung độ là _______ và cao độ là _______.
 Xem đáp án
Xem đáp án
Hình chiếu của điểm M trên mặt phẳng (P) có hoành độ là 4 , tung độ là -1 và cao độ là 0 .
Giải thích
Gọi \(d\) là đường thẳng đi qua \(M\) và vuông góc với mặt phẳng \((P)\).
\( \Rightarrow \) Phương trình đường thẳng \(d:\left\{ {\begin{array}{*{20}{c}}{x = 3 + t}\\{y = 1 - 2t}\\{z = - 1 + t}\end{array}} \right.\).
Gọi \(H\) là hình chiếu của điểm \(M\) trên mặt phẳng \((P)\).
\( \Rightarrow H = d \cap (P) \Rightarrow \) Tọa độ điểm \(H\) thỏa mãn hệ phương trình :
\(\left\{ {\begin{array}{*{20}{c}}{x = 3 + t}\\{y = 1 - 2t}\\{z = - 1 + t}\\{x - 2y + z - 6 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{t = 1}\\{x = 4}\\{y = - 1}\\{z = 0}\end{array} \Rightarrow H(4; - 1;0).} \right.} \right.\)
Câu 92:
Một quả cầu rỗng có bán kính ngoài \(4\;{\rm{cm}}\) và dày \(3\;{\rm{cm}}\) được làm từ thép. Biết khối lượng riêng của thép là \(7,850\;{\rm{kg}}/{{\rm{m}}^3}\). Khối lượng của quả cầu là bao nhiêu? (Kết quả làm tròn đến chữ số thập phân thứ nhất).
 Xem đáp án
Xem đáp án
Thể tích phần làm bằng thép của quả cầu là:
\(V = \frac{4}{3}\pi {.4^3} - \frac{4}{3}\pi .{(4 - 3)^3} = 84\pi \left( {{\rm{c}}{{\rm{m}}^3}} \right) = 84\pi {.10^{ - 6}}\left( {\;{{\rm{m}}^3}} \right)\).
Vậy khối lượng của quả cầu là: \(7,850\;{\rm{V}} = 7,850.84\pi {.10^{ - 6}}(\;{\rm{kg}}) \approx 2,1\,\,(\;{\rm{g}})\).
Câu 93:
Cho các số thực \(a,b,c \in (1; + \infty )\) thỏa mãn \({a^{10}} \le b\) và \({\log _a}b + 2{\log _b}c + 5{\log _c}a = 12\). Giá trị nhỏ nhất của biểu thức \(P = 2{\log _a}c + 5{\log _c}b + 10{\log _b}a\) bằng
 Xem đáp án
Xem đáp án
Đặt \(x = {\log _a}b;\,\,y = {\log _b}{\rm{c}};\,\,z = {\log _c}a\). Ta có \(\left\{ {\begin{array}{*{20}{l}}{x,y,z > 0}\\{x.y.z = 1}\\{x \ge 10}\\{x + 2y + 5z = 12}\end{array}} \right.\)
Khi đó :
\(P = \frac{2}{z} + \frac{5}{y} + \frac{{10}}{x} = \frac{2}{z} + \frac{5}{y} + \frac{{100}}{x} - \frac{{90}}{x} \ge 3\sqrt[3]{{\frac{2}{z}.\frac{5}{y}.\frac{{100}}{x}}} - 9 = 30 - 9 = 21\)
Suy ra \[{P_{min}} = 21\;\] đạt được khi
\(\left\{ {\begin{array}{*{20}{l}}{x.y.z = 1}\\{\frac{2}{z} = \frac{5}{y} = \frac{{100}}{x}}\\{x + 2y + 5z = 12}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 10}\\{y = \frac{1}{2}}\\{z = \frac{1}{5}}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{{\log }_a}b = 10}\\{{{\log }_b}c = \frac{1}{2}}\\{{{\log }_c}a = \frac{1}{5}}\end{array} \Rightarrow b = {c^2} = {a^{10}}} \right.} \right.} \right.\)
Câu 94:
Cho dãy số \(\left( {{u_n}} \right)\) được xác định bởi \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1,{u_2} = 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\{{u_{n + 2}} + {u_n} = 2\left( {{u_{n + 1}} + 1} \right),n \in {\mathbb{N}^*}}\end{array}} \right.\). Giới hạn \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{n^2}}}\) bằng (1) ________.
 Xem đáp án
Xem đáp án
Đáp án: “1”
Giải thích
\(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1,{u_2} = 3\quad {\rm{ (1)}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{ }}}\\{{u_{n + 2}} + {u_n} = 2\left( {{u_{n + 1}} + 1} \right)\quad (2)}\end{array}\quad (n \ge 1).} \right.\)
Đặt \({v_n} = {u_{n + 1}} - {u_n}\).
Ta có \((2) \Leftrightarrow {u_{n + 2}} - {u_{n + 1}} = {u_{n + 1}} - {u_n} + 2 \Leftrightarrow {v_{n + 1}} = {v_n} + 2\).
Suy ra \(\left( {{v_n}} \right)\) lập thành một cấp số cộng có số hạng đầu \({v_1} = 2\) và công sai \(d = 2\).
Nên \({v_n} = 2 + (n - 1).2 = 2n\).
Khi đó: \({u_n} = \left( {{u_n} - {u_{n - 1}}} \right) + \left( {{u_{n - 1}} - {u_{n - 2}}} \right) + \ldots + \left( {{u_2} - {u_1}} \right) + {u_1}\)
\( = {v_{n - 1}} + {v_{n - 2}} + \ldots + {v_1} + {u_1} = 2((n - 1) + (n - 2) + \ldots + 1) + 1\)
\( = 2\frac{{n(n - 1)}}{2} + 1 = n(n - 1) + 1.\)
Do đó: \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{n^2}}} = \mathop {\lim }\limits_{n \to + \infty } \frac{{n(n - 1) + 1}}{{{n^2}}} = \mathop {\lim }\limits_{n \to + \infty } \frac{{{n^2} - n + 1}}{{{n^2}}} = 1\). Vậy \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{u_n}}}{{{n^2}}} = 1\).
Câu 95:
Cho hình trụ có bán kính đáy \(r\). Gọi \(O\) và \({O^\prime }\) là tâm của hai đường tròn đáy với \(O{O^\prime } = 2r\). Một mặt cầu tiếp xúc với hai đáy của hình trụ tại \(O\) và \({O^\prime }\). Gọi \({V_c}\) và \({V_t}\) lần lượt là thể tích của khối cầu và khối trụ. Khi đó \(\frac{{{V_c}}}{{{V_t}}}\) bằng
 Xem đáp án
Xem đáp án
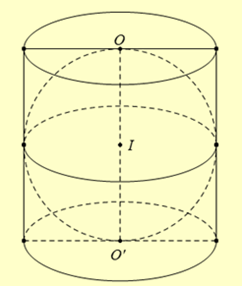
Ta có thể tích khối trụ là \({V_t} = \pi .{r^2}.O{O^\prime } = 2\pi {r^3}\).
Mặt cầu tiếp xúc với hai đáy của hình trụ nên mặt cầu có bán kính \(R = \frac{1}{2}O{O^\prime } = r\), suy ra thể tích khối cầu là \({V_c} = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {r^3}\).
Khi đó, \(\frac{{{V_c}}}{{{V_t}}} = \frac{{\frac{4}{3}\pi {r^3}}}{{2\pi {r^3}}} = \frac{2}{3}\).
Câu 96:
Cho các số thực dương a, b, c thỏa mãn \({a^{{{\log }_3}7}} = 27,\,\,{b^{{{\log }_7}11}} = 49,\,\,{c^{{{\log }_{11}}25}} = \sqrt {11} {\rm{. }}\)
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
\(\sqrt[3]{{{a^{{{\left( {{{\log }_3}7} \right)}^2}}}}} = 14\) |
¡ |
¡ |
|
\({c^{{{\left( {{{\log }_{11}}25} \right)}^2}}} = 5\) |
¡ |
¡ |
|
\(\sqrt[3]{{{a^{{{\left( {{{\log }_3}7} \right)}^2}}}}} + \sqrt {{b^{{{\left( {{{\log }_7}11} \right)}^2}}}} + {c^{{{\left( {{{\log }_{11}}25} \right)}^2}}} = 23\) |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
Đúng |
Sai |
|
\(\sqrt[3]{{{a^{{{\left( {{{\log }_3}7} \right)}^2}}}}} = 14\) |
¡ |
¤ |
|
\({c^{{{\left( {{{\log }_{11}}25} \right)}^2}}} = 5\) |
¤ |
¡ |
|
\(\sqrt[3]{{{a^{{{\left( {{{\log }_3}7} \right)}^2}}}}} + \sqrt {{b^{{{\left( {{{\log }_7}11} \right)}^2}}}} + {c^{{{\left( {{{\log }_{11}}25} \right)}^2}}} = 23\) |
¤ |
¡ |
Giải thích
\(\sqrt[3]{{{a^{{{\left( {{{\log }_3}7} \right)}^2}}}}} = \sqrt[3]{{{{\left( {{a^{{{\log }_3}7}}} \right)}^{{{\log }_3}7}}}} = \sqrt[3]{{{{27}^{{{\log }_3}7}}}} = \sqrt[3]{{{{\left( {{3^{{{\log }_3}7}}} \right)}^3}}} = 7\)
\(\sqrt {{b^{{{\left( {{{\log }_7}11} \right)}^2}}}} = \sqrt {{{\left( {{b^{{{\log }_7}11}}} \right)}^{{{\log }_7}11}}} = \sqrt {{{49}^{{{\log }_7}11}}} = \sqrt {{{\left( {{7^{{{\log }_7}11}}} \right)}^2}} = 11.\)
\({c^{{{\left( {{{\log }_{11}}25} \right)}^2}}} = {\left( {{c^{{{\log }_{11}}25}}} \right)^{{{\log }_{11}}25}} = {(\sqrt {11} )^{{{\log }_{11}}25}} = \sqrt {{{11}^{{{\log }_{11}}25}}} = \sqrt {25} = 5\)
Vậy \(\sqrt[3]{{{a^{{{\left( {{{\log }_3}7} \right)}^2}}}}} + \sqrt {{b^{{{\left( {{{\log }_7}11} \right)}^2}}}} + {c^{{{\left( {{{\log }_{11}}25} \right)}^2}}} = 7 + 11 + 5 = 23\).
Câu 97:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng \(a\sqrt 2 \). Góc giữa đường thẳng SA và mặt phẳng đáy bằng
 Xem đáp án
Xem đáp án
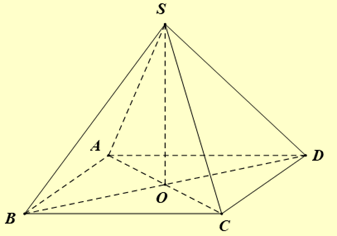
Gọi \(O\) là giao điểm của AC và BD.
Vì hình chóp S.ABCD là hình chóp đều nên \(SO \bot (ABCD)\) suy ra AO là hình chiếu của AS trên mặt phẳng \((ABCD) \Rightarrow \widehat {(SA,(ABCD))} = (\widehat {SA;AO}) = \widehat {SAO}\).
Tứ giác ABCD là hình vuông cạnh bằng \(a\) suy ra \(AO = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\).
Trong tam giác vuông \(SOA:\cos \widehat {SAO} = \frac{{AO}}{{SA}} = \frac{1}{2} \Rightarrow \widehat {SAO} = {60^^\circ }\).
Vậy góc giữa đường thẳng SA và mặt phẳng đáy bằng \({60^^\circ }\).
Câu 98:
Một cái thùng đựng đồ khô có dạng hình nón cụt rỗng với đường kính đáy dưới là 25 cm, đáy trên là 28 cm và chiều cao là 35 cm. Dùng một cái lon hình trụ rỗng có đường kính đáy là 6 cm và chiều cao là 10 cm đong đầy hạt vừng đổ vào thùng đựng đồ khô. Giả sử các hạt vừng lấp vừa kín lon và mỗi lần đong vừng đều như nhau. (Lấy π ≈ 3,14).
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Thể tích thùng đựng đồ khô là 19,42 lít. |
¡ |
¡ |
|
Thể tích hạt vừng chứa trong mỗi lon là 0,2826 lít. |
¡ |
¡ |
|
Cần tối thiểu 67 lon hạt vừng để đổ đầy thùng đựng đồ khô. |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
Đúng |
Sai |
|
Thể tích thùng đựng đồ khô là 19,42 lít. |
¡ |
¤ |
|
Thể tích hạt vừng chứa trong mỗi lon là 0,2826 lít. |
¤ |
¡ |
|
Cần tối thiểu 67 lon hạt vừng để đổ đầy thùng đựng đồ khô. |
¡ |
¤ |
Giải thích
Thể tích thùng đựng đồ khô là:
\({V_{NC}} = \frac{1}{3}\pi h\left( {{R^2} + {r^2} + Rr} \right) = \frac{1}{3}\pi .35\left[ {{{\left( {\frac{{28}}{2}} \right)}^2} + {{\left( {\frac{{25}}{2}} \right)}^2} + \frac{{28}}{2}.\frac{{25}}{2}} \right] = 6151,25\pi \left( {{\rm{c}}{{\rm{m}}^3}} \right) \approx 19,314925\)(lít)
Thể tích cái lon là: \({V_T} = \pi r_0^2{h_0} = \pi .{\left( {\frac{6}{2}} \right)^2}.10 = 90\pi \left( {{\rm{c}}{{\rm{m}}^3}} \right) \approx 0,2826\) (lít)
Ta thấy \(\frac{{6151,25\pi }}{{90\pi }} \approx 68,35\). Vậy cần tối thiểu 69 lon hạt vừng để đổ đầy thùng đựng đồ khô.
