Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 28)
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 28)
-
356 lượt thi
-
97 câu hỏi
-
150 phút
Danh sách câu hỏi
Câu 1:
Phần tư duy đọc hiểu
Theo bài viết, tế bào gốc đang được nghiên cứu để ứng dụng vào điều trị vấn đề gì về sức khỏe của con người?
 Xem đáp án
Xem đáp án
Đọc và xác định thông tin trong đoạn [0] của bài viết, kết hợp với phương pháp loại trừ: Ghép tế bào gốc đang dần trở thành phương pháp tiềm năng trong việc điều trị bệnh lý thoái hoá, tổn thương hệ miễn dịch hay các tổn thương mất mô, cơ quan. Trong các phương án trả lời, nội dung bài viết chỉ nhắc tới việc điều trị các vấn đề về thoái hóa mắt.
Chọn B
Câu 2:
Điền từ thích hợp (không quá hai tiếng) để hoàn thành câu sau:
“Cơ thể chúng ta được tạo ra khi trứng gặp tinh trùng, tế bào gốc đầu tiên và lớn nhất được gọi là (1) _______ tiếp tục thực hiện quá trình nhân lên về số lượng, biệt hóa chức năng để hình thành nên cơ thể và các cơ quan.”
 Xem đáp án
Xem đáp án
Đáp án
“Cơ thể chúng ta được tạo ra khi trứng gặp tinh trùng, tế bào gốc đầu tiên và lớn nhất được gọi là (1) hợp tử tiếp tục thực hiện quá trình nhân lên về số lượng, biệt hóa chức năng để hình thành nên cơ thể và các cơ quan.”
Giải thích
Đọc và xác định thông tin trong đoạn [2] của bài viết: Cơ thể được tạo ra khi trứng của mẹ và tinh trùng của cha gặp nhau, tạo thành một tế bào gốc đầu tiên có tên gọi là hợp tử. Hợp tử là tế bào gốc lớn nhất, tiếp tục nhân lên về số lượng để tạo thành phôi rồi hình thành thai.
Câu 3:
Theo thông tin trong bài viết, tất cả các cơ quan trên cơ thể người đều được hình thành dựa trên cơ chế hoạt động, phát triển của tế bào gốc. Đúng hay sai?
 Xem đáp án
Xem đáp án
Đọc và xác định thông tin trong đoạn [2] của bài viết: Trong suốt giai đoạn hình thành và phát triển, cơ quan và cả cơ thể được tiếp tục hoàn thiện chức năng và kích thước thông qua nhiều cơ chế hoạt động của tế bào gốc.
Chọn A
Câu 4:
Hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí.
cơ chế, chức năng, dữ trữ, tăng sinh
Tế bào gốc trong cơ thể hoạt động theo nhiều _______ khác nhau nhằm duy trì số lượng và tạo nguồn _______ tế bào gốc trong cơ thể, hình thành nên những tế bào _______; chính vì vậy, tế bào gốc sẽ được huy động và dùng để thay thế, bổ sung những tế bào thiếu hụt do nhiều nguyên nhân khác nhau.
 Xem đáp án
Xem đáp án
Đáp án
Tế bào gốc trong cơ thể hoạt động theo nhiều cơ chế khác nhau nhằm duy trì số lượng và tạo nguồn dự trữ tế bào gốc trong cơ thể, hình thành nên những tế bào chức năng; chính vì vậy, tế bào gốc sẽ được huy động và dùng để thay thế, bổ sung những tế bào thiếu hụt do nhiều nguyên nhân khác nhau.
Giải thích
Đọc và xác định thông tin trong đoạn [3] của bài viết:
+ Tế bào gốc hoạt động theo các cơ chế khác nhau
+ một tế bào gốc nhân lên để thành hai tế bào gốc con giống hệt nhau và giống hệt tế bào gốc ban đầu. Hoạt động này nhằm duy trì số lượng và tạo nguồn dự trữ tế bào gốc trong cơ thể
+ một tế bào gốc ban đầu nhân lên thành hai tế bào, trong đó có một tế bào gốc giống hệt tế bào mẹ ban đầu, một tế bào còn lại sẽ biệt hóa để trở thành tế bào chức năng.
Câu 5:
 Xem đáp án
Xem đáp án
Đọc và xác định thông tin trong đoạn [4] của bài viết: Ví dụ khi chúng ta bị trầy da, các tế bào bị tổn thương sẽ tạo ra tín hiệu để các yếu tố cận tiết và yếu tố tự tiết theo dòng máu đi tới hệ thần kinh trung ương, từ đây hệ thần kinh phát ra các tín hiệu báo hiệu cho cơ thể biết chính xác vị trí của vết thương. Khi đó, tế bào gốc tại vùng tổn thương hoặc tế bào gốc từ vùng lân cận và từ tủy xương sẽ được huy động và kích hoạt để làm nhiệm vụ theo một hoặc nhiều trong số các cơ chế đã nêu nhằm sửa chữa các tổn thương quanh vùng da bị đứt. Từ đó xác định, thông qua tín hiệu được truyền về, hệ thần kinh trung ương nhận diện vị trí và huy động, kích hoạt tế bào gốc để tiến hành sửa chữa tổn thương.
Chọn A
Câu 6:
Điền từ thích hợp (không quá hai tiếng) để hoàn thành câu sau:
“Có nhiều yếu tố khác nhau ảnh hưởng đến quá trình chữa lành các vết thương trên cơ thể, nhưng có thể nói, (1) ______ là yếu tố chính vì số lượng tế bào gốc ở những người trẻ sẽ có nhiều hơn so với người lớn tuổi.”
 Xem đáp án
Xem đáp án
Đáp án
“Có nhiều yếu tố khác nhau ảnh hưởng đến quá trình chữa lành các vết thương trên cơ thể, nhưng có thể nói, (1) tuổi tác là yếu tố chính vì số lượng tế bào gốc ở những người trẻ sẽ có nhiều hơn so với người lớn tuổi.”
Giải thích
Đọc, xác định thông tin trong đoạn [5]: Tốc độ lành của vết thương phụ thuộc nhiều yếu tố khác nhau như diện tích vùng tổn thương, đặc tính sinh học của từng cơ thể (cơ địa), mức độ hoạt động, giới tính hay tuổi tác… Trong đó, tuổi tác là một trong các yếu tố chính tác động đến tốc độ lành vết thương do lượng tế bào gốc trong cơ thể trẻ nhiều hơn so với người lớn.
Câu 7:
 Xem đáp án
Xem đáp án
Đọc và tổng hợp thông tin trong đoạn [6] của bài viết: Đặc tính của tế bào gốc là chúng tự biết khi nào sẽ phải làm gì và làm thế nào cho đúng. Khác với tế bào ung thư, tế bào gốc tăng sinh với số lượng đủ để bù đắp cho số lượng tế bào đã lão hóa, tế bào tổn thương hay tế bào chết. Chúng chỉ hoạt động (tăng sinh và/hoặc biệt hóa) khi nhận được tín hiệu phù hợp, ở đúng vị trí thiếu hụt tế bào.
Chọn B
Câu 8:
Theo thông tin trong đoạn [5], tế bào gốc có hoạt động tốt trong quá trình khắc phục những vết thương của cơ thể hay không phụ thuộc rất nhiều vào sự giải phóng các yếu tố sinh trưởng từ tiểu cầu. Đúng hay sai?
 Xem đáp án
Xem đáp án
Theo thông tin trong đoạn [5], tế bào gốc có hoạt động tốt trong quá trình khắc phục những vết thương của cơ thể hay không phụ thuộc rất nhiều vào sự giải phóng các yếu tố sinh trưởng từ tiểu cầu. Đúng hay sai?
Chọn A
Câu 9:
 Xem đáp án
Xem đáp án
Đọc và xác định thông tin trong đoạn [6]: Khác với tế bào ung thư, tế bào gốc tăng sinh với số lượng đủ để bù đắp cho số lượng tế bào đã lão hóa, tế bào tổn thương hay tế bào chết. Chúng chỉ hoạt động (tăng sinh và/hoặc biệt hóa) khi nhận được tín hiệu phù hợp, ở đúng vị trí thiếu hụt tế bào; ngược lại, tế bào ung thư có thể tăng sinh ở mọi cơ quan, mọi vị trí và tăng sinh vượt mức số lượng tế bào vốn có của cơ quan.
Chọn A
Câu 10:
 Xem đáp án
Xem đáp án
Giải thích
Đọc và xác định thông tin trong đoạn [6] của bài viết: Hoạt động của tế bào gốc đã tạo ra sự cân bằng về số lượng và chất lượng của các loại tế bào trong cơ thể. Nhờ đó mà hoạt động sống của cơ thể có thể diễn ra bình thường. Vì vậy, có thể nói tế bào gốc là chìa khóa quan trọng của sự sống.
Chọn B
Câu 11:
Để cạnh tranh với các nền tảng xuyên biên giới như Facebook, Google, các nhà cung cấp dịch vụ truyền hình trực tuyến trong nước đang làm gì?
 Xem đáp án
Xem đáp án
Đọc và xác định thông tin trong đoạn [1] của bài viết: "người Việt ngày càng thích xem video ngắn trên mạng xã hội. Các đài truyền hình cũng đang đẩy nội dung lên những nền tảng này để kết nối với người xem", từ đó nhận thấy, do thói quen của người dùng mà các nhà cung cấp đang phải xử lý các sản phẩm cũ để thích ứng, tăng doanh thu từ Facebook, Youtube.
Chọn A
Câu 12:
Tại hội thảo về quản lý dịch vụ phát thanh truyền hình, bà Phạm Thanh Phương đã đề cập đến sự thay đổi nào trong sở thích xem video của người Việt?
 Xem đáp án
Xem đáp án
Căn cứ vào cụm từ "hội thảo về quản lý dịch vụ phát thanh truyền hình", xác định thông tin nằm trong đoạn [1] của bài viết: "dẫn báo cáo của Research and Market cho thấy người Việt ngày càng thích xem video ngắn trên mạng xã hội", "Việc người dùng ngày càng chuyển dịch từ truyền hình truyền thống lên nền tảng số như Facebook, YouTube kéo theo sự dịch chuyển doanh thu". Tổng hợp thông tin cho thấy, người Việt đang thay đổi thói quen của mình từ việc xem truyền hình TV chuyển sang sử dụng các nền tảng số.
Chọn B
Câu 13:
Theo bài viết, nguyên nhân của việc lợi nhuận thu từ quảng cáo video trên mạng xã hội không bằng quảng cáo truyền hình là gì?
 Xem đáp án
Xem đáp án
Xác định lợi nhuận là phần thu được của doanh nghiệp sau khi trừ đi chi phí, đọc nội dung đoạn [2] và xác định thông tin: "doanh thu quảng cáo video trên mạng xã hội của các đơn vị sản xuất tăng nhưng không tương xứng với số tiền đầu tư", "Giá trị kinh doanh trên mạng xã hội rất nhỏ so với doanh thu quảng cáo truyền hình trả".
Chọn D
Câu 14:
Hoàn thành câu sau bằng cách kéo thả các từ vào đúng vị trí.
khuyến cáo, phụ thuộc, đề nghị, chia sẻ, chủ động
Để giải quyết bài toán _______ doanh thu, tránh _______ vào nền tảng nước ngoài, bà Phạm Thanh Phương đưa ra _______ các doanh nghiệp OTT hợp tác và chia sẻ tài nguyên để phục vụ tốt hơn cho người dùng.
 Xem đáp án
Xem đáp án
Đáp án
Để giải quyết bài toán chủ động doanh thu, tránh phụ thuộc vào nền tảng nước ngoài, bà Phạm Thanh Phương đưa ra đề nghị các doanh nghiệp OTT hợp tác và chia sẻ tài nguyên để phục vụ tốt hơn cho người dùng.
Giải thích
Căn cứ vào cụm từ “hợp tác và chia sẻ”, đọc lướt bài viết và xác định thông tin nằm trong đoạn [3]: “Bà Phương đề nghị doanh nghiệp OTT trong nước và nhà đài nên hợp tác với nhau, chia sẻ nội dung thế mạnh của từng bên để phục vụ tốt hơn cho người dùng, từ đó chủ động doanh thu từ quảng cáo, thay vì phụ thuộc vào nền tảng nước ngoài”.
Câu 15:
Theo lãnh đạo của VieON, các doanh nghiệp OTT Việt đang gặp cản trở rất lớn về vấn đề doanh thu quảng cáo, thậm chí thua lỗ khi quá phụ thuộc vào nền tảng Google Ads. Đúng hay sai?
 Xem đáp án
Xem đáp án
Căn cứ vào từ khóa "lãnh đạo VieON" xác định thông tin nằm trong đoạn [3] của bài viết: Ông Huỳnh Long Thủy, Tổng giám đốc VieON, đề xuất mô hình hợp tác mới, giúp doanh nghiệp OTT Việt có thể chủ động doanh thu quảng cáo thay vì phụ thuộc vào nền tảng Google Ads. "Hầu hết các đơn vị dùng nền tảng quảng cáo của Google. Tuy nhiên thực tế chứng minh, nhiều nơi doanh thu quảng cáo không đủ bù đắp chi phí cho nhà cung cấp. Doanh nghiệp càng làm càng lỗ", ông nói.
Chọn A
Câu 16:
Đại diện Bộ Thông tin và Truyền thông đã đề cập đến khó khăn nào trong việc doanh nghiệp cùng nhau đo đếm và xây dựng chân dung người dùng?
 Xem đáp án
Xem đáp án
Đọc và xác định thông tin trong đoạn [4] của bài viết: “...việc doanh nghiệp cùng nhau đo đếm, xây dựng chân dung người dùng tưởng đơn giản nhưng khó nhất là làm sao có thể bắt tay cùng làm, tránh tâm lý sợ thiệt, không công bằng. “Chúng ta hoài nghi với nhau trong khi lại tuân theo luật chơi của nền tảng nước ngoài, chính điều này đã tự làm mình yếu đi”.”
Chọn C
Câu 17:
Điền từ thích hợp (không quá hai tiếng) để hoàn thành câu sau:
Khi tiến hành xây dựng và công bố các chỉ số đánh giá về dữ liệu người dùng, Bộ TT&TT mong muốn nhận được những ý kiến đóng góp, (1) _____ để tìm ra một số liệu chính xác nhất về chân dung người dùng.
 Xem đáp án
Xem đáp án
Đáp án
Khi tiến hành xây dựng và công bố các chỉ số đánh giá về dữ liệu người dùng, Bộ TT&TT mong muốn nhận được những ý kiến đóng góp, (1) tranh luận để tìm ra một số liệu chính xác nhất về chân dung người dùng.
Giải thích
Đọc và xác định thông tin trong đoạn [5] của bài viết: Bộ sẽ công bố các chỉ số, bộ đếm đo lường của cơ quan chức năng, kết hợp cùng số liệu từ các nền tảng OTT. Tuy nhiên, đại diện Bộ cũng lưu ý, khi chỉ số này được công bố, chắc chắn sẽ có những khác nhau tương đối lớn giữa các bộ đếm. “Chúng tôi mong chờ những tranh luận để xem cái nào chính xác nhất, tuy nhiên ít nhất sẽ có một số liệu chính thống, do nhà nước đo, công bố và xếp hạng”, ông Lâm nói.
Câu 18:
Theo bài viết, Facebook đã đầu tư một số tiền lớn vào việc gì?
 Xem đáp án
Xem đáp án
Đọc và xác định thông tin trong đoạn [5] của bài viết: “Facebook từng bỏ ra 270 triệu USD mua bản quyền bóng đá Ngoại hạng Anh tại Việt Nam ba mùa 2019-2022”.
Chọn C
Câu 19:
Theo bài viết, doanh nghiệp trong nước đang cân nhắc việc hợp tác và chia sẻ nội dung để cạnh tranh với nền tảng nước ngoài. Đề xuất nào sau đây có thể giúp tối ưu hóa giá trị quảng cáo?
 Xem đáp án
Xem đáp án
Đọc và xác định thông tin trong đoạn [5] của bài viết: “Đại diện VieON kiến nghị các nhà cung cấp OTT Việt có thể xây dựng một gói dịch vụ đặc biệt, tập hợp nội dung đặc sắc của mình và bán cho người dùng. Nhà đài cũng có thể hợp tác với doanh nghiệp OTT, doanh thu gói cước sẽ chia sẻ với bên cung cấp dịch vụ”.
Chọn D
Câu 20:
Nội dung nào sau đây được đề cập trong nội dung bài viết?
 Xem đáp án
Xem đáp án
Đọc lại thông tin trong bài viết và tiến hành loại trừ. Bài viết để cập tới việc các doanh nghiệp bị sụt giảm doanh thu do sự thay đổi thói quen của người dùng, lợi nhuận từ quảng cáo không đảm bảo được số tiền đã đầu tư nên đáp án là D.
Câu 21:
Phần tư duy khoa học / giải quyết vấn đề
Phát biểu nào sau đây là đúng khi nói về đặc điểm của ánh sáng khả kiến?
 Xem đáp án
Xem đáp án
Ánh sáng khả kiến là các bức xạ điện từ có bước sóng nằm trong vùng quang phổ nhìn thấy được bằng mắt thường của con người.
Chọn D
Câu 22:
Dựa vào hình 1, cho biết bước sóng nào sau đây của ánh sáng khả kiến sẽ được hấp thụ để thúc đẩy hoạt động quang hợp mạnh nhất ở cây xanh?
 Xem đáp án
Xem đáp án
Nhìn vào hình 1, ta thấy ở bước sóng 440 nm, có sự hấp thụ lớn đối với cả 3 sắc tố quang hợp.
Chọn B
Câu 23:
Dựa vào thông tin được cung cấp trong hình 1 và bảng 1, cho biết phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Nhìn vào hình 1, ta thấy diệp lục a và diệp lục b có độ hấp thụ thấp nhất ở phần quang phổ từ 525 đến 625 nm, tương ứng với độ phản xạ lớn nhất.
Chọn C
Câu 24:
Điền từ thích hợp vào chỗ trống dưới đây
Sắc tố có độ hấp thụ cao nhất trong vùng ánh sáng đỏ của quang phổ là (1) _______.
 Xem đáp án
Xem đáp án
Đáp án
Sắc tố có độ hấp thụ cao nhất trong vùng ánh sáng đỏ của quang phổ là (1) chlorophyll a.
Giải thích
Ánh sáng đỏ có bước sóng 620 – 750 nm, nhìn vào hình 1, trong phạm vi bước sóng đó, diệp lục a có độ hấp thụ cao nhất.
Câu 25:
 Xem đáp án
Xem đáp án
Nhìn vào hình 1, ta thấy quang hợp xảy ra ở miền ánh sáng đỏ và miền ánh sáng xanh tím.
Chọn A
Câu 26:
Phát biểu sau đây đúng hay sai?
Màu xanh của lá cây mà mắt người có thể nhìn thấy được là vì diệp lục có khả năng hấp thụ tốt ánh sáng màu xanh lá của quang phổ khả kiến, đồng thời phản xạ lại môi trường ánh sáng đỏ và tím.
 Xem đáp án
Xem đáp án
Mắt người có khả năng nhìn thấy màu xanh của diệp lục vì ở vùng ánh sáng màu xanh lá của quang phổ khả kiến, diệp lục gần như không hấp thụ chúng và phản xạ toàn bộ lại môi trường, phản lại mắt ta khiến ta nhìn thấy lá có màu xanh.
Chọn B
Câu 27:
Phát biểu sau đây là đúng hay sai?
Trong 4 Nghiên cứu trên thì dòng điện chạy qua đường ray đều theo một chiều nhất định, đúng hay sai?
 Xem đáp án
Xem đáp án
Dựa vào Bảng 4, ta thấy các giá trị của dòng điện đều âm.
→ Nghiên cứu 4 có dòng điện chạy theo hướng ngược lại so với các nghiên cứu khác.
Chọn b
Câu 28:
Trong Nghiên cứu 2, khi chiều dài của thanh nam châm là 1 m thì dòng điện cần thiết trong đường ray có cường độ là
 Xem đáp án
Xem đáp án
Dựa vào dữ liệu trong Bảng 2, khi chiều dài của thanh nam châm là 1 m thì cường độ dòng điện cần thiết trong đường ray là 84 A.
Chọn B
Câu 29:
Trong mỗi thử nghiệm, dòng điện trong đường ray đệm từ được tạo ra bởi một điện áp khác không. Thử nghiệm nào sau đây trong Nghiên cứu 3 có điện áp là lớn nhất?
 Xem đáp án
Xem đáp án
Ta có, khi dòng điện tăng là kết quả của điện áp tăng.
Từ dữ liệu của Bảng 3, ta thấy trong 4 phương án lựa chọn thì Thử nghiệm 14 có dòng điện lớn nhất, vì vậy nó cũng phải có điện áp lớn nhất.
Chọn A
Câu 30:
Trong Nghiên cứu 1, khi cường độ dòng điện I = 500 A thì giá trị của v là (1) ______ m/s.
 Xem đáp án
Xem đáp án
Đáp án
Trong Nghiên cứu 1, khi cường độ dòng điện I = 500 A thì giá trị của v là (1) _400_ m/s.
Giải thích
Theo dữ liệu trong Bảng 1, ta thấy khi dòng điện (I) tăng gấp đôi thì vận tốc (v) của đoàn tàu cũng tăng gấp đôi.
→ Khi dòng điện I = 500 A phải tương ứng với vận tốc của đoàn tàu là
Câu 31:
Theo tính toán lý thuyết, tàu đệm từ sử dụng hệ thống EDS phải di chuyển _______ ít nhất 4 inch so với đường ray.
 Xem đáp án
Xem đáp án
Đáp án
Theo tính toán lý thuyết, tàu đệm từ sử dụng hệ thống EDS phải di chuyển cao hơn ít nhất 4 inch so với đường ray.
Giải thích
Theo phần dẫn, ta có: Về mặt lý thuyết, tàu đệm từ trong EDS phải di chuyển cao hơn ít nhất 4 inch so với đường ray.
Câu 32:
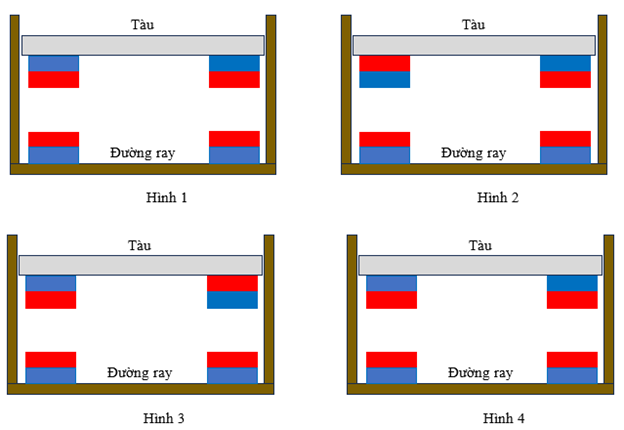
Cách sắp xếp các nam châm trong mô hình của tàu điện từ nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Theo phần dẫn, ta có: Dòng điện có thể tạo ra từ trường cảm ứng trong các thanh nam châm siêu dẫn của đường ray, kết quả là xuất hiện lực đẩy liên tục giữa các thanh nam châm khiến tàu được nâng lên, duy trì một khoảng cách phía trên đường ray được gọi là “khe không khí” và di chuyển về phía trước.
Vì vậy giữa các nam châm cần tạo ra lực đẩy hay có nghĩ là các nam châm cùng cực thì được đặt gần nhau nên Hình 1 đúng.
Chọn A
Câu 33:
Dòng điện chạy trong các thanh nam châm siêu dẫn của đường ray là dòng điện (1) _____.
 Xem đáp án
Xem đáp án
Đáp án
Dòng điện chạy trong các thanh nam châm siêu dẫn của đường ray là dòng điện (1) xoay chiều.
Giải thích
Dòng điện chạy trong các thanh nam châm siêu dẫn của đường ray có thể tạo ra từ trường cảm ứng nên dòng điện sử dụng ở đây là dòng điện xoay chiều (AC).
Câu 34:
Người mẹ 1 mắc bệnh mù màu đỏ và xanh lục sẽ có kiểu gene là _______.
 Xem đáp án
Xem đáp án
Đáp án
Người mẹ 1 mắc bệnh mù màu đỏ và xanh lục sẽ có kiểu gene là XaXa.
Giải thích
Nhìn vào bảng 1, ta thấy người nữ mắc bệnh sẽ có kiểu gene XaXa.
Câu 35:
Trường hợp cặp vợ chồng nào sau đây đều sinh ra con đều mắc bệnh mù màu đỏ - xanh lục?
 Xem đáp án
Xem đáp án
Người mẹ có kiểu gene XaXa luôn cho con giao tử Xa, người bố có kiểu gene XaY cho con gái giao tử Xa, con trai giao tử Y. Sự kết hợp ngẫu nhiên các giao tử luôn tạo ra kiểu gene: XaXa hoặc XaY quy định kiểu hình mù màu đỏ và xanh lục.
Chọn B
Câu 36:
Phát biểu sau đây đúng hay sai?
Người bố không mắc bệnh mù màu đỏ - xanh lục thì chắc chắn con gái sẽ không bị mắc bệnh mù màu đỏ - xanh lục.
 Xem đáp án
Xem đáp án
Người bố bình thường sẽ cho con gái giao tử XA, nên chắc chắn con gái sinh ra cũng sẽ không mắc bệnh mù màu đỏ - xanh lục.
Chọn A
Câu 37:
Giả sử người con gái số 3 lấy chồng mắc bệnh mù màu đỏ - xanh lục. Phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Người con gái 3 sẽ có kiểu gene XAXa lấy chồng mắc bệnh mù màu đỏ - xanh lục sẽ có kiểu gene XaY luôn cho con gái giao tử Xa. Như vậy họ không thể sinh ra người con gái có kiểu gene XAXA.
Chọn B
Câu 38:
Điền số thích hợp vào chỗ trống:
Nếu cặp bố mẹ trên sinh thêm một người con trai thì xác suất để người con đó bị bệnh là (1) ____ %.
 Xem đáp án
Xem đáp án
Đáp án
Nếu cặp bố mẹ trên sinh thêm một người con trai thì xác suất để người con đó bị bệnh là (1) 100%.
Giải thích
Do người mẹ 1 bị mắc bệnh mù màu đỏ - xanh lục có kiểu gene XaXa nên luôn cho người con trai giao tử Xa, người bố cho giao tử Y. Sự tổ hợp lại làm cho người con trai luôn có kiểu gene XaY – quy định bệnh mù màu đỏ - xanh lục.
Câu 39:
trội, con trai, lặn, con gái
Đối với bệnh do gene _______ quy định nằm trên nhiễm sắc thể giới tính X, khi người mẹ bị bệnh thì _______ chắc chắn sẽ bị bệnh, khi người bố không bị bệnh thì _______ chắc chắn không bị bệnh.
 Xem đáp án
Xem đáp án
Đáp án
Đối với bệnh do gene lặn quy định nằm trên nhiễm sắc thể giới tính X, khi người mẹ bị bệnh thì con trai chắc chắn sẽ bị bệnh, khi người bố không bị bệnh thì con gái chắc chắn không bị bệnh.
Giải thích
Đối với bệnh do gene lặn quy định nằm trên nhiễm sắc thể giới tính X, khi người mẹ bị bệnh thì con trai chắc chắn sẽ bị bệnh, khi người bố không bị bệnh thì gái chắc chắn không bị bệnh.
Câu 40:
Phát biểu sau đúng hay sai?
Dựa trên kết quả của Thí nghiệm 2, độ hấp thụ hiệu chỉnh của mơ khô có giá trị lớn nhất.
 Xem đáp án
Xem đáp án
Theo Bảng 2, độ hấp thụ hiệu chỉnh của nho khô có giá trị lớn nhất (0,941).
Chọn B
Câu 41:
Các phát biểu sau đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Dựa trên kết quả của Thí nghiệm 1, nếu một dung dịch có nồng độ SO32− là 3 ppm được thử nghiệm thì độ hấp thụ hiệu chỉnh sẽ xấp xỉ 0,5. |
||
|
Nếu Thí nghiệm 1 và 2 được lặp lại bằng cách sử dụng một chất tạo màu khác, cần có những thay đổi sau trong quy trình: + Chất tạo màu mới cần được thêm vào dung dịch A nhưng không cần thêm vào dung dịch mẫu. + Máy quang phổ UV-vis cần được cài đặt để đo ở bước sóng tương ứng với khả năng hấp thụ ánh sáng của chất tạo màu mới. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Dựa trên kết quả của Thí nghiệm 1, nếu một dung dịch có nồng độ SO32− là 3 ppm được thử nghiệm thì độ hấp thụ hiệu chỉnh sẽ xấp xỉ 0,5. |
X | |
|
Nếu Thí nghiệm 1 và 2 được lặp lại bằng cách sử dụng một chất tạo màu khác, cần có những thay đổi sau trong quy trình: + Chất tạo màu mới cần được thêm vào dung dịch A nhưng không cần thêm vào dung dịch mẫu. + Máy quang phổ UV-vis cần được cài đặt để đo ở bước sóng tương ứng với khả năng hấp thụ ánh sáng của chất tạo màu mới. |
X |
Giải thích
1. Đúng, vì: Dựa vào Bảng 1, dung dịch thử nghiệm có nồng độ sulfite là 3 ppm (nằm giữa 2,0 ppm và 4,0 ppm), sẽ có độ hấp thụ hiệu chỉnh nằm ở khoảng giữa 0,302 và 0,600. Do đó, một dung dịch có nồng độ SO32− là 3 ppm được thử nghiệm thì độ hấp thụ hiệu chỉnh sẽ xấp xỉ 0,5.
2. Sai, vì:
Nếu Thí nghiệm 1 và 2 được lặp lại bằng cách sử dụng một chất tạo màu khác, cần có những thay đổi sau trong quy trình:
+ Cả hai chất tạo màu nên được thêm vào dung dịch A và cho tất cả các mẫu.
+ Theo đoạn văn, máy quang phổ UV-vis là một thiết bị đo khả năng hấp thụ ánh sáng của mẫu chất. Bởi vì các màu khác nhau có bước sóng khác nhau, máy quang phổ UV-vis cần cài đặt để đo ở bước sóng tương ứng với khả năng hấp thụ ánh sáng của chất tạo màu mới.
Câu 42:
Điền từ/cụm từ thích hợp vào chỗ trống.
Mẫu trái cây có nồng độ SO32− thấp nhất là (1) ________.
 Xem đáp án
Xem đáp án
Đáp án
Mẫu trái cây có nồng độ SO32− thấp nhất là (1) chuối sấy.
Giải thích
Theo Bảng 2, chuối sấy có nống độ SO32− thấp nhất (0,2 ppm).
Câu 43:
Trong Thí nghiệm 2, một mẫu dứa khô cũng được đo độ hấp thụ và giá trị độ hấp thụ hiệu chỉnh xác định được là 0,603. Các mẫu được sắp xếp theo thứ tự nồng độ SO32− giảm dần là:
_______, _______, _______, _______, _______, _______.
 Xem đáp án
Xem đáp án
Trong Thí nghiệm 2, một mẫu dứa khô cũng được đo độ hấp thụ và giá trị độ hấp thụ hiệu chỉnh xác định được là 0,603. Các mẫu được sắp xếp theo thứ tự nồng độ SO32− giảm dần là:
nho khô, mơ khô, việt quất khô, dứa khô, mận khô, chuối sấy.
Giải thích
Dựa vào Bảng 2, ta thấy nồng độ của SO32− và độ hấp thụ hiệu chỉnh tỉ lệ thuận với nhau. Dứa khô có độ hấp thụ hiệu chỉnh hay nồng độ của SO32− cao hơn mận khô và thấp hơn việt quất khô.
Do đó, thứ tự nồng độ SO32− giảm dần sẽ tương ứng với thứ tự độ hấp thụ hiệu chỉnh giảm dần: nho khô (0,941), mơ khô (0,774), việt quất khô (0,668), dứa khô (0,603), mận khô (0,562), chuối sấy (0,031).
Câu 44:
Dựa trên kết quả của Thí nghiệm 1, nếu nồng độ SO32− trong dung dịch tăng gấp đôi, thì độ hấp thụ hiệu chỉnh của dung dịch
 Xem đáp án
Xem đáp án
Cả Bảng 1 và Hình 1 đều chỉ ra rằng, khi nồng độ sulfite tăng gấp đôi, độ hấp thụ hiệu chỉnh cũng tăng gần gấp đôi: khi nồng độ sulfite tăng từ 1 ppm lên 2 ppm (tăng gấp đôi) thì độ hấp thụ hiệu chỉnh tương ứng tăng từ 0,153 lên 0,302 (tăng gần gấp đôi).
Chọn C
Câu 45:
Dựa trên kết quả của Thí nghiệm 1, nếu một dung dịch có nồng độ SO32− là 1,5 ppm được thử nghiệm thì độ hấp thụ hiệu chỉnh sẽ gần nhất với giá trị nào sau đây?
 Xem đáp án
Xem đáp án
Dựa vào Bảng 1, dung dịch thử nghiệm có nồng độ sulfite là 1,5 ppm (nằm giữa 1,0 ppm và 2,0 ppm), sẽ có độ hấp thụ hiệu chỉnh nằm ở khoảng giữa 0,153 và 0,302. Do đó, phương án 0,240 là lựa chọn chính xác.
Chọn B
Câu 46:
Nếu một số thành phần hòa tan trong nước được tìm thấy trong tất cả các loại trái cây được thử nghiệm trong Thí nghiệm 2 hấp thụ ánh sáng có cùng bước sóng với hợp chất được hình thành bởi SO32− và chất tạo màu. So với nồng độ SO32− thực tế, nồng độ SO32− đo được sẽ
 Xem đáp án
Xem đáp án
Giả thiết cho rằng hàm lượng chất phụ gia trong trái cây có khả năng hấp thụ ánh sáng ở cùng bước sóng với hợp chất được hình thành bởi SO32− và chất tạo màu, có nghĩa là độ hấp thụ sẽ cao hơn. Mà nồng độ SO32− và độ hấp thụ hiệu chỉnh tỉ lệ thuận với nhau nên so với nồng độ SO32− thực tế, nồng độ SO32− đo được sẽ cao hơn.
Chọn A
Câu 47:
Phát biểu sau đúng hay sai?
Gold là kim loại có tính khử yếu nên không bị hòa tan trong acid kể cả HNO3 nhưng lại bị hòa tan trong nước cường toan. Sau phản ứng thu được kết tủa gold(III) chloride theo phương trình sau:
Au + HNO3 + 3HCl → AuCl3↓ + 2H2O + NO↑
 Xem đáp án
Xem đáp án
Sai, vì: gold(IIII) chloride tồn tại ở dạng dung dịch, không phải kết tủa.
Chọn B
Câu 48:
Các phát biểu sau đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Có thể trung hòa nước cường toan bằng sodium bicarbonate hoặc sodium hydroxide. |
||
|
Al, Fe và Cr đều bị thụ động trong dung dịch nước cường toan. |
||
|
Khi bảo quản nước cường toan cần bảo quản trong bình thủy tinh không có nắp đậy, vì khí sinh ra có thể tích tụ và tạo áp suất làm bình chứa bị vỡ. |
||
|
Cho phương trình hóa học sau: Pt + HNO3 + HCl → H2PtCl6 + H2O + NO2↑ Sau khi cân bằng, tổng hệ số tối giản của các chất trong phản ứng này là 18. |
 Xem đáp án
Xem đáp án
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Có thể trung hòa nước cường toan bằng sodium bicarbonate hoặc sodium hydroxide. |
X | |
|
Al, Fe và Cr đều bị thụ động trong dung dịch nước cường toan. |
X | |
|
Khi bảo quản nước cường toan cần bảo quản trong bình thủy tinh không có nắp đậy, vì khí sinh ra có thể tích tụ và tạo áp suất làm bình chứa bị vỡ. |
X | |
|
Cho phương trình hóa học sau: Pt + HNO3 + HCl → H2PtCl6 + H2O + NO2↑ Sau khi cân bằng, tổng hệ số tối giản của các chất trong phản ứng này là 18. |
X |
Giải thích
1. Đúng, vì:
Sodium bicarbonate và sodium hydroxide đều có tính base, tham gia phản ứng trung hòa được với nước cường toan có tính acid.
2. Sai, vì: Al, Fe và Cr đều tham gia phản ứng được với nước cường toan.
3. Đúng, vì: khi trộn hydrochloric acid đậm đặc (HCl) với nitric acid đậm đặc (HNO3) để thu được nước cường toan, xảy ra phản ứng:
2HNO3(aq) + 6HCl(aq) + O2(g) → 2NO2(g)↑ + 4H2O(l) + 3Cl2(g)↑
4. Sai, vì: Phương trình phản ứng sau khi cân bằng như sau:
Pt + 4HNO3 + 6HCl → H2PtCl6 + 4H2O + 4NO2↑
Tổng hệ số tối giản của phương trình này là 20.
Câu 49:
Điền số thích hợp vào chỗ trống
Hòa tan hoàn toàn 24,3 gam silver trong hỗn hợp 1 thể tích HNO3 đặc và 3 thể tích HCl đặc thu được V lít một chất khí không màu, hóa nâu trong không khí (ở đktc). Giá trị của V là (1) _____ lít.
 Xem đáp án
Xem đáp án
Đáp án
Hòa tan hoàn toàn 24,3 gam silver trong hỗn hợp 1 thể tích HNO3 đặc và 3 thể tích HCl đặc thu được V lít một chất khí không màu, hóa nâu trong không khí (ở đktc). Giá trị của V là (1) 1,68 lít.
Giải thích
Số mol silver tham gia phản ứng là: 24,3:108 = 0,225 mol
Theo phương trình phản ứng:
3Ag + HNO3 + 3HCl → 3AgCl↓ + 2H2O + NO↑
0,225 → 0,075(mol)
Giá trị của V là: 0,075.22,4 = 1,68 lít.
Câu 50:
Kéo thả ô vuông vào vị trí thích hợp: 1:2, 4:1, 2:3
Tỉ lệ về thể tích của hydrochloric acid đậm đặc và nitric acid đậm đặc cần dùng để pha chế nước cường toan là _______.
 Xem đáp án
Xem đáp án
Đáp án
Tỉ lệ về thể tích của hydrochloric acid đậm đặc và nitric acid đậm đặc cần dùng để pha chế nước cường toan là 4:1.
Giải thích
Theo đoạn văn “Nitric acid đậm đặc có khối lượng riêng khoảng 1,44 g/ml, trong khi hydrochloric acid đậm đặc có khối lượng riêng khoảng 1,2 g/ml. Vì phản ứng cần tỉ lệ HCl : HNO3 là 3 : 1, điều này có nghĩa là cần tối thiểu 3,6 ml hydrochloric acid đậm đặc cho mỗi 1 ml nitric acid đậm đặc. Tỉ lệ này có thể được tăng lên đến 4:1 để bù cho sự thất thoát do bay hơi của nitric acid đậm đặc.”
Do đó, tỉ lệ về thể tích của hydrochloric acid đậm đặc và nitric acid đặc dùng để pha chế nước cường toan là 4 : 1.
Câu 51:
Điền công thức hóa học hoặc số thích hợp vào chỗ trống
Hòa tan hoàn toàn 29,125 gam muối sulfide của kim loại X trong dung dịch nước cường toan thu được muối X(II) chloride, 4 gam chất rắn màu vàng và V lít chất khí không màu, hóa nâu trong không khí (ở đktc). Công thức của muối sulfide ban đầu là (1) ______ và giá trị của V là (2)_______ lít (làm tròn kết quả đến phần thập phân thứ ba)
 Xem đáp án
Xem đáp án
Đáp án
Hòa tan hoàn toàn 29,125 gam muối sulfide của kim loại X trong dung dịch nước cường toan thu được muối X(II) chloride, 4 gam chất rắn màu vàng và V lít chất khí không màu, hóa nâu trong không khí (ở đktc). Công thức của muối sulfide ban đầu là (1) _HgS _ và giá trị của V là (2) __1,867_ lít (làm tròn kết quả đến phần thập phân thứ ba)
Giải thích
Chất rắn màu vàng thu được là S và chất khí không màu hóa nâu trong không khí là NO.
Ta có phương trình phản ứng:
3XS + 2HNO3 + 6HCl → 3XCl2 + 3S + 2NO↑ + 4H2O
Số mol S thu được là: nS = 4:32 = 0,125 mol
3XS + 2HNO3 + 6HCl → 3XCl2 + 3S + 2NO↑ + 4H2O
0,125 ← 0,125 → \(\frac{1}{{12}}\) (mol)
\[ \to {M_{XS}} = \frac{{29,125}}{{0,125}} = 233 \to {M_X} = 233 - 32 = 201\,\,\left( {g/mol} \right)\]
→ X là Hg
→ Công của muối sulfide là HgS
VNO = 22,4.\(\frac{1}{{12}}\)≈ 1,867 lít.
Câu 52:
 Xem đáp án
Xem đáp án
Khi cho silver phản ứng với nước cường toan thì thu được hiện tượng: xuất hiện kết tủa trắng và có khí không màu hóa nâu trong không khí thoát ra.
Phương trình phản ứng:
3Ag + HNO3 + 3HCl → 3AgCl↓ + 2H2O + NO↑
Chọn B
Câu 53:
Cho các phát biểu sau:
(1) Nước cường toan được sử dụng để tinh chế một số kim loại quý như gold, platinum.
(2) Có thể bảo quản nước cường toan trong thời gian dài.
(3) Khi bị cường toan tiếp xúc với da, hãy trung hòa bằng dung dịch sodium hydroxide và rửa lại nhiều lần với nước.
(4) Nước cường toan cũng được sử dụng trong phòng thí nghiệm để làm sạch dụng cụ thí nghiệm bằng thủy tinh.
Số phát biểu đúng là
 Xem đáp án
Xem đáp án
Giải thích
Các phát biểu đúng là: (1) và (4).
(2) sai, vì: nước cường toan không ổn định, nên được sử dụng ngay.
(3) sai, vì: sodium hydroxide có tính base mạnh, có thể gây ăn mòn da nên không khuyến khích sử dụng để trung hòa nước cường toan.
Chọn B
Câu 54:
Theo hình vẽ, tốc độ trung bình của sóng có biên độ/độ căng cao gần nhất với giá trị nào sau đây?
 Xem đáp án
Xem đáp án
Dựa vào hình vẽ, ta có:
+ Tại t1 = 0,5s ứng với s1 ≈ 0,55 m
+ Tại t2 = 3,5s ứng với s2 ≈ 3,85 m
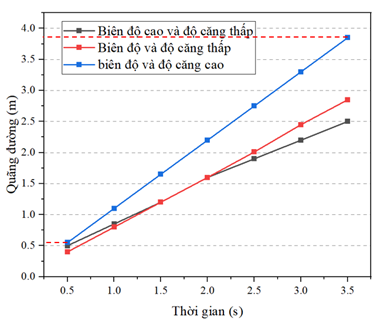
Tốc độ trung bình: \[{v_{tb}} = \frac{s}{t} = \frac{{{s_2} - {s_1}}}{{{t_2} - {t_1}}} = \frac{{3,85 - 0,55}}{{3,5 - 0,5}} = 1,1\;\]m/s.
Chọn D
Câu 55:
Điền từ/cụm từ thích hợp vào chỗ trống.
Khi so sánh sự ảnh hưởng của lực căng của lò xo thì có thể kết luận rằng khi lực căng của lò xo tăng dẫn đến (1) ______ tăng.
 Xem đáp án
Xem đáp án
Đáp án
Khi so sánh sự ảnh hưởng của lực căng của lò xo thì có thể kết luận rằng khi lực căng của lò xo tăng dẫn đến (1) tốc độ truyền sóng tăng.
Giải thích
Dựa vào Hình 2.
Khi so sánh đồ thị quãng đường – thời gian với hai trường hợp sóng có biên độ/độ cứng cao và biên độ cao/ độ cứng thấp ta thấy rằng độ dốc của đồ thị trong trường hợp biên độ/độ cứng cao lớn hơn. Hay nói cách khác trong trường hợp sóng có biên độ/độ cứng cao thì quãng đường sóng truyền đi được trong một đơn vị thời gian là lớn hơn.
Câu 56:
Phát biểu nào sau đây là đúng hoặc sai?
Sóng truyền trong trường hợp biên độ và độ căng thấp thì tốc độ truyền sóng được duy trì không đổi.
 Xem đáp án
Xem đáp án
Đồ thị biểu diễn mối liên hệ quãng đường – thời gian sóng truyền trong trường hợp biên độ và độ căng thấp là đường thẳng. Vậy với mỗi quãng đường đi được trong 0,1 s là như nhau nên tốc độ không đổi và được duy trì.
Chọn A
Câu 57:
Điền số từ thích hợp vào chỗ trống.
Sóng truyền trên lò xo có bước sóng là (1) ______ m.
 Xem đáp án
Xem đáp án
Đáp án
Sóng truyền trên lò xo có bước sóng là (1) __1,6__ m.
Giải thích
Dựa theo Hình 1, ta thấy trong đoạn từ 0 đến 10 m tương ứng với
\( \to 6,25\lambda = 10 \to \lambda = \frac{{10}}{{6,25}} = 1,6\;{\rm{m}}{\rm{.}}\)
Câu 58:
Vì âm thanh cũng có tính chất giống như sóng nên dựa vào kết quả trên Hình 1 và Hình 2, người ta có thể suy ra rằng âm thanh lớn
 Xem đáp án
Xem đáp án
Dựa trên Hình 1 và Hình 2, ta có biên độ sóng không ảnh hưởng đến tốc độ truyền sóng
→ Âm thanh phát ra lớn và âm thanh phát ra nhỏ trong cùng một môi trường truyền sóng thì có tốc độ bằng nhau.
Chọn A
Câu 59:
Lúc t = 0 đầu O của lò xo căng nằm ngang bắt đầu dao động đi lên biên độ A, chu kì 1 s. Hai điểm gần nhau nhất trên lò xo dao động ngược pha cách nhau 3 cm. Thời điểm đầu tiên để M cách O một khoảng 12 cm đang đi xuống qua vị trí cân bằng là (1) _______ s.
 Xem đáp án
Xem đáp án
Đáp án
Lúc t = 0 đầu O của lò xo căng nằm ngang bắt đầu dao động đi lên biên độ A, chu kì 1 s. Hai điểm gần nhau nhất trên lò xo dao động ngược pha cách nhau 3 cm. Thời điểm đầu tiên để M cách O một khoảng 12 cm đang đi xuống qua vị trí cân bằng là (1) __2,5__ s.
Giải thích
Bước sóng: \(\lambda = 6\;{\rm{cm}} \to \) tốc độ truyền sóng là: \({\rm{v}} = v = \frac{\lambda }{T} = \frac{6}{1} = 6\;{\rm{cm}}/{\rm{s}}\)
Khoảng thời gian để \(M\) nhận sóng (bắt đầu đi lên) từ nguồn O là: \(\Delta t = \frac{{OM}}{v} = \frac{{12}}{6} = 2s\)
Khoảng thời gian điểm \({\rm{M}}\) từ lúc nhận sóng (bắt đầu dao động đi lên) đến khi qua VTCB đi xuống là: \(\frac{T}{2} = \frac{1}{2}\;{\rm{s}}\)
Thời điểm cần tìm là: \(t' = \Delta t + \frac{T}{2} = 2 + \frac{1}{2} = 2,5\;{\rm{s}}\).
Câu 60:
Trong không gian \(Oxyz\), cho điểm \(I\left( {1;2; - 2} \right)\) và mặt phẳng \(\left( P \right):2x + 2y + z + 5 = 0\). Mặt cầu \(\left( S \right)\) có tâm \(I\) cắt mặt phẳng \(\left( P \right)\) theo một đường tròn có chu vi bằng \(8\pi \).
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
ĐÚNG |
SAI |
|
Bán kính mặt cầu \(\left( S \right)\) bằng 3 . |
¡ |
¡ |
|
Mặt cầu \(\left( S \right)\) tiếp xúc với mặt phẳng có phương trình \(2x + 2y + z + 11 = 0\). |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Bán kính mặt cầu \(\left( S \right)\) bằng 3 . |
¡ |
¤ |
|
Mặt cầu \(\left( S \right)\) tiếp xúc với mặt phẳng có phương trình \(2x + 2y + z + 11 = 0\). |
¤ |
¡ |
Giải thích
Gọi \(H\) là hình chiếu của \(I\) trên mặt phẳng \(\left( P \right)\).
Ta có \(IH = d\left( {I,\left( P \right)} \right) = \frac{{\left| {2.1 + 2.2 + 1.\left( { - 2} \right) + 5} \right|}}{{\sqrt {{2^2} + {2^2} + {1^2}} }} = 3\).
Gọi \(r\) là bán kính đường tròn và \(R\) là bán kính mặt cầu.
Ta có chu vi đường tròn là \(2\pi r = 8\pi \Rightarrow r = 4\).
Bán kính mặt cầu là \(R = \sqrt {I{H^2} + {r^2}} = \sqrt {{3^2} + {4^2}} = 5\).
Gọi \(\left( \alpha \right):2x + 2y + z + 11 = 0\).
Ta có \(d\left( {I,\left( \alpha \right)} \right) = \frac{{\left| {2.1 + 2.2 + 1.\left( { - 2} \right) + 11} \right|}}{{\sqrt {{2^2} + {2^2} + {1^2}} }} = 5 = R\).
\( \Rightarrow \left( S \right)\) tiếp xúc với \(\left( \alpha \right)\).
Câu 61:
Cho hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} - 3x + 2}}{{\left| {x - 1} \right|}}\,\,khi\,\,x \ne 1\\a\,\,khi\,\,x = 1\end{array} \right.\) .
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
ĐÚNG |
SAI |
|
Với \(a = 1\) hàm số liên tục trái tại \(x = 1\). |
¡ |
¡ |
|
Với \(a = 1\) hàm số liên tục phải tại \(x = 1\). |
¡ |
¡ |
|
Với \(a = \pm 1\) hàm số liên tục tại \(x = 1\). |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Với \(a = 1\) hàm số liên tục trái tại \(x = 1\). |
¤ |
¡ |
|
Với \(a = 1\) hàm số liên tục phải tại \(x = 1\). |
¡ |
¤ |
|
Với \(a = \pm 1\) hàm số liên tục tại \(x = 1\). |
¡ |
¤ |
Giải thích
Ta có: \(f(x) = \left\{ \begin{array}{l}x - 2\,\,khi\,\,x > 1\\a\,\,khi\,\,x = 1\\2 - x\,\,khi\,\,x < 1{\rm{\;}}\end{array} \right.\)
a) Để \(f\left( x \right)\) liên tục trái tại \(x = 1 \Leftrightarrow \mathop {{\rm{lim}}}\limits_{x \to {1^ - }} f\left( x \right)\) tồn tại và \(\mathop {{\rm{lim}}}\limits_{x \to {1^ - }} f\left( x \right) = f\left( 1 \right)\).
Ta có: \(\mathop {{\rm{lim}}}\limits_{x \to {1^ - }} f\left( x \right) = \mathop {{\rm{lim}}}\limits_{x \to {1^ - }} \left( {2 - x} \right) = 1\) và \(f\left( 1 \right) = a\).
Vậy với \(a = 1\) hàm số liên tục trái tại \(x = 1\).
b) Để \(f\left( x \right)\) liên tục phải tại \(x = 1 \Leftrightarrow \mathop {{\rm{lim}}}\limits_{x \to {1^ + }} f\left( x \right)\) tồn tại và \(\mathop {{\rm{lim}}}\limits_{x \to {1^ + }} f\left( x \right) = f\left( 1 \right)\).
Ta có: \(\mathop {{\rm{lim}}}\limits_{x \to {1^ + }} f\left( x \right) = \mathop {{\rm{lim}}}\limits_{x \to {1^ + }} \left( {x - 2} \right) = - 1\) và \(f\left( 1 \right) = a\).
Vậy với \(a = - 1\) hàm số liên tục phải tại \(x = 1\).
c) Do \(\mathop {{\rm{lim}}}\limits_{x \to {1^ - }} f\left( x \right) \ne \mathop {{\rm{lim}}}\limits_{x \to {1^ + }} f\left( x \right)\) nên hàm số không liên tục tại \(x = 1\).
Câu 62:
Điền các số nguyên dương thích hợp vào những chỗ trống.
Cho bảng ô vuông sau:
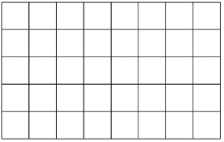
Số hình chữ nhật có trên hình là: (1) _________.
Số hình vuông có trên hình là: (2) _________.
 Xem đáp án
Xem đáp án
Số hình chữ nhật có trên hình là: (1) ___540__.
Số hình vuông có trên hình là: (2) ___100___.
Giải thích
Cứ hai đường kẻ ngang phân biệt và 2 đường kẻ dọc phân biệt cho ta một hình chữ nhật. Vậy số hình chữ nhật là: \(C_9^2 \times C_6^2 = 540\).
Số hình vuông là: \(8 \times 5 + 7 \times 4 + 6 \times 3 + 5 \times 2 + 4 \times 1 = 100\).
Câu 63:
Một nhà bán buôn cung cấp sản phẩm cho 10 cửa hàng bán lẻ, mỗi cửa hàng đặt hàng độc lập và có cùng xác suất đặt hàng trong một ngày là 0,4 . Trong một ngày, nhà bán buôn đó cung cấp sản phẩm cho bao nhiêu cửa hàng bán lẻ để xác suất nhà buôn cung cấp sản phẩm cho các cửa hàng là lớn nhất?
 Xem đáp án
Xem đáp án
Xác suất bán cho \(k\) cửa hàng trong một ngày là \(C_{10}^k.{(0,4)^k}.{(0,6)^{10 - k}}\).
Thử lần lượt các giá trị của \(k\), thì giá trị lớn nhất đạt tại \(k = 4\).
Câu 64:
Có bao nhiêu số tự nhiên có 3 chữ số có dạng \(\overline {abc} \) thỏa mãn \(a,b,c\) là độ dài 3 cạnh của một tam giác cân?
 Xem đáp án
Xem đáp án
Gọi độ dài cạnh bên và cạnh đáy của tam giác cân là \(x,y\) (thỏa mãn \(x,y\) là các chữ số)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{1 \le x \le 9}\\{1 \le y \le 9}\\{1 \le y < 2x}\end{array}} \right.\)
TH1: \(\left\{ {\begin{array}{*{20}{l}}{1 \le y \le 9}\\{5 \le x \le 9}\end{array} \Rightarrow } \right.\) có \(9.5 = 45\) cặp số \(\left( {x;y} \right)\).
TH2: \(\left\{ {\begin{array}{*{20}{l}}{1 \le x \le 4}\\{x = i}\\{1 \le y \le 2i - 1}\end{array}} \right.\)
Với mỗi giá trị của \(i\) có \(2i - 1\) cặp số thỏa mãn, do đó ta có:
\(\left( {2.1 - 1} \right) + \left( {2.2 - 1} \right) + \left( {2.3 - 1} \right) + \left( {2.4 - 1} \right) = 16\) cặp số \(\left( {x;y} \right)\)
Suy ra có 61 cặp số \(\left( {x;y} \right)\) mà với mỗi cặp, ta có thể viết số có 3 chữ số trong đó có 2 chữ số \(x\) và 1
chữ số \(y\). Trong 61 cặp số này có:
+ 9 cặp \(x = y\) thì viết được 9 số.
+ 52 cặp \(x \ne y\) thì mỗi cặp viết được 3 số \(\left( {\overline {xxy} ,\overline {xyx} ,\overline {yxx} } \right)\) nên có \(52.3 = 156\) số.
Vậy tất cả viết được 165 số.
Câu 65:
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Gọi \(K\) là một điểm thuộc cạnh \(DD'\) (\(K\) khác \(D\) và \(D'\)) sao cho khoảng cách giữa hai đường thẳng \(CK\) và \(A'D\) bằng \(\frac{a}{3}\). Tỉ số \(\frac{{DK}}{{DD'}}\) bằng
(1) __________.
 Xem đáp án
Xem đáp án
Đáp án: “1/2”
Giải thích
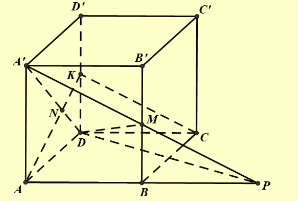
Đặt \(\frac{{DK}}{{DD'}} = x\).
Gọi \(M\) là điểm thuộc cạnh \(BB'\) sao cho \(\frac{{B'M}}{{B'B}} = x\).
Ta có \(A'M//KC\) nên \(d\left( {CK;A'D} \right) = d\left( {CK;\left( {A'MD} \right)} \right) = d\left( {K;\left( {A'MD} \right)} \right)\).
Gọi \(N = AK \cap A'D;P = AB \cap A'M\). Khi đó \(\frac{{d\left( {K;\left( {A'MD} \right)} \right)}}{{d\left( {A;\left( {A'MD} \right)} \right)}} = \frac{{NK}}{{NA}} = \frac{{DK}}{{AA'}} = x\).
Suy ra \(d\left( {CK;A'D} \right) = x.d\left( {A;\left( {A'MD} \right)} \right) = x.d\left( {A;\left( {A'DP} \right)} \right)\).
\(\frac{{A'B'}}{{BP}} = \frac{{B'M}}{{BM}} = \frac{x}{{1 - x}}\) suy ra \(BP = \frac{{A'B'\left( {1 - x} \right)}}{x} = \frac{{a\left( {1 - x} \right)}}{x}\) nên \(AP = BP + AB = \frac{{a\left( {1 - x} \right)}}{x} + a = \frac{a}{x}\).
Tứ diện \(A.A'DP\) vuông tại \(A\) nên \(\frac{1}{{{d^2}\left( {A;\left( {A'DP} \right)} \right)}} = \frac{1}{{A'{A^2}}} + \frac{1}{{A{D^2}}} + \frac{1}{{A{P^2}}} = \frac{{{x^2} + 2}}{{{a^2}}}\)
Suy ra \(d\left( {A;\left( {A'DP} \right)} \right) = \frac{a}{{\sqrt {{x^2} + 2} }}\). Do đó \(d\left( {CK;A'D} \right) = \frac{{ax}}{{\sqrt {{x^2} + 2} }}\)
Mà \(d\left( {CK;A'D} \right) = \frac{a}{3}\) suy ra \(\frac{x}{{\sqrt {{x^2} + 2} }} = \frac{1}{3}\). Giải phương trình này thu được \(x = \frac{1}{2}\).
Vậy \(\frac{{DK}}{{DD'}} = \frac{1}{2}\).
Câu 66:

Cho hàm số \(y = \frac{{{\rm{sin}}x}}{{1 + {\rm{cos}}x}} + \frac{1}{{1 - {\rm{cos}}x}} + {\rm{cot}}x\left( C \right)\). Số giao điểm của đồ thị hàm số \(\left( C \right)\) với đường thẳng \(y = 2\) trên đọan \(\left[ { - \pi ;\pi } \right]\) là _______, trong đó điểm có hoành độ \(\frac{{\pi a}}{b}\) với \(a = \)_______,\(b = \) _______\((a,b \in \mathbb{Z};b > 0;\left( {a;b} \right) = 1)\)nằm gần trục tung nhất.
 Xem đáp án
Xem đáp án
Cho hàm số \(y = \frac{{{\rm{sin}}x}}{{1 + {\rm{cos}}x}} + \frac{1}{{1 - {\rm{cos}}x}} + {\rm{cot}}x\left( C \right)\). Số giao điểm của đồ thị hàm số \(\left( C \right)\) với đường thẳng \(y = 2\) trên đọan \(\left[ { - \pi ;\pi } \right]\) là 3 , trong đó điểm có hoành độ \(\frac{{\pi a}}{b}\) với \(a = \)-1 ,\(b = \) 4 \((a,b \in \mathbb{Z};b > 0;\left( {a;b} \right) = 1)\)nằm gần trục tung nhất.
Giải thích
Điều kiện xác định của hàm số \(\left( C \right):\left( {\begin{array}{*{20}{c}}{{\rm{cos}}x \ne \pm 1}\\{{\rm{sin}}x \ne 0}\end{array}} \right) \Leftrightarrow x \ne k\pi \left( {k, \in ,\mathbb{Z}} \right)\).
Xét phương trình hoành độ giao điểm:
\(\frac{{{\rm{sin}}x}}{{1 + {\rm{cos}}x}} + \frac{1}{{1 - {\rm{cos}}x}} + {\rm{cot}}x = 2\,\,\left( * \right)\)
\( \Leftrightarrow \frac{{{\rm{sin}}x\left( {1 - {\rm{cos}}x} \right) + 1 + {\rm{cos}}x}}{{{\rm{si}}{{\rm{n}}^2}x}} + \frac{{{\rm{cos}}x}}{{{\rm{sin}}x}} = 2\)
\( \Rightarrow {\rm{sin}}x - {\rm{sin}}x{\rm{cos}}x + 1 + {\rm{cos}}x + {\rm{sin}}x{\rm{cos}}x = 2{\rm{si}}{{\rm{n}}^2}x\)
\( \Leftrightarrow {\rm{sin}}x + {\rm{cos}}x + 1 - 2{\rm{si}}{{\rm{n}}^2}x = 0\)
\( \Leftrightarrow {\rm{sin}}x + {\rm{cos}}x + {\rm{cos}}2x = 0\)
\( \Leftrightarrow \left( {{\rm{sin}}x + {\rm{cos}}x} \right)\left( {1 + {\rm{cos}}x - {\rm{sin}}x} \right) = 0\)
\( \Leftrightarrow \left( {\begin{array}{*{20}{c}}{\sin x + \cos x = 0}\\{1 + \cos x - \sin x = 0}\end{array}} \right) \Leftrightarrow \left( {\begin{array}{*{20}{c}}{\tan x = - 1}\\{\sin \left( {x, - ,\frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}}\end{array}} \right) \Leftrightarrow \left( {\begin{array}{*{20}{c}}{x = - \frac{\pi }{4} + k\pi (t,m)}\\{x = \frac{\pi }{2} + k2\pi (t,m)}\\{x = \pi + k2\pi (L)}\end{array}} \right)(k, \in ,\mathbb{Z})\)
Xét \( - \pi \le - \frac{\pi }{4} + k\pi \le \pi \Leftrightarrow - \frac{3}{4} \le k \le \frac{5}{4} \Leftrightarrow k \in \left\{ {0;1} \right\}\).
Xét \( - \pi \le \frac{\pi }{2} + k2\pi \le \pi \Leftrightarrow - \frac{3}{4} \le k \le \frac{1}{4} \Leftrightarrow k = 0\).
Vậy có 3 nghiệm của (*) trên \(\left[ { - \pi ;\pi } \right]\) hay số giao điểm của đồ thị hàm số \(\left( C \right)\) với đường thẳng \(y = 2\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) là 3 , trong đó điểm có hoành độ \(\frac{{ - \pi }}{4}\) nằm gần trục tung nhất \( \Rightarrow a = - 1;{\rm{\;}}b = 4\).
Câu 67:
Cho \(x,y\) là các số thực dương thỏa mãn \({\rm{lo}}{{\rm{g}}_{2023}}\left( {17x} \right) + {\rm{lo}}{{\rm{g}}_{2023}}\left( {119y} \right) - 1 \ge {\rm{lo}}{{\rm{g}}_{2023}}\left( {{x^2} + y + 1} \right)\). Giá trị nhỏ nhất của biểu thức \(x + y\) bằng (1) ________.
 Xem đáp án
Xem đáp án
Đáp án: “7”
Giải thích
Ta có:
\({\rm{lo}}{{\rm{g}}_{2023}}\left( {17x} \right) + {\rm{lo}}{{\rm{g}}_{2023}}\left( {119y} \right) - 1 \ge {\rm{lo}}{{\rm{g}}_{2023}}\left( {{x^2} + y + 1} \right)\)
\( \Leftrightarrow {\rm{lo}}{{\rm{g}}_{2023}}\left( {17x} \right) + {\rm{lo}}{{\rm{g}}_{2023}}\left( {119y} \right) + {\rm{lo}}{{\rm{g}}_{2023}}\frac{1}{{2023}} \ge {\rm{lo}}{{\rm{g}}_{2023}}\left( {{x^2} + y + 1} \right)\)
\( \Leftrightarrow {\rm{lo}}{{\rm{g}}_{2023}}\left( {17x.119y.\frac{1}{{2023}}} \right) \ge {\rm{lo}}{{\rm{g}}_{2023}}\left( {{x^2} + y + 1} \right)\)
\( \Leftrightarrow xy \ge {x^2} + y + 1\)
\( \Leftrightarrow y\left( {x - 1} \right) \ge {x^2} + 1\)
\( \Leftrightarrow y \ge \frac{{{x^2} + 1}}{{x - 1}}\) (vì \(y > 0,y\left( {x - 1} \right) \ge {x^2} + 1 > 0\) nên \(x - 1 > 0\))
\( \Rightarrow x + y \ge x + \frac{{{x^2} + 1}}{{x - 1}}\forall x > 1;y > 0\).
Khi đó bài toán đã cho trở thành: Tìm giá trị nhỏ nhất của \(x + \frac{{{x^2} + 1}}{{x - 1}}\) với \(x > 1\).
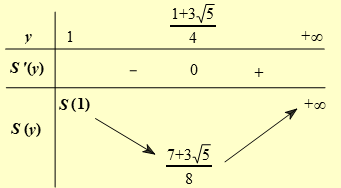
Ta có: \(x + \frac{{{x^2} + 1}}{{x - 1}} = \frac{{{x^2} - x + {x^2} + 1}}{{x - 1}} = \frac{{2{x^2} - x + 1}}{{x - 1}} = f\left( x \right)\).
\( \Rightarrow f'\left( x \right) = \frac{{2{x^2} - 4x}}{{{{(x - 1)}^2}}};f'\left( x \right) = 0 \Leftrightarrow x = 2\) (vì \(x > 1\)).
Ta có: \(\mathop {{\rm{lim}}}\limits_{x \to {1^ + }} f\left( x \right) = \mathop {{\rm{lim}}}\limits_{x \to {1^ + }} \frac{{2{x^2} - x + 1}}{{x - 1}} = + \infty ,f\left( 2 \right) = \frac{{{{2.2}^2} - 2 + 1}}{{2 - 1}} = 7\),
\(\mathop {{\rm{lim}}}\limits_{x \to + \infty } f\left( x \right) = \mathop {{\rm{lim}}}\limits_{x \to + \infty } \frac{{2{x^2} - x + 1}}{{x - 1}} = + \infty \).
Do đó \(\mathop {{\rm{min}}}\limits_{\left( {1; + \infty } \right)} f\left( x \right) = f\left( 2 \right) = 7\).
Vậy giá trị nhỏ nhất của \(x + y\) là 7 .
Câu 68:
Một chất điểm chuyển động với quãng đường được cho bởi công thức \(s\left( t \right) = \frac{1}{4}{t^4} - {t^3} + \frac{5}{2}{t^2} + 10t\), trong đó thời gian \(t\) được tính bằng giây \(\left( s \right)\) và quãng đường \(s\) được tính bằng mét \(\left( m \right)\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Tại thời điểm \(t = 3\), chất điểm chuyển động với gia tốc bằng _______ m/s2.
Tại thời điểm \(t = 2\), chất điểm chuyển động với vận tốc bằng _______ m/s.
Vận tốc chuyển động của chất điểm tại thời điểm chất điểm có gia tốc chuyển động nhỏ nhất bằng _______ m/s.
 Xem đáp án
Xem đáp án
Tại thời điểm \(t = 3\), chất điểm chuyển động với gia tốc bằng 14 m/s2.
Tại thời điểm \(t = 2\), chất điểm chuyển động với vận tốc bằng 16 m/s.
Vận tốc chuyển động của chất điểm tại thời điểm chất điểm có gia tốc chuyển động nhỏ nhất bằng 13 m/s.
Giải thích
Gọi \(v\left( t \right),a\left( t \right)\) lần lượt là vận tốc và gia tốc của chất điểm.
Theo ý nghĩa hình học của đạo hàm, ta suy ra \(\left\{ {\begin{array}{*{20}{c}}{v\left( t \right) = s'\left( t \right) = {t^3} - 3{t^2} + 5t + 10}\\{a\left( t \right) = v'\left( t \right) = 3{t^2} - 6t + 5}\end{array}} \right.\).
Tại thời điểm \(t = 3\), chất điểm chuyển động với gia tốc bằng
\(a\left( 3 \right) = {3.3^2} - 6.3 + 5 = 14\left( {{\rm{m}}/{{\rm{s}}^2}} \right)\).
Tại thời điểm \(t = 2\), chất điểm chuyển động với vận tốc bằng
\(v\left( 2 \right) = {2^3} - {3.2^2} + 5.2 + 10 = 16\left( {{\rm{m}}/{\rm{s}}} \right)\).
Ta có: \(a\left( t \right) = 3{t^2} - 6t + 5 = 3{(t - 1)^2} + 2 \ge 2\) với mọi \(t\), dấu "=" xảy ra khi chỉ khi \(t = 1\).
Suy ra gia tốc chuyển động của chất điểm nhỏ nhất bằng 2 khi \(t = 1\).
Vận tốc chuyển động của chất điểm tại thời điểm gia tốc nhỏ nhất là
\(v\left( 1 \right) = {1^3} - {3.1^2} + 5.1 + 10 = 13\left( {{\rm{m}}/{\rm{s}}} \right)\).
Câu 69:
Cho khối chóp \(S.ABC\) có đáy là tam giác đều, \(SA \bot \left( {ABC} \right),SC = a\sqrt 3 \) và \(SC\) hợp với đáy một góc \({30^ \circ }\).
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
ĐÚNG |
SAI |
|
Chiều cao của khối chóp bằng \(\frac{{a\sqrt 3 }}{2}\). |
¡ |
¡ |
|
Độ dài mỗi cạnh của tam giác \(ABC\) bằng \(\frac{a}{3}\). |
¡ |
¡ |
|
Thể tích của khối chóp là \(\frac{{9{a^3}}}{{32}}\). |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Chiều cao của khối chóp bằng \(\frac{{a\sqrt 3 }}{2}\). |
¤ |
¡ |
|
Độ dài mỗi cạnh của tam giác \(ABC\) bằng \(\frac{a}{3}\). |
¡ |
¤ |
|
Thể tích của khối chóp là \(\frac{{9{a^3}}}{{32}}\). |
¤ |
¡ |
Giải thích
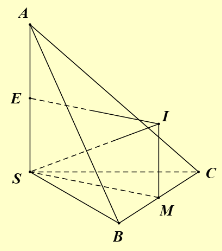
Ta có: \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AC\).
\(SC\) hợp với đáy một góc \({30^ \circ } \Rightarrow \widehat {SCA} = {30^ \circ }\).
Xét vuông tại \(A\) có: \({\rm{sin}}{30^ \circ } = \frac{{SA}}{{SC}} \Rightarrow SA = \frac{{a\sqrt 3 }}{2},AC = \sqrt {S{C^2} - S{A^2}} = \frac{{3a}}{2}\).
Tam giác \(ABC\) đều cạnh \(AC = \frac{{3a}}{2}\) nên \({S_{ABC}} = {\left( {\frac{{3a}}{2}} \right)^2}.\frac{{\sqrt 3 }}{4} = \frac{{9\sqrt 3 {a^2}}}{{16}}\) (đvdt).
Thể tích khối chóp \(S.ABC\) là: \({V_{S.ABC}} = \frac{1}{3}SA.{S_{ABC}} = \frac{1}{3}.\frac{{a\sqrt 3 }}{2}.\frac{{9\sqrt 3 {a^2}}}{{16}} = \frac{{9{a^3}}}{{32}}\) (đvtt).
Câu 70:
Cho hàm số \(y = f\left( x \right) = {x^3} + 1\) có đồ thị hàm số là \(\left( C \right)\). Phát biểu nào dưới đây là sai?
 Xem đáp án
Xem đáp án
Ta có: \(f'\left( x \right) = {\left( {{x^3} + 1} \right)^{\rm{'}}} = 3{x^2} \Rightarrow f''\left( x \right) = {\left( {3{x^2}} \right)^{\rm{'}}} = 6x\) và \(f'\left( 2 \right) = {3.2^2} = 12\).
Có: \(f'\left( 1 \right) = {3.1^2} = 3 \Rightarrow \) Hệ số góc của phương trình tiếp tuyến của \(\left( C \right)\) tại điểm \(M\left( {1;1} \right)\) là \(k = f'\left( 1 \right) = 3\).
Câu 71:
Cho khối chóp \(S.ABC\) có ba cạnh \(SA,SB,SC\) bằng nhau và đôi một vuông góc.
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
ĐÚNG |
SAI |
|
Thể tích khối chóp \(S.ABC\) là \({V_{S.ABC}} = \frac{1}{3}SA.{S_{ABC}}\). |
¡ |
¡ |
|
Diện tích mặt cầu ngoại tiếp khối chóp \(S.ABC\) là \(S = 3S{A^2}\). |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Thể tích khối chóp \(S.ABC\) là \({V_{S.ABC}} = \frac{1}{3}SA.{S_{ABC}}\). |
¡ |
¤ |
|
Diện tích mặt cầu ngoại tiếp khối chóp \(S.ABC\) là \(S = 3S{A^2}\). |
¤ |
¡ |
Giải thích
Ta có: \({V_{S.ABC}} = \frac{1}{3}SA.{S_{SBC}}\)
Bán kính mặt cầu ngoại tiếp khối chóp \(S.ABC\) là:
\(IS = R = \sqrt {\frac{{S{A^2}}}{4} + M{S^2}} = \sqrt {\frac{{S{A^2}}}{4} + \frac{{B{C^2}}}{4}} = \sqrt {\frac{{S{A^2}}}{4} + \frac{{2S{B^2}}}{4}} = \frac{{SA\sqrt 3 }}{2}\).
Khi đó, diện tích mặt cầu ngoại tiếp khối chóp \(S.ABC\) là: \(S = 4\pi {R^2} = 3S{A^2}\).
Câu 72:
Cho hàm số \(y = {x^3} - \left( {m - 2} \right){x^2} + 3x - 1\left( C \right)\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:Với \(m = 2\), đồ thị \(\left( C \right)\) có _______ điểm cực trị.
Có _______ giá trị nguyên âm của tham số \(m\) để đồ thị \(\left( C \right)\) cắt trục hoành tại đúng một điểm.
 Xem đáp án
Xem đáp án
Với \(m = 2\), đồ thị \(\left( C \right)\) có 0 điểm cực trị.
Có 1 giá trị nguyên âm của tham số \(m\) để đồ thị \(\left( C \right)\) cắt trục hoành tại đúng một điểm.
Giải thích
Với \(m = 2\) ta có \(:y = {x^3} + 3x - 1 \Rightarrow y' = 3{x^2} + 3 > 0,\forall x \in \mathbb{R}\).
\( \Rightarrow \) Hàm số đã cho không có điểm cực trị.
Phương trình hoành độ giao điểm là : \({x^3} - \left( {m - 2} \right){x^2} + 3x - 1 = 0\,\,\left( {\rm{*}} \right)\).
Vì \(x = 0\) không là nghiệm của phương trình \(\left( {\rm{*}} \right)\) nên ta có :
\(\frac{{{x^3} + 3x - 1}}{{{x^2}}} = m - 2 \Leftrightarrow x + \frac{3}{x} - \frac{1}{{{x^2}}} = m - 2\).
Xét hàm số \(f\left( x \right) = x + \frac{3}{x} - \frac{1}{{{x^2}}} \Rightarrow f'\left( x \right) = 1 - \frac{3}{{{x^2}}} + \frac{2}{{{x^3}}} = \frac{{{x^3} - 3x + 2}}{{{x^3}}}\).
\(f'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = - 2}\end{array}} \right.\).
Bảng biến thiên :
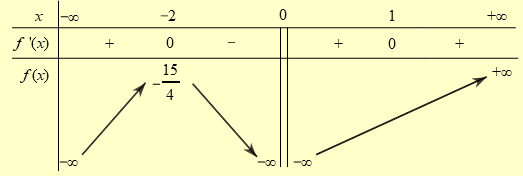
Dựa vào bảng biến thiên, ta thấy \(f\left( x \right) = m - 2\) có nghiệm duy nhất \( \Leftrightarrow m - 2 > - \frac{{15}}{4} \Leftrightarrow m > - \frac{7}{4}\).
Vậy có duy nhất một giá trị nguyên âm của tham số \(m\) để đồ thị hàm số \(\left( C \right)\) cắt trục hoành tại đúng một điểm.
Câu 73:
Cho hình trụ \(\left( T \right)\) có hai hình tròn đáy là \(\left( O \right)\) và \(\left( {O'} \right)\). Xét hình nón \(\left( N \right)\) có đỉnh \(O'\), đáy là hình tròn \(\left( O \right)\) và đường sinh hợp với đáy một góc \(\alpha \). Biết tỉ số giữa diện tích xung quanh hình trụ \(\left( T \right)\) và diện tích xung quanh hình nón \(\left( N \right)\) bằng \(\sqrt 3 \). Tính số đo góc \(\alpha \).
 Xem đáp án
Xem đáp án
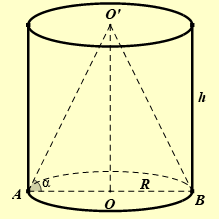
Giả sử hình trụ \(\left( T \right)\) có chiều cao \(h\), bán kính đáy \(R\).
Khi đó \(\left( T \right)\) có \({S_{xq\left( {tru} \right)}} = 2\pi Rh\).
Vì đường sinh hợp với đáy một góc \(\alpha \) nên \(\widehat {O'AO} = \alpha \Rightarrow O'A = \frac{h}{{{\rm{sin}}\alpha }}\).
Diện tích xung quanh hình nón \(\left( N \right):{S_{xq\left( {non} \right)}} = \pi Rl = \pi R\frac{h}{{{\rm{sin}}\alpha }}\).
Tỉ số giữa diện tích xung quanh hình trụ \(\left( T \right)\) và diện tích xung quanh hình nón \(\left( N \right)\) bằng \(\sqrt 3 \).
Suy ra: \(\frac{{{S_{xq}}_{\left( {{\rm{tru\;}}} \right)}}}{{{S_{xq\left( {{\rm{non\;}}} \right)}}}} = \sqrt 3 \Leftrightarrow \frac{{2\pi Rh.{\rm{sin}}\alpha }}{{\pi Rh}} = \sqrt 3 \Leftrightarrow {\rm{sin}}\alpha = \frac{{\sqrt 3 }}{2} \Leftrightarrow \alpha = {60^ \circ }\).
Câu 74:
Điền số tự nhiên vào chỗ trống
Mô đun của số phức \({(3 - 4i)^2}\) là (1) ______.
 Xem đáp án
Xem đáp án
Mô đun của số phức \({(3 - 4i)^2}\) là (1) __25__.
Câu 75:
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, biết \(AB = 2a,AD = a,SA = 3a\) và \(SA\) vuông góc với mặt phẳng đáy. Gọi \(M\) là trung điểm cạnh \(CD\), điểm \(E \in SA\) sao cho \(SE = a\). Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
ĐÚNG |
SAI |
|
Khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {BME} \right)\) bằng \(\frac{{a\sqrt {70} }}{7}\). |
¡ |
¡ |
|
Cosin của góc giữa hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {BME} \right)\) bằng \(\frac{1}{{\sqrt {15} }}\). |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {BME} \right)\) bằng \(\frac{{a\sqrt {70} }}{7}\). |
¡ |
¤ |
|
Cosin của góc giữa hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {BME} \right)\) bằng \(\frac{1}{{\sqrt {15} }}\). |
¤ |
¡ |
Giải thích
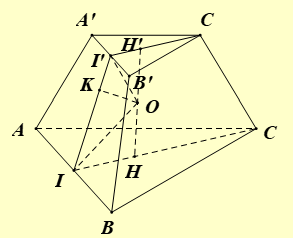
Góc giữa hai mặt phẳng (α) và (β) là góc \(\left\{ {\begin{array}{*{20}{c}}{\frac{1}{a} + \frac{4}{b} + \frac{9}{c} = 1\,\,\,\,\,\,\,\,\,\,\,\,}\\{\frac{1}{a} = \frac{2}{b} = \frac{3}{c}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\{a + b + c = {{(1 + 2 + 3)}^2}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 6}\\\begin{array}{l}b = 12\\c = 18\end{array}\end{array}} \right.\).
Khi đó \(\sin \varphi = \frac{{d(A;\alpha )}}{{d(A;\Delta )}}\).
Gọi \(O = AC \cap BD\).
Gọi điểm \(G\) là trọng tâm , kéo dài tia \(BM\) cắt \(AD\) tại \(F\).
Ta có \(\left( {SAC} \right) \cap \left( {BEF} \right) = EG\)
Khi đó góc giữa hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {BME} \right)\) là góc \(\varphi \) có \({\rm{sin}}\varphi = \frac{{d\left( {A;\left( {BEF} \right)} \right)}}{{d\left( {A;EG} \right)}}\).
Trong \(\left( {SAC} \right)\), kẻ \(AK \bot EG\left( {K \in EG} \right)\).
Ta có: \(AE = SA - SE = 2a;AG = AC - GC = AC - \frac{2}{3}OC = \frac{2}{3}AC = \frac{{2a\sqrt 5 }}{3}\)
\( \Rightarrow d\left( {A,EG} \right) = AK = \frac{{AE.AG}}{{\sqrt {A{E^2} + A{G^2}} }} = \frac{{a\sqrt {70} }}{7}\)
Gọi \(h = d\left( {A;\left( {BEF} \right)} \right)\).
Ta có: \(\frac{{FD}}{{FA}} = \frac{{DM}}{{AB}} = \frac{1}{2} \Rightarrow FA = 2a\)
Vì \(AE,AB,AF\) đôi một vuông góc nên
\(\frac{1}{{{h^2}}} = \frac{1}{{A{E^2}}} + \frac{1}{{A{B^2}}} + \frac{1}{{A{F^2}}} = \frac{1}{{{{(2a)}^2}}} + \frac{1}{{{{(2a)}^2}}} + \frac{1}{{{{(2a)}^2}}} = \frac{3}{{4{a^2}}} \Rightarrow h = \frac{{2a\sqrt 3 }}{3}\)
\( \Rightarrow {\rm{sin}}\varphi = \frac{{d\left( {A;\left( {BEF} \right)} \right)}}{{d\left( {A;EG} \right)}} = \frac{{\sqrt {14} }}{{\sqrt {15} }} \Rightarrow {\rm{cos}}\varphi = \frac{1}{{\sqrt {15} }}\).
Câu 76:
Tập hợp các giá trị của tham số \(m\) để hàm số \(y = {x^3} + 6{x^2} + 3\left( {m + 2} \right)x - m - 1\) đạt cực trị tại các điểm \({x_1}\) và \({x_2}\) thỏa mãn \({x_1} < - 1 < {x_2}\) là
 Xem đáp án
Xem đáp án
Ta có \(y' = 3{x^2} + 12x + 3\left( {m + 2} \right);y' = 0 \Leftrightarrow {x^2} + 4x + m + 2 = 0\,\,\left( {\rm{*}} \right)\).
Hàm số có hai điểm cực trị \({x_1}\) và \({x_2}\) thỏa mãn \({x_1} < - 1 < {x_2} \Leftrightarrow \) phương trình (*) có hai nghiệm phân biệt \({x_1}\) và \({x_2}\) thỏa mãn \(\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right) < 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{\Delta '}} = 4 - \left( {m + 2} \right) > 0}\\{{x_1}{x_2} + {x_1} + {x_2} + 1 < 0}\end{array}} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m < 2}\\{m < 1}\end{array} \Leftrightarrow m < 1} \right.\)
Câu 77:
Cho hình chóp cụt tam giác đều ngoại tiếp một hình cầu có bán kính \(r = \sqrt 3 \). Biết hình chóp cụt có độ dài cạnh đáy lớn gấp đôi độ dài cạnh đáy nhỏ. Thể tích khối chóp cụt bằng
 Xem đáp án
Xem đáp án
Giả sử ta có hình chóp cụt tam giác đều ABC.A′B′C′ như hình vẽ.
\( \Rightarrow \Delta ABC,\Delta A'B'C'\) đều.
Gọi \(H,H'\) lần lượt là tâm đường tròn nội tiếp các tam giác đều \(ABC,A'B'C'\).
\( \Rightarrow HH' \bot \left( {ABC} \right)\) và tâm mặt cầu nội tiếp hình chóp cụt thuộc \(HH'\).
Gọi \(I,I'\) lần lượt là trung điểm cạnh \(AB,A'B'\).
Ta có: \(\left. {\begin{array}{*{20}{c}}{AB \bot CI}\\{AB \bot HH'}\end{array}} \right\} \Rightarrow AB \bot \left( {CHH'} \right) \Rightarrow \left( {ABB'A'} \right) \bot \left( {CII'C'} \right)\)
\( \Rightarrow OK \bot \left( {CII'C'} \right)\)
\( \Rightarrow \) Hình cầu nội tiếp hình chóp cụt \(ABC.A'B'C'\) tiếp xúc với hai mặt phẳng đáy tại \(H,H'\) và tiếp xúc với mặt bên \(\left( {ABB'A'} \right)\) tại điểm \(K \in II'\).
Gọi \(O\) là trung điểm cạnh \(HH'\). Khi đó, \(O\) là tâm mặt cầu nội tiếp hình chóp cụt và \(OK \bot II'\).
\( \Rightarrow OK = r = \sqrt 3 \)
Đặt \(A'B' = x \Rightarrow AB = 2x\). Ta có: \(I'K = I'H = \frac{1}{3}I'C' = \frac{{x\sqrt 3 }}{6};IK = IH = \frac{1}{3}IC = \frac{{x\sqrt 3 }}{3}\)
Ta có: \(\widehat {KIO} = \widehat {HIO};\widehat {KI'H'} = \widehat {H'{I^ \top }O}\) (tính chất hai tiếp tuyến cắt nhau).
\( \Rightarrow \widehat {KIO} + \widehat {KI'O} = {90^ \circ } \Rightarrow \widehat {IOI'} = {90^ \circ }\)
\( \Rightarrow {\rm{\Delta }}IOI'\) vuông tại \(O \Rightarrow O{K^2} = IK.I'K\)
\( \Leftrightarrow 3 = \frac{{x\sqrt 3 }}{3}.\frac{{x\sqrt 3 }}{6} \Leftrightarrow x = 3\sqrt 2 \)
\( \Rightarrow {S_{ABC}} = \frac{{{{(2x)}^2}\sqrt 3 }}{4} = 18\sqrt 3 ;{S_{A'B'C'}} = \frac{{{x^2}\sqrt 3 }}{4} = \frac{{9\sqrt 3 }}{2}\)
Thể tích khối chóp cụt \(ABC.A'B'C'\) là:
\(V = \frac{{HH'}}{3}\left( {{S_{ABC}} + {S_{A'B'C'}} + \sqrt {{S_{ABC}}.{S_{A'B'C'}}} } \right) = 63\)
Câu 78:
Cho 5 đoạn thẳng có độ dài là \(1;2;3;4;5\). Lấy ngẫu nhiên ba đoạn thẳng. Xác suất để độ dài ba đoạn thẳng này là độ dài ba cạnh của một tam giác là (1) _______.
 Xem đáp án
Xem đáp án
Đáp án: “3/10”
Giải thích
Số phần tử của không gian mẫu là: \(n\left( {\rm{\Omega }} \right) = C_5^3 = 10\).
Để độ dài ba đoạn thẳng là độ dài ba cạnh của tam giác thì tổng độ dài hai cạnh lớn hơn độ dài cạnh còn lại.
Do đó, các khả năng xảy ra là bộ các độ dài \(\left\{ {\left( {2;3;4} \right),\left( {2;4;5} \right),\left( {3;4;5} \right)} \right\}\).
Vậy xác suất cần tìm là: \(P = \frac{3}{{10}}\).
Câu 79:
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{\sqrt {2x + 3} - \sqrt {x + 6} }}{{x - 3}}}&{{\rm{\;khi\;\;}}x \ne 3}\\{a + 2}&{{\rm{\;khi\;\;}}x = 3}\end{array}} \right.\). Tổng tất cả các giá trị thực của tham số \(a\) để hàm số liên tục tại \({x_0} = 3\) là
 Xem đáp án
Xem đáp án
Hàm số liên tục tại \(x = 3\) khi \(f\left( 3 \right) = \mathop {\lim }\limits_{x \to 3} f\left( x \right)\).
Ta có \(f\left( 3 \right) = a + 2\);
\(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = \mathop {\lim }\limits_{x \to 3} \frac{{\sqrt {2x + 3} - \sqrt {x + 6} }}{{x - 3}} = \mathop {\lim }\limits_{x \to 3} \frac{{2x + 3 - x - 6}}{{\left( {x - 3} \right)\left( {\sqrt {2x + 3} + \sqrt {x + 6} } \right)}} = \mathop {\lim }\limits_{x \to 3} \frac{1}{{\sqrt {2x + 3} + \sqrt {x + 6} }} = \frac{1}{6}\)
Suy ra \(f\left( 3 \right) = \mathop {\lim }\limits_{x \to 3} f\left( x \right) \Leftrightarrow a + 2 = \frac{1}{6} \Leftrightarrow a = - \frac{{11}}{6}\).
Câu 80:
Điền số nguyên vào chỗ trống
Cho hai số thực \(x,y\) lớn hơn 1 thỏa mãn \({\rm{cos}}\left( {x + y + 1} \right) + 4 = {\rm{cos}}\left( {4xy} \right) + 16xy - 4x - 4y\). Giá trị nhỏ nhất của biểu thức \(S = x\left( {y + 2} \right)\) bằng \(\frac{{a + b\sqrt 5 }}{c}\left( {a,b,c \in \mathbb{R}} \right)\) với \(abc\) bằng (1) _______.
 Xem đáp án
Xem đáp án
Đáp án: “168”
Giải thích
Ta có: \({\rm{cos}}\left( {x + y + 1} \right) + 4 = {\rm{cos}}\left( {4xy} \right) + 16xy - 4x - 4y\)
\( \Leftrightarrow {\rm{cos}}\left( {x + y + 1} \right) + 4\left( {x + y + 1} \right) = {\rm{cos}}\left( {4xy} \right) + 4.4xy\).
Xét hàm \(f\left( t \right) = {\rm{cos}}t + 4t\) với \(t \in \mathbb{R}\). Ta có \(f'\left( t \right) = - {\rm{sin}}t + 4 > 0,\forall t \in \mathbb{R} \Rightarrow f\left( t \right)\) đồng biến trên \(\mathbb{R}\).
Mà \(f\left( {x + y + 1} \right) = f\left( {4xy} \right)\) nên \(x + y + 1 = 4xy \Leftrightarrow x = \frac{{y + 1}}{{4y - 1}}\).
Khi đó \(S = \frac{{\left( {y + 1} \right)\left( {y + 2} \right)}}{{4y - 1}} = \frac{{{y^2} + 3y + 2}}{{4y - 1}}\) với \(y > 1\).
\(S'\left( y \right) = \frac{{4{y^2} - 2y - 11}}{{{{(4y - 1)}^2}}}\).
Bảng biến thiên:
Vậy \({\rm{min}}S = \frac{{7 + 3\sqrt 5 }}{8} \Rightarrow abc = 168\).
Câu 81:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm xác định và liên tục trên \(\mathbb{R}\). Biết đồ thị hàm số \(f'\left( x \right)\) như hình vẽ
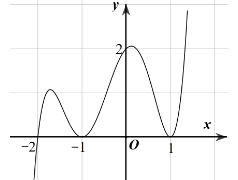
![]()
Hàm số \(y = f\left( x \right)\) có _______ điểm cực trị.
Hàm số \(y = f\left( x \right)\) đạt giá trị nhỏ nhất tại _______.
Hàm số \(y = f\left( x \right) - x\) có _______ điểm cực trị.
 Xem đáp án
Xem đáp án
Hàm số \(y = f\left( x \right)\) có 1 điểm cực trị.
Hàm số \(y = f\left( x \right)\) đạt giá trị nhỏ nhất tại -2 .
Hàm số \(y = f\left( x \right) - x\) có 5 điểm cực trị.
Giải thích
Đồ thị hàm số \(f'\left( x \right)\) cắt (nhưng không tiếp xúc) trục \(Ox\) tại 1 điểm nên hàm số \(y = f\left( x \right)\) có 1 điểm cực trị.
Ta có BBT của hàm số \(y = f\left( x \right)\):
Vậy hàm số \(y = f\left( x \right)\) đạt giá trị nhỏ nhất tại \(x = - 2\).
Hàm số \(y = f\left( x \right) - x\) có \(y' = f'\left( x \right) - 1\).
\(f'\left( x \right) - 1 = 0 \Leftrightarrow f'\left( x \right) = 1\)
Ta thấy đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = f'\left( x \right)\) tại 5 điểm phân biệt. Vậy hàm số \(y = f\left( x \right) - x\) có 5 điểm cực trị.
Câu 82:
Cho hình nón \(\left( N \right)\) có đường cao \(SO = 9\) và bán kính đáy bằng \(R\), gọi \(M\) là điểm trên đoạn \(SO\) sao cho \(OM = x(0 < x < 9)\). Mặt phẳng \(\left( P \right)\) vuông góc với trục \(SO\) tại \(M\) giao với hình nón \(\left( N \right)\) theo thiết diện là đường tròn \(\left( C \right)\). Giá trị của \(x\) bằng (1) ______ để khối nón có đỉnh là điểm \(O\) và đáy là hình tròn \(\left( C \right)\) có thể tích lớn nhất?
 Xem đáp án
Xem đáp án
Đáp án: “3”
Giải thích
Gọi BC là đường kính của \((C)\) và AD là đường kính của đường tròn đáy của \((N)\) sao cho \(BC//AD\). S, A, B thẳng hàng \( \Rightarrow S,C,D\) thẳng hàng.
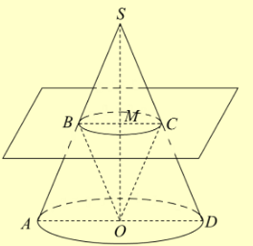
Ta có \(r = BM\) là bán kính đường tròn \(\left( C \right)\).
Vì nên \(\frac{{BM}}{{AO}} = \frac{{SM}}{{SO}} \Leftrightarrow r = \frac{{AO.SM}}{{SO}} \Leftrightarrow r = \frac{{R\left( {9 - x} \right)}}{9}\).
Thể tích của khối nón có đỉnh là \(O\), đáy là \(\left( C \right)\) là
\(V = \frac{1}{3}\pi {r^2}.OM = \frac{1}{3}\pi {\left[ {\frac{{R\left( {9 - x} \right)}}{9}} \right]^2}x = \frac{1}{{243}}\pi {R^2}{(9 - x)^2}x\).
Xét hàm số \(f\left( x \right) = \frac{1}{{243}}\pi {R^2}{(9 - x)^2}x,(0 < x < 9)\) ta có:
Ta có \(f'\left( x \right) = \frac{1}{{243}}\pi {R^2}\left( {9 - x} \right)\left( {9 - 3x} \right)\); \(f'\left( x \right) = 0 \Leftrightarrow \frac{1}{{243}}\pi {R^2}\left( {9 - x} \right)\left( {9 - 3x} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 9\left( L \right)}\\{x = 3\left( {tm} \right)}\end{array}} \right.\)
Lập bảng biến thiên ta có:
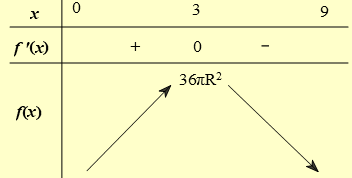
Từ bảng biến thiên ta có thể tích khối nón có đỉnh là \(O\), đáy là \(\left( C \right)\) lớn nhất khi \(x = 3\).
Câu 83:
Cho các phát biểu sau:
(1) Hình hộp là một hình lăng trụ.
(2) Hình lăng trụ có tất cả các cạnh song song.
(3) Hình lăng trụ có tất cả các mặt bên là hình bình hành.
(4) Hình hộp có tất cả các mặt bên bằng nhau.
(5) Hình lăng trụ là một hình hộp.
Số phát biểu đúng là
 Xem đáp án
Xem đáp án
Các phát biểu (1), (3) đúng.
Câu 84:
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ?
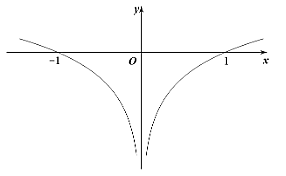
 Xem đáp án
Xem đáp án
Ta thấy đồ thị hàm số nhận trục \(Oy\) làm trục đối xứng nên hàm số là hàm số chẵn.
Mặt khác, đồ thị hàm số nhận đường thẳng \(x = 0\) làm đường tiệm cận đứng nên chỉ có hàm số \(y = {\rm{log}}\left| x \right|\) thỏa mãn.
Câu 85:
Cho \(n\) là số tự nhiên thỏa mãn: \(C_n^0 + 2C_n^1 + 4C_n^2 + \ldots + {2^n}C_n^n = 243\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:

Giá trị của \(n\) bằng _______.
Khi đó hệ số của số hạng chứa \(x\) của khai triển \({(3x - 1)^n}\) là _______.
Giá trị của biểu thức \(C_n^0 + C_n^1 + C_n^2 + \ldots + C_n^n\) bằng _______.
 Xem đáp án
Xem đáp án
Giá trị của \(n\) bằng 5.
Khi đó hệ số của số hạng chứa \(x\) của khai triển \({(3x - 1)^n}\) là 15.
Giá trị của biểu thức \(C_n^0 + C_n^1 + C_n^2 + \ldots + C_n^n\) bằng 32.
Giải thích
Xét khai triển: \({(1 + x)^n} = C_n^0 + xC_n^1 + {x^2}C_n^2 + \ldots + {x^n}C_n^n\).
Thay \(x = 2\) ta có: \(C_n^0 + 2C_n^1 + 4C_n^2 + \ldots + {2^n}C_n^n = {(1 + 2)^n} = {3^n}\).
Theo đề bài: \({3^n} = 243 \Leftrightarrow n = 5\).
Với \(n = 5\) thì:
+) \({(3x - 1)^n} = {(3x - 1)^5} = \sum\limits_{k = 0}^5 {C_5^k{{(3x)}^{5 - k}}.{{( - 1)}^k}} = \sum\limits_{k = 0}^5 {C_5^k{3^{5 - k}}.{{( - 1)}^k}.{x^{5 - k}}} \)
Ta có: \(5 - k = 1 \Leftrightarrow k = 4\).
Hệ số của số hạng chứa \(x\) của khai triển là \(C_5^4{.3^{5 - 4}}.{( - 1)^4} = 15\).
+) \(C_n^0 + C_n^1 + C_n^2 + \ldots + C_n^n = {(1 + 1)^n} = {2^n} = {2^5} = 32\).
Câu 86:
Một lớp học trong một trường đại học có 60 sinh viên, trong đó có 40 sinh viên học tiếng Anh, 30 sinh viên học tiếng Pháp và 20 sinh viên học cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên 2 sinh viên của lớp học này. Tính xác suất để 2 sinh viên được chọn không học ngoại ngữ. Biết rằng trường này chỉ dạy hai loại ngoại ngữ là tiếng Anh và tiếng Pháp.
 Xem đáp án
Xem đáp án
Ta có sơ đồ Ven như hình vẽ.
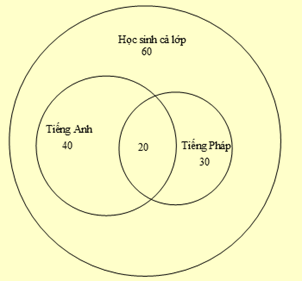
Số lượng sinh viên học ít nhất một môn ngoại ngữ là: \(40 + 30 - 20 = 50\) (học sinh).
Số lượng sinh viên không học ngoại ngữ là: \(60 - 50 = 10\) (học sinh).
Ta xét phép thử: Chọn 2 sinh viên bất kỳ trong số 60 sinh viên của lớp học.
\( \Rightarrow \) Số phần tử của không gian mẫu là: \(n\left( {\rm{\Omega }} \right) = C_{60}^2\).
Xét biến cố \(A\): "Chọn ra 2 sinh viên không học ngoại ngữ".
\( \Rightarrow \) Số phần tử của biến cố \(A\) là: \(n\left( A \right) = C_{10}^2\).
Vậy xác suất để chọn được 2 sinh viên không học ngoại ngữ là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( {\rm{\Omega }} \right)}} = \frac{{C_{10}^2}}{{C_{60}^2}} = \frac{3}{{118}}\).
Câu 87:
Cho hình tứ diện được tô màu tại các đỉnh, trung điểm các cạnh, trọng tâm các mặt và trọng tâm tứ diện. Số cách chọn 4 điểm tô màu là 4 đỉnh của một tứ diện bằng
 Xem đáp án
Xem đáp án
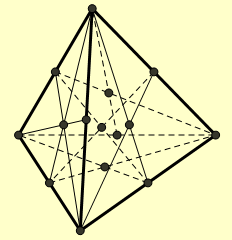
Có tất cả 15 điểm được tô màu gồm 4 đỉnh tứ diện, 6 trung điểm của 6 cạnh, 4 trọng tâm của 4 mặt bên và 1 trọng tâm của tứ diện.
Chọn 4 điểm trong 15 điểm có \(C_{15}^4\) cách.
Để chọn 4 điểm đồng phẳng trong 15 điểm, ta có các trường hợp sau:
TH1: 4 điểm cùng thuộc 1 mặt bên
+ Mỗi mặt bên có 7 điểm được tô màu nên chọn 4 điểm trong 7 điểm có \(C_7^4\) cách.
+ Có tất cả 4 mặt bên.
\( \Rightarrow 4.C_7^4\) cách cho TH1.
TH2: 4 điểm cùng thuộc 1 mặt phẳng chứa 1 cạnh của tứ diện và trung điểm của cạnh đối diện với cạnh đó
+ Mỗi mặt phẳng này có 7 điểm được tô màu nên chọn 4 điểm trong 7 điểm có \(C_7^4\) cách.
+ Tứ diện có 6 cạnh nên có tất cả 6 mặt phẳng như vậy.
\( \Rightarrow 6.C_7^4\) cách cho TH2.
TH3: 4 điểm cùng thuộc 1 mặt phẳng chứa 1 đỉnh và đường trung bình của tam giác đối diện với đỉnh đó
+ Mỗi mặt phẳng này có 5 điểm được tô màu nên chọn 4 điểm trong 5 điểm có \(C_5^4\) cách.
+ Tứ diện có 4 đỉnh và mỗi tam giác có 3 đường trung bình nên có tất cả 12 mặt phẳng như vậy.
\( \Rightarrow 12.C_5^4\) cách cho TH3.
TH4: 4 điểm cùng thuộc 1 mặt phẳng chứa 2 đường nối 2 trung điểm của các cạnh đối diện
+ Mỗi mặt phẳng này có 5 điểm được tô màu nên chọn 4 điểm trong 5 điểm có \(C_5^4\) cách.
+ Có tất cả 3 đường nối 2 trung điểm của các cạnh đối diện nên chọn 2 đường trong 3 đường để tạo ra mặt phẳng có \(C_3^2\) cách.
\( \Rightarrow C_3^2\).\(C_5^4\) cách cho TH4.
Vậy số cách chọn 4 điểm không đồng phẳng hay chính là chọn 4 điểm là 4 đỉnh của một tứ diện là \(C_{15}^4 - 4.C_7^4 - 6.C_7^4 - 12.C_5^4 - C_3^2.C_5^4 = 940\).
Câu 88:
Phần nguyên của \(x\), kí hiệu là \(\left[ x \right]\), là số nguyên lớn nhất không vượt quá \(x\).Tìm \(\left[ x \right]\) biết \(x = \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + \ldots + \frac{1}{{n.\left( {n + 1} \right)}}\left( {n \in {\mathbb{N}^{\rm{*}}}} \right)\).
 Xem đáp án
Xem đáp án
Ta có: \(x = \left( {1 - \frac{1}{2}} \right) + \left( {\frac{1}{2} - \frac{1}{3}} \right) + \ldots + \left( {\frac{1}{n} - \frac{1}{{n + 1}}} \right) = 1 - \frac{1}{{n + 1}}\).
Vì \(n \in {\mathbb{N}^{\rm{*}}}\) nên \(n + 1 > 1 \Leftrightarrow 0 < \frac{1}{{n + 1}} < 1 \Rightarrow 0 < 1 - \frac{1}{{n + 1}} < 1 \Leftrightarrow 0 < x < 1 \Rightarrow \left[ x \right] = 0\).
Câu 89:
Một hộp đựng 8 quả cầu giống nhau được đánh số từ 1 đến 8.
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
a) Lấy ngẫu nhiên 2 quả cầu từ hộp thì xác suất để lấy được 2 quả cầu ghi số có tổng bằng 5 là _______.
b) Lấy ngẫu nhiên từ hộp một số quả cầu. Cần phải lấy ít nhất _______ quả cầu để xác suất lấy được ít nhất 1 quả ghi số chia hết cho 3 lớn hơn \(\frac{3}{4}\).
 Xem đáp án
Xem đáp án
a) Lấy ngẫu nhiên 2 quả cầu từ hộp thì xác suất để lấy được 2 quả cầu ghi số có tổng bằng 5 là \(\frac{1}{7}\).
b) Lấy ngẫu nhiên từ hộp một số quả cầu. Cần phải lấy ít nhất 4 quả cầu để xác suất lấy được ít nhất 1 quả ghi số chia hết cho 3 lớn hơn \(\frac{3}{4}\).
Giải thích
a) Lấy ngẫu nhiên 2 quả cầu từ hộp thì số phần tử của không gian mẫu là \(n\left( {\rm{\Omega }} \right) = C_8^2\).
Gọi biến cố \(A\): "Lấy được 2 quả cầu ghi số có tổng bằng 5".
Hai quả cầu ghi số có tổng bằng 5 thì số trên 2 quả là 1 và 4 hoặc 2 và \(3 \Rightarrow n\left( A \right) = 2 + 2 = 4\).
Vậy xác suất cần tìm là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( {\rm{\Omega }} \right)}} = \frac{4}{{C_8^2}} = \frac{1}{7}\).
b) Nhận thấy trong 8 quả cầu đã cho, có 2 quả ghi số chia hết cho 3 là 3 và \(6;6\) quả còn lại ghi số không chia hết cho 3.
Giả sử rút ra \(x\) quả \((1 \le x \le 8,x \in \mathbb{N}\) ). Lấy ngẫu nhiên \(x\) quả từ 8 quả trong hộp thì số phần tử của không gian mẫu là \(n\left( {\rm{\Omega }} \right) = C_8^x\).
Gọi biến cố \(A\) : "Trong \(x\) quả lấy ra có ít nhất 1 quả ghi số chia hết cho 3 ".
Biến cố đối của \(A\) là \(\overline A \) : "Trong \(x\) quả lấy ra không có quả nào ghi số chia hết cho 3" \( \Rightarrow n\left( {\overline A } \right) = C_6^x\).
\( \Rightarrow P\left( {\overline A } \right) = \frac{{n\left( {\overline A } \right)}}{{n\left( {\rm{\Omega }} \right)}} = \frac{{C_6^x}}{{C_8^x}} = \frac{{6!}}{{x!\left( {6 - x} \right)!}}:\frac{{8!}}{{x!\left( {8 - x} \right)!}} = \frac{{\left( {8 - x} \right)\left( {7 - x} \right)}}{{56}}\).
Theo đề bài
\(P\left( A \right) > \frac{3}{4} \Rightarrow 1 - P\left( {\overline A } \right) > \frac{3}{4} \Leftrightarrow 1 - \frac{{\left( {8 - x} \right)\left( {7 - x} \right)}}{{56}} > \frac{3}{4} \Leftrightarrow \frac{{\left( {8 - x} \right)\left( {7 - x} \right)}}{{56}} < \frac{1}{4} \Leftrightarrow {x^2} - 15x + 42 < 0\)
\( \Leftrightarrow 3,7 \approx \frac{{15 - \sqrt {57} }}{2} < x < \frac{{15 + \sqrt {57} }}{2} \approx 11,3\) mà \(1 \le x \le 8,x \in \mathbb{N}\)
\( \Rightarrow \) Giá trị nhỏ nhất của \(x\) là 4 .
Vậy cần phải lấy ít nhất 4 quả cầu.
Câu 90:
Trong không gian \(Oxyz\), cho vật thể có mặt đáy là hình tròn có tâm trùng gốc tọa độ, bán kính bằng 1 nằm trên \(\left( {Oxy} \right)\) (minh họa như hình vẽ). Khi cắt vật thể bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\left( { - 1 \le x \le 1} \right)\) thì được thiết diện là một tam giác đều. Thể tích \(V\) của vật thể đó là
 Xem đáp án
Xem đáp án
Tại vị trí có hoành độ \(x\left( { - 1 \le x \le 1} \right)\) thì tam giác thiết diện có độ dài cạnh là \(2\sqrt {1 - {x^2}} \).
Do đó tam giác thiết diện có diện tích \(S\left( x \right) = {\left( {2\sqrt {1 - {x^2}} } \right)^2}\frac{{\sqrt 3 }}{4} = \sqrt 3 \left( {1 - {x^2}} \right)\).
Vậy thể tích \(V\) của vật thể là \(\int\limits_{ - 1}^1 {\sqrt 3 \left( {1 - {x^2}} \right)dx = \frac{{4\sqrt 3 }}{3}} \).
Câu 91:
Bạn Xuân là thành viên trong một nhóm gồm 15 người.
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
Đúng |
Sai |
|
Chọn ngẫu nhiên 3 người từ nhóm để lập một ban đại diện. Xác suất để Xuân là 1 trong 3 người được chọn là 0,2. |
¡ |
¡ |
|
Chọn ngẫu nhiên 2 người từ nhóm để làm nhóm trưởng và nhóm phó. Xác suất để Xuân không làm nhóm trưởng cũng như nhóm phó nhỏ hơn 0,8. |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
Đúng |
Sai |
|
Chọn ngẫu nhiên 3 người từ nhóm để lập một ban đại diện. Xác suất để Xuân là 1 trong 3 người được chọn là 0,2. |
¤ |
¡ |
|
Chọn ngẫu nhiên 2 người từ nhóm để làm nhóm trưởng và nhóm phó. Xác suất để Xuân không làm nhóm trưởng cũng như nhóm phó nhỏ hơn 0,8. |
¡ |
¤ |
Giải thích
+) Chọn ngẫu nhiên 3 người từ nhóm để lập một ban đại diện thì số phần tử của không gian mẫu là \(n\left( {\rm{\Omega }} \right) = C_{15}^3 = 455\).
Gọi \(A\) là biến cố: "Xuân là một trong ba người được chọn".
Có 1 cách chọn Xuân trong nhóm 15 người.
Có \(C_{14}^2\) cách chọn 2 người trong 14 người còn lại.
Suy ra \(n\left( A \right) = 1.C_{14}^2 = 91\).
Xác suất cần tìm là \(P\left( A \right) = \frac{{91}}{{455}} = 0,2\).
+) Chọn ngẫu nhiên 2 người từ nhóm để làm nhóm trưởng và nhóm phó thì số phần tử của không gian mẫu là \(n\left( {\rm{\Omega }} \right) = 15.14 = 210\).
Gọi \(A\) là biến cố: "Xuân không làm nhóm trưởng cũng như nhóm phó".
Trong 14 người còn lại, chọn nhóm trưởng có 14 cách, chọn nhóm phó có 13 cách.
Suy ra \(n\left( A \right) = 14.13 = 182\).
Xác suất cần tìm là \(P\left( A \right) = \frac{{182}}{{210}} = \frac{{13}}{{15}} \approx 0,87 > 0,8\).
Câu 92:
Có bao nhiêu bộ số \(\left( {a;b;c;d} \right)\) thỏa mãn \(a;b;c;d;\,\,a + c;\,\,b + c;\,\,a + d;\,\,b + d\) là tám số tự nhiên khác nhau từ 1 đến 8 và \(a\) là số lớn nhất?
 Xem đáp án
Xem đáp án
Vì \(a;b;c;d;a + c;b + c;a + d;b + d\) là tám số tự nhiên khác nhau từ 1 đến 8 nên tổng của 8 số này là: \(a + b + c + d + \left( {a + c} \right) + \left( {b + c} \right) + \left( {a + d} \right) + \left( {b + d} \right) = 1 + 2 + \ldots + 8\).
\( \Leftrightarrow 3\left( {a + b + c + d} \right) = 36 \Leftrightarrow a + b + c + d = 12\).
Mà \(b + c + d \ge 1 + 2 + 3 = 6 \Rightarrow a = 12 - \left( {b + c + d} \right) \le 6\).
Mặt khác, \(a\) là số lớn nhất nên \(4a > a + b + c + d \Leftrightarrow a > 3\).
Với \(a = 4\) ta có: \(b + c + d = 8\) mà \({\rm{max}}\left( {b + c + d} \right) = 1 + 2 + 3 = 6\) nên không thỏa mãn.
Với \(a = 5\) ta có: \(\left\{ {\begin{array}{*{20}{l}}{b + c + d = 7}\\{b,c,d \in \left\{ {1;2;3;4} \right\}(a > b,c,d)}\end{array} \Rightarrow b,c,d \in \left\{ {1;2;4} \right\}} \right.\). Vì \(a + c;a + d \le 8\) nên
\(\left\{ {\begin{array}{*{20}{l}}{b = 4}\\{c;d \in \{ 1;2\} }\end{array} \Rightarrow \left[ {\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{c = 1;d = 2}\\{a + c = b + d = 6}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{c = 2;d = 1}\\{a + d = b + c = 6}\end{array}} \right.}\end{array}} \right.} \right.\) (vô lí).
Với \(a = 6\) ta có: \[\left\{ {\begin{array}{*{20}{l}}{b + c + d = 6}\\{b,c,d \in \{ 1;2;3;4;5\} (a > b,c,d)}\end{array} \Rightarrow b;c;d \in \{ 1;2;3\} } \right.\]. Vì \(a + c;a + d \le 8\)
nên \(\left\{ {\begin{array}{*{20}{l}}{b = 3}\\{c;d \in \left\{ {1;2} \right\}}\end{array} \Rightarrow \left[ {\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{c}}{c = 1;d = 2}\\{a + c = 7;b + c = 4;a + d = 8;b + d = 5}\end{array}{\rm{\;}}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{c = 2;d = 1}\\{a + c = 8;b + c = 5;a + d = 7;b + d = 4}\end{array}} \right.}\end{array}} \right.} \right.\)(thỏa mãn).
Vậy có 2 bộ số \(\left( {a;b;c;d} \right)\) thỏa mãn.
Câu 93:
Cho \(z\) là số phức thoả mãn \(\left| {z - 2 + 3i\left| = \right|iz - 1} \right|\). Gọi \(M\left( {x;y} \right)\) là điểm biểu diễn số phức \(z\) ở trên mặt phẳng phức.
Kéo các ô vuông thả vào vị trí thích hợp trong các câu sau:
Tập hợp các điểm \(M\left( {x;y} \right)\) là đường thẳng có phương trình: _______.
Giá trị nhỏ nhất của \[P = \left| {z - 1 - 2i} \right|\] là: _______.
 Xem đáp án
Xem đáp án
Tập hợp các điểm \(M\left( {x;y} \right)\) là đường thẳng có phương trình: \(x - y - 3 = 0\).
Giá trị nhỏ nhất của \[P = \left| {z - 1 - 2i} \right|\] là: \(2\sqrt 2 \).
Giải thích
Do \(M\left( {x;y} \right)\) là điểm biểu diễn của số phức \(z \Rightarrow z = x + yi\).
\(\left| {z - 2 + 3i\left| = \right|iz - 1\left| \Leftrightarrow \right|x + yi - 2 + 3i\left| = \right|x.i - y - 1} \right|\)
\( \Leftrightarrow {(x - 2)^2} + {(y + 3)^2} = {x^2} + {(y + 1)^2}\)
\( \Leftrightarrow - x + y + 3 = 0\).
Tập hợp các điểm \({\rm{M}}\) là đường thẳng \(\left( a \right): - x + y + 3 = 0\) hay \(x - y - 3 = 0\).
Ta có \(P = \left| {z - 1 - 2i} \right| = MI,{\rm{\;}}I\left( {1;2} \right)\).
Do đó \({P_{{\rm{min\;}}}} = I{M_{{\rm{min\;}}}} = d\left( {I,\left( a \right)} \right) = \frac{{\left| {1 - 2 - 3} \right|}}{{\sqrt 2 }} = 2\sqrt 2 \).
|
Lí do lựa chọn phương án |
Ô 1 |
Vị trí 1. |
|
Ô 2 |
Nhiễu: học sinh sai dấu khi tìm \(\left( a \right)\). |
|
|
Ô 3 |
Vị trí 2. |
|
|
Ô 4 |
Nhiễu: ứng với lỗi sai ở phương trình \(\left( a \right)\) ở trên. |
Câu 94:
Một loại vi khuẩn sau mỗi phút số lượng tăng gấp đôi biết rằng sau 5 phút người ta đếm được có 64000 con. Hỏi sau bao nhiêu phút thì có được 2048000 con?
 Xem đáp án
Xem đáp án
Số lượng vi khuẩn tăng sau mỗi phút lên là cấp số nhân \(\left( {{u_n}} \right)\) với công bội \(q = 2\).
Ta có: \({u_6} = 64000 \Rightarrow {u_1}.{q^5} = 64000 \Rightarrow {u_1} = 2000\).
Sau \(n\) phút thì số lượng vi khuẩn là \({u_{n + 1}}\).
\({u_{n + 1}} = 2048000 \Rightarrow {u_1}.{q^n} = 2048000 \Rightarrow {2000.2^n} = 2048000 \Rightarrow n = 10\).
Vậy sau 10 phút thì có được 2048000 con.
Câu 95:
Cho hàm số \(f\left( x \right) = \left( {2x - 7} \right){\rm{ln}}\left( {x + 1} \right)\).
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
ĐÚNG |
SAI |
|
Tập xác định của hàm số là \(D = \left( {\frac{7}{2}; + \infty } \right)\). |
¡ |
¡ |
|
Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt. |
¡ |
¡ |
|
Đồ thị hàm số không cắt trục tung. |
¡ |
¡ |
 Xem đáp án
Xem đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Tập xác định của hàm số là \(D = \left( {\frac{7}{2}; + \infty } \right)\). |
¡ |
¤ |
|
Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt. |
¤ |
¡ |
|
Đồ thị hàm số không cắt trục tung. |
¡ |
¤ |
Giải thích
Điều kiện xác định: \(x + 1 > 0 \Leftrightarrow x > - 1\).
\( \Rightarrow \) Tập xác định của hàm số là \(D = \left( { - 1; + \infty } \right)\).
Xét \[f(x) = 0 \Leftrightarrow (2x - 7){\rm{ln(}}x + 1) = 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2x - 7 = 0}\\{{\rm{ln(}}x + 1) = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = \frac{7}{2}\,\,\left( {t/m} \right)}\\{x = 0\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.\]
\( \Rightarrow \) Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt.
Tại \(x = 0 \Rightarrow f\left( 0 \right) = 0\).
\( \Rightarrow \) Đồ thị hàm số cắt trục tung tại điểm duy nhất.
Câu 96:
Trong không gian \(Oxyz\), cho ba điểm \(A\left( {0;1;2} \right),B\left( {3;0; - 1} \right),C\left( { - 1; - 2;0} \right)\). Diện tích tam giác \(ABC\) là \(\frac{{\sqrt a }}{2}\) với \(a = \) (1) ______.
 Xem đáp án
Xem đáp án
Đáp án: “230”
Giải thích
\(\overrightarrow {AB} = \left( {3; - 1; - 3} \right)\).
\(\overrightarrow {AC} = \left( { - 1; - 3; - 2} \right)\).
\(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( { - 7;9; - 10} \right)\)
Diện tích tam giác \(ABC\) là \(S = \frac{1}{2}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]} \right| = \frac{{\sqrt {230} }}{2}\).
Câu 97:
Gọi \(S\) là tập hợp tất cả các giá trị của tham số \(m\) để bất phương trình \({\rm{lo}}{{\rm{g}}_3}\left( {{x^2} - 5x + m} \right) > {\rm{lo}}{{\rm{g}}_3}\left( {x - 2} \right)\) có tập nghiệm chứa khoảng \(\left( {2; + \infty } \right)\). Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Ta có: \({\rm{lo}}{{\rm{g}}_3}\left( {{x^2} - 5x + m} \right) > {\rm{lo}}{{\rm{g}}_3}\left( {x - 2} \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x - 2 > 0}\\{{x^2} - 5x + m > x - 2}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x > 2}\\{m > - {x^2} + 6x - 2}\end{array}} \right.} \right.\).
Bất phương trình \({\rm{lo}}{{\rm{g}}_3}\left( {{x^2} - 5x + m} \right) > {\rm{lo}}{{\rm{g}}_3}\left( {x - 2} \right)\) có tập nghiệm chứa khoảng \(\left( {2; + \infty } \right)\) \( \Leftrightarrow m > - {x^2} + 6x - 2\) có nghiệm với mọi \(x \in \left( {2; + \infty } \right)\).
Xét hàm số \(f\left( x \right) = - {x^2} + 6x - 2\) trên \(\left( {2; + \infty } \right)\).
Ta có \(f'\left( x \right) = - 2x + 6,f'\left( x \right) = 0 \Leftrightarrow x = 3\)
Bảng biến thiên
Dựa vào bảng biến thiên ta có: \(m > - {x^2} + 6x - 2\) có nghiệm với mọi \(x \in \left( {2; + \infty } \right) \Leftrightarrow m > 7\).
