Giải SGK Toán 11 Cánh Diều Bài Hàm số lượng giác và đồ thị
-
714 lượt thi
-
57 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Guồng nước (hay còn gọi là cọn nước) không chỉ là công cụ phục vụ sản xuất nông nghiệp, mà đã trở thành hình ảnh quen thuộc của bản làng và là một nét văn hoá đặc trưng của đồng bào dân tộc miền núi phía Bắc.

Một chiếc guồng nước có dạng hình tròn bán kính 2,5 m; trục của nó đặt cách mặt nước 2 m. Khi guồng quay đều, khoảng cách h (m) từ một ống đựng nước gắn tại một điểm của guồng đến mặt nước được tính theo công thức h = |y|, trong đó \(y = 2,5\sin \left( {2\pi x - \frac{\pi }{2}} \right) + 2\), với x (phút) là thời gian quay của guồng (x ≥ 0).
(Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2020).
Khoảng cách h phụ thuộc vào thời gian quay x như thế nào?
 Xem đáp án
Xem đáp án
Với x ≥ 0, xét hàm số \[y = 2,5\sin \left( {2\pi x - \frac{\pi }{2}} \right) + 2\]
\[ = - 2,5\sin \left( {\frac{\pi }{2} - 2\pi x} \right) + 2\]
\[ = - 2,5\cos \left( {2\pi x} \right) + 2\]
Khi đó h = |y| = |‒2,5cos2πx + 2|.
Vậy khoảng cách h phụ thuộc vào thời gian quay x theo công thức h = |‒2,5cos2πx + 2|.
Câu 2:
Cho hàm số f(x) = x2.
• Với x ∈ ℝ, hãy so sánh f(‒x) và f(x).
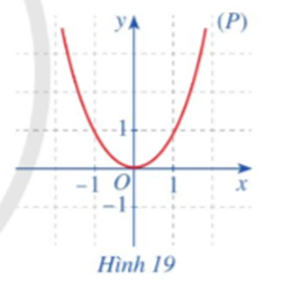
• Quan sát parabol (P) là đồ thị của hàm số f(x) = x2 (Hình 19) và cho biết trục đối xứng của (P) là đường thẳng nào.
 Xem đáp án
Xem đáp án
Xét hàm số f(x) = x2.
• Với x ∈ ℝ, ta có: f(‒x) = (‒x)2 = x2.
Do đó f(‒x) = f(x).
• Trục đối xứng của (P) là đường thẳng x = 0, hay chính là trục Oy.
Câu 3:
Cho hàm số g(x) = x.
• Với x ∈ ℝ, hãy so sánh g(‒x) và ‒g(x).
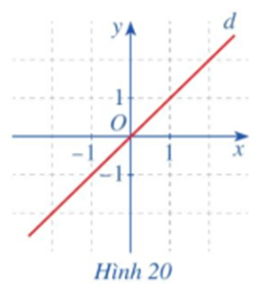
• Quan sát đường thẳng d là đồ thị của hàm số g(x) = x (Hình 20) và cho biết gốc toạ độ O có là tâm đối xứng của đường thẳng d hay không.
 Xem đáp án
Xem đáp án
Xét hàm số g(x) = x.
• Với x ∈ ℝ, ta có: g(‒x) = ‒x và ‒g(x) = ‒x.
Do đó g(‒x) = ‒g(x).
• Gốc tọa độ O là tâm đối xứng của đường thẳng d.
Câu 4:
 Xem đáp án
Xem đáp án
Xét hàm số g(x) = x3 có tập xác định D = ℝ.
∀x ∈ ℝ thì ‒x ∈ ℝ, ta có: g(‒x) = (‒x)3 = ‒x3 = ‒g(x).
Do đó hàm số g(x) = x3 là hàm số lẻ.
Câu 5:
Cho ví dụ về hàm số không là hàm số chẵn và cũng không là hàm số lẻ.
 Xem đáp án
Xem đáp án
Ví dụ về hàm số không là hàm số chẵn và cũng không là hàm số lẻ:
f(x) = x2 + x; g(x) = 2x3 – 3x2; …
Câu 6:
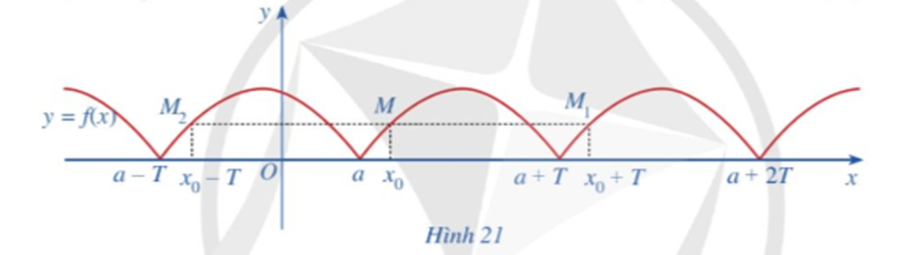
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị như Hình 21.
Có nhận xét gì về đồ thị hàm số trên mỗi đoạn [a ; a + T], [a + T; a + 2T], [a – T; a]?
 Xem đáp án
Xem đáp án
Câu 7:
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị như Hình 21.
![Lấy điểm M(x0; f(x0)) thuộc đồ thị hàm số với x0 thuộc [a; a + T]. So sánh mỗi giá trị (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid4-1689050996.png)
Lấy điểm M(x0; f(x0)) thuộc đồ thị hàm số với x0 ∈ [a; a + T]. So sánh mỗi giá trị f(x0 + T), f(x0 − T) với f(x0).
 Xem đáp án
Xem đáp án
Ta có f(x0 + T) = f(x0);
f(x0 − T) = f(x0).
Câu 8:
Cho ví dụ về hàm số tuần hoàn.
 Xem đáp án
Xem đáp án
Ví dụ về hàm số tuần hoàn:
Cho T là một số hữu tỉ và hàm số f(x) được cho bởi công thức sau:
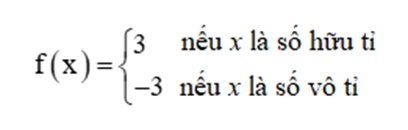
Ta thấy, hàm số xác định trên ℝ. Xét một số thực tùy ý.
Nếu x là số hữu tỉ thì x + T cũng là số hữu tỉ;
Nếu x là số vô tỉ thì x + T cũng là số vô tỉ.
Do đó f(x + T) = f(x) với mọi x.
Vậy hàm số f(x) là hàm số tuần hoàn.
Câu 9:
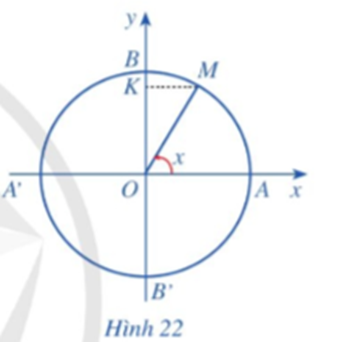
Với mỗi số thực x, tồn tại duy nhất điểm M trên đường tròn lượng giác sao cho (OA, OM) = x (rad) (Hình 22). Hãy xác định sinx.
 Xem đáp án
Xem đáp án
Giả sử tung độ của điểm M là y.
Khi đó ta có sinx = y.Câu 10:
Cho hàm số y = sinx.
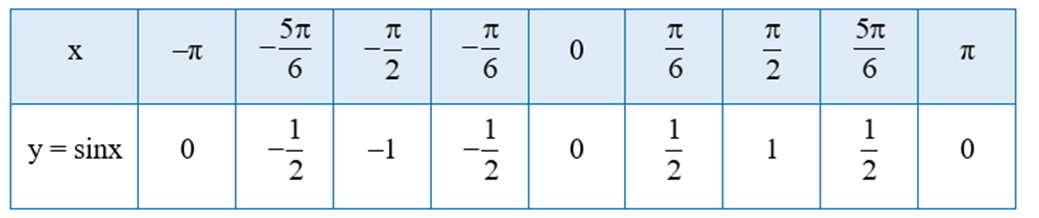
Tìm giá trị y tương ứng với giá trị của x trong bảng sau

 Xem đáp án
Xem đáp án
Thay từng giá trị của x vào hàm số y = sinx ta có bảng sau:
Câu 11:
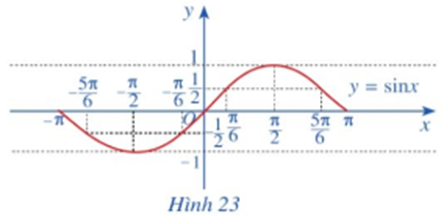
Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x ; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; sinx) với x ∈ [‒π; π] và nối lại ta được đồ thị hàm số y = sinx trên đoạn [‒π; π] (Hình 23).
 Xem đáp án
Xem đáp án
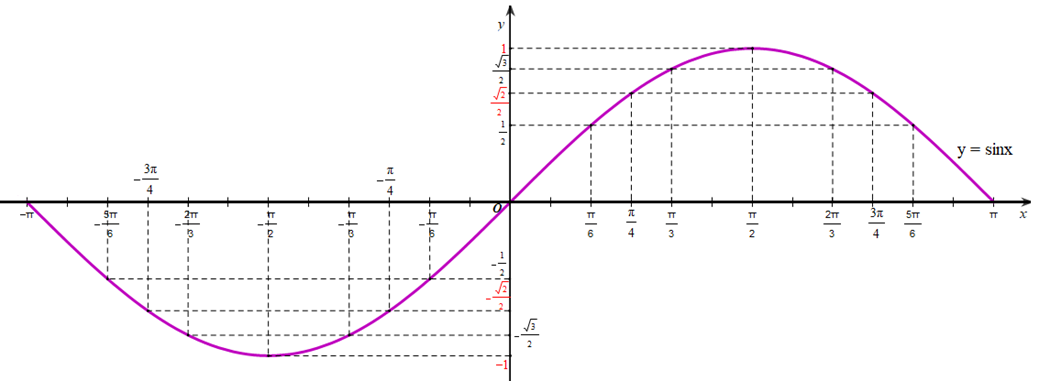
Lấy thêm một số điểm (x; sinx) với x ∈ [‒π; π] trong bảng sau và nối lại ta được đồ thị hàm số y = sinx trên đoạn [‒π; π] (hình vẽ).

Câu 12:
Làm tương tự như trên đối với các đoạn [‒3π; ‒π], [π; 3π], …, ta có đồ thị hàm số y = sin x trên ℝ được biểu diễn ở Hình 24.
![Làm tương tự như trên đối với các đoạn [-3pi; -pi], [pi; 3pi], …, ta có đồ thị hàm số y (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid12-1689051143.png)
 Xem đáp án
Xem đáp án
Làm tương tự như trên đối với các đoạn [‒3π; ‒π], [π; 3π], …, ta có đồ thị hàm số y = sin x trên ℝ được biểu diễn ở hình vẽ sau:
![Làm tương tự như trên đối với các đoạn [-3pi; -pi], [pi; 3pi], …, ta có đồ thị hàm số y (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid13-1689051150.png)
Câu 13:
Quan sát đồ thị hàm số y = sinx ở Hình 24.
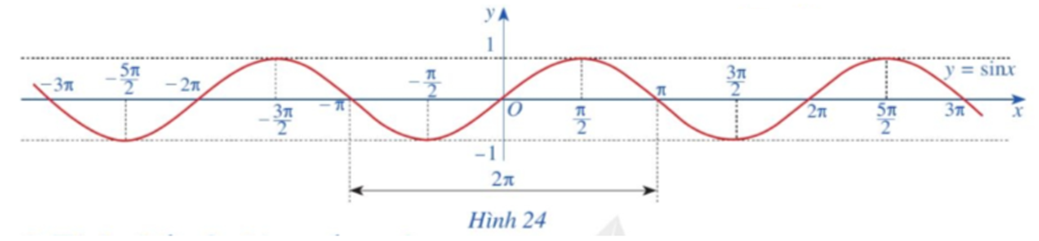
Nêu tập giá trị của hàm số y = sinx.
 Xem đáp án
Xem đáp án
Tập giá trị của hàm số y = sinx là [‒1; 1].
Câu 14:
Quan sát đồ thị hàm số y = sinx ở Hình 24.
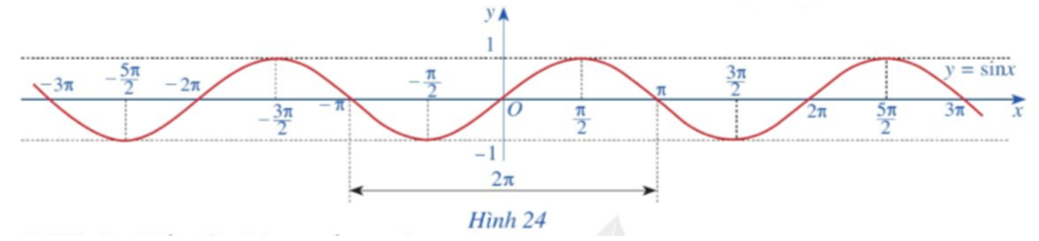
Gốc toạ độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y = sinx.
 Xem đáp án
Xem đáp án
Gốc toạ độ O là tâm đối xứng của đồ thị hàm số.
Do đó hàm số y = sinx là hàm số lẻ.
Câu 15:
Quan sát đồ thị hàm số y = sinx ở Hình 24.
![Bằng cách dịch chuyển đồ thị hàm số y = sinx trên đoạn [-pi; pi] song song với trục (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid15-1689051202.png)
Bằng cách dịch chuyển đồ thị hàm số y = sinx trên đoạn [‒π; π] song song với trục hoành sang phải theo đoạn có độ dài 2π, ta có nhận được đồ thị hàm số y = sinx trên đoạn [π; 3π] hay không? Hàm số y = sinx có tuần hoàn hay không?
 Xem đáp án
Xem đáp án
‒ Bằng cách dịch chuyển đồ thị hàm số y = sinx trên đoạn [‒π; π] song song với trục hoành sang phải theo đoạn có độ dài 2π, ta sẽ nhận được đồ thị hàm số y = sinx trên đoạn [π; 3π].
Làm tương tự như trên ta sẽ được đồ thị hàm số y = sinx trên ℝ.
‒ Xét hàm số f(x) = y = sinx trên ℝ, với T = 2π và x ∈ ℝ ta có:
• x + 2π ∈ ℝ và x – 2π ∈ ℝ;
• f(x + 2π) = f(x)
Do đó hàm số y = sinx là hàm số tuần hoàn với chu kì T = 2π.
Câu 16:
Quan sát đồ thị hàm số y = sinx ở Hình 24.
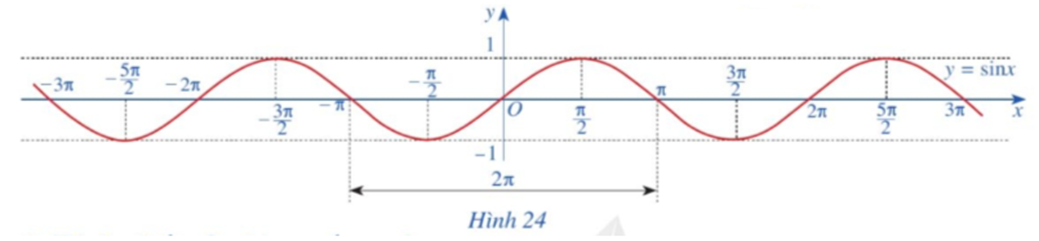
Tìm khoảng đồng biến, nghịch biến của hàm số y = sinx.
 Xem đáp án
Xem đáp án
Quan sát đồ thị hàm số y = sinx ta thấy:
• Hàm số đồng biến trên mỗi khoảng \(\left( { - \frac{{5\pi }}{2}; - \frac{{3\pi }}{2}} \right);\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right);\left( {\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right);...\)
Ta có: \(\left( { - \frac{{5\pi }}{2}; - \frac{{3\pi }}{2}} \right) = \left( { - \frac{\pi }{2} - 2\pi ;\frac{\pi }{2} - 2\pi } \right)\);
\[\left( {\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right) = \left( { - \frac{\pi }{2} + 2\pi ;\frac{\pi }{2} + 2\pi } \right)\];
…
Do đó ta có thể viết hàm số đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) với k ∈ ℤ.
• Hàm số nghịch biến trên mỗi khoảng \(\left( { - \frac{{7\pi }}{2}; - \frac{{5\pi }}{2}} \right);\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right);\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right);...\)
Ta có: \[\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right) = \left( {\frac{\pi }{2} - 2\pi ;\frac{{3\pi }}{2} - 2\pi } \right)\];
…
Do đó ta có thể viết hàm số nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\) với k ∈ ℤ.
Câu 17:
 Xem đáp án
Xem đáp án
Do \(\left( { - \frac{{7\pi }}{2}; - \frac{{5\pi }}{2}} \right) = \left( {\frac{\pi }{2} - 4\pi ;\frac{{3\pi }}{2} - 4\pi } \right) = \left( {\frac{\pi }{2} + \left( { - 2} \right).2\pi ;\frac{{3\pi }}{2} + \left( { - 2} \right).2\pi } \right)\) nên hàm số y = sinx nghịch biến trên khoảng \(\left( { - \frac{{7\pi }}{2}; - \frac{{5\pi }}{2}} \right)\).
Câu 18:
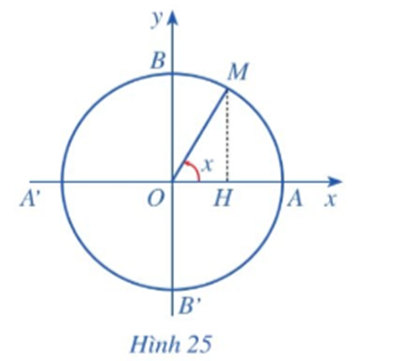
Với mỗi số thực x, tồn tại duy nhất điểm M trên đường tròn lượng giác sao cho (OA, OM) = x (rad) (Hình 25). Hãy xác định cosx.
 Xem đáp án
Xem đáp án
Giả sử hoành độ của điểm M là y.
Khi đó ta có cosx = y.
Câu 19:
Cho hàm số y = cosx.
Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

 Xem đáp án
Xem đáp án
Thay từng giá trị của x vào hàm số y = cosx ta có bảng sau:

Câu 20:
Làm tương tự như trên đối với các đoạn [‒3π; ‒π], [π; 3π], ta có đồ thị hàm số y = cosx trên ℝ được biểu diễn ở Hình 27.
![Làm tương tự như trên đối với các đoạn [-3pi; -pi], [pi; 3pi], ta có đồ thị hàm số y (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid23-1689051624.png)
 Xem đáp án
Xem đáp án
Làm tương tự như trên đối với các đoạn [‒3π; ‒π], [π; 3π], …, ta có đồ thị hàm số y = cosx trên ℝ được biểu diễn ở hình vẽ sau:
![Làm tương tự như trên đối với các đoạn [-3pi; -pi], [pi; 3pi], ta có đồ thị hàm số y (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid24-1689051631.png)
Câu 21:
Quan sát đồ thị hàm số y = cosx ở Hình 27.
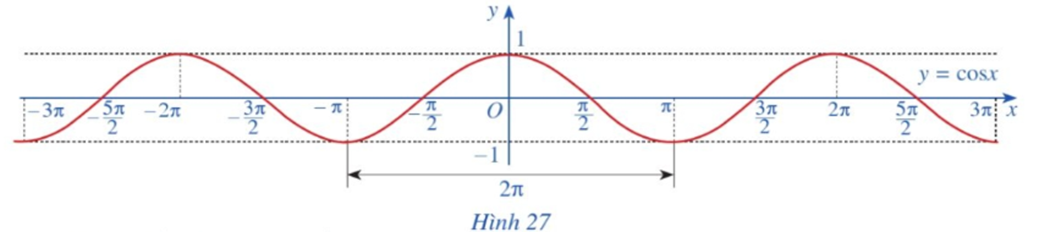
Nêu tập giá trị của hàm số y = cosx.
 Xem đáp án
Xem đáp án
Tập giá trị của hàm số y = cosx là [‒1; 1].
Câu 22:
Quan sát đồ thị hàm số y = cosx ở Hình 27.
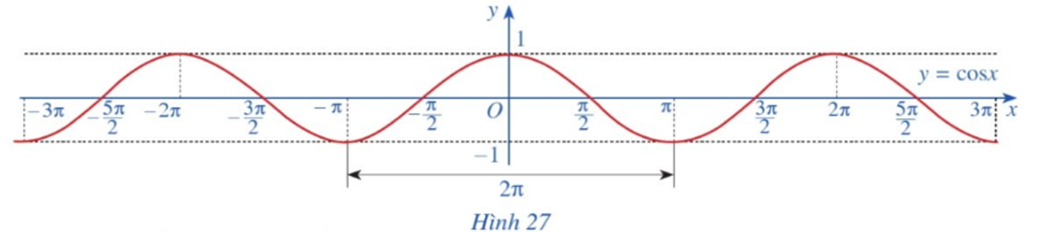
Trục tung có là trục đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y = cosx.
 Xem đáp án
Xem đáp án
Trục tung là trục đối xứng của đồ thị hàm số.
Do đó hàm số y = cosx là hàm số chẵn.
Câu 23:
Quan sát đồ thị hàm số y = cosx ở Hình 27.
![Bằng cách dịch chuyển đồ thị hàm số y = cosx trên đoạn [-pi; pi] song song với trục (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid27-1689051716.png)
Bằng cách dịch chuyển đồ thị hàm số y = cosx trên đoạn [‒π; π] song song với trục hoành sang phải theo đoạn có độ dài 2π, ta nhận được đồ thị hàm số y = cosx trên đoạn [π; 3π] hay không? Hàm số y = cosx có tuần hoàn hay không?
 Xem đáp án
Xem đáp án
‒ Bằng cách dịch chuyển đồ thị hàm số y = cosx trên đoạn [‒π; π] song song với trục hoành sang phải theo đoạn có độ dài 2π, ta sẽ nhận được đồ thị hàm số y = cosx trên đoạn [π; 3π].
Làm tương tự như trên ta sẽ được đồ thị hàm số y = cosx trên ℝ.
‒ Xét hàm số f(x) = y = cosx trên ℝ, với T = 2π và x ∈ ℝ ta có:
• x + 2π ∈ ℝ và x – 2π ∈ ℝ;
• f(x + 2π) = f(x)
Do đó hàm số y = cosx là hàm số tuần hoàn với chu kì T = 2π.
Câu 24:
Quan sát đồ thị hàm số y = cosx ở Hình 27.
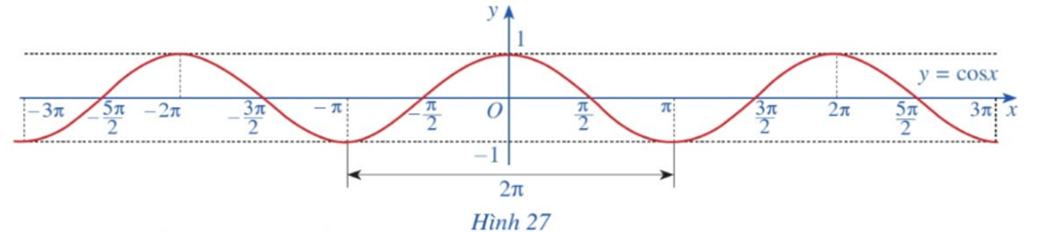
Tìm khoảng đồng biến, nghịch biến của hàm số y = cosx.
 Xem đáp án
Xem đáp án
Quan sát đồ thị hàm số y = cosx ta thấy:
• Hàm số đồng biến trên mỗi khoảng (‒3π; ‒2π); (‒π; 0); (π; 2π); …
Ta có: (‒3π; ‒2π) = (‒π ‒ 2π; 0 ‒ 2π);
(π; 2π) = (‒π + 2π; 0 + 2π);
…
Do đó ta có thể viết hàm số đồng biến trên mỗi khoảng (‒π + k2π; k2π) với k ∈ ℤ.
• Hàm số nghịch biến trên mỗi khoảng (‒2π; ‒π); (0; π); (2π; 3π); …
Ta có: (‒2π; ‒π) = (0 ‒ 2π; π ‒ 2π);
(2π; 3π) = (0 + 2π; π + 2π);
…
Do đó ta có thể viết hàm số nghịch biến trên mỗi khoảng (k2π; π + k2π) với k ∈ ℤ.
Câu 25:
Hàm số y = cosx đồng biến hay nghịch biến trên khoảng (‒2π; ‒π)?
 Xem đáp án
Xem đáp án
Do (‒2π; ‒π) = (0 – 2π; π – 2π) nên hàm số nghịch biến trên khoảng (‒2π; ‒π).
Câu 26:
Xét tập hợp \[D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\]. Với mỗi số thực x ∈ D, hãy nêu định nghĩa tanx.
 Xem đáp án
Xem đáp án
Nếu cosx ≠ 0, tức \[x \in \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\] hay x ∈ D thì ta có: \(\tan x = \frac{{\sin x}}{{\cos x}}\).
Câu 27:
Cho hàm số y = tanx.
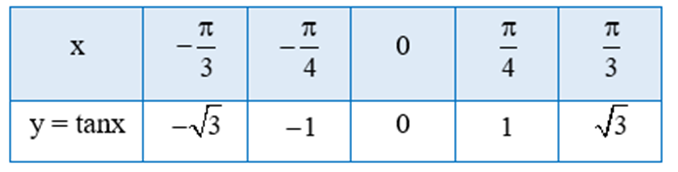
Tìm giá trị y tương ứng với giá trị của x trong bảng sau
 Xem đáp án
Xem đáp án
Thay từng giá trị của x vào hàm số y = tanx ta có bảng sau:
Câu 28:
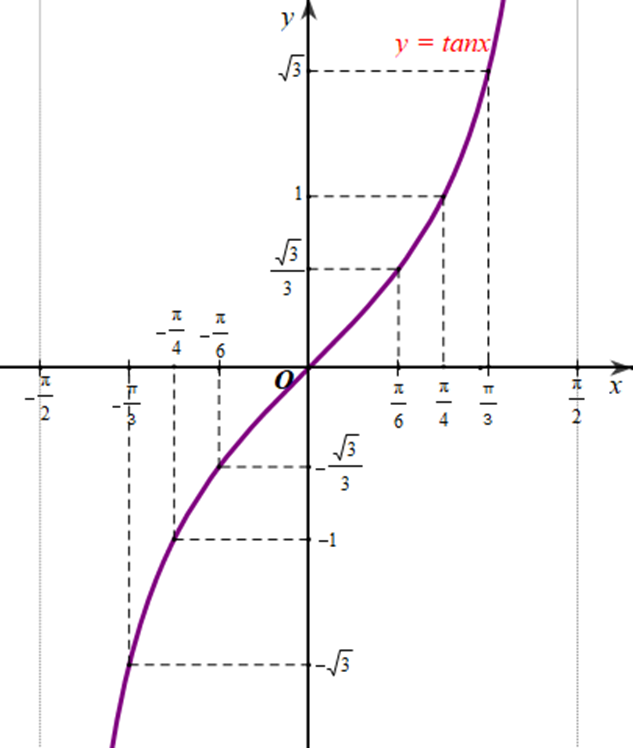
Trong mặt phẳng toạ độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; tanx) với \(x \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) và nối lại ta được đồ thị hàm số y = tan x trên khoảng \(x \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) (Hình 28).
 Xem đáp án
Xem đáp án
Lấy thêm một số điểm (x; tanx) với \(x \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) trong bảng sau và nối lại ta được đồ thị hàm số y = tanx trên khoảng \(x \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) (hình vẽ).
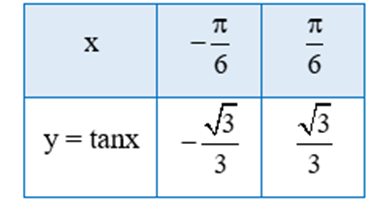
Câu 29:
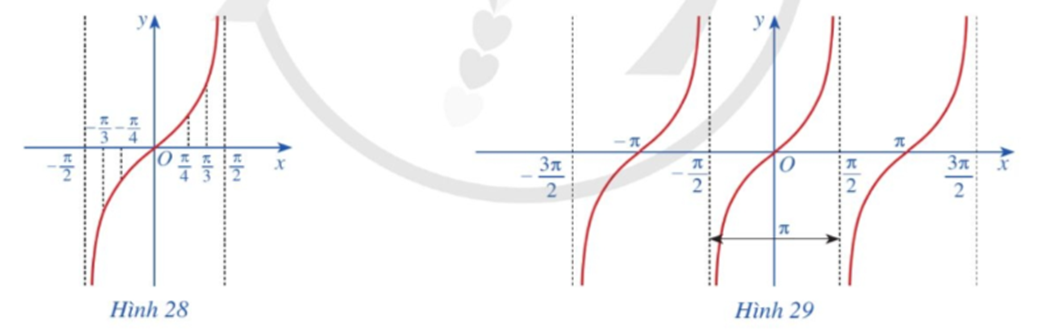
Làm tương tự như trên đối với các khoảng \[\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right),\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right)\], …, ta có đồ thị hàm số y = tan x trên D được biểu diễn ở Hình 29.
 Xem đáp án
Xem đáp án
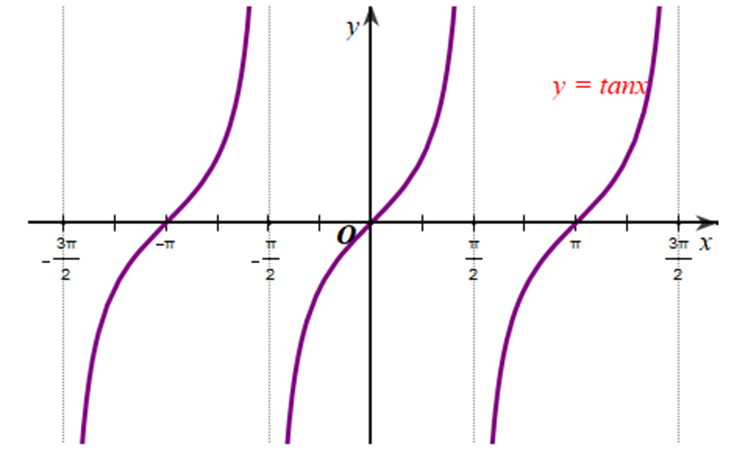
Làm tương tự như trên đối với các \[\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right),\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right)\], …, ta có đồ thị hàm số y = tanx trên D được biểu diễn ở hình vẽ sau:
Câu 30:
Quan sát đồ thị hàm số y = tanx ở Hình 29.
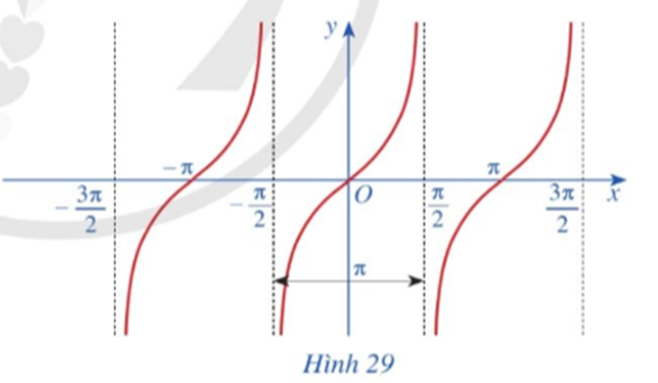
Nêu tập giá trị của hàm số y = tanx.
 Xem đáp án
Xem đáp án
Tập giá trị của hàm số y = tanx là ℝ.
Câu 31:
Quan sát đồ thị hàm số y = tanx ở Hình 29.
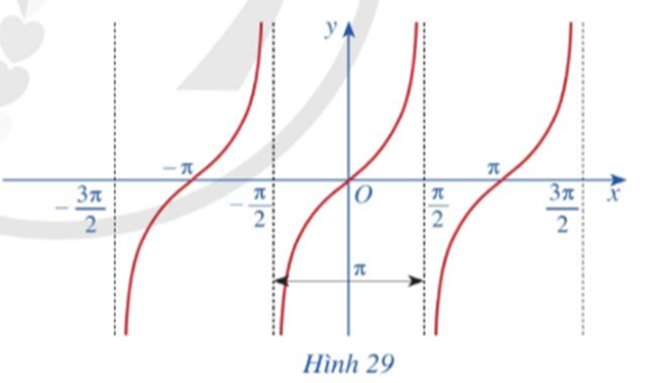
Gốc toạ độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y = tanx.
 Xem đáp án
Xem đáp án
Gốc toạ độ là tâm đối xứng của đồ thị hàm số y = tanx.
Do đó hàm số y = tanx là hàm số lẻ.
Câu 32:
Quan sát đồ thị hàm số y = tanx ở Hình 29.

Bằng cách dịch chuyển đồ thị hàm số y = tanx trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) song song với trục hoành sang phải theo đoạn có độ dài π, ta nhận được đồ thị hàm số y = tanx trên khoảng \(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\) hay không? Hàm số y = tanx có tuần hoàn hay không?
 Xem đáp án
Xem đáp án
‒ Bằng cách dịch chuyển đồ thị hàm số y = tanx trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) song song với trục hoành sang phải theo đoạn có độ dài π, ta sẽ nhận được đồ thị hàm số y = tanx trên khoảng \(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\).
Làm tương tự như trên ta sẽ được đồ thị hàm số y = tanx trên \[\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\].
‒ Xét hàm số f(x) = y = tanx trên \[D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\], với T = π và x ∈ D ta có:
• x + π ∈ D và x – π ∈ D;
• f(x + π) = f(x)
Do đó hàm số y = tanx là hàm số tuần hoàn với chu kì T = π.
Câu 33:
Quan sát đồ thị hàm số y = tanx ở Hình 29.

Tìm khoảng đồng biến, nghịch biến của hàm số y = tanx.
 Xem đáp án
Xem đáp án
Quan sát đồ thị hàm số y = tanx ở Hình 29, ta thấy: đồ thị hàm số đồng biến trên mỗi khoảng \(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right);\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right);\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right);...\)
Ta có: \(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right) = \left( { - \frac{\pi }{2} - \pi ;\frac{\pi }{2} - \pi } \right);\)
\(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right) = \left( { - \frac{\pi }{2} + \pi ;\frac{\pi }{2} + \pi } \right);\)
…
Do đó ta có thể viết đồ thị hàm số y = tanx đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\) với k ∈ ℤ.
Câu 34:
Với mỗi số thực m, tìm số giao điểm của đường thẳng y = m và đồ thị hàm số y = tanx trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
 Xem đáp án
Xem đáp án
Xét đồ thị của hàm số y = m và đồ thị của hàm số y = tanx trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) (hình vẽ).
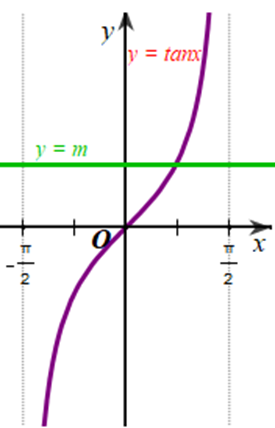
Từ đồ thị của hai hàm số trên hình vẽ, ta thấy mọi m ∈ ℝ thì hai đồ thị trên luôn cắt nhau tại 1 điểm.
Vậy số giao điểm của đường thẳng y = m (m ∈ ℝ) và đồ thị hàm số y = tanx trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) là 1.
Câu 35:
Xét tập hợp E = ℝ \ {kπ | k ∈ ℤ}. Với mỗi số thực x ∈ E, hãy nêu định nghĩa cotx.
 Xem đáp án
Xem đáp án
Nếu sinx ≠ 0, tức x ∈ ℝ \ {kπ | k ∈ ℤ} hay x ∈ E thì ta có: \(\cot x = \frac{{\cos x}}{{\sin x}}\).
Câu 36:
Cho hàm số y = cotx.
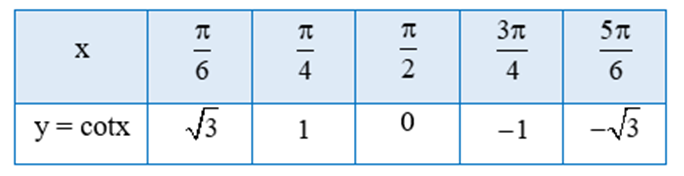
Tìm giá trị y tương ứng với giá trị của x trong bảng sau

 Xem đáp án
Xem đáp án
Thay từng giá trị của x vào hàm số y = cotx ta có bảng sau:
Câu 37:
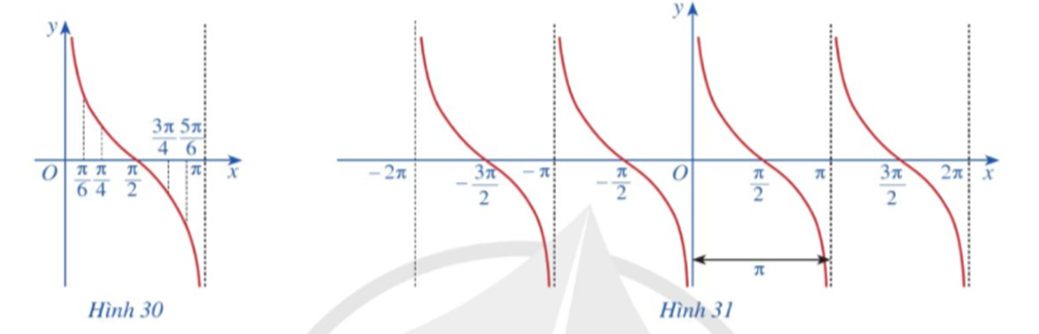
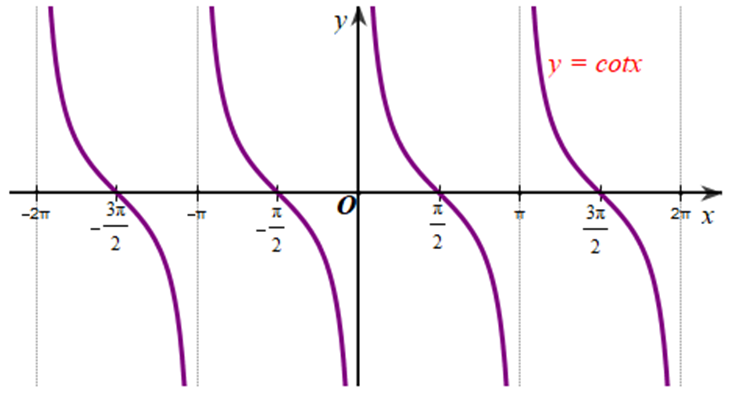
Làm tương tự như trên đối với các khoảng (π; 2π), (‒π; 0), (‒2π; ‒π), …, ta có đồ thị hàm số y = cotx trên E được biểu diễn ở Hình 31.
 Xem đáp án
Xem đáp án
Làm tương tự như trên đối với các \[\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right),\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right)\], …, ta có đồ thị hàm số y = cotx trên D được biểu diễn ở hình vẽ sau:
Câu 38:
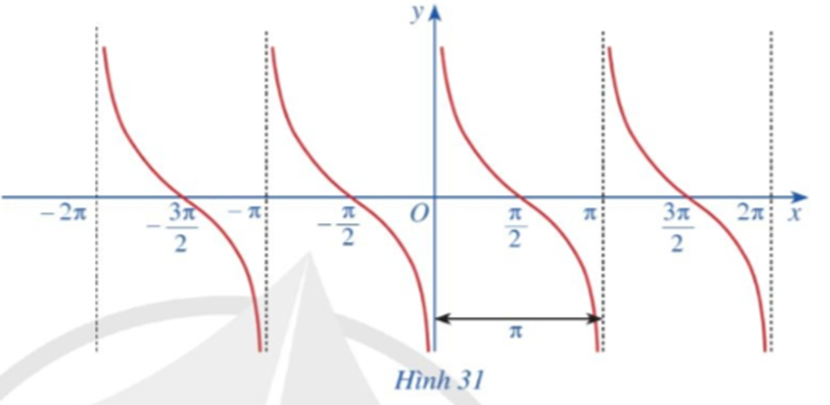
Quan sát đồ thị hàm số y = cotx ở Hình 31.
 Xem đáp án
Xem đáp án
Tập giá trị của hàm số y = cotx là ℝ.
Câu 39:
Quan sát đồ thị hàm số y = cotx ở Hình 31.
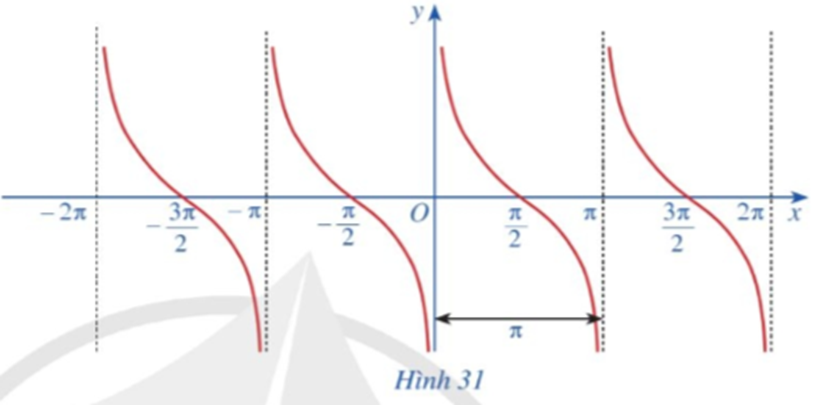
Gốc toạ độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y = cotx.
 Xem đáp án
Xem đáp án
Gốc toạ độ là tâm đối xứng của đồ thị hàm số y = cotx.
Do đó hàm số y = cotx là hàm số lẻ.
Câu 40:
Bằng cách dịch chuyển đồ thị hàm số y = cotx trên khoảng (0; π) song song với trục hoành sang phải theo đoạn có độ dài π, ta nhận được đồ thị hàm số y = cotx trên khoảng (π; 2π) hay không? Hàm số y = cotx có tuần hoàn hay không?
 Xem đáp án
Xem đáp án
‒ Bằng cách dịch chuyển đồ thị hàm số y = cotx trên khoảng (0; π) song song với trục hoành sang phải theo đoạn có độ dài π, ta sẽ nhận được đồ thị hàm số y = cotx trên khoảng (π; 2π).
Làm tương tự như trên ta sẽ được đồ thị hàm số y = cotx trên ℝ \ {kπ | k ∈ ℤ}.
‒ Xét hàm số f(x) = y = cotx trên D = ℝ \ {kπ | k ∈ ℤ}, với T = π và x ∈ D ta có:
• x + π ∈ D và x – π ∈ D;
• f(x + π) = f(x)
Do đó hàm số y = cotx là hàm số tuần hoàn với chu kì T = π.
Câu 41:
Quan sát đồ thị hàm số y = cotx ở Hình 31.
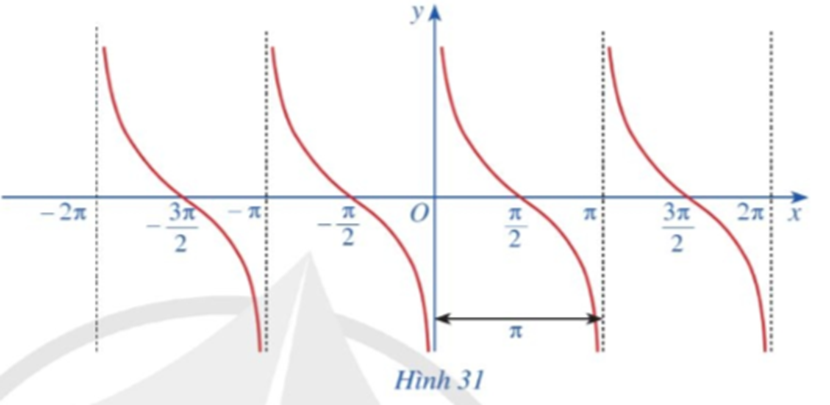
Tìm khoảng đồng biến, nghịch biến của hàm số y = cotx.
 Xem đáp án
Xem đáp án
Quan sát đồ thị hàm số y = cotx ở Hình 31, ta thấy: đồ thị hàm số nghịch biến trên mỗi khoảng (‒2π; ‒π); (‒π; 0); (0; π); (π; 2π); …
Ta có: (‒2π; ‒π) = (0 ‒ 2π; π – 2π);
(‒π; 0) = (0 – π; π ‒ π);
(π; 2π) = (0 + π; π + π);
…
Do đó ta có thể viết đồ thị hàm số y = cotx nghịch biến trên mỗi khoảng (kπ; π + kπ) với k ∈ ℤ.
Câu 42:
Với mỗi số thực m, tìm số giao điểm của đường thẳng y = m và đồ thị hàm số y = cotx trên khoảng (0; π).
 Xem đáp án
Xem đáp án
Xét đồ thị của hàm số y = m và đồ thị của hàm số y = cotx trên khoảng (0; π) (hình vẽ).
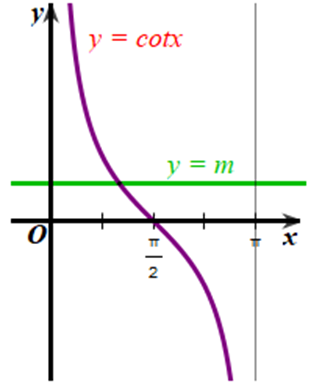
Từ đồ thị của hai hàm số trên hình vẽ, ta thấy mọi m ∈ ℝ thì hai đồ thị trên luôn cắt nhau tại 1 điểm.
Vậy số giao điểm của đường thẳng y = m (m ∈ ℝ) và đồ thị hàm số y = cotx trên khoảng (0; π) là 1.
Câu 43:
Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [‒2π; 2π] để:
Hàm số y = sinx nhận giá trị bằng 1; Xem đáp án
Xem đáp án
Đồ thị hàm số y = sinx:
![Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [-2pi; 2pi] để: Hàm số y = sinx nhận giá trị bằng 1 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid50-1689052523.png)
Quan sát đồ thị hàm số y = sinx trên đoạn [‒2π; 2π] ta thấy hàm số y = sinx nhận giá trị bằng 1 tại \(x \in \left\{ { - \frac{{3\pi }}{2};\frac{\pi }{2}} \right\}\).
Câu 44:
Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [‒2π; 2π] để:
Hàm số y = sinx nhận giá trị bằng 0;
 Xem đáp án
Xem đáp án
Đồ thị hàm số y = sinx:
![Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [-2pi; 2pi] để Hàm số y = sinx nhận giá trị bằng 0 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid51-1689052542.png)
Quan sát đồ thị hàm số y = sinx trên đoạn [‒2π; 2π] ta thấy hàm số y = sinx nhận giá trị bằng 0 tại x ∈ {‒2π; ‒π; 0; π; 2π}.
Câu 45:
Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [‒2π; 2π] để:
Hàm số y = cosx nhận giá trị bằng ‒1;
 Xem đáp án
Xem đáp án
Đồ thị hàm số y = cosx:
![Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [-2pi; 2pi] Hàm số y = cosx nhận giá trị bằng -1 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid52-1689052604.png)
Quan sát đồ thị hàm số y = cosx trên đoạn [‒2π; 2π] ta thấy hàm số y = cosx nhận giá trị bằng ‒1 tại x ∈ {‒π; π}.
Câu 46:
Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [‒2π; 2π] để:
Hàm số y = cosx nhận giá trị bằng 0.
 Xem đáp án
Xem đáp án
Đồ thị hàm số y = cosx:
![Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [-2pi; 2pi] để Hàm số y = cosx nhận giá trị bằng 0 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid53-1689052870.png)
Quan sát hai đồ thị hàm số y = cosx trên đoạn [‒2π; 2π] ta thấy hàm số y = cosx nhận giá trị bằng 0 tại \(x \in \left\{ { - \frac{{3\pi }}{2}; - \frac{\pi }{2};\frac{\pi }{2};\frac{{3\pi }}{2}} \right\}\).
Câu 47:
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\) để:
Hàm số y = tanx nhận giá trị bằng ‒1;
 Xem đáp án
Xem đáp án
Xét đồ thị hàm số y = ‒1 và đồ thị hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\):
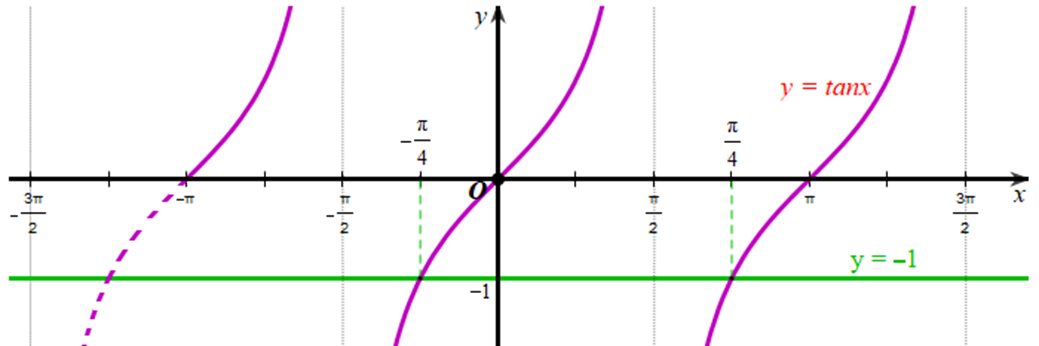
Quan sát đồ thị của hai hàm số, ta thấy hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\) nhận giá trị bằng ‒1 tại \[x \in \left\{ { - \frac{\pi }{4};\frac{\pi }{4}} \right\}\].
Câu 48:
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\) để:
Hàm số y = tanx nhận giá trị bằng 0;
 Xem đáp án
Xem đáp án
Xét đồ thị hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\):
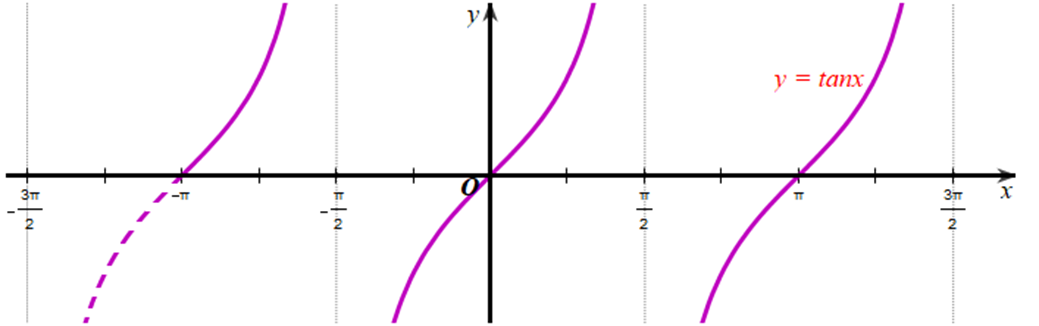
Quan sát hình vẽ, ta thấy hàm số y = tanx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\) nhận giá trị bằng 0 tại x ∈ {0; π}.
Câu 49:
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\) để:
Hàm số y = cotx nhận giá trị bằng 0. Xem đáp án
Xem đáp án
Xét đồ thị hàm số y = cotx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\):
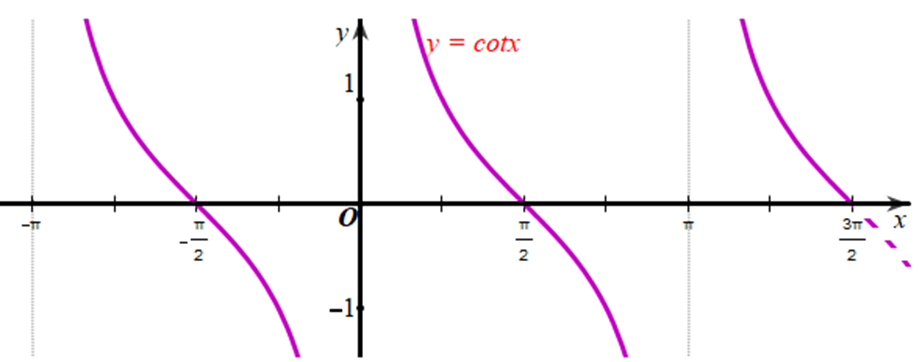
Quan sát hình vẽ, ta thấy hàm số y = cotx trên khoảng \(\left( { - \pi ;\frac{{3\pi }}{2}} \right)\) nhận giá trị bằng 0 tại \[x \in \left\{ { - \frac{\pi }{2};\frac{\pi }{2}} \right\}\].
Câu 50:
Xét sự biến thiên của hàm số sau trên các khoảng tương ứng:
y = cosx trên khoảng (‒20π; ‒19π), (‒9π; ‒8π).
 Xem đáp án
Xem đáp án
Xét hàm số y = cosx:
Do (‒20π; ‒19π) = (0 ‒ 20π; π ‒ 20π) nên hàm số y = cosx nghịch biến trên khoảng (‒20π; ‒19π).
Do (‒9π; ‒8π) = (‒π – 8π; 0 ‒ 8π) nên hàm số y = cosx đồng biến trên khoảng (‒9π; ‒8π).
Câu 51:
Dùng đồ thị hàm số, hãy cho biết:
 Xem đáp án
Xem đáp án
Xét đồ thị hàm số y = m (m ∈ [‒1;1]) và đồ thị hàm số y = cosx trên [0; π]:
![Với mỗi m thuộc [-1;1], có bao nhiêu giá trị alpha thuộc [0; pi] sao cho cos alpha = m (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid1-1689053423.png)
Từ đồ thị của hai hàm số ở hình vẽ trên, ta thấy với mỗi m ∈ [‒1;1] thì hai đồ thị cắt nhau tại 1 điểm.
Vậy m ∈ [‒1;1] sẽ có 1 giá trị α ∈ [0; π] sao cho cosα = m.
Câu 52:
Dùng đồ thị hàm số, hãy cho biết:
Với mỗi m ∈ ℝ, có bao nhiêu giá trị \(\alpha \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) sao cho tanα = m;
 Xem đáp án
Xem đáp án
Xét đồ thị hàm số y = m (m ∈ ℝ) và đồ thị hàm số y = tanx trên \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\):
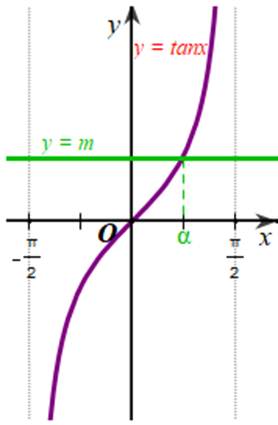
Từ đồ thị của hai hàm số ở hình vẽ trên, ta thấy với mỗi m ∈ ℝ thì hai đồ thị cắt nhau tại 1 điểm.
Vậy với mỗi m ∈ ℝ sẽ có 1 giá trị \(\alpha \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) sao cho tanα = m.
Câu 53:
Dùng đồ thị hàm số, hãy cho biết:
Với mỗi m ∈ ℝ, có bao nhiêu giá trị α ∈ (0; π) sao cho cotα = m.
 Xem đáp án
Xem đáp án
Xét đồ thị hàm số y = m (m ∈ ℝ) và đồ thị hàm số y = cotx trên (0; π):
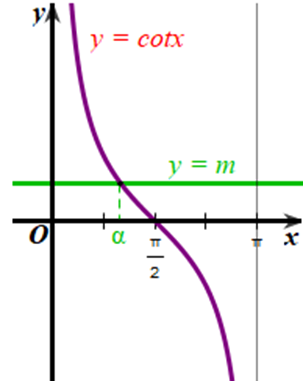
Từ đồ thị của hai hàm số ở hình vẽ trên, ta thấy với mỗi m ∈ ℝ thì hai đồ thị cắt nhau tại 1 điểm.
Vậy với mỗi m ∈ ℝ sẽ có 1 giá trị α ∈ (0; π) sao cho cotα = m.
Câu 54:
Xét tính chẵn, lẻ của các hàm số:
a) y = sinx cosx;
b) y = tanx + cotx;
c) y = sin2x.
 Xem đáp án
Xem đáp án
a) Xét hàm số f(x) = y = sinx cosx có tập xác định D = ℝ:
• ∀x ∈ D thì ‒x ∈ D;
• f(‒x) = sin(‒x) . cos(‒x) = ‒sinx cosx = ‒f(x).
Do đó hàm số y = sinx cosx là hàm số lẻ.
b) Xét hàm số f(x) = y = tanx + cotx có tập xác định \(D = \mathbb{R}\backslash \left\{ {k\pi ;\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\):
• ∀x ∈ D thì ‒x ∈ D;
• f(‒x) = tan(‒x) + cot(‒x) = (‒tanx) + (‒cotx) = ‒(tanx + cotx) = ‒f(x).
Do đó hàm số y = tanx + cotx là hàm số lẻ.
c) Xét hàm số f(x) = y = sin2x có tập xác định D = ℝ:
• ∀x ∈ D thì ‒x ∈ D;
• f(‒x) = sin2(‒x) = (‒sinx)2 = sin2x = f(x).
Do đó hàm số y = sin2x là hàm số chẵn.
Câu 55:
Một dao động điều hoà có phương trình li độ dao động là: x = Acos(ωt + φ), trong đó A, φ, ω là các hằng số (ω > 0). Khi đó, chu kì T của dao động là \(T = \frac{{2\pi }}{\omega }\).
Xác định giá trị của li độ khi t = 0, \(t = \frac{T}{4},t = \frac{T}{2},t = \frac{{3T}}{4}\), t = T.
 Xem đáp án
Xem đáp án
Từ \(T = \frac{{2\pi }}{\omega }\) ta có \(\omega = \frac{{2\pi }}{T}\).
Khi đó ta có phương trình li độ là \(x = A\cos \left( {\frac{{2\pi }}{T}.t + \varphi } \right)\).
• t = 0 thì \(x = A\cos \left( {\frac{{2\pi }}{T}.0 + \varphi } \right) = A\cos \varphi \);
• \(t = \frac{T}{4}\) thì \(x = A\cos \left( {\frac{{2\pi }}{T}.\frac{T}{4} + \varphi } \right) = A\cos \left( {\frac{\pi }{2} + \varphi } \right)\);
• \(t = \frac{T}{2}\) thì \(x = A\cos \left( {\frac{{2\pi }}{T}.\frac{T}{2} + \varphi } \right) = A\cos \left( {\pi + \varphi } \right) = - A\cos \varphi \);
• \(t = \frac{{3T}}{4}\) thì \(x = A\cos \left( {\frac{{2\pi }}{T}.\frac{{3T}}{4} + \varphi } \right) = A\cos \left( {\frac{{3\pi }}{2} + \varphi } \right) = - A\cos \left( {\frac{\pi }{2} + \varphi } \right)\);
• t = T thì \(x = A\cos \left( {\frac{{2\pi }}{T}.T + \varphi } \right) = A\cos \left( {2\pi + \varphi } \right) = A\cos \varphi \).
Câu 56:
Một dao động điều hoà có phương trình li độ dao động là: x = Acos(ωt + φ), trong đó A, φ, ω là các hằng số (ω > 0). Khi đó, chu kì T của dao động là \(T = \frac{{2\pi }}{\omega }\).
Vẽ đồ thị biểu diễn li độ của dao động điều hoà trên đoạn [0; 2T] trong mỗi trường hợp sau:
A = 3 và φ = 0; A = 3 và \(\varphi = - \frac{\pi }{2}\); A = 3 và \(\varphi = \frac{\pi }{2}\).
 Xem đáp án
Xem đáp án
Từ \(T = \frac{{2\pi }}{\omega }\) ta có \(\omega = \frac{{2\pi }}{T}\).
Khi đó ta có phương trình li độ là \(x = A\cos \left( {\frac{{2\pi }}{T}.t + \varphi } \right)\).
* Với A = 3 và φ = 0 thay vào phương trình li độ \(x = A\cos \left( {\frac{{2\pi }}{T}.t + \varphi } \right)\) ta có:
\(x = 3\cos \left( {\frac{{2\pi }}{T}.t} \right)\).
• t = 0 thì x = 3cos0 = 3;
• \(t = \frac{T}{4}\) thì \(x = 3\cos \left( {\frac{{2\pi }}{T}.\frac{T}{4}} \right) = 3\cos \frac{\pi }{2} = 0\);
• \(t = \frac{T}{2}\) thì \(x = 3\cos \left( {\frac{{2\pi }}{T}.\frac{T}{2}} \right) = 3\cos \pi = - 3\)
• \(t = \frac{{3T}}{4}\) thì \(x = 3\cos \left( {\frac{{2\pi }}{T}.\frac{{3T}}{4}} \right) = 3\cos \frac{{3\pi }}{2} = 0\);
• t = T thì \(x = 3\cos \left( {\frac{{2\pi }}{T}.T} \right) = 3\cos 2\pi = 3\)
‒ Vẽ đồ thị biểu diễn li độ của dao động điều hoà \(x = 3\cos \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [0; 2T]:
Xét hàm số \(x = 3\cos \left( {\frac{{2\pi }}{T}.t} \right)\) có chu kì là T.
Ta vẽ đồ thị hàm số \(x = 3\cos \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [0; T] theo bảng sau:
![Vẽ đồ thị biểu diễn li độ của dao động điều hoà trên đoạn [0; 2T] trong mỗi trường (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid4-1689053734.png)
Bằng cách dịch chuyển đồ thị hàm số \(x = 3\cos \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [0; T] song song với trục hoành sang phải theo đoạn có độ dài T, ta sẽ nhận được đồ thị hàm số \(x = 3\cos \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [T; 2T].
Từ đó ta vẽ được đồ thị biểu diễn li độ của dao động điều hoà \(x = 3\cos \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [0; 2T] như sau:
![Vẽ đồ thị biểu diễn li độ của dao động điều hoà trên đoạn [0; 2T] trong mỗi trường (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid5-1689053744.png)
* Với A = 3 và \(\varphi = - \frac{\pi }{2}\) thay vào phương trình li độ \(x = A\cos \left( {\frac{{2\pi }}{T}.t + \varphi } \right)\) ta có:
\(x = 3\cos \left( {\frac{{2\pi }}{T}.t - \frac{\pi }{2}} \right)\)\[ = 3\cos \left( {\frac{\pi }{2} - \frac{{2\pi }}{T}.t} \right) = 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\]
• t = 0 thì \(x = 3\sin \left( {\frac{{2\pi }}{T}.0} \right) = 3\sin 0 = 0\)
• \(t = \frac{T}{4}\) thì \(x = 3\sin \left( {\frac{{2\pi }}{T}.\frac{T}{4}} \right) = 3\sin \frac{\pi }{2} = 3\);
• \(t = \frac{T}{2}\) thì \(x = 3\sin \left( {\frac{{2\pi }}{T}.\frac{T}{2}} \right) = 3\sin \pi = 0\);
• \(t = \frac{{3T}}{4}\) thì \[x = 3\sin \left( {\frac{{2\pi }}{T}.\frac{{3T}}{4}} \right) = 3\sin \frac{{3\pi }}{2} = - 3\];
• t = T thì \[x = 3\sin \left( {\frac{{2\pi }}{T}.T} \right) = 3\sin 2\pi = 0\].
‒ Vẽ đồ thị biểu diễn li độ của dao động điều hoà \(x = 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [0; 2T]:
Xét hàm số \(x = 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\) có chu kì là T.
Ta vẽ đồ thị hàm số \(x = 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [0; T] theo bảng sau:
![Vẽ đồ thị biểu diễn li độ của dao động điều hoà trên đoạn [0; 2T] trong mỗi trường (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid6-1689053755.png)
Bằng cách dịch chuyển đồ thị hàm số \(x = 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [0; T] song song với trục hoành sang phải theo đoạn có độ dài T, ta sẽ nhận được đồ thị hàm số \(x = 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [T; 2T].
Từ đó ta vẽ được đồ thị biểu diễn li độ của dao động điều hoà \(x = 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [0; 2T] như sau:
![Vẽ đồ thị biểu diễn li độ của dao động điều hoà trên đoạn [0; 2T] trong mỗi trường (ảnh 4)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid7-1689053764.png)
* Với A = 3 và \(\varphi = \frac{\pi }{2}\) thay vào phương trình li độ \(x = A\cos \left( {\frac{{2\pi }}{T}.t + \varphi } \right)\) ta có:
\[x = 3\cos \left( {\frac{{2\pi }}{T}.t + \frac{\pi }{2}} \right) = - 3\cos \left[ {\pi - \left( {\frac{{2\pi }}{T}.t + \frac{\pi }{2}} \right)} \right]\]
\( = - 3\cos \left( {\frac{\pi }{2} - \frac{{2\pi }}{T}.t} \right) = - 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\).
• t = 0 thì \(x = - 3\sin \left( {\frac{{2\pi }}{T}.0} \right) = - 3\sin 0 = 0\)
• \(t = \frac{T}{4}\) thì \[x = 3\sin \left( {\frac{{2\pi }}{T}.\frac{T}{4}} \right) = - 3\sin \frac{\pi }{2} = - 3\];
• \(t = \frac{T}{2}\) thì \(x = - 3\sin \left( {\frac{{2\pi }}{T}.\frac{T}{2}} \right) = - 3\sin \pi = 0\);
• \(t = \frac{{3T}}{4}\) thì \[x = - 3\sin \left( {\frac{{2\pi }}{T}.\frac{{3T}}{4}} \right) = - 3\sin \frac{{3\pi }}{2} = 3\];
• t = T thì \[x = - 3\sin \left( {\frac{{2\pi }}{T}.T} \right) = - 3\sin 2\pi = 0\].
‒ Vẽ đồ thị biểu diễn li độ của dao động điều hoà \(x = - 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\) trên đoạn [0; 2T]:
Đồ thị hàm số \(x = - 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\) là hình đối xứng với đồ thị hàm số \(x = 3\sin \left( {\frac{{2\pi }}{T}.t} \right)\) qua trục hoành:
![Vẽ đồ thị biểu diễn li độ của dao động điều hoà trên đoạn [0; 2T] trong mỗi trường (ảnh 5)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid8-1689053775.png)
Câu 57:
Trong bài toán mở đầu, hãy chỉ ra một số giá trị của x để ống đựng nước cách mặt nước 2 m.
 Xem đáp án
Xem đáp án
Để ống đựng nước cách mặt nước 2 m thì h = |y| = 2
\( \Leftrightarrow \left| {2,5\sin \left( {2\pi x - \frac{\pi }{2}} \right) + 2} \right| = 2 \Leftrightarrow \left| { - 2,5\cos \left( {2\pi x} \right) + 2} \right| = 2\)
\( \Leftrightarrow \left[ \begin{array}{l} - 2,5\cos \left( {2\pi x} \right) + 2 = 2\\ - 2,5\cos \left( {2\pi x} \right) + 2 = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\cos \left( {2\pi x} \right) = 0\\\cos \left( {2\pi x} \right) = \frac{8}{5}\end{array} \right.\)
Ta loại trường hợp \[{\rm{cos}}\left( {2\pi x} \right) = \frac{8}{5} > 1\] vì ‒1 ≤ cos(2πx) ≤ 1 với mọi x.
Do đó ta có cos(2πx) = 0.
Ta đã biết cosα = 0 tại những giá trị \[\alpha = \frac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
Suy ra cos(2πx) = 0 \( \Leftrightarrow 2\pi x = \frac{\pi }{2} + k\pi \Leftrightarrow x = \frac{1}{4} + \frac{k}{2}\,\,\left( {k \in \mathbb{Z}} \right)\).
Khi k = 0 thì \(x = \frac{1}{4}\) (phút);
Khi k = 1 thì \(x = \frac{1}{4} + \frac{1}{1} = \frac{5}{4}\) (phút);
Khi k = 2 thì \(x = \frac{1}{4} + \frac{2}{1} = \frac{9}{4}\) (phút);
…
Vậy khi guồng quay được \(\frac{1}{4}\) phút; \(\frac{5}{4}\) phút; \(\frac{9}{4}\) phút; … thì ống đựng nước cách mặt nước 2 m.
