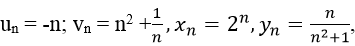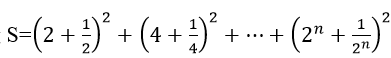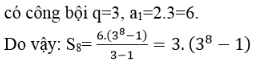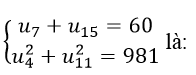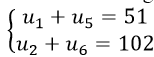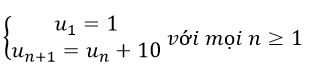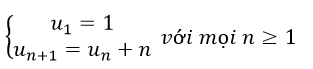Trắc nghiệm Đại số và Giải tích 11 Bài 4(Có đáp án): Cấp số nhân
-
2748 lượt thi
-
31 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 3:
Cho một cấp số nhân có 5 số hạng với công bội dương. Biết rằng số hạng thứ hai bằng 3, số hạng thứ tư bằng 6. Tính tổng của cấp số nhân đó?
 Xem đáp án
Xem đáp án
Kí hiệu u1,u2,u3,u4,u5 là các số hạng của cấp số nhân
Ta có :
Lấy (2) chia (1)
![]()
![]()
![]()
![]()
![]()
Đáp án C
Câu 4:
Cho tam giác ABC cân tại A, có đáy BC, đường cao AH, cạnh bên AB theo thứ tự đó lập thành một cấp số nhân. Hãy tính công bội q của cấp số nhân đó.
 Xem đáp án
Xem đáp án
Theo giả thiết AB=AC, BC,AH,AB lập thành cấp số nhân nên ta có hệ:
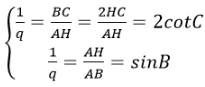
Suy ra: 2cotC =sinB
Mà tam giác ABC cân tại A nên
Từ đó ta có kết quả sau: 2cotC = sinC ⇔ 2cosC =sin2C = 1-cos2C
⇔ cos2C + 2cosC -1 =0 ⇒cosC = -1 +√2 (0° < C < 90°)
Do C là góc nhọn nên :
![]()
Cho nên công bội của cấp số nhân là:
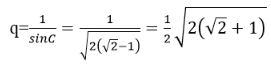
Đáp án C.
Câu 5:
Tìm các số (x,y) biết y < 0 và các số x+6y, 5x+2y, 8x+y theo thứ tự lập thành cấp số cộng đồng thời các số x+5/3, y -1, 2x – 3y theo thứ tự đó lập thành một cấp số nhân.
 Xem đáp án
Xem đáp án
Ta có hệ phương trình:
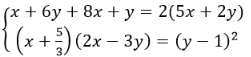
Từ đó ta suy ra
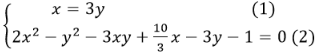
Thế (1) vào (2) ta được:
8y2+ 7y - 1=0⇒ y = -1 hoặc y=1/8
Do y < 0 , ta được y = -1, x = -3
Đáp án B
Câu 6:
Số hạng đầu tiên của cấp số nhân (un) thoả mãn hệ :
 Xem đáp án
Xem đáp án
Chọn B
Lấy (2) chia (1) ta được: q = 2
Thay vào (1) ta được:
Vậy .
Câu 7:
Công bội nguyên dương của cấp số nhân thoả mãn :
 Xem đáp án
Xem đáp án
Chọn B
Gọi 3 số cần tìm là
Theo giả thiết ta có:
Giải (*)
Theo đề là công bội nguyên dương do đó q = 2
Câu 8:
Cho ba số phân biệt tạo thành một cấp số nhân mà tổng của chúng bằng 93. Ta có thể sắp xếp chúng (theo thứ tự của cấp số nhân kế trên) như là số hạng thứ nhất, thứ hai và thứ bảy của một cấp số cộng. Tìm tích của 3 số đó.
 Xem đáp án
Xem đáp án
Gọi ba số cần tìm là theo thứ tự là số hạng thứ 1, thứ 2 và thứ 7 của cấp số cộng, công sai d.
Suy ra:
Ba số này có tổng là 93 nên:
Ba số này là ba số hạng liên tiếp của cấp số nhân nên:
+ Nếu ( không thỏa mãn (3) ) nên số hạng đầu khác 0.
Chia cả 2 vế của (3) cho ta được:
+ Nếu Thay vào (2)
Tích ba số cần tìm là 3.15. 75 = 3375
+ Nếu thay vào (2) ta được
( loại vì 3 số này trùng nhau)
Đáp án A
Câu 9:
Độ dài các cạnh của một tam giác ABC lập thành một cấp số nhân. Tam giác ABC có tối đa mấy góc không vượt qua 60°?
 Xem đáp án
Xem đáp án
Chọn C
Giả sử ba cạnh của tam giác ABC là a,b,c.
Không mất tính tổng quát, ta giả sử 0 < a ≤b ≤c,
Nếu chúng tạo thành cấp số nhân thì theo tính chất của cấp số nhân ta có: b2=ac.
Theo định lý hàm côsin Ta có:
![]()
![]()
Mặt khác
Vậy góc ,mà , cho nên tam giác ABC có hai góc không quá 60°
Câu 10:
Tìm số hạng đầu của cấp số nhân có bốn số hạng (công bội , biết tổng ba số hạng đầu bằng , đồng thời theo thứ tự, chúng là số hạng thứ nhất, thứ tư và thứ tám của một cấp số cộng.
 Xem đáp án
Xem đáp án
Chọn A
Gọi u1,u2,u3,u4 là 4 số hạng đầu tiên của cấp số nhân, với công bội q. gọi (vn) là cấp số cộng tương ứng với công sai là d. Theo giả thuyết Ta có:
Khử d từ (2) và (3) ta thu được:
Lấy vế trừ vế ta thu được
Do
Theo giả thiết, suy ra
Thay vào (1) ta được
Câu 11:
Cho 3 số x, 3, y lập thành một cấp số nhân và . Tìm công bội q của cấp số đó
 Xem đáp án
Xem đáp án
Chọn B
Theo giả thuyết:
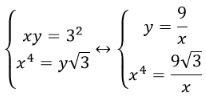
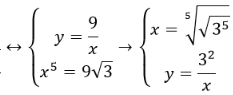
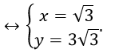
![]()
Câu 12:
Cho dãy số (un):
Khi đó số hạng thứ năm của dãy số là:
 Xem đáp án
Xem đáp án
Chọn A
Ta có u2=u1+1=2, u3=u2+2=4, u4=u3+3=7, u5=u4+4=11
Câu 14:
Trong các dãy số:
có bao nhiêu dãy số bị chặn trên
 Xem đáp án
Xem đáp án
Chọn B
![]()
![]()
nên có hai dãy bị chặn trên
Câu 15:
Cho tam giác ABC có các cạnh tương ứng a,b,c. Biết A =90° và a,, c theo thứ tự lập thành một cấp số nhân. Tìm số đo góc B.
 Xem đáp án
Xem đáp án
Chọn D
Theo tính chất cấp số nhân, Ta có: ac=2/3 b2. Theo hệ thức lượng trong tam giác vuông, Ta có: b=a.sinB, c=a.cosB. vậy Ta có
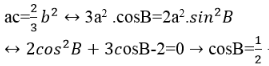
![]()
Câu 16:
Tìm m để phương trình có bốn nghiệm lập thành một cấp số cộng.
 Xem đáp án
Xem đáp án
Giả sử 4 nghiệm phân biệt của phương trình là x1,x2,x3,x4.
Đặt x2= y ≥0, ta được phương trình y2-(3m+5)y+(m+1)2=0(1)
Ta phải tìm m sao cho (1) có hai nghiệm dương phân biệt 0 < y1 < y2.
Khi đó thì (1) có bốn nghiệm là:
Theo đầu bài bốn nghiệm lập thành một cấp số cộng, nên x3+x1=2x2 và x4+x2=2x3
![]()
![]()
Áp dụng định lý Vi-et cho phương trình (1). Ta có hệ:
và
Thay vào định lí Viet
Thay (*) vào hệ trên ta được :
Thay (1) vào (2) ta được:
Chọn B
Câu 17:
Tính tổng :
 Xem đáp án
Xem đáp án
Ta có
Áp dụng công thức tính tổng n số hạng đầu tiên của cấp số nhân:
Chọn C
Câu 18:
Giẳ sử các số lập thành một cấp số cộng, còn các số lập thành cấp số nhân . Hiệu của x- y dương bằng?
 Xem đáp án
Xem đáp án
Từ giả thiết ta có:
Như vậy có 2 trường hợp xảy ra:
hoặc
Suy ra, có 1 trường hợp .
Chọn đáp án B.
Câu 19:
Từ 0 giờ đến 12 giờ trưa, đông dồ đánh bao nhiêu tiếng chuông nếu nó chỉ đánh chuông báo giờ và tiếng chuông bằng số giờ?
 Xem đáp án
Xem đáp án
Chọn B
Lúc 1h , đồng hồ đánh chuông 1 lần
2h, đồng hồ đánh chuông 2 lần
....12 h đồng hồ đánh chương 12 lần.
Số tiếng chuông đồng hồ bằng S=1+2+3+4+…+12 = =78 tiếng
( đây là tổng của 1 cấp số cộng có , công sai d = 1)
Câu 20:
Giả sử a,b,c ,d lập thành một cấp số nhân. Tính giá trị biểu thức
 Xem đáp án
Xem đáp án
Chọn D
Gọi công bội của cấp số nhân đã cho là q.
Ta có
Câu 21:
Công bội nguyên dương của cấp số nhân thoả mãn :
 Xem đáp án
Xem đáp án
Chọn B
Ta giải hệ:
Giải (*)
TH1:
TH2;
Vậy q=2
Câu 23:
Người ta thiết kế 1 cái tháp gồm 11 tầng. Diện tích bề mặt của mỗi tầng bằng nửa diện tích của bề mặt của tầng ngay bên dưới và diện tích của bề mặt tầng một bằng nửa diện tích của đế tháp. Biết diện tích của đế tháp là . Diện tích bề mặt của tầng trên cùng là:
 Xem đáp án
Xem đáp án
Chọn C
Diện tích bề mặt của tầng 1 là
Diện tích bề mặt của mỗi tầng bằng nửa diện tích của bề mặt của tầng ngay bên dưới .
Do đó, dãy số diện tích bề mặt mỗi tầng lập thành cấp số nhân với , công bội
Diện tích mặt trên cùng là:
Câu 24:
Một công sai của cấp số cộng () thoả mãn:
 Xem đáp án
Xem đáp án
Chọn A
Ta có:
Từ (1); thay vào(2) ta được:
Câu 25:
Tìm tổng 5 số hạng đầu tiên của cấp số nhân, biết
 Xem đáp án
Xem đáp án
Chọn D
Ta giải hệ
Lấy (2) chia (1) ta tìm được q=2
Thay vào (1), suy ra
Câu 26:
Cho dãy số :
Khi đó số hạng thứ 10 của dãy số là
 Xem đáp án
Xem đáp án
Chọn D
Vì
Suy ra,dãy (un) là cấp số cộng có công sai d=10
Do đó, u10 = u1+9d = 1 + 9.10 = 91
Câu 27:
Giá tiền công khoan giếng ở cơ sở B được tính như sau: giá của mét khoan đầu tiên là 6000 đồng và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm 7% so với giá của mét khoan ngay trước đó. Vậy muốn khoan 20 mét thì tốn bao nhiêu tiền (tính bằng đồng)?
 Xem đáp án
Xem đáp án
Chọn C
Giá của các mét khoan lập thành cấp số nhân với , công bội
Suy ra, giá khi khoan 20 mét là:
![]()
Câu 28:
Tìm công sai dương của cấp số cộng ba số hạng, biết tổng của chúng bằng 9 và tổng bình phương bằng 125.
 Xem đáp án
Xem đáp án
Chọn A
Gọi d là công sai. Ba số phải tìm là: (x-d); x; (x+d). Ta có hệ phương trình
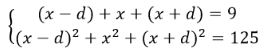
Vì công sai dương nên d = 7
vậy 3 số cần tìm là : - 4; 3; 10
Câu 29:
Cho các dãy số :
Trong các dãy số trên có bao nhiêu dãy bị chặn trên?
 Xem đáp án
Xem đáp án
Chọn A
Trong bốn dãy số chỉ có yn=n/(n+1) < 1 nên có 1 dãy bị chặn trên
Câu 30:
Một cấp số nhân dương có 4 số hạng, công bội q bằng 1/4 lần số hạng thứ nhất, tổng của hai số hạng đầu bằng 24. Tìm tích các số hạng cấp số nhân đó?
 Xem đáp án
Xem đáp án
Vì công bội bằng 1/4 lần số hạng thứ nhất nên:
Vì tổng của hai số hạng đầu bằng 24 nên:
Khi đó, q = 2.
Vậy cấp số nhân cần tìm là : 8; 16; 32; 64
Tích các số hạng đó là: 8. 16. 32. 64 = 262 144
Chọn D
Câu 31:
Cho dãy số :
Khi đó số hạng thứ 5 của dãy số là:
 Xem đáp án
Xem đáp án
Chọn A
Ta có u2=u1+1=2, u3=u2+2=4, u4=u3+3=7, u5=u4+4=11