Dạng 1: Xác định và tính góc giữa hai đường thẳng có đáp án
-
161 lượt thi
-
10 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Cho hình hộp ABCD.A'B'C'D'. Giả sử tam giác AB'C và A'DC' đều có 3 góc nhọn. Góc giữa hai đường thẳng AC và A'D là góc nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
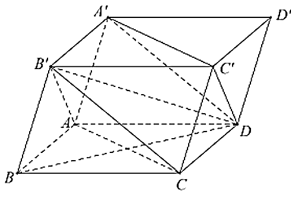
Ta có: AC // A'C' (do ABCD.A'B'C'D') là hình hộp.
Do đó, (AC, A'D) = (A'C', A'D) = (do giả thiết tam giác DA'C' nhọn).
Câu 2:
Cho tứ diện đều ABCD có tất cả các cạnh bằng nhau. Số đo góc giữa hai đường thẳng CD và AB là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
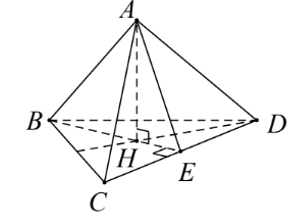
Gọi H là tâm đường tròn ngoại tiếp tam giác BCD
Do đó, AH vuông góc với (BCD).
ABCD là tứ diện đều tất cả các cạnh bằng nhau nên tam giác BCD đều.
Gọi E là trung điểm của CD ⇒ BE vuông góc với CD.
Do AH vuông góc với (BCD) nên AH vuông góc với CD.
Ta có: .Câu 3:
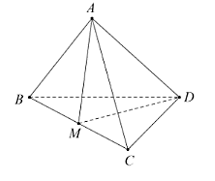
Cho tứ diện đều ABCD, M là trung điểm của BC. Khi đó cos(AB, DM) bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Không mất tính tổng quát, giả sử tứ diện ABCD có cạnh bằng a.
Gọi H là tâm đường tròn ngoại tiếp tam giác BCD nên AH vuông góc với (BCD).
Gọi E là trung điểm AC, ta có:
ME // AB ⇒ (AB, DM) = (ME, MD)
Ta có: cos(AB, DM) = cos(ME, MD)
Do các mặt của tứ diện đều là tam giác đều, từ đó ta dễ dàng tính được độ dài các cạnh của tam giác MED: ME = ; ED = MD = .
Xét tam giác MED, ta có:
.
Từ đó .
Câu 4:
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo của góc (MN, SC) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
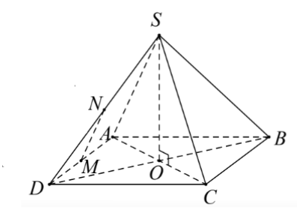
Gọi O là tâm của hình vuông ABCD, do đó, O là tâm đường tròn ngoại tiếp của hình vuông ABCD (1)
Ta có: SA = SB = SC = SD nên S nằm trên trục của đường tròn ngoại tiếp hình vuông ABCD (2).
Từ (1) và (2) ta có: SO vuông góc với (ABCD).
Từ giả thiết ta có: MN song song với SA (do MN là đường trung bình của tam giác SAD)
⇒ (MN, SC) = (SA, SC)
Xét tam giác SAC có:
SA2 + SC2 = a2 + a2 = 2a2
AC2 = AD2 + DC2 = 2a2
Suy ra SA2 + SC2 = AC2.
Do đó, tam giác SAC vuông tại S nên SA vuông góc với SC.
Vậy (MN, SC) = (SA, SC) = 90°.
Câu 5:
Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo của góc (IJ, CD) bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
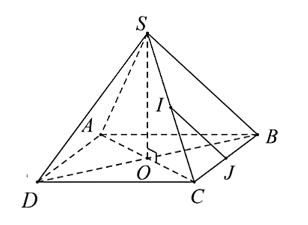
Gọi O là tâm của hình vuông ABCD
Do đó, O là tâm của đường tròn ngoại tiếp của hình vuông ABCD (1)
Ta có: SA = SB = SC = SD nên S nằm trên trục của đường tròn ngoại tiếp hình vuông ABCD (2)
Từ (1) và (2) ⇒ SO vuông góc với (ABCD)
Ta lại có: IJ // SB (do IJ là đường trung bình của tam giác SAB)
⇒ (IJ, CD) = (SB, AB)
Mặt khác, ta lại có tam giác SAB đều, do đó ⇒ (IJ, CD) = (SB, AB) = .
Câu 6:
Cho tứ diện ABCD có AB = CD. Gọi I, J, E, F lần lượt là trung điểm của AC, BC, BD, AD. Góc giữa (IE, JF) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
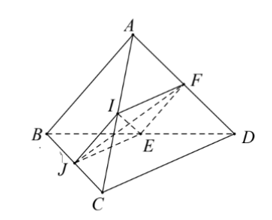
Do I, J, E, F lần lượt là trung điểm của AC, BC, BD, AD. Do đó IJ là đường trung bình của tam giác ABC, EF là đường trung bình của tam giác ABD, JE là đường trung bình của tam giác BCD, IF là đường trung bình của tam giác ACD.
Từ đó, ta có:
IJ // EF // AB
JE // IF // CD
Do đó, tứ giác IJEF là hình bình hành
Mặt khác: AB = CD ⇒ IJ = AB =
Do đó, ABCD là hình thoi.
Do đó, IE vuông góc với JF (tính chất hai đường chéo của hình thoi)
⇒ .
Câu 7:
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa hai đường thẳng AB, DH bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
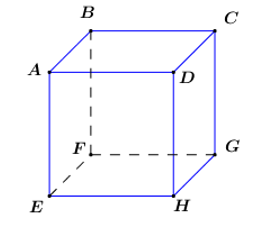
Ta có:
AE // DH (do ABCD.EFGH là hình lập phương)
AE cắt AB tại A
⇒ (AB, DH) = (AE, AB)
Mà AE vuông góc với AB nên (AB, DH) = (AE, AB) = .
Câu 8:
Trong không gian cho hai hình vuông ABCD và ABC'D' có chung cạnh AB và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm O và O'. Hãy xác định góc giữa hai đường thẳng AB và OO'?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
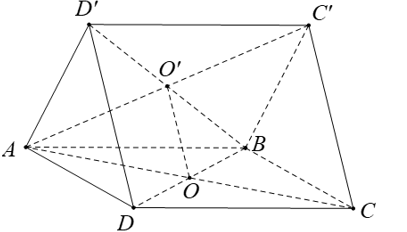
Vì ABCD và ABC'D' là hình vuông nên AD // BC'; AD = BC'
⇒ ADBC' là hình bình hành
Mà O, O' là tâm của 2 hình vuông nên O, O' là trung điểm của BD và AC'
Do đó, OO' là đường trung bình của ADBC'.
Do đó, OO' song song với AD.
Mặt khác, AD vuông góc với AB nên OO' vuông góc với AD nên (OO', AB) = .
Câu 9:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Giả sử cạnh của tứ diện là a.
Ta có:
Mặt khác:
.Câu 10:
Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo của góc (IJ, CD) bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
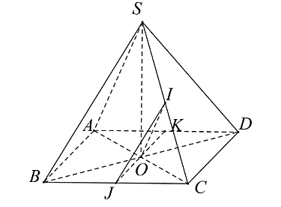
Gọi O là tâm của hình thoi ABCD
Ta có: OJ // CD
Nên (IJ, CD) = (IJ, OJ)
Nên góc giữa IOJ và CD bằng góc giữa IJ và OJ
Xét tam giác IOJ có:
Nên tam giác IOJ đều
Vậy (IJ, CD) = (IJ, OJ) = = .
