Đề kiểm tra Cuối kì 1 Toán 11 Cánh Diều có đáp án - Đề 01
-
116 lượt thi
-
38 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Trên đường tròn lượng giác, gọi \(M\left( {{x_0};{y_0}} \right)\) là điểm biểu diễn cho góc lượng giác có số đo \(\alpha \). Mệnh đề nào đúng trong các mệnh đề sau?
Xem đáp án
Chọn A
Câu 4:
Xem đáp án
Chọn A
Câu 5:
Tập xác định của hàm số \[y = \tan \left( {x + \frac{\pi }{3}} \right)\] là
Xem đáp án
Chọn A
Câu 9:
Với những giá trị nào của \(m\) thì phương trình \({\cos ^2}x - m = 2\) có nghiệm?
Xem đáp án
Chọn D
Câu 11:
Cho dãy số \(\left( {{u_n}} \right)\), biết \(\left\{ \begin{array}{l}{u_1} = 1\\{u_{n + 1}} = {u_n} + n\end{array} \right.\) với \(n \ge 1\). Số hạng thứ 3 của dãy số đó là:
Xem đáp án
Chọn A
Câu 12:
Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_1} = 5\) và \({u_2} = 1.\) Công sai của cấp số cộng đã cho bằng
Xem đáp án
Chọn B
Câu 13:
Cho tam giác \(ABC\) có số đo của ba góc lập thành cấp số cộng và số đo góc nhỏ nhất bằng \(30^\circ .\) Góc có số đo lớn nhất trong ba góc của tam giác này là
Xem đáp án
Chọn B
Câu 14:
Cho cấp số nhân có các số hạng lần lượt là \(2;\,\,4;\,\,8;\,\,16;...\) Số hạng tổng quát \({u_n}\) của cấp số nhân đó là
Xem đáp án
Chọn C
Câu 15:
Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = - 2\) và công bội \(q = \frac{1}{2}\). Số hạng thứ \(10\) của cấp số nhân là
Xem đáp án
Chọn A
Câu 16:
Cho hai dãy \(\left( {{u_n}} \right)\) và \(\left( {{v_n}} \right)\) thỏa mãn \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = \frac{1}{2}\) và \(\mathop {\lim }\limits_{n \to + \infty } {v_n} = - 2.\) Giá trị của \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n}.{v_n}} \right)\) bằng
Xem đáp án
Chọn A
Câu 17:
Biết \(\mathop {\lim }\limits_{n \to + \infty } \frac{{{{\left( {1 - 2n} \right)}^3}}}{{a{n^3} + 2}} = 4\) với \(a\) là tham số. Khi đó \(a - {a^2}\) bằng
Xem đáp án
Chọn B
Câu 18:
Xem đáp án
Chọn A
Câu 19:
Kết quả của giới hạn \(\mathop {\lim }\limits_{x \to - 1} \left( {x + 1} \right)\) là
Xem đáp án
Chọn A
Câu 20:
Hàm số \(y = f\left( x \right)\) có đồ thị như hình dưới đây:
Hàm số gián đoạn tại điểm
Xem đáp án
Chọn A
Câu 21:
Cho các hàm số \(y = \cos x\,\,\,\left( I \right)\), \(y = \sin \sqrt x \,\,\left( {II} \right)\) và \(y = \tan x\,\,\,\left( {III} \right)\). Hàm số nào liên tục trên \(\mathbb{R}\)?
Xem đáp án
Chọn B
Câu 22:
Tìm khẳng định đúng trong các khẳng định sau:
I. \[f\left( x \right)\] liên tục trên đoạn \[\left[ {a;b} \right]\] và \[f\left( a \right) \cdot f\left( b \right) < 0\] thì phương trình \[f\left( x \right) = 0\] có nghiệm.
II. \[f\left( x \right)\] không liên tục trên \[\left[ {a;b} \right]\] và \[f\left( a \right) \cdot f\left( b \right) \ge 0\] thì phương trình \[f\left( x \right) = 0\] vô nghiệm.
Xem đáp án
Chọn A
Câu 23:
Cho hình chóp tứ giác \(S.ABCD.\) Gọi \(O\) là giao điểm của \(AC\) và \[BD.\] Trong các mặt phẳng sau, điểm \(O\) không nằm trên mặt phẳng nào?
Xem đáp án
Chọn B
Câu 25:
Cho tứ diện \(ABCD,\) vị trí tương đối của hai đường thẳng \(AC\) và \(BD\) là
Xem đáp án
Chọn C
Câu 26:
Cho tứ diện \(ABCD.\) Gọi \(I,\,\,J\) lần lượt là trọng tâm của các tam giác \(ABC\) và \(ABD.\) Khẳng định nào sau đây đúng?
Xem đáp án
Chọn D
Câu 27:
Cho đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) không có điểm chung. Kết luận nào sau đây đúng?
Xem đáp án
Chọn C
Câu 28:
Cho hình chóp tứ giác \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Khẳng định nào sau đây sai?
Xem đáp án
Chọn D
Câu 29:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\) là đường thẳng song song với mặt phẳng nào sau đây?
Xem đáp án
Chọn A
Câu 31:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O.\) Gọi \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(SA,\,\,SD,\,\,AB.\) Khẳng định nào sau đây đúng?
Xem đáp án
Chọn B
Câu 33:
Cho hình lăng trụ \[ABC.{A_1}{B_1}{C_1}.\] Trong các khẳng định sau, khẳng định nào sai?
Xem đáp án
Chọn D
Câu 36:
Tính các giới hạn sau:
a) \[\mathop {\lim }\limits_{n \to + \infty } \left( {1 + n - {n^2}} \right).\] b) \[\mathop {\lim }\limits_{x \to 2} \frac{{{x^3} - 8}}{{{x^2} - 4}}.\]
Xem đáp án
a) Ta có: \[1 + n - {n^2} = {n^2}\left( {\frac{1}{{{n^2}}} + \frac{1}{n} - 1} \right).\]
Mặt khác: \(\mathop {\lim }\limits_{n \to + \infty } {n^2} = + \infty ;\)
\(\mathop {\lim }\limits_{n \to + \infty } \left( {\frac{1}{{{n^2}}} + \frac{1}{n} - 1} \right) = \mathop {\lim }\limits_{n \to + \infty } \frac{1}{{{n^2}}} + \mathop {\lim }\limits_{n \to + \infty } \frac{1}{n} - \mathop {\lim }\limits_{n \to + \infty } 1 = 0 + 0 - 1 = - 1 < 0.\)
\( \Rightarrow \mathop {\lim }\limits_{n \to + \infty } \left( {1 + n - {n^2}} \right) = \mathop {\lim }\limits_{n \to + \infty } \left[ {{n^2}\left( {\frac{1}{{{n^2}}} + \frac{1}{n} - 1} \right)} \right] = \mathop {\lim }\limits_{n \to + \infty } {n^2}.\mathop {\lim }\limits_{n \to + \infty } \left( {\frac{1}{{{n^2}}} + \frac{1}{n} - 1} \right) = - \infty .\)
b) \[\mathop {\lim }\limits_{x \to 2} \frac{{{x^3} - 8}}{{{x^2} - 4}} = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right)}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} + 2x + 4}}{{x + 2}} = \frac{{{2^2} + 2.2 + 4}}{{2 + 2}} = 3.\]
Câu 37:
Cho hình lăng trụ tam giác \(ABC.A'B'C'\). Gọi \(M,\,N\) lần lượt là trung điểm của \(A'B'\) và \(AB\).
a) Chứng minh \(CB'\,\,{\rm{//}}\,\left( {AMC'} \right)\).
b) Mặt phẳng \(\left( P \right)\) đi qua \(N\) song song với hai cạnh \(AB'\) và \(AC'\). Tìm giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( {BB'C'} \right)\).
Xem đáp án
a)
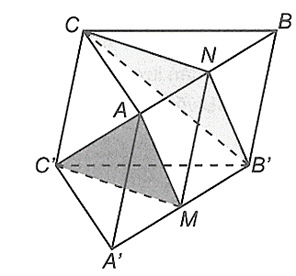
Vì \(M,\,N\) lần lượt là trung điểm của \(A'B'\) và \(AB\) nên \(MN\) là đường trung bình của hình thang \(ABB'A'\). Suy ra \(MN{\rm{//}}AA'\) và \(MN\, = \,AA'\) (do \(ABB'A'\) là hình bình hành).
Ta có: \[MN{\rm{//}}AA'\] và \[AA'{\rm{//}}CC'\] (tính chất hình lăng trụ).
\[ \Rightarrow MN{\rm{//AA'}}{\rm{.}}\]
Lại có \(AA' = CC'\) (tính chất hình lăng trụ), mà \(MN\, = \,AA'\) nên \[MN = CC'\].
Do đó, tứ giác \[MNCC'\] là hình bình hành. Suy ra \[CN{\rm{//}}MC'.\]
Ta có \[\left\{ \begin{array}{l}CN{\rm{ // }}MC'\\MC' \subset \left( {AMC'} \right)\end{array} \right. \Rightarrow CN{\rm{ // }}\left( {AMC'} \right).\]
Mặt khác ta chứng minh được \[AN{\rm{//}}B'M;\,\,AN = B'M\] nên tứ giác \[ANB'M\] là hình bình hành. Suy ra \[NB'{\rm{//}}MA.\]
Ta có \[\left\{ \begin{array}{l}NB'{\rm{//}}MA\\MA \subset \left( {AMC'} \right)\end{array} \right. \Rightarrow NB'{\rm{//}}\left( {AMC'} \right).\]
Lại có \[\left\{ \begin{array}{l}CN{\rm{//}}\left( {AMC'} \right)\\NB'{\rm{//}}\left( {AMC'} \right)\\CN,NB' \subset \left( {CNB'} \right)\\CN \cap NB' = \left\{ N \right\}\end{array} \right. \Rightarrow \left( {AMC'} \right){\rm{//}}\left( {CNB'} \right).\]
Mà \[CB' \subset \left( {CNB'} \right).\,\,\,{\rm{Suy}}\,\,{\rm{ra}}\,\,\,CB'\,{\rm{//}}\,\left( {AMC'} \right)\].
b)
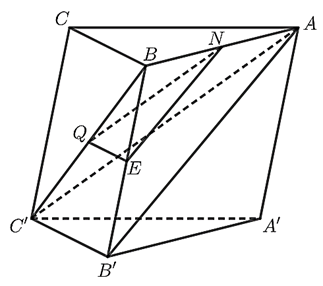
Trong mặt phẳng \(\left( {ABB'A'} \right)\), kẻ đường thẳng qua \(N\) song song với \(AB'\), cắt \(BB'\) tại \(E\).
Trong mặt phẳng \(\left( {ABC'} \right)\), kẻ đường thẳng qua \(N\) song song với \(AC'\), cắt \(BC'\) tại \(Q\).
Khi đó, mặt phẳng \(\left( P \right)\) chính là mặt phẳng \(\left( {NQE} \right)\).
Vì \(E \in BB'\) nên \(E \in \left( {BB'C'} \right)\); vì \(Q \in BC'\) nên \(Q \in \left( {BB'C'} \right)\). Do đó, \(EQ \subset \left( {BB'C'} \right)\).
Vậy \[\left( {NQE} \right) \cap \left( {BB'C'} \right)\,\, = \,\,EQ\] hay \[\left( P \right) \cap \left( {BB'C'} \right)\,\, = \,\,EQ\].
Câu 38:
Xem đáp án
Hình vuông đầu tiên \(\left( {{C_1}} \right)\) có cạnh bằng \(a\) và diện tích là \({S_1} = {a^2}\).
Từ đề bài, ta thấy cạnh của hình vuông \(\left( {{C_2}} \right)\) là \({a_2} = \sqrt {{{\left( {\frac{3}{4}a} \right)}^2} + {{\left( {\frac{1}{4}a} \right)}^2}} = \frac{{a\sqrt {10} }}{4}\).
Khi đó diện tích của hình vuông \(\left( {{C_2}} \right)\) là \({S_2} = {\left( {\frac{{a\sqrt {10} }}{4}} \right)^2} = \frac{5}{8}{a^2} = \frac{5}{8}{S_1}\).
Cạnh của hình vuông \(\left( {{C_3}} \right)\) là \({a_3} = \sqrt {{{\left( {\frac{3}{4}{a_2}} \right)}^2} + {{\left( {\frac{1}{4}{a_2}} \right)}^2}} = \frac{{{a_2}\sqrt {10} }}{4} = a{\left( {\frac{{\sqrt {10} }}{4}} \right)^2} = \frac{5}{8}a.\)
Khi đó diện tích của hình vuông \(\left( {{C_3}} \right)\) là \({S_3} = {\left( {\frac{5}{8}a} \right)^2} = {\left( {\frac{5}{8}} \right)^2}{a^2} = {\left( {\frac{5}{8}} \right)^2}{S_1}.\)
Lý luận tương tự ta có \({S_1},\,\,{S_2},\,\,{S_3},\,\,...,\,{S_n},\,...\) tạo thành một dãy cấp số nhân \({u_1} = {S_1} = {a^2}\) và công bội \(q = \frac{5}{8}\).
Vì \(\left| q \right| = \frac{5}{8} < 1\) nên \({S_1},\,\,{S_2},\,\,{S_3},\,\,...,\,{S_n},\,...\) là một cấp số nhân lùi vô hạn với \({u_1} = {S_1} = {a^2}\) và công bội \(q = \frac{5}{8}.\)
Tổng của cấp số nhân lùi vô hạn này là
\(T = {S_1} + {S_2} + {S_3} + ... + {S_n} + ...\)\( = \frac{{{S_1}}}{{1 - q}} = \frac{{{a^2}}}{{1 - \frac{5}{8}}} = \frac{{8{a^2}}}{3}\).
Mà \(T = \frac{{32}}{3}\) nên \(\frac{{8{a^2}}}{3} = \frac{{32}}{3} \Leftrightarrow {a^2} = 4\). Suy ra \(a = 2\) (do độ dài cạnh là số dương).