Đề thi Toán lớp 6 có đáp án Giữa kì 1 (Đề 4)
-
3343 lượt thi
-
32 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
Biển báo có dạng là tam giác đều là biển báo 1
Chọn đáp án C.
Câu 2:
Xem đáp án
5.5.5.5 = 54(tích của 4 thừa số 5).
Chọn đáp án B.
Câu 3:
Xem đáp án
Để tìm ước của 15 ta chia lần lượt số đó cho 2; 5; 6; 4 để xét xem 15 chia hết cho những số nào, khi đó số được chia hết sẽ là ước của 15.
Ta thấy trong 4 đáp án thì 15 chỉ chia hết cho 5.
Chọn đáp án D.
Câu 4:
Xem đáp án
Dấu hiệu chia hết cho 2: “Các số có chữ số tận cùng là 0; 2; 4; 6; 8 thì chia hết cho 2.”
Vây trong 4 số 326; 124; 963; 148 có 3 số chia hết cho 2.
Chọn đáp án D.
Câu 5:
Xem đáp án
Khẳng định đúng là 1 ∈ P.
Chọn đáp án A.
Câu 6:
Xem đáp án
11 lớn hơn 1, chỉ chia hết cho 1 và chính nó → Số nguyên tố
15 lớn hơn 1, chia hết cho 1, 3, 5 và chính nó → Hợp số
26 lớn hơn 1, chia hết cho 1, 2, 13 và chính nó → Hợp số
12 lớn hơn 1, chia hết cho 1, 2, 3, 4, 6, và chính nó → Hợp số
31 lớn hơn 1, chỉ chia hết cho 1 và chính nó → Số nguyên tố
Vậy có 3 hợp số.
Chọn đáp án D.
Câu 7:
Xem đáp án
Trong thiết kế logo Mitsubishi được tạo nên bởi 3 hình thoi.
Chọn đáp án A.
Câu 8:
Xem đáp án
Trong các số trên, số nguyên tố là 17, vì 17 lớn hơn 1, chỉ có hai ước là 1 và 17.
Chọn đáp án A.
Câu 9:
Xem đáp án
Dấu hiệu chia hết cho 5: “Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5.”
Vậy số chia hết cho 5 trong các số trên là: 125.
Chọn đáp án B.
Câu 10:
Xem đáp án
79 + 114 + 21 + 86
= (79 + 21) + (114 + 86)
= 100 + 200 = 300
Chọn đáp án A.
Câu 11:
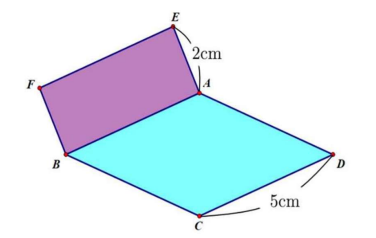
Xem đáp án
ABCD là hình thoi nên AB = BC = AD = CD = 5cm
Diện tích hình chữ nhật ABCD là: AB. AE = 5.2 = 10 (cm2).
Chọn đáp án C.
Câu 12:
Xem đáp án
Các số tự nhiên lẻ nhỏ hơn 7 là: 1, 3, 5.
Vậy tập hợp E gồm các số tự nhiên lẻ, nhỏ hơn 7 là: E = {1; 3; 5}
Chọn đáp án D.
Câu 13:
Xem đáp án
22 – 2.(32+ 1)
= 22 – 2.(9 + 1)
= 22 – 2.10
= 22 – 20
= 2
Chọn đáp án D.
Câu 14:
Xem đáp án
Ta có: 100 = 4.25 = 22.52
Chọn đáp án C.
Câu 15:
Xem đáp án
Chu vi hình chữ nhật là:
(8 + 6).2 = 28 (cm)
Chu vi hình thoi có công thức P = 4a
Do đó một cạnh của hình thoi bằng:
28 : 4 = 7 (cm)
Chọn đáp án B.
Câu 16:
Xem đáp án
36.29 + 36.71
= 36.(29 + 71)
= 36.100
= 3600
Chọn đáp án A.
Câu 17:
Xem đáp án
Ta có: 121 = 11 . 11
Do đó một cạnh của hình vuông là: 11 (cm)
Chu vi hình vuông là:
11.4 = 44 (cm)
Chọn đáp án D.
Câu 18:
Xem đáp án
Ta có: 7 + 1 + * = 8 + *
Để \(\overline {71*} \) chia hết cho 9 thì (8 + *) chia hết cho 9
Số * thỏa mãn là 1.
Chọn đáp án D.
Câu 19:
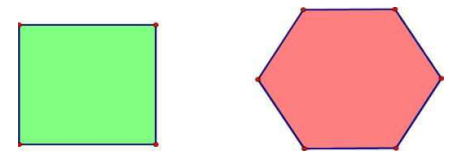
Xem đáp án
Chu vi hình vuông là:
6.4 = 24 (cm)
Chu vi hình vuông bằng chu vi lục giác đều và bằng 24 cm
Độ dài cạnh của lục giác đều là:
24 : 6 = 4 (cm)
Chọn đáp án C.
Câu 20:
Xem đáp án
Cách 1:
Ta có:
12 = 22.3
20 = 22.5
BCNN(12, 20) = 22.3.5 = 60
BC(12, 20) = B(60) = {0; 60; 120;…}
Cách 2: Trong các số đã cho ở phần đáp án, ta thấy chỉ có số 60 vừa chia hết cho 12, vừa chia hết cho 20 nên 60 là bội chung của 12 và 20.
Chọn đáp án D.
Câu 21:
Xem đáp án
Ta có:
20 = 22.5
30 = 2.3.5
ƯCLN(20, 30) = 2.5 = 10
ƯC(20, 30) = Ư(10) = {1; 2; 5; 10}
Chọn đáp án B.
Câu 22:
Xem đáp án
Để \(\overline {x54y} \) chia hết cho cả 2 và 5 thì chữ số tận cùng phải là 0.
Nên y = 0
Ta có: x + 5 + 4 + 0 = 9 + x
Để \(\overline {x540} \) ⁝ 3 thì (9 + x) chia hết cho 3.
Chữ số x (khác 0, vì là chữ số đầu tiên) thỏa mãn là: 3; 6; 9.
Vậy có 3 chữ số x thỏa mãn.
Chọn đáp án D.
Câu 23:
Xem đáp án
Đáp án A: 2 là số nguyên tố chẵn duy nhất → Đúng
Đáp án B: Tổng của hai số nguyên tố lớn hơn 2 luôn là số chẵn → Đúng
Vì các số nguyên tố lớn hơn 2 đều là số lẻ. Nên khi cộng hai số lẻ ta được tổng của chúng là số chẵn.
Ví dụ: 3 + 5 = 8; 79 + 83 = 162
Đáp án C: Không có số nguyên tố nào chia hết cho 3 → Sai
Vì số 3 là số nguyên tố và chia hết cho 3
Đáp án D: Mọi số tự nhiên lớn hơn 5 và chia hết cho 5 đều là hợp số → Đúng
Chọn đáp án C.
Câu 24:
Xem đáp án
40 = 23.5
60 = 22.3.5
ƯCLN(60, 40) = 22.5 = 20
x ∈ ƯC(60, 40) = Ư(20) = {1; 2; 4; 5; 10; 20}
Vì x >4 nên x {5; 10; 20}
Tổng các giá trị của x bằng: 5 + 10 + 20 = 35.
Chọn đáp án B.
Câu 25:
Xem đáp án
Gọi số học sinh khối 6 của trường Nghĩa Tân là x (học sinh) \(\left( {x \in {\mathbb{N}^*}} \right)\).
Để xếp số học sinh thành hàng 12, hàng 18 và hàng 20 đều vừa đủ thì
x phải chia hết cho 12, 18 và 20
Hay x ∈ BC(12, 18, 20)
12 = 22.3
18 = 2.32
20 = 22.5
BCNN(12, 18, 20) = 22.32.5 = 180
BC(12, 18, 20) = B(180) = {0; 180; 360; 540; 900;…}
Biết rằng số học sinh khối 6 có khoảng từ 500 đến 600 học sinh.
Vậy số học sinh khối 6 của trường Nghĩa Tân là 540 học sinh.
Chọn đáp án C.
Câu 26:
Xem đáp án
Ư(20) = {1; 2; 4; 5; 10; 20}
Vì x >5 nên x ∈ {10; 20}
Tổng các giá trị bằng: 10 + 20 = 30.
Chọn đáp án C.
Câu 27:
Xem đáp án
Để \(\overline {1x23y} \) chia hết cho 5 nhưng không chia hết cho 2 thì chữ số tận cùng phải là 5.
Nên y = 5
Ta có: 1 + x + 2 + 3 + 5 = 11 + x
Để \(\overline {1x235} \,\,\, \vdots \,\,\,9\) thì (11 + x) phải chia hết cho 9.
Có chữ số x = 7 thỏa mãn (11 + 7 = 18 chia hết cho 9)
Vậy x + y = 7 + 5 = 12.
Chọn đáp án A.
Câu 28:
Xem đáp án
Gọi số nhóm là x (nhóm, \(x \in {\mathbb{N}^*}\))
Để số học sinh nam và nữ của mỗi nhóm là như nhau và số nhóm là nhiều nhất thì: x = ƯCLN(24, 30)
24 = 23.3
30 = 2.3.5
ƯCLN(24, 30) = 2.3 = 6
Nên x = 6 (t/m)
Vậy cô giáo có thể chia lớp thành nhiều nhất là 6 nhóm.
Chọn đáp án B.
Câu 29:
Xem đáp án
B(3) = {0; 3; 6; 9; 12; 15; 18; …}
Vì 6 x ≤ 18 nên x ∈ {9; 12; 15; 18}
Vậy có 4 giá trị thỏa mãn yêu cầu của bài.
Chọn đáp án D.
Câu 30:
Xem đáp án
P = 19924+ 20212020
= (…2)4+ (…1)2020
= (…6) + (…1)
= …7
Vậy P có chữ số tận cùng là 7.
Chọn đáp án D.
Câu 31:
Xem đáp án
(x + 2)(y – 1) = 7
Suy ra (x + 2) và (y – 1) ∈ Ư(7) = {1; 7}
Vì x, y là các số tự nhiên nên x + 2 ≥ 2
Nên x + 2 = 7 và y – 1= 1
Suy ra x = 5 và y = 2
Vậy x.y = 5.2 = 10
Chọn đáp án C.
Câu 32:
Xem đáp án
x2+ 117 = y2
Dễ thấy y2>117
nên y >10
Do y là số nguyên tố nên y lẻ suy ra y2lẻ
Mà x2+ 117 = y2nên x2chẵn suy ra x chẵn
Mà x là nguyên tố nên x = 2 (vì 2 là số nguyên tố chẵn duy nhất).
Thay vào đề bài ta có:
22+ 117 = y2
121 = y2
112= y2
Suy ra y = 11
Vậy x + 2y = 2 + 2.11 = 24
Chọn đáp án D.