Đường tiệm cận của đồ thị hàm số
-
1382 lượt thi
-
25 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Nếu thì đường thẳng là:
 Xem đáp án
Xem đáp án
Nếu thì đường thẳng là tiệm cận đứng của đồ thị hàm số.
Đáp án cần chọn là: B
Câu 2:
 Xem đáp án
Xem đáp án
Đường thẳng là tiệm cận ngang của đồ thị hàm số nếu
Đáp án cần chọn là: A
Câu 3:
Tiệm cận ngang của đồ thị hàm số là?
 Xem đáp án
Xem đáp án
Đồ thị hàm số có TCN là
Đáp án cần chọn là: D
Câu 4:
Cho hàm số có đồ thị (C). Tìm tọa độ giao điểm I của hai đường tiệm cận của đồ thị (C)
 Xem đáp án
Xem đáp án
Đồ thị hàm số đã cho có hai đường tiệm cận
nên giao 2 đường tiệm cận là I(−2;1).
Đáp án cần chọn là: D
Câu 5:
Đồ thị hàm số có tiệm cận ngang và tiệm cận đứng thì bằng
 Xem đáp án
Xem đáp án
Ta có là tiệm cận ngang của ĐTHS
Và là tiệm cận đứng của ĐTHS
Vậy tổng
Đáp án cần chọn là: B
Câu 6:
Cho hàm số có đồ thị (H). Số đường tiệm cận của (H) là:
 Xem đáp án
Xem đáp án
Ta có là tiệm cận ngang của đồ thị hàm số.
Và là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có 2 đường tiệm cận.
Đáp án cần chọn là: A
Câu 7:
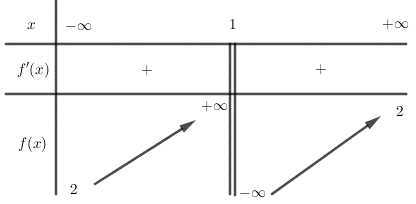
Cho hàm số có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Vì nên là tiệm cận ngang của đồ thị hàm số.
Vì nên là tiệm cận đứng của đồ thị hàm số.
Đáp án cần chọn là: C
Câu 8:
Đồ thị hàm số nào sau đây có 3 đường tiệm cận?
 Xem đáp án
Xem đáp án
Đáp án A: Đồ thị hàm số chỉ có 1 đường tiệm cận .
Đáp án B: Đồ thị hàm số có 1 TCN là và 2 TCĐ là nên có 3 tiệm cận.
Đáp án C: Đồ thị hàm số có 2 tiệm cận là
Đáp án D:
và
Đồ thị hàm số chỉ có 2 tiệm cận là
Đáp án cần chọn là: B
Câu 9:
Số tiệm cận ngang của đồ thị hàm số là
 Xem đáp án
Xem đáp án
Ta có
Lại có
Vậy là tiệm cận ngang của đồ thị hàm số đã cho.
Đáp án cần chọn là: B
Câu 10:
 Xem đáp án
Xem đáp án
TXĐ:
Ta có:
Suy ra là tiệm cận đứng của đồ thị hàm số.
Suy ra là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có tất cả 3 đường tiệm cận.
Đáp án cần chọn là: C
Câu 11:
Tất cả phương trình tiệm cận ngang của đồ thị hàm số là:
 Xem đáp án
Xem đáp án
Dễ dàng tính được và do đó là hai tiệm cận ngang của đồ thị hàm số.
Đáp án cần chọn là: B
Câu 12:
Đồ thị hàm số có bao nhiêu đường tiệm cận ngang:
 Xem đáp án
Xem đáp án
là đường tiệm cận ngang của đồ thị hàm số
là đường tiệm cận ngang của đồ thị hàm số
Đáp án cần chọn là: C
Câu 13:
Phương trình đường tiệm cận đứng của đồ thị hàm số là:
 Xem đáp án
Xem đáp án
Ta có:
Ngoài ra nên x=4 không là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số chỉ có 1 tiệm cận đứng
Đáp án cần chọn là: B
Câu 14:
Đồ thị hàm số có bao nhiêu đường tiệm cận đứng?
 Xem đáp án
Xem đáp án
Dễ thấy đa thức dưới mẫu có hai nghiệm và và hai nghiệm này đều không phải nghiệm của tử thức.
⇒ Đồ thị hàm số đã cho có 2 tiệm cận đứng.
Đáp án cần chọn là: C
Câu 15:
Số đường tiệm cận của đồ thị hàm số là:
 Xem đáp án
Xem đáp án
Đồ thị hàm số có 2 đường tiệm cận là
- Tiệm cận đứng
- Tiệm cận ngang
Đáp án cần chọn là: C
Câu 16:
Phương trình đường tiệm cận xiên của đồ thị hàm số là:
 Xem đáp án
Xem đáp án
Ta có:
Do đó đường thẳng là đường tiệm cận xiên của đồ thị hàm số.
Đáp án cần chọn là: D
Câu 17:
Đồ thị hàm số có bao nhiêu đường tiệm cận ngang?
 Xem đáp án
Xem đáp án
Tập xác định :
Vậy, đồ thị hàm số có 2 tiệm cận ngang là
Đáp án cần chọn là: A
Câu 18:
Cho hàm số Với giá trị nào của thì đường tiệm cận đứng, đường tiệm cận ngang của đồ thị hàm số cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 8?
 Xem đáp án
Xem đáp án
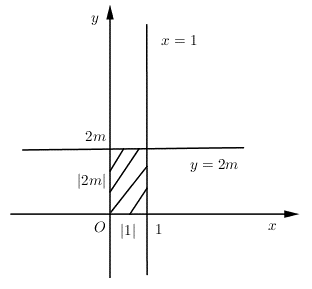
Đáp án cần chọn là: C
Câu 19:
Cho hàm số . Tất cả các giá trị của m để (C) có 3 đường tiệm cận là:
 Xem đáp án
Xem đáp án
Suy ra là tiệm cận ngang của đồ thị hàm số
Để đồ thị hàm số có 3 đường tiệm cận ⇔ Đồ thị hàm số phải có hai đường tiệm cận đứng
có 2 nghiệm phân biệt khác 2
Đáp án cần chọn là: D
Câu 20:
Cho hàm số . Để đồ thị hàm số không có tiệm cận đứng thì các giá trị của tham số m là:
 Xem đáp án
Xem đáp án
Cách 1: Thử đáp án
Với ta có là nghiệm của đa thức trên tử
không có tiệm cận đứng.
Với ta có là nghiệm của đa thức trên tử
không có tiệm cận đứng.
Cách 2: Chia đa thức
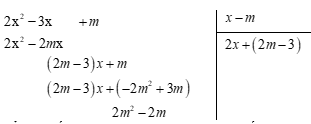
Để hàm số không có tiệm cận đứng thì tử số phải chia hết cho mẫu số
hoặc m = 1
Đáp án cần chọn là: B
Câu 21:
Cho hàm số thỏa mãn và . Có bao nhiêu giá trị thực của tham số m để đồ thị hàm số có duy nhất một tiệm cận ngang.
 Xem đáp án
Xem đáp án
Đồ thị hàm số có TCN y=1
Để đồ thị hàm số có duy nhất một tiệm cận ngang thì hoặc là không xác định hoặc là bằng 1.
Khi đó
Vậy có 2 giá trị thực của m thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: C
Câu 22:
Cho hàm số có bảng biến thiên như sau:
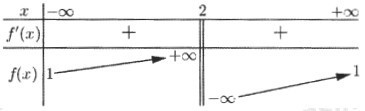
Trong các số a,b và c có bao nhiêu số dương ?
 Xem đáp án
Xem đáp án
Dựa vào BBT ta thấy đồ thị hàm số có TCĐ:
TCN:
Ta có:
Hàm số đồng biến trên các khoảng và
Vậy trong ba số a,b,c có 1 số dương.
Đáp án cần chọn là: C
Câu 23:
Cho hàm số có bảng biến thiên như sau:
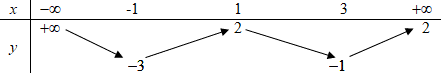
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
 Xem đáp án
Xem đáp án
Ta có: do đó đồ thị hàm số có TCN y=1
do đó đồ thị hàm số có TCN y=0.
Số đường tiệm cận đứng của đồ thị hàm số là số nghiệm của phương trình
Dựa vào đồ thị hàm số ta thấy đường thẳng cắt đồ thị hàm số tại 4 điểm phân biệt nên phương trình có 4 nghiệm phân biệt. Suy ra đồ thị hàm số có 4 đường tiệm cận đứng.
Vậy đồ thị hàm số có tổng cộng 6 đường tiệm cận.
Đáp án cần chọn là: B
Câu 24:
Cho hàm số có đồ thị như hình vẽ bên.
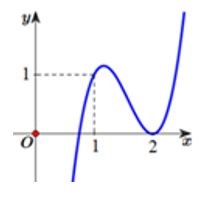
Hỏi đồ thị hàm số có bao nhiêu tiệm cận đứng?
 Xem đáp án
Xem đáp án
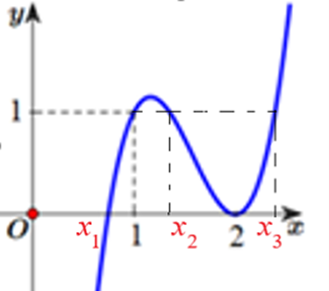
ĐKXĐ:
Nhận xét: là hàm số bậc ba, đồng thời, quan sát đồ thị ta thấy:
có 2 nghiệm phân biệt (nghiệm đơn) và x = 2(nghiệm kép).
+) có 3 nghiệm phân biệt x = 1 (nghiệm đơn), (nghiệm đơn) và (nghiệm đơn).
Khi đó hàm số được viết dưới dạng :
Do đó, đồ thị hàm số g(x) có 3 đường tiệm cận đứng là:
Đáp án cần chọn là: B
Câu 25:
 Xem đáp án
Xem đáp án
+ Nếu thì đồ thị hàm số này có tiệm cận đứng và tiệm cận ngang nên A, C sai.
+ Nếu thì nên là đường tiệm cận xiên của đồ thị hàm số.
Khi đó luôn đi qua điểm (−1;0) với mọi .
Đáp án cần chọn là: B
