10 câu hỏi trắc nghiệm thuộc Dạng 4: Hình chóp đều, hình lăng trụ đứng và các trường hợp đặc biệt có đáp án

Câu 1:

Cho khối hộp chữ nhật ABCD.A'B'C'D' có đáy là hình vuông, BD = 2a, góc phẳng nhị diện [A', BD, A] bằng 30° . Tính độ dài cạnh AA'.

A. $\frac{2 a \sqrt{3}}{3}$

B. $\frac{a}{3}$

C. $\frac{a \sqrt{3}}{6}$

D. $\frac{a \sqrt{3}}{3}$

Xem đáp án

Đáp án đúng là: D

Cho khối hộp chữ nhật ABCD.A'B'C'D' có đáy là hình vuông, BD = 2a, góc phẳng nhị diện [A', BD, A] bằng 30 . Tính độ dài cạnh AA'. (ảnh 1)

Gọi O là tâm của hình vuông ABCD.

Vì ABCD là hình vuông nên AO ^ BD.

Vì AA' ^ (ABCD) ⇒ AA' ^ BD mà AO ^ BD nên BD ^ (AOA') ⇒ BD ^ A'O.

Khi đó: $\{\begin{cases} (A^{'} B D) \cap (A B D) = B D \\ A^{'} O ⊥ B D \\ A O ⊥ B D \end{cases} \Rightarrow [A^{'}, B D, A] = \hat{A^{'} O A} = 30 °$ .

Vì ABCD là hình vuông nên AC = BD mà O là tâm hình vuông nên $A O = \frac{A C}{2} = a$ .

Xét DA'AO vuông tại A, ta có:

tan \hat{A^{'} O A} = \frac{A A^{'}}{A O} \Rightarrow A A^{'} = \frac{1}{\sqrt{3}} . a = \frac{a \sqrt{3}}{3}

.

Câu 2:

Xét các mệnh đề sau:

(1) Hình hộp là hình lăng trụ đứng.

(2) Hình hộp chữ nhật là hình lăng trụ đứng.

(3) Hình lập phương là hình lăng trụ đứng.

(4) Hình lăng trụ tứ giác đều là lăng trụ đứng.

Số mệnh đề đúng trong các mệnh đề trên là:

A. 4;

B. 3;

C. 2;

D. 1.

Xem đáp án

Đáp án đúng là: B

Mệnh đề (1) sai. Các cạnh bên không vuông góc với mặt đáy.

Câu 3:

Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình vuông. Khẳng định nào sau đây đúng?

A. (AB'C) ^ (B'BD);

B. (AB'C) ^ (BA'C');

C. (AB'C) ^ (D'BC);

D. (AB'C) ^ (D'AB).

Xem đáp án

Đáp án đúng là: A

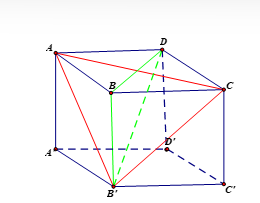
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình vuông. Khẳng định nào sau đây đúng? (ảnh 1)

Vì BB' ^ (ABCD) ⇒ BB' ^ AC (1).

Do ABCD là hình vuông nên BD ^ AC (2).

Từ (1) và (2), suy ra AC ^ (BB'D) mà AC Ì (AB'C) nên (AB'C) ^ (BB'D).

Câu 4:

Cho hình lập phương ABCD.A'B'C'D' cạnh a. Cắt hình lập phương bởi mặt phẳng trung trực của AC'. Diện tích của thiết diện là:

A. $\frac{3 \sqrt{3} a^{2}}{2}$

B. $\frac{\sqrt{3} a^{2}}{4}$

C. $\frac{3 \sqrt{3} a^{2}}{4}$

D. $\frac{\sqrt{3} a^{2}}{16}$

Xem đáp án

Đáp án đúng là: C

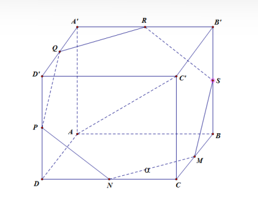
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Cắt hình lập phương bởi mặt phẳng trung trực của AC'. Diện tích của thiết diện là: (ảnh 1)

Gọi M là trung điểm BC, khi đó $M A = M C' = \sqrt{a^{2} + {(\frac{a}{2})}^{2}} = \frac{a \sqrt{5}}{2}$ nên M thuộc mặt phẳng trung trực của AC'. Tương tự ta cũng có các điểm N, P, Q, R, S lần lượt là trung điểm DC, DD', D'A', A'B', B'B và cũng thuộc mặt phẳng trung trực.

Vậy thiết diện cần tìm là lục giác đều MNPQRS.

Có $M N = \sqrt{\frac{a^{2}}{4} + \frac{a^{2}}{4}} = \frac{a \sqrt{2}}{2}$ .

Do đó diện tích của lục giác đều bằng

6. {(\frac{a \sqrt{2}}{2})}^{2} . \frac{\sqrt{3}}{4} = \frac{3 \sqrt{3}}{4} a^{2}

Câu 5:

Cho hình lăng trụ lục giác đều ABCDEF.A'B'C'D'E'F' có cạnh bên bằng a và ADD'A' là hình vuông. Cạnh đáy của lăng trụ bằng:

A. a;

B. $\frac{\sqrt{2} a}{2}$

C. $\frac{\sqrt{3} a}{3}$

D. $\frac{a}{2}$

Xem đáp án

Đáp án đúng là: D

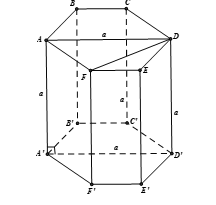
Cho hình lăng trụ lục giác đều ABCDEF.A'B'C'D'E'F' có cạnh bên bằng a và ADD'A' là hình vuông. Cạnh đáy của lăng trụ bằng: (ảnh 1)

Tổng số đo các góc của hình lục giác là 720°. Vì ABCDEF là hình lục giác đều nên mỗi góc của hình lục giác đều ABCDEF là 120° $\Rightarrow \hat{F A B} = 120 °$ .

Vì ABCDEF là hình lục giác đều nên ta suy ra:

AD là tia phân giác của góc $\hat{F A B}$ và $\hat{E D C}$ . $\Rightarrow \hat{F A D} = \frac{\hat{F A B}}{2} = 60 °$

Tam giác AFD vuông tại F có $\hat{F A D} = 60 °$ và AD = a ta suy ra: $\cos \hat{F A D} = \frac{A F}{A D} \Rightarrow A F = A D . \cos \hat{F A D} = a . \cos 60 ° = a . \frac{1}{2} = \frac{a}{2}$ .

Câu 6:

Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng a, góc giữa hai mặt phẳng (ABCD) và (ABC') có số đo bằng 60°. Cạnh bên của hình lăng trụ bằng:

A. 3a

B. $a \sqrt{3}$

C. 2a

D. $a \sqrt{2}$

Xem đáp án

Đáp án đúng là: B

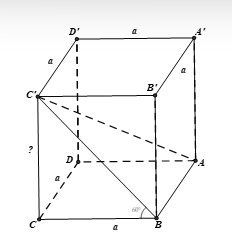
Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng a, góc giữa hai mặt phẳng (ABCD) và (ABC') (ảnh 1)

Ta có: (ABCD) Ç (ABC') = AB.

Vì BB' ^ (ABCD) ⇒ BB' ^ AB mà AB ^ BC ⇒ AB ^ (BB'C'C) ⇒ AB ^ BC'.

Do đó góc giữa hai mặt phẳng (ABCD) và (ABC') bằng góc giữa hai đường thẳng BC và BC'.

Mà (BC, BC') = $\hat{C B C^{'}} = 60 °$ .

Xét DCBC' vuông tại C, có $\tan \hat{C B C^{'}} = \frac{C C^{'}}{C B} \Rightarrow C C^{'} = C B . \tan \hat{C B C^{'}} = a . \tan 60 ° = a \sqrt{3}$ .

Câu 7:

Cho hình chóp tam giác đều có tất cả các cạnh bằng a. Côsin của góc giữa mặt bên và mặt đáy bằng

A. $\frac{1}{\sqrt{3}}$

B. $\frac{1}{3}$

C. $\frac{1}{2}$

D. $\frac{1}{\sqrt{2}}$

Xem đáp án

Đáp án đúng là: B

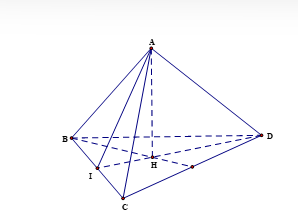
Cho hình chóp tam giác đều có tất cả các cạnh bằng a. Côsin của góc giữa mặt bên và mặt đáy bằng (ảnh 1)

Hình chóp tam giác đều A.BCD có H là trọng tâm của tam giác đáy BCD và DH cắt BC tại I.

Ta có AH ^ (BCD) ⇒ AH ^ BC (1).

Tam giác BCD đều và H là trọng tâm của tam giác BCD nên DI ^ BC (2).

Từ (1) và (2), suy ra BC ^ (AHI) ⇒ BC ^ AI.

Do đó góc giữa mặt bên (ABC) và mặt đáy (BCD) là $\hat{A I H}$ .

Tam giác ABC đều có AI là đường trung tuyến nên AI là đường cao và $A I = \frac{a \sqrt{3}}{2}$ .

Tam giác BCD đều có H là trọng tâm nên $I H = \frac{1}{3} D I = \frac{a \sqrt{3}}{6}$ .

Có AH ^ (BCD) nên tam giác AIH vuông tại H. Khi đó $\cos \hat{A I H} = \frac{I H}{A H} = \frac{1}{3}$ .

Câu 8:

Cho hình chóp tứ giác đều S.ABCD với O là tâm của đáy và chiều cao $S O = \frac{\sqrt{3}}{2} A B$ . Tính góc giữa mặt phẳng (SAB) và mặt phẳng đáy.

A. 90°;

B. 60°;

C. 30°;

D. 45°.

Xem đáp án

Đáp án đúng là: B

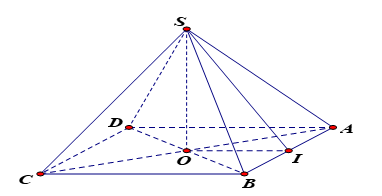
Cho hình chóp tứ giác đều S.ABCD với O là tâm của đáy và chiều cao (ảnh 1)

.

Vì SO ^ (ABCD) ⇒ SO ^ AB mà OI ^ AB nên AB ^ (SOI) ⇒ AB ^ SI.

Do đó góc giữa mặt phẳng (SAB) và mặt phẳng (ABCD) là .

Vì OI là đường trung bình của DABC nên $O I = \frac{B C}{2} = \frac{a}{2}$ và $S O = \frac{\sqrt{3}}{2} A B = \frac{\sqrt{3}}{2} a$ .

Xét DSOI vuông tại O, có $\tan \hat{S I O} = \frac{S O}{O I} = \frac{\frac{\sqrt{3}}{2} a}{\frac{1}{2} a} = \sqrt{3} \Rightarrow \hat{S I O} = 60 °$ .

Câu 9:

Lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a. Gọi M là điểm trên cạnh AA' sao cho $A M = \frac{3 a}{4}$ . Tang của góc hợp bởi hai mặt phẳng (MBC) và (ABC) là:

A. 2;

B. $\frac{1}{2}$

C. $\frac{\sqrt{3}}{2}$

D. $\frac{\sqrt{2}}{2}$

Xem đáp án

Đáp án đúng là: C

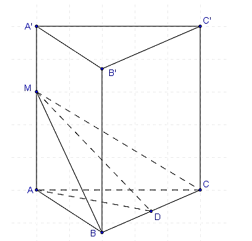
Lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a. Gọi M là điểm trên cạnh AA' (ảnh 1)

Gọi D là trung điểm của BC.

Vì DABC đều nên AD ^ BC và $A D = \frac{a \sqrt{3}}{2}$ .

Vì AA' ^ (ABC) nên AM ^ BC mà AD ^ BC ⇒ BC ^ (ADM) ⇒ BC ^ MD.

Do đó góc hợp bởi hai mặt phẳng (MBC) và (ABC) là $\hat{M D A}$ .

Xét DMAD vuông tại A, có $\tan α = \frac{A M}{A D} = \frac{3 a}{4} . \frac{2}{a \sqrt{3}} = \frac{\sqrt{3}}{2}$ .

Câu 10:

Cho hình chóp đều S.ABC có cạnh đáy bằng a, góc giữa mặt bên và mặt đáy bằng 60°. Tính độ dài đường cao SH của khối chóp

A. $S H = \frac{a \sqrt{3}}{2}$

B. $S H = \frac{a \sqrt{2}}{3}$

C. $S H = \frac{a}{2}$

D. $S H = \frac{a \sqrt{3}}{2}$

Xem đáp án

Đáp án đúng là: C

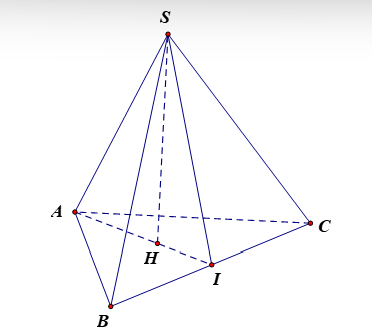
Cho hình chóp đều S.ABC có cạnh đáy bằng a, góc giữa mặt bên và mặt đáy bằng 60. Tính độ dài đường cao SH của khối chóp (ảnh 1)

Vì S.ABC là hình chóp đều nên SH ^ (ABC) (H là trọng tâm DABC).

Gọi I là trung điểm của BC.

Vì ABC là tam giác đều nên AI ^ BC (1) và $A I = \frac{a \sqrt{3}}{2}$ .

Mà SH ^ (ABC) nên SH ^ BC (2).

Từ (1) và (2), suy ra BC ^ (SAI) ⇒ BC ^ SI.

Do đó góc giữa mặt phẳng (SBC) và (ABC) là $\hat{S I H} = 60 °$ .

Vì H là trọng tâm tam giác ABC nên $H I = \frac{1}{3} A I = \frac{a \sqrt{3}}{6}$ .

Xét DSHI vuông tại H, có SH = HI.tan60° = $\frac{a \sqrt{3}}{6} . \sqrt{3} = \frac{a}{2}$ .