25 câu hỏi trắc nghiệm thuộc 75 câu trắc nghiệm Giới hạn nâng cao (P3)

Câu 1:

Cho hàm số $f (x) = \{\begin{cases} \frac{x + 1 + \sqrt[3]{x - 1}}{x} k h i x k h á c 0 \\ 2 k h i x = 0 \end{cases}$ Khẳng định nào sau đây đúng nhất

A. Hàm số liên tục tại x = 0

B. Hàm số liên tục tại mọi điểm

C. Hàm số không liên tục tại x = 0

D. Tất cả đều sai

Xem đáp án

Chọn C

Ta có: f(0) = 2

Vậy hàm số liên tục tại x = 0.

Câu 2:

Cho hàm số $f (x) = \{\begin{cases} \frac{x^{2} - x - 2}{\sqrt{x - 2}} + 2 x k h i x > 2 \\ x^{2} - x + 3 k h i x \leq 2 \end{cases}$ Khẳng định nào sau đây đúng nhất

A. Hàm số liên tục tại x = 2

B. Hàm số liên tục tại mọi điểm

C. Hàm số không liên tục tại x = 2

D. Tất cả đều sai

Xem đáp án

Chọn C.

Ta có:

Hàm số không liên tục tại x = 2.

Câu 3:

Tìm a để hàm số sau liên tục tại x = 0.

A. 1/2

B. 1/4

C. -1/6

D. 1

Xem đáp án

Chọn C.

Ta có :

Hàm số liên tục tại .

Câu 4:

Tìm a để các hàm số $f (x) \{\begin{cases} \frac{\sqrt{3 x + 1} - 2}{x^{2} - 1} K h i x > 1 \\ \frac{a (x^{2} - 2)}{x - 3} K h i x \leq 1 \end{cases}$ liên tục tại x = 1

A. 1/2

B. 1/4

C. 3/4

D. 1

Xem đáp án

Chọn C.

Suy ra hàm số liên tục tại

Câu 5:

Tìm khẳng định đúng trong các khẳng định sau:

$(I) f (x) = \frac{1}{\sqrt{x^{2} - 1}}$ liên tục với mọi x.

$(II) f (x) = \frac{\sin x}{x}$ có giới hạn khi x → 0.

$(III) f (x) = \sqrt{9 - x^{2}}$ liên tục trên đoạn [-3; 3].

A. Chỉ (I) và (II).

B. Chỉ (II) và (III).

C. Chỉ (II).

D. Chỉ (III).

Xem đáp án

Chọn B.

* Dễ thấy (I) sai

Vì hàm số này có tập xác định D = (- 1; 1).

Với mọi x không thuộc tập xác định thì hàm số gián đoạn tại điểm đó.

* Khẳng định (II) là lí thuyết.

* Hàm số: liên tục trên khoảng (-3; 3). Liên tục phải tại 3 và liên tục trái tại -3.

Nên liên tục trên đoạn [-3; 3].

Câu 6:

Tìm khẳng định đúng trong các khẳng định sau:

(I) $f (x) = \frac{\sqrt{x + 1}}{x - 1}$ liên tục với mọi $x \neq$ 1

(II) f(x) = sinx liên tục trên R.

(III) $f (x) = \frac{|x|}{x}$ liên tục tại x = 1

A. Chỉ (I) đúng.

B. Chỉ (I) và (II).

C. Chỉ (I) và (III).

D. Chỉ (II) và (III).

Xem đáp án

Chọn B.

* (I) : Hàm số có tập xác định $D = [- 1; + \infty) \ {1}$

Khi đó, với mọi x không thuộc tập xác định thì hàm số gián đoạn

Do đó, (I) là sai.

*Ta có (II) đúng vì hàm số lượng giác liên tục trên từng khoảng của tập xác định.

Ta có (III) đúng vì

* Khi đó

Vậy hàm số liên tục tại x = 1.

Câu 7:

Cho hàm số . Tìm khẳng định đúng trong các khẳng định sau:

(I). f(x) liên tục tại x= $\sqrt{3}$

(II). f(x) gián đoạn tại x= $\sqrt{3}$ .

(III). f(x) liên tục trên R.

A. Chỉ (I) và (II).

B. Chỉ (II) và (III).

C. Chỉ (I) và (III).

D. Cả (I), (II), (III) đều đúng.

Xem đáp án

Chọn C.

Với ta có hàm số liên tục trên khoảng và , (1).

Với ta có và nên hàm số liên tục tại , (2)

Từ (1) và (2) ta có hàm số liên tục trên R.

Câu 8:

Tìm khẳng định đúng trong các khẳng định sau:

$(I) f (x) = x^{5} - x^{2} + 1$ liên tục trên R

$(II) f (x) = \frac{1}{\sqrt{x^{2} - 1}}$ liên tục trên khoảng (-1; 1).

$(III) f (x) = \sqrt{x - 2}$ liên tục trên đoạn [2; +∞).

A. Chỉ (I) đúng.

B. Chỉ (I) và (II).

C. Chỉ (II) và (III).

D. Chỉ (I) và (III).

Xem đáp án

Chọn D.

Ta có (I) đúng vì f(x) = x⁵ – x² + 1 là hàm đa thức nên liên tục trên R..

Ta có (III) đúng vì liên tục trên (2; +∞) và nên hàm số liên tục trên [2; +∞)

(II) sai vì hàm số này có tập xác định D = (- ∞; -1)∪ (1; + ∞)

Với mọi x thuộc khoảng (-1; 1), hàm số không xác định nên hàm số gián đoạn tại các điểm đó.

Câu 9:

Cho hàm số $f (x) = \{\begin{cases} \frac{3 - \sqrt{9 - x}}{x}, 0 < x < 9 m, x = 0 \\ \frac{3}{x}, x \geq 9 \end{cases}$ Tìm m để f(x) liên tục trên [0; +∞) là.

A. 1/3.

B. 1/2.

C. 1/6.

D. 1.

Xem đáp án

Chọn C.

TXĐ: D = [0; +∞).

Với x = 0 ta có f(0) = m.

Ta có .

Vậy để hàm số liên tục trên [0; +∞) thì hàm số phải liên tục tại điểm x = 0 nên :

.

Câu 10:

Cho hàm số $f (x) = \frac{x^{2} + 1}{x^{2} + 5 x + 6}$ Khi đó hàm số y = f(x) liên tục trên các khoảng nào sau đây?

A. (-3; 2).

B. (-2; +∞).

C. (-∞; 3).

D. (2; 3).

Xem đáp án

Chọn B.

Hàm số có nghĩa khi $x^{2} + 5 x + 6 \neq 0 \Leftrightarrow x ≢ - 2; x \neq - 3$

Vậy theo định lí, hàm số đã cho liên tục trên khoảng (-∞; -3); (-3; -2) và (-2; +∞).

Câu 11:

Cho hàm số $f (x) = \{\begin{cases} \frac{x^{2} - 5 x + 6}{2 x^{3} - 16} k h i x < 2 \\ 2 - x k h i x \geq 2 \end{cases}$ Khẳng định nào sau đây đúng nhất.

A. Hàm số liên tục với mọi x.

B. Hàm số liên tục tại mọi điểm

C. Hàm số không liên tục trên (2 ; +∞)

D. Hàm số gián đoạn tại điểm x = 2.

Xem đáp án

Chọn D.

TXĐ : D = R \ {2}

Với hàm số liên tục

Với x > 2 ⇒ f(x) = 2 – x ⇒ hàm số liên tục

Tại x = 2 ta có : f(2) = 0

Hàm số không liên tục tại x = 2.

Câu 12:

Cho hàm số $f (x) = \{\begin{cases} \frac{\sqrt[3]{x} - 1}{\sqrt{x} - 1} k h i x > 1 \\ \frac{\sqrt[]{1 - x} + 2}{x + 2} k h i x \leq 1 \end{cases}$ Khẳng định nào sau đây đúng nhất.

A. Hàm số liên tục trên R

B. Hàm số không liên tục trên R.

C. Hàm số không liên tục trên (1 ; +∞)

D. Hàm số gián đoạn tại các điểm x = 1.

Xem đáp án

Chọn A.

Hàm số xác định với mọi x thuộc R.

- Với hàm số liên tục

Tại x = 1 ta có : f(1) = 2/3

Hàm số liên tục tại x = 1.

Vậy hàm số liên tục trên R.

Câu 13:

Cho hàm số $f (x) = \{\begin{cases} \frac{\tan x}{x}; x k h á c 0 \land x k h á c \frac{π}{2} + k π; k \in ℤ \\ 0; x = 0 \end{cases}$ Hàm số y = f(x) liên tục trên các khoảng nào sau đây?

Xem đáp án

Chọn A.

TXĐ: .

Với x = 0 ta có f(0) = 0.

hay .

Vậy hàm số gián đoạn tại x = 0.

+ Trên khoảng (0; $\frac{π}{2}$ ) hàm số xác định và liên tục

Câu 14:

Cho hàm số $f (x) = \{\begin{cases} a^{2} x^{2}, x \leq \sqrt{2}, a \in ℝ \\ (2 - a) x^{2}, x > \sqrt{2} \end{cases}$ Giá trị của a để f (x) liên tục trên R là:

A. 1 và 2.

B. 1 và -1.

C. -1 và 2.

D. 1 và -2.

Xem đáp án

Chọn D.

Với $x < \sqrt{2}$ ta có hàm số f(x) = a²x² liên tục trên khoảng $(- \infty; \sqrt{2})$ .

Với $x > \sqrt{2}$ ta có hàm số f(x) = (2 – a)x² liên tục trên khoảng $(\sqrt{2}; + \infty)$ .

Với ta có .

Để hàm số liên tục tại

Vậy a = 1 hoặc a = -2 thì hàm số liên tục trên R.

Câu 15:

Cho hàm số $f (x) = \{\begin{cases} x^{2}, x \geq 1 \frac{2 x^{3}}{1 + x}, 0 \leq x \leq 1 \\ x \sin x, x < 0 \end{cases}$ Tìm khẳng định đúng trong các khẳng định sau:

A. f(x) liên tục trên R.

B. f(x) liên tục trên R \ {0}.

C. f(x) liên tục trên R \ {1}.

D. f(x) liên tục trên R \ {0; 1}.

Xem đáp án

Chọn A.

* Với x >1 ta có hàm số f(x) = x² là hàm đa thức nên liên tục trên khoảng (1; +∞). (1)

* Với 0 < x < 1 ta có hàm số là hàm phân thức, xác định trên khoảng đó nên liên tục trên khoảng (0; 1). (2)

* Với x < 0 ta có f(x) = x.sinx- hàm số xác định trên khoảng đó nên liên tục trên khoảng (-∞; 0). (3)

* Với x = 1 ta có f(1) = 1;

Suy ra .

Vậy hàm số liên tục tại x = 1.

* Với x = 0 ta có f(0) = 0; ;

suy ra .

Vậy hàm số liên tục tại x = 0. (4)

Từ (1), (2), (3) và (4) suy ra hàm số liên tục trên R.

Chọn A.

Câu 16:

Cho hàm số $f (x) = \sqrt{3 x^{2} - 1}$ . Khẳng định nào sau đây đúng nhất.

A. Hàm số liên tục trên R.

B. Hàm số liên tục tại mọi điểm

C. TXĐ :

D. Hàm số liên tục tại mọi điểm

Xem đáp án

Chọn B.

TXĐ :

Ta có hàm số liên tục tại mọi điểm

hàm số liên tục trái tại

hàm số liên tục phải tại

Hàm số gián đoạn tại mọi điểm

Câu 17:

Xác định a ; b để các hàm số $f (x) = \{\begin{cases} \sin x k h i |x| \leq \frac{π}{2} \\ a x + b k h i |x| > \frac{π}{2} \end{cases}$ liên tục trên R

Xem đáp án

Chọn D.

Hàm số liên tục trên R thì hàm số liên tục tại 2 điểm $x = \pm \frac{π}{2}$

Từ (1) và (2) ta có hệ phương trình

Câu 18:

Tìm m để các hàm số $f (x) = \{\begin{cases} \frac{\sqrt[3]{x - 2} + 2 x - 1}{x - 1}, k h i x k h á c 1 \\ 3 m - 2, k h i x = 1 \end{cases}$ liên tục trên R

A. 7/ 6

B. 13/6

C. 2

D. 0

Xem đáp án

Chọn B.

Với x ≠ 1 ta có nên hàm số liên tục trên khoảng R \{1}

Do đó hàm số liên tục trên R khi và chỉ khi hàm số liên tục tại x = 1

Ta có: f(1) = 3m - 2

$= 1 + \frac{1 + 1 + 2}{1 - (- 1) + 1} = \frac{7}{3}$

Nên hàm số liên tục tại x = 1 ⇔ 3m – 2 = $\frac{7}{3}$ ⇔ m = 13/6.

Câu 19:

Tìm m để các hàm số $f (x) = \{\begin{cases} \frac{\sqrt{x + 1} - 1}{x} k h i x > 0 \\ 2 x^{2} + 3 m + 1 k h i x \leq 0 \end{cases}$ liên tục trên R.

A. 1

B. -1/6

C. 2

D. 0

Xem đáp án

Chọn B.

- Với x > 0 ta có nên hàm số liên tục trên (0; +∞)

- Với x < 0 ta có f(x) = 2x² + 3m + 1 nên hàm số liên tục trên (-∞; 0).

Do đó hàm số liên tục trên R khi và chỉ khi hàm số liên tục tại x = 0

Ta có: f(0) = 3m + 1

Do đó hàm số liên tục tại .

Câu 20:

Tìm m để các hàm số $f (x) = \{\begin{cases} \sqrt{2 x - 4} + 3 K h i x \geq 2 \\ \frac{x + 1}{x^{2} - 2 m x + 3 m + 2} K h i x < 2 \end{cases}$ liên tục trên R

A. 1

B. 2

C. 5

D. 4

Xem đáp án

Chọn C.

Với x > 2 ta có hàm số liên tục

Để hàm số liên tục trên R thì hàm số phải liên tục trên khoảng (-∞; 2) và liên tục tại x = 2.

- Hàm số liên tục trên (-∞; 2) khi và chỉ khi tam thức

TH 1:

TH 2:

Nên thì

Hàm số liên tục tại (thỏa (*))

Câu 21:

Cho hàm số $f (x) = \{\begin{cases} \sqrt{x^{2} - 5} k h i x \geq 3 (1) \\ \frac{x^{2} - 5}{x + 2} k h i x < 3 (2) \end{cases}$

Trong biểu thức (2) ở trên, cần thay số 5 bằng số nào để hàm số f(x) có giới hạn khi x → 3?

A. 19.

B. 1.

C. -1.

D. Không có số nào thỏa mãn.

Xem đáp án

Chọn C.

Ta có

Đặt khi x < 3 (m là tham số).

Ta có .

Để hàm số f(x) có giới hạn khi x → 3 thì .

Câu 22:

Cho hàm số f(x) có đồ thị như hình dưới đây:

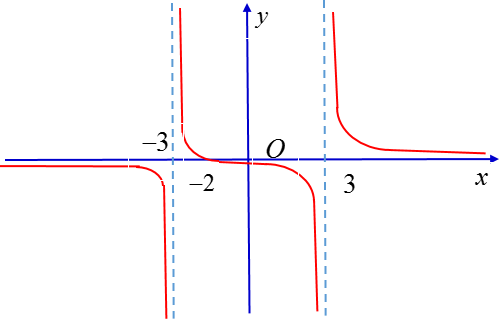
Quan sát đồ thị và cho biết trong các giới hạn sau, giới hạn nào là +∞ ?

Xem đáp án

Chọn C.

Khi x → -3⁺, đồ thị hàm số là một đường cong đi lên từ phải qua trái

Do đó .

Tương tự như vậy ta có

Câu 23:

$\lim_{x \to a} \frac{\sin x - \sin a}{x - a}$ bằng

A. tana.

C. sina.

D. cosa.

Xem đáp án

Chọn D.

Ta có

Mà

Vậy

Câu 24:

Cho a và b là các số nguyên dương thỏa mãn $\lim_{x \to 0} \frac{e^{a x} - 1}{\sin b x} = \frac{5}{3}$ .Tích ab có thể nhận giá trị bằng số nào trong các số dưới đây?