Đề kiểm tra Giữa kì 1 Toán 11 CTST có đáp án - Đề 01
-
528 lượt thi
-
37 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 2:
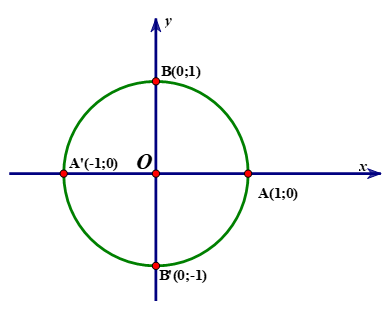
Trong mặt phẳng tọa độ $Oxy,$cho đường tròn lượng giác như hình vẽ bên dưới. Hỏi góc lượng giác nào sau đây có số đo là $90^\circ ?$
 Xem đáp án
Xem đáp án
Chọn C
Câu 3:
Trong mặt phẳng tọa độ $Oxy,$ trên đường tròn lượng giác gọi điểm $M$là điểm biểu diễn của góc $\alpha = \frac{\pi }{6}.$ Lấy điểm $N$ đối xứng với $M$ qua gốc tọa độ. Hỏi $N$ là điểm biểu diễn của góc có số đo bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn A
Câu 4:
Cho $\alpha $ thuộc góc phần phần tư thứ nhất của đường tròn lượng giác. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Chọn A
Câu 6:
Cho góc $\alpha $ thỏa mãn $\cos \alpha = - \frac{{\sqrt 5 }}{3}$ và $\pi < \alpha < \frac{{3\pi }}{2}$. Tính $\tan \alpha $.
 Xem đáp án
Xem đáp án
Chọn B
Câu 8:
Cho các đẳng thức sau:
1) $\cos x - \sin x = \sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right)$. 2) $\cos x - \sin x = \sqrt 2 \cos \left( {x + \frac{\pi }{4}} \right)$.
3) $\cos x - \sin x = \sqrt 2 \cos \left( {x - \frac{\pi }{4}} \right)$. 4) $\cos x - \sin x = \sqrt 2 \sin \left( {\frac{\pi }{4} - x} \right)$.
Có bao nhiêu đẳng thức dưới đây là đồng nhất thức?
 Xem đáp án
Xem đáp án
Chọn B
Câu 9:
Cho góc $\alpha $ thỏa mãn $\cos 2\alpha = \frac{2}{3}$. Tính $P = {\sin ^4}\alpha + {\cos ^4}\alpha $.
 Xem đáp án
Xem đáp án
Chọn C
Câu 10:
Tìm tập xác định ${\text{D}}$ của hàm số $y = \frac{{1 + \sin x}}{{\cos x - 1}}.$
 Xem đáp án
Xem đáp án
Chọn D
Câu 11:
Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D.
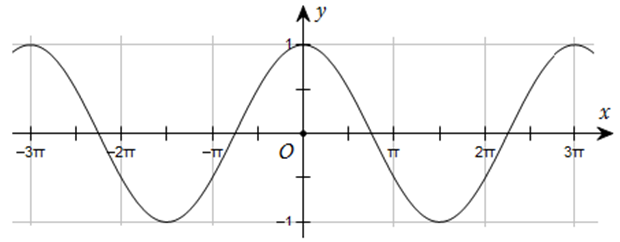
Hỏi hàm số đó là hàm số nào?
 Xem đáp án
Xem đáp án
Chọn A
Câu 13:
Trong các phương trình sau, phương trình tương đương với phương trình ${x^2} - 1 = 0$ là
 Xem đáp án
Xem đáp án
Chọn B
Câu 15:
Tất cả nghiệm của phương trình $\tan \left( {30^\circ - 3x} \right) = \tan 75^\circ $ là
 Xem đáp án
Xem đáp án
Chọn D
Câu 16:
Nghiệm âm lớn nhất của phương trình lượng giác $\cos 2x = \cos \left( {x + \frac{\pi }{3}} \right)$ là
 Xem đáp án
Xem đáp án
Chọn A
Câu 17:
Cho dãy số \[\left( {{u_n}} \right)\] là dãy số tự nhiên lẻ theo thứ tự tăng dần và ${u_1} = 3$. Năm số hạng đầu của dãy số \[\left( {{u_n}} \right)\] là:
 Xem đáp án
Xem đáp án
Chọn C
Câu 19:
Cho dãy số $\left( {{u_n}} \right)$với ${u_n} = \frac{{n + a}}{n}$, $a$ là số thực. Tìm một giá trị của $a$ để $\left( {{u_n}} \right)$ là dãy số giảm.
 Xem đáp án
Xem đáp án
Chọn B
Câu 22:
Cho hai số $ - 3$ và $23$. Xen kẽ giữa hai số đã cho $n$ số hạng để tất cả các số đó tạo thành cấp số cộng có công sai $d = 2$. Tìm $n$.
 Xem đáp án
Xem đáp án
Chọn A
Câu 23:
Tìm $n$ số hạng đầu tiên của một cấp số cộng \[{S_n} = {n^2} + 4n\] với $n \in \mathbb{N}*$. Tìm số hạng tổng quát ${u_n}$ của cấp số cộng đã cho.
 Xem đáp án
Xem đáp án
Chọn A
Câu 26:
Tìm tất cả giá trị của $x$ để ba số $2x - 1;\,\,x;\,\,2x + 1$ theo thứ tự đó lập thành một cấp số nhân.
 Xem đáp án
Xem đáp án
Chọn A
Câu 27:
Cho cấp số nhân $\left( {{u_n}} \right)$ có tổng $n$ số hạng đầu tiên là ${S_n} = \frac{{{3^n} - 1}}{{{3^{n - 1}}}}$. Tìm số hạng thứ 5 của cấp số nhân đã cho.
 Xem đáp án
Xem đáp án
Chọn A
Câu 30:
Cho mặt phẳng \[\left( \alpha \right)\], cho 4 điểm $A,\,\,B,\,\,C,\,\,D$ trong đó không có ba điểm nào thẳng hàng. Điểm $S$ không thuộc mặt phẳng \[\left( \alpha \right)\]. Có mấy mặt phẳng tạo bởi $S$ và 2 trong 4 điểm nói trên?
 Xem đáp án
Xem đáp án
Chọn D
Câu 31:
Cho bốn điểm $A,\,\,B,\,\,C,\,\,D$ không đồng phẳng. Gọi $M,\,\,N$ lần lượt là trung điểm của $AC$ và $BC$. Trên đoạn $BD$ lấy điểm $P$ sao cho $BP = 2PD$. Giao điểm của đường thẳng $CD$ và mặt phẳng $\left( {MNP} \right)$ là giao điểm của
 Xem đáp án
Xem đáp án
Chọn A
Câu 33:
Trong không gian, cho ba đường thẳng phân biệt $a,\,\,b,\,\,c$ trong đó $a\,{\text{//}}\,b$. Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Chọn B
Câu 34:
Cho hình chóp $S.ABCD$ có $ABCD$ là hình bình hành. Gọi $d$ là giao tuyến của hai mặt phẳng $(SAD)$ và $(SBC)$. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn A
Câu 35:
Gọi $G$ là trọng tâm tứ diện $ABCD$. Gọi $A'$ là trọng tâm của tam giác $BCD$. Tính tỉ số $\frac{{GA}}{{GA'}}$.
 Xem đáp án
Xem đáp án
Chọn B
Câu 36:
Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ $t$ của năm $2017$ được cho bởi một hàm số $y = 4\sin \left[ {\frac{\pi }{{178}}\left( {t - 60} \right)} \right] + 10$ với $t \in \mathbb{Z}$ và $0 < t \leqslant 365$. Vào ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất?
 Xem đáp án
Xem đáp án
Vì $\sin \left[ {\frac{\pi }{{178}}\left( {t - 60} \right)} \right] \leqslant 1 \Rightarrow y = 4\sin \left[ {\frac{\pi }{{178}}\left( {t - 60} \right)} \right] + 10 \leqslant 14.$
Ngày có ánh sáng mặt trời nhiều nhất khi và chỉ khi
$y = 14 \Leftrightarrow \sin \left[ {\frac{\pi }{{178}}\left( {t - 60} \right)} \right] = 1$
$ \Leftrightarrow \frac{\pi }{{178}}\left( {t - 60} \right) = \frac{\pi }{2} + k2\pi \Leftrightarrow t = 149 + 356k.$
Do $0 < t \leqslant 365 \Rightarrow 0 < 149 + 356k \leqslant 365$
$ \Leftrightarrow - \frac{{149}}{{356}} < k \leqslant \frac{{54}}{{89}}$.
Mà $k \in \mathbb{Z}$ nên $k = 0$.
Với $k = 0 \Rightarrow t = 149$ rơi vào ngày 29 tháng 5 (vì ta đã biết tháng 1 và 3 có 31 ngày, tháng 4 có 30 ngày, riêng đối với năm 2017 thì không phải năm nhuận nên tháng 2 có 28 ngày hoặc dựa vào dữ kiện $0 < t \leqslant 365$ thì ta biết năm này tháng 2 chỉ có 28 ngày).
Câu 37:
Một du khách vào chuồng đua ngựa đặt cược, lần đầu đặt $20\,\,000$ đồng, mỗi lần sau đặt gấp đôi lần cọc trước. Người đó thua 9 lần liên tiếp và thắng ở lần thứ 10. Hỏi du khách trên thắng hay thua bao nhiêu?
 Xem đáp án
Xem đáp án
Du khách thu trong 9 lần đầu tiên nên tổng số tiền thua là:
${S_9} = {u_1} + {u_2} + ... + {u_9} = \frac{{{u_1}\left( {1 - {p^9}} \right)}}{{1 - p}} = 10\,\,220\,\,000$ (đồng)
Số tiền mà du khách thắng trong lần thứ 10 là:
\[{u_{10}} = {u_1}{p^9} = 10\,\,240\,\,000\] (đồng)
Ta có \[{u_{10}} - {S_9} = 10\,\,240\,\,000 - 10\,\,220\,\,000 = 20\,\,000 > 0\] nên du khách thắng $20\,\,000$ đồng.
