Đề kiểm tra Cuối kì 1 Toán 11 CTST có đáp án - Đề 01
-
335 lượt thi
-
39 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Cho góc hình học $uOv$ có số đo $50^\circ $. Xác định số đo của góc lượng giác $\left( {Ou,Ov} \right)$ trong hình dưới đây?
Xem đáp án
Chọn A
Câu 2:
Cho góc $\alpha $ thỏa mãn $\cos \alpha = \frac{3}{5}$. Giá trị của $P = \cos 2\alpha $ là
Xem đáp án
Chọn B
Câu 6:
Có bao nhiêu giá trị nguyên của $m$ để phương trình $\sin x - 2m = 1$ có nghiệm?
Xem đáp án
Chọn B
Câu 8:
Dãy số \[ - 1;1; - 1;1; - 1; \cdots \]có số hạng tổng quát là công thức nào dưới đây?
Xem đáp án
Chọn A
Câu 9:
Cho dãy số $\left( {{u_n}} \right)$, biết ${u_n} = \frac{{2{n^2} - 1}}{{{n^2} + 3}}$. Tìm số hạng ${u_5}$.
Xem đáp án
Chọn B
Câu 11:
Cho cấp số cộng $\left( {{u_n}} \right)$ có ${u_3} = 9;{u_4} = 3$. Khi đó công sai là
Xem đáp án
Chọn D
Câu 12:
Cho cấp số cộng $\left( {{u_n}} \right)$ có ${u_1} = - 5;d = 3$. Mệnh đề nào sau đây đúng?
Xem đáp án
Chọn B
Câu 14:
Cho dãy số $\left( {{u_n}} \right)$ biết $\left\{ \begin{gathered}
{u_1} = 3 \hfill \\
{u_{n + 1}} = 3{u_n} \hfill \\
\end{gathered} \right.,\forall n \in {\mathbb{N}^*}$. Tìm số hạng tổng quát của dãy số $\left( {{u_n}} \right).$
Xem đáp án
Chọn C
Câu 15:
Cho hai dãy $\left( {{u_n}} \right)$ và $\left( {{v_n}} \right)$ thỏa mãn $\mathop {\lim }\limits_{n \to + \infty } {u_n} = \frac{1}{2}$ và $\mathop {\lim }\limits_{n \to + \infty } {v_n} = - 2.$ Giá trị của $\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n}.{v_n}} \right)$ bằng
Xem đáp án
Chọn A
Câu 17:
Tính $\mathop {\lim }\limits_{n \to + \infty } {\left( {\frac{{ - 3}}{4}} \right)^n}.$
Xem đáp án
Chọn D
Câu 18:
Cho hàm số $f\left( x \right)$ thỏa mãn $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2.$ Giá trị $\mathop {\lim }\limits_{x \to + \infty } 3f\left( x \right)$ bằng
Xem đáp án
Chọn A
Câu 21:
Hàm số $y = f\left( x \right)$ có đồ thị như hình dưới đây:
Hàm số gián đoạn tại điểm
Xem đáp án
Chọn A
Câu 23:
Cho hình chóp tứ giác $S.ABCD$ có đáy là hình bình hành tâm $O$. Điểm $M$ thuộc cạnh $SO$ ($M$ khác $S,O$). Trong các mặt phẳng sau, điểm $M$ thuộc mặt phẳng nào?
Xem đáp án
Chọn B
Câu 25:
Cho tứ diện $ABCD.$ Gọi $M,\,N$ lần lượt là các điểm thuộc các cạnh $AB,\,AC$ sao cho $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}$; $I,\,J$ lần lượt là trung điểm của $BD$ và $CD.$
Khẳng định nào sau đây đúng?
Xem đáp án
Chọn B
Câu 26:
Cho đường thẳng $a$ và mặt phẳng $\left( P \right)$ không có điểm chung. Kết luận nào sau đây đúng?
Xem đáp án
Chọn C
Câu 27:
Cho hình chóp tứ giác $S.ABCD.$ Gọi $M,\,N$ lần lượt là trung điểm của $SA,\,SC.$ Đường thẳng $MN$ song song với mặt phẳng nào dưới đây?
Xem đáp án
Chọn A
Câu 28:
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $O.$ Gọi $M,$ $N,\,\,P$ lần lượt là trung điểm của $SA,$ $SD,$$AB.$ Khẳng định nào sau đây đúng?
Xem đáp án
Chọn B
Câu 29:
Cho hình hộp $ABCD.A'B'C'D'$. Mặt phẳng $\left( {BC'D} \right)$ song song với mặt phẳng nào trong các mặt phẳng sau đây?
Xem đáp án
Chọn A
Câu 30:
Cho các đường thẳng không song song với phương chiếu. Khẳng định nào sau đây là đúng?
Xem đáp án
Chọn D
Câu 31:
Cho hình lăng trụ tam giác $ABC.A'B'C'.$
Hình chiếu của tam giác $ACB$ trên mặt phẳng $\left( {A'B'C'} \right)$ theo phương $CC'$ là
Xem đáp án
Chọn A
Câu 32:
Bảng xếp loại học lực của học sinh lớp 11A của trường năm học 2022 - 2023, được cho như sau:
|
Học lực |
Kém |
Yếu |
Trung bình |
Khá |
Giỏi |
|
Điểm |
$\left[ {0;3} \right)$ |
$\left[ {3;5} \right)$ |
$\left[ {5;6,5} \right)$ |
$\left[ {6,5;8} \right)$ |
$\left[ {8;10} \right]$ |
|
Số học sinh |
2 |
10 |
15 |
12 |
6 |
Số học sinh của lớp 11A trên là bao nhiêu?
Xem đáp án
Chọn A
Câu 33:
Điều tra về chiều cao của học sinh khối lớp 10 của trường thu được mẫu số liệu ghép nhóm sau:
|
Chiều cao (cm) |
Số học sinh |
|
$\left[ {150;152} \right)$ |
11 |
|
$\left[ {152;154} \right)$ |
18 |
|
$\left[ {154;156} \right)$ |
38 |
|
$\left[ {156;158} \right)$ |
26 |
|
$\left[ {158;160} \right)$ |
20 |
|
$\left[ {160;162} \right)$ |
7 |
Nhóm chứa mốt của mẫu số liệu trên là:
Xem đáp án
Chọn C
Câu 34:
Người ta ghi lại tuổi thọ (năm) của $50$ bình ắc quy của một hãng xe ô tô cho kết quả như sau:
|
Tuổi thọ (năm) |
\[\left[ {2;2,5} \right)\] |
$\left[ {2,5;3} \right)$ |
$\left[ {3;3,5} \right)$ |
$\left[ {3,5;4} \right)$ |
$\left[ {4;4,5} \right)$ |
$\left[ {4,5;5} \right)$ |
|
Tần số |
4 |
9 |
14 |
11 |
7 |
5 |
Trung vị của mẫu số liệu trên thuộc nhóm nào trong các nhóm dưới đây?
Xem đáp án
Chọn B
Câu 35:
Người ta ghi lại tuổi thọ (năm) của 50 bình ắc quy của một hãng xe ô tô của cho kết quả như sau:
|
Tuổi thọ (năm) |
\[\left[ {2;2,5} \right)\] |
$\left[ {2,5;3} \right)$ |
$\left[ {3;3,5} \right)$ |
$\left[ {3,5;4} \right)$ |
$\left[ {4;4,5} \right)$ |
$\left[ {4,5;5} \right)$ |
|
Tần số |
4 |
9 |
14 |
11 |
7 |
5 |
Tứ phân vị thứ nhất của mẫu số liệu trên gần với giá trị nào trong các giá trị sau đây?
Xem đáp án
Chọn B
Câu 36:
Tính các giới hạn sau:
a) \[\mathop {\lim }\limits_{n \to + \infty } \left( {1 + n - {n^2}} \right)\]; b) \[\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {{x^2} + 4} - 2}}{x}.\]
Xem đáp án
a) Ta có: \[1 + n - {n^2} = {n^2}\left( {\frac{1}{{{n^2}}} + \frac{1}{n} - 1} \right).\]
Ta có: $\mathop {\lim }\limits_{n \to + \infty } {n^2} = + \infty ;$ $\mathop {\lim }\limits_{n \to + \infty } \left( {\frac{1}{{{n^2}}} + \frac{1}{n} - 1} \right) = \mathop {\lim }\limits_{n \to + \infty } \frac{1}{{{n^2}}} + \mathop {\lim }\limits_{n \to + \infty } \frac{1}{n} - \mathop {\lim }\limits_{n \to + \infty } 1 = 0 + 0 - 1 = - 1 < 0.$
$ \Rightarrow \mathop {\lim }\limits_{n \to + \infty } \left( {1 + n - {n^2}} \right) = \mathop {\lim }\limits_{n \to + \infty } \left[ {{n^2}\left( {\frac{1}{{{n^2}}} + \frac{1}{n} - 1} \right)} \right] = \mathop {\lim }\limits_{n \to + \infty } {n^2}.\mathop {\lim }\limits_{n \to + \infty } \left( {\frac{1}{{{n^2}}} + \frac{1}{n} - 1} \right) = - \infty .$
b) \[\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {{x^2} + 4} - 2}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{\left( {\sqrt {{x^2} + 4} - 2} \right).\left( {\sqrt {{x^2} + 4} + 2} \right)}}{{x\left( {\sqrt {{x^2} + 4} + 2} \right)}} = \mathop {\lim }\limits_{x \to 0} \frac{{{x^2} + 4 - 4}}{{x\left( {\sqrt {{x^2} + 4} + 2} \right)}}\]
$ = \mathop {\lim }\limits_{x \to 0} \frac{{{x^2}}}{{x\left( {\sqrt {{x^2} + 4} + 2} \right)}} = \mathop {\lim }\limits_{x \to 0} \frac{x}{{\sqrt {{x^2} + 4} + 2}} = \frac{0}{{\sqrt {0 + 4} + 2}} = 0.$
Câu 37:
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $G,N$ lần lượt là trọng tâm của tam giác $SAB,ABC$.
a) Tìm giao tuyến của hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SBD} \right)$.
b) Chứng minh rằng $NG$ song song với mặt phẳng $\left( {SAC} \right)$.
Xem đáp án
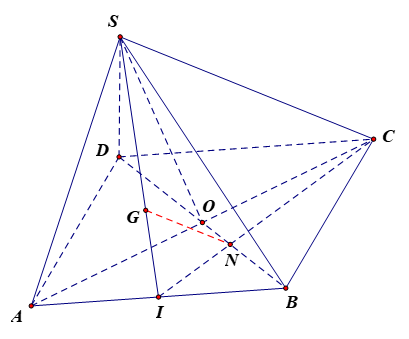
a) Gọi $O$là giao điểm của $AC$ và $BD$.
Khi đó: $\left\{ \begin{gathered}
O \in AC \hfill \\
AC \subset (SAC) \hfill \\
\end{gathered} \right. \Rightarrow O \in (SAC)$.
$\left\{ \begin{gathered}
O \in BD \hfill \\
BD \subset (SBD) \hfill \\
\end{gathered} \right. \Rightarrow O \in (SBD)$.
$ \Rightarrow O \in \left( {SAC} \right) \cap (SBD)\,\,(1)$
Mặt khác $S \in \left( {SAC} \right) \cap (SB{\text{D}})\,\,\,\,(2)$
Từ (1) và (2) suy ra $\left( {SAC} \right) \cap (SB{\text{D}}) = SO$.
b) Gọi $I$ là trung điểm của $AB$.
Vì $G$ là trọng tâm tam giác $SAB$ nên $\frac{{IG}}{{GS}} = \frac{1}{2}$.
Vì $N$ là trọng tâm tam giác $ABC$nên $\frac{{IN}}{{NC}} = \frac{1}{2}$.
Xét $\Delta SIC$ có $\frac{{IG}}{{GS}} = \frac{{IN}}{{NC}} = \frac{1}{2} \Rightarrow GN{\text{//}}SC$ (Định lý đảo của định lí Thalès).
Khi đó ta có $\left\{ \begin{gathered}
GN{\text{//}}SC \hfill \\
SC \subset (SAC) \hfill \\
GN \not\subset (SAC) \hfill \\
\end{gathered} \right. \Rightarrow GN{\text{//}}(SAC)$.
Câu 38:
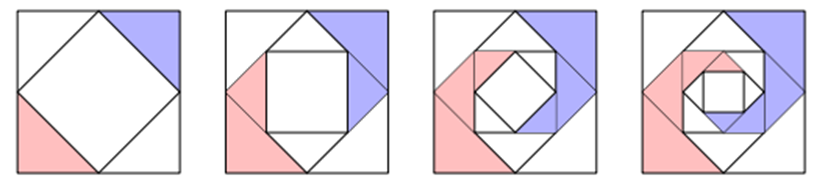
Một thợ thủ công muốn vẽ trang trí một hình vuông kích thước $4\;{\text{m}} \times 4\;{\text{m}}$ bằng cách vẽ một hình vuông mới với các đỉnh là trung điểm các cạnh của hình vuông ban đầu và tô kín màu lên hai tam giác đối diện (như hình vẽ dưới đây). Quá trình vẽ và tô theo quy luật đó được lặp lại 10 lần. Tính số tiền nước sơn để người thợ đó hoàn thành trang trí hình vuông trên? Biết tiền nước sơn 1 ${{\text{m}}^{\text{2}}}$ là 80 000 đồng.
Xem đáp án
Theo quy luật trang trí một hình vuông trên thì ta có các tam giác được tô màu sẽ là tam giác vuông cân.
Gọi ${u_n}$ là diện tích của hai tam giác được tô màu sau lần vẽ thứ $n$, với $n \in {\mathbb{N}^*}.$
Độ dài cạnh góc vuông của hai tam giác vuông cân được tô màu theo lần vẽ đầu tiên là $\frac{4}{2} = 2\,\,\left( {\text{m}} \right).$ Khi đó diện tích của hai tam giác được tô màu sau lần vẽ đầu tiên là
${u_1} = 2\left( {\frac{1}{2}.2.2} \right) = 4$ $\left( {{{\text{m}}^{\text{2}}}} \right).$
Độ dài cạnh góc vuông của hai tam giác vuông cân được tô màu theo lần vẽ thứ hai là $\frac{1}{2}.\sqrt {{2^2} + {2^2}} \, = \sqrt 2 \left( {\text{m}} \right).$ Khi đó diện tích của hai tam giác được tô màu sau lần vẽ thứ hai là
${u_2} = 2\left( {\frac{1}{2}.\sqrt 2 .\sqrt 2 } \right) = 4.\frac{1}{2}$ $\left( {{{\text{m}}^{\text{2}}}} \right).$
Độ dài cạnh góc vuông của hai tam giác vuông cân được tô màu theo lần vẽ thứ ba là$\frac{1}{2}.\sqrt {{{\left( {\sqrt 2 } \right)}^2} + {{\left( {\sqrt 2 } \right)}^2}} = 1\,\left( {\text{m}} \right).$ Khi đó diện tích của hai tam giác được tô màu sau lần vẽ thứ ba là
${u_3} = 2\left( {\frac{1}{2}.1.1} \right) = 4.{\left( {\frac{1}{2}} \right)^2}$ $\left( {{{\text{m}}^{\text{2}}}} \right).$
Khi đó, dãy số $\left( {{u_n}} \right)$ là một cấp số nhân với số hạng đầu ${u_1} = 4$ và công bội $q = \frac{1}{2}.$
Ta có công thức số hạng tổng quát ${u_n} = 4.{\left( {\frac{1}{2}} \right)^{n - 1}}$ $\left( {{{\text{m}}^{\text{2}}}} \right).$
Tổng diện tích của các tam giác được tô màu sau lần vẽ thứ 10 là:
${S_{10}} = \frac{{4\left[ {1 - {{\left( {\frac{1}{2}} \right)}^{10}}} \right]}}{{1 - \frac{1}{2}}} = \frac{{1\,\,023}}{{128}}$ $\left( {{{\text{m}}^{\text{2}}}} \right).$
Vậy số tiền nước sơn là $\frac{{1\,\,023}}{{128}}.80\,\,000 = 639\,\,375$ đồng.
Câu 39:
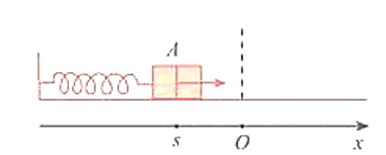
Trong hình sau, khi được kéo ra khỏi vị trí cân bằng ở điểm $O$ và buông tay, lực đàn hồi của lò xo khiến vật $A$ gắn ở đầu của lò xo dao động quanh $O$. Toạ độ $s\left( {{\text{cm}}} \right)$ của $A$ trên trục $Ox$ vào thời điểm $t$ (giây) sau khi buông tay được xác định bởi công thức $s = 10\sin \left( {10t + \frac{\pi }{2}} \right)$. Vào các thời điểm nào thì $s = - 5\sqrt 3 \left( {{\text{cm}}} \right)$?
Xem đáp án
Theo đề ra ta có phương trình:
\[10\sin \left( {10t + \frac{\pi }{2}} \right) = - 5\sqrt 3 \]
\[ \Leftrightarrow \sin \left( {10t + \frac{\pi }{2}} \right) = \frac{{ - \sqrt 3 }}{2} = \sin \left( {\frac{{ - \pi }}{3}} \right)\]
\[ \Leftrightarrow \left[ \begin{gathered}
10t + \frac{\pi }{2} = \frac{{ - \pi }}{3} + k2\pi \hfill \\
10t + \frac{\pi }{2} = \frac{{4\pi }}{3} + k2\pi \hfill \\
\end{gathered} \right.,k \in \mathbb{Z} \Leftrightarrow \left[ \begin{gathered}
t = \frac{{ - \pi }}{{12}} + k\frac{\pi }{5} \hfill \\
t = \frac{\pi }{{12}} + k\frac{\pi }{5} \hfill \\
\end{gathered} \right.,k \in \mathbb{Z}\].
Vậy vào các thời điểm $t = \frac{{ - \pi }}{{12}} + k\frac{\pi }{5},\left( {k \geqslant 1,k \in \mathbb{Z}} \right)$ và $t = \frac{\pi }{{12}} + k\frac{\pi }{5}$$\left( {k \geqslant 0,k \in \mathbb{Z}} \right)$ thì $s = - 5\sqrt 3 $cm.