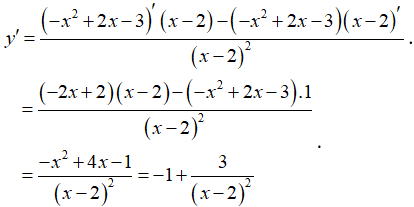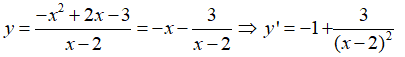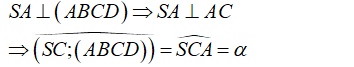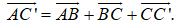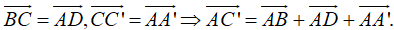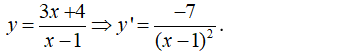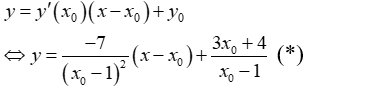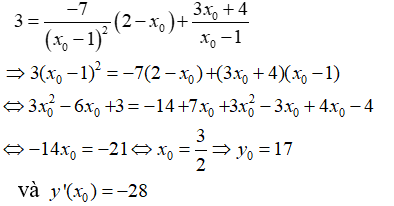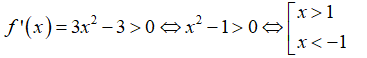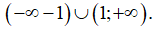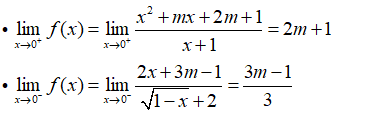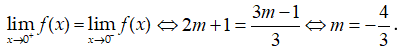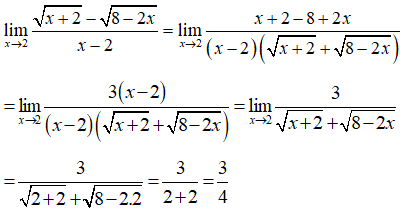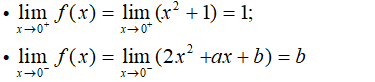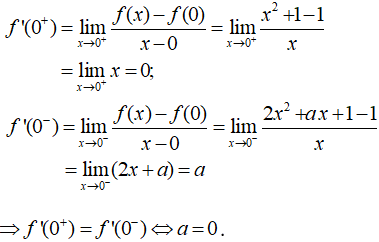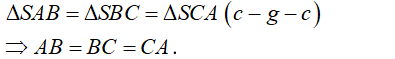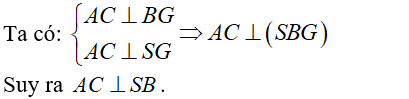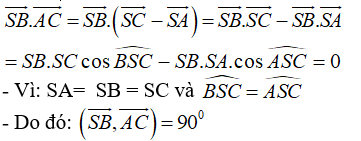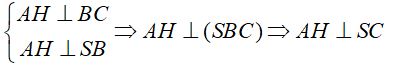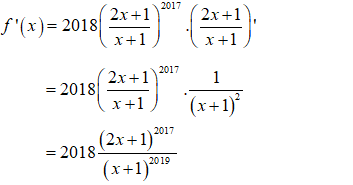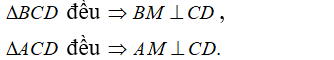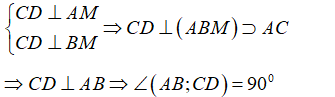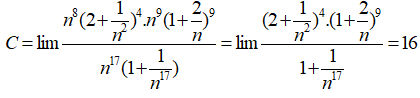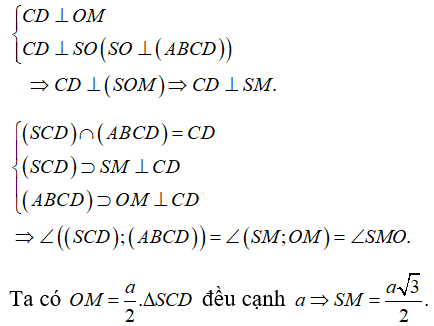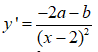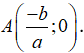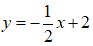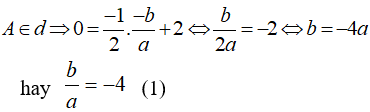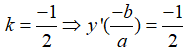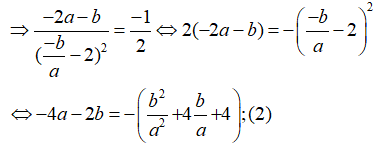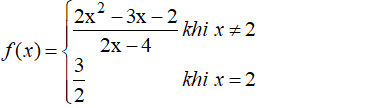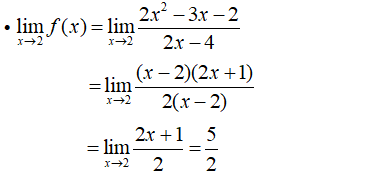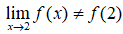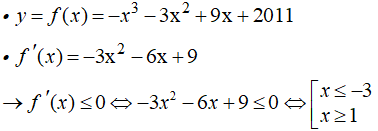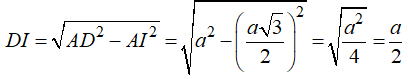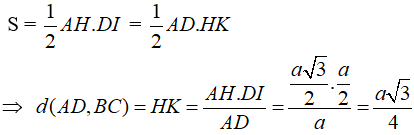26 câu hỏi trắc nghiệm thuộc Đề thi Toán 11 Học kì 2 có đáp án (Đề 3)

Câu 1:

Phần I: Trắc nghiệm

Cho hàm số $y = \frac{- x^{2} + 2 x - 3}{x - 2}$ . Đạo hàm y’ của hàm số là biểu thức nào sau đây?

A. $- 1 - \frac{3}{{(x - 2)}^{2}}$

B. $1 + \frac{3}{{(x - 2)}^{2}}$

C. $- 1 + \frac{3}{{(x - 2)}^{2}}$

D. $1 - \frac{3}{{(x - 2)}^{2}}$

Xem đáp án

Đáp án C

Cách 1: Ta có:

Cách 2: Ta có:

Câu 2:

Cho dãy số $(u_{n})$ xác định bởi $u_{n} = \frac{2^{n} \sin n}{9^{n}}$ . Tính $l i m u_{n}$

A. 0

B. $\frac{2}{9}$

C. $+ \infty$

D. $\frac{9}{2}$

Xem đáp án

Đáp án A

- Theo công thức giới hạn đặc biệt, ta có:

Câu 3:

Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng a và SA ⊥ (ABCD). Biết $S A = \frac{a \sqrt{6}}{3}$ . Tính góc giữa SC và mp (ABCD).

A. $30 °$

B. $45 °$

C. $60 °$

D. $75 °$

Xem đáp án

Đáp án A.

- Ta có:

- Vì ABCD là hình vuông cạnh a.

Câu 4:

Cho hình lập phương ABCD.A’B’C’D’. Hệ thức nào sau đây đúng?

A. $\vec{A C'} = \vec{A B} + \vec{A C} + \vec{A A'}$

B. $\vec{A C'} = \vec{A B} + \vec{C B} + \vec{A A'}$

C. $\vec{A C'} = \vec{A B} + \vec{A D} + \vec{A A'}$

D. $\vec{A C'} = \vec{B D} + \vec{A C} + \vec{A A'}$

Xem đáp án

Đáp án C.

- Phương pháp: Sử dụng công thức ba điểm và các vectơ bằng nhau.

- Cách giải:

+ Ta có:

+ Mà:

Câu 5:

Viết phương trình tiếp tuyến kẻ từ điểm A (2; 3) tới đồ thị hàm số $y = \frac{3 x + 4}{x - 1}$ là

A. y = -28x+59; y = x+1

B. y = -24x+51; y = x+1

C. y = -28x+59

D. y = -28x+59; y = -24x+51

Xem đáp án

Đáp án C.

- Ta có:

- Phương trình tiếp tuyến của đồ thị (C): $y = \frac{3 x + 4}{x - 1}$ tại điểm $M (x_{0}; y_{0}) \in (C)$ với $x_{0} \neq 1$ là:

- Vì tiếp tuyến đi qua điểm A(2; 3) nên ta có:

- Vậy có một tiếp tuyến thỏa đề bài là:

Câu 6:

Cho hàm số $f (x) = x^{3} - 3 x + 2018 .$ Tập nghiệm của bất phương trình f'(x) > 0 là:

A. (-1;1)

B. [-1;1]

C. $(- \infty; - 1) \cup (1; + \infty)$

D. $(- \infty; - 1] \cup [1; + \infty)$

Xem đáp án

Đáp án C.

- Phương pháp:

+) Tính f'(x).

+) Sử dụng quy tắc trong trái ngoài cùng giải bất phương trình bậc hai.

- Cách giải:

+ Ta có:

→ Vậy tập nghiệm của bất phương trình là

Câu 7:

Tìm m để các hàm số $f (x) = \{\begin{cases} x^{2} + m x + 2 m + 1 k h i x \geq 0 \\ \frac{2 x + 3 m - 1}{\sqrt{1 - x} + 2} k h i x < 0 \end{cases}$ có giới hạn khi x → 0.

A. $m = \frac{1}{3}$

B. $m = - \frac{1}{3}$

C. $m = - \frac{2}{3}$

D. $m = - \frac{4}{3}$

Xem đáp án

Đáp án D.

- Ta có:

- Hàm số có giới hạn khi x → 0 khi và chỉ khi:

Câu 8:

Giới hạn $\lim_{x \to 2} \frac{\sqrt{x + 2} - \sqrt{8 - 2 x}}{x - 2}$ bằng:

A. $+ \infty$

B. $- \infty$

C. 0

D. $\frac{3}{4}$

Xem đáp án

Đáp án D.

- Phương pháp: Nhân cả tử và mẫu với biểu thức liên hợp của tử.

- Cách giải:

+ Ta có:

Chú ý: HS có thể sử dụng chức năng CALC trên MTCT để tìm giới hạn của hàm số.

Câu 9:

Tìm a,b để hàm số $f (x) = \{\begin{cases} x^{2} + 1 k h i x \geq 0 \\ 2 x^{2} + a x + b k h i x < 0 \end{cases}$ có đạo hàm tại x = 0?

A. a = 10; b = 11

B. a = 0; b = -1

C. a = 0; b = 1

D. a = 20; b = 1

Xem đáp án

Đáp án C.

- Để hàm số đã cho có đạo hàm tại x = 0 khi và chỉ khi:

+ Hàm số liên tục tại x = 0.

+ Đạo hàm bên trái và đạo hàm bên phải tại điểm x = 0 bằng nhau.

+) Ta có:

- Do đó, để hàm số liên tục tại x= 0 khi b = 1 .

+) Ta có: f(0) = 1.

- Vậy a = 0, b = 1 là những giá trị cần tìm.

Câu 10:

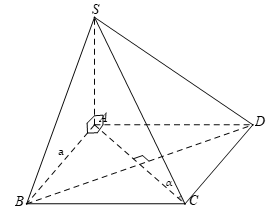
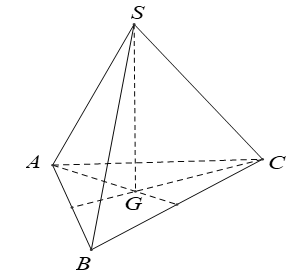
Cho hình chóp S.ABC có SA = SB = SC và $\hat{A S B} = \hat{B S C} = \hat{C S A}$ . Hãy xác định góc giữa cặp vectơ $\vec{S B}$ và $\vec{A C}$ ?

A. $60 °$

B. $120 °$

C. $45 °$

D. $90 °$

Xem đáp án

Đáp án D

Cách 1:

- Ta có: SA = SB = SC nên:

- Do đó, tam giác ABC đều. Gọi G là trọng tâm của tam giác ABC.

- Vì hình chóp S.ABC có SA = SB = SC nên hình chiếu của S trùng với G. Hay SG ⊥ (ABC).

- Vậy góc giữa cặp vectơ 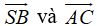bằng $90 °$ .

Cách 2:

- Ta có:

Câu 11:

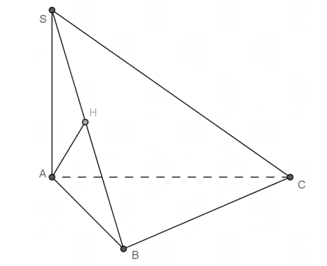
Cho hình chóp S.ABCD có SA ⊥ (ABCD) và ΔABC vuông ở B, AH là đường cao của ΔSAB. Khẳng định nào sau đây sai?

A. $S A ⊥ B C$

B. $A H ⊥ B C$

C. $A H ⊥ A C$

D. $A H ⊥ S C$

Xem đáp án

Chọn C.

+) Do SA ⊥ (ABCD) ⇒ SA ⊥ BC nên câu A đúng.

+) Tam giác ABC vuông ở B nên AB ⊥ BC

- Lại có: SA ⊥ BC (vì SA ⊥ (ABCD))

→ Do đó: BC ⊥ (SAB) ⇒ AH ⊥ BC.

nên câu B đúng.

+) Theo trên ta có:

⇒ D đúng.

- Vậy câu C sai.

Câu 12:

Giới hạn $\lim_{x \to - \infty} (- x^{2} - 10 x^{5} - 10 x)$ bằng:

A. $+ \infty$

B. $- \infty$

C. 1

D. -4

Xem đáp án

Đáp án A.

- Ta có:

Câu 13:

Đạo hàm của hàm số $f (x) = {(\frac{2 x + 1}{x + 1})}^{2018}$ là:

A. $f' (x) = 2018 {(\frac{2 x + 1}{x + 1})}^{2017} (\frac{- 1}{x + 1})$

B. $f' (x) = 2018 \frac{{(2 x + 1)}^{2017}}{{(x + 1)}^{2019}}$

C. $f' (x) = 2018 {(\frac{2 x + 1}{x + 1})}^{2017}$

D. $f' (x) = {(\frac{2 x + 1}{x + 1})}^{2017} {(\frac{1}{x + 1})}^{2}$

Xem đáp án

Đáp án B.

- Phương pháp: Sử dụng công thức tính đạo hàm của hàm hợp

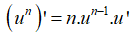
và công thức tính nhanh

- Cách giải:

Câu 14:

Cho hàm số $y = k x^{3} + \sqrt{x^{2} + x - 2}$ . Với giá trị nào của k thì $y' (2) = \frac{53}{4}$ ?

A. k = -1

B. k = 1

C. k = -2

D. k = 3

Xem đáp án

Đáp án B

- Ta có:

Câu 15:

Cho chuyển động thẳng xác định bởi phương trình $s = t^{3} - 3 t^{2} - 9 t + 2$ (t tính bằng giây; s tính bằng mét). Khẳng định nào sau đây đúng?

A. Vận tốc của chuyển động bằng 0 khi t = 0 hoặc t = 2.

B. Vận tốc của chuyển động tại thời điểm t= 2 là v = 18m/s.

C. Gia tốc của chuyển động tại thời điểm t = 3 là $a = 12 m / s^{2}$ .

D. Gia tốc của chuyển động bằng 0 khi t = 0.

Xem đáp án

Đáp án C.

- Phương trình vận tốc của chuyển động là:

- Phương trình gia tốc của chuyển động là:

Câu 16:

Cho tứ diện đều ABCD. Góc giữa hai đường thẳng AB và CD bằng:

A. $60 °$

B. $90 °$

C. $45 °$

D. $30 °$

Xem đáp án

Đáp án B.

- Phương pháp: Tứ diện đều có các cặp cạnh đối vuông góc.

- Cách giải:

+ Gọi M là trung điểm của CD ta có:

+ Ta có:

Câu 17:

Cho hình lăng trụ ABC.A'B'C', M là trung điểm của BB’. Đặt $\vec{C A} = \vec{a}; \vec{C B} = \vec{b}; \vec{A A'} = \vec{c}$ . Khẳng định nào sau đây đúng?

A. $\vec{A M} = \vec{b} + \vec{c} - \frac{1}{2} \vec{a}$

B. $\vec{A M} = \vec{a} - \vec{c} + \frac{1}{2} \vec{b}$

C. $\vec{A M} = \vec{a} + \vec{c} - \frac{1}{2} \vec{b}$

D. $\vec{A M} = \vec{b} - \vec{a} + \frac{1}{2} \vec{c}$

Xem đáp án

Đáp án D.

- Ta phân tích như sau:

Câu 18:

Giá trị của $C = l i m \frac{(2 n^{2} + 1)^{4} (n + 2)^{9}}{n^{17} + 1}$ bằng:

A. $+ \infty$

B. $- \infty$

C. 16

D. 1

Xem đáp án

Đáp án C.

- Ta có:

Câu 19:

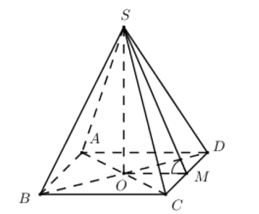
Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Tan của góc giữa mặt bên và mặt đáy bằng:

A. $\sqrt{2}$

B. $\frac{\sqrt{2}}{2}$

C. $\frac{\sqrt{3}}{2}$

D. $\sqrt{3}$

Xem đáp án

Đáp án A.

- Phương pháp:

+) Xác định góc giữa mặt bên và đáy là góc giữa hai đường thẳng lần lượt thuộc 2 mặt phẳng và vuông góc với giao tuyến của hai mặt phẳng đó.

+) Tính tan của góc xác định được.

Cách giải:

- Gọi O = AC ∩ BD. Do S.ABCD là chóp đều ⇒ SO ⊥ (ABCD).

- Gọi M là trung điểm của CD ta có: OM là đường trung bình của tam giác BCD ⇒ OM // BC ⇒ OM ⊥ CD.

- Ta có:

- Áp dụng định lý Pytago trong tam giác vuông SOM ta có:

Câu 20:

Cho hàm số $y = \frac{a x + b}{x - 2}$ , có đồ thị là (C). Tìm biết tiếp tuyến của đồ thị (C) tại giao điểm của (C) và trục Ox có phương trình là $y = - \frac{1}{2} x + 2$ ?

A. a = -1; b = 1

B. a = -1; b = 2

C. a = -1; b = 3

D. a = -1; b = 4

Xem đáp án

Đáp án D.

- Ta có:

+) Giao điểm của tiếp tuyến của đồ thị (C) tại giao điểm của (C) và trục Ox là

+ ) Tiếp tuyến tại A có phương trình:

+) Tiếp tuyến tại A có hệ số góc

- Giải hệ phương trình (1) và (2) ta được: a = -1, b = 4.

Câu 21:

Phần II: Tự luận

Tìm các giới hạn sau: $\lim_{x \to 1} \frac{3 x^{2} - 2 x - 1}{x^{3} - 1}$

Xem đáp án

Câu 22:

Tìm các giới hạn sau: $\lim_{x \to 3 -} \frac{x + 3}{x - 3}$

Xem đáp án

Câu 23:

Tìm các giới hạn sau: $\lim_{x \to 1} \frac{x - \sqrt{2 x - 1}}{x^{2} - 12 x + 11}$

Xem đáp án

Câu 24:

Xét tính liên tục của hàm số sau tại điểm $x_{0} = 2$

$f (x) = \{\begin{cases} \frac{2 x^{2} - 3 x - 2}{2 x - 4} k h i x \neq 2 \\ \frac{3}{2} k h i x = 2 \end{cases}$

Xem đáp án

- Tập xác định D = R.

- Ta có: f(2) = 3/2.

- Vì

Nên hàm số không liên tục tại x = 2.

Câu 25:

Cho hàm số $y = f (x) = - x^{3} - 3 x^{2} + 9 x + 2011$ có đồ thị (C).

a) Giải bất phương trình: f'(x) ≤ 0.

b) Viết phương trình tiếp tuyến với đồ thị (C) tại điểm có hoành độ bằng 1.

Xem đáp án

a) Ta có:

b) Với $x_{0} = 1$ thì $y_{0} = 2016$ và f’(1) = 0.

- Do đó, phương trình tiếp tuyến tại điểm có hoành độ x= 1 là

y = 0(x- 1) + 2016 hay y = 2016.

Câu 26:

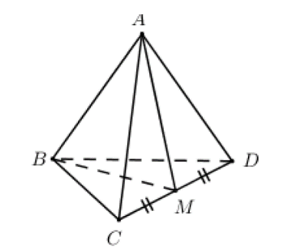
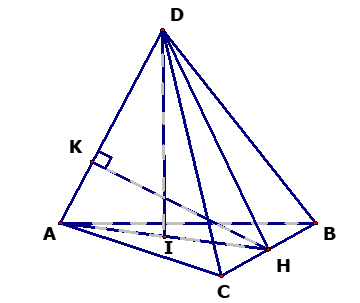
Cho tứ diện ABCD có tam giác ABC là tam giác đều cạnh a, AD vuông góc với BC, AD = a và khoảng cách từ điểm D đến đường thẳng BC là a. Gọi H là trung điểm BC, I là trung điểm AH.

1) Chứng minh rằng đường thẳng BC vuông góc với mặt phẳng (ADH) và DH = a.

2) Chứng minh rằng đường thẳng DI vuông góc với mặt phẳng (ABC).

3) Tính khoảng cách giữa AD và BC.

Xem đáp án