20 câu hỏi trắc nghiệm thuộc Đề thi Toán 11 Học kì 2 có đáp án (Đề 5)

Câu 1:

Hàm số nào dưới đây liên tục trên ℝ?

A. f(x) = x² – 1.

B. f(x) = \(\frac{1}{{x - 1}}.\)

C. f(x) = \(\sqrt x - 1.\)

D. f(x) = \(\frac{1}{{\sqrt x }}.\)

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Đáp án B: tập xác định D = ℝ\{1}.

Đáp án C: tập xác định D = [0;+¥).

Đáp án D: tập xác định D = (0;+¥).

Đáp án A; tập xác định D = ℝ.

Vậy hàm số f(x) = \(\frac{1}{{\sqrt x }}\) liên tục trên ℝ.

Câu 2:

Cho hàm số y = f(x) liên tục trên ℝ và thỏa mãn \(\mathop {\lim }\limits_{x \to 1} \frac{{f(x) - f(1)}}{{x - 1}} = 2.\) Tính f '(1).

A. f '(1) = −2.

B. f '(1) = 2.

C. f '(1) = 1.

D. f '(1) = 0.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Theo định nghĩa, ta có: \[f'(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(x) - f(1)}}{{x - 1}}\] Þ f'(1) = 2.

Câu 3:

Trên khoảng (0; +¥), hàm số y = \(\sqrt x \) có đạo hàm là

A. y' = \(\frac{1}{2}\sqrt x .\)

B. y' = \(\frac{2}{{\sqrt x }}.\)

C. y' = \(\frac{1}{{\sqrt x }}.\)

D. y' = \(\frac{1}{{2\sqrt x }}.\)

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Ta có y = \(\sqrt x \) Þ y' = \(\frac{1}{{2\sqrt x }}.\)

Câu 4:

Tính đạo hàm của hàm số y = sin2x + 1.

A. y' = 2cos2x.

B. y' = −2cos2x.

C. y' = cos2x.

D. y' = −cos2x.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Ta có y = sin2x + 1

Þ y' = (2x)'.cos2x = 2cos2x.

Câu 5:

Đạo hàm của hàm số y = \(\frac{1}{{5x + 1}}\) là

A. y' = \(\frac{1}{{{{(5x + 1)}^2}}}\)

B. y' = \( - \frac{5}{{{{(5x + 1)}^2}}}\)

C. y' = \( - \frac{1}{{{{(5x + 1)}^2}}}\)

D. y' = \(\frac{5}{{{{(5x + 1)}^2}}}\)

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Ta có y = \(\frac{1}{{5x + 1}}\) Þ y' = \( - \frac{5}{{{{(5x + 1)}^2}}}\).

Câu 6:

Tiếp tuyến của đồ thị hàm số y = −x³ + 3x + 2 tại điểm M(2; 0) có hệ số góc bằng

A. 3.

B. −15.

C. −9.

D. 9.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Ta có: y' = −3x² + 3 Þ y'(2) = −9.

Vậy hệ số góc của tiếp tuyến đồ thị hàm số y tại điểm M(2; 0) bằng −9.

Câu 7:

Cho hàm số f(x) = x³ – 3x² – 9x + 5. Tập nghiệm của bất phương trình f '(x) < 0 là

A. (−¥; −3) È (1; +¥).

B. (−¥; −1) È (3; +¥).

C. (−3; 1).

D. (−1; 3).

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Ta có: f '(x) = 3x² – 6x – 9

Giải f '(x) < 0 Û 3x² – 6x – 9 < 0

Û x² – 2x – 3 < 0 Û −1 < x < 3.

Câu 8:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Các mặt phẳng (SAB) và (SAD) cũng vuông góc với đáy. Mặt phẳng (SBD) vuông góc với mặt phẳng nào dưới đây?

A. (ABCD).

B. (SAC).

C. (SAB).

D. (SAD).

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

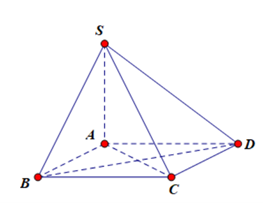
Ta có (SAB) và (SAD) vuông góc với mặt phẳng đáy

Þ SA ^ (ABCD) Þ SA ^ BD.

Mà AC ^ BD (đường chéo hình thoi ABCD).

Þ BD ^ (SAC) mà BD Ì (SBD) Þ (SAC) ^ (SBD).

Câu 9:

Một chất điểm chuyển động thẳng với vận tốc được xác định bởi v(t) = 6t – t² (m/s), t là thời gian tính bằng giây. Tính vận tốc tức thời của chuyển động tại thời điểm gia tốc triệt tiêu.

A. 3 (m/s).

B. 6 (m/s).

C. 9 (m/s).

D. 12 (m/s).

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Ta có: a(t) = v'(t) = 6 – 2t = 0

Þ t = 3(s) Þ v(3) = 9 (m/s).

Vậy vận tốc tức thời của chuyển động tại thời điểm gia tốc triệt tiêu là 9 m/s.

Câu 10:

Cho hàm số y = f(x) liên tục trên ℝ thỏa mãn \(\mathop {\lim }\limits_{x \to 2} \left[ {f(x) - 3} \right] = 4.\) Tính f(2).

A. f(2) = 7.

B. f(2) = −7.

C. f(2) = 1.

D. f(2) = −1.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Ta có: \(\mathop {\lim }\limits_{x \to 2} \left[ {f(x) - 3} \right] = 4\) Û f(2) – 3 = 4 Û f(2) = 7.

Câu 11:

Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng 2a, cạnh bên bằng nửa cạnh đáy. Tính khoảng cách từ điểm A tới mặt phẳng (A’BC).

A. \(\frac{{2a\sqrt 7 }}{7}.\)

B. \(\frac{{a\sqrt 3 }}{3}.\)

C. \(a\sqrt 3 .\)

D. \(\frac{{a\sqrt 3 }}{2}.\)

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

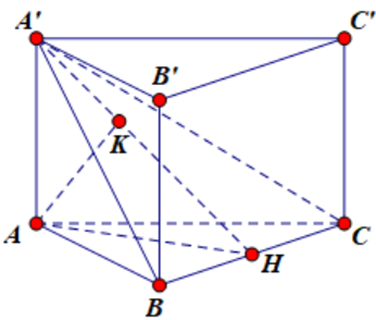
Gọi H là trung điểm BC.

Trong mặt phẳng AA’H dựng AK ^ A’H tại K.

Þ d[A,(A’BC)] = AK.

AH = a\(\sqrt 3 \), AA’ = a.

AK = \[\frac{{AA'.AH}}{{\sqrt {AA{'^2} + A{H^2}} }} = \frac{{a.a\sqrt 3 }}{{{{\sqrt {{a^2} + \left( {a\sqrt 3 } \right)} }^2}}} = \frac{{a\sqrt 3 }}{2}.\]

Câu 12:

Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−10;10] sao cho đồ thị hàm số y = \(\frac{1}{3}\)x³ – mx² + (m + 9)x + 2022 có đúng hai tiếp tuyến với hệ số góc bằng 3?

A. 13.

B. 6.

C. 15.

D. 17.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Tập xác định: D = ℝ.

Hệ số góc của tiếp tuyến tại M(x;y) là: k = y' = x² – 2mx + m + 9.

Theo đề bài, ta có: k = 3

Û x² – 2mx + m + 9 = 3

Û x² – 2mx + m + 6 = 0 (1)

Đồ thị hàm số có đúng 2 tiếp tuyến với hệ số góc bằng 3

Û phương trình (1) có 2 nghiệm phân biệt.

Û ∆' = (−m)² – (m + 6) = m² – m – 6 > 0

Û \(\left[ {\begin{array}{*{20}{c}}{m > 3}\\{m < - 2}\end{array}} \right.\).

Vì m Î [−10;10] và m nguyên nên m Î [−10;-3] È [4;10].

Vậy có 15 giá trị m thỏa mãn yêu cầu bài toán.

Câu 13:

Tính các giới hạn sau:

\(\mathop {\lim }\limits_{x \to 2} \frac{{5x - 10}}{{{x^2} + x - 6}}\)

Xem đáp án

Hướng dẫn giải

\(\mathop {\lim }\limits_{x \to 2} \frac{{5x - 10}}{{{x^2} + x - 6}}\)

\( = \mathop {\lim }\limits_{x \to 2} \frac{{5(x - 2)}}{{(x - 2)(x + 3)}} = \mathop {\lim }\limits_{x \to 2} \frac{5}{{(x + 3)}} = 1.\)

Câu 14:

Tính các giới hạn sau:

\(\mathop {\lim }\limits_{x \to + \infty } \left( {2x - 3 - \sqrt {{x^2} + x + 1} } \right).\)

Xem đáp án

Hướng dẫn giải

\(\mathop {\lim }\limits_{x \to + \infty } \left( {2x - 3 - \sqrt {{x^2} + x + 1} } \right).\)

\(\mathop { = \lim }\limits_{x \to \infty } \left( {2 - \frac{3}{x} - \sqrt {1 + \frac{1}{x} + \frac{1}{{{x^2}}}} } \right) = + \infty .\)

Câu 15:

Tính đạo hàm của các hàm số sau:

a) y = x⁴ – 2x² – 15.

b) y = x.cosx.

c) y = \(\sqrt {{x^2} + 1} \).

Xem đáp án

Hướng dẫn giải

a) Ta có y = x⁴ – 2x² – 15.

Do đó y' = 4x³ – 4x.

b) Ta có y = x.cosx.

Do đó y' = (x)'.cosx + x.(cosx)' = cosx – x.sinx.

c) Ta có y = \(\sqrt {{x^2} + 1} \)

Do đó y' = \(\frac{{\left( {{x^2} + 1} \right)'}}{{2\sqrt {{x^2} + 1} }} = \frac{{2x}}{{2\sqrt {{x^2} + 1} }} = \frac{x}{{\sqrt {{x^2} + 1} }}.\)

Câu 16:

Cho hàm số y = \(\frac{{2x + 1}}{{x - 1}}\) có đồ thị là (C). Viết phương trình tiếp tiếp của đồ thị (C) tại điểm có hoành độ bằng 2.

Xem đáp án

Hướng dẫn giải

Với x = 2 Þ y = 5 Þ M(2;5).

Ta có y' = \( - \frac{3}{{{{(x - 1)}^2}}}.\)

Hệ số góc của tiếp tuyến tại M là k = y'(2) = −3.

Phương trình tiếp tuyến cần tìm là y = −3(x – 2) + 5 Û y = −3x + 11.

Vậy phương trình tiếp tiếp của đồ thị (C) tại điểm có hoành độ bằng 2 là y = −3x + 11.

Câu 17:

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB = BC = \(\frac{1}{2}\)AD = 2a. Cạnh bên SA vuông góc với mặt phẳng đáy là SA = \(2\sqrt 2 a.\)

Chứng minh rằng (SBC) ^ (SAB).

Xem đáp án

Hướng dẫn giải

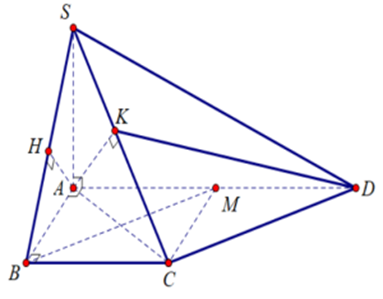
Ta có SA ^ (ABCD) Þ SA ^ BC (1).

Lại có ABCD là hình thang vuông tại B nên AB ^ BC (2).

Từ (1), (2) suy ra BC ^ (SAB) Þ (SBC) ^ (SAB).

Câu 18:

Tính khoảng cách từ điểm A tới mặt phẳng (SBC).

Xem đáp án

Hướng dẫn giải

Trong mặt phẳng (SAB) dựng AH ^ SB tại H, chứng minh được AH ^ (SBC).

Từ đó d[A,(SBC)] = AH.

Trong tam giác SAB ta có:

AH = \(\frac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }}\)= \(\frac{{\left( {2a\sqrt 2 } \right).2a}}{{\sqrt {{{\left( {2a\sqrt 2 } \right)}^2} + {{\left( {2a} \right)}^2}} }} = \frac{{2a\sqrt 6 }}{3}.\)

Vậy d[A,(SBC)] = \(\frac{{2a\sqrt 6 }}{3}.\)

Câu 19:

Tính góc giữa hai mặt phẳng (SAB) và (SCD).

Xem đáp án

Hướng dẫn giải

Gọi M là trung điểm AD

Suy ra tứ giác ABCM là hình vuông

Do đó AC ^ BM.

Ta thấy BC // MD, BC = MD = 2a

Suy ra tứ giác BCDM là hình bình hành nên BM // CD.

Từ đó Þ CD ^ AC và ta có CD ^ SA (do SA ^ (ABCD)) nên CD ^ (SAC).

Trong mặt phẳng (SAC) dựng AK ^ SC tại K, chứng minh được AK ^ (SCD) (3).

Lại có AD ^ SA, AD ^ AB Þ AD ^ (SAB) (4).

Từ (3) và (4) Þ [(SAB),(SCD)] = (AK,AD) = \(\widehat {KAD}.\)

Ta có AC = \(2a\sqrt 2 \) và SA = \(2a\sqrt 2 \) Þ AK = 2a.

Trong tam giác vuông AKD vuông tại K ta có:

cos\(\widehat {KAD}\)= \(\frac{{AK}}{{AD}}\)= \(\frac{1}{2}\)Þ \(\widehat {KAD}\)= 60°.

Vậy [(SAB),(SCD)] = 60°.

Câu 20:

Cho hàm số y = f(x) có đạo hàm trên ℝ. Biết tiếp tuyến của đồ thị các hàm số y = f(x⁴) và y = x². f(2x² – 1) tại điểm có hoành độ bằng −1 vuông góc với nhau. Tìm giá trị nhỏ nhất của biểu thức T = 4[f(1)]² – 4f(1) – 5.

Xem đáp án

Huớng dẫn giải

∙ y = f(x⁴) Þ y' = (4x³).f '(x⁴)

Þ K₁ = y'(1) = 4.f '(1).

∙ y = x².f(2x² – 1) Þ y' = 2x.f(2x² – 1) + 4x³.f '(2x² – 1).

Þ K₂ = y'(1) = 2f(1) + 4f '(1).

Theo đề bài ta có 2 tiếp tuyến vuông góc với nhau nên K₁.K₂ = −1

Û 4. f '(1).[2f(1) + 4f '(1)] = −1.

Đặt t = f'(1) Þ f(1) = \( - \frac{1}{{8t}} - 2t\)

Þ |f(1)| ≥ \(2\sqrt {\frac{1}{{8t}}.2t} = 1\)

Þ \(\left[ {\begin{array}{*{20}{c}}{f(1) \le - 1}\\{f(1) \ge 1}\end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{c}}{2f(1) - 1 \le - 3}\\{2f(1) - 1 \ge 1}\end{array}} \right.\)

Þ |2f(1) – 1| ≥ 1 Þ (2f(1) – 1)² ≥ 1.

Khi đó: T = [2f(1) – 1]² – 6 ≥ 1 – 6 = −5.

Vậy MinT = −5 khi f(1) = 1.