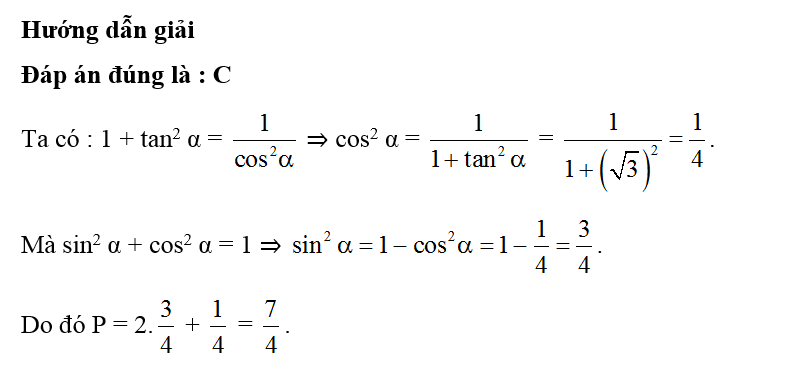10 câu hỏi trắc nghiệm thuộc Dạng 6. Tính giá trị của biểu thức liên quan đến các giá trị lượng giác

Trắc nghiệm Toán 11 Bài 1. Giá trị lượng giác của góc lượng giác có đáp án

Dạng 6. Tính giá trị của biểu thức liên quan đến các giá trị lượng giác

269 lượt thi
10 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho x = 30°. Khi đó giá trị của biểu thức A = sin 2x – 3cos x là:

A. 3;

B. $\sqrt{3}$ ;

C. $- \sqrt{3}$ ;

\frac{\sqrt{2}}{2}

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Thay x = 30° vào biểu thức A ta có:

A = sin (2.30°) – 3cos 30° = sin 60° – 3cos 30° = $\frac{\sqrt{3}}{2}$ – 3. $\frac{\sqrt{3}}{2}$ = – $\sqrt{3}$ .

Câu 2:

Cho α + β = π. Khi đó biểu thức A = sin² (π – β) + cos² (π – α) là:

A. 1;

B. 2;

C. –1;

D. –2.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Ta có: α + β = π ⇒ α = π – β.

Do đó A = sin² (π – β) + cos² (π – α) = (sin α)² + (– cos α)² = sin² α + cos² α = 1.

Câu 3:

Cho sin x = $\frac{1}{4}$ . Biểu thức A = $\frac{4}{3} \sin^{2} α$ + $c {os}^{2} α$ = $\frac{a}{b}$ (với (a, b) = 1). Khi đó giá trị của a – b là:

A. 2;

B. 1;

C. 3;

D. 4.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Ta có: sin² x + cos² x = 1 ⇒ cos²x = 1 – sin²x = $1 - \frac{1}{16} = \frac{15}{16}$ .

Do đó A = $\frac{4}{3}$ . $\frac{1}{16}$ + $\frac{15}{16}$ = $\frac{49}{48}$ .

Như vậy a = 49, b = 48 ⇒ a – b = 1.

Câu 4:

Cho tan α = $\sqrt{3}$ . Biểu thức P = 2sin² α + cos² α có giá trị bằng

A. $\frac{4}{5}$ ;

B. $\frac{5}{4}$ ;

C. $\frac{7}{4}$ ;

\frac{7}{3}

Xem đáp án

Cho tan alpha = căn bậc hai 3 . Biểu thức P = 2sin^ 2 alpha + cos2 alpha có giá trị bằng (ảnh 1)

Câu 5:

Cho sin x = $\frac{1}{2}$ , biết cos x nhận giá trị âm, giá trị của biểu thức A = $\frac{s in x - c os x}{\sin x + c os x}$ là

A. $- 2 - \sqrt{3}$ ;

B. $2 + \sqrt{3}$ ;

C. $- 2 + \sqrt{3}$ ;

2 - \sqrt{3}

Xem đáp án

Cho sin x = 1/2 , biết cos x nhận giá trị âm, giá trị của biểu thức A = sin x - cos x /sin x + cos x là (ảnh 1)

Câu 6:

Cho sin α = $\frac{2}{3}$ biết 90° < α < 180°. Đáp án nào sau đây là đúng?

A. 4sin² α + 2cos² α = 3;

B. 4sin² α + 2cos² α = – 3;

C. 4sin α + 2cos α = $\frac{8 - 2 \sqrt{5}}{3}$ ;

D. 4sin α + 2cos α =

\frac{8 + 2 \sqrt{5}}{3}

Xem đáp án

Cho sin alpha = 2/3 biết 90° < alpha < 180°. Đáp án nào sau đây là đúng? (ảnh 1)

Câu 7:

Cho tan x = 3. Khi đó giá trị biểu thức A = $\frac{4 s in x + c os x}{\sin x + 2 \cos x}$ là

A. $\frac{- 13}{5}$ ;

B. 3;

C. $\frac{- 4}{5}$ ;

\frac{13}{5}

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Vì tan x = 3 nên cos x ≠ 0. Chia cả tử và mẫu biểu thức A cho cos x ta có:

A = $\frac{4. \frac{\sin x}{cos x} + 1}{\frac{\sin x}{cos x} + 2}$ = $\frac{4 \tan x + 1}{\tan x + 2}$ = $\frac{4.3 + 1}{3 + 2}$ = $\frac{13}{5}$ .

Câu 8:

Cho cot x = 2. Giá trị của biểu thức P = $\frac{3 \cos x - \sin x}{\cos x + \sin x}$ là

A. $\frac{4}{3}$ ;

B. $- \frac{4}{3}$ ;

C. $- \frac{5}{3}$ ;

\frac{5}{3}

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Vì cot x = 2 ⇒ sin x ≠ 0. Chia cả tử và mẫu biểu thức P cho sin x ta có:

$P = \frac{3. \frac{cos x}{\sin x} - 1}{\frac{cos x}{\sin x} + 1}$ = $\frac{3 \cot x - 1}{\cot x + 1} = \frac{3.2 - 1}{2 + 1} = \frac{5}{3}$ .

Câu 9:

Cho cos α = $- \frac{1}{2}$ , 90° < α < 180°. Khi đó C = $\frac{2 \tan^{2} α + \cot^{2} α}{4 \tan^{2} α - 3 \cot^{2} α}$ = $\frac{a}{b}$ , với $\frac{a}{b}$ là phân số tối giản. Tổng a + b bằng:

A. 52;

B. 35;

C. 34;

D. 51.

Xem đáp án

Cho cos α = 1/2, 90° < α < 180°. Khi đó C =2 tan ^2 alpha + cot ^2 alpha / 4 tan ^2 alpha - 3 cot ^2 alpha = a/b, với a/b là phân số tối giản (ảnh 1)

Câu 10:

Cho tan x = 2. Biểu thức M = $\frac{\sin x - 3 \cos^{3} x}{5 \sin^{3} x - 2 c osx}$ = $\frac{a}{b}$ (với (a, b) = 1). Giá trị của hiệu b – a là:

A. 9;

B. 8;

C. 7;

D. 23.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Do tan x = 2 nên cos x ≠ 0 nên cos³ x ≠ 0.

Chia cả tử và mẫu biểu thức M cho cos³ x ta có:

M = $\frac{\frac{\sin x}{{cos}^{3} x} - 3}{5. \frac{\sin^{3} x}{{cos}^{3} x} - \frac{2}{{cos}^{2} x}} = \frac{\frac{\sin x}{cos x} . \frac{1}{{cos}^{2} x} - 3}{5. \tan^{3} x - 2. \frac{1}{{cos}^{2} x}}$ $= \frac{\tan x (1 + \tan^{2} x) - 3}{5 \tan^{3} x - 2 (1 + \tan^{2} x)}$

$= \frac{2 (1 + 2^{2}) - 3}{{5.2}^{3} - 2 (1 + 2^{2})} = \frac{7}{30} .$

Như vậy, a = 7; b = 30 ⇒ b – a = 23.

Bắt đầu thi ngay