Trắc nghiệm Toán 11 Bài 3: Đường thẳng vuông góc với mặt phẳng có đáp án (Mới nhất)
Dạng 1: Chứng minh đường thẳng vuông góc với mặt phẳng và đường thẳng vuông góc đường thẳng có đáp
-
1825 lượt thi
-
35 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Chọn C.
Do nên câu A đúng.
Do nên câu B và D đúng.
Vậy câu C sai.Câu 2:
Cho tứ diện SABC có là tam giác ABC vuông tại B và
a) Khẳng định nào sau đây là đúng nhất. Chứng minh
 Xem đáp án
Xem đáp án
a) Ta có nên
Do đó
Câu 3:
 Xem đáp án
Xem đáp án
Chọn B
b) Ta có
Vậy
Câu 4:
 Xem đáp án
Xem đáp án
Chọn D.
Gọi E là trung điểm của BC .
Khi đó ta có
Câu 5:
 Xem đáp án
Xem đáp án
Chọn D
Có là tam giác vuông tại B
Ta có là các tam giác vuông tại A
Mặt khác là tam giác vuông tại B
Vậy bốn mặt của tứ diện đều là tam giác vuông. Nên đáp án D đúng.
Câu 6:
 Xem đáp án
Xem đáp án
Tam giác SAC cân tại S có SO là trung tuyến => SO cũng là đường cao
Tam giác SBD cân tại S có SO là trung tuyến => SO cũng là đường cao
Từ đó suy ra .
Do ABCD là hình thoi nên CD không vuông góc với BD . Do đó CD không vuông góc với (SBD) .
Câu 7:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, Gọi AE, AF lần lượt là các đường cao của tam giác SAB và tam giác SAD. Chọn khẳng định đúng trong các khẳng định sau ?
 Xem đáp án
Xem đáp án
Chọn D
Ta có:
Vậy:
Tương tự :
Từ vậy đáp án D đúng.
Câu 8:
Cho hình chóp S.ABC có cạnh và đáy ABC là tam giác cân ở C . Gọi H và K lần lượt là trung điểm của AB và SB . Khẳng định nào sau đây sai?
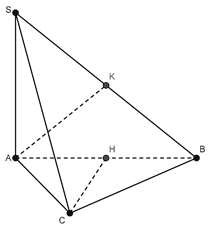
 Xem đáp án
Xem đáp án
Chọn D.
Do tam giác ABC cân tại C nên . Suy ra . Vậy các câu A, B, C đúng nên D sai.
Câu 9:
Cho tứ diện ABCD . Vẽ . Biết H là trực tâm tam giác BCD. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn D
Câu 10:
 Xem đáp án
Xem đáp án
Chọn D
Ta có
Từ đó suy ra nên A, B, C đúng.
Đáp án D sai trong trường hợp SA và AB không bằng nhau -> Chọn đáp án D.
Câu 11:
 Xem đáp án
Xem đáp án
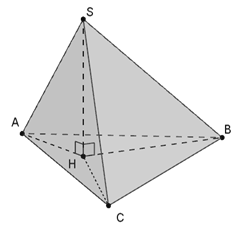
Xét ba tam giác vuông có
chính là tâm đường tròn ngoại tiếp
Câu 12:
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc với nhau. Gọi Hlà hình chiếu của O trên mp(ABC) . Mệnh đề nào sai trong các mệnh đề sau:
 Xem đáp án
Xem đáp án
Chọn B
Ta có và
Tương tự, ta có , suy ra đáp án A, D đúng.
Ta có , với , suy ra đáp án C đúng.
Câu 13:
 Xem đáp án
Xem đáp án
Câu 14:
Cho hình chóp SABC có Gọi H, K lần lượt là trực tâm các tam giác SBC và ABC. Mệnh đề nào sai trong các mệnh đề sau?
 Xem đáp án
Xem đáp án
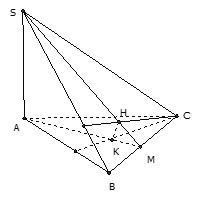
Ta có
Ta có
Mặt khác có hay tương tự nên
Gọi M là giao điểm của SH và BC. Do hay đường thẳng
AM trùng với đường thẳng AK. Hay SH, AK, BC đồng quy.
Do đó sai
Câu 15:
Cho hai hình chữ nhật ABCD và ABEF nằm trong hai mặt phẳng khác nhau sao cho hai đường thẳng AC và BF vuông góc với nhau. Gọi CH và FK lần lượt là đường cao của hai tam giác BCE và ADF. Chứng minh rằng :
a) Khẳng định nào sau đây là đúng về 2 tam giác và ? Xem đáp án
Xem đáp án
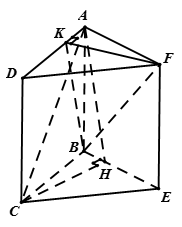
Chọn A
a) Ta có
Vậy
hay vuông tại H
Tương tự
vuông tại K
Câu 17:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết SA = SC, SB = SD.
a)Khẳng định nào sau đây là sai? Xem đáp án
Xem đáp án
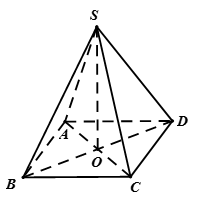
a) Ta có O là trung điểm của và
Tương tự
Vậy
Câu 18:
 Xem đáp án
Xem đáp án
Chọn D
b) Ta có (do ABCD là hình thoi).
Lại có ( do )
Suy raCâu 19:
 Xem đáp án
Xem đáp án
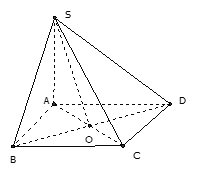
Ta có
Do tứ giác ABCD là hình thoi nên mà nên
AD không vuông góc SCCâu 20:
 Xem đáp án
Xem đáp án
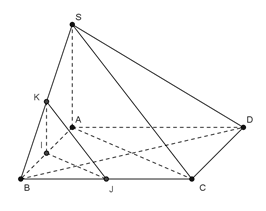
Do IJ // AC và IK // SA nên (IJK) // (SAC) . Vậy A đúng.
Do và nên nên D đúng.
Do và (IJK) // (SAC) nên nên B đúng.
Vậy C sai.
Câu 21:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, Gọi H là trung điểm của AB và . Gọi K là trung điểm của cạnh AD.
a) Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
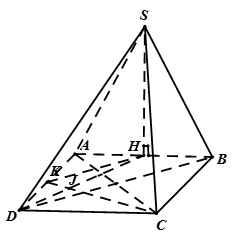
a) Ta có lại có
Câu 23:
 Xem đáp án
Xem đáp án
Chọn D
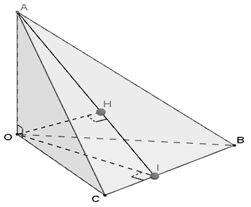
đáp án A đúng.
Tương tự chứng minh được
Hạ
Ta có:Đáp án B đúng.
Ta có: Tương tự
Từ (1) và (2) => H là trực tâm Đáp án C đúng.
Câu 24:
 Xem đáp án
Xem đáp án
Chọn D

Gọi O là trung điểm của AD
Từ giả thiết ta có Vậy vuông tại C.
Do đó OA = OC = OD (1)
Mặt khác vuông tại B
Do đó OA = OB = OD (2)
Từ (1) và (2) ta có OA = OB = OC = OD.
Câu 25:
 Xem đáp án
Xem đáp án
Chọn D.
Gọi E là trung điểm của BC. Khi đó ta có
Câu 26:
Cho tứ diện ABCD. Vẽ . Biết H là trực tâm tam giác BCD. Khẳng định nào sau đây không sai?
 Xem đáp án
Xem đáp án
Chọn C.
Do
Mặt khác, H là trực tâm nên
Suy ra nên
Câu 27:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều và . Gọi H, K lần lượt là trung điểm của các cạnh AB và AD.
a) Khẳng định nào sau đây là sai?.
 Xem đáp án
Xem đáp án
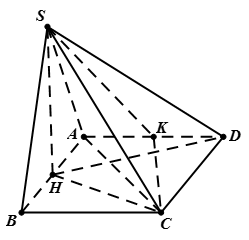
a) Vì H là trung điểm của AB và tam giác SAB đều nên
Lại có
Do đó
vuông tại
VậyCâu 29:
 Xem đáp án
Xem đáp án
Câu 30:
 Xem đáp án
Xem đáp án
Chọn C
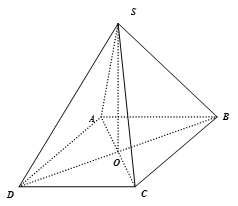
Ta có: SA = SC => SAC là tam giác cân
Mặt khác: O là trung điểm của AC (tính chất hình thoi)
Khi đó ta có:
Câu 31:
 Xem đáp án
Xem đáp án
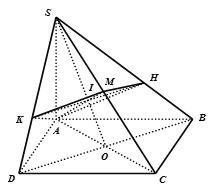
Ta có:
Gọi
(P) là mặt phẳng A và vuông góc với SC
Qua I kẻ
Khi đó:
Ta có: , mà không vuông góc với HK
Câu 32:
 Xem đáp án
Xem đáp án
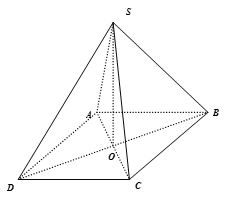
Ta có
Giả sử (vô lý)
Hay không thể là tam giác vuông
Câu 33:
 Xem đáp án
Xem đáp án
Chọn B
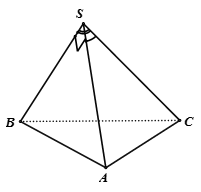
Gọi
Ta có: đều => AC = SA = a
vuông cân tại
vuông tại A
Gọi I là trung điểm của AC thì I là tâm đường tròn ngoại tiếp tam giác ABC
Gọi d là trục của tam giác ABC thi d đi qua I và
Mặt khác: nên . Vậy nên I là hình chiếu vuông góc của S lên mặt phẳng (ABC)
Vì H và K lần lượt là trực tâm của tam giác ABC và SBC nên H và K lần lượt thuộc AA' và SA'
Vậy AH, SK, BC đồng quy tại A'
Câu 34:
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Xét các mệnh đề sau :
I. Vì nên
II. Do nên
III. Có và nên
IV. Từ (1) và (2) Xem đáp án
Xem đáp án
Chọn A
Ta có:
Vậy I đúng.
Vậy II đúng.
Vậy III đúng.
Vậy IV đúng.
Câu 35:
 Xem đáp án
Xem đáp án
Chọn B
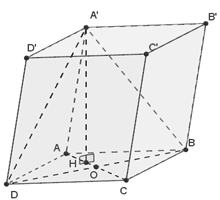
Vì A'A = A'B = A'D => hình chiếu của A' trên (ABCD) trùng với H là tâm đường tròn ngoại tiếp
Mà tứ giác ABCD là hình thoi và nên là tam giác đều (2)
Từ (1) & (2) => H là trọng tâm