Trắc nghiệm Toán 11 Bài 3: Đường thẳng vuông góc với mặt phẳng có đáp án (Mới nhất)
Dạng 2: Tính góc giữa đường thẳng và mặt phẳng có đáp án
-
1830 lượt thi
-
31 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Từ giả thiết ta có
Do đó
Câu 2:
 Xem đáp án
Xem đáp án
Câu 3:
 Xem đáp án
Xem đáp án
Chọn B
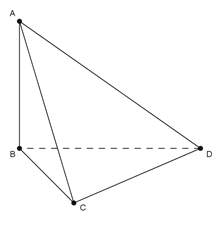
Do AB, BC, BD vuông góc với nhau từng đôi một nên , suy ra BC là hình chiếu của AC lên
Câu 4:
 Xem đáp án
Xem đáp án
Chọn C.
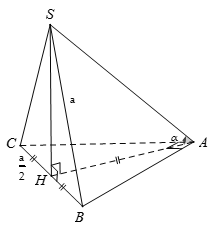
Gọi H là trung điểm của BC suy ra
Ta có:
Câu 5:
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh bằng a và . Biết . Tính góc giữa SC và (ABCD)
 Xem đáp án
Xem đáp án
Chọn A.
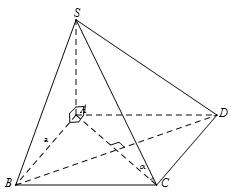
Ta có:
ABCD là hình vuông cạnh aCâu 6:
 Xem đáp án
Xem đáp án
Chọn C
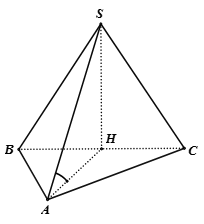
Do H là hình chiếu của S lên mặt phẳng (ABC) nên
Vậy AH là hình chiếu của SH lên mp(ABC)
Ta có:
Mà:
Vậy tam giác SAH vuông cân tại H
Câu 7:
 Xem đáp án
Xem đáp án
Chọn B.
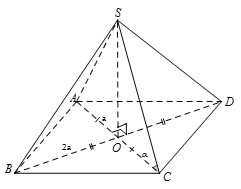
Ta có:
Mặt khác
Suy ra số đo của góc giữa SC và (ABCD) bằng 45°
Câu 8:
 Xem đáp án
Xem đáp án
Chọn B
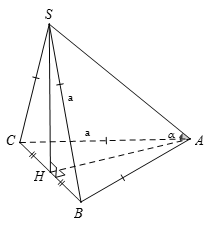
Ta có:
và là hai tam giác đều cạnh a
vuông cân tại H
Câu 9:
 Xem đáp án
Xem đáp án
Chọn D
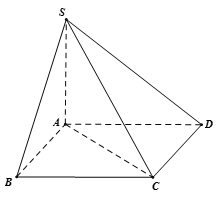
Vì nên AC là hình chiếu vuông góc của SC lên (ABCD)
=> Góc giữa giữa SC và mp (ABCD) bằng góc SC và SA
Xét tam giác SAC vuông tại A có:
Câu 10:
 Xem đáp án
Xem đáp án
Chọn A
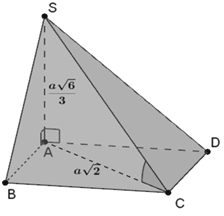
Tứ giác ABCD là hình vuông cạnh a nên
là hình chiếu vuông góc của SC lên là góc giữa SC và (ABCD)
Tam giác SAC vuông tại A nên
Câu 11:
 Xem đáp án
Xem đáp án
Chọn D
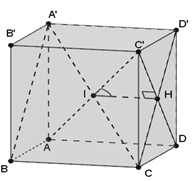
Gọi
mà là hình chiếu vuông góc của AC' lên là góc giữa AC' và (A'BCD')Câu 12:
 Xem đáp án
Xem đáp án
Chọn B
Gọi . Ta có và
Ta lại có
Mà , suy raCâu 13:
 Xem đáp án
Xem đáp án
Chọn C
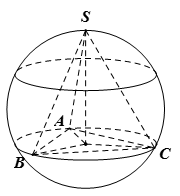
Do hình chóp S.ABC có SA = SB = SC và 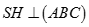 nên SH là trục của hình chóp S.ABC. => HA = HB = HC. Nên H là tâm đường tròn ngoại tiếp tam giác ABC
nên SH là trục của hình chóp S.ABC. => HA = HB = HC. Nên H là tâm đường tròn ngoại tiếp tam giác ABC
Câu 14:
 Xem đáp án
Xem đáp án
Chọn C
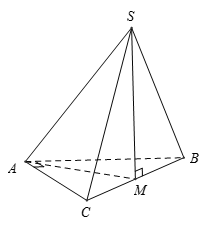
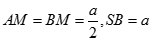
Có 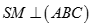 nên AM là hình chiếu của SA lên mp(ABC)
nên AM là hình chiếu của SA lên mp(ABC)
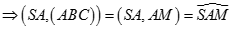
Áp dụng định lý Pytago
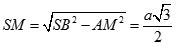
Xét tam giác SAM có
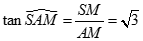
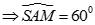
Câu 15:
 Xem đáp án
Xem đáp án
Chọn C
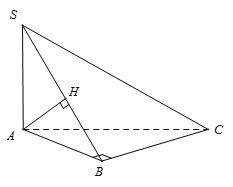
Do 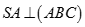 nên
nên 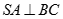 . Nên Phương án A đúng.
. Nên Phương án A đúng.
Có 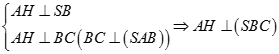 . Phương án D đúng.
. Phương án D đúng.
Suy ra 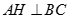 ,
, 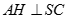 . Phương án B, D đúng.
. Phương án B, D đúng.
Phương án C sai. Thật vậy với 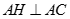 , ta có
, ta có 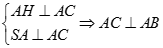 (vô lý).
(vô lý).
Câu 17:
 Xem đáp án
Xem đáp án
Chọn D
Xét có
đều => BC = a
có
Từ đó tam giác ABC vuông tại C
Câu 18:
 Xem đáp án
Xem đáp án
Chọn C
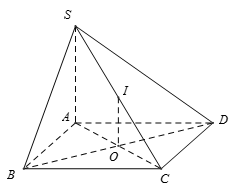
Có IO là đường trung bình tam giác SAC nên IO // SA nên 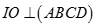 . Phương án A đúng.
. Phương án A đúng.
Có . Phương án B đúng
Và nên phương án D đúng.
Phương án C sai. Thật vậy nếu (SAC) là mặt phẳng trung trực của (vô lý).
Câu 19:
 Xem đáp án
Xem đáp án
Chọn D
Phương án A sai vì nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng thuộc mặt phẳng này vuông góc với giao tuyến sẽ vuông góc với mặt phẳng kia.
Phương án B sai vì còn trường hợp hai mặt phẳng cắt nhau.
Phương án C sai.Câu 20:
 Xem đáp án
Xem đáp án
Chọn B
Do nên SB là hình chiếu của SC lên (SAB)
Xét tam giác SBC có
Câu 21:
 Xem đáp án
Xem đáp án
Chọn D
Thiết diện là hình thang vuông đi qua trung điểm các cạnh AB, CD, CS, SB nên diện tích thiết diện là
Câu 22:
 Xem đáp án
Xem đáp án
Chọn C
Theo bài ra hình chóp S.ABC là hình chóp tam giác đều. Gọi H là trung điểm của BC, ta có
Mặt khác ta có:
Câu 23:
 Xem đáp án
Xem đáp án
Chọn C
Câu 24:
 Xem đáp án
Xem đáp án
Chọn B
Sử dụng tính chất trung điểm của tam giác vuông
Câu 25:
 Xem đáp án
Xem đáp án
Chọn C
Do hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, SA = SC, SB = SD nên
Câu 26:
 Xem đáp án
Xem đáp án
Chọn D
Câu 27:
 Xem đáp án
Xem đáp án
Chọn A
Gọi H là hình chiếu của A lên mp(BCD), a là độ dài cạnh của tứ diện ABCD.
Ta cóCâu 28:
 Xem đáp án
Xem đáp án
Chọn D
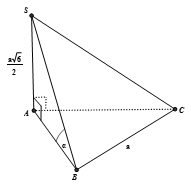
Câu 29:
Cho hình lập phương ABCD.A1B1C1D1 Gọi là góc giữa AC1 và mp(ABCD). Chọn khẳng định đúng trong các khẳng định sau?
 Xem đáp án
Xem đáp án
Chọn B
Ta có:
Câu 30:
 Xem đáp án
Xem đáp án
Chọn C
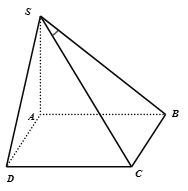
Ta có:
là hình chiếu của S trên (SAB) (1)
=> B là hình chiếu của trên (2)
Từ
Xét tam giác SAB vuông tại A ta có:
Xét tam giác SBC vuông tại B ta có: