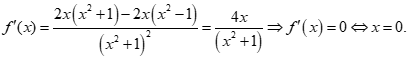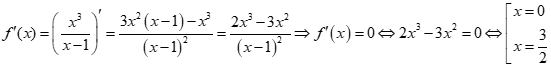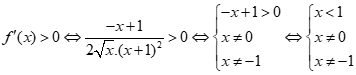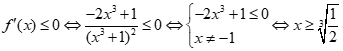26 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 11 Dạng 3: Đạo hàm và các bài toán giải pt, bpt có đáp án (Mới nhất)

Câu 1:

Cho hàm số $y = {x^3} - 3{x^2} - 9x - 5$. Phương trình $y' = 0$ có nghiệm là:

A. $\left\{ { - 1;2} \right\}$.

B. $\left\{ { - 1;3} \right\}$.

C. $\left\{ {0;4} \right\}$.

D. $\left\{ {1;2} \right\}$.

Xem đáp án

Hướng dẫn giải:

Chọn B.

Ta có : $y' = 3{x^2} - 6x - 9$

$y' = 0 \Leftrightarrow 3{x^2} - 6x - 9 = 0 \Leftrightarrow x = - 1;x = 3$.

Câu 2:

Cho hàm số \[f\left( x \right) = k\sqrt[3]{x} + \sqrt x \]\[(k \in \mathbb{R})\]. Để \[f'\left( 1 \right) = \frac{3}{2}\] thì ta chọn:

A. \[k = 1\].

B. \[k = - 3\].

C. \[k = 3\].

D. \[k = \frac{9}{2}\].

Xem đáp án

Hướng dẫn giải:

Chọn C.

Ta có: \[f\left( x \right) = k\sqrt[3]{x} + \sqrt x \]\[ \Rightarrow f'\left( x \right) = {\left( {k\sqrt[3]{x} + \sqrt x } \right)^\prime } = k{\left( {\sqrt[3]{x}} \right)^\prime } + {\left( {\sqrt x } \right)^\prime }\]

Đặt $y = \sqrt[3]{x} \Rightarrow {y^3} = x \Rightarrow 3{y^2}y' = 1 \Rightarrow y' = \frac{1}{{3{y^2}}} = \frac{1}{{3{{\left( {\sqrt[3]{x}} \right)}^2}}}$.

\[f'\left( x \right) = k{\left( {\sqrt[3]{x}} \right)^\prime } + {\left( {\sqrt x } \right)^\prime }\]\[ = \frac{k}{{3{{\left( {\sqrt[3]{x}} \right)}^2}}} + \frac{1}{{2\sqrt x }}\].Vậy để \[f'\left( 1 \right) = \frac{3}{2}\] thì \[\frac{k}{3} + \frac{1}{2} = \frac{3}{2} \Rightarrow k = 3\].

Câu 3:

Cho hàm số \[f\left( x \right) = \frac{1}{3}{x^3} - 2\sqrt 2 {x^2} + 8x - 1\]. Tập hợp những giá trị của \[x\] để \[f'\left( x \right) = 0\] là:

A. \[\left\{ { - 2\sqrt 2 } \right\}\].

B. \[\left\{ {2;\sqrt 2 } \right\}\].

C. \[\left\{ { - 4\sqrt 2 } \right\}\].

D. \[\left\{ {2\sqrt 2 } \right\}\].

Xem đáp án

Hướng dẫn giải:

Chọn D

Ta có $f'(x) = {x^2} - 4\sqrt 2 x + 8$

$f'(x) = 0 \Leftrightarrow {x^2} - 4\sqrt 2 x + 8 = 0 \Leftrightarrow x = 2\sqrt 2 $.

Câu 4:

Cho hàm số $y = 4x - \sqrt x $. Nghiệm của phương trình $y' = 0$ là

A. $x = \frac{1}{8}.$

B. $x = \sqrt {\frac{1}{8}} .$

C. $x = \frac{1}{{64}}.$

D. $x = - \frac{1}{{64}}.$

Xem đáp án

Hướng dẫn giải:

Chọn C

$y' = 4 - \frac{1}{{2\sqrt x }}$

$y' = 0 \Leftrightarrow 4 - \frac{1}{{2\sqrt x }} = 0 \Leftrightarrow 8\sqrt x - 1 = 0 \Leftrightarrow \sqrt x = \frac{1}{8} \Rightarrow x = \frac{1}{{64}}$.

Câu 5:

Cho hàm số $y = - 4{x^3} + 4x$. Để $y' \ge 0$ thì \[x\]nhận các giá trị thuộc tập nào sau đây ?

A. $\left[ { - \sqrt 3 ;\sqrt 3 } \right].$

B. $\left[ { - \frac{1}{{\sqrt 3 }};\frac{1}{{\sqrt 3 }}} \right].$

C. $\left( { - \infty ; - \sqrt 3 } \right] \cup \left[ {\sqrt 3 ; + \infty } \right).$

D. $\left( { - \infty ; - \frac{1}{{\sqrt 3 }}} \right] \cup \left[ {\frac{1}{{\sqrt 3 }}; + \infty } \right).$

Xem đáp án

Hướng dẫn giải:

Chọn B

Ta có $y = - 4{x^3} + 4x$$ \Rightarrow y' = - 12{x^2} + 4$.

Nên $y' \ge 0 \Leftrightarrow - 12{x^2} + 4 \ge 0 \Leftrightarrow x \in \left[ { - \frac{1}{{\sqrt 3 }};\frac{1}{{\sqrt 3 }}} \right].$

Câu 6:

$f'(x) \ge 0$ với $f(x) = 2{x^3} - 3{x^2} + 1$

A. $\left[ \begin{array}{l}x \le 0\\x \ge 1\end{array} \right.$

B. $x \le 1$

C. $x \ge 0$

D. $0 \le x \le 1$

Xem đáp án

Hướng dẫn giải:

Chọn A

TXĐ: $D = \mathbb{R}$

Ta có: $f'(x) = 6{x^2} - 6x$, suy ra $f'(x) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le 0\\x \ge 1\end{array} \right.$

Câu 7:

$f'(x) < 0$ với $f(x) = - 2{x^4} + 4{x^2} + 1$

A. $\left[ \begin{array}{l} - 1 < x < 0\\x > 1\end{array} \right.$

B. $ - 1 < x < 0$

C. $x > 1$

D. $x < 0$

Xem đáp án

Hướng dẫn giải:

Chọn A

TXĐ: $D = \mathbb{R}$

Ta có: $f'(x) = - 8{x^3} + 8x$, suy ra $f'(x) < 0 \Leftrightarrow \left[ \begin{array}{l} - 1 < x < 0\\x > 1\end{array} \right.$

Câu 8:

Cho hàm số $y = - 3{x^3} + 25.$ Các nghiệm của phương trình \[y' = 0\] là.

A. $x = \pm \frac{5}{3}$.

B. $x = \pm \frac{3}{5}$.

C. $x = 0$.

D. $x = \pm 5$.

Xem đáp án

Hướng dẫn giải: :

Chọn A

Ta có: $y' = - 9{x^2} + 25$

$y' = 0 \Leftrightarrow - 9{x^2} + 25 = 0 \Leftrightarrow x = \pm \frac{5}{3}.$

Câu 9:

Cho hàm số

. Các nghiệm của phương trình

là

A.

B.

C.

D.

Xem đáp án

Hướng dẫn giải:

Chọn D.

Câu 10:

Cho hàm số . Tập nghiệm của phương trình là

A.

B.

C.

D.

Xem đáp án

Hướng dẫn giải:

Chọn A.

Câu 11:

Cho hàm số . Tập nghiệm của phương trình là

A.

B.

C.

D.

Xem đáp án

Hướng dẫn giải:

Chọn C.

Ta có

Câu 12:

Tìm số \[f\left( x \right) = {x^3} - 3{x^2} + 1.\] Đạo hàm của hàm số \[f\left( x \right)\] âm khi và chỉ khi.

A. \[0 < x < 2\].

B. \[x < 1\].

C. \[x < 0\] hoặc \[x > 1.\]

D. \[x < 0\] hoặc \[x > 2.\]

Xem đáp án

Hướng dẫn giải:

Chọn A

Ta có: $f'\left( x \right) = 3{x^2} - 6x.$

$f'\left( x \right) < 0 \Leftrightarrow 3{x^2} - 6x < 0 \Leftrightarrow 0 < x < 2.$

Câu 13:

Cho hàm số . Để thì x nhận các giá trị thuộc tập nào sau đây?

A.

B.

C.

D.

Xem đáp án

Hướng dẫn giải:

Chọn C.

Câu 14:

Cho hàm số . Để thì x nhận các giá trị thuộc tập nào sau đây?

A.

B.

C.

D.

Xem đáp án

Hướng dẫn giải:

Chọn C.

Câu 15:

Cho hàm số

. Để

thì x nhận các giá trị thuộc tập nào sau đây?

A.

B.

C.

D.

Xem đáp án

Hướng dẫn giải:

Chọn D.

Câu 16:

Cho hàm số $y = \frac{3}{{1 - x}}$. Để $y' < 0$ thì x nhận các giá trị thuộc tập nào sau đây?

A. 1.

B. 3.

C. $\emptyset$ .

D. $\mathbb{R}$.

Xem đáp án

Hướng dẫn giải:

Chọn C.

Tập xác định $D = R\backslash \left\{ 1 \right\}$.

${y^\prime } = \frac{3}{{{{\left( {1 - x} \right)}^2}}} > 0\forall x \in D$.

Câu 17:

Cho hàm số $f(x) = \frac{{1 - 3x + {x^2}}}{{x - 1}}$. Tập nghiệm của bất phương trình $f'(x) > 0$ là

A. $\mathbb{R}\backslash \left\{ 1 \right\}.$

B. $\emptyset .$

C. $\left( {1; + \infty } \right)$.

D. $\mathbb{R}.$

Xem đáp án

Hướng dẫn giải:

Đáp án A

$\begin{array}{l}f'(x) = {\left( {\frac{{1 - 3x + {x^2}}}{{x - 1}}} \right)^\prime }\\\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{{{\left( {1 - 3x + {x^2}} \right)}^\prime }\left( {x - 1} \right) - \left( {1 - 3x + {x^2}} \right){{\left( {x - 1} \right)}^\prime }}}{{{{\left( {x - 1} \right)}^2}}}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{\left( { - 3 + 2x} \right)\left( {x - 1} \right) - \left( {1 - 3x + {x^2}} \right)}}{{{{\left( {x - 1} \right)}^2}}} = \frac{{{x^2} - 2x + 2}}{{{{\left( {x - 1} \right)}^2}}}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{{{\left( {x - 1} \right)}^2} + 1}}{{{{\left( {x - 1} \right)}^2}}} > 0,\,\forall x \ne 1\end{array}$

Câu 18:

Cho hàm số $y = 3{x^3} + {x^2} + 1$. Để $y' \le 0$ thì $x$ nhận các giá trị thuộc tập nào sau đây

A. $\left[ { - \frac{2}{9};0} \right].$

B. $\left[ { - \frac{9}{2};0} \right].$

C. $\left( { - \infty ; - \frac{9}{2}} \right] \cup \left[ {0; + \infty } \right).$

D. $\left( { - \infty ; - \frac{2}{9}} \right] \cup \left[ {0; + \infty } \right).$

Xem đáp án

Hướng dẫn giải:

Đáp án A

$\begin{array}{l}y = 3{x^3} + {x^2} + 1 \Rightarrow y' = 9{x^2} + 2x\\y' \le 0 \Rightarrow - \frac{2}{9} \le x \le 0\end{array}$

Câu 19:

Cho hàm số . Tập nghiệm của bất phương trình là

A.

B. \{0}.

C.

D.

Xem đáp án

Hướng dẫn giải:

Lưu ý: Công thức đạo hàm nhanh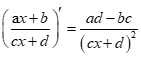

vô nghiệm.

Chọn A.

Câu 20:

$2 x f^{'} (x) - f (x) \geq 0$ với $f(x) = x + \sqrt {{x^2} + 1} $

A. $x \ge \frac{1}{{\sqrt 3 }}$

B. $x > \frac{1}{{\sqrt 3 }}$

C. $x < \frac{1}{{\sqrt 3 }}$

D. $x \ge \frac{2}{{\sqrt 3 }}$

Xem đáp án

Hướng dẫn giải:

TXĐ: $D = \mathbb{R}$

Ta có: $f'(x) = 1 + \frac{x}{{\sqrt {{x^2} + 1} }} = \frac{{f(x)}}{{\sqrt {{x^2} + 1} }}$

Mặt khác: $f(x) > x + \sqrt {{x^2}} = x + \left| x \right| \ge 0,{\rm{ }}\forall x \in \mathbb{R}$

Nên $2xf'(x) - f(x) \ge 0 \Leftrightarrow \frac{{2xf(x)}}{{\sqrt {{x^2} + 1} }} - f(x) \ge 0$

$ \Leftrightarrow 2x \ge \sqrt {{x^2} + 1} \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\3{x^2} \ge 1\end{array} \right. \Leftrightarrow x \ge \frac{1}{{\sqrt 3 }}$.

Câu 21:

$f'(x) > 0$ với $f(x) = x + \sqrt {4 - {x^2}} $.

A. $ - 2 \le x \le \sqrt 2 $

B. $x \le \sqrt 2 $

C. $ - 2 \le x$

D. $x < 0$

Xem đáp án

Hướng dẫn giải:

TXĐ: $D = \left[ { - 2;2} \right]$

Ta có: $f'(x) = 1 - \frac{x}{{\sqrt {4 - {x^2}} }} \Rightarrow f'(x) > 0 \Leftrightarrow \sqrt {4 - {x^2}} > x$

$ \Leftrightarrow \left[ \begin{array}{l} - 2 \le x < 0\\\left\{ \begin{array}{l}x \ge 0\\4 - {x^2} > {x^2}\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - 2 \le x < 0\\0 \le x < \sqrt 2 \end{array} \right. \Leftrightarrow - 2 \le x < \sqrt 2 $.

Đáp án: A

Câu 22:

Cho hàm số . Tập nghiệm của bất phương trình là

A.

B.

C.

D.

Xem đáp án

Hướng dẫn giải:

Chọn A.

Media VietJack .

Câu 23:

Cho hàm số

. Tập nghiệm của bất phương trình

là

A.

B.

C.

D.

Xem đáp án

Hướng dẫn giải:

Chọn D.

Media VietJack .

Câu 24:

Cho hàm số \[f(x) = 2mx - m{x^3}\]. Số \[x = 1\] là nghiệm của bất phương trình \[f'(x) \le 1\] khi và chỉ khi:

A. \[m \ge 1.\]

B. \[m \le - 1.\]

C. \[ - 1 \le m \le 1.\]

D. \[m \ge - 1.\]

Xem đáp án

Hướng dẫn giải:

Chọn D

Có \[f(x) = 2mx - m{x^3}\]$ \Rightarrow $$f'(x) = 2m - 3m{x^2}.$Nên\[f'(1) \le 1\]\[ \Leftrightarrow \]$2m - 3m \le 1$\[ \Leftrightarrow \]\[m \ge - 1.\]

Câu 25:

Tìm $m$ để các hàm số $y = (m - 1){x^3} - 3(m + 2){x^2} - 6(m + 2)x + 1$ có $y' \ge 0,{\rm{ }}\forall x \in \mathbb{R}$

A. $m \ge 3$

B. $m \ge 1$

C. $m \ge 4$

D. $m \ge 4\sqrt 2 $

Xem đáp án

Hướng dẫn giải:

Chọn C

Ta có: $y' = 3\left[ {(m - 1){x^2} - 2(m + 2)x - 2(m + 2)} \right]$

Do đó $y' \ge 0 \Leftrightarrow (m - 1){x^2} - 2(m + 2)x - 2(m + 2) \ge 0$ (1)

$ \bullet $ $m = 1$ thì (1) $ \Leftrightarrow - 6x - 6 \ge 0 \Leftrightarrow x \le - 1$ nên $m = 1$ (loại)

$ \bullet $ $m \ne 1$ thì (1) đúng với $\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a = m - 1 > 0\\\Delta ' \le 0\end{array} \right.$

$ \Leftrightarrow \left\{ \begin{array}{l}m > 1\\(m + 1)(4 - m) \le 0\end{array} \right. \Leftrightarrow m \ge 4$

Vậy $m \ge 4$ là những giá trị cần tìm.

Câu 26:

Tìm $m$ để các hàm số $y = \frac{{m{x^3}}}{3} - m{x^2} + (3m - 1)x + 1$ có $y' \le 0,{\rm{ }}\forall x \in \mathbb{R}$.

A. $m \le \sqrt 2 $

B. $m \le 2$

C. $m \le 0$

D. $m < 0$

Xem đáp án

Hướng dẫn giải:

Chọn C

Ta có: $y' = m{x^2} - 2mx + 3m - 1$

Nên $y' \le 0 \Leftrightarrow m{x^2} - 2mx + 3m - 1 \le 0$ (2)

$ \bullet $ $m = 0$ thì (1) trở thành: $ - 1 \le 0$ đúng với $\forall x \in \mathbb{R}$

$ \bullet $ $m \ne 0$, khi đó (1) đúng với $\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a = m < 0\\\Delta ' \le 0\end{array} \right.$

$ \Leftrightarrow \left\{ \begin{array}{l}m < 0\\m(1 - 2m) \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 0\\1 - 2m \ge 0\end{array} \right. \Leftrightarrow m < 0$

Vậy $m \le 0$ là những giá trị cần tìm.